Ultrasound-based stroke/cardiovascular risk stratification using Framingham Risk Score and ASCVD Risk Score based on “Integrated Vascular Age” instead of “Chronological Age”: a multi-ethnic study of Asian Indian, Caucasian, and Japanese cohorts

Abstract

Background

Vascular age (VA) has recently emerged for CVD risk assessment and can either be computed using conventional risk factors (CRF) or by using carotid intima-media thickness (cIMT) derived from carotid ultrasound (CUS). This study investigates a novel method of integrating both CRF and cIMT for estimating VA [so-called integrated VA (IVA)]. Further, the study analyzes and compares CVD/stroke risk using the Framingham Risk Score (FRS)-based risk calculator when adapting IVA against VA.

Methods

The system follows a four-step process: (I) VA using cIMT based using linear-regression (LR) model and its coefficients; (II) VA prediction using ten CRF using a multivariate linear regression (MLR)-based model with gender adjustment; (III) coefficients from the LR-based model and MLR-based model are combined using a linear model to predict the final IVA; (IV) the final step consists of FRS-based risk stratification with IVA as inputs and benchmarked against FRS using conventional method of CA. Area-under-the-curve (AUC) is computed using IVA and benchmarked against CA while taking the response variable as a standardized combination of cIMT and glycated hemoglobin.

Results

The study recruited 648 patients, 202 were Japanese, 314 were Asian Indian, and 132 were Caucasians. Both left and right common carotid arteries (CCA) of all the population were scanned, thus a total of 1,287 ultrasound scans. The 10-year FRS using IVA reported higher AUC (AUC =0.78) compared with 10-year FRS using CA (AUC =0.66) by ~18%.

Conclusions

IVA is an efficient biomarker for risk stratifications for patients in routine practice.

Introduction

Mortality and mobility due to cardiovascular diseases (CVD) are the major challenges in global public health (1). Annually, ~17.7 million people experience CVD, out of which 85% die due to heart attack and stroke (1). The prevalence of CVD is even higher in low- or middle-income countries (1). This is due to the lack of resources for the management of CVD (1). In the last decade, the cost for CVD prevention has also boosted to a great extent (2). Especially in the United States, the current annual cost for CVD prevention is around $600 billion which is estimated to reach up to $1.1 trillion in 2035 (2). Thus, in order to prevent the mortalities due to CVD, it is important to look for preventive solutions that can provide the estimate of long-term risk at a reduced cost (3). Furthermore, such preventive tools should also provide an easy understanding of CVD/stroke risk to patients (3,4). This will help them to manage the CVD by controlling the behavioral risk factors such as weight, body mass index (BMI), low-density lipoproteins (LDL) cholesterol, and physical inactivity (4).

At present, conventional cardiovascular risk calculators (CCVRC) models are available that provide an estimate of 10-year CVD/stroke risk to the patients (5-11). Once the risk level is known to the physicians, then using a set of clinical practice guidelines (7,12-16) the strategy and the potential targets can be decided to prevent the onset of CVD events. One common challenge associated with such types of CCVRC is that their absolute risk sometimes underestimates or overestimates the risk profile of the patients (17,18). The reasons for such underestimation or overestimation are (I) ethnicity-specific nature of each risk calculator, (II) varying patients’ demographics or the combination of demographics and blood biomarkers, or (III) dependence on only conventional risk factors (CRF) (17).

Ultrasound imaging has recently shown promising outcomes in atherosclerosis imaging (19-22). There has been a quest to standardize the image-based phenotype measurements from B-mode ultrasound (23). Recently, robust automated tools were developed for quantification of wall thickness and carotid plaque measurements, so-called image phenotypes (24,25) and its morphological characterization (26). Recently, robust methods for wall thickness and carotid plaque measurements were developed using various engineering methods such as signal processing approaches (24), classification-based approaches, boundary-based approaches or fusion of these. These included cIMT (27) and distance measurement methods (28), IMTV (29) and TPA (30) measurements for CCA. This was extended for all segments including bulb (31,32) and further validated using gold standard and computed tomography (33,34) and tested for inter- and intra-observer variability studies (35). Further, we recently demonstrated that these image phenotypes under the automated paradigm can capture both wall thickness and carotid plaque (25). We will use these automated paradigms for our biomarker studies. One solution can be including all the biomarkers of CVD including ultrasound-based imaging phenotypes presented above (19,36) into the risk prediction model (37-40). Another solution can be the development of a tool that provides an easy understating of risk to patients so that they can modify their lifestyle to prevent CVD (41).

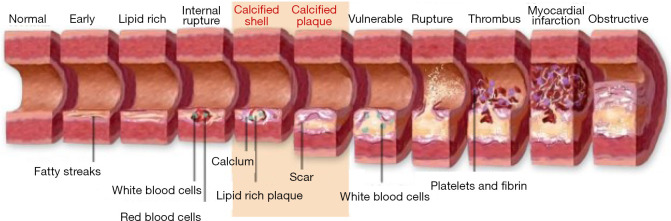
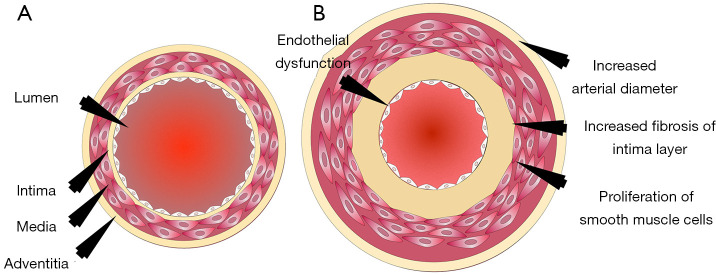
One such preventive tool is “Vascular Age (VA)”. Chronological age (CA) is generally converted into an age that is modulated by conventional cardiovascular risk factors (CCVRF) or image-based phenotypes (5,42-46). CRFs such as hyperlipidemia, diabetes mellitus, hypertension, and smoking, all contribute towards the development of atherosclerosis as shown in Figure 1. It shows the changes in the vascular geometry blood vessels, starting from the normal blood vessels at the left side to the completely modified geometry at the right side. This process further results in the aging of the artery. The cross-sectional view can be visualized in Figure 2 which depicts the difference in vascular geometry of the young and the elderly persons. Vascular aging increases the fibrosis that results in increased thickness of the intimal and medial layers (47). Furthermore, the aging of the blood vessels leads to an increase in arterial stiffness (47,48). The VA is an easily understood tool for the patients since it directly relates the cardiovascular risk to the age of blood vessels arteries (42,44). The accurate and easy understanding of the VA leads to an improved lifestyle change of the patients (44). This modifies their routine practice such as consumption of healthier diet, seizing of smoking, reducing/quitting alcohol consumption, and improves physical fitness (44). This was the reason for both Canadian (14) and European guidelines (49) to recommend using the VA measurement during the CVD risk assessment. At present, there is no solid guideline/consensus available that provides the protocols for measuring the VA (43). There exist several models, to compute the VA of a person (5,45,46,50-52). Some of the models are focused on using the CCVRF (5,52) while others use the image-based phenotypes such as carotid intima-media thickness (45,46,50) or total carotid plaque area (53). Although the CCVRF-based VA models are widely adopted for VA computation, such models do not provide the morphological variations in atherosclerotic plaque components. This morphological variation in atherosclerotic plaque tends to change the healthy behaviors in the blood vessels that may lead to an increase in overall VA of a person (4,48). At present, none of the studies have tried to investigate the effect of combining both image-based phenotypes and CCVRF for VA computation for a screening patient. This is the first study that presents an online system for computing integrated vascular age (IVA) by combining both carotid ultrasound image-based phenotype (CUSIP) and CCVRF. The spirit of this design comes from designing online systems by our team (54,55). The concept of integration has been in existence for a while, where the ultimate effect is to improve the performance of the system (56) or improve the prediction of the system. Since the CUS is a non-invasive, economical, and user-friendly imaging modality (57), it was therefore adapted for for developing the IVA. Once the IVA is known, it can then be used to investigate the CVD risk profile of the patients by replacing them with CA in risk prediction models (45,50,51,53,58-60).

Figure 1.

The vascular aging process (Courtesy AtheroPointTM, Roseville, CA, USA).

Figure 2.

The cross-sectional view of the blood vessels of the (A) young and (B) aged person (Courtesy AtherpPointTM, Roseville, USA).

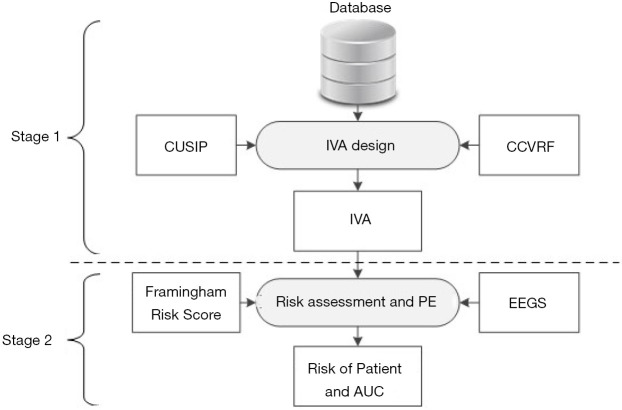
The objectives of this proposed study are depicted in Figure 3 and are as follows: (I) to investigate the effect of combining both CUSIP and CCVRF on the VA of person, (II) to develop a non-invasive and easy-to-understand tool called IVA, that can provide a true measure of the VA of person, (III) to investigate the improvement in the risk stratification of patients by replacing the CA with the IVA, and (IV) to benchmark the IVA-based risk stratification against the risk stratification perform using CCVRF-driven VA. In this study, a combination of cIMT and glycated hemoglobin was used as a surrogate biomarker for the CVD/stroke events.

Figure 3.

Two-stage system for IVA design and performance evaluation. Stage 1: integrated vascular age computation and stage 2: risk stratification and performance evaluation. CCVRF, conventional cardiovascular risk factors; CUSIP, carotid ultrasound image-based phenotypes, IVA, integrated vascular age; EEGS, event-equivalence gold standard; PE, performance evaluation; AUC, area-under-the-curve.

Methods

Study population

A multi-ethnic cohort of 648 patients was selected for this retrospective study. Out of 648 patients, 202 were Japanese (Ohashi Medical Center, Toho University, Japan), 314 were Asian-Indian (MV Hospital, Chennai, India), and 132 were Caucasian (Hospital del Mar, Barcelona, Spain). All the patients were approved by the Institutional Review Board. Written consent was obtained from all the study participants. A total of 1,296 CUS scans (648 patients ×2 CUS scans) were collected from both left and right carotid arteries of the patients. Nine CUS scans were excluded from this study due to the poor quality of ultrasound scans showing no visualization of atherosclerotic plaque. Thus, a total of 1,287 CUS scans were used to model the integrated VA and to test the hypothesis of this study. Two expert operators with 15 years of experience in radiology examined all the CUS scans.

Ultrasound image acquisition

Carotid arteries of all the study participants were scanned using a linear array of transducers with a center frequency of 10 MHz (General Electric, India), 7.5 MHz (Aplio XG, Xario, Aplio XV, Toshiba Inc., Tokyo, Japan), and 10 MHz (Sonosite Microma, Spain) respectively, for Asian-Indian, Japanese, and Caucasian patients, respectively. All the patients have analyzed in the supine position with their head tilted backward. The location of the carotid artery was first identified by the transverse scan. After locating the carotid artery, the CUS probe was rotated by 90 degrees to obtain the longitudinal scans of the anterior and posterior walls of the CCA. A measurement guideline recommended by the American Society of Echocardiography was followed during the measurement. A detailed protocol for image acquisition was discussed in our previous publications (24,37,40,61).

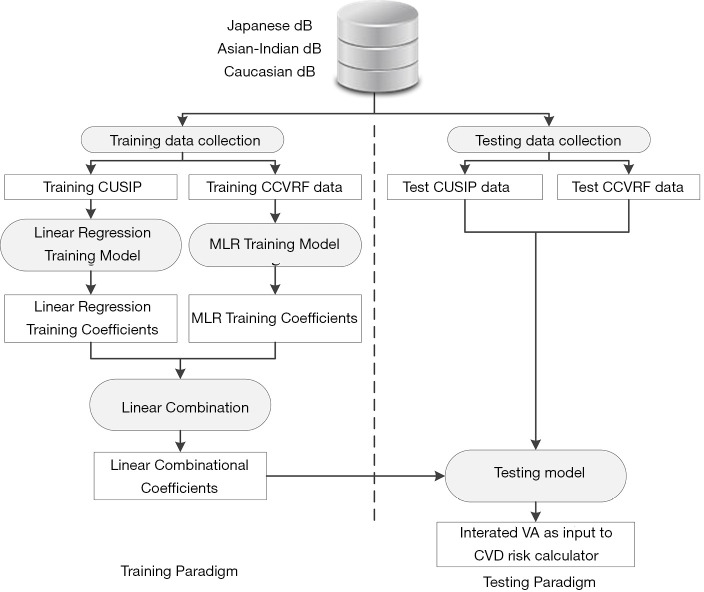
Development of IVA

Figure 4 shows the IVA development architecture of the proposed system. At first, CUSIP and the CRF from three different databases (Japan, Asian Indian, and Italy) were combined to form a complete dataset of 1,287 samples. Then, the system architecture was divided into two parts: (I) training paradigm and (II) testing paradigm. K-fold data-partitioning protocol (K =5, 10, N-1, where N is the sample size) was followed to obtain the training and testing dataset. The details of the K-fold data-partitioning have been given in our previous publications (62,63). In the training paradigm, the average cIMT (cIMTave) and CRF were labeled as “training CUSIP” and “training CCVRF”. Both the training CUSIP” and “training CCVRF” were then separated into three risk categories (low-risk, moderate-risk, and high-risk) based on the average cIMT (cIMTave) threshold points (lower threshold of 0.5 mm and an upper threshold of 0.9 mm). These risk-category dependent CUSIP and CCVRF were then used as input covariates for the linear regression and the multivariate linear regression (MLR) models, respectively. In both the linear regression and MLR models, the CA was used as the dependent variable.

Figure 4.

The internal architecture of the proposed system. CUSIP, carotid ultrasound image-based phenotypes; CCVRF, conventional cardiovascular risk factors; MLR, multivariate linear regression; VA, vascular age; CVD, cardiovascular diseases.

Since the age in both the statistical models was determined by the CUSIP and the CCVRF, it was termed as ‘CUSIP-driven vascular age’ and ‘CCVRF-driven vascular age’, respectively. The corresponding coefficients of the linear regression-based CUSIP-driven VA model and the MLR-based CCVRF-driven VA model were then combined using a linear combination, which when combined can be used to transform the test patient to predict an IVA of a test patient. Note that the IVA considers the effect of both the CCVRF and the cIMT. The IVA was then replaced with CA in the FRS-based calculator to risk stratify the patients. A combination of cIMT and HbA1c was used as a response variable or event equivalence gold standard to perform the risk stratification. This study hypothesized that the FRS with IVA as input covariate (FRS_IVA) can provide a better CVD risk stratification compared to the FRS with CA as input covariate (FRS_CA). From here on, when we call FRS_IVA, means FRS is computed using IVA. Similarly, FRS_CA, means FRS is computed using CA. Such a combinational approach of using two different types of risk factors as discussed in our previous studies (37,63,64). The performance of FRS_IVA was evaluated against the FRS_CA based on the area-under-the-curve (AUC) analysis.

Validation of risk stratification using atherosclerosis CVD (ASCVD) calculator

In order to validate the performance of IVA against the CA, CVD risk stratification was performed using the ASCVD risk calculator, which was proposed by the American College of Cardiology (ACC) and the American Heart Association (AHA) (7). The CVD risk stratification was performed (I) by computing the 10-year risk using ASCVD calculator with IVA, instead of CA, as input covariate and (II) stratifying the patients into low- or high-risk category using a predefined risk threshold of 7.5% (7). The performance of ASCVD_IVA was also evaluated against the ASCVD_CA based on the AUC analysis. At last, to validate the hypothesis, we showed that the risk stratification performed using the FRS calculator (5) and ASCVD calculator (7) should provide a higher AUC with IVA, instead of CA as input covariate.

Statistical analysis

All the baseline characteristics presented in Table 1 are expressed as mean ± standard deviation for continuous variables and as a percentage for categorical variables. The statistical significance was tested using a two-tailed students’ t-test for continuous variables and chi-square tests for categorical variables. A statistical significance was determined for P value <0.05. All the statistical analysis was performed using SPSS23.0 and MATLAB17b. Receiver operating characteristics (ROC) was used to compare FRS_IVA and FRS_CA. An FRS threshold of 20% was selected to risk-stratify the patients into either low-risk (FRS <20%) or high-risk (FRS ≥20%) category. An AUC was used as a primary performance evaluation metric for this proposed study. A combination of cIMT and HbA1c was used as a response variable to perform the ROC analysis. This response variable also serves the purpose of combinational event equivalence gold-standard to risk stratify the patients. A similar type of combinational approach of deriving a response variable using two risk factors was proposed the Cuadrado-Godia et al. (64) and Khanna et al. (37). At baseline, patients were classified into the high-risk category if cIMT ≥0.9 mm and HbA1c ≥6.5%.

Table 1. Baseline characteristics for the study participants.

SN	C1	C2	C3	C4	C5
	Parameter	Overall	Low-risk†	High-risk#	P value
R1	Total (n)	648	592	56	–
R2	Male, n (%)	486 (75.00%)	444 (91.36%)	42 (8.64%)	1.00
R3	Age (years)	56.83±13.86	56.00±13.81	65.59±11.11	<0.05
R4	HbA1c (%)	7.26±2.06	7.16±2.04	8.36±1.94	<0.05
R5	LDL (mg/dL)	103.13±37.08	103.82±37.63	95.88±30.06	0.07
R6	HDL (mg/dL)	42.81±13.57	42.74±13.53	43.59±14.08	0.67
R7	TC (mg/dL)	174.98±49.92	175.89±50.50	165.45±42.48	0.09
R8	SBP (mmHg)	128.44±13.26	128.01±13.15	133.05±13.73	0.03
R9	DBP (mmHg)	80.13±8.59	80.07±8.50	80.71±9.61	0.01
R10	HT, n (%)	232 (35.80%)	204 (87.93%)	28 (12.07%)	0.63
R11	Smoking, n (%)	140 (21.60%)	121 (86.43%)	19 (13.57%)	0.05
R12	TG (mg/dL)	159.49±148.28	160.86±152.56	145.04±91.19	0.25
R13	cIMTave (mm)	0.75±0.25	0.71±0.21	1.14±0.27	<0.05

^†, significant confounding factors; ^#, stenosis was used for risk stratification. SN, serial number; HbA1c, glycated hemoglobin; LDL-C, low-density lipoprotein cholesterol; HDL-C, high-density lipoprotein cholesterol; TC, total cholesterol; SBP, systolic blood pressure; DBP, diastolic blood pressure; FH, family history; PS, plaque score.

Power analysis and sample size

In general, data samples should not be identical. In this proposed study, a standardized protocol was followed that selects the data samples at different locations of the same human body (23,65,66). Although the left and right carotid arteries have similar genetic formation and functionality, they work independently along two different pathways (19,40,67). Furthermore, the deposition of atherosclerotic plaque within the blood vessel is completely random and multifocal. Thus, a CUS scan from the left and right carotid artery was collected, yielding a total sample size of 1,287. The validity of the selected sample size of 1,287 CUS scans was tested using a power analysis. Power analysis suggests the smallest sample size required to perform the risk stratification of patients with higher predictive power. In this study, the population refers to the multicenter cohort of Japan, South-India, and Spain. A confidence level of 95% was selected for this study with a margin of error (MoE) of 5% and a data proportion () of 0.5. The desired sample size (n) for the true population was computed using, $n=\left[{\left(Z^{*}\right)}^2\times \left(\frac{\hat{P}\left(1-\hat{P}\right)}{{\rm M}O{{\rm E}}^2}\right)\right]$ (68). The resultant sample size with a 95% confidence level and 5% of MoE was ~384. Thus recruited sample size (1,287) was ~235% higher compared to the desired sample size of 384. This indicates that the selected sample size was sufficient to perform the statistical analysis.

Results

Baseline characteristics

Table 1 indicates the baseline characteristics of the study participants. A cohort of 648 patients (486 males and 162 females) was analyzed in this study. In a pool of 648 patients, average CA was 56.83±13.86 years (ranging between 24 and 88 years), HbA1c was 7.26%±2.06% (ranging between 4.80% and 14.30%), LDL cholesterol was 103.13±37.08 mg/dL (ranging between 26 and 259 mg/dL), HDL cholesterol was 42.81±13.57 mg/dL (ranging between 19 and 119 mg/dL), total cholesterol was 174.98±49.92 mg/dL (ranging between 60 and 435 mg/dL), SBP was 128.44±13.26 mmHg (ranging between 90 and 182 mmHg), DBP was 80.13±8.59 mmHg (ranging between 90 and 182 mmHg), and triglyceride was 159.49 mg/dL. Out total patients, 232 (35.80%) patients were hypertensive, 351 patients were diabetic, and 140 (21.60%) patients were smokers. The criteria for hypertension were SBP ≥130 or DBP ≥80 mmHg or treatment with hypertensive medication. Similarly, the criteria for diabetes were HbA1c ≥6.5%. Table 1 also shows the baseline characteristics of patients based on two risk categories: low- and high-risk.

CA vs. VA for different risk categories and different partition protocols (K)

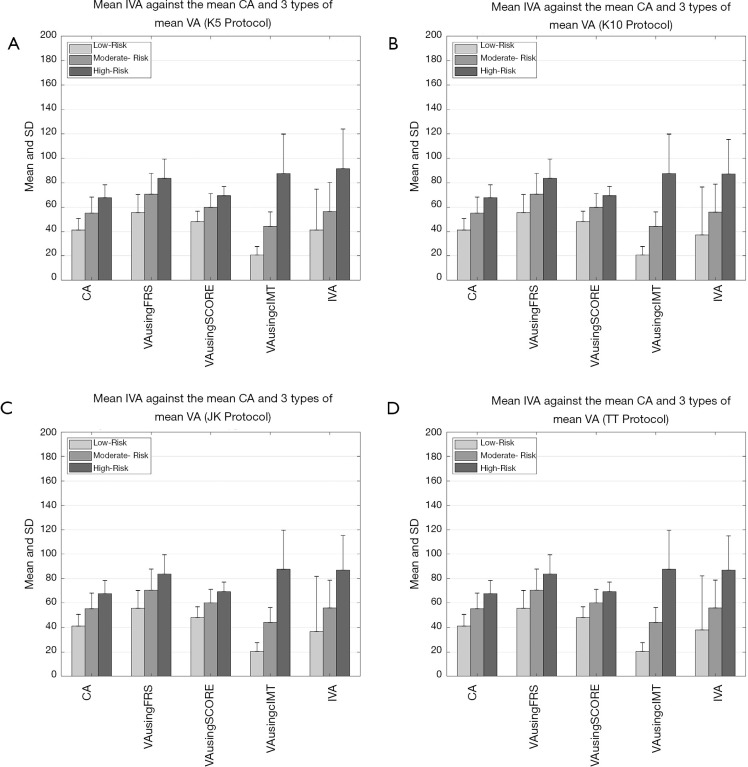
Figure 5A,B,C,D shows the comparison between (I) average values of IVA, (II) three types of VA (FRS-based, SCORE chart-based, and cIMTave-based), and (III) CA using four types of data-partitioning protocols (5-, 10-fold, Jack-Knife, and TT). The comparison between all the four types of VA techniques and the CA was made using the three risk classes (low-, moderate-, and high-risk). The risk classes were determined using cIMTave values. From the Figure 5A,B,C,D it was found that mean IVA of all the samples was (I) comparable to mean CA in low-risk category (mean CA =41 years, mean IVA =41 years), (II) slightly higher/comparable than the mean CA in moderate risk category (mean CA =55 years, mean IVA =57 years), and (III) significantly higher compared to mean CA of the high-risk category (mean CA =68 years, mean IVA =92 years). A similar trend of increment in VA was also observed in the other three types of VA techniques (FRS-based, SCORE chart-based, and cIMTave-based). Table S1 in the Appendix compares the average IVA (row R5) against (I) the three types average VA (row R2: FRS-based, row R3: SCORE chart-based, and row R4: cIMTave-based) and the (II) average CA (row R1: CA). This comparison was made based on the three different risk categories (column C1 to column C3) which were derived using cIMTave threshold points (lower threshold of 0.5 mm and an upper threshold of 0.9 mm). This identification of risk categories has already been discussed in the “Development of Integrated Vascular Age” section.

Figure 5.

Comparison between the average values of IVA, the types of the average values of VA [FRS-based (5), SCORE chart-based (52), and cIMTave-based (46)], and chronological age for four types of data-partitioning protocols. (A) 5-fold data-partitioning, (B) 10-fold data-partitioning, (C) Jack-Knife data-partitioning, and (D) TT data-partitioning. IVA, integrated vascular age; VA, vascular age; FRS, framingham risk score.

Table S1. Risk category-based comparison between average IVA against (I) the three types of average VA [FRS-based (5), SCORE chart-based (52), and cIMTave-based (46)] and (II) average chronological age.

Sr#	C1		C2	C3	C4
	Type of age		cIMTave-based risk categories
			Low-risk	Moderate-risk	High-risk
R1	CA (years)		41±9	55±13	68±11
R2	VA using FRS (years)		56±15	70±17	84±16
R3	VA using SCORE (years)		48±9	60±11	69±8
R4	VA using cIMTave (years)		20±8	44±12	88±32
R5	IVA (years)		41±34	57±24	92±32

IVA, integrated vascular age; CA, chronological age; VA, vascular age.

FRS using Integrated Vascular Age (FRS_IVA) vs. Chronological Age (FRS_CA)

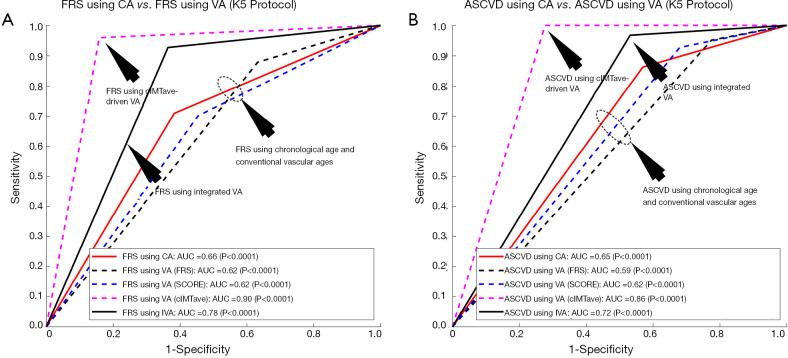
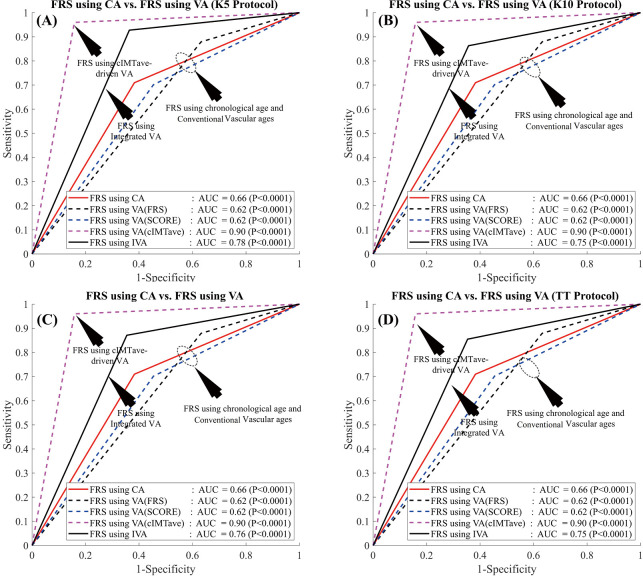
In order to evaluate the performance of the proposed IVA, the 10-year risk of CVD was computed using FRS (5) in two different scenarios: (I) considering IVA as input covariate (FRS_IVA) and (II) by considering the CA as input covariate (FRS_CA). FRS computed using both of these scenarios were used to risk-stratify the patients into two risk categories (low- or high-risk) using the response variable. Figure 6A shows the ROC curve that evaluates the performance of FRS_IVA [solid black curve in Figure 6A] as against the FRS_CA (solid red curve in Figure 6A). FRS_IVA reported the higher AUC (AUC =0.78, P<0.0001) compared to FRS_CA (AUC =0.66, P<0.0001) by ~18%. This has clearly indicated the higher risk prediction ability of the IVA when used in FRS instead of the CA. A similar trend was also observed for four types of data-partitioning protocols as indicated by Figure S1 of the Appendix.

Figure 6.

Receiver operating characteristics curve indicating the performance of integrated vascular age against the chronological age and the three types of VA computations methods. (A) FRS computed using IVA against the FRS computed using chronological age, VA computed using FRS (5), VA computed using SCORE chart (52), and VA computed using cIMT-based model developed by Linda model (46); (B) ASCVD computed using IVA against the ASCVD computed using chronological age, VA computed using FRS, VA computed using SCORE chart, and VA computed using Linda model. FRS, framingham risk score; CA, chronological age; VA, vascular age; ASCVD, atherosclerosis CVD; IVA, integrated vascular age.

Figure S1.

Comparison of performance of risk stratification using IVA, risk stratification using three types of VA [FRS-based (5), SCORE chart-based (52), and cIMTave-based (46)], and risk stratification using chronological age for four types of data-partitioning protocols. (A) 5-fold data-partitioning, (B) 10-fold data-partitioning, (C) Jack-Knife data-partitioning, and (D) TT data-partitioning. FRS, framingham risk score; CA, chronological age; VA, vascular age; IVA, integrated vascular age; AUC, area-under-the-curve; TT, time-triggered.

FRS using IVA vs. FRS using three types of VA techniques (VA_cIMT, VA_FRS, and VA_score)

Figure 6 also compares the performance of IVA against the three different types of VA: (I) VA computed using Linda’s model (VA_cIMT) (46), (II) VA computed using FRS calculator (5) (VA_FRS), and (III) VA computed using SCORE chart (52) (VA_score). Among all these types of techniques, VA computed using the cIMT-based model developed by Linda’s (46) was solely based on cIMT values whereas the VA computed using the FRS calculator (5) and SCORE chart (52) used the CRFs. The AUC values for the 10-year risk computed using FRS calculator (Figure 6A, Table 2) with all three types of vascular ages are: (I) VA using Linda’s model (AUC =0.90, P<0.0001), (II) VA using FRS (AUC =0.62, P<0.0001), and (III) VA using SCORE chart (AUC =0.62, P<0.0001). From Figure 6A, it should be noted that the AUC values of FRS_IVA (black solid line) and FRS_VA(cIMT) (pink dotted line) were higher compared to FRS_VA(SCORE) (blue dotted line) and FRS_VA(FRS) (black dotted line). Furthermore, the AUC value for FRS_IVA (AUC =0.78, P<0.0001) was higher than the AUC values of both the CCVRF-based FRS_VA(SCORE) and FRS_VA(FRS) by ~26%. However, the AUC value for FRS_IVA (black solid line) was found to be comparable with the AUC value for FRS_VA(cIMT) (pink dotted line). The reason for the lower AUC value for the IVA model was due to the proprietary dataset used by Linda et al. (46), which only contained low-to-moderate risk patients (cIMTave ~0.6 mm). Thus, such linear regression coefficients may not be suitable for patients with high baseline risk (for example in the proposed study) which could further provide a bias during risk stratification. This was the reason for a difference in AUC values between Linda’s model and all the other VA models including IVA.

Table 2. Comparing the performance of IVA-based risk stratification using FRS against chronological age and three types of VA technique.

SN	PE metric	CA	VA using FRS	VA using SCORE	VA using cIMTave	IVA
1	Sensitivity	70.93	87.83	70.17	95.97	92.70
2	Specificity	61.74	36.80	54.60	84.18	63.63
3	Accuracy	62.63	41.73	62.63	62.63	66.44
4	PPV	16.52	12.91	14.17	39.54	21.74
5	NPV	95.22	96.67	94.49	99.49	98.77
6	MCC	0.20	0.15	0.15	0.56	0.34
7	AUC	0.66	0.62	0.62	0.90	0.78

All the results are obtained for the 20 trials using K5 protocol. IVA, integrated vascular age; FRS, framingham risk score; PE, performance evaluation; CA, chronological age; VA, vascular age; FRS, framingham risk score.

Validation and consistency analysis against ASCVD calculator

The atherosclerosis CVD (ASCVD) risk calculator was developed by the American College of Cardiology/American Heart Association and is widely used for 10-year CVD risk estimation (7). In this proposed study, the performance of the IVA was also tested by replacing with CA in the ASCVD calculator (Figure 6B and Table S2). The ASCVD computed using IVA (ASCVD_IVA) reported the higher AUC (AUC =0.72, P<0.0001) compared to the ASCVD computed using CA (ASCVD_CA) (AUC =0.65, P<0.0001) by ~9%. This further provided validation of our results obtained using FRS_IVA. Furthermore, when the risk stratification based on ASCVD_IVA was compared against the risk stratification using three types of VA [FRS-based VA (5), SCORE chart-based (52), cIMTave-based VA by Linda et al. (46)], the AUC values showed consistent results as observed using FRS calculator (Figure 6B).

Table S2. Risk stratification metrics for 10-year risk computed using IVA against the 10-year risk computed using (I) chronological age and (II) 3 types of traditional vascular ages.

PE metric	FRS calculator vs. response variable						ASCVD calculator vs. response variable
	CA	VA using FRS	VA using SCORE	VA using cIMTave	IVA		CA	VA using FRS	VA using SCORE	VA using cIMTave	IVA
Sensitivity (%)	70.93	87.83	70.17	95.97	92.70		86.23	95.10	92.67	100.00	96.70
Specificity (%)	61.74	36.80	54.60	84.18	63.63		43.08	22.53	32.07	72.31	46.86
Accuracy (%)	62.63	41.73	62.63	62.63	66.44		47.24	29.53	47.24	47.24	51.68
PPV (%)	16.52	12.91	14.17	39.54	21.74		13.92	11.58	12.71	27.98	16.36
NPV (%)	95.22	96.67	94.49	99.49	98.77		96.74	97.89	97.69	100.00	99.35
MCC	0.20	0.15	0.15	0.56	0.34		0.18	0.13	0.16	0.45	0.26
AUC	0.66	0.62	0.62	0.90	0.78		0.65	0.59	0.62	0.86	0.72

IVA, integrated vascular age; PE, performance evaluation; FRS, framingham risk score; ASCVD, atherosclerosis CVD; CA, chronological age; VA, vascular age; PPV, positive prediction value; NPV, negative predication value; AUC, area-under-the-curve.

Discussion

In this study, a novel IVA was proposed that combines the effect of both CRFs and the CUSIP such as cIMTave. The IVA was then used as input covariate to FRS for risk stratification. We showed that FRS_IVA (AUC =0.78, P<0.0001) performed better compared against FRS_CA, (AUC =0.66, P<0.0001) by 18%. The risk-stratification results with IVA were also validated using the ASCVD calculator. The risk stratification using ASCVD_IVA reported higher AUC (AUC =0.72, P<0.0001) compared to the ASCVD_VA (AUC =0.65, P<0.0001) by ~11%. This clearly indicates that the IVA can be replaced with CA while performing the long-term cardiovascular risk assessment. Furthermore, while performing the risk CVD risk stratification, this study showed a higher predictive power of integrated risk factors (CUSIP + CRF) compared to CCVRF or CRF alone.

Benchmarking

The proposed IVA was benchmarked against 11 studies (row R1 to row R11) that were presented in Table 3. Eight out of 11 studies (column C3, row R1-R3, R5-R6, R8-R9, R11) used the CUSIPs such as cIMT or TPA for vascular age measurement. The studies presented D’Agostino et al. (5) (row R4) and Cuende et al. (52) (row R7) used the CCVRF to measure the vascular age of patients. All the studies that used CUSIP for VA measurement have used the linear regression-based percentile models (or nomograms) to compute the VA. Whereas the CCVRF-based vascular age measurement uses the proportional hazard models such as cox-regression [used by FRS-based point model (5)] or Weibull regression models [used by SCORE chart et al. (52,70)]. Except for the proposed study (row R12), none of the previously published studies have tried to combine the effect of both CCVRF and the CUSIP for VA measurement (column C4). It should also be noted that the proposed IVA calculator was modeled using the three different types of ethnicities (row R12 and column C2). In order to test the performance of vascular age for risk stratification of patients, most of the studies (column C10) used the FRS as a risk calculator. In our proposed study we also tested the performance of IVA using FRS which was further validated using the ASCVD calculator. The ASCVD is the recently developed CCVRC by the American College of Cardiology/American Heart Association (ACC/AHA) which is widely used for CVD risk assessment.

Table 3. Studies that used the concept of vascular age for CVD risk assessment.

SN	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11
	Author	Ethnicity	Covariates	Integrated approach	VA Technique	N	Mean CA (years)	Mean VA (years)	Risk stratification	CCVRC	Results
R1	Stein et al. [2004] (45)	American	cIMT		Linear Regression	82	55.8±9.0	65.5±18.9		FRS	NA
R2	Gepner et al. [2006] (50)	American	cIMT		Linear Regression	506	55.0±7.4	61.8±11.6		FRS	NA
R3	Junyent et al. [2006] (58)	Spanish	cIMT		Linear Regression	409	49±11	Mean CA +14.5		FRS	FRS (CA) =9.2%±8.3%; FRS (VA) =9.8%±8.5%
R4	D’Agostino et al. [2008] (5)	White American	CCVRF		Point-based system	8,491	NA	NA
R5	Naqvi et al. [2010] (59)		cIMT		Linear Regression	136	56.9±10.1	61.6±11.4		FRS	NA
R6	Khalil et al. [2010] (51)	American	cIMT		Linear Regression	20	55.8	68.5		FRS	NA
R7	Cuende et al. [2010] (52)	European	CCVRF		SCORE chart-based	205,178	NA	NA		SCORE
R8	Adolphe et al. [2011] (46)	Asian	cIMT		Linear Regression	2,291	40.7±11.7	32.2±15.8		NA	NA
R9	Romanens et al. [2014] (53)	Swiss	TPA		Linear Regression	1,500	59.9±9	49±21		AGLA	AGLAca vs. AGLAaa: mean risk =8% vs. 9%; AUC =0.65 vs. 0.78
R10	Sharma et al. [2015] (69)	Indian	CCVRF		FRS point Based	2,483	46±8	53±34
R11	Andrade et al. [2016] (60)	Brazil	cIMT		Linear Regression	96	44.4±6.4	53.8±12.5		FRS	FRS (VA) =17.2%±10%; FRS (CA) =12.5%±7.8%
R12	Proposed [2019]	Japanese, Indian, Caucasian	CUSIP + CCVRF		Linear Regression and MLR	648				FRS & ASCVD	FRS (CA): AUC =0.62; FRS (IVA): AUC =0.78; ASCVD (CA): AUC =0.67; ASCVD (IVA): AUC =0.72

CVD, cardiovascular diseases; VA, vascular age; CCVRC, conventional cardiovascular risk calculators; FRS, framingham risk score; CA, chronological age; ASCVD, atherosclerosis CVD; AUC, area-under-the-curve.

Comparison of complete MLR model vs. partial MLR model

The proposed model of IVA measurement comprised of both the linear regression (for cIMT-based vascular age) and MLR (for CCVRF-based vascular age). This was also referred to as a partial MLR-based model. On the contrary, we also tested a complete MLR model with both CCVRF and cIMT as input covariates. The CA of a person was used as a dependent variable for the MLR analysis. Such completely MLR-based IVA when added to the FRS by replacing the CA, resulted in an improvement in the AUC by ~5% (AUC of FRS using IVA =0.74 and AUC of FRS using CA =0.70). Figure 7 shows the ROC curve for FRS using CA and VA as an input argument. Although there is an improvement in AUC by 5%, it is less compared to the partial MLR-based IVA proposed in this study resulted in improvement in AUC by ~18%. Thus a partial MLR-based model opted for this study.

Figure 7.

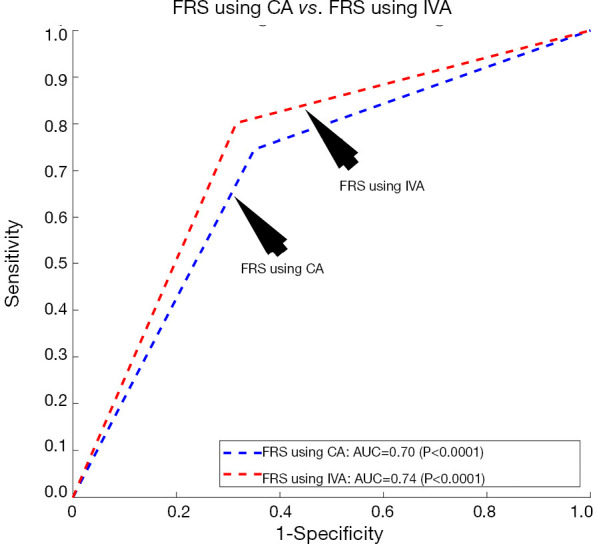
Receiver operating characteristics curve for the FRS calculator using (I) CA as input argument (blue curve) and (II) complete MLR-based integrated VA as input argument (red curve). FRS, framingham risk score; CA, chronological age; IVA, integrated vascular age; AUC, area-under-the-curve.

Strengths, limitations, and future scope

The proposed study had following strengths: (I) this was the first study which combined the effect of CCVRF and cIMT to measure the vascular age of person, (II) this was the first attempt to combined three different types of ethnicities (Japanese, Asian-Indian, and Caucasian) to measure the vascular age, and (III) the propose integrated calculator was validated with two types 10-year CCVRC such FRS and ASCVD.

Although the power analysis validated the selected sample size, we intend to extend the analysis to a longitudinal trial with a large diversified cohort of varying ethnicities. Furthermore, it should be noted that the 10-year risk stratification using the proposed IVA provides a trade-off performance between the cIMT-based vascular and CCVRF-based vascular age. This is because of the (I) higher AUC value for the 10-year risk stratification using cIMT-based vascular age compared to the proposed IVA and (II) lower AUC value for the 10-year risk stratification using CCVRF-based vascular age compared to the IVA.

The proposed study development of IVA can further be extended to an automated machine learning-based risk assessment system (3,71) where IVA can be used as an important input feature. More features such as grayscale information from the images can be added (55,72,73). Another extension can be accomplished where CUSIP can be used from deep learning paradigms (74-77).

Conclusions

The proposed study reported the higher potential of integrated vascular compared to (I) CA and (II) to the CRF-based vascular age. Thus, replacing the “chronological age” with the “integrated vascular age” could provide a better CVD risk assessment. CUSIPs such as cIMT can provide a better understanding of the atherosclerosis plaque build-up in the blood vessels. They reflect the overall health of arteries and can provide information about the true arterial age of a person. This was the primary reason for boosting the AUC when cIMT was integrated with the CCVRFs in the vascular age model.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). All the patients were approved by the Institutional Review Board. Written consent was obtained from all the study participants.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.