Abstract
Targeted drugs disrupting proteins that are dysregulated in cancer have emerged as promising treatments because of their specificity to cancer cell aberrations and thus their improved side effect profile. However, their success remains limited, largely due to existing or emergent therapy resistance. We suggest that this is due to limited understanding of the entire relevant cellular landscape. A class of mathematical models called discrete dynamic network models can be used to understand the integrated effect of an individual tumor's aberrations. We review the recent literature on discrete dynamic models of cancer and highlight their predicted therapeutic strategies. We believe dynamic network modeling can be used to drive treatment decision-making in a personalized manner to direct improved treatments in cancer.
Keywords: Network model, Dynamic model, Discrete dynamical system, Boolean model, Cancer phenotypes, Signal transduction networks, Targeted cancer therapy, Drug resistance, Combinatorial therapy, Personalized therapy
Highlights
-
•
Cancer is rooted in incorrect cellular decisions caused by genetic alterations.
-
•
Dynamic models of signaling networks can map the relevant repertoire of alterations.
-
•
Discrete dynamic network models can predict therapeutic interventions.
-
•
Progress in personalized medicine needs integration of multiple data and model types.
Introduction
Cancer, a disease characterized by uncontrolled cell growth, can lead to devastating effects on the human body. Cancer is one of the most common causes of deaths worldwide. Normal working cells over time accumulate genetic and epigenetic changes that lead to dysregulation of the signaling pathways that regulate cellular behavior and the acquisition of the hallmark features of cancer. These hallmark features include proliferation, evasion of growth suppression and cell death, invasion, and metastasis [1]. More recently, modulation of the immune response has emerged as an important additional feature of cancer [2].
Traditional medical modalities of cancer treatment (when surgical removal is not an option) include chemotherapy and radiation, which disrupt DNA synthesis of all cells and lead to cessation of proliferation and induction of cell death. More recently, targeted and immunological therapy have emerged as promising modalities of cancer treatment. Targeted therapies are drugs that target a specific protein within a signaling pathway that is critical to one of the above cancer hallmarks. They tend to be less toxic than chemotherapy because the targeted protein is usually not expressed in healthy cells. With the growing arsenal of targeted therapies for cancer and other diseases, the question becomes how to most effectively use targeted therapy.
Individualization of oncologic treatment: where we stand now
Currently, targeted therapies are approved as first or second line agents in multiple cancer types and are generally used as single agents. Personalized tumor information is currently used to a very limited extent. There are initiatives for screening for specific genetic or expression features of cancers and targeting the treatment accordingly but the benefit they have so far demonstrated is limited 3, 4. For example, in non-small cell lung cancer, if a tumor contains an EGFR inhibitor sensitizing mutation, the treatment decision would be an EGFR inhibitor such as gefitinib [5]. Gefitinib, compared to traditional chemotherapy, has a slightly improved progression-free period (about 11 months versus 5 months) and overall survival (30 months versus 24 months) [6]. This trend is similar for many targeted therapies in lung cancer [7] and other cancer types 8, 9. But just like traditional chemotherapy, the efficiency of targeted therapies is thwarted by either intrinsic resistance to the drug or the development of drug resistance. We propose that models that incorporate comprehensive tumor information would help improve treatment efficacy beyond the current “single mutation, single treatment” strategy. For example, multivariate models using clinical and epidemiologic information are frequently and successfully used for making clinical decisions 10, ∗11, 12. At present there are no clinical multivariate models that incorporate molecular/genomic information.
The critical information required to determine which patients should get a targeted therapy can be formulated as a set of questions:
-
•
What are the characteristics of a specific tumor that would lead it to respond in some way or be outright resistant to a targeted therapy?
-
•
Should we target multiple aspects of cancer in combination? Which targeted drug combinations are optimal?
-
•
As a cancer acquires resistance to our current treatment regimen, how should we augment the regimen to effectively treat this evolved cancer?
We propose that answers to these questions can be elicited by systems biology approaches. Systems biology provides a powerful set of tools that allows the integration of signaling and gene regulatory networks, genomic, and epigenomic information into system-level models 13, ∗∗14, 15, 16, ∗∗17. These models can be used to incorporate such information from individual cancer cells to understand these cells’ individual dynamics, their response or resistance to treatment. Here we describe how these network models can help to understand cancer cell dynamics and to rationally develop individualized targeted strategies to improve oncologic treatment.
Oncogenic signaling networks underlie cancer
Molecular networks inside healthy cells contain so-called proto-oncogenes and tumor suppressor genes. Proto-oncogenes may acquire a mutation that then makes the cell adopt a cancer hallmark phenotype (e.g. proliferation); these altered genes in cancer cells are referred to as oncogenes. Tumor suppressor genes ward against aberrant phenotypes when they are active; alterations that cause their inactivation lead to cancer development. Alterations that activate oncogenes, combined with alterations that inactivate tumor suppressor genes, perturb the cell's signaling pathways, lead to incorrect cellular decisions and behaviors (proliferation instead of quiescence, survival instead of apoptosis), and ultimately to a cancer phenotype [1].
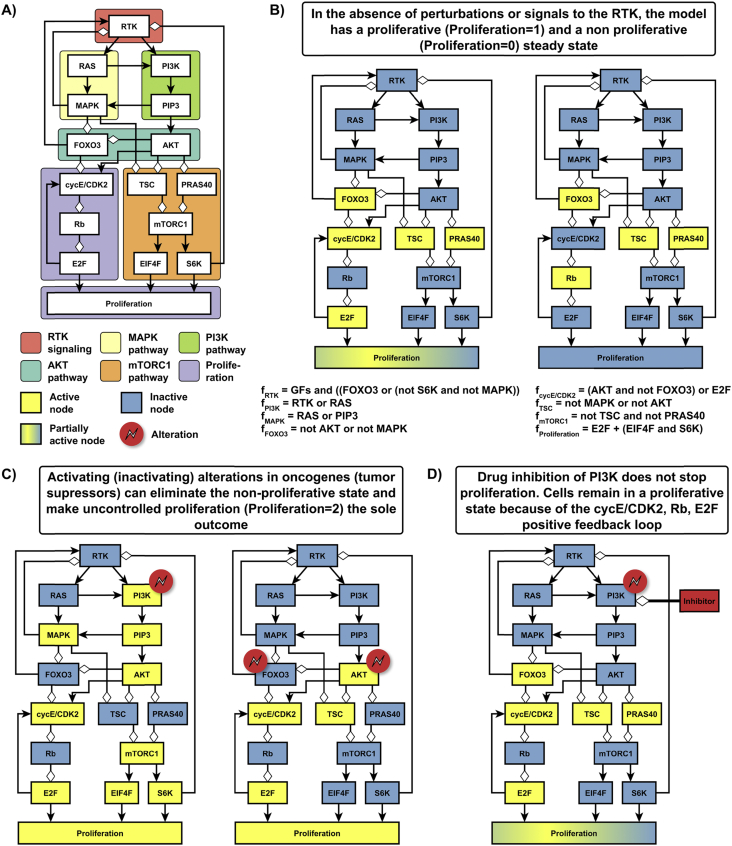
In order to understand the often indirect connection between an alteration and a cellular outcome, we need to consider the network of interactions and regulatory relationships the alteration is embedded in. In a within-cell network, nodes represent proteins, RNA, or small molecules and the edges are the interactions and regulatory relationships between nodes. The edges are directed (indicating the direction of mass- or information flow) and can be positive (activating) or negative (inhibitory). This network usually also involves proxies for one or more cellular outcomes and the external signals that can lead to these cellular outcomes. The receptor tyrosine kinase (RTK) signaling network shown in Figure 1 and described in detail in Box 1 illustrates several features of signaling networks that underlie cancer phenotypes.
Figure 1.
Illustrative example of a signal transduction network relevant to a cancer hallmark phenotype, uncontrolled proliferation. In the normal context cell proliferation is driven by growth factors that bind to receptor tyrosine kinases (RTKs); yet it can also be an outcome of alterations in signal transduction proteins. In panel A, the six subgraphs that are typically referred to as separate pathways in the biological literature are colored differently. Panels B–D indicate select outcomes of a discrete dynamic model of this network, whose regulatory functions are indicated in the bottom of panel B. The unperturbed system (B) has two possible steady states, a non-proliferative one and one with controlled proliferation (Proliferation = 1), among which it may select depending on environmental signals. (C) Alterations in certain oncogenes or tumor suppressor genes yield a single outcome: uncontrolled proliferation (Proliferation = 2). (D) Targeted inhibition of an oncogene (here, PI3K) may not eliminate the proliferating phenotype. Further details are provided in Box 1.
Box 1. Illustrative example of systems biology methods applied to cancer.
Figure 1A illustrates signal transduction networks relevant to cancer cell phenotypes by a simplified version of receptor tyrosine kinase (RTK) signaling through the MAPK, PI3K, AKT, and mTORC1 pathways in the context of breast cancer [17], and leading to the cellular outcome of proliferation, which is denoted by the node “Proliferation”. RTKs signal through two parallel pathways, the PI3K/AKT and the RAS/MAPK pathways, and this is encoded in the network by RTK activating two nodes, RAS and PI3K, each of which is a key component of these pathways. Note that although these pathways are referred to as parallel 47, 48, there are multiple examples of cross-talk between these pathways (e.g. RAS→PI3K and PIP3→MAPK). This cross-talk between pathways is quite general, and makes defining what is or is not part of a certain pathway a sometimes ill-posed task.
Signaling networks often have multiple feedback loops, as illustrated in Figure 1A by the negative feedback loops RTK has with MAPK, S6K, and FOXO3, and the positive feedback loop between the cell cycle proteins cyclE/CDK2, Rb, and E2F. This network contains several proteins encoded by oncogenes (e.g. RAS, PI3K, mTOR) and tumor suppressors (e.g. Rb, FOXO3). The oncogene nodes can reach the outcome node Proliferation through positive paths (e.g. the path RAS, MAPK, FOXO3, CycE/CDK2, Rb, E2F, Proliferation); tumor suppressor nodes can reach Proliferation through negative paths. (Paths that have an even number of negative edges are positive.) Most oncogene nodes can also reach proliferation through longer, negative paths, due to the negative feedback loops mediated by the RTK node, making their influence on proliferation ambivalent. If we add the effect of positive and negative paths weighted by their length [49], the path influence of the oncogenes on proliferation is positive (with a normalized value ranging between 0.34 and 0.84), consistent with expectations.
In a DDNM of this network based on [17], all nodes variables are Boolean, shown with blue (for 0) or yellow (for 1) background colors in Figure 1B–D, except for the outcome node Proliferation, whose three states represent a non-proliferative (0), proliferative (1 or partially active), and uncontrolled proliferative (2 or active) state. The meaning of the active state of each protein (which we represent with the protein/node name) and of its regulatory function depends on the protein. For example, if a protein is active if (un)phosphorylated (e.g. (Rb) AKT), the node name refers to the (un)phosphorylated form, and its regulatory function expresses the condition under which the protein is (un)phosphorylated. The five nodes that have a single positive regulator will follow their regulator with a time delay, e.g. the regulatory function of RAS is fRAS = RTK. The four nodes that have a single negative regulator adopt the negation of their regulator's state, e.g. the regulatory function of E2F is fE2F = not Rb. The rest of the regulatory functions are shown in Figure 1B, where GFs in fRTK denotes the status of growth factor signals to the RTK.
The unperturbed system in the absence of GFs has two steady states (see Figure 1B), a proliferative (Proliferation = 1) and nonproliferative one (Proliferation = 0), which arise because of the bistability of the cycE/CDK2, Rb, E2F, cycE/CDK2 positive feedback loop. This feedback loop may activate or deactivate due to signals encountered by the cell that are not represented in this network. Constitutive activation of either of the oncogenes PI3K, RAS, or constitutive activation of AKT or mTORC1 combined with constitutive inactivity of the tumor suppressor Rb yields an attractor that corresponds to uncontrolled proliferation (Proliferation = 2) even in the absence of GFs (Figure 1C). The fraction of constitutive (in)activity-inducing alterations that yield uncontrolled proliferation is low (3 of 28 possible single-node alterations, 7 of 182 possible double-node alterations). The DDNM agrees well with the expected properties of oncogenes and tumor suppressor genes with the exception of FOXO3, for which both constitutive inactivity (in combination with AKT constitutive activity) or constitutive activity (in the presence of GFs) can lead to abnormally high proliferation. This illustrates that the same node may be classified as an oncogene or tumor suppressor depending on the network context [50].
This model also illustrates that targeted inhibition of an oncogene responsible for driving a cancer hallmark phenotype may not completely eliminate that phenotype (Figure 1D). Drug-induced inactivation of PI3K inactivates the majority of pathways through which constitutive PI3K activity led to proliferation, but it does not disrupt the cycE/CDK2, Rb, E2F, cycE/CDK2 positive feedback loop, which is a stable motif [51]. Stable motifs are generalized positive feedback loops that can maintain an associated state regardless of the state of nodes outside of the motif. Stabilization of a stable motif acts as a point of no return in a system's dynamics, thus driving a system into an attractor must involve control of the stable motifs [52].
The network representation of a signal transduction process, such as the one shown in Figure 1A, is static, while biological processes happen over time. In order to understand the dynamic behavior of a system, each node needs to be characterized by a state variable that can change in time and that is affected by the state variable of the nodes that regulate it. Both quantitative models (using continuous state variables) and qualitative models (using discrete state variables) exist. Quantitative models, generally using systems of ordinary or partial differential equations, can be highly accurate and provide quantitative information (e.g. drug dosage information, drug response time, or fold-changes of protein concentrations) that is either difficult or impossible to obtain with qualitative models because of their use of discrete state variables. Phenomenological pharmacokinetic/pharmacodynamic models of the physiological response to drugs are an integral part of drug testing and discovery. The use of quantitative models for mechanistic modeling of signal transduction networks is highly desirable, and there are multiple examples of the unique insights such a quantitative approach can provide 18, 19, 20, 21, ∗22, ∗23, but their widespread use is limited by the scarcity of high-quality quantitative data these models require, such as kinetic and temporal information about individual nodes in the network and/or quantitative microscopy time course data to fit the unknown model parameters. Discrete and quantitative models are often consistent in capturing the response repertoire of signaling networks (e.g. their potential bistability or response to perturbations) ∗∗17, 20, 21, 24, 25.
Discrete dynamic network models in biology
Discrete dynamic network models (DDNMs) can be constructed using widely available biological information. In DDNMs each node is assigned a variable that can take one of a small number of discrete states, where each state is characterized (and defined) by its influence on the state of the nodes that have an incoming edge from node . Thus, the direct regulators of each node determine its future state, and this is encoded in the regulatory function of the node. In the simplest case, the Boolean scenario, each node takes one of two states: or , assuming that an implicit threshold exists above which the node is sufficiently active to regulate its target nodes. Each regulatory function can be expressed in terms of Boolean logical operators (e.g. AND, OR, NOT). A DDNM must specify a method for when the regulatory functions are applied to modify the node states (i.e. an updating scheme). The most common updating schemes are the synchronous and the stochastic asynchronous updating schemes, and several others exist. A number of review articles offer insights into the construction and use of DDNMs ∗26, 27, 28, 29, 30, 31, ∗32.
DDNMs were introduced as prototypical models for gene regulatory networks underlying cell fate decisions and cell differentiation processes 33, 34, 35, 36. The focus of the initial studies was on the long-term behavior of the models, that is, the attractors of the system (e.g. steady states or limit cycles), which were found to be identifiable with the expected cell fates or stable patterns of cell activity. As biological information on the regulatory networks of diverse organisms increased, DDNMs of more complex gene regulatory networks, cell differentiation processes, and signal transduction networks were constructed 37, 38, 39, 40, 41, 42, 43, 44, 45, 46. These models reaffirmed the observation that the attractors of the modeled system correspond to stable patterns of cell activity, and supported an intrinsic hypothesis of DDNMs: that the network topology and the regulatory logic (without the need for specifying kinetic details) can be sufficient to explain several dynamical aspects of the modeled system, including its response to perturbations. This work was done in parallel to biophysical and mathematical modeling of well-characterized genetic and signal transduction networks, e.g. Refs. 18, 19.
Network-based discrete dynamic models have become a useful and common tool in systems biology and mathematical modeling due to their ability to (i) encode the current knowledge of a biological process of interest, (ii) check the consistency (or lack thereof) of the current knowledge by testing the model's ability to recapitulate observed behavior based on the known interactions and their logic, (iii) fill gaps of knowledge with hypothesized interactions, and (iv) predict the behavior of the system under untested circumstances (e.g. test the consequences of two competing hypotheses on the model's behavior). In Figure 1B–D and Box 1 we illustrate the types of results generated by these models.
Discrete dynamic network models in cancer
Given the ability of DDNMs to mathematically model signal transduction and gene regulation, they have increasingly been used to model oncogenic signaling, its effect on several hallmarks of cancer, and to predict therapeutic interventions. The networks and regulatory functions were typically constructed based on literature curation and followed by an iterative procedure that refines the regulatory functions according to the model's ability to reproduce key experimental outcomes ∗∗17, 25, ∗∗53, 54, 55, ∗∗56, 57, 58, 59. In several cases this was combined with bioinformatics or network inference methods ∗∗14, ∗∗60, ∗61. Some of these models consider the effect of cell heterogeneity by using stochastic updating schemes (which simulates the effect of each cell having different kinetic parameters) or by simulating the model using different initial states or node alterations ∗∗56, 57, 58, ∗61. The models identified the key mechanisms that underlie cancer phenotypes and predicted therapeutic interventions that disrupt these phenotypes; many of these predictions were validated experimentally. In the following we summarize the main findings of recent DDNMs.
Grieco et al. modeled MAPK signaling downstream of the RTKs EGFR and FGFR3 in bladder cancer, and predicted that the less aggressive phenotype of FGFR3-driven tumors is due to a low proliferation state, which they found is dependent on ERK and independent of PI3K [54]. A three-state DDNM of EGFR inhibition in colon cancer in the presence of various concomitant mutations correctly predicted whether or not a tumor would be sensitive to an EGFR inhibitor [25], in agreement with a quantitative model [21]. Modeling apoptosis and proliferation in estrogen-receptor-positive breast cancer, Zañudo et al. predicted that MAPK signaling, FOXO3 and MYC upregulation act as resistance mechanisms against PI3K inhibitors [17]. The model also predicted that the combination of a PI3K inhibitor with a CDK4/6 inhibitor would be synergistic to a similar degree to the combination of PI3K and estrogen receptor inhibitors, and that prior or simultaneous application of an mTOR inhibitor would sensitize cells to PI3K inhibition by priming them for apoptosis.
Evasion of cell death and uncontrolled growth (and how to prevent them) are the most studied outcomes in models of oncogenic signaling, yet the interplay of oncogenic signaling in invasion and metastasis is equally important and less understood. Several groups have recently developed mathematical models of the biological processes underlying cancer cell invasion and metastasis ∗∗14, ∗22, ∗23, ∗∗56, 57, ∗61, 62, ∗63, with a particular emphasis on the epithelial-to-mesenchymal transition (EMT), a developmental process hijacked by cancer that is thought to be necessary for the initiation of metastatic spreading. On the discrete network modeling side, one of the initial efforts was by Steinway et al., who constructed a model of EMT in the context of hepatocellular carcinoma ∗∗56, 62. The model predicted that EMT is a robust outcome, induced by a variety of external and internal signals, many of which sustain each other (e.g. the growth factor TGFβ concurrently induces the Wnt and Shh signaling pathways), a prediction that was validated experimentally in vitro [56]. Steinway et al. used the model and the network control approach of [51] to predict, and cell line experiments to confirm, that the combinatorial inhibition of SMAD and proteins in the RAS or NOTCH pathways, but not SMAD alone, can suppress TGFβ-driven EMT [62]. They also predicted that certain perturbations (e.g. SMAD knockout) give rise to hybrid states intermediate between the epithelial and mesenchymal states, which might retain some invasive properties, thus emphasizing the need for combinatorial therapies to fully suppress EMT and invasion.
Cohen et al. constructed a logical model of signaling and regulatory mechanisms leading to EMT, invasion, and metastasis, and predicted that the Notch gain-of-function and p53 loss-of-function double mutant is the most efficient in inducing metastasis, that the TGFβ pathway is required for metastasis in this mutant, and that the characteristic set of mutations for colorectal cancer tumorigenesis is sufficient for EMT and invasion but not for metastasis [57]. Colorectal cancer was also the focus of Kim et al.'s analysis aiming to revert a cancer attractor landscape (with respect to proliferation, EMT and stemness) to a more normal landscape [13]. Experimental data from engineered intestinal stem cells informed the development of a proximity-to-normal score. Systematic search in the space of interventions recapitulated known beneficial interventions and predicted new ones: inhibition of ARF or Rb and restoration of the normal level of MMP and BRCA1. This study suggested that the key strategy for cancer reversion is to increase the responsiveness of cancer cells to external signals by disturbing stable functional motifs of cancer cells, in agreement with Refs. ∗∗51, 62.
Udyavar et al. constructed a network model of transcription factors (TFs) for the epithelial-like and mesenchymal-like phenotypes in small-cell lung cancer (SCLC) using a mixed bioinformatics and literature-based approach [14]. They identified the nodes of this network by clustering the gene expression profiles of SCLC cell lines and tumors into two subtypes, identifying coexpressed gene modules that separated the two subtypes, and using TF databases to identify TFs whose targets are enriched in the gene modules. They then constructed an interaction network among these TFs using alternative TF databases and literature search. The model predicted the existence of epithelial-like and mesenchymal-like attractors, a prediction that was confirmed experimentally in cell lines and tumors. However, the model was unable to predict the hybrid phenotypes observed in cell lines and tumors, indicating that these hybrid phenotypes may arise due to alterations and mutations in the networks [62] or the existence of intermediate levels of gene expression [22].
Modeling gene regulatory processes underlying senescence, inflammation, and EMT in cancers of epithelial origin, Méndez-López et al. found that the commonly observed progression by which epithelial cells first become senescent and then acquire a mesenchymal phenotype can be reproduced through perturbation-driven phenotype transitions [58]. The model predicted that the transition into the mesenchymal phenotype is accelerated by inflammation, consistent with the poor prognosis of pro–inflammatory conditions. Khan et al. developed a DDNM of E2F1-mediated epithelial-to-mesenchymal transition in the context of bladder and breast cancer [61]. The authors first constructed a comprehensive interaction map centered on E2F1, then they selected key genes and feedback loops by ranking them according to a metric that combined biological and network criteria. The model's prediction that combined alteration of E2F1, TGFβR1, and FGFR1 in bladder cancer, and E2F1, TGFβR2, and EGFR in breast cancer corresponds to the most aggressive phenotype was confirmed by in vitro experiments, and supported by patient survival data.
Outlook for network models in cancer – drug resistance and drug combinations
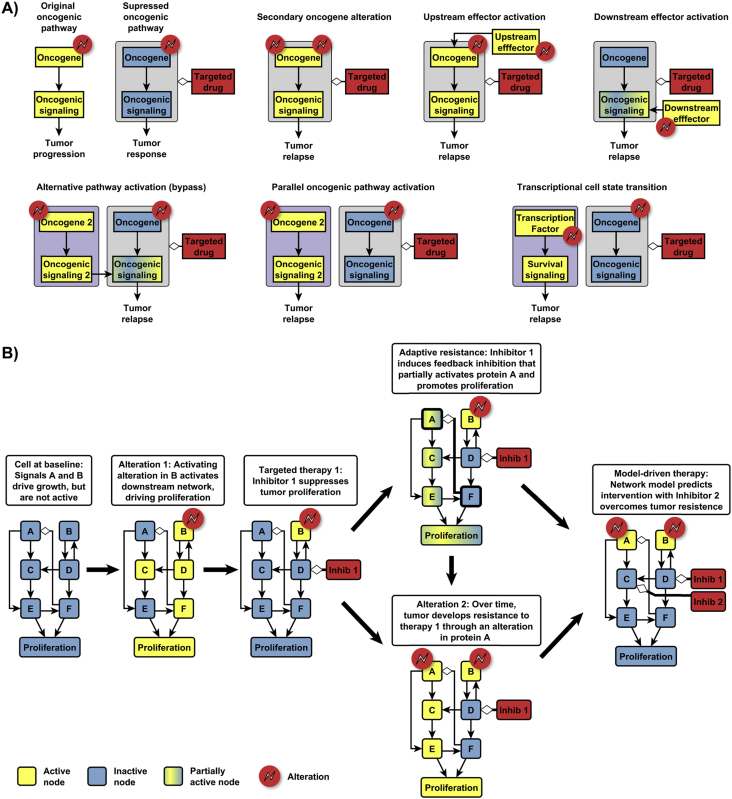
The examples reviewed in the previous section point to the multiple ways in which network-based dynamic modeling can be used to answer the questions we posed at the beginning. For any targeted therapy, cells that rely on a different signaling network and cancer phenotype will be resistant to the therapy. A partial response will be observed if the targeted therapy can only partially deactivate the network that leads to the relevant cancer phenotype, as in our example of Figure 1. If the targeted therapy does not eliminate all the cancer cells (as is usually the case), the remaining cells can survive treatment through adaptive resistance mechanisms or by developing acquired resistance mechanisms, illustrated in Figure 2. Dynamic modeling can be used not only to find the most effective treatment at each stage of the cancer evolution process (Figure 2B), but also to anticipate the repertoire of oncogenic alterations relevant to a cancer type. This repertoire will be a subset of all alterations that yield an advantage to cancer cells. Discrete dynamic modeling can be used to identify all such advantageous alterations. In the example described in Figure 1 and Box 1, 3 out of 28 possible single-node alterations yield uncontrolled proliferation; we expect it is generally true that the advantageous alterations represent a small subset of all possible alterations. The empirically observed ways to escape targeted treatment seem to be an even smaller subset of the advantageous alterations; further research is needed to identify all the factors that play a role in the selection of alterations during cancer evolution. Having determined a potential repertoire of alterations represented in cancer cell subpopulations, the model can be used to devise a combinatorial treatment that is simultaneously effective for all of them, or a sequential treatment that takes them on in an optimal way, which may include driving them to apoptosis or to more benign phenotypes. While we focused on within-cell models in this review, multi-scale models, which consider the population dynamics of cancer cell subtypes [64] and the interactions among them or with surrounding healthy cells, will be most successful in predicting the most efficacious treatment strategies.
Figure 2.
Illustration of resistance mechanisms to targeted therapies and effective combinatorial treatments. (A) The identified mechanisms of resistance to targeted inhibition of signaling through an oncogene 65, 66 include the reactivation of the oncogene or of nodes that mediate its effect on a cancer phenotype, alterations that drive the same cancer phenotype through an overlapping or parallel pathway, or alterations that drive different cancer hallmark phenotypes. All of these resistance mechanisms can be mapped to relevant intra-cellular networks through systems biology methods. Panel B illustrates a network-based view of a cancer emergence, evolution and finally eradication trajectory. Cancer cells may develop adaptive (e.g. negative feedback-driven) or acquired resistance to a targeted treatment. Adaptive resistance may also aid the selection of certain alterations in the population of cancer cells. Dynamic modeling of the relevant intra-cellular networks can anticipate these resistance mechanisms and predict the most effective targeted therapy.
Conclusion
Network-based dynamic modeling has the potential to fundamentally change the way we make treatment decisions in medicine. These models can be used to understand the mechanistic effect of signals and alterations on a homeostatic process and the ways in which they can lead to disease. Importantly, the effect of inhibiting these disease-driving signals can also be modeled, aiding in identification of therapeutic interventions.
We propose that the limited current success of the initiatives to target treatment to specific genetic or expression features of cancers is a consequence of the limitations of the current methods of targeting treatments to individuals and a lack of understanding of the combined effect of oncogenic alterations on the signaling networks underlying each individual patient. An important benefit of network modeling is that it can be tailored to the individual alterations of an individual's disease, an important goal of personalized medicine. We believe that integration of molecular and genomic data 67, 68 and models at multiple scales (within-cell network models 20, 21, ∗26, 31, models of cell populations 64, 69, and clinical multivariate models 10, ∗11) is the way forward toward making optimal personalized treatment decisions.
Acknowledgements
Discrete dynamic modeling of cancer-related networks by the authors is supported by the National Science Foundation (grant PHY 1545832), the Stand Up to Cancer Foundation, and a Stand Up to Cancer Foundation/The V Foundation Convergence Scholar Award (D2015-039) to J.G.T.Z.
This review comes from a themed issue on Mathematical modelling (2018)
Edited by Leah Edelstein-Keshet and William Holmes
References
- 1.Hanahan D., Weinberg R.A. The hallmarks of cancer. Cell. 2000;100:57–70. doi: 10.1016/s0092-8674(00)81683-9. [DOI] [PubMed] [Google Scholar]
- 2.Hanahan D., Weinberg R.A. Hallmarks of cancer: the next generation. Cell. 2011;144:646–674. doi: 10.1016/j.cell.2011.02.013. [DOI] [PubMed] [Google Scholar]
- 3.Prasad V., Fojo T., Brada M. Precision oncology: origins, optimism, and potential. Lancet Oncol. 2016;17:e81–e86. doi: 10.1016/S1470-2045(15)00620-8. [DOI] [PubMed] [Google Scholar]
- 4.Letai A. Functional precision cancer medicine—moving beyond pure genomics. Nat Med. 2017;23:1028–1035. doi: 10.1038/nm.4389. [DOI] [PubMed] [Google Scholar]
- 5.Lynch T.J., Bell D.W., Sordella R., Gurubhagavatula S., Okimoto R.A., Brannigan B.W. Activating mutations in the epidermal growth factor receptor underlying responsiveness of non–small-cell lung cancer to Gefitinib. N Engl J Med. 2004;350:2129–2139. doi: 10.1056/NEJMoa040938. [DOI] [PubMed] [Google Scholar]
- 6.Maemondo M., Inoue A., Kobayashi K., Sugawara S., Oizumi S., Isobe H. Gefitinib or chemotherapy for non-small-cell lung cancer with mutated EGFR. N Engl J Med. 2010;362:2380–2388. doi: 10.1056/NEJMoa0909530. [DOI] [PubMed] [Google Scholar]
- 7.Mayekar M.K., Bivona T.G. Current landscape of targeted therapy in lung cancer. Clin Pharmacol Ther. 2017;102:757–764. doi: 10.1002/cpt.810. [DOI] [PubMed] [Google Scholar]
- 8.Masoud V., Pagès G. Targeted therapies in breast cancer: new challenges to fight against resistance. World J Clin Oncol. 2017;8:120–134. doi: 10.5306/wjco.v8.i2.120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wong D.J.L., Ribas A. Targeted therapy for melanoma. Cancer Treat Res. 2016;167:251–262. doi: 10.1007/978-3-319-22539-5_10. [DOI] [PubMed] [Google Scholar]
- 10.Maddrey W.C., Boitnott J.K., Bedine M.S., Weber F.L., Jr., Mezey E., White R.I., Jr. Corticosteroid therapy of alcoholic hepatitis. Gastroenterology. 1978;75:193–199. [PubMed] [Google Scholar]
- Ntaios G., Lip G.Y.H., Makaritsis K., Papavasileiou V., Vemmou A., Koroboki E. CHADS2, CHA2S2DS2-VASc, and long-term stroke outcome in patients without atrial fibrillation. Neurology. 2013;80:1009–1017. doi: 10.1212/WNL.0b013e318287281b. [DOI] [PubMed] [Google Scholar]; An example of a clinical multi-variate model, the CHA2S2DS2 -VASc model determines, based on age, sex, and clinical history, which patients are at highest risk of developing blood clots and which patients might benefit from receiving a blood thinner.
- 12.Lip G.Y.H., Nieuwlaat R., Pisters R., Lane D.A., Crijns H.J.G.M. Refining clinical risk stratification for predicting stroke and thromboembolism in atrial fibrillation using a novel risk factor-based approach: the euro heart survey on atrial fibrillation. Chest. 2010;137:263–272. doi: 10.1378/chest.09-1584. [DOI] [PubMed] [Google Scholar]
- 13.Kim Y., Choi S., Shin D., Cho K.-H. Quantitative evaluation and reversion analysis of the attractor landscapes of an intracellular regulatory network for colorectal cancer. BMC Syst Biol. 2017;11:45. doi: 10.1186/s12918-017-0424-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Udyavar A.R., Wooten D.J., Hoeksema M., Bansal M., Califano A., Estrada L. Novel hybrid phenotype revealed in small cell lung cancer by a transcription factor network model that can explain tumor heterogeneity. Cancer Res. 2017;77:1063–1074. doi: 10.1158/0008-5472.CAN-16-1467. [DOI] [PMC free article] [PubMed] [Google Scholar]; The authors constructed a transcription factor network model of small-cell lung cancer using a methodology combining in vitro and in vivo gene expression, transcription factor databases, and manual curation. The model predicted attractors that corresponded to the observed epithelial and mesenchymal states in small-cell lung cancer cell lines and tumors.
- 15.Módos D., Bulusu K.C., Fazekas D., Kubisch J., Brooks J., Marczell I. Neighbours of cancer-related proteins have key influence on pathogenesis and could increase the drug target space for anticancer therapies. NPJ Syst Biol Appl. 2017;3:2. doi: 10.1038/s41540-017-0003-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Li Z., Ivanov A.A., Su R., Gonzalez-Pecchi V., Qi Q., Liu S. The OncoPPi network of cancer-focused protein-protein interactions to inform biological insights and therapeutic strategies. Nat Commun. 2017;8:14356. doi: 10.1038/ncomms14356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gómez Tejeda Zañudo J., Scaltriti M., Albert R. A network modeling approach to elucidate drug resistance mechanisms and predict combinatorial drug treatments in breast cancer. Cancer Convergence. 2017;1 doi: 10.1186/s41236-017-0007-6. [DOI] [PMC free article] [PubMed] [Google Scholar]; A discrete network model of apoptosis and proliferation in estrogen-receptor-positive breast cancer built with the objective of determining resistance mechanisms to targeted drugs and effective drug combinations. The model recapitulated several drug synergies and resistance mechanisms and predicted new ones.
- 18.Tyson J.J., Chen K.C., Novak B. Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell. Curr Opin Cell Biol. 2003;15:221–231. doi: 10.1016/s0955-0674(03)00017-6. [DOI] [PubMed] [Google Scholar]
- 19.Alon U. CRC Press; 2006. An Introduction to systems biology: design principles of biological circuits. [Google Scholar]
- 20.Tyson J.J., Baumann W.T., Chen C., Verdugo A., Tavassoly I., Wang Y. Dynamic modelling of oestrogen signalling and cell fate in breast cancer cells. Nat Rev Cancer. 2011;11:523–532. doi: 10.1038/nrc3081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Iyengar R., Zhao S., Chung S.-W., Mager D.E., Gallo J.M. Merging systems biology with pharmacodynamics. Sci Transl Med. 2012;4 doi: 10.1126/scitranslmed.3003563. 126ps7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu M., Jolly M.K., Levine H., Onuchic J.N., Ben-Jacob E. MicroRNA-based regulation of epithelial-hybrid-mesenchymal fate determination. Proc Natl Acad Sci USA. 2013;110:18144–18149. doi: 10.1073/pnas.1318192110. [DOI] [PMC free article] [PubMed] [Google Scholar]; A differential equation model of the transcriptional and microRNA core of the epithelial-to-mesenchymal transition. The model predicts that this core can act as a tri-stable switch and allows for a hybrid phenotype between the epithelial and mesenchymal phenotypes.
- Zhang J., Tian X.-J., Zhang H., Teng Y., Li R., Bai F. TGF-β-induced epithelial-to-mesenchymal transition proceeds through stepwise activation of multiple feedback loops. Sci Signal. 2014;7 doi: 10.1126/scisignal.2005304. ra91. [DOI] [PubMed] [Google Scholar]; The authors use a differential equation model of the transcriptional and microRNA core of the epithelial-to-mesenchymal transition to predict that two sequential bistable switches underlie EMT, and experimentally confirm this result in cell lines at the single cell and population level.
- 24.Kraeutler M.J., Soltis A.R., Saucerman J.J. Modeling cardiac β-adrenergic signaling with normalized-Hill differential equations: comparison with a biochemical model. BMC Syst Biol. 2010;4:157. doi: 10.1186/1752-0509-4-157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Steinway S.N., Wang R.-S., Albert R. Discrete dynamic modeling: a network approach for systems pharmacology. AAPS Adv Pharm Sci Series. 2016:81–103. [Google Scholar]
- Morris M.K., Saez-Rodriguez J., Sorger P.K., Lauffenburger D.A. Logic-based models for the analysis of cell signaling networks. Biochemistry. 2010;49:3216–3224. doi: 10.1021/bi902202q. [DOI] [PMC free article] [PubMed] [Google Scholar]; This review of logic-based models in mammalian cell signaling describes qualitative and quantitative variants of logic-based models and provides case studies of how logic-based models can be used to answer biological questions.
- 27.Abou-Jaoudé W., Traynard P., Monteiro P.T., Saez-Rodriguez J., Helikar T., Thieffry D. Logical modeling and dynamical analysis of cellular networks. Front Genet. 2016;7:94. doi: 10.3389/fgene.2016.00094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wynn M.L., Consul N., Merajver S.D., Schnell S. Logic-based models in systems biology: a predictive and parameter-free network analysis method. Integr Biol. 2012;4:1323–1337. doi: 10.1039/c2ib20193c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Laubenbacher R., Hinkelmann F., Murrugarra D., Veliz-Cuba A. Algebraic models and their use in systems biology. Nat Comput Series. 2013:443–474. [Google Scholar]
- 30.Cho K.-H., Lee S., Kim D., Shin D., Joo J.I., Park S.-M. Cancer reversion, a renewed challenge in systems biology. Curr Opin Syst Biol. 2017;2:49–58. [Google Scholar]
- 31.Wang R.-S., Saadatpour A., Albert R. Boolean modeling in systems biology: an overview of methodology and applications. Phys Biol. 2012;9:055001. doi: 10.1088/1478-3975/9/5/055001. [DOI] [PubMed] [Google Scholar]
- Bloomingdale P., Nguyen V.A., Niu J., Mager D.E. Boolean network modeling in systems pharmacology. J Pharmacokinet Pharmacodyn. 2018 doi: 10.1007/s10928-017-9567-4. [DOI] [PMC free article] [PubMed] [Google Scholar]; This review describes in detail the methods used for the construction and analysis of Boolean network models, and illustrates these models' use in identifying novel drug targets and combinatorial interventions.
- 33.Glass L., Kauffman S.A. The logical analysis of continuous, non-linear biochemical control networks. J Theor Biol. 1973;39:103–129. doi: 10.1016/0022-5193(73)90208-7. [DOI] [PubMed] [Google Scholar]
- 34.Thomas R. Boolean formalization of genetic control circuits. J Theor Biol. 1973;42:563–585. doi: 10.1016/0022-5193(73)90247-6. [DOI] [PubMed] [Google Scholar]
- 35.Glass L. Classification of biological networks by their qualitative dynamics. J Theor Biol. 1975;54:85–107. doi: 10.1016/s0022-5193(75)80056-7. [DOI] [PubMed] [Google Scholar]
- 36.Kauffman S.A. Metabolic stability and epigenesis in randomly constructed genetic nets. J Theor Biol. 1969;22:437–467. doi: 10.1016/0022-5193(69)90015-0. [DOI] [PubMed] [Google Scholar]
- 37.Mendoza L., Thieffry D., Alvarez-Buylla E.R. Genetic control of flower morphogenesis in Arabidopsis thaliana: a logical analysis. Bioinformatics. 1999;15:593–606. doi: 10.1093/bioinformatics/15.7.593. [DOI] [PubMed] [Google Scholar]
- 38.Espinosa-Soto C., Padilla-Longoria P., Alvarez-Buylla E.R. A gene regulatory network model for cell-fate determination during Arabidopsis thaliana flower development that is robust and recovers experimental gene expression profiles. Plant Cell. 2004;16:2923–2939. doi: 10.1105/tpc.104.021725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sánchez L., Thieffry D. A logical analysis of the Drosophila gap-gene system. J Theor Biol. 2001;211:115–141. doi: 10.1006/jtbi.2001.2335. [DOI] [PubMed] [Google Scholar]
- 40.Albert R., Othmer H.G. The topology of the regulatory interactions predicts the expression pattern of the segment polarity genes in Drosophila melanogaster. J Theor Biol. 2003;223:1–18. doi: 10.1016/s0022-5193(03)00035-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Naldi A., Carneiro J., Chaouiya C., Thieffry D. Diversity and plasticity of Th cell types predicted from regulatory network modelling. PLoS Comput Biol. 2010;6:e1000912. doi: 10.1371/journal.pcbi.1000912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mendoza L. A network model for the control of the differentiation process in Th cells. Biosystems. 2006;84:101–114. doi: 10.1016/j.biosystems.2005.10.004. [DOI] [PubMed] [Google Scholar]
- 43.Li F., Long T., Lu Y., Ouyang Q., Tang C. The yeast cell-cycle network is robustly designed. Proc Natl Acad Sci USA. 2004;101:4781–4786. doi: 10.1073/pnas.0305937101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Huang S., Ingber D.E. Shape-dependent control of cell growth, differentiation, and apoptosis: switching between attractors in cell regulatory networks. Exp Cell Res. 2000;261:91–103. doi: 10.1006/excr.2000.5044. [DOI] [PubMed] [Google Scholar]
- 45.Li S., Assmann S.M., Albert R. Predicting essential components of signal transduction networks: a dynamic model of guard cell abscisic acid signaling. PLoS Biol. 2006;4:e312. doi: 10.1371/journal.pbio.0040312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Saez-Rodriguez J., Simeoni L., Lindquist J.A., Hemenway R., Bommhardt U., Arndt B. A logical model provides Insights into T Cell receptor signaling. PLoS Comput Biol. 2007;3:e163. doi: 10.1371/journal.pcbi.0030163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.She Q.-B., Solit D.B., Ye Q., O'Reilly K.E., Lobo J., Rosen N. The BAD protein integrates survival signaling by EGFR/MAPK and PI3K/Akt kinase pathways in PTEN-deficient tumor cells. Canc Cell. 2005;8:287–297. doi: 10.1016/j.ccr.2005.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Penuel E., Martin G.S. Transformation by v-Src: Ras-MAPK and PI3K-mTOR mediate parallel pathways. Mol Biol Cell. 1999;10:1693–1703. doi: 10.1091/mbc.10.6.1693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Campbell C., Thakar J., Albert R. Network analysis reveals cross-links of the immune pathways activated by bacteria and allergen. Phys Rev E Stat Nonlin Soft Matter Phys. 2011;84:031929. doi: 10.1103/PhysRevE.84.031929. [DOI] [PubMed] [Google Scholar]
- 50.Ikushima H., Miyazono K. Cellular context-dependent “colors” of transforming growth factor-beta signaling. Cancer Sci. 2010;101:306–312. doi: 10.1111/j.1349-7006.2009.01441.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zañudo J.G.T., Albert R. Cell fate reprogramming by control of intracellular network dynamics. PLoS Comput Biol. 2015;11:e1004193. doi: 10.1371/journal.pcbi.1004193. [DOI] [PMC free article] [PubMed] [Google Scholar]; Developed the concept of stable motifs (intersecting positive feedback loops with a specified node state) and their role in determining the attractors of a Boolean model. In the leukemia model of [53], it identified a stable motif (PDGFR, SPHK1, S1P, and Ceramide) as the key determinant of the leukemic attractor.
- 52.Zañudo J.G.T., Yang G., Albert R. Structure-based control of complex networks with nonlinear dynamics. Proc Natl Acad Sci USA. 2017;114:7234–7239. doi: 10.1073/pnas.1617387114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang R., Shah M.V., Yang J., Nyland S.B., Liu X., Yun J.K. Network model of survival signaling in large granular lymphocyte leukemia. Proc Natl Acad Sci USA. 2008;105:16308–16313. doi: 10.1073/pnas.0806447105. [DOI] [PMC free article] [PubMed] [Google Scholar]; One of the first discrete dynamic models in cancer, it predicted and experimentally validated (in blood samples from patients) several therapeutic targets whose inhibition causes apoptosis of leukemic cells.
- 54.Grieco L., Calzone L., Bernard-Pierrot I., Radvanyi F., Kahn-Perlès B., Thieffry D. Integrative modelling of the influence of MAPK network on cancer cell fate decision. PLoS Comput Biol. 2013;9:e1003286. doi: 10.1371/journal.pcbi.1003286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Sahin Ö., Fröhlich H., Löbke C., Korf U., Burmester S., Majety M. Modeling ERBB receptor-regulated G1/S transition to find novel targets for de novo trastuzumab resistance. BMC Syst Biol. 2009;3:1. doi: 10.1186/1752-0509-3-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinway S.N., Zañudo J.G.T., Ding W., Rountree C.B., Feith D.J., Loughran T.P., Jr. Network modeling of TGFβ signaling in hepatocellular carcinoma epithelial-to-mesenchymal transition reveals joint sonic hedgehog and Wnt pathway activation. Cancer Res. 2014;74:5963–5977. doi: 10.1158/0008-5472.CAN-14-0225. [DOI] [PMC free article] [PubMed] [Google Scholar]; The first discrete dynamic network model of the epithelial-to-mesenchymal transition, built in the context of hepatocellular carcinoma. It predicted that several signals and pathways can mutually activate and maintain each other and result in EMT, and experimentally confirmed this for TGFβ and the Wnt and Shh pathways.
- 57.Cohen D.P.A., Martignetti L., Robine S., Barillot E., Zinovyev A., Calzone L. Mathematical modelling of molecular pathways enabling tumour cell invasion and migration. PLoS Comput Biol. 2015;11:e1004571. doi: 10.1371/journal.pcbi.1004571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Méndez-López L.F., Davila-Velderrain J., Domínguez-Hüttinger E., Enríquez-Olguín C., Martínez-García J.C., Alvarez-Buylla E.R. Gene regulatory network underlying the immortalization of epithelial cells. BMC Syst Biol. 2017;11:24. doi: 10.1186/s12918-017-0393-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Chudasama V.L., Ovacik M.A., Abernethy D.R., Mager D.E. Logic-based and cellular pharmacodynamic modeling of Bortezomib responses in U266 human myeloma cells. J Pharmacol Exp Ther. 2015;354:448–458. doi: 10.1124/jpet.115.224766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saez-Rodriguez J., Alexopoulos L.G., Epperlein J., Samaga R., Lauffenburger D.A., Klamt S. Discrete logic modelling as a means to link protein signalling networks with functional analysis of mammalian signal transduction. Mol Syst Biol. 2009;5:331. doi: 10.1038/msb.2009.87. [DOI] [PMC free article] [PubMed] [Google Scholar]; The authors propose an innovative method to integrate an initial network with phospho-proteomics information to develop a parsimonious model. Application of this method to hepatocellular carcinoma predicted interactions in the initial database-derived network that are not functional in this context, as well as new interactions.
- Khan F.M., Marquardt S., Gupta S.K., Knoll S., Schmitz U., Spitschak A. Unraveling a tumor type-specific regulatory core underlying E2F1-mediated epithelial-mesenchymal transition to predict receptor protein signatures. Nat Commun. 2017;8:198. doi: 10.1038/s41467-017-00268-2. [DOI] [PMC free article] [PubMed] [Google Scholar]; The authors developed an algorithm to construct a network model based on an interaction map of the process of interest (E2F1-mediated EMT) and selecting genes according to a metric combining biological and network criteria. They model predicted and validated alterations with aggressive phenotypes in bladder and breast cancer.
- 62.Steinway S.N., Zañudo J.G.T., Michel P.J., Feith D.J., Loughran T.P., Albert R. Combinatorial interventions inhibit TGFβ-driven epithelial-to-mesenchymal transition and support hybrid cellular phenotypes. NPJ Syst Biol Appl. 2015;1 doi: 10.1038/npjsba.2015.14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jolly M.K., Levine H. Computational systems biology of epithelial-hybrid-mesenchymal transitions. Curr Opin Syst Biol. 2017;3:1–6. [Google Scholar]; A review of systems and computational biology work on the epithelial-to-mesenchymal transition, encompassing both quantitative and qualitative mechanistic “bottom-up” models, and data-driven “top-down” models.
- 64.Komarova N.L., Wodarz D. Springer Science & Business Media; 2013. Targeted cancer treatment in Silico: small molecule inhibitors and oncolytic viruses. [Google Scholar]
- 65.Wagle N., Emery C., Berger M.F., Davis M.J., Sawyer A., Pochanard P. Dissecting therapeutic resistance to RAF inhibition in melanoma by tumor genomic profiling. J Clin Oncol. 2011;29:3085–3096. doi: 10.1200/JCO.2010.33.2312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Garraway L.A., Jänne P.A. Circumventing cancer drug resistance in the era of personalized medicine. Cancer Discov. 2012;2:214–226. doi: 10.1158/2159-8290.CD-12-0012. [DOI] [PubMed] [Google Scholar]
- 67.Malod-Dognin N., Petschnigg J., Pržulj N. Precision medicine ― A promising, yet challenging road lies ahead. Current Opinion in Systems Biology. 2018;7:1–7. [Google Scholar]
- 68.Kristensen V.N., Lingjærde O.C., Russnes H.G., Vollan H.K.M., Frigessi A., Børresen-Dale A.-L. Principles and methods of integrative genomic analyses in cancer. Nat Rev Cancer. 2014;14:299–313. doi: 10.1038/nrc3721. [DOI] [PubMed] [Google Scholar]
- 69.Altrock P.M., Liu L.L., Michor F. The mathematics of cancer: integrating quantitative models. Nat Rev Cancer. 2015;15:730–745. doi: 10.1038/nrc4029. [DOI] [PubMed] [Google Scholar]