Turgor-driven plant growth applied in a soybean functional–structural plant model

Abstract

Background and Aims

Turgor pressure within a plant cell represents the key to the mechanistical descriptiion of plant growth, combining the effects of both water and carbon availability. The high level of spatio-temporal variation and diurnal dynamics in turgor pressure within a single plant make it a challenge to model these on the fine spatial scale required for functional–structural plant models (FSPMs). A conceptual model for turgor-driven growth in FSPMs has been established previously, but its practical use has not yet been explored.

Methods

A turgor-driven growth model was incorporated in a newly established FSPM for soybean. The FSPM simulates dynamics in photosynthesis, transpiration and turgor pressure in direct relation to plant growth. Comparisons of simulations with field data were used to evaluate the potential and shortcomings of the modelling approach.

Key Results

Model simulations revealed the need to include an initial seed carbon contribution, a more realistic sink function, an estimation of respiration, and the distinction between osmotic and structural sugars, in order to achieve a realistic model of plant growth. However, differences between simulations and observations remained in individual organ growth patterns and under different environmental conditions. This exposed the need to further investigate the assumptions of developmental and environmental (in)sensitivity of the parameters, which represent physiological and biophysical organ properties in the model, in future research.

Conclusions

The model in its current form is primarily a diagnostic tool, to better understand and model the behaviour of water relations on the scale of individual plant organs throughout the plant life cycle. Potential future applications include its use as a phenotyping tool to capture differences in plant performance between genotypes and growing environments in terms of specific plant characteristics. Additionally, focused experiments can be used to further improve the model mechanisms to lead to better predictive FSPMs, including scenarios of water deficit.

INTRODUCTION

The function of water in driving plant growth is often under-represented in models, whether it be large-scale global vegetation models, or small-scale plant models such as functional–structural plant models (FSPMs). The historic availability and ease of use of measurement and modelling tools for source-related processes such as photosynthesis have led to an uneven representation in modelling complexity, where sink-related controls are often minimized or ignored entirely (Körner, 2015; Fatichi et al., 2019). In the last two decades, a prevailing sentiment is arising that incorporation of sink controls is essential for moving forward in growth models across all spatial scales (Fatichi et al., 2014; Steppe et al., 2015a; Fatichi et al., 2019). The incorporation of realistic water fluxes plays a fundamental role in achieving mechanistic sink control, as water availability is more directly linked to plant growth than photosynthetic activity (Boyer, 1970; Muller et al., 2011; Steppe et al., 2016) due to its role in controlling turgor pressure in plant cells (Lockhart, 1965).

The link between turgor pressure and plant growth has already been successfully demonstrated in relation to model stem diameter variations and fruit growth (Génard et al., 2001; Steppe et al., 2006, 2015a; De Swaef et al., 2015) and has been applied to a variety of plant and tree species [e.g. tomato (De Swaef and Steppe, 2010), oak and beech (De Schepper and Steppe, 2010), peach (De Swaef et al., 2014), grape (Baert and Steppe, 2017) and the mangrove species Avicennia marina (Steppe et al., 2018)]. The incorporation of this direct link between turgor pressure and plant growth is still missing in FSPMs; however, a theoretical framework for their incorporation has recently been suggested (Coussement et al., 2018a). FSPMs distinguish themselves by including a realistic 3D structural component in plant models. As a result, they are able to operate on a fine spatial scale, where, for example, each plant organ is an individual functional unit. Incorporation of plant–water relations therefore also requires the solving of flow equations on the same spatial scale, which can lead to complex hydraulic networks. While this adds considerable modelling complexity and computational cost as opposed to the more prevalent carbon-driven approach in functional–structural plant modelling, it is a necessary step towards a more mechanistic description of plant growth and the performance of FSPMs under a wider range of environments. Additionally, such a model relates growth to biochemical cell wall properties, which can be linked to genotypic differences between varieties. As a result, incorporation of turgor-driven growth is a crucial requirement to improve FSPM suitability in plant phenotyping and breeding, as more realistic and stable virtual genotypes can be generated to be evaluated in virtual environments.

Before such goals can be achieved, however, it is paramount that the integration of turgor driven-growth in an FSPM leads to realistic simulated plant growth when compared with observed patterns of plant growth. This validation is important even under well-watered conditions, as unfavourable turgor pressure constraining plant growth occurs on a daily basis due to transpirational water losses. Realistic conditions were not evaluated in the conceptual framework of Coussement et al. (2018a), where turgor-driven growth was modelled using several theoretical inputs and an arbitrary 3D structure. Therefore, in this paper the turgor-driven growth concept was incorporated in a new soybean (Glycine max ‘Adsoy’) FSPM equipped with a realistic light model and a coupled photosynthesis, stomatal conductance and transpiration model. The model was then evaluated in its potential to simulate the effect of different planting densities, which heavily affects the patterns of photosynthesis and transpiration, on plant growth.

It is the goal of this paper to explore these innovative model dynamics under realistic conditions to gain insight into the validity of the turgor-driven growth concept as well as the potential to describe plant growth as a function of parameters representing direct biochemical cell wall properties. To do so, (1) model simulations were compared with observations to improve the original concept assumptions, (2) the environmental (in)sensitivity of the parameters was evaluated by conducting virtual simulations with identical parameter sets under different growing conditions, and (3) local sensitivities of model outputs to the model parameters and inputs were explored. Furthermore, the current possibilities and shortcomings of the model are discussed as well as future perspectives on the turgor-driven modelling approach as a whole.

MATERIALS AND METHODS

Experimental description and data processing

A total of three soybean field trials with the same cultivar (‘Adsoy’) were conducted in the growing seasons of 2015, 2016 and 2017. For model calibration, spatio-temporal series of plant architecture, dry matter and leaf chlorophyll content were obtained during a field trial in 2015. Additionally, a field trial in 2017 was used to link measurements of leaf chlorophyll content index (CCI) to leaf spectral characteristics (method in Coussement et al., 2018b) and photosynthesis. For model validation, the final architecture and dry matter distribution in three different planting densities were evaluated in the 2016 growing season. The field trials are described in more detail in Supplementary Data S1 and are further referred to by year. Environmental data for all years were not directly measured but taken from a nearby weather station in Melle (50°58′47.7ʺ N, 3°49′9.25ʺ E). These data included daily measurements of minimum and maximum temperatures, the daily sum of incoming short-wave radiation and mean relative humidity.

The spatio-temporal discrete data obtained during the 2015 trial was used to first create a continuous descriptive model for soybean to gain insight into the temporal evolution of variables that are difficult to measure, such as whole-plant photosynthesis Supplementary Data S2. To do so, growth curves from Yin et al. (2003) were fitted to the architectural data to represent individual plant organ dimensions in terms of thermal time. These growth curves describe the progression of the organ dimension in terms of parameters related to the timing of their growth (i.e. ${\mathrm{t}}_{\mathrm{m}}$ and ${\mathrm{t}}_{\mathrm{e}}$), with ${\mathrm{t}}_{\mathrm{m}}$ representing the thermal time at which an organ reaches half its maximal size and ${\mathrm{t}}_{\mathrm{e}}$ the thermal time at which an organ is fully grown. The thermal time between the development of consecutive phytomers was modelled as a constant value (i.e. the phyllochron, PHYLLO) as is often done in developmental models (Evers et al., 2005; Watanabe et al., 2005). Modelling the spatio-temporal evolution of leaf CCI was done using an adapted curve of relative growth rate as a function of both thermal leaf age and thermal plant age (Supplementary Data S2). Internodes and petioles were approximated using cylinders, while leaflet shapes were determined by fitting a leaf shape function (Coussement et al., 2018c) to a dataset of dissected leaflet scans (Supplementary Data S2) and modelled using meshes.

The light response curves obtained during the 2017 experiment were used to calibrate the coupled photosynthesis–stomatal conductance–transpiration (P-SC-T) model of Kim and Lieth (2003). The Kim–Lieth model combines the biochemical C3 photosynthesis model of Farquhar, von Caemmerer and Berry (FvCB model, Farquhar et al., 1980), the stomatal conductance model of Ball, Woodrow and Berry (BWB model, Ball et al., 1987) and an energy balance model (Campbell and Norman, 1998). The model thus couples well-established mechanistic models taking into account biochemical photosynthetic limitations as well as stomatal limitations on CO₂ supply. The energy balance model is used to estimate leaf temperature and transpiration as a function of environmental variables, stomatal conductance and boundary layer resistance. The Kim–Lieth model additionally adds photosynthetic restraints based on leaf age, a variable that was not measured when photosynthesis measurements were obtained. As a workaround, the leaf age parameter (f_age) was linked to leaf CCI based on the observations that leaf CCI was correlated with the thermal leaf age. A second adaptation was made to replace the use of a fixed parameter that represents the percentage of non-absorbed photosynthetically active radiation (PAR). This parameter was made dependent upon the actual leaf spectral characteristics calculated using the CCI and the PROSPECT-D model (Coussement et al., 2018b). A final adaptation was made of the parameter for residual stomatal conductance in the absence of light. In the Kim–Lieth model this is represented as a fixed value; however, we found it to be dependent upon the leaf age parameter. These adaptations are described in more detail in Supplementary Data S3.

The descriptive model with the calibrated P-SC-T model was then implemented in the GroIMP modelling platform (Kniemeyer et al., 2007). The observed daily environmental variables were converted to hourly values for simulation. The data regarding daily radiation sum were first used to make a theoretical calculation to establish a fixed degree of daily cloud cover, necessary to differentiate the fraction of direct and diffuse radiation at any given day (Spitters et al., 1986). Then, these data were split across daylight hours, based on the theoretical distribution of sunlight for a given day (Spitters et al., 1986) and the position of the sun in the light model was updated to correspond to the correct hour of the day. The diffuse light sources in the model were approximated using a dome of 72 directional light sources (Evers et al., 2007; Buck-Sorlin et al., 2011) while the direct light sources were set at 5-min intervals within the 1-h windows (adapted from Evers et al., 2010). The irradiance distribution also related to the daily behaviour of temperature and relative humidity as no data were available at a higher temporal resolution. Using daily values of ${\mathrm{T}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ and ${\mathrm{T}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$, the time of ${\mathrm{T}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ corresponds to the time of sunrise and ${\mathrm{T}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ was assumed to occur 2 h after maximum solar radiation (Chow and Levermore, 2007). This behaviour was modelled using the Sin (14R-1) method (Chow and Levermore, 2007). Modelling of the relative humidity was done based on the calculated hourly values of temperature using the minimal method (Waichler and Wigmosta, 2003) as no more accurate data were available. A simulation of this descriptive model was then conducted over the course of the entire growing season to obtain insight into the continuous evolution of whole-plant photosynthesis, sink strength distribution and plant volume.

Model description

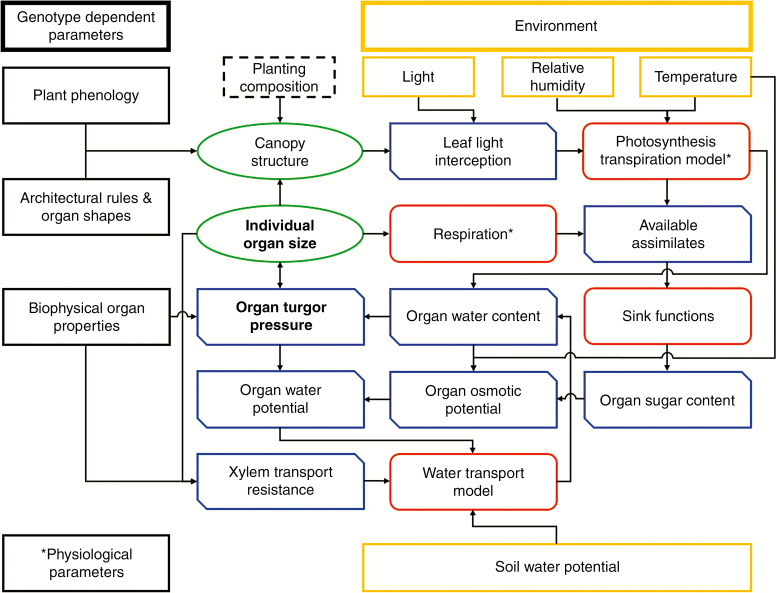
The turgor-driven growth model (Coussement et al., 2018a; summary given in Box A) was integrated in the descriptive soybean FSPM. Concretely, this means that the timeframes of plant development obtained from fitting growth curves to the data (i.e. t_m, t_e, PHYLLO) remain as independent parameters, but the growth rate (i.e. the change in organ volume) and final organ size were deduced from the complex interactions between environment, plant morphology, plant carbon and plant water status. Rather than a theoretical input function used in the conceptual turgor-driven growth model (Coussement et al., 2018a), photosynthesis and transpiration were realistically modelled with the combined P-SC-T model based on light interception. The carbohydrates obtained from photosynthesis are then distributed among the growing plant organs based on their individual relative sink strengths (see below). Alongside changes in water content due to transpiration and sap flow, the osmotic potential and turgor potential in each plant organ can be evaluated; the latter of these results in irreversible changes in organ volume (i.e. growth) when turgor is favourable. Seed development is established at a fixed thermal plant age throughout the entire plant, corresponding to observations in the field. Several adaptations, which are explained in detail below, were made to the conceptual turgor-driven growth model with the goal of improving model performance and realism. A complete overview of the model and the interactions between model components are given in Fig. 1.

BOX A: THE THEORETICAL TURGOR-DRIVEN GROWTH (SUB-)MODEL SUMMARIZED.

The conceptual turgor-driven growth model introduced by Coussement et al., 2018a is based on the flow- and storage model by Steppe et al., 2006. Water flow (${\mathrm{F}}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}(\mathrm{i})}$) is driven in the model by the hydraulic system approach (Darcy’s law):

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{F}}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}(\mathrm{i})}=\frac{{\mathrm{\psi }}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}(\mathrm{i}-1)}-{\mathrm{\psi }}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}(\mathrm{i})}}{{\mathrm{R}}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}(\mathrm{i}-1)\to \mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}(\mathrm{i})}^{\mathrm{x}}}}\end{array}}$$

and is thus defined as the difference in water potential (${\mathrm{\psi }}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}$) between two neighbouring organs ($\mathrm{i}-1;\mathrm{i}$) taking account the flow resistance $\left({\mathrm{R}}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}(\mathrm{i}-1)\to \mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}(\mathrm{i})}^{\mathrm{x}}\right)$ between the two organs, which, in turn, depends on the travelling distance and the cross-sectional area between those organs.

Knowledge of the internal flows of water, alongside knowledge of leaf transpiration (${\mathrm{E}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}$) allows evaluation of the overall change in internally stored water in each element (${\mathrm{W}}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}$):

$${\displaystyle \begin{array}{l}{\displaystyle \frac{\mathrm{d}{\mathrm{W}}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}(\mathrm{i})}}{\mathrm{d}\mathrm{t}}={\mathrm{F}}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}(\mathrm{i})}-\sum {\mathrm{F}}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}(\mathrm{i}+1)}}\end{array}}$$

$${\displaystyle \begin{array}{l}{\displaystyle \frac{\mathrm{d}{\mathrm{W}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}}{\mathrm{d}\mathrm{t}}={\mathrm{F}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}-{\mathrm{E}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}}\end{array}}$$

With flows going from an internode to any number of higher-positioned organs (i.e., internodes, petioles), water flowing through petioles to leaves, and through leaves supplying transpiration.

The change in organ volume (${\mathrm{V}}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}$) associated with this change in internally stored water is approximated by using the density of water (${\mathrm{\rho }}_{\mathrm{w}}$):

$${\displaystyle \begin{array}{l}{\displaystyle \frac{\mathrm{d}{\mathrm{W}}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}{\mathrm{d}\mathrm{t}}={\mathrm{\rho }}_{\mathrm{w}}\left(\frac{\mathrm{d}{\mathrm{V}}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}{\mathrm{d}\mathrm{t}}\right)}\end{array}}$$

As plant volumes are considered in three dimensions, this change in organ volume will not be uniform. This non-uniform volume change was achieved by decomposing the plant volume into its specific dimensions, and applying the Lockhart (1965) equation on each dimensional component. Using the derivation from Coussement et al., 2018a, this allows an evaluation of the change in turgor pressure in each plant organ:

$${\displaystyle \begin{array}{ll}{\displaystyle \frac{\mathrm{d}{\mathrm{\psi }}_{\mathrm{p},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}{\mathrm{d}\mathrm{t}}=}& [\frac{1}{{\mathrm{\rho }}_{\mathrm{w}}{\mathrm{V}}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}\frac{\mathrm{d}{\mathrm{W}}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}{\mathrm{d}\mathrm{t}}-({\varphi }_{\mathrm{z},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}+{\varphi }_{\mathrm{x},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}+{\varphi }_{\mathrm{y},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}})\\ & (\mathrm{m}\mathrm{a}\mathrm{x}({\mathrm{\psi }}_{\mathrm{p},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}},\mathrm{\Gamma })-\mathrm{\Gamma })\\ & \ast \left(\frac{{\epsilon }_{\mathrm{z},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}{\epsilon }_{\mathrm{x},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}{\epsilon }_{\mathrm{y},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}{{\epsilon }_{\mathrm{z},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}{\epsilon }_{\mathrm{x},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}+{\epsilon }_{\mathrm{z},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}{\epsilon }_{\mathrm{y},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}+{\epsilon }_{\mathrm{x},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}{\epsilon }_{\mathrm{y},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}\right)]\end{array}}$$

where dimension-specific extensibilities (${\varphi }_{\mathrm{z},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}};{\varphi }_{\mathrm{x},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}};{\varphi }_{\mathrm{y},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}$) and elasticities (${\epsilon }_{\mathrm{z},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}};{\epsilon }_{\mathrm{x},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}};{\epsilon }_{\mathrm{y},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}$) determine the differences in cell wall properties in the different dimensions. A uniform threshold turgor ($\mathrm{\Gamma }$) is also defined as the minimal turgor required for irreversible growth.

The osmotic potential (${\mathrm{\psi }}_{\mathrm{o},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}$) of each plant organ is evaluated by the total amount of soluble sugar (${\mathrm{m}}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}$; driven by photosynthesis, source-sink relations, and ratio structural/soluble sugars) and water in the storage compartment of the organ (${\mathrm{V}}_{{}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}^{\mathrm{s}}$):

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{\psi }}_{\mathrm{o},\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}=-\mathrm{R}\mathrm{T}\frac{{\mathrm{m}}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}{{\mathrm{V}}_{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}^{\mathrm{s}}{\mathrm{M}}_{\mathrm{s}\mathrm{u}\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{e}}}}\end{array}}$$

With R the universal gas constant, T the organ temperature, and ${\mathrm{M}}_{\mathrm{s}\mathrm{u}\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{e}}$ the molar mass of sucrose. As both osmotic and turgor pressure are now known, this allows the change in organ water potentials, and thus, the water flow, to be updated.

Fig. 1.

Schematic build-up of the full turgor-driven growth FSPM containing all the interactions and influences within the model. The model is driven by an independently acting environment (yellow), fixed genotype-dependent parameters (black) and the planting composition (dashed). Internally, the plant/canopy structure (green) is interwoven with the plants functioning affecting, and being affected by, various plant variables (blue) and sub-models (orange). Due to the complexity of the feedback loops within this system, plant morphology is considered fixed at the start of each (hourly) simulation step for the purpose of independently calculating respiration, photosynthesis, transpiration and xylem transport resistance. These values are then used to dynamically calculate water transport and turgor-driven growth. At the end of the simulation step, individual organ sizes are then updated, in turn changing canopy structure. Such an approach vastly increased model stability and performance as it removed some of the inherent dependencies of the model and allowed a single light model calculation per time step.

3D plant structure

The structural component of the model was considerably more complex than the theoretical model (Coussement et al., 2018a), which considered solely a linear series of phytomers. In the soybean model, branching was introduced and leaves were modelled as trifoliate leaflets, which added considerable complexity by increasing the number of equations to solve. To increase model performance without compromising accuracy, trifoliate leaves were considered as a single unit for the water transport equations (Supplementary Data S4). Below-ground development and interactions between soil and roots were not yet included in the model. Instead, a fixed root water potential is used and root growth is not considered.

Radial stem growth

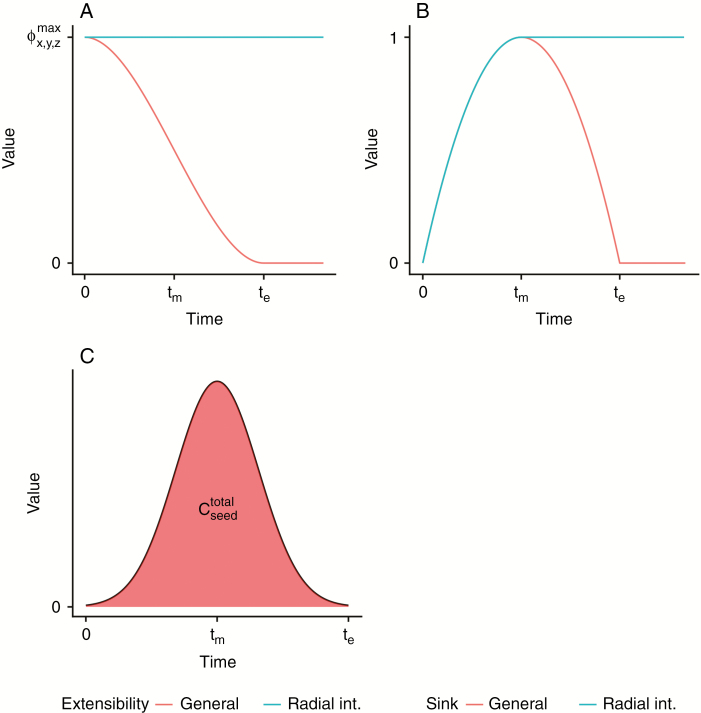
The theoretical model assumed a uniform formulation for the evolution of extensibility within a plant organ, where extensibility was maximal at organ initiation and decreased with organ age to reach zero at organ maturity. This formulation is consistent with experimental observations of internode elongation (e.g. Nonami and Boyer, 1990b for soybean) but not for the radial internode growth, which does not cease simultaneously with elongation. Rather, (secondary) radial growth in soybean can continue even during generative growth (Alerding et al., 2018). Therefore, the extensibility of the radial direction of the internodes was defined to remain constant (Fig. 2A).

Fig. 2.

Theoretical functions of temporal evolution of organ extensibility, sink strength and seed assimilate contribution. (A) Organ extensibility is defined as maximal at organ initiation with a gradual decrease to zero at the end of organ growth. This definition is identical to the one in the theoretical model (Coussement et al., 2018a) and agrees with experimental observations (e.g. Nonami and Boyer, 1990b for soybean). Radial internode growth is defined so that (secondary) radial stem growth continues throughout plant development. (B) Scale factor for the sink function of the plant organ gradually increases to a maximal value and decreases towards organ maturity (eqn 3 with fixed ${\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}$). As a result, the timing of the highest sink strength overlaps with the timing of the highest relative growth rate. Sink strength of the radial internodes remains constant after reaching its highest value to maintain sugar supply for radial stem growth (eqn 5). Note that the true sink function of the plant organ also depends on the temporal evolution of ${\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}$, which is linked to volumetric extensibility. (C) Seed assimilate contribution totals to ${\mathrm{C}}_{\mathrm{s}\mathrm{e}\mathrm{e}\mathrm{d}}^{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}$, which is the total area under the curve between 0 and t_e (eqn 6).

Seed development

A similar approach was taken to modelling the seed development. In this model, it was decided to approach seed development as a simple carbon sink rather than implementing the turgor-driven growth approach that is taken in other plant organs. This is because seed development occurs throughout the plant and would considerably influence model performance through an increase in complexity of the plant organ network. Therefore, we considered total seed carbon content (dry weight) as the primary output variable rather than individual seed size. While this decision was made with regard to the modelling goals, it does not exclude the possibility of fruit growth in future models. Therefore, seed sink strength was modelled with a single variable representing relative sink strength.

Carbon balance: structural biomass, respiration, sink strength and seed assimilate contribution

The conceptual model (Coussement et al., 2018a) did not incorporate structural biomass and considered all carbon supply to be in the form of sucrose and to be osmotically contributing to the water potential of the plant organ. Realistically, some of the sugar imported into the growing plant organ is used to create structural biomass, which does not contribute to the osmotic potential. By not considering this distinction in the model, the osmotic response of a plant organ to an increase in sugar content was overstated. In turn, this resulted in an exaggerated change in turgor and consequently plant growth (an example of the magnitude of this simplification is shown in Supplementary Data S5). As a result, sugar supply was split into a fixed structural fraction and an osmotic fraction depending on the measured mean density (i.e. dry matter content per plant volume) of each organ type (i.e. petiole, internode, leaf) by simply attributing the appropriate fraction of the total sugar content to be contributing to the osmotic potential (see also Box A).

The absence of high-resolution spatio-temporal data regarding plant carbon cycling made it unfeasible to mechanistically integrate respiration, carbon storage and translocation. However, as respiration accounts for a significant loss of available carbon, a simple empirical function was introduced to indirectly capture this. Within this function, respiration depends on total plant volume (in direct relation to plant biomass), including a linear decrease in terms of thermal plant age. This linear decrease is necessary to capture the additional source of carbon supply that is not considered in the model, being carbon translocation of senescent leaves and petioles towards the seeds (Benner and Noodén, 1984; Htwe et al., 2011). This additional supply is closely linked to generative carbon demand. In fact, depodding of soybean leads to suppression of leaf senescence (Htwe et al., 2011). As a result, carbon translocation from leaves is expected to increase as generative demand grows with increasing plant age, a mechanism that is not yet included in the model. Therefore, the combined effect of carbon translocation growth and maintenance respiration [GMR (g sucrose)] was modelled as:

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{G}\mathrm{M}\mathrm{R}={\mathrm{a}}_{\mathrm{G}\mathrm{M}\mathrm{R}}\mathrm{D}{\mathrm{W}}_{\mathrm{i}\mathrm{n}\mathrm{t}+\mathrm{p}\mathrm{e}\mathrm{t}+\mathrm{s}\mathrm{e}\mathrm{e}\mathrm{d}}}\end{array}}$$ (1)

where the magnitude of respiration was linked to the total dry weight of internodes, petioles and seeds [$\mathrm{D}{\mathrm{W}}_{\mathrm{i}\mathrm{n}\mathrm{t}+\mathrm{p}\mathrm{e}\mathrm{t}+\mathrm{s}\mathrm{e}\mathrm{e}\mathrm{d}}$ (g dry matter)], as leaf respiration was already considered in the P-SC-T model. The reduction term a_GMR was modelled as a function of plant age (t^plant), with ${\mathrm{t}}_{\mathrm{e}}^{\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{t}}$ the thermal time at plant maturity:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{t}}^{\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{t}}\le {\mathrm{t}}_{\mathrm{e}}^{\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{t}}}\end{array}}$$

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{a}}_{\mathrm{G}\mathrm{M}\mathrm{R}}=\mathrm{G}\mathrm{M}{\mathrm{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}}(1-\frac{{\mathrm{t}}^{\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{t}}}{{\mathrm{t}}_{\mathrm{e}}^{\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{t}}})}\end{array}}$$ (2)

where $\mathrm{G}\mathrm{M}{\mathrm{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ [g sucrose g⁻¹ dry matter] represents the maximum relative respiration cost for daylight hours.

The sink functions were changed from those in the theoretical model (Coussement et al., 2018a), where the relative sink strength of the different organ types depended on their extensibility. However, as extensibility is maximal at organ initiation, this meant that initially very small organs immediately demanded a disproportionate amount of assimilates compared with their organ size. This created large spikes in osmotic potential and turgor potential in the model, and resulted in a growth pattern that deviated from observations (i.e. fast initial growth spike followed by a period of slow growth as opposed to a logistic growth pattern). Therefore, the absolute sink strength (${\mathrm{P}}_{\mathrm{a}\mathrm{b}\mathrm{s}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}$) was defined to be minimal at organ initiation, and to follow the pattern of a relative growth function corresponding to the observed patterns of logistic growth in a plant organ (Yin et al., 2003, Fig. 2B)

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{t}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}\le {\mathrm{t}}_{\mathrm{e}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}\end{array}}$$

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{P}}_{\mathrm{a}\mathrm{b}\mathrm{s}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}={\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}\left(\frac{{\mathrm{t}}_{\mathrm{e}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}-{\mathrm{t}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}{{\mathrm{t}}_{\mathrm{e}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}-{\mathrm{t}}_{\mathrm{m}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}\right){\left(\frac{{\mathrm{t}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}{{\mathrm{t}}_{\mathrm{m}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}\right)}^{\frac{{\mathrm{t}}_{\mathrm{m}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}{{\mathrm{t}}_{\mathrm{e}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}-{\mathrm{t}}_{\mathrm{m}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}}}\end{array}}$$ (3)

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{t}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}>{\mathrm{t}}_{\mathrm{e}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}\end{array}}$$

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{P}}_{\mathrm{a}\mathrm{b}\mathrm{s}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}=0}\end{array}}$$

with the maximal absolute sink strength (${\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}$) being a fixed value per organ type and sink strength being zero at organ initiation and organ age (${\mathrm{t}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}$) equal to or larger than the thermal time of organ maturity (${\mathrm{t}}_{\mathrm{e}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}$). Absolute sink strength is maximal at the time the organ reaches half of its final size (${\mathrm{t}}_{\mathrm{m}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}$).

The relative sink strength of each plant organ was still given by:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{P}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}=\frac{{\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{P}}_{\mathrm{a}\mathrm{b}\mathrm{s}}^{\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{a}\mathrm{n}}}}\end{array}}$$ (4)

The result of this change is that the sink function is defined similarly to a classical source-sink model for plant growth.

For radial internode growth, which continues over the entire course of plant development, an adjusted version of eqn (3) that maintains maximal sink strength was used:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{t}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}\le {\mathrm{t}}_{\mathrm{m}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}}\end{array}}$$

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{P}}_{\mathrm{a}\mathrm{b}\mathrm{s}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}={\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}\left(\frac{{\mathrm{t}}_{\mathrm{e}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}-{\mathrm{t}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}}{{\mathrm{t}}_{\mathrm{e}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}-{\mathrm{t}}_{\mathrm{m}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}}\right){\left(\frac{{\mathrm{t}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}}{{\mathrm{t}}_{\mathrm{m}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}}\right)}^{\frac{{\mathrm{t}}_{\mathrm{m}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}}{{\mathrm{t}}_{\mathrm{e}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}-{\mathrm{t}}_{\mathrm{m}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}}}}\end{array}}$$ (5)

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{t}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}>{\mathrm{t}}_{\mathrm{m}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}}\end{array}}$$

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{P}}_{\mathrm{a}\mathrm{b}\mathrm{s}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}={\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{x},\mathrm{i}\mathrm{n}\mathrm{t}}}\end{array}}$$

where the superscript x,int indicates that these functions are specific to the radial internode growth.

After introducing these new elements in the model, preliminary model simulations revealed problems for the virtual plant in establishing enough initial leaf area (and therefore an adequate photosynthetic assimilate supply) to flourish, regardless of the model parameters. This indicated a need to introduce a contribution of sucrose from the seed to provide an initial source of sugars to initial plant growth at early developmental stages. This required a function to facilitate the gradual release of sucrose into the plant. Therefore, a Gaussian function is suggested (eqn 6) as an empirical replacement of realistic seed sucrose supply (Fig. 2C):

$${\text{t}}^{\text{plant}}\le {\text{t}}_e^{\text{seed}}{\text{C}}_{\text{plant}}^{\text{net}}={\displaystyle \sum {\text{P}}_n+}{\text{C}}_{\text{seed}}^{\text{total}}\left(\frac{\Delta {\text{t}}_{\text{step}}}{\sqrt{2\pi {\text{a}}_{\text{seed}}}}\text{e-}\frac{\left({\text{t}}_{\text{plant}}-\frac{{\text{t}}_e^{\text{seed}}}{2}\right)}{2^{{\text{a}}_{\text{seed}}}}\right){\text{t}}^{\text{plant}}{\text{>t}}_{\text{e}}^{\text{seed}}{\text{C}}_{\text{plant}}^{\text{net}}={\displaystyle \sum {\text{P}}_n}$$ (6)

This function describes the total supply of assimilates (${\mathrm{C}}_{\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{t}}^{\mathrm{n}\mathrm{e}\mathrm{t}}$ [g sucrose]) at any time step as the sum of net photosynthesis across all leaves ($\sum {\mathrm{P}}_{\mathrm{n}}$, [g sucrose]) and the seed sucrose contribution, which continues up to ${\mathrm{t}}_{\mathrm{e}}^{\mathrm{s}\mathrm{e}\mathrm{e}\mathrm{d}}$. For the latter, the use of a Gaussian function was chosen so that the area under the curve could be guaranteed to be equal to 1. As a result, a parameter (${\mathrm{C}}_{\mathrm{s}\mathrm{e}\mathrm{e}\mathrm{d}}^{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}\left[{\mathrm{g}}_{\mathrm{s}\mathrm{u}\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{e}}\right]$) could be chosen to set the total seed sucrose contribution. The function contributes sucrose at a gradually increasing rate, reaching its maximal contribution at half of ${\mathrm{t}}_{\mathrm{e}}^{\mathrm{s}\mathrm{e}\mathrm{e}\mathrm{d}}$ after which a mirrored decrease occurs. The dimensionless empirical parameter ${\mathrm{a}}_{\mathrm{s}\mathrm{e}\mathrm{e}\mathrm{d}}$ determines the slope of the increase and decrease (i.e. the variance of the Gaussian function). Step size is $\mathrm{\Delta }{\mathrm{t}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}$ (in thermal time). A summary of the shapes of the temporal functions for the extensibility, absolute sink strength and seed assimilate contribution for a single plant organ is given in Fig. 2.

Computational efficiency

The large number of feedback loops within the model structure (Fig. 1) creates a computationally complex system. As individual organ size influences many of the model variables (i.e. photosynthesis, transpiration, respiration and transport resistance) and has a feedback effect on turgor pressure, dynamically solving all of these interactions becomes unnecessarily complex and computationally intensive. While the interaction between organ size and turgor pressure is fundamental, it can be assumed that within the timespan of a single step (i.e. 1 h) the effect of changes in organ size on the other model variables is negligible. As a result, the system of differential and algebraic equations that needs to be solved for the turgor-driven growth sub-model is greatly simplified. This represents a drastic improvement in model stability and computational speed.

Due to the complexity of the model architecture and its effect on model performance, it was opted to simulate a single soybean plant with the turgor-driven growth model. As this would yield unrealistic results with regard to light interception and mutual shading in a realistic soybean canopy, the function GridClonerNode() from GroIMP was used to simulate a canopy of 25 × 25 identical plants. GridClonerNode provides identical copies of the simulated plant for the purpose of light modelling, without the corresponding computational cost of simulating plant growth in each of these clones.

Model calibration

The inherent complexity of FSPMs makes a global optimization of the model parameters a challenging task (Lin et al., 2012). One of the more prominent approaches to calibrating FSPMs is to combine the use of experimental data, independent parameterization of sub-models, and parameter values derived from literature (Evers et al., 2018). This strategy was also applied to deal with the complexity of the soybean model and therefore several sub-models of the FSPM were considered independently for model calibration. As stated earlier, the parameters related to plant phenology, timing of organogenesis and time-dependence of leaf CCI were taken from calibration with data from the 2015 field trial (Supplementary Data S2). The relationships between leaf CCI, light absorption, reflection and transmission, and photosynthesis were separately calibrated based on the 2017 trial. The remaining parameters relate to the turgor-driven growth model, for which a combination of literature values and manual fine-tuning was applied. Specifically, the remaining parameters that needed to be estimated were the individual organ extensibilities (ϕ) and elasticities (𝜀), xylem transport resistance (${\mathrm{R}}_{\mathrm{x}}$), threshold turgor (Γ), and the newly introduced respiration parameter ($\mathrm{G}\mathrm{M}{\mathrm{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$).

From the literature a value for threshold turgor specific to soybean was found for both internodes and leaves. A range of 0.30–0.50 MPa was reported for internodes (Nonami and Boyer, 1990b). For leaves, a range of 0.20–0.32 MPa was reported for well-watered, expanding leaves, noting, however, that the threshold turgor increases during leaf growth up to almost 0.90 MPa (Randall and Sinclair, 1989). As we did not incorporate this relation and preferred a fixed value across all organ types for model simplicity, we chose a fixed value of 0.40 MPa, well within the range for both internodes and leaves.

Elasticity values for soybean were hard to find. Nonami and Boyer (1990b) reported elastic compliance of the elongating (0.025 MPa⁻¹) and mature (0.015 MPa⁻¹) zones of a soybean hypocotyl with an approximate fourth of the hypocotyl being in the elongation phase throughout its development. This reported elastic compliance was recalculated to a value of elasticity of 57 MPa for the internodes. Identical values were assumed in both internode directions and the same values were taken for the petioles. Elasticity values for soybean leaves were not found in the literature.

The final parameters were manually fine-tuned. The goal was to use the temporal patterns of plant length, volume and photosynthesis obtained from the descriptive simulation of the 2015 field trial as a blueprint for fine-tuning the model parameters, which could not be obtained from literature, while maintaining realistic model dynamics and parameter values. Firstly, the sink function that describes resource allocation in our model (eqns 3–5) depends solely on: (1) the timeframe of phytomer development; (2) organ composition of the phytomers; (3) the timeframe of individual organ growth; and (4) the fixed sink parameter per organ type. As these were all fixed parameters in our model, this sink function was essentially deterministic as a function of thermal time. Moreover, only the organ-specific sink parameters to establish this sink function were unknown at this point of the calibration. As a result, the sink function obtained from measurements (Supplementary Material S2) could be used to independently calibrate organ-specific sink parameters that lead to the sink function.

Calibration of absolute values of the extensibilities and the other parameters was made possible due to the specific sensitivities of the model dynamics to the different parameter values. The absolute values of organ extensibilities (ϕ) determine the rate of plant volume accumulation, whereas relative extensibility values determine the individual organ 3D structure. Xylem transport resistance (${\mathrm{R}}_{\mathrm{x}}$) influences the time delay between water loss and supply, impacting the magnitudes of the diel patterns of water potential and organ volumes. Organ elasticity (𝜀) impacts the effect of water availability on turgor pressure. The empirical respiration reduction (eqn 2), related to a relative decrease in growth respiration and increase in assimilate contribution of senescent leaves, affects late growth. If this term is not included, a point in the development is reached where respiration exceeds assimilate production due to a reduction in healthy leaf area. Lastly, the magnitude of the respiration term influences the availability of assimilates.

The complexity of FSPMs, and this model specifically, regarding the number of parameters and high computation time, makes it difficult to quantify parameter sensitivities with classical methods for global sensitivity analyses (Wu, 2012; Mathieu et al., 2018). Though extremely useful for model evaluation and recalibration, such analysis is out of the scope of this paper. However, to gain some insight into the individual impacts of the newly introduced biophysical plant parameters on the main model outputs, a one-at-a-time variation of 10 % on the calibrated values was simulated. Similarly, sensitivity of main model outputs towards water-related model inputs, namely relative humidity of the air and soil water potential, was explored.

Alternative growing scenarios

A number of actual and theoretical scenarios were simulated to evaluate both the validity of the physiological parameters and the environmental sensitivity of certain physiological and morphological parameters on the model development. Evaluating the validity of the physiological parameters was done by comparing simulations of the calibrated model under other environmental conditions.

A first scenario was simulated for validation by changing only environmental data to simulate the differences between the 2015 and 2016 growing seasons. As the measured plant data from the 2016 experiment in the same planting densities were significantly different, an agreement between observed and simulated plant architecture would therefore serve as a first validation of the model parameters and dynamics.

Three additional scenarios were simulated to evaluate the effect of plant spacing on model simulations. Under different plant spacings, plant hydraulics are impacted due to differences in leaf light interception, and thus photosynthesis and transpiration. However, plant spacing also impacts the development (or inhibition) of branches, a mechanism that is not included in the current version of the model. To make realistic comparisons of plant behaviour under these conditions, the plant’s branching rules were manually adjusted in the model to match the experimental observations to allow evaluation of the effect of plant spacing on the hydraulic components of the model dynamics. A first theoretical simulation was conducted on the environmental data of 2015, where only branching was inhibited but all other parameters and planting density remained the same. Such a simulation serves as an exploration of the influence branching has on the overall model dynamics, such as the distribution of resources, plant yield and plant length. However, it cannot be compared with experimental data, as branching always occurs at this planting density in the ‘Adsoy’ cultivar. Therefore, more realistic simulations were also conducted, where branching was manually inhibited or increased under planting densities where this was experimentally observed to occur in the 2016 field trials. Such simulations are useful for assessing the predictive value of the model. A first simulation was conducted at a planting density that was observed to not (or very rarely) develop branches (i.e. 15 cm × 6 cm). A second simulation was based on a more widely spaced (i.e. 50 cm × 50 cm) trial, which also very frequently developed branches on the second and third phytomer. Note that branches always develop in the leaf axils, and therefore trifoliate phytomers support a maximum of one branch per phytomer (unlike the hypocotyl or unifoliate phytomer, which can develop up to two, one in each cotyledon or leaf axil). As a result, the total number of branches in the 50 cm × 50 cm scenario is six. See Table 1 for a full overview.

Table 1.

Overview of the calibration and alternative model scenarios and their altered parameters. In the growing season of 2015 only a single field trial was conducted which was used to calibrate the models parameters (calibration). An alternative scenario was simulated where only the branching of the individual plants was (theoretically) inhibited for the same growing year and planting density (branchless). In the growing season of 2016, final plant dimensions and seed yield were measured for a plot with the same planting density (validation) and two alternative planting densities which respectively resulted in plants that did not develop branches (branchless) or developed an additional branch on the second and third phytomer (fullbranch). Dates are given as respective day of the year (DOY)

Simulation year	2015		2016
Simulation reference name	2015_ calibration	2015_ branchless	2016_ validation	2016_ branchless	2016_ fullbranch
Germination	146	146	147	147	147
Generative induction	183	183	184	184	184
End of vegetative development	216	216	217	217	217
Thermal time at full leaf senescence	966	966	1025	1025	1025
Based on experimental conditions	yes	no	yes	yes	yes
Branching on phytomers [rank]	0, 1	-	0, 1	-	0, 1, 2, 3
Row spacing [cm]	25	25	25	15	50
Plant spacing within rows [cm]	25	25	25	6	50

RESULTS

Model implementation and performance

Implementing the conceptual turgor-driven growth model (Coussement et al., 2018a) in the soybean FSPM was relatively straightforward as the conceptual model was inherently able to deal with the added complexity of branching structures. Similarly, from a programming standpoint, integration of transpiration and photosynthesis (P-SC-T model) based on realistic light modelling was simply a matter of replacing the theoretical inputs used in the conceptual model of Coussement et al. (2018a). The complexity of trifoliate leaves in soybean was simplified (Supplementary Data S4) since this is not expected to affect model accuracy much, but greatly improves model computation time. The only information lost with this simplification is the ability to distinguish differences in response between the leaflets of a trifoliate leaf as a result of local shading, which was considered less important in this study than computation time. The introduction of a more realistic leaf shape within the model (compared with the simplified rectangles used in Coussement et al. (2018a) only affects leaf light interception; it does not require changes to any of the fundamental equations of the turgor-driven growth model (besides a correct calculation of leaf volume).

Model computation time hinges on the number of plant organs in the scene, which quickly adds up with the branched complexity of soybean plants. One full soybean growing season, from germination to harvest, takes ~114 d, which means 2736 timesteps (i.e. hours) to be computed. The model simulation time with 25 × 25 plant clones on a single core of a high-performance computing cluster (2 × 12-core Intel E5-2680v3 [Haswell-EP @ 2.5 GHz]) with 50 GB of memory assigned to the simulation took ~24–25 h, of which the light simulation accounted for ~8.5 h. Light simulation time of a single simulation step during daylight ranged from 1 s at model start to 32 s at maximal leaf area due to the higher number of objects in the scene.

Model calibration

Model calibration revealed some of the shortcomings with the initial conceptual model design (Coussement et al., 2018a) that were previously discussed in the model description, such as the incorporation of an initial carbon source and constant radial stem growth. The latter is important because the bottom-most internodes provide a bottleneck for water transport throughout the plant. As a result, both from a biological and a mechanistic standpoint, development of thicker internodes higher on the stem was an unnatural and unnecessary carbon investment. Some further exceptions were made in this regard, firstly for the hypocotyl, where the radial sink strength was set to twice the radial sink strength of the other stem segments, to provide sufficient investment in radial stem growth. Otherwise, at equal radial sink strength across all internodes, the hypocotyl radius would lag behind the first internodes due to a lower sugar supply during the initial growth phase (i.e. when elongation is still taking place), which also contributes to radial stem growth. Secondly, the first phytomer, which contains the unifoliate leaves, is a special case with very small petioles and was observed to have a much higher relative leaf sink strength than other phytomers [Supplementary Data S3]. These observations were included in the model by fine-tuning the petiole sink strength of the unifoliate phytomer to 5 % of the other petioles and quadrupling the sink strength of the unifoliate leaves.

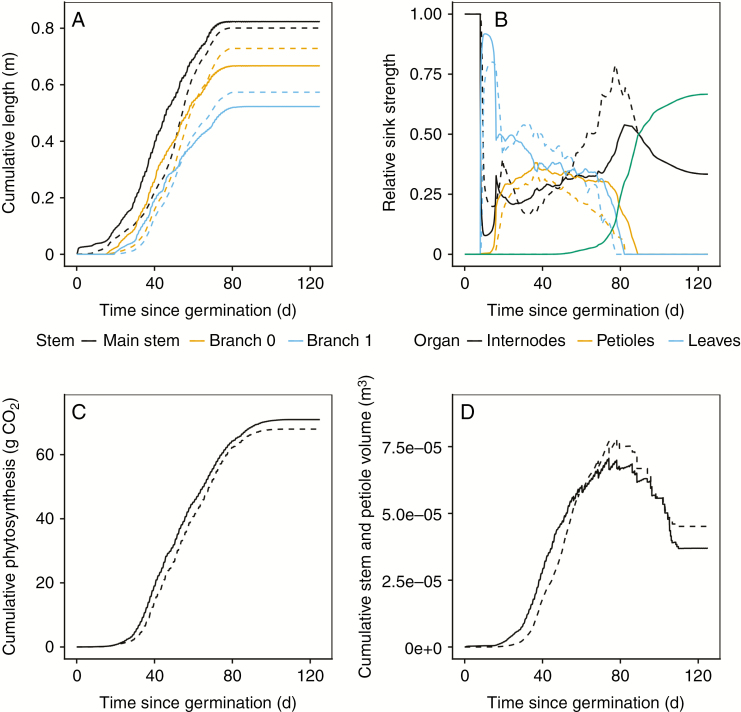
The turgor-driven soybean FSPM simulation with calibrated model parameters (summary of calibrated values and a comparison with literature-reported values is given in Supplementary Data S6) was able to reach a good agreement with the observed values in terms of plant length, sink function, cumulative photosynthesis and internode and petiole volumes (as cumulative leaf area is already related to cumulative photosynthesis) (Fig. 3) while being constrained by realistic dynamics of water transport and turgor pressure. Carbon distribution in the soybean FSPM, governed by the sink function (Fig. 3B) and by the rate of carbon assimilation throughout plant development (Fig. 3C), was largely in agreement with the measured value as illustrated by the dry weight of the plant stem (9.48 g simulated, 8.02 ± 2.52 [SD] g measured) and seeds (16.14 g simulated, 15.71 ± 7.40 g measured). Comparison of main stem and branch lengths between the soybean FSPM and plant measurements showed relatively shorter branches compared with main stem length. The calibrated model simulation overestimated main stem length by 2.5 %, while the branches on the hypocotyl and the first phytomer were underestimated by 8.4 and 8.9 %, respectively (Fig. 3A).

Fig. 3.

Comparison of the turgor-driven soybean FSPM (continuous lines) with calibrated parameter values (Supplementary Data S6) with the descriptive model obtained directly from measured data (S2, dashed lines). (A) Cumulative length of the main stem and branches originating on the hypocotyl (branch 0) and unifoliate phytomer (branch 1). (B) Temporal sink functions describing the relative resource allocation over time. The function of the descriptive model (Supplementary Data S2) was rescaled using the seed sink strength of the predictive model as no temporal measurements of the seeds were taken and thus included in the descriptive model. (C) Cumulative photosynthesis, which is directly related to the temporal development of leaf area, as the timings of leaf spectral characteristics, phenology and leaf angle development are equal in the two models. (D) Evolution of stem and petiole volume. The sudden decreases in this graph are due to shedding of senesced leaves (and petioles). At full senescence, the remaining value shows only the final internode volume.

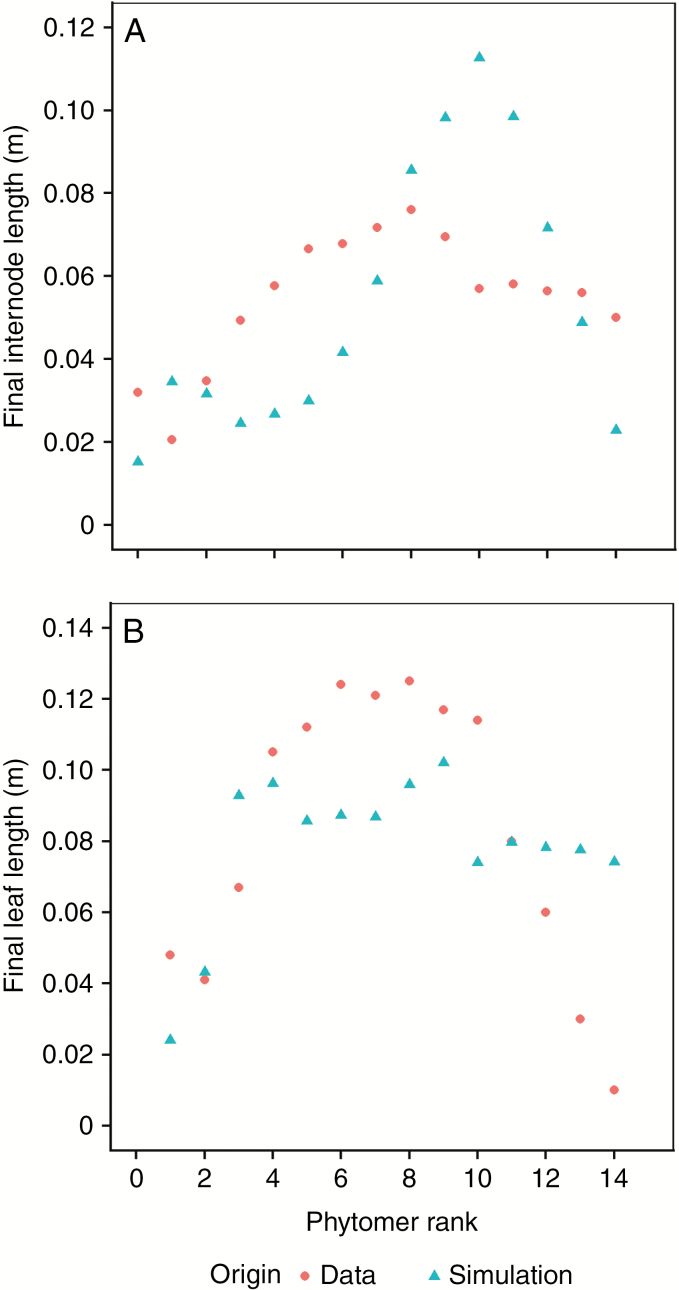
As the model calibration was conducted on whole-plant variables, the simulated growth progression of individual organs in the FSPM was not yet considered. Clear differences were observed between the expected (i.e. simulated) and measured growth patterns. The measured final length of the main stem internodes consistently showed distinct similarity to an asymmetrical unimodal curve (Fig. 4A) while the simulations coincided with a lower, symmetrical unimodal curve. The measurements of final leaf length on the main stem also coincided with a symmetrical unimodal curve. The corresponding simulated values were largely in line with observations, but slightly underestimated the middle ranks, while overestimating the top ranks (Fig. 4B). In terms of individual organ growth patterns, simulations consistently overestimated the growth rate of newly conceived organs (data not shown). At organ initiation simulations showed an initial peak in osmotic potential and turgor pressure. Even though extensibility was at its highest and sink strength was still relatively low during this initial phase of organ growth, the influx of a limited amount of soluble sugars had a strong effect on the initial plant organs due to their small initial size. As a result, the physiological response in terms of potential components was significantly stronger in primordial organs than when the organ had already amassed some volume.

Fig. 4.

Comparison of the final length of main stem internodes (A) and leaves (B) between observations and simulations with the calibrated model. Patterns of simulated final organ lengths are similar between the two organ types, with a gradual increase in earlier ranks, maximal lengths in middle ranks, and shorter lengths in final ranks. These values coincide with the gradual increase and decrease in overall resources, total overall sinks (e.g. seed development) and environmental conditions during development. Observed final leaf lengths follow a pattern that is similar to the simulations, though more distinct. Observed final internode lengths deviate from this pattern with a distinct depression in ranks 2–5. This depression coincides with the timing of branch development, which may interfere with main stem internode elongation in a mechanism not yet captured by the model. Upper internode ranks are also distinctly longer than simulated, which may relate to canopy closure and related shade-avoidance response.

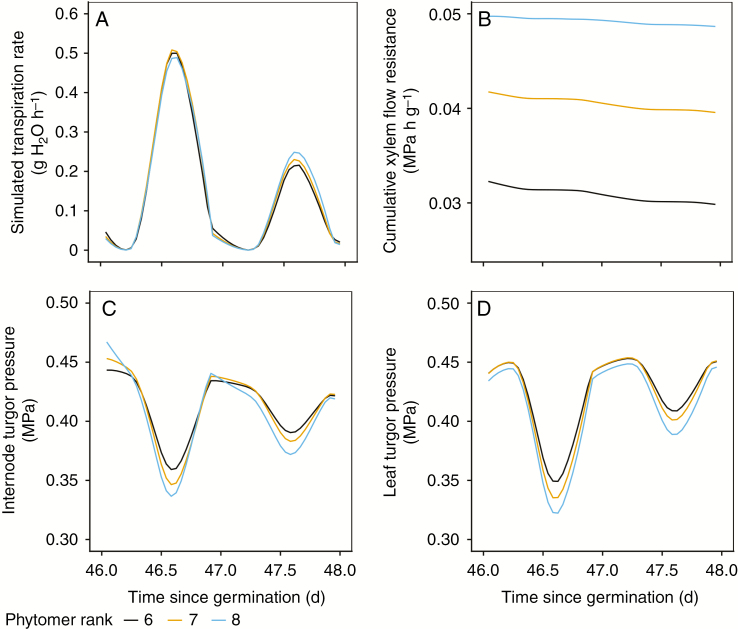
The environmental conditions that drive the model had a strong influence on leaf transpiration. These day-to-day variations strongly influenced the dynamics of leaf turgor and osmotic and total water potential in the model (Fig. 5). Aside from environmental influences, these dynamics were also influenced by the size of the individual organs, their extensibility and sink strength. Turgor pressure varied between different plant organs and with position on the plant (Fig. 5), related to differences in hydraulic resistance, which increased with travelling distance to the organ. Hydraulic resistance from the bottom to the top also varied strongly during the growing season due to changes in e.g. cumulative stem length and total transpiration demand.

Fig. 5.

Detail of the model dynamics within three selected phytomers on two consecutive days with different environmental conditions. During this timeframe, phytomers 6 and 7 were already fully grown (with the exception of radial internode growth), while phytomer 8 was still in its growth phase. Simulated transpiration rates (A) showed only minor differences for the three leaves, but strong differences between the two days. Due to differences in cumulative xylem flow resistance from soil to respective phytomer internodes (B), daily decline in turgor pressure in response to transpiration was stronger in phytomers higher in the plant (C and D). Turgor pressure in phytomer 8 showed a decline during night-time hours (as opposed to the fully grown phytomers) resulting from cell relaxation under its irreversible growth.

Analysis of the local sensitivity of calibrated biophysical and empirical seed and respiration parameters in relation to selected output variables is given in Table 2. While interaction between different parameters was expected (which cannot be analysed by this method), some conclusions can be drawn. The length of the main stem was largely insensitive to parameters not related to extensibility. Elasticity values had little impact on the overall model outputs. Seed dry weight strongly depended on the relative extensibilities in the model, which directly impacted seed sink strength. Elemental xylem flow resistivity had a relatively low effect on the model outputs; however, a strong interaction with extensibility parameters is expected due to its relationship with individual organ sizes. Interestingly, a relatively low influence of leaf extensibility values was found for each output variable, including total photosynthesis. However, this relates to the use of uniform extensibility in both the longitudinal and the normal direction. Therefore, the organ shape does not alter, unlike changes made to the directional extensibility components of the other plant organs. Input variables related to water availability (i.e. relative humidity of the air and soil water potential) impacted all selected output variables to varying degrees, illustrating the direct dependence of plant growth on water availability in the model.

Table 2.

Local sensitivities of selected model outputs of the newly introduced biophysical and empirical seed and respiration parameters. Each row represents a full simulation where the selected parameter was either increased or decreased by 10 % compared with its calibrated value, while keeping all other parameters at their calibrated values. Every column presents relative change in outputs ( %) obtained from these simulations compared with the model simulation where no parameters were changed. Highest sensitivity parameters per output variable are highlighted. Additionally, the effect of the input variables relative humidity (RH) and soil water on the model outputs was tested in variations of 10 and 25 %. In the case of RH, these variations were applied on the difference between 100 % and current RH (e.g., an increase of 25 % in RH is calculated as $1-(100\mathrm{\%}-\mathrm{R}\mathrm{H}\left(\mathrm{t}\right))\ast (100\mathrm{\%}-25\mathrm{\%})$; similarly, a decrease of 10 % RH is calculated as $1-(100\mathrm{\%}-\mathrm{R}\mathrm{H}\left(\mathrm{t}\right))\ast (100\mathrm{\%}+10\mathrm{\%})$; with $\mathrm{R}\mathrm{H}\left(\mathrm{t}\right)$ the current relative humidity) so that RH does not exceed 100 % at high RH

Parameter	Change	Total photosynthesis	Final plant length	Seed dry weight	Final stem volume
${\varphi }_{\mathbf{z}}^{\mathbf{i}\mathbf{n}\mathbf{t}\mathbf{e}\mathbf{r}\mathbf{n}\mathbf{o}\mathbf{d}\mathbf{e}}$	+	1.10	12.52	1.80	1.45
	-	-0.60	-12.56	-0.68	-0.72
${\varphi }_{\mathbf{x}}^{\mathbf{i}\mathbf{n}\mathbf{t}\mathbf{e}\mathbf{r}\mathbf{n}\mathbf{o}\mathbf{d}\mathbf{e}}$	+	-0.47	-11.04	-0.54	-0.54
	-	1.17	13.33	1.90	1.51
$\epsilon {}_{\mathbf{x}\mathbf{,}\mathbf{z}}^{\mathbf{i}\mathbf{n}\mathbf{t}\mathbf{e}\mathbf{r}\mathbf{n}\mathbf{o}\mathbf{d}\mathbf{e}}$	+	-0.01	-0.04	0.00	0.00
	-	-0.01	0.03	0.00	-0.01
${\varphi }_{\mathbf{z}\mathbf{,}\mathbf{y}}^{\mathbf{l}\mathbf{e}\mathbf{a}\mathbf{f}}$	+	0.32	0.22	0.21	0.28
	-	-0.45	-0.32	-0.29	-0.39
$\epsilon {}_{\mathbf{x}\mathbf{,}\mathbf{y}\mathbf{,}\mathbf{z}}^{\mathbf{l}\mathbf{e}\mathbf{a}\mathbf{f}}$	+	-0.25	-0.18	-0.14	-0.21
	-	0.28	0.20	0.16	0.24
${\varphi }_{\mathbf{z}}^{\mathbf{p}\mathbf{e}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{l}\mathbf{e}}$	+	0.80	0.67	0.66	0.69
	-	-0.30	-0.27	-0.20	-0.16
${\varphi }_{\mathbf{x}}^{\mathbf{p}\mathbf{e}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{l}\mathbf{e}}$	+	-0.22	-0.24	-0.16	-0.12
	-	0.95	0.77	0.91	0.91
$\epsilon {}_{\mathbf{x},\mathbf{z}}^{\mathbf{p}\mathbf{e}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{l}\mathbf{e}}$	+	0.00	0.00	-0.02	-0.01
	-	-0.01	-0.01	0.01	-0.01
${\mathbf{R}}_{\mathbf{f}\mathbf{l}\mathbf{o}\mathbf{w}}^{\mathbf{x}}$	+	-0.17	-0.33	-0.09	-0.12
	-	0.17	0.34	0.09	0.12
${\mathbf{C}}_{\mathbf{s}\mathbf{e}\mathbf{e}\mathbf{d}}^{\mathbf{t}\mathbf{o}\mathbf{t}\mathbf{a}\mathbf{l}}$	+	1.58	1.44	0.73	1.33
	-	-0.57	-0.52	-0.26	-0.48
$\mathbf{G}\mathbf{M}{\mathbf{R}}_{\mathbf{m}\mathbf{a}\mathbf{x}}$	+	-0.96	-1.86	-2.82	-2.83
	-	0.95	1.87	3.01	2.97
Input variable	Change	Total photosynthesis	Final plant length	Seed dry weight	Final stem volume
Relative humidity	+25 %	3.29	2.67	2.50	2.98
	+10 %	1.34	1.09	1.04	1.22
	-10 %	-1.37	-1.09	-1.08	-1.25
	-25 %	-3.74	-2.79	-2.99	-3.41
Soil water potential	+25 %	4.37	5.83	1.53	8.12
	+10 %	1.74	2.31	0.69	3.17
	-10 %	-1.61	-2.19	-0.55	-2.92
	-25 %	-3.90	-5.35	-1.36	-7.02

Alternative growing scenarios

The different scenarios resulted in large differences in simulation results (summarised in Table 3). The first scenario, which simulated the same experimental setup as that used in 2015 under 2016 conditions, was unable to fully explain the rather drastic differences observed between the plants in the different growing years. Compared with the 2015 simulation (2015_calibration), the 2016 simulation (2016_validation) predicted plants of near equal height, with a slight increase in stem and seed dry weight. However, the measured data showed slightly shorter plants in the 2016 experiment, with vastly increased stem and seed dry weight.

Table 3.

Comparison of the model simulations of the five different scenarios from Table 1 using identical parameter values for each simulation with their respective measured plant length and dry weight at the end of the growing season (where relevant). Measured variables are shown with a single standard deviation

Simulation year	2015		2016
Simulation reference name	2015_ calibration	2015_ branchless	2016_ validation	2016_ branchless	2016_ fullbranch
Density [cm x cm]	25 x 25	25 x 25	25 x 25	15 x 6	50 x 50
Number of branches per plant	4	0	4	0	6
Simulated plant length [m]	0.82	1.47	0.84	0.71	1.09
Measured plant length [m]	0.80 ± 0.05	-	0.65 ± 0.09	1.07 ± 0.16	0.62 ± 0.06
Simulated total photosynthesis [g CO2]	70.94	46.30	74.16	13.71	189.45
Simulated seed dry weight [g]	16.14	18.55	16.96	4.04	46.58
Measured seed dry weight [g]	15.71 ± 7.40	-	20.71 ± 8.93	3.60 ± 2.25	55.54 ± 15.52
Simulated stem dry weight [g]	9.48	10.11	10.02	2.70	26.60
Measured stem dry weight [g]	8.02 ± 2.52	-	14.33 ± 6.23	3.76 ± 2.16	45.92 ± 12.13
Total simulation time [h]	24.35	10.18	24.80	10.29	40.41

Scenarios without branching had drastic effects on plant development. Under 2015 conditions, and with the same planting density (2015_branchless), the simulation resulted in significantly longer plants with less photosynthesis but a higher seed yield. Such a scenario was unrealistic, however, because branching is only inhibited under high planting densities such as the branchless simulation of 2016 (2016_branchless). This simulation, with planting density of 15 × 6 cm, reported a drastic reduction in photosynthesis and a decrease in plant length and biomass for both stem and seed. While the measured plants in this scenario were substantially longer, the drastic reduction in stem and seed biomass corresponded to the model simulation. This indicated that soybean actively adapts its stem elongation under high densities, a process that is not yet incorporated in the model. The last scenario, where extra branches developed on the second and third phytomers due to a wider planting density (2016_fullbranch), led to a vast increase in total carbon assimilation, seed yield and stem biomass per plant with a relatively limited effect on plant length. The predictions of a strong biomass increase per plant was in line with the observations, but still underestimated the magnitude of their increase. This could once more be related to the active adaptation of stem elongation related to planting density, as our simulation predicted longer plants than the reference, while in reality the observed plants were shorter. As a result, the plant simulated in this setup overinvested resources in stem elongation that could have been used for further leaf area or seed development.

DISCUSSION

Opportunity cost of turgor-driven growth in FSPMs

Water transport is essential for plant growth and survival but is still largely absent in most FSPMs. Several studies (e.g. Fatichi et al., 2014; De Swaef et al., 2015; Körner, 2015; Steppe et al., 2016) have outlined the importance of including water status in models of plant growth, even in conditions where water is not limited. However, the translation to FSPMs is not an easy thing to consider, as the complexity of mechanisms involved in dynamic water transport inevitably leads to more complex models which operate at a smaller temporal scale than is required for carbon-based growth models. The associated high computational cost can hinder simultaneous simulation of complex architectures and canopies (Nikinmaa et al., 2014), as was also demonstrated by our decision to model only a single plant. However, constant improvements are seen in overall available computational power. Additionally, the increasing availability of tools for monitoring of plant water status continuously and non-destructively (Steppe et al., 2016) alongside growth models with dynamic water transport may increase real-time insight into plant growth status.

The increase in modelling complexity associated with turgor-driven growth in FSPMs should therefore be correctly justified. Firstly, an approach could be considered for an increase in predictive power, to create an FSPM that results in valid simulations under any scenario of water availability. While such scenarios were not evaluated within the current study, the mechanistic integration of both water and carbon availability as key drivers of plant growth has not yet been attempted in FSPMs, and may prove an important stepping stone for evaluating and improving model performance under such scenarios. Secondly, these mechanisms allow the expression of plant growth in terms of plant characteristics (e.g. extensibility and elasticity of the cell wall) that are, in part, under genetic control (Mirabet et al., 2011). This provides a better understanding of the differences in plant performance between genotypes and growing environments, which could be an important phenotyping tool for improved breeding strategies (van Eeuwijk et al., 2019). This work was meant as an evaluation of turgor-driven growth in FSPMs under realistic conditions to provide a better insight into the hurdles and opportunities associated with this approach, as well as an evaluation of the assumptions made. From a programming perspective, the integration of the conceptual model in a realistic FSPM was straightforward, though the associated computational costs limited possibilities with regard to simulating a large number of plants simultaneously and more efficient methods for global model calibration. The mechanistic nature of the model allows insight into the origin of discrepancies between observed and simulated growing patterns. For example, in the conceptual turgor-driven growth model of Coussement et al. (2018a) a more direct coupling of extensibility and sink strength was proposed, but was here discarded due to unrealistic simulation results in the initial growing stage of a plant organ. The positive coupling of extensibility and sink strength defined maximal sink strength at organ initiation, resulting in a disproportionately large influx of assimilates for the initially very small plant organ. As a result, turgor pressure spiked and an immediate growth spurt was initiated. This is an indication that extensibility might not be a good proxy for capturing sink strength, at least not in the early growth stages of a plant organ. At organ formation, cell differentiation receives priority over cell expansion and evidence suggests that during these stages organ growth is driven metabolically rather than hydraulically (Pantin et al., 2011). The importance of hydraulic control increases over the course of the organ’s development (Pantin et al., 2011). As this is considerably more complex, a more classical sink approach was therefore chosen in an attempt to accurately capture sink strength behaviour with a minimal amount of parameters.

In comparison with a simulation with a classical source–sink model, results are expected to be similar under conditions of non-limiting water such as those used in this study, even though significant model complexity is added. As long as extensibility and turgor pressure remain favourable for plant growth, plant organ dimensions grow towards an equilibrium based on the carbon availability in the model (Supplementary Data S5). The extensibility and turgor pressure determine the rate at which this occurs in the model, but not the final size of the organ. Rather, the total potential volumetric change associated with an increase in carbon availability is governed by the threshold turgor, organ temperature and soil water potential. Under water-limiting conditions, plant organ growth slows down in the model and osmotic pressure accumulates. If re-watering occurs at a stage when extensibility is no longer favourable, the final organ size will be affected. Such scenarios were not evaluated in this study, and may need further improvement of some model mechanics (e.g. the accumulation of starch and non-structural carbohydrates under water-limiting conditions, with associated downregulation of photosynthesis (Fatichi et al., 2014) (downregulation of photosynthesis and transpiration under water deficit due to stomatal closure). However, validation under non-limiting conditions is a necessary first step in moving towards model evaluation under limiting conditions in future research.

Current model performance

As the turgor-driven growth concept is new within full-plant FSPMs and our data for model calibration were limited, several conceptual simplifications were introduced to maintain the proof of concept but also avoid overfitting. Measurements of model variables (e.g. sap flow and stem diameter variations) were not available in this study but are a top priority for future model development and evaluation, as these data could aid in further identifying possible shortcomings in our modelling assumptions. Simplifications within the model include several parameters that were kept constant (e.g. threshold turgor) or simplifications with regard to sub-models (e.g. respiration). The use of identical parameters for each organ type not only allows a strong reduction in parameters to be estimated (without which the model would not be identifiable) but is also supported by observations that, for example, diel growth patterns of soybean leaflets are identical, and independent of their position on the plant (Friedli and Walter, 2015). However, comparison of the calibrated turgor-driven FSPM with the measured progression of plant growth and development showed that fixed model parameters for each organ type were capable of explaining the whole-plant observations (Fig. 3) but deviated on organ-specific observations (Fig. 4) and when faced with different growing scenarios (Table 3). Therefore, it was clear that not all model parameters are truly developmentally and environmentally insensitive, and may therefore require further consideration before using them to make predictions under different environmental conditions.

In terms of final plant dry weight (i.e. stem and seed), the model was able to capture the measured trends of increased or decreased dry weight in the three validation scenarios (Table 3). However, the trends in terms of plant length between the different planting densities were not correctly simulated. This was expected as this is related to active adaptation of stem elongation as shade avoidance (Franklin and Whitelam, 2005), with densely planted plants investing significantly in stem elongation while widely spaced plants are shorter and develop more branches (Carpenter and Board, 1997). This effect can increase with increasing canopy closure, and may also be responsible for the distinct pattern in observed main stem internode lengths at higher ranks (Fig. 4A), which deviates from the symmetrical unimodal curve that is visible in the observed main stem leaf lengths (Fig. 4B). A symmetrical unimodal curve is expected if a uniform logistic growth pattern is present across the main stem, with cumulative whole-plant assimilate availability following a logistic pattern as well (Fig. 3C). As a result, this pattern is distinguishable in both the simulated internode and leaf lengths (Fig. 4) as adaptive internode elongation is not included in the model. Rather, internode elongation is modelled using a discrepancy between radial and longitudinal extensibility, with an equidirectional, constant threshold turgor. Mechanistically, this represents dimensional differences in growth potential related to cellulose microfibril orientation, which govern the primary direction of cell elongation and organ shape as a result (Schopfer, 2006). However, the process of cell elongation can be governed by active processes of cell wall loosening or stiffening, which influence both extensibility and threshold turgor (Kutschera, 1994; Schopfer, 2006; Kutschera and Niklas, 2013). Shoot elongation for shade avoidance therefore relates to an active adaptation of cell wall extensibility (Sasidharan et al., 2008) as well as a change in sink distribution (Franklin and Whitelam, 2005). As the current version of the model used fixed values for extensibility regardless of environmental conditions, an increase in plant resources due to wider spacing was expected to result in a balanced increase in plant growth across all organ types, including stem elongation. However, even without incorporation of active shade avoidance, the response of internode elongation was not linearly related to the total amount of assimilated carbon (Table 3). For example, the assimilated carbon of the validation simulation in 2016 was over five times higher than the branchless simulation of the same year, while the final plant length was only 17 % higher. This indicates that the simple act of not developing branches already contributes to an increase in available assimilates for stem elongation.

Potential for future model improvements

The possibility of identifying missing aspects (such as the dynamic adaptation of stem elongation) in the model simulation originates from the mechanistic nature of the model, which expresses parameters and variables with tangible plant properties and dynamics. As a result, comparing model simulations with both realistic variable boundaries and measured structural and photosynthesis data allowed further exploration of the shortcomings of the modelling approach. Some of these inadequacies were dynamically identified and improved upon in this paper when model calibration revealed them (e.g. the necessity of seed carbon contribution), while others point to missing aspects of plant growth that may be important for future model development (e.g. shade avoidance) or aspects that were (over)simplified.

Simplifications are a necessity for model development, but are still important to consider for determining why simulated results do not always correspond with observations, especially when data are limited. Thus, some further considerations must be made with regard to the decisions taken in this paper and how they may influence future simulations. It has already been shown that cell wall extensibility can be influenced by external factors such as shade avoidance, but it is also susceptible to changing water deficit (Wu et al., 2005). Another factor that was considered constant was a standardized measure for xylem water transport resistance. While a dependency on organ size was incorporated, hydraulic resistance of leaves (Cochard et al., 2007), stem (Steppe et al., 2012) and roots (Vandeleur et al., 2014) is directly influenced by transpiration demand. Furthermore, drought stress affects hydraulic resistance through embolism formation in xylem vessels (Buchard et al., 1999; Steppe et al., 2015b; Vergeynst et al., 2015).

Photosynthesis was modelled using the P-SC-T model (Kim and Lieth, 2003) combined with realistic values for light absorption obtained from the complex interaction between canopy structure, leaf CCI and direct and diffuse sunlight. The P-SC-T model also takes into account measured values of temperature and relative humidity of the air to model stomatal conductance and leaf temperature, which influence both photosynthesis and transpiration. However, a direct feedback loop, linking leaf water potential and stomatal closure, is not included in this model. As a result, there is no physiological response of stomatal conductance to water loss. In leaves higher up in the plant, and with resulting higher transport resistance from soil to leaf, the absence of this feedback loop can lead to (temporary) simulated negative turgor pressures at high light intensities depending on both xylem transport resistance and organ elasticity. Even in these extreme cases of local water deficit, modelled stomatal conductance remains unaffected, pointing to a possibly important interaction between stomatal closure at low turgor, which is not included in the current model. A solution to this could be to include a P-SC-T model that incorporates the relationship between leaf water potential and stomatal closure (e.g. Tuzet et al., 2003; Zweifel et al., 2007). Carbon distribution, storage, remobilization and respiration are additional aspects of the model that were captured in a simple empirical function. Incorporation of these aspects in the model was fundamental for achieving realistic results, indicating that monitoring and modelling of carbon processes may be required for future model development. The importance of carbon storage may increase even further when considering that an accumulation of carbon storage directly downregulates photosynthesis (Goldschmidt and Huber, 1992; Paul and Foyer, 2001; Körner, 2015; Mahmud et al., 2018).

Conclusions

Overall, the introduction of turgor-driven growth in an FSPM has potential to be used as a tool to better understand the performance of plant growth in terms of internal plant properties and their response to environmental triggers. The use of this tool in combination with data from future experiments, focused specifically on water deficit, to provide insight into the simulated model dynamics such as sap flow or stem diameter variations can alleviate the need for some model simplifications introduced into the current model. This will be the next fundamental step before an FSPM will be applicable as a predictive model to evaluate plant growth under a wide range of conditions, such as drought. Current model simulations already display large differences under different growing scenarios, which highlight the adaptive nature of the model, in which changes in plant architecture result in differences in plant hydraulics. The different transpiration rates in these scenarios resulting from contrasting light interception (due to the different planting densities) facilitate differences in spatio-temporal variation in turgor pressure which, in turn, result in the observed different growth patterns.

SUPPLEMENTARY DATA

Supplementary data are available online at https://academic.oup.com/aob and consist of the following: S1: the field trials and resulting measurements used throughout this paper are more thoroughly described. S2: describes the steps taken to convert these discrete measurements to create a descriptive soybean model, capable of simulating the continuous progression of e.g. plant length, photosynthesis and transpiration. S3: contains some minor adaptations to the photosynthesis–stomatal conductance–transpiration model used in the FSPM. S4: contains the reasoning and effect of simplifying trifoliate leaflets in the model. S5: explains the effects of extensibility, threshold turgor and assimilate supply on plant growth. S6: contains an overview of all model parameters and their calibrated values, as well as a thorough comparison with literature-reported values.

FUNDING

This work was supported by a personal PhD grant issued by the Agency for Innovation by Science & Technology (IWT 141434) to J.C.