Simulating the effects of water limitation on plant biomass using a 3D functional–structural plant model of shoot and root driven by soil hydraulics

Abstract

Background and Aims

Improved modelling of carbon assimilation and plant growth to low soil moisture requires evaluation of underlying mechanisms in the soil, roots, and shoots. The feedback between plants and their local environment throughout the whole spectrum soil-root-shoot-environment is crucial to accurately describe and evaluate the impact of environmental changes on plant development. This study presents a 3D functional structural plant model, in which shoot and root growth are driven by radiative transfer, photosynthesis, and soil hydrodynamics through different parameterisation schemes relating soil water deficit and carbon assimilation. The new coupled model is used to evaluate the impact of soil moisture availability on plant productivity for two different groups of flowering plants under different spatial configurations.

Methods

In order to address different aspects of plant development due to limited soil water availability, a 3D FSP model including root, shoot, and soil was constructed by linking three different well-stablished models of airborne plant, root architecture, and reactive transport in the soil. Different parameterisation schemes were used in order to integrate photosynthetic rate with root water uptake within the coupled model. The behaviour of the model was assessed on how the growth of two different types of plants, i.e. monocot and dicot, is impacted by soil water deficit under different competitive conditions: isolated (no competition), intra, and interspecific competition.

Key Results

The model proved to be capable of simulating carbon assimilation and plant development under different growing settings including isolated monocots and dicots, intra, and interspecific competition. The model predicted that (1) soil water availability has a larger impact on photosynthesis than on carbon allocation; (2) soil water deficit has an impact on root and shoot biomass production by up to 90 % for monocots and 50 % for dicots; and (3) the improved dicot biomass production in interspecific competition was highly related to root depth and plant transpiration.

Conclusions

An integrated model of 3D shoot architecture and biomass development with a 3D root system representation, including light limitation and water uptake considering soil hydraulics, was presented. Plant-plant competition and regulation on stomatal conductance to drought were able to be predicted by the model. In the cases evaluated here, water limitation impacted plant growth almost 10 times more than the light environment.

INTRODUCTION

Water availability is one of the main constraints of carbon assimilation (Rogers et al., 2017) and crop productivity (Lynch et al., 2014). Climate change is expected to decrease mean crop yield around the world mainly due to changes in precipitation patterns (Knox et al., 2012; Lombardozzi et al., 2018) and, therefore, it is important to increase the predictability of productivity loss for different ecosystems. The increase of atmospheric CO₂ is strongly related to observed variations in global land water storage and present-day carbon cycle models underestimate this relationship (Humphrey et al., 2018).

To explore the effects of environmental resources such as the light environment, water, and nutrients on plant and crop performance, different biogeophysical modelling techniques can be used. For example, processes linking soil moisture, stomata opening, and the internal CO₂ concentration in the leaf are known, working to eventually reduce photosynthesis and transpiration (Ball et al., 1987; Leuning, 1995; Medlyn et al., 2011; Lin et al., 2015). Mechanistic modelling approaches offer the possibility to integrate knowledge of plant development and plant physiology at different spatial and temporal levels of detail. These different approaches can assess the influence of different model parameterisations and parameters on ecosystem functioning and understanding.

The Farquhar, von Caemmerer, and Berry (FvCB) photosynthetic model (Farquhar et al., 1980; Von Caemmerer and Farquhar 1981; Collatz et al. 1991) is widely used to predict steady-state CO₂ assimilation rates of leaves under different environmental conditions of light intensity, temperature, CO₂ and O₂ partial pressures in C3 photosynthesis pathway of the Calvin Cycle (Von Caemmerer, 2013). According to the photosynthetic model firstly described in Farquhar et al. (1980), photosynthesis is highly sensitive to the parameters expressed as the maximum rate of carboxylation (V_cmax) and the maximum rate of electron transport (J_max) in ecophysiology models (Zaehle et al., 2005; Bonan et al., 2011; Verheijen et al., 2013). Increasing evidence also suggests that V_cmax is affected by low soil moisture, possibly due to lower values of mesophyll conductance (Keenan et al., 2010; Egea et al., 2011; Zhou et al., 2013). A lack of water in the soil can reduce the biochemical capacity of photosynthesis through V_cmax and J_max in ecophysiology models, but the relative balance of stomatal conductance and biochemical limitations of water availability in the soil is still subject to significant debate (Chaves et al., 2009).

There are different types of approaches to simulate the effects of soil moisture on carbon assimilation by plants, including simple supply constraint approaches in which plant transpiration cannot exceed the potential supply of soil water; physiological approaches, hydraulic limitations, and empirical reduction factors (Rogers et al., 2017). The empirical reduction factor approach involves multiplying parameters by a ‘soil water stress factor’ (β) in response to shortage of water. However, land surface models disagree (Nearing et al., 2016; Ukkola et al., 2016) on to whether this factor should be applied to the carbon assimilation (A_n) and/or autotrophic respiration (R_d), to the photosynthetic parameter, V_cmax only, or to V_cmax and J_max, together.

These different models present a large divergence in the response of carbon assimilation to drought (Rogers et al., 2017). Whilst much of this divergence could be explained by the different approaches taken by each model, the method used to estimate soil water availability also varies between models. Some models estimate soil water availability using soil moisture content, e.g. O-CN (Zaehle and Friend, 2010), while others make use of soil moisture potential, e.g. CLM (Bonan et al., 2014). A major source of model divergence is the highly nonlinear soil water retention curves that strongly depend on soil type (Medlyn et al., 2016), as well as soil water conductance that decreases soil drying. Therefore, soil hydraulic properties should also be considered when estimating photosynthesis.

Current ecosystem modelling approaches treat soil properties and root systems in a very simplified way, resulting in unrealistic and uncertain responses of carbon assimilation to soil moisture (De Kauwe et al., 2013; Dietze, 2014; De Kauwe et al., 2016). Improved model representation of carbon assimilation and plant growth to low soil moisture requires the evaluation of underlying mechanisms in the soil, roots, and shoots, all together. Therefore, a modelling tool coupling soil, roots, and shoots is necessary to quantify the interactions between the light environment, root development, and soil properties (Dunbabin et al., 2013), which could contribute to promote agricultural strategies, such as crop species mixtures (Cardinale et al., 2012; Zhu et al., 2015) for increased plant productivity and increased water use efficiency.

Crop species mixtures, or intercropping, are often more efficient in the use of available resources for plant growth, such as water, light, and nutrients, in comparison to individual crops (Bedoussac et al., 2015). The development of a detailed model capable to test the performance of plant growth in different competition settings (e.g. intraspecific competition, such as in a monocrop, or interspecific competition, such as in intercropping) is important.

Functional-structural plant (FSP) models have been used to simulate plant development in different contexts with highly detailed calculations in three dimensions as a function of physiological processes driven by environmental changes, such as shortwave radiation (Evers and Bastiaans, 2016), nutrients availability (Gérard et al., 2017), and water acquisition and transportation (Lynch et al., 2014; Ndour et al., 2017). However, the feedback between plants and their local environment, especially the soil, is the foundation for simulating plant–plant interactions, as well as, the feedback plant-environment is often misrepresented or lacking representation in FSP models (Dunbabin et al., 2013; Tournier et al., 2015; Gérard et al., 2017; Postma et al., 2017; Schnepf et al., 2018). Therefore, it is important to describe the whole plant as coupled system with the soil and the atmosphere in order to accurately evaluate the impact of environmental changes on plant development (Evers et al., 2019).

The goal of this study is to evaluate how soil water availability affects the ecophysiological signatures in isolated plants, intraspecific competition (one species), and interspecific competition settings (two or more species). To this end, we present and assess qualitatively the coupling of a shoot FSP model with a 3D model of root architecture, water uptake, and soil hydrodynamics that can be used in the broader context of research on root-related drought tolerance, in single and dual plant systems. First, we present how these different model compartments were coupled with full plant physiology and functional soil hydraulics used for drought studies. We then present different parameterisation schemes in order to integrate photosynthetic rate with root water uptake within these sub-models, and evaluate how those different schemes can impact the simulation of the development of a whole plant system. Finally, we evaluate how plant growth is impacted by soil water deficit under different competitive conditions.

MATERIALS AND METHODS

ArchiSimple

Models of root system architecture have been often used for studying plant-soil interactions. These models are required to simulate the structural and spatial distribution of the root system in 3D, the integration of root level processes (e.g. elongation, branching) with soil properties, and root interaction with the airborne part of a plant. Only a few of them, however, have been integrated into larger crop or ecosystem models because they are too difficult to parameterise, and they require large amounts of computational power.

The ArchiSimple model has been designed to enable the representation of the architectural diversity of various plant species in interaction with environmental factors using a relatively small set of parameters (Pagès et al., 2014). It is a dynamic architectural and functional model, in which the root system is represented as a set of small segments and meristems. The root system is modified by functions describing their development, including emission of new roots from the shoot, elongation of existing roots, acropetal branching, radial growth, and self-pruning following root decay. Model parameters can be estimated independently from observations or from the literature. Calibration and evaluation for 6 species (Musa spp., Pisum sativum, Prunus persica, Teucrium botrys, Thlaspi perfoliatum, and Zea mays) were performed in Pagès et al. (2014).

Min3P

The Min3P model is designed to simulate 3D flow and multicomponent reactive transport in variably saturated media involving a set of homogeneous and heterogeneous reactions (Mayer et al., 2002). Several geochemical processes can be considered within Min3P including: aqueous speciation, mineral dissolution-precipitation, redox, intra-aqueous reactions, gas exchange, ion exchange, and competitive as well as non-competitive sorption.

Rainfall and irrigation can easily be included as boundary condition as a prescribed flux (e.g. Gérard et al., 2004; Maier et al., 2009; Jia et al., 2019). This can be performed by setting boundary conditions at discrete locations, in order to reproduce the presence of several irrigation spots or irregular rainfall.

Reactions that are microbiologically mediated can also be considered by Min3P. Regarding mass transport processes in porous media, the Min3P model solves Richard’s equation to simulate variably-saturated flow and both, solute and gas transport, that are solved using standard convective-dispersion equations.

This reactive transport model has been used to support multiple field and laboratory investigations including reactions of inorganic and organic substances and it has been developed to account for plant-soil interactions (Mayer et al., 2012). Accordingly, the Min3P model can also simulate water and solute dynamics in the rhizosphere. To this end, several biophysical processes have been implemented including: plant transpiration and soil evaporation, solute uptake/release by plants, and preferential flow (equilibrium scheme). The implementation of plant transpiration and preferential flow was required to accurately simulate soil moisture variations in a forest soil (Gérard et al., 2004, 2006). Plant uptake of solutes was added to support the modelling investigation of the Si-cycle (Gérard et al., 2008).

Note that the reduction function proposed by Battaglia and Sands (1997) was initially implemented into Min3P in order to cope with the effect of water deficit on plant transpiration (Gérard et al., 2004). Since then, the more conventional Feddes function (Feddes et al., 1978; Simunek and Hopmans, 2009) was implemented into Min3P.

Shoot FSP model

The shoot FSP model, implemented in the modelling platform GroIMP (Hemmerling et al., 2008; Zhu et al., 2015; Evers and Bastiaans, 2016), simulates growth and development of the aboveground parts of plants in 3D, at daily time steps, following internal physiological processes under the influence of external driving factors, such as light, temperature, vapour pressure deficit, and air pressure.

The virtual shoots are composed of: leaves, internodes, and spikes. The spikes function only as sinks for assimilates, while leaves and internodes work as sinks and sources (suppliers of assimilates via photosynthesis). Further description on light absorption, assimilate production, potential and actual organ growth, development and architecture can be found in Evers and Bastiaans (2016). Photosynthesis is calculated according to the Farquhar model of photosynthesis (Farquhar et al., 1980; von Caemmerer and Farquhar, 1981; von Caemmerer, 2000) as a function of leaf nitrogen content, leaf light capture, ambient temperature, and CO₂ level. Shoot development was simulated using rules that describe the production of new phytomers over time, as driven by air temperature. Anthesis occurred when a given number of leaves has been produced. Water limitation on photosynthesis is not considered in this model. The effect of fertilization is included as the gradient in leaf nitrogen content.

Besides the highly detailed light environment and aerial plant 3D architecture, the shoot model does not consider any sort of soil water or nutrients limitation into the calculations of carbon assimilation, mainly because of the simple representation of the root system as a sink of assimilates.

Modelling scenes

In order to address different aspects of plant development due to limited soil water availability, a 3D FSP model including shoot, root, and soil was constructed by linking three different well-stablished models: Min3P (Mayer et al., 2002; Mayer et al., 2012), ArchiSimple (Pagès et al., 2014), and a shoot FSP model (Hemmerling et al., 2008; Evers and Bastiaans, 2016). The new coupled model was evaluated in two different approaches: first, through the evaluation of the impact of soil moisture availability on plant productivity, in an experiment setup with one single plant of type cereal performed over 95 days; and second, through the evaluation of the impact of soil moisture on plant productivity in a virtual experiment simulated over 60 days using: i) a single plant (Iso) of two different species – monocot (cereal) and dicot (legume) –; ii) two plants of the same species (Mono); and, iii) two plants of different species (Inter).

The monocot and dicot phenotypes were chosen such that they capture general characteristics of typical cereal and broadleaf species, without being designed to represent particular species or varieties. In that way, the explorations done with the model have broad relevance rather than being significant for particular species or varieties only.

The goal of this study is to present and demonstrate the abilities of this new coupling framework between three well-developed and thoroughly tested models, and not to perform actual modelling predictions, which would require a totally different approach, such as the collection of real observed data, calibration, measuring of a large set of specific parameters, etc. This new modelling tool, however, opens up an innovative approach to explore different research questions at very fine scales with a vast number of parameters describing shoot, root, and soil properties.

The 3D FSP model with shoot-root-soil

For this study, three different models developed in different computing languages, different platforms, and by different teams from different disciplines were used to study heterogeneous intercropping systems with FSP models. One challenge of this approach is to couple different existing models that have been built separately (Marshall-Colon et al., 2017; Long et al., 2018). To do so, we followed the software strategy developed in OpenAlea (Pradal et al., 2008) where each model is viewed as a Python component. Rather than letting one component driving the others, each component can be viewed as a knowledge source with a well-defined interface in Python. The central loop is managed in Python while the different algorithms are executed in their respective computing language. To implement this strategy, we have built a Fortran/Python wrapper for Min3P using f2py and a C/Python wrapper for ArchiSimple using ctypes. The shoot FSP model is run in Java from Python and the result is retrieved through source files.

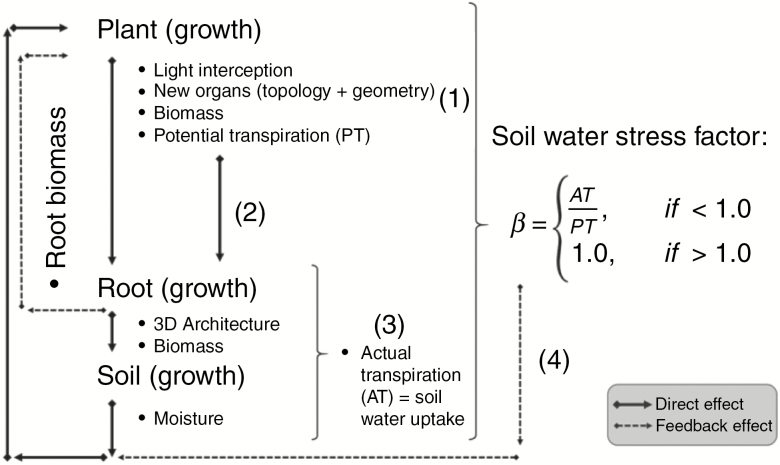
A scheme representing the coupling method is presented in Fig. 1. First, non-water limited potential photosynthesis is calculated by the shoot FSP model, following its default set of equations related to light, temperature, and nitrogen distribution.

Fig. 1.

Scheme describing the method used to couple MIN3P – ArchiSimple with the shoot FSP model. (1) photosynthesis is calculated; (2) potential transpiration (PT) is used to drive root growth in MIN3P – ArchiSimple; (3) actual transpiration (AT), i.e. root water uptake is calculated; (4) β is used to modulate photosynthesis based on soil water deficit and a new limited root biomass is calculated to generate a feedback effect for root growth before the next time step.

The shoot FSP model was adapted in order to calculate potential transpiration (PT) from stomatal conductance (g_s) following the original equation of Ball-Berry (Ball et al., 1987) and further implemented by Leuning (1995), considering that stomata respond to vapour pressure deficit (VPD) as:

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{P}\mathrm{T}={\mathrm{g}}_{\mathrm{s}}.1.56.\left(\mathrm{V}\mathrm{P}\mathrm{D}/{\mathrm{P}}_{\mathrm{a}\mathrm{i}\mathrm{r}}\right)}\end{array}}$$ (1)

where P_air is the atmospheric pressure. The ratio 1.56 is the inverse ratio of the square root of the molecular weights CO₂/air and H₂O/air, the latter referring equally to the diffusion of air through water vapour and water vapour through air. Details on equations and parameters used in the FvCB model of photosynthesis for C3 and C4 plants used in the shoot FSP model are given in Yin and Struik (2009).

Second, PT is used to drive root growth in Min3P – ArchiSimple. In Min3P, the potential physical evaporation is given by the product of potential evapotranspiration rate, PET (m.s^-1), and the solar energy ratio, R (dimensionless). This solar energy ratio corresponds to the ratio between the solar energy at the ground surface and the solar energy above the vegetation cover. Therefore, this variable ranges from unity in bare soils to less in the presence of a vegetation cover. Physical evaporation is not considered in these experiments, i.e. physical evaporation equals zero, and so, PET is equal PT. However, physical evaporation can be easily represented in Min3P. In Min3P, the flux of water leaving the system by physical evaporation is taken as a sink term in the Richards equation.

The reactive transport model Min3P was coupled with the root system architecture model, ArchiSimple, using a macroscopic approach at the plot or field scale by representing the root system in terms of root surface density in each control volume used to represent the soil domain (Gérard et al., 2017).

The coupling between Min3P and ArchiSimple was performed using a non-interactive sequential method. This novel soil-root coupling can describe geochemical processes using state-of-the-art thermodynamic and kinetic formalisms. Gérard et al. (2017) studied phosphorus acquisition from hydroxyapatite and pH variations in the root zone of an alkaline soil. Although the simulation of water uptake was also possible using the standalone Min3P-ArchiSimple version, this was not used by Gérard et al. (2017) since the authors neglected water uptake and considered a soil profile at hydrostatic equilibrium. Root growth is limited in ArchiSimple through a maximum value of root biomass given by the shoot FSP model.

Third, actual transpiration (AT), i.e. root water uptake is calculated based on the actual size of the root (given by ArchiSimple), i.e. the surface of the root in direct contact with the soil, and the water flux leaving the soil driven by PT. In the root water uptake model defined by Feddes et al. (1978, 2001), the sink term is a function of potential transpiration, the vertical root distribution, and the pressure head, which depends on soil intrinsic properties and soil moisture (Cai et al., 2018).

Finally, the soil water stress factor (β) is calculated as AT divided by PT and it is used to modulate photosynthesis based on soil water deficit. A new limited photosynthesis and a new root biomass are calculated to generate a feedback effect for root growth before the next time step. The ways water deficit limits photosynthesis is discussed in the next section.

Parameterisation schemes of soil moisture stress due to water deficit

To account for soil moisture deficit on carbon assimilation and plant development, the β factor was used to modulate different variables within the shoot FSP model depending on the applied parameterisation scheme. Three different approaches based on different parameterisation schemes used in land surface models were applied to the new coupled model, in order to capture the spread of the impact on carbon assimilation and plant development caused by the application of different parameterisation schemes of soil water stress in response to water shortage. Approximately 40–80 % of the intermodel variability of carbon assimilation by land surface models is due to the functional form of the utilised parameterisation scheme of soil water limitation alone (Powell et al., 2013; Trugman, et al., 2018).

The first scheme used to simulate the impact of soil water availability on carbon assimilation and plant development was based on an empirical reduction factor described in Cox et al. (1998) and tested (Egea et al., 2011) in the land surface model of the UK Earth System Model, JULES (Best et al., 2011; Clark et al., 2011). This method consists in multiplying the carbon assimilation rate and plant respiration by the soil moisture availability factor (β), which is defined as the ratio between actual transpiration (AT) and potential transpiration (PT) calculated by the shoot FSP model. In the first limitation scheme, β factor is multiplied by the rate of gross photosynthesis (A_n) and autotrophic respiration (R_d), as described in eqn 2:

$${\displaystyle \begin{array}{l}{\displaystyle \begin{array}{ll}& {\displaystyle {{\mathrm{A}}_{\mathrm{n}}}^{\mathrm{l}\mathrm{i}\mathrm{m}}=\beta .{\mathrm{A}}_{\mathrm{n}}}\\ & {\displaystyle {{\mathrm{R}}_{\mathrm{d}}}^{\mathrm{l}\mathrm{i}\mathrm{m}}=\beta .{\mathrm{R}}_{\mathrm{d}}}\end{array}}\end{array}}$$ (2)

The second parameterisation scheme was based on an empirical reduction function described in Thornton and Zimmermann (2007), where a soil moisture limitation function acts on the leaf-scale maximum carboxylation capacity of Rubisco (V_cmax) only. This method was thoroughly tested (Oleson et al., 2008) in the land surface model CLM (Bonan et al., 2014). The second parameterisation scheme was implemented in the new coupled model and it is described in eqn 3:

$${\displaystyle \begin{array}{l}{\displaystyle {{\mathrm{V}}_{\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}}^{\mathrm{l}\mathrm{i}\mathrm{m}}=\beta .{\mathrm{V}}_{\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}}\end{array}}$$ (3)

The third and last parameterisation scheme implemented in the shoot FSP model is applied by modifying the photosynthetic parameters V_cmax and J_max at the same time. This scheme is used in the land surface model G’DAY (Comins and McMurtrie, 1993; Medlyn et al. 2000; Corbeels et al. 2005a,b) and it is given by eqn 4:

$${\displaystyle \begin{array}{l}{\displaystyle \begin{array}{ll}& {\displaystyle {{\mathrm{V}}_{\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}}^{\mathrm{l}\mathrm{i}\mathrm{m}}=\beta .{\mathrm{V}}_{\mathrm{c}\mathrm{m}\mathrm{a}\mathrm{x}}}\\ & {\displaystyle {{\mathrm{J}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}^{\mathrm{l}\mathrm{i}\mathrm{m}}=\beta .{\mathrm{J}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}\end{array}}\end{array}}$$ (4)

Although the Ball-Berry parameterisation scheme is based on a linear approximation of the relationship between stomatal conductance and carbon assimilation, its implementation in models requires the closure of a rather complex system with three equations and three unknows, i.e. net carbon assimilation, stomatal conductance, and leaf internal CO₂ concentration. This first requires an estimate of carbon assimilation through the FvCB photosynthesis model (Farquhar et al., 1980). In the FvCB model, the Rubisco-limited CO₂ assimilation rate, or carbon limited regime, the RuBP regeneration-limited CO₂ assimilation rate, or light limited regime, and the leaf respiration rate are calculated. However, both limiting regimes depend on leaf internal CO₂ concentration, which itself depends on carbon assimilation rate and stomatal conductance through the leaf CO₂ diffusion equation. Iterative numerical solutions are needed to account for dependences of stomatal conductance and net photosynthesis on VPD and temperature (Collatz et al., 1991; Franks et al., 2017).

Simulation protocol

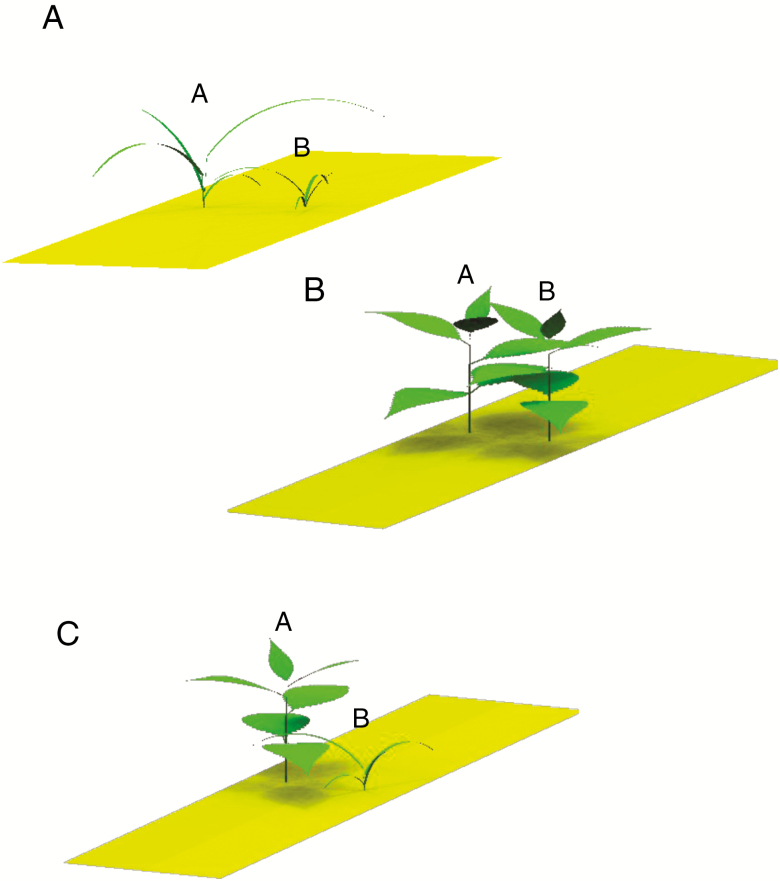
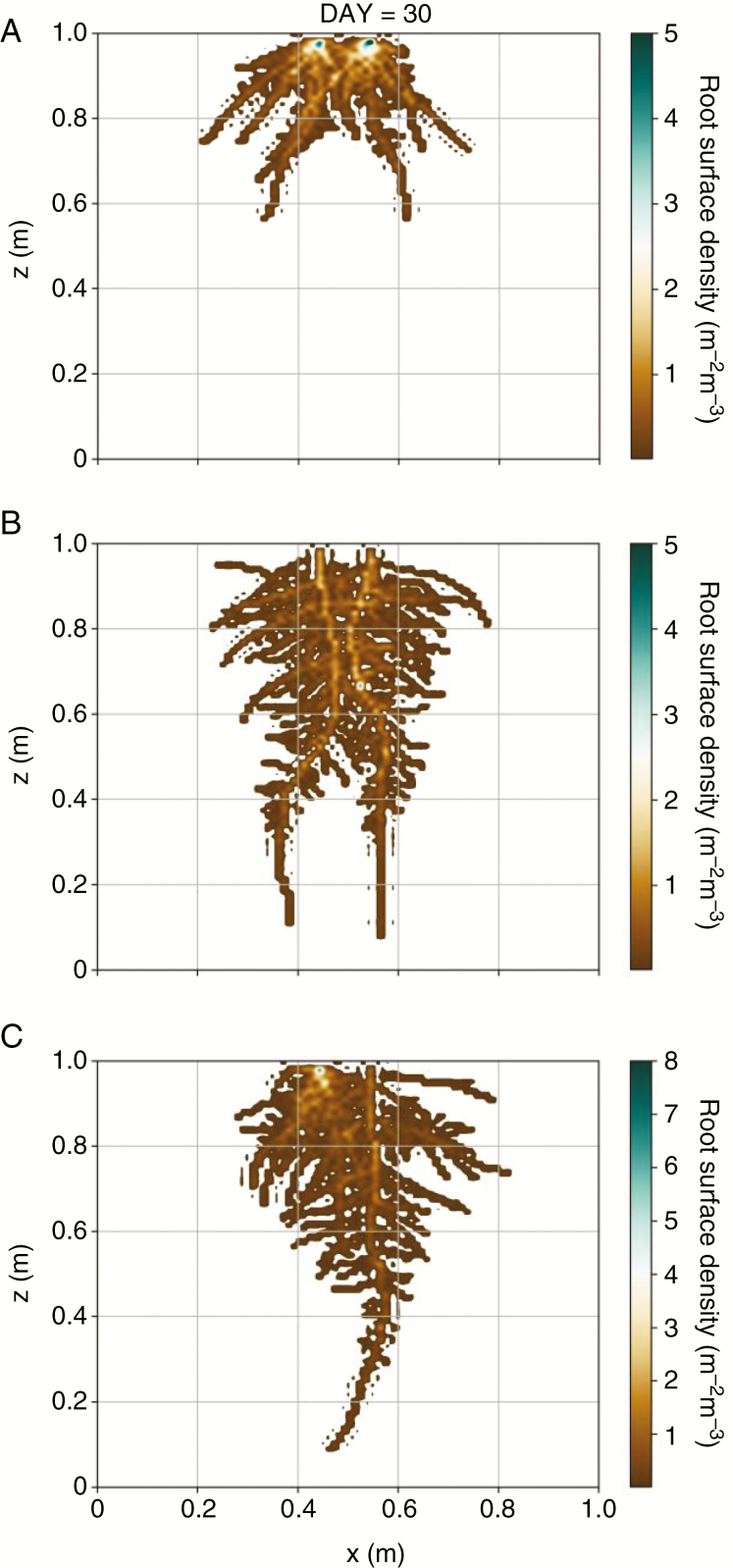
For evaluation purposes, we applied the coupled model to different domains, including: i) a sensitivity analysis of carbon assimilation and plant development to different parameterisation schemes of soil water stress due to reduced soil water availability; and ii) simulation of plant growth under different scenarios including isolated plants, intraspecific competition (two plants of the same species), and interspecific competition (two plants of different species) (Fig. 2 and Fig. 3).

Fig. 2.

Representation of shoots in three different modelling setups corresponding to day 30 after sowing; A: two monocot shoots (Intra monocot); B: two dicot shoots (Intra dicot); and C: one monocot shoot and one dicot shoot (Inter). Plant A is the one on the left of the plot and Plant B is the one in the right of the plot.

Fig. 3.

Representation of root systems in three different modelling setups corresponding to day 30 after sowing; A: two monocot root systems (Intra monocot); B: two dicot root systems (Intra dicot); and C: one monocot and one dicot root systems (Inter).

In a first evaluation of the impact of soil moisture availability on plant productivity, an experiment with one single plant of type cereal was performed over 95 days. The section of the soil profile was 1 m² (1 m × 1 m), and 1 m depth. In this modelling exercise, soil hydraulic properties were representative of a silty soil (Schaap and Van Genuchten, 2006) and the water table was set at 5 m depth as bottom boundary condition. No water flux was set at the sides or top boundary of the evaluated soil profile. Initial soil moisture profile corresponds to hydrostatic equilibrium, i.e. when water is at rest, or when the flow velocity at each point is constant over time.

The β values varied from 0 to 1 in 0.01 intervals and they were set constant throughout each one of the 95 days for 100 runs performed with the shoot model. The β values were applied to the shoot model following each one of the three parameterisation schemes described in the previous section and referred to as: Scheme 1 (eqn 1), Scheme 2 (eqn 2), and Scheme 3 (eqn 3). The results shown are associated with the development stage referred to as ‘dough’ in day 60.

As a second evaluation of the impact of soil moisture on plant biomass, several simulations were performed over a shorter time, 60 days, but using either a single plant (Iso) of two different species – monocot (cereal) and dicot (legume) –, or two plants of the same species (Mono), or two plants of different species (Inter). The impact of water limitation was evaluated by running the coupled model with β parameterisation scheme 1 turned on (Iso_β, Intra_β, and Inter_β) and turned off (Iso, Intra, and Inter). In this modelling exercise, the seed of an isolated plant was placed 10 cm deep and positioned at the centre of the soil profile. In the case with two plants, the two seeds were placed 10 cm apart from one another. We arbitrarily set the space in between plants to 10 cm for simplicity. Our goal in this study is to present and demonstrate the abilities of an innovative coupling framework, and not to model actual data.

All parameters describing a monocot plant of type cereal in the shoot FSP model are described in Supplementary data Table S1 and describing a dicot plant of type legume is described in Supplementary data Table S2. Atmospheric variables used in the run are described in Supplementary data Table S3. Parameters describing a root of type cereal in ArchiSimple are described in Supplementary data Table S4 and parameters describing a root of type legume are described in Supplementary data Table S5. Soil hydraulic properties and parameters of the reduction function for the effect of water deficit on plant transpiration (Feddes) are shown in Supplementary data Table S6. Soil hydraulic parameters used for a representative silty soil are shown in Supplementary data Table S7.

RESULTS

Sensitivity of plant productivity to soil water stress due to water shortage

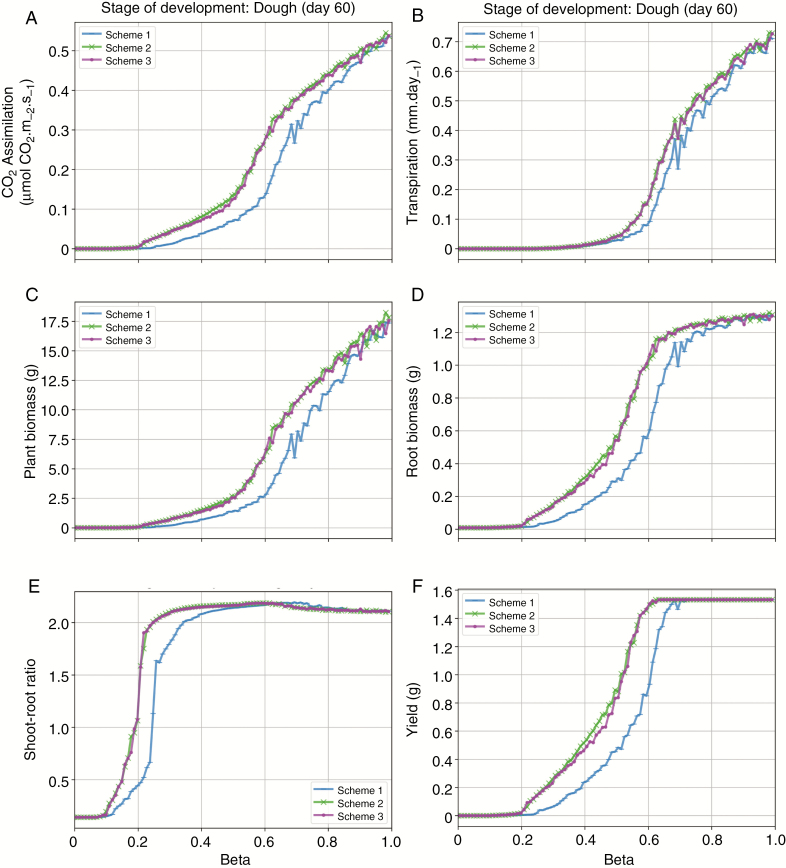
It can be seen in Fig. 4 that for all the evaluated variables, a β value below 0.2 completely stopped CO₂ assimilation, as well as plant and root biomass growth, and plant yield in the dough stage of development.

Fig. 4.

Effects of three different parameterisation schemes of soil water stress factor in response to water shortage, β on single cereal plant variables: A: CO₂ assimilation (μmol CO₂ m^-2 s^-1), B: transpiration (mm.day^-1), C: plant biomass, D: root biomass (g), E: shoot-root ratio, and F: yield (g) for the dough development stage (day 60 after sowing).

For transpiration, the same is verified for β under 0.4, and for shoot-root ratio, changes start to appear from β approximately equal to 0.1. This behaviour of the model indicates that for the three evaluated parameterisation schemes of soil water stress in response to water shortage, a value of root water uptake equal to or smaller than 20 % of the potential plant transpiration should be fatal for plant development.

Results of this first model evaluation also showed that the variables CO₂ assimilation and transpiration were more impacted by β parameterisation schemes in comparison to the variables plant and root biomass, as well as yield. For example, for β = 0.5, transpiration and CO₂ assimilation were 4 times smaller than in a scenario with β = 1.0 in the dough stage of development. For the other variables, root biomass and yield, β = 0.5 gave values approximately 2.5 times smaller than for β = 1.0. This result indicates that variables directly related to photosynthesis are more sensitive to β than variables that depend on biomass allocation, for example.

For root biomass and yield (Fig. 4), β over 0.7 had little or no impact on the final output, which indicates that, according to the new model, in episodes of root water uptake equal or greater than 70 % of the required potential transpiration, cereals can allocate biomass, even though the photosynthesis is reduced. In this sensitivity analysis, it was possible to observe a higher impact of soil water deficit in photosynthesis than in carbon allocation for an individual plant of type cereal.

The shoot-root ratio is impacted by water deficit in this stage of development when water supply is between 10 % and 30 % of water demand (Fig. 4). If water supply is smaller than 10 % of the demand, there is no plant growth, and if it is above 30 % the shoot has 2 times more biomass than the root.

Between β = 0.1 and β = 0.2, carbon assimilation, shoot biomass, and root biomass were all very close to zero. However, this behaviour is not due to the divergence between ArchiSimple and shoot FSP model. All plots in Fig. 4 come from shoot FSP model alone, before the coupling. We believe this behaviour is triggered by the way in which the shoot FSP model deals with carbon allocation. The model allocates most part of the carbon very quickly to the shoot instead of to the root, which makes shoot-root ratio increase substantially at a high rate for small β values.

Among the evaluated β factor parameterisation schemes, Scheme 1 presents the strongest impact on all evaluated variables, and because of that, only Scheme 1 is used on the following evaluations.

The impact of limited water uptake and spatial plant distribution on plant biomass

In the second evaluation, the maximum total plant biomass of isolated monocot with soil water limitation considered was 3.2 g plant^-1, which corresponds to 43.7 % less total plant biomass than the case without soil water limitation. In the case of a dicot plant, the maximum total plant biomass of isolated dicot with soil water limitation was 16.7 g plant^-1, which corresponds to 6.9 % less total plant biomass than the case without soil water limitation considered (Table 1).

Table 1.

The maximum biomass and water uptake of monocot and dicot estimated for a single plant (Iso) of two different species – monocot (cereal) and dicot (legume) –, or two plants of the same species (Intra), or two plants of different species (Inter). The impact of water limitation was evaluated by running the coupled model with β parameterisation scheme 1 turned on (Iso_β, Intra_β, and Inter_β).

		Monocot						Dicot
		Iso	Isoβ	Intra	Intraβ	Inter	Interβ	Iso	Isoβ	Intra	Intraβ	Inter	Interβ
Max. biomass (g.plant -1)	Total	5.62	3.16	5.55	5.01	5.56	0.61	17.92	16.68	17.88	9.4	17.89	16.45
	Shoot	4.30	2.42	4.26	3.92	4.26	0.46	16.06	14.93	16.02	8.43	16.03	14.72
	Root	1.32	0.74	1.29	1.09	1.30	0.16	1.86	1.75	1.86	0.97	1.86	1.73
	Shoot/root	3.26	3.26	3.29	3.59	3.29	2.95	8.62	8.54	8.62	8.72	8.62	8.52
Max. water uptake (g.plant -1)	Total	2.72	1.10	2.24	1.85	1.59	0.25	14.46	13.77	8.79	3.92	11.25	10.59

Similarly, the maximum shoot and root biomass of isolated monocot with soil water limitation considered was 43.7 % and 43.9 %, respectively lower than that of the isolated monocot without soil water limitation. For a dicot plant, these values were 7.0 % and 6.2 % lower for shoot and root biomass respectively, when comparing the case with soil water limitation and the one without it. The change in the value of shoot biomass caused by soil water deficit applied through the parameterisation scheme 1 among monocot was slightly smaller than the change in root biomass. The opposite behaviour is observed among dicot.

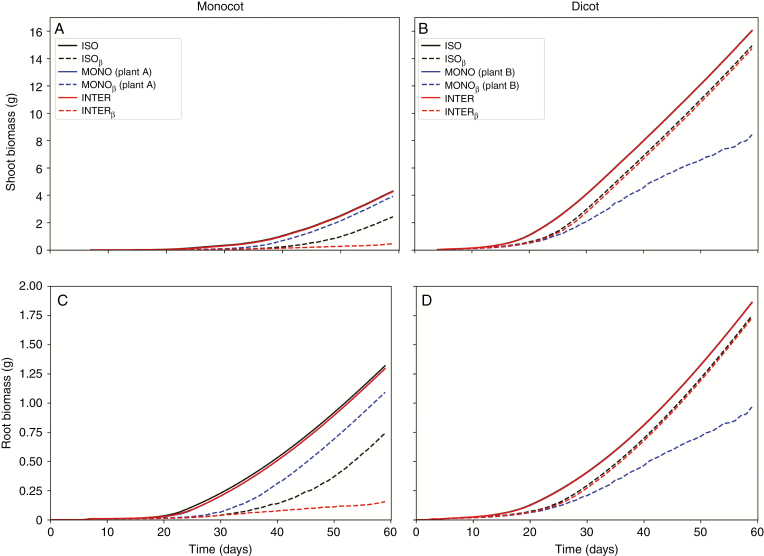
Divergences of biomass production between curves with and without soil water limitation can be seen in shoot of a monocot plant from day 30, and in root biomass from day 20, becoming pronounced towards day 60 (Fig. 5).

Fig. 5.

Cumulative biomass production. A, B: shoot biomass of monocot and dicot, respectively; C, D: root biomass of monocot and dicot, respectively. ISO: isolated plants without water limitation; ISO_β: isolated plants with water limitation; MONO: monocropped plants without water limitation; MONO_β: monocropped plants with water limitation. INTER: intercropped plants without water limitation; INTER_β: intercropped plants with water limitation. Plant A is the one on the left and Plant B is the one in the right of the plot indicated in Fig. 2.

Changes in the order of 1 % probably have no biological significance, but they are communicated either way in order to inform the reader about theoretical differences between the evaluated cases. The maximum total plant biomass of monocropped monocot without soil water limitation considered was 5.6 g plant^-1, which corresponds to 1.2 % more total plant biomass than the isolated case without soil water limitation considered. In the case of dicot, the maximum total plant biomass of intercropped dicot without soil water limitation considered was 17.9 g plant^-1, which corresponds to less than 1.0 % more total plant biomass than the case without soil water limitation considered (Table 1). Similarly, the maximum shoot biomass and root biomass of monocropped monocot without soil water limitation considered was, respectively, 1.9 % and 1.0 % less than that of isolated monocot without soil water limitation. Differences in shoot and root biomass were 8.0 % and 15.6 % lower in the monocropped monocot with soil water limitation than without soil water limitation. The difference in shoot biomass caused by monocropped monocot species without considering water limitation was smaller than the difference in root biomass.

For dicots, the maximum shoot and root biomass of monocropped plants without soil water limitation was 0.2 % less than that of the isolated monocot without soil water limitation. Differences were 47.4 % less shoot biomass and 48.0 % less root biomass when comparing monocropped dicot with and without soil water limitation. The difference in shoot biomass in monocropped dicot species without water limitation was smaller than the difference in root biomass.

The maximum total plant biomass of intercropped monocot without soil water limitation was 5.6 g plant^-1, which corresponds to 1.1 % less total plant biomass than that of the isolated case without soil water limitation considered. In the case of dicot, the maximum total plant biomass of intercropped dicot without soil water limitation was 17.9 g plant^-1, which corresponds to less than 0.2 % in total plant biomass than the isolated case (Table 1). Similarly, the maximum shoot and root biomass of intercropped monocot without soil water limitation was 0.9 % and 1.8 %, respectively lower than that of the isolated monocot without soil water limitation. Differences were 8.2 % less shoot biomass and 7.1 % less root biomass when comparing intercropped dicot without soil water limitation and with soil water limitation. The difference in shoot biomass caused by intercropped monocot and dicot species without considering water limitation was larger than the difference in root biomass for dicot and smaller for monocot.

When considering both effects together, i.e. soil water limitation and intercropped species, the maximum total plant biomass of intercropped monocot with soil water limitation considered was 0.6 g plant^-1, which corresponds to 80.7 % less total plant biomass than the isolated case with soil water limitation considered. In the case of dicot, the maximum total plant biomass of intercropped dicot with soil water limitation considered was 16.5 g plant^-1, which corresponds to 1.4 % less total plant biomass than the isolated case with soil water limitation (Table 1).

Through our modelling framework it is possible to categorize imbalanced resource access by plants. For example, the effects of water limitation can be determined through the evaluation of runs with versus runs without the β parameterisation. In the same way, the comparison between an isolated plant versus a plant growing next to another one of the same, or of a different species enable us to determine the influence of the light environment on plant growth. In the scenarios simulated here, the total biomass of a monocot at day 60 after sowing is 43.6 % smaller when water limitation is considered, while it is only 3.9 % smaller when growing next to a dicot plant. In the conditions set in these scenarios, water limitation is almost 10 times more impacting for plant growth than the light environment. The coupled model can simulate whether a plant A is able to dominate the light environment as much as the water resource, and if so whether the outcompeted plant B loses more assimilation because of water deficit or shading.

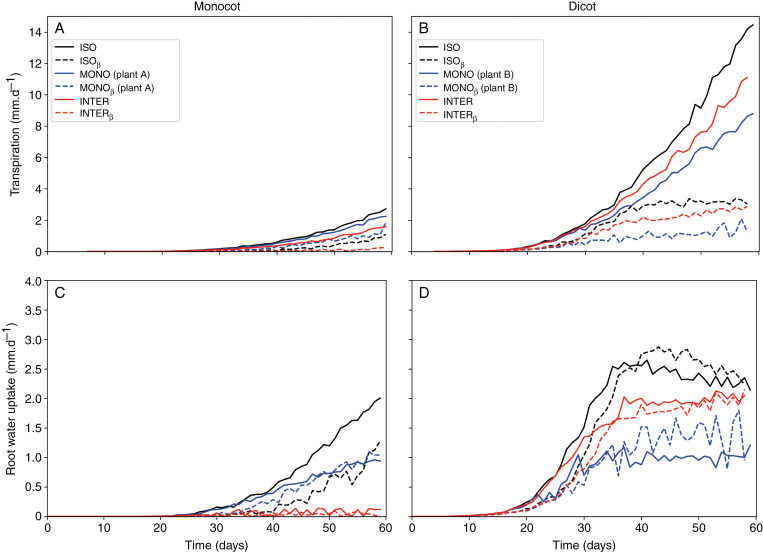
Impact of limited root water uptake and plant spatial distribution on transpiration

The maximum transpiration of both species was influenced by soil water availability and intercropping (Fig. 6A). In Fig. 6 and throughout the manuscript, evapotranspiration is equal to transpiration. In the cases where β is considered (all scenarios described as ‘scenario_β’), root water uptake is approximately equal to actual transpiration, and the missing root water uptake to support the current transpiration is carried into the next time step in order to reduce photosynthesis and therefore transpiration. For runs without β, potential transpiration is always higher than root water uptake, which indicates that the shoot model standalone always requires more water to support photosynthesis than the current soil state can support. The shoot model uses more water than the root model is supposedly sending to it and considering β to reduce shoot productivity, i.e. β < 1, is crucial for a realistic representation of plant productivity. Making use of the β parameterisation scheme to account for the effects of soil water deficit on plant productivity is indirectly accounting for the effects of hydraulic conductivity in the soil by Min3P through the Mualem-Van Genuchten scheme (Mualem, 1976; van Genuchten, 1980) in combination with the root water uptake function originally proposed by Feddes et al. (1978).

Fig. 6.

Cumulative water fluxes. A, B: total transpiration in mm.day^-1 of monocot and dicot; C, D: total root water uptake in mm.day^-1 of monocot and dicot. ISO: isolated plants without water limitation; ISO_β: isolated plants with water limitation; MONO: monocropped plants without water limitation; MONO_β: monocropped plants with water limitation. INTER: intercropped plants without water limitation; INTER_β: intercropped plants with water limitation. Plant A is the one on the left and Plant B is the one in the right of the soil profile.

Maximum transpiration by intercropped monocot was 41.5 % smaller than that of isolated monocot without soil water limitation and 77.3 % with soil water limitation. In contrast to transpiration in monocot, interaction of neighbouring dicot had a weaker effect on transpiration, which was 22.2 % smaller than the isolated plant without considering water limitation and 23.1 % larger than the isolated plant when considering water limitation. Dicot had a greater maximum transpiration per plant than monocot in both, isolated and intercropped systems (Fig. 6B).

The maximum root water uptake of both species was also influenced by soil water availability and intercropping (Figs. 6C, D). The root water uptake by intercropped monocot was 99.9 % smaller than that of isolated monocot with soil water limitation. Interaction of neighbouring dicot had a negative impact on transpiration, which was in average 11.5 % smaller than the isolated plant considering water limitation. Dicot had a greater maximum root water uptake per plant than monocot in all cases, isolated, monocropped, and intercropped systems, increasing with time until about day 40 (Fig. 6D) and decreasing afterwards for an isolated plant, and stabilizing for the monocropped and intercropped scenarios.

The monocropped scenario for dicot had in general lower transpiration and root water uptake than the isolated plant and the intercropped case. Two dicot plants 10 cm apart from each other exhausted soil water content more rapidly than the other two evaluated cases. That was not observed for monocot plants. In the case of a monocot plant, the isolated case presented highest rates of transpiration and root water uptake, followed by the monocropped case, while the intercropped case presented very low values for both variables.

Soil water limitation also works by delaying the peak of root water uptake. For an isolated and monocropped dicot, root water uptake with soil water limitation reaches its peak in average 5 days later than in cases without soil water limitation. This can be explained by the fact that water limitation impacts carbon assimilation and therefore plant development. Plants growing under the effect of soil water limitation reach their peak on transpiration later than the ones growing without this effect. By comparing root water uptake of an isolated dicot in the cases with and without β, it is possible to notice that while in the non-water limited case the peak occurs around day 35 after sowing, in the water limited case, the peak occurs around day 45 after sowing.

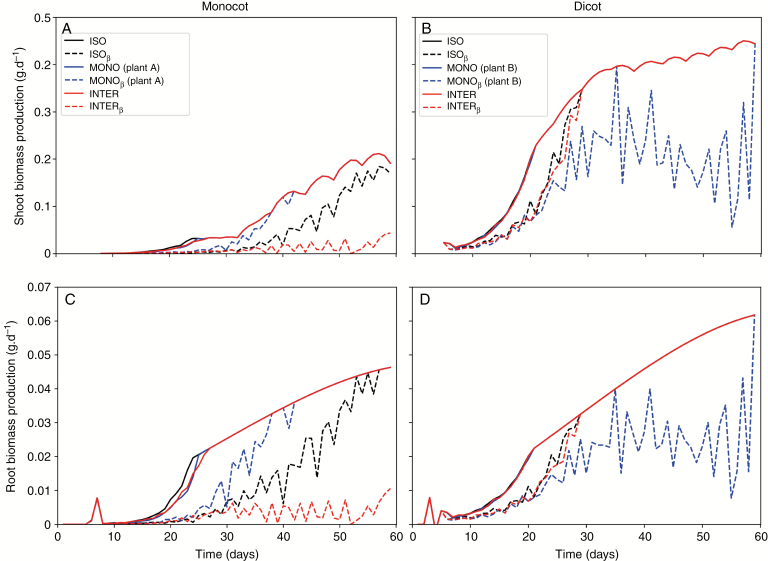
Despite the large variability among monocot and dicot plants, for a dicot plant in this study, the impact of intercropping on biomass production rate seems to be negligible (see Fig. 5). However, soil water limitation impacts biomass production rate until approximately day 30 by reducing it in average of 37.6 ± 5.8 % in the intercropped case, and 39.2 ± 5.6 % in the isolated case. Although a plant of type dicot has biomass production rate less impacted by soil water availability than a monocot plant, the intercropped case seems to be also less impacted by soil water limitation than the isolated case for a monocot plant.

Soil water availability and different spatial configurations on planting monocots and dicots also impact the rate of biomass production (Fig. 7). Throughout all 60 days, monocot and dicot plants presented roughly the same biomass production rate for shoots and roots when comparing different spatial plots, with only observable variations on a critical period from day 10 to 25 for monocot, and 5 to 20 for dicot. After these critical periods biomass production rate converges to the same values for all cases without soil water limitation considered.

Fig. 7.

Biomass production rate (g.plant^-1.d^-1). A, B: shoot biomass of monocot and dicot; C, D: root biomass of monocot and dicot. ISO: isolated plants without water limitation; ISO_β: isolated plants with water limitation; MONO: monocropped plants without water limitation; MONO_β: monocropped plants with water limitation. INTER: intercropped plants without water limitation; INTER_β: intercropped plants with water limitation. Plant A is the one on the left and Plant B is the one in the right.

For the cases considering soil water limitation, monocots presented major impact when intercropped, followed by the isolated plant, and finally, by monocropped. The differences in all three scenarios is pronounced, but especially regarding the intercropped case where the biomass production rate is much lower than the other two cases and does not converge for the case where soil water limitation is not considered.

Dicots on the other hand presented major impact when monocropped, followed by the isolated and intercropped presenting roughly the same behaviour. Biomass production rate for the isolated and intercropped plant with soil water limitation differs from the scenarios where soil water limitation is not considered between the beginning of plant development until about day 30, converging to the case without soil water limitation after that. The monocropped presents the most impacted biomass production rates with values twice smaller than the case without soil water limitation.

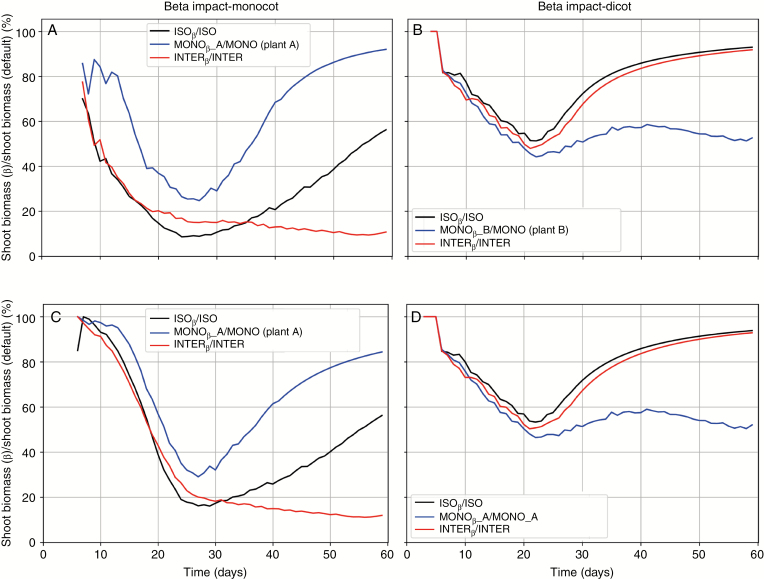
Plant-plant competition, as well as the effect of soil water limitation were both captured by the model. Fig. 8 summarises the relative difference in shoot and root biomass (%) over three different spatial configurations for effects of soil water deficit on biomass production. Soil water deficit impacted shoot and root biomass of both plant species by increasingly reducing them during the critical growth period, i.e. from day 10 after sowing to approximately day 25 for monocot; and for day 8 after sowing to approximately day 22 for dicot. After the critical period, soil moisture deficit also impacted biomass but relatively less towards the end of the growing period.

Fig. 8.

Relative difference in biomass (%). A, B: shoot biomass with soil water limitation divided by the shoot biomass without soil water limitation for a single plant, monocropped, and intercropped for monocot and dicot; C, D: root biomass with soil water limitation divided by the root biomass without soil water limitation for a single plant, monocropped, and intercropped for monocot and dicot; ISO_β: isolated plants with water limitation; MONO: monocropped plants without water limitation; MONO_β: monocropped plants with water limitation. INTER: intercropped plants without water limitation; INTER_β: intercropped plants with water limitation. Plant A is the one on the left and Plant B is the one in the right.

DISCUSSION

This study presented a novel approach to model 3D plants in intra- and interspecific competition, in conditions of soil water limitation and hydrodynamics. We first implemented three parameterisation schemes at plant scale. These parameterisation schemes are based on the following hypothesis: at every time step of the simulation, calculating the water demand by the plant through plant transpiration (eqn 1). The information on water demand is passed on to the root system by taking up water from the soil. Soil conditions and root architecture determine the amount of available water to the whole plant through a macroscopic approach, in which more root density corresponds to more root water uptake, as long as soil moisture is available. An eventual lack of water is calculated through the equation presented in Fig. 1 and may impact plant carbon assimilation on the following time step of the simulation. Before moving on the next time step, the shoot model calculates a new value of root biomass, which may or may not be limited by water, and this new value limits root growth in the next time step of the coupled model, a feedback effect of limitation in shoot growth on root growth. It is possible that the model time step could impact the outcome of these simulations. However, the same time step of one day was used throughout all runs, including control runs.

Concerning the rules of soil water limitation on plant growth, we assumed that in the case of complete water demand being not satisfied, the reduction factor coefficient (β) can impact a group of different variables following each one of the three proposed parameterisation schemes: 1) limiting carbon assimilation (A_n) plus autotrophic respiration (R_d) (eqn 2); 2) reducing the maximum rate of carboxylation (V_cmax) only (eqn 3); and 3) reducing V_cmax and the maximum rate of electron transport (J_max) at the same time (eqn 4). In all tested parameterisation schemes, modifying total carbon assimilation and autotrophic respiration presented a higher impact on carbon assimilation, transpiration, plant and root biomass, and yield than modifying V_cmax only, or V_cmax and J_max at the same time. These assumptions allowed testing a simple implementation to evaluate an increased intrinsic water user efficiency of a monocot plant (e.g. wheat) when grown with a dicot plant (e.g. faba bean, common bean) reported from experimental observations (Chapagain and Riseman, 2015). Simulations for interspecific plant competition were performed with the parameterisation scheme 1, because it showed greater impact on all the evaluated variables. They allowed reproducing the impacts of soil water limitation on plant growth over all cases (isolated, intra, and interspecific competition), as intercropping benefits had been previously demonstrated experimentally with an enhanced water use efficiency and yield production of a cereal-legume intercrop compared to an isolated plant (Chen et al., 2018).

The results simulated in this study indicated a general negative impact of a dry soil on plant biomass, root water uptake, and plant biomass production rate for both evaluated plant species, but more emphasized on monocot than on dicot. Despite the large variation in each plant group, it has been previously reported that monocot plants usually present lower drought-induced yield reduction compared to dicot plants (Daryanto et al., 2017). However, their study did not focus directly on plant biomass production. Also, the study cases evaluated in here depend on a number of different parameters defining the competition between species for water acquisition. For example, in the cases presented in here, the dicot plant had a growth coefficient of 2.5, while the monocot had a growth coefficient of 1.5 (see Supplementary data Tables S4 and S5). In this case, the root system of the dicot plant presented deeper elongation than its peer monocot causing a higher level of soil water stress in the monocot plant than the dicot plant. In different combinations of monocots and dicots, for example, a monocot species that extends its roots deeper than the dicot plant could present an advantage to access deeper available water in the soil.

The processes by which one plant species improves the environmental condition to another species are referred to as facilitation. Usually facilitation occurs by a dicot providing nitrogen/phosphorus to a monocot, but some species with deep root systems can supply water to other species by hydraulic lift (Bybee-Finley and Ryan, 2018). Even though the current coupled model does not explicitly take hydraulic lift into account, the effect of soil water capillarity is considered by Min3P, and it indirectly impacts the water availability of one plant next to another plant with access to deep water tables.

Interspecific competition has an impact on vertical root density distribution for both plant species (Supplementary data Fig. S1). On day 60, the vertical distribution of root surface density of a monocot did not present major differences in the first 40 cm depth when comparing soil water limitation or different spatial arrangements. However, after around 40 cm depth, the interspecific competition case presented a smaller root system than the intraspecific competition and isolated plant.

For the dicot plant the vertical distribution of root surface density had its peak ranging from 20 cm and 40 cm depth, with the intraspecific case presenting the lower mean root surface density than the other two evaluated cases.

It is reported that during critical growth stages, it is particularly important to maintain plant water supply (McLaughlin and Boyer, 2004) and plants seem to regulate their water loss as a function of the amount of available water in the soil (Jones, 1990). This effect suggests that plants must be able to ‘perceive’ the degree of soil water deficit and respond to it, for example, by regulating their stomatal conductance (Du et al., 2015). The current coupled model was able to replicate stomatal conductance regulation by decreasing it in scenarios with soil water deficit (Figs. 6A and B).

This new coupled model adds to the ongoing challenge of efficiently coupling models of multiple plant and soil compartments, and it presents an exclusive approach when in contrast with other models of the same kind. For example, much previous work on intercropping has used models that ignored the light environment, considering only soil resources (e.g. Postma and Lynch 2012), while other models specifically designed for intercropping (e.g. Dupraz et al. 2019) may consider light environment and soil resources (e.g. water and nitrogen) but be designed to work on very different scales.

The potential of this new coupled model is related to its use as a tool for the development and testing of concepts, as well as the prediction of mechanisms and trends on single, monocropped, or intercropped plants. The model may be further extended to different phenotypes by estimating genotype performance based on measured root/shoot phenotypes.

The impact on respiration was not directly evaluated in this study mainly because the FSP shoot model treats autotrophic respiration as a fraction of assimilated CO₂. Maintenance respiration is 0.015 gr CO₂/ gr plant biomass/ per day and growth respiration is 0.3 in fraction biomass. Heterotrophic respiration is not directly modelled in this study, but the ecological importance of this variable should be taken into account in future model development.

Future development may include new processes, such as root plasticity due to drought responses, as well as soil chemistry once our mechanistic understanding of water limited processes can be analogously implemented to nitrogen and phosphorus limitation for plant growth (Fisher et al., 2010; Brzostek et al., 2014). V_cmax and J_max have been linked to leaf nitrogen concentration and phosphorus availability, which impacts distinct aspects of plant physiology, such as membrane solubility, ATP, and NADPH production (Walker et al., 2014). Therefore, the implementation of nutrients limitation into the FvCB model of photosynthesis can lead us to new insights in our understanding of plant and crop resource development.

CONCLUSION

This study demonstrated that it is possible to simulate an integrated system of shoot 3D architecture and biomass development with a 3D root system representation, and water uptake, with both, light limitation and soil hydraulics. This novel macroscopic approximation for plant growth enables integrated simulations of crop development under different conditions of light, temperature, and carbon concentrations, as well as available water in the soil. This new approach also makes possible studies using virtual plant models to better understand competition between crops both above- and below-ground. A comparison study with two different types of plants (monocot and dicot) growing in three different arrangements (isolated, intra, and interspecific competition) showed that the model is a tool capable to simulate soil water limitation to plant development and to explore the processes involved in soil-root-shoot-atmosphere interactions, of particular importance for the analysis and exploration of intercropping scenarios.

SUPPLEMENTARY DATA

Supplementary data are available online at https://academic.oup.com/aob and consist of the following.

Table S1 Parameters related to cereal plant in the shoot FSP model.

Table S2 Parameters related to dicot plant in the shoot FSP model.

Table S3 Environmental and spectral variables used in the shoot FSP model.

Table S4 Monocot root parameters in ArchiSimple .

Table S5 Dicot root parameters in ArchiSimple.

Table S6 Parameters related to the soil in MIN3P.

Table S7 Soil hydraulic parameters used for a representative silty soil.

Fig. S1.Vertical and horizontal profiles of mean root surface density for all cases.

Fig. S2. Spatial distribution of root surface density for intercropped monocot and dicot.

Fig. S3 Spatial distribution of root surface density for an isolated monocot and dicot, and monocropped monocot and dicot.

Fig. S4. Vertical profile of soil moisture availability for an individual monocot plant growing without soil limitation.

Fig. S5. Water saturation profile at hydrostatic equilibrium set as initial condition for the modelling.

FUNDING

This research was supported by the European Research Council under the European Union’s Horizon 2020 research and innovation program Remix (Redesigning European cropping systems based on species mixtures, https://www.remix-intercrops.eu/) [grant number 727217].