Abstract
Background and Aims
Understanding how climate change influences crop productivity helps in identifying new options to increase crop productivity. Soybean is the most important dicotyledonous seed crop in terms of planting area. Although the impacts of elevated atmospheric [CO2] on soybean physiology, growth and biomass accumulation have been studied extensively, the contribution of different factors to changes in season-long whole crop photosynthetic CO2 uptake [gross primary productivity (GPP)] under elevated [CO2] have not been fully quantified.
Methods
A 3-D canopy model combining canopy 3-D architecture, ray tracing and leaf photosynthesis was built to: (1) study the impacts of elevated [CO2] on soybean GPP across a whole growing season; (2) dissect the contribution of different factors to changes in GPP; and (3) determine the extent, if any, of synergism between [CO2] and light on changes in GPP. The model was parameterized from measurements of leaf physiology and canopy architectural parameters at the soybean Free Air CO2 Enrichment (SoyFACE) facility in Champaign, Illinois.
Key Results
Using this model, we showed that both a CO2 fertilization effect and changes in canopy architecture contributed to the large increase in GPP while acclimation in photosynthetic physiological parameters to elevated [CO2] and altered leaf temperature played only a minor role in the changes in GPP. Furthermore, at early developmental stages, elevated [CO2] increased leaf area index which led to increased canopy light absorption and canopy photosynthesis. At later developmental stages, on days with high ambient light levels, the proportion of leaves in a canopy limited by Rubisco carboxylation increased from 12.2 % to 35.6 %, which led to a greater enhancement of elevated [CO2] to GPP.
Conclusions
This study develops a new method to dissect the contribution of different factors to responses of crops under climate change. We showed that there is a synergestic effect of CO2 and light on crop growth under elevated CO2 conditions.
Keywords: Canopy architecture, photosynthesis, atmospheric change, climate change, food security, growth, leaf temperature, canopy absorbance, leaf area index, light extinction coefficient, soybean, SoyFACE
INTRODUCTION
Soybean is the most important dicotyledonous seed crop in terms of area planted and mass produced at the global scale. It is also the largest single source of vegetable protein for food and feed in the world. Understanding the response of soybean growth and productivity to global atmospheric change will be critical to an accurate projection of future soybean production and global food security (Parry et al., 2004; Long et al., 2006). The impacts of elevated [CO2] on soybean physiology, growth, development and yield have been extensively documented (Kimball, 1983; Ainsworth et al., 2002; Bernacchi et al., 2005, 2006, 2007; Morgan et al., 2005). Soybean grown under free air [CO2] enrichment shows a 37 % increase of biomass dry weight and 24 % increase in yield with a [CO2] increase to about 700 ppm (Ainsworth et al., 2002). When [CO2] is increased to about 550 ppm, above-ground biomass increases by 17–18 % and yield increases by 15 % (Morgan et al., 2005). The yield increase is significant, but less than the expected increase under elevated [CO2] (Long et al., 2006). Similar observations of lower than expected increase in crop yields under elevated [CO2] have been made in other species as well (Long et al., 2004).
To a first approximation, the yield of a crop under optimal growth conditions is the product of the solar radiation receipt for the growing season and the efficiencies with which the crop intercepts that radiation (ε i), converts it into biomass (ε c) and partitions the biomass into the harvested organ (ε p), i.e. seed in the case of soybean (Monteith, 1972). Under elevated [CO2], the partitioning efficiency (also known as harvest index) of soybean is only slightly reduced, compared to under ambient [CO2]. Measured harvest index is about 0.55 and 0.53 for soybean grown under atmospheric [CO2] of 370 and 550 ppm, respectively (Morgan et al., 2005). Furthermore, given that the root : shoot ratio changes relatively little for soybean under elevated [CO2] (Ainsworth et al., 2002), the increase in yield and biomass can mainly be attributed to an increase in total CO2 uptake of the whole canopy, i.e. gross primary productivity (GPP). GPP includes the photosynthetic CO2 uptake of all leaves in the canopy, including not only those leaves at the top of the canopy which are mostly light-saturated, but also those at lower layers which are mostly light-limited.
GPP is affected by many environmental factors besides light, including [CO2], temperature, humidity and plant water status. It is affected also by canopy size, canopy architecture, leaf chlorophyll content and leaf photosynthetic parameters. When soybean is grown under elevated [CO2] many physiological parameters change (Long et al., 2004; Ainsworth & Long, 2005), such as leaf area index (LAI) (Dermody et al., 2006), the maximal rate of carboxylation under RuBP and CO2 saturation (Vcmax) (Long et al., 2004; Morgan et al., 2004), stomatal conductance (Bernacchi et al., 2005) and microclimatic parameters especially leaf temperature (Long et al., 2006). These changes differentially influence GPP. Increasing LAI at early crop developmental stages leads to increased GPP, but at later developmental stages an increase in LAI may decrease GPP (Srinivasan et al., 2016). Decreasing Vcmax can monotonically decrease GPP, decreasing stomatal conductance (gs) can similarly monotonically decrease GPP, while changes in leaf temperature (Tleaf) influence GPP in an non-linear manner dependent on ambient temperature. Given the complexity and non-linearity in the impacts of these factors on GPP, it is difficult to dissect the contribution of these individual factors and their interactions on changes in GPP and correspondingly observed increases in biomass and seed production.
In this study, we used a mathematical modelling approach to dissect the contribution of different factors to change in GPP. In fact, many mathematical models of canopy photosynthesis have been developed and used to study GPP. The sunlit–shaded canopy photosynthesis model, which divides leaves in a canopy dynamically into those that are sunlit and those that are shaded, has been used widely in predicting canopy photosynthesis of plants under different conditions (Norman, 1980; Givnish, 1988; DePury & Farquhar, 1997). This method has been used to evaluate the consequences of altering Rubisco kinetic properties and changing the speed of relaxation of photoprotection on GPP (Zhu et al., 2004a, b). It has also been used to evaluate the potential changes in GPP under elevated [CO2] and to dissect the factors controlling changes in GPP (Wittig et al., 2005). The sunlit–shaded model uses aggregated parameters to represent canopy architectural features. Recently, 3-D canopy models were developed which use canopy architectural features directly and can be used to predict fine details of canopy light distribuiton (Song et al., 2013; Kim et al., 2016). Such models can be used to study the impacts of changes in architecture on canopy photosynthesis. For example, these models have been used to evaluate the optimal architectures that maximize canopy photosynthetic CO2 uptake rate under different ambient [CO2] (Song et al., 2013), and to predict the impacts of assymetric row spacing and row orientation on GPP in sugarcane agronomy (Wang et al., 2017).
In this study, we use a 3-D canopy photosynthesis model to dissect the contribution of different environmental, architectural and physiological parameters to the changes in GPP under elevated CO2. Using the model, we further show that there is a synergistic effect between [CO2] and light for soybean grown under elevated CO2.
MATERIALS AND METHODS
SoyFACE facility
The data used for model parameterization in this study were collected from the SoyFACE facility (www.soyface.uiuc.edu), which employs a free air concentration enrichment (FACE) technology. SoyFACE is a 32-ha facility at the University of Illinois at Urbana-Champaign (40°03′21.3″N, 88°12′3.4″W, 230 m elevation). The soil at SoyFACE is a Drummer-Flanagan series (fine-silty, mixed, mesic Typic Endoaquoll; Morgan et al., 2005), typically very deep and formed from loess and silt parent material deposited on the till and outwash plains. The average ground surface slope is <1 % at this site, with tile drains at a depth of 1–2 m below the ground surface. This rain-fed field site has been following a continuous crop rotation practice typical for the US Midwestern corn belt of soybean and maize. Extended descriptions of site, including micrometeorology and climate, have been previously described (Leakey et al., 2004; Rogers et al., 2004).
SoyFACE elevated [CO2] treatments consist of four blocks each with two octagonal plots of 20 m diameter within the 16 ha planted with soybean. Each block contains one control plot at an ambient [CO2] of 370 ppm and one fumigated plot to a target [CO2] of 550 ppm, using the FACE technology of Miglietta et al. (2001). Fumigation was performed between sunrise and sunset and began 3 d after planting and operated over the remainder of the growing season until crop harvest.
Leaf photosynthetic parameters
V cmax and Jmax of canopy top leaves for ambient and elevated [CO2] were taken from Morgan et al. (2005). An exponential distribution model was used to predict Vcmax and Jmax for leaves at different depth (z) of the canopy (eqn 1) following previous observations of Vcmax, Jmax and leaf nitrogen content in different layers of tghe canopy (Morgan et al., 2004; Srinivasan et al., 2016). The relationship between Vcmax and cumulative leaf area index (cLAI) from the top of the canopy was based on the vertical distribution of leaf nitrogen content in the canopy. Vcmax,top is the Vcmax of leaves in the top layer of a canopy.
| (1) |
Meteorological parameters
Air temperature (°C), relative humidity, photosynthetic photon flux density (PPFD) and diffuse PPFD were recorded with 10-min intervals at the weather station located at SoyFACE.
Calculation of GPP
The overall workflow used to calculate GPP was as follows: (1) development of a 3-D soybean canopy photosynthesis model; (2) simulation of the light environments inside a canopy; (3) calculation of the photosynthetic rate of each leaf; and (4) calculation of the canopy photosynthetic rate by integrating the total photosynthetic rate for all leaves in a canopy. These steps are described in detail in the following sections.
3-D soybean canopy model
A 3-D soybean canopy model was developed based on the 3-D canopy modelling algorithm of Song et al. (2013) (the MATLAB-based program, mCanopy-soybean, is available from the authors upon request).
The different measurements required for the 3-D canopy model development are summarized in Supplementary Data Tables S1–S8. Leaf lengths, leaf widths, petiole lengths and angles for the left, middle and right trifoliate leaves (Tables S1–S3) were obtained using digital photography and image processing. An in-situ non-destructive leaf photo scanner was used to obtain a picture of the soybean trifoliate leaves at all nodes for five plants per plot. The scanner holds a leaf between two flat sheets, with the top sheet being transparent, to obtain a photo of the leaf. A standard length was placed within the frame of the picture for reference. The camera was mounted normal to the leaf plane and the leaf image was recorded using a digital camera. Leaf widths, lengths and the angles were digitally processed using the java-based image processing and analysis software ImageJ (1.48j 11 December 2013, https://imagej.nih.gov/ij/).
The internode lengths and petiole lengths (Supplementary Data Table S4) for each node in the main stem and the branches were measured for the same five plants in each plot using a ruler. Petiole angle, branch angle and leaf angle were measured using a protractor (iGaging digital protractor, http://www.igaging.com/) at midday. These measurements were made for the same five plants in each plot.
Measurements of leaf senescence were made on the same five plants in each plot, recorded twice a week for each node. Leaves that turned pale yellow to brown were considered non-photosynthetic and senesced. Note that there was a finite duration of time between post-yellowing of leaves and complete litterfall (a few days to a week). In our 3-D model, we assume all leaves that turned yellow have senesced. During the growing season, ten plants from each plot were identified to measure development, and the presence of branches and their node lengths were measured. Using these data, a branching probability was computed (Supplementary Data Tables S5–S7).
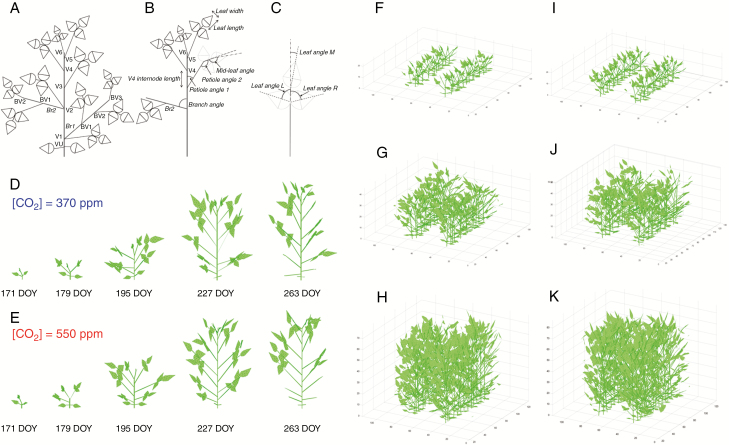
A soybean architecture model (features in Fig. 1A–C) was developed based on these measured architecture data. The description of nodes and branches is given in Table 1. In the main stem, the base node before the first node is the VU node, which is the node growing unifoliate leaves (Fig. 1A), and the first trifoliate leaf is on the first node V1. The second trifoliate leaf grows on the second node V2 and so on. The first branch (Br1) grows from the V1 node and the second branch (Br2) from the V2 node and so on. Internode length is the distance between two nodes (e.g. V3 internode length was the length between nodes V3 and V2). Branch angle is the angle between the main stem and branch (Fig. 1B), petiole angle 1 is the angle between the main stem (or branch) and the common petiole of a trifoliate leaf (Fig. 1C), and petiole angle 2 (Fig. 1B) is the angle between a common petiole and the petiole of the mid-leaf of the trifoliate leaf. Mid-leaf angle is the angle between the petioles of the mid-leaf and the main vein of the mid-leaf (Fig. 1b). Leaf length and leaf width are the maximal length and width of a leaf. Leaf angle L, leaf angle R and leaf angle M (Fig. 1C) are the angles between the common petiole of a trifoliate leaf and the main veins of left, right and middle leaves when these leaves are laid on a horizontal plane.
Fig. 1.
Representations of the canopy architectural features for soybean. (A) VU, V1, V2, etc., are nodes of the main stem, Br1 and Br2 are branches from the main stem, and BV1, BV2 and BV3 are branch nodes. (B) The parameters internode length, branch angles, petiole angle 1, petiole angle 2 and mid-leaf angle. (C) Leaf width and length are the maximal width and length of a leaf; leaf angle L, leaf angle R and leaf angle M are shown when the trifoliolate was placed in a plane. (D, E) 3-D models of a single soybean plant at different developmental stages during a growing season under ambient CO2 (D) and elevated CO2 (E). (F–K) 3-D models of soybean canopy under ambient (F, G, H) and elevated CO2 (I, J, K) at stages V4 (DOY 180), V7 (DOY 195) and V11 (DOY 210).
Table 1.
Description of measured nodes and branches, which are used to develop the 3-D soybean canopy model at different stages in this study.
| ID | Nodes and branches | Description |
|---|---|---|
| VU | Unifoliate node | Fully developed leaves at the unifoliate node |
| V1 | The first node | Fully developed trifoliate leaf at the node above the unifoliate node |
| V2 | The second node | Two nodes on the main stem with fully developed trifoliate leaves |
| V(n) | The nth node | n nodes on the main stem with fully developed trifoliate leaves |
| BV1 | The first node of a branch | First fully developed trifoliate leaf at the first node of a branch |
| BV2 | The second node of a branch | Two nodes on a branch with fully developed trifoliate leaves |
| BV(n) | The nth node of a branch | n nodes on a branch with fully developed trifoliate leaves |
| Br1 | The first branch | Branch developed on the main stem at V1 |
| Br2 | The second branch | Branch developed on the main stem at V2 |
| Br(n) | The nth branch | Branch developed on the main stem at V(n) |
3-D soybean canopy models applied to different days in the growing season
Row spacing was 38 cm and the planting distance was 5 cm under both ambient and elevated CO2 conditions. The integrated model was run for the year 2002 between days 168 (V1) and 267 (V16) every 3 d (Fig. 1D, E).
To simulate canopy photosynthesis throughout a growing season (Fig. 1), canopy architectural parameters (i.e. leaf length, leaf width, leaf angle, internode length, etc.) were measured at different stages of plant growth (Supplementary Data Tables S1–S4). To model the variation of node number among different plants, we used a randomization algorithm to determine the node number (Vx) for each main stem and branch as follows.
First, the maximal node number (Vx_max) for the main stem and branches for different days of the year (DOY) were determined based on previous measurements (Castro et al., 2009). Second, the probability p(n) (probability for node number = n) of the main stem or branches on different days were calculated based on measurement data collected in the field (Supplementary Data Table S5). A random value i between 0 and 1 (uniform distribution) was then generated and if i > sum(p(n<N)) and i < sum(p(n>N+1)), N is used for Vx_r, which is the randomized node number. Lastly, if Vx_r is less than Vx_max, Vx_r is used as the node number, and if Vx_r is larger than Vx_max, Vx_max is used as the node number (Tables S5–S7). Pseudocode for the above process is given in the Supplementary data Methods.
Senescenced leaves were excluded from the model. The number of senescenced leaves was counted during the growing season and the number of senescenced leaves every 3 d was based on measurement data (Supplementary Data Table S8). The total number of senescenced leaves (Ns) on a DOY is the sum of the senescenced leaf number from the start day (168 DOY) to the current day. If Ns is not an integer, a randomization algorithm is used to determine the total senescenced leaf number. For example, if Ns = 2.3, then leaf number being 2 is used with a probability of 0.7 and leaf number being 3 is used with a probability of 0.3. In the model, newly formed leaves were smaller than mature leaves. The sizes of the top three newest formed leaves (from top to bottom) were assumed to be 25 %, 50 % and 75 % of their mature sizes.
Ray tracing algorithm
The light environment in the soybean canopy was simulated using a ray tracing algorithm, fastTracer (Song et al., 2013). The program for fastTracer is available upon request from the corresponding author. Measured ambient direct and diffuse photosynthetic photon flux density (PPFD) data were used as input to fastTracer. The ray tracing algorithm simulates the direct PPFD, diffuse PPFD and leaf scattering PPFD absorbed by every leaf. The simulations were conducted 15 times a day, from 0500 to 1900 h with intervals of 1 h. Using ray tracing, the calculation of PPFD distribution in the canopy was accurate for evaluating the impacts of small differences in canopy architecture, such as leaf size and leaf number and the PPFD distribution under different weather conditions, both of which were important for this study.
Leaf photosynthesis calculation
Leaf photosynthetic CO2 uptake rate was calculated with the steady-state biochemical model of C3 leaf photosynthesis (Farquhar et al., 1980).
Leaf photosynthesis rate at any given CO2, light, O2 and temperature conditions was calculated from eqn (2):
| (2) |
where: Γ* is the CO2 compensation point in the absence of dark respiration, Ci is the leaf intercellular CO2 concentration, Wc is the Rubisco-limited rate of carboxylation and Wj is the RuBP regeneration-limited rate of carboxylation, which were calculated from eqns (3) and (4):
| (3) |
| (4) |
where Kc is the Michaelis constant for CO2 (404.9 μmol mol−1), Ko is the Michaelis constant for O2 (278.4 mmol mol−1) and J is the potential photosynthetic electron transport rate. The parameters describing impacts of temperature on Rubisco kinetics follow Bernacchi et al. (2001). Leaf temperature was assumed to be equal to air temperature T for the ambient condition and leaf temperature was assumed to be 1.5 °C higher under elevated CO2 than under ambient conditions based on the data from Long et al. (2006).
The potential electron transport rate, J, was calculated as:
| (5) |
where Θ PSII (0.864 was used) is the convexity of the non-rectangular curve, I2 is the PPFD absorbed by photosystem II (PSII), and Jmax is the maximal electron transport rate (Chen, Zhu & Long, 2008). I2 was calculated from:
| (6) |
where Isun is the PPFD incident upon a facet in a leaf simulated by the ray tracing algorithm described by Song et al. (2013), αl is leaf absorbance (0.85 was used), Φ PSII,max is the maximal quantum yield of PSII (0.85 was used) and β (0.5 was used) is the maximal fraction of quanta that reaches PSII (Chen et al., 2008). The parameters used in describing the temperature response were taken from Long & Bernacchi (2003).
Estimation of Ci and gs
During the calculation of leaf photosynthesis, Ci and gs were estimated using eqns (7)–(12) as in previous studies (Humphries & Long, 1995; Song et al., 2013) based on Ball et al. (1987). Equation (12) shows the calculation of intercellular CO2 partial pressure (Ci, µbar) based on the CO2 partial pressure on the leaf surface (Cs, µbar), photosynthetic CO2 assimilation rate (A, µmol m−2 s−1), stomatal conductance (gs, mmol m−2 s−1) and air pressure (Pa, bar). Equation (11) shows the calculation of CO2 partial pressure on the leaf surface (Cs) based on the ambient CO2 partial pressure (Ca, µbar), photosynthetic CO2 assimilation rate (A), leaf boundary conductance (gb, mmol m−2 s−1) and air pressure (Pa). The parameters a, b and c calculated in eqns (8)–(10) are those used in eqn (7), which is an empirical equation used to calculate gs based on the CO2 partial pressure on the leaf surface (Cs), photosynthetic CO2 assimilation rate (A), leaf boundary conductance (gb), relative humidity (RH), partial pressure of the saturated water vapour for the air temperature (eair, mbar) and for leaf temperature (eleaf, mbar), stomatal coefficient g0 (20) and stomatal coefficient g1 (11.35). The equations used in this study to calculate stomatal conductance are suitable to model plants without water stress (Ball et al., 1987). To adapt the Ball–Berry model to simulate plants under water stress conditions, additional factors associated with leaf water potential or soil water content are needed (Buckley et al., 2003; Li et al., 2012).
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
Temperature response of photosynthetic parameters
Leaf temperature affects photosynthetic parameters and eqns (13)–(21) were used to describe the temperature responses of photosynthetic parameters.
| (13) |
| (14) |
| (15) |
At 25 °C, Ci = 0.7 Ca
| (16) |
At 25 °C, Oi =Oa
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
Iterative calculation of Ci, gs and P under constant leaf temperature
Equations (1)–(21) together form a system of equations, which was solved by using the Newton–Raphson method. During this computation, the initial Ci was calculated (eqn 15) and then used to calculate P (eqn 2) and gs (eqn 7); Ci was updated using eqn (12). The calculation was terminated when either Ci reached a stable value or the maximum number of iterations was reached.
Calculation of GPP
GPP was calculated by integrating the photosynthesis rates of all leaves in a canopy (eqn 22).
| (22) |
where Pi is leaf photosynthesis rate for the ith leaf facet (the ‘i’ here is the sequence ID of a facet in the data file, ‘leaf ID’ is used to label a leaf for parameterization of leaf photosynthetic parameters) and Si is the corresponding leaf area of the leaf facet. Sground is the ground area occupied by the canopy.
To study GPP on different days during the growing season and to compare the whole season GPP of soybean under ambient and elevated CO2 conditions, the GPP per day or per season was calculated by integrating GPP during a day or throughout the growing season (eqn 23).
| (23) |
where GPPday is the GPP per day, Pc,t is total canopy photosynthetic CO2 uptake for a unit ground area during a particular hour; Pc,u is total canopy photosynthetic CO2 uptake at the mid-point of an hour, i.e. at the 30th minute in each hour.
Cumulative GPP (cGPP) from the start day (168 DOY) to different days (n) between 168 DOY and 267 DOY was calculated by adding GPPday from the start day to day n (eqn 24).
| (24) |
Calculation of GPP under ambient and elevated CO2
The model was parameterized for both ambient and elevated CO2 conditions (Table 2). The parameters used include [CO2], Vcmax, Jmax, air temperature and canopy structure on different days from 168 DOY to 267 DOY (for each day, the model was run three times).
Table 2.
The different environmental (CO2 concentration, air temperature), physiological (Vcmax and Jmax), and plant structural and developmental characteristics (leaf size, growth stage and leaf senescence) between the elevated CO2 and normal CO2 conditions.
| Factor | Ambient [CO2] | Elevated [CO2] |
|---|---|---|
| CO2 concentration (ppm) | 370 | 550 |
| Air temperature (°C) | T | T+1.5 |
| V cmax and Jmax | (+) | Higher in early stages and lower in later stages (+) |
| Leaf size (area of single leaf) | S (+) | 1.1–1.9 × S (+) |
| Growth stages | (+) | Earlier than ambient (+) |
| Leaf senescence | (+) | Earlier than ambient (+) |
(+) Detailed data are presented in the supporting tables.
Estimation of above-ground biomass from cGPP
Model-estimated above-ground biomass was calculated based on cGPP, the harvest index, carbon content in different organs and root : shoot ratio. Briefly, we first calculated the total carbon in biomass (Wc) by subtracting respiration from cGPP assuming that respiration is 57.5 % of total photosynthetic CO2 uptake (Amthor, 2000). Second, the proportion of carbon for the whole plant was calculated based on the harvest index, the proportion of carbon in pod and seed, and the proportion of carbon in other parts of the soybean, which was assumed as (C6H10O5)n. We assumed that the composition of soybean pod and seed was carbohydrate (29 %), protein (37 %), lipid (18 %), lignin (6 %), organic acid (5 %) and mineral (5 %); this results in a proportion of carbon (Cpod+seed) of 53 % in pod and seed (Amthor, 2000). We also assumed that the composition of root, stem and leaf biomass was (C6H10O5)n, which results in a proportion of carbon (Cother) being 44.4 %. We further assumed a harvest index η of 0.57 (Pedersen & Lauer, 2004; Spaeth et al., 2010), and then calculated the proportion of carbon in a whole soybean plant (Cplant) as:
| (25) |
Whole plant biomass was given by:
| (26) |
Finally, assuming a ratio of root to total biomass (proot) as 18.7 % (Clough & Peet, 1981), we calculated above-ground biomass:
| (27) |
Dissecting the factors contributing to changes in GPP under elevated CO2
To evaluate the relative contribution of physiological parameters (i.e. Vcmax and Jmax), architectural parameters and environmental factors (i.e. air temperature and CO2) to the changed GPP under elevated CO2, we simulated GPP under different scenarios. The method was adapted from the sensitivity analysis of a model that is commonly used in previous studies (Zhu et al., 2007; Wu & Cournède, 2010). The different scenarios are listed in Table 3. The contribution of all four factors, i.e. CO2 (C), canopy structure (S), temperature (T), and Vcmax and Jmax (V) can be split into the contribution of single factors c(C), c(S), c(T) and c(V), interactions between two factors c(CS), c(CT), c(CV), c(ST), c(SV) and c(TV), interactions between three factors c(CST), c(CSV), c(CTV) and c(STV), and interaction between four factors c(CSTV) as shown in eqn (28). The contribution of any single factor c(X) was calculated from eqn (29); the contribution of an interaction of any two factors c(XY) was calculated from eqns (29) and (30); and the contribution of an interaction among any three factors c(XYZ) was calculated from eqns (29–31). In this study, the relative contributions of each factor and the interactions between factors were calculated by solving a system of linear equations where c(X), c(XY), c(XYZ) and c(CSTV) are variables.
Table 3.
Scenarios used to calculate GPP, which is used to dissect the contributions of individual factors ([CO2], Vcmax and Jmax, T, canopy structure) and their interactions to changes in GPP
| Scenarios | Elevated CO2 (X), Ambient CO2 (–) | |||
|---|---|---|---|---|
| [CO2] | V cmax, Jmax | T | Canopy structure | |
| O | – | – | – | – |
| C | X | – | – | – |
| V | – | X | – | – |
| T | – | – | X | – |
| S | – | – | – | X |
| C,V | X | X | – | – |
| C,T | X | – | X | – |
| C,S | X | – | – | X |
| V,T | – | X | X | – |
| V,S | – | X | – | X |
| T,S | – | – | X | X |
| C,V,T | X | X | X | – |
| C,V,S | X | X | – | X |
| C,T,S | X | – | X | X |
| V,T,S | – | X | X | X |
| C,V,T,S | X | X | X | X |
A dash (‘–’) represents a factor under ambient CO2 conditions, and ‘X’ represents a factor under elevated CO2 conditions. The scenarios include all the combinations of four factors, i.e. [CO2], Vcmax and Jmax, air temperature (T) and canopy structure, under two conditions, i.e. elevated [CO2] and ambient [CO2].
| (28) |
| (29) |
| (30) |
| (31) |
Statistical analysis
Pearson’s correlation coefficient was calculated with the R software function cor. Student’s t-test was calculated with the R software function t.test.
RESULTS
Canopy architectural and physiological data used to develop soybean canopy models
Soybean grown under elevated [CO2] revealed about a 10–90 % increase in leaf lengths and leaf widths for different leaves (Supplementary Data Tables S1 & S2). Leaf angle distributions were assumed to be the same for both CO2 treatments based on field observations (Table S3). Internode distances were obtained from direct measurements under ambient [CO2] conditions (Table S4). Internode distances for soybean grown under elevated [CO2] were 6 % longer than under ambient [CO2] conditions (Ainsworth et al., 2002). The probabilities of node numbers of the main stem and branches at the final stage were assumed to be the same between the two [CO2] conditions and were measured (Table S5). For the main stem, all measured plants had more than ten nodes; 95 % of plants had more than 11 nodes; with an increase in node number, the percentage of plants having more than the node number gradually decreased (Table S5). Node probabilities differed dramatically between branches. For example, the probability of having more than one node was 10 % for Br1, 50 % for Br2 and 30 % for Br3 (Table S5). Maximal node numbers of the main stem and different branches during a growing season under ambient and elevated [CO2] conditions are given in Tables S6 and S7, which was compiled based on a previous study (Castro et al., 2009). Growth of the main stem and branch was faster under elevated [CO2] than under ambient [CO2] (Tables S6 and S7). We used the number of leaves defoliated from stands to quantify leaf senescence. Leaves senescenced faster under elevated [CO2] than under ambient [CO2] (Table S8). Leaf photosynthetic parameters, Vcmax and Jmax, collected based on Bernacchi et al. (2005), are shown in Table S9.
GPP during a growing season under elevated and ambient CO2 conditions
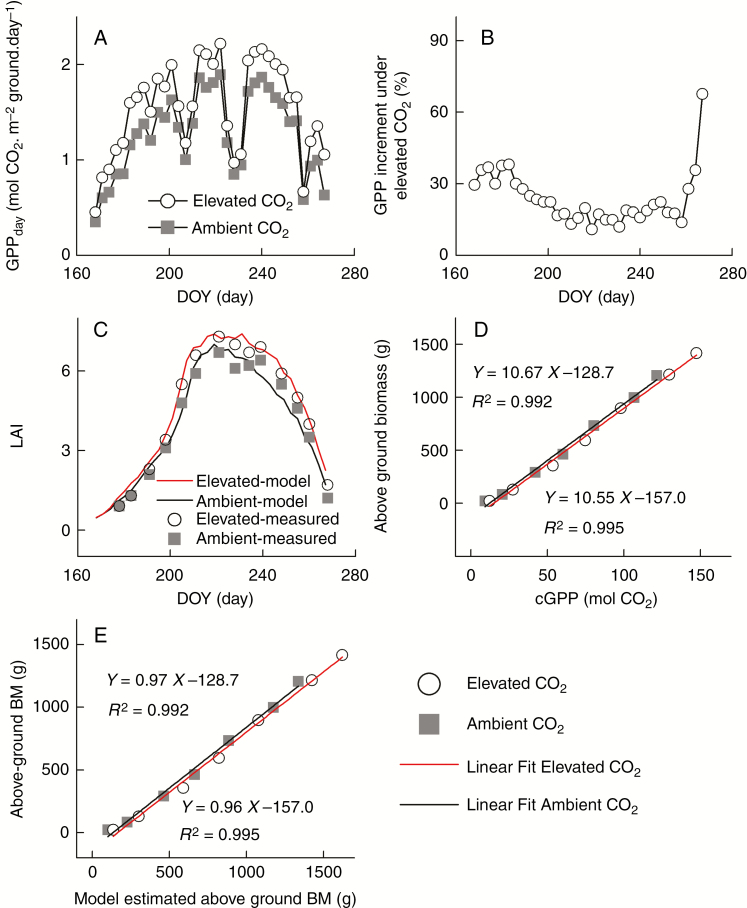
Simulated GPPday was higher under elevated [CO2] compared to ambient [CO2] throughout the growing season (Fig. 2A), with the relative increase in simulated GPPday being higher in the early growth season (DOY<200) (Fig. 2B). The seasonal trends in simulated daily GPP (GPPday) mimicked the behaviour of measured LAI with an initial fast increase, followed by a peak in GPPday near the date of peak LAI and a final decline towards the end of the growing season (Fig. 2A, C). Simulated cGPP showed a high degree of correlation (Pearson coefficient > 0.99) with measured aBM (Morgan et al., 2005), under both ambient and elevated [CO2] conditions (Fig. 2D) (Supplementary Data Table S10). To compare the model simulation with measured data, we further estimated the above-ground biomass with cGPP. The model-estimated above-ground biomass was linearly correlated with measured values, with slope being 0.96 and 0.97 under elevated and ambient CO2, respectively (Fig. 2E). The R2 values for these two relationships were 0.995 and 0.992 for elevated and ambient CO2 respectively (Fig. 2E).
Fig. 2.
(A) Daily GPP of a soybean canopy (GPPday) under either elevated or ambient [CO2] conditions. (B) Relative increase of GPP under elevated [CO2] condition as compared to the ambient [CO2] condition. GPP in A and B was model-simulated. (C) Leaf area index (LAI) simulated using the canopy models, as compared to the measured data (Dermody et al., 2006) for soybean grown under elevated [CO2] and ambient [CO2] conditions. (D) Correlation between above-ground biomass (Morgan et al., 2005) and calculated cumulative GPP (cGPP) at different stages. The R2 of linear fitting was > 0.99 for both ambient [CO2] and elevated [CO2] conditions. (E) Correlation between the measured above-ground biomass and model-estimated above-ground biomass from cGPP.
Contributions of CO2 concentration, canopy structure, leaf temperature and Vcmax and Jmax to the increase of GPP under elevated [CO2]
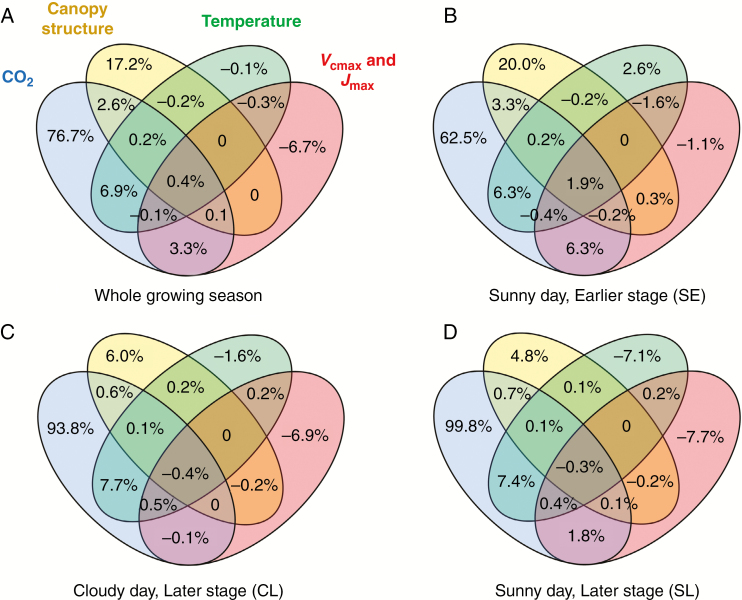
Between soybean plants grown under elevated [CO2] and ambient [CO2], four factors (i.e. CO2 concentration, temperature, Vcmax and Jmax, and canopy structure, which includes leaf size and leaf number) differed (Table 2). Here we used canopy photosynthesis models to dissect the contribution of each of these factors, and their interactions, to increase GPP in elevated [CO2] compared to ambient [CO2] (ΔGPP) (Fig. 3). Figure 3A shows the averaged contributions over the growing season of CO2 (76.7 %), canopy structure (17.2 %) and their interaction (2.6 %) to increases in ΔGPP (Fig. 3A). The increase in air temperature under elevated CO2 showed a mild negative impact (−0.1 %) on ΔGPP, but the interaction between CO2 and temperature showed a substantial positive impact (6.9 %) on ΔGPP (Fig. 3A). Vcmax and Jmax negatively influenced ΔGPP, i.e. decreasing GPP by −6.7 % of ΔGPP, but their interactions with CO2 had a positive impact of 3.3 % on ΔGPP (Fig. 3A). The contributions of other interactions on ΔGPP are not significant (<1 %) (Fig. 3A).
Fig. 3.
Venn diagrams showing the contributions of different factors and their interactions to the increase in GPP under elevated CO2 conditions as compared to that under ambient CO2 conditions for the whole growing season (A), dissected contributions on a sunny day during the early developmental stage (195 DOY) (B), dissected contributions on a cloudy day during the later developental stage (231 DOY) (C), and dissected contributions on a sunny day during the later developmental stage (234 DOY) (D).
To further investigate the impacts of these factors on ΔGPP in different growth stages and weather conditions, we chose a Sunny day in the Early developmental stage (SE), a Cloudy day in the Late developmental stage (CL), and a Sunny day at a Later developmental stage (SL) for analysis (Fig. 3B–D). The contribution of CO2 concentration was smaller in SE (62.5 %) than in SL (99.8 %) and the contribution of canopy structure was larger in SE (20 %) than in SL (4.8 %) (Fig. 3B, D). The contribution of [CO2] was smaller in CL (93.8 %) than in SL (99.8 %) and the contribution of canopy structure was greater in CL (6 %) than in SL (4.8 %) (Fig. 3C, D).
Canopy absorbance and PPFD distribution in different stages and weather conditions
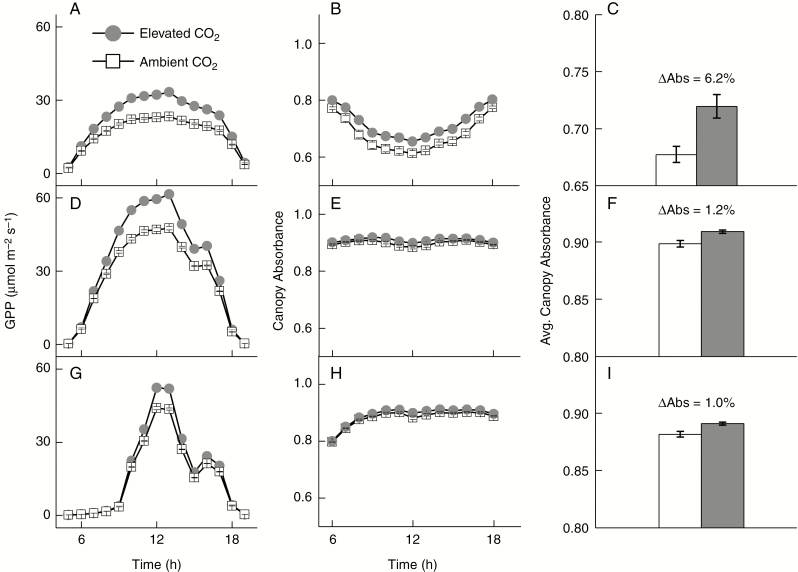
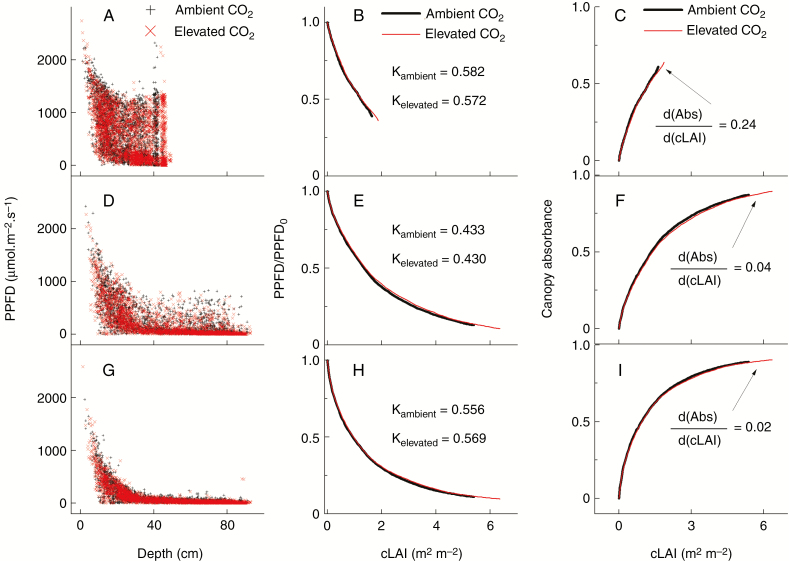
To explore the greater relative contribution of canopy structure to ΔGPP in the earlier growth stages, we analysed the canopy absorbance for SE, SL and CL days (Fig. 4). In the earlier stages, canopy absorbance decreased with time in the morning and increased in the afternoon because the canopy was not closed to fully cover the ground (LAI = 2.6 for ambient and 2.9 for elevated [CO2]), resulting in more light penetrating through the canopy and reaching the soil surface when solar elevation angle increased (Fig. 4B). In later growth stages, canopy absorbance was relatively constant over the course of a day (Fig. 4E, H). The difference in daily averaged canopy absorbance between the two [CO2] conditions was larger in SE (6.2 %) than SL (1.2 %) and CL (1.0 %) (Fig. 4C, F, I).
Fig. 4.
Diurnal GPP (A, D, G), diurnal canopy absorbance (B, E, H) and daily averaged canopy absorbance (C, F, I) of soybean canopy on a sunny day during the early developmental stage (A, B, C), on a sunny day during the later developmental stage (D, E, F) and on a cloudy day during the later developmental stage (G, H, I). The error bar shows the standard deviation of six replicates of individual model simulations.
The PPFD distribution in SE was more uniform than in SL (Fig. 5A, D). The canopy in SL experienced more scattered PPFD or sunflecks in the botttom layers than that in CL (Fig. 5D, G). The light extinction coefficients for canopies developed under elevated [CO2] and ambient [CO2] were almost the same in either SL, CL or SE days (Fig. 5B, E, H). With increasing cLAI, canopy absorbance increased but did not saturate in SE, increased and approached saturation at about cLAI = 6 in SL, and increased and approached saturation at about cLAI = 3 in CL. The marginal canopy absorbance, defined as d(Abs)/d(cLAI), was much higher (0.24) in SE, comparing to those at the later stages (0.04 for SL and 0.02 for CL) (Fig. 5C, F, I).
Fig. 5.
Distribution of PPFD absorbed by leaves at different depths of a canopy (A, D, G), relative PPFD (PPFD/PPFD0) as a function of cumulative LAI (cLAI) (B, E, H) and canopy absorbance as a function of cLAI (C, F, I) on a sunny day during an earlier developmental stage (195 DOY, A, B, C), on a sunny day during a later developmental stage (234 DOY, D, E, F) and on a cloudy day during a later developmental stage (231 DOY, G, H, I). Relative PPFD and canopy absorbance were calculated based on the distribution of PPFD.
Synergistic effect of PPFD on the contribution of [CO2] to ΔGPP
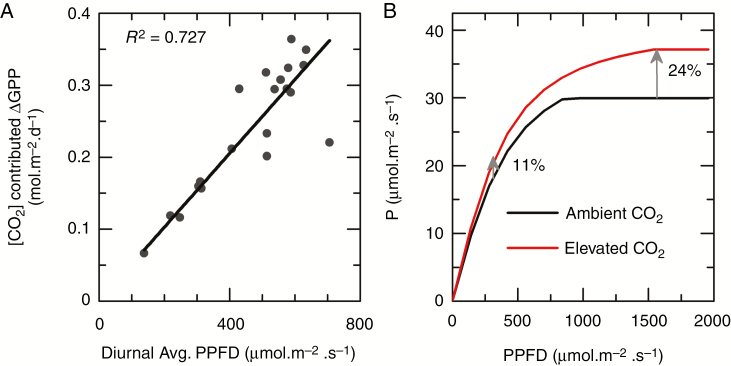
For mature canopies (DOY > 207), daily ΔGPPCO2 was positively correlated (R2 = 0.727) with the daily averaged ambient solar PPFD (Fig. 6A). In Fig. 6A, diurnal average PPFD is the diurnal averaged ambient solar PPFD, while points represent PPFD of different days of the later developmental stages. For these days, we also calculated ΔGPP contributed by elevated [CO2], and found that on days with high ambient PPFD (i.e. sunny days), ‘ΔGPP contributed by elevated CO2’ was higher; on days with low ambient PPFD (i.e. cloudy days), the ‘ΔGPP contributed by elevated CO2’ was lower. Although daily GPP is a function of daily total intercepted solar radiation, here we used the average ambient PPFD as the x-axis to ease comparison with Fig. 6B, which shows the simulated light response curves of leaf photosynthetic CO2 uptake rate (AQ curve) for both ambient and elevated CO2 conditions on 219 DOY (Fig. 6B) (data of AQ curves for 210–252 DOY are given in Supplementary Data Table S11). When PPFD was lower than about 800 µmol m−2 s−1 and photosynthesis was limted by RuBP regeneration, the increase in leaf photosynthesis rate (ΔP) was about 11 % under elevated CO2 compared to ambient CO2 condition (Fig. 6B). When PPFD was greater than 800 µmol m−2 s−1 and photosynthesis was limited by Rubisco, ΔP was as high as 24 % (Fig. 6B).
Fig. 6.
(A) The relationship between ambient PPFD above the canopy and the contribution of [CO2] to the increase of GPP (ΔGPP) for a mature soybean canopy from the V10 stage to the V18 stage (207 to 264 DOY). Different points show data from different days and the R2 of the linear fitting is 0.727. (B) Light response curves of leaf photosynthetic CO2 uptake rates under elevated [CO2] and ambient [CO2] conditions on the 219 DOY. The curves were drawn based on the Vcmax and Jmax measured on 219 DOY.
DISCUSSION
This study presents a new integrative framework that coupled an explicit 3-D soybean architecture model with a ray tracing algorithm (Song et al., 2013) and a leaf photosynthesis model (Farquhar et al., 1980; Ball et al., 1987; Monteith & Unsworth, 2007) to compute whole canopy photosynthetic response under different environments. In addition, the integrated model also incorporated the responses of photosynthetic parameters to temperature (Bernacchi et al., 2001, 2003). The integrated model was employed in this study to dissect the contribution of different factors to the changes in GPP of soybean grown under elevated [CO2]. Model simulations over the entire growing season demonstrated that CO2 fertilization and structural acclimation significantly increased whole canopy ΔGPP, while photosynthetic acclimation and leaf temperature changes played a minor effect (Fig. 3). Furthermore, we show that the impacts of these different factors on the observed ΔGPP varied with different canopy architecture parameterizations and weather conditions (Fig. 3). Finally, we demonstrate a synergetic effect of CO2 and light on ΔGPP. Specifically, an increase in LAI under elevated [CO2] during the early developmental stage dramatically increased light absorption and hence canopy photosynthesis (Figs 4 and 5); at later developmental stages, on days with high ambient light (i.e. on bright sunny days), the contribution of elevated CO2 to GPP was larger than that under lower ambient light (i.e. on cloudy days), because the proportion of leaves in a canopy undertaking Rubisco-limited photosynthesis increased when ambient PPFD increased (Fig. 6).
A new method to dissect the contribution of different factors and their interactions to ΔGPP
This study used the canopy architectural parameters for each devleopmental stage to construct 3-D canopy models along the growing season (Fig. 1). This enabled quantification of GPP for plants at each developmental stage (Fig. 2A, B). Previous studies have used the sunlit–shaded model to simulate light environments inside the canopy and canopy photosynthesis (DePury & Farquhar, 1997; Wang & Leuning, 1998). In this study, we applied a ray tracing algorithm coupled with 3-D canopy architecture model to simulate the fine details or heterogeneities of light environments in the soybean canopies (Fig. 5A, D, G).
Another major feature of the model was the 3-D canopy photosythesis model along the growing season. In some previous studies, 3-D canopy photosynthesis models have been built for a particular developmental stage (Zheng et al., 2008; Song et al., 2013; Pound et al., 2014). Here we developed a routine to extrapolate the architectural parameters along the whole growth cycle using architectural parameters measured in a representative developmental stage. Our method uses probability tables to randomize node numbers on the main stem and branches (Supplementary Data Tables S5 and S6). The senescence of soybean leaves begins from the bottom of a canopy, with senescent leaves dropping to the ground causing a decrease in LAI at later developmental stages (Setiyono et al., 2008). Such leaf senescence has been modelled by decreasing the LAI (Yin, 2000). In this study, we modelled the number of senescent leaves with a probability table and those senescenced leaves was removed directly from the 3-D canopy model (Table S8; Fig. 1).
The model-calculated GPP was linearly correlated with the measured above-ground biomass (Morgan et al., 2005) along the growing season, and the obtained coefficient of determination, R2, was higher than 0.99 (Fig. 2D), which suggests that the model can be uesd to study factors influencing variations of GPP and hence biomass production. Assuming a fixed root : shoot ratio (Ainsworth et al., 2002) and a fixed fraction of dark respiration (Amthor et al., 2001), the model predicted a 21.4 % increase in above-ground biomass when increasing [CO2] from 370 to 550 ppm (Fig. 2; Supplementary Data Table S10). Our model prediction is largely consistent with results from earlier studies. Previous studies showed that when [CO2] is increased to about 700 ppm, total biomass increases by about 37 % (Ainsworth et al., 2002); when [CO2] is increased to about 550 ppm, above-ground biomass increases by about 17–18 % (Morgan et al., 2005). The difference between the measured and predicted increase in biomass can be attributed to a number of factors: difference between the predicted vs. measured Vcmax and Jmax for leaves at different layers of a canopy, and potential heterogeneity of microclimatic factors other than light (e.g. CO2, humidity) inside canopies. These areas need to be improved in future canopy photosynthesis modelling studies.
Dissection of the contribution of different factors to ΔGPP
This model provides a unique opportunity to dissect the contribution of different factors to changes in GPP (ΔGPP) under elevated [CO2] as compared to that under ambient [CO2]. The CO2 fertilization effect showed the greatest contribution (76.7 %), followed by canopy architecture (17.2 %), to ΔGPP (Fig. 3A). This dominant role of elevated [CO2] to ΔGPP is consistent with an earlier study which showed that changes in the canopy photosynthetic energy conversion efficiency contributed 80 % and the interception efficiency contributed 20 % to the increase in soybean yield under elevated [CO2] (Dermody et al., 2008). The contribution of canopy structure, as shown in the present study, can be further divided into the contribution of LAI and contribution from architecture. LAI directly determines the total photosynthesis leaf area and greatly influences canopy photosynthesis (Song et al., 2013). In this study, the leaf size of soybean was 1.1–1.9 times larger under elevated [CO2] than under ambient [CO2] depending on the growth stages (Supplementary Data Tables S1 and S2). The architecture of the canopy was not changed under elevated [CO2] compared with ambient [CO2].
Changes in leaf temperature showed a minor influence (−0.1 %) on ΔGPP. Temperature can influence a number of factors related to ΔGPP. First, it influenced leaf photosynthetic rates. In SoyFACE, the soybean growth temperature was around the optimal temperature for soybean leaf photosynthesis (Supplementary Data Fig. S1), which was reported to be at about 28 °C based on the temperature response to photosynthesis (Bernacchi et al., 2001, 2003; Medlyn et al., 2002). A further increase in leaf temperature in SoyFACE decreased canopy photosynthesis. Second, temperature can alter leaf respiration. In a previous study, the negative impact of temperature on rice yield has been attributed to increased respiration at night (Peng et al., 2004). Increased leaf temperature can increase leaf respiration rate, which is usually modelled via the Q10 parameter. Note that total canopy respiration is usually positively correlated with LAI and canopy total nitrogen content. LAI increased by about 19 % under elevated [CO2] (cLAI in Fig. 5E, H) which caused and increase in total canopy respiration; however, the leaf nitrogen content on a leaf area basis decreases by an average of 3.9 % in crops under elevated [CO2] as result of Rubisco acclimation (Leakey et al., 2009).
Under elevated [CO2] conditions, while Rubisco content decreases by 19 %, Vcmax at 25 °C decreases only by 15 % due to increased Rubisco activation state (Ainsworth & Long, 2005). The photosynthetic acclimation to growth under elevated [CO2] observed in later developmental stages under the elevated [CO2] condition increases the nitrogen use efficiency of the photosynthesis system (Long et al., 2004) and contributed to ΔGPP by about −6.7 % (Fig. 3).
Synergetic effect of CO2 and light on ΔGPP
This study reveals a synergetic effect of CO2 and light on ΔGPP. On the one hand, elevated CO2 promoted photosynthesis and growth of the plant canopy, which resulted in a higher LAI. The higher LAI led to more light absorption, which increased canopy photosynthesis. At early developmental stages, when LAI was relatively low, canopy absorbance under elevated [CO2] can be 6.2 % higher than that under ambient [CO2] (Fig. 4C). This positive effect of LAI on light absorbance decreased with increasing LAI; at later developmental stages, the difference in canopy absorbance between canopies grown under elevated vs. ambient [CO2] was only about 1–1.2 % because the canopy intercepted about 90 % of total PPFD when LAI > 6 (Fig. 5F, I). The increase in leaf area under elevated CO2 can increase canopy respiration, which decreased the positive impact of increasing LAI on net canopy photosynthesis. In fact, greater than optimal LAI can even lead to decreased canopy photosynthesis (McCree & Troughton, 1966; Anten et al., 1995; Song et al., 2013).
The synergistic effect between CO2 and light on ΔGPP is shown by the correlation between daily averaged PPFD and ΔGPP (Fig. 6A), which shows that the impact of elevated [CO2] on ΔGPP was positively correlated with ambient PPFD. Canopy photosynthetic rate is the integral of photosynthetic rates of all leaves in a canopy. Every facet of the every leaf in a canopy is under either Rubisco limitation or RuBP-regeneration limitation depending on its photosynthetic parameters and the absorbed PPFD. The proportion of leaves in which photosynthesis is limited by Rubisco is higher on sunny days than on cloudy days. CO2 can influence photosynthesis through two mechanisms, i.e. suppressing photorespiration and increasing substrate availability to Rubisco (Long et al., 2004). When photosynthesis was limited by RuBP regeneration, leaf photosynthetic rate under a [CO2] of 550 ppm was 11 % higher than that under a [CO2] of 370 ppm, mainly due to suppression of photorespiration (at low light in Fig. 6B); in contrast, when photosynthesis was limited by Rubisco, a potential 24 % increase in leaf photosynthetic rate was predicted as a result of both suppressing photorespiration and increased substrate availablity for Rubisco (at high light in Fig. 6B). Therefore, with an increase in ambient PPFD, the proportion of leaves under Rubisco-limited photosynthesis increases from 12.2 % under low PPFD to 35.6 % under high PPFD (Supplementary Data Fig. S2), which leads to an increased contribution of elevated CO2 on canopy photosynthesis or ΔGPP.
CONCLUSION
We integrated an existing 3-D canopy photosynthesis model (Song et al., 2013) with data describing the architectural and physiological changes of soybean grown under ambient and elevated [CO2] to build a soybean canopy model throughout the whole growing season. The integrated 3-D soybean models were then used to dissect the contribution of the different acclimation responses, i.e. [CO2], Vcmax, Jmax, canopy architecture, leaf temperature and their interactions, on whole-canopy GPP. The study demostrates the synergetic effect of [CO2] and light on GPP under elevated [CO2].
SUPPLEMENTARY DATA
Supplementary data are available online at https://academic.oup.com/aob and consist of the following. Table S1: Leaf length of soybean in the mature stage under both ambient and elevated CO2 conditions. Table S2: Leaf widths of soybean in the mature stage under both ambient and elevated CO2 conditions. Table S3: Branch angle, petiole angle, mid-leaf angle and leaf angles of leaf, middle and right leaves in a trifoliate leaf in the mature stage used for parameterization of the soybean architecture models under both ambient and elevated CO2 conditions. Table S4: Internode and petiole lengths for each node in the main stem and those for branches used for parameterization of models under ambient CO2 conditions. Table S5: Probabilities of node numbers for the main stem and the branches used for parameterization of the canopy architecture model under both ambient and elevated CO2 conditions. Table S6: Maximal node numbers of the main stem and the branches for Br1 to Br2 of soybean under ambient and elevated CO2 conditions. Table S7: Maximal node numbers of the main stem and branches for Br3 to Br6 of soybean under ambient and elevated CO2 conditions. Table S8: Senescence leaf numbers in every 3 d for soybean grown under ambient and elevated CO2 conditions. Table S9: Vcmax and Jmax for top leaves of soybean grown under ambient and elevated CO2 conditions during a growing season. Table S10: Biomass, model-calculated cumulative GPP. Table S11: Leaf photosynthesis at different PPFD under both ambient and elevated [CO2] conditions. Figure S1: Air temperature, relative humidity and photosynthetic photon flux density during the growing season from 168 DOY to 267 DOY used for modelling canopy photosynthesis. Figure S2: The proportion of Rubisco-limited photosynthesis under high light and under low light. Methods: Pseudocode for the randomized process.
ACKNOWLEDGEMENT
The authors declare no conflicts of interest.
FUNDING
The authors acknowledge funding from the Bill and Melinda Gates Foundation grant (grant no. OPP1172157), National Natural Science Foundation of China (grant nos. 31970378, 31870214), Ministry of Science and Technology (grant no. 2015CB150104) and Strategic Priority Research Program of the Chinese Academy of Sciences (grant no. XDB27020105).
LITERATURE CITED
- Ainsworth EA, Davey PA, Bernacchi CJ, et al. . 2002. A meta-analysis of elevated [CO2] effects on soybean (Glycine max) physiology, growth and yield. Global Change Biology 8: 695–709. [Google Scholar]
- Ainsworth EA, Long SP. 2005. What have we learned from 15 years of free-air CO2 enrichment (FACE)? A meta-analytic review of the responses of photosynthesis, canopy properties and plant production to rising CO2. New Phytologist 165: 351–372. [DOI] [PubMed] [Google Scholar]
- Amthor JS. 2000. The McCree-de Wit-Penning de Vries-Thornley respiration paradigms: 30 years later. Annals of Botany 86: 1–20. [Google Scholar]
- Amthor JS, Koch GW, Willms JR, Layzell DB. 2001. Leaf O2 uptake in the dark is independent of coincident CO2 partial pressure. Journal of Experimental Botany 52: 2235–2238. [DOI] [PubMed] [Google Scholar]
- Anten NPR, Schieving F, Medina E, Werger MJA, Schuffelen P. 1995. Optimal leaf area indices in C3 and C4 mono- and dicotyledonous species at low and high nitrogen availability. Physiologia Plantarum 95: 541–550. [Google Scholar]
- Ball JT, Woodrow IE, Berry JA. 1987. A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions. In: Biggins J, ed. Progress in photosynthesis research. Dordrecht: Springer, 221–224. [Google Scholar]
- Bernacchi CJ, Kimball BA, Quarles DR, Long SP, Ort DR. 2007. Decreases in stomatal conductance of soybean under open-air elevation of [CO2] are closely coupled with decreases in ecosystem evapotranspiration. Plant Physiology 143: 134–144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernacchi CJ, Leakey ADB, Heady LE, et al. . 2006. Hourly and seasonal variation in photosynthesis and stomatal conductance of soybean grown at future CO2 and ozone concentrations for 3 years under fully open-air field conditions. Plant, Cell & Environment 29: 2077–2090. [DOI] [PubMed] [Google Scholar]
- Bernacchi CJ, Morgan PB, Ort DR, Long SP. 2005. The growth of soybean under free air [CO2] enrichment (FACE) stimulates photosynthesis while decreasing in vivo Rubisco capacity. Planta 220: 434–446. [DOI] [PubMed] [Google Scholar]
- Bernacchi CJ, Pimentel C, Long SP. 2003. In vivo temperature response functions of parameters required to model RuBP-limited photosynthesis. Plant, Cell & Environment 26: 1419–1430. [Google Scholar]
- Bernacchi CJ, Singsaas EL, Pimentel C, Portis AR Jr, Long SP. 2001. Improved temperature response functions for models of Rubisco-limited photosynthesis. Plant, Cell & Environment 24: 253–259. [Google Scholar]
- Buckley TN, Mott KA, Farquhar GD. 2003. A hydromechanical and biochemical model of stomatal conductance. Plant, Cell & Environment 26: 1767–1785. [Google Scholar]
- Castro JC, Dohleman FG, Bernacchi CJ, Long SP. 2009. Elevated CO2 significantly delays reproductive development of soybean under Free-Air Concentration Enrichment (FACE). Journal of Experimental Botany 60: 2945–2951. [DOI] [PubMed] [Google Scholar]
- Chen CP, Zhu X-G, Long SP. 2008. The effect of leaf-level spatial variability in photosynthetic capacity on biochemical parameter estimates using the Farquhar model: a theoretical analysis. Plant Physiology 148: 1139–1147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clough JM, Peet MM. 1981. Effects of intermittent exposure to high atmospheric CO2 on vegetative growth in soybean. Physiologia Plantarum 53: 565–569. [Google Scholar]
- DePury DGG, Farquhar GD. 1997. Simple scaling of photosynthesis from leaves to canopies without the errors of big-leaf models. Plant, Cell & Environment 20: 537–557. [Google Scholar]
- Dermody O, Long SP, DeLucia EH. 2006. How does elevated CO2 or ozone affect the leaf-area index of soybean when applied independently? New Phytologist 169: 145–155. [DOI] [PubMed] [Google Scholar]
- Dermody O, Long SP, Kelly M, DeLucia EH. 2008. How do elevated CO2 and O3 affect the interception and utilization of radiation by a soybean canopy? Global Change Biology 14: 556–564. [Google Scholar]
- Farquhar GD, Von Caemmerer S, Berry JA. 1980. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149: 78–90. [DOI] [PubMed] [Google Scholar]
- Givnish TJ. 1988. Adaptation to sun and shade : a whole-plant perspective. Australian Journal of Plant Physiology 15: 63–92. [Google Scholar]
- Humphries SW, Long SP. 1995. WIMOVAC: a software package for modelling the dynamics of plant leaf and canopy photosynthesis. Computer Applications in the Biosciences 11: 361–371. [DOI] [PubMed] [Google Scholar]
- Kim JH, Lee JW, Ahn TI, Shin JH, Park KS, Son JE. 2016. Sweet pepper (Capsicum annuum L.) canopy photosynthesis modeling using 3D plant architecture and light ray-tracing. Frontiers in Plant Science 7: 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimball BA. 1983. Carbon dioxide and agricultural yield: an assemblage and analysis of 430 prior observations. Agronomy Journal 75: 779–788. [Google Scholar]
- Leakey ADB, Ainsworth EA, Bernacchi CJ, Rogers A, Long SP, Ort DR. 2009. Elevated CO2 effects on plant carbon, nitrogen, and water relations: six important lessons from FACE. Journal of Experimental Botany 60: 2859–2876. [DOI] [PubMed] [Google Scholar]
- Leakey ADB, Bernacchi CJ, Dohleman FG, Ort DR, Long SP. 2004. Will photosynthesis of maize (Zea mays) in the US Corn Belt increase in future [CO2] rich atmospheres? An analysis of diurnal courses of CO2 uptake under free-air concentration enrichment (FACE). Global Change Biology 10: 951–962. [Google Scholar]
- Li G, Lin L, Dong Y, et al. . 2012. Testing two models for the estimation of leaf stomatal conductance in four greenhouse crops cucumber, chrysanthemum, tulip and lilium. Agricultural and Forest Meteorology 165: 92–103. [Google Scholar]
- Long SP, Ainsworth E A, Leakey ADB, Nösberger J, Ort DR. 2006. Food for thought: lower-than-expected crop yield stimulation with rising CO2 concentrations. Science 312: 1918–21. [DOI] [PubMed] [Google Scholar]
- Long SP, Ainsworth E A, Rogers A, Ort DR. 2004. Rising atmospheric carbon dioxide: plants FACE the future. Annual Review of Plant Biology 55: 591–628. [DOI] [PubMed] [Google Scholar]
- Long SP, Bernacchi CJ. 2003. Gas exchange measurements, what can they tell us about the underlying limitations to photosynthesis? Procedures and sources of error. Journal of Experimental Botany 54: 2393–2401. [DOI] [PubMed] [Google Scholar]
- McCree KJ, Troughton JH. 1966. Non existence of an optimal leaf area index for the production rate of white clover grown under constant conditions. Plant Physiology 41: 1615–1622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medlyn BE, Dreyer E, Ellsworth D, et al. . 2002. Temperature response of parameters of a biochemically based model of photosynthesis. II. A review of experimental data. Plant, Cell & Environment 25: 1167–1179. [Google Scholar]
- Miglietta F, Peressotti A, Vaccari FP, Zaldei A, Deangelis P, Scarascia-mugnozza G. 2001. Free-air CO2 enrichment (FACE) of a poplar plantation: the POPFACE fumigation system. New Phytologist 150: 465–476. [Google Scholar]
- Monteith J, Unsworth M, eds.2007. Principles of environmental physics, 3rd edn. Elsevier, London. [Google Scholar]
- Monteith JL. 1972. Solar radiation and productivity in tropical ecosystems. Journal of Applied Ecology 9: 747–766. [Google Scholar]
- Morgan PB, Bernacchi CJ, Ort DR, Long SP. 2004. An in vivo analysis of the effect of season-long open-air elevation of ozone to anticipated 2050 levels on photosynthesis in Soybean. Plant Physiology 135: 2348–2357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgan PB, Bollero G a, Nelson RL, Dohleman FG, Long SP. 2005. Smaller than predicted increase in aboveground net primary production and yield of field-grown soybean under fully open-air [CO2] elevation. Global Change Biology 11: 1856–1865. [Google Scholar]
- Norman J. 1980. Interfacing leaf and canopy irradiance interception models. In: Hesketh JD, Jones JW, eds. Predicting photosynthesis for ecosystem models. Boca Raton, FL: CRC Press, 49–67. [Google Scholar]
- Parry M., Rosenzweig C, Iglesias A, Livermore M, Fischer G. 2004. Effects of climate change on global food production under SRES emissions and socio-economic scenarios. Global Environmental Change 14: 53–67. [Google Scholar]
- Pedersen P, Lauer JG. 2004. Response of soybean yield components to management system and planting date. Agronomy Journal 96: 1372–1381. [Google Scholar]
- Peng S, Huang J, Sheehy JE, et al. . 2004. Rice yields decline with higher night temperature from global warming. Proceedings of the National Academy of Sciences of the United States of America 101: 9971–9975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pound MP, French A P, Murchie EH, Pridmore TP. 2014. Automated recovery of 3D models of plant shoots from multiple colour images. Plant Physiology 166: 1688–1698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogers A, Allen DJ, Davey PA, et al. . 2004. Leaf photosynthesis and carbohydrate dynamics of soybeans grown throughout their life-cycle under free-air. Plant, Cell & Environment 27: 449–458. [Google Scholar]
- Setiyono TD, Weiss A, Specht JE, Cassman KG, Dobermann A. 2008. Leaf area index simulation in soybean grown under near-optimal conditions. Field Crops Research 108: 82–92. [Google Scholar]
- Song Q, Zhang G, Zhu X-G. 2013. Optimal crop canopy architecture to maximise canopy photosynthetic CO2 uptake under elevated CO2 – a theoretical study using a mechanistic model of canopy photosynthesis. Functional Plant Biology 40: 109–124. [DOI] [PubMed] [Google Scholar]
- Spaeth SC, Randall HC, Sinclair TR, Vendeland JS. 2010. Stability of Soybean Harvest Index1. Agronomy Journal 76: 482. [Google Scholar]
- Srinivasan V, Kumar P, Long SP. 2016. Decreasing, not increasing, leaf area will raise crop yields under global atmospheric change. Global Change Biology 23: 1626–1635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Leuning R. 1998. A two-leaf model for canopy conductance, photosynthesis and partitioning of available energy I: Model description and comparison with a multi-layered model. Agricultural and Forest Meteorology 91: 89–111. [Google Scholar]
- Wang Y, Song Q, Jaiswal D, de Souza AP, Long SP, Zhu XG. 2017. Development of a three-dimensional ray-tracing model of sugarcane canopy photosynthesis and tts application in assessing impacts of varied row spacing. Bioenergy Research 10: 626–634. [Google Scholar]
- Wittig VE, Bernacchi CJ, Zhu X-G, et al. . 2005. Gross primary production is stimulated for three Populus species grown under free-air CO2 enrichment from planting through canopy closure. Global Change Biology 11: 644–656. [Google Scholar]
- Wu Q, Cournède PH. 2010. Sensitivity analysis of GreenLab model for maize. In: Plant growth modeling, simulation, visualization and applications, proceedings – PMA, Vol.09 Beijing: IEEE, 311–318. [Google Scholar]
- Yin X. 2000. A generic equation for nitrogen-limited leaf area index and its application in crop growth models for predicting leaf senescence. Annals of Botany 85: 579–585. [Google Scholar]
- Zheng B, Shi L, Ma Y, Deng Q, Li B, Guo Y. 2008. Comparison of architecture among different cultivars of hybrid rice using a spatial light model based on 3-D digitising. Functional Plant Biology 35: 900–910. [DOI] [PubMed] [Google Scholar]
- Zhu X-G, Ort DR, Whitmarsh J, Long SP. 2004a The slow reversibility of photosystem II thermal energy dissipation on transfer from high to low light may cause large losses in carbon gain by crop canopies: a theoretical analysis. Journal of Experimental Botany 55: 1167–1175. [DOI] [PubMed] [Google Scholar]
- Zhu X-G, de Sturler E, Long SP. 2007. Optimizing the distribution of resources between enzymes of carbon metabolism can dramatically increase photosynthetic rate: a numerical simulation using an evolutionary algorithm. Plant Physiology 145: 513–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X, Portis JR, Long SP. 2004b Would transformation of C3 crop plants with foreign Rubisco increase productivity? A computational analysis extrapolating from kinetic properties to canopy. Plant, Cell & Environment 27: 155–165. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.