A functional–structural model of upland rice root systems reveals the importance of laterals and growing root tips for phosphate uptake from wet and dry soils

Abstract

Background and Aims

Upland rice is often grown where water and phosphorus (P) are limited. To better understand the interaction between water and P availability, functional–structural models that mechanistically represent small-scale nutrient gradients and water dynamics in the rhizosphere are needed.

Methods

Rice was grown in large columns using a P-deficient soil at three P supplies in the topsoil (deficient, sub-optimal and non-limiting) in combination with two water regimes (field capacity vs. drying periods). Root system characteristics, such as nodal root number, lateral types, interbranch distance, root diameters and the distribution of biomass with depth, as well as water and P uptake, were measured. Based on the observed root data, 3-D root systems were reconstructed by calibrating the structural architecure model CRootBox for each scenario. Water flow and P transport in the soil to each of the individual root segments of the generated 3-D root architectures were simulated using a multiscale flow and transport model. Total water and P uptake were then computed by adding up the uptake by all the root segments.

Key Results

Measurements showed that root architecture was significantly affected by the treatments. The moist, high P scenario had 2.8 times the root mass, double the number of nodal roots and more S-type laterals than the dry, low P scenario. Likewise, measured plant P uptake increased >3-fold by increasing P and water supply. However, drying periods reduced P uptake at high but not at low P supply. Simulation results adequately predicted P uptake in all scenarios when the Michaelis–Menten constant (K_m) was corrected for diffusion limitation. They showed that the key drivers for P uptake are the different types of laterals (i.e. S- and L-type) and growing root tips. The L-type laterals become more important for overall water and P uptake than the S-type laterals in the dry scenarios. This is true across all the P treatments, but the effect is more pronounced as the P availability decreases.

Conclusions

This functional–structural model can predict the function of specific rice roots in terms of P and water uptake under different P and water supplies, when the structure of the root system is known. A future challenge is to predict how the structure root systems responds to nutrient and water availability.

INTRODUCTION

Although only 4 % of the world’s rice (Oryza spp.) production is grown under upland conditions (GRiSP, 2013; Chauhan et al., 2017), upland rice systems are an important food source for subsistence farmers in Asia, Africa and Central America. Upland rice is often cultivated in marginal environments without appriopriate management, leading to large yield gaps. Drought events and phosphorus (P) deficiency in soils comprise two major challenges for upland rice production, and these limiting factors often co-occur (Mueller et al., 2012; Diagne et al., 2013). To cope with drought and/or P-deficient soils, efficient rice root systems for resource acquisition under limiting conditions are of crucial importance (Wissuwa and Ae, 2001; Rose et al., 2013; Mori et al., 2016). Interestingly, soil water status and P availability are highly inter-related, and both resources have specific behaviour and dynamics in the soil (Lal and Stewart, 2016). The soil water status influences the P supply through diffusion, aeration and sorption, while the accumulation of P in topsoil layers affects rooting patterns which indirectly influences the water acquisition from deeper layers (Ho et al., 2005). Due to these complex interactions and the heterogeneous spatial distribution of both P (often stratified in top layers) and water (often more available in deeper layers) in soils, trade-offs and synergisms between P and water uptake efficiency of roots with respect to root architectural traits may exist (Ho et al., 2005). It is currently not known to what extent certain root types or root responses contribute to a crop’s tolerance against drought and/or low P availability. Hence, it is unclear how the root responses to limitations of one soil resource affect the uptake of another soil resource (i.e. water or P).

With experimental studies, we can evaluate the impact of P and/or water stress on the root development of rice. For example, an increased rooting depth and a decreased thickness of the nodal roots [emerging from both apical and basal sites of each shoot unit (Abe and Morita, 1994)] were previously observed with reduced water availability, while reduced root growth was observed in response to low P availability (De Bauw et al., 2019). Plant root systems comprise a set of phenes, or traits, that interact. Phenes are the units of the plant phenotype, and phene states represent the variation in form and function a particular phene may take (York et al., 2013). Multiple studies have identified single root phene responses to environmental changes (e.g. Rose et al., 2013; Gao and Lynch, 2016; Hazman and Brown, 2018), but studies on root system responses integrating multiple phenes into a holistic root system performance are generally scarce. Obtaining information about single phene responses to P and water availability is very important, but understanding of the functionality of these responses for water and P uptake requires a whole soil–root system approach. This approach should integrate the responses of all root phenes, which constitute the root system, with flow and transport processes in the soil that define how the outer environment of the root system interacts with root activity. Direct experimental observations of the root system interacting with its environment are nowadays possible using dedicated non-invasive measurement and tracer techniques (Zarebanadkouki et al., 2013; Koch et al., 2019), but these techniques are still too elaborated and limited to allow for larger scale studies (in terms of both size of the root systems and the number of plants investigated). Simulation models are therefore interesting tools as they allow these limitations to be overcome by investigating responses and interactions in the soil–root system in silico. Dynamic structural root system models have been previously developed (Dunbabin et al., 2013; Schnepf et al. (2018) enabling the integration of multiple root phenes into root systems. Integrated virtual root systems could then be linked with soil water flow and P transport models, in order to acquire insights into root performance and function, and unravel the underlying processes of water and P uptake.

Such functional–structural models allow the identification of important phenes contributing to tolerance under contrasting scenarios, and they form a useful tool to guide breeding of ideotypes adapted to specific soil environments (Lynch, 2011; Lynch and Brown, 2012; Ahmadi et al., 2014). Therefore functional–structural models of the interactions between root systems and soil are increasingly used to enhance physical understanding of nutrient transport and water flow in root–soil systems, along with experiments (Dunbabin et al., 2013; Postma et al., 2017; Schnepf et al., 2018; Zhu et al., 2018; Koch et al., 2019; Zhou et al., 2020). However, the major challenge in such approaches is to capture rhizosphere gradients in the whole root system scale simulation and to transfer results from a single root scale to a larger scale efficiently and accurately. With this perspective, a continuum multiscale model that explicitly defines the 3-D root architecture, water and nutrient flow in both soil and roots as well as rhizosphere gradients around each root segment was recently developed by Mai et al. (2018).

Unfortunately, it remains very challenging to parameterize models so that they can predict specific root responses of certain crops or contrasting varieties to environmental factors. Currently, models have to be parameterized according to particular reactions of plant roots to soil and environmental conditions. Combining experimentally measured single root phene datasets with such 3-D continuum multiscale soil–root models would theoretically allow the evaluation of integrated root responses to water content and P level in the soil. However, such a combined approach has never been thoroughly validated with real root data. In this work, we aim to highlight the potential of integrating experimental datasets of individual root phenes of upland rice with in silico simulations of water and P uptake by this 3-D continuum multiscale soil–root model.

Specifically, the objectives of this study were to (1) evaluate the integrated root system responses of upland rice to changing P and water availability; (2) evaluate the parameterized 3-D continuum multiscale soil–root model for the observed rice root system architectures in predicting water and P uptake from the soil under contrasting conditions; (3) use the developed model to make predictions about the specific soil layers and depths from which water and P are taken up; and (4) evaluate the role of different root types and characteristics for P and water uptake under contrasting scenarios.

MATERIALS AND METHODS

Laboratory experiments

Soil preparation, P treatments and pot filling

A pot trial was set up in a greenhouse located at the Sokoine University of Agriculture (Tanzania). More details on this experimental set-up are descibed in Supplementary data Text S1. Initially, a P-deficient soil (0.035 mg P L^–1 in soil solution) was collected from an upland rice field in Matombo (07°02'46.8''S; 37°47'11.6''E; Tanzania). This soil was classified as a ferralsol (World Reference Base for Soil Resources) and was characterized by a soil pH(CaCl₂) = 5.7, a particle size distribution of 9 % sand, 57 % silt and 34 % clay, and an oxalate-extractable Al_ox = 1073 mg kg^–1, Fe_ox = 1730 mg kg^–1, Mn_ox = 2559 mg kg^–1 and P_ox = 122 mg kg^–1. After sampling, the bulk soil was shade dried, crushed to an aggregate size of 4 mm and amended with nutrients (Supplementary data Text S1), in order to avoid any deficiency other than P.

As P generally accumulates in the topsoil, no P was initially added to the bulk soil in order to mimic a P-deficient sub-soil. Large pots (height 55 cm, diameter 16 cm) were then filled with 7.3 kg of the P-deficient sub-soil. The remainder of this bulk soil was then subjected to three different P treatments. One-third was amended with a non-limiting amount of ground Triple Super Phosphate (TSP) (70.8 mg P ${\mathrm{k}\mathrm{g}}_{\mathrm{t}\mathrm{o}\mathrm{p}\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}^{-1}$ or 354 mg P per pot) up to a theoretical P concentration of 0.5 mg P L^–1 in soil solution (PlusP), which was based on the previously determined P adsorption isoterm. Another third was amended with a sub-optimal amount of ground TSP (25.0 mg P ${\mathrm{k}\mathrm{g}}_{\mathrm{t}\mathrm{o}\mathrm{p}\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}^{-1}$ or 125.2 mg P per pot) up to a theoretical P concentration of 0.1 mg P L^–1 in soil solution (SubP). The remaining part was not amended with TSP (NoP), and CaCl₂ was used to equalize the amended Ca in all treatments. Pots were then filled with 5 kg of topsoil, affixed on top of each sub-soil. The layer of the sub-soil was 30 cm and the topsoil was 20 cm thick. Pots were then irrigated to bring the whole pot to field capacity (38 %, w/w).

Sowing, maintenance and water treatments

One pre-germinated seed of the typical upland rice variety (NERICA4) was sown into the pots (1 cm depth) at the centre of the surface, which is closely related to a conventional spacing density of 20 × 20 cm for rice on the field.

Pots were irrigated daily to field capacity (based on pot weight) until 25 days after sowing (DAS), and two contrasting water treatments were then initiated and maintained until the end of the trial. Half of the pots were irrigated daily to field capacity (FC), while the other half was subjected to drying periods (DP). To represent drying cycles during erratic rainfall, pots were re-watered up to FC after a period of approx. 4 d (pre-set as an average period of drying). Each treatment combination was replicated four times. The amount of irrigated water was consistently monitored to assess evapotranspiration, water use and water productivity (Supplementary data Fig. S1; Table S1). Pot weight was monitored, and the water potential could hence be derived by using a pF curve determined on this soil. An estimate of the evaporation was monitored by daily weighing and re-irrigating six unsown pots, randomly placed through the experiment.

Data collection

Plant development was monitored by measuring plant height and counting tillers and leaves twice a week. At 52 DAS, shoots were cut, oven-dried (60 °C), weighed and manually ground using a mortar and pestle. P concentrations in the shoot tissues were then determined by inductively coupled plasma atomic emission spectroscopy (ICP-OES; Thermo Scientific iCAP 7000 series) after digestion in HNO₃.

Immediately after removing the shoot, the soil cylinder was carefully taken out of the pot and precisely cut into three segments. One part comprised a segment (A) from 0 to 15 cm depth which included the ‘shallow roots’; another segment (B) comprised soil from 15 to 30 cm depth including the ‘intermediate roots’; and the last segment incorporated the ‘deep roots’ below a depth of 30 cm. The latter segment (C) was defined according to most rice studies, where deep roots are defined as roots below 30 cm (Kato et al., 2006, 2013; Gowda et al., 2011). For each soil segment, roots were carefully washed by gently shaking the soil segments on a 2 mm net in water. After removing the soil from the roots, roots of each segment were placed in a dish with clean water, and root architectural variables were determined as follows.

The number of nodal roots was counted and the average nodal root diameter was measured using a transparent ruler (0.1 mm). For each soil segment, the transparent ruler was placed on the nodal roots, and the average thickness was visually determined. S-type lateral root density (i.e. the branching distance of the first-order laterals on the nodal root) was scored using the ‘shovelomics scoreboard’ developed by Trachsel et al. (2011). The shovelomics scoreboard is a resource for phenotyping roots of soil-grown crops after excavation. S-type laterals are short and thin, emerging at the root base on the nodal roots, and they do not have higher order branches. L-type laterals are longer and generally thicker, and they branch further into higher order branches (Nestler et al., 2016). The density of the S-type laterals was determined by placing the different scoring classes from the scoreboard next to the roots and comparing the densities from the board with the actual density on the root. These scores were then translated into actual values of distance. Lateral root thickness (both at the base and at the deeper roots) was visually scored according to five classes, each corresponding to a thickness class with actual diameter values. The secondary branching distance on L-type roots was also scored based on the ‘shovelomics scoreboard’. After analysing root architecture in the different segments, the roots from each segment were oven-dried (60 °C) and weighed to determine root distribution and biomass allocation. Total P uptake was calculated by assuming an equal P concentration in root and shoot.

The continuum multiscale model for growing root systems and virtual experiment set-up

Model description

The CRootBox root architectural model is a tool to create root geometries based on root growth mechanisms such as elongation, branching and death (Schnepf et al., 2018). The root is represented as a branched network discretized into connected segments with attributes such as root radius and age that are related to hydraulic properties. In this work, the root architecture model parameters were obtained by calibrating the model based on the available data from the lab experiment. A growing root system was reconstructed for each scenario. These root system models were then linked to water and P dynamics, without feedback mechanisms on root development.

The resulting root grid was used in a numerical simulator, DuMu^x (Flemisch et al., 2011), in which the root network is embedded within a 3-D soil domain. Water flow equations are solved in both domains: 3-D Richards equation (Richards, 1931) for the soil domain and linear flow equation for the 3-D root segment network using the approach developed by Doussan et al. (2006). The exchange of water between domains is modelled based on source/sink terms that are defined with regards to radial root conductances and water potential differences between the soil and the root xylem (Koch et al., 2018). Potential transpiration and irrigation events are the main drivers for water flow, and they are prescribed as boundary conditions at the root collar and the soil surface. The 3-D solute transport equation (convection dispersion equation), which is coupled to the soil water flow equation, is solved for the soil domain to describe P transport. The main factors influencing P dynamics are diffusion, which depends on soil water content, convection, (non-linear) sorption and P uptake by the root system. P uptake by each root segment was prescribed by the Michaelis–Menten kinetics using the simulated P concentrations at the soil–root interface of the root segment. Our multiscale approach handles small-scale concentration gradients at sub-millimetre scale around single root segments by assigning a 1-D radially symmetric rhizosphere model to each root segment as in the Barber–Cushman model (Barber, 1995). It combines in a mass conservative way the Barber–Cushman model approach for single root segments with the 3-D macroscopic model, which describes at centimetre-scale resolution the water flow and nutrient transport in the soil volume that contains the entire root system (Mai et al, 2018). So far, we have not considered kinetic sorption–desorption or multispecies sorption–desorption processes or other biogeochemical reactions in the rhizosphere which can be influenced by root exudation. To simulate the water and nutrient transport in the soil columns, the multiscale model developed by Mai et al. (2018) was further upgraded to consider root growth and, consequently, a dynamic root system. The mathematical equations and their implementation are described in Supplementary data Text S2.

Root growth is simulated by adding, after each time step, root segments to the root system that developed during this particular time step. During a time step, only uptake by root segments that were present at the beginning of the time step is simulated. If a new root segment is added in a soil control volume that already contains other root segments, the radii of the cylindrical rhizosphere models for the existing root segments are decreased (Eqn 4 in Supplementary data Text S2). The rhizosphere concentration profiles around already existing root segments are maintained but clipped at their outer ends. The initial solute concentration in the cylindrical rhizosphere model of the new segment is uniform and is calculated using a mass balance from the mass in the clipped outer volumes of the already existing rhizopshere models.

Implementation

The cylindrical soil domain with a diameter of 16 cm and a height of 55 cm was represented by a structured grid using hexahedral elements. The numerical mesh was generated using the mesh generator GMesh (Geuzaine and Remacle, 2009), with a vertical resolution of 2 cm and a horizontal resolution varying between 1 cm and 3 cm. In total, the soil mesh has 1839 elements (Supplementary data Fig. S2). The grid elements of the root system (root segments) had a standard length of 1 cm along the roots. Some root segments were smaller to accommodate branches to appear in specific positions. The simulations of water flow and solute transport in the coupled soil–root domains were performed using the simulation framework for soil–root interaction (Koch et al., 2018; Mai et al., 2018), utilizing a cell-centred finite volume scheme. The code is written in C++ and combines the DuMu^x framework (Flemisch et al., 2011) with the structural root model CRootBox (Schnepf et al., 2018). The code that was used for the specific application of this study is shared on GitHub (https://github.com/Plant-Root-Soil-Interactions-Modelling/dumux-rosi/tree/pub/Mai2019).

Virtual experiment set-up

Based on the data from the lab experiment, simulation scenarios were set up to study the water and P transport in the soil–rice column as well as the functions of the root system in plant water and nutrient uptake. Two water regimes were considered in the model: (1) optimal conditions where the soil water content was maintained at field capacity (FC) by daily compensating evapotranspiration; and (2) conditions with drying periods (DP) where the soil columns were not irrigated for several days. Similar to the lab experiment, P availability in the simulations comprised three contrasting concentrations in the topsoil: P deficient (NoP), a sub-optimal (SubP) and a non-P limited scenario (PlusP). Combining these three P rates and two water regimes resulted in six contrasting scenarios to be simulated.

Soil and root hydraulic and physicochemical properties

The soil is considered as a homogenous medium with constant hydraulic properties and sorption capacity for P which is characterized by the Freundlich isotherm (Table 1). The Freundlich coefficient and the Freundlich power were derived from a P adsorption experiment. Briefly, the soil was dried and sieved. Replicate samples of 3 g were suspended in 30 mL of water and amended with KH₂PO₄ at various rates between 0 and 30 mg P L^–1. The soils were equilibrated with an end-over-end shaker for 24 h followed by centrifugation and filtration (0.45 μm) and P was analysed by inductively coupled plasma mass spectrometry (ICP-MS; Agilent7700X). The Freundlich coefficient was 124.8 mg^0.6 kg^–1 L^0.4 and the Freundlich power was 0.4. Regarding the distribution of the P concentration in the soil column, the P concentration in the topsoil layer (the first 20 cm layer from the soil surface) varied according to the P rate, while the P concentration in the deeper sub-soil (from 20 cm to the bottom) remained constant and deficient. The root hydraulic properties and Michaelis–Menten parameters necessary for root water and nutrient uptake simulations are taken from the literature and are presented in Table 1.

Table 1.

Soil and root parameters in the multiscale simulations

Soil parameters	Value	Sources
Hydraulic characteristic
Van Genuchten alpha (m–1)	0.1	Fitting curve
Van Genuchten n (–)	2.5	Fitting curve
Residual water content (–)	0.03	Fitting curve
Porosity (–)	0.345	Measured
Saturated hydraulic conductivity (m d–1)	0.286	Pedotransfer function (Schaap et al. 2001)
Sorption characteristic
Freundlich coefficient (mg0.6 kg–1 L0.4)	124.8	Measured
Freundlich power (–)	0.4	Measured
Root parameters	Value	Sources
Hydraulic characteristic
Axial conductance (m4 s–1 Pa–1)	2e-16	Matsuo et al. (2009)
Radial conductivity (m s–1 Pa–1)	6.3e-14	Miyamoto et al. (2001)
Michaelis–Menten kinetics for P uptake
Maximum uptake rate (kg m–2 s–1)	3.844e-10	(Teo et al. (1992a)
Michaelis constant (kg m–3)	1.054e-4	(Teo et al. (1992b)

Reconstruction of rice root systems

For each scenario, a 3-D root architecture was generated with CRootBox using scenario-specific parameters, as presented in Fig. 1. Some of the necessary model parameters were directly obtained from the measurements (i.e. the number and thickness of nodal roots, lateral root density near the proximal end of the nodals, S-type and L-type lateral root radius and secondary branching distance on L-type roots). To obtain the remaining parameters, CRootBox was calibrated. The emergence coefficient k of the nodal roots, the transition depth z₀ of the distribution of L- and S-type lateral roots and the scaling factor of the interbranch distance at the bottom of the soil column Ks were adjusted to fit with the root mass distribution derived from the experiment (Supplementary data Fig. S3; Text S2). The parameter sets that were used in CRootBox to simulate the 3-D root architectures for the different scenarios are presented in Table 2. The number of root segments in the root systems varied between 11 509 segments in the combined water and P stress scenario and 27 659 segments in the case of optimal water conditions (FC) and surplus P in top soil.

Fig. 1.

Simulated root systems (3-D architture) from CRootBox of upland rice grown on a P-deficient soil with three P treatments in the topsoil [no P amendment (NoP), a sub-optimal rate (SubP) and a non-limiting rate (PlusP)] and two water regimes (field capacity (FC) and drying periods (DP)]. The colour of the root represents the P uptake rate of the root, while the colour on the discs represents the soil P sink. The transition between topsoil and sub-soil (at 20 cm depth) can be observed by the shift in P uptake rate in SubP and PlusP.

Table 2.

CRootBox parameter values used for the reconstruction of the rice root system of NERICA4 grown under contrasting conditions. P availability comprised three levels: NoP, SubP and PlusP, while water included two levels: field capacity (FC) vs. drying cycles (DP)

	FC			DP
	NoP	SubP	PlusP	NoP	SubP	PlusP
Nodal roots
Number of nodals* (–)	60	69	100	43	55	69
Nodal diameter* (cm)	1.080	1.075	1.350	1.045	1.055	1.250
Emerging coefficient† (d–1)	12	8.5	13.5	10	5	12.5
Maximal root length‡ (cm)	90	90	90	90	90	90
Initial elongation rate† (cm d–1)	2	2	2	2	2	2
Length of basal zone§ (cm)	1	1	1	1	1	1
Length of apical zone§ (cm)	1	1	1	1	1	1
Insertion angle† (rad)	0.7	0.8	0.8	0.7	0.8	0.8
Tropism type§ (–)	1	1	1	1	1	1
Tropism strength* (–)	0.7	0.7	0.7	0.7	0.7	0.7
Root flexibility§ (cm–1)	0.2	0.2	0.2	0.2	0.2	0.2
First-order lateral root distribution (on the nodal roots)
Lateral type transition steepness, s Eqn 7 S2† (cm–1)	0.3	1.5	1.5	0.3	0.3	1.5
Lateral type transition depth, z0 Eqn 7 S2† (cm)	–12	–20	–20	–15	–18	–15
Inter-branch distance at proximal end of nodal roots* (i.e. only S-types) (cm)	0.35	0.19	0.21	0.35	0.30	0.27
Inter-branch distance scaling factor at distal end of nodal roots, ks,∞ Eqn 8 S2† (–)	1.6	1.85	2.3	1.8	1.9	1.65
Inter-branch distance transition depth, z0 Eqn 8 S2† (cm)	–13	–20	–20	–25	–15	–20
Inter-branch distance slope, s Eqn 8 S2† (cm–1)	1.5	1.5	1.5	1.5	1.5	1.5
S-type lateral roots (do not create second-order laterals)
S-type radius* (µm)	131.3	118.8	106.3	118.8	112.5	100.0
Maximal root length‡ (cm)	1.5	1.5	1.5	1.5	1.5	1.5
Initial elongation rate§ (cm d–1)	1	1	1	1	1	1
Tropism type§ (–)	1	1	1	1	1	1
Tropism strength§ (–)	3.5	3.5	3.5	3.5	3.5	3.5
Root flexibility§ (cm–1)	1	1	1	1	1	1
L-type lateral roots (create second-order laterals)
L-type radius* (µm)	187.5	175.0	168.8	206.3	150.0	209.4
Maximal root length† (cm)	6.5	4	4	6.5	4	4
Initial elongation rate† (cm d–1)	1.5	1	1	1.5	1	1.5
Length of basal zone† (cm)	0.5	0.5	0.5	0.5	0.4	0.37
Length of apical zone† (cm)	0.5	0.5	0.5	0.5	0.4	0.37
Inter-branch distance* † (cm)	0.7	0.7	0.6	0.5	0.4	0.37
Insertion angle§ (rad)	1.2	1.2	1.2	1.2	1.2	1.2
Tropism type§ (–)	1	1	1	1	1	1
Tropism strength§ (–)	3.5	3.5	3.5	3.5	3.5	3.5
Root flexibility§ (cm–1)	0.2	0.2	0.2	0.2	0.2	0.2
Second-order lateral roots (branching from L-type laterals)
Maximal root length‡ (cm)	0.8	0.8	0.8	0.8	0.8	0.8
Initial elongation rate‡ (cm d–1)	1.5	1	1	1.5	1.5	1.5
Tropism type§ (–)	1	1	1	1	1	1
Tropism strength§ (–)	1	1	1	1	1	1
Root flexibility§ (cm–1)	0.2	0.2	0.2	0.2	0.2	0.2

*Parameters from direct measurements in the laboratory experiment.

^†Manually calibrated parameters to fit the measured root mass fractions in each soil section.

^‡Parameters set to match the generally observed rice root systems (derived from pictures and/or few measurements).

^§Standard parameters from CRootBox.

Top boundary condition and initial P concentrations

To simulate the water conditions in the virtual experiment, the daily irrigation data as well as the evaporation rate monitored in the real experiment were used as the boundary condition at the soil surface (Supplementary data Fig. S1). Hence, the soil water balance in the simulations was set to match exactly the water balance of the lab columns. The daily evaporation rate varied in the range of 18–120 mL d^–1. In order to keep the soil column saturated in the FC treatment, the irrigation rate compensated the evaporation and transpiration of rice plant which increased over time following plant development. For the DP scenario, four cycles of drying (no irrigation) were reproduced from the 25th day of the experiment by virtually withholding irrigation. Total transpiration in each scenario was derived by extracting the measured evaporation from the monitored irrigation. The daily transpiration rates were then calculated proportional to the growing number of leaves. Evapotranspiration rates per unit surface calculated in this trial were relatively high, which probably can be attributed to the fact that the rice canopy exceeds the pot surface. At the bottom and sides of the soil column, zero-flux boundary conditions were imposed. In the sub-soil, the initial P concentration in the pore water was 0.035 mg P L^–1 for all scenarios. In contrast, the initial P concentration in the topsoil was varied corresponding to the P availability in solution after the three P fertilization levels in the real experiment: 0.035 mg P L^–1 (NoP), 0.1 mg P L^–1 (SubP) and 0.5 mg P L^–1 (PlusP).

RESULTS

Evaluating the rice root responses to changing P and water availability in the laboratory experiment

For rice grown in the laboratory experiment, the shoot and root biomass significantly responded to the P and water treatments, with a significant interaction between P and water treatments (details not shown). The same was true for the measured total (root + shoot) P uptake that significantly increased with increased P supply and increased water supply (Fig. 2), and there was a significant treatment interaction on P uptake. That interaction shows a larger effect of the water regime on P uptake at higher P supply and no effect of the water regime under P-deficient conditions (Fig. 2).

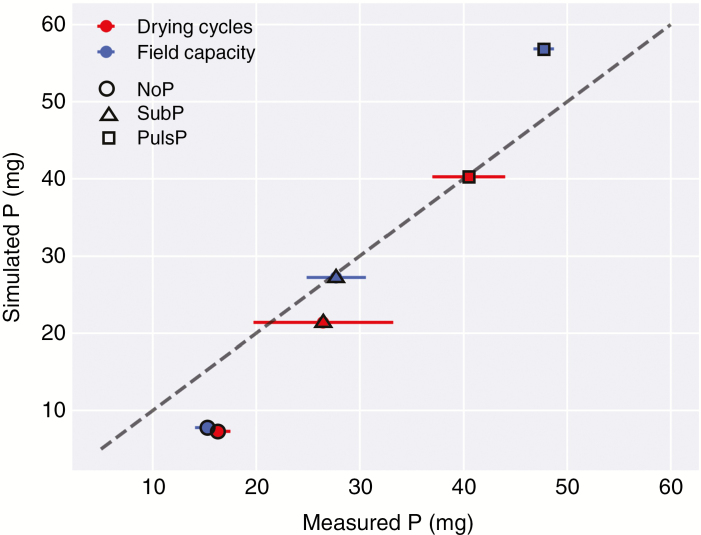
Fig. 2.

The simulated P uptake per plant (mg per plant or mg per pot, one plant per pot) vs. the measured P uptake per plant in the lab experiment (including the s.e.m.). The latter value of total P uptake was calculated for the shoot and the root after measuring shoot P concentration, and assuming an equal P concentration in the root. Rice root systems were grown and simulated on a P-deficient soil with three P treatments in the topsoil [no P amendment (NoP), a sub-optimal rate (SubP) and a non-limiting rate (PlusP)] and two water regimes [field capacity (FC) and drying periods (DP)].

Table 3 presents the root responses of upland rice to combinations of contrasting P rates and subjected to FC and DP for the determined root parameters in the laboratory experiment (top) and the derived parameters in CRootBox after calibration of the latter observations (bottom). Data from the pot experiment reveal that the total root mass increased with increasing P rates and decreased under DP compared with FC. Both the absolute root mass and the mass fraction in the shallow layer (0–15 cm) decreased with DP (Table 3; Supplementary data Fig. S3). The mass fraction in the intermediate layer remained unaffected by water but increased with increasing P rate. The absolute root mass in the deep layer (>30 cm) remained unaffected by the water regime, but the root mass fraction (% of total root mass) in this deep layer systematically increased under DP. (Table 3; Supplementary data Fig. S3)

Table 3.

Rice root characteristics determined in the lab experiment (top) and root system properties derived from CRootBox simulations of growing virtual 3-D root systems, which could not be observed directly (bottom). Root architectural parameters extracted from the lab experiment (top) were used to define input parameters for CRootBox (Table 2). The mass fraction distribution measured in the lab experiment was used to simulate equal volume fractions in the corresponding layers at a similar time. For both the laboratory experiment and the simulations, rice was grown on a P-deficient soil with three P treatments in the topsoil [no P amendment (NoP), a sub-optimal rate (SubP) and a non-limiting rate (PlusP)] and two water levels [field capacity (FC) and drying periods (DP)]. The L-type laterals only emerge in deeper layers, and their interbranch distance was not measured but was calibrated as presented in Table 2.

Lab experiment			Total root mass	Mass fraction A (0–15 cm)	Mass fraction B (15–30 cm)	Mass fraction C (>30 cm)	Nodal number	Nodal diameter		S-type radius	L-type radius	S-type distance	Secondary distance
			(g)	(%)	(%)	(%)		(mm)		(µm)	(µm)	(cm)	(cm)
	NoP	DP	1.6 (0.3)	44.0 (4.4)	26.9 (1.0)	29.1 (4.0)	43 (6)	1.045 (0.13)		118.8	206.3	0.35	0.51
		FC	2.0 (0.2)	56.2 (2.0)	20.6 (1.7)	23.2 (2.7)	60 (1)	1.080 (0.07)		131.3	187.5	0.35	0.93
	SubP	DP	2.7 (0.2)	41.3 (5.6)	24.6 (3.6)	34.1 (3.7)	55 (7)	1.055 (0.07)		112.5	150.0	0.30	0.32
		FC	3.0 (0.1)	49.4 (3.7)	26.5 (1.3)	24.1 (2.5)	69 (5)	1.075 (0.06)		118.8	175.0	0.19	0.81
	PlusP	DP	3.0 (0.3)	42.0 (2.0)	28.6 (1.8)	29.4 (3.4)	69 (6)	1.250 (0.09)		100.0	209.4	0.27	0.38
		FC	4.5 (0.7)	55.6 (0.8)	28.7 (0.7)	15.7 (0.9)	100 (8)	1.350 (0.06)		106.3	168.8	0.29	0.63
	Water		*	**	n.s.	***	***	n.s.		n.s.	*	*	**
	P		***	n.s.	*	n.s.	***	*		n.s.	***	*	n.s.
	Water × P		n.s.	n.s.	n.s.	n.s.	n.s.	n.s.		n.s.	**	n.s.	n.s.
CRootBox			Total root surface	Root volume	Total root length	Surface topsoil	Surface subsoil	Root tips	Tips-volume ratio	Surface-volume ratio	Halfmean distance	Root tips in topsoil	Root tips in subsoil
			(cm2)	(cm3)	(cm)	(cm2)	(cm2)	(n)	(cm–3)	(cm–1)	(cm)	(n)	(n)
	NoP	DP	863	11.09	7622	439	424	4663	420	77.87	0.680	2323	2340
		FC	957	13.25	7828	560	397	4579	346	72.27	0.671	2427	2152
	SubP	DP	1597	18.53	16539	689	908	8116	438	86.20	0.461	3129	4987
		FC	1678	19.82	16472	882	796	7836	395	84.68	0.462	4074	3762
	PlusP	DP	1644	21.63	15504	750	894	8238	381	76.00	0.476	3608	4630
		FC	1831	30.10	17047	1111	720	7992	266	60.83	0.454	4862	3130

Significance was based on a P-level of *P < 0.05, **P < 0.01, and ***P < 0.001; n.s. = not significant.

The number of nodal roots of rice grown in the laboratory experiment varied from 43 to 100 depending on the water and P conditions during the growth, and the number of nodal roots was largest under PlusP and decreased with DP. Nodal thickness was largest under PlusP. It showed a decreasing trend under DP, but this was not significant. The density of S-type laterals was smallest under NoP, and it generally decreased under DP, while the density of the secondary laterals on the L-type roots strongly increased under DP. The radius of the L-type laterals under dry periods was smallest for SubP compared with NoP and PlusP (Table 3, top).

Root system responses to changing P and water availability simulated by CRootBox

Root mass distribution in the soil column was calibrated in CRootBox with a good agreement based on the observed distribution in the pot experiment (Supplementary data Fig. S3). Following these distributions, the interbranch scaling factor and the calibrated transition depth of the L-type laterals were derived (Supplementary data Figs S4 and S5). The 3-D structure of the contrasting root systems and the distribution of the root types (simulated in CRootBox) virtually grown in contrasting environments are presented in Supplementary data Fig. S6, while Fig. 1 illustrates the reconstructed 3-D architecture of these root systems with the corresponding simulated P uptake rates by the root system. An example of this virtual root growth is shown in Supplementary data Video S1. The 3-D root systems reveal that the total root surface and root volume generally increased with increasing P rate and water availability (bottom part of Table 3). Results from CRootBox also show that a similar increase with P rate is true for root length under FC, but not under DP. The 3-D simulations reveal that the root surface in the topsoil generally decreased under DP, while the root surface (and root length) in the sub-soil increased. The total number of root tips (i.e. the terminal portion of each root type including S-type laterals, L-type laterals, secondary laterals and nodal roots) generally increased with increasing P rate, and it also increased under DP compared with FC, which mainly follows an increased number of secondary laterals on the L-type roots under DP (data not shown). Under DP, the number of root tips in the sub-soil exceeded the number of root tips in the topsoil, while the reverse was true under FC. (Table 3)

The surface–volume ratio (i.e. the ratio of the root surface to the volume of the root system) and root tip–volume ratio (i.e. the ratio of the total number of root tips to the total volume of the root system) were generally largest under SubP, and increased under DP compared with FC within each P treatment (Table 3). The surface–volume ratio generally reached its maximum before 10 DAS and it subsequently decreased with growth (data not shown). Simulations further reveal that this root surface per root volume was consistently largest for the L-type laterals, followed by S-type laterals, and was smallest for nodal roots (data not shown). The half mean distance between roots was largest under NoP due to its low root density in the soil column, and this value decreases under PlusP (Table 3).

Analysis of the reconstructed root systems further shows that under DP, the total contribution of L-type roots to both root mass and root surface increased compared with FC, while the contribution of S-type laterals decreased. The total root surface comprised by the L-type laterals (which include the secondary laterals on these L-types) was generally larger than the surface comprised by S-type roots, but S-type roots are located more in the upper layer. Interestingly, the root surface of L-type roots in the topsoil dramatically increased under DP, while the root surface of the S-type roots in the topsoil decreased (data not shown).

Simulated water dynamics and effects on P diffusion

The change of the water content in the soil column during the simulated drying cycles of the DP treatments is shown in Supplementary data Fig. S7, and these data match the water balance in the laboratory experiment following implementation of the boundary conditions. Under FC, the water content stayed relatively constant near saturation (despite some minor daily fluctuations). During the drying cycles, plants continued transpiring, although irrigation was stopped. Therefore, the water content in the soil dropped about 4–8 volume% (Supplementary data Fig. S7). The soil water content dropped to a greater extent when higher P levels were applied in the topsoil due to the higher transpiration. It is also observed that the effective P diffusion at the root surface under FC generally remained constant, with minor daily fluctuations (Supplementary data Fig. S8). In contrast, under DP, the effective P diffusion coefficient dramatically decreased 30–50 % during the drying cycles.

Evaluating simulated vs. measured P uptake

Figure 2 presents the P uptake by the reconstructed 3-D root systems simulated with the multiscale model vs. the averages of the measured P uptake in the lab experiment. Both simulations and measurements show that the total P uptake greatly increased with P supply. Under DP, both the measured and simulated P uptake are reduced in the PlusP and SubP scenario. The negative effect of DP on total P uptake thus increased with increasing P rate in both simulations and actual measurements. At first glance, the predicted P uptake is close to the measured values from the real experiment. However, the predicted P uptake was underestimated for NoP (approx. 50 % underestimation), while it was slightly overestimated for PlusP under FC (approx. 15 % overestimation). Neither the observed nor the predicted P uptake was influenced by the drying cycles under deficiency (NoP), whereas water uptake was indeed affected by drying cycles. Under sub-optimal and optimal P conditions, dry periods also triggered a lower P uptake (measured and simulated).

Determining the location of the water and P uptake with the multiscale model

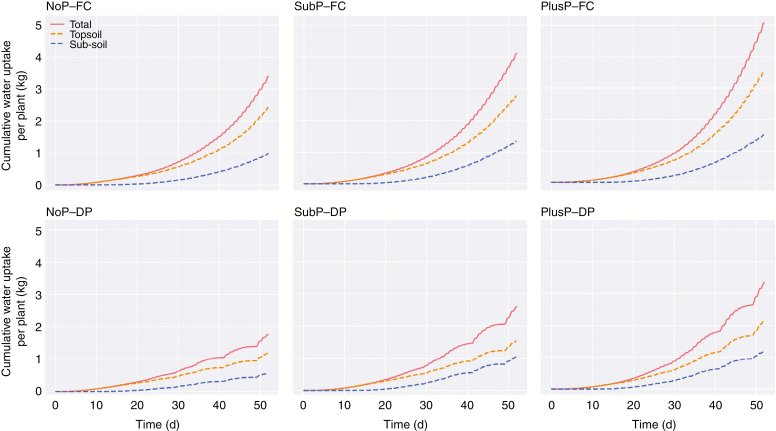
The cumulative water uptake by rice in the pot experiment increased with increasing P rate and it decreased under DP. Simulations of the water uptake predict that most water was taken up in the topsoil. Under FC, approx. 70 % of the total water uptake was acquired from the topsoil at 52 DAS. Interestingly, the relative contribution of the sub-soil to water uptake increased under DP as this share increased to approx. 37 % (compared with approx. 30 % under FC). (Fig. 3)

Fig. 3.

The simulated cumulative water uptake per plant (in kg) of rice roots during a growing period of 52 d. Rice roots were grown under contrasting P rates [P deficiency (NoP), a sub-optimal P amendment in the topsoil (SubP) and a non-limiting P rate in the topsoil (PlusP)] and contrasting water regimes [field capacity (FC) vs. drying periods (DP)]. These simulations enable the differentiation among total water uptake, water uptake from the topsoil (0–20 cm depth) and water uptake from the sub-soil (>20 cm depth).

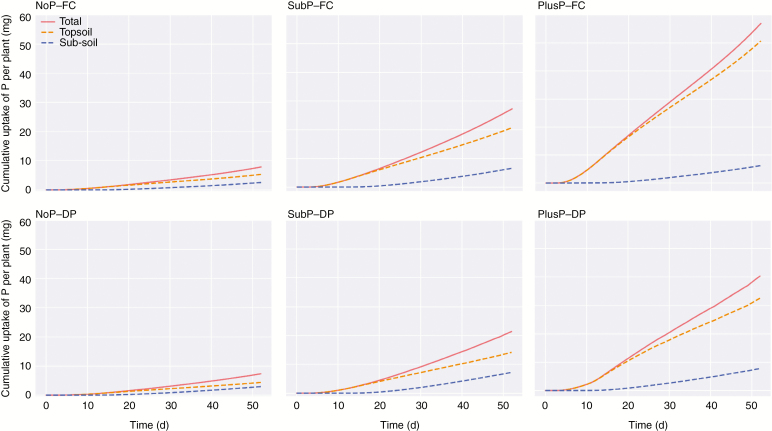
Similar to water uptake, simulations reveal that P uptake was mainly located in the topsoil, also when the P availability in the top- and sub-soil were equally low (NoP; Fig. 4). With increasing P supply, the percentage of P acquired from the topsoil increased (71 % under NoP, 75 % under SubP and 88 % under PlusP at 52 DAS, FC). In the scenarios without P application (NoP), the simulated P uptake rate towards the end of the experiment (roughly after DAS 40) in topsoil was equal to the uptake rate in the sub-soil (illustrated by the parallel lines in Fig. 4). Interestingly, P acquisition from the sub-soil slightly increased under DP compared with FC for all P treatments (an increase in the contribution of approx. 10 %), while the acquisition in the topsoil decreased (Fig. 4). Supplementary data Fig. S9 illustrates the relationship between the P uptake and the total water uptake. Interestingly, both experimental data and simulation results reveal that the lower water uptake under drying cycles has only a minor effect on the total P uptake.

Fig. 4.

The simulated cumulative P uptake per plant of upland rice roots during a growing period of 52 d. Rice roots were grown under contrasting P rates [P deficiency (NoP), a sub-optimal P amendment in the topsoil (SubP) and a non-limiting P rate in the topsoil (PlusP)] and contrasting water regimes [field capacity (FC) vs. drying periods (DP)]. These simulations enable the differentiation among total P uptake, P uptake from the topsoil (0–20 cm depth) and P uptake from the sub-soil (>20 cm depth).

The role of different root types and root characteristics for P and water uptake

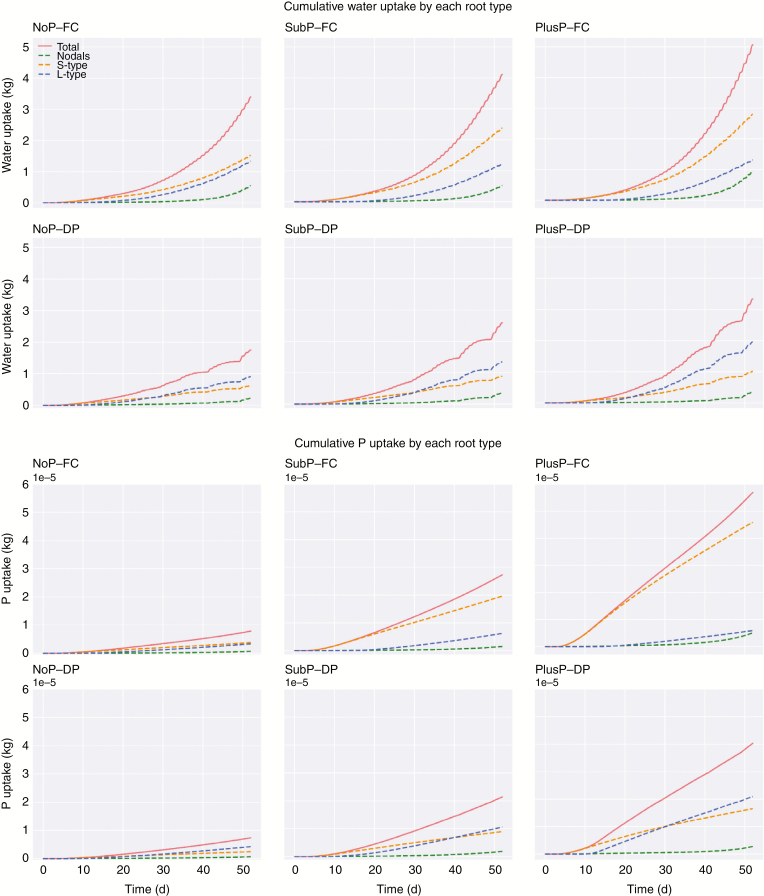
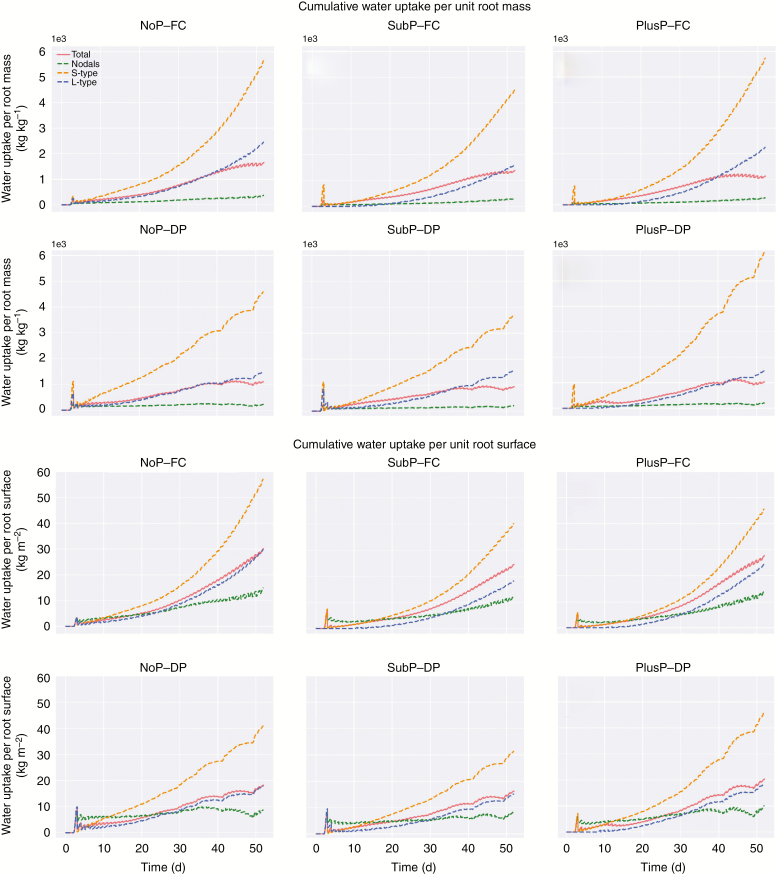
Figure 5 displays the predicted contributions of each root type to water uptake. Under FC, the largest share in water uptake was attributed to S-type roots (47–59 %). This trend altered under DP where the contribution of the L-type roots to water uptake (50–60 %) exceeded the contribution of S-types (31–37 %). Nodal roots consistently displayed only a minor contribution to water uptake (Fig. 5) and they showed a minor cumulative water uptake per unit root mass.

Fig. 5.

The cumulative water uptake per plant (top) and cumulative P uptake per plant (bottom) by the different root types of rice during a growing period of 52 d. Rice roots were grown under contrasting P rates [P deficiency (NoP), a sub-optimal P amendment in the topsoil (SubP) and a non-limiting P rate in the topsoil (PlusP)] and contrasting water regimes [field capacity (FC) vs. drying periods (DP)]. These simulations enable the differentiation among the water and P uptake by the nodal roots, the S-type lateral roots and the L-type lateral roots.

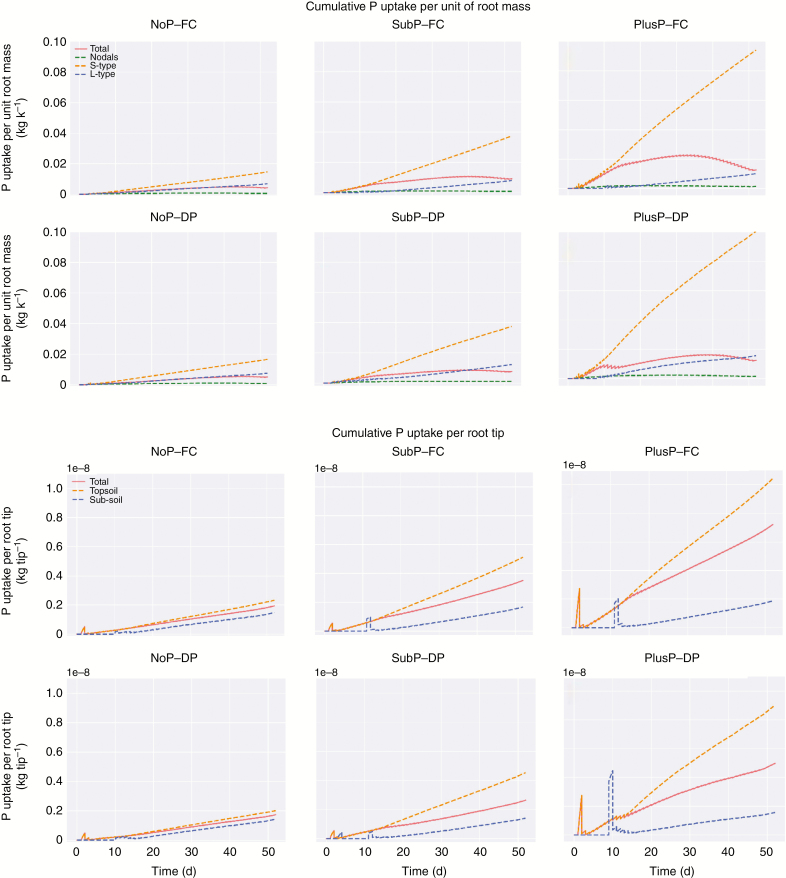
Similar to water uptake, nodal roots are predicted to have only a minor contribution to P uptake under FC while S-type laterals displayed the largest contribution (Fig. 5). Under DP, the contribution of the L-type roots to P uptake increased during the growth and the development of the root system, and its contribution to P acquisition finally overrode the contribution of the S-type roots during development. With increasing P rates, the relative contribution of the S-type roots to P uptake increased under both FC (from approx. 44 % under NoP to 79 % under PlusP) and DP (from approx. 31 % to 44 %), while the reverse was true for L-type roots. The cumulative P uptake per unit root mass increased equally with time for S- and L-type roots under NoP, while this ‘efficiency’ strongly increased for S-type roots under SubP and PlusP (Fig. 6).

Fig. 6.

The simulated cumulative P uptake per unit of root mass for each root type (top) and the cumulative P uptake per root tip in each soil layer (bottom). When root tips start entering the sub-soil (approx. 10 d), segment co-ordinates may be assigned to the sub-soil, while a large part of the segment is still located in the topsoil. Therefore. the P uptake is larger due to a larger availability, and hence peaks can be observed.

Normalizing P and water uptake to root mass, root surface, root length and root tips, and the importance of root elongation

Under P limitations (NoP), a larger root mass was obtained under FC compared with that under DP (Table 3). However, this larger root mass did not lead to a large increase in P uptake (Fig. 6), but it indeed resulted in a much larger increase in water uptake under FC compared with DP (Fig. 7). In contrast, under optimal P availability (PlusP), the larger root mass under FC compared with DP (Table 3) did lead to a larger increase in P uptake, whereas the increase in water uptake per increase in root mass was smaller (Figs 6 and 7).

Fig. 7.

The simulated cumulative water uptake per unit of root mass for each root type (top) and cumulative water uptake per unit surface for each root type (bottom).

Towards the end of the simulation period, the cumulative P uptake per unit of root mass (Fig. 6) started to decrease in all scenarios. This trend is also observed for the cumulative P uptake per root surface (not shown), however to a smaller extent. Both observations indicate a decline in P uptake rate per unit of root mass or surface. In contrast, for the cumulative P uptake per number of root tips, one can observe a consistent linear increase towards the end of the simulation period, indicating a constant P uptake rate per root tip (Fig. 6), which is additionally supported by the findings displayed in Supplementary data Fig. S10. Supplementary data Fig. S10 shows a general low P uptake rate by a single nodal root under NoP (left) compared with SubP (middle). Under SubP, the P uptake rate suddenly decreases when the root penetrates into the P-deficient sub-soil (i.e. at 20 cm depth). Interestingly, the P uptake rate at the tip is generally large, but it dramatically decreases when the root does not continue to grow (middle vs. right plot in Supplementary data Fig. S10).

For water uptake, the trends are different. The cumulative water uptake per root surface area still increases by the end of the simulation period, and the uptake rate remains relatively constant (with exceptions during the periods of water stress when the uptake per unit area decreases). This indicates a consistent increase in water uptake with increasing root surface (Fig. 7).

DISCUSSION

Integrated responses of root system architecture

Multiple single root phenes (the number of nodal roots, nodal radius, lateral density, etc.) all contribute to the performance of a root system, but the utility of a root phene depends on other phenes, which can be either synergistic or antagonistic. Therefore, functional–structural modelling is the most practical approach to assess the large number of root phene interactions with other phenes or environmental variables (Lynch, 2011, 2019; Ahmadi et al., 2014; Rangarajan et al., 2018). This work demonstrated how multiple co-occurring root phene responses can be integrated in CRootBox.

Responses of single root phenes (such as deep root ratio, root angle and branching) to drought events were previously observed for upland rice (Kato et al., 2006; Gowda et al., 2011; Henry, 2013; Menge et al., 2016). However, to our knowledge, this is the first study demonstrating the holistic, integrated responses of the root system architecture, and its function with respect to P and water uptake. This modelling approach allows the evaluation of the root system architecture by combining multiple root phenes directly associated with water and nutrient acquisition (e.g. total surface, surface distribution, number of root tips and total root length).

In particular, these simulations reveal how combined responses of root mass, nodal root number, root radii and branching density contribute to a decreased total root surface under decreasing P supply or water level. The simulations demonstrate that the total number of root tips and total root surface in the sub-soil generally increased under drying periods compared with field capacity, independent of P availability.

Generally, ‘root system efficiency’ of a crop is defined as the amount of P acquisiton per unit root size (Mori et al., 2016). Hence, root system efficiency can be evaluated by the surface to volume ratio, as soil exploration occurs at a lower carbon cost when this ratio is high (Lynch and Ho, 2005). With this perspective, this modelling study illustrates how multiple root phenes (i.e. number of nodal roots, nodal diameter, S-type radius, L-type radius, S-type distance and secondary distance) contribute to the utility of a root system under sub-optimal P availability and drying periods. This corresponds to the general theory of ‘rhizoeconomics’ (Lynch and Ho, 2005; Lambers et al., 2006). It is now proven that upland rice indeed reduces the cost of soil exploration under sub-optimal P availability and drying periods by optimizing its surface/volume ratio, but also by an increased root tip/volume ratio.

This work highlights the importance of growing root tips for P uptake from deficient soils, and P uptake is thus not only driven by the root surface. Hence, we argue that root functionality and efficiency should be assessed by the parameters that actually drive the uptake of a particular resource under a particular condition. In terms of P uptake, root system efficiency should be assessed by the ratio of emerging root tips over the total root system volume, while root system efficiency in terms of water uptake should be assessed by the ratio of root surface over the total root system volume.

Deep water acquisition increases under dry events, but the contribution to total water uptake remains relatively small

Simulations allow the evaluation of soil resource uptake from certain soil layers, and they allow quantification throughout the depth. For upland rice, water is preferentially extracted from the top layer and more water is taken up from deeper layers only after drying of the topsoil (Kondo et al., 2000; Price et al., 2002). However, to our knowledge, this has never been quantified. Deep rooting enhances deep water acquisition (Fukai and Cooper, 1995; Uga et al., 2013; Lynch and Wojciechowski, 2015), and deep water acquisition was generally regarded as a drought adaptation in crops (Comas et al., 2013). Interestingly, this work reveals that ‘deep water acquisition’ in upland rice only comprises a relatively small fraction of the total cumulated water uptake, even under dry events. During the final phase of the simulated experiments, the water uptake rate from the sub-soil became similar to the uptake rate in the topsoil. Although the total fraction of water uptake over the total growing period from the sub-soil is small, deeper roots contribute to plant survival under water stress.

Growing root tips are driving P uptake and are responsible for top soil P foraging in P-deficient soils

Similarly, we quantified the importance of P acquisition from the topsoil vs. P uptake from deeper layers. Topsoil foraging of P generally follows from P accumulation in upper layers (Fei et al., 2011; Lal and Stewart, 2016). However, this study shows that this trend also holds when P availability is equally distributed throughout the depth, even with a larger root surface in the sub-soil. The latter trend could be explained by the longer residence time of roots in top layers (grown from root base to bottom), but this is unlikely to be the only explanatory factor as P is rather immobile. Interestingly, a higher number of root tips is also observed in the topsoil (NoP and FC) and this elucidates the greater P uptake from the topsoil. Hence, topsoil foraging of P does not result only from the higher P availability in the upper soil layers. The acropetal development of the root surface distribution throughout the depth during the growing period should also be considered.

Our simulations indicate a general depletion of P along the root axis which results in a reduced P uptake rate from the tip towards the basal end of the roots (Fig. 6; Supplementary data Fig. S6). These simulations highlight the importance of root tips and root elongation for P uptake. Hence, root tips that grow in previously undepleted soil are the main contributors to overall P uptake of a growing root system. Several studies have found that the regions close to the root tip are biochemically more active, following a higher density of phosphate transporters (Smith, 2002; Péret et al., 2011; Kanno et al., 2016). However, we show that the greater importance of the root tips for overall P uptake can also be explained by physical principles alone, i.e. due to the high depletion of P near the root surface, root tips that grow into still undepleted soil have a greater contribution even when the same amount of transporters/same Michaelis–Menten parameters are prescribed along the root axis. In our model, we assumed that the ‘uptake capacity’ of a root did not change along the root, but we show that this uptake capacity becomes ‘latent’ behind the root tip because of P transport limitations in the soil. Thus, it would not make sense for a plant to have many transporters near the base of the root.

In this model, a depletion zone around each root segment develops with nutrient uptake. Hence, the gradient of nutrient concentration is largest at the root surface. We defined the depletion radius as the distance from the root centre to the position where the nutrient concentration gradient decreases to 1 % of that at the root surface. Compared with the half mean distance values, the depletion radii in the NoP scenario (Supplementary data Fig. S12) are generally twice as small (Table 3), while they are comparable in the PlusP scenario. This indicates that competition among roots for P uptake is more likely to occur in the PlusP scenarios following the large depletion radii and large root density in the soil. Furthermore, simulations indicate that under NoP and SubP, P uptake by newly developed root tips will not be influenced by the P uptake of the other root segments or by depletion of the P stock in the soil due to previous uptake. These findings suggest that, when developing low P-tolerant rice varieties, it is more interesting to strive for root systems having many primary and secondary laterals, so having many new emerging, growing root tips, rather than a large root surface area (Rose et al., 2013), and this would further enhance root penetration and tolerance to drying periods (Bengough et al., 2011).

L-type laterals and their branches can contribute to the combined tolerance of upland rice against drought and P deficiency in soils

This study shows that nodal roots have only a minor contribution to water or P uptake, and nodal roots thus rather function as the ‘skeleton’ determining the spatial distribution of roots in soil (Fageria, 2013). However, a reduced nodal thickness might still contribute to a more efficient biomass utilization, as long as this does not compromise the transport function for water and nutrients of nodal roots. S-type roots are found to have a large contribution to P uptake, and De Bauw et al. (2019) previously related a higher density of such S-types to an increased P uptake capacity under deficient conditions. Interestingly, the upland rice variety simulated in this study (i.e. NERICA4) was previously found to have a very sparse S-type density compared with other varieties (e.g. NERICA-L-19, Mudgo and DJ123), and for these varieties the role of S-type roots in P uptake would thus be even more important.

This study demonstrates that the P uptake by L-type roots should definitely not be ignored in upland conditions as their contribution in P uptake even overrides the uptake of S-type roots under dry periods. Using simulations, we demonstrate that increased P uptake efficiency in response to reduced water availability (De Bauw et al., 2019) is mainly attributed to a higher secondary branching density of L-type roots. This produces a more efficient water and P uptake. Previous studies in maize have highlighted the importance of reduced lateral branching to drought tolerance (Gao and Lynch, 2016). However, this work demonstrates that S-type roots have the largest contribution to water uptake under field capacity, while L-type roots increase water acquisition during dry periods. It was previously not possible to qualify root characteristics beneficial under both P deficiency and dry periods. However, this study indicates that the key to a synergistic tolerance to drought and low P can be found in the secondary branching of L-type roots.

Potential model improvements by adjusting the Michaelis–Menten parameters for diffusion limitations

We have demonstrated that the coupled 3-D continuum multiscale model of Mai et al. (2018) can be applied to simulate nutrient uptake from any crop grown in specific environments. Given the fact that there was no calibration of P dynamics, this model fairly predicted the P uptake for both water regimes and the different P supplies (validation shown in Fig. 2). It is possible to evaluate effects of drying periods on the P uptake by a growing root system in a highly P-fixing soil, and the interactions of drying periods with nutrient availability throughout the depth can be assessed. The simulations strongly underestimated the P uptake only in the scenarios without P application, which can be explained by four factors. (1) Under P deficiency, the interaction of roots with the soil microbiome (e.g. mycorrhyzae) becomes highly important for soil exploration and this is not included (Maiti et al., 2011, 2017). To tackle this issue in a modelling study, a Matlab version of RootBox exists which considers primary and secondary infection of a growing root system with arbuscular mycorrhizal fungi (Schnepf et al., 2016) and which can be coupled to the model developed in this study. (2) Root exudates may mobilize immobile P to enhance acquisition in response to P deficiency (Kirk et al., 1999; Schnepf et al., 2012; Tawaraya et al., 2013; Bhattacharyya et al., 2013). (3) Root hairs might play a key role in P uptake under limited availability (Leitner et al., 2010; Nestler and Wissuwa, 2016), and these are not included in the root model. Hence, it should be considered that these simulations only assess physical aspects and therefore they might underestimate the actual P (or other nutrients) uptake when deficient in soils. (4) The high root absorbing power for P (ratio of uptake flux to free ion concentration in solution; Nye and Tinker, 1969) suggests that diffusion-limited plant uptake is likely for P, even in nutrient solutions. As a consequence, the Michaelis constant, K_m, derived from nutrient solution or sand cultures (as used here) are overestimated when based on the bulk solution ion concentration (Winne, 1973). The K_m values determined under diffusion limitations are therefore apparent values reflecting the physical process (diffusion limitation), and are not characteristic for the biological transport process (transporter affinity towards the transported ion). Santner et al. (2012) argued that the true K_m values for plant root P transporters would be much lower than the values usually reported in the literature. For models where Michaelis–Menten kinetics are used, they recommended using a low value for K_m (e.g. the one estimated in buffered solutions: K_m approx. 0.5 µmol L^–1) rather than a value determined in unbuffered solutions. As the K_m value used in this model was determined on gravel and nutrient solution (Teo et al., 1992b), diffusion limitation might have occurred. Hence we re-simulated our model for two scenarios with a smaller K_m value as suggested by Santner et al. (2012) (i.e. 0.5 µmol L^–1, which is seven times smaller than the K_m value used in this study), and also using a smaller V_max (i.e. 1.84 × 10^–6 kg m^–2 s^–1; which was determined by using the average uptake rate initially simulated in the PlusP–FC scenario, from which the interface concentration was derived. The new V_max was derived so that for this interface concentration and new K_m value, the Michaelis–Menten uptake reproduced the same uptake rate. Interestingly, when using this small K_m and smaller V_max, the simulated P uptake under the NoP scenario greatly improved (Supplementary data Fig. S11) while the simulations under SubP and PlusP barely changed. This highlights the need for using buffered K_m values when simulating root P uptake under deficient conditions and it might indeed suggest that the general K_m values for P uptake currently available in the literature are too large (Santner et al., 2012).

Conclusions

Combining experimentally measured single root phene datasets with a 3-D continuum multiscale soil–root model enhances the mechanistic insights in soil–root processes that are important for water and P uptake. We showed that functional–structural root models can predict the function of the root system under different P and water conditions when its structure is known. Therefore, we could use functional–structural root models to demonstrate how multiple co-occuring single root phene responses of upland rice to environmental stimuli such as drying cycles and sub-optimal P availability contribute to the development of a more efficient root system.

We found that root tips that grow in previously undepleted soil are the main contributors to the overall P uptake of a growing rice root system in low P soil. Quantification of the contribution of distinct root types to both P and water uptake revealed the most relevant root characteristics enhancing low P and/or drought tolerance. The S-type roots are important for P uptake, but the L-types and their branches additionally improve water uptake under drying periods, hence potentially contributing to the combined tolerance against drought and P deficiency in soils for upland rice. The model would need some further improvements to adjust for the low simulated P uptake under deficient conditions. Modellers should consider the use of Michaelis–Menten kinetic parameters that are derived from solutions in which the low P concentrations are buffered and models may be refined by including the effects of root exudates, root hairs and colonization by mycorrhizae.

SUPPLEMENTARY DATA

Supplementary data are available online at https://academic.oup.com/aob and consist of the following. Figure S1: boundary conditions for six in silico experiments of the virtual soil–root system. Figure S2: a picture of the simulated pot mesh. Figure S3: the observed root mass distribution along the depth in the pot experiment and the corresponding distribution simulated in CRootBox in all scenarios. Figure S4: the interbranch distance scaling factor along the soil depth. Figure S5: the probability of the S-type roots along the soil depth. Figure S6: the simulated root systems from CRootBox showing the different root types and the corresponding emergence. Figure S7: the dynamics of the water content in the soil during the simulation period. Figure S8: the effective P diffusion coefficient at the root surface. Figure S9: the relationship between water uptake and the measured and simulated P uptake for each scenario. Figure S10: the simulated P uptake rate along a nodal root vs. the distance from the root origin. Figure S11: the re-simulated P uptake per plant vs. the measured P uptake per plant in the lab experiment by using a small K_m and a small V_max. Figure S12: depletion radii in the rhizospheres and the P uptake rates of root segments in the rhizospheres for each scenario during the simulation period of 52 d. Table S1: daily irrigation rate per treatment. Text: S1: detailed information about the laboratory experiment. Text S2: detailed information on the model descriptors and the mathematical equations. Video S1: the simulated root growth, P uptake rates and soil P sink during the growing period of 52 d for the scenario under sub-optimal P and field capacity.

FUNDING

The pot trial and lab analyses were partly conducted at and financed by the Africa Rice Center in Tanzania and the KU Leuven in Belgium, and the work was additionally supported by the Belgian VLIR-UOS through a scholarship (VLADOC grant awarded to P.D.B.). T.H.M. was funded by the German Federal Ministry of Education and Research (BMBF) in the framework of the funding initiative ‘Soil as a Sustainable Resource for the Bioeconomy BonaRes’, project ‘BonaRes (Module A): Sustainable Subsoil Management – Soil3; subproject 3’ (grant 031B0026C).