Parameter estimation for functional–structural plant models when data are scarce: using multiple patterns for rejecting unsuitable parameter sets

Abstract

Background and Aims

Functional–structural plant (FSP) models provide insights into the complex interactions between plant architecture and underlying developmental mechanisms. However, parameter estimation of FSP models remains challenging. We therefore used pattern-oriented modelling (POM) to test whether parameterization of FSP models can be made more efficient, systematic and powerful. With POM, a set of weak patterns is used to determine uncertain parameter values, instead of measuring them in experiments or observations, which often is infeasible.

Methods

We used an existing FSP model of avocado (Persea americana ‘Hass’) and tested whether POM parameterization would converge to an existing manual parameterization. The model was run for 10 000 parameter sets and model outputs were compared with verification patterns. Each verification pattern served as a filter for rejecting unrealistic parameter sets. The model was then validated by running it with the surviving parameter sets that passed all filters and then comparing their pooled model outputs with additional validation patterns that were not used for parameterization.

Key Results

POM calibration led to 22 surviving parameter sets. Within these sets, most individual parameters varied over a large range. One of the resulting sets was similar to the manually parameterized set. Using the entire suite of surviving parameter sets, the model successfully predicted all validation patterns. However, two of the surviving parameter sets could not make the model predict all validation patterns.

Conclusions

Our findings suggest strong interactions among model parameters and their corresponding processes, respectively. Using all surviving parameter sets takes these interactions into account fully, thereby improving model performance regarding validation and model output uncertainty. We conclude that POM calibration allows FSP models to be developed in a timely manner without having to rely on field or laboratory experiments, or on cumbersome manual parameterization. POM also increases the predictive power of FSP models.

INTRODUCTION

Functional–structural plant (FSP) models have been used widely for over two decades to understand the complex interactions between plant architecture and underlying processes driving plant growth (Kurth, 1994; Sievänen et al., 1997; Godin and Sinoquet, 2005; Vos et al., 2007, 2010; Fourcaud et al., 2008; DeJong et al., 2011; Evers, 2016). They are constructed to explicitly describe the growth of plant architecture over time based on internal physiological processes, which in turn are determined by external environmental processes. The development of such models has also provided insights into potential applications in agriculture and horticulture, such as for kiwifruit (Actinidia deliciosa) (Cieslak et al., 2011a, b), cucumber (Cucumis sativus) (Kahlen and Stützel, 2011; Wiechers et al., 2011; Chen et al., 2018), macadamia (Macadamia integrifolia, M. tetraphylla, and various hybrids) (White and Hanan, 2016), apple (Malus domestica) (Saudreau et al., 2011; Pallas et al., 2016; Poirier-Pocovi et al., 2018), avocado (Persea americana ‘Hass’) (Wang et al., 2018), peach (Prunus persica) (Allen et al., 2005), tomato (Solanum lycopersicum) (Sarlikioti et al., 2011), grapevine (Vitis vinifera) (Pallas et al., 2010; Zhu et al., 2018), legumes (Han et al., 2010, 2011; Louarn and Faverjon, 2018) and root systems (Barczi et al., 2018; Schnepf et al., 2018), as well as for insect–plant interactions (Hanan et al., 2002; de Vries et al., 2017, 2018, 2019).

Regardless, due to their inherent complexity, parameterization of FSP models remains challenging. Here, the term ‘parameterization’ refers to the involved process of estimation of parameters rather than of deciding which parameters to use. While field or laboratory experiments are the best method for determining parameter values, it can be difficult or impossible to collect all of the data that are needed to directly determine all parameters, and therefore some have to be determined indirectly, via calibration. In recent years, efforts have been made to develop methods for parameter estimation of FSP models (Guo et al., 2006; Ma et al., 2007; Cournède et al., 2011; Trevezas and Cournède, 2013; Trevezas et al., 2014; Baey et al., 2016, 2018; Mathieu et al., 2018). Most of these techniques are based on statistical inference, in particular on maximum-likelihood estimation that relies on detailed component-level experimental data for parameter fitting. The values of unknown parameters can be estimated via optimization where the best parameter value minimizes the difference between model outputs and empirical observations.

Despite the successful application of such techniques to FSP modelling mostly for annual crops, they can be limited by the stochastic nature of biological systems (Toni et al., 2009; Hartig et al., 2011). This limitation is perhaps exacerbated for complex plants such as tree crops, due to them being long-lived with cumulative effects of growth and of development on tree structure. Such effects are caused by the environment (e.g. climatic and soil conditions as well as pest infestation) and management (e.g. horticultural practices) over many years, as well as other complex cycles that have impacts from one year to the next (e.g. alternate/biennial bearing cycles). If FSP models are developed to simulate such complex plants, both biological and physical processes occurring in the models are generally implemented discretely and stochastically. In turn, model behaviours (emergent properties) are determined by interactions among these discrete and stochastic processes. Calibration of such models via optimization can thus be difficult, as the hierarchy of the internal stochastic processes in the model often makes formulating likelihood functions cumbersome or even impossible (Hartig et al., 2011).

The complexity of interactions between biological and physical processes and the high variability of plant growth (Godin and Sinoquet, 2005; DeJong et al., 2011) implies that parameter uncertainty is inevitable. When the processes underlying unknown parameters interact with each other, it is unlikely to find a single, optimal value for each unknown parameter that leads to realistic simulations under all conditions. This phenomenon can be explained by the concept of equifinality or parameter identifiability (Beven and Freer, 2001; Beven, 2006; Slezak et al., 2010). It refers to the situation where calibration results in multiple parameter sets (i.e. the different parameter value combinations) that make the model reproduce the observations equally well for specific objectives, due to the complex interactions among the components of a system. Optimization approaches might not capture these interactions, and favour specific parameter values or sets, which could limit the flexibility of the model in terms of possible applications.

To overcome these limitations, simulation-based inference techniques for parameter estimation have been suggested (Hartig et al., 2011). Simulation-based inference refers to a type of model calibration where the values of unknown parameters in high-dimensional parameter space are inversely determined via stochastic simulation; this usually results in multiple parameter sets that can make the model reproduce observed data equally well under certain criteria (Wiegand et al., 2003, 2004; Hartig et al., 2011).

Here, we adopt the pattern-oriented modelling (POM) strategy (Grimm et al., 1996, 2005; Wiegand et al., 2003; Grimm and Railsback, 2012) to improve on parameterization for cases when measured data are scarce, by systematically exploiting the information included in an entire set of patterns that characterize the growth and structure of a plant.

In this pattern-oriented calibration approach, we use multiple observed patterns as filters for rejecting unrealistic parameter combinations. A pattern is defined as any observation beyond random variation and therefore containing information related to underlying mechanisms (Grimm et al., 1996). There are strong patterns and weak patterns. A strong pattern, such as changes in the length of a shoot over time, often contains a lot of information and can reflect the underlying mechanisms strongly, whereas a weak pattern is usually descriptive and can be characterized by a few numbers or words, such as the number of shoots in a branching architecture. The distinction between strong patterns and weak patterns is qualitative, based on the power of a pattern to reject unsuitable sub-models and parameter combinations. Nevertheless, several weak patterns used together can be more powerful in rejecting unsuitable parameter sets than a single strong pattern. This is a key advantage of POM calibration because often data supporting strong patterns are not available (Wiegand et al., 2004).

In POM calibration, the model is run with a large number of possible sets of parameter values and multiple patterns are then used simultaneously as ‘filters’ to determine the entire sets of unknown parameters inversely. In contrast to the traditional automatic model calibration approach, this approach is based on categorical calibration, i.e. looking for parameter values that make model outputs lie within a category/range that we define as acceptably close to the observations (Railsback and Grimm, 2019, p. 267). The concept of using POM calibration is not to obtain an optimally fitted value for each unknown parameter against a single pattern, but to obtain several parameter sets that can make the model reproduce an entire set of patterns sufficiently well, because of limited knowledge on the complex interactions among the components of a system. This approach, also known as inverse modelling or Monte Carlo filtering, is a simulation-based inference technique and is similar to the simplest approach in Approximate Bayesian Computing (ABC), the so-called Rejection ABC (Beaumont, 2010; van der Vaart et al., 2015, 2016). ABC is a calibration approach based on Bayesian statistics. If a model simultaneously reproduces multiple patterns, observed at different levels of organization and different scales, it is more likely that it captures the internal organization of the modelled system sufficiently well for the intended purpose of the model.

The aims of this study are to present an automated procedure, i.e. a simulation-based inference technique, for parameterization of FSP models and to demonstrate how POM can make the parameterization of FSP models more systematic, efficient and powerful, in contrast to manual calibration, and how it can reduce uncertainty when direct parameterization with experiments is not possible.

MATERIALS AND METHODS

As a case study of applying a simulation-based inference technique of parameter estimation for FSP models, POM was used to parameterize an existing stochastic FSP model of avocado branching architecture (Wang et al., 2018). Our model, which has six unknown parameters (Table 1), was previously successfully parameterized manually (Wang et al., 2018), thereby allowing us to check whether POM calibration would converge to the same results. To test the predictive power of the model after POM calibration, we also checked how well the calibrated model matches an independent set of further patterns, here termed ‘validation patterns’.

Table 1.

Overview of six unknown parameters and their possible values

Parameter	Description	Possible values	Units	References
SyllepticShootsLocation*	Location of sylleptic shoots – the sylleptic shoots appear in an acropetal direction	2–11		Based on Thorp et al. (1994)
ProlepticShootsLocation	Location of proleptic shoots – the proleptic shoots appear in a basipetal direction	1–10		Based on Thorp et al. (1994)
SYLLEPTIC_LIMB_PRO	Probability of a sylleptic shoot developing from an axillary bud on the primary growth axis (PGA) in one of the positions noted above	0–100	%	T. G. Thorp, Plant & Food Research Australia Pty Ltd, Australia, ‘pers. comm.’
SYLLEPTIC_AXILLARY_PRO	Probability of a sylleptic shoot developing from an axillary bud on a second-order growth axis in one of the positions noted above	0–50	%	T. G. Thorp, Plant & Food Research Australia Pty Ltd, Australia, ‘pers. comm.’
PROLEPTIC_LIMB_PRO	Probability of a proleptic shoot developing from an axillary bud on the PGA in one of the positions noted above	0–100	%	T. G. Thorp, Plant & Food Research Australia Pty Ltd, Australia, ‘pers. comm.’
PROLEPTIC_AXILLARY_PRO	Probability of a proleptic shoot developing from an axillary bud on a second-order growth axis in one of the positions noted above	0–50	%	T. G. Thorp, Plant & Food Research Australia Pty Ltd, Australia, ‘pers. comm.’

*The possible values of the parameter for the location of sylleptic shoots is actually from 1 to 10, but due to programming conventions in the model, the value of 2 is the first node in an axis where a sylleptic shoot may be developed from.

Pattern-oriented calibration

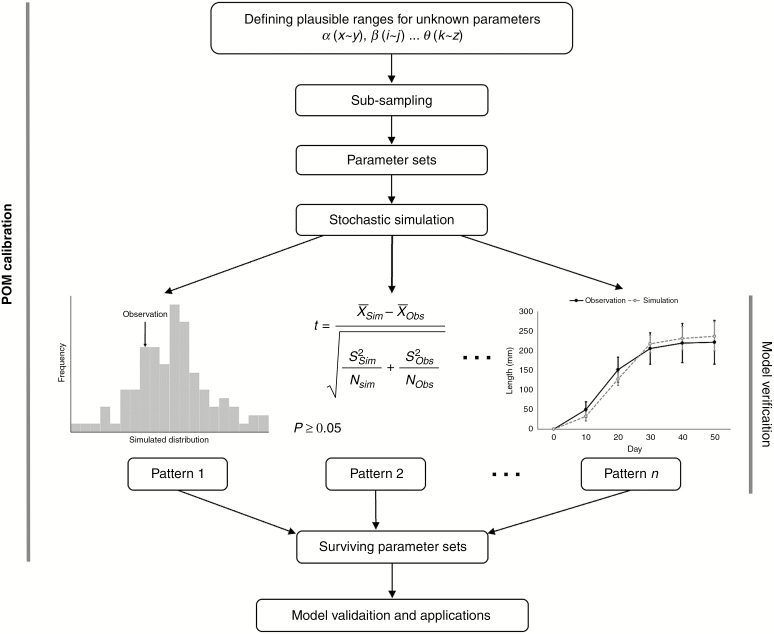
The pattern-oriented calibration approach (Fig. 1) has been used widely in ecological modelling (e.g. Wiegand et al., 2004; Kriticos et al., 2009; Grimm and Railsback, 2012; De Villiers et al., 2016; Kriticos et al., 2016). To apply POM calibration, for each pattern to be reproduced by the model, quantitative criteria need to be specified to decide whether that pattern was reproduced, i.e. matched by the model output. These criteria should be neither too restrictive nor too broad. If they are too restrictive, we may reject too many parameter sets; by contrast, if they are too broad, this would make model outputs too uncertain and less useful.

Fig. 1.

The flowchart of POM calibration. During model verification, multiple observed patterns at different scales are used as filters to screen out unsuitable parameter sets by comparison between simulations and observations under the specified criteria.

In our case, all patterns used are scalar metrics, i.e. specific numbers (Table 2). Hence, if the cited articles reported the observed mean values with s.e. or s.d. as well as the number of replications, for pattern matching we required that there should be no statistically significant difference (P ≥ 0.05) between model outputs and verification patterns, and the absolute value of relative difference between model outputs and observations should be less than 20 %. Otherwise, when only the mean values were reported, we required that the absolute value of relative difference between model outputs and observations should be less than 20 %, or the t-distribution (95 % confidence interval) of model outputs should encompass the observed mean values. When statistical analysis was applicable, the unequal variance t-test also known as the Welch t-test was used in R (R Core Team, 2018) as suggested by Ruxton (2006).

Table 2.

Overview of seven patterns used for model verification (Thorp and Sedgley, 1993a). Note that here the patterns are scalar (i.e. numbers) whereas in general patterns for POM can be more complex, including spatial (geographical distributions), temporal (time series patterns) or structural patterns (e.g. size distributions)

Pattern	Description	Values
P1	The number of sylleptic shoots on the primary growth axis (PGA)	7.8 ± 3.0 (mean ± s.e.; n = 5)
P2	The number of proleptic shoots on the PGA	12.6 ± 1.5 (mean ± s.e.; n = 5)
P3	The number of growth units (GUs)	64 ± 18.9 (mean ± s.e.; n = 5)
P4	The number of terminal GUs	49 ± 12.3 (mean ± s.e.; n = 5)
P5	The number of GUs per axillary shoot	3.7 ± 0.5 (mean ± s.e.; n = 5)
P6	The number of flushes per year	3
P7	Flush growth timing	*

*Flush growth occurs in three seasons: spring, summer and autumn.

For each unknown parameter, a range of plausible values was specified based on expert knowledge or reasonable biological arguments regarding the studied system (Table 1), and within these specified ranges, only integers were chosen, due to the biological properties of growth of avocado [e.g. the number of nodes (location of different shoot types on an axis) must be an integer]. Exploring all possible combinations of the six parameters would have been impossible, even though the model runs relatively quickly. For the parameter space explored here, there are ~2.65 × 10⁹ combinations. Given that it takes a little over 2 s to run the model and even allowing for parallel runs using eight processes, it would take nearly 20 years to complete. Clearly, sub-sampling techniques must be used to scan parameter space in a systematic way, resulting in a much smaller number of parameter sets (Thiele et al., 2014). We used such a technique, i.e. Latin Hypercube Sampling (LHS), to sample 10 000 parameter sets, effectively and systematically. The resulting 10 000 parameter sets were generated using the lhs function within the package ‘tgp’ version 2.4-14 (Gramacy, 2007; Gramacy and Taddy, 2010) in R.

The model was then run 50 times using each of these 10 000 parameter sets, and the model outputs were compared to the seven observed verification patterns (Table 2), all of them scalar metrics. They characterize structural features of the avocado annual growth module (AGM) developed from an indeterminate compound inflorescence (thyrse) that does not set fruit over an annual growing period. It consisted of one mixed reproductive and vegetative (spring) and two vegetative (summer and autumn) growth flushes (Thorp and Sedgley, 1993a).

The model outputs were compared with the verification patterns one at a time, under the specified criteria. Only parameter sets that made the model output fulfil these criteria for the first verification pattern were tested with the next pattern, and so on. Each pattern thus served as a filter to reject unsuitable parameter combinations. The resulting suite of parameter sets that passed or ‘survived’ from all filters was then used for model validation and/or application.

Because parameters may interact, i.e. different combinations may lead to the same model outputs, we checked correlations among the values of the unknown parameters that resulted from POM calibration by calculating a correlation matrix using R.

Model verification and validation

The term ‘verification’ is defined as the comparison of model outputs with patterns that guided model design and were used for calibration (Augusiak et al., 2014). This process was described in the POM calibration section above. It was used to determine whether a parameter set should be kept as a surviving one that passed all verification ‘filters’. To take stochasticity into account in the model’s dynamics, each parameter set was tested by running the model 50 times and comparing means and variations in the model outputs with those in the observed patterns.

For model validation, defined as the comparison of model predictions with independent patterns that were not used when the model was parameterized (Augusiak et al., 2014), we ran the model with all surviving parameter sets that resulted from the POM parameterization. Fifty replications were run for each surviving set and we then pooled their outputs (1100 replications in total). Model outputs were compared with six validation patterns (quantitative patterns specifying specific mean values and/or variances) (Table 3) that were not used for parameterization, based on the specified criteria. These pooled outputs (1100 replications in total) were also compared with all verification patterns to confirm that the model was able to reproduce them sufficiently well, just like the outputs for verification demonstrated in the POM calibration section above were generated by each 50 replications.

Table 3.

Overview of six quantitative patterns used for model validation

Pattern	Description	Values	References
P8	Mean length (mm) of spring growth flush on the primary growth axis (PGA) on non-fruit-bearing shoots in south-east Queensland, Australia	191.9 (mean)	Wolstenholme et al. (1990, p. 318)
P9	Mean length (mm) of summer growth flush on the PGA on non-fruit-bearing shoots in south-east Queensland, Australia	238.2 (mean)	Whiley et al. (1991, p. 594)
P10	Mean length (mm) of autumn growth flush on the PGA on non-fruiting shoots in a commercial orchard in South Australia, Australia	193 ± 66 (mean ± s.e.; n = 15)	Thorp and Sedgley (1993b, p. 152)
P11	Mean length (mm) of the PGA over a 1-year growing period on non-fruiting shoots on 2-year-old ‘Hass’ trees in south-east Queensland, Australia	720 ± 131 (mean ± s.e.; n = 5)	Thorp and Sedgley (1993a, p. 92)
P12	Mean leaf area (mm2) per shoot on non-fruit-bearing shoots in south-east Queensland, Australia	4060 (mean)	Wolstenholme et al. (1990, p. 318)
P13	Mean number of nodes (leaf nodes only) per growth unit on non-fruit-bearing shoots found on 4-year-old ‘Hass’ trees in a commercial orchard in central Queensland, Australia	6.5 ± 0.24 (mean ± s.e.; n = 16)	The Queensland Department of Agriculture and Fisheries (unpubl. res.)

Note that in POM calibration, the filtering process is only applied for model verification (Fig. 1), where verification patterns are used as filters to reject unrealistic model structures and parameter sets. The result of this filtering is a suite of parameter sets, which is then pooled for model applications, where the model is run for all these parameter sets. In the surviving parameter sets, each individual parameter usually still varies over a wide range, which reflects interactions among model parameters and their corresponding processes respectively that cannot be resolved, given the initial parameter and process uncertainty. However, the variation in these pooled model outputs generated by running the model with the entire suite of surviving parameter sets is much smaller than that caused by the original uncertainty in the initial 10 000 parameter sets. POM calibration thus takes equifinality of the given model structure into account by using the entire suite of surviving parameter sets resulting from the calibration for applications.

To improve the ‘structural realism’ of a model, i.e. the likelihood that a model reproduces empirical observations for the right reasons (Wiegand et al., 2003; Grimm et al., 2005; Grimm and Railsback, 2012), a second, independent set of patterns can then be used for model validation. This set of patterns is not used, and preferably not even known, when the model is constructed, parameterized and verified. Such validation patterns are used to test secondary or independent predictions (emergent properties at the system level) generated from the model, and to check whether these predictions are reliable. In ecological modelling, this is kind of validation is rarely done, i.e. testing a POM-calibrated model with further validation patterns, because of the lack of patterns and the usually high uncertainty in model structure (Railsback and Grimm, 2019). For FSP models, however, validation patterns are more likely to exist and can guide the refinement of models by indicating structure, processes and parameter values that should be explored in experiments to enable direct parameterization. In our study, the validation patterns are emergent properties observed at the system level as a result of carbon allocation and production of metamers by independent apical meristems.

If the pooled model outputs resulting from simulations run with all surviving parameter sets fail to fulfil model validation, or are overly sensitive to the quantitative criteria used to decide whether a pattern was reproduced by the model, this indicates that both model structure and the data used for calibration should be improved, and which kind of data are subsequently needed most. Therefore, the whole process of POM calibration may need iterations until the pooled model outputs can agree with all validation patterns.

We also evaluated the performance of each individual surviving parameter set, again with 50 replications, to further explore how POM calibration performed in contrast to possible manual calibration.

RESULTS

Pattern-oriented calibration

After pattern-oriented calibration, there were 22 parameter sets that passed all verification patterns (Table 4). One set (Set 9207) was similar to the manually calibrated set shown in the last row of Table 4.

Table 4.

The parameter sets that can pass all verification patterns with the possible values

Set number	SyllepticShootsLocation	ProlepticShootsLocation	SYLLEPTIC_LIMB_PRO	SYLLEPTIC_AXILLARY_PRO	PROLEPTIC_LIMB_PRO	PROLEPTIC_AXILLARY_PRO
714	6	9	65	3	90	21
1557	4	7	71	39	96	4
1570	4	8	77	2	82	34
1893	4	10	70	36	82	4
2580	5	6	57	6	100	35
2702	4	10	73	5	76	35
3142	4	9	79	3	68	40
3440	5	8	77	4	92	19
4717	8	9	33	10	82	23
4778	6	10	50	1	83	23
4972	4	10	72	18	74	18
5084	6	10	52	26	78	10
5137	6	9	58	22	96	0
5317	4	8	97	7	94	22
6036	7	9	42	20	89	14
6198	4	9	96	3	80	21
6526	9	8	31	18	85	11
7755	9	9	34	9	82	15
7996	6	8	46	11	87	23
8313	4	8	93	9	76	16
9095	4	7	68	1	85	39
9207	4	7	74	21	99	22
Manually calibrated set	4	7	70	20	90	20

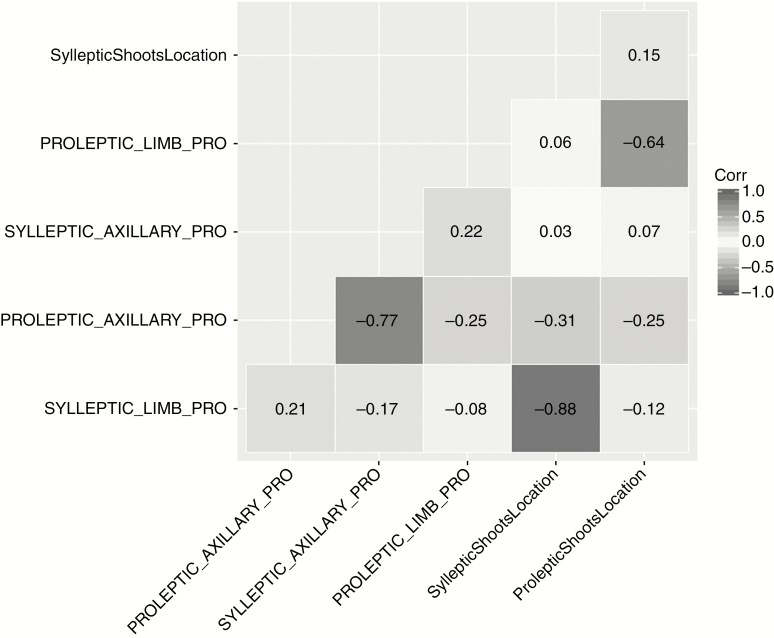
After POM calibration, the overall correlation was low among the 15 paired unknown parameters, but there were three pairs (SyllepticShootsLocation vs. SYLLEPTIC_LIMB_PRO; ProlepticShootsLocation vs. PROLEPTIC_LIMB_PRO; SYLLEPTIC_AXILLARY_PRO vs. PROLEPTIC_AXILLARY_PRO) that were significantly negatively correlated, within pairs (Fig. 2 and Table 5).

Fig. 2.

Comparison of correlation among the 15 paired unknown parameters that resulted from POM calibration, including all 22 surviving parameter sets with their correlation coefficients.

Table 5.

Comparison of correlation P-values among the 15 paired unknown parameters resulting from POM calibration, including all 22 surviving parameter sets (not significantly correlated at P = 0.05)

	SyllepticShoots Location	ProlepticShoots Location	SYLLEPTIC_ LIMB_PRO	SYLLEPTIC_ AXILLARY_PRO	PROLEPTIC_ LIMB_PRO	PROLEPTIC_ AXILLARY_ PRO
SyllepticShootsLocation	NA	0.494	<0.001	0.912	0.801	0.166
ProlepticShootsLocation	0.494	NA	0.585	0.746	0.001	0.270
SYLLEPTIC_LIMB_PRO	<0.001	0.585	NA	0.440	0.710	0.339
SYLLEPTIC_AXILLARY_ PRO	0.912	0.746	0.440	NA	0.319	<0.001
PROLEPTIC_LIMB_PRO	0.801	0.001	0.710	0.319	NA	0.267
PROLEPTIC_AXILLARY_ PRO	0.166	0.270	0.339	<0.001	0.267	NA

NA, not applicable.

Model verification and validation using the entire parameter sets

The existing avocado branching architecture model, fitted with the 22 parameter sets that resulted from POM calibration, reproduced all seven verification patterns sufficiently well. There was no significant difference between model outputs and observations, as shown in Table 6, with the maximum absolute value of the relative difference between them being 14.16 %.

Table 6.

Comparison (mean ± s.e.) of model outputs, generated by fitting the model with the 22 surviving parameter sets, and verification patterns, including results of the t-test (not significantly different at P = 0.05), and absolute and relative differences between model outputs and observations

Pattern	Model (n = 1100)	Observation (n = 5)	t	d.f.	P	Difference	Relative difference (%)*
P1	7.3 ± 0.06	7.8 ± 3.0	−0.17	4.00	0.88	−0.50	−6.36
P2	10.82 ± 0.09	12.6 ± 1.5	−1.19	4.03	0.30	−1.78	−14.16
P3	66.69 ± 0.51	64 ± 18.9	0.14	4.00	0.89	2.69	4.20
P4	47.17 ± 0.39	49 ± 12.3	−0.15	4.01	0.89	−1.83	−3.74
P5	3.7 ± 0.02	3.7 ± 0.5	0.005	4.02	0.996	0.00	0.00
P6	3	3	–	–	–		–
P7	†	†	–	–	–		–

*The relative difference is calculated from model minus observation (difference) then divided by observation.

^†Flush growth occurs in three seasons: spring, summer and autumn.

For the validation patterns, model predictions were similar to observations (Table 7), with the maximum absolute value of the relative difference between them being 31.49 % associated with P8. The cited article for P8 did not report whether the mean length of the spring flush included a reproductive zone. Hence, two simulation scenarios (P8E and P8I) were conducted: the spring flush excluded and included a reproductive zone, respectively. Scenario P8I resulted in a relative difference of 31.49 % between the predicted and observed lengths (mean ± s.d.: 252.34 ± 54.42 mm; n = 1100, and 191.9 mm), while the predicted length (mean ± s.d.: 209.26 ± 54.42 mm; n = 1100) generated from the scenario of the spring flush excluding a reproductive zone (P8E) was very similar to the observed value (191.9 mm), with the relative difference being 9.04 %. In spite of the fact that the relative difference between the model prediction and observation was 31.49 % for scenario P8I, the mean observed value (191.9 mm) was located in the t-distribution of the model prediction (252.34 ± 106.77; d.f. = 1099). Thus, the model is capable of predicting the observed mean value.

Table 7.

Comparison of model outputs, generated by fitting the model with the 22 surviving parameter sets, and validation patterns, including results of the t-test (not significantly different at P = 0.05), and absolute and relative differences between model outputs and observations

Model (n = 1100)				Observation
Pattern	Mean	s.d.	s.e.	Mean	s.e.	n	t	d.f.	P	Difference	Relative difference (%)*	t-distribution (d.f. = 1099)
P8E†	209.26	54.42		191.9‡						17.36	9.04
P8I†	252.34	54.42		191.9‡						60.44	31.49	252.34 ± 106.77
P9	187.64	64.83		238.2‡						−50.56	−21.23	187.64 ± 127.20
P10	192.11		1.95	193	66	15	−0.01	14.02	0.99	−0.89	−0.46
P11	632.09		4.24	720	131	5	−0.67	4.01	0.54	−87.91	−12.21
P12	4279.03	200.35		4060‡						219.03	5.39
P13	6.82		0.07	6.5	0.24	16	1.26	17.94	0.23	0.32	4.85

*The relative difference is calculated from model minus observation (difference) then divided by observation.

^†P8E refers to the mean length of spring growth flush excluding the reproductive zone, whereas P8I indicates the mean length of spring growth flush including the reproductive zone.

^‡Statistical analysis methods were not applicable, because the cited articles did not report the s.d. or s.e. and n for the observed mean values.

Note: for P8 we did not know whether the length of the spring growth flush from the cited article included a reproductive zone. Therefore, we compared our model prediction with two scenarios, spring growth flush including a reproductive zone and spring growth flush excluding a reproductive zone, to see how they differed. The observed mean for P8I lies in the range 252.34 ± 106.77 (t-distribution; d.f. = 1099).

The same situation occurred for P9. Although the absolute value of the relative difference between the predicted and observed lengths (mean ± s.d.: 187.64 ± 64.83 mm; n = 1100, and 238.2 mm) of summer growth flush (21.23 %) was slightly more than 20 %, the mean observed length (238.2 mm) was within the t-distribution of the model prediction (187.64 ± 127.20; d.f. = 1099). Therefore, the observation is similar to what the model would predict.

The results for P10 and P11 indicated statistical similarity between model predictions and observations. For the mean length (mean ± s.e.) of autumn growth flush, the model gave 192.11 ± 1.95 mm (n = 1100), which was similar to 193 ± 66 mm (n = 15) observed on non-fruit-bearing shoots (t = −0.01, d.f. = 14.02, P = 0.99). Over a 1-year growth period, the length (mean ± s.e.) of the primary growth axis (PGA) was 632.09 ± 4.24 mm (n = 1100), which was similar to the field observation (720 ± 131 mm; n = 5) of non-fruit-bearing shoots (t = −0.67, d.f. = 4.01, P = 0.54).

For comparison of the mean leaf area per non-fruiting shoot (P12) between the model prediction and observation, leaf area predicted by the model was 4279.03 ± 200.35 mm² (mean ± s.d.; n = 1100), which was similar to the value (4060 mm²) observed in the field, with the relative difference between them being 5.39 %.

For P13 – the number of nodes (leaf nodes only) per growth unit (GU) – the model prediction was 6.82 ± 0.07 (mean ± s.e.; n = 1100), matching the value (6.5 ± 0.24; n = 16) found on non-fruiting shoots in the field (t = 1.26, d.f. = 17.94, P = 0.23).

Model verification and validation using individual surviving parameter sets

For the 22 surviving sets, each can make the model reproduce all verification patterns, because they resulted from POM calibration. Additionally, most individual sets could also make the model predict all observed patterns for validation, except for two sets: Sets 1557 and 5137. They failed to make the avocado model predict P13: the number (mean ± s.e.) of nodes (leaf nodes only) per GU. There was a statistically significant difference between model outputs and observations indicated by the Welch t-test. For Set 1557, the model prediction was 7.67 ± 0.44 (mean ± s.e.; n = 50) for P13, which was significantly different from the observation (6.5 ± 0.24; n = 16) of non-fruiting shoots in the orchard (t = 2.33, d.f. = 63.99, P = 0.02). Comparison of P13 between the model prediction (7.43 ± 0.37; mean ± s.e.; n = 50) and the observation (6.5 ± 0.24; n = 16) for Set 5137 also showed a significant difference (t = 2.12, d.f. = 62.57, P = 0.04).

DISCUSSION

We present a simulation-based inference technique for parameter estimation for FSP models. The calibration method presented here deals with a common situation in which direct estimation of parameters does not exist or is infeasible due to a lack of time or resources, so the values of unknown parameters have to be determined indirectly in a reliable and robust way. We used POM to calibrate an existing FSP model of an avocado branching architecture. POM calibration led to several parameter sets (22 in total), which indicates strong interactions among the processes underlying those unknown parameters. Interestingly, POM calibration also identified one set that was similar to the manually calibrated set shown in the previous study (Wang et al., 2018).

Importantly, when fitted with these multiple parameter sets, our model had the capacity to reproduce the verification patterns, as well as to predict further independent validation patterns that were not used for model parameterization simultaneously. Despite not delivering one single, ‘optimal’ parameter set, using the pooled outcome of POM calibration, the model captured the development of an AGM sufficiently well. It was thus able to make reliable predictions of emergent system behaviours; that is, architectural and growth patterns such as the number of nodes (leaf nodes only) per GU and the length of the growth flush emerged from the interactions among the physical and biological processes occurring in the model. It is thus likely that the model has a realistic structure to provide realistic representations of processes. This interpretation is also supported by the low correlation among unknown parameter values resulting from calibration (Whittaker et al., 2010).

Ideally, parameters should have no strong correlations, but should have an unambiguous biological meaning in terms of representing the underlying processes for a given system modelled. In our study, following calibration there were three out of the 15 paired unknown parameters that were negatively correlated. A reason for this could be incomplete information on the location and likelihood of development of sylleptic and proleptic shoots within an AGM. Nevertheless, these correlated parameters appear to be meaningful in describing the biological processes underlying the growth of an AGM. For example, an increase in the number of locations (nodes) for sylleptic shoots (basal nodes) or proleptic shoots (nodes closest to the apex) on the PGA is associated with a decrease in the probability of a shoot for both types developing from an axillary bud on the PGA in one of those locations. Also, with the increase in the probability of a sylleptic shoot developing from an axillary bud on a second-order growth axis, the probability of a proleptic shoot developing from an axillary bud on the same order axis will decrease. The compensatory effect between the correlated parameters appears to represent plausible biological mechanisms that could explain the number/proportion of sylleptic or proleptic shoots existing within an AGM, which reflects the natural growth habits of avocado as observed by Thorp and Sedgley (1993a) and Mickelbart et al. (2012).

In the parameter sets passing all verification patterns used as filters, most individual parameters varied over a large range (Table 4) so that only the entire parameter sets (22 sets in our case) should be used for model applications. This is because the interactions between the values of unknown parameters can make the model produce equally acceptable model outputs. For example, both a low value of a parameter (α) and a high one for the second parameter (β), or vice versa, may lead to the same model output, depending on the value of another parameter (θ). Such interactions, which could also be termed compensation, are underlying the equifinality, i.e. the fact that different models can ‘explain’ the same set of observations (Beven and Freer, 2001; Beven, 2006; Slezak et al., 2010). To take these interactions into account fully, the entire suite of surviving parameter sets that passed all the verification filters should therefore be used together for model validation and/or applications.

However, the occurrence of equifinality does not imply poor model performance. In fact, the multiple parameter sets can improve model performance for validation and reduce parameter uncertainty (Her and Chaubey, 2015). This has been confirmed by our findings. Our study demonstrates that it would be risky to focus on just one single parameter set. The single set may make the model work perfectly under certain observed patterns, but when new patterns are observed, it may not result in the model producing the reliable outputs that match with the new observations. In our case, as an essential modelling exercise, we tested the surviving sets individually against all validation patterns. Two sets (Sets 1557 and 5137) failed to make the avocado model predict P13, but they made the model work well for the remaining validation patterns. Also, other ‘successful’ sets might fail for new observed patterns in the future, and thus keeping all of them has many advantages. The key point of POM calibration is to use the entire suite of surviving parameter sets, rather than using each individual parameter set or few parameter sets, to fully capture these interactions among the processes underlying the unknown parameters.

Comparing pooled model outputs with validation patterns is not an integral part of POM calibration, but is an option for guiding model improvement if validation patterns exist. Generally, it is not expected that all surviving parameter sets make the model match all validation patterns in POM calibration. However, in our study there are only two such sets, perhaps due to the relatively well-known modular structure of plant architecture and growth rules that often are used as verification patterns to guide the design of the conceptual framework of FSP models. This leads to considerably less uncertainty in model structure than that in most ecological models (Wiegand et al., 2004; Railsback and Grimm, 2019), thereby effectively constraining most unrealistic parameter values during the process of calibration. As a consequence, 20 out of the 22 parameter sets resulting from POM calibration can individually make the model predict all validation patterns in the current study.

Nevertheless, there is always uncertainty, more or less, in model structure due to the limited knowledge about the modelled system and assumptions made in designing the model. In our study, the occurrence of equifinality is the result of a limited number of verification patterns that were available and used for model design and parameterization. To the best of our knowledge, there were only seven verification patterns (Table 2) that we could use to guide model development, while the validation patterns were identified only after model development and calibration were finished.

It is well known that the values of the single best parameter set fitting some experimental data optimally are not necessarily the best from a biological perspective (Slezak et al., 2010). POM calibration can overcome this limitation by using multiple parameter sets together. For our avocado model, the use of multiple sets made the model produce those reliable predictions. This outcome is supported by the findings in many modelling studies from various scientific disciplines (Wiegand et al., 2004; Rossmanith et al., 2007; Colwell and Rangel, 2010; Whittaker et al., 2010; Grimm and Railsback, 2012; Her and Chaubey, 2015; Luo et al., 2015; May et al., 2016; Sukumaran et al., 2016; Boer et al., 2017; He et al., 2017; Teixeira et al., 2018). Consequently, modellers should consider using multiple parameter sets instead of choosing the single best set of parameters for achieving better model performance, because of the inherent uncertainty related to each parameter set. Further experimental work can be conducted to quantify the proper values of unknown parameters under the guidance of the resultant parameter sets from POM calibration, if possible. For example, experiments can be designed to target only a certain range of values for each unknown parameter based on the frequency distribution of these values, resulting from POM calibration. In such a way, time and resources can be better focused on experiments showing the greatest likelihood of success. In turn, the model can be refined by fitting with new parameter values gathered from such experimental data-gathering, in terms of the model development cycle (Grimm and Railsback, 2005, p. 27), so that the structural realism of the model can be enhanced and increased, thereby reducing uncertainty in model structure. This would lead to a lower number of parameter sets surviving from the calibration process (i.e. a lower level of equifinality), and the interactions among the processes underlying these unknown parameters can thus be better understood.

Conventionally, most parameter estimation techniques applied to FSP models are based on statistical inference (e.g. maximum likelihood estimation), which rely largely on detailed component-level experimental data for parameter fitting. Such techniques have been successfully used to estimate parameters mostly for annual crops (Guo et al., 2006; Ma et al., 2007; Cournède et al., 2011; Trevezas and Cournède, 2013; Trevezas et al., 2014; Baey et al., 2016, 2018; Mathieu et al., 2018). However, Toni et al. (2009) and Hartig et al. (2011) pointed out that the statistical inference approaches can be constrained by the stochastic nature of biological systems. Calibration of such FSP models could therefore be difficult using statistical inference approaches, because these non-linear interactions can make their analytical formulae (i.e. the likelihood functions) intractable.

In addition to traditional parameter estimation techniques, simulation inference approaches such as ABC and POM are valuable for parameterizing FSP models in the plant modelling community. For FSP models that are not analytically tractable, their unknown parameter values can be identified inversely via stochastic simulation. In principle, stochastic simulation fitted with different parameter sets can be used to generate the approximate distributions of observed data by multiple model runs. Summary statistics can then be used to quantify similarity between simulated data and observed data. Unsuitable parameter sets can be screened out using such a process (Hartig et al., 2011). This is particularly useful to filter unsuitable parameter sets when using multiple observed patterns at different levels and scales (Wiegand et al., 2003; Grimm et al., 2005; Grimm and Railsback, 2012). The main advantage of using POM to parameterize FSP models is that it enables the use of multiple observed patterns at the system level to inversely determine the values of unknown parameters at the component level. Here, model parameterization avoids relying heavily on data-gathering at the organ level, because emergent system properties at the macro-level are more easily observed than properties at the micro-level.

It is also noteworthy that sometimes POM even allows us to inversely infer information that was not reported in the original literature. For P8, it was not reported whether measurements of the mean length of the spring flush included a reproductive zone. We thus ran scenarios with and without the reproductive zone and found that it was more likely that the reproductive zone was not included. This indicates that POM is not only useful for inversely determining parameters, but also for identifying processes. Indeed, the rationale for selecting the most suitable representation of a certain process, for example habitat selection of fish (Railsback and Harvey, 2002), or information transfer among birds (Cortés-Avizanda et al., 2014), is exactly the same as for parameterization: use multiple patterns to identify the most plausible representation of a process. This approach has been termed ‘pattern-oriented theory development’ (Railsback and Grimm, 2019) and also has high potential to be useful for FSP modelling.

In summary, we demonstrate a simulation inference technique to parameterize FSP models. Such techniques are suitable for parameterizing FSP models that are analytically intractable or are constructed based on sparse and noisy data at the component level. The POM calibration approach allows FSP models to be developed in a timely manner without relying heavily on field or laboratory experiments, or on cumbersome manual calibration. More importantly, the accuracy of model performance (predictive power) for validation can be increased.

FUNDING

This work was supported by an Australian Government Research Training Program Scholarship from the Australian Federal Government, a Queensland Alliance for Agriculture and Food Innovation (QAAFI) Postgraduate Award and a Graduate School International Travel Award from The University of Queensland; and Horticulture Innovation Australia Ltd (HIA) (‘The Small Trees High Productivity Initiative’ project – AI13004 ‘Transforming subtropical/tropical tree crop productivity’).