An overview of agent-based models in plant biology and ecology

Abstract

Agent-based modelling (ABM) has become an established methodology in many areas of biology, ranging from the cellular to the ecological population and community levels. In plant science, two different scales have predominated in their use of ABM. One is the scale of populations and communities, through the modelling of collections of agents representing individual plants, interacting with each other and with the environment. The other is the scale of the individual plant, through the modelling, by functional–structural plant models (FSPMs), of agents representing plant building blocks, or metamers, to describe the development of plant architecture and functions within individual plants. The purpose of this review is to show key results and parallels in ABM for growth, mortality, carbon allocation, competition and reproduction across the scales from the plant organ to populations and communities on a range of spatial scales to the whole landscape. Several areas of application of ABMs are reviewed, showing that some issues are addressed by both population-level ABMs and FSPMs. Continued increase in the relevance of ABM to environmental science and management will be helped by greater integration of ABMs across these two scales.

Introduction

Over the past few decades, agent-based modelling (ABM), also called individual-based modelling (IBM), has revolutionized many areas of biology, not least the modelling of individual plants, plant populations and plant communities (Shugart et al., 1992; Judson, 1994; Kurth, 1994; Grimm, 1999; DeJong et al., 2011). Two general areas of application of ABM to plant science have developed.

ABM at the population and community levels aims at predicting plant population or community dynamics by modelling multiple individual plants (agents) that interact with their environment and each other. Each agent has a set of state variables, which can include age, size, condition and spatial location, as well as adaptations, which can include both physiological traits and behavioural traits. This is critical because plant traits play a crucial role in plant ecology via determining the success or failure of species in a given environment. These traits govern an individual’s growth, reproduction, dispersal, allocation of nutrients and energy, and mortality in relation to environmental factors. Traits may vary among the individuals due to genetic variation but may also change through time due to ontogeny and plasticity. ABMs differ from differential equation (DE) population and matrix model (MM) size–structure models, in which a top-down description is imposed on populations through population-level parameters (i.e. birth and death rates at the population level). ABMs are bottom up-models such that population-level behaviours emerge from the interactions that autonomous individuals have with each other and their environment. The number of individual-level attributes that an individual can have in an ABM is virtually unlimited, in contrast to DE or MM models of populations, in which it is awkward to include more than a few attributes. Therefore, complex questions concerning how populations and communities respond to environmental conditions can be addressed by ABMs through the effects of those conditions on individuals and interactions among individuals.

Historically, the first use of ABM in plant ecology, describing multiple interacting individual trees, was probably the JABOWA model (Botkin et al., 1972). This was termed a ‘gap-phase replacement’ model, because it described succession of tree communities in gaps created in forests due to the death of a canopy tree (typically 100 m² or 0.01 ha) by taking into account the differential effects of shading on trees of different species and different heights in relation to their neighbours. Tree models were the earliest ABMs partly because forest succession has been a key area of ecology since its inception and partly because the long history of forest mensuration has provided data on growth of important commercial species. The initial successes of JABOWA in describing succession and altitudinal change in tree communities inspired many variations of forest models, including extensions beyond small plots to landscapes, such as FORET (Shugart and West, 1977), FORTNITE (Aber, 1982), LINKAGES (Post and Pastor, 1996), FORMIND (Kohler and Huth, 1998), FORMAN (Chen and Twilley, 1998), iLand (Seidl et al., 2012a, b) and TEMFORM (Zhang et al., 2013; Kolobov and Frisman, 2016b). Reviews include Bugmann (2001), Porté and Bartelink (2002), Xi et al. (2009) and Wallentin et al. (2008).

The second scale at which there are now decades of application of ABM is at the level of development of individual plants. The agents in this case are modules (metamers) within the plant and algorithms are used to model repetitive branching patterns by which the plants grow, with different morphologies for different species. Among methods of plant morphological modelling is the formal language of L-systems pioneered by Lindenmayer (1968), Lindenmayer and Prusinkiewicz (1990), and Prusinkiewicz (1998), and described and reviewed by Kurth (1994), Prusinkiewicz and Runions (2012), as well as the AMAP methodology (de Reffye and Houllier, 1997). These methods arose out of interest in the development of 3-D spatial structure of individual woody and herbaceous plants and in the visualization of their structures, which led to these models of plant morphology. Because the development of plant structure interacts with light capture and material flows, these can be integrated into a general methodology that combines geometric structure with function; that is, functional–structural plant modelling (FSPM), in which plant architecture, including roots, is explicitly modelled in 3-D and linked to process-based modelling (e.g. Landsberg and Waring, 1997) of functional aspects, such a light capture, and carbon and nutrient flows. These are discussed in a Special Issue of Annals of Botany (Cieslak et al., 2011; DeJong et al., 2011; Han et al., 2011; Sarlikioti et al., 2011; Xu et al., 2011), as well as Faverjon et al. (2019). This approach, while focusing on the internal structure and function of plants, is also used at the scale of multi-plant combinations to provide better understanding of the details of plant interactions.

There are a number of other related modelling approaches with the same purpose as ABM of allowing macroscale dynamics to emerge from microscale actions. In particular, cellular automata (CA) models are spatially explicit, and the agents are discrete spatial cells, in which the variables are different occupancy states of vegetation of the cells (Czárán, 1998). Cells can interact with neighbouring cells through propagule dispersal and competition and change state through those interactions.

Our goal here is to (1) provide an overview of the basic structure of ABMs, used in the modelling of plants, plant populations and communities; (2) provide examples of applications of ABMs in several areas of biological and ecological research; and (3) discuss the future challenges and opportunities ahead for under for this modelling. In particular, the limitations of the variations of these models are discussed, as well as ways of integrating modelling at the individual plant level, population level and community level. Although this review covers both ABMs at the population/community level and individual plant level (e.g. FSPMs), the emphasis is on applications of the former, with the focus on FSPMs being largely directed to those with the most relevance or potential application to issues at the population level.

INDIVIDUAL PLANT PROCESSES

Plant growth

Plant growth has been modelled in different ways, including by empirical growth functions, by process-based models, and by models that combine development of architecture with biomass increase. The last way can include both clonal and non-clonal growth.

Gap phase replacement (gap) models such as JABOWA use empirically based equations to describe the life cycle processes of the trees, and in general do not go into detail concerning the actual physiological processes. JABOWA simulates plant succession in a 0.01-ha plot, with a given set of tree species and environmental conditions. Each tree is simulated individually from the sapling stage. JABOWA requires input of parameters supplied by the user, as described in detail by Botkin (1993). The basic equation for growth involves computing the yearly increment of growth of the tree volume, as follows:

$${\displaystyle \begin{array}{l}{\displaystyle \delta \left(D^{2}H\right)=LA(1-DH/D_{max}{H}_{max})f\left(environment\right)}\end{array}}$$ (1)

where $D^{2}H$ is the volume of a tree idealized as a cylinder and where D = tree diameter, H = tree height, D_max = maximum diameter of a given tree of species, H_max = maximum height of the tree species of species, LA is the leaf area of the tree, and the constant R is the maximum growth rate per unit leaf area. The relationships between tree height and leaf area with diameter in JABOWA are given by the allometric relationships:

$${\displaystyle \begin{array}{l}{\displaystyle H=137+b_{2}D-b_3{D}^{2}LA=C{D}^2}\end{array}}$$ (2)

where b₂, b₃ and C are empirical parameters that can be fit to a species. Other variables such as vertical leaf profile, etc., are deduced from stem diameter via species-specific allometric relationships and growth is allocated accordingly. Different species have different empirically based growth and allometric parameters, but the same model structures. The effect of the environment, f(environment) = f(AL)*Q*s(BAR), is composed of effects of light shading, f(AL), where AL is available light, site quality, Q, and an upper limit on basal area s(BAR), each of which decreases the growth rate of a tree from its maximum. Site quality involves a temperature factor, a wilting factor for effect of drought, a wetness factor for effect of soil wetness, a nitrogen factor for effect of soil nitrogen, and a light shading effect, which is covered below in Plant Competition. The key limitations of the gap models are that individual spatial locations are not taken into account, and that empirical growth parameters are available largely for common or commercial tree species.

The use of plant functional types, where physiological process-based models for tree growth replace the empirical parameterization in ABMs, expands the ability of population dynamics to be simulated in terms of plant responses (e.g. Kazmierczak et al., 2014). An example of this more mechanistic modelling approach is PLATHO (PLAnts as Tree and Herb Objects), which simulates the growth of plants, including their carbon and nitrogen fluxes. Its basic processes are morphological development, phenological development, photosynthesis, respiration, biomass growth and allocation to biochemical pools, water uptake, nitrogen uptake and senescence (Gayler and Priesack, 2006). An array of submodels is used for the different processes. PLATHO models plant growth and competition in a spatial setting that can simulate up to 20 competing individuals.

The version of the model described by Gayler et al. (2008), which includes allocation to secondary compounds, focuses on the behaviour of a few carbon-based components of the model, including available carbon assimilates, A_av, structural biomass (wood for trees), carbon-based secondary compounds and reserves, R. All are measured in terms of grams of glucose. The formation of carbon based-compounds requires sufficient nitrogen levels but is less strongly dependent on nitrogen concentration, N, than on carbon. There is a tradeoff in potential allocation to defensive compounds and plant growth rate.

An equation for the current assimilates can be written, using the authors’ notation:

$${\displaystyle \begin{array}{l}{\displaystyle A_{av}=(P_{act}+R{\tau }_R)\mathrm{\Delta }t-D_M+A_{old}}\end{array}}$$ (3)

Here P_act is the current photosynthesis rate, R is the potential amount of reserves that can be remobilized, τ _R the rate of remobilization of reserves, D_M is the demand for maintenance, A_old is the assimilate remaining from the previous time step and Δt is the time step of a year.

In addition to assimilates, a limiting nutrient, assumed to be nitrogen, N, here, is obtained from soil and nitrogen remobilization, respectively:

$${\displaystyle \begin{array}{l}{\displaystyle N_{av}=N_{upt,pot}+N_{trans,pot}}\end{array}}$$ (4)

The modelling approach in PLATHO is hierarchical priority type (Le Roux et al., 2001) in that there is a hierarchy of priorities for meeting demands of internal components of the plant. Pools of carbonates and nitrogenous compounds are assumed, which are augmented daily by carbon assimilation and nitrogen uptake, plus mobilization of reserves. These are distributed by a priority scheme. Meeting maintenance costs is the first priority for the allocation of carbonates. Reproduction is the second priority and vegetative growth the third priority after blooming. If the available carbon is greater than what is needed for growth, then the remaining assimilate can be converted into defence compounds. If the amount of available assimilates exceeds both growth and defence demands, then the last priority is replenishment of reserves. The demands on nitrogen compounds are proportional to the demands on carbon.

In other models of the hierarchical approach for utilization of energy by an individual plant, priorities may also depend on the proximity of a component to the source [e.g. PEACH of Grossman and DeJong (1994), and TREGRO of Weinstein and Yanai (1994) and Retzlaff et al. (1996)]. In TREGRO above-ground components have first access to new photosynthate. Both PEACH and TEGRO are used for individual trees, and are divided, as in PLATHO, into a small number of functional components within the trees.

The modelling of Maréchaux and Chave (2017) took process-based modelling beyond the application to just one or a few trees. Their spatially explicit forest growth simulator, TROLL, for tropical forests, like other models of complex multi-species systems (e.g. Bossel and Krieger, 1991; Köhler and Huth, 1998, 2004; Fischer et al., 2016; Liu et al., 2016; Zakharova et al., 2019), uses species-specific functional traits. Tree geometry is set by allometric relations, as in JABOWA, but leaf area varies dynamically as a balance between allocation and losses. At the leaf level, the model uses the Farquhar et al. (1980) model for photosynthesis, with photosynthesis limited by either Rubisco activity or ribulose bisphosphate regeneration. The maximum rate of carboxylation and maximal electron capacity are co-limited by nitrogen and phosphorus, and stomatal conductance varies with the whole-plant water use efficiency and abiotic conditions. Stomatal behaviour is regulated by an optimization criterion based on Cowan and Farquhar (1977). This theory postulates that stomata should act to maximize carbon gain, photosynthesis, while at the same time minimizing water lost by transpiration. Allocation of net primary production is to canopy and wood based on empirical relationships, and then, within the canopy, different fractions go to leaves, twigs and fruits. Empirical relationships are also used for respiration. Using species-specific parameters for 163 species, TROLL simulated the successional dynamics of a tropical forest from bare soil in an area of 400 × 400 m on monthly time steps.

A further step towards combining physiological processes with greater structural detail was taken by Grote and Pretzsch (2002), who simulated individual tree development in stands of beech and spruce depending on carbon, nitrogen and water balance of individual trees, designed to calculate growth as a function of climatic driving variables. A tree is assumed to be partitioned into pipes and the growth in dry matter of the tree equals the collective growth in dry matter of all of the pipes. The pipe model (Shinozaki et al., 1964), of functional equilibrium theory, assumes that there must be a long-term balance between the acquisition of carbon by foliage and nutrient by roots with the use of these for growth, so that the relationship between the leaf mass and the pipe cross-section area in branches and in the stem of a tree does not change through time. It is assumed that the relative allocations of carbon and nutrients serve some optimization goal such as the maximization of carbon production. This type of model is defined as a teleonomic model by Thornley and Johnson (1990). These models can show how a tree should optimally behave in response to environmental conditions. For example, a model of carbon and nitrogen allocation in a forest stand in steady state (Mäkelä et al., 2008) showed that increasing nitrogen availability to the roots should optimally lead to a decrease in carbon allocation to fine roots, as might be expected, but, less intuitively, to increased allocation to wood rather than to foliage, which remains stable in the model. Grote and Pretzsch (2002) simulated the growth of a 5312-m² stand of 215 beech and spruce trees in southern Bavaria over 5 years.

The full integration of tree 3-D structure with function is taken by the FSPM approach, which is based on the L-system formalism (Lindenmayer and Prusinkiewicz, 1990) in an environment of light interception above ground and transfer of water and mineral nitrogen from below-ground sources. As parts of a modular organism, the common feature of all plant shoots is that they are built from elementary subunits, or building blocks, called phytomers (White, 1979) (same as metamers). Shoot morphogenesis arises from the initiation of new metamers by shoot meristems, from the growth of the individual organs produced, and from the differentiation of support tissues. Metamer responses include branching, apical growth, radial growth, death and dormancy. Typically, the plant grows on daily time steps, and the rates of branching are affected by genotype, carbon availability, spatial position and light conditions. The FSPM approach is able to take into account details of foliage architecture such as leaf orientation (Sterck et al., 2005). Light capture is integrated over that captured by all leaves and nitrogen uptake is limited by root length within the soil. Biomass allocation between shoots and roots is assumed to follow an allometric relationship. Further partitioning between organs within the shoots is then assumed to follow the relative carbon demands of organs to sustain maximum expansion in dimensions. 3-D root models using FSPM have been developed in the same way to simulate root–soil interactions (e.g. Dunbabin et al., 2013). The specific root architecture can be important in plant competition (e.g. Van Noordwijk et al., 2015).

The modelling of clonal plants has combined physiological structure with horizontal structure. Such ABMs, e.g. CLONAL (Mony et al., 2011) may consist of two types of agents, potentially autonomous shoots (ramets) connected by horizontal stems, along which resources may be conducted. CLONAL simulates 2-D growth of a clonal plant during a growing season as the horizontal stems forming branches on a landscape (or model lattice) of hexagonal grid cells. A ramet may be formed at the end of a connecting unit. It performs photosynthesis and nutrient uptake, the results of which can be stored in the connecting stems or used for further growth of the clone through the formation of a new connecting unit branching from the ramet. The probability of branching from a ramet, creation of a new ramet or extension of an existing connector depends on a set of rules, and is dependent on carbon metabolism and storage. Different strategies may involve short branches to create a highly ramified plant (termed phalanx), or few, long branches (termed guerilla). CLONAL has been used for modelling competing populations of clonal plants (Bittebiere et al., 2012). ABM includes stochasticity in the simulation of the effects of the network structure of plants on the growth strategy of clonal plants (Campillo and Champagnat, 2012; Vincenot et al., 2016).

Carbon allocation within plants

Plants allocate their acquired resources, energy (or carbon) and nutrients, to meet their several essential functions. In order to grow and reproduce, plants allocate resources to capture solar radiation by growing leaf biomass and to acquire nutrients by growing fine root biomass. Investment in stem wood, beyond what is needed structurally by the foliage and roots, also is employed to obtain a competitive height advantage for capturing light (Givnish et al., 2008). Plants exist within the constraints that only a certain amount of solar radiation is available per unit area of land, and only a fraction of that energy can potentially be captured by photosynthesis. Therefore, the amount of carbon that can be allocated is limited, and allocation of carbon to one function necessarily decreases the carbon that could be allocated to other functions.

The ability to adjust carbon allocation in response to environmental conditions is widely documented (Litton et al., 2007) and the basic processes involved in allocation are reviewed by Lacointe (2000). The trade-off in investment between root and shoot (foliage) is well known and has been the subject of many studies and models (e.g. Wilson, 1988; Ingestad and Agren, 1991; Thornley, 1995; Hermans et al., 2006). Seidl et al. (2012a), in their model, iLand, used a process-based approach with variable hierarchical allocation of carbohydrates among leaves, fine and coarse roots, and reserve and stem pools in order to predict changes in productivity and mortality in 100 × 100-m cells across spatial transects in which radiation, nutrients and water availability varied. Nutrient deficiency can stimulate biomass allocation to root biomass and morphology (Hermans et al., 2006), whereas increased resources and stand age result in increased partitioning to above-ground wood production and decreased it to below-ground production (reviewed by Litton et al., 2007). However, shading of leaves can lead to higher leaf area per unit biomass and higher allocation of above-ground growth to leaves in shade than in the sun in deciduous saplings (King, 2003). Investment in additional stem wood, beyond what is needed structurally by the foliage and roots, to obtain a height advantage in capturing light, is another possible destination of carbon allocation. PLATHO (Gayler et al., 2008), which was described earlier, is another example of a model that is used to explore allocation strategies. Gayler et al. (2008) used PLATHO with data from apple trees to simulate the effects of different levels of nitrogen fertilizer on apple trees, which they compared with growth data. They found that increased growth rates resulting from high fertilization were associated with decreased levels of defence compounds in leaves, suggesting a general conclusion concerning the strategy of apple trees for allocation of assimilate. When nitrogen is abundant, the apple tree invests assimilates into shoot growth, rather than towards the defensive pool of phenolic compounds, which are usually less needed when nutrients are abundant.

A model of dry matter portioning applied to Douglas fir and beech (Bartelink, 1998), which incorporated the effects of site conditions, dominance position and thinning, showed that over time for trees in a stand, there should be a gradual increase in branches and a decrease in fine roots and foliage in response to thinning. A model for carbon and nitrogen dynamics in an even-aged coniferous forest (King, 1993) showed that optimal fine root allocation for a competing individual was less than 5 % of total production for adequate nitrogen, but rose to 30 % as nitrogen became more limiting with growth of the stand. This shift to roots had the benefit of decreasing the losses of nutrients from the stand by leaching, although it slowed the production of wood.

Assimilate allocation is a key component in FSPMs. In the short term, partitioning of the whole-plant carbon among the different sink organs (those that are growing and need carbon input) and/or functions determines the relative growth rates of the various plant components, including structural as well as harvestable parts. However, assimilate allocation is involved in a number of feedback processes that make it even more central in the longer term. As a significant example, young leaves, which are sinks for carbon, the growth of which is dependent on current assimilate allocation, will later become carbon sources, thus affecting the future carbon inputs. As another example, the growth of sinks is both the result of carbon allocation to them and a major determinant of the carbon allocation pattern. Unfortunately, lack of precise knowledge of carbon partitioning remains a weak point in current models, although its basic principles and mechanism are relatively simple and fairly well understood. An additional problem is that different models discretize plant components in different ways (from individual metamers up to larger groupings), making model comparisons difficult. However, Reyes et al. (2019) have developed a multi-scale carbon allocation model (MuSCA), which allows simulation of carbon allocation to be defined at multiple scales. This approach will help in identifying the topological scale at which allocation can be modelled that is the best compromise between model accuracy and simplicity.

Plant competition

Extension of modelling of individual plants towards populations and communities requires modelling intra- and inter-specific competition. Gap models such as JABOWA are not spatially explicit. Such gap models assume that the conditions in the gap of area 0.01 ha or so are homogeneous; that is, although the trees may differ in size and species, no specific locations of the trees with the gap are given, so every tree in principle competes for light with every other tree, according to their relative heights and leaf area. Therefore, interactions are averaged over all of the trees of the plot. The light response function, which is part of the factor f_i(environment) = f_i(AL)*Q_i*s(BAR) of eqn (1), i.e. the shading response, is f_i(AL) = $k_1(1-e^{-k_2(AL-k_3)})$, where AL = available light and $AL=PHI\ast e^{-k_{4}SLA}$, PHI = light incident above the canopy, SLA = shading leaf area, calculated from the leaf areas of all of the trees higher than the ‘target’ tree, and k₁, k₂, k₃ and k₄ are constant parameters.

The assumptions of the gap models miss the fine-scale effects of spatial interaction between trees that are a function of inter-tree distances. In spatially explicit ABMs, on the other hand, every tree has a specific location and affects other trees according to both size relationships and distance, so that effects of competition depend on the relative sizes and distances between neighbouring trees. The model FOREST (Ek and Monserud, 1974) was perhaps the first spatially explicit forest ABM. Other early models include that of Green (1989), which simulated two species on a CA spatial grid to study the effects of fire. Pacala et al. (1993) and Pacala and Deutschman (1995), in SORTIE, extended modelled space beyond the 0.01-ha range of local interactions by including spatial locations of each tree. SORTIE is capable of including the realistic detail of individual trees having specific locations and competing with local neighbours, by changing the local available light environment at each location and height. The light a plant receives is calculated in detail by the number, sizes, species-identities and relative locations of neighbours that cast shade. Fine-scale spatial patterns of tree stems and biomass emerge from the simulations (Canham et al., 2004). Pacala and Deutschman (1995) show that including spatial explicitness has system-level consequences that might not be captured in ‘mean field’ approximations that leave out horizontal spatial structure. The authors’ model of a hardwood forest predicted twice the old growth basal area predicted by the mean field approximation.

Although in most ABMs light is the main resource competed for, competition for nutrients is included in some models, such as nitrogen in LINKAGES (Post and Pastor, 1996) and soil water in LES (Liénard and Strigul, 2016) and in Reineking et al. (2006). A number of approaches developed to model plant competition that include both light and nutrient competition are reviewed by Berger et al. (2008). In CA and grid-based models, in which several plants may occur together with no spatial structure within a given grid cell, they may all compete with other within each spatial cell in the same way as in forest gap models. In spatially explicit models where space is continuous, a variety of approaches for representing competition are used. Fixed-radius-neighbourhood (FRN) models assume a circular area for each plant, roughly corresponding to the adult canopy area, such that competition occurs where the circles of different plants overlap. A refinement on the FRN is the ‘zone-of-influence’ (ZOI) approach, in which, again, the ZOIs represent the circular areas on which plants acquire resources (Wyszomirski, 1983; Weiner et al., 2001). But as the plants grow in size, their ZOIs also grow. Competition occurs where the ZOIs overlap, but the mode of competition (e.g. whether symmetric or asymmetric) must be defined by the user. Because the ZOI is not spatially structured, if, for example, a seedling is within the ZOI of a larger plant, no difference is assumed as to how far within the ZOI the seedling is. The ZOI approach has also been applied to competition of clonal plants (Bittebiere et al., 2012). The geometry of light extinction in heterogeneous vegetation is reviewed by Boulain et al. (2007).

The ZOI approach has been modified to include more realistic geometries of spatial interactions (field of neighbourhood, FON). Unlike the ZOI, which assumes a constant effect of competition across the zone around the plant, in the FON, the strength of competition decreases exponentially from each plant in the population (Berger and Hildenbrandt, 2000; Berger et al., 2002, 2004). The competitive effect of one tree (A) on another (B) is a function of the strength of the competitive strength of tree A, which depends on its size, and its distance from tree B. The total effect on growth of a given tree depends on the competitive effects of all other trees whose FONs overlap with that tree. The FON approach has been applied to above- and below-ground interactions of grass (May et al., 2009), to growth models based on metabolic theory (Lin et al., 2013), and to facilitation of growth of some plants through positive feedbacks by others (Lin et al., 2012). The FON approach captures essential aspects of spatial competition and appears to be a reasonable standard way of modelling interactions. However, the FON method has limitations, discussed by Berger et al. (2008). First, the effect of the plant on local nutrient resources through exploitation is generally not considered. Even in Grote and Pretzsch (2002), where water and nutrients are modelled in some detail, their availabilities are set externally, although the tree can have some negative effect on water reaching the soil by interception of precipitation. Second, phenotypic plasticity in response to heterogeneity and competition by other plants is not considered, at least in the types of models, forest models, reviewed by Berger et al. (2008). Detailed root and soil modelling can help overcome both deficiencies. Dunbabin et al. (2004) and Dunbabin et al. (2013) review six root system 3-D architecture (RSA) models of root–soil interactions. These models are able to simulate, to different degrees, the structural development through time, and uptake of water and nutrients, including their local depletions. Carbon dynamics has been incorporated in the model SimRoot (Clausnitzer and Hopmans, 1994; Lynch et al., 1997). Incorporated into FSPMs, the root system can respond plastically to changes in water and nutrients and through changes in carbon allocation (Han et al., 2011; Louarn and Faverjon, 2018). There are still major challenges in such models of root architecture, however, due to computational intensity in simulating nutrient uptake.

As another example of a detailed process modelling approach to competition, Gayler et al. (2006) extended PLATHO to competition experiments in phytotrons of mixed cultures of juvenile beech and spruce, in which spruce dominated. The model indicated the importance of the starting conditions and spacing densities. Beech has greater plasticity in allocation of assimilates, which was a disadvantage when beech and spruce were started with similar heights and high densities, as beech allocated more to diameter growth, while the less plastic spruce increased in height faster and outcompeted the beech for light. These process-based models were used for the limited purpose of simulating individual trees or small assemblages of competing trees.

Plant mortality

There are two main mortality processes in most models. The first is simple age-dependent mortality not due to competition, where, in JABOWA, $M_i=1-{(1-{\epsilon }_i)}^{AGEMA{X}_i}$, is the yearly probability of mortality, where AGEMAX_i is maximum age of an individual of species i and ${\epsilon }_i=4/AGEMA{X}_i$. The second mortality process is from effects of stress due to competition. Trees that grow poorly are much more likely to die than healthy trees. JABOWA, for example, tests whether the last annual growth increment is less than a minimum value, set as the parameter AINC_i. It is assumed that a tree whose diameter increment falls below this minimum would have only a 1 % chance of surviving those 10 years. A random number is selected, and if it is less than AINC_i, the tree dies. Other models use other measures of stress, such as stemwood increment relative to leaf area (FORKSA: Price and Apps, 1995) and whole tree carbon balance (e.g. HYBRID: Friend et al., 1997; and model 4C of Bugmann et al., 1997).

In models of individual plants, such as FSPMs, mortality usually refers to particular organs within the plant. Root hairs have a high rate of turnover, and leaves are shed seasonally. In the architecture model ALMIS (Eschenbach, 2005), leaves that have net negative carbon balance may be shed at other times, and a branch is dead when the terminal apex stops functioning and all the organs on the branch are dead (Mathieu et al., 2009).

Reproduction

Modelling of individual-level reproduction has largely been applied to trees, and has been implemented in different ways. In JABOWA, for example, for shade-intolerant species, saplings can enter only if the light intensity at the forest floor (i.e. available light, AL) is greater than 99 % of incident sunlight (AL > 0.99) and if the site quality, Q_i, is greater than zero. Saplings of a shade-intermediate-tolerant species can be added even if the light intensity at the soil surface is less than 99 % of the incident sunlight, but greater than the empirical species-specific minimum. If light intensity is in this range, then a certain number of saplings can enter in a given year. How many individuals of a shade-tolerant species i can enter is a stochastic function of the environmental conditions. For both shade-intermediate-tolerant and shade-tolerant species, if the inequality regarding light availability is true, then a number of saplings for the species can enter. In other models lack of adequate moisture and freezing events (FORENA: Solomon, 1986), lack of chilling (FORSKA: Prentice et al., 1993) and spring frost events (FORECE: Kienast, 1987) are specific effects that are taken into consideration. Models limited to the development of individual plants that we know of do not simulate population growth through reproduction, but they may simulate fruit production and thus fecundity, which can be a basis for extending to population growth.

Scaling to greater spatial areas

Forest simulators of the JABOWA type cover only areas of 0.01 ha or so, a scale at which competitive effects can be averaged. This approach could be used with no further model development to simulate a landscape by combining many spatial cells, but the cells would be independent, so this would ignore both effects such as shading coming from outside the cell and seed dispersal between cells.

Methods that allow scaling up to larger areas, while at the same time having the important properties of ABMs, have been reviewed (e.g. Pacala and Silander, 1990; Gratzer et al., 2004; Strigul et al., 2008; Xi et al., 2009). However, simulating the patchiness of the light regime, which is essential for predicting dynamics of the full forest community, including understorey and forest floor species and processes, relies on fine-resolution spatially explicit models such as SORTIE (Canham et al., 1994; Coates et al., 2003; Adams et al., 2007). Spatially explicit models such as SORTIE and TROLL can cover larger areas, but may be constrained by computational limits.

Scaling to larger areas involves taking into consideration heterogeneity (Jeltsch et al., 2008). Some models have dealt with this issue. In order to simulate forest landscape pattern, while still maintaining the ABM approach, Smith and Urban (1988) developed ZELIG, which uses a grid of contiguous 0.01 cells. They modelled 9-ha stands by using this grid, taking into account the edge effects on tree establishment and growth that comes from the surrounding four cells. Urban et al. (1999) extended 10 × 10-m cells with individual trees to the heterogeneous landscape scale, which could include spatially contagious processes of tree colonization and fire. TROLL (Chave, 1999) is also an example of an individual-based tree model that has been used to simulate natural forest dynamics at the landscape scale. At an even larger scale, Friend et al. (1997) proposed the Hybrid 3.0 model in which multiple plots of an individual-based tree and plant model are linked together with biogeochemical factors. Other models sacrifice some fine-scale spatial resolution and either link many gap-sized plots together, connected by seed dispersal (Urban et al., 1999; Moorcroft et al., 2001; Mladenoff, 2004; Elkin et al., 2012; Fischer et al., 2016; Liu et al., 2016), or simply scatter independent gap models across large regions (Bugmann et al., 1997; Shuman et al., 2011).

In another approach to scaling up to larger spatial areas, Liu and Ashton (1998a) developed the FORMOSAIC ABM to similarly simulate landscape-level tree dynamics. In FORMOSAIC the location of each individual tree is modelled within a 0.01 grid cell. It is assumed that each cell is linked to others by seed dispersal. Liu and Ashton (1998b) applied their model to a 50-ha permanent plot in the Pasoh Nature Reserve in Malaysia, but the model can be applied to areas of any size, depending on computer capability. At a still larger scale, the ecosystem demography (ED) model (Moorcroft et al., 2001) again started with ABM dynamics of individual tree functional types in individual 15 × 15-m cells, coupled with biogeochemical models of fluxes of water, nitrogen and carbon. However, they converted the output of individual cells into age- and size-structured approximations described by partial differential equations that are the first moment (or mean) of a stochastic process involving many simulations. This approach allows scaling spatially by taking into account the heterogeneity without having to keep track of every individual tree. The authors applied their model to the area of South America between 15°N and 15°S. The ED model forms the basis of the dynamic global vegetation model (DGVM), in which terrestrial biosphere vegetation is linked to biophysical and physiological cycles and is driven by climate (see also Sato, 2009). Although based on traits of individual plants, these models do not simulate the structure of tree communities, and are thus referred to as vegetation models rather than plant population models (Jeltsch et al., 2008). These models may capture key aspects of the effects of global change on vegetation, but because they lack the high degree of species and functional diversity of real forests, they may be limited to coarse projections.

APPLICATIONS

Models can be created for understanding, for predicting, for guiding management or for some combination of those goals. ABMs are especially suited for specific applications, as they can take into account details of a given situation. Therefore, ABMs have been used for practical applications in both forestry and agriculture. A few examples of modelling at the individual plant scale and the population and community scales are described below. Some additional examples from the last 12 years are listed in Table 1.

Table 1.

Agent-based modelling used to address species and/or applied ecology questions (published since 2006).

ABM	Reference
Plant intercropping	Gaudio et al. (2019)
Orange tree structure–function modelling	Qu et al. (2012)
Forest management; Araucaria angustofolia in Brazil	Valeriano et al. (2014)
Competition and tree growth; Cryptomeria japonica in Japanese plantation	Inoue et al. (2008)
Forest restoration for diversity in Australia	Ngugi et al. (2011)
Effects of agricultural landscape on aphid dynamics	Perry and Millington (2008)
Effects of control on a pest carabid beetle	Topping and Lagisz (2012)
Estimating cost/benefit of weed control	Steel et al. (2014)
Forest management; effects of frequency of prescribed burning	Karsai et al. (2016)
Integrated pest management strategies; banana weevil	Vinatier et al. (2012)
Prediction of range expansion of invasive species	Travis et al. (2011)
Prediction of effects of climate change on alpine plants	Cotto et al. (2017)
Predicting invasive plant dispersal; Gunnera tinctorial in Ireland	Fennell et al. (2012)
Predicting effect of dispersal limitation of species under climate change; Pinus uncinate in Pyrenees	Martinez et al. (2012)
Deforestation in Yucatan, reforestation in Midwest USA	Manson and Evans (2007)
Grassland management; claspleaf pennycress, southern Germany	Pagel et al. (2008)
Growth of wetland sedges, south-east Michigan	Wildova et al. (2007)
Succession in Oregon forest landscapes	Busing (1991)
Invading giant hogweed	Nehrbass and Winkler (2007)
Phenotypic plasticity; black alder	Reuter et al. (2008)
Alpine tree line; Austrian central Alps	Wallentin et al. (2008)
Light interception in the canopy; tomatoes	Sarlikioti et al. (2011)
Leaf inclination effects in wheat stands	Barillot et al. (2019)

Predicting forest succession and productivity

Models have been used to make and test predictions in both forest succession and forest productivity. Predictions are important for making long-term decisions regarding future forest composition in the face of global change, invasion by non-native trees and effects of forest fragmentation. So the predictive power of ABMs has been emphasized (Loehle, 2000; Perry and Millington, 2008). Because forests play an important role in the carbon cycle and, therefore, in the effects on the global climate system to carbon dioxide emissions, accurate projections of the carbon budget, including carbon sequestration, are also important (Yan and Zhao, 2007).

Forest gap ABMs, such as JABOWA (Botkin et al., 1972) and the many forest ABMs that followed, have been used to predict forest succession, composition and effects of environmental changes on forests. As pointed out by Purves et al. (2008), these models have successfully reproduced the species composition of old-growth, semi-natural forests. As an example, Ngugi et al. (2011) used the Ecosystem Dynamics Simulator (EDS), based on JABOWA, to project growth dynamics of remnant Australian brigalow forest communities. After parameterization of the model for 34 tree and shrub species, it was tested with independent long-term measurements. The model provided close approximation of the actual development trajectories of mature forests and the regrowth of thickets. This included projection of changes in species composition in remnant forests to within a 10 % error. EDS projections between 1966 and 2005 (39 years) explained 89.3 % of the observed basal area of the plots. In another case, an ABM was applied to understand forest succession of a monoculture of mangroves to try to understand the observed fact that annual stem wood production tends to decline after a certain age. The modelling was able to attribute the net loss with age to an imbalance of wood production due to higher death rate of larger trees that was not compensated for by greater growth of smaller trees (Berger et al., 2004).

Although the ability of ABMs to handle any degree of complexity is an advantage, it usually makes them analytically intractable. However, a simplified version of the forest gap ABM, called the perfect-plasticity approximation (PPA), was developed as a model of forest dynamics (Purves et al., 2008). As in other ABMs, this approximation is based on individual tree parameters, including allometry, growth and mortality, and uses height relationships in determining the outcome of competition. However, many other details are discarded, so that analytical predictions can be made. In that study, the timing and magnitude of basal area dynamics and ecological succession on different soil types for eight common species in the USA were found to be accurate, and predictions for the diameter distribution of 100-year-old stands were qualitatively correct in their shape. Another suggestion for dealing with the difficulty of fully analysing large complex models was the proposal by Mony et al. (2011) of using volunteer computing in computational ecology to systematically browse the parameter space and analyse the simulation results. This technology will enable modellers to proceed to large-scale landscape experiments that provide insight into ecological processes linked to plant ecology.

Despite the existence of some data that are sufficiently long-term to allow predictions to be tested for certain forest stands, such as those that are fast-growing, the fact that forest succession can take centuries to reach its final state is still a serious obstacle to model testing. Therefore, ‘space-for-time’ substitutions are frequently used (Pickett, 1989). As an example, Clebsch and Busing (1989) empirically measured forests after 63 years of agricultural abandonment. Forest composition at 63 years was used as the starting condition for a particular forest gap succession simulator (FORET: Shugart et al., 1981). The prediction of 300 years ahead closely matched the state of a nearby old-growth forest that was approximately that age.

The economic importance of forests has led to abundant data on individual tree and stand growth for many commercially important species. For orchard tree species, sufficient data are available to parameterize FSPMs to accurately simulate such commercial species as orange trees (Qu et al., 2012) and peach trees (Grossman and DeJong, 1994). However, parameterization of models of diverse natural forests is difficult, as fewer data are available (Evans and Moustakas, 2016). New developments may ameliorate some of these limitations, as they require less data to upscale in a computationally efficient manner. The FSPM approach has also been applied to estimate crop production in general and in specific crops such as pepper (Ma et al., 2017), and wheat production (Evers et al., 2010), which may be more suitable than process-based models that do not take architecture into account, especially when competition for resources is important.

Spatial patterns and biodiversity

Spatially explicit models are able to simulate not only changes in tree community composition, but also the changing small-scale spatial arrangement of trees, as Busing (1991) demonstrated for 0.07- to 0.4-ha patches of deciduous forest. The model predicted nearest-neighbour distances well, although the simulated trees were more regularly spaced than the empirical stands with which they were compared. Ford and Diggle (1981) showed that in an even-aged plant monoculture, slight initial differences in height can be amplified by competition and lead to a bimodal distribution of trees, and thus to a two-tiered stand structure that is commonly observed. The forest model by Ribbens et al. (1994) introduced a technique for calibrating a model of tree seedling dispersal and demonstrated the effect of spatial variation in seedling recruitment on forest dynamics. Using SORTIE, they were able to describe growth, probability of survival, production of recruits and resource density on a spatial domain. Earlier ABMs of forest dynamics made simple assumptions concerning seedling dependence on parent distribution. Ribbens et al. (1994) used data on the spatial distribution of parent trees, as well as transect data on seedlings in mixed stands. These data were used to calibrate and validate a seedling dispersal submodel. Because this analysis showed that seedling establishment can be a limiting factor in forest dynamics, the authors next included their seedling submodel in SORTIE, and demonstrated that seedling recruitment limitation could significantly affect the dynamics of a forest.

Life cycle variation in traits provides possible mechanisms for maintaining biodiversity of plants in a biodiversity model by (Chave et al., 2002). Such mechanisms include (a) life history niche-differentiation mediated by competitive trade-offs, (b) frequency dependence due to species-specific pests, (c) recruitment limitation due to localized dispersal and (d) a speciation-extinction dynamic equilibrium mediated by stochastic drift. The relative importance of these mechanisms was assessed using a spatially explicit ABM with individual-level processes of birth, death, speciation, dispersal and immigration from outside a 4096 × 4096-m lattice. Community-level patterns, such as species–area curves, relative-abundance distributions and spatial distributions were extracted from the simulation output and compared with those in real communities. All mechanisms studied contributed to species richness, but only (a) and (b) produced robust coexistence. The scale of dispersal was the most important factor affecting species–area curves (steep at small scales, then shallower and finally steep across large scales). The model was successful because of its unifying nature in explaining many spatial patterns. Kolobov and Frisman (2016a) showed the importance of disturbances in maintaining diversity in an East Asian forest. Parrott and Lange (2004) used the model WIST to study such complexity more generally. Mailly et al. (2000) used the spatially explicit model DRYADES for the coniferous forest of North America.

Biodiversity has value also for agro-ecosystems, where mixed species, or intercropping, is widely used (Vandermeer, 1992). The use of FSPM for mixed-species agriculture was reviewed by Evers et al. (2019) and Gaudio et al. (2019). The advantage of FSPM for such models is that the competition or complementarity between species can emerge as an outcome of their individual interactions with light and nutrient environments, rather than being imposed as extra equations for competition. FSPM can in principle be used to explore optimal combinations of plants for use in mixed-species agriculture or agro-forestry. A step in this direction is the Virtual Grassland model of Louarn et al. (2020). The model was designed to test for overyielding (additional yield of mixed crops over monoculture). The model showed that highest overyielding was found when there was high trait divergence in light and nitrogen acquisition between N-fixers (legumes) and the second crop.

ABMs reveal aspects of the relationships of local- and regional-level processes that were not seen in simpler models. In an example of a non-forest model, Weiss et al. (2014) simulated grassland plant functional types on a lattice model of 1-cm² cells to identify the drivers of species diversity. By accounting only for local plant interactions and local seed dispersal, the model captured observed levels of community diversity and productivity, as well as their response to gradients of resource availability and grazing intensity. The non-intuitive result emerged that increasing regional seed dispersal decreased the ability of the model to simulate empirical data.

Changes in communities along gradients

Ecotones, or transitions between different vegetation types, are a particular type of spatial pattern that often exist along environmental gradients and can often be explained by the changes in certain environmental factors such as precipitation and temperature. However, some ecotones are far sharper than can be explained by the more gradual changes in the underlying gradient. There can be various explanations for such sharp ecotones, and ABMs can help quantify these explanations.

Because altitudinal climate gradients are much sharper than latitudinal gradients and thus altitudinal ecotones are easier to study, they have been the focus of much study, including modelling. Using an individual-based simulation model (FORET), Shugart et al. (1980) simulated a transition from beech to yellow poplar along elevational gradients in which there was change of both mean annual temperature and growing degree days. They showed that a sharp transition occurred from American beech to yellow poplar as either of these factors increased (thus from higher to lower elevation). The competition for light between the two species played a role, where beech had an advantage in that respect, but the faster growing yellow poplar could outgrow beech at lower elevations. The authors showed that, in the simulations, a property of alternative stable states, hysteresis, occurred; that is, once one vegetation type was established, a large change in temperature was needed in the mode to re-establish the other type.

The well-known alpine treeline, which marks the altitudinal limit of tree growth, is characterized by an ecotone from upright closed-canopy forest to tundra. This can sometimes be very abrupt (Alftine and Malanson, 2004). Both temperature and wind are major factors in determining the treeline (Bunn et al., 2005), inhibiting seedling and tree survival, and thus preventing movement into tundra zones. However, trees that occur in groups can act to shelter each other from wind, so survival is enhanced. Alftine and Malanson (2004) studied the treeline on Lee Ridge, Glacier National Park, Montana, and showed that the wind there has a net directionality, so a seedling has a higher chance of survival in an area slightly downwind of a tree. Those authors built that effect into a CA simulation model and, using it, were able to show that the mechanism of mutual sheltering could explain much of the structure of the treeline ecotone on Lee Ridge. Another landscape model, LandClim, scaling up from individual-tree growth, was used to simulate alpine community zonation with elevation (Elkin et al., 2012). A key point made by the authors is that the exact way fine-scale effects, such as the way individual tree growth is modelled, are important. The authors showed, for example, that a high disturbance rate favours Larix species at high elevations.

In a study of a climatic transition zone in south-western USA, a gap dynamics model was used to examine the relationship between plant life history traits and patterns in dominance and composition at a grassland–shrubland transition zone in order to predict shifts in dominance with directional changes in climate. The model, ECOTONE, simulates below-ground resources and dynamic individual plant root distribution. This work demonstrated that the ABM approach is capable of representing complex interactions among herbaceous and woody species as well as between congeneric species with different life history traits at a biome transition zone (Peters, 2002).

Part of the explanation for these sharp ecotones may be the strong competition between the types, to create a sharper transition between types than would be explained by environmental gradients alone. This can occur if each vegetation type affects its local environment in a way that favours itself, through building soil, stabilizing nutrient availability, moderating temperature, changing soil pH, adding structure and changing conditions in many other ways (e.g. Callaway, 1995). This occurs during the plant successional process, in which there is a sequence of changing dominant plant types or species in a given place following a disturbance (e.g. old-field succession following abandonment of cultivated land). This ability of vegetation to alter its local environment can create spatial patterns, as well as form much sharper boundaries between two vegetation types than the gradual changes in the externally imposed environmental conditions.

Another example of formation of a sharp ecotone is where there are gradients in salinity of ground water. This can occur in both coastal zones and inland areas where salt pans exist. Sharp ecotones can be formed between halophytic (salinity-tolerant) and glycophytic (salinity-intolerant) vegetation (e.g. Burchill and Kenkel, 1991; Grosshans and Kenkel, 1997; Sternberg et al., 2007; Teh et al., 2008; Jiang et al., 2012a, 2014). This appears again to be a case where positive feedbacks between each vegetation type and certain abiotic conditions create the boundary. For example, in southern Florida, mangrove communities and tropical hardwood hammock communities (with species such as Quercus virginiana, Lysiloma bahamensis, Bursera simaruba, etc.) can form sharp boundaries when they occur in proximity to each other. The hammocks are restricted to areas with salinities below 7 ppt, but mangroves are able to tolerate a wide range of salinities (Sternberg and Swart, 1987; Ross et al., 1992; Sternberg et al., 2007), so they can compete for space with the hardwood hammock species. The sharp boundary between the vegetation types is accompanied by a sharp difference in vadose- (unsaturated soil) zone salinity level, even though there is only a gradual change in the underlying ground water salinity. Jiang et al. (2012b) used an ABM to simulate the mangrove–hardwood hammock interaction, including effects of gradually varying ground water salinity, precipitation and tides. In the presence of these effects, the combination of salinity gradient and vegetation positive feedback created a sharp boundary.

Although the results described here matched empirical observations, the models were based on simple empirical data, and need to be extended to include physiological detail to better understand how plants and abiotic resources interact to produce change along gradients. The FSPM approach has an opportunity here. To our knowledge, FSPMs have rarely been used to simulate plants along environmental gradients. However, Bornhofen et al. (2011) used an FSPM to study plant evolution along gradients of both stress (low nutrients) and disturbance. Over evolutionary time, the mutable physiological traits evolved towards the three general strategy types of Grime’s (1977) competitor–stress tolerant–ruderal theory. Another interesting study of plant–soil interactions in a heterogeneous environment was done using various simulated root system architectures (RSMs) by Draye et al. (2010). The authors show that under suboptimal water conditions, water uptake to plants is a function of external water supply, soil hydraulic conductivity and the plants’ RSM. This approach could be useful in projecting changes in plant growth along resource gradients.

Effects of global change

Global changes over the coming decades are expected to initiate large changes in the types of vegetation cover in different places across the Earth. A number of studies have applied ABMs to attempt to project the changes in vegetation due to climate change (e.g. Solomon, 1986; Botkin, 1993; Shugart and Smith, 1996; He and Mladenoff, 1999; Miller and Urban, 1999; Fischer et al., 2014; Ma et al., 2017), including using ABMs to help estimate the relative importance of tree age, size and competition in studies of previous climate change using tree rings (Rozas, 2015).

One of the areas where temperature increase may lead to important vegetation change is the vast boreal forest of Siberia. In particular, areas of this forest that are now covered with deciduous larch (Larix spp.) have been hypothesized to potentially shift to dominance by more temperature-tolerant spruce (Picea spp) and fir (Abies spp.) species. Because larch is deciduous, it sheds leaves in the winter, so that the land surface is generally white, due to snow, and has high albedo. Evergreen spruces and firs, on the other hand, do not shed their foliage, and thus have lower albedo. Thus, such a species shift would affect climate. Shuman et al. (2011) applied a version of a gap ABM specialized to East Asian forests, FAREAST, to project through simulations the possible transition of larch forests in Siberia to spruce and fir. FAREAST was run on 372 sites in Siberia and the Russian Far East. It incorporated monthly climate parameters and data on soil characteristics at each site. It simulated 58 different tree species, including those of the three genera of interest, in different communities across the region. Scenarios involved different assumed changes in temperature and precipitation, including a linear 4 °C increase in temperature over the time period of the simulations. The model showed some geographical variation in the response of the vegetation communities. There was a strong shift from larch to evergreen conifers in the geographical areas of low species diversity , but a lesser response in high-diversity areas. In some areas where change is projected, it was shown to occur rapidly, through collapse of the larch community. The decrease in albedo resulting from the vegetation shift was projected to lead to increased regional warming.

Future changes in species distributions will occur due to changes in temperature and precipitation, as indicated above (Zhang et al., 2019). But how fast they will change is not easy to answer. Species distribution models (SDMs) can project potential equilibrium species distribution based on climatic variables, but climate may change faster than a species population, limited by dispersal rates, can stay in equilibrium with the changing climate conditions. Martinez et al. (2012) used a spatially explicit ABM for treeline dynamics to estimate how fast a pine species, Pinus uncinata, could migrate in elevation, given estimates of future changes in temperature, and what its extinction rate would be in its current lower elevations. They found that, while SDMs accurately described the current distribution of the species, the ABM projection for year 2100 was only about half the possible habitat area estimated by SDM, the difference in part being due to the AMB taking into account competition across the changing range.

Global change will have various types of indirect effects through its impact on forests, and these can also be projected by ABM. For example, plants release volatile organic compounds (VOCs) that affect air quality. Wang et al. (2018) used an ABM to study possible effects of increased temperatures on release of forest VOC emissions at the individual tree level, including ecological competition among the individuals of differing size and age, and radiative transfer and leaf function through the canopy. They found that climate warming only sometimes stimulates isoprene emissions (the single largest source of non-methane hydrocarbon) in a south-eastern US forest (Wang et al., 2018).

Along with changes in climatic variables, there will be a unidirectional change in atmospheric CO₂. This has prompted modelling of changes to primary production, which could potentially increase along with increased CO₂, bringing with it the possibility of increased terrestrial carbon storage. The extent to which a concomitant increase can occur is not straightforward, however, as other factors, such as nitrogen, may become limiting to the increased growth that CO₂ can stimulate. Risk et al. (2014) simulated both C and N using a community of plant functional types in a patch-sized ABM. Assuming projected trends in CO₂ and temperature increase, as well as the effect of increases in N mineralization due to warmer soil, the authors’ model projects a slight increase in the rate of C sequestration, compared with decreased sequestration in some previous studies.

Invading weedy species, pest and beneficial insect species, and epidemics

Biological invasions are a leading cause of recent extinctions (Clavero and Garcia-Berthou, 2005; Bellard et al., 2016), and are becoming increasingly common with the accelerating impact of anthropogenic climate change, habitat alteration, species introductions, and their combination (Simberloff et al., 2013). ABMs have been used not only to predict the long-term dynamics of invasive plant species, but also to take account of the native community in the model (e.g. Krug et al., 2009; Maines et al., 2013). In addition, environmental factors, such as soils and climatic conditions, can also be included in simulating invasive species dynamics (Higgins et al., 1996; Goslee et al., 2001). The effects of herbivory on plant succession and production have been studied using ABM (e.g. Dyer and Shugart; 1992; Seagle and Liang, 2001), so it is reasonable to apply ABM to the study of biocontrol of weedy plants.

As an example, a serious problem in southern Florida is the invasion of Melaleuca quinquenervia (hereafter melaleuca), which is a tree from Australia that has spread over the freshwater ecosystems of southern Florida, displacing native vegetation, and thus threatening native biodiversity. A programme to suppress melaleuca, begun in 1997 with insect herbivore agents, including the melaleuca weevil Oxyops vitiosa and the psyllid Boreioglycaspis melaleucae (Meyerson and Mooney, 2007; Tipping et al., 2008, 2009; Center et al., 2012) appears to be highly successful where applied. The combined effects of these herbivores cause losses of leaves, forcing melaleuca to switch resource allocation from seed production to production of new, often unseasonal growth (Tipping et al., 2008). Field studies (Tipping et al., 2009) show that melaleuca weevils attack new lead tissue preferentially and relentlessly, thereby contributing to continuous defoliation and re-foliation cycles.

However, the extent to which melaleuca can be controlled to low levels, primarily through biocontrol, is important to estimate, because of the costs of mechanical and chemical methods. Also, what the long-term recovery of native plant communities will be as melaleuca is gradually suppressed remains unknown. Therefore, predicting the efficacy of control on invading species such as melaleuca is of current interest because of the ecological and environmental damage of many invading species. Zhang et al. (2017) used JABOWA to project probable future changes in plant communities, by simulating successional processes occurring in two types of southern Florida habitat, cypress swamp and bay swamp, occupied by native species and melaleuca, with the impact of insect herbivores. Modelling is possible because a substantial amount of information is available on the melaleuca and stand dynamics for the period prior to the release of insect herbivores (Rayamajhi et al., 2008, 2010).

Computer simulations show melaleuca invasion leads to decreases in density and basal area of native species in the two swamps, but that herbivory would effectively control melaleuca to low levels, resulting in a recovery of native species. The results suggest the introduction of insect herbivory appears sufficient to suppress melaleuca over the long term and major native species may show substantial recovery within about 50 years.

ABM is important in modelling the interaction of various insects, both useful and harmful, with plants, as ABMs can simulate the configurations of plants. For example, Dupont et al. (2014) followed the movements and flower visits of marked bumblebee individuals within a population of thistle plants in a 50 × 50-m study plot. Their individual-based and animal-centred approach of sampling ecological networks provided new insights on incorporating foraging behaviour and trait variation into spatial analyses of plant–animal interactions. Dattilo et al. (2014) structured an individual-based ant-plant network to evaluate the importance of considering nocturnal records in ant-plant network sampling design.

Plant pathogens and pest herbivorous insects act on a finer scale than the whole plant, so that understanding and controlling them may be greatly aided by FSPMs. Garin et al. (2014) created a generic ‘fungal foliar pathosystem’ as a framework for modelling both the plant and the development of the parasite population. The model consists of plants and their organs in 3-D space. The geometric configurations of the tissues and their properties determines their exposure to pathogens. The infection cycle of the fungal pathogens and their spread of spores are simulated as well. The authors applied their model to septoria leaf blotch of wheat and grapevine powdery mildew of grape orchards.

Insect movements are also influenced by plant architecture, along with light and microclimate variation, although the patterns are not well understood. Wang et al. (2016) developed a model for the Queensland fruit fly and applied it to an orange tree canopy. Model simulations were shown to be consistent with empirical observations of the flies’ movement patterns on the plant. Models of this type can be used in making predictions and save time and resources for control of these pest insects that would otherwise have to rely on expensive empirical studies.

Theoretical models

In a review of ABM, Grimm (1999) distinguished between ‘pragmatic’ and ‘paradigmatic’ models, where pragmatic models, such as those reviewed above, address applied problems, whereas paradigmatic models are aimed at theoretical understanding. Grimm noted that by 1999, pragmatic ABMs far outnumbered paradigmatic ABMs. We will not consider paradigmatic models in this review except to list a few that have been developed over the past 12 years (Table 2).

Table 2.

Agent-based modelling used to address theoretical ecology questions (published since 2006).

ABM	Reference(s)
Plant–soil feedback effects on evolution of plant traits	Schweitzer et al. (2014)
Estimating tropical forest productivity	Fyllas et al. (2014)
Niche vs. neutral theory	Adler et al. (2010)
Explaining plant community patterns	Brown et al. (2016)
Effects of root herbivory on grassland plant coexistence	Pfestorf et al. (2016)
Factors affecting local adaptation at margins of a population’s range	Bridle et al. (2010)
Predicting spread of an invasive plant	Travis et al. (2011)
Testing predictions of metabolic scaling theory	Lin et al. (2013)
Vegetation self-organizing patterns in space	Vincenot et al. (2016)
Carbon allocation and plant allometry	Dybzinski et al. (2011)
Plant–pollinator networks	Dupont et al. (2014)
Tree-morphological plasticity	Strigul et al. (2008)
Filtering and competition in assembly of tree sapling communities	Carlucci et al. (2012)
Clonal growth and competition	Mony et al. (2011), Wong et al. (2011), Bittebiere et al. (2012), Wang et al. (2016)
Individual plant growth in heterogeneous environment	Qu et al. (2010)
Herbivorous insect–plant interactions	Wang et al. (2016)
Population resilience to disturbances	Pena-Alzate and Barriga (2017)
Factors affecting plant competition	Boyden et al. (2008)
Ecotone formation	Jiang et al. (2012b), Wiegand et al. (2006)
Plant morphogenesis	Louarn and Faverjon (2018)
Tree dynamics in savanna	Calabrese et al. (2010)
Root–soil interactions	Dunbabin et al. (2013)
Estimating effective plant dispersal distance	Anand and Langille (2010)
Grassland community yield and stoichometry	Faverjon et al. (2019)
Tropical tree diversity	Maréchaux and Chave (2017)
Grazing effects on plant diversity; below-ground competition	May et al. (2009)
Post-fire succession in shrubland/grassland	Chakraborty and Li (2009)
Above-ground/below-ground linked processes	van der Putten et al. (2009)
Evolutionarily stable state plant height	Xiao et al. (2007)
Plant growth under crowded conditions	Damgaard and Weiner (2008)
Mangrove forests	Berger et al. (2008)
Competition; ABM to mathematical model	Finkelshtein et al. (2009)

Discussion

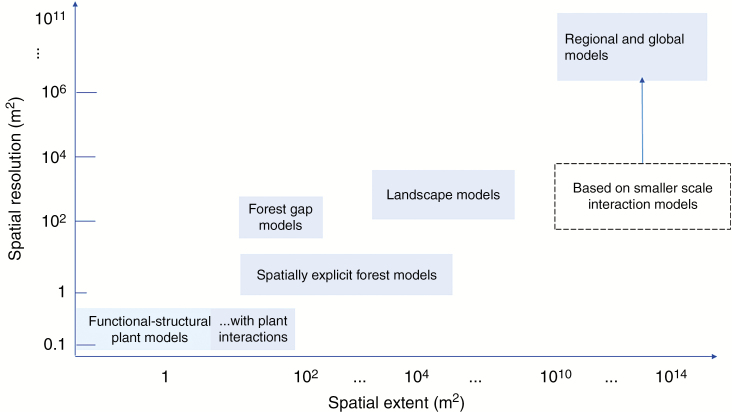
Altogether, plant ABMs cover a huge range of styles, levels of detail and applications, so there is no easy way to sort these out along a small number of axes. However, all ABMs can be viewed in terms of two spatial scales, their scale of spatial resolution and the scale of spatial extent. Resolution here refers to the smallest spatial area needed in the model, while extent refers to the size of the area to which the model is being applied. Figure 1 classifies models into five general groups, starting with FSPMs (1) at the lowest spatial scales of resolution and extent. Although population models are all based on characteristics of individual trees, non-spatial gap ABMs (2), because they average over plant interactions, have both resolution and extent roughly around 0.01–0.08, while spatially explicit gap ABMs (3) use finer resolution and often greater extent. Landscape ABMs usually link together many gap models and make some simplifications. Regional ABMs extract information on plant interactions from fine spatial scale models but integrate these into models with spatial cells with resolutions such as 1⁰ × 1⁰ or ~12 000 km². This spatial perspective on ABMs shows that together they cover spatial scales from plant metamers to the globe.

Fig. 1.

Types of ABMs with the ranges of spatial extent and resolution. (1) Functional structural plant models (FSPMs): for example, PEACH (Grossman and DeJong, 1994), and Tomato model (Sarlikioti et al., 2011). (2) FSPMs with plant–plant interactions: for example, PLATHO (Gayler et al., 2006), Virtual Grassland (Louarn et al., 2020, ROOTMAP (Diggle, 1988). (3) Gap phase models: for example, JABOWA (Botkin et al., 1972), FORET (Shugart and West, 1977), LINKAGES (Post and Pastor, 1996), FORMAN (Chen and Twilley, 1998), EDS (Ngugi et al., 2011) and FORCLIM (Bugmann and Solomon, 2000). (4) Spatially explicit forest models: for example, SORTIE (Pacala et al., 1993), MANGRO (Berger et al., 2008) and TROLL (Maréchaux and Chave, 2017). (5) Landscape models (linking gap models): for example, ZELIG (Miller and Urban, 1999), LANDIS (Mladenoff, 2004), FORMIND (Kohler and Huth, 1998), TREEGRASS (Simioni et al., 2000) and PSS (Fennel et al., 2012). (6) Regional models: for example, SEIB-DDVM (Sato et al., 2007) and ED (Moorcroft et al., 2001).

In disciplinary terms, ABM for individual plants (FSPM) and for population and community-level modelling (population-level ABM) have developed largely independently as distinct scientific programmes. However, in terms of their methodologies and objectives, it may be more appropriate to consider them as occupying ranges along a continuum of spatial and mechanistic detail, with substantial overlap. One aspect of the continuum is the level of detail with which growth and competition are modelled. For example, plant growth rates are described by allometric equations in JABOWA, as whole-plant process models in, for example, Maréchaux and Chave (2017), as multi-organ process models in, for example, Pretzsch et al. (2008), and finally as 3-D plant architecture at the mechanistically detailed end of the continuum. Plant competition is similarly described by a spectrum of methods, from coarse to detailed. At one end, competition is determined by height differences averaged over 0.01 ha in JABOWA, in spatially explicit models by increasingly detailed fixed-radius neighbourhood models, zones of influence and field-of-neighbourhood models, and finally to fine-scale competition for light and nutrients at the scale of leaves and roots in FSPMs.

Overlapping of objective was seen in the survey of several types of applications, which showed that population-level ABMs and FSPMs are addressing some of the same issues of primary production, biodiversity, spatial heterogeneity and pest problems, although at different spatial scales. Even where obvious differences between the population-level ABMs and FSPMs occur, it is not complete. For example, although FTPMs do not deal with population growth through seed dispersal, they do simulate fruit and thus fecundity.

Despite this near continuum of model mechanisms and applications, there are distinctions between the practice of modelling at the population and community scale and at the scale of plant architecture. This may be due to a few factors. One is the disciplinary border that can exist between academic departments of ‘botany’ and ‘ecology and evolutionary biology’. Also, the complexity and computational intensity of modelling 3-D plant architecture may inhibit expansion to the larger spatial scale problems that ecologists deal with. Even though FSPMs have been developed to deal with many of the same issues as population-level ABMs, it does not yet seem possible computationally to extend them to landscapes. In addition, there are basic differences between individual plants and plant communities. Plants have internal integration and signalling between organs, while plant communities, despite some ‘superorganism’ theories in the early history of ecology, are importantly made up of individualistic plants within individualistic species.

Nevertheless, it is possible that the time is right to make use of the complementarity of the approaches to facilitate overall progress in ABM. One sign is that modelling methodologies such as Overview, Design and Details (Grimm et al., 2010) and pattern-oriented modelling (Grimm et al., 2005) are being adopted in some FSPM papers (e.g. Garin et al., 2014).

The need for convergence of the approaches is clear in much of the review literature. A review of models for forecasting effects of climate change (Botkin et al., 2007) pointed out the need for adding mechanistic details of plant physiology, including plasticity of responses to temperature and disturbance, response, and life history trade-offs, or, alternatively for improving the models’ empirical basis (Loehle, 2000; Norby et al., 2001; Botkin et al., 2007). Along these lines, although it is difficult to extend FSPMs to large spatial scales, it may be possible, for example, to use them at the 0.01-ha scale to compare results with current gap models. We are not aware of any current extensions of FSPMs to that scale, but it would be interesting to compare FSPM-based modelling with current spatially explicit community-level ABMs at that scale.

Jeltsch et al. (2008) assessed the overall state of plant population modelling, particularly in comparing the bottom-up mechanistic approach of ABMs with the more top-down approaches such as DGVMs (Longo et al., 2018), climatic envelope models (CEMs) (McKenney et al., 2007) and SDMs (Guisan and Thuiller, 2005). Correlative models such as CEMs and SDMs are easier to parameterize and validate, making them an attractive alternative to detailed mechanistic models and shift interest away from ABMs as a way of forecasting effects of climate change, etc. It should be admitted that these ABM may not be the appropriate method for every issue in plant biology and ecology, particularly at the global level, where more aggregated models are simpler and easier to parameterize. However, ABMs have advantages that will make them relevant to certain types of problems, particularly where plant–plant interactions are important, and these are places where progress can be focused. Jeltsch et al. (2008) discussed three general areas where progress will be key to increasing the relevance of ABMs to important environmental issues. One is that of scaling up from individual plants to large scales. Some progress is being made in this area, as in the modelling of Reynolds (2002) and Mladenoff (2004). Also, despite the advantages of top-down models such as DGVMs mentioned above, those models rely on the assumption that processes at large scales have the same functional forms as those at small scales (Shugart et al., 2018). Those authors argue that, in parallel with models such as the DGVMs, multiple local ABMs be used to simulate changes in forest structure, where they have the advantage, under the constraints that the productivities be consistent with DGVMs, where those models have the advantage of integrating biogeochemical and physiological constraints (see also Morin and Thuiller, 2009).

A second area where progress is needed is in the assembly and availability of data to parameterize and test models, because lack of data has been a bottleneck for modelling large numbers of species. The TRY initiative (Kattge et al., 2011) and LEDA (Kleyer et al., 2008) are examples of this effort. TRY is compiling plant trait data from the different aspects of plant functioning on the global scale. Traits of vegetation in North-West Europe are included in LEDA.

The third area of progress called for by Jeltsch et al. (2008) is generalization across species–plant functional-type population models. Plant functional types (PFTs), as noted earlier, are used in DGVMs to replace species by a smaller number of functional types, which greatly reduces the data needed to parameterize the models and can relate them to basic physiological traits. However, such aggregated models are not suited to capture ecological processes such as competition. Jeltsch et al. suggest extending the features of functional types to ‘functional species’, or virtual species that fill the whole trait space. Recent models, such as that of Maréchaux and Chave (2017), do this and so represent a likely future for further development of ABMs for application to landscape and global problems.

Finally, Jeltsch et al. (2008) emphasize the need for moving towards a more unified science of forecasting using models. The proliferation of ABMs has not been accompanied by needed underlying theory, although some methodological advances, such as unified methods of describing ABMs (Grimm et al., 2010) have gained wide acceptance. Concepts such as ‘pattern-oriented modelling’ (Grimm et al., 2005) may be one way to standardize the development and testing of ABMs. However, it is also important that tools, such as hierarchical Bayesian statistics, which can enable model testing in a rigorous way, need to be extended from simple models to complex ABMs. Greater interdisciplinary collaboration between population- and community-level ABM and FSPM modellers could facilitate than kind of unified science.

Future progress will continue to be made in ABM through greater ability to obtain data at the individual plant level, greater computer capacity for increasing detail at the individual level and increasing spatial scale, and increasing availability of modelling packages for population ABMs (e.g. Falster et al., 2016) and for FSPM (Qu et al., 2012). Several directions include developing a spatially explicit trait-based ABM of microbes (Allison, 2012), considering dispersal and demography in spatial population models for conservation and control management (Jongejans et al., 2008), and applications in land-use change (Verburg, 2006). It should also be noted that there is an increasing interest of integrating analytical and ABM models together because the two approaches offer different, but complementary, advantages and combining the two together can facilitate the understanding of plant ecology (Travis et al., 2011). It is also crucial to integrate biodiversity and the ecosystem in plant ecology. As stated in Grimm et al. (2017), next-generation scientists should include the individual-based approach in their toolkit and focus on addressing real systems by developing theory for individual behaviours just detailed enough to reproduce and explain patterns observed at the system level. If some or all of these trends can be accelerated, the next decade in plant ABM will be very exciting.

Funding

D.L.D. was supported in part by the U.S. Geological Survey’s Greater Everglades Priority Ecosystem Science Program, grant number DD (C) GEPES ATLSS T5.17. B.Z. was supported by the Greater Everglades Priority Ecosystem Science Program and UC Davis Chancellors’ postdoc fellowship. Any use of trade, firm or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.