Abstract
We experimentally identify coherent spin pumping in the magnon-magnon hybrid modes of yttrium iron garnet/permalloy (YIG/Py) bilayers. By reducing the YIG and Py thicknesses, the strong interfacial exchange coupling leads to large avoided crossings between the uniform mode of Py and the spin wave modes of YIG enabling accurate determination of modification of the linewidths due to the dampinglike torque. We identify additional linewidth suppression and enhancement for the in-phase and out-of-phase hybrid modes, respectively, which can be interpreted as concerted dampinglike torque from spin pumping. Furthermore, varying the Py thickness shows that both the fieldlike and dampinglike couplings vary like , verifying the prediction by the coupled Landau-Lifshitz equations.
Coherent phenomena have recently become an emerging topic for information processing with their success in quantum computing [1, 2]. In spintronics, exchange-induced magnetic excitations, called spin waves, or magnons [3, 4], are good candidates for coherent information processing because information can be encoded by both the amplitude and the phase of spin waves. For example, the interference of coherent spin waves can be engineered for spin wave logic operations [5–7]; the coherent interaction of spin-torque oscillators leads to mutual synchronization [8–13], which can be applied in artificial neural networks [14, 15]; and the coherent coupling between magnons and microwave cavities [16–23] opens up new opportunities for magnon-based quantum information science [24, 25].
Recently, strong coupling between two magnonic systems has enabled excitations of forbidden spin wave modes [26–28] and high group velocity of propagating spin waves [29, 30]. The coupling is dominated by the exchange interaction at the interface of the magnetic bilayers, providing a new pathway to coherently transfer magnon excitations between two magnetic systems possessing distinctive properties: from conductor to insulator, from uniform to nonuniform mode and from high-damping to low-damping systems. However, the underlying physical mechanisms of the coupling are still not fully understood. First, what are the key parameters that dictate the coupling efficiency and enable one to reach the strong-coupling regime? Second, with the interfacial exchange coupling acting as a fieldlike torque, is there a dampinglike torque associated with spin pumping [31–34]? To resolve both questions, large separations of the two hybrid modes are required in order to quantitatively analyze the coupling mechanism. The second question is also important for optimizing the coherence of spin wave transfer in hybrid systems. Furthermore, the parasitic effect on the incoherent spin current from the conduction band is absent [35–37] when using magnetic insulators such as yttrium iron garnet (Y3Fe5O12, YIG) [30, 38, 39], which facilitates the study of spin pumping coherency.
In this work, we study YIG/permalloy (Ni80Fe20, Py) bilayers. By using much thinner YIG and Py films than studied in previous works [26, 28], we achieve an exchange-induced separation of the two hybrid modes much larger than their linewidths, allowing us to study the evolution of their linewidths in the strong coupling regime. We find a pronounced suppression of the total linewidth for the in-phase hybrid modes and a linewidth enhancement for the out-of-phase hybrid modes. The linewidths can be understood from the Landau-Lifshitz-Gilbert (LLG) equation with interfacial exchange coupling and mutual spin pumping, which provide the fieldlike and dampinglike interlayer coupling torques, respectively. Furthermore, the thickness dependence of the two coupling strengths agrees with the modeling of coupled LLG equations with mutual spin pumping. The sign of the fieldlike torque also reconfirms that the YIG and Py are coupled antiferromagnetically [26]. Our results provide important insights for improving the coupling strength and coherence in magnon-magnon hybrid systems and pave the way for coherent information processing with exchange coupled magnetic heterostructures.
The samples consist of YIG(100 nm)/Py(tPy) bilayers where tPy varies from 5 nm to 60 nm. YIG(100 nm) films were deposited by magnetron sputtering from a YIG target onto Gd3Ga5O12(111) substrates and annealed in air at 850°C for 3 hrs to reach low-damping characteristics [40]. Before the deposition of Py films on top of YIG, the YIG surfaces were ion milled in-situ for one minute in order to enable good exchange coupling between Py and YIG [41]. For each Py thickness, one additional reference Py film was deposited on a Si/SiO2 substrate during the same deposition.
The hybrid magnon dynamics were characterized by broad-band ferromagnetic resonance with field modulation on a coplanar waveguide (Fig. 1a). An in-plane magnetic field HB saturates both the YIG and Py magnetizations. Their Kittel modes, which describe spatially uniform magnetization precession, are formulated as , where ω is the mode frequency, γ/2π = (geff/2) × 27.99 GHz/T is the gyromagnetic ratio, Hr is the resonance field and Ms is the magnetization [42]. For YIG, the spatially nonuniform perpendicular standing spin wave (PSSW) modes can be also measured. An effective exchange field Hex will lower the resonance field by µ0Hex(k) = (2Aex/Ms)k2, where Aex is the exchange stiffness, k = nπ/t, n labels the index of PSSW modes, and t is the film thickness [43].
FIG. 1.
(a) Illustration of the magnetization excitations in the YIG/Py bilayers with a coplanar waveguide. (b) Lineshapes of the YIG(100 nm)/Py(9 nm) sample for the first three resonance modes of YIG and the uniform mode of Py. The field axis is shifted so that the resonance field of the YIG(n=0) mode is zero. (c) Unshifted evolution of the four modes in (b). Curves show the fits as uncoupled modes. The vertical dashed line denotes where the YIG(n = 2) and Py(n = 0) modes cross on the frequency axis at ωc/2π = 9.4 GHz.
Fig. 1(b) shows the line shapes of the resonance fields for the first three resonance modes of YIG (n = 0, 1, 2) and the Py uniform mode (n = 0) measured for tPy = 9 nm. For illustration, the YIG (n = 0) resonance is shifted to zero field. An avoided crossing is clearly observed when the Py uniform mode is degenerate with the YIG (n = 2) mode. This is due to the exchange coupling at the YIG/Py interface [26–28] providing a fieldlike coupling torque. Both in-phase and out-of-phase YIG/Py hybrid modes are strongly excited because the energy of the Py uniform mode is coherently transferred to the YIG PSSW modes through the interface [26]. The full-range frequency dependencies of the extracted resonance fields are plotted in Fig. 1(c). To analyze the two hybrid modes, we analyze our results with two independent Lorentzians because it facilitates a transparent physical picture and the fit lineshapes agree well with our measurements. The mode crossing happens at ωc/2π = 9.4 GHz (black dashed line), which corresponds to the minimal resonance separation of the two hybrid modes. Fitting to the Kittel equation, we extract , . From the exchange field offset as shown in Fig. 1(b), an exchange stiffness Aex = 2.6 pJ/m is calculated for YIG, which is similar to previous reports [44].
The avoided crossing can be fitted to a phenomenological model of two coupled harmonic oscillators, as previously shown in magnon polaritons [16–18, 20]:
| (1) |
where is the resonance field of YIG (Py), and gc is the interfacial exchange coupling strength. and are both functions of frequency and are equal at ωc. Note that for in-plane biasing field the resonance field is nonlinear to the excitation frequency. This nonlinearity will be accounted for the analytical reproduction of Eq. 1. The fitting yields gc = 8.4 mT for tPy = 9 nm.
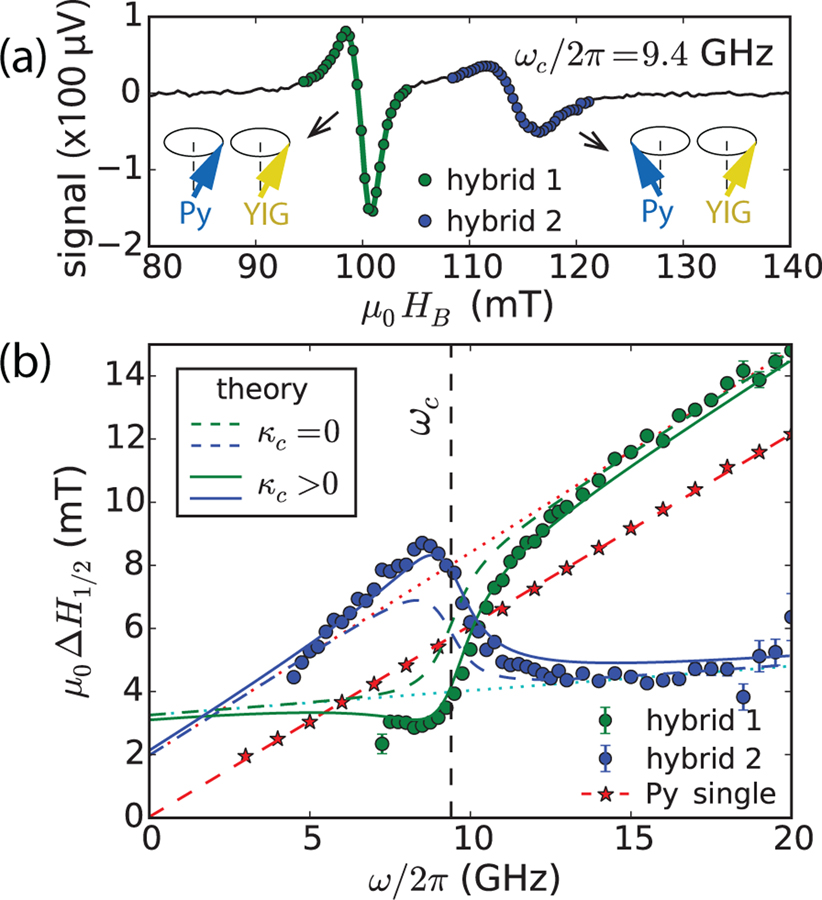
Next, we focus on the linewidths of the YIG-Py hybrid modes. Fig. 2(a) shows the line shape of the two hybrid modes for tPy = 7.5 nm at ωc/2π = 9.4 GHz (same value as for 9-nm Py). These two eigenmodes correspond to the in-phase and out-of-phase magnetization precession of Py and YIG with the same weight, so they should yield the same total intrinsic damping. Nevertheless, a significant linewidth difference is observed, with the extracted full-width-half-maximum linewidth µ0∆H1/2 varying from 3.5 mT for the lower field resonance to 8.0 mT for the higher field resonance. Fig. 2(b) shows the full-range evolution of linewidth. Compared with the dotted lines which are the linear extrapolations of the YIG (n = 2) and Py linewidths, the linewidth of the higher-field hybrid mode (blue circles) exceeds the Py linewidth and the linewidth of the lower-field hybrid mode (green circles) reduces below the YIG linewidth when the frequency is near ωc. This is the central result of the paper. It suggests a coherent dampinglike torque which acts along or against the intrinsic damping torque depending on the phase difference of the coupled dynamics of YIG and Py, same as the fieldlike torque acting along or against the Larmor precession. The dominant mechanism for the dampinglike torque is the spin pumping from the concerted dynamics of YIG and Py [31, 32]
FIG. 2.
(a) The lineshape of the YIG(100 nm)/Py(7.5 nm) sample at ωc/2π = 9.4 GHz, showing different linewidths between the two hybrid modes of YIG(n = 2) and Py(n = 0) resonances. (b) Linewidths of the two hybrid modes as a function of frequency. Dotted lines show the linear fit of the linewidths for the two uncoupled modes. Dashed curves show the theoretical values with κc = 0. Solid curves show the fits with finite κc.
Because spin pumping is dissipative, we determine the mode with a broader (narrower) linewidth as the out-of-phase (in-phase) precession mode. In Fig. 2(a) the broader-linewidth mode exhibit a higher resonance field than the narrower-linewidth mode. This is a signature of antiferromagnetic exchange coupling at the YIG/Py interface [26]. From the resonance analysis we also find that all the SiO2/Py samples show lower resonance fields than the Py samples grown on YIG [45], which agrees with the antiferromagnetic nature of the YIG/Py interfacial coupling.
To reproduce the data in Fig. 2(b), we introduce the linewidths as the imaginary parts of the resonance fields in Eq. (1):
| (2) |
where κYIG(Py) is the uncoupled linewidth of YIG (Py) from the linear extraction (dotted lines) in Fig. 2(b), and is the complex interfacial coupling strength with an additional dampinglike component κc from spin pumping.
In order to show the relationship between the spin pumping from the coherent YIG-Py dynamics and the incoherent spin pumping from the individual Py dynamics, we identify the latter as the linewidth enhancement of Py(7.5 nm), , between the linearly extrapolated YIG/Py [red dots in Fig. 2(b)] and Si/SiO2/Py [red stars in Fig. 2(b)]. Then, we quantify the coherent dampinglike coupling strength κc as , where β is a unitless and frequency-independent value measuring the ratio between the coherent and incoherent spin pumping. For the best fit value, β = 0.82, Eq. (2) nicely reproduces the data in Fig. 2(b). For comparison, if we set κc(ω) = 0 in Eq. (2), we obtain the blue and green dashed curves, which result in identical linewidth at ωc as opposed to the data in Fig. 2(a).
In order to understand the physical meaning of , we consider the coupled Landau-Lifshitz-Gilbert (LLG) equations of YIG/Py bilayer [26, 32, 34] in the macrospin limit:
| (3) |
where mi,j is the unit magnetization vector, Heff is the effective field including HB, Hex and the demagnetizing field, αi is the intrinsic Gilbert damping. The index is defined as (i, j) = (1, 2) or (2, 1). In the last two coupling terms, J is the interfacial exchange energy and Δαi = γiħg↑↓/(4πMiti) is the spin pumping damping enhancement with g↑↓ the spin mixing conductance. The two terms provide the fieldlike and dampinglike coupling torques, respectively, between mi and mj. To view the dampinglike coupling on a similar footage, we define its coupling energy J′ as:
| (4) |
Here J′ describes the number of quantum channels per unit area (g↑↓) for magnons (ħω) to pass through [31, 34]; similarly, J describes the number and strength of exchange bonds between YIG and Py per unit area. From the definition, we can express the spin pumping linewidth enhancement as , in pair with the exchange field term in Eq. (3). By solving Eq. (3) we find:
| (5a) |
| (5b) |
| (5c) |
with the dimensionless factor f (ω) accounting for the precession elliptical asymmetry. f (ω) = 1 for identical ellipticity (M1 = M2) and f (ωc) = 0.9 in the case of YIG and Py; See the Supplmental Information for details [45].
Eq. (5) shows that both gc and κc(ωc) are proportional to , which comes from the geometric averaging of the coupled magnetization dynamics. This is in contrast to the 1/ti dependence of the uncoupled exchange field and spin pumping damping enhancement for a single layer, as shown in Eq. (5a). In Fig. 3(a), a good fitting of gc to rather than 1/tPy validates the model. In the limit of zero Py thickness, the model breaks down due to the significance of boundary pinning and the assumption of macrospin dynamics, as reflected in the reduction of gc at tPy = 5 nm.
FIG. 3.
(a) Extracted gc as a function of tPy. (b) Extracted β2 as a function of tPy. In both figures, the solid and dashed curves are the fits of data to the coherent and incoherent models, respectively. In (b), the red and cyan dotted arrows show the theoretical predictions for the coherent models based on the macrospin and spin wave approximations, respectively. Error bars indicate single standard deviations found from the fits to the lineshape.
For the dampinglike coupling, we plot β instead as a function of tPy in order to minimize the variation in the quality of interfacial coupling and the frequency dependence of κc(ωc). By taking the ratio between κc(ωc) and from the analytical model, we obtain the macrospin expression with f (ωc) = 0.9. Fig. 3(b) shows that the extracted β2 varies linearly with tPy, rather than being independent of it as would be expected for incoherent spin pumping. The fit is not perfect, which may be caused by i) the variation of inhomogeneous broadening of Py in YIG/Py bilayers, or ii) the multi-peak lineshapes in YIG (see YIG n = 0 lineshapes in Fig. 1b) due to possible damage during the ion milling process.
If we calculate β from the macrospin approximation, the prediction, shown in the red dashed arrow in Fig. 3(b), differs significantly from the experimental data. To account for the difference, we consider a spin wave model for the YIG/Py bilayer, where finite wavenumbers exist in both layers and are determined from the boundary condition [46]. For simplicity, we consider free pinning at the two exterior surfaces of YIG and Py and Hoffmann exchange boundary conditions for the interior interface of YIG/Py [47]. From the spin wave model, we find an additional factor of in Eqs. (5b) and (5c); see the Supplemental Information for details [45]. This factor arises because the nonuniform profile of the PSSW mode in YIG reduces the effective mode volume by a factor of two compared with the uniform mode. A similar effect has been previously discussed in spin pumping from PSSW modes [48, 49]. In Fig. 3(b) the theoretical calculation from the spin wave model (cyan dashed arrow) is close to the experimental values. This is an additional evidence of the coherent spin pumping in YIG/Py bilayers.
Fig. 4 compares the values of J and J′ obtained from the hybrid dynamics. For convenience we estimate the value of J′ from Eq. (5c), as . Noting the frequency dependence of J′(ω), all the values of J′(ω) in this work are obtained around ωc/2π = 9 GHz. We can also calculate J′(ωc) from uncoupled spin pumping effect, as . For the YIG/Py interface, the value of J stays at the same level; the value of J′(ωc) fluctuates with samples but is well aligned with , which again supports that the dampinglike interfacial coupling comes from spin pumping. Furthermore, we have also repeated the experiments for a thinner YIG(50 nm)/Py(t) sample series and obtained similar values of J and J′(ωc), as shown in Fig. 4.
FIG. 4.
Thickness dependence of J (circles) and J′ (triangles), which are calculated from gc and κc(ωc), respectively. Blue points denote the results for YIG(100 nm)/Py(tPy) and red points for YIG(50 nm)/Py(tPy). The blue stars denote , in which is calculated from the Py linewidth enhancement from Py(tPy) to YIG(100 nm)/Py(tPy). Error bars indicate single standard deviations found from the fits to the lineshape.
Table I summarizes the values of J, J′ and g↑↓ for YIG/Py interface, where J′ is taken from the vicinity of ωc/2π = 9 GHz and g↑↓ is calculated from J′(ωc) by Eq. (4). The value of J is much smaller than a perfect exchange coupled interface, which is not surprising given the complicated and uncharacterized nature of the YIG/Py interface. For Py, the interfacial exchange energy can be estimated [46] by 2Aex/a, where for Py Aex = 12 pJ/m [49] and the lattice parameter a = 0.36 nm. We find 2Aex/a = 68 mJ/m2, three orders of magnitude larger than J. Comparing with similar interfaces, our reported J is similar to YIG/Ni (0.03 mJ/m2 [27]) and smaller than YIG/Co (0.4 mJ/m2 [26]). A different interlayer exchange coupling from Ruderman-Kittel-Kasuya-Yosida interaction may generate a larger J [50–52] but a smaller g↑↓ [53]. There could also be a fieldlike contribution of J from g↑↓ [26, 54–57]. But since the exchange J dominates in the coupled dynamics, it is difficult to distinguish the spin mixing conductance contribution in our experiments.
TABLE I.
Fieldlike, dampinglike coupling energy and spin mixing conductance for the YIG/Py interface. The value of J′ is calculated around ωc/2π = 9 GHz
| J(mJ/m2) | J′(mJ/m2) | g↑↓ (nm−2) | |
|---|---|---|---|
| YIG/Py | 0.060 ± 0.011 | 0.019 ± 0.009 | 42 ± 21 |
In conclusion, we have characterized the dampinglike coupling torque between two exchange-coupled ferromagnetic thin films. By exciting the hybrid dynamics in the strong coupling regime, this dampinglike torque can either increase or suppress the total damping in the out-of-phase or in-phase mode, respectively. The origin of the dampinglike torque is the coherent spin pumping from the coupling magnetization dynamics. Our results reveal new insight for tuning the coherence in magnon-magnon hybrid dynamics and are important for magnon-based coherent information processing.
Supplementary Material
Acknowledgments
Work at Argonne on sample preparation was supported by the U.S. DOE, Office of Science, Office of Basic Energy Sciences, Materials Science and Engineering Division under Contract No. DE-AC02-06CH11357, while work at Argonne and National Institute of Standards and Technology (NIST) on data analysis and theoretical modeling was supported as part of Quantum Materials for Energy Efficient Neuromorphic Computing, an Energy Frontier Research Center funded by the U.S. DOE, Office of Science. Work on experimental design at Oakland University was supported by AFOSR under grant no. FA9550-19-1-0254 and the NIST Center for Nanoscale Science and Technology, Award No. 70NANB14H209, through the University of Maryland. Work on microwave spectroscopy at Columbia University was supported by NSF under grant NSF-DMR1411160.
References
- [1].Devoret MH and Schoelkopf RJ, Science 339, 1169 (2013). [DOI] [PubMed] [Google Scholar]
- [2].Awschalom DD, Bassett LC, Dzurak AS, Hu EL, and Petta JR, Science 339, 1174 (2013). [DOI] [PubMed] [Google Scholar]
- [3].Dyson FJ, Phys. Rev 102, 1217 (1956). [Google Scholar]
- [4].Chumak AV, Vasyuchka VI, Serga AA, and Hillebrands B, Nature Physics 11, 453 (2015). [Google Scholar]
- [5].Khitun A, Bao M, and Wang KL, IEEE Trans. Magn 44, 2141 (2008). [Google Scholar]
- [6].Schneider T, Serga AA, Leven B, Hillebrands B, Stamps RL, and Kostylev MP, Appl. Phys. Lett 92, 022505 (2008). [Google Scholar]
- [7].Kruglyak VV, Demokritov SO, and Grundler D, J Phys. D: Appl. Phys 43, 264001 (2010). [Google Scholar]
- [8].Kaka S, Pufall MR, Rippard WH, Silva TJ, Russek SE, and Katine JA, Nature 437, 389 (2005). [DOI] [PubMed] [Google Scholar]
- [9].Mancoff FB, Rizzo ND, Engel BN, and Tehrani S, Nature 437, 393 (2005). [DOI] [PubMed] [Google Scholar]
- [10].Locatelli N, Hamadeh A, Abreu Araujo F, Belanovsky AD, Skirdkov PN, Lebrun R, Naletov VV, Zvezdin KA, Muñoz M, Grollier J, Klein O, Cros V, and de Loubens G, Sci. Rep 5, 17039 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Li Y, de Milly X, Abreu Araujo F, Klein O, Cros V, Grollier J, and de Loubens G, Phys. Rev. Lett 118, 247202 (2017). [DOI] [PubMed] [Google Scholar]
- [12].Lebrun R, Tsunegi S, Bortolotti P, Kubota H, Jenkins AS, Romera M, Yakushiji K, Fukushima A, Grollier J, Yuasa S, and Cros V, Nat. Commun 8, 15825 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Awad A, D urrenfeld P, Houshang A, Dvornik M, Iacocca E, Dumas RK, and Åkerman J, Nature Phys 13, 292 (2017). [Google Scholar]
- [14].Vodenicarevic D, Locatelli N, Abreu Araujo F, Grollier J, and Querlioz D, Sci. Rep 7, 44772 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Romera M, Talatchian P, Tsunegi S, Abreu Araujo F, Cros V, Bortolotti P, Trastoy J, Yakushiji K, Fukushima A, Kubota H, Yuasa S, Ernoult M, Vodenicarevic D, Hirtzlin T, Locatelli N, Querlioz D, and Grollier J, Nature 563, 230 (2018). [DOI] [PubMed] [Google Scholar]
- [16].Huebl H, Zollitsch CW, Lotze J, Hocke F, Greifenstein M, Marx A, Gross R, and Goennenwein STB, Phys. Rev. Lett 111, 127003 (2013). [DOI] [PubMed] [Google Scholar]
- [17].Tabuchi Y, Ishino S, Ishikawa T, Yamazaki R, Usami K, and Nakamura Y, Phys. Rev. Lett 113, 083603 (2014). [DOI] [PubMed] [Google Scholar]
- [18].Zhang X, Zou C-L, Jiang L, and Tang HX, Phys. Rev. Lett 113, 156401 (2014). [DOI] [PubMed] [Google Scholar]
- [19].Goryachev M, Farr WG, Creedon DL, Fan Y, Kostylev M, and Tobar ME, Phys. Rev. Applied 2, 054002 (2014). [Google Scholar]
- [20].Bai L, Harder M, Chen YP, Fan X, Xiao JQ, and Hu C-M, Phys. Rev. Lett 114, 227201 (2015). [DOI] [PubMed] [Google Scholar]
- [21].Li Y, Polakovic T, Wang Y-L, Xu J, Lendinez S, Zhang Z, Ding J, Khaire T, Saglam H, Divan R, Pearson J, Kwok W-K, Xiao Z, Novosad V, Hoffmann A, and Zhang W, Phys. Rev. Lett 123, 107701 (2019). [DOI] [PubMed] [Google Scholar]
- [22].Hou JT and Liu L, Phys. Rev. Lett 123, 107702 (2019). [DOI] [PubMed] [Google Scholar]
- [23].McKenzie-Sell L, Xie J, Lee C-M, Robinson JWA, Ciccarelli C, and Haigh JA, Phys. Rev. B 99, 140414 (2019). [Google Scholar]
- [24].Tabuchi Y, Ishino S, Noguchi A, Ishikawa T, Yamazaki R, Usami K, and Nakamura Y, Science 349, 405 (2015). [DOI] [PubMed] [Google Scholar]
- [25].Lachance-Quirion D, Tabuchi Y, Ishino S, Noguchi A, Ishikawa T, Yamazaki R, and Nakamura Y, Science Advances 3 (2017), 10.1126/sciadv.1603150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Klingler S, Amin V, Geprags S, Ganzhorn K, Maier-Flaig H, Althammer M, Huebl H, Gross R, McMichael RD, Stiles MD, Goennenwein STB, and Weiler M, Phys. Rev. Lett 120, 127201 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Chen J, Liu C, Liu T, Xiao Y, Xia K, Bauer GEW, Wu M, and Yu H, Phys. Rev. Lett 120, 217202 (2018). [DOI] [PubMed] [Google Scholar]
- [28].Qin H, Hamalainen SJ, and van Dijken S, Sci. Rep 8, 5755 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Liu C, Chen J, Liu T, Heimbach F, Yu H, Xiao Y, Hu J, Liu M, Chang H, Stueckler T, Tu S, Zhang Y, Zhang Y, Gao P, Liao Z, Yu D, Xia K, Lei N, Zhao W, and Wu M, Nature Commun 9, 738 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].An K, Bhat V, Mruczkiewicz M, Dubs C, and Grundler D, Phys. Rev. Applied 11, 034065 (2019). [Google Scholar]
- [31].Tserkovnyak Y, Brataas A, and Bauer GEW, Phys. Rev. Lett 88, 117601 (2002). [DOI] [PubMed] [Google Scholar]
- [32].Heinrich B, Tserkovnyak Y, Woltersdorf G, Brataas A, Urban R, and Bauer GEW, Phys. Rev. Lett 90, 187601 (2003). [DOI] [PubMed] [Google Scholar]
- [33].Lenz K, Toliński T, Lindner J, Kosubek E, and Baberschke K, Phys. Rev. B 69, 144422 (2004). [Google Scholar]
- [34].Tserkovnyak Y, Brataas A, Bauer GEW, and Halperin BI, Rev. Mod. Phys 77, 1375 (2005). [Google Scholar]
- [35].Zhang SS-L and Zhang S, Phys. Rev. B 86, 214424 (2012). [Google Scholar]
- [36].Amin VP, Zemen J, and Stiles MD, Phys. Rev. Lett 121, 136805 (2018). [DOI] [PubMed] [Google Scholar]
- [37].Chen YS, Lin JG, Huang SY, and Chien CL, Phys. Rev. B 99, 220402 (2019). [Google Scholar]
- [38].Miao BF, Huang SY, Qu D, and Chien CL, Phys. Rev. Lett 111, 066602 (2013). [DOI] [PubMed] [Google Scholar]
- [39].Hyde P, Bai L, Kumar DMJ, Southern BW, Hu C-M, Huang SY, Miao BF, and Chien CL, Phys. Rev. B 89, 180404 (2014). [Google Scholar]
- [40].Li S, Zhang W, Ding J, Pearson JE, Novosad V, and Hoffmann A, Nanoscale 8, 388 (2016). [DOI] [PubMed] [Google Scholar]
- [41].Jungfleisch MB, Lauer V, Neb R, Chumak AV, and Hillebrands B, Appl. Phys. Lett 103, 022411 (2013). [Google Scholar]
- [42].Kittel C, Phys. Rev 73, 155 (1948). [Google Scholar]
- [43].Herring C and Kittel C, Phys. Rev 81, 869 (1951). [Google Scholar]
- [44].Klingler S, Chumak AV, Mewes T, Khodadadi B, Mewes C, Dubs C, Surzhenko O, Hillebrands B, and Conca A, J. Phys. D: Appl. Phys 48, 015001 (2014). [Google Scholar]
- [45].See the Supplemental Information for details.
- [46].Hillebrands B, Phys. Rev. B 41, 530 (1990). [DOI] [PubMed] [Google Scholar]
- [47].Hoffmann F, Stankoff A, and Pascard H, J. Appl. Phys 41, 1022 (1970). [Google Scholar]
- [48].Kapelrud A and Brataas A, Phys. Rev. Lett 111, 097602 (2013). [DOI] [PubMed] [Google Scholar]
- [49].Li Y and Bailey WE, Phys. Rev. Lett 116, 117602 (2016). [DOI] [PubMed] [Google Scholar]
- [50].Parkin SSP, More N, and Roche KP, Phys. Rev. Lett 64, 2304 (1990). [DOI] [PubMed] [Google Scholar]
- [51].Belmeguenai M, Martin T, Woltersdorf G, Maier M, and Bayreuther G, Phys. Rev. B 76, 104414 (2007). [Google Scholar]
- [52].Fallarino L, Sluka V, Kardasz B, Pinarbasi M, Berger A, and Kent AD, Appl. Phys. Lett 109, 082401 (2016). [Google Scholar]
- [53].Yang H, Li Y, and Bailey WE, Appl. Phys. Lett 108, 242404 (2016). [Google Scholar]
- [54].Zhang W, Jungfleisch MB, Freimuth F, Jiang W, Sklenar J, Pearson JE, Ketterson JB, Mokrousov Y, and Hoffmann A, Phys. Rev. B 92, 144405 (2015). [Google Scholar]
- [55].Sklenar J, Zhang W, Jungfleisch MB, Jiang W, Chang H, Pearson JE, Wu M, Ketterson JB, and Hoffmann A, Phys. Rev. B 92, 174406 (2015). [DOI] [PubMed] [Google Scholar]
- [56].Nan T, Emori S, Boone CT, Wang X, Oxholm TM, Jones JG, Howe BM, Brown GJ, and Sun NX, Phys. Rev. B 91, 214416 (2015). [Google Scholar]
- [57].Zhu L, Ralph DC, and Buhrman RA, Phys. Rev. Lett 123, 057203 (2019). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.