Fabrication and characterization of femtosecond laser induced microwave frequency photonic fiber grating

Abstract

We proposed and fabricated a microwave-frequency photonic fiber grating (MPFG) by femtosecond laser micromachining on optical fibers. Illuminated by low coherent light source, the MPFG can be interrogated using proposed microwave photonic system to show the resonant peaks in microwave frequency domain. We studied the working principle and characteristics of this device. After that, we discussed the influence of fiber type, apodization and light source coherence lengths on this device. The device can also respond to ambient temperature change like fiber optic sensors.

I. INTRODUCTION

During recent years, microwave photonics technologies have been applied to help interrogating complex sensing systems as the technology combines the advantage of both microwave and optics[1–4]. It is specifically successful when trying to interrogate interferometric fiber sensors on special fibers such as silica rod[5] and sapphire fibers[6], because they are highly multimode fibers. Traditional fiber Fabry-Perot interferometer and FBGs cannot work on them, while microwave photonic method interferes in microwave domain, which is virtually not affected by optical multimode operation. With the help of Fourier transform of both the amplitude and phase information in the microwave frequency response, this technique can also be used to interrogate a series of interferometers consists of weak reflectors on an optical fiber[7]. In these kinds of interrogation systems, the interferogram or resonant peaks frequency are all in the microwave frequency range.

Inspired by the very successful fiber Bragg gratings (FBGs), it has been demonstrated that Bragg gratings can be made in microwave frequency domain by making longer periodic structure on microwave waveguides such as coaxial cables[8]. However, it does not have much applications because coaxial cables have significantly higher loss comparing to optical fibers, making the working distance of coaxial cable Bragg gratings (CCBG) relatively short, usually a few hundred meters.

With the help of microwave photonics technologies, it would be interesting to develop a microwave frequency domain Bragg grating on optical fiber. Because the signal is transmitted on optical fibers, it can reach very long distance, and preserve the various advantage of fiber base devices and sensors, such as immunity to EM interference, resistance to harsh environments, resistance to corrosion, etc[9–11]. At the same time, it can be interrogated in microwave frequency, which will have the potential advantage of fabrication flexibility and multimode operations.

In this paper, we propose, study and realize such a device fabricated by femtosecond laser micromachining[12], which provides great fabrication flexibility for the intensity and period of the grating. The working principle and microwave domain characteristic of this microwave-frequency photonic fiber grating (MPFG) device is studied, and possible application in sensing is demonstrated. We also discussed the influence of the light source, as well as the possibility of apodization because of the flexibility of the FS laser fabrication process. Such a device could have other application such as a microwave photonic filter with desired frequency response.

The rest of the paper is organized as follows. In section two, the fabrication and interrogation method of the MPFG is demonstrated. In section three, we study the grating behavior theoretically to show how the spectrum is formed. In section four, we show the result of a 21 periods grating and the evolution of the spectrum during the fabrication process. We then use this device as a temperature sensor to show its response to ambient temperature change. The influence of light source and the possibility of apodization are also discussed. In section five, the characteristics of the device and the experiment results are summarized.

II. GRATING FABRICATION AND INTERROGATION SETUP

In this section, we first demonstrate the fabrication method of the proposed MPFG. After that, the interrogation system of the device is introduced. The time domain and frequency domain signal of such a device with 13 grating periods is shown to verify the fabrication process and the interrogation system.

A. Femtosecond laser fabrication of reflectors and grating structure in fiber

Fiber based gratings usually mean periodic refractive index change on the fiber. In this paper, it is made of multiple weak reflectors evenly distributed along the fiber. These reflectors are fabricated by femtosecond laser micromachining. A section of single mode optical fiber is mounted on a computer-controlled three-axis translation stage (PM500 series, Newport, Inc.) with a resolution of 0.1 μm. The laser beam is focused inside the fiber using an oil immersion lens (100X) with a NA of 1.3. The diameter of the focused beam is about 0.5μm. A dichroic mirror and a charge-coupled device (CCD) camera connected to the computer are involved to in-situ monitor the fabrication process. The actual laser energy used for processing silica is approximately 0.4 ~ 0.5 μJ per pulse.

During fabrication, the femtosecond laser focal point is scanned in a raster scanning pattern to cover the fiber core area at a specific position along the fiber. Starting from the bottom of the fiber core, the focused laser beam scans horizontally in a line, and after each line is finished, it moves up by a small step (usually about0.5 μm to 1 μm) and then scans the next line. The intensity of the reflector under fabrication can be tuned by adjusting the scanning or exposure parameters, such as number of line scans, distance between two lines, repeating scanning times, scanning speed, laser power, etc.

The schematic of the femtosecond laser irradiation process for the reflector fabrication is shown in Figure 1.

Figure 1.

Fabrication with FS. (a)Schematic of the fabrication process. The FS laser beam is focused into the fiber core by an oil immersion objective lens. (b) Enlarged view of the laser beam scanning pattern at the fiber core. (c) The picture of a fiber after one scan of the FS laser beam and the reflector is formed, fiber axis is perpendicular to the raster pattern.

The grating structure proposed in this paper consists of a series of the femtosecond laser induced reflectors evenly distributed along a fiber. It is well known that the grating period of a FBG is a few hundred nanometers; the grating period of a long period fiber grating is a few hundred micrometers. Here, if the period of the grating, or the separation between two adjacent reflectors, is in millimeter to centimeter range, the resulted resonant frequency will be in microwave frequency.

B. Interrogation of the MWP grating

The system to interrogate a microwave frequency photonic grating is shown in Figure 2. A laser beam from a proper low-coherence laser source is first modulated by an electro-optic modulator (EOM) in microwave frequency. The EOM is connected to the port one of a vector network analyzer (VNA, Keysight E8363B) via an RF amplifier, and a DC bias is also connected. The light then goes through the circulator and interact with the MPFG. The reflected light from the grating again go through the circulator and reach the high speed photodetector (PD). The output of the photodetector is connected to the port two of the VNA. The RF domain frequency response of the device is recorded as the S21 on the VNA.

Figure 2.

Interrogation setup.

The VNA can record the amplitude and phase response of the device, and a time domain reflectometry response can be obtained as a built-in function of the VNA, which is basically a Fourier transform. Typical time domain and frequency domain will be shown later in Figure 4 and Figure 5 in part IV. We will discuss the theory behind this phenomenon in section III, and in section IV we will further study the measured spectrum of this kind of device through experiments.

Figure 4.

Time domain signal of the 21-periods MPFG.

Figure 5.

Frequency domain signal of the 21-period MPFG.

III. THEORETICAL ANALYSIS OF THE GRATING BEHAVIOR IN MICROWAVE DOMAIN

Assume an optical wave of one polarization is

$$E_0=A_0\exp [-j(\omega t+\phi )]$$

where t is the time; E₀ is electric field; A₀ is the amplitude and φis the phase of the corresponding electric field; ω is the angular optical frequency.

The modulating microwave signal is

$$s(t)=M\cos (\mathrm{\Omega }t+\varphi )$$

where M is the amplitude, Ω is the angular frequency, and ϕ is the phase.

The electric field after modulation is

$$E=m(t)E_0$$

Where m(t) is the amplitude modulation term, which is

$$m(t)=\sqrt{1+h\cdot s(t)}=\sqrt{1+h\cdot M\cos (\mathrm{\Omega }t+\varphi )}$$

Where h is the modulation index.

Assume that this modulated lightwave is diffracted by a general diffraction grating which has N total slots, and the optical wave going through the ith slot at time t and position (path length) z is Ei(t,z). And the recombined optical beams at the receiving point is

$$E_{total}=\sum _{i=1}^N{E}_i$$

The electric field of the ith beam wave that propagate through an optical path length of zi in a media which has an effective refractive index of neff is now represented by

$$E_i\left(t,z_i\right)=m\left(t,z_i\right)E_{0i}\left(t,z_i\right)$$ (1)

Where

$$E_{0i}(t,z)=A_0\exp \{-j\left[\omega \left(t+\frac{z_i{n}_{eff}}{c}\right)+\phi \right]\}$$

And the microwave amplitude is

$$m\left(t,z_i\right)=\sqrt{1+h\cdot M\cos [\mathrm{\Omega }\left(t+\frac{w}{c}+\frac{z_i{n}_{eff}}{c}\right)]}$$

Assume that the optical source has a spectrum width from ω_min to ω_max. The total optical power at the receiving point is then

$$\begin{gathered} I_{total}=\left(\frac{{\epsilon }_{0}c}{2}\right)\frac{1}{{\omega }_{max}-{\omega }_{min}}{\int }_{{\omega }_{min}}^{{\omega }_{max}}\left(E_{total}{E}_{total}^{*}\right)d\omega \\ =\left(\frac{{\epsilon }_{0}c}{2}\right)\frac{1}{{\omega }_{max}-{\omega }_{min}}{\int }_{{\omega }_{min}}^{{\omega }_{max}}\left({\sum }_{i=1}^N{\sum }_{j=1}^N{E}_i{E}_j^{*}\right)d\omega \end{gathered}$$ (2)

Expand the right hand side of the equation, we can obtain N² terms. We denote the terms as ‘self-product terms’ when i=j, and the terms as ‘cross-product terms’ when i≠j. And we can write the total power as

$$I_{total}=I_{cross-produ}+I_{self-product}$$

We first examine the cross product terms (i≠j). Substitute Eq. (1) to Eq. (2), for each term on right side of Eq. (2), we have

$$\begin{gathered} \left(\frac{{\epsilon }_{0}c}{2}\right)\frac{1}{{\omega }_{max}-{\omega }_{min}}{\int }_{{\omega }_{min}}^{{\omega }_{max}}\left(E_i{E}_j^{*}\right)d\omega =\left(\frac{{\epsilon }_{0}c}{2}\right)\frac{1}{{\omega }_{max}-{\omega }_{min}}. \\ m\left(t,z_i\right)\cdot m\left(t,z_j\right)\cdot {\int }_{{\omega }_{min}}^{{\omega }_{max}}\exp \left\{-j\left[\frac{\omega }{c}\left(z_i-z_j\right)\cdot n_{eff}\right]\right\}d\omega \end{gathered}$$ (3)

As mentioned before, in this system we use a low coherent broadband light source, so that the optical path difference (OPD) is sufficiently larger than the coherence length of the optical source, i.e., $\left(z_i-z_j\right)n_{eff}\gg \frac{2\pi c}{{\omega }_{max}-{\omega }_{min}}$, As a result, the integral term in Eq. (3) approaches zero, thus the cross-production terms will vanish. This means that I_{cross–produ} = 0, thus I_total = I_{self–produc}.

Then we examine the self-product terms. When i=j, E_i=E_j, so,

$$\begin{gathered} I_{self-product}=I_{total}= \\ \left(\frac{{\epsilon }_{0}c}{2}\right)\frac{1}{{\omega }_{max}-{\omega }_{min}}{\int }_{{\omega }_{{}_{min}}}^{{\omega }_{max}}\left(\sum _{i=1}^N{E}_i{E}_i^{*}\right)d\omega \end{gathered}$$ (4)

For a grating structure, the optical path length z_i are evenly separated from each other, which means that we can write z_i as

$$z_i=z_0+i\cdot \mathrm{\Delta }z$$ (5)

Where z₀ is a fixed common optical length plus fixed electrical length of the transmission line in the system, and Δz is the optical path difference between 2 adjacent grating slots induced beam length, which is closely related to the grating period.

From Eq. (1), we have

$$\begin{gathered} E_i{E}_i^{*}={\left[m\left(t,z_i\right)\right]}^2\cdot {\left|E_{0i}(t,z)\right|}^2= \\ {A}_0^2\cdot \left\{1+h\cdot M\cos \left[\mathrm{\Omega }\left(t+\frac{z_i{n}_{eff}}{c}\right)\right]\right\} \end{gathered}$$ (6)

Substitute the Eq. (5) and Eq. (6) to Eq. (4), we obtain

$$\begin{gathered} I_{total}=\left(\frac{{\epsilon }_{0}c}{2}\right)\frac{1}{{\omega }_{max}-{\omega }_{min}}{\int }_{{\omega }_{min}}^{{\omega }_{max}}({\sum }_{i=1}^N{A}_0^2\cdot \{1+h\cdot \\ M\cos \mathrm{\Omega }t+\mathit{(}z\mathit{0}+i·\Delta z\mathit{)}neffcd\omega \\ =\frac{A_0^2{\epsilon }_{0}c}{2}+\frac{A_0^2{\epsilon }_0\mathit{ch}M}{2}\frac{1}{{\omega }_{max}-{\omega }_{min}}{\int }_{{\omega }_{{}_{min}}}^{{\omega }_{max}}\{{\sum }_{i=1}^N\cos \left[\mathrm{\Omega }\right(t+ \\ \mathit{(}z\mathit{0}+i\cdot \Delta z\mathit{)}neffcd\omega \end{gathered}$$ (7)

In Eq. (7), the optical frequency terms (terms that contain ω) have gone because the cross-product terms zero out. In the integration, it is actually a calculation for a multi-slit grating with slit separation Δz, excited by microwave with frequency Ω. The summation inside the integral, let us refer to as K, can be written as

$$\begin{gathered} K={\sum }_{i=1}^N\cos \left[\mathrm{\Omega }\left(t+\frac{\left(z_0+i\cdot \mathrm{\Delta }z\right)n_{eff}}{c}\right)\right]= \\ \mathit{Re}\left\{{\sum }_{i=1}^{N}exp\left[j\mathrm{\Omega }\left(t+\frac{\left(z_0+i\cdot \mathrm{\Delta }z\right)n_{eff}}{c}\right)\right]\right\} \end{gathered}$$

When we measure the S21 on the VNA, the resulted value is in proportion to

$$\begin{gathered} S21\propto \frac{K}{s(t)}=\frac{\mathit{Re}\left\{{\sum }_{i=1}^{N}exp\left[j\mathrm{\Omega }\left(t+\frac{\left(z_0+i\cdot \mathrm{\Delta }z\right)n_{eff}}{c}\right)\right]\right\}}{Re\{M\exp \text{j}(\mathrm{\Omega }t+\varphi )\}} \\ =Re\left\{\frac{1}{M}{\sum }_{i=1}^{N}exp\left[j\mathrm{\Omega }\left(\frac{\left(z_0+i\cdot \mathrm{\Delta }z\right)n_{eff}}{c}-\varphi \right)\right]\right\} \end{gathered}$$

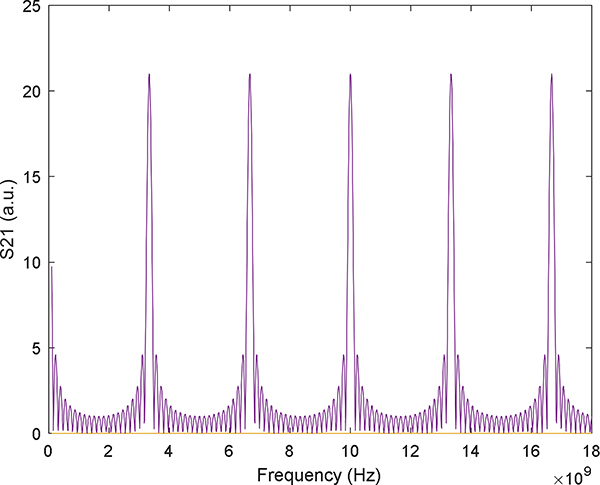
Evaluate the value inside the curly bracket, with N=21, c=3e8, n_eff =1.5, Δz=0.03 and random ϕ, the result is shown in Figure 3. There will be multiple resonant peaks occur at

$$\mathrm{\Omega }=2\mathrm{\pi }\mathrm{f}=c\frac{m\pi }{\mathrm{\Delta }z{n}_{eff}}$$

Figure 3.

Simulation result of the frequency domain spectrum.

Where m = 0, ±1, ±2, … …

With the assumed parameters, the resonant frequency f will be multiples of 3.33GHz. This is a typical grating pattern, and we should note that the frequency here is microwave frequency Ω.

IV. EXPERIMENT AND DISCUSSION

In this section, experiments of fabrication and tests of MPFG are demonstrated. We then discuss various characteristic of the MPFG.

A. Grating fabrication and resulted spectra

A MPFG with 21 periods has been fabricated by inscribing 21 weak reflectors on a single mode fiber (The last one is a little weaker comparing to others due to fabrication error), the time domain signal of which is shown in Figure 4. The distance between adjacent reflectors is 3 cm. We did not use a linear motor stage to control the distance because the total length is about 60cm, and it happened that we do not have a linear stage with that long range in the lab, so we control the distance manually. Before fabrication, we measured the distance with a ruler, and mark the position on the coating of the fiber with a thin marker. We then put the marked fiber section below the femtosecond laser micromachining system to fabricate the reflector. Because we control the distance manually, the positional error of the inscribed reflector should be about the width of the mark, which is about 0.5mm. In time domain, the signal strength is about −107dB to −97dB, while the noise floor is about −125dB. The variation of peak strength is maybe due to that the fiber is repositioned when inscribing each reflector, and smaller position difference and laser energy variation may cause the reflection strength to be different for the same scanned area. If very uniform strength is wanted, we could monitor the time domain signal while doing the laser fabrication and adjust the laser power and scanned area in real time. However, this could be very time consuming. For this paper, we just fabricate each reflector with the same laser parameters. The resulted peaks are not so uniform, but should be enough for us to demonstrate the properties of a MPFG.

Figure 4 shows the time domain reflection signal from the VNA. About 21 weak reflectors are fabricated in the fiber, and each reflector exhibit itself as a peak in the time domain signal.

The frequency domain signal is show in Figure 5. Multiple resonant peaks can be observed at frequency of about 3.5G Hz, 7G Hz, 10.5G Hz, 14G Hz and 17.5G Hz.

The measured resonant peaks are very close to our simulated resonant peaks of multiples of 3.33GHz. The difference might come from the error in the assumption of effective index value (1.5 in assumption), and the period is slightly different than the 3cm design value in experiment by fabrication error. We can observe that the resonant peaks are decreasing at higher frequency. This is because of higher loss of the coaxial cable at higher frequency used in our experiment. This can also be verified as the noise level is also decreasing at higher frequency.

As we inscribe the reflectors one by one on the fiber, the frequency domain resonant peaks become more and more clear. We recorded the spectra of the grating when inscribed 6, 11, 16 and 21 periods and they are shown in Figure 6 respectively. When only a few periods are inscribed (for example the signal of 6 reflectors or periods), the resonant peak is relatively wide, and there are also side-lobes appear in between two resonant peaks. With more reflectors inscribed, the resonant peaks become narrower and higher, while the side-lobes gradually disappear.

Figure 6.

Evolution of the frequency domain signal when inscribed 6, 11, 16 and 21 periods of the MPFG.

This phenomenon is similar to what happens to traditional uniform fiber Bragg gratings. To show this similarity, a simple uniform FBG spectrum calculation program is used. In the program, all the parameters are set to as in traditional FBG, except that the grating period is set to 3cm, to show similar frequency position as in our experiment. The refractive index of the fiber is set to 1.5, the inscribed grating is uniform with sinusoidally modulated RI, modulation depth is set to 1*10⁻⁴ RIU. The following figure shows the calculated spectrum peak at about 3G Hz, with number of period set to 6, 11, 16 and 21 respectively.

B. Grating spectra change in response to temperature change

Similar to FBG sensors, the MPFG can be used as sensors because it can respond to outside conditions change such as temperature and strain. When exposed to ambient temperature change, thermo-optic effect will cause the resonant peak frequency to move. To verify it, a MPFG is put in a digitally controlled furnace and the spectrum of the MPFG is recorded at different furnace temperature from 25 °C to 75 °C. The peak frequency near 1.35G Hz is recorded, and the frequency shift with regard to the furnace temperature is shown in Figure 8(a). A linear response with R² value of 0.9893 can be observed. Figure 8(b) shows the different MPFG spectra near 1.35G Hz during the temperature change.

Figure 8.

(a) The frequency shift with regard to the furnace temperature near 1.35G Hz. (b) The MPFG spectra near 1.35G Hz during temperature change.

C. Influence of the coherence of light sources

From the analysis in section III, we know that it is important that the grating period should be much longer than the coherence length of the light source, so that the optical interference is canceled out (I_{cross–product} = 0), and only the microwave frequency components are resonating to form the grating spectrum. Here we use three different light sources with different coherent length to verify it. The MPFG is still the 21 periods MPFG we fabricated in section IV (A). The measured frequency domain results are shown in Figure 9. The first light source is HP 81554SM laser source module shown as the blue curve in the figure. It is a Fabry-Perot source that has 4nm linewidth which is about 0.2mm in coherence length, much smaller than the 3cm grating period. We can see that the grating resonant peaks are very clear in the blue curve, about 10dB SNR at the peak near 3.5G Hz. The second light source is the same HP 81554SM laser but filtered with a 0.1nm grating filter, the resulted spectrum shown as the red curve in the figure. This filtered light source has a coherence length of about 7.6mm. It is still 4 times smaller than the grating period of 3cm, so we can still see the resonant peaks in the grating. However, as the coherence length become longer, we can see that the resonant peak at 3.5G Hz becomes lower than the blue curve, while the noise level in the frequency domain increased. The third light source is an Agilent 81680A tunable laser, shown as the green curve in the figure. Its linewidth is 100 kHz, so the coherence length is about 954m. This is much larger than the grating period, and we cannot observe any resonant peak of the MPFG illuminated by this light source in the green curve. This experiment verifies that a low coherent source is needed to interrogate the MPFG. The shorter the coherence length, the stronger the resonant peak would be.

Figure 9.

Frequency domain spectra when the MPFG is illuminated with light sources of different coherence length.

D. Apodization of the grating

Apodization is a technique that is usually used in FBG to optimize the spectrum by controlling the grating profile. As the grating in MPFG is actually inscribed point by point, apodization should be also easy to implement in this grating. The index modification strength can be controlled by laser power and scanned area, and the position of the reflector can be controlled because the period is relatively big. In our experiment above, it seems that the position error is an issue, but that is because we control distance manually. As long as a linear stage is used, the position could be precisely controlled. Here we consider two examples in simulation for apodization discussion.

The first is a phase shifted grating, which means that one of the periods in the grating has a phase shift, such as a π phase shift, comparing to the other periods. A phase shifted grating usually exhibit itself as a split peak at resonant frequency. In Figure 10, the red curve is the 21 periods grating that have 3cm period as we see before. We take the time domain complex signal from this spectrum, then expand the length of the 11th period from 3cm to 4.5cm using interpolation methods in both amplitude and phase. This modified time domain signal is used to simulate the phase shifted grating that the 11th period has a π phase shift. We then using Fourier transform to convert this modified time domain signal to frequency domain. The new simulated signal is shown in Figure 10 as the blue curve. We can clearly observe the split peak in microwave domain as in traditional phase shifted fiber gratings.

Figure 10.

Simulated spectrum of phase shifted MPFG comparing to original grating spectrum.

Another typical apodization scheme is Gaussian apodization, which means that the distribution of the intensity of the reflectors shows a Gaussian profile. Just like our processing methods in phase shifted grating simulation, here we take the time domain MPFG signal and multiply it by a Gaussian window. We then Fourier transform it back to frequency domain to obtain the simulated Gaussian apodized grating spectrum. Comparing to uniform gratings, the apodized grating will have less side-lobe, as shown in Figure 11. The blue curve is the simulated Gaussian apodized grating, while the red curve is the original spectrum in experiment.

Figure 11.

Simulated spectrum of Gaussian apodized MPFG comparing to original grating spectrum.

V. CONCLUSION

In this paper, we proposed and fabricated MPFGs by femtosecond laser micromachining on optical fibers. The working principle and the microwave domain characteristics of this device is studied. The temperature response of the MPFG is demonstrated for possible sensing applications. We also studied the influence of the coherence length by changing the illuminating light source in the experiment. Because of the flexibility of the femtosecond laser fabrication process, possibility of apodization is studied and demonstrated in simulation results. Other than sensing, this microwave photonic device could have other potential applications such as a microwave photonic filter.

Figure 7.

Simulated traditional uniform FBG spectra that have 6, 11, 16 and 21 periods. The grating period is set to 3cm; other parameters are chosen as in traditional FBG.