Quantitating denaturation by formic acid: imperfect repeats are essential to the stability of the functional amyloid protein FapC

Abstract

Bacterial functional amyloids are evolutionarily optimized to aggregate, so much so that the extreme robustness of functional amyloid makes it very difficult to examine their structure-function relationships in a detailed manner. Previous work has shown that functional amyloids are resistant to conventional chemical denaturants, but they dissolve in formic acid (FA) at high concentrations. However, systematic investigation requires a quantitative analysis of FA's ability to denature proteins. Amyloid formed by Pseudomonas sp. protein FapC provides an excellent model to investigate FA denaturation. It contains three imperfect repeats, and stepwise removal of these repeats slows fibrillation and increases fragmentation during aggregation. However, the link to stability is unclear. We first calibrated FA denaturation using three small, globular, and acid-resistant proteins. This revealed a linear relationship between the concentration of FA and the free energy of unfolding with a slope of m_FA+pH (the combined contribution of FA and FA-induced lowering of pH), as well as a robust correlation between protein size and m_FA+pH. We then measured the solubilization of fibrils formed from different FapC variants with varying numbers of repeats as a function of the concentration of FA. This revealed a decline in the number of residues driving amyloid formation upon deleting at least two repeats. The midpoint of denaturation declined with the removal of repeats. Complete removal of all repeats led to fibrils that were solubilized at FA concentrations 2–3 orders of magnitude lower than the repeat-containing variants, showing that at least one repeat is required for the stability of functional amyloid.

The term amyloid is normally associated with misfolding of different proteins, resulting in neurodegenerative diseases like Alzheimer's and Parkinson's disease, but the number of cases where the amyloid structure is used for functional purposes is steadily increasing (1, 2). The first functional amyloids to be identified and purified were the curli fibrils expressed by Escherichia coli and Salmonella enteritidis (3, 4). Since their discovery, curli have been shown to be widely expressed among different bacteria, spanning at least four different phyla (5). Curli fibrils serve an architectural role in bacterial biofilm but are also involved in cell attachment and invasion (6–8). Curli are composed primarily of the protein CsgA, which, for bacterial strains within the Enterobacteriales and the Vibrionales, is expressed from the csgBAC operon together with the nucleator protein CsgB and the chaperone CsgC (5, 9, 10). Furthermore, four additional Csg proteins are expressed from the csgDEFG operon, and they act as a transcription regulator of the csgBAC operon (CsgD), chaperones (CsgE/CsgF), and an outer membrane pore protein (CsgG) (9–11). All Csg proteins, except CsgD, are targeted for Sec-dependent secretion across the inner bacterial membrane to the periplasm (12).

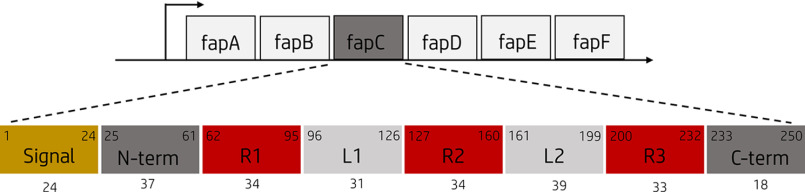
A decade ago, we identified a similar amyloid system in Pseudomonas, termed functional amyloid in Pseudomonas (fap) (13). The fap system encodes proteins FapA–F, expressed from a single fapA–F operon. Like the curli system, it encodes an outer membrane pore protein (FapF) and possible chaperones (FapA and FapD), besides the primary amyloid-forming protein FapC, and a potential nucleator FapB (14) (Fig. 1). Like the curli system, fap fibrils contribute to biofilm formation (15, 16) and play roles in virulence (17), and the individual Fap proteins are also secreted across the inner membrane via Sec (15, 18, 19). However, the fap system is evolutionarily younger than the curli system and only exists within a single phylum, the Proteobacteria (20).

Figure 1.

The fapA–F operon and the FapC protein. The fapA–F operon encodes the six Fap proteins, FapA–F. The Pseudomonas sp. strain UK4 FapC protein consists of a 24-aa N-terminal signal peptide (yellow) and three imperfect repeats (R1–R3, red) separated by two linker regions (L1–L2, light gray). Start and end amino acid positions for the different regions are shown in the upper corners, and the length is shown below.

Both amyloid proteins CsgA and FapC consist of multiple imperfect repeats. CsgA has five, each ca. 20 residues in length and folded as individual β-hairpins separated by a tight turn (4–5 residues), according to a computationally predicted structure (21). In support of this, peptides corresponding to three of the individual repeats (repeats 1, 3, and 5) readily form amyloid on their own (22). FapC has 3 longer repeats (ca. 35 residues long) that are also predicted to form β-hairpins (14). However, in FapC the repeats are separated by linker regions of variable lengths; the second linker shows especially large variations in size, with lengths ranging from 39 (in the Pseudomonas sp. strain UK4 used in this study) to more than 250 residues for Pseudomonas putida F1 (13). For FapC, stepwise removal of these repeats has only relatively little effect on the rapidity of fibrillation but increases the ensuing fibrils' tendency to fragment during shaking, thereby forming new growing fibrils (23). Whereas that study focused on the mechanistic roles of the different repeats, we here address the question of how removal of these repeats affects the stability of the formed fibrils. Given that functional amyloids are largely made for structural reasons, it is their stability (thermodynamics) rather than the ease of their formation (kinetics) that is critical to their functionality. This aspect has not been addressed for functional amyloids. However, to answer this question thoroughly, we need a reliable assay to determine fibril stability.

For globular monomeric proteins, stability is defined by the distribution between native and denatured states. Analogously, there is an equilibrium between the fibrillated and monomeric state; the higher the concentration of the monomeric species (corresponding to a critical aggregation concentration, or cac), the less stable the fibril. Consequently, the free energy of fibrillation can be expressed as –RT ln cac (24), and for relatively unstable amyloids formed by misfolded proteins involved in neurodegenerative diseases, this can be further analyzed by displacing the equilibrium toward the monomeric state by, e.g. addition of denaturants (25). This formalism has been used to evaluate the stability of the Aβ peptide, aided by the relatively high Aβ cac (24). However, fibrillation of functional amyloids such as FapC is very efficient and typically leads to impracticably low levels of monomer (13), even in the presence of high concentrations of denaturant (data not shown) or boiling SDS (13). Fortunately, other organic solvents are able to dissociate functional amyloids. For example, CsgA fibrils can be disassembled in a 1:1 mixture of hexafluoroisopropanol and TFA and subsequently reassembled in water or buffer (26), whereas fungal amyloids consisting of hydrophobins can be extracted with TFA and formic acid (FA) (27). Overall, the simplest approach is to use the high concentrations (typically >80%) of FA that have been shown to solubilize functional amyloids. This phenomenon even serves as an operational basis to identify functional amyloid in complex mixtures (28). Therefore, the extent to which a protein fibril is dissolved by a progressive increase in FA may provide a measure of the fibril's stability. To investigate this systematically, however, we need a more general analysis of the denaturation potency of FA. To the best of our knowledge, such an analysis has not been performed yet, and here we provide it as part of our analysis of the stability of functional amyloid.

Formic acid, HC(O)OH, is the simplest carboxylic acid. As a protein solvent, FA is superior to most common organic solvents (e.g. glycerol, DMSO, or TFA), solubilizing the protein polypeptide chain through protonation, destabilization of hydrogen bonds, and hydrophobic residue interactions (29, 30). High concentrations (>70%, v/v) of FA solubilize large, fibrous protein complexes, such as collagen, wool keratin, and silk fibroin (31–33). Interestingly, the FA-solubilized form of fibroin seems to be more compact than that when solubilized in water, although fibroin is in random coil conformation in both solutions (31). Solubilization does not involve chemical modification (31); FA can formylate Thr and Ser (O-formylation) as well as Lys (N-formylation), but this requires high concentrations (>80%, v/v) and extended time intervals (many hours) (29). The amide derivative of FA, formamide (FM), is also able to solubilize and unfold globular proteins, such as myoglobin, cytochrome c, and insulin (34, 35). Although not an acid, it still interacts with proteins through hydrogen bond disruption and solubilization of hydrophobic surfaces (36). Thus, FM constitutes a protonation-free comparison to FA.

Our objectives for this study were 2-fold: (1) to establish a quantitative basis for the use of FA to determine protein stability and (2) to employ this approach to determine the contribution of the individual repeats in FapC to fibril stability. To achieve goal 1, we investigate the impact of FA on the stability of proteins that unfold according to a simple two-state system, making it straightforward to assess the impact of FA on their stability. However, given FA's properties as an acid, the simple lowering of pH will, in itself, make a major contribution to FA's destabilizing properties. To extract the non-protonation-related denaturing properties of FA, we need to be able to subtract the contributions that a simple drop in pH would make to destabilization. This restricts our investigations to proteins that do not unfold at low pH unless other denaturing measures are involved, such as heat. Therefore, we have selected three acid-resistant proteins (hen egg white lysozyme [37–40], S6 from Thermus thermophilus [41–44], and bovine ubiquitin [45–51]) whose stabilities all have been extensively analyzed under a range of conditions. For all three proteins, we determine their stability in FA based on near-UV CD thermal scans over a range of FA concentrations. For each FA concentration, we carry out a thermal scan at the corresponding pH adjusted with HCl and subtract this effect from that of FA to quantitate the intrinsic contribution of FA to protein stability. Furthermore, we carry out these experiments using <30%, v/v, FA to minimize formylation (29). To achieve goal 2, we use the obtained relationship between FA concentration and its denaturation potency (m-values) to evaluate the FA depolymerization assays of eight different FapC constructs (Fig. S1) and thereby quantify the aggregative effect of individual repeats of FapC.

Results and discussion

Near-UV CD reveals reversible and cooperative thermal unfolding of acid-stable proteins in formic acid despite local relaxation of the native structure of S6 and Ubi

To quantitate the denaturing potency of formic acid (FA), we used near-UV CD to carry out thermal scans of three model proteins in different concentrations of FA. The proteins are the 129-residue hen egg white lysozyme, the 101-residue ribosomal protein S6 from Thermus thermophiles, and the 76-residue bovine ubiquitin (Ubi). These proteins were selected for a number of reasons. First, they are well-characterized small proteins in a range of sizes (from 8.6 kDa through 12 kDa to 16.2 kDa) that have previously been used as model systems for fundamental studies in protein stability and folding (37–51). Second, they unfold in a single step without equilibrium intermediates. Third, they remain folded under acidic conditions, allowing us to carry out thermal scans at low pH to determine melting temperatures in the presence of FA. The protein solutions were not buffered beforehand, so addition of even small amounts of FA led to a large drop in pH. Because of the high absorption of FA in the far-UV range, we monitored protein unfolding using near-UV CD. Near-UV CD is highly sensitive to correct folding of the protein; indeed, it can be just as sensitive to loss of native structure as enzyme activity (52). Therefore, before we proceed further, we will describe the impact of FA on the structures of our 3 model proteins, as indicated by near-UV.

The near-UV signal of lysozyme in FA at room temperature (RT) is essentially identical to that in pure water (Fig. S2, A and B), showing that the protein remains natively folded in FA. In the case of S6, there is a 4- to 5-fold reduction in signal intensity in FA at RT compared with that in water, but there is still a distinct spectroscopic signature centered around 280 nm that disappears at 90 °C and is largely regained upon cooling down (Fig. S2, D and E). We have previously observed that S6 adopts a more flexible or “quasi-native” (but not molten globule-like) (53) structure at low pH. The single Trp residue in S6 (position 62) hydrogen bonds to Glu5 and Glu41 in the crystal structure of S6 (PDB entry 1RIS [54]), and these residues are likely to be protonated at low pH. This will most likely disrupt hydrogen bonding with Trp and increase its mobility, leading to a reduction in near-UV CD. In 10 mm HCl (pH 2), S6 still folds and unfolds according to a two-state transition with well-defined kinetics (53), but the change in compactness upon unfolding (as determined by the so-called m value, which describes how the free energy of unfolding changes with denaturant concentration) is reduced by ca. 40%. This is most likely because of an expansion of the native state, as indicated by the loss in near-UV signal combined with an increased affinity for the fluorescent probe ANS, which preferably binds to exposed hydrophobic patches, as well as decreased sensitivity of this low-pH state to mutagenesis (53). Far-UV spectra of S6 in MilliQ (MQ) and HCl are nearly identical, suggesting that the secondary structure is fully conserved at low pH (Fig. S2F). Rather than a loss of structure, lysozyme and Ubi actually show a small increase in CD signal intensity when the pH is decreased to 2.0 (Fig. S2, C and I). Ubi also shows a shift in the relative intensities of the 3 peaks seen in the near-UV CD signal at 265, 275, and 281 nm (Fig. S2, G and H). In water, these peaks all rise above the downward turn seen from ca. 295 nm down to 287 nm to reach positive ellipticity values. In FA, they are still visible but do not rise so much, suggesting a less asymmetric (rigid) environment for the aromatic groups at low pH. The spectrum is similar to the structure of the V62A mutant of ubiquitin assumed at pH 2–4, which, according to NMR, retains native secondary and tertiary structure, except for the unfolding of a long loop between two β-strands (47). Thus, both S6 and Ubi retain large parts of their original structure and overall compactness in FA but undergo some loosening of the tertiary fold.

Despite S6 and Ubi spectroscopic changes, all three proteins unfold reversibly and cooperatively in thermal scans, leading to a sigmoidal denaturation curve that can be fitted to a two-state unfolding transition from the (quasi-)native state, N, to the denatured state, D (Fig. 2). Furthermore, the refolded protein curves retain most of the signal after cooling the protein back to RT (Fig. S2, A, D, and G). This justifies the use of a reversible unfolding model to fit the data. The fits provide both the temperature midpoint of denaturation, T_m (in units of K), and the enthalpy of denaturation at T_m, ΔH_Tm. As shown for lysozyme in Fig. S3, the protein undergoes no significant acid hydrolysis in either HCl or FA at 60 °C, although there is significant accumulation of hydrolysis degradation products after 30–60 min at 90 °C. Because all proteins unfold below 60 °C at most FA concentrations (Fig. 3) and are only exposed to elevated temperatures for a short period of time, we conclude that acid hydrolysis does not significantly contribute to thermal unfolding in formic acid. It should also be noted that across the thermal scan temperatures applied here (5–95 °C), the pK_a of FA is only slightly changed, from 3.79 to 3.91 (55); the change is even smaller (well below 0.1 pH unit) in the temperature ranges where unfolding takes place. Finally, we point out that FA remains >99% undissociated at concentrations of >1 M (ca. 3.8%, v/v); at 0.2 M, <3% is dissociated. Thus, FA remains essentially undissociated under all conditions used in our experiments.

Figure 2.

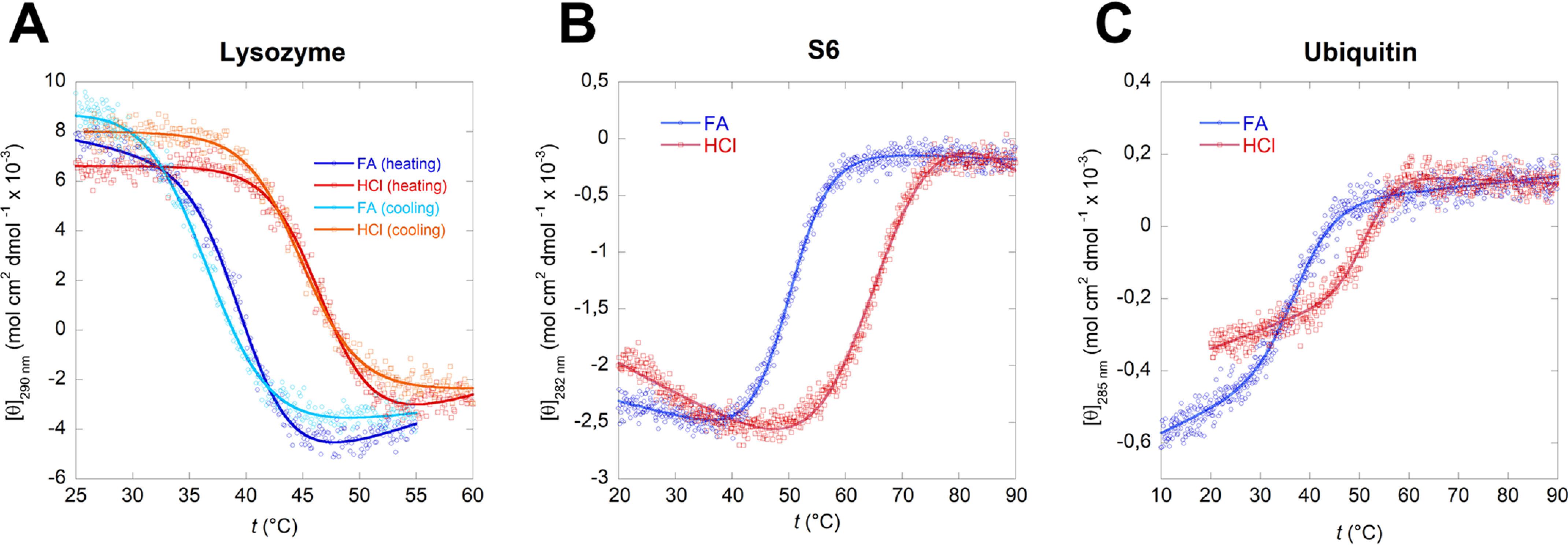
Thermal unfolding curves of lysozyme (A), S6 (B), and ubiquitin (C) in 10%, v/v, FA and in HCl solutions with the corresponding pH. In 10% FA all three proteins show significantly reduced thermal stability while maintaining a reversible two-state unfolding (Fig. S2). The sigmoidal curves were fitted using Equation 1.

Figure 3.

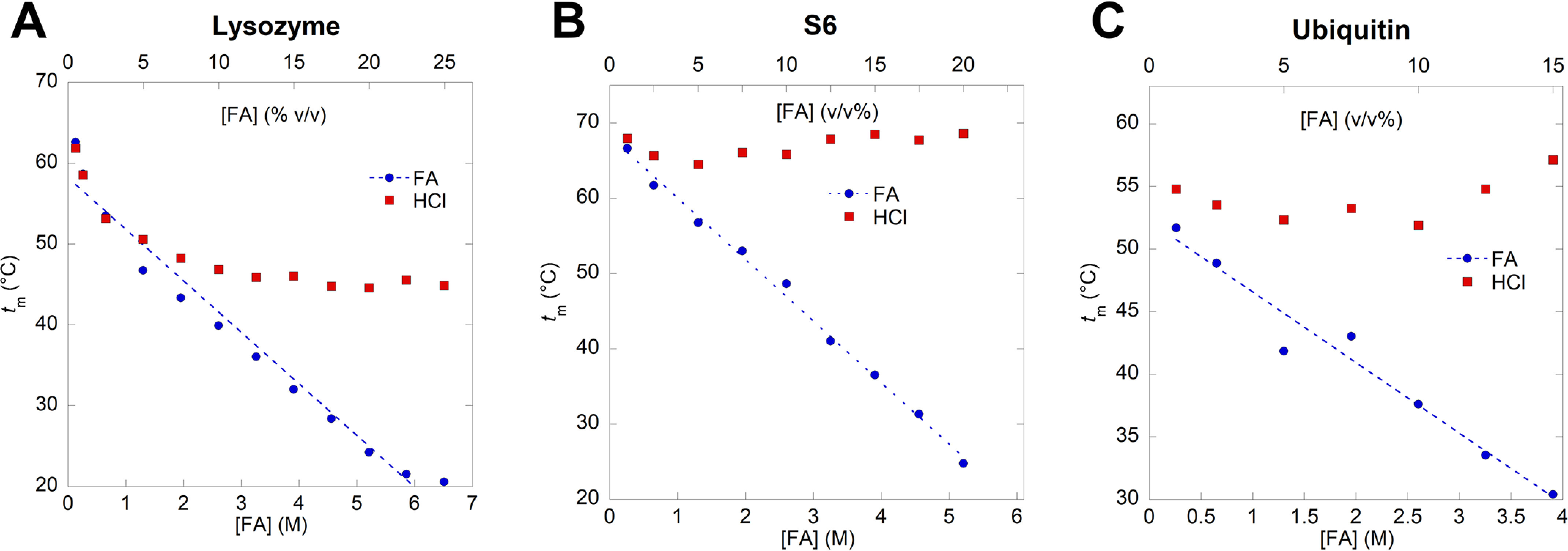
Melting temperature of lysozyme (A), S6 (B), and ubiquitin (C). The FA concentration is represented both as molar concentration (M) and volume percentage (v/v%). Each melting temperature, t_m, is obtained by thermal unfolding of the proteins at a given concentration of FA or HCl followed by fitting the sigmoidal unfolding curves of Equation 1 (Fig. 2). t_m values for all three proteins decrease significantly at high FA concentrations compared with HCl solutions of the corresponding pH.

Formic acid reduces T_m more than HCl at similar pH values

Thermal scans were performed on protein solutions containing 0.1–25%, v/v, FA (equal to 0.27–6.63 M given FA's density of 1.22 g/ml and molecular weight of 46 Da in the protonated form). All three proteins show a linear decrease in T_m (and, thus, t_m) with FA concentration (Fig. 3). To separate effects of low pH from those of the FA molecule, we carried out thermal scans in HCl at the same pH values as those obtained with FA. At low FA concentrations, t_m values of unfolding in FA follow those in HCl (Fig. 4), indicating that denaturation at those concentrations is a simple pH effect. However, as FA rises above 0.5 M, the pH effect caused by HCl starts to level out (t_m remains essentially constant for S6 and Ubi at all pH values and levels out for lysozyme around pH 1.4, which corresponds to an FA concentration of 3 M), whereas the denaturation effect of FA continues unabated.

Figure 4.

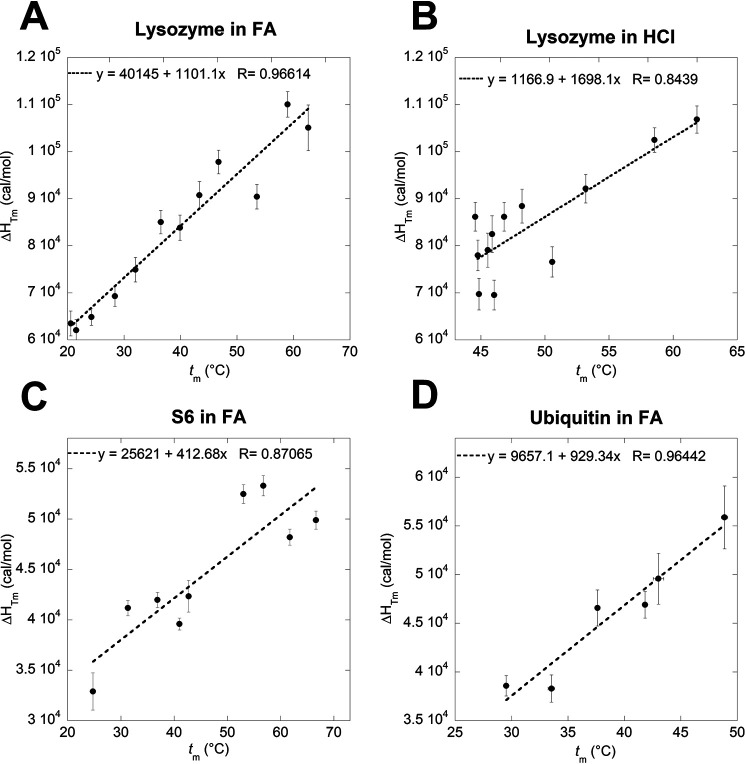
Determination of the specific heat capacity of denaturation (ΔC_p) of lysozyme in FA (A) and HCl (B), S6 in FA (C) and ubiquitin in FA (D) by plotting δH_Tm versus t_m. ΔC_p of S6 and ubiquitin in HCl could not be determined because of insignificant difference in measured t_m values at different concentrations of HCl.

Heat capacity changes upon unfolding are reduced in FA compared with HCl and GdmCl, which may reflect a more compact unfolded state and a more expanded native state

To quantify this denaturation effect, we calculated the free energy of unfolding (ΔG_D-N) of the different proteins in HCl and FA at matching pH values and subtracted the effect of HCl. To achieve this, we needed to calculate the specific heat capacity change upon unfolding (ΔC_p) of the different proteins under our denaturation conditions. Standard thermodynamics predicts a linear relationship between T_m and ΔH_Tm, with a slope of ΔC_p (assuming that ΔC_p is temperature independent) (56). Indeed, plots of ΔH_Tm versus t_m provide reasonably linear plots (Fig. 4). Based on these plots, ΔC_p of lysozyme is calculated to 1.10 ± 0.10 kcal mol⁻¹ K⁻¹ in FA and 1.70 ± 0.34 kcal mol⁻¹ K⁻¹ in HCl. An early calorimetric study of lysozyme denaturation reported a ΔC_p of 1.37 kcal mol⁻¹ K⁻¹ when the protein was denatured in guanidinium chloride (GdmCl) but a similar ΔC_p of 1.57 kcal mol⁻¹ K⁻¹ when denatured in HCl (57). FA is reported to induce a more compact state when used as a solvent (31), and considering that the ΔC_p value is correlated to the change in solvent-accessible surface area (SASA) upon unfolding (58) (i.e. the change in compaction upon unfolding), this may explain the difference in ΔC_p values between FA and HCl.

For both S6 and Ubi, we determined ΔC_p using FA-based scans, since the small variation in t_m with pH in the HCl-based thermal scans prevented the determination of meaningful t_m–ΔH_Tm plots. The ΔC_p of S6 in FA is found to be 0.41 kcal mol⁻¹ K⁻¹, which is significantly lower than the value of 0.93 ± 0.05 kcal mol⁻¹ K⁻¹ obtained when denaturing with GdmCl (59). We attribute this to the previously mentioned “loosening” of the native state of S6 at low pH, which, together with a likely more compact unfolded state in FA compared with that of GdmCl, means that the increase in SASA upon unfolding will be smaller. Nevertheless, the satisfactory linear correlation between t_m and ΔH_Tm for S6 is consistent with a well-defined, reasonably compact species populated prior to thermal unfolding.

Somewhat surprisingly in view of the previous results, ΔC_p of Ubi in FA was found to be 0.93 ± 0.13 kcal mol⁻¹ K⁻¹, which is essentially identical to the value of 0.90 ± 0.20 kcal mol⁻¹ K⁻¹ obtained from calorimetric studies in different concentrations of GdmCl (49).

pH effects can be factored out to reveal the intrinsic contribution of formic acid to protein stability 3-fold weaker than that of GdmCl

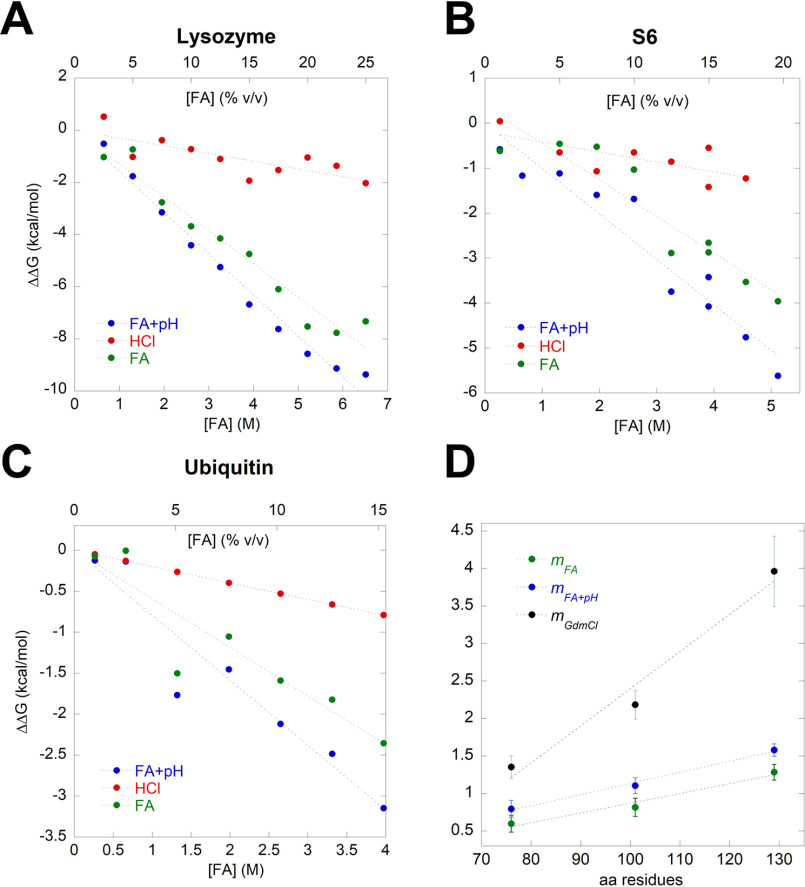
Having determined ΔC_p, ΔG_D-N can be calculated from each thermal scan based on their individual ΔH_Tm and T_m values (eq. 2). For all three proteins, ΔG_D-N (here denoted ΔG_D-N^FA+pH to emphasize the joint contribution of FA as a chemical denaturant and as an acid) decreases linearly with [FA] (blue points and lines in Fig. 5). Each FA-ΔG_D-N data point has an HCl-ΔG_D-N counterpoint, in which ΔG_D-N has been determined from a thermal scan performed in an HCl solution with the same pH value as the corresponding FA data point (ΔG_D-N^pH, red points and lines in Fig. 5). The low ΔG_D-N values of the HCl-based data points compared with the FA-based points make it clear that the stability decrease caused by a given concentration of FA (which can be considered driven by the combined effect of lowered pH and increased [FA]) is significantly larger than the stability decrease solely caused by the equivalent decrease in pH. This emphasizes the strong effect of FA as a denaturant and not merely as an acid. Thanks to these pairwise measurements of stability in FA and HCl at the same pH value, it is possible to subtract the isolated pH effect for FA at every data point and, thus, calculate the “true” FA effect, denoted ΔG_D-N^FA, as a function of [FA]. This corrected series is shown in green points and lines in the graphs in Fig. 5 For all three proteins, there is a satisfactory linear relationship between ΔG_D-N^FA and [FA], whose slope is the m_FA value. Lysozyme's m_FA value of 1.28 ± 0.10 kcal mol⁻¹ M⁻¹ is close to the m value of 1.29 kcal mol⁻¹ M⁻¹ reported for lysozyme when denatured in urea (58, 60), but significantly lower than the value of 3.96 ± 0.47 kcal mol⁻¹ M⁻¹ in GdmCl (37). A similar analysis for S6 yields an m_FA value of 0.81 ± 0.12 kcal mol⁻¹ M⁻¹, which is again considerably smaller than the value of 2.33 ± 0.12 kcal mol⁻¹ M⁻¹ in GdmCl (41) (note that this value is based on the average m-value of 1.71 ± 0.09 M⁻¹ from reference 41 and has to be multiplied by –RT ln10). Finally, the m_FA value of Ubi in FA was found to be 0.59 ± 0.11 kcal mol⁻¹ M⁻¹, which differs from 1.35 kcal mol⁻¹ M⁻¹ in GdmCl (45). M values reflect the molar efficacy of a given denaturant in reducing the stability of a protein and can be correlated to effects such as the ability to increase solubility of nonpolar amino acids that are normally buried within a protein core, as well as hydrogen bonding to peptide bonds and other polar groups in proteins (61–63). Such values may be further substantiated by e.g. measuring the free energy of transfer of individual amino acids and small peptides to the denaturant in question to determine solubility effects (64). Overall, the m_FA values are ∼1/3 of the corresponding m_GdmCl values, illustrating that FA is only 1/3 as efficient as GdmCl as a denaturant on a per-mole basis (discounting the pH effect).

Figure 5.

Correlation between the change in the free energy of unfolding ΔΔG_D-N and FA concentration (blue), HCl (red), and HCl-subtracted effect of FA (green) of lysozyme (A), S6 (B), and ubiquitin (C). D, the m values found in panels A–C are plotted versus the number of residues of the model proteins. These FA-based m values can be compared to m values for the same three proteins in GdmCl, resulting in a slope that is 3–4 times more steep for GdmCl reflecting FA's comparatively lower strength as a denaturant.

Isothermal titration with formic acid confirms results from thermal scans

As a final control, we sought to validate the obtained m-values described above through an analysis of FA-induced denaturation under isothermal denaturation (25 °C), measured by intrinsic aromatic fluorescence. Note that we observe only m_FA+pH values and not the corrected m_FA, as the pH effect cannot be subtracted in a simple manner in this type of experiment. In addition, we also measure [FA]^50%, which is the FA concentration at which half of the protein is unfolded. We were able to predict the fraction of folded protein in FA under isothermal conditions based on the ΔG_D-N^FA+pH and m_FA+pH values from the thermal unfolding experiments using Equation 3 (Fig. 6, A–C). For all 3 proteins, there is excellent overlap between isothermal data and folding fractions predicted from thermal scans. For both lysozyme and Ubi, there is a good agreement between m_FA+pH obtained from both thermal and isothermal experiments. Lysozyme unfolding, represented by a red shift in Trp fluorescence, overlaps the predicted f_N very well and shows an m_FA+pH value of 1.43 ± 12 kcal mol⁻¹ M⁻¹, which is close to the value of 1.58 ± 0.08 kcal mol⁻¹ M⁻¹ measured by near-UV CD (Fig. 6A). Ubi unfolding was followed as a change in emission at 320 nm (Trp+Tyr) and overlaps the predicted curve almost perfectly (Fig. 6C). Both thermal and isothermal measurements of Ubi unfolding show a strikingly similar m_FA+pH value of 0.79 ± 0.11 kcal mol⁻¹ M⁻¹. Isothermal measurements of S6 were measured by the change in near-UV ellipticity to avoid complications from protonation of Trp that affect fluorescence without affecting structure. The isothermal m_FA+pH value of 0.66 ± 0.22 kcal mol⁻¹ M⁻¹ is within error, the same as the value of 0.81 ± 0.12 kcal mol⁻¹ M⁻¹ from thermal unfolding (Fig. 6B). These values are summarized in Table 1.

Figure 6.

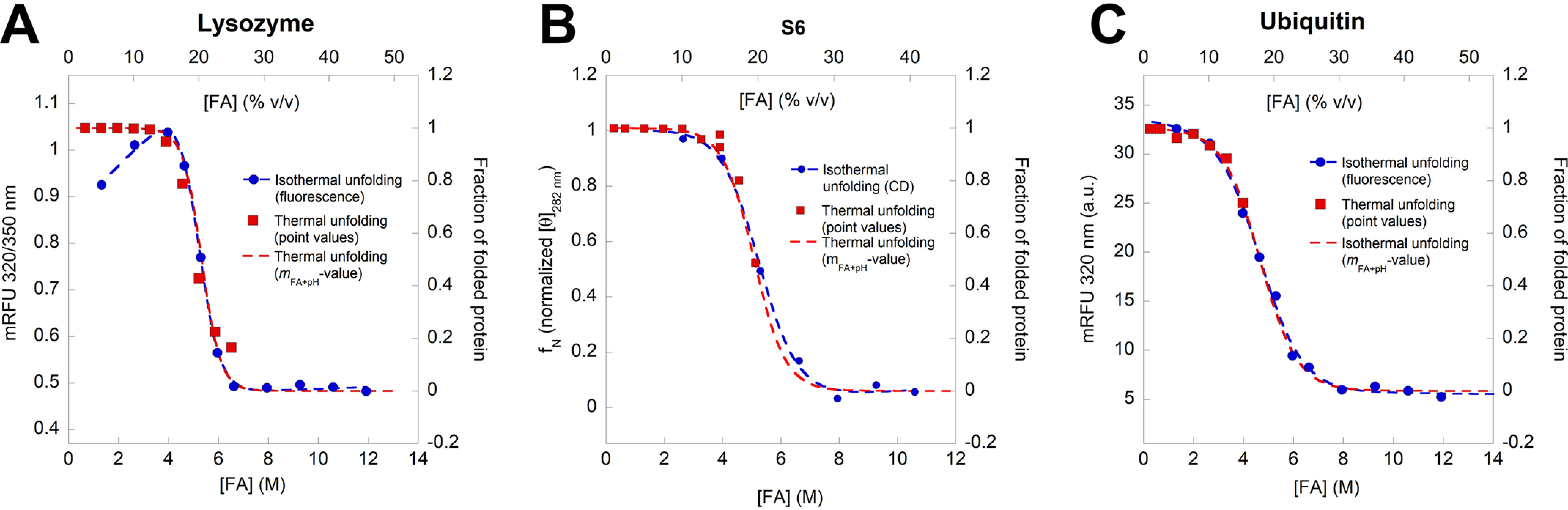
Unfolding of lysozyme (A), S6 (B), and ubiquitin (C), measured by intrinsic aromatic fluorescence (lysozyme and ubiquitin) and near-UV CD (S6). Blue points are measured equilibrium values, whereas red points represent the predicted fraction of folded protein at 25 °C based on thermal unfolding values. The red stippled curves are best fits of Equation 4 to the red points. These show a very good correspondence with the measured isothermal equilibrium data set.

Table 1.

Thermodynamic parameters of lysozyme, S6, and ubiquitin denaturation in FA derived from the thermal and isothermal unfolding experiments, measured by near-UV CD and aromatic fluorescence, respectively

Method and parameter	Lysozyme	S6	Ubiquitin
Near-UV CD (thermal)
ΔCpFA (cal mol−1 K−1)a	1101 ± 93	412.7 ± 88	928.3 ± 13
mFA+pH (kcal mol−1 M−1)b	1.58 ± 0.08	1.10 ± 0.11	0.79 ± 0.11
mFA (kcal mol−1 M−1)c	1.28 ± 0.10	0.81 ± 0.12	0.59 ± 0.11
Fluorescence (isothermal)
[FA]50% (M)d	5.18 ± 0.05	4.86 ± 1.3	4.69 ± 0.40
mFA+pH (kcal mol−1 M−1)d	1.43 ± 12	0.66 ± 0.21	0.79 ± 0.11

^aSlope of linear plots in Fig. 4.

^bSlopes of linear plots (Fig. 5, A–C, blue data points).

^cSlopes of linear plots with pH contribution subtracted (Fig. 5, A–C, green data points).

^dFrom fits of data in plots in Fig. 6 to Equation 4.

Gratifyingly, the m values of all three proteins scale with their size measured as residue number (Fig. 5D). Similarly, m values for denaturation with classical denaturants, such as urea and GdmCl, scale linearly with the change in SASA upon unfolding, which in turn scales with the number of residues per protein (58), as shown in Fig. 2D. These linear correlations are attributed to weak binding effects, and the interaction between the denaturant and the protein is therefore determined by the SASA rather than specific interaction regions. This can also be quantified as the increase in solubilization power of the denaturant, i.e. their interactions with protein functional groups which become exposed upon unfolding. Thus, the better the solvation, the stronger the denaturation potency, cfr. the seminal work by Nozaki and Tanford on the solubility of amino acids in GdmCl (64), which has subsequently been used to develop activity coefficients for GdmCl denaturation (37). FA must work in the same unspecific manner given its scaling properties, indicating that it has a conventional denaturing effect as a weak binder to the protein surface in addition to the effect of lowering the solution pH. However, the slope of the plot for GdmCl (−0.049 ± 0.009 kcal/mol/M/residue) is 3–4 times steeper than that of FA (0.013 ± 0.002 kcal/mol/M/residue), illustrating the greater solubilization power of GdmCl (Fig. 5D). Simple comparison of the unfolding of lysozyme in 1M GdmCl and 5% FA separately and together indicates that the two denaturants have an additive effect on lysozyme stability, indicating that they do not interfere with or strengthen each other but act in independent fashion (Fig. S4A).

Formate does not show any denaturating potency, and formamide is ∼3-fold weaker as a denaturant than formic acid, indicating lower solvating abilities

We also attempted to quantify the denaturation potency of the ionized version of FA, sodium formate, as well as its amidated counterpart, formamide (FM). However, thermal denaturation of lysozyme in formate was challenged by the high levels of precipitation accompanying unfolding (Fig. S4, B and C). In addition, the t_m of unfolding increased from 72.4 °C (0 M formate) to 78–80 °C (0.8–2.6 M formate) (Fig. S4D). This stabilization by formate indicates that only the protonated form of FA has denaturing properties. Because of the low value of the formate K_a (10^−3.75 at 25 °C), the dissociation of FA to H⁺ and formate is very low (0.4–1.7%) in the FA concentration range (2.5–40%) used for the vast majority of the experiments in this study; therefore, we consider the contributions from formate to be insignificant. FM, on the other hand, showed a more classical denaturation effect (Fig. S5A), and denaturation was completely reversible up to 45%, above which it became progressively less reversible (data not shown). t_m decreased linearly with [FM] up to 80% (Fig. S5B). A plot of ΔH_Tm as a function of t_m was satisfactorily linear (Fig. S5C), leading to a predicted lysozyme ΔC_p of 1.25 ± 0.11 kcal mol⁻¹K⁻¹, which is identical, within error, to the value of 1.10 ± 0.10 kcal mol⁻¹K⁻¹ in FA, suggesting a comparable level of unfolding and, thus, hydration in the denatured state. In the FM concentration range we probed here (0–80%, corresponding to 0–23 M), the pH of the solution only increased from 8.45 to 10.1, and, unsurprisingly, the T_m of lysozyme only decreased by ∼6 °C in the corresponding control experiments where pH was adjusted with NaOH buffer. The very modest decline in stability induced by the shift in pH alone was nevertheless subtracted from the overall ΔG_D-N, analogous to Fig. 5, A–C. This led to a linear correlation between ΔG_D-N and [FM] (Fig. S5D) with an m_FM value of 0.47 ± 0.02 kcal mol⁻¹ M⁻¹, which is 2.7-fold less than m_FA for lysozyme (1.28 ± 0.10 kcal mol⁻¹ M⁻¹). Equilibrium fluorescence measurements at isothermal conditions show an even lower estimate of m_FM value of 0.29 ± 0.06 kcal mol⁻¹ M⁻¹ (Fig. S5E), although the denaturation curve and the curve constructed from thermal scans overall overlap well. Thus, FM is significantly less efficient than FA as a denaturant, even though the only difference between these two molecules is the replacement of a carboxylic acid with an amide group. Therefore, we conclude that the acidic −OH group of FA must interact with and solvate protein functional groups (particularly amides and hydrocarbon groups) better than the amide −NH₂ group (cfr. similar solubilization measurements for amide-amide and amide-hydrocarbon interactions) (65). Similar considerations apply for –OH (FA) versus –O⁻ (formate). Future studies using appropriate model compounds may put these empirical observations on an even firmer basis.

Solubilization of FapC variants by formic acid reveals that FapC imperfect repeats stabilize fibrils

Having quantified the denaturating potency of FA, we now analyze the contribution of the different imperfect repeats to FapC fibril stability. We designed different FapC mutant proteins where either one repeat (FapC ΔR1, FapC ΔR2, and FapC ΔR3), two repeats (FapC ΔR1R2, FapC ΔR1R3, and FapC ΔR2R3), or all three repeats (FapC ΔR1R2R3) were removed (Fig. S1). These proteins were fibrillated and their secondary structure analyzed with FTIR. Consistent with previous observations (23, 66), all fibrils showed an intense peak around 1620 cm⁻¹, indicating that they contain the characteristic amyloid cross-β structure as opposed to conventional β-sheets, which absorb at wavenumbers of >1630 cm⁻¹ (Fig. 7A). This is caused by the stacking of the β-sheets in the fibril structure, which shifts the frequencies toward lower wavenumbers (67).

Figure 7.

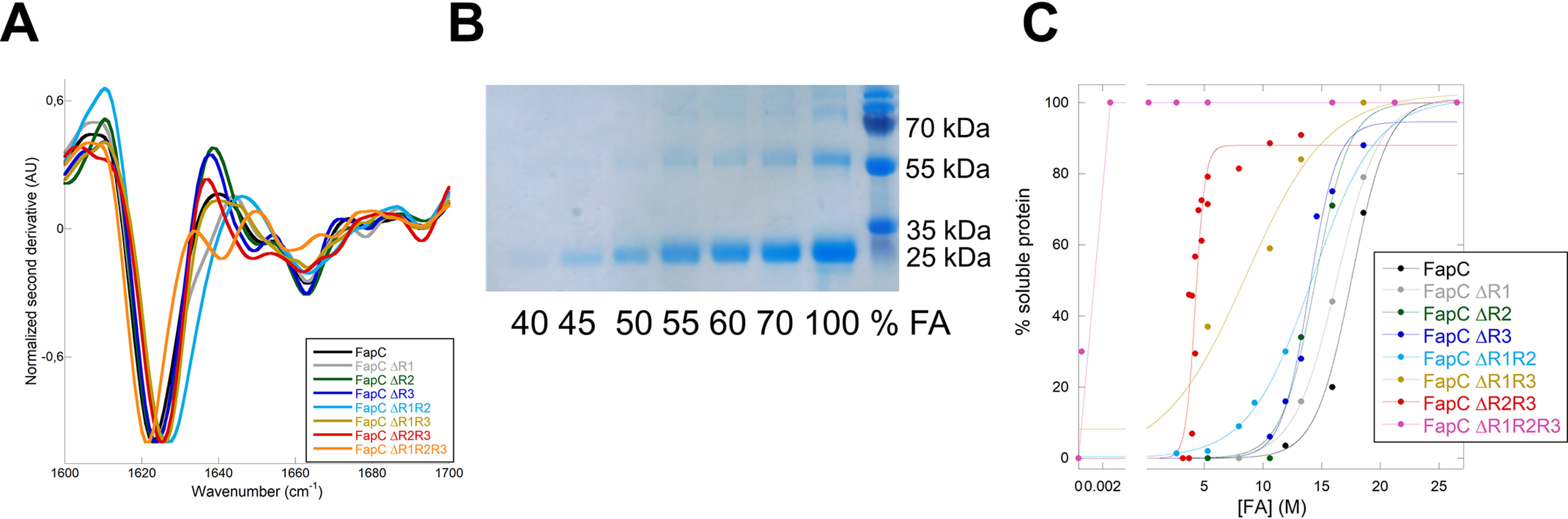
All FapC proteins can form amyloid fibrils. A, FapC variants were desalted from 8 M GdmCl into MQ water and immediately fibrillated before FTIR analysis was performed on the formed fibrils. The normalized second derivative shown here validates the amyloid nature of the different fibrils. B, representative gel of the supernatants after treatment with FA (here shown for FapC ΔR3 protein). The band around 25 kDa is FapC solubilized by FA. C, percentage of total protein present in supernatant after FA treatment as a function of FA concentration. Gel bands were quantified with ImageJ, normalized to the 100% FA band, and fitted to Equation 8. There is a marked decrease in stability when the number of repeats is reduced.

We used FA to measure the stability of the different FapC constructs as follows. Equal amounts of fibril mass were treated with different concentrations of FA, and the amount of fibrils that was dissolved by FA was quantified from SDS-PAGE gels (an example is shown in Fig. 7B). All quantifications were normalized to the sample treated with 100% FA, where the fibrils are fully dissolved. FA treatment of all eight proteins showed a stepwise displacement of the midpoint values of denaturation ([FA]^50%) toward lower values of FA as more and more repeats were removed (Fig. 7C, summarized in Table 2). The stability toward FA is dependent not only on how many repeats but also on which repeats are removed from the protein. Based on the decline in [FA]^50%, removal of R1 has a relatively modest impact on fibril stability compared with R2 and R3. In good agreement with these results, bioinformatic investigations of the sequences for the three repeats using the FISH Amyloid tool (68) show that R1 is the least aggregation-prone repeat (and, by implication, contributes the least to fibril stability), with an average amyloidogenicity score pr. amino acid of 0.0353 compared with 0.0588 for R2 and 0.0437 for R3 (Fig. S6). However, its m-value is slightly decreased compared with the two other mutants, leading to a lower overall stability. Importantly, removing two repeats leads to a significant decrease in either [FA]^50% (ΔR1R3 or ΔR2R3) or the m_FA+pH value (ΔR1R2 and ΔR1R3) and a consequent dip in the overall stability of the protein. Besides the FapC ΔR1R2R3 mutant (see below), fibrils formed from the FapC ΔR2R3 and FapC ΔR1R3 proteins are the most destabilized compared with wt FapC, indicating an important role for R3 in stabilizing the fibrils. That the different FapC repeats play different roles in fibril formation has also been observed for CsgA, where the last repeat (R5) is the most aggregation prone and is also critical for polymerization (22).

Table 2.

Summary of FA stability of different FapC constructs based on solubilization measurements

Construct	mFA+pH (kcal mol−1 M−1)a	[FA]50% (M)a	No. of aa involvedb	Nc	ΔGd-Nwater (kcal mol−1)d	ΔGd-Nwater /N (cal mol-1 residue−1) e
FapC wt	0.38 ± 0.07	17.56 ± 0.34	50 ± 9	226	6.7 ± 1.2	29.5 ± 5.5
FapC ΔR1	0.33 ± 0.01	16.31 ± 0.09	46 ± 1	193	5.4 ± 0.1	27.9 ± 0.7
FapC ΔR2	0.41 ± 0.05	14.47 ± 0.17	52 ± 6	192	5.9 ± 0.7	30.9 ± 3.8
FapC ΔR3	0.50 ± 0.09	13.94 ± 0.25	58 ± 10	193	7.0 ± 1.3	36.1 ± 6.5
FapC ΔR1R2	0.22 ± 0.01	14.21 ± 0.29	39 ± 2	158	3.1 ± 0.2	19.8 ± 1.0
FapC ΔR1R3	0.17 ± 0.04	8.56 ± 1.03	35 ± 8	159	1.5 ± 0.4	9.2 ± 2.4
FapC ΔR2R3	1.44 ± 0.41	4.25 ± 0.13	121 ± 34	159	6.1 ± 1.8	38.5 ± 11.0
FapC ΔR1R2R3		<0.01		125

^aBased on data in Fig. 7C fitted to eq. 8.

^bBased on the linear correlation in Fig. 5D, m_FA+pH = 0.0148 × no. of amino acids − 0.354.

^cThe total number of residues in the protein, cfr. Fig. S1.

^dΔG_D-N^water = -m_FA*[FA]^50% (Equation 6).

The repeatless mutant (FapC ΔR1R2R3) is extremely sensitive to FA; already at 0.001% FA (0.3 mm) 30% is dissolved, and at 0.1% FA there is no amyloid left. This mutant is composed entirely of FapC's linker regions but nevertheless still forms fibrils on the hours-days timescale, although the fibrillation process is much less reproducible than that for the other FapC constructs (23, 66). Clearly, the fibrils formed by this mutant are much less resistant to FA than any of the other mutants; in fact, its properties are similar to those of fibrils formed by misfolded proteins such as α-synuclein, which dissolves completely around 0.1% FA (data not shown). Thus, fibrils containing as little as a single repeat retain a moderate resistance to FA, whereas there is a dramatic collapse of stability upon complete removal of repeats. This strongly indicates that repeats are indeed the key to functional amyloid stability.

Analysis of the FapC sequence using the ZipperDB tool (69) reveals that the N-terminal part (excluding the signal peptide), both linkers (L1 and L2), and the C-terminal all have segments of high fibrillation propensity (below −23 kcal/mol) (Fig. S7). These segments may rationalize the ability of this highly amputated mutant to form fibrils with amyloid characteristics, although the ensuing fibrils' high sensitivity to FA indicates that the linkers only make minor contributions to the exceptional stability of the functional amyloid. Indeed, linker regions are completely missing from the functional amyloid in E. coli, CsgA, whose five repeats are connected by only enough residues (4–5) to form a tight turn (22).

Solubility in SDS correlates well with stability against FA

To obtain complementary evidence for the quantification of destabilization of the different FapC variants, we turned to solubilization in SDS. FapC fibrils are largely resistant to strongly denaturing anionic surfactants such as SDS; boiling SDS is even used to remove less robust proteins as a way to purify FapC fibrils (13). Nevertheless, the effect has not been investigated systematically and even modest solubilization levels will be indicative of fibril stability. Accordingly, we incubated FapC fibrils in 58 mm SDS (corresponding to the concentration of SDS in SDS-PAGE loading buffer when loading samples on a gel) at a range of temperatures (21–95 °C) for 10 min. Supernatants from these incubations were then analyzed by SDS-PAGE to determine the amount of soluble protein. We observed a strong temperature dependence, with estimated solubilities rising from ∼ 0.2% at 21 °C to ∼5% at 95 °C (Fig. 8A). Solubility was only slightly increased under reducing conditions (1 mm TCEP, Fig. 8A). FapC contains two conserved Cys residues in a CXXC motif near the C terminus (position 213 and 216, Fig. S1), which may form intermolecular disulfide bonds during the early on-pathway FapC oligomerization steps, but this does not affect stability significantly (70). We also observe that disulfide bond formation is not important in FapC fibrillation, as FapC in the presence of the reducing agent DTT or FapC without the C₂₁₃XXC₂₁₆ motif (FapC-SS) show fibrillation kinetics similar to those of WT FapC (Fig. S8). This has also been observed previously for FapC from P. aeruginosa PAO1 (70). We carried out similar studies with the other 7 FapC deletion mutants and observed a significant increase in solubility for several of the mutants (Fig. 8B), up to 30–35% for the double mutant FapC ΔR2R3 and the triple mutant FapC ΔR1R2R3. We observe a very significant correlation between solubility in SDS at 20 °C (both under reducing and oxidizing conditions) and the midpoint of denaturation in FA (Fig. 8C). This corroboration by an independent approach indicates that solubility in FA is indeed a credible way of estimating fibrils' intrinsic ability to dissociate.

Figure 8.

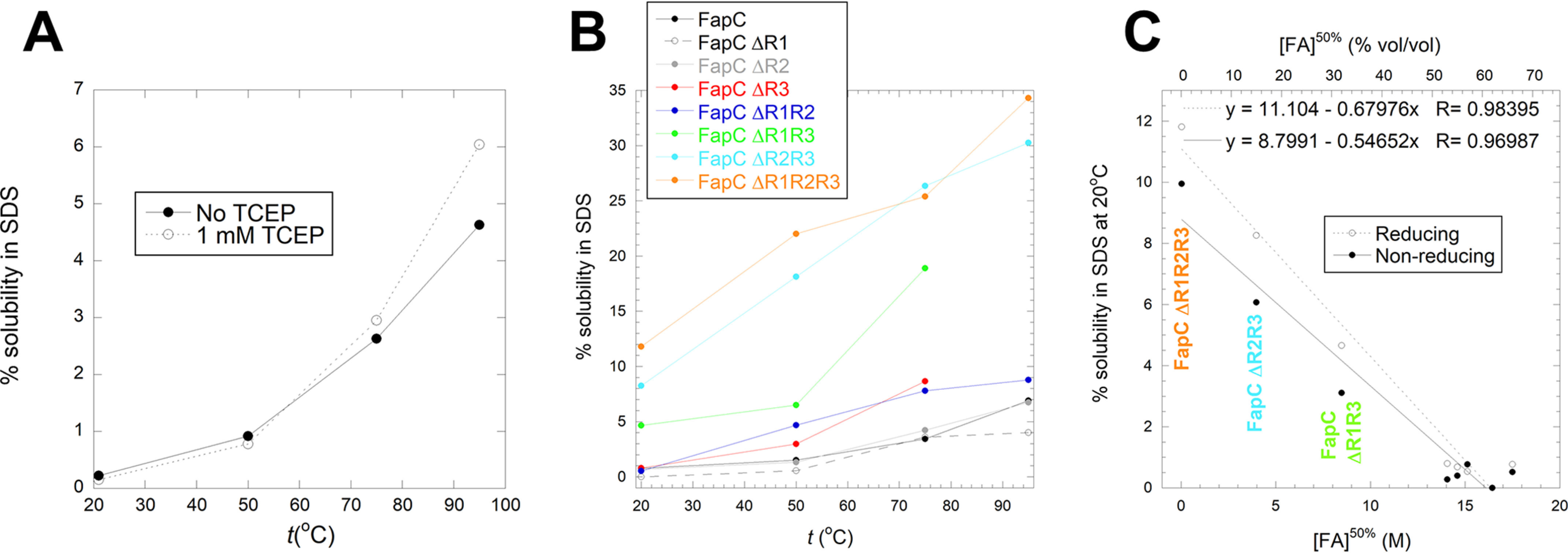
Solubilization of FapC fibrils in SDS. A, solubility of WT FapC in SDS at 20–95°C under reducing (1 mm TCEP) or nonreducing conditions. Solubility was quantified as in Fig. 7C. B, solubility under reducing conditions in SDS at 20–95°C for all 8 FapC variants. C, correlation between solubility in SDS at room temperature and the midpoint of denaturation in FA, shown for all 8 FapC variants. The three most destabilized variants are indicated with the same colors as those in panel B.

FapC fibril solubilization by FA predicts a relatively low stability compared with other fibrils; superior performance by FA is not easy to explain

We transformed the solubility data of FapC mutants in Fig. 7 to apparent stability as follows. Based on our previous analysis of the stabilities of lysozyme, S6 and Ubi in FA, we assume a linear relationship between [FA] and the free energy of unfolding, ΔG_D-N. The associated equilibrium constant of unfolding is formally defined as the ratio between dissolved and aggregated protein. We also considered the option of assuming that the equilibrium constant corresponds to the concentration of free protein, inspired by the use of free monomer concentration to determine the stability of Aβ fibrils (24) as well as other fibril stability studies (25); however, this approach does not yield a linear relationship between the free energy and [FA] and, therefore, does not allow us to extrapolate robustly to 0 M FA (data not shown). Data are instead fitted with Equation 2 and summarized in Table 2. In line with the general decline in values of [FA]^50%, they reveal a remarkable reduction in stability upon removal of two repeats. The decrease is less significant when only one repeat is removed because of the errors associated with the measurement, but they still reveal a reducing trend, particularly when viewed from the perspective of the midpoint of denaturation.

The overall stability of the fibrils (6.7 kcal/mol for full-length FapC and less for the variants) is very modest compared with naturally occurring globular proteins, which have stabilities in the 5–15 kcal/mol range (71). The value is comparable with, but certainly not higher than, the stabilities of fibrils formed from a range of other proteins, which are associated with neurodegenerative diseases or other misfolding conditions (25) but not otherwise optimized to form fibrils. The free energy per residue for FapC (ca. 30 cal/mol/residue) is actually substantially lower than any of the measured stabilities for these proteins and peptides, for which the values vary from ca. 40 to 500 cal/mol/residue. The highest stability contribution per residue in this study is assumed by small peptides whose entire sequence is most likely integrated into the amyloid structure, whereas larger proteins with more extensive regions of nonamyloid structure lead to lower scores (25). For FapC, it is likely that the linker regions are not involved in amyloid formation (72); however, restricting the analysis to the 3 imperfect repeats as contributors to fibril stability only doubles this figure and still leaves it on the low end of the scale. Assuming that our method of fibril stability estimation is correct, this raises the question of why a chemical denaturant such as GdmCl, which effectively unfolds very stable proteins, such as OmpA (ΔG_D-N = 16 kcal/mol and t_½^unfolding at 0 M GdmCl ∼800 years [73]) is quite unable to dissolve these fibrils. The point is made all the stronger by the fact that m-values for GdmCl based on our 3 globular proteins are ∼3 times higher than those for FA, illustrating the high efficacy of solubilization by GdmCl. Nevertheless, even a crass anionic surfactant like SDS only confers limited solubilization at temperatures as high as 95 °C. We speculate that the unique solubilization properties of FA reflect (1) a high activation barrier for FapC unfolding, which is selectively reduced by FA because of favorable solvation of the transition state, (2) very favorable solvation of the denatured state, or (3) a combination of the two phenomena. In the absence of kinetic data (which are currently not feasible to record by e.g. near-UV CD because of the high concentrations of FA needed and the low near-UV CD signal of FapC fibrils), it is not possible to provide any direct support for transition state stabilization, but it is worth noting the cooperative nature of the fibril build-up, which, in itself, constitutes a significant activation barrier to dissociation. Thus, each FapC monomer is stabilized not only by interactions with other monomers in the fibril (at least two monomers on either side in the fibril and possibly also intersheet contacts between multiple protofilaments in a given fibril) but also by contacts between the individual imperfect repeats, which most likely constitute β-hairpin helices (14, 21).

Using FA stability to predict the level of involvement of amino acids in fibrillation

Based on the correlation in Fig. 5D between m_FA and protein size, we use the m_FA values in Table 2 to predict the number of residues involved in FapC amyloid formation (Table 2). This assumes that the average degree of burial per residue (i.e. the reduction in solvent-accessible surface area) is the same for the 3 globular proteins as that for the residues forming amyloid structures. Such an assumption may be questioned. Loops can remain significantly exposed in the native state, and generally β-sheet proteins bury more surface area than α-helices and turns/loops, leading to ∼10, 20, and 30% accessibility, respectively, compared with the denatured state (74). A higher level of burial per residue means that a smaller number of residues is required to achieve the same level of burial; therefore, transfer of data based on e.g. pure α-helical properties to analysis of β-sheet proteins may lead to an overestimation of the number of residues involved in a given folding process. Lysozyme, S6, and ubiquitin contain significant amounts (10/46/34%, respectively) of β-sheet structure but also a major proportion of less organized structure, like coils and turns (49/27/43%, respectively), leading to a lower level of burial than all-β-sheet structures.

Full-length FapC and all single-repeat mutants show the same overall level of amino acids involved (49–59); this declines to ∼40 for two double repeats but then rises steeply to ∼120 for the third double repeat (FapC ΔR2R3). The number of residues in the imperfect repeats are ca. 105 for full-length FapC, declining to 70 for single repeats and 35 for double repeats. Thus, there is an overall satisfactory prediction for single repeats and two double repeats (with the caveats on m_FA values described above). The breakdown in the relationship between repeat length and m-values for FapC ΔR2R3 may be caused by a change in the nature of the fibril structure relative to the FA-denatured state. A greater m-value indicates a greater difference between compactness of the two ground states (FA-denatured and fibrillar states). Thus, either or both of the two states could change compactness; the denatured state could become more expanded and/or the fibrillar state more compact. The denatured state of FapC in FA has not been characterized in any detail, but we note that aggregated species are found at the very beginning of the aggregation of wt FapC, according to small-angle X-ray scattering (75, 76). This might be explained by a high propensity even in the denatured state to engage in intermolecular contacts; removal of repeats could destabilize these transient interactions and lead to a more fully expanded state. It seems unlikely that removal of fibrillar repeats would lead to a more compact structure unless the protein changes architecture to a fundamental extent, e.g. by integrating otherwise exposed regions, such as the linker sequences into the fibrillar state. This is a possibility in view of the ability of the repeat-free mutant to form (admittedly very FA-sensitive) fibrils (23, 77). More detailed but also methodologically demanding studies on the denatured and fibrillated states of FapC ΔR2R3, as well as the kinetics of their interconversion, are needed to address these questions.

Conclusions

We have quantitated the denaturing potency of formic acid against globular proteins using thermal scans and isothermal titration, monitored by near-UV CD. FA unfolds globular proteins reversibly and cooperatively; the effects go beyond simple pH-driven denaturation and show a linear relationship between unfolding free energy and FA concentration, revealing that FA is ∼3-fold less effective on a molar scale than guanidinium chloride as a denaturing agent. Nevertheless, protonated FA is radically different from its ionized formate counterpart, which actually stabilizes proteins. Formamide is ca. 3 fold weaker than FA as a denaturant, highlighting the role of the acidic −OH group. Heat capacity changes indicate that the unfolded state is more compact in FA than in chemical denaturants. The m_FA value of unfolding scales with protein size, suggesting weak binding interactions between FA and the polypeptide chain. FA was used to solubilize fibrils of the functional amyloid FapC, revealing a surprisingly low stability. Importantly, stepwise removal of the imperfect repeats progressively decreased stability. Complete removal, whereas not preventing fibrillation, led to fibrils that were extraordinarily sensitive to FA, indicating that these repeats are central to the stability of functional amyloid.

Experimental procedures

Materials

Hen egg white lysozyme (130 residues, 14.7 kDa), bovine ubiquitin (Ubi, 76 residues, 8.6 kDa), and all other chemicals were from Sigma-Aldrich.

Design and purification of the FapC repeat deletion mutant proteins

Seven FapC mutant proteins (based on FapC from the Pseudomonas sp. strain UK4) lacking 1–3 of the imperfect repeats (FapC ΔR1, ΔR2, ΔR3, ΔR1R2, ΔR1R3, ΔR2R3, and ΔR1R2R3) were cloned into an ampicillin-resistant pET31b vector without the N-terminal signal peptide (aa 1–24) and with a C-terminal 6× His tag, although the FapC wt was cloned into a kanamycin-resistant pET28a vector. A variant of FapC wt in which Cys213 and Cys216 were replaced with Ser213 and Ser216 was prepared as described previously (70). The full amino acid sequences are included in Fig. S1. All proteins were expressed in E. coli BL21(DE3) and purified as described previously (23, 66). Eluted protein fractions were immediately frozen in liquid nitrogen and stored at −80 °C until further use.

Purification of S6

For reasons of availability, we used a double mutant of S6 rather than wt S6. Two Cys residues were inserted in the N- and C-terminal parts of the protein, which show high mobility in the crystal structure and therefore are expected to have little, if any, effect on overall protein stability. Accordingly, a pET28(+) expression vector was produced by GenScript (Piscataway, NJ) to express the 101-aa S6 from Thermus thermophilus containing the mutations Met1Cys and Phe97Cys (S6^{M1C, F97C}). The protein was expressed using a protocol based on the original procedure (41). The plasmid was transformed into E. coli BL21(DE3) using single-pulse electroporation at 1800 V in an Electroporator 2510 (Eppendorf, Hamburg, Germany). The transformed cells were incubated for 1 h at 37 °C in Super Optimal with catabolite repression medium, spread on an LB agar plate containing 50 μg/ml kanamycin, and grown overnight (O/N) at 37 °C. A single colony was resuspended in ∼ 2 ml LB medium, spread on freshly prepared LB agar plates, and grown O/N at 37 °C, after which the cells were resuspended in a few milliliters of LB medium and used to inoculate 4 L LB medium. The cells were grown at 37 °C at 180 rpm, induced with 1 mm IPTG at an optical density at 600 nm of ∼0.8, and grown for additional 4 h before being harvested by centrifugation (4000 rpm, 4 °C, 20 min). The cell pellet was dissolved in a few milliliters of 50 mm Tris, pH 7.4, containing 1 mm TCEP, 50 mg/L RNase, 50 mg/L DNase, and a tablet of Roche cOmplete Mini Protease Inhibitor mixture and stored at −80 °C. After thawing, the cells were lysed by sonication using a Q500 sonicator (Qsonica, Connecticut USA) set to ten 20-s pulses with a 10-s pause at 20% intensity, using a 1.6-mm Microtip probe. The lysate was centrifuged (30,000 × g, 4 °C, 30 min) and the pellet discarded. Nucleic acid contaminants were removed by addition of 0.5%, w/v, polyethyleneimine and stirring for 20 min at 4 °C, after which the solution was centrifuged again. The protein content was precipitated from the supernatant with 70% (NH₄)₂SO₄ and stirring for 1 h at 4 °C. The solution was centrifuged (34,000 × g, 45 min) and the supernatant discarded. The pellet was resuspended in MQ water with 1 mm TCEP and dialyzed against 50 mm Tris-HCl (pH 7.5) and 1 mm TCEP for 24 h. After filtration through a 0.22-μm filter, the solution was loaded onto a CM-Sepharose column coupled to an Äkta Pure system (GE Healthcare Life Sciences, Brøndby, Denmark). The sample was loaded on a column equilibrated with buffer A (50 mm Tris-HCl, 1 mm TCEP, pH 7.5) and run with 1 ml/min. The protein was eluted with a gradient of buffer B (buffer A plus 1 M NaCl) in 1-ml fractions. Based on SDS-PAGE, S6 was identified in the second major peak on the chromatogram (data not shown), and the S6-containing fractions were pooled and dialyzed against 50 mm Tris-HCl (pH 7.5) and 1 mm TCEP for 24 h. Protein concentration was determined using an ε₂₈₀ of 12,700 M⁻¹ cm⁻¹ and a molecular weight of 11.97 kDa on a NanoDrop 1000 (Thermo Scientific). S6 was aliquoted into 1-ml fractions of 1 mg/ml, frozen, and lyophilized for later use.

CD spectroscopy

CD measurements were performed on a Chirascan-plus CD spectropolarimeter (Applied Photophysics, Leatherhead, UK). Lyophilized protein was weighed out on an analytical scale and dissolved directly in FA (or FM) of different concentrations. Both protein concentration and solution pH were measured afterward. In control experiments, protein solutions were adjusted to similar pH values using HCl or NaOH. FA and FM absorb strongly below 240 nm, precluding the use of far-UV CD measurements. Protein denaturation was instead monitored in the near-UV (aromatic) CD region, which reports on tertiary structure. All three proteins contain aromatic amino acids to different extents (lysozyme, 6 Trp and 3 Tyr; S6, 1 Trp and 4 Tyr; Ubi, 1 Tyr). Denaturation was followed with 1 mg/ml protein at 290, 282, and 285 nm for lysozyme, S6, and Ubi, respectively. The samples were transferred into a 3-mm quartz cuvette with a cap to avoid evaporation. Thermal scans were carried out between 5 °C and 95 °C with a scan rate of 1 °C/min, step resolution of 0.1 °C, 1 s time points and bandwidth of 2 nm. Data were fitted in KaleidaGraph using the following equation:

$$\mathrm{E}\mathrm{l}\mathrm{l}\mathrm{i}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}=\hspace{0.17em}\frac{\left({\alpha }_N+{\beta }_{N}T\right)+\left({\alpha }_{\mathrm{D}}+{\beta }_{D}T\right)\hspace{0.17em}{e}^{-\frac{\Delta H_{T_m}\left(1-\frac{T}{T_m}\right)}{RT}}}{1+e^{-\frac{\Delta H_{T_m}\left(1-\frac{T}{T_m}\right)}{RT}}}$$ (1)

Here, α_N and α_D are the ellipticity values of the native (N) and denatured (D) state, respectively, at 25 °C, and β_N and β_D describe the linear temperature dependence of the ellipticities of these two states. ΔH_Tm is the enthalpy of denaturation at the midpoint of denaturation, T_m. (T_m is in units of Kelvin; we use the term t_m to refer to the value in centigrade.) This equation does not include specific heat capacity, ΔC_p, because this value cannot be determined with sufficient accuracy from a single thermal scan. However, by determining ΔC_p separately (see Results and discussion), the free energy, ΔG_T, at 25 °C can be determined using the following equation:

$$\begin{array}{c}\Delta G_T=\Delta H_{T_m}\left(1-\frac{T}{T_m}\right)-\Delta C_p\left(T_m-T+T\hspace{0.17em}\ln \left(\frac{T}{T_m}\right)\right)\end{array}$$ (2)

Using these ΔG values, we calculate the fraction of natively folded protein (f_N) as

$$\begin{array}{c}{f}_N=\frac{\left[N\right]}{\left[D\right]+\left[N\right]}=\frac{1}{1+K_{D-N}}=\frac{1}{1+e^{\frac{-\Delta G}{RT}}\hspace{0.17em}}\end{array}$$ (3)

Fluorescence spectroscopy

2 mg/ml protein stocks of lysozyme, S6, and ubiquitin were prepared from lyophilized material solubilized in MQ. The protein stocks were diluted into 1-ml samples with final concentrations of 1 mg/ml (lysozyme), 0.5 mg/ml (S6), or 0.25 mg/ml (ubiquitin) in FA concentrations ranging from 0–45% (v/v). Lysozyme was also treated with 10–90% (v/v) FM. The samples were incubated at RT for 30 min before measurements to ensure that equilibrium was achieved. Fluorescence measurements were performed on a Cary eclipse fluorescence spectrophotometer (Agilent) using a 10-mm quartz cuvette under isothermal conditions (25 °C). Trp fluorescence was measured by excitation at 295 nm (5 nm slit), and the emission spectrum was recorded between 305 and 450 nm (2.5 nm slit), whereas combined Trp and Tyr fluorescence was recorded by excitation at 280 nm and emission at 295–450 nm. All spectra were recorded with 1 nm resolution and scanning speed of 0.5 nm/s. Shift in Trp or Trp+Tyr emission intensity as a function of FA or FM concentration was fitted to the following equation:

$$\begin{array}{c}\mathit{Fluorescence}=\frac{\left({\alpha }_N+{\beta }_N\left[FA\right]\right)+\left({\alpha }_D+{\beta }_D\left[FA\right]\right){10}^{\frac{m_{D-N}\left(\left[FA\right]-{\left[FA\right]}^{50\mathrm{\%}}\right)}{-RTln\left(10\right)}}}{1+{10}^{\frac{m_{D-N}\left(\left[FA\right]-{\left[FA\right]}^{50\mathrm{\%}}\right)}{-RTln\left(10\right)}}}\hspace{0.17em}\end{array}\left(4\right)$$ (4)

Here, analogously to Equation 2, α_N and α_D are fluorescence signal amplitudes of the native and the denatured states, respectively, whereas β_N and β_D are the respective baseline slopes. [den]^50% is the denaturant concentration at which [N] and [D] are equal. The factor –RT ln(10) = −1.36 kcal/mol ensures that the m_D-N value reports on the linear dependence of ΔG_D-N (rather than ln K_D-N) on [FA]. This equation was also used to monitor unfolding of 1 mg/mL S6 in 0–40% FA at RT using the near-UV CD signal at 282 nm.

Lysozyme chemical stability

Lysozyme was incubated at a concentration of 1 mg/ml in 100 µl of either MQ water, HCl (pH2) 10% FA, or 30% FA at either 60 °C or 90 °C in a thermoblock. 20-µl samples were taken out after 10, 30, and 60 min, mixed with reducing loading buffer (G Biosciences), and run on SDS-PAGE at 150 V for ∼70 min, together with a prestained PageRuler protein ladder (Mark 12, Thermo Scientific). Gels were stained for 45 min in Coomassie brilliant blue (CBB) solution (1.2 mm CBB, 5% ethanol, 7% acetic acid) and destained O/N in destaining solution (5% ethanol, 5% acetic acid).

Fibril stability toward SDS

Fibrils formed by wt FapC and FapC mutants were produced as follows. The FapC solution was desalted from elution buffer (8 M GdmCl, 50 mm Tris-HCl, 300 mm imidazole, pH 8) into 50 mm Tris-HCl, pH 7.4, in 0.5-ml fractions using a pre-equilibrated PD-10 desalting column (GE Healthcare), and concentration was measured on a NanoDrop using a theoretical extinction coefficient of 10,095 M⁻¹ cm⁻¹, calculated from the amino acid sequences (all FapC variants contain 1 Trp, 3 Tyr, and 2 Cys) using the website ExPASy (https://web.expasy.org/protparam/). Protein solutions were then allowed to fibrillate O/N at 37 °C with 900 rpm shaking in a tabletop Eppendorf shaker (Thermo Scientific). After 24 h of incubation, equal amounts of the fibrillated sample were aliquoted into 8 tubes, the fibrils were pelleted by centrifugation (13,500 rpm, 15 min) in a MicroStar12 tabletop centrifuge (VWR), the supernatants were removed, and the concentration of unfibrillated monomer was measured to determine the exact amount of fibrillated protein. Next, a nonreducing (58 mm SDS, 83 mm Tris-HCl, pH 6.8) and a reducing (58 mm SDS, 83 mm Tris-HCl, 1 mm TCEP, pH 6.8) SDS solution were prepared. The fibril samples were resuspended in 60 μl of either nonreducing or reducing SDS solution, yielding a final FapC concentration of 3.25 mg/ml. The samples were then incubated at 21 °C, 50 °C, 75 °C, or 95 °C for 10 min. All samples were centrifuged as described previously, and the supernatant of each sample was transferred to new tubes. Glycerol (10% [w/v]) and bromphenol blue (0.005% [w/v]) were added to the supernatants, and the samples were analyzed with SDS-PAGE as described above. The intensity of the protein bands was quantified using ImageJ. The percentage of solubilized FapC fibril was calculated for each sample by comparing their values to a dilution series of monomeric FapC protein of known concentrations.

Fibril stability toward FA

FapC wt and FapC mutants, purified in 8 M GdmCl, were desalted directly from 8 M GdmCl into pure MQ as described in the preceding section. Concentration was measured by UV absorbance at 280 nm, and the samples were fibrillated as described above. α-Synuclein was included for comparison, and lyophilized α-synuclein was solubilized in MQ and filtrated through 0.22-μm filters, and concentration was determined by UV₂₈₀. α-Synuclein was fibrillated for 80 h at 300 rpm, 37 °C, and was followed by ThT to make sure an end plateau was reached (data not shown). Fibrils were spun down (13,500 rpm, 15 min), and the concentration of protein remaining in the supernatant was measured. This allows for calculation of the amount of pelleted protein fibrils. The fibrils were then resuspended in MQ to a concentration of 1 mg/ml and aliquoted into Eppendorf tubes. The fibrils were pelleted again and the supernatant discarded before resuspending them at 1 mg/ml in different concentrations of FA, followed by 10 min of incubation at room temperature. The samples were again centrifuged, and 20 μl of each supernatant was lyophilized for ∼1 h. The lyophilized material was resuspended in 20 μl of MQ and run on SDS-PAGE. Gels were quantified using Gel Analyzer 2010a (78) and normalized to the band where fibrils were dissolved in 100% FA. From these gel quantifications, we can determine the percent dissolution for a given mutant at the investigated FA concentrations by comparing with the 100% FA-treated sample where everything is dissolved. We derive a predicted relationship between the fraction of dissolved protein and [FA] as follows. We assume a linear relationship between the free energy of unfolding in FA (ΔG_D-N^FA) and [FA]:

$$\Delta G_{D-N}^{FA}=\Delta G_{D-N}^{water}+m_{FA}·\left[FA\right]=m_{FA}·{\left(\left[FA\right]-[FA\right]}^{50\mathrm{\%}})=-RT·\mathrm{l}\mathrm{n}\hspace{0.17em}(10)·\mathrm{l}\mathrm{o}\mathrm{g}\hspace{0.17em}(K_{D-N}^{FA})=-1.36\times \hspace{0.17em}\mathrm{l}\mathrm{o}\mathrm{g}\hspace{0.17em}(K_{D-N}^{FA})\hspace{0.17em}$$ (5)

where [FA]^50% is the FA concentration where the fibrillar state (F) and the monomeric state (M) are equally stable, i.e.

$$\Delta G_{D-N}{}^{FA50\%}=0\iff \Delta G_{D-N}{}^{water}=\hspace{0.17em}-m_{FA}*{\left[FA\right]}^{50}{}^{\%}$$ (6)

and operationally define

$$K_{D-N}{}^{FA}=\left[M\right]/\left[F\right]$$ (7)

(analogous to the relationship between native and unfolded protein in conventional unfolding). This leads to the following expression for the percentage dissolved protein, y_diss, as function of [FA]:

$$\begin{array}{c}{y}_{diss}=100·\frac{\left[M\right]}{\left[M\right]+\left[F\right]}=100·\frac{1}{1+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$K_{D-N}^{FA}$}\right.}\\ =\frac{100}{1+{10}^{\frac{m_{FA}·\left({\left[FA\right]}^{50\mathrm{\%}}-\left[FA\right]\right)}{1.36}}}\hspace{0.17em}\end{array}$$ (8)

In this model, no protein dissolves in the absence of FA and all protein is dissolved at high [FA]. This is consistent with our observations.

FTIR spectroscopy of the different fibrils

2.0 μl of fibrillated sample was dried onto an attenuated total reflection (ATR) crystal with dry nitrogen on a Tensor 27 FTIR instrument (Bruker Optics, Billerica, MA). OPUS version 5.5 was used to process the data, including calculating atmospheric compensation, baseline subtraction, and second-derivative analysis. All spectra were made as accumulations of 68 scans with a resolution of 2 cm⁻¹ in the range of 1000–3998 cm⁻¹. Only the 1600–1700 cm⁻¹ range, comprised of information about secondary structure, is shown.

Data availability

All data are available in the manuscript.