Abstract
The current situation with the SARS-CoV-2 pandemic indicates the importance of new approaches in vaccine design. In order to design new attenuated vaccines, to decrease virulence of virus wild types, it is important to understand what allows a virus to hijack its host cell's metabolism, a property of all viruses. RNA and protein sequences obtained from databases were used to count the number of atoms of each element in the virions of SARS, MERS and SARS-CoV-2. The number of protein copies and carbohydrate composition were taken from the literature. The number of lipid molecules was estimated from the envelope surface area. Based on elemental composition, growth equations were balanced, and thermodynamic properties of the viruses were determined using Patel-Erickson and Battley equations. Elemental and molecular compositions of SARS, MERS and SARS-CoV-2 were found, as well as their standard thermodynamic properties of formation and growth. Standard Gibbs energy of growth of virus nucleocapsids was found to be significantly more negative than that of their host tissue. The ratio of Gibbs energies of growth of virus nucleocapsids and host cell is greater than unity. The more negative Gibbs energy of growth of viruses implies that virus multiplication has a greater driving force than synthesis of host cell components, giving a physical explanation of why viruses are able to hijack their host cell's metabolism. Knowing the mechanism of viral metabolism hijacking can open new paths for vaccine design. By manipulating chemical composition of viruses, virulence can be decreased by making the Gibbs energy of their growth less negative, resulting in decreased multiplication rate, while preserving antigenic properties.
Keywords: Biophysics, Microbiology, Virology, Thermodynamics, Viruses, Viral disease, SARS, MERS, SARS-CoV-2, Gibbs energy, Virus multiplication rate
Biophysics; Microbiology; Virology; Thermodynamics; Viruses; Viral disease; SARS; MERS; SARS-CoV-2; Gibbs energy; Virus multiplication rate.
1. Introduction
SARS, MERS and SARS-CoV-2 are three related RNA viruses, belonging to the family Coronaviridae and sharing the same morphology (Figure 1) and similar (but not identical) chemical composition. The nucleic acid sequences of all three viruses, SARS (He et al., 2004), MERS (van Boheemen et al., 2012) and SARS-CoV-2 (Wu et al., 2020) have been determined. The lipid constituents of the viral envelopes of all three viruses are similar, since all three viruses attack the same host tissue and hence their envelopes are formed by budding from the same kind of cell membrane (Riedel et al., 2019). The protein components of the envelope differ between SARS, MERS and SARS-CoV-2 (Table 1). There are no data on capsid structure for the three viruses, except that they are of helical symmetry, since they are difficult to culture and therefore poorly characterized (Riedel et al., 2019).
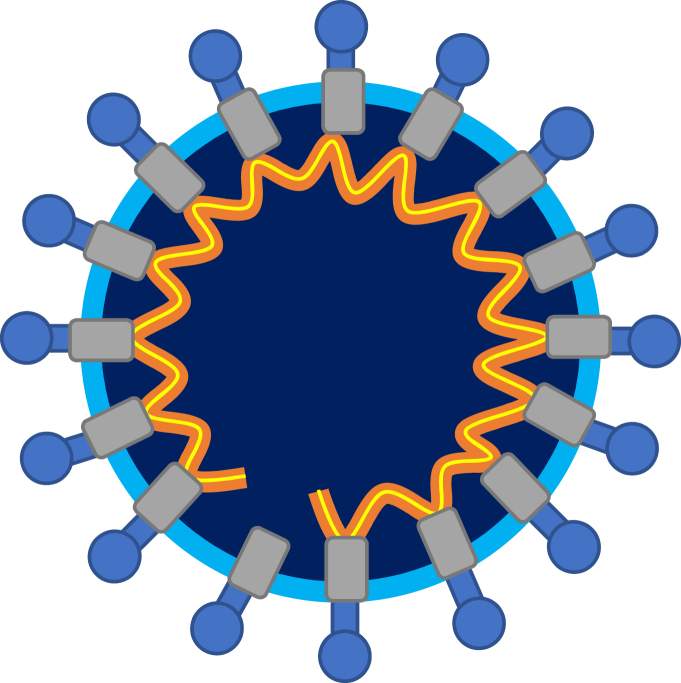
Figure 1.
Schematic representation of a virus from the family Coronaviridae. The yellow line represents RNA, orange – nucleoproteins lining the RNA (yellow and orange combined represent the nucleocapsid), grey – membrane proteins, light blue – lipids in the envelope, blue spikes – spike proteins.
Table 1.
RNA and protein data for the viruses analyzed in this work. The number of protein copies per virion varies, even within a single species (Neuman et al., 2011, 2006). For example, the number of spike protein trimers can vary between 50 and 100 per virion. The average number is 74 trimers, giving 74 × 3 = 222 spike proteins in total (Neuman et al., 2011, 2006).
| Virus | Name | Number of copies | ID number | Source |
|---|---|---|---|---|
| SARS | Genome | 1 | NC_004718.3 | NCBI |
| Nucleoprotein | 2368 | P59595 | UniProt | |
| Membrane protein | 1184 | Q3S2C1 | UniProt | |
| Spike protein | 222 | P59594 | UniProt | |
| MERS | Genome | 1 | NC_019843.3 | NCBI |
| Nucleoprotein | 2368 | R9UM87 | UniProt | |
| Membrane protein | 1184 | QGW51926.1 | NCBI | |
| Spike protein | 222 | A0A140AYZ5 | UniProt | |
| SARS-CoV-2 | Genome | 1 | NC_045512.2 | NCBI |
| Nucleoprotein | 2368 | QIK50455.1 | NCBI | |
| Membrane protein | 1184 | QHR63293.1 | NCBI | |
| Spike protein | 222 | QHR63290.2 | NCBI | |
Empirical formulas of the three viruses allow calculation of thermodynamic properties (enthalpy, entropy, Gibbs energy) of formation and growth of each of the three viruses. Gibbs energy allows estimation of the spontaneity of formation of new virions and the rate of their multiplication (Popovic and Minceva 2020a).
Viral multiplication is fundamentally a chemical process that can be represented by a growth reaction (Von Stockar, 2014; Battley, 1998; Popovic and Minceva, 2020a). Gibbs energy of growth, through nonequilibrium thermodynamics, allows comparison of growth reaction rates of host cells and viruses (Popovic and Minceva, 2020a; Popovic and Minceva, 2020b). Knowledge of growth reaction rates allows us to gain insight into multiplication dynamics of the microorganisms (Westerhoff et al., 1982; Von Stockar, 2014). The multiplication dynamics can be of benefit to epidemiologists and infectologists, to estimate the maximal virus multiplication rate and to quantitatively estimate viral reservoir in a patient or a population. Thus, the knowledge of reservoir size and basic reproductive number can enable epidemiologists to estimate virus transmission dynamics (Kucharski et al., 2020; Fang et al., 2020).
Composition of viruses can be estimated, based on their nucleic acid and protein sequences. Based on nucleic acid composition, protein sequences and capsid structures, Jover et al. (2014) determined compositions of icosahedral and spherical DNA bacteriophages, and described their impact on oceanic cycling of the elements. Virus shapes were approximated by geometric figures, such as spheres and cylinders. A virus head was represented by a ball with a fraction of its internal volume filled by DNA. On the surface of the ball, a spherical shell with a uniform thickness was used to represent the capsid and estimate the quantity of proteins in the virion. When present, virus tails were approximated by hollow cylinders made of protein. The method gave accurate predictions for viruses of known composition (Jover et al., 2014).
Some aspects of life cycles of various virus species have already been analyzed using thermodynamics. Katen and Zlotnick (2009) analyzed the thermodynamics of capsid assembly for several viruses, treating it as a polymerization reaction and providing new insights into the assembly mechanisms of spherical virus capsids, as well as into the biology of the viral life cycle. Ceres and Zlotnick (2002) used thermodynamics to analyze hepatitis B virus capsid assembly and found that it has a negative Gibbs energy change, implying that the process is thermodynamically spontaneous. Casasnovas and Springer (1995) studied the kinetics and thermodynamics of human rhinovirus interaction with its receptor, determining the enthalpy and Gibbs energy of their association, and analyzing their influence on virus disruption. Gale (2020) analyzed thermodynamics of virus binding to host cell receptors and proposed new directions for designing antiviral therapies. Mahmoudabadi et al. (2017) developed a quantitative description of viral infection energetics and they made predictions about viral evolution. In addition to studies of viral component synthesis and self-assembly, Tzlil et al. (2004) made a statistical thermodynamic description of viral budding and found that complete budding (full wrapping of nucleocapsids) can only take place if the adhesion energy exceeds a certain, critical, bending Gibbs energy. However, there is still insufficient quantitative understanding of infection energetics (Mahmoudabadi et al., 2017).
The goal of this research is to determine the elemental and molecular composition of SARS, MERS and SARS-CoV-2, and make thermodynamic characterization of the three viruses, by finding enthalpy, entropy and Gibbs energy of formation and growth of all three viruses.
2. Methods
Elemental and molecular composition of the three viruses was determined by counting atoms coming from each of the four principal molecular constituent of virions: nucleic acid, proteins, lipids and non-nucleic acid carbohydrates (Knight, 1975). For this to be done, two pieces of information had to be known: (1) the number of atoms of each element in the molecular constituents and (2) the number of molecules of each constituent in the virion.
2.1. Virus elemental and molecular composition
The four main molecular components of viruses are: nucleic acids, proteins, lipids and non-nucleic acid carbohydrates (Knight, 1975). Since each of these molecular classes has a well-defined elemental composition, it was possible to find the elemental composition of virions. The calculations for SARS, MERS and SARS-CoV-2 were done using custom made software.
2.1.1. Nucleic acids
The number of atoms of each element coming from nucleic acids was calculated using an atom counting method. Nucleic acid sequences were obtained from the NCBI database (National Center for Biotechnology Information, 2020) and are listed in Table 1. Since the elemental composition of each nucleotide residue in the sequence is known, the number of atoms of each element in the nucleic acid was found by going along the sequence and adding atoms of each element coming from each residue. Coronaviruses contain only one copy of their single stranded RNA genomes.
The composition of viral nucleic acids was determined using an atom counting method. First, nucleic acid sequences were obtained from the NCBI database (National Center for Biotechnology Information, 2020) and are listed in Table 1. Since the elemental composition of each nucleotide residue in the sequence is known, the number of atoms of each element in the nucleic acid was found by going along the sequence and adding atoms of each element coming from each residue. The result of such a calculation is a nucleic acid formula of the form CNnaCHNnaHONnaONNnaNSNnaS, where NC(NA), NH(NA), NO(NA), NN(NA) and NS(NA) are the number of C, H, O, N and S atoms in the nucleic acid. The molar mass of the nucleic acid, m (NA) can be calculated using the formula
| (1) |
where NA is Avogadro's number and AJ is the atomic mass of element J.
2.1.2. Proteins
The atom counting method was also used to find the number of atoms coming from proteins. Protein sequences were taken from the UniProt database (The UniProt Consortium, 2019) and the NCBI database (National Center for Biotechnology Information, 2020), and are listed in Table 1. Coronavirus particles consist of four kinds of proteins: nucleoproteins (N), membrane proteins (M), envelope proteins (E) and spike proteins (S) (Neuman and Buchmeier, 2016). Envelope proteins were not considered due to their low abundance in the virus (Neuman and Buchmeier, 2016). They improve, but are not required, for the functioning of the virus (Neuman and Buchmeier, 2016; DeDiego et al., 2007; Kuo and Masters, 2010). Thus, they do not have a significant influence on elemental composition and thermodynamic properties of the viruses. The number of protein copies in coronavirus particles was reported by Neuman et al. (2011, 2006) and is summarized in Table 1.
Similarly to nucleic acids, protein composition was found by counting atoms coming from each amino acid residue. The protein sequences were taken from the UniProt database (The UniProt Consortium, 2019) and the NCBI database (National Center for Biotechnology Information, 2020), and are listed in Table 1. The result of such a calculation is a protein formula of the form CNprCHNprHONprONNprNSNprS, where Npr,C, Npr,H, Npr,O, Npr,N and Npr,S are the number of C, H, O, N and S atoms in a single protein molecule (Table 2). From the formula, the protein's molar mass in Daltons, Mr,pr, can be calculated
| (2) |
where Npr,J is the number of atoms of element J in the protein. Mr,pr is converted into the mass of a single protein molecule, mpr, molecule by dividing it by Avogadro's number
| (3) |
Table 2.
Calculated viral protein data.
| Virus | Protein name | Number of copies | Mr (Da) | Atoms per protein molecule |
||||
|---|---|---|---|---|---|---|---|---|
| C | H | O | N | S | ||||
| SARS-CoV-2 | Nucleoprotein | 2368 | 45624.58 | 1971 | 3137 | 629 | 607 | 7 |
| Membrane protein | 1184 | 25146.01 | 1165 | 1823 | 301 | 303 | 8 | |
| Spike protein | 222 | 141175.1 | 6336 | 9770 | 1894 | 1656 | 54 | |
| MERS | Nucleoprotein | 2368 | 45047.17 | 1965 | 3102 | 611 | 594 | 7 |
| Membrane protein | 1184 | 24516.27 | 1128 | 1756 | 302 | 282 | 13 | |
| Spike protein | 222 | 149380.5 | 6681 | 10245 | 2029 | 1737 | 63 | |
| SARS | Nucleoprotein | 2368 | 46023.9 | 1985 | 3150 | 633 | 618 | 7 |
| Membrane protein | 1184 | 25059.92 | 1155 | 1809 | 300 | 303 | 10 | |
| Spike protein | 222 | 139121.8 | 6252 | 9593 | 1871 | 1609 | 59 | |
However, unlike nucleic acids, structural proteins in viruses are present in multiple copies. Thus, the number of atoms in each capsid protein was multiplied by the number of the protein copies present in the capsid.
Coronaviridae virions consitst of four proteins: spike proteins (S), envelope proteins (E), membrane proteins (M) and nucleoproteins (N) (Neuman and Buchmeier, 2016) (Figure 1). The most distinctive feature of Coronaviridae are the spikes on the virion surface made of spike proteins (Neuman and Buchmeier, 2016). On the average, a coronavirus has 74 spikes, each consisting of a spike protein trimer, giving 222 spike proteins per virion (Neuman et al., 2011). The envelope protein is encoded by all known coronavirus genomes, but its role is still under debate (Neuman and Buchmeier, 2016). The envelope protein is probably best viewed as a multifunctional accessory protein that contributes to both virus growth and pathogenesis (Neuman and Buchmeier, 2016). Since the E protein is present in virions in small amounts (Neuman and Buchmeier, 2016), its contribution to virion chemical composition will be neglected. The most important role in coronavirus particle assembly is that of the membrane protein (Neuman and Buchmeier, 2016). The membrane proteins span through the viral envelope (Neuman et al., 2011). On the outer side, M proteins hold the spikes, while on the inside they bind the nucleoproteins, thus connecting the ribonucleoprotein core to the envelope (Neuman et al., 2011). For each S protein trimer, there are 8 M protein dimers (Neuman et al., 2011). Thus, in an average coronavirus there are 1184 copies of the M protein (Neuman et al., 2011). The nucleoprotein surrounds the viral RNA. Analysis of coronaviruses has shown that M and N proteins come in a fixed ratio, although the value differs between 1 and 3 in various studies (Neuman et al., 2011). In this work, the mean value of 2 N proteins per an M protein will be taken.
The number of atoms of element J coming from the all viral proteins is
| (4) |
c(X) the number of copies of protein X in the virion and N(X) is the number of atoms of element J in a single molecule of X. Here, X represents S, M and N proteins. The total mass of all proteins in the virion is
| (5) |
2.1.3. Lipids
Lipids are located in the viral envelope. Since enveloped viruses bud off their host cells, their lipid composition resembles that of the host cell membrane. Thus, the lipid composition of the viral envelopes was represented with that of the human cell membrane: 17% phosphatidylcholine, 6% phosphatidylserine, 16% phosphatidylethanolamine, 17% sphingomyelin, 2% glycolipids and 45% cholesterol (mole fractions) (Cooper, 2000). More information on the lipid constituents can be found in Table 3. The number of lipid molecules was determined from the envelope surface area and the average surface area taken by a single lipid molecule, taken from Ingólfsson et al. (2014). The envelope surface area was calculated from virus particle diameter, reported by Neuman and Buchmeier (2016). A correction was made for the envelope surface area taken by membrane proteins, using the average protein density (Serdyuk et al., 2007; Jover et al., 2014) and viral envelope thickness (Neuman and Buchmeier, 2016).
Table 3.
Virus lipid representative molecules, their chemical formulas and abundances. The abundances are mole fractions of the total lipid content and were taken from (Cooper, 2000).
| Class | Representative name | Formula | Mole fraction |
|---|---|---|---|
| Phosphatidylcholine | 1-Oleoyl-2-palmitoylphosphatidylcholine | C42H82O8NP | 17% |
| Phosphatidylserine | Phosphatidylserine (18:0/18:1) (PubChem CID: 9547087) | C42H79O10NP | 6% |
| Phosphatidylethanolamine | Phophatidylethanolamine(15:0/20:0) (ChemSpider ID: 394115) | C40H80O8NP | 16% |
| Sphingomyelin | C18 Sphingomyelin | C41H85O6N2P | 17% |
| Glycolipids | Stearoyl-glucose | C24H46O7 | 2% |
| Cholesterol | Cholesterol | C27H46O | 45% |
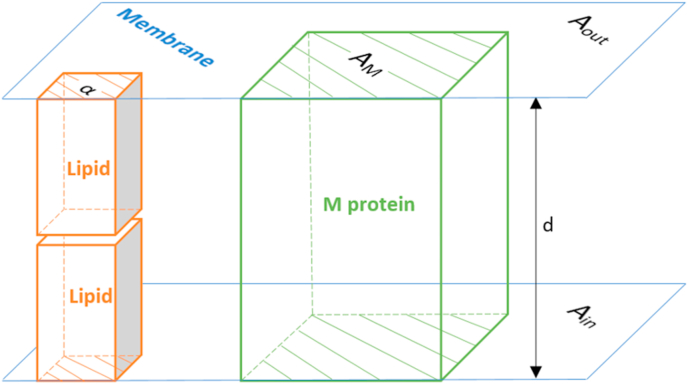
The total number of lipid molecules in the envelope was calculated from its surface area (Figure 2). The total area of the envelope, A, is equal to the sum of the envelope inner, Ain, and outer surface area, Aout
| (6) |
Figure 2.
Schematic representation of the viral envelope. The envelope is a lipid bilayer membrane of thickness d, consisting of lipids and membrane (M) proteins. It has two surface areas: one facing outside the virion, Aout, and one inside the virion, Ain. The total area taken by M proteins, on both sides of the membrane, is AM. The average area covered by a lipid molecule is α.
The outer surface area is the surface area of a sphere with a radius equal to the radius of the virus, r,
| (7) |
Radii of coronaviruses vary, even within a single species, but an average coronavirus has a radius of r = 45 nm (Neuman and Buchmeier, 2016). The inner surface area is the area of the inner surface of the viral envelope, which has a thickness of d = 8 nm (Neuman and Buchmeier, 2016). Thus,
| (8) |
The virus surface area, A, is covered with M proteins and lipids. The surface area covered by M proteins, AM, can be determined from their mass and the average protein density, ρ = 1.36986 ∙ 10−21 g/nm3, reported in (Serdyuk et al., 2007; Jover et al., 2014).
| (9) |
In the equation above the molar mass of M, Mr(M), was divided with the Avogadro's number, NA, to find the mass of a single M protein molecule. This mass was then multiplied with the number of M proteins in the envelope, c(M), to find the total mass of M proteins in the envelope. The total mass of M proteins in the envelope was then divided by the average protein density, ρ, to find the volume taken by M proteins in the envelope, and then divided by the envelope thickness, d, to find the surface area. Multiplication with 2 is due to the fact that the proteins take an area on both the inner and outer surfaces of the envelope.
The area covered by the M proteins, AM, was then subtracted from the total envelope area, A, to find the area of the envelope covered by lipids, ALip.
| (10) |
When ALip is divided by the average area per lipid molecule, α = 0.533 nm2 (Ingólfsson et al., 2014), the result is the total number of lipid molecules in the envelope, c (Lip).
| (11) |
Finally, the number of molecules of lipid constituent X, c(X), was determined by multiplying c (Lip) with the mole fraction of that lipid, x(X),
| (12) |
The number of atoms of element J in all lipids present, NJ (Lip), was determined from the equation
| (13) |
where NJ(X) is the number of atoms of element J in a single molecule of X. Here X represents the lipid components: phosphatidylcholine, phosphatidylserine, phosphatidylethanolamine, sphingomyelin, glycolipids and cholesterol. The properties of the considered lipid constituents are given in Table 3. The total mass of lipids in the virion was calculated using the equation
| (14) |
where Mr(X) is the molar mass of lipid constituent X.
2.1.4. Non-nucleic acid carbohydrates
Non-nucleic acid carbohydrates are present in virions bound in glycolipids and glycoproteins, as parts of viral envelopes. Glycolipids were represented by stearoyl-glucose, C24H46O7, the glucose residue of which belongs to non-nucleic acid carbohydrates. Glycoproteins were represented by attaching oligosaccharide molecules onto spike proteins. Oligosaccharide composition was set to be equal to that of Orthomyxoviridae: for each spike protein molecule, 14 000 Da of oligosaccharides was added, composed of mannose and 2 N-acetyglucosamine residues in a ratio of 5:2 (Kuroda et al., 1990).
Non-nucleic acid carbohydrates are present in glycolipids and glycoproteins, as parts of viral envelopes. Glycolipids were represented by stearoyl-glucose, C24H46O7, the glucose residue of which, C6H10O5 (molar mass 162 Da) belongs to non-nucleic acid carbohydrates. Thus, for each glycolipid molecule (2% of the envelope lipids), 6 C, 10 H and 5 O atoms were added to the virion composition. Glycoproteins were represented by attaching oligosaccharide molecules onto spike proteins (S). Oligosaccharide composition was set to be equal to that of Orthomyxoviridae: for each spike protein molecule (S), 14 000 Da of oligosaccharides was added, composed of mannose and N-acetyglucosamine residues in a ratio of 5:2 (C46H76O35N2, molar mass 1217 Da) (Kuroda et al., 1990).
| (15a) |
| (15b) |
| (15c) |
| (15d) |
where NJ (CH) is the number of atoms of element J in the virion coming from non-nucleic acid carbohydrates. The total mass of non-nucleic acid carbohydrates in the virion was found using the equation
| (16) |
2.1.5. Complete virus composition
The total number of atoms in the virion is the sum of contributions from the four classes of molecules
| (17) |
The results are presented in Table 4. The empirical formula or UCF of the virus has the form CHnHOnONnNPnPSnS, where nJ is the number of moles of element J in the virus UCF and can be found using the equation
| (18) |
Table 4.
Total number of atoms constituting viruses, obtained by the atom counting method. For each virus, the number of atoms is given for the entire virion (nucleocapsid + envelope) and the nucleocapsid. The last column presents the molar mass of entire virions, in Daltons. The molar masses of all three viruses are similar.
| Name | Total atoms per virion |
|||||||
|---|---|---|---|---|---|---|---|---|
| C | H | O | N | P | S | Total | Molar mass (Da) | |
| SARS-CoV-2: Entire virus | 1.010E+07 | 1.656E+07 | 2.881E+06 | 2.325E+06 | 6.523E+04 | 3.804E+04 | 3.197E+07 | 2.200E+08 |
| SARS-CoV-2: Nucleocapsid | 4.951E+06 | 7.778E+06 | 1.709E+06 | 1.547E+06 | 2.990E+04 | 1.658E+04 | 1.603E+07 | 1.178E+08 |
| MERS: Entire virus | 1.014E+07 | 1.654E+07 | 2.875E+06 | 2.287E+06 | 6.569E+04 | 4.595E+04 | 3.195E+07 | 2.200E+08 |
| MERS: Nucleocapsid | 4.938E+06 | 7.697E+06 | 1.669E+06 | 1.516E+06 | 3.012E+04 | 1.658E+04 | 1.587E+07 | 1.165E+08 |
| SARS: Entire virus | 1.011E+07 | 1.654E+07 | 2.883E+06 | 2.340E+06 | 6.511E+04 | 4.151E+04 | 3.198E+07 | 2.203E+08 |
| SARS: Nucleocapsid | 4.983E+06 | 7.807E+06 | 1.717E+06 | 1.573E+06 | 2.975E+04 | 1.658E+04 | 1.613E+07 | 1.187E+08 |
The total mass of the virion is similarly calculated as
| (19) |
The mass fractions of each of the molecular constituents are calculated using the equations
| (20a) |
| (20b) |
| (20c) |
| (20d) |
Similarly, the total number of atoms element J in the nucleocapsid is the sum of atoms of J coming from the nucleic acid, NJ (NA), and all the nucleoproteins (N), NJ(N).
| (21) |
The coefficients in the nucleocapsid UCF, nnucleocapsid, J, can be found from the equation
| (22) |
The total mass of the nucleocapsid is
| (23) |
The mass fractions of nucleic acid, wnucleocapsid (NA), and proteins in the nucleocapsid, wnucleocapsid (Prot), are
| (24a) |
| (24b) |
The molecular mass of the virus is determined by adding the masses of each element in the virus
| (25a) |
| (25b) |
where NJ is the number of atoms of element J and AJ is the molar mass of element J.
2.2. Thermodynamic properties of live matter
Based on the determined elemental composition, standard thermodynamic properties of SARS, MERS and SARS-CoV-2 were determined (the standard state is defined as dry virus particles at a temperature of 298.15 K and pressure of 101.3 kPa). The main product of growth of any organism are biological molecules and structures, which are contained in the organism's dry matter. Thus, organism dry matter is the main constituent of an organism and will in the further text be denoted as live matter. There are two ways to determine standard thermodynamic properties of live matter: Battley and Roels methods. In the Battley method, standard enthalpy of formation and standard molar entropy are determined using the Patel-Erickson and Battley equations, respectively. These are then combined to determine standard Gibbs energy of formation. In the Roels method, Gibbs energy is determined directly, using the Roels equation. Thermodynamic properties of SARS, MERS and SARS-CoV-2 were determined using both methods. Since the Battley method is more accurate (Von Stockar and Liu, 1999), all the presented results (Sections 3.1, 3.2 and 3.3.1) are based on it. The Roels method was used to see whether changing the method of estimating thermodynamic properties has influence on the conclusions (Section 3.3.2). The uncertainties in determining thermodynamic properties are 5.36% for Patel-Erickson (Popovic, 2019) and 19.7% for Battley equation (Battley, 1999; Popovic, 2019).
2.2.1. Battley method
Standard enthalpy of formation of live matter, ΔfH⁰(bio), was calculated from its standard molar enthalpy of combustion, ΔCH⁰,
| (26) |
where nJ is the number of atoms of element J in the live matter empirical formula, bio denotes live matter, and ΔfH⁰(X) is standard enthalpy of formation of substance X (Patel and Erickson, 1981; Battley, 1998). ΔCH⁰ was calculated from the Patel-Erickson equation
| (27) |
where the term in the parentheses represents the number of electrons transferred to oxygen during complete combustion of live matter (Patel and Erickson, 1981; Battley, 1998). Next, standard molar entropy, S⁰m (bio), of live matter was calculated using the Battley equation (Battley, 1999)
| (28) |
where nJ is the number of atoms of element J in the empirical formula of the live matter, S⁰m(J) is standard molar entropy of element J and aJ is the number of atoms per molecule of element J in its standard state elemental form. Standard molar entropy of formation of live matter, ΔfS⁰(bio), was calculated using the equation (Battley, 1999)
| (29) |
Finally, standard Gibbs energy of formation of live matter, ΔfG⁰(bio), was found through the equation
| (30) |
where T is temperature.
2.2.2. Roels method
Gibbs energy of live matter can be determined directly using the Roels equation. The Roels equation is analogous to the Patel-Erickson equation, giving standard Gibbs energy of combustion, ΔCG⁰, of live matter
| (31) |
where E is the number of electrons transferred to oxygen during combustion to CO2(g), H2O(l), N2(g), P4O10(s) and SO3(g) (Roels, 1983; Von Stockar and Liu, 1999). ΔCG⁰ is then converted into standard Gibbs energy of formation of live matter, ΔfG⁰(bio), using an equation analogous to Eq. (26).
| (32) |
The Roels Battley methods are complementary ways of finding Gibbs energy of formation of live matter. However, the Battley equation was calibrated on a better dataset than the Roels equation, making it more precise (Von Stockar and Liu, 1999). Thus, all results presented in Tables 5 and 6, are based on the Battley method. The Roels method was used to make a parallel calculation of ΔfG⁰(bio), to determine whether the conclusions of this research are dependent on the method used to find live matter thermodynamic properties.
Table 5.
Standard thermodynamic properties of formation and growth of SARS, MERS and SARS-CoV-2. The thermodynamic properties of formation of Lung – parenchyma were taken from (Popovic and Minceva, 2020b) and [Woodard and White, 1986], respectively.
| Name | Formation |
Growth |
||||
|---|---|---|---|---|---|---|
| ΔfH⁰bio (kJ/C-mol) | S⁰m,bio (J/C-mol K) | ΔfG⁰bio (kJ/C-mol) | ΔrH⁰ (kJ/C-mol) | ΔrS⁰ (J/C-mol K) | ΔrG⁰ (kJ/C-mol) | |
| SARS-CoV-2: Entire virus | -64.7 ± 30.5 | 30.7 ± 6.1 | -24.8 ± 32.3 | -4.8 ± 60.1 | 6.9 ± 13.2 | -6.9 ± 64.0 |
| SARS-CoV-2: Nucleocapsid | -75.9 ± 29.4 | 32.5 ± 6.4 | -33.7 ± 31.3 | -233.4 ± 59.0 | -37.7 ± 13.6 | -222.2 ± 63.0 |
| MERS: Entire virus | -63.8 ± 30.5 | 30.5 ± 6.0 | -24.3 ± 32.3 | -5.2 ± 60.1 | 7.7 ± 13.2 | -7.5 ± 64.0 |
| MERS: Nucleocapsid | -73.9 ± 29.4 | 32.1 ± 6.3 | -32.3 ± 31.3 | -218.8 ± 59.0 | -34.8 ± 13.5 | -208.5 ± 63.0 |
| SARS-1: Entire virus | -64.5 ± 30.5 | 30.7 ± 6.1 | -24.7 ± 32.3 | -4.5 ± 60.1 | 6.6 ± 13.2 | -6.5 ± 64.0 |
| SARS-1: Nucleocapsid | -75.6 ± 29.4 | 32.5 ± 6.4 | -33.5 ± 31.3 | -242.0 ± 58.9 | -39.2 ± 13.6 | -230.3 ± 63.0 |
| Lung - parenchyma | -65.6 ± 30.7 | 31.4 ± 6.2 | -24.9 ± 32.6 | -50.5 ± 60.3 | -2.8 ± 13.4 | -49.8 ± 64.3 |
Table 6.
The influence of uncertainty on the conclusions of this research. The column “Worst-case ΔrG⁰” contains uncertainty combinations that are the most unfavorable for the conclusions of this research: the Gibbs energies of growth of viruses was increased by the error, making them less negative, while that of the host tissue was decreased to make it more negative.
| Name | ΔrG⁰ (kJ/C-mol) | Worst-case ΔrG⁰ (kJ/C-mol) |
|---|---|---|
| SARS-CoV-2: Entire virus | -6.9 ± 64.0 | 57.2 |
| SARS-CoV-2: Nucleocapsid | -222.2 ± 63.0 | -159.2 |
| MERS: Entire virus | -7.5 ± 64.0 | 56.5 |
| MERS: Nucleocapsid | -208.5 ± 63.0 | -145.5 |
| SARS-1: Entire virus | -6.5 ± 64.0 | 57.5 |
| SARS-1: Nucleocapsid | -230.3 ± 63.0 | -167.4 |
| Lung - parenchyma | -49.8 ± 64.3 | -114.1 |
2.3. Growth stoichiometry and thermodynamics
In this research, a growth medium was chosen that resembles human blood. The main source of N and S, and partly C is an equimolar mixture of amino acids, with the empirical formula CH1.7978O0.4831N0.2247S0.0225. The remaining C comes from carbohydrates with the empirical formula CH2O. The source of P is the hydrogen phosphate ion HPO42-, while the sources of inorganic ions are Na+, K+, Mg2+, Ca2+ and Cl−. Since S in amino acids come in a quantity greater than needed for growth, the excess S is removed as the SO42- ion. The pH of the growth mixture is regulated by the bicarbonate buffer. Thus, the general unbalanced growth reaction has the form
| CH1.7978O0.4831N0.2247S0.0225 + CH2O + O2 + HPO42- + HCO3- + Na+ + K+ + Cl− → (Bio) + SO42- + H2O + H2CO3 | (33) |
where Bio denotes live matter. The stoichiometric coefficients are given in Table 7.
Table 7.
Growth stoichiometries of SARS, MERS and SARS-CoV-2 viruses, and their host tissue. The coefficients given in this table are for reaction (1). (Bio) represents the UCF of live matter, the composition of which is given in Table 3.
| Name | Reactants |
→ | Products |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Amino acid | CH2O | O2 | HPO42- | HCO3- | Na+ | K+ | Cl- | Bio | SO42- | H2O | H2CO3 | ||
| SARS-CoV-2: Entire virus | 1.0238 | 0.0098 | 0.0000 | 0.0065 | 0.0256 | 0.0000 | 0.0000 | 0.0000 | → | 1 | 0.0192 | 0.0674 | 0.0591 |
| SARS-CoV-2: Nucleoprotein | 1.3905 | 0.0000 | 0.4937 | 0.0060 | 0.0437 | 0.0000 | 0.0000 | 0.0000 | → | 1 | 0.0279 | 0.0551 | 0.4342 |
| MERS: Entire virus | 1.0035 | 0.0349 | 0.0000 | 0.0065 | 0.0231 | 0.0000 | 0.0000 | 0.0000 | → | 1 | 0.0180 | 0.0748 | 0.0615 |
| MERS: Nucleoprotein | 1.3657 | 0.0000 | 0.4623 | 0.0061 | 0.0425 | 0.0000 | 0.0000 | 0.0000 | → | 1 | 0.0273 | 0.0644 | 0.4081 |
| SARS-1: Entire virus | 1.0302 | 0.0016 | 0.0000 | 0.0064 | 0.0252 | 0.0000 | 0.0000 | 0.0000 | → | 1 | 0.0190 | 0.0683 | 0.0570 |
| SARS-1: Nucleoprotein | 1.4047 | 0.0000 | 0.5121 | 0.0060 | 0.0445 | 0.0000 | 0.0000 | 0.0000 | → | 1 | 0.0282 | 0.0553 | 0.4492 |
| Lung - parenchyma | 1.1266 | 0.0000 | 0.1070 | 0.0074 | 0.0206 | 0.0100 | 0.0059 | 0.0097 | → | 1 | 0.0146 | 0.0661 | 0.1472 |
The term live matter refers to viruses and their host cells. Growth reaction thermodynamic parameters, including standard enthalpy of growth, ΔrH⁰, standard entropy of growth, ΔrS⁰, and standard Gibbs energy of growth, ΔrG⁰, were calculated using the principles of thermochemistry [Atkins and de Paula, 2014, 2011]. Growth reaction thermodynamic parameters were calculated using the equations
| (34) |
| (35) |
| (36) |
where ν′s are stoichiometric coefficients of species participating the reaction (Atkins and de Paula, 2014, 2011).
2.4. Uncertainties
Thermodynamic properties (ΔfH⁰(bio), S⁰m (bio) and ΔfG⁰(bio)) were determined from elemental composition using empirical relations and thus have some uncertainty. ΔCH⁰ was found using the Patel-Erickson equation, the uncertainty of which is 5.36% (Popovic, 2019). The determined ΔCH⁰ values were then subtracted from standard enthalpies of formation of oxides (Eq. (26)) to find ΔfH⁰(bio). Since standard enthalpies of formation of oxides were precisely determined by experiment (more details in (Chase, 1998)), they have a negligible error compared to that in ΔCH⁰. Thus, the uncertainty in standard enthalpy of formation of live matter, δ(ΔfH⁰(bio)), is equal to the error in ΔCH⁰.
| (37) |
S⁰m (bio) was determined using the Battley equation, which was calibrated on a wide range of organic molecule and live matter data (Battley, 1999). The uncertainty in estimation of entropy using the Battley equation is 2% for dry matter and 19.7% for hydrated matter (Battley, 1999). Therefore, the uncertainty in standard molar entropy of live matter, δ(S⁰m (bio)), is
| (38) |
ΔfS⁰(bio) is the entropy of the reaction
| nc C + ½ nH H2 + ½ nO O2 + ½ nN N2 + nP P + nS S + nNa Na + nK K + nMg Mg + nCa Ca + ½ nCl Cl → CnCHnHOnONnNPnPSnSNanNaKnKMgnMgCanCaClnCl | (39) |
and is defined as the difference in S⁰m (bio) and standard molar entropies of the elements, which have been determined with great accuracy by experiment (Chase, 1998). Thus, the uncertainty in ΔfS⁰(bio) is equal to that in S⁰m (bio) (Popovic, 2019).
ΔfH⁰(bio) and ΔfS⁰(bio) are used to find ΔfG⁰(bio). Therefore, the uncertainty in the standard Gibbs energy of formation of live matter, δ(ΔfG⁰(bio)), is (Popovic, 2019)
| (40) |
Finally, the uncertainty in ΔfG⁰(bio) is equal to that in ΔrG⁰, since it is the greatest source of uncertainty in its determination. ΔrG⁰ is determined using Eq. (36), as the difference of ΔfG⁰ values of reactants and products. The ΔfG⁰ values of all reaction participants, except for live matter have been determined with great accuracy by experiment (Chase, 1998). Thus, uncertainty in Gibbs energy of growth, δ(ΔrG⁰), is equal to δ(ΔfG⁰(bio)). Similarly, δ(ΔrH⁰) and δ(ΔrS⁰) are equal to δ(ΔfH⁰(bio)) and S⁰m (bio), respectively.
3. Results and discussion
3.1. Elemental composition and thermodynamic properties of SARS, MERS and SARS-CoV-2
Wimmer (2006) persuasively portrays viruses as chemicals. Using the methodology described above, elemental and molecular composition of SARS, MERS and SARS-CoV-2 were calculated and are given in Table 8. The empirical formulas of entire virions are SARS CH1.6362O0.2852N0.2315P0.0064S0.0041, MERS CH1.6308O0.2835N0.2255P0.0065S0.0045, and SARS-CoV-2 CH1.6390O0.2851N0.2301P0.0065S0.0038. The empirical formulas of nucleocapsids only are SARS CH1.5668O0.3446N0.3157P0.0060S0.0033, MERS CH1.5586O0.3380N0.3069P0.0061S0.0034 and SARS-CoV-2 CH1.5708O0.3452N0.3125P0.0060S0.0033. Thus, there is a difference in empirical formulas of both the nucleocapsids and entire viruses between SARS, MERS and SARS-CoV-2. For comparison, the empirical formulas of other classes of organisms are: bacteria CH1.7O0.4N0.2, fungi CH1.7O0.5N0.1, algae CH1.7O0.5N0.1 (Popovic, 2019) and human soft tissue average CH1.7296O0.2591N0.1112P0.0134S0.0030Na0.0027K0.0031Ca0.0173Cl0.0018 (Popovic and Minceva, 2020a). The empirical formulas are similar to those of other classes of organisms.
Table 8.
Elemental and molecular compositions per C-mole of SARS, MERS and SARS-CoV-2. The general unit carbon formula (UCF) has the form CHnHOnONnNPnPSnS, where nH, nO, nN, nP and nS are coefficients given in this table. The elemental and molecular composition of Lung – parenchyma were taken from (Popovic and Minceva, 2020b) and (Woodard and White, 1986), respectively.
| Name | Elemental composition |
Molecular composition |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| nH | nO | nN | nP | nS | Nucleic acid | Proteins | Lipids | Non-RNA carbohydrates | |
| SARS-CoV-2: Entire virus | 1.6390 | 0.2851 | 0.2301 | 0.0065 | 0.0038 | 4% | 77% | 17% | 2% |
| SARS-CoV-2: Nucleocapsid | 1.5708 | 0.3452 | 0.3125 | 0.0060 | 0.0033 | 8% | 92% | 0% | 0% |
| MERS: Entire virus | 1.6308 | 0.2835 | 0.2255 | 0.0065 | 0.0045 | 4% | 77% | 17% | 2% |
| MERS: Nucleocapsid | 1.5586 | 0.3380 | 0.3069 | 0.0061 | 0.0034 | 8% | 92% | 0% | 0% |
| SARS-1: Entire virus | 1.6362 | 0.2852 | 0.2315 | 0.0064 | 0.0041 | 4% | 77% | 17% | 2% |
| SARS-1: Nucleocapsid | 1.5668 | 0.3446 | 0.3157 | 0.0060 | 0.0033 | 8% | 92% | 0% | 0% |
| Lung - parenchyma | 1.6268 | 0.2836 | 0.2532 | 0.0074 | 0.0107 | <5% | 88.1% | 6.7% | <5% |
Based on the calculated elemental compositions, growth stoichiometry and standard thermodynamic properties of formation of the three viruses were determined, which are given in Tables 5 and 7, respectively. Moreover, these were used to find standard thermodynamic properties of growth, which are given in Table 5.
Standard molar entropies of live matter are around 30 J/C-mol K (Table 5), laying between that of graphite, 5.740 J/mol K, and carbon in gaseous state, 158.10 J/mol K (Atkins and de Paula, 2014). This indicates that the mobility of C atoms in live matter is greater than in graphite, but lower than in the gaseous state.
3.2. Thermodynamic properties and virus multiplication
SARS, MERS and SARS-CoV-2 cause respiratory infections. As all other viruses, they are obligatory intracellular parasites. The processes of replication, transcription and translation of viruses compete with metabolic processes of the host cell. Thus, it is necessary to know Gibbs energies of growth of the host tissue. The Gibbs energies of formation and growth of lung parenchymal tissue (Popovic and Minceva, 2020a) is given in Table 5. It can be seen that the Gibbs energy of growth of nucleocapsids of all three viruses is significantly more negative than Gibbs energy of growth of the host tissue. Due to this, the viruses are able to hijack cellular metabolism and their components are synthesized at a greater rate than those of the host. Notice that the highly negative Gibbs energies of growth indicate a great driving force for viral multiplication.
Multiplication rate of a virus is analogous to its growth reaction rate, r, which is proportional to the Gibbs energy of growth, ΔrG, the Gibbs energy change of reaction (33)
| (41) |
where L is a constant (phenomenological coefficient) and T is temperature (Demirel, 2014, p. 149), a relationship that has been applied to multiplication of microorganisms (Von Stockar, 2014, p. 416; Demirel, 2014, p. 407; Westerhoff et al., 1982; Hellingwerf et al., 1982), including viruses (Popovic and Minceva, 2020a). The exponential dependence of reaction rate on temperature is contained in L (Demirel, 2014). However, physiological processes occur in a very narrow temperature range. Thus, physiological temperature of a species can be assumed to be constant. The L constant also includes the influence of various kinetic factors, such as enzymes that lower activation energies.
Gibbs energy of growth, ΔrG, is the Gibbs energy change when live matter is formed from nutrients, as in reaction (33). ΔrG should not be confused with Gibbs energy of formation of live matter, ΔfG, the change in Gibbs energy when live matter is formed from elements. The elements here are just a reference state, which is used because there is no way of knowing the absolute Gibbs energies of substances (Atkins and de Paula, 2011). Thus, ΔfG is a property of live matter, independent of the environment in which it grows, while ΔrG is a property of the growth process.
Gibbs energy of growth depends on the chemical nature of the organism and the growth medium. However, it is also influenced by conditions in the medium, in particular on temperature, reactant and product concentrations, and intermolecular forces between reaction participants. The dependence is given by the equation
| (42) |
where ΔrG⁰ is the standard Gibbs energy of growth, Rg the universal gas constant, while Q is the reaction quotient (Atkins and de Paula, 2014). The first term, ΔrG⁰, describes the chemical properties of the organism and the growth medium (Atkins and de Paula, 2014). The second term on the right hand side describes the influence of the conditions in the medium through the reaction quotient, Q, which is defined as
| (43) |
where Ci, γi and νi are concentration, activity coefficient and stoichiometric coefficient of substance i, respectively (Atkins and de Paula, 2014). However, the focus of this research is comparison of driving forces of growth of viruses and their host cells. Viruses and their host cells are subjected to the same environment, but they differ in chemical composition. Thus, the principal difference in Gibbs energies of growth of viruses and their host cells comes from the difference in their chemical composition, which is quantified by ΔrG⁰. Thus, in this work ΔrG in Eq. (41) can be approximated with ΔrG⁰ values of viruses and their host cells (Von Stockar, 2014),
| (44) |
By comparing growth reaction rates of viruses and their host tissues, their ratio, R, is greater than one (Popovic and Minceva, 2020a)
| (45) |
Since viruses and their host perform transcription, translation and replication at the same temperature and using the same cellular machinery, T and L are the same for both. Viruses do not possess their own multiplication machinery and must use that of their host. The process of transcription, translation and replication is identical in a virus and its host. Therefore, virus and its host cell share the same phenomenological coefficient L. R indicates the ratio between the growth (multiplication) rate of the virus and growth rate of the host cell (Popovic and Minceva, 2020a). The fact that R > 1 leads to the conclusion that in the competition of metabolic processes of viruses and their hosts, the virus will dominate (Popovic and Minceva, 2020a). Thus, viral multiplication will dominate over the metabolism of the infected tissue.
By performing its life cycle, a virus performs several chemical processes: binding of the virus to the receptor on the cell surface, transcription, replication, translation and self-assembly (Popovic and Minceva 2020a). Within self-assembly, new virions are formed from replicated RNA and synthesized nucleoproteins. However, the envelope originates from the host cell membrane. The rate of each of the mentioned chemical processes depends on their Gibbs energy, because the host cell and virus use the same metabolic machinery and are at the same temperature (Popovic and Minceva, 2020a). Since the envelope originates from the host cell, during self-assembly, the virus passively takes it from the host cell. Thus, the model suggested here focuses on determination of Gibbs energy of the nucleocapsid, since it is formed in self-assembly processes from components coded in the viral nucleic acid. However, Gibbs energies of formation and growth were determined both for the nucleocapsid and the entire virion. Based on the data in Table 5, the R-values for nucleocapsids were found to be 4.6 for SARS, 4.2 for MERS and 4.5 for SARS-CoV-2. The nucleocapsids of all three viruses have similar R-values.
The R-values were calculated comparing Gibbs energies of growth of nucleocapsids and host cells, because only nucleocapsids are formed in a chemical process, involving polymerization and self-assembly. On the other hand, entire virions are formed in the physical process of budding, from the already present nucleocapsid and cell membrane. The cell membrane is not synthesized during budding. It is already there, synthesized by the host cell, and is taken by the virion. R relates to the synthesis process and is thus not directly related to budding.
3.3. The influence of assumptions on the results
The discussion above rests on two assumptions: the Battley method for estimating thermodynamic properties of live matter and approximating Gibbs energy of growth with standard Gibbs energy of growth. The influence of these assumptions on the results is considered in this section. The discussion begins with the uncertainty in thermodynamic properties. Then, it is considered whether the results are dependent on the method used to find thermodynamic properties. Finally, the influence of approximating ΔrG with ΔrG⁰ is considered.
3.3.1. The influence of uncertainties
Uncertainties in the determined Gibbs energies of growth were calculated as described in Section 2.4. and are presented in Table 5. Their influence on the results of this research is analyzed in Table 6. The most unfavorable combination of uncertainties was considered. The Gibbs energies of growth of the viruses were increased by the uncertainty, making them less negative. On the other hand, the Gibbs energy of growth of the host tissue was decreased by the uncertainty, making it more negative. As can be seen, Gibbs energy of growth of the host tissue remains more negative that of the virus nucleocapsids.
The trend in the R-values is also preserved. To repeat, the original R-values were found to be 4.6 for SARS, 4.2 for MERS and 4.5 for SARS-CoV-2, while those of entire virions are 0.13 for SARS, 0.15 for MERS and 0.14 SARS-CoV-2. The worst-case R-values for virus nucleocapsids are 1.5 for SARS, 1.3 for MERS and 1.4 for SARS-CoV-2. The worst-case R-values for entire virions are -0.50 for SARS, -0.50 for MERS and -0.50 for SARS-CoV-2. The R-values of entire virions are negative, because their ΔrG⁰ is only slightly negative and adding maximum uncertainty makes them positive, while that of the host tissue remain negative. However, this does not represent a problem for virus multiplication. The R-values of the nucleocapsids are greater than unity. Thus, virus nucleocapsid synthesis in the cytoplasm dominates over that of host cell components. Once a nucleocapsid is formed, it takes a part of the already existing cell membrane as its envelope, during the budding process, and leaves the cell. Since virions are constantly leaving the cell by budding, the process is shifted towards the products – budding of new virions.
3.3.2. The influence of thermodynamic property models
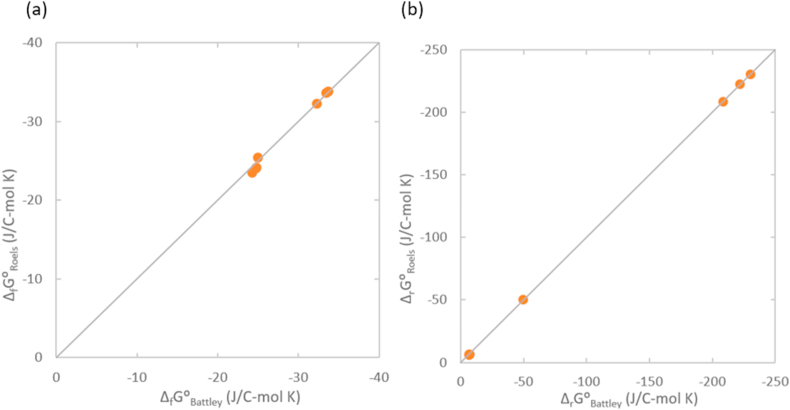
Gibbs energy of formation and growth of the three viruses and their host tissue have been calculated using the Battley and Roels methods (Section 2.2.), to see whether changing the thermodynamic properties model will have influence of the conclusions. The results are presented in Table 9 and Figure 3. As can be seen from Figure 3a, both models give very similar Gibbs energies of formation for both the viruses and their host tissue. Figure 3b shows a comparison of Gibbs energies of growth based on the two models. For higher values of ΔrG⁰ the results are very similar, a slight discrepancy appears at lower ΔrG⁰ values, due to subtraction of large numbers. However, Table 9 shows that for both models, ΔrG⁰ of virus nucleocapsids is more negative than that of the host tissue. Thus, changing the thermodynamic property model has no influence on the results of this research.
Table 9.
Comparison of Gibbs energies of formation and growth calculated using the Battley and Roels methods.
| Name | Formation |
Growth |
||||
|---|---|---|---|---|---|---|
| ΔfG⁰Battley (kJ/C-mol) | ΔfG⁰Roels (kJ/C-mol) | Relative deviation | ΔrG⁰Battley (kJ/C-mol) | ΔrG⁰Roels (kJ/C-mol) | Relative deviation | |
| SARS-CoV-2: Entire virus | -24.84 | -24.17 | -2.7% | -6.9 | -6.2 | -9.7% |
| SARS-CoV-2: Nucleocapsid | -33.73 | -33.85 | 0.4% | -222.2 | -222.4 | 0.1% |
| MERS: Entire virus | -24.28 | -23.52 | -3.1% | -7.5 | -6.7 | -10.2% |
| MERS: Nucleocapsid | -32.26 | -32.22 | -0.1% | -208.5 | -208.4 | 0.0% |
| SARS-1: Entire virus | -24.68 | -24.05 | -2.5% | -6.5 | -5.9 | -9.6% |
| SARS-1: Nucleocapsid | -33.46 | -33.64 | 0.5% | -230.3 | -230.5 | 0.1% |
| Lung - parenchyma | -24.94 | -25.37 | 1.7% | -49.8 | -50.2 | 0.9% |
Figure 3.
Comparison of Gibbs energies of (a) formation and (b) growth, calculated using the Battley and Roels methods.
3.3.3. The influence of reaction quotient Q
In the discussion above ΔrG was approximated with ΔrG⁰, simplifying Eqs. (41), (42), (43), and (44). To find the influence of this approximation, ΔrG was calculated using Eqs. (42) and (43), and compared to ΔrG⁰. The concentrations of substances in reaction (33) were taken from the literature (Fuggle, 2018; Blinn et al., 2006): amino acids 2.76 mol/dm3 (total blood protein 70 g/l, molar mass 25.39 g/C-mol), CH2O 0.036 mol/dm3 (blood glucose 6 mmol/l), O2 14 kPa, HPO42- 0.0012 mol/dm3, HCO3- 0.025 mol/dm3, Na+ 0.14 mol/dm3, K+ 0.0042 mol/dm3, Cl− 0.1 mol/dm3, SO42- 3.2 ∙ 10−5 mol/dm3, and CO2 5 kPa. The stoichiometric coefficients were taken from Table 7, while the activity coefficients were assumed to be 1 (activity coefficients make a correction for Q, which is itself a correction for ΔrG⁰). The results are summarized in Table 10.
Table 10.
Influence of the reaction quotient on Gibbs energy of growth. The table compares the influences of standard Gibbs energy of growth, ΔrG⁰, and the reaction quotient Q on Gibbs energy of growth, ΔrG. The last column %Q contains the relative size of the correction to ΔrG made by Q, calculated as (%Q) = [ RgT ln(Q) ]/ΔrG. Also, notice that the size of the correction RgT ln(Q) is in all cases lower than the uncertainty in ΔrG⁰ (Table 5).
| Name | Q | ΔrG⁰ (kJ/C-mol) | RgT ln(Q) (kJ/C-mol) | ΔrG (kJ/C-mol) | %Q |
|---|---|---|---|---|---|
| SARS-CoV-2: Entire virus | 0.289 | -6.890 | -3.077 | -9.967 | 31% |
| SARS-CoV-2: Nucleocapsid | 0.169 | -222.236 | -4.413 | -226.648 | 2% |
| MERS: Entire virus | 0.320 | -7.491 | -2.827 | -10.318 | 27% |
| MERS: Nucleocapsid | 0.176 | -208.466 | -4.313 | -212.779 | 2% |
| SARS-1: Entire virus | 0.281 | -6.545 | -3.143 | -9.688 | 32% |
| SARS-1: Nucleocapsid | 0.165 | -230.342 | -4.468 | -234.810 | 2% |
| Lung - parenchyma | 0.269 | -49.758 | -3.252 | -53.009 | 6% |
From the data in Table 10, it can be seen that approximating ΔrG with ΔrG⁰ does not influence the main conclusions of this research. The correction made by the Q-term in Eq. (42) is 2% for the nucleocapsids and 6% for the host tissue, while for entire virions it goes up to 32%, due to their small ΔrG value. However, the trend in the ΔrG values is preserved: nucleocapsids have a much more negative Gibbs energy of growth than the host tissue. Moreover, the absolute size of the RgT ln(Q) terms is much lower than the uncertainty in ΔrG⁰ (Table 5). Therefore, approximating Eq. (41) with Eq. (44) seems to be a reasonable assumption.
3.4. Outlook
Pathogenicity (capacity of a microbe to cause damage on affected cell/tissue) of viruses is a consequence of more efficient multiplication of a virus compared to its host cell. Multiplication of viruses leads to cell and tissue damage (Albrecht et al., 1996). Decrease in multiplication rate leads to decreased production and accumulation, as well as less cell and tissue damage. This leaves the organism enough time to develop an immune response, with less tissue damage and milder clinical symptoms. Examples are the BCG (artificially designed) and Jenner (designed by nature) vaccine, attenuated vaccines capable of making local inflammatory changes followed by a general development of immune response. Moreover, Human diploid cell rabies vaccines are made using the attenuated Pitman-Moore L503 strain of the virus, while the purified Vero cell rabies vaccine uses the attenuated Wistar strain of the rabies virus (WHO, 2018).
Virulence represents a pathogen's or microbe's ability to infect or damage a host. Virulence factors allow a virus to enter its host, replicate, modify host defenses (in multicellular host organisms) and spread within a multicellular host (Flint et al., 2009). Entrance into a host and replication capability (ability to replicate more efficiently than the host cell) are chemical reactions governed by change in thermodynamic properties, i.e. Gibbs energy. Thus, if Gibbs energy of growth of an attenuated virus strain is made less negative, it is possible to decrease its rate of binding to the specific receptor or its replication rate. Thus, the result of Gibbs energy increase is the decrease in virulence of the attenuated virus. If the Gibbs energy of growth of the virus is less negative than that of its host tissue, then the virus loses its virulence. If the attenuated virus strain loses its virulence and keeps its antigenic properties, it can become an attenuated vaccine. Since the attenuated strain has a lower multiplication rate, it is not capable of destroying the host cell. Thus, during vaccine design, an attempt should be made to increase the Gibbs energy of growth of the nucleocapsid, by changing the chemical composition of the wild-type virus. In this way, R would be made equal to or lower than unity.
4. Conclusions
SARS-CoV-2 (COVID-19), in addition to being a medical problem, is also a biological and biothermodynamic phenomenon. Biothermodynamics attempts to find the driving forces and mechanisms that lead to biological phenomena. All processes in nature are a consequence of interactions between various systems. Organisms represent thermodynamic systems, while their life cycles are processes that appear as interactions with the environment. If the environment, as in the case of viruses, is another organism (human), then the interaction is infection. The driving force for all processes in nature is Gibbs energy. In this paper, Gibbs energies of growth of SARS, MERS and SARS-CoV-2 were compared to those of their host. The comparison implies a great spontaneity of virus multiplication, leading to high virus multiplication rate. High multiplication rate leads to formation of a great reservoir of viruses, which enables extensive transmission through the population.
Declarations
Author contribution statement
Marko Popovic: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Mirjana Minceva: Analyzed and interpreted the data; Wrote the paper.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- Albrecht T., Fons M., Boldogh I., Rabson A.S. Effects on cells. In: Baron S., editor. Medical Microbiology. fourth ed. University of Texas Medical Branch at Galveston; 1996. https://www.ncbi.nlm.nih.gov/books/NBK7979/ Galveston (TX) chapter 44. Available from: [PubMed] [Google Scholar]
- Atkins P., de Paula J. second ed. W.H. Freeman and Company; New York: 2011. Physical Chemistry for the Life Sciences. [Google Scholar]
- Atkins P., de Paula J. tenth ed. W.H. Freeman and Company; New York: 2014. Physical Chemistry: Thermodynamics, Structure, and Change. [Google Scholar]
- Battley E.H. The development of direct and indirect methods for the study of the thermodynamics of microbial growth. Thermochim. Acta. 1998;309:17–37. [Google Scholar]
- Battley E.H. An empirical method for estimating the entropy of formation and the absolute entropy of dried microbial biomass for use in studies on the thermodynamics of microbial growth. Thermochim. Acta. 1999;326:7–15. [Google Scholar]
- Blinn C.M., Biggee B.A., McAlindon T.E., Nuite M., Silbert J.E. Sulphate and osteoarthritis: decrease of serum sulphate levels by an additional 3-h fast and a 3-h glucose tolerance test after an overnight fast. Ann. Rheum. Dis. 2006;65(9):1223–1225. doi: 10.1136/ard.2006.052571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casasnovas J.M., Springer T.A. Kinetics and thermodynamics of virus binding to receptor: studies with rhinovirus, intercellular adhesion molecule-1 (ICAM-1), and surface plasmon resonance. J. Biol. Chem. 1995;270(22):13216–13224. doi: 10.1074/jbc.270.22.13216. [DOI] [PubMed] [Google Scholar]
- Ceres P., Zlotnick A. Weak protein-protein interactions are sufficient to drive assembly of hepatitis B virus capsids. Biochemistry. 2002;41(39):11525–11531. doi: 10.1021/bi0261645. [DOI] [PubMed] [Google Scholar]
- Chase M.W. NIST-JANAF thermochemical tables, fourth edition. J. Phys. Chem. Ref. Data, Monograph. 1998;9:1–1951. [Google Scholar]
- Cooper G.M. second ed. Sinauer Associates; Sunderland (MA): 2000. The Cell: A Molecular Approach.https://www.ncbi.nlm.nih.gov/books/NBK9928/ Cell Membranes. Available from: [Google Scholar]
- DeDiego M.L., Alvarez E., Almazán F., Rejas M.T., Lamirande E., Roberts A., Shieh W.J., Zaki S.R., Subbarao K., Enjuanes L. A severe acute respiratory syndrome coronavirus that lacks the E gene is attenuated in vitro and in vivo. J. Virol. 2007;81(4):1701–1713. doi: 10.1128/JVI.01467-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demirel Y. third ed. Elsevier; Amsterdam: 2014. Nonequilibrium Thermodynamics: Transport and Rate Processes in Physical, Chemical and Biological Systems. [Google Scholar]
- Fang Y., Nie Y., Penny M. Transmission dynamics of the COVID-19 outbreak and effectiveness of government interventions: a data-driven analysis. J. Med. Virol. 2020 doi: 10.1002/jmv.25750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flint S.J., Enquist L.W., Racaniello V.R., Skalka A.M. third ed. II. Wiley; Hoboken, NJ: 2009. Principles of Virology. (Pathogenesis and Control). [Google Scholar]
- Fuggle S. National Health Service; Leeds, UK: 2018. Clinical Biochemistry Reference Ranges Handbook. [Google Scholar]
- Gale P. How virus size and attachment parameters affect the temperature sensitivity of virus binding to host cells: predictions of a thermodynamic model for arboviruses and HIV. Microb. Risk Anal. 2020;15:100104. doi: 10.1016/j.mran.2020.100104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He R., Dobie F., Ballantine M., Leeson A., Li Y., Bastien N., Cutts T., Andonov A., Cao J., Booth T.F., Plummer F.A., Tyler S., Baker L., Li X. Analysis of multimerization of the SARS coronavirus nucleocapsid protein. Biochem. Biophys. Res. Commun. 2004;316(2):476–483. doi: 10.1016/j.bbrc.2004.02.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hellingwerf K.J., Lolkema J.S., Otto R., Neijssel O.M., Stouthamer A.H., Harder W., van Dam K., Westerhoff H.V. Energetics of microbial growth: an analysis of the relationship between growth and its mechanistic basis by mosaic non-equilibrium thermodynamics. FEMS (Fed. Eur. Microbiol. Soc.) Microbiol. Lett. 1982;15(1):7–17. [Google Scholar]
- Ingólfsson H.I., Melo M.N., van Eerden F.J., Arnarez C., Lopez C.A., Wassenaar T.A., Periole X., de Vries A.H., Tieleman D.P., Marrink S.J. Lipid organization of the plasma membrane. J. Am. Chem. Soc. 2014;136(41):14554–14559. doi: 10.1021/ja507832e. [DOI] [PubMed] [Google Scholar]
- Jover L.F., Effler T.C., Buchan A., Wilhelm S.W., Weitz J.S. The elemental composition of virus particles: implications for marine biogeochemical cycles. Nat. Rev. Microbiol. 2014;12(7):519–528. doi: 10.1038/nrmicro3289. [DOI] [PubMed] [Google Scholar]
- Katen S., Zlotnick A. The thermodynamics of virus capsid assembly. In: Johnson M.L., Holt J.M., Ackers G.K., editors. Vol. 455. Academic Press; Cambridge, MA: 2009. pp. 395–417. (Methods in Enzymology). [Google Scholar]
- Knight C.A. Springer; Berlin: 1975. Chemistry of Viruses. [Google Scholar]
- Kucharski A.J., Russell T.W., Diamond C., Liu Y., Edmunds J., Funk S., Eggo R.M. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect. Dis. 2020 doi: 10.1016/S1473-3099(20)30144-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo L., Masters P.S. Evolved variants of the membrane protein can partially replace the envelope protein in murine coronavirus assembly. J. Virol. 2010;84(24):12872–12885. doi: 10.1128/JVI.01850-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuroda K., Geyer H., Geyer R., Doerfler W., Klenk H.D. The oligosaccharides of influenza virus hemagglutinin expressed in insect cells by a baculovirus vector. Virology. 1990;174(2):418–429. doi: 10.1016/0042-6822(90)90095-9. [DOI] [PubMed] [Google Scholar]
- Mahmoudabadi G., Milo R., Phillips R. Energetic cost of building a virus. Proc. Natl. Acad. Sci. Unit. States Am. 2017;114(22):E4324–E4333. doi: 10.1073/pnas.1701670114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- National Center for Biotechnology Information . 2020. NCBI Database [online]https://www.ncbi.nlm.nih.gov/ [Google Scholar]
- Neuman B.W., Buchmeier M.J. Supramolecular architecture of the coronavirus particle. Adv. Virus Res. 2016;96:1–27. doi: 10.1016/bs.aivir.2016.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuman B.W., Adair B.D., Yoshioka C., Quispe J.D., Orca G., Kuhn P., Milligan R.A., Yeager M., Buchmeier M.J. Supramolecular architecture of severe acute respiratory syndrome coronavirus revealed by electron cryomicroscopy. J. Virol. 2006;80(16):7918–7928. doi: 10.1128/JVI.00645-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuman B.W., Kiss G., Kunding A.H., Bhella D., Baksh M.F., Connelly S., Droese B., Klaus J.P., Makino S., Sawicki S.G., Siddell S.G., Stamou D.G., Wilson I.A., Kuhn P., Buchmeier M.J. A structural analysis of M protein in coronavirus assembly and morphology. J. Struct. Biol. 2011;174(1):11–22. doi: 10.1016/j.jsb.2010.11.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel S.A., Erickson L.E. Estimation of heats of combustion of biomass from elemental analysis using available electron concepts. Biotechnol. Bioeng. 1981;23:2051–2067. [Google Scholar]
- Popovic M. Thermodynamic properties of microorganisms: determination and analysis of enthalpy, entropy, and Gibbs free energy of biomass, cells and colonies of 32 microorganism species. Heliyon. 2019;5(6) doi: 10.1016/j.heliyon.2019.e01950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popovic M., Minceva M. A thermodynamic insight into viral infections: do viruses in a lytic cycle hijack cell metabolism due to their low Gibbs energy? Heliyon. 2020;6(5) doi: 10.1016/j.heliyon.2020.e03933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popovic M., Minceva M. Thermodynamic properties of human tissues. Therm. Sci. 2020 [Google Scholar]
- Riedel S., Hobden J.A., Miller S., Morse S.A., Mietzner T.A., Detrick B., Mitchell T.G., Sakanari J.A., Hotez P., Mejia R. 28thed. McGraw-Hill; New York: 2019. Jawetz, Melnick and Adelberg’s Medical Microbiology. [Google Scholar]
- Roels J.A. Energetics and Kinetics in Biotechnology. Elsevier; Amsterdam: 1983. [Google Scholar]
- Serdyuk I.N., Zaccai N.R., Zaccai J. Cambridge University Press; Cambridge: 2007. Methods in Molecular Biophysics: Structure, Dynamics, Function. [Google Scholar]
- The UniProt Consortium UniProt: a worldwide hub of protein knowledge. Nucleic Acids Res. 2019;47:D506–515. doi: 10.1093/nar/gky1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzlil S., Deserno M., Gelbart W.M., Ben-Shaul A. A statistical-thermodynamic model of viral budding. Biophys. J. 2004;86(4):2037–2048. doi: 10.1016/S0006-3495(04)74265-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Boheemen S., de Graaf M., Lauber C., Bestebroer T.M., Raj V.S., Zaki A.M., Osterhaus A.D., Haagmans B.L., Gorbalenya A.E., Snijder E.J., Fouchier R.A. Genomic characterization of a newly discovered coronavirus associated with acute respiratory distress syndrome in humans. mBio. 2012;3(6) doi: 10.1128/mBio.00473-12. 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Von Stockar U. EPFL Press; Lausanne: 2014. Biothermodynamics: the Role of Thermodynamics in Biochemical Engineering. [Google Scholar]
- Von Stockar U., Liu J.-S. Does microbial life always feed on negative entropy? Thermodynamic analysis of microbial growth. Biochim. Biophys. Acta Bioenerg. 1999;1412(3):191–211. doi: 10.1016/s0005-2728(99)00065-1. [DOI] [PubMed] [Google Scholar]
- Westerhoff H.V., Lolkema J.S., Otto R., Hellingwerf K.J. Thermodynamics of growth. Non-equilibrium thermodynamics of bacterial growth: the phenomenological and the Mosaic approach. Biochim. Biophys. Acta Rev. Bioenerg. 1982;683(3-4):181–220. doi: 10.1016/0304-4173(82)90001-5. [DOI] [PubMed] [Google Scholar]
- WHO Rabies vaccines: WHO position paper – april 2018. Wkly. Epidemiol. Rec. 2018;16(93):201–220. [Google Scholar]
- Wimmer E. The test-tube synthesis of a chemical called poliovirus. The simple synthesis of a virus has far-reaching societal implications. EMBO Rep. 2006;7 doi: 10.1038/sj.embor.7400728. (Spec No), S3–S9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodard H.Q., White D.R. The composition of body tissues. Br. J. Radiol. 1986;59:1209–1219. doi: 10.1259/0007-1285-59-708-1209. [DOI] [PubMed] [Google Scholar]
- Wu F., Zhao S., Yu B., Chen Y.M., Wang W., Song Z.G., Hu Y., Tao Z.W., Tian J.H., Pei Y.Y., Yuan M.L., Zhang Y.L., Dai F.H., Liu Y., Wang Q.M., Zheng J.J., Xu L., Holmes E.C., Zhang Y.Z. A new coronavirus associated with human respiratory disease in China. Nature. 2020;579:265–269. doi: 10.1038/s41586-020-2008-3. [DOI] [PMC free article] [PubMed] [Google Scholar]