Complexity trees of the sequence of some nonahedral graphs generated by triangle

Abstract

Calculating the number of spanning trees of a graph is one of the widely studied graph problems since the Pioneer Gustav Kirchhoff (1847). In this work, using knowledge of difference equations we drive the explicit formulas for the number of spanning trees in the sequence of some Nonahedral (nine faced polyhedral) graphs generated by triangle using electrically equivalent transformations and rules of the weighted generating function. Finally, we evaluate the entropy of graphs in this manuscript with different studied graphs with an average degree being 4, 5 and 6.

Mathematics; Number of spanning trees; Entropy; Electrically equivalent transformations.

1. Introduction

The trouble of counting spanning trees turns to be essential and more importantly, interesting. For instance, it has been shown that, if the graph represents an electrical community with each edge a unit resistor, the effective resistance of an edge is equal to the proportion of spanning trees that the edge is in. Also, the wide variety of spanning trees is used as an invariant for computing the entropy of certain networks related to physical processes. In addition, there are various applications of the wide variety of spanning trees within mathematics as well [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12].

A spanning tree of a connected graph is a subgraph that is a tree reaching all vertices.

There exist numerous strategies for finding the number of spanning trees $\tau \left(G\right)$ of a graph $G$.

A classic technique called the matrix tree theorem, also called Kirchhoff''s matrix-tree theorem [13] which states that the number of nonidentical spanning trees of a graph $G$ is same to any cofactor of its Laplacian matrix $L=D-A$, in which $D$ is the degree matrix and $A$is the adjacency matrix of the graph $G$.

Another method to count this number is using Laplacian eigenvalues. Kelmans and Chelnoknov [14] derived the following formula:

$$\tau \left(G\right)=\frac{1}{p}\prod _{i=1}^{p-1}{\lambda }_i.$$ (1.1)

in which $G$ is a connected graph with $p$vertices and $p={\lambda }_1\ge {\lambda }_2\ge ...\ge {\lambda }_p=0$ are the eigenvalues of the Laplacian matrix $L$.

One popular technique for finding the number of spanning tress, $\tau \left(G\right)$, is the deletion-contraction method. This technique is a reliable method which lets into enumerate the number of spanning trees of a multigraph $G$. This method makes use of the fact that

$$\tau \left(G\right)=\tau \left(G-e\right)+\tau \left(G/e\right)$$ (1.2)

where $G-e$denotes the graph obtained by deleting an arbitrary edge $e$, and $G/e$denotes the graph obtained by contracting an arbitrary edge $e$ [15, 16]. For more results, see [17, 18, 19, 20].

2. Electrically equivalent transformations

An electrical network is an interconnection of electrical components (e.g. inductors, capacitors, batteries, resistors, switches, etc).

Kirchhoff's motivation was studied of electrical networks: an edge-weighted graph can be regarded as an electrical network, where weights are the conductance of the respective edges. The effect conductance between two specific nodes $u,v$can be written as the quotient of (weighted) number of spanning trees and the (weighted) number of so called thickets, i.e., spanning forests with exactly two components and property that each of the components contains precisely one of the nodes $u,v$[21, 22]. Next, we list the effect of some simple transformations on the number of spanning trees, suppose that $G$ is an edge weighted graph, $G^{\text{'}}$is the corresponding electrically equivalent graph and $\tau \left(G\right)$denotes the weighted number of spanning trees of $G$.

• i.Parallel edges: when two parallel edges with conductances $u$and $v$ in $G$ are merged into a single edge with conductances $u+v$in $G^{\text{'}}$, then $\tau \left(G^{\text{'}}\right)=\tau \left(G\right).$
• ii.Serial edges: when two serial edges with conductances $u$ and $v$ in $G$ are merged into a single edge with conductance $\frac{uv}{u+v}$ in $G^{\text{'}}$, then $\tau \left(G^{\text{'}}\right)=\frac{1}{u+v}\tau \left(G\right).$.
• iii$\Delta -Y$transformation: when a triangle with conductances $u,v$ and $w$ in $G$ is changed into an electrically equivalent star graph with conductances $r=\frac{uv+vw+uw}{u},s=\frac{uv+vw+uw}{v}$ and $t=\frac{uv+vw+uw}{w}$ in $G^{\text{'}}$, then $\tau \left(G^{\text{'}}\right)=\frac{{\left(uv+vw+uw\right)}^2}{uvw}\tau \left(G\right).$
• iv$Y-\Delta$ transformation: when a star graph with conductances $u,v$ and $w$in $G$ is changed into an electrically equivalent triangle with conductances $r=\frac{vw}{u+v+w},s=\frac{uw}{u+v+w}$ and $t=\frac{uv}{u+v+w}$ in $G^{\text{'}}$, then $\tau \left(G^{\text{'}}\right)=\frac{1}{u+v+w}\tau \left(G\right).$

3. Main results

In mathematics, one constantly attempts to get new structure from given once. This also applies to the realm of graphs, where one can generate many new graphs from given one.

In the following we take into account six nonahedral graphs generated by triangle and we derive the explicit formulas for the number of spanning trees of sequences of those graphs.

Consider the sequence of graphs $G_1=K_3,G_2,\mathrm{...},G_n$ formed as illustrated in Figure 1.

Figure 1.

Some sequences of the graph G_n.

According to this formation, the number of total vertices $\left|V\left(G_n\right)\right|$ and edges $\left|E\left(G_n\right)\right|$are $\left|V\left(G_n\right)\right|=6n-3$,$\left|E\left(G_n\right)\right|=15n-12,n=\mathrm{1,2},\dots$ It is obvious that the average degree is convergently $5$for a large $n$.

Theorem 1

The number of spanning trees in the sequence of the graph $G_n$ , where $n\ge 1$, is given by

$$\frac{2^{n-5}{\left(97+17\sqrt{33}\right)}^2{\left(-1+{\left(\frac{1}{32}\left(329-57\sqrt{33}\right)\right)}^n\right)}^2{\left({\left(19-3\sqrt{33}\right)}^n\left(33+\sqrt{33}\right)-\left(-33+\sqrt{33}\right){\left(19+3\sqrt{33}\right)}^n\right)}^2}{3267{\left(8\left(29+5\sqrt{33}\right)+{32}^n{\left(329+57\sqrt{33}\right)}^{1-n}\right)}^2}$$

Proof: Let us be using the electrically equivalent transformation to transform $G_i$ to $G_{i-1}$. Figure 2 clarifies the transformation process from $G_2$ to $G_1=$$K_3.$

Figure 2.

The transformations from G₂ to G₁.

By utilizing the properties that are given in section 2, the following the transformations are given:

$$\tau \left(G_1^{\text{'}}\right)=\frac{1}{27}\tau \left(G_2\right),\tau \left(G_2^{\text{'}}\right)=\tau \left(G_1^{\text{'}}\right),\tau \left(G_3^{\text{'}}\right)=9k_2\tau \left(G_2^{\text{'}}\right),\tau \left(G_4^{\text{'}}\right)={\left(\frac{3}{9k_2+8}\right)}^3\tau \left(G_3^{\text{'}}\right),\tau \left(G_5^{\text{'}}\right)=\tau \left(G_4^{\text{'}}\right),\tau \left(G_6^{\text{'}}\right)=\left(\frac{9k_2+8}{72k_2}\right)\tau \left(G_5^{\text{'}}\right)\text{and}\tau \left(G_1\right)=\tau \left(G_6^{\text{'}}\right).$$

Merging these seven transformations, we get

$$\tau \left(G_2\right)=8{\left(9k_2+8\right)}^2\tau \left(G_1\right).$$ (3.1)

Moreover,

$$\tau \left(G_n\right)=\prod _{i=2}^{n}8{\left(9k_i+8\right)}^2\tau \left(G_1\right)=3\times 8^{n-1}{k}_1^2{\left[\prod _{i=2}^n\left(9k_i+8\right)\right]}^2$$ (3.2)

_where $k_{i-1}=\frac{11k_i+8}{9k_i+8},i=\mathrm{2,3},\mathrm{...},n.$

Its characteristic equation is $9x^2-3x-8=0$ which has two roots $x_1=\frac{1-\sqrt{33}}{6}$ and $x_2=\frac{1+\sqrt{33}}{6}$. Subtracting these two roots into both sides of $k_{i-1}=\frac{11k_i+8}{9k_i+8}$, we have

$$k_{i-1}-\frac{1-\sqrt{33}}{6}=\frac{11k_i+8}{9k_i+8}-\frac{1-\sqrt{33}}{6}=\left(19+3\sqrt{33}\right).\frac{k_i-\left(\frac{1-\sqrt{33}}{6}\right)}{2\left(9k_i+8\right)}$$ (3.3)

$$k_{i-1}-\frac{1+\sqrt{33}}{6}=\frac{11k_i+8}{9k_i+8}-\frac{1+\sqrt{33}}{6}=\left(19-3\sqrt{33}\right).\frac{k_i-\left(\frac{1+\sqrt{33}}{6}\right)}{2\left(9k_i+8\right)}$$ (3.4)

Let $h_i=\frac{k_i-\frac{1-\sqrt{33}}{6}}{k_i-\frac{1+\sqrt{33}}{6}}$. Then by Eqs. (3.3) and (3.4), we get $h_{i-1}=\left(\frac{329+57\sqrt{33}}{32}\right)h_i$ and $h_i={\left(\frac{329+57\sqrt{33}}{32}\right)}^{n-i}{h}_n.$

Thus $k_i=\frac{{\left(\frac{329+57\sqrt{33}}{32}\right)}^{n-i}\left(\frac{1+\sqrt{33}}{6}\right)h_n-\frac{1-\sqrt{33}}{6}}{{\left(\frac{329+57\sqrt{33}}{32}\right)}^{n-i}{h}_n-1}.$ Therefore,

$$k_1=\frac{{\left(\frac{329+57\sqrt{33}}{32}\right)}^{n-1}\left(\frac{1+\sqrt{33}}{6}\right)h_n-\frac{1-\sqrt{33}}{6}}{{\left(\frac{329+57\sqrt{33}}{32}\right)}^{n-1}{h}_n-1}.$$ (3.5)

Utilizing the expression $k_{n-1}=\frac{11k_n+8}{9k_n+8}$ and indicating the coefficients of $11k_n+8$ and $9k_n+8$ as $a_n$ and $b_n$, we obtain

$$\begin{array}{l}9k_n+8=a_0\left(11k_n+8\right)+b_0\left(9k_n+8\right),\\ 9k_{n-1}+8=\frac{a_1\left(11k_n+8\right)+b_1\left(9k_n+8\right)}{a_0\left(11k_n+8\right)+b_0\left(9k_n+8\right)},\\ 9k_{n-2}+8=\frac{a_2\left(11k_n+8\right)+b_2\left(9k_n+8\right)}{a_1\left(11k_n+8\right)+b_1\left(9k_n+8\right)},\\ ⋮\\ 9k_{n-i}+8=\frac{a_i\left(11k_n+8\right)+b_i\left(9k_n+8\right)}{a_{i-1}\left(11k_n+8\right)+b_{i-1}\left(9k_n+8\right)},\end{array}$$ (3.6)

$$\begin{array}{l}9k_{n-\left(i+1\right)}+8=\frac{a_{i+1}\left(11k_n+8\right)+b_{i+1}\left(9k_n+8\right)}{a_i\left(11k_n+8\right)+b_i\left(9k_n+8\right)},\\ ⋮\\ 9k_2+8=\frac{a_{n-2}\left(11k_n+8\right)+b_{n-2}\left(9k_n+8\right)}{a_{n-3}\left(11k_n+8\right)+b_{n-3}\left(9k_n+8\right)},\end{array}$$ (3.7)

Thus, we get

$$\tau \left(G_n\right)=3\times 8^{n-1}{k}_1^2{\left[a_{n-2}\left(11k_n+8\right)+b_{n-2}\left(9k_n+8\right)\right]}^2$$ (3.8)

where a₀ = 0, b₀ = 1 and a₁ = 9, b₁ = 8. By the expression $k_{n-1}=\frac{11k_n+8}{9k_n+8}$ and Eqs. (3.6) and (3.7), we obtain

$$a_{i+1}=19a_i-16a_{i-1};b_{i+1}=19b_i-16b_{i-1}$$ (3.9)

The characteristic equation of Eq. (3.9) is $y^2-19y+16=0$ which has two roots $y_1=\frac{19+3\sqrt{33}}{2}$ and $y_2=\frac{19-3\sqrt{33}}{2}$. The general solution of Eq. (3.9) are $a_i={\lambda }_1{y}_1^i+{\lambda }_2{y}_2^i;b_i={\mu }_1{y}_1^i+{\mu }_2{y}_2^i$.

Utilizing the initial conditions $a_0=0,b_0=1$ and $a_1=9,b_1=8$, yields

$$a_i=\frac{\sqrt{33}}{11}{\left(\frac{19+3\sqrt{33}}{2}\right)}^i-\frac{\sqrt{33}}{11}{\left(\frac{19-3\sqrt{33}}{2}\right)}^i;b_i=\left(\frac{33-\sqrt{33}}{66}\right){\left(\frac{19+3\sqrt{33}}{2}\right)}^i+\left(\frac{33+\sqrt{33}}{66}\right){\left(\frac{19-3\sqrt{33}}{2}\right)}^i$$ (3.10)

If $k_n=1$, yields $G_n$ has no any electrically equivalent transformation. Substituting Eq. (3.10) into Eq. (3.8), we get

$$\tau \left(G_n\right)=3\times 8^{n-1}{k}_1^2{\left[\left(\frac{561+97\sqrt{33}}{66}\right){\left(\frac{19+3\sqrt{33}}{2}\right)}^{n-2}+\left(\frac{561-97\sqrt{33}}{66}\right){\left(\frac{19-3\sqrt{33}}{2}\right)}^{n-2}\right]}^2,n\ge 2.$$ (3.11)

When $n=1$, $\tau \left(G_1\right)=3$ which verifies Eq. (3.11). Thus, the number of spanning trees in the sequence of the graph$G_n$ is given by

$$\tau \left(G_n\right)=3\times 8^{n-1}{k}_1^2{\left[\left(\frac{561+97\sqrt{33}}{66}\right){\left(\frac{19+3\sqrt{33}}{2}\right)}^{n-2}+\left(\frac{561-97\sqrt{33}}{66}\right){\left(\frac{19-3\sqrt{33}}{2}\right)}^{n-2}\right]}^2,n\ge 1.$$ (3.12)

Where

$$k_1=\frac{{\left(\frac{329+57\sqrt{33}}{32}\right)}^{n-1}\left(97+17\sqrt{33}\right)+2\left(1-\sqrt{33}\right)}{3{\left(\frac{329+57\sqrt{33}}{32}\right)}^{n-1}\left(29+5\sqrt{33}\right)+12},n\ge 1.$$ (3.13)

Putting Eq. (3.13) into Eq. (3.12), the result is obtained.

Consider the sequence of graphs $H_1=K_3,H_2,\mathrm{...},H_n$ formed as illustrated in Figure 3.

Figure 3.

Some sequences of the graph H_n.

According to this formation, the number of total vertices $\left|V\left(H_n\right)\right|$and edges $\left|E\left(H_n\right)\right|$are $\left|V\left(H_n\right)\right|=6n-3$,$\left|E\left(H_n\right)\right|=12n-9,n=\mathrm{1,2},\dots$ It is obvious that the average degree is convergently $4$for a large $n$.

Theorem 2

The number of spanning trees in the sequence of the graph $H_n$ , where $n\ge 1$, is given as $\frac{3\times 2^{n-3}{\left(3{\left(8+3\sqrt{7}\right)}^n\left(161+61\sqrt{7}\right)+\left(-49+10\sqrt{7}\right){\left(2024+765\sqrt{7}\right)}^n+9{\left(8-3\sqrt{7}\right)}^n\left(3458+1307\sqrt{7}\right)\right)}^2}{49{\left(-9\left(127+48\sqrt{7}\right)+\left(16+5\sqrt{7}\right){\left(127+48\sqrt{7}\right)}^n\right)}^2}$

Proof: The electrically equivalent transformation to transform $H_i$ to $H_{i-1}$ is using. Figure 4 clarifies the transformation process from $H_2$ to $H_1=K_3.$

Figure 4.

The transformations from H₂ to H₁.

By utilizing the properties that are given in section 2, the following the transformations are given:

$$\tau \left(H_1^{\text{'}}\right)=9k_2\tau \left(H_2\right),\tau \left(H_2^{\text{'}}\right)=\frac{1}{{\left(3k_2+1\right)}^3}\tau \left(H_1^{\text{'}}\right),\tau \left(H_3^{\text{'}}\right)=\left(\frac{3k_2+1}{9k_2}\right)\tau \left(H_2^{\text{'}}\right),\tau \left(H_4^{\text{'}}\right)=\tau \left(H_3^{\text{'}}\right),\tau \left(H_5^{\text{'}}\right)=9\left(\frac{4k_2+1}{3k_2+1}\right)\tau \left(H_4^{\text{'}}\right),\tau \left(H_6^{\text{'}}\right)={\left(\frac{3k_2+1}{18k_2+5}\right)}^3\tau \left(H_5^{\text{'}}\right),\tau \left(H_7^{\text{'}}\right)=\tau \left(H_6^{\text{'}}\right),\tau \left(H_8^{\text{'}}\right)=\left(\frac{18k_2+5}{72k_2+18}\right)\tau \left(H_7^{\text{'}}\right)\text{and}\tau \left(H_1\right)=\tau \left(H_8^{\text{'}}\right).$$

Merging these nine transformations, we get

$$\tau \left(H_2\right)=2{\left(18k_2+5\right)}^2\tau \left(H_1\right).$$ (3.14)

Moreover,

$$\tau \left(H_n\right)=\prod _{i=2}^{n}2{\left(18k_i+5\right)}^2\tau \left(H_1\right)=3\times 2^{n-1}{k}_1^2{\left[\prod _{i=2}^n\left(18k_i+5\right)\right]}^2$$ (3.15)

where $k_{i-1}=\frac{11k_i+3}{18k_i+5},i=\mathrm{2,3},\mathrm{...},n.$

Its characteristic equation is $6x^2-2x-1=0$ which has two roots $x_1=\frac{1-\sqrt{7}}{6}$ and $x_2=\frac{1+\sqrt{7}}{6}$. Subtracting these two roots into both sides of $k_{i-1}=\frac{11k_i+3}{18k_i+5}$, we get

$$k_{i-1}-\frac{1-\sqrt{7}}{6}=\frac{11k_i+3}{18k_i+5}-\frac{1-\sqrt{7}}{6}=\left(8+3\sqrt{7}\right).\frac{a_i-\left(\frac{1-\sqrt{7}}{6}\right)}{18k_i+5}$$ (3.16)

$$k_{i-1}-\frac{1+\sqrt{7}}{6}=\frac{11k_i+3}{18k_i+5}-\frac{1+\sqrt{7}}{6}=\left(8-3\sqrt{7}\right).\frac{k_i-\left(\frac{1+\sqrt{7}}{6}\right)}{18k_i+5}$$ (3.17)

Let $h_i=\frac{k_i-\frac{1-\sqrt{7}}{6}}{k_i-\frac{1+\sqrt{7}}{6}}$. Then by Eqs. (3.16) and (317), we get $h_{i-1}=\left(127+48\sqrt{7}\right)h_i$ and $h_i={\left(127+48\sqrt{7}\right)}^{n-i}{h}_n.$

Thus $k_i=\frac{{\left(127+48\sqrt{7}\right)}^{n-i}\left(\frac{1+\sqrt{7}}{6}\right)h_n-\frac{1-\sqrt{7}}{6}}{{\left(127+48\sqrt{7}\right)}^{n-i}{h}_n-1}.$ Therefore,

$$k_1=\frac{{\left(127+48\sqrt{7}\right)}^{n-1}\left(\frac{17+7\sqrt{7}}{3}\right)-\left(1-\sqrt{7}\right)}{2{\left(127+48\sqrt{7}\right)}^{n-1}\left(\frac{16+5\sqrt{7}}{3}\right)-6}.$$ (3.18)

Utilizing the expression $k_{n-1}=\frac{11k_n+3}{18k_n+5}$ and indicating the coefficients of $11k_n+3$ and $18k_n+5$ as $a_n$ and $b_n$, we obtain

$$\begin{array}{l}18k_n+5=a_0\left(11k_n+3\right)+b_0\left(18k_n+5\right),\\ 18k_{n-1}+5=\frac{a_1\left(11k_n+3\right)+b_1\left(18k_n+5\right)}{a_0\left(11a_n+3\right)+b_0\left(18k_n+5\right)},\\ 18k_{n-2}+5=\frac{a_2\left(11k_n+3\right)+b_2\left(18k_n+5\right)}{a_1\left(11k_n+3\right)+b_1\left(18k_n+5\right)},\\ ⋮\\ 8k_{n-i}+5=\frac{a_i\left(11k_n+3\right)+b_i\left(18k_n+5\right)}{a_{i-1}\left(11k_n+3\right)+b_{i-1}\left(18k_n+5\right)},\end{array}$$ (3.19)

$$\begin{array}{l}18k_{n-\left(i+1\right)}+5=\frac{a_{i+1}\left(11k_n+3\right)+b_{i+1}\left(18k_n+5\right)}{a_i\left(11k_n+3\right)+b_i\left(18k_n+5\right)},\\ ⋮\\ 18k_2+5=\frac{a_{n-2}\left(11k_n+3\right)+b_{n-2}\left(18k_n+5\right)}{a_{n-3}\left(11k_n+3\right)+b_{n-3}\left(18k_n+5\right)},\end{array}$$ (3.20)

Thus, we obtain

$$\tau \left(H_n\right)=3\times 2^{n-1}{k}_1^2{\left[a_{n-2}\left(11k_n+3\right)+b_{n-2}\left(18k_n+5\right)\right]}^2$$ (3.21)

where $a_0=0,b_0=1$ and $a_1=18,b_1=5$. By the expression $k_{n-1}=\frac{11k_n+3}{18k_n+5}$ and Eqs. (3.19) and (3.20), we have

$$a_{i+1}=16a_i-a_{i-1};b_{i+1}=16b_i-b_{i-1}$$ (3.22)

The characteristic equation of Eq. (3.22) is $y^2-16y+1=0$ which has two roots $y_1=8+3\sqrt{7}$ and $y_2=8-3\sqrt{7}$. The general solution of Eq. (3.22) are $a_i={\lambda }_1{y}_1^i+{\lambda }_2{y}_2^i;b_i={\mu }_1{y}_1^i+{\mu }_2{y}_2^i$.

Utilizing the initial conditions $a_0=0,b_0=1$ and $a_1=18,b_1=5$, yields

$$a_i=\frac{3\sqrt{7}}{7}{\left(8+3\sqrt{7}\right)}^i-\frac{3\sqrt{7}}{7}{\left(8-3\sqrt{7}\right)}^i;b_i=\left(\frac{7-\sqrt{7}}{14}\right){\left(8+3\sqrt{7}\right)}^i+\left(\frac{7+\sqrt{7}}{14}\right){\left(8-3\sqrt{7}\right)}^i$$ (3.23)

If $k_n=1$, yields $H_n$ has no any electrically equivalent transformation. Substituting Eq. (3.23) into Eq. (3.21), we get

$$\tau \left(H_n\right)=3\times 2^{n-1}{k}_1^2{\left[\left(\frac{161+61\sqrt{7}}{14}\right){\left(8+3\sqrt{7}\right)}^{n-2}+\left(\frac{161-61\sqrt{7}}{14}\right){\left(8-3\sqrt{7}\right)}^{n-2}\right]}^2,n\ge 2.$$ (3.24)

When $n=1$, $\tau \left(H_1\right)=3$which verifies Eq. (3.24). Thus, the number of spanning trees in the sequence of the graph $H_n$ is given by

$$\tau \left(H_n\right)=3\times 2^{n-1}{k}_1^2{\left[\left(\frac{161+61\sqrt{7}}{14}\right){\left(8+3\sqrt{7}\right)}^{n-2}+\left[\frac{161-61\sqrt{7}}{14}\right]{\left(8-3\sqrt{7}\right)}^{n-2}\right]}^2,n\ge 1.$$ (3.25)

where

$$k_1=\frac{{\left(127+48\sqrt{7}\right)}^{n-1}\left(\frac{17+7\sqrt{7}}{3}\right)-\left(1-\sqrt{7}\right)}{2{\left(127+48\sqrt{7}\right)}^{n-1}\left(\frac{16+5\sqrt{7}}{3}\right)-6}.$$ (3.26)

Putting Eq. (3.26) into Eq. (3.25), we obtain the result.

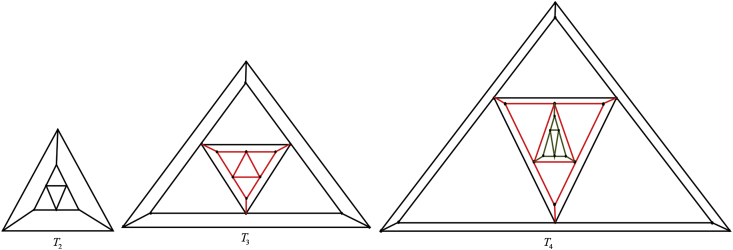
Consider the sequence of graphs $T_1=K_3,T_2,\mathrm{...},T_n$formed as illustrated in Figure 5.

Figure 5.

Some sequences of the graph T_n.

According to this formation, the number of total vertices $\left|V\left(T_n\right)\right|$ and edges $\left|E\left(T_n\right)\right|$are $\left|V\left(T_n\right)\right|=6n-3$, $\left|E\left(T_n\right)\right|=12n-9,n=\mathrm{1,2},\dots .$ It is obvious that the average degree is convergently $4$ for a large $n$.

Theorem 3

The number of spanning trees in the sequence of the graph $T_n$ , where $n\ge 1$, is given by $\frac{3\times 2^{n-3}{\left({\left(2(8+3\sqrt{7}\right)}^n\left(98+37\sqrt{7}\right)-3{\left(8-3\sqrt{7}\right)}^n\left(1897+717\sqrt{7}\right)+\left(7+5\sqrt{7}\right){\left(2024+765\sqrt{7}\right)}^n\right)}^2}{49{\left(381+144\sqrt{7}+\left(11+4\sqrt{7}\right){\left(127+48\sqrt{7}\right)}^n\right)}^2}$

Proof: The electrically equivalent transformation to transform $T_i$ to $T_{i-1}$is using. Figure 6 clarifies the transformation process from $T_2$ to $T_1=K_3.$

Figure 6.

The transformations from T₂ to T₁.

By utilizing the properties that are given in section 2, the following the transformations are given:

$$\tau \left(T_1^{\text{'}}\right)=9k_2\tau \left(T_2\right),\tau \left(T_2^{\text{'}}\right)=\frac{1}{{\left(3k_2+2\right)}^3}\tau \left(T_1^{\text{'}}\right),\tau \left(T_3^{\text{'}}\right)=\tau \left(T_2^{\text{'}}\right),\tau \left(T_4^{\text{'}}\right)=\left(\frac{3k_2+2}{18k_2}\right)\tau \left(T_3^{\text{'}}\right),\tau \left(T_5^{\text{'}}\right)=\tau \left(T_4^{\text{'}}\right),\tau \left(T_6^{\text{'}}\right)={\left(\frac{18k_2+9}{3k_2+2}\right)}^3\tau \left(T_5^{\text{'}}\right),\tau \left(T_7^{\text{'}}\right)={\left(\frac{3k_2+2}{9k_2+5}\right)}^3\tau \left(T_6^{\text{'}}\right),\tau \left(T_8^{\text{'}}\right)=\left(\frac{9k_2+5}{18k_2+9}\right)\tau \left(T_7^{\text{'}}\right)\text{and}\tau \left(T_1\right)=\tau \left(T_8^{\text{'}}\right).$$

Merging these nine transformations, we get

$$\tau \left(T_2\right)=2{\left(9k_2+5\right)}^2\tau \left(T_1\right).$$ (3.27)

Moreover,

$$\tau \left(T_n\right)=\prod _{i=2}^{n}2{\left(9k_i+5\right)}^2\tau \left(T_1\right)=3\times 2^{n-1}{k}_1^2{\left[\prod _{i=2}^n\left(9k_i+5\right)\right]}^2$$ (3.28)

where

$$k_{i-1}=\frac{11k_i+6}{9k_i+5},i=\mathrm{2,3},\mathrm{...},n.$$

Its characteristic equation is $3x^2-2x-2=0$ which has two roots $x_1=\frac{1-\sqrt{7}}{3}$ and $x_2=\frac{1+\sqrt{7}}{3}$. Subtracting these two roots into both sides of $k_{i-1}=\frac{11k_i+6}{9k_i+5}$, we have

$$k_{i-1}-\frac{1-\sqrt{7}}{3}=\frac{11k_i+6}{9k_i+5}-\frac{1-\sqrt{7}}{3}=\left(8+3\sqrt{7}\right).\frac{a_i-\left(\frac{1-\sqrt{7}}{3}\right)}{9k_i+5}$$ (3.29)

$$k_{i-1}-\frac{1+\sqrt{7}}{3}=\frac{11k_i+6}{9k_i+5}-\frac{1+\sqrt{7}}{3}=\left(8-3\sqrt{7}\right).\frac{k_i-\left(\frac{1+\sqrt{7}}{3}\right)}{9k_i+5}$$ (3.30)

Let $h_i=\frac{k_i-\frac{1-\sqrt{7}}{3}}{k_i-\frac{1+\sqrt{7}}{3}}$. Then by Eqs. (3.29) and (3.30), we have $h_{i-1}=\left(127+48\sqrt{7}\right)h_i$ and $h_i={\left(127+48\sqrt{7}\right)}^{n-i}{h}_n.$

Thus $k_i=\frac{{\left(127+48\sqrt{7}\right)}^{n-i}\left(\frac{1+\sqrt{7}}{3}\right)h_n-\frac{1-\sqrt{7}}{3}}{{\left(127+48\sqrt{7}\right)}^{n-i}{h}_n-1}.$ Therefore,

$$k_1=\frac{{\left(127+48\sqrt{7}\right)}^{n-1}\left(\frac{13+5\sqrt{7}}{3}\right)+\left(\frac{1-\sqrt{7}}{3}\right)}{{\left(127+48\sqrt{7}\right)}^{n-1}\left(\frac{11+4\sqrt{7}}{3}\right)+1}.$$ (3.31)

Utilizing the expression $k_{n-1}=\frac{11k_n+6}{9k_n+5}$ and indicating the coefficients of $11k_n+6$ and $9k_n+5$ as $a_n$ and $b_n$, we obtain

$$\begin{array}{l}9k_n+5=a_0\left(11k_n+6\right)+b_0\left(9k_n+5\right),\\ 9k_{n-1}+5=\frac{a_1\left(11k_n+6\right)+b_1\left(9k_n+5\right)}{a_0\left(11a_n+6\right)+b_0\left(9k_n+5\right)},\\ 9k_{n-2}+5=\frac{a_2\left(11k_n+6\right)+b_2\left(9k_n+5\right)}{a_1\left(11k_n+6\right)+b_1\left(9k_n+5\right)},\\ ⋮\\ 9k_{n-i}+5=\frac{a_i\left(11k_n+6\right)+b_i\left(9k_n+5\right)}{a_{i-1}\left(11k_n+6\right)+b_{i-1}\left(9k_n+5\right)},\end{array}$$ (3.32)

$$\begin{array}{l}9k_{n-\left(i+1\right)}+5=\frac{a_{i+1}\left(11k_n+6\right)+b_{i+1}\left(9k_n+5\right)}{a_i\left(11k_n+6\right)+b_i\left(9k_n+5\right)},\\ ⋮\\ 9k_2+5=\frac{a_{n-2}\left(11k_n+6\right)+b_{n-2}\left(9k_n+5\right)}{a_{n-3}\left(11k_n+6\right)+b_{n-3}\left(9k_n+5\right)},\end{array}$$ (3.33)

Thus, we get

$$\tau \left(T_n\right)=3\times 2^{n-1}{k}_1^2{\left[a_{n-2}\left(11k_n+6\right)+b_{n-2}\left(9k_n+5\right)\right]}^2$$ (3.34)

where $a_0=0,b_0=1$ and $a_1=9,b_1=5$. By the expression $k_{n-1}=\frac{11k_n+6}{9k_n+5}$ and Eqs. (3.32) and (3.33), we obtain

$$a_{i+1}=16a_i-a_{i-1};b_{i+1}=16b_i-b_{i-1}$$ (3.35)

The characteristic equation of Eq. (3.35) is $y^2-16y+1=0$which has two roots $y_1=8+3\sqrt{7}$ and $y_2=8-3\sqrt{7}$. The general solution of Eq. (3.35) are $a_i={\lambda }_1{y}_1^i+{\lambda }_2{y}_2^i;b_i={\mu }_1{y}_1^i+{\mu }_2{y}_2^i$.

Utilizing the initial conditions $a_0=0,b_0=1$ and $a_1=9,b_1=5$, yields

$$a_i=\frac{3\sqrt{7}}{14}{\left(8+3\sqrt{7}\right)}^i-\frac{3\sqrt{7}}{14}{\left(8-3\sqrt{7}\right)}^i;b_i=\left(\frac{7-\sqrt{7}}{14}\right){\left(8+3\sqrt{7}\right)}^i+\left(\frac{7+\sqrt{7}}{14}\right){\left(8-3\sqrt{7}\right)}^i$$ (3.36)

If $k_n=1$, yields$T_n$ has no any electrically equivalent transformation. Substituting Eq. (3.36) into Eq. (3.34), we get

$$\tau \left(T_n\right)=3\times 2^{n-1}{k}_1^2{\left[\left(\frac{98+37\sqrt{7}}{14}\right){\left(8+3\sqrt{7}\right)}^{n-2}+\left(\frac{98-37\sqrt{7}}{14}\right){\left(8-3\sqrt{7}\right)}^{n-2}\right]}^2,n\ge 2.$$ (3.37)

When $n=1$ , $\tau \left(T_1\right)=3$ which verifies Eq. (3.37). Thus, the number of spanning trees in the sequence of the graph $H_n$ is given by

$$\tau \left(T_n\right)=3\times 2^{n-1}{k}_1^2{\left[\left(\frac{98+37\sqrt{7}}{14}\right){\left(8+3\sqrt{7}\right)}^{n-2}+\left(\frac{98-37\sqrt{7}}{14}\right){\left(8-3\sqrt{7}\right)}^{n-2}\right]}^2,n\ge 1.$$ (3.38)

where

$$k_1=\frac{{\left(127+48\sqrt{7}\right)}^{n-1}\left(\frac{13+5\sqrt{7}}{3}\right)+\left(\frac{1-\sqrt{7}}{3}\right)}{{\left(127+48\sqrt{7}\right)}^{n-1}\left(\frac{11+4\sqrt{7}}{3}\right)+1}.$$ (3.39)

Putting Eq. (3.39) into Eq. (3.38), then the result is obtained.

Consider the sequence of graphs $X_1=K_3,X_2,...,X_n$ formed as illustrated in Figure 7.

Figure 7.

Some sequences of the graph X_n.

According to this formation, the number of total vertices $\left|V\left(X_n\right)\right|$ and edges $\left|E\left(X_n\right)\right|$are $\left|V\left(X_n\right)\right|=6n-3$,$\left|E\left(X_n\right)\right|=18n-15,n=\mathrm{1,2},\dots .$ It is obvious that the average degree is convergently $6$ for a large $n$.

Theorem 4

The number of spanning trees in the sequence of the graph $X_n$ , where $n\ge 1$, is given by

$$\frac{8^{n-3}{\left(\left(55-23\sqrt{5}\right){\left(14+6\sqrt{5}\right)}^n+\left(55+23\sqrt{5}\right){\left(14-6\sqrt{5}\right)}^n\right)}^2{\left(-{192}^n\left(29+13\sqrt{5}\right)+\left(41+25\sqrt{5}\right){\left(47+21\sqrt{5}\right)}^n\right)}^2}{75{\left(19\times 2^n\left(47+21\sqrt{5}\right)+\left(42+8\sqrt{5}\right){\left(47+21\sqrt{5}\right)}^n\right)}^2}$$

Proof: The electrically equivalent transformation to transform $X_i$ to $X_{i-1}$is using. Figure 8 clarifies the transformation process from $X_2$ to $X_1=K_3.$

Figure 8.

The transformations from X₂ to X₁.

By utilizing the properties that are given in section 2, the following the transformations are given:

$$\tau \left(X_1^{\text{'}}\right)=\frac{1}{27}\tau \left(X_2\right),\tau \left(X_2^{\text{'}}\right)=\tau \left(X_1^{\text{'}}\right),\tau \left(X_3^{\text{'}}\right)=9k_2\tau \left(X_2^{\text{'}}\right),\tau \left(X_4^{\text{'}}\right)={\left(\frac{3}{9k_2+8}\right)}^3\tau \left(X_3^{\text{'}}\right),\tau \left(X_5^{\text{'}}\right)=\tau \left(X_4^{\text{'}}\right),\tau \left(X_6^{\text{'}}\right)=\left(\frac{9k_2+8}{72k_2}\right)\tau \left(X_5^{\text{'}}\right)\text{and}\tau \left(X_1\right)=\tau \left(X_6^{\text{'}}\right)\text{.}$$

Merging these seven transformations, we get

$$\tau \left(X_2\right)=8{\left(9k_2+8\right)}^2\tau (\left(X_1\right).$$ (3.40)

Moreover,

$$\tau \left(X_n\right)=\prod _{i=2}^{n}8{\left(9k_i+8\right)}^2\tau \left(X_1\right)=3\times 8^{n-1}{k}_1^2{\left[\prod _{i=2}^n\left(9k_i+8\right)\right]}^2$$ (3.41)

where

$$k_{i-1}=\frac{20k_i+16}{9k_i+8},i=\mathrm{2,3},\mathrm{...},n.$$

Its characteristic equation is $9x^2-12x-16=0$ which has two roots $x_1=\frac{2-2\sqrt{5}}{3}$ and $x_2=\frac{2+2\sqrt{5}}{3}$. Subtracting these two roots into both sides of $k_{i-1}=\frac{20k_i+16}{9k_i+8}$, we have

$$k_{i-1}-\frac{2-2\sqrt{5}}{3}=\frac{20k_i+16}{9k_i+8}-\frac{2-2\sqrt{5}}{3}=2\left(7+3\sqrt{5}\right).\frac{a_i-\left(\frac{2-2\sqrt{5}}{3}\right)}{9k_i+8}$$ (3.42)

$$k_{i-1}-\frac{2+2\sqrt{5}}{3}=\frac{20k_i+16}{9k_i+8}-\frac{2+2\sqrt{5}}{3}=2\left(7-3\sqrt{5}\right).\frac{k_i-\left(\frac{2+2\sqrt{5}}{3}\right)}{9k_i+8}$$ (3.43)

Let $h_i=\frac{k_i-\frac{2-2\sqrt{5}}{3}}{k_i-\frac{2+2\sqrt{5}}{3}}$. Then by Eqs. (3.42) and (3.43), we get $h_{i-1}=\left(\frac{47+21\sqrt{5}}{2}\right)h_i$ and $h_i={\left(\frac{47+21\sqrt{5}}{2}\right)}^{n-i}{h}_n.$

Thus $k_i=\frac{{\left(\frac{47+21\sqrt{5}}{2}\right)}^{n-i}\left(\frac{2+2\sqrt{5}}{3}\right)h_n-\frac{2-2\sqrt{5}}{3}}{{\left(\frac{47+21\sqrt{5}}{2}\right)}^{n-i}{h}_n-1}.$ Therefore,

$$k_1=\frac{2{\left(\frac{47+21\sqrt{5}}{2}\right)}^{n-1}\left(\frac{41+25\sqrt{5}}{57}\right)+\left(\frac{2-2\sqrt{5}}{3}\right)}{{\left(\frac{47+21\sqrt{5}}{2}\right)}^{n-1}\left(\frac{21+4\sqrt{5}}{19}\right)+1}.$$ (3.44)

Utilizing the expression $k_{n-1}=\frac{20k_n+16}{9k_n+8}$ and indicating the coefficients of $20k_n+16$ and $9k_n+8$ as $a_n$ and $b_n$, we obtain

$$\begin{array}{l}9k_n+8=a_0\left(20k_n+16\right)+b_0\left(9k_n+8\right),\\ 9k_{n-1}+8=\frac{a_1\left(20k_n+16\right)+b_1\left(9k_n+8\right)}{a_0\left(20a_n+16\right)+b_0\left(9k_n+8\right)},\\ 9k_{n-2}+8=\frac{a_2\left(20k_n+16\right)+b_2\left(9k_n+8\right)}{a_1\left(20k_n+16\right)+b_1\left(9k_n+8\right)},\\ ⋮\\ 9k_{n-i}+8=\frac{a_i\left(20k_n+16\right)+b_i\left(9k_n+8\right)}{a_{i-1}\left(20k_n+16\right)+b_{i-1}\left(9k_n+8\right)},\end{array}$$

$$9k_{n-i}+8=\frac{a_i\left(20k_n+16\right)+b_i\left(9k_n+8\right)}{a_{i-1}\left(20k_n+16\right)+b_{i-1}\left(9k_n+8\right)},$$ (3.45)

$$\begin{array}{l}9k_{n-\left(i+1\right)}+8=\frac{a_{i+1}\left(20k_n+16\right)+b_{i+1}\left(9k_n+8\right)}{a_i\left(20k_n+16\right)+b_i\left(9k_n+8\right)},\\ ⋮\\ 9k_2+8=\frac{a_{n-2}\left(20k_n+16\right)+b_{n-2}\left(9k_n+8\right)}{a_{n-3}\left(20k_n+16\right)+b_{n-3}\left(9k_n+8\right)},\end{array}$$ (3.46)

Thus, we obtain

$$\tau \left(X_n\right)=3\times 8^{n-1}{k}_1^2{\left[a_{n-2}\left(20k_n+16\right)+b_{n-2}\left(9k_n+8\right)\right]}^2$$ (3.47)

where $a_0=0,b_0=1$ and $a_1=9,b_1=8$. By the expression $k_{n-1}=\frac{20k_n+16}{9k_n+8}$ and Eqs. (3.45) and (3.46), we get

$$a_{i+1}=28a_i-16a_{i-1};b_{i+1}=28b_i-16b_{i-1}$$ (3.48)

The characteristic equation of Eq. (3.48) is $y^2-28y+16=0$which has two roots $y_1=14+6\sqrt{5}$ and $y_2=14-6\sqrt{5}$. The general solution of Eq. (3.48) are $a_i={\lambda }_1{y}_1^i+{\lambda }_2{y}_2^i;b_i={\mu }_1{y}_1^i+{\mu }_2{y}_2^i$.

Utilizing the initial conditions $a_0=0,b_0=1$ and $a_1=9,b_1=8$, yields

$$a_i=\frac{3\sqrt{5}}{20}{\left(14+6\sqrt{5}\right)}^i-\frac{3\sqrt{5}}{20}{\left(14-6\sqrt{5}\right)}^i;b_i=\left(\frac{5-\sqrt{5}}{10}\right){\left(14+6\sqrt{5}\right)}^i+\left(\frac{5+\sqrt{5}}{10}\right){\left(14-6\sqrt{5}\right)}^i$$ (3.49)

If $k_n=1$, yields $X_n$ has no any electrically equivalent transformation. Substituting Eq. (3.49) into Eq. (3.47), we get

$$\tau \left(X_n\right)=3\times 8^{n-1}{k}_1^2{\left[\left(\frac{85+37\sqrt{5}}{10}\right){\left(14+6\sqrt{5}\right)}^{n-2}+\left(\frac{85-37\sqrt{5}}{10}\right){\left(14-6\sqrt{5}\right)}^{n-2}\right]}^2,n\ge 2.$$ (3.50)

When $n=1$ , $\tau \left(X_1\right)=3$which verifies Eq. (3.50). Thus, the number of spanning trees in the sequence of the graph$X_n$ is given by

$$\tau \left(X_n\right)=3\times 8^{n-1}{k}_1^2{\left[\left(\frac{85+37\sqrt{5}}{10}\right){\left(14+6\sqrt{5}\right)}^{n-2}+\left(\frac{85-37\sqrt{5}}{10}\right){\left(14-6\sqrt{5}\right)}^{n-2}\right]}^2,n\ge 1.$$ (3.51)

where

$$k_1=\frac{2{\left(\frac{47+21\sqrt{5}}{2}\right)}^{n-1}\left(\frac{41+25\sqrt{5}}{57}\right)+\left(\frac{2-2\sqrt{5}}{3}\right)}{{\left(\frac{47+21\sqrt{5}}{2}\right)}^{n-1}\left(\frac{21+4\sqrt{5}}{19}\right)+1}.$$ (3.52)

Putting Eq. (3.52) into Eq. (3.51), the result is obtained.

Consider the sequence of graphs $Y_1=K_3,Y_2,...,Y_n$ formed as illustrated in Figure 9.

Figure 9.

Some sequences of the graph Y_n.

According to this formation, the number of total vertices $\left|V\left(Y_n\right)\right|$ and edges $\left|E\left(Y_n\right)\right|$ are $\left|V\left(Y_n\right)\right|=6n-3,$ $\left|E\left(Y_n\right)\right|=15n-12,n=\mathrm{1,2},\dots .$It is obvious that the average degree is convergently $5$ for a large $n$.

Theorem 5

The number of spanning trees in the sequence of the graph $Y_n$ , where $n\ge 1$, is given by

$$\frac{2^{n-5}{\left(\left(10+7\sqrt{2}\right){\left(17-12\sqrt{2}\right)}^n+\left(10-7\sqrt{2}\right){\left(17+12\sqrt{2}\right)}^n\right)}^2{\left(1055+746\sqrt{2}-\left(11+8\sqrt{2}\right){\left(577+408\sqrt{2}\right)}^n\right)}^2}{3{\left(577+408\sqrt{2}+\left(3+2\sqrt{2}\right){\left(577+408\sqrt{2}\right)}^n\right)}^2}$$

Proof: The electrically equivalent transformation to transform $Y_i$ to $Y_{i-1}$ is using. Figure 8 clarifies the transformation process from $Y_2$ to $Y_1=K_3.$ (see Figure 10).

Figure 10.

The transformations from Y₂ to Y₁.

By utilizing the properties that are given in section 2, the following the transformations are given:

$$\tau \left(Y_1^{\text{'}}\right)=9k_2\tau \left(Y_2\right),\tau \left(Y_2^{\text{'}}\right)={\left(\frac{1}{3k_2+2}\right)}^3\tau \left(Y_1^{\text{'}}\right),\tau \left(Y_3^{\text{'}}\right)=\tau \left(Y_2^{\text{'}}\right),\tau \left(Y_4^{\text{'}}\right)=\left(\frac{3k_2+2}{18k_2}\right)\tau \left(Y_3^{\text{'}}\right),\tau \left(Y_5^{\text{'}}\right)=\tau \left(Y_4^{\text{'}}\right),\tau \left(Y_6^{\text{'}}\right)=\left(\frac{45k_2+27}{3k_2+2}\right)\tau \left(Y_5^{\text{'}}\right),\tau \left(Y_7^{\text{'}}\right)={\left(\frac{3k_2+2}{18k_2+11}\right)}^3\tau \left(Y_6^{\text{'}}\right),\tau \left(Y_8^{\text{'}}\right)=\left(\frac{18k_2+11}{45k_2+27}\right)\tau \left(Y_7^{\text{'}}\right)\text{and}\tau \left(Y_1\right)=\tau \left(Y_8^{\text{'}}\right).$$

Merging these nine transformations, we obtain

$$\tau \left(Y_2\right)=2{\left(18k_2+11\right)}^2\tau \left(Y_1\right).$$ (3.53)

Moreover,

$$\tau \left(Y_n\right)=\prod _{i=2}^{n}2{\left(18k_i+11\right)}^2\tau \left(Y_1\right)=3\times 2^{n-1}{k}_1^2{\left[\prod _{i=2}^n\left(18k_i+11\right)\right]}^2$$ (3.54)

where $k_{i-1}=\frac{23k_i+14}{18k_i+11},i=\mathrm{2,3},\mathrm{...},n.$

Its characteristic equation is $9x^2-6x-7=0$ which has two roots $x_1=\frac{1-2\sqrt{2}}{3}$ and $x_2=\frac{1+2\sqrt{2}}{3}$. Subtracting these two roots into both sides of $k_{i-1}=\frac{23k_i+14}{18k_i+11}$, we have

$$k_{i-1}-\frac{1-2\sqrt{2}}{3}=\frac{23k_i+14}{18k_i+11}-\frac{1-2\sqrt{2}}{3}=\left(17+12\sqrt{2}\right).\frac{k_i-\left(\frac{1-2\sqrt{2}}{3}\right)}{18k_i+11}$$ (3.55)

$$k_{i-1}-\frac{1+2\sqrt{5}}{3}=\frac{23k_i+14}{18k_i+11}-\frac{1+2\sqrt{2}}{3}=\left(17-12\sqrt{2}\right).\frac{k_i-\left(\frac{1+2\sqrt{2}}{3}\right)}{18k_i+11}$$ (3.56)

Let $h_i=\frac{k_i-\frac{1-2\sqrt{2}}{3}}{k_i-\frac{1+2\sqrt{2}}{3}}$. Then by Eqs. (3.55) and (3.56), we have t $h_{i-1}=\left(577+408\sqrt{2}\right)h_i$ and $h_i={\left(577+408\sqrt{2}\right)}^{n-i}{h}_n.$

Thus $k_i=\frac{{\left(577+408\sqrt{2}\right)}^{n-i}\left(\frac{1+2\sqrt{2}}{3}\right)h_n-\frac{1-2\sqrt{2}}{3}}{{\left(577+408\sqrt{2}\right)}^{n-i}{h}_n-1}.$ Therefore,

$$k_1=\frac{{\left(577+408\sqrt{2}\right)}^{n-1}\left(\frac{11+8\sqrt{2}}{3}\right)+\left(\frac{1-2\sqrt{2}}{3}\right)}{{\left(577+408\sqrt{2}\right)}^{n-1}\left(3+2\sqrt{2}\right)+1}.$$ (3.57)

Utilizing the expression $k_{n-1}=\frac{23k_n+14}{18k_n+11}$ and indicating the coefficients of $23k_n+14$ and $18k_n+11$ as $a_n$ and $b_n$, we obtain

$$\begin{array}{l}18k_n+11=a_0\left(23k_n+14\right)+b_0\left(18k_n+11\right),\\ 18k_{n-1}+11=\frac{a_1\left(23k_n+14\right)+b_1\left(18k_n+11\right)}{a_0\left(23a_n+14\right)+b_0\left(18k_n+11\right)},\\ 18k_{n-2}+11=\frac{a_2\left(23k_n+14\right)+b_2\left(18k_n+11\right)}{a_1\left(23k_n+14\right)+b_1\left(18k_n+11\right)},\\ ⋮\\ 18k_{n-i}+11=\frac{a_i\left(23k_n+14\right)+b_i\left(18k_n+11\right)}{a_{i-1}\left(23k_n+14\right)+b_{i-1}\left(18k_n+11\right)},\end{array}$$ (3.58)

$$\begin{array}{l}18k_{n-\left(i+1\right)}+11=\frac{a_{i+1}\left(23k_n+14\right)+b_{i+1}\left(18k_n+11\right)}{a_i\left(23k_n+14\right)+b_i\left(18k_n+11\right)},\\ ⋮\\ 18k_2+11=\frac{a_{n-2}\left(23k_n+14\right)+b_{n-2}\left(18k_n+11\right)}{a_{n-3}\left(23k_n+14\right)+b_{n-3}\left(18k_n+11\right)},\end{array}$$ (3.59)

Thus, we have

$$\tau \left(Y_n\right)=3\times 2^{n-1}{k}_1^2{\left[a_{n-2}\left(23k_n+14\right)+b_{n-2}\left(18k_n+11\right)\right]}^2$$ (3.60)

where $a_0=0,b_0=1$and $a_1=18,b_1=11$. By the expression $k_{n-1}=\frac{23k_n+14}{18k_n+11}$ and Eqs. (3.58) and (3.59), we have

$$a_{i+1}=34a_i-a_{i-1};b_{i+1}=34b_i-b_{i-1}$$ (3.61)

The characteristic equation of Eq. (3.61) is $y^2-34y+1=0$which has two roots $y_1=17+12\sqrt{2}$ and $y_2=17-12\sqrt{5}$. The general solution of Eq. (3.61) are $a_i={\lambda }_1{y}_1^i+{\lambda }_2{y}_2^i;b_i={\mu }_1{y}_1^i+{\mu }_2{y}_2^i$.

Utilizing the initial conditions $a_0=0,b_0=1$ and $a_1=18,b_1=11$, yields

$$a_i=\frac{3\sqrt{2}}{8}{\left(17+12\sqrt{2}\right)}^i-\frac{3\sqrt{2}}{8}{\left(17-12\sqrt{2}\right)}^i;b_i=\left(\frac{4-\sqrt{2}}{8}\right){\left(17+12\sqrt{2}\right)}^i+\left(\frac{4+\sqrt{2}}{8}\right){\left(17-12\sqrt{2}\right)}^i$$ (3.62)

If $k_n=1$, yields $Y_n$ has no any electrically equivalent transformation. Substituting Eq. (3.62) into Eq. (3.60), we get

$$\tau \left(Y_n\right)=3\times 2^{n-1}{k}_1^2{\left[\left(\frac{58+41\sqrt{2}}{4}\right){\left(17+12\sqrt{2}\right)}^{n-2}+\left(\frac{58-41\sqrt{2}}{4}\right){\left(17-12\sqrt{2}\right)}^{n-2}\right]}^2,n\ge 2.$$ (3.63)

When $n=1$, $\tau \left(Y_1\right)=3$ which verifies Eq. (3.63). Thus, the number of spanning trees in the sequence of the graph$Y_n$ is given by

$$\tau \left(Y_n\right)=3\times 2^{n-1}{k}_1^2{\left[\left(\frac{58+41\sqrt{2}}{4}\right){\left(17+12\sqrt{2}\right)}^{n-2}+\left(\frac{58-41\sqrt{2}}{4}\right){\left(17-12\sqrt{2}\right)}^{n-2}\right]}^2,n\ge 1.$$ (3.64)

where

$$k_1=\frac{{\left(577+408\sqrt{2}\right)}^{n-1}\left(\frac{11+8\sqrt{2}}{3}\right)+\left(\frac{1-2\sqrt{2}}{3}\right)}{{\left(577+408\sqrt{2}\right)}^{n-1}\left(3+2\sqrt{2}\right)+1}.$$ (3.65)

Putting Eq. (3.65) into Eq. (3.64), then the result is obtained.

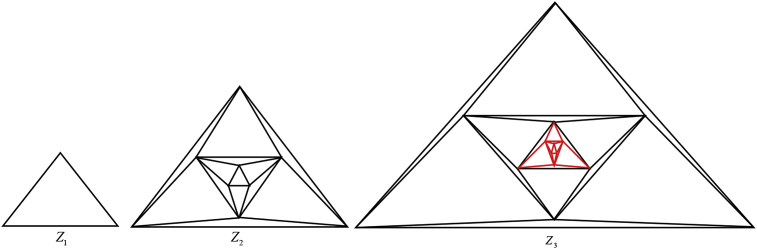
Consider the sequence of graphs $Z_1=K_3,Z_2,...,Z_n$formed as illustrated in Figure 11.

Figure 11.

Some sequences of the graph Z_n.

According to this formation, the number of total vertices $\left|V\left(Z_n\right)\right|$ and edges $\left|E\left(Z_n\right)\right|$ are $\left|V\left(Z_n\right)\right|=6n-3$, $\left|E\left(Z_n\right)\right|=18n-15,n=\mathrm{1,2},\dots .$ It is obvious that the average degree is convergently $6$ for a large $n$.

Theorem 6

The number of spanning trees in the sequence of the graph $Z_n$, where $n\ge 1$, is given by $G_n$ , where $n\ge 1$, is given by $\frac{{3(47+21\sqrt{5})}^{2n}{\left(2^{n+1}\left(85+38\sqrt{5}\right)+(15-7\sqrt{5}){\left(2207+987\sqrt{5}\right)}^n+\left(88555+93603\sqrt{5}\right){\left(2207-987\sqrt{5}\right)}^n\right)}^2}{100{\left(2^n\left(2207+987\sqrt{5}\right)+(3+\sqrt{5}){\left(2207+987\sqrt{5}\right)}^n\right)}^2}$

Proof: Let us be using the electrically equivalent transformation to transform $z_i$ to $z_{i-1}$. Figure 2 clarifies the transformation process from $z_2$to $z_1=$$K_3.$

Proof: The electrically equivalent transformation to transform $Z_i$to $Z_{i-1}$is using. Figure 12 clarifies the transformation process from $Z_2$to $Z_1=K_3.$

Figure 12.

The transformations from Z₂ to Z₁.

By utilizing the properties that are given in section 2, the following the transformations are given:

$$\tau \left(Z_1^{\text{'}}\right)=9k_2\tau \left(Z_2\right),\tau \left(Z_2^{\text{'}}\right)={\left(\frac{1}{3k_2+2}\right)}^3\tau \left(Z_1^{\text{'}}\right),\tau \left(Z_3^{\text{'}}\right)=\tau \left(Z_2^{\text{'}}\right),\tau \left(Z_4^{\text{'}}\right)=\frac{3k_2+2}{18k_2}\tau \left(Z_3^{\text{'}}\right),\tau \left(Z_5^{\text{'}}\right)=\tau \left(Z_4^{\text{'}}\right),\tau \left(Z_6^{\text{'}}\right)=9\left(\frac{5k_2+3}{3k_2+2}\right)\tau \left(Z_5^{\text{'}}\right),\tau \left(Z_7^{\text{'}}\right)={\left(\frac{3k_2+2}{21k_2+13}\right)}^3\tau \left(Z_6^{\text{'}}\right),\tau \left(Z_8^{\text{'}}\right)=\tau \left(Z_7^{\text{'}}\right),\tau \left(Z_9^{\text{'}}\right)=\frac{21k_2+13}{9\left(10k_2+6\right)}\tau \left(Z_8^{\text{'}}\right)\text{and}\tau \left(Z_1\right)=\tau \left(Z_9^{\text{'}}\right).$$

Merging these nine transformations, we obtain

$$\tau \left(Z_2\right)=4{\left(21k_2+13\right)}^2\tau \left(Z_1\right).$$ (3.66)

Moreover,

$$\tau \left(Z_n\right)=\prod _{i=2}^{n}4{\left(21k_i+13\right)}^2\tau \left(Z_1\right)=3\times 4^{n-1}{k}_1^2{\left[\prod _{i=2}^n\left(21k_i+13\right)\right]}^2$$ (3.67)

where $k_{i-1}=\frac{34k_i+21}{21k_i+13},i=\mathrm{2,3},\mathrm{...},n.$

Its characteristic equation is $x^2-x-1=0$ which has two roots $x_1=\frac{1-\sqrt{5}}{2}$ and $x_2=\frac{1+\sqrt{5}}{2}$. Subtracting these two roots into both sides of $k_{i-1}=\frac{34k_i+21}{21k_i+13}$, we have

$$k_{i-1}-\frac{1-\sqrt{5}}{2}=\frac{34k_i+21}{21k_i+13}-\frac{1-\sqrt{5}}{2}=\left(47+21\sqrt{5}\right).\frac{a_i-\left(\frac{1-\sqrt{5}}{2}\right)}{2\left(21k_i+13\right)}$$ (3.68)

$$k_{i-1}-\frac{1+\sqrt{5}}{2}=\frac{34k_i+21}{21k_i+13}-\frac{1+\sqrt{5}}{2}=\left(47-21\sqrt{5}\right).\frac{k_i-\left(\frac{1+\sqrt{5}}{2}\right)}{2\left(21k_i+13\right)}$$ (3.69)

Let $h_i=\frac{k_i-\frac{2-2\sqrt{5}}{3}}{k_i-\frac{2+2\sqrt{5}}{3}}$. Then by Eqs. (3.68) and (3.69), we have $h_{i-1}=\left(\frac{2207+987\sqrt{5}}{2}\right)h_i$ and $h_i={\left(\frac{2207+987\sqrt{5}}{2}\right)}^{n-i}{h}_n.$

Thus $k_i=\frac{{\left(\frac{2207+987\sqrt{5}}{2}\right)}^{n-i}\left(\frac{1+\sqrt{5}}{2}\right)h_n-\frac{1-\sqrt{5}}{2}}{{\left(\frac{2207+987\sqrt{5}}{2}\right)}^{n-i}{h}_n-1}.$ Therefore,

$$k_1=\frac{{\left(\frac{2207+987\sqrt{5}}{2}\right)}^{n-1}\left(2+\sqrt{5}\right)+\left(\frac{1-\sqrt{5}}{2}\right)}{{\left(\frac{2207+987\sqrt{5}}{2}\right)}^{n-1}\left(\frac{3+\sqrt{5}}{2}\right)+1}.$$ (3.70)

Utilizing the expression $k_{n-1}=\frac{34k_n+21}{21k_n+13}$ and indicating the coefficients of $34k_n+21$ and $21k_n+13$ as $a_n$ and $b_n$ , we obtain

$$\begin{array}{l}21k_n+13=a_0\left(34k_n+21\right)+b_0\left(21k_n+13\right),\\ 21k_{n-1}+13=\frac{a_1\left(34k_n+21\right)+b_1\left(21k_n+13\right)}{a_0\left(34a_n+21\right)+b_0\left(21k_n+13\right)},\\ 21k_{n-2}+13=\frac{a_2\left(34k_n+21\right)+b_2\left(21k_n+13\right)}{a_1\left(34k_n+21\right)+b_1\left(21k_n+13\right)},\\ ⋮\\ 21k_{n-i}+13=\frac{a_i\left(34k_n+21\right)+b_i\left(21k_n+13\right)}{a_{i-1}\left(34k_n+21\right)+b_{i-1}\left(21k_n+13\right)},\end{array}$$ (3.71)

$$\begin{array}{l}21k_{n-\left(i+1\right)}+13=\frac{a_{i+1}\left(34k_n+21\right)+b_{i+1}\left(21k_n+13\right)}{a_i\left(34k_n+21\right)+b_i\left(21k_n+13\right)},\\ ⋮\\ 21k_2+13=\frac{a_{n-2}\left(34k_n+21\right)+b_{n-2}\left(21k_n+13\right)}{a_{n-3}\left(34k_n+21\right)+b_{n-3}\left(21k_n+13\right)},\end{array}$$ (3.72)

Thus, we get

$$\tau \left(Z_n\right)=3\times 4^{n-1}{k}_1^2{\left[a_{n-2}\left(34k_n+21\right)+b_{n-2}\left(21k_n+13\right)\right]}^2$$ (3.73)

where $a_0=0,b_0=1$and $a_1=21,b_1=13$. By the expression $k_{n-1}=\frac{34k_n+21}{21k_n+13}$ and Eqs. (3.71) and (3.72), we have

$$a_{i+1}=47a_i-a_{i-1};b_{i+1}=47b_i-b_{i-1}$$ (3.74)

The characteristic equation of Eq. (3.74) is $y^2-47y+1=0$ which has two roots $y_1=\frac{47+21\sqrt{5}}{2}$ and $y_2=\frac{47-21\sqrt{5}}{2}$. The general solution of Eq. (3.74) are $a_i={\lambda }_1{y}_1^i+{\lambda }_2{y}_2^i;b_i={\mu }_1{y}_1^i+{\mu }_2{y}_2^i$.

Utilizing the initial conditions $a_0=0,b_0=1$ and $a_1=21,b_1=13$, yields

$$a_i=\frac{\sqrt{5}}{5}{\left(\frac{47+21\sqrt{2}}{2}\right)}^i-\frac{\sqrt{5}}{5}{\left(\frac{47-21\sqrt{5}}{2}\right)}^i;b_i=\left(\frac{5-\sqrt{5}}{10}\right){\left(\frac{47+21\sqrt{5}}{2}\right)}^i+\left(\frac{5+\sqrt{5}}{10}\right){\left(\frac{47-21\sqrt{5}}{2}\right)}^i$$ (3.75)

If $k_n=1$, yields Z_n has no any electrically equivalent transformation. Substituting Eq. (3.75) into Eq. (3.73), we get

$$\tau \left(Z_n\right)=3\times 4^{n-1}{k}_1^2{\left[\left(\frac{85+38\sqrt{5}}{10}\right){\left(\frac{47+21\sqrt{5}}{2}\right)}^{n-2}+\left(\frac{85-38\sqrt{5}}{10}\right){\left(\frac{47-21\sqrt{5}}{2}\right)}^{n-2}\right]}^2,n\ge 2.$$ (3.76)

When $n=1$,$\tau \left(Z_1\right)=3$ which verifies Eq. (3.76). Thus, the number of spanning trees in the sequence of the graph Z_n is given by

$$\tau \left(Z_n\right)=3\times 4^{n-1}{k}_1^2{\left[\left(\frac{85+38\sqrt{5}}{10}\right){\left(\frac{47+21\sqrt{5}}{2}\right)}^{n-2}+\left(\frac{85-38\sqrt{5}}{10}\right){\left(\frac{47-21\sqrt{5}}{2}\right)}^{n-2}\right]}^2,n\ge 1.$$ (3.77)

where

$$k_1=\frac{{\left(\frac{2207+987\sqrt{5}}{2}\right)}^{n-1}\left(2+\sqrt{5}\right)+\left(\frac{1-\sqrt{5}}{2}\right)}{{\left(\frac{2207+987\sqrt{5}}{2}\right)}^{n-1}\left(\frac{3+\sqrt{5}}{2}\right)+1}.$$ (3.78)

Putting Eq. (3.77) into Eq. (3.78), hence the result is obtained.

4. Numerical results

Next tables illustrate some the values of the number of spanning trees in the graphs $G_n,H_n,T_n,X_n,Y_n$ and Z_n.

$n$	$\tau \left(G_n\right)$	$\tau \left(H_n\right)$	$\tau \left(T_n\right)$
$1$	3	3	3
2	8664	1176	1734
3	22852800	596748	881292
4	60019201536	303141984	447690264
5	157597728780288	153993738288	227423130672
6	413814073710182400	78227606477184	115529159623776

n	$\tau \left(X_n\right)$	$\tau \left(Y_n\right)$	$\tau \left(Z_n\right)$
1	3	3	3
2	31104	8214	36300
3	188940288	18960588	320498688
4	1136394240000	43761009624	2829362006208
5	6833482751803392	101000334380592	24977602663502592
6	41091617468631220224	233108596706389344	220502231043611492352

5. Spanning tree entropy

After having explicit formulas for the number of spanning trees of the sequence of the six graphs $G_n,H_n,T_n,X_n,Y_n$ and Z_n, we can calculate its spanning tree entropy Z which is a finite number and a very interesting quantity characterizing the network structure, defined in [23, 24] : for a graph $G$,

$$Z\left(G\right)=\underset{n\to \infty }{lim}\frac{\ln \tau \left(G\right)}{\left|V\left(G\right)\right|}.$$ (5.1)

$$Z\left(G_n\right)=\frac{1}{6}\left(\ln \left[2\right]+2\ln \left[19+3\sqrt{33}\right]\right)=1.312187627,$$

$$Z\left(H_n\right)=\frac{1}{6}\left(ln\left[2\right]-2ln\left[127+48\sqrt{7}\right]+2ln\left[2024+765\sqrt{7}\right]\right)=1.038,$$

$$Z\left(T_n\right)=\frac{1}{6}\left(ln\left[2\right]-2ln\left[127+48\sqrt{7}\right]+2ln\left[2024+765\sqrt{7}\right]\right)=1.038,$$

$$Z\left(X_n\right)=\frac{1}{6}\left(\ln \left[8\right]+2\ln \left[14+6\sqrt{5}\right]\right)=1.45,$$

$$Z\left(Y_n\right)=\frac{1}{6}\left(\ln \left[2\right]+2\ln \left[17+12\sqrt{2}\right]\right)=1.291,$$

$$Z\left(Z_n\right)=\frac{1}{3}\left(\ln \left[47+21\sqrt{5}\right]\right)=1.514.$$

By comparing the value of entropy in our graphs with other graphs, we notice that the entropy of the graph $G_n$ is larger than the entropy of the graph $Y_n$ of the same average degree 5. Also, the entropy of the graph Z_n is larger than the entropy of the graph $X_n$ of the same average degree 6. In addition the entropy of the graphs $H_n\text{and}{T}_n$ of the same average degree 4 are equal and smaller than the entropy of the fractal scale-free lattice [25] which has the entropy $1.040$, two dimensional Sierpinski gasket [26] which has the entropy $1.166$ and the 3-prism graph [27] which has the entropy $1.0445\text{of the same averagre degree}4$.

6. Conclusions

In this paper, we have calculated the number of spanning trees in the sequences of some nonahedral (polyhedral graphs having nine vertices) graphs generated by triangle using electrically equivalent transformations. The feature of this technique lies in the parry of strenuous computation of Laplacian spectra that is prerequisite for a generic method for determining spanning trees. Also, our results have been shown that entropy is related to the average degree of the graphs.

Declarations

Author contribution statement

S. Daoud, W. Saleh: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

Authors were supported by Taibah University.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.