Lateral heterogeneity and domain formation in cellular membranes

Highlights

• •Review article describing recent experimental and theoretical membrane lateral heterogeneity research.
• •Describes the static and dynamic physical concepts behind domain formation in model membranes.
• •Describes coarse-grained, phenomenological approaches that result in phases associated with lipid lateral heterogeneity.

Abstract

As early as the development of the fluid mosaic model for cellular membranes, researchers began observing the telltale signs of lateral heterogeneity. Over the decades this has led to the development of the lipid raft hypothesis and the ensuing controversy that has unfolded, as a result. Here, we review the physical concepts behind domain formation in lipid membranes, both of their structural and dynamic origins. This, then leads into a discussion of coarse-grained, phenomenological approaches that describe the wide range of phases associated with lipid lateral heterogeneity. We use these physical concepts to describe the interaction between raft-lipid species, such as long-chain saturated lipids, sphingomyelin, and cholesterol, and non-raft forming lipids, such as those with short acyl chains or unsaturated fatty acids. While debate has persisted on the biological relevance of lipid domains, recent research, described here, continues to identify biological roles for rafts and new experimental approaches have revealed the existence of lipid domains in living systems. Given the recent progress on both the biological and structural aspects of raft formation, the research area of membrane lateral heterogeneity will not only expand, but will continue to produce exciting results.

1. Introduction

The fluid mosaic model of membranes was proposed by Singer and Nicolson in 1972 (Singer and Nicolson, 1972) and almost immediately there were reports showing the existence of membrane lateral heterogeneity (Shimshick and McConnell, 1973, Lee et al., 1974). By the late 1970s, it was suggested that lipids could segregate into liquid disordered and liquid ordered domains (Wunderlich et al., 1978). Over the next decade, research showed that proteins could also co-localize (Thomas et al., 1982, Karnovsky et al., 1982, Florine and Feigenson, 1987, Dibble et al., 1993), and in some cases, preferentially associate with lipids such as, sphingomyelin (Curtain et al., 1980). In the early 1990s, experiments focusing on cholesterol in model membranes showed the sterol's ability to increase lateral heterogeneity (Sankaram and Thompson, 1991, Vist and Davis, 1990), and other studies, such as those using detergents to extract biomolecules from natural membranes, soon followed demonstrating protein co-localization with sphingomyelin and cholesterol (Schroeder et al., 1994, Levental et al., 2010, Brown and Rose, 1992, Fridriksson et al., 1999, Pike et al., 2002). Eventually, these data led to the hypothesis that sphingomyelin and cholesterol formed liquid ordered domains, called “rafts”, in which proteins could associated with (Simons and Ikonen, 1997, Lingwood and Simons, 2010). Although it was shown that some proteins had a preference for certain lipids, the idea that these would form large domains of functional significance remained controversial. However, recent research has revealed evidence for domain formation, consistent with lipid rafts, in fully functional, living cells (Swamy et al., 2006, Nickels et al., 2017). In this review, we discuss the concepts behind lipid domain formation in membranes, the biomolecules that they are made of, and their biological significance.

2. Concepts of domain formation

2.1. Line tension and scale invariance

The propensity for domain formation results from the interaction energy between chemically distinct lipids and proteins. For example, unfavorable interaction energies can result from lipids with different length fatty acid chains forming differering thickness membranes residing next to each other. Some of these unfavorable interactions can be eliminated or minimized by sequestering lipids of similar length within a domain. To model this, an interaction energy, i.e., the so-called called line tension, λ, is used, and is defined as:

$$\lambda =E_b/L_b,$$ (1)

where E _b is the total interaction energy at the domain boundary and L _b is the length of the domain boundary (Keller et al., 1987). Note, that the total interaction energy is proportional to the domain boundary length, but the line tension, is not.

In general, the greater the line tension, the greater the propensity for domain formation. Line tension can be thought of as a string surrounding the domain perimeter that tightens as a function of an increasing unfavorable interaction energy between the domain and its surroundings. Note, that line tension should be considered in relation to the repulsive electrostatic forces that exist between the different lipids. For example, two systems of similar intrinsic line tension can have drastically different domain sizes if one system happens to have charged lipids, while the other, does not. Theoretically, a constant line tension obeys the property of scale invariance (Fischer and Vink, 2011). This means, that at any scale – if treated as a continuous system – one observes a small number of large domains and an increasing number of smaller domains. The consequence of this, is that statistical properties such as, average domain size increase with the size of the system explaining why simulations of small membrane patches “observe” more mixing than what is observed experimentally.

However, domain size as a function of system size is not only the result of general scale invariance principles. For example, computer simulations have found size dependant critical points in phase separation studies (Pantelopulos et al., 2017, Bolmatov et al., 2020a). Further, experiments have revealed that domain formation, is to some extent, dependent on collective membrane material properties and long-range fluctuations (Galimzyanov et al., 2017), which will be discussed later. Thus, line tension, itself, can vary as a function of system size under certain circumstances.

In addition to domain size having an effect on line tension, it is known that lipid-lipid repulsive interactions – which limit domain formation – also affect line tension. One way to account for lipid-lipid repulsive forces that counteract line tension, is to treat each lipid phase as a density of dipoles. What is important here, is not the absolute dipolar density, but the dipole density difference, Δm, where lipids of one phase redistribute into the other phase in order to reduce repulsive dipolar interactions. The energy per molecule, E/N, for a circular domain can be written in terms of the opposing line tension and dipolar density difference as:

$$\frac{E}{N}=\frac{2a_0}{R}\left[\lambda -\frac{{\left(\mathrm{\Delta }m\right)}^2}{4\pi \epsilon {\epsilon }_0}ln\left(\frac{4R}{e^2\delta }\right)\right],$$ (2)

where a ₀ is the area per molecule, R is the domain radius, ε is the dielectric constant of the interfacial water, ε ₀ is the permittivity of free space, e is Euler's number, and δ is the molecular cut-off distance ∼0.5 nm (Lee et al., 2011, Lee and McConnell, 1993). While the circular domain assumption is not necessarily valid for liquid-solid domain coexistence, it generally applies to liquid-liquid domain coexistence, as shown in Fig. 3a. In Eq. (2), the line tension contribution to the energy density decreases at a greater rate than the dipolar density difference contribution with respect to domain radius. Thus, an increasing dipolar density difference reduces the average size of large domains. For a given line tension, and using Eq. (2) within a statistical framework, the result is a distribution of domain sizes (Lee et al., 2011). In the following subsections we will discuss formulations for the line tension and the physical origins of domain formation.

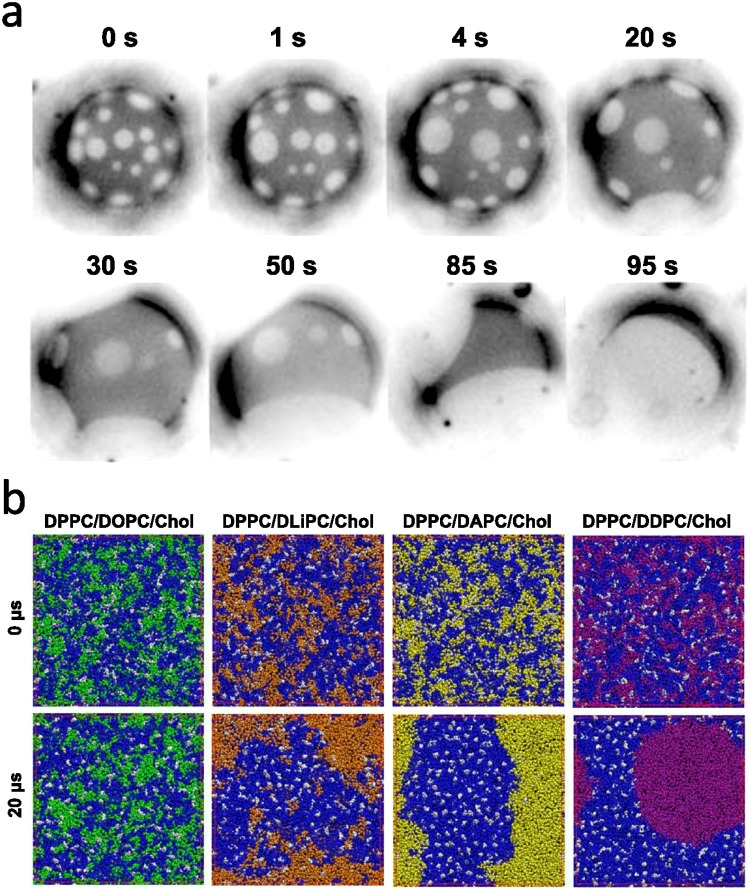
Fig. 3.

Using epifluorescence microscopy with Texas Red-DPPE dye, Veatch and Keller were able to observe domain formation over time, (a) in a 2:2:1 DOPC/DPPC/cholesterol model membrane system (Veatch and Keller, 2003). (b) Lin et al. observed increased domain formation with polyunsaturated lipids using coarse-grained molecular dynamics simulations (Lin et al., 2016).

2.2. Hydrophobic mismatch and membrane deformation

Lipids and membrane proteins have varying intrinsic hydrophobic thicknesses. Coexistence of these species within a membrane results in local deformations at boundaries where lipids splay and tilt to accommodate different thicknesses (see Fig. 1 ). However, these deformations have an associated energy cost that results in line tension. Energetics of local deformation can be discussed in terms of material properties, such as the splay elastic modulus (B), tilt modulus (K), and the intrinsic curvature (J) between two domains. If we consider two domains with thickness difference, δ, and an average thickness, h ₀, the line tension at the domain boundary can be written as:

$$\lambda =\left(\frac{{\delta }^2}{h_0^2}\right)\frac{\sqrt{B_d{K}_d{B}_o{K}_o}}{\sqrt{B_d{K}_d}+\sqrt{B_o{K}_o}}-\left(\frac{1}{2}\right)\frac{{(B_d{J}_d-B_o{J}_o)}^2}{\sqrt{B_d{K}_d}+\sqrt{B_o{K}_o}},$$ (3)

where the subscripts d and o denote the disordered (thinner) and ordered (thicker) domains, respectively (Kuzmin et al., 2005).

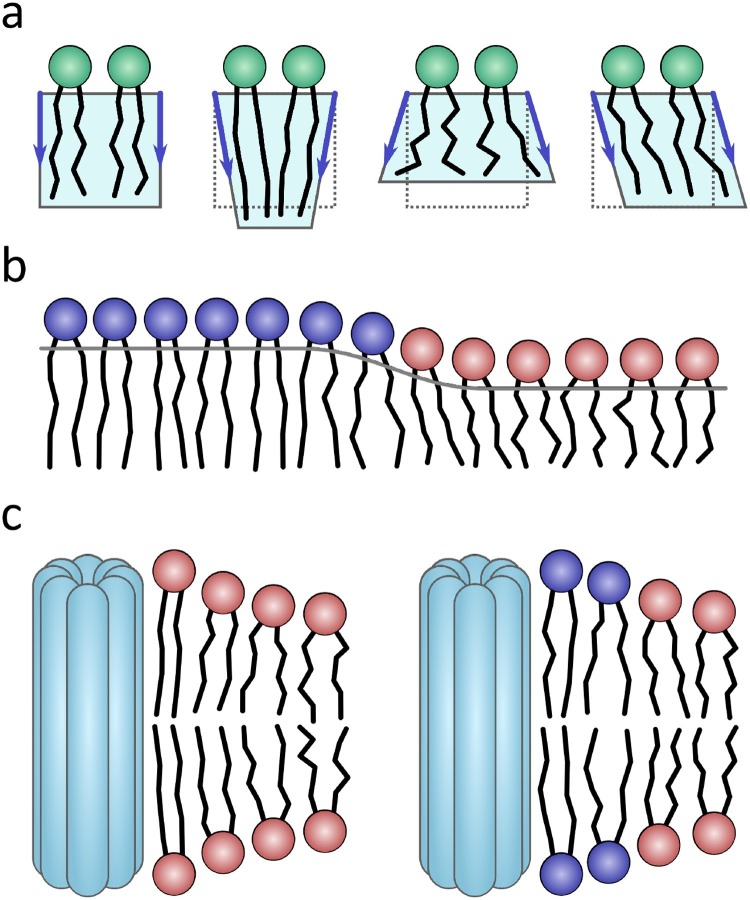
Fig. 1.

(a) Membrane deformations can be represented (from left to right) in terms of an undisturbed lipid monolayer, and ones with negative splay, positive splay, and tilt. When splay and tilt are energetically costly, they produce line tension at domain boundaries (b). (c) Proteins can also introduce deformation and line tension in membranes through hydrophobic mismatch. Line tension can be reduced/eliminated in the vicinity of proteins via the clustering of ordered lipids (dark blue). (a) and (b) were adapted from Kuzmin et al. (2005), while (c) was adapted from Akimov et al. (2008)gr1

From Eq. (3) we can deduce the following. Firstly, increasing bilayer thickness mismatch between two membrane patches (in relation to their average) results in greater line tension. In addition, having species that form rigid domains, such as for proteins shown in Fig. 1c, also increases line tension due to an increased energy cost during deformation. It should be pointed out, that intrinsic curvature can also play a role in line tension, where the intrinsic curvature difference between domains can reduce line tension, as described by Eq. (3). This is the result of curvature stress being reduced or eliminated at the domain boundary. Moreover, introducing a third biomolecular species into a membrane with intrinsic curvature can reduce curvature stress at the boundaries, thus reducing the system's overall line tension. Since biological membranes contain a variety of lipid species, this is used to explain why it is easier to observe lipid domain formation in model systems, compared to natural systems, as it is likely that natural systems have lipids with intrinsic curvatures capable of relieving deformation stress. We also note, that fundamental membrane material properties can vary as a function of temperature. In general, with increasing temperature membranes become more flexible (Pan et al., 2008, Bolmatov et al., 2018, Zhernenkov et al., 2016) and their lipids experience increased negative curvature (Marsh, 1996). Thus they can undergo phase transitions where large domains are no longer observed (Gerstle et al., 2018, Veatch and Cicuta, 2018).

2.3. Packing defects and dynamics

A feature of increasing importance is the packing defects between membrane lipids. These are introduced when the structure of a lipid is unable to conform to its neighbor. Defects can therefore be introduced as a result of the presence of unsaturated acyl chains or methylated segments that do not pack well with rigid moieties, such as the hydrocarbon rings in sterols, as shown in Fig. 2 c. Akin to material rigidities – as discussed in the previous section – increasing biomolecule rigidity enhances packing mismatch, which in turn increases line tension. In terms of specific theoretical energetics, this contribution to line tension is less well understood. However, simulations (and experiment Bakht et al., 2007, Wassall and Stillwell, 2009) have shown lipid packing to be important (Pitman et al., 2004, Leng et al., 2018). In general, packing defects reduce the interaction energies between lipid species and promote disorder (Wassall and Stillwell, 2009, Jaikishan et al., 2010). Therefore, this loss in interaction energy can equivalently be understood in terms of an increasing line tension.

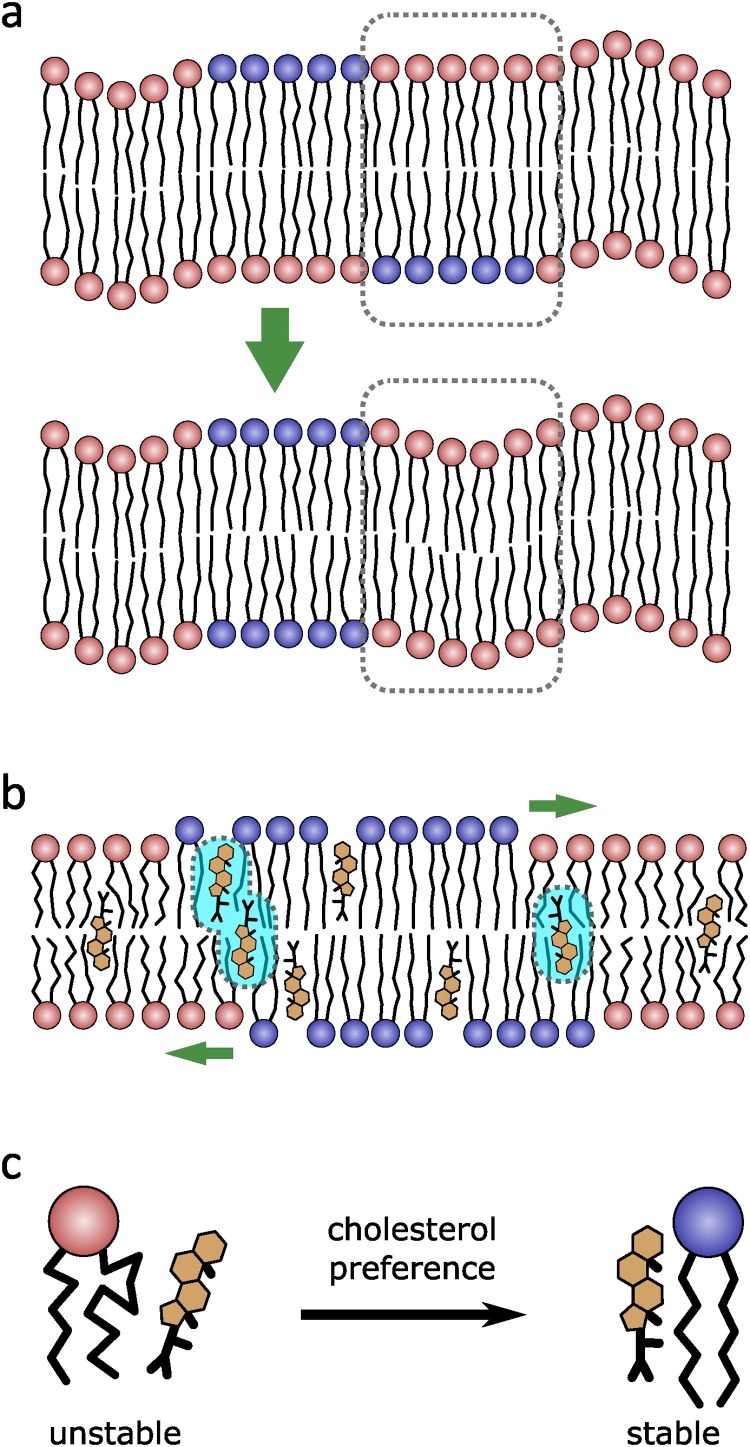
Fig. 2.

(a) The registration of domains across membrane leaflets maximizes dynamics, is entropically favorable, and is one mechanism for domain coalescence (adapted from Haataja, 2017). (b) Cholesterol (yellow) may also play a role in domain coalescence. In the case of thinner domains (red), cholesterol resides closer to the bilayer center and results in entropically unfavorable interactions (light blue highlights) when near ordered domains (blue) or at domain boundaries (adapted from Thallmair et al., 2018). (c) Further, cholesterol experiences unfavorable packing conditions when near unsaturated and methylated lipids, which can drive the sterol toward ordered domains, increasing the possibility of domain formation.

It should be pointed out, that it is not only lateral lipid dynamics (e.g., diffusion) that enable the spontaneous formation of domains, but that longitudinal dynamics in terms of membrane undulations (Helfrich and Servuss, 1984) can lead to the co-localization of domains and perhaps, even to domain formation. For example, theoretical analysis has shown that stiffer domains align in areas of a monolayer that undergo less pronounced membrane fluctuations (Galimzyanov et al., 2017), as shown in Fig. 2a. For example, Galimzyanov et al. found that the energetic cost for domain anti-registration across leaflets to be approximately:

$$W\approx \left(\frac{k_{B}T}{4a^2}\right)ln\left[\frac{{\left(B_d+B_o\right)}^2}{4B_d{B}_o}\right],$$ (4)

where a is the characteristic length of the monolayer that lies between the lipid headgroup diameter and monolayer thickness (Galimzyanov et al., 2017). An increasing bending rigid difference between ordered and disordered lipid phases increases the value of the logarithm in Eq. (4). This repulsive energy increase can result in co-alignment of rigid domains across bilayer leaflets or domains aggregating to more rigid areas of the membrane, such as those with proteins. For the case of domain registration across bilayer leaflets, it has been determined experimentally that domains with similar bending rigidities can coalesce (Nickels et al., 2015a). It has also been observed that domains are able to coalesce across adjacent bilayers (Tayebi et al., 2012) and membrane undulations are thought to play a similar role (Kollmitzer et al., 2015, Haataja, 2017, Galimzyanov et al., 2017). Moreover, effects of acyl chain packing across bilayer leaflets should not be discounted, as there is evidence that leaflets can influence each other's molecular order (Heberle et al., 2016). Thus the packing between leaflets may influence domain registration and ultimately, domain formation (Fig. 3 ).

3. Lipid interactions in domain formation

3.1. Ordered lipids and rafts

Evidence for lipid-driven lateral heterogeneity in membranes began to appear in lipid mixtures, such as dimyristoylphosphatidylcholine (14 carbon acyl chains) mixed with distearoylphosphatidylcholine (18 carbon acyl chains) (Mabrey and Sturtevant, 1976, Van Dijck et al., 1977, Wilkinson and Nagle, 1979, Knoll et al., 1981). In general, longer-chained, unsaturated lipids tend to be more ordered (Lu et al., 1995), have higher phase transition temperatures (Silvius, 1982), and form thicker bilayers (Kučerka et al., 2011, Petrache et al., 2000, Nagle and Tristram-Nagle, 2000). Thus, one accepted mechanism for domain formation in mixtures of ordered/disordered lipids is hydrophobic mismatch with line tension appearing as a result of local deformation (Kuzmin et al., 2005, Heberle et al., 2013).

While lateral heterogeneity has been widely observed in model membranes, existence of domain formation and its role in living systems has been contentious. This is partly the result that living systems contain a large variety of chemically diverse lipids (van Meer, 2005, Shevchenko and Simons, 2010, Harayama and Riezman, 2018). Eventually, and even after years of study, sphingomyelin emerged as a central candidate responsible for the formation of ordered domains in biological membranes (Lingwood and Simons, 2010). In general, sphingomyelin does not form large domains in the absence of cholesterol (Bartels et al., 2008). It is also widely thought that cholesterol hydrogen bonds to sphingomyelin's functional amide group, binding the two molecules and increasing domain size (Sodt et al., 2015, Róg and Pasenkiewicz-Gierula, 2006, Matsumori et al., 2011). However, recent research has suggested that sphingomyelin also has strong homophilic interactions and that cholesterol's interactions take place deeper within the membrane's acyl chain region, i.e., lower than sphingomyelin's functional amide group (Yano et al., 2018). Moreover, in systems that form large domains, there is evidence of cholesterol segregating within ordered domains (Javanainen et al., 2017, Soloviov et al., 2020). Currently, it is safe to say that cholesterol's role within ordered domains remains a topic of current research and controversy .

Interestingly, new mechanisms have been proposed where cholesterol participates in increasing lateral heterogeneity. Early work on cholesterol-containing model membrane systems demonstrated that the sterol increased the bilayer thickness of liquid-disordered phase membranes (Hui and He, 1983, Nezil and Bloom, 1992, Smondyrev and Berkowitz, 1999). A possible mechanism for cholesterol stabilizing domains could be that it favors liquid ordered domains over liquid disordered domains, and in doing so, enhances membrane thickness mismatch. On the other hand, there is research showing that cholesterol does not lead to a significant increase in membrane thickness (Mitra et al., 2004). While cholesterol's ability to increase hydrophobic mismatch as a mechanism for increased domain size should not be neglected, other mechanisms may play equally important roles. One such mechanism may be cholesterol's ability to increase local bending rigidity (Brown et al., 2002, Song and Waugh, 1993, Evans and Rawicz, 1990), enabling liquid ordered domains containing sphingomyelin to coalescence with each other (Nickels et al., 2015b; Galimzyanov et al., 2017; Gracià et al., 2010) to form larger domains. However, this scenario neglects cholesterol's interactions with disordered and unsaturated lipids, a topic that will be discussed in the next section.

3.2. Disordered lipids and non-raft domains

Ordered lipids, such as those participating in the formation of lipid rafts, are "more ordered" relative to more disordered lipids. Early on, the role of disordered lipids on lateral heterogeneity became a topic of interest (Massari and Colonna, 1986, Salmon et al., 1987). These lipids differ from ordered lipids in that they form thinner membranes with lower bending rigidities, and possess physical characteristics that allow rafts and more ordered domains to form. However, short acyl chain lipids are not necessarily the main determinant for the formation of larger size domains. For example, lipids with highly disordered polyunsaturated fatty acids (PUFAs), such as eicosapentaenoic acid and docosahexaenoic acid (Feller, 2008), when incorporated into bilayers are able to form larger domains, compared to lipids with shorter acyl chains, such as oleic acid (Williams et al., 2012, Kinnun et al., 2018, Shaikh et al., 2015), and may be the result of how PUFAs interact with cholesterol.

For the most part, cholesterol has an aversion for PUFA lipids and tends to associate with saturated fatty acid lipids (Kučerka et al., 2010, Lin et al., 2016, Yasuda et al., 2015) – saturated lipids, even mono-unsaturated lipids, have a lesser effect on cholesterol distribution (Lindblom et al., 2006, Bunge et al., 2008, Kinnun et al., 2018, Lin et al., 2016). It is also generally accepted that the cis double bonds of unsaturated acyl chain lipids result in less well-packed membranes, which deter interactions with cholesterol (Leng et al., 2018, Pitman et al., 2004). In support of this notion, methylation of lipid chains (resulting in increased disorder) has been shown to reduce cholesterol's affinity with the methylated fatty acid chains (Jaikishan et al., 2010), presumably due to packing defects. However, it isn’t simply acyl chain disorder that cholesterol is averse to, as short saturated, but disordered acyl chain lipids, such as DMPC are better able at accommodating cholesterol, compared to their unsaturated lipid counterparts (Kučerka et al., 2010). Even in the case where thickness mismatch is not a major factor, cholesterol has been shown to enable the formation of micron-sized domains in model systems with unsaturated lipids (Georgieva et al., 2015). For lipid compositions that do not contain polyunsaturated lipids, but exhibit domain formation, cholesterol is known to reduce domain size – if evenly distributed between domains (Tsai and Feigenson, 2019). This is likely due to cholesterol's ability to increase bilayer thickness without increasing thickness mismatch, thus not affecting line tension to any great extent (see Eq. (3)). This further lends validity to the notion that acyl chain packing is a factor when considering line tension at domain boundaries, particularly when cholesterol is present.

Recently, an interesting mechanism for cholesterol's ability to promote domain formation has come to light. It was observed that cholesterol resided near the bilayer center in thinner membranes, such as those made up of highly disordered lipids, e.g., PUFAs (Kučerka et al., 2010, Marrink et al., 2008, Harroun et al., 2006, Harroun et al., 2008). This is in contrast to what has been observed in membranes comprised of ordered lipids, such as sphingomyelin, where cholesterol resides closer to the lipid-water interface and is less dynamic (Thallmair et al., 2018). The entropic difference between these two states results in a tension at domain boundaries (Thallmair et al., 2018, Weiner and Feigenson, 2018) (see Fig. 2b) and adds another possible mechanism for cholesterol increasing domain size through domain registration.

Although specific bonding between cholesterol and sphingomyelin may play a major role in cholesterol's ability to increase the size of domains, the effect of non-raft domains should not be discounted. There is research showing that increasing the unsaturated lipid content of non-raft lipid constituents drives increasing domain size, implying that acyl packing may be a big contributor to domain size. It has also been suggested that the “push” mechanism that drives cholesterol from non-raft domains is equally important as the “pull” mechanism, where cholesterol is incorporated into rafts (Krause et al., 2014, Wang et al., 2015). This debate opens up new avenues for future theoretical and experimental research on the effects of membrane packing efficiency and domain formation.

3.3. Protein interactions in domain formation

Many proteins are relatively rigid and require a bilayer of sufficient thickness for “proper” incorporation into the membrane. Differences between the protein's hydrophobic portions and those of the surrounding lipid membrane can result in hydrophobic mismatch, i.e., increased line tension (see Fig. 1c). For example, research in membranes extracted from eukaryotic cells has shown that proteins can increase bilayer thickness to accommodate the protein's hydrophobic amino acids (Mitra et al., 2004). This can result in proteins acting as nucleation sites for ordered lipids and domain formation (Akimov et al., 2008, Hoferer et al., 2019). Furthermore, the fact that many of these rigid proteins span the membrane can result in domain registration and domain coalescence (Galimzyanov et al., 2017).

Early on, some research indicated that certain proteins preferential interact with sphingomyelin (Brown and Rose, 1992, Okamoto et al., 1998). Since proteins can increase membrane thickness, it is likely that the ordering nature of sphingomyelin reduces membrane tension by deforming the membrane around proteins. Also, it has been discussed that the nature of sphingomyelin's acyl chains allows for them to be compatible with the rigid cholesterol. Since proteins can also be rigid, it is then possible that sphingomyelin is able to interact with proteins in a manner similar to that with cholesterol. It should also be pointed out that proteins, themselves, can form domains on the membrane surface, e.g., scaffolding proteins (Okamoto et al., 1998, Whitmarsh, 2006). Often their organization is guided by electrostatics through specific charged amino acids, leading to oligomerization (Horner et al., 2012). Although some of these proteins do not penetrate into the bilayer, they do introduce a region of increased local rigidity which may be sufficient to cause ordered domain registration of apposing bilayer leaflets (Galimzyanov et al., 2017).

4. Continuum models and modulated phases

Continuum models play a pivotal role in understanding lipid heterogeneity, since complex lipid mixtures are often amenable to thermodynamic analysis in terms of a coarse-grained, continuous order parameter. For example, liquid–liquid phase separation into liquid-ordered and liquid-disordered regions (discussed in previous sections) can be described phenomenologically via a free energy, $\mathcal{F}[\varphi ]$, for a scalar field, ϕ(x). This scalar field represents the presence of different lipid phases, given a location, x, via some constant values ϕ(x) = ϕ _o, ϕ _d for the liquid-ordered and liquid-disordered regions, respectively. A thermodynamic potential, V[ϕ], describes the stability of these phases. For example, in the liquid-liquid phase separated regime, V[ϕ] will have local minima at ϕ = ϕ _o, ϕ _d. In such continuum models, line tension represents a free energy cost for spatial variations of ϕ(x). The result of combining V[ϕ] with the line tension is the standard Landau-Ginzburg free energy, namely:

$$\mathcal{F}[\varphi ]=\int \mathrm{d}\text{x}\left[\frac{1}{2}{[{\nabla }^2\varphi ]}^2+\frac{\kappa }{2}|\nabla \varphi {|}^2+\underset{V[\varphi ]}{\underbrace{\frac{r}{2}{\varphi }^2+\frac{\mu }{3}{\varphi }^3+\frac{1}{4}{\varphi }^4}}\right],$$ (5)

where the units are defined such that the coefficients of the quartic terms are unitless. This simple model has three parameters: i.e., κ, r, and μ, with the latter two parameters derived from the thermodynamic potential V[ϕ], and where κ is the rescaled surface tension.

Often, the fourth-order derivative term is ignored. This is acceptable as long as κ > 0 in Eq. (5). As a result, the fourth-order derivative term becomes irrelevant with respect to the renormalization group and the dominant term becomes the second-order derivative. r is a tunable parameter across the mixing/demixing phase transition, which, in the mean-field, would occur at r = μ ²/4 or where phase separation takes place. Conversely, for r > μ ²/4, the potential V[ϕ] is minimized around ϕ = 0 and we would expect no phase separation, but rather a fluctuating, disordered mixture of the liquid-ordered and liquid-disordered regions with a characteristic correlation length $\xi \sim \sqrt{\kappa /r}$.

We may also be somewhat more specific and identify the constant values ϕ _o,d for which the potential is at a minimum in the phase separated regime with r < μ ²/4. For 0 < r < μ ²/4, the potential V[ϕ] has two minima at constant values ϕ = ϕ _d = 0 and $\varphi ={\varphi }_o=-\mu /2-\sqrt{{\mu }^2/4-r}$. When r < 0, the two values are $\varphi ={\varphi }_{d,o}=-\mu /2\pm \sqrt{{\mu }^2/4-r}$, respectively. Note that when μ ≠ 0, this transition would have a first-order character and the potential will have a local maximum between the two minima (i.e., a thermodynamic barrier to transitioning between the liquid-disordered and liquid-ordered phases). If μ = 0, the two minima in the free energy become degenerate at ϕ = 0 at the transition (r = 0) so that there is no thermodynamic barrier and the transition is second-order (continuous). However, thermal fluctuations change this picture, somewhat, as the distinction between an unstable and a metastable phase becomes ambiguous when thermal fluctuations are taken into account (Langer, 1975).

In lipid vesicles, it is easy to tune across the mixing/demixing transition by varying the temperature. In biological cells, however, the situation is more complicated as it is unclear whether or not the cell membrane is at equilibrium, whereby these phases may not be meaningful. Nevertheless, the free energy in Eq. (5) is useful as a conceptual tool. We may use it as a basis for constructing the dynamics of the lipid phases by employing an appropriate dynamical model (Hohenberg and Halperin, 1977). For instance, it has been recently argued that natural cells tune their membranes such that, they have compositions near criticality (μ = 0 and r ≈ 0) (Veatch et al., 2008a; Machta et al., 2012).

Through dynamical processes, such as lipid diffusion, the free energy in Eq. (5) trends towards minimization. As the lipid membrane is fluid, the most appropriate model would include the hydrodynamic coupling of the lipids across the membrane (Camley and Brown, 2010). Another crucial aspect of the dynamics is the conservation of total lipids, which means that the integrated order parameter, ∫dx ϕ(x), is a constant (typically zero for equal proportions of liquid-ordered and liquid-disordered regions). Excluding hydrodynamics and thermal fluctuations, the time-dependence of the order parameter is given by:

$${\partial }_t\varphi (\text{x},t)=\mathrm{\Gamma }{\nabla }^2\frac{\delta \mathcal{F}}{\delta \varphi },$$ (6)

with Γ representing the mobility of the phase. Eq. (6) may be evolved for various initial conditions, for example, to study the evolution of the phase separation of domains in the r < μ ²/4 region. With such conserved dynamics, we would typically expect Lifshitz–Slyosov domain evolution, where domains grow as ℓ ∼ t ^1/3 (Lifshitz and Slyozov, 1961). However, hydrodynamic effects may modify this scaling in more realistic scenarios (Camley and Brown, 2011).

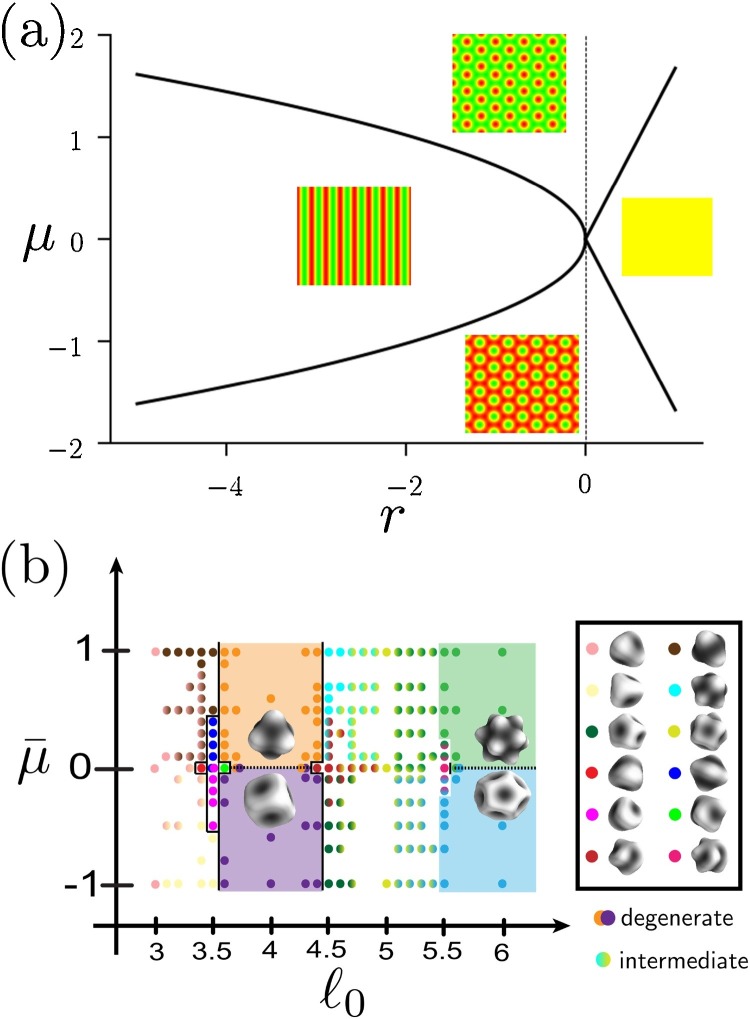
The different phase-separated regions in a lipid vesicle may exhibit different preferred curvatures of the membrane, due to the particular geometry of the constituent lipid molecules (Frolov et al., 2011). Here, the shape of the membrane couples to the dynamics of ϕ, and we have to combine the free energy in Eq. (5) with elastic terms for the membrane and a coupling between ϕ and membrane curvature. Leibler and Andelman (Leibler and Andelman, 1987) showed that in the presence of such couplings, the line tension term, κ| ∇ ϕ|²/2, gets contributions from membrane curvature and can even change signs. When κ is driven to negative values, the quartic derivative term, | ∇ ² ϕ|²/2, must be included in the theory and the free energy, $\mathcal{F}$, is now minimized by spatially modulated configurations. Microscopic models also reveal that a coupling to membrane curvature is sufficient to drive the surface tension term negative (Amazon et al., 2013). By including sign changes in κ, this makes the phase space of the theory in Eq. (5) much richer, and the various possibilities present a unified way of thinking about lipid membrane heterogeneity (Shlomovitz et al., 2014). In the mean-field (ignoring thermal fluctuations), the phase portrait of the model is shown in Fig. 4 .

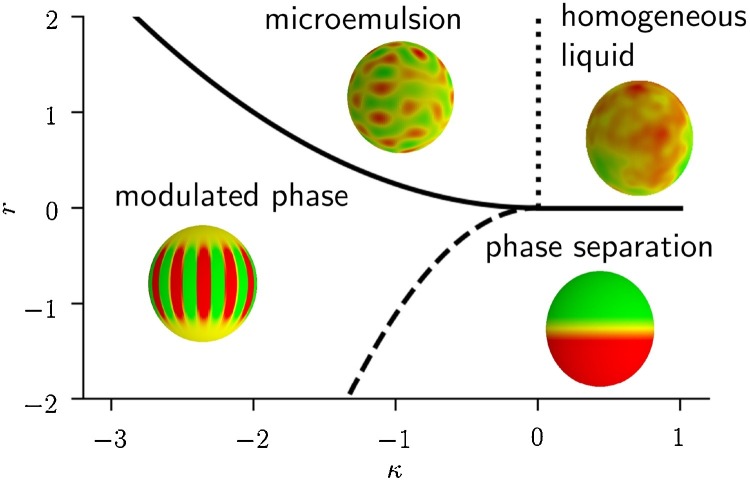
Fig. 4.

Schematic of the various phases described by the free energy in Eq. (5) for μ = 0. The phase boundaries are given in the single-mode mean-field approximation (Shlomovitz et al., 2014). We see that when the gradient term κ < 0, it is possible to form an ordered modulated (patterned) phase and a disordered “microemulsion”, with a characteristic wave number q₀. Here we have shown possibilities for the phases on the surface of a vesicle, which introduces its own complications due to the finite spherical geometry. For example, the striped modulated phase shown has stripes terminating at the poles. Moreover, any of the modulated phases will have defects induced by the spherical topology.

When κ < 0, the free energy develops minima with configurations of ϕ(x) with non-zero Fourier modes. In particular, using a simple single-mode approximation, one can show that in the mean-field, the preferred wave number is $|\text{q}|=q_0=\sqrt{-\kappa /2}$ (see Eq. (5)), which corresponds to a length scale of λ ₀ = 2π/q ₀. For the modulated phase (see Figs. 4 and 5 ), this length scale sets the size of the patterns. For μ = 0 in our thermodynamic potential, and a flat, infinite substrate, the pattern is striped. Otherwise, the balance between the two different liquid phases may be different, resulting in hexagonal or inverted hexagonal patterns, as shown in Fig. 5 a. In a lipid membrane, these patterns would also manifest as undulations in the lipid as the two different liquid phases would correspond to different spontaneous curvatures.

Fig. 5.

(a) Mean-field phase diagram for the modulated phases with a fixed κ < 0 in Eq. (5) and a flat and infinite two-dimensional substrate. We see that the cubic term μ tunes between the striped phase (middle), the hexagonal phase (top), and the inverted hexagonal phase (bottom). When r > 0, we also find a microemulsion region, denoted by the yellow. (b) Modulated phases on a sphere have a more complex structure, since the pattern has to wrap the sphere ℓ₀ = q₀R times, and has defects. We show the various possible shapes for small values of ℓ₀. Note the wide range of shapes, including continuously varying “intermediate” states. In general, on the sphere the free energy landscape becomes much more complicated than for a flat, infinite substrate. The phase diagram is adapted from Radja et al. (2019). Here, we have a rescaled cubic term $\overline{\mu }\propto \mu$. r is fixed to a negative value ensuring that we are always in a modulated phase.

Modulated phases on a sphere present a particular challenge as neither the hexagonal nor the striped patterns we find on infinite substrates (see phases in Fig. 5) can wrap around the surface of the sphere uniformly – i.e., the spherical topology induces defects in the pattern. This creates a much richer phase diagram for the modulated phases, as can be seen when comparing Fig. 5 a and b. These patterned phases on a sphere are particularly relevant for cells and lipid vesicles. For example, the diversity of patterns on a sphere within a relatively small range of the phenomenological parameters helps explain the natural diversity of pollen grain surface patterns (Radja et al., 2019, Lavrentovich et al., 2016). Pollen grains are single cells that secrete a phase separating substance during development, which buckles the cellular membrane. Although such phases are also readily observable in synthetic lipid vesicles (Konyakhina et al., 2011, Baumgart et al., 2003), living cells typically have nanoscopic domains and are more likely to be in the disordered “microemulsion” phase instead of these highly ordered patterned phases. Note that we may incorporate dynamics by using an equation such as Eq. (6). In the case of a free energy with parameters corresponding to a modulated phase, the dynamics reduce to the so-called “phase field crystal” (Elder et al., 2002). The dynamics of the modulated phases include interesting cases such as, the formation of a foam after a rapid quench into the modulated phase (Guttenberg et al., 2010). Such foamy states appear to be relevant for pollen grain patterns, as well (Radja et al., 2019). Foamy structures may also be observed in synthetic lipid vesicles with specific compositions (Konyakhina et al., 2013).

If κ is large and negative, then we will be deep in the modulated phase/microemulsion regime and we can expand our free energy around the dominant Fourier modes with |q| = q ₀. For a spherical vesicle, Fourier modes are inappropriate and one has to expand the field ϕ(x) in spherical harmonics: $\varphi (\text{x})={\sum }_{\ell =0}^{\infty }{\sum }_{m=-\ell }^{\ell }{c}_{\ell }^m{Y}_{\ell }^m(\theta ,\varphi )$, where x = (θ, ϕ) is the location on the spherical membrane in spherical coordinates. We also have the usual spherical harmonics $Y_{\ell }^m(\theta )$, with ℓ=0, 1, 2, … the “total angular momentum” mode number and m =− ℓ , − ℓ +1, …, ℓ the azimuthal mode number. Then, we expect that the field has contributions primarily around the spherical harmonic modes with ℓ ≈ ℓ ₀ ≈ q ₀ R, with R the vesicle radius. This parameter will strongly influence the kinds of patterned phases that can form, as shown in Fig. 5 . We can rewrite the free energy in Eq. (5) on the sphere in the following (rescaled) Landau–Brazovskii (Radja et al., 2019, Luo and Maibaum, 2018) form:

$$\begin{array}{ccc}\hfill \mathcal{F}[\varphi ]& \hfill =\hfill & \frac{1}{2}\sum _{\ell ,m}\left[{(\ell -{\ell }_0)}^2+\overline{r}\right]|c_{\ell }^m{|}^2+\frac{\overline{\mu }}{6}\sum _{{\{{\ell }_i,m_i\}}_{i=1}^3}{\mathrm{\Upsilon }}_{m_1,m_2,m_3}^{{\ell }_1,{\ell }_2,{\ell }_3}{c}_{{\ell }_1}^{m_1}{c}_{{\ell }_2}^{m_2}{c}_{{\ell }_3}^{m_3}\hfill \\ \hfill & \hfill \hfill & +\frac{1}{24}\sum _{{\{{\ell }_i,m_i\}}_{i=1}^4,\overline{\ell },\overline{m}}{\mathrm{\Upsilon }}_{m_1,m_2,\overline{m}}^{{\ell }_1,{\ell }_2,\overline{\ell }}{\mathrm{\Upsilon }}_{m_3,m_4,-\overline{m}}^{{\ell }_3,{\ell }_4,\overline{\ell }}{c}_{{\ell }_1}^{m_1}{c}_{{\ell }_2}^{m_2}{c}_{{\ell }_3}^{m_3}{c}_{{\ell }_4}^{m_4},\hfill \end{array}$$ (7)

where ${\mathrm{\Upsilon }}_{m_1,m_2,m_3}^{{\ell }_1,{\ell }_2,{\ell }_3}$ are the so-called Gaunt coefficients (Edmonds, 1957) coming from integrations of products of three spherical harmonics. We see here that the cubic and quartic terms in the thermodynamic potential will couple different spherical harmonic modes. Minimizing Eq. (7) over the set of coefficients $c_{\ell }^m$ yields a rich set of possibilities for modulated phases, some of which are illustrated in Fig. 5 (b). A free energy of this type is not only useful for understanding lipid vesicles and pollen grains, but also viral capsid formation (Dharmavaram et al., 2017).

We have spent some time considering the modulated phases (κ, r < 0 in Eq. (5)). However, as mentioned previously, lipid heterogeneities in living cells and in many synthetic lipid mixtures are best thought of as disordered, microemulsion phases. The main difficulty of this hypothesis is explaining the origin of the sign change of κ. However, one possibility is that differences in composition between lipid leaflets can induce such a sign change via a mechanism similar to spontaneous curvature (Schick, 2012). This is plausible as living cells are known to maintain asymmetric lipid compositions on their inner and outer membrane leaflets (Nickels et al., 2015a). In this phase, the order parameter remains, on average, zero (〈ϕ〉=0), but exhibits particular fluctuations with dominant contributions at the characteristic wavevectors with |q| = q ₀ (or modes ℓ = ℓ ₀ on the sphere), resulting in a structure factor S(q).

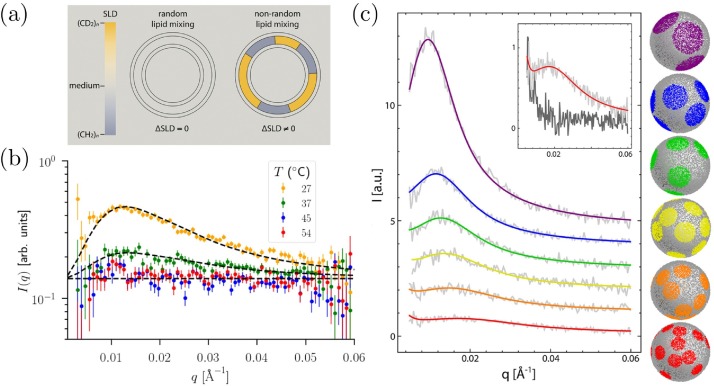
The structure factor, S(q), for the lipid membrane can be measured via a scattering (neutron or X-ray) experiment (Anghel et al., 2018). Small angle neutron scattering is particularly valuable as it provides better contrast to probe the lateral membrane heterogeneity, even when these heterogeneities are nanoscopic (Pan et al., 2013, Anghel et al., 2019). To get good contrast on the lateral heterogeneity within the membrane, deuterated lipid mixtures may be used to mask one of the liquid phases, for example. A schematic of the idea is shown in Fig. 6 a. Here, lipid vesicles are prepared with particular deuteration levels such that, at high temperatures when the lipids remain mixed, the SLD of the acyl tails match the SLD of the surrounding fluid. Thus, the lipid vesicles become “invisible” to neutrons, as shown by the flat curves at high temperatures in Fig. 6 b. At lower temperatures, we have the liquid-liquid phase separation (or possibly microemulsion or modulated phase formation) and the SLDs of the liquid-ordered and liquid-disordered regions will be different, creating contrast for the neutron scattering as shown in Fig. 6 a. In this case, the neutron scattering will come from fluctuations in the lipid composition. Therefore, it is a direct probe of our order parameter, ϕ(x). For scattering from lipid vesicles, the scattering intensity, I, is a probe of the fluctuations $〈|c_{\ell }^m{|}^2〉$ of the spherical harmonic modes of ϕ(x). For a microemulsion phase, we expect that $〈|c_{\ell }^m{|}^2〉\propto {[{(\ell -{\ell }_0)}^2+R^2/{\xi }^2]}^{-1}$, where R is the vesicle radius and ξ the correlation length.

Fig. 6.

(a) Contrast matching scheme of lipid vesicles for small angle neutron scattering, adapted from Heberle et al. (2013). Lipid deuteration is tuned such that, the neutron scattering length density (SLD) of the lipids matches that of the surrounding fluid when the lipids are mixed. When the lipids phase separate, an SLD contrast is developed and the neutrons scatter from the compositional variations, directly probing our order parameter ϕ(x). (b) Neutron scattering data from lipid vesicles (points) and fits to the microemulsion theory reviewed here (dashed lines), taken from Bolmatov et al. (2019). (c) Neutron scattering data fit to a more detailed, microscopic model of lipid domain configurations, taken from Heberle et al. (2013). The inset shows lipid mixtures at low (20 °C, dark gray line) and high (50 °C, light gray line) temperatures.

Such a phenomenological approach was used successfully to interpret scattering data of lipid vesicles in the presence of melatonin (Bolmatov et al., 2019) – although a true microemulsion phase could not be established as the scattering data was also consistent with ℓ₀ = 0 (a regular phase-separated phase). Fits using the microemulsion theory are shown in Fig. 6 b. Note, that this theory works well even when compared to a more microscopic model of domain configurations shown in Fig. 6 c. In other words, the simple phenomenological free energy approach presented here provides a conceptual framework for understanding the scattering data and interpreting the wide range of phase behaviors observed for lateral lipid organization in cell membranes.

So far we have focused on the mean field properties of the modulated phase free energy, but thermal fluctuations play an important role in modifying the phase diagrams we have constructed in Figs. 4 and 5 . The nature of the phase transitions also gets modified. For example, Brazovskii (1975) showed that thermal fluctuations modify the second-order phase transition at μ, r = 0, to one of first-order. This is due to the much larger phase space afforded to thermal fluctuations as ϕ(q) fluctuates around a shell of configurations in momentum space with |q| ≈ q ₀. Similar behavior is observed on a spherical surface (Lavrentovich et al., 2016), but the analysis there, is additionally complicated by finite size effects. This more detailed study, including a proper understanding of how fluctuations renormalize the parameters of the free energy, remains a theoretical challenge. Importantly, the fundamental principles in these coarse-grained Landau–Ginzburg approaches allows for a guiding perspective when discussing lipid interactions and domain formation in natural systems.

5. Domain formation and function in living systems

Proteomics studies demonstrate that signaling proteins, including some tyrosine kinases and receptors, have high specificity for raft forming lipids such as, cholesterol and sphingomyelin (Foster et al., 2003, Filipp et al., 2004). The depletion of cholesterol within living cells has been shown to interrupt signaling pathways, presumably due to the disruption of rafts, thus implicating the importance of raft lipid species for proper cell function (Pike and Miller, 1998, Simons and Toomre, 2000). Further, there is evidence that suggests that ordered lipids, such as sphingomyelin, aid in the coupling of receptors to the actin cytoskeleton (Holowka and Baird, 2016). Although there is evidence of raft lipid species playing an important role in biological function, the importance of domain formation continues to be studied and is evolving (Milovanovic et al., 2015, Stone et al., 2017).

As evidence has mounted that lipids can segregate into domains in model systems, questions have arisen as to the presence of lipid domains in living cells. Using fluorescence microscopy techniques, cholesterol-dependant phase separation was inferred that was consistent with the lipid-raft hypothesis in canine (Zacharias et al., 2002) and human (Gaus et al., 2003) cells. However, these were indirect measurements. Clearer evidence of domain formation in living systems was obtained by extracting intact cell membranes from living cells (Baumgart et al., 2007, Sezgin et al., 2012, Huang et al., 2019), which allowed for more detailed studies, but with the caveat that one was looking at extracted membranes and not functional natural membranes in situ. It was revealed that the difficulty in observing raft domains optically could be due to their physical size. Specifically, it has been determined that rafts are typically in the range of nanometers in size (Eggeling et al., 2009, Frisz et al., 2013, Lozano et al., 2016, Kinnun et al., 2018), and likely transient (Hancock, 2006). Domains of this nature are difficult to observe by the optical techniques that have, for the most part, performed well in studying living systems (Sezgin et al., 2017, Levental and Wang, 2020). Recently, neutron scattering studies have revealed the presence of lipid rafts, approximately 40 nm in size, in intact, fully functional living cells (Nickels et al., 2017).

The idea of the transient nature of rafts leads to speculation that lipid rafts can respond to external stimuli by modulating their composition and size (Simons and Toomre, 2000, Bolmatov et al., 2020b). This is consistent with observations of domain miscibility taking place at near physiological temperatures (Veatch et al., 2008b; Gerstle et al., 2018, Dietrich et al., 2001, Samsonov et al., 2001, Baumgart et al., 2007). Being near a phase transition allows for small changes in the environment to have a large effect on the appearance and size of rafts. One proposed scenario is that rafts may provide a buffering role in stabilizing membrane physiological properties across a range of temperatures (Nickels et al., 2015b). Here, high-melting temperature raft lipids diffuse into the disordered phase as temperature increases, maintaining membrane bending rigidity and viscosity. It has also been theorized that cells vary their lipid composition to control the formation of rafts (Heerklotz, 2002). Moreover, there is research indicating that some anesthetics lower the miscibility phase transition of lipid rafts (Gray et al., 2013, Machta et al., 2016), giving additional validity to the notion of dynamic domain formation as a relevant mode of biological function.

It is important to note that the chemical composition of non-raft lipids may modulate raft size and stability. It has been proposed, for example, that the dietary health benefits derived from PUFAs is their ability to increase raft domain size (i.e., increasing the miscibility phase transition) (Wassall and Stillwell, 2008, Turk and Chapkin, 2013). In general PUFA containing lipids are more unstable than other disordered lipids, due to their susceptibility to oxidation as a result of their multiple double bonds (Yakubenko and Byzova, 2017). As mentioned, domain formation can also occur with smaller and more saturated lipids, a combination that results in hydrophobic mismatch that increases domain formation (Kuzmin et al., 2005, Heberle et al., 2013). However, these systems tend to form domains with lipids in the solid ordered and liquid disordered phases, where membranes become extremely permeable to various ions and other small molecules, compromising cell viability (Clerc and Thompson, 1995). Since cholesterol can broaden phase transitions, it can address the solid ordered domain phase problem by favoring the liquid ordered state and by redistributing thinner saturated lipids – with the caveat of reducing line tension and domain size (Tsai and Feigenson, 2019). However, PUFA lipids can segregate cholesterol into ordered domains, allowing for liquid-liquid domain formation, something less easily attainable with saturated lipids. Thus, despite PUFA lipids being susceptible to oxidation, one of their biological roles may be to maintain liquid–liquid domain co-existence.

While the biological importance of lipid domains is becoming clearer, there is research that shows that lipid domains can be used by some viruses to promote fusion with host cells (Yang et al., 2016). For example, it was found that cells depleted of cholesterol and of rafts (Zheng et al., 2009, Shaikh, 2012), were less likely to fuse with HIV (Mañes et al., 2000, Dick et al., 2012, Lorizate et al., 2013) and influenza (Liu and Boxer, 2020) viruses. It is speculated that viruses, such as influenza utilize rafts to increase local concentration of viral proteins in order to enhance processes such as viral budding from host cells (Takeda et al., 2003). Further, there is evidence that the viral envelopes of the semliki forest and sindbis viruses require the presence of both cholesterol and sphingomyelin in the host cell for fusion, also suggesting a raft dependence (Waarts et al., 2002). Thus raft interactions may be important for the entry viruses into host cells. To combat this, it has been suggested that molecules which lower line tension, such as vitamin E (Muddana et al., 2012), may help in preventing such viral fusion events (Yang et al., 2016). Thus research studying the modulation of raft formation and virus inhibition has attracted much attention as of lately, especially with regard to the COVID-19 pandemic.

6. Conclusions

Even as the notion of the fluid mosaic model of the membrane was being evaluated, evidence for lateral heterogeneity had started to accumulate. Experiments on model systems were able to determine which combination of lipids resulted in domain formation. Contemporary to these experiments, research demonstrated the specificity of proteins for certain lipid species, hinting at a biological role for lipid domains. This then fueled further speculation as to which lipids were able to form domains and their underlying mechanisms that enabled them to do so.

Using the concept of line tension, differences in domain size and shape can be interrogated theoretically. Structural considerations, such as hydrophobic mismatch and packing defects hint at, and sometimes are able to estimate line tension. Furthermore, membrane dynamics, can in theory, also lead to domain coalescence and registration. Recently, studies on cholesterol's location within membranes have yielded unique mechanisms for domain formation, which has sparked renewed interest in what is cholesterol's role in membrane lateral heterogeneity.

Over the last couple few decades we have established, to a great extent, the lipid characteristics that lead to domain formation. In general, long-chain saturated lipids, sphingomyelins, and cholesterol contribute to ordered raft-like domains, while short-chain and unsaturated lipids form non-raft phases. The thickness mismatch between long-chain and short-chain lipids accentuates hydrophobic mismatch, thus promoting domain formation. Furthermore, saturated and unsaturated lipids modulate cholesterol's affinity to lipids, thus modulating domain formation while maintaining a liquid membrane phase.

In order to understand the wide range of phase behaviors observed in synthesized lipid vesicles – including domain formation, patterned phases, and disordered structures – phenomenological, coarse-grained approaches have been developed that capture the wide spectrum of phases with just a few parameters. We have reviewed the essence of such Landau–Ginzburg approaches. A key feature is that the lipid composition and membrane shape may be strongly coupled, yielding a scenario that is different from the typical Ising-like, liquid-liquid phase separation. Lipid membranes are observed to exhibit spatially-modulated or patterned phases with a characteristic pattern size λ ₀. This points toward the possibility that the small lipid heterogeneities in living membranes are manifestations of the corresponding disordered phase (i.e., a microemulsion). These coarse-grained theories are also valuable for interpreting scattering data, which necessarily represents an average over many vesicles or over a large region of a model membrane. Thus coarse-grained theories provide a way of describing lateral heterogeneities in membrane systems whether synthetic or biological.

As lipid species became established in biologically relevant roles, the direct observation of domains in living systems remained elusive. Some techniques focusing on protein interactions inferred the existence of rafts, but lacked a direct measurement of them. The extraction of membranes from living cells was useful in determining the size of rafts, which was revealed to be below optical wavelengths. Finally, in recent years neutron diffraction was used on living cells to observe nanoscale lipid domains.

Lateral heterogeneity in membranes has been a long-debated topic, particularly in terms of its biological relevance. However, new mechanisms behind domain formation continue to be discovered and biological roles continue to be inferred. Membrane systems, such cholesterol-containing membranes have attracted renewed interest as exceptions to their accepted roles have been discovered. And now, that measurements on fully functional living cells are showing the presence of nanoscopic lipid domains, the role of rafts in biology is going to spur new experiments and insights. Recent developments in experimental techniques may answer the question how rafts appear and disappear in living cells, and why. Instead of once being thought as static structures, lipid rafts are increasingly understood as dynamic entities within biological membranes that modulate function.

Declaration of Competing Interest

The authors report no declarations of interest.