Lead-time bias in esophageal cancer screening in high-risk areas in China

Abstract

Objective

To investigate what extent lead-time bias is likely to affect endoscopic screening effectiveness for esophageal cancer in the high-risk area in China.

Methods

A screening model based on the epidemiological cancer registry data, yielding a population-level incidence and mortality rates, was carried out to simulate study participants in the high-risk area in China, and investigate the effect of lead-time bias on endoscopic screening with control for length bias.

Results

Of 100,000 participants, 6,150 (6.15%) were diagnosed with esophageal squamous dysplasia during the 20-year follow-up period. The estimated lead time ranged from 1.67 to 5.78 years, with a median time of 4.62 years [interquartile range (IQR): 4.07−5.11 years] in the high-risk area in China. Lead-time bias exaggerated screening effectiveness severely, causing more than a 10% overestimation in 5-year cause-specific survival rate and around a 43% reduction in cause-specific hazard ratio. The magnitude of lead-time bias on endoscopic screening for esophageal cancer varied depending on the screening strategies, in which an inverted U-shaped and U-shaped effects were observed in the 5-year cause-specific survival rate and cause-specific hazard ratio respectively concerning a range of ages for primary screening.

Conclusions

Lead-time bias, usually causing an overestimation of screening effectiveness, is an elementary and fundamental issue in cancer screening. Quantification and correction of lead-time bias are essential when evaluating the effectiveness of endoscopic screening in the high-risk area in China.

Introduction

Esophageal cancer is one of the most common cancers worldwide, and nearly half of the newly reported cases occur in China, especially for esophageal squamous cell carcinoma ( 1). The main etiology of esophageal cancer remains unclear ( 2). Secondary prevention, such as endoscopic screening with subsequent intervention, has therefore been considered to be an appropriate strategy ( 3- 5). Screening has been recommended for the most prevalent cancers, such as breast ( 6), lung ( 7), prostate ( 8), colorectal ( 9), and cervical ( 10) cancer because it is a tenet of cancer prevention that earlier detection through screening leads to a better prognosis if tumors can be detected before the symptomatic diagnosis (or clinical detectable). However, in practice, the apparent benefit conferred by screening is often more favorable than expected due to the existence of lead-time and length biases, which further causes huge flawed impacts on academics and the public ( 11). Herein, lead time refers to the time interval between the screen-detected and symptomatic diagnosis time, of which the screening effectiveness may be exaggerated, inducing lead-time bias ( 12); and length time is the increment in survival among screen-detected patients because of the selection of slowly growing cancers, based on which length bias happens due to the overestimation of survival time for those detected cases with asymptomatically slowly progressing ( 13).

When the roles of lead-time and length biases on cancer screening are hotly debated, but experimental evidence is limited, the modelling study provides a useful tool to investigate the effect of lead-time bias on esophageal cancer screening ( 12- 17). Notably, it is quite challenging to identify whether any of this apparent benefit is real as lead-time and length biases cannot be quantified directly in practice. Therefore, emphasizing the limitation of the study in the discussion section by stating that the effectiveness of screening may exaggerate due to lead-time and length biases, is often encountered in published papers ( 18, 19). However, it would be much helpful if the magnitude of lead-time bias could be estimated, or what extent lead-time bias would be required to achieve a positive result. Fortunately, for past decades, surrogate measurements (e.g., the tumor doubling time and expected additional follow-up time) have been developed to quantify and correct lead-time or length bias ( 20). Based on these methods, the estimated lead time due to prostatic specific antigen screening obtained from different studies ranged from 3 to 12 years ( 18, 21, 22), and those in breast cancer screening varied from 4 to 9 years ( 17). To date, this estimate for esophageal cancer screening remains unclear, especially in the high-risk area in China, although endoscopic screening has been proved to be effective for esophageal cancer in the high-risk area in China ( 4, 5). Hence, knowing whether or what extent lead-time bias has contributed to the endoscopic screening for esophageal cancer is a matter of the utmost importance, as more ongoing endoscopic cancer screening programs have been launching for upper gastrointestinal cancer screening in the high-risk area in China ( 4, 5, 23).

In this study, we investigate the effect of lead-time bias on esophageal cancer screening in the high-risk area in China, with control for length bias concerning various patterns of screening by the severity of esophageal squamous dysplasia (ESD), and provide a well-established model for quantifying or even correcting lead-time bias when evaluating the effectiveness of endoscopic screening for esophageal cancer in observational studies.

Materials and methods

Screening model for esophageal cancer

In this study, we first developed a conceptual esophageal cancer screening model ( Supplementary materials ). In brief, the model consists of a hypothetical cohort, three-phase disease history, and patterns of cancer screening based on the severity of ESD and their benefits, which are simulated to mimic those in the high-risk area in China. Under this framework, we leveraged available demographic and age-specific incidence ( Supplementary Table S1 ) of esophageal cancer in the high-risk area in China to simulate cancer progression in terms of time to onset, diagnosis, and death or the end of the study ( 24). We investigate the effect of lead-time bias on endoscopic screening by comparing the changes of the 5-year cause-specific survival rate with and without the implementation of endoscopic screening. Further details of the model structure and model input parameters were presented in Supplementary Figure S1 , Table S1, 2 .

Table S1. Age-specific incidence rates of esophageal cancer in high-risk area (Cixian county, Hebei province, per 10,000 persons) in Mainland China, 2012.

Age (year)	Incidence rate
0−	0.00
20−	2.12
25−	0.00
30−	7.89
35−	6.01
40−	31.77
45−	82.32
50−	150.50
55−	869.65
60−	1,116.44
65−	1,164.32
70−	1,152.65
75−	1,986.21
80−	1,759.30
85−	2,144.30

Figure S1.

A schematic of mathematical model for investigating, quantifying, and correcting lead-time bias on cancer screening. Cancer stages and grades can be adjusted based on the cancer type of clinical interest.

Table S2. Model input parameters for esophageal endoscopic screening of esophageal cancer in high-risk area in China.

Model parameters	Description	Sources
ESD, esophageal squamous dysplasia.
Baseline characteristics
Number of participants	100,000	Assumption
Cancer characteristics
Incidence rate	Age-specific incidence rate of upper gastrointestinal cancer in Cixian county, Hebei province, China in 2012	Song et al. ( 24)
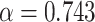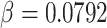
Tumor growth model	Gompertz model: the initial proliferation rate at V 0 = 1 mm 3 is ; the rate of exponential decay of this proliferation is	Benzekry et al. ( 25)
Natural history of cancer		Wang et al. ( 3)
Premalignant (Volume, mm 3)		Assumption
Mild ESD	V 1 = 80−120 with the proportion being 0.70
Moderate ESD	V 2 = 480−520 with the proportion being 0.20
Severe ESD	V 3 = 980−1,020 with the proportion being 0.10
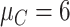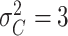
Preclinical phase	The mean and variance are and	Assumption
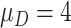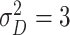
Clinical phase	The mean and variance are and	Assumption
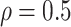
Correlation	The correlation between the length of the preclinical and clinical phases is	Assumption
Screening strategy		Chen et al. ( 23)
Age at primary screening	40-year old
Screening interval
Mild ESD	Every 3-year
Moderate ESD	Every 1-year
Severe ESD	Every half-year
Age at end of screening	69-year old
Screening sensitivity		Assumption
Mild ESD	0.80
Moderate ESD	0.85
Severe ESD	0.90
Benefit time		Assumption
Mild ESD	The mean and variance are 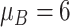and
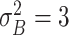
Moderate ESD	The mean and variance are 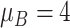and
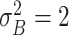
Severe ESD	The mean and variance are 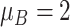and
Study period	20-year follow-up	Assumption

Model assumptions

Our model assumed three-phase cancer progression, i.e., the premalignant, preclinical, and clinical phases, with a Gompertz model for fitting tumor’s growth ( 25). Considering the length of pre-clinical and clinical phases were highly correlated, a bivariate Gamma distribution with prespecified means and variances were employed. Supposing cancer screening began at the age of 40 years old, and then was performed every three years until the age of 69 years old, with a constant screening sensitivity during the follow-up period for all undiagnosed patients. For screen-detected patients, patterns of screening were modified according to the severity of ESD during the mid-course of the study. To simplify the screening model, we combined the effect of an intervention on the screen-detected patients with the benefits of screening (referred as to the benefit time) and assumed that the benefit time was relevant to the length of the clinical phase. Moreover, to ensure the 5-year cause-specific survival rate of patients with and without receiving cancer screening respectively being around the previously reported level of 60% and 20% ( 26, 27), we calibrated the benefit time with several additional constraints (more details can be found in Supplementary materials ). Finally, the model assumed that the sojourn time followed an exponential distribution with a constant rate of λ for participants being changed to symptomatic-detected patients, which further leads to an identical distribution of lead time ( 12). Under these assumptions, we quantified and corrected lead-time bias by subtracting the expected additional follow-up time derived from Duffy et al. method ( 12), in which the lead time was estimated via a homogeneous Poisson process ( Supplementary materials ). Last but not least, we simulated participants with three commonly encountered subtypes of ESD (i.e., mild, moderate, and severe) in practice, and implemented corresponding screening strategies to reduce the potential effect of length bias with an additional assumption of no overdiagnosis. In such a case, all cases would be detected and dead from esophageal cancer. Although overdiagnosis did exist in practice with an uncertain magnitude ( 13).

Modeled scenarios and outcomes

Considering the relatively low crude incidence rate (i.e., overall crude incidence rate 21.62 per 100,000 person-year, 2011) of esophageal cancer in China ( 28- 30), we employed the age-specific incidence rate of upper gastrointestinal cancer in Cixian county, Hebei province, China in 2012 to represent the incidence rate of esophageal cancer in the high-risk area in China ( 24). According to the protocol of the National Cohort of Esophageal Cancer-Prospective Cohort Study of Esophageal Cancer and Precancerous Lesions based on High-Risk Population in China (NCEC-HRP), we simulated 100,000 participants to ensure that we can observe adequate ESD and cancer cases at the end of the study based on the corresponding incidence rate in Cixian county ( 23). We followed the simulated participants with and without undergoing endoscopic screening, and modified the patterns of screening and benefit times for screen-detected patients by the severity of ESD during the mid-course of study ( Supplementary Table S2 ) ( 23). The follow-up time was set to be 20 years, with the primary outcome being death from esophageal cancer. To quantify the effectiveness of endoscopic screening, a 5-year cause-specific survival rate and cause-specific hazard ratio (CSHR) were estimated, respectively. For calculating the 5-year cause-specific survival rate, the model assumed that the subtype-specific survival rate and the benefits of endoscopic screening for esophageal cancer were unchanged; that is, the increment of the survival rate was entirely due to endoscopic screening.

Quantifying effect of lead-time bias on endoscopic screening

To investigate the effect of lead-time bias on endoscopic screening, we quantified and corrected the lead-time via the described method in Supplementary materials ( 12). As such, we could further evaluate the performance of the established model in terms of bias, corrected, and uncorrected results.

Sensitivity analysis

In practice, the effectiveness of endoscopic is affected by several factors, such as the age of primary screening and study period. When the age of primary screening is young, the benefits of screening would be higher, with more resources being needed. Subsequently, participants enrolled in the study would be followed for a long period of time to obtain enough cancer cases. On the other hand, if the incidence rate is low, more participants would be required to ensure an adequate power of the study. Hence, it is necessary to evaluate the effect of age of primary screening and the period of follow-up on the magnitude of lead-time bias and screening effectiveness. Additionally, parameters corresponding to the aforementioned factors were considered in a one-way analysis, compliance with all model assumptions. All simulations and analyses were performed using R software (Version 3.5.1; R Foundation for Statistical Computing, Vienna, Austria) ( http://www.r-project.org).

Results

Of 100,000 simulated participants, 6,150 (6.15%) were diagnosed with ESD up to the 20-year follow-up, among which 3,005 (3.00%) patients were diagnosed with moderate or severe ESD. Table 1 presents the baseline characteristics of the simulated participants by the severity of ESD. No significant differences were observed for both age and gender between the healthy and ESD participants. As expected, the length of the premalignant phase increases along with the increasing severity of ESD.

Table 1. Baseline characteristics of simulated participants.

Baseline characteristics	Healthy	ESD
		Mild	Moderate	Severe
ESD, esophageal squamous dysplasia.
Number of patients [n (%)]	93,850 (93.85)	3,145 (3.15)	1,894 (1.89)	1,111 (1.11)
Age (year) ( 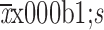)	55.35±3.88	57.74±3.15	57.77±3.18	57.58±3.05
Gender, male [n (%)]	65,500 (69.80)	2,213 (70.40)	1,322 (69.80)	789 (71.00)
Disease history (year) ( )
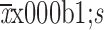Premalignant period	−	0.71±0.03	1.14±0.01	1.40±0.01
Preclinical period	−	5.99±1.71	6.00±1.69	6.06±1.76
Clinical period	−	3.95±1.72	3.99±1.73	3.95±1.73

During the 20-year follow-up period, the estimated lead time varied from 1.67 to 5.78 years, with a median value of 4.62 years [interquartile range (IQR): 4.07−5.11], which was comparable with the true value (median: 4.64, IQR: 3.41−6.02). Such results suggested that our model could quantify the lead time among the screen-detected patients adequately. More results can be found in Supplementary Figure S2, 3 , Table S3 .

Figure S2.

Biases and 95% CI of 5-year cause-specific survival rate (A) and causal-specific hazard ratio (CSHR) with (B) and without (C) correction of lead-time bias by severity of esophageal squamous dysplasia based on developed model for esophageal endoscopic screening in the high-risk area in China. 95% CI, 95% confidence interval.

Figure S3.

True and estimated distributions of lead time (year) in endoscopic screening for esophageal cancer in high-risk area in China.

Table S3. True and estimated of lead time (year) for screen-detected patients.

ESD	Min	Q5	Q25	Q50	Q75	Q95	Max
ESD, esophageal squamous dysplasia.
Total
Estimator	1.67	3.21	4.07	4.62	5.11	5.56	5.78
True	0.01	1.52	3.41	4.64	6.02	8.13	15.14
Mild
Estimator	1.67	3.34	4.20	4.72	5.18	5.43	5.56
True	0.01	1.04	2.80	4.11	5.50	7.70	12.29
Moderate
Estimator	1.98	3.15	3.99	4.53	5.05	5.56	5.56
True	0.05	2.22	3.69	4.87	6.03	7.92	12.38
Severe
Estimator	2.14	3.03	3.80	4.40	4.97	5.69	5.78
True	1.67	3.22	4.61	5.75	7.11	9.12	15.14

Table 2 shows the effect of lead-time bias on screening effectiveness in terms of both 5-year cause-specific survival rate and CSHR. It is straightforward to show that the effectiveness of endoscopic screening for esophageal cancer was overstated in presence of lead-time bias, with more than 10% of overestimation concerning 5-year cause-specific survival rate and more than 43% reduction concerning CSHR. Furthermore, the magnitude of the lead-time bias heavily depended on the severity of ESD. In contrast, the estimates with correcting lead-time bias were practically identical to the true values in terms of both 5-year cause-specific survival rate (67.63%, bias: 4.54%) and CSHRs (CSHR=0.27, 95% CI: 0.26−0.29, bias: −10.0%; adjusted CSHR=0.30, 95% CI: 0.28−0.31, bias: −6.25%). However, it is worth noting that the accuracy for correcting lead-time bias varies, depending on the severity of ESD, especially for patients with severe ESD. This reason may lie in that the exponential assumption of the sojourn time and lead time and the proportional hazard assumption of screening effectiveness during the follow-up time may be satisfied in the whole participants, but not satisfied in each stratum of participants according to the severity of ESD. In such a case, the estimates of the sojourn time and lead time in each stratum could be biased, resulting in a slight deterioration in the performance of the proposed model.

Table 2. Summary of 5-year cause-specific survival rate and CSHR with and without an additional correction for lead-time bias.

ESD	5-year cause-specific survival rate (95% CI, %)	Bias (5-year cause-specific survival rate, %)	CSHR (95% CI)	Bias (CSHR, %)	Adjusted CSHR (95% CI)	Bias (Adjusted CSHR, %)
CSHR, cause-specific hazard rate; ESD, esophageal squamous dysplasia; 95% CI, 95% confidence interval.
Total (n=430)
Uncorrected	72.44 (71.33−73.56)	11.98	0.17 (0.16−0.17)	−43.33	0.18 (0.17−0.19)	−43.75
Corrected	67.63 (66.47−68.81)	4.54	0.27 (0.26−0.29)	−10.00	0.30 (0.28−0.31)	−6.25
True	65.69 (64.41−66.79)	Ref	0.30 (0.28−0.31)	Ref	0.32 (0.30−0.33)	Ref
Mild (n=174)
Uncorrected	73.67 (71.25−75.23)	3.15	0.15 (0.14−0.16)	−28.57	0.16 (0.15−0.17)	−27.27
Corrected	70.53 (68.95−72.14)	−1.25	0.23 (0.22−0.25)	9.52	0.25 (0.23−0.26)	13.64
True	71.42 (69.85−73.01)	Ref	0.21 (0.20−0.22)	Ref	0.22 (0.21−0.24)	Ref
Moderate (n=191)
Uncorrected	70.43 (68.41−72.52)	11.35	0.19 (0.17−0.21)	−42.42	0.21 (0.20−0.23)	−41.67
Corrected	64.78 (62.67−66.97)	2.42	0.31 (0.29−0.33)	−6.06	0.34 (0.32−0.37)	−5.56
True	63.25 (61.12−65.46)	Ref	0.33 (0.31−0.36)	Ref	0.36 (0.34−0.39)	Ref
Severe (n=65)
Uncorrected	72.23 (69.78−75.05)	36.10	0.17 (0.16−0.20)	−65.31	0.19 (0.17−0.22)	−62.75
Corrected	64.27 (61.51−67.15)	21.10	0.33 (0.30−0.36)	−32.65	0.36 (0.32−0.39)	−29.41
True	53.07 (50.22−56.09)	Ref	0.49 (0.45−0.54)	Ref	0.51 (0.47−0.56)	Ref

Figure 1 presents the biases of both 5-year cause-specific survival rate and CSHR in terms of various ages of primary screening due to the effect of lead time. An inverted U-shaped effect of lead-time bias on 5-year cause-specific survival rate was observed ( Figure 1A ); and a similar effect of lead-time bias on CSHR was also observed ( Figure 1C ), which confirmed that the magnitude of lead-time bias was heavily depended on the age of primary screening, especially for the patients with the primary screening age ranged from 40 to 55 years. This is expected because the age-specific incidence rate of esophageal cancer increases rapidly after 40 years ( 28). Therefore, participants undergoing endoscopic screening were more likely to be diagnosed early and receiving the subsequent intervention, and thus suffered the most of lead-time bias. These phenomena were also verified in Figure 1B , D . Furthermore, it is worth noting that the true benefit pattern of cancer screening was unchanged concerning the primary screening age, no matter whether lead-time bias was corrected or not. Last but not least, we found that participants receiving primary endoscopic screening for esophageal cancer at 45 or 50 years would benefit the most.

Figure 1.

Sensitivity analyses in terms of various ages of primary screening. (A) Biases of effect of lead-time bias on 5-year cause-specific survival; (B) 5-year cause-specific survival rate and 95% confidence interval (95% CI) with and without correction of lead-time bias; (C) Biases of effect of lead-time bias on cause-specific hazard ratio (CSHR); (D) CSHR and 95% CI with and without correction of lead-time bias.

Figure 2 shows the biases of both 5-year cause-specific survival rate and CSHR in terms of various study periods due to the effect of lead time. The magnitude of lead-time bias increased as the study period becomes longer and finally held at a high level ( Figure 2B , D ). This is reasonable as the proposed model simulated the fixed cohort, rather than a dynamic population. As a consequence, the total benefits of endoscopic screening would be fixed and could be observed if the follow-up period was long enough.

Figure 2.

Sensitivity analyses in terms of various study periods. (A) Biases of effect of lead-time bias on 5-year cause-specific survival rate; (B) 5-year cause-specific survival rate and 95% confidence interval (95% CI) with and without correction of lead-time bias; (C) Biases of effect of lead-time bias on cause-specific hazard ratio (CSHR); (D) CSHR and 95% CI with and without correction of lead-time bias.

Discussion

Lead-time bias has caused debates and controversies in the literature hotly when conveying the effectiveness of cancer screening derived from observational studies ( 13, 31- 34). In this study, we investigated the effect of lead-time bias on the perception of screening effectiveness in the high-risk area in China based on a well-established screening model. However, no endoscopic screening programming is recommended for esophageal cancer in adults by the current clinical practice guidelines ( 35). The model used common sources of cancer registry data under several assumptions. We found that lead-time bias presents a significant impact when deriving screening effectiveness from observational studies. Considering the endoscopic screening is an invasive procedure, ignoring its impact could not only overestimate the effectiveness of cancer screening massively but also cause severe adverse effects, such as, perforation, cardiopulmonary events and aspirations, and bleeding requiring hospitalization, which may further cause flawed impacts on both academic and public. Although quantifying and correcting of lead-time bias is quite difficult in practice, it is still indispensable. In addition, it is not surprising for the relatively high degree of variation of the corrected results based on the well-established model given different screening strategies under these assumptions. In contrast, the high degree of variation in results reflects uncertainties in the interpretation of screening effectiveness, which should be cautious. Additionally, our estimates of lead-time bias on cancer screening are broadly consistent with the current knowledge, which has been intensely discussed for the past few decades ( 12- 14, 14, 18, 21, 22, 31, 34).

Notably, it is also necessary to point out that we do not doubt the effectiveness of cancer screening, although the effect of endoscopic screening on esophageal cancer has not yet been proved effective. Herein, we emphasize the concept and issue of lead-time and length biases in cancer screening, especially when conveying screening effectiveness of an invasive procedure to the public. For example, in the sensitivity analysis, we found an inverted U-shaped effect of lead-time bias on the 5-year cause-specific survival rate in terms of different ages of primary screening, with which participants with primary screening aged 45 or 50 years old would benefit the most.

Alongside with lead-time bias, length bias is much more subtle and even more critical, as patients with less aggressive tumors have a longer sojourn time, which further results in a higher chance to be detected by screening than patients with fast-growing or more aggressive tumors ( 13). The most extreme case of length bias is overdiagnosis, in which the early diagnosis of the disease has no benefit on the prognosis of patients ( 18). In this study, to reduce the impact of length bias, our model simulated the fixed cohort of participants based on the pathological grade of ESD with an additional assumption about no overdiagnosis. However, from a public health perspective, our findings should be interpreted cautiously because overdiagnosis may still exist in practice and leads to an uncertain overestimation of endoscopy screening effectiveness. Additionally, we set up a relatively long follow-up period of 20 years and used stratified analyses to estimate both the 5-year cause-specific survival rate and CSHR to mitigate its effect.

What’s more, there are several strengths. First, our model simulated the study participants based on the population-level data in the high-risk area in China and incorporated a three-phase cancer progression. Second, our model allowed various patterns of screening by the severity of ESD during the mid-course of the study, compliance with the real strategies in the high-risk area in China ( 23). Third, our model provided a useful toolbox to quantify and correct the impact of lead-time bias and investigate screening effectiveness with respect to different screening strategies. Finally, such kinds of screening models have been widely used by the US Preventive Services Task Force to aid in the understanding of the effectiveness of screening combing with clinical therapy ( 36).

Nevertheless, there still exist several limitations to this study. First, the model was developed with several assumptions, and the violation of these assumptions often happens in practice, which may limit the applicability of our findings. For example, our model assumed an exponential distribution of the sojourn time, whereas some cases did have negative sojourn times; that is, these patients became symptomatic before they could be detected by endoscopic screening ( 13). Second, the benefits of the clinical intervention were combined into cancer screening, rather than considered separately. Third, the 5-year cause-specific survival rate and CSHR may be affected by other factors or the unmeasured confounders (e.g., health status at the baseline), rather than endoscopic screening alone.

Despite these limitations, our finding of lead-time bias in endoscopic screening for esophageal cancer will hopefully be able to help researchers and policymakers to become wary of the appeared benefits derived from observational studies. We emphasize the critical impact of lead-time bias on cancer screening and provide a well-established model for quantifying and correcting lead-time bias to avoid promoting endoscopic screening based on flawed evidence. In practice, a simulation study is highly recommended to be conducted to estimate the magnitude of lead-time bias when evaluating the effect of endoscopic screening on esophageal cancer in China.

Conclusions

Lead-time bias, usually causing an overestimation of screening effectiveness, is an elementary and fundamental issue in cancer screening. Quantification and correction of lead-time bias are essential when evaluating the effectiveness of endoscopic screening in the high-risk area in China.

Footnote

Conflicts of Interest: The authors have no conflicts of interest to declare.

Supplementary materials

Screening model for esophageal cancer

The proposed mathematical model consists of six components, as shown in Supplementary Figure S1 . In detail, the first component involves a hypothetically fixed cohort, which was generated based on the population-level age-specific esophageal cancer incidence rate obtained from Cixian county, Hebei province, China. The second component refers to a three-phase progression model, including the premalignant, preclinical, and clinical phases. Supposing the tumor growth follows a Gompertz model, and the lengths of preclinical and clinical phases are assumed to follow a bivariate Gamma distribution with a moderate correlation, e.g., 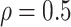. Then, the simulated cohort of participants was followed up with and without undergoing esophageal endoscopy screening. For the screen-detected patients, we modified patterns of screening based on the severity of esophageal squamous dysplasia (ESD) during the mid-course of the study and assigned them benefit times. The benefit time was assumed to be correlated with the length of the clinical phase and was combined with the subsequent interventions after screening. The model assumed an exponential distribution for the sojourn time. We estimated the expected additional follow-up time to substitute lead time. The primary outcome was deaths from mild, moderate and severe ESD, in which the mild dysplasia was diagnosed with the criteria: atypical cells are distributed mainly in the basement embrace, less than 1/3 of the epithelium; the moderate and severe dysplasia were respectively diagnosed with atypical cells involved in the top layer of epithelium, or less than 2/3 of the epithelium and precursor lesions involved the epithelium without invading the basement membrane, or atypical cells are fully or almost fully distributed in the epithelium with a clear structure of the basement membrane. Finally, we estimated both 5-year cause-specific survival rate and causal-specific hazard ratio (CSHR) to evaluate screening effectiveness and the magnitude of lead-time bias. Last but not least, we assumed that the cause-specific survival rate was constant during the follow-up period for each subtype of ESD, in such a case, the increment of 5-year cause-specific survival rate is only due to the benefit of cancer screening. It is worth noting that in this mathematical model, we can calculate lead time directly as the progression of ESD is known given a specific screening strategy. In the following sections, we described our model briefly.

Onset of cancer and its natural history

Assume the patients with each subtype of ESD possesses a similar three-phase history. As such, the onset of ESD can be simulated based on the population-level age-specific incidence rate, as described in Supplementary Table S1 . In detail, we assumed that the tumor grows without any limitation and invention at the beginning of onset, and a Gompertz model was employed to fit the tumor’s growth ( 1). Consider the length of the premalignant phase depends on the minimum screen-detected volume of tumor size. Given the tumor volume, the length of the premalignant phase can be computed. The preclinical phase begins at the end premalignant and ends when ESD-related symptoms appear. Once the preclinical period ends, the clinical phase begins. In practice, it is worth noting that the length of the clinical phase is highly correlated with the preclinical phase. Hence, we employed a bivariate Gamma distribution with means and variances as well as a correlation, i.e., 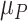, , 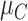, , 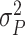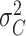and 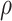, to simulate their lengths, which can be described as follows:

Step 1. Calculate the shapes and rates of gamma distributions for both the preclinical and clinical phases,

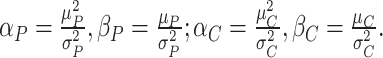Step 2. Generate a bivariate random variable based on the standard bivariate normal distribution with a correlation 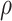, and then calculate the probability of the bivariate random variable being less than or equal to the generated random variables,

Step 3. Simulate the bivariate gamma-distributed lengths of the preclinical and clinical phases,

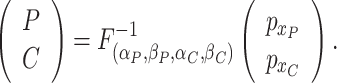where 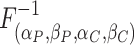is the inverse cumulative distribution function for the gamma distribution.

Patterns of cancer screening

Assuming participants had received endoscopic screening for esophageal cancer at the age of 40 years, and then were performed every three years until the age of 69 years. For the screen-detected patients, the patterns of screening were modified by the severity of ESD, as detailed in Supplementary Table S2 . Furthermore, the screening sensitivity was assumed to be constant during the follow-up period for all undiagnosed patients. As such, lead time (L) for the screen-detected patients can be calculated as

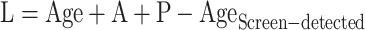where A and P are lengths of premalignant and preclinical phases. For the interval patients, which refer to patients with a misdiagnosis at the current screening but symptomatic diagnosed before the next round of screening, the lead time is 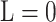. In addition, for the screen-detected patients, we assigned them benefit times (B) based on the approach proposed by Kafadar and Prorok ( 2) with an assumption that benefit times are relevant to the length of clinical phase, which can be described as follows,

where g, h, and M are respectively the lower, upper, maximum value of lead time, and C is the length of the clinical phase. Last but not least, to avoid the negative value of benefit time, another constraint is employed,

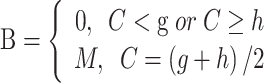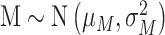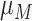where h > g >0 and , and and 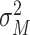are mean and variance of the maximum value of benefit times. Under these conditions, the possible effects of subsequent interventions for the screen-detected patients were also incorporated into the benefit time by calibrating the 5-year relative overall survival rate for patients with and without cancer screening being around 60% and 20%, respectively.

Death due to other causes

We estimated 5-year cause-specific survival rate and CSHR by treating death from ESD or esophageal cancer as the outcome of interest and death from other causes being competing events through a causal-specific proportional-hazard model ( 3- 5). The survival time is defined either as the period of diagnosis of cancer and death or the end of the follow-up. In such situations, for the screen-detected patients, the survival time consists of lead time, clinical phase, and the corresponding benefit time; for the interval and unscreened patients, it solely consists of the length of the clinical phase.

Estimating lead time (L) and magnitude of lead-time bias

To estimate lead time, we employed Duffy et al. approach ( 6) by using the expected additional follow-up time to substitute lead time with an assumption that the sojourn time follows an exponential distribution with a constant hazard rate of λ. Under this assumption, lead time has also followed an identical exponential with the parameter λ. Then, for a screen-detected patient with survival time t, the expected additional follow-up time l is the lead time conditional on its being smaller than t; that is,

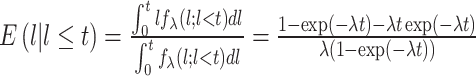Then, we can correct lead time by subtracting E( l) from the observed survival time t. It is of note that the only unknown parameter is λ. To estimate the value of λ, we used a homogeneous Poisson process, in which the diagnostic time between two consecutive patients follows an exponential distribution with an average diagnostic time interval being 1/λ. Finally, the value of λ can be estimated numerically. Last but not least, the magnitude of lead-time bias was measured by

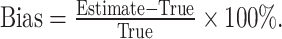Furthermore, to adequately quantify the performance of the developed model, we calculated average bias and its 95% confidence interval (95% CI), (LCI and UCI) by using the following definition,

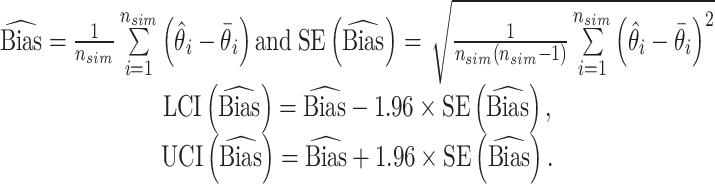where 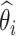and 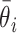are the estimated value and the truth for the 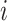th simulated study, and 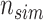is the total number of simulated studies.

Validation of developed model

Supplementary Figures S2 show biases and 95% CIs in terms of 5-year cause-specific survival rate and CSHRs with and without correction of lead-time bias based on 200 simulation studies using the developed model under the aforementioned settings ( Table 1 in the main text) concerning the severity of ESD. The developed model could quantify and correct lead-time bias accurately, although the performance becomes worse among the patients with severity ESD. The reason may lie in that the exponential assumption of the sojourn time may not satisfy in each subpopulation stratified by the severity of ESD, which further results in an inaccurate estimate of the sojourn time distribution as well as the lead time.

References

1.　Benzekry S, Lamont C, Beheshti A, et al. Classical mathematical models for description and prediction of experimental tumor growth. PLoS Comput Biol 2014;10:e1003800.

2.　Kafadar K, Prorok PC. Computer simulation of randomized cancer screening trials to compare methods of estimating lead time and benefit time. Computational Statistics & Data Analysis 1996;23:263-91.

3.　Fine JP, Gray RJ. A proportional hazards model for the subdistribution of a competing risk. J American Statistical Association 1999;94:496-509.

4.　van Walraven C, Hawken S. Competing risk bias in Kaplan-Meier risk estimates can be corrected. J Clin Epidemiol 2016;70:101-5.

5.　Austin PC, Lee DS, Fine JP. Introduction to the analysis of survival data in the presence of competing risks. Circulation 2016;133:601-9.

6.　Duffy SW, Nagtegaal ID, Wallis M, et al. Correcting for lead time and length bias in estimating the effect of screen detection on cancer survival. Am J Epidemiol 2008;168:98-104.