Discrete-Event Simulation Modeling of Critical Care Flow: New Hospital, Old Challenges

Supplemental Digital Content is available in the text.

Abstract

Objectives:

As the demand for critical care beds rises each year, hospitals must be able to adapt. Delayed transfer of care reduces available critical care capacity and increases occupancy. The use of mathematic modeling within healthcare systems has the ability to aid planning of resources. Discrete-event simulation models can determine the optimal number of critical care beds required and simulate different what-if scenarios.

Design:

Complex discrete-event simulation model was developed using a warm-up period of 30 days and ran for 30 trials against a 2-year period with the mean calculated for the runs. A variety of different scenarios were investigated to determine the effects of increasing capacity, increasing demand, and reduction of proportion and length of delayed transfer of care out of the ICU.

Setting:

Combined data from two ICUs in United Kingdom.

Patients:

The model was developed using 1,728 patient records and was validated against an independent dataset of 2,650 patients.

Interventions:

None.

Measurements and Main Results:

During model validation, the average bed utilization and admittance rate were equal to the real-world data. In the what-if scenarios, we found that increasing bed numbers from 23 to 28 keeping the arrival rate stable reduces the average occupancy rate to 70%. We found that the projected 4% yearly increase in admissions could overwhelm even the 28-bedded unit, without change in the delayed transfer of care episodes. Reduction in the proportion of patients experiencing delayed transfer of care had the biggest effect on occupancy rates, time spent at full capacity, and average bed utilization.

Conclusions:

Using discrete-event simulation of commonly available baseline patient flow and patient care data produces reproducible models. Reducing the proportion of patients with delayed transfer of care had a greater effect in reducing occupancy levels than simply increasing bed numbers even when demand is increased.

Demand for critical care services has increased significantly over the last 20 years in the United Kingdom, with a disproportionate increase in demand for the elderly population (1). Critical care bed numbers in United Kingdom are the lowest in Europe with an average of 6.2 beds per 100,000 residents (2). Hospitals must be able to adapt to the rising demand for critical care beds due to an increasing population with extensive comorbidities as well as introduction of new and extensive curative surgical options for cancer and immunomodulatory therapies such as chimeric antigen receptor T-cell treatment among other improvements in medical care, all requiring critical care support for monitoring and treatment of potential complications (3).

Our previous work using queuing theory analyzed the potential effects of merging two critical care units to determine the optimal number of beds needed (4). This analysis could not take into account the significant variability in admission rates from emergency and elective cases and to a lesser extent the overcrowding caused by delayed transfer of care (DTOC) once patients are ready to be discharged from the critical care unit.

Using simulation modeling as an approach within critical care redesign allows for the effects of potential improvements within the unit to be explored and potential failures identified (5).

Simulation packages, such as Simul8 (www.simul8.com; SIMUL8 Corp, Boston, MA), can be used to generate complex systems. To date, there are only limited applications of discrete-event simulation (DES) in critical care modeling and these efforts also lacked taking into account the effect of DTOC on patient flow and bed occupancy levels (6).

In order to determine how the new critical care unit, opening in 2021 and combining two currently existing ICUs into one large unit, will change over time, a DES model was developed and validated to determine the optimal number of critical care beds required and to simulate different what-if scenarios.

METHOD AND DATA ANALYSIS

The Aneurin Bevan University Health Board Research Governance Committee reviewed the study and waived the need for informed consent as it used two anonymized datasets. First, data from the standalone critical care database WardWatcher (Critical Care Audit, Yorkshire, United Kingdom) were used for initial analysis to determine the current occupancy levels from April 2017 to March 2018 consisting of 1,637 patient records. The second set of data was acquired from the Intensive Care National Audit and Research Centre (ICNARC) for the two currently existing critical care units from January 2016 to December 2017, detailing each individual patient’s stay, including length of stay (LOS), level of care, and DTOC for 2,650 patient records. For both these datasets, data had been merged from the two current hospitals and analyzed as one unit. More information about the setting can be found in Supplemental Digital Content 1 (http://links.lww.com/CCX/A237).

Model Generation and Replication

To determine how the bed occupancy of the unit will change through different and potential future scenarios, we used the simulation software, Simul8 (SIMUL8 Corp), to generate a replica model of the new Grange University Hospital critical care unit.

Figure 1 demonstrates the flow of patients through the model: entering, their LOS, and leaving the critical care unit. The entry point is a patient being admitted into the unit with the variable of an interarrival rate that can be adjusted depending on the average time between two consecutive patients arriving.

Figure 1.

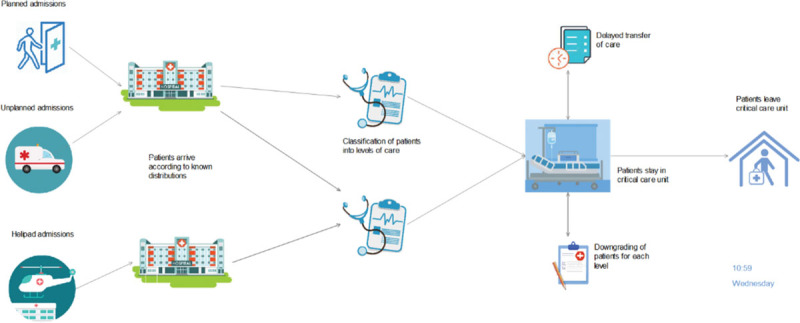
The Simul8 (SIMUL8 Corp) model of the proposed combined critical care unit.

The classification node takes the probability of each possible route a patient can take through the critical care unit and uses a label-based distribution within Simul8 (SIMUL8 Corp) to assign an LOS for each of these patient groups. Due to this labeling system, the patient pathway and their corresponding LOS are then predetermined.

Once a patient has completed treatment and is ready to be discharged, the patient either is discharged within 4 hours or classified as experiencing DTOC. When a patient leaves the system, the statistics concerning that patient, for example, total time within the system, is collected and the averages and CIs for the model run are calculated.

Within modeling, to recreate a system and establish a patient flow, a warm-up period is used to ensure the system is not initially empty. The model based on the data of 1,728 patients from the WardWatcher (Critical Care Audit) dataset used a warm-up period set to 30 days (to reach a steady state) and was run for 30 trials (to account for variation) against a 2-year period with the mean calculated for the runs.

The model variables have been derived using historic data and where required distributions have been fitted to these variables using the Stat::Fit tool within Simul8 (SIMUL8 Corp). This provides a more realistic model that accounts for known variability seen in arrival and LOS distributions (Supplemental Digital Content 2, http://links.lww.com/CCX/A238). For example, it was found that an exponential distribution best described the emergency arrival rate with an average elective arrival rate being the most appropriate fit. To emulate the flow of patients through the varying levels of care, the model uses a random assignment based on the known proportions.

The model generated is specific to our unit, although some variables, such as interarrival times, LOS, and the number of beds available, can be changed, with the structure of the model remaining the same. For further information on configuring the model used, please access the Simul8 (SIMUL8 Corp) template file (https://tinyurl.com/y4oovlnh) and the step-by-step instructions (Supplemental Digital Content 3, http://links.lww.com/CCX/A292).

Model Validation

To determine whether the model generated reflects the real-world scenario of bed occupancies and LOS, we validated it against real-world data. The simulation was run for 30 simulations for a 2-year period and the average results were compared with the ICNARC dataset consisting 2,650 patient episodes.

Table 1 shows the key results produced from the simulation model compared with the real-world data. The average bed utilization was shown to be equal, with a total number of 2,650 patients admitted into the unit. The LOS is slightly higher in the simulation model; however, these discrepancies are due to the software allowing for queuing, where in reality, operational flexibility would be used to accommodate the urgent admissions and 100% occupancy would be exceeded. In the independent validation cohort, the LOS on level 3, level 2, and level 1 care was 60.48, 54.28, and 30.72 hours, respectively. The similarity in results shows that the model follows a close resemblance to the actual data and allows further analysis.

Table 1.

Validation Results From the Simul8 (SIMUL8 Corp) Model

	Model Results	Intensive Care National Audit and Research Centre Data Results
Average number entering system	2,650	2,650
Average number discharged within 4 hr	975	973
Average number of delayed transfer of care patients	1,675	1,677
Average bed utilization, %	84.74	84.74
Percentage of time above 75% capacity, %	72.50	80.41
Percentage of time above 95% capacity, %	21.03	19.73
Average length of stay (d)	5.67	5.14

Simulation model was built from detailed patient flow description and data available for the two critical care units between 2016 and 2018. Model results are an average obtained over 30 independent random trials of our model, where each trial uses a different initial random seed to sample from the defined distributions.

What-If Scenarios

A variety of different scenarios were investigated using the model to determine the effects on the new merged critical care unit. The different scenarios were analyzed using the current bed capacity of 23 beds, as well as the proposed 25 and 28 beds.

Table 2 shows the effect of increasing the bed numbers under the current conditions for a 2-year period (Scenario A). By increasing the number of beds to 28, the average occupancy rate reduces to 70%, reducing the pressure on the system.

Table 2.

Simulation of the Proposed Changes Increasing the Bed Capacity From 23 to 25 or to 28 Beds Using the Simul8 (SIMUL8 Corp) Model (Scenario A)

No. of Beds	23	25	28
Average number entering system	2,650.46	2,650.46	2,650.46
Average bed utilization, %	84.74	78.72	70.43
Percentage of time above 75% capacity, %	72.50	58.45	35.27
Percentage of time at 100% capacity, %	23.44	9.09	1.31

Simulation model was built from detailed patient flow description and data available for the two critical care units between 2016 and 2018. Model results are an average obtained over 30 independent random trials of our model, where each trial uses a different initial random seed to sample from the defined distributions.

The demand for critical care beds within the National Health Service (NHS) is expected to increase by 4–5% per year (1). Table 3 shows the model results and highlights the pressure the critical care unit will face even by a small 4% increase (Scenario B). This shows that at 23 beds and current DTOC time and proportion, the unit will struggle to cope with the expected demand. With an 8% increase, the 92% of the time spent at full occupancy on the 23-bedded unit is infeasible. Even by increasing bed numbers to 28, 75% of time is spent above 75% occupancy levels.

Table 3.

Simulation Results on the Effects of Increasing the Patient Admission Rate for 23 and 28 Beds (Scenario B)

No. of Beds	23			28
Percentage increase in arrival rates, %	0	4	8	0	4	8
Total number of arrivals (per year)	1,455.23	1,510.54	1,569.73	1,455.23	1,510.54	1,569.73
Percentage of time at or above 75% utilization, %	92.86	95.52	98.69	64.23	70.94	75.05
Percentage of time at 100% utilization, %	68.37	77.02	91.70	10.17	11.55	18.86

Simulation model was built from detailed patient flow description and data available for the two critical care units between 2016 and 2018. Model results are an average obtained over 30 independent random trials of our model, where each trial uses a different initial random seed to sample from the defined distributions. Bold indicates percentage changes compared to baseline.

Scenario C investigated the effect of reducing the proportion of DTOC patients (Table 4). With an increase to 28 beds alongside a 20% reduction in the proportion of DTOC patients to 51%, the pressure on the system reduces greatly with only 4% of time spent at full occupancy.

Table 4.

Simulation Results on the Effects of Reducing the Proportion and Length of Time of Delayed Discharges (Scenarios C and D)

	No. of Beds	23			28
Scenario C: DTOC patient reduction	Proportion, %	0	10	20	0	10	20
	Percentage bed utilization, %	93.17	91.74	88.74	76.29	74.54	74.00
	Percentage of time at or above 75% utilization, %	92.86	88.46	81.97	64.23	53.68	51.47
	Percentage of time at 100% utilization, %	68.37	56.24	41.01	10.17	4.35	3.63
Scenario D: DTOC time reduction	Proportion, %	0	10	25	0	10	25
	Percentage bed utilization, %	93.17	90.83	88.61	76.29	74.86	72.68
	Percentage of time at or above 75% utilization, %	92.86	85.75	83.76	64.23	57.05	47.94
	Percentage of time at 100% utilization, %	68.37	50.85	47.93	10.17	5.49	3.32

DTOC = delayed transfer of care.

Simulation model was built from detailed patient flow description and data available for the two critical care units between 2016 and 2018. Model results are an average obtained over 30 independent random trials of our model, where each trial uses a different initial random seed to sample from the defined distributions. Bold indicates percentage changes compared to baseline.

Scenario D investigated reducing the DTOC time (Table 4). By increasing to 28 beds alongside a 25% reduction in DTOC time, the average bed utilization reduces. Reducing either the DTOC time by 25% or the DTOC proportion by 20%, the results produced are very similar for 28 beds. If the unit can increase bed numbers as well as reduce the proportion of patients or their time spent in DTOC, occupancy levels will be reduced to safe operating conditions.

DISCUSSION

In this in silico study using DES strategy with the commercially available software, we have shown that modeling of commonly available baseline patient flow and patient care data can result in reproducible models to real-life data, using separate development and validation dataset of similar size. We were able to simulate different scenarios with constant or increasing demand on critical care services to examine how these pressures will manifest in a new hospital, yet to open its doors.

Improving access to critical care services by increasing bed numbers has been a high priority for the critical care community in United Kingdom, and our data from this study further emphasize the need for expansion (2, 7). DTOC has been shown to be a significant problem in the Welsh NHS, where more than half of the critical care patients experience delay in timely discharge, with a quarter of them still occupying a critical care bed 24 hours after they were deemed fit for ward-based care (2).

Our findings that the reduction in either the proportion of patients experiencing DTOC or the length of DTOC period would provide benefits for patient flow provides an important starting point for the executive stakeholders, not just within our organization, but internationally. In general, DTOC is associated with high occupancy levels, which in turn has been shown to have detrimental effect on mortality due to the increased acuity of admitted patients (8). Our data support the previous findings that reducing congestion may improve timely access to critical care, with potentially improved patient outcomes (9, 10). Based on our simulation data, with the planned increase first to 25 then to 28 critical care beds alone, the new hospital could still cope with the projected increase in admissions. However, this may lead to detrimental patient outcomes due to overcrowding and increased staff burnout unless the DTOC problem is tackled at the same time (8, 11–13).

Queuing theory and DES models are the most widely applied system engineering and operation research methods used for system analysis and justification of operational business decisions (14). Queuing theory is used widely in engineering and industry for modeling of processes that involve waiting lines. In the past, queuing theory analysis was applied to a variety of hospital activities, including critical care units, obstetric services, operating rooms, and emergency departments, as a mean of directing the allocation of increasingly scarce resources (14, 15). Unfortunately, most proposed queuing models lack real-world validation and, perhaps for this reason, have yet to be embraced by physicians and hospital administrators (16). An early study using these methods was used to model accurately a large ICU within Microsoft Excel (Microsoft Corp., Redmond, WA) (14). However, queuing equations usually examine a limited number of predetermined simplified models of the real processes for which analytic formulas can be developed. Within the hospital, modeling critical care flow is complicated, as this depends on admission rates, patients’ LOS, current bed occupancy levels, critical care bed capacity, and availability of discharge destinations. Contrary to the main assumptions used in general queuing theory models, the majority of critical care admissions do not follow a predictable pattern. Similarly, discharge from critical care depends on patient factors and hospital flow. Patient factors vary widely and depend on the disease process, including acute physiologic disturbance at admission and the underlying comorbidities (17). Although these complex variables can be accounted for in the queuing models, all the required calibrations, adjustments, and fitting to the actual data can make the model lose its main advantage: its analytic simplicity and transparency (17). Nevertheless, queuing models in different simulation packages can be used to generate more complex systems (18). In an elegant study, Hagen et al (19) used Rockwell Arena 13.5 (Rockwell Automation, Coraopolis, PA) to aid development of the process flow of five ICUs, with submodels for each ICU and then analyzed six different queuing methods with differing priority methods. The results showed that if a healthcare organization solely focuses on operating at the highest efficiency, the quality of patient care may be killed, whereas some priority methods raised overall waiting times and lowered the quantity of patients seen, but improved patient mortality and preserved quality of care. The authors of this study acknowledged the general drawbacks of the queuing methods, in particular the inflexibility of the model to cater for changing patient characteristics (19). It has been previously noted that when generating mathematical models for critical care units, the model must cater for both planned and unplanned patients in regard to admission and LOS (19). Our model has taken into account both the varying levels of patient acuity at ICU admission and during the critical care stay and was also adapted for both emergency and elective admissions.

There have been other modeling approaches to evaluate the effect of the growing demand on the need for critical care provision. To determine the effect on increasing bed numbers within a critical care unit, Lawton and McCooe (20) generated a Monte Carlo simulation within R (R Foundation for Statistical Computing, Vienna, Austria). After successful validation, they analyzed staffing and bed numbers to determine the effect on occupancy on the current 16 bed unit. Contrary to our findings, they have not observed any significant effect on the reduction of DTOC on occupancy levels (20). This is probably due to their relatively simplistic model, which did not take into account the full effect of the exit block that DTOC can create in the critical care flow.

An alternative to queuing theory is to develop a DES model to create a visual representation of the system that allows testing a range of scenarios (21). DES has been increasingly used in the context of healthcare research, as it enables the modeling of patients at the individual level, including the evolution of their clinical course over time and how a patient moves through the different domains of the healthcare system (22). Different general patient-related attributes such as age and gender and clinical specific attributes such as disease phase and treatment mode can also be integrated in the DES model (23). As time progresses, patients’ attributes may be altered to reflect changes in their status. This allows the tracking of patients, as they evolve in the care system including the events they experience at different points of time. DES provides the flexibility to incorporate capacity and resource constraints explicitly and to capture the resource-allocation policies and priority rules where entities compete for limited resources (5). This feature is extremely important in health contexts, as clinical activities such as diagnosis, treatment, and consultations require a mix of specialized resources (doctors, nurses, beds, operating theaters, and so on), and these resources are, in most cases, not sufficient to meet the required level of demand (24). DES has been successfully applied to a variety of healthcare problems such as patient flow modeling in hospitals and emergency departments, reconfiguring of the primary- and secondary-care services and previously evaluation of bed occupancy and cost-effectiveness of critical care units and tele-ICU workflows (5, 6, 22, 25). To our knowledge, our description is the first published reference to use the Simul8 (SIMUL8 Corp) software package to produce a visualization and complex simulation models in the critical care arena. The strengths of our study are that we used contemporary real-life data including variable times between admissions, delineated emergency and elective admissions, and used patient-level factors to produce a closely calibrated baseline model validated against the performance metrics of two hospitals. The model is significantly more complex than the previously used queuing theory methods and provides closer resemblance of the real-life operation of a busy critical care department (18).

There are obvious limitations. First, our data only apply to our centers and as with any simulation could be affected by inconsistencies in the baseline variables. However, we have previously shown that similar levels of activity and DTOC issues are affecting the whole of NHS Wales, making our model applicable outside the future combined ICU (2). Second, the model developed in Simul8 (SIMUL8 Corp) has not incorporated potentially important patient and organizational factors, such as acuity of admissions and staffing problems on the critical care unit. There is a valid argument that with increased ICU bed strain, patients are admitted in a worse physiologic status, in turn increasing their LOS (8, 26). DES models can be configured to add this element to the simulation; however, for our current model, we could not quantify the unmet need for critical care from the available data (9). Another limitation of the data was that we only recorded how many days a patient spent at each level of care and we assumed that they move through the system with decreasing level of dependency. Third, we have not used sophisticated financial modeling to understand whether increasing ICU bed numbers or reducing DTOC would provide better value for money. In very simplistic terms, in the Welsh NHS, a critical care bed attracts approximately £1,900 as a daily tariff, whereas a general ward bed is costed at £413 per day. If we were to provide a new investment of a fixed amount of money to the system, it appears that improving the general provision of ward beds to unblock the critical care backlog would provide a better avenue to reduce ICU occupancy. Fourth, our model was constructed using a commercial software package, limiting the access of this approach. Simul8 (SIMUL8 Corp) is one of the leading software packages for DES models, which offers educational and research discounts. There are a limited number of open-source alternatives available, which lack the ability to run continuous simulations and visualization of the data. For readers prepared to adapt our DES model to their own needs, we provide the Simul8 (SIMUL8 Corp) template file (https://tinyurl.com/y4oovlnh) and a user guide (Supplemental Digital Content 3, http://links.lww.com/CCX/A292).

CONCLUSIONS

Using DES, we have shown that modeling of commonly available baseline patient flow and patient care data can result in reproducible models to real life. Based on the simulation of a variety of different scenarios, we found that reducing either the proportion of patients with a DTOC or the length of the DTOC had a significant effect in reducing the occupancy levels, which could complement the increase in bed numbers. Applying a DES model to critical care occupancy and flow problems is a more sophisticated way of managing the variation in demand that is experienced by healthcare organizations worldwide and produces results that are more accurate and visual than spreadsheets.