Engineering Person-Specific Behavioral Interventions to Promote Physical Activity

Abstract

Physical activity is dynamic, complex, and often regulated idiosyncratically. In this paper, we review how techniques used in control systems engineering are being applied to refine physical activity theory and interventions. We hypothesize that person-specific adaptive behavioral interventions grounded in system identification and model predictive control will lead to greater physical activity than more generic, conventional intervention approaches.

Summary for Table of Contents:

Computational modeling approaches can be applied with intensive longitudinal data on physical activity to refine behavioral theories and improve interventions.

INTRODUCTION

The majority of American adults fail to attain recommended levels of physical activity (1). Insufficient population-level physical activity adversely impacts health and creates substantial burden for healthcare systems (2). Significant time and resources have been invested to promote physical activity. Yet, to date, these investments by policy makers, the health care industry, employers, and consumers have not been sufficient to meet the challenge. A fundamental barrier to addressing the inactivity crisis is the misalignment between the nomothetic assumptions of behavioral theories and interventions that seek to work at the population-level and the idiographic nature of behavioral dynamics at the individual level. Put simply, a one-size-fits-all approach to theory and behavioral intervention development is unlikely to be sufficient for complex, multiply-determined behavioral phenomena such as physical activity. We propose that methods developed in the field of control systems engineering can be integrated with behavioral science to optimize the explanatory and predictive power of person-specific models of behavior. These person-specific models can provide a basis for refining theories to explain individual behavior and developing person-specific adaptive intervention approaches. These approaches use periodically updated models of behavioral responses to intervention to refine decision rules for delivering interventions. In this paper, we review research applying system identification methods to develop person-specific models of physical activity dynamics and propose that this research sets the stage for improving physical activity interventions using model predictive control tools to deliver person-specific adaptive behavioral interventions.

ALIGNING THEORY, DATA, AND METHODS FOR DYNAMIC PHENOMENA

Most theories used to explain physical activity were developed to differentiate between people engaged in more versus less physical activity (3). Static summaries of individual differences in physical activity have been common in this literature. This approach has been effective for explaining infrequent health behavior decisions (e.g., whether to get vaccinated against flu or screened for cancer) but may not be as effective for explaining and predicting health behavior decision processes (e.g., whether to move or not) that vary continuously in time (4).

Studies using ecological momentary assessment and ambulatory monitoring methods for capturing intensive longitudinal data are increasingly common and important in the physical activity literature (5). Advances in mobile and sensor technology have made it possible to capture intensive longitudinal data on physical activity and associated psychological processes in the natural context of daily life with limited expense for researchers or burden for participants (6,7). Intensive longitudinal data have energized the research community because of their potential to reveal processes involved in initiating and maintaining behavior change (8). Access to intensive longitudinal data on behavior is necessary but not sufficient to study behavioral dynamics. Appropriate modeling strategies are also needed (7).

To date, multilevel modeling has been the most common technique applied to model intensive longitudinal data (9,10). These models have been applied profitably to test hypotheses about synchronicity and sequentiality but, for reasons noted below, they are not suitable for all modeling purposes with intensive longitudinal data (5). Multilevel models provide fixed effect estimates that represent the average within-person association between two variables (11–13). Caution is needed when attempting to generalize associations at the inter-individual level to explain within-person processes or system dynamics because those population-level estimates may not adequately describe any individuals in the dataset (14). At the individual level, within-person associations can vary quite dramatically from person to person so multilevel models often include random effects to capture that variance. Even with random effects in a model, conclusions about fixed effects are conditioned on an assumption that observations of each participant were made under similar conditions (15). Just as scientists are cautious about generalizing conclusions about behavior in the lab to behavior in the natural context of daily life, they should also be cautious in generalizing conclusions about behavior observed in different contexts of daily life (15). Collecting more data to represent more diverse contextual exposures is not the answer to this problem by itself. Approaches that predict future responses of an individual based on incoming data about that individual are needed to create a cumulative understanding of dynamics at the individual level. Multilevel models are not well suited to that challenge.

Dynamic approaches assume that systems evolve as a function of both past and present conditions of the system. These systems require a memory of recent conditions because past states and behaviors may impose constraints on future states and behaviors. For example, future physical activity may be constrained by physiological limits on energy availability or psychological limits for tolerating fatigue or pain. The science of physical activity promotion will advance most rapidly if person-specific psychological, contextual, and behavioral dynamics can be leveraged to adapt or “tune” interventions to the specific requirements of each individual. With person-specific models generated, one could then go on to the latter step of identifying principles that do (and do not) generalize across members of the population (16).

TRANSLATING BEHAVIORAL THEORIES INTO COMPUTATIONAL MODELS OF PHYSICAL ACTIVITY

Behavioral interventions to promote physical activity are always either explicitly or implicitly grounded in a theory or conceptual model of behavior change. In our view, theories are explanatory tools that integrate principled reasoning and evidence to make sense of observations; they explain why relations exist between variables. In contrast, conceptual models are descriptive tools for organizing observations and specifying hypothesized causal influences (including feedback loops); they summarize how variables are related. Conceptual models are useful because they can be used to operationalize theories mathematically and allow users to simulate how changes in one variable might influence change in another.

Conceptual models can vary in complexity. At one end of the spectrum, models can be quite simple, merely describing the expected direction of an association between two variables. At the opposite end, models can be formal mathematical expressions of systems of relations that unfold between constructs, behaviors or contexts and may even change over time. Computational models refer to a broad class of approaches used to specify beliefs about the dynamic behavior of complex systems (17). These models can be used to simulate how future behavior would unfold over time under a variety of conditions. Most models of physical activity – indeed all health behaviors – have been closer to the simple than complex end of this continuum because they rarely address the dynamics of behavior directly (18). This simplicity is constraining theory and intervention development for complex health behaviors. To advance the science of physical activity promotion, behavioral models need to be refined – that is, formally expressed, expanded, and elaborated – into testable computational models. These models can then be used to guide development of experiments, such as system identification experiments, that formally test these computational models.

This work is underway. Computational models of health behavior emerged in the past decade, initially based on the theories of reasoned action and planned behavior (19,20). The first attempts to translate social-cognitive theory into formal computational models of physical activity occurred shortly thereafter (6,21). This work implemented a specific class of computational modeling techniques that describe system dynamics. Figure 1 illustrates a simplified dynamic system in which an input alters a network of states in the system to effect change on an output. Inputs represent external factors that influence the states and outputs being studied. Some inputs are controllable using behavior change techniques; others are exogenous and not controllable (e.g., weather conditions). States describe internal processes that can be modified indirectly (e.g., self-efficacy beliefs). Outputs represent measurable outcomes connected to the behavior being studied (e.g., step counts). Proof-of-concept for computational modeling of physical activity was provided via secondary analysis of bottom-up change processes in a small data set from a sub-sample of data from the Mobile Interventions for Lifestyle Exercise and Eating at Stanford study (6,21,22). Martín, Rivera, Riley, Hekler and colleagues specified a computational model with two inputs (skills training and reminders to set goals) and two outputs (self-efficacy beliefs and daily step counts) (23). The model was used to simulate values for self-efficacy and daily step counts under varying conditions. When predicted values were compared to observed values, the model accounted for approximately a third of the variance in efficacy beliefs and half of the variance in physical activity levels.

Figure 1.

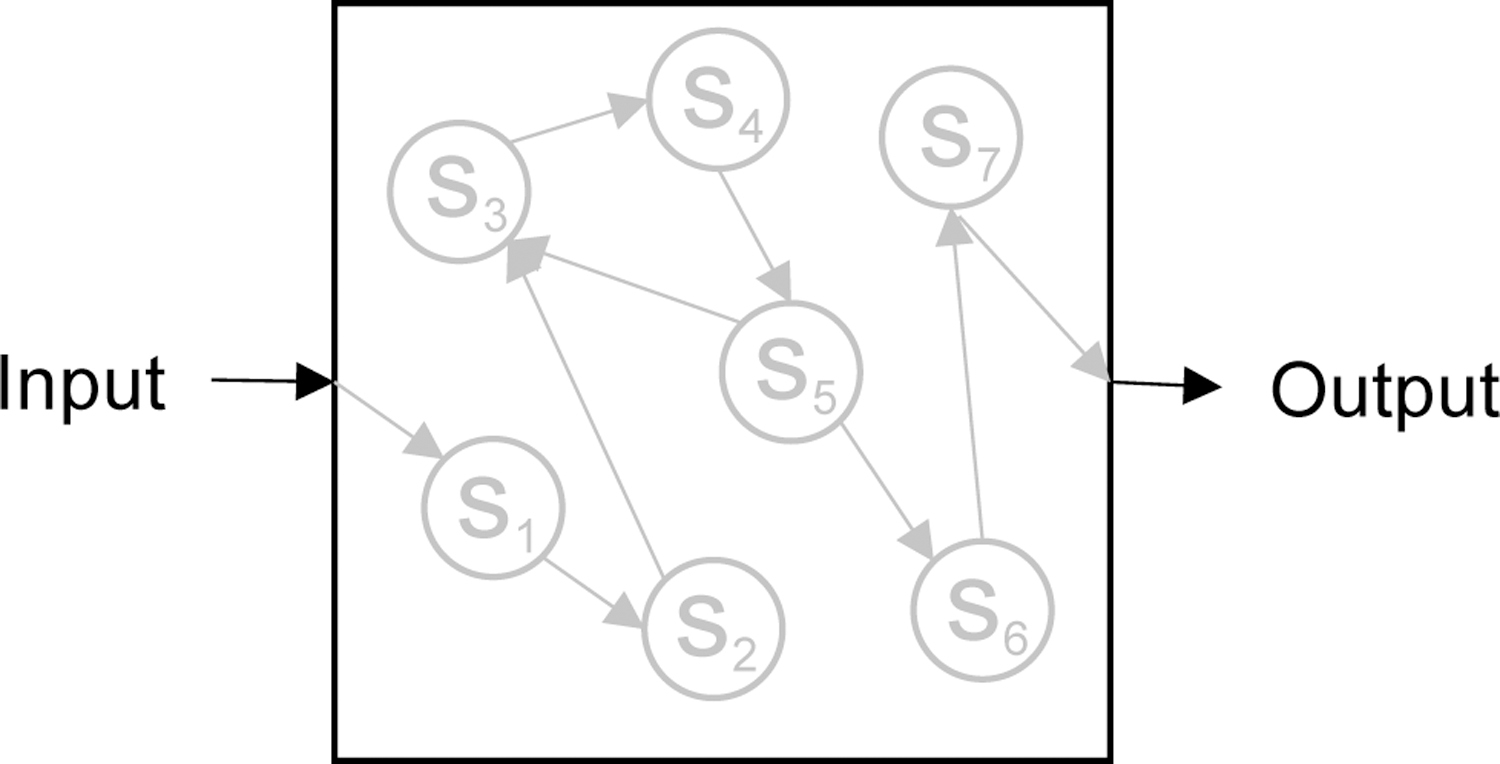
Generic dynamical system model showing inputs influencing states which influence outputs. This system evolves over time borrowing information about the recent and present inputs and states to predict future outputs.

Martín, Riley, and colleagues extended that approach in a top-down manner to represent social-cognitive theory more fully (21,24). Their model, shown in Figure 2, applied a fluid analogy model commonly used to manage supply-chain dynamics. Psychological processes were represented as flowing from inputs through states to outputs, much like fluid flow between tanks, or energy traveling between capacitators in the power grid. It included dynamic variables that functioned as both states and behavior, including self-management skills (e.g., goal-setting, self-monitoring), outcome expectancies, self-efficacy beliefs, cues to action (e.g., invitations to walk with someone), behavior, and behavioral outcomes (e.g., well-being). For example, the output of physical activity was expressed as a function of a network of states involving outcome expectancies, self-efficacy beliefs, and cues to action. In this model, recycle flows were introduced to accommodate feedback loops where recent or present values of one construct influence future values of another construct and those values subsequently influence future values of the original construct. For example, self-efficacy beliefs served as an inflow to physical activity outputs, and physical activity served as an input to self-efficacy belief outputs. This arrangement represents what Bandura described as reciprocal determinism based on agency (self-efficacy beliefs influencing future physical activity) and mastery experiences (physical activity influencing future self-efficacy beliefs) (25). The extended model also incorporated a set of variables that served exclusively as inputs to the model, such as skills training for enhancing self-management skills, observed behavior, verbal persuasion and social support, perceived barriers, intrapersonal states, environmental context, and a variety of internal and external cues that influence cues to action.

Figure 2.

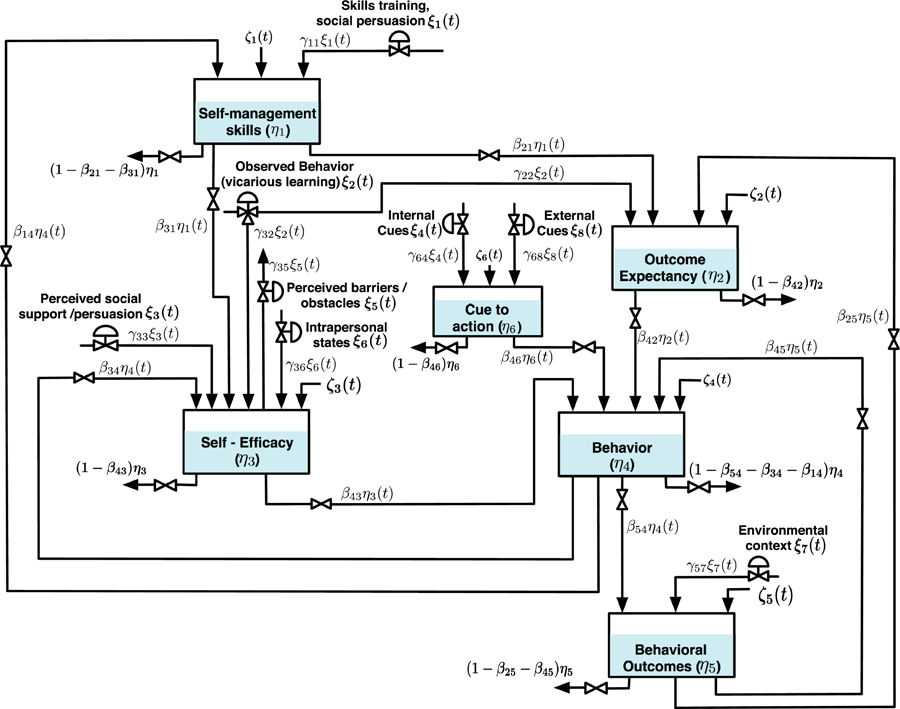
Social-cognitive theory expressed as a computational model (Reprinted from (21). Copyright © 2020 IEEE. Used with permission.)

A series of simulations were conducted by varying a limited number of parameters in the model to observe responses in outputs (24). Results of those simulations aligned with predictions of the theory. For example, self-efficacy moderated the effects of cues to action on behavior; cues had a limited effect when self-efficacy was low but a sustained positive effect when self-efficacy was high. These effects were not unbounded. Increasing the frequency of cues to action for several days led to diminishing returns and ultimately became counterproductive. This model holds promise for application with real participant data and can yield new insights for designing and refining behavioral interventions (18).

SYSTEM IDENTIFICATION OF DAILY PHYSICAL ACTIVITY RESPONSES TO INTERVENTION

Control systems engineering provides a set of tools for (1) specifying computational models of dynamic systems, (2) identifying model coefficients from intensive longitudinal data (system identification), and (3) simulating how outputs are expected to respond to different inputs over time (26). When multi-component behavioral interventions introduce components at different occasions, system identification can be applied retrospectively to identify which components actively stimulated behavior change (and which were inert). This bottom-up approach uses interventions to excite the system so its dynamics can be characterized.

Identifying Inputs Associated with Maintenance of Daily Physical Activity

The earliest-known application of system identification for decomposing the effects of a multi-component treatment package involved a secondary analysis of daily physical activity reports from a subsample of participants in the Active Adult Mentoring Program (27). Participants were selected from the treatment group of a 16-week randomized controlled trial that used peer volunteers to deliver a physical activity intervention grounded in social-cognitive theory. This intervention involved multiple components, including self-monitoring, gym memberships, behavioral initiation training, and maintenance training. At the end of the 16-week intervention period, both the treatment group and the control group increased their physical activity but only the treatment group maintained some of those gains at an 18-month follow-up (28).

In secondary analyses, participants in the treatment group who completed the intervention period (n=34) were divided into subsamples of maintainers (n=10) and nonmaintainers (n=24) based on whether they reported engaging in 150 minutes or more of moderate-to-vigorous physical activity at the 18-month follow-up (participants who did not report that level of activity were classified as nonmaintainers). Hekler and colleagues then applied system identification tools to model daily self-reported physical activity (output variable) as a function of the onset and offset of individual intervention components and time-varying determinants of physical activity (input variables). Using continuous-time linear models, physical activity was modeled as a first-order system, meaning that physical activity was modeled as a function of previous-day states and activity and inputs from time-varying intervention components (note: higher-order systems would involve more than one previous day of data, increasing the memory built into the model).

System identification modeling yielded different models for maintainers and non-maintainers. Nonmaintainers’ physical activity was a function of inputs that included self-monitoring, having a gym membership, and engaging in more exercise bouts outdoors. In contrast, maintainers’ physical activity was a function of inputs that included self-monitoring, behavioral initiation training, maintenance training, and engaging in more exercise bouts outdoors. Thus, system identification provided the unique insights that (1) having gym memberships did not discriminate maintainers from non-maintainers, but (2) uptake of behavioral initiation and maintenance training were critical for discriminating those sub-groups at follow-up. One implication of this system identification analysis for optimizing future interventions is that it may be useful to reconsider the cost-benefit analysis of providing gym memberships as a part of this multicomponent package. This component adds expense but neither stimulated a greater behavioral response during the intervention period nor supported maintenance of physical activity at follow-up. Indeed, the data suggesting better maintenance among those who exercised outdoors, suggests a plausible iatrogenic effect to gym membership related to maintenance, which makes sense when considering the gym membership was removed at that time. Thus, any behavioral routines generated in the context of a gym were no longer available to the person. A second implication is that the behavioral initiation and maintenance trainings used should be refined to address the needs of nonmaintainers more effectively.

Identifying Person-Specific Intervention Inputs of Daily Physical Activity

Another bottom-up application of system identification was used to test a dynamic formulation of social cognitive theory using data from the Just Walk intervention (29,30). After a 2-week baseline period of activity monitoring with a consumer device, 20 adult participants received a pseudo-randomized schedule of daily step count goals with varying reward values for a 12-week intervention period. The pseudo-randomized schedule was designed to produce the behavioral variation (excitation) needed for dynamic modeling of two independent inputs on behavior. In this case, those inputs were the two intervention components: daily step goals and reward values. The ability to experimentally manipulate these inputs allows for estimation and validation of computational models, thus, allowing system identification to be used to test these models.

Daily step goals were tailored based on initial activity levels during the baseline period. They varied from ‘doable’ (matching the median daily steps during baseline) to ‘ambitious’ (up to 175–250% of the median daily steps during baseline depending on initial step counts). Whenever participants met their daily step goal, they earned reward points that could be exchanged for gift cards. These values were announced with the step goal in a message at the beginning of every day. Daily reward values ranged from 100 to 500 points (corresponding to monetary equivalents ranging from $0.20 to $1.00). These two intervention components were manipulated in an orthogonal manner so participants could be incentivized with small or large rewards for attaining doable or ambitious goals. Daily reward receipt was a third input but was not experimentally manipulated. Prior to delivering intervention messages, participants were prompted to self-report other hypothesized time-varying determinants of physical activity (e.g., expected stress, expected busyness, expected typicality of the day).

System identification modeling was used to estimate the effects of controllable (manipulated) inputs, the intervention components, as well as the uncontrollable (disturbance) inputs and states, on daily step counts. This experiment was open loop because the output (behavior change) in this dynamic system was not used to provide information that would be used to modify subsequent inputs (whereas closed loop experimentation uses changes in the output variable to adjust subsequent inputs). Separate linear systems with exogenous inputs were estimated for every participant. For each participant, 16 separate models were estimated. The base model included the daily steps goal, expected reward value, and rewards received. The 15 additional models included all possible combinations of five inputs: expected busyness, expected stress, expected typicality, and whether it was a weekend or weekday (separate binary variables). Final model selection for each participant was based on theoretical plausibility, empirical consistency and reliability.

This process resulted in individual models of varying complexity (e.g., 45% of the final models had four inputs, 40% of the final models had five inputs). Model fit was calculated by comparing observed daily steps with model-simulated daily steps for each individual. Fit for the 20 participants ranged from 6.3% to 46.0% of the observed daily step variance (M=19.2, SD=9.3, median=19.1). The most common input variables in the 20 individual models were whether it was a weekend or weekday and the expected typicality of the day. These findings revealed potential tailoring variables that could inform decisions about whether to deliver incentivized step goals to participants.

Implications for Developing Person-Specific Behavioral Interventions

The person-specific dynamical models estimated for system identification can also be used to simulate treatment responses under varying conditions. Freigoun et al. provided an example of an individual’s step responses to different goal intensities, expected rewards, granted rewards and expected busyness (30). Simulated responses from individual dynamical models can be used to determine the optimal combinations of intervention components for a given individual. These response simulations can reveal components that are more likely to be active versus inactive for stimulating behavior change. That information can be leveraged to optimize interventions by including only active components.

These examples of system identification from the Active Adult Mentoring Program and the Just Walk intervention modeled physical activity at a daily time scale. It is also possible to predict behavioral responses to physical activity interventions on faster time scales (e.g., hourly), provided that corresponding behavioral data are available, if interventions are expected to be delivered on a more frequent schedule. Faster time scales can be attractive for dynamical modeling because they yield the required intensive data in shorter periods. Yet there is a danger in selecting a time scale that is too fast because noise can drown out the signal from intervention responses. Noise represents unique variance in measurements that is unrelated to the signal in the sensor measurements (similar to unique variance of item responses unassociated with a latent variable in a latent factor model). Thus, researchers need to exercise their judgment and test different measurement time scales to select one that balances the duration of data acquisition with an acceptable signal-to-noise ratio.

These two examples also assume that a common model underlies person-specific behavioral dynamics across all contexts. Developing person-specific models to describe real-world behavior represents a major advance in physical activity research. It is also possible that behavioral dynamics differ systematically across contexts. For example, consistent with national physical activity data, the Just Walk study models indicated that physical activity varied consistently between weekends and weekdays (29,31). In this instance, there may be advantages to modeling behavior as a switched system by constructing sub-models with (a) separate functions for modeling behavior on weekends versus weekdays, and (b) rules for determining when to switch to each model when predicting behavior. Switched systems are useful when behavioral dynamics differ under specific known conditions, such as on weekends versus weekdays. The next example extends applications of system identification to model the dynamics of acute behavioral responses to physical activity interventions in a switch model that allows for different control dynamics on weekends and weekdays.

SYSTEM IDENTIFICATION OF MOMENTARY PHYSICAL ACTIVITY RESPONSES TO INTERVENTION

Text messages represent a common mode of physical activity interventions that can be delivered multiple times every day at very little cost (32–36). The conventional approach to evaluating text message interventions is to treat them as a treatment package by comparing the physical activity of groups who received text messages and groups who did not receive text messages at the end of an intervention period. This approach has shown that, as a treatment package, text messages appear to have small-to-medium sized positive effects on physical activity (34–36). Yet little is known about the parameters for optimizing messaging effects. Interventionists are left with little guidance to answer important dosing questions: When should messages be sent? Which messages should be sent? How many messages should be sent? In what contexts and states should a message be sent? How long does it take for the build-up of an effect? How long is the half-life or degradation of an effect? How long is a given message expected to have an active effect on behavior before another message is needed? System identification can be applied to answer these questions.

In a recent study, Conroy, Lagoa and colleagues enrolled 10 adults to receive text messages and wear activPAL activity monitors for 16 weeks (37,38). Participants received five text messages distributed in equal-sized blocks from 8:00am to 8:00pm, with message delivery constrained so all messages were separated by at least one hour to avoid message pile-up. Messages were drawn randomly from one of three content libraries – ‘move more,’ ‘sit less,’ and trivial facts. The ‘move more’ and ‘sit less message content was informed by social-cognitive theory for consistency with prior messaging interventions as well as existing evidence for physical activity motivation (34,39,40). Participants were incentivized to confirm message receipt with a brief, timely reply. Message confirmation rates (>98%) suggested high fidelity of treatment delivery and receipt throughout the study (41).

One of the challenges in modeling these data was the intensity of data from the physical activity monitors which sampled at 20 Hz and provided output in 15-second epochs. Assuming 16 waking hours daily, each participant produced over 430,000 physical activity measurements over the 4-month study period. To produce a suitable signal-to-noise ratio, data were aggregated up to 15-minute epochs (after exploring a number of possibilities). Using a bottom-up approach, dynamical models were specified to estimate the effects of receiving each type of text message (input) on activity behavior (output) in the subsequent 15-minute epoch. Past behavior also predicts future behavior. Memory of past behavior was added to the model by including recent activity behaviors as inputs. Model order (the number of previous epochs of behavior used as inputs) was varied to evaluate effects on model uncertainty. A 5^th-order model (i.e., using the last 5 epochs of behavior as inputs) was selected. Next, separate piecewise models were specified to estimate the effects of text message and recent behavior (inputs) on weekend and weekday physical activity (outputs).

Conroy, Lagoa and colleagues then used coefficients generated from observed data to simulate impulse responses to each type of text message. As seen in the left panel of Figure 3, impulse response curves indicate the expected change in activity behavior (output) during each 15-minute epoch following delivery of a single message of each type. Impulse responses reveal how long it takes for that single message to have its peak momentary effect (i.e., whether it changes behavior instantly or 30 minutes after message delivery). They also suggest when messages may become inert and no longer have an effect on activity behavior. This information can be useful for optimizing the frequency of message delivery schedules. We have also found it helpful to examine cumulative step response curves. As seen in the right panel of Figure 3, cumulative response curves indicate the overall effect of an individual message over time, as indicated by the steady state achieved at the asymptote of the curve. These two curves summarize (a) the latency for a single message to initiate its expected momentary effect (delay of initial change), (b) the latency for a single message to achieve its expected peak momentary effect (delay of peak instantaneous change), (c) the magnitude of a single message’s peak expected effect (peak instantaneous change), (d) the duration a message is actively exerting an effect on behavior before behavior achieves a steady state (settling time), and (e) the expected overall effect of a single message (steady state). This information is important when individual messages are used to stimulate desired behavior change in a system.

Figure 3.

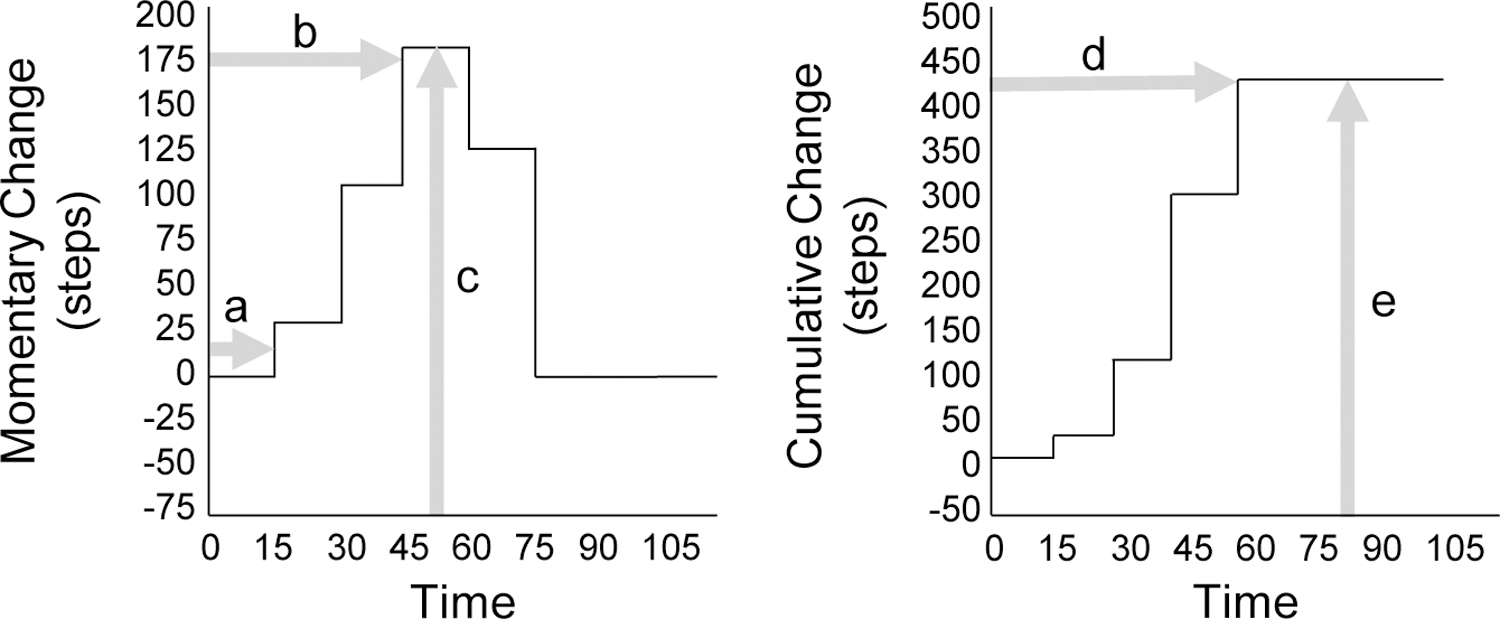
Impulse response (left panel) and cumulative step response curves (right panel) depicting the simulated response to an individual message. These curves reveal a number of important response features, including the latency to initiate a momentary message effect (a), latency to peak momentary message effects (b), magnitude of peak momentary message effects (c), settling time for responses to a message (d), and steady state response to a message (e).

These two plots can reveal the heterogeneity of behavioral responses to individual text messages. Figure 4 presents simulated impulse response (panels a, c, e, and g) and corresponding step response (panels b, d, f, and h; cumulative behavior change) curves following delivery of three types of messages for two participants. These curves represent simulated responses based on the empirically-generated person-specific models of behavior change. The output of these models, represented by the y-axis, involved changes in the number of minutes moving following message delivery relative to what would be expected if a message had not been delivered. The maximum impulse response is theoretically constrained by the size of the epoch (e.g., an individual cannot exceed 15 minutes of movement time during a 15-minute epoch) but also practically constrained by model-predicted outputs in the absence of message delivery (e.g., if 4 minutes of movement time were predicted for an epoch without a message, the maximum impulse response during that epoch would be 11 minutes with a message).

Figure 4.

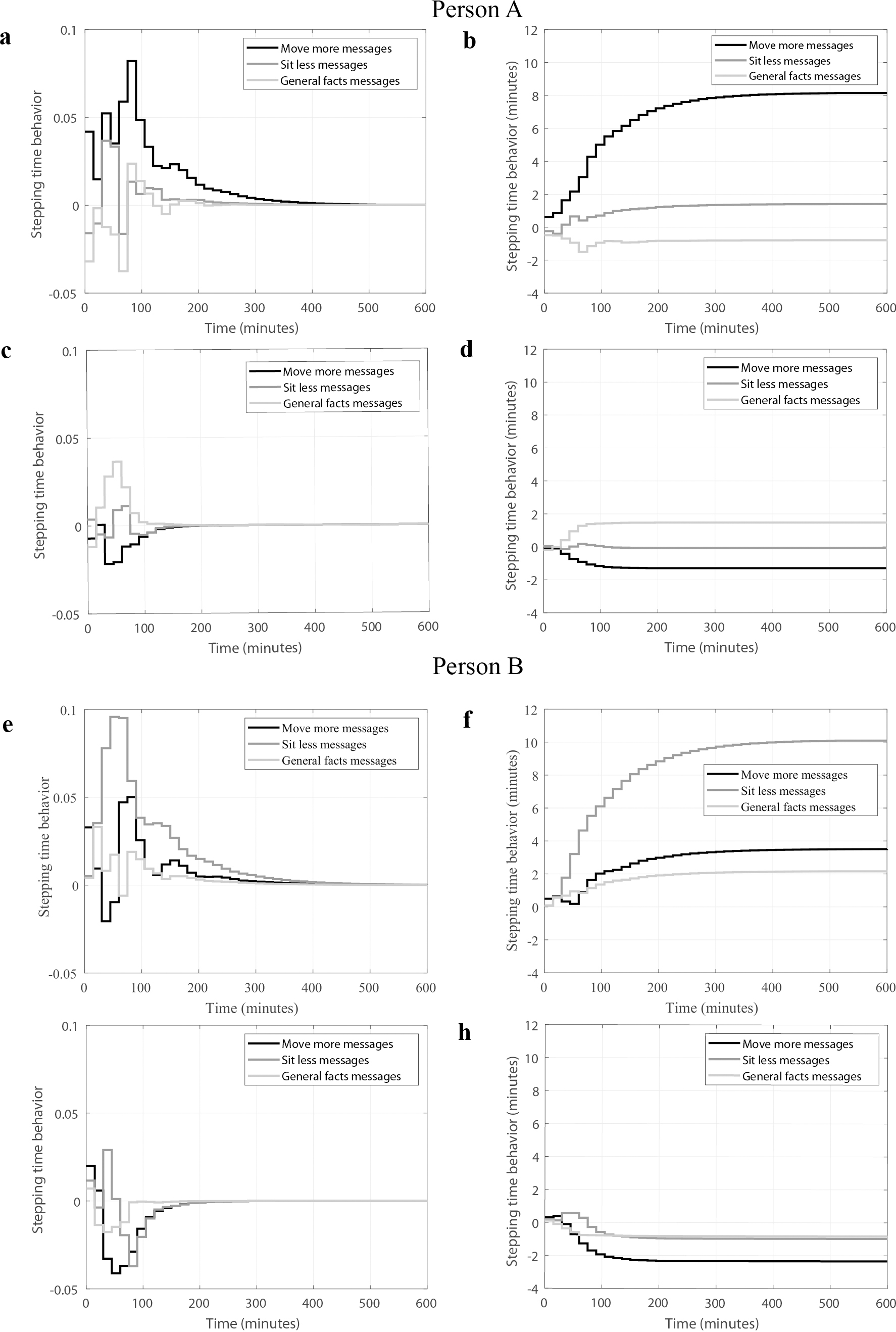
Heterogeneity of physical activity responses to different message types on weekends (panels a, b, e, and f) and weekdays (panels, c, d, g, and h) for two individuals (top and bottom halves; panels a-d and e-h).

Both participants in this example were more responsive to messages delivered on weekends (panels a, b, e, and f) than on weekdays (panels c, d, g, and h). This difference suggests that occupational or social factors during weekdays may have constrained their ability to respond to messages. On weekends, each participant showed a behavioral response to a specific type of message but these responses differed. The first participant (top half of Figure 4; panels a and b) responded to ‘move more’ messages by moving for an additional 8 minutes over the next 5 hours but had only trivial responses to the other messages. The second participant (bottom half of Figure 4, panels e and f) responded to ‘sit less’ messages by moving for an additional 10 minutes over the next 5 hours. Taken together, these results can be used to deliver messages on schedules specific to each participant. They can inform a decision rule that controls when messages are sent (i.e., on weekends rather than on weekdays), which messages are sent (i.e., ‘move more’ messages for the first participant, ‘sit less’ messages for the second participant), and how many messages are sent to achieve a behavior change goal (i.e., five messages for the first participant, four for the second participant). Similar heterogeneity of responses was found when sedentary time was the output in each model (37).

USING COMPUTATIONAL MODELS TO INFORM PERSON-SPECIFIC BEHAVIORAL INTERVENTIONS

The promise of precision medicine has been hyped (42). Genetic applications have captured the greatest interest and largely failed to live up to the hype (so far) (43). Precision medicine approaches could be expanded to address public health needs to focusing on prevention and addressing social determinants of health (44,45). The approach described here provides a basis for developing context-sensitive, person-specific adaptive behavioral interventions informed by intensive longitudinal data. A rich variety of data types can be incorporated in these models and interventions, including behavioral or physiological data from wearable sensors, psychological data from self-reports or personal sensing, contextual data linked to spatial locations, and temporal data.

Building on the text message intervention described above, the system identification coefficients provide a basis for developing person-specific decision rules for selecting and timing message delivery based on recent behavior, historical responses to different messages, and contextual tailoring variables (e.g., weekend vs weekday, location, weather conditions, built environment features). In this way, decision rules can ensure that people only receive messages they respond to, when they are likely to respond, and as often as needed to achieve their behavior change goals. Automating the design of these context-sensitive, person-specific decision rules can promote health equity by making behavior change accessible across a variety of social contexts that constrain physical activity.

This extension of system identification to develop person-specific decision rules will rely on another set of tools from control systems engineering. Model predictive control is a real-time framework for developing decision rules (controllers) that directly incorporate system identification models (46,47). These controllers are effectively optimization algorithms that implement the decision rules for intervention delivery, and can be configured for multi-component interventions, while recognizing constraints that limit dosages or keep outcomes of interest at acceptable levels. Figure 5 presents one pipeline for person-specific adaptive behavioral interventions. System identification tools are used to develop a dynamical model of the behavior. That model is used to design a controller for achieving a specific objective, such as increasing physical activity by 30 minutes daily. The controller draws on information about recent and present values of the state to determine whether to deliver an intervention, which intervention to deliver, when to deliver the intervention, and how often to deliver the intervention. Behavioral responses to the intervention are tracked and used to adapt future intervention decisions by the controller as well as to adapt the model underpinning the controller. This integration of system identification and model predictive control in this way has been described as a control optimization trial (46). This approach can even be extended to permit periodic adaptations as the intervention algorithm learns more about how a specific individual responds to different interventions (inputs) under different conditions (states and external factors such as the day of week or weather conditions). This intervention approach would be adaptive (in the control systems sense) because the person-specific decision rules are refined as new information about that person’s behavioral dynamics accumulates. It is akin to the continuous tuning interventions described by Hekler and colleagues (45).

Figure 5.

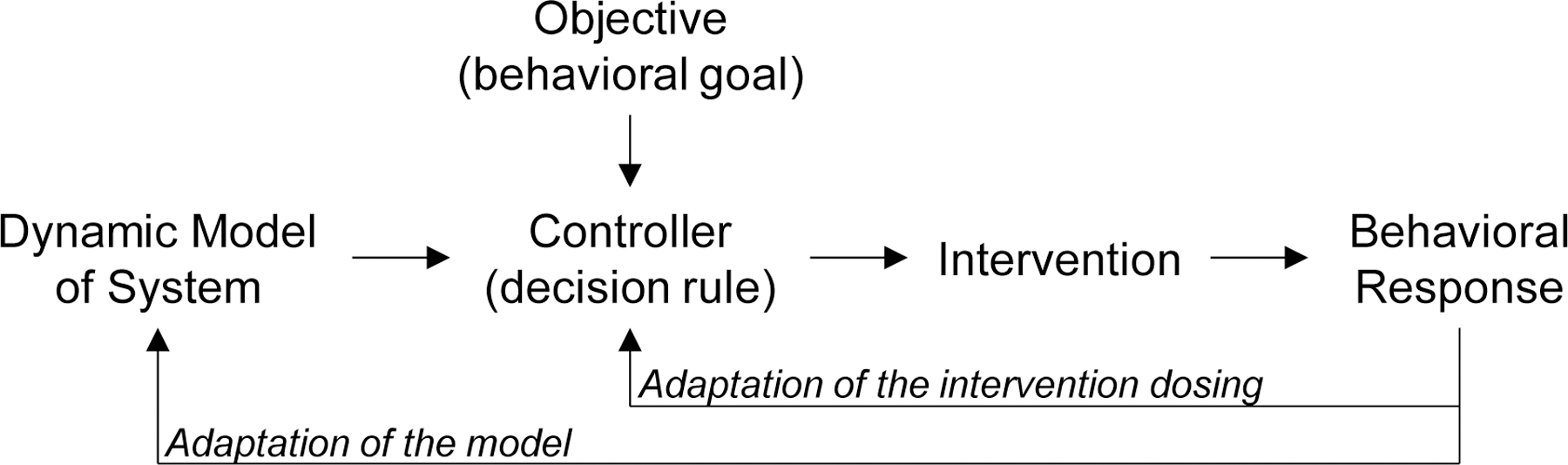
Precision behavioral intervention pipeline.

System identification can also be used to develop just-in-time adaptive interventions (JITAI; 48). The JITAI approach was developed to deliver context-sensitive behavioral interventions at moments of vulnerability/opportunity and receptivity. These interventions require that intervention developers specify decision points (the frequency of determining whether or not to intervene), a tailoring variable that will be used to determine vulnerability/opportunity at each decision point, a decision rule that will be used to determine whether the level of the tailoring variable should trigger an intervention, one or more intervention options that can be delivered, and proximal and distal outcomes that are targeted. The decision rule in most just-in-time adaptive intervention approaches (JITAI) is generic, meaning that the same rule is applied for all participants. The person-specific adaptive intervention approach described here is different. It may start with a generic decision rule but it progressively adapts that rule to be increasingly person-specific over time as it acquires new information about an individual’s behavioral responses to different interventions under different conditions. Unlike many existing JITAI approaches, this model also has built-in memory that stores recent values of the state and behavior to inform decisions about whether or not to intervene. Another difference between these approaches is that existing JITAI approaches do not monitor responses to interventions to inform whether future interventions should be delivered.

To be sure, system identification and model predictive control are not the only approaches available to model intensive longitudinal data and inform intervention development. Mixed-effect location-scale modeling is an approach for estimating individual differences in variance adjusted for means (49). Time-varying effect models are useful for characterizing how (instantaneous) relations between variables change over time (50). Machine learning is a buzzword used to describe a large family of methods for classification and prediction tasks. Machine learning approaches can overlap with the system identification described herein because both use past or current information to predict future behavior, a critical feature for intervention development.

With respect to intervention development, if a generic decision rule can be applied to all participants, then the established JITAI framework can be applied to develop context-specific behavioral interventions (48,51). Micro-randomized trials can be used to provide an experimentally-derived, generic decision rule for delivering these interventions (52). The HeartSteps intervention was the first example of a micro-randomized trial for physical activity promotion (53). Another approach to personalizing interventions involves recommender systems. For example, the MyBehavior app uses a multi-arm bandit method to provide personalized physical activity recommendations (54,55). This intervention incorporated an explore-and-exploit algorithm to leverage both the familiarity of frequently-enacted physical activities with the novelty of new physical activities to stimulate behavior change. If one has access to large volumes of data, it may even be possible to develop a model and controller simultaneously using reinforcement learning tools; however, this approach has yet to be applied to develop a physical activity intervention (56). As these and other approaches for personalizing physical activity interventions become more popular, it will be valuable to compare them directly to determine which approaches lead to the most effective interventions in the least amount of time.

CHALLENGES OF DEVELOPING PHYSICAL ACTIVITY INTERVENTIONS USING COMPUTATIONAL MODELING

Control systems engineering offers a powerful suite of tools that can be applied to develop person-specific behavioral interventions but it presents unique challenges for researchers. These challenges include research design, data processing, and communicating results to a research community that may be unfamiliar with these methods.

From a research design perspective, intensive longitudinal data are clearly needed. The question is, how much? The factors used to inform statistical power analyses – sample size, effect size, and Type-1 error rates – are less informative for planning studies using system identification. Instead, the relevant considerations involve the time scale of interest (e.g., daily vs hourly), the types and timing of inputs, the potency of the inputs (relative to potential unmeasured influences), whether feedback is included in the design, model complexity, and uncertainty in the model.

Sensors, such as accelerometers, have enabled high-frequency data collection. Raw sensor signals are typically processed by software or firmware for an activity monitor to provide physical activity indices at different levels of abstraction (e.g., counts/minute, steps/minutes, daily duration of moderate-to-vigorous physical activity). Our experience has shown that more frequent data is not always better because the noise-to-signal ratio can be inflated. As a part of data processing, researchers will need to explore a variety of sampling frequencies to determine the optimal one for their applications.

Finally, system identification approaches are well-established in control system engineering but largely unfamiliar to the physical activity promotion community. These models have unique evaluation and reporting requirements. Researchers may need to educate reviewers and editors who are not accustomed to this type of work. None of these challenges are insurmountable but they will require a flexible, team science approach to introduce computational modeling approaches into the world of physical activity promotion.

CONCLUSIONS

In sum, we reviewed early-stage research applying a well-established suite of tools from control systems engineering to develop, identify and interpret computational models of physical activity. These models provide a basis for designing, refining and optimizing physical activity interventions at a variety of time scales. Whether a single time scale is sufficient to model physical activity dynamics is not clear and efforts are underway to develop multi-time scale models of physical activity dynamics (18). We propose that single or multi-time scale models can be extended using model predictive control tools to deliver interventions that are sensitive to recent behavior, historical responses to treatments, and a variety of contexts under which behavior is executed over time. As information is acquired about behavior in new contexts and about different responses to treatment, these models can be adapted to ensure they remain person-specific as people develop and change. Although intervention development has been our focus, the accumulation of person-specific dynamic models has potential to accelerate theory development (16). To date, health behavior theories have not been articulated in ways that describe the dynamics of physical activity. The accumulation of person-specific dynamic models can be used to identify common processes as well as distinct subgroups characterized by predictable boundary conditions or processes (16). We look forward to further applications of system identification and model predictive control tools to improve the science and practice of physical activity promotion.

Key Points.

• Physical activity has largely been studied as a static individual difference instead of a dynamic process.

• Control systems engineering approaches can reveal how behavioral interventions influence daily and momentary physical activity dynamics.

• System identification of behavioral responses to interventions provides the basis for developing and adapting person-specific decision rules to select and time behavioral interventions.

• Person-specific behavioral interventions can be developed, adapted, and scaled to refine health behavior theories and address broad and unmet public health needs.

• Whether person-specific adaptive behavioral interventions are superior to more generic intervention approaches is an open empirical question.