Abstract
Suppose the same contestants play in tournaments of chess, shogi, and Go. Per-tournament rankings can be estimated. We may also try to recover a latent board game skill that accounts for some proportion of the variance in per-board game rankings. To accomplish this, a factor model is introduced. Identification issues with the ordinal paired item model are discussed. Simulation studies are presented to provide some guidance about sample size requirements. Both single item and multivariate correlation and factor model are validated using simulation-based calibration. We recommend leave-one-out cross-validation to assess model fit. To ease application of the methods described, an open-source companion R extension, pcFactorStan, is published on the Comprehensive R Archive Network. Application of pcFactorStan is demonstrated by analysis of a real-world dataset.
Keywords: Mathematics, Psychology, Bayesian methods, Bradley-Terry model, Factor model, Ordinal paired comparison, Thurstonian model
Mathematics; Psychology; Bayesian methods; Bradley-Terry model; Factor model; Ordinal paired comparison; Thurstonian model
1. Introduction
The notion that latent constructs such as general intelligence can partially account for more specific measurable attributes like reading comprehension has spawned a whole branch of productive research known as factor analysis [1]. Factor analysis has generally been applied to items that record absolute as opposed to relative judgments. Absolute measures are interpreted in reference to some fixed maximum and minimum. In contrast, relative measures are judgments about the relative worth of objects within a set. These judgments are relative because the worth of a given object depends on which other contrasting objects are included in the set. Here we introduce a novel type of factor model built on relative indicators.
For example, consider a survey to compare chocolate pudding recipes on facets of taste, color, and texture. Each prompt consist of two competing recipes (i.e., two objects) and a facet or item. A set of prompts might include,
Carob Milk has
taste compared to Cocoa Milk.
Cocoa Soy has
texture compared to Cocoa Milk.
Carob Soy has
color compared to Carob Milk.
where a judge fills  with better, worse, or the same. Ignoring any potential judge effect, recipes can be ranked per-facet (i.e., on taste, texture, and color). The Bradley-Terry-Luce model is often used to conduct analyses that rank one facet at a time [2]. For example, recipes might be ranked on texture alone. However, we can also imagine that there might be a latent Pudding Greatness factor that accounts for some proportion of the variance in item-wise (i.e., facet-wise) rankings.
with better, worse, or the same. Ignoring any potential judge effect, recipes can be ranked per-facet (i.e., on taste, texture, and color). The Bradley-Terry-Luce model is often used to conduct analyses that rank one facet at a time [2]. For example, recipes might be ranked on texture alone. However, we can also imagine that there might be a latent Pudding Greatness factor that accounts for some proportion of the variance in item-wise (i.e., facet-wise) rankings.
While correlations among facets have been modeled [3], a factor model is absent from the literature. Factor models can be fit to correlation data. However, in such a two-stage analysis, uncertainty is not accurately propagated from response data to correlation data, and then to factor scores and loadings. Inferential statistics at the factor model level cannot accurately reflect the uncertainly arising from the response model. Here we introduce a Bayesian paired comparison factor model. Item and factor parameters are estimated simultaneously and estimates of parameter uncertainty do not rely on asymptotic arguments.
To further clarify our aims, we acknowledge that factor analysis is a general mathematical technique that can be used in diverse ways. Indeed, factor models have appeared with some frequency in paired comparison literature. For example, the worth of each object can be modeled as a latent variable and a factor model built on top, treating the latent worths as indicators [e.g., 4]. This application of factor analysis can discern subtle relationships among objects, but it remains a single item analysis in terms of object comparison.
Factor models can also appear in a superficially similar model [e.g., 5]. In this strand of research, multivariate models are employed to combat social desirability bias [6]. Items are ranked within blocks wherein each item within a block is associated with a different latent dimension. An example block of size three to measure the Big Five personality traits is
I am relaxed most of the time.
I start conversations.
I catch on to things quickly.
A participant ranks the items within a block by marking one as most like me and another as least like me [7]. The first item is associated with Neuroticism, the second with Extraversion, and the third with Openness. This kind of survey is multidimensional, but researchers have no intention to posit a latent Personality factor that would account for some of the variance in the five traits.
We have reviewed some examples of paired comparison factor models from prior literature. However, these analytic methods do not try to assess an inaccessible, latent quality of objects by measuring multiple accessible facets of these objects. The models and associated topics required to perform a factor analysis of the type indicated will be introduced. A series of simulation studies will attest to the accuracy of our proposed models. Finally, our proposed methodology will be applied to a real-world dataset.
Before we start, a word on mathematical convention. For Bayesian inference we use Stan, a state-of-the-art probabilistic programming language [8]. To promote clarity, we follow Stan's mathematical conventions. Specifically, matrix Cholesky factors are lower (not upper) triangular, and for the univariate case of the normal distribution , the second argument is a standard deviation not a variance.
2. Model
2.1. Item model
Let N be the number of objects with latent worths . Let index two objects such that . Let be an odd number of response options and denote thresholds with and . Let observed data where response 1 is the most favorable for m and H the most favorable for n. Let be a continuous latent stochastic variable associated with such that when then . We model paired comparisons as
| (1) |
where is a cumulative distribution function. Both [9] and [2] described this same model, but [9] used the cumulative normal for while [2] used the logistic. This is a traditional, abstract style of presentation for a single item. Later, we will add index i in the set to accommodate I items. For example, Carob Milk might be compared to Cocoa Soy on three items: taste, texture, and color.
Our particular item model is inspired by the graded response model [10] from Item Response Theory [11]. We do not need to review the graded response model; the presentation here is self-contained, but a reader who is already familiar with it will notice the similarities. Probability is assigned to less-than inequalities and a difference is used to obtain the probability of an observation,
| (2) |
The graded response model is adapted to paired comparisons mainly through the use of particular thresholds. We assume the symmetry ; object comparison order has no effect other than a change of sign. Hence, thresholds can be completely parameterized by for where . Let the cumulative sum for . We define our paired comparison response inequality as
| (3) |
where are the cumulative thresholds arranged in descending and then ascending order ; is a discrimination parameter; and controls the scale. Since probability (Equation (2)) must be positive, we also require all . The relationship between α and s will be elaborated in the next section.
2.2. Identification
Since we only have ordinal information about worth differences , the scale is arbitrary and, given N latent worths , we can only estimate of them. Without loss of generality, we would like to center latent worths ∑μ at zero. One solution is to employ a hard constraint, . Alternately, we could use a soft constraint such as prior with some scale σ. Both solutions would result in equivalent estimates. We should choose whichever is easier to sample. Adopting the same approach used by Stan models for Item Response Theory [12], we employ a soft constraint.
The traditional response model (Equation (1)) will estimate a spread of μ limited only by the number of objects N when observations imply that objects are arranged like beads on a string, , , …, . This arbitrary scale is inconvenient for statistical modeling; software often performs better when variables are scaled to have a variance near 1.0. The s parameter in response model (Equation (3)) facilitates scaling. Regardless of the number of objects N, the distribution of μ can be standardized by using s to zoom in (or out) on μ differences. The utility of s differs from α. The discrimination parameter α quantifies how easy it is to discriminate the difference between two worths, analogous to the role this parameter plays in the graded response model [10].
Parameters s and α cannot be simultaneously identified. Two scenarios, a sensitive item comparing similar objects and an insensitive item comparing dissimilar objects, are not distinguishable. We will describe how the distribution of worths μ is standardized in the Section 2.6.
2.3. Correlation and factor models
To accommodate I items, we add an index to worths , number of response options , discriminations , thresholds , and observed data . For the polychoric correlation model, object worths are distributed with correlation [cf. 13]. The factor model takes a different tack and does not use a correlation matrix to relate items. Instead, a parameter expansion approach adds a parameter for each latent factor score [14], [15]. Object worths are modeled as
| (4) |
where is the factor-to-item loadings matrix, is the latent factor scores matrix, and is an array of zero mean, normally distributed residuals.
To recap, we have presented the likelihoods for three distinct models: a single item model (Equation (2)), a correlation model that binds I item models together with correlation matrix , and a factor model that binds I item models together with a factor structure (Equation (4)). As usual, the model log likelihood is the sum of item response (Equation (2)) log likelihoods, where are all the comparisons on item i for objects , with the sum over observations omitted for brevity. To reiterate, all three models specify the same likelihood for observed data but differ in latent, unobserved structure. This concludes our discussion of likelihood, but for Bayesian estimation we also need to specify priors distributions for all parameters, to be covered next.
2.4. Bayesian statistical inference with Stan
An open-source companion software package to this paper, pcFactorStan version 1.5, is published on the Comprehensive R Archive Network (CRAN).1 This package contains Stan implementations of the univariate, correlation, and factor models that we will continue to describe in the next sections. To use these models competently, it is crucial to have a rudimentary understanding of Stan fit diagnostics. We summarize diagnostic guidelines in Appendix A.
In this article, all reported results have met the recommended diagnostic thresholds and exhibit no geometric divergences. The key to efficient sampling is careful scaling, parameterization, and priors. These details provide insight into how the data generating processes are communicated to the Stan sampler and assist in the interpretation of parameter estimates.
2.5. Item thresholds
We drop the item index i since the following applies to all items independently. Initially, we experimented with an exponential distribution prior for thresholds. However, the sampler occasionally explored pathologically large thresholds, regardless of the rate parameter. We argue that the largest sensible threshold is . For example, if there is only one threshold and then the model (Equation (2)) would predict for all . This would be an overwhelmingly frequent use of a response category. We can a priori cap thresholds at this extreme value. Although there is often plenty of data to estimate thresholds, the Stan sampler has trouble with exactly uniform priors. Dropping the index d, as all thresholds receive the same treatment, we can parameterize and estimate the proportion . This beta distribution favors proportions near 0.09. The precise shape of the beta distribution seems to have little influence on the posterior.
2.6. Scale
Due to computational limitations, the standard multivariate normal is easier to fit than a general multivariate normal with arbitrary scale. As a first step in any analysis, we estimate on a per-item basis, ignoring any potential relationship among items. This will not affect analysis results, even for multi-item models, because the choice of s only affects worth scale, , not interpretation or inferential statistics. Some point estimate of s will suffice.
We estimate variance and standardized worths for . This permits a non-centered parameterization that separates scale and location type parameters, [16, p. 255]. By setting for some constant , the adaptive or profiled posterior tends to aim at 1.0. We fix to scale the logistic function to closely match the normal cumulative distribution function [17].
The constant j controls the strength of the adaptation. We conducted a simulation study to demonstrate this approach with 30 objects and 450 round-robin comparisons. Worths μ were drawn from for and comparisons generated with item discrimination α set to for . Object variance and α could not be much larger because there were only 30 objects; the maximum spread is obtained when comparisons imply that objects are arranged along a line like , , …, . For each condition, models were fit with j set to integers 1 to 9. Each condition was replicated 4 times with different random seeds.
The results are displayed in Fig. 1. The larger error in the upper right of the panel evidence that this is a mild correction. As j increases to 5, the error in the upper right decreases to below 0.2 all the way to the corner. Accuracy seemed adequate with and did not improve much with . Models in the lower left are never recovered accurately because the discrimination is so poor and variance so small that most of the comparisons obtain an endorsement of equal or are contradictory. We did not explore ; as j increases extreme posterior curvature will eventually cause sampling problems.
Figure 1.
Root mean squared error of recovered mean worth point estimates compared to true locations by simulated variance and item discrimination α split into nine panels by j.
2.7. Item discrimination
In the previous section, we approximately standardized the distribution of worths μ by estimating a per-item scale s. Since s and discrimination α cannot be identified simultaneously, α was fixed to 1.749 to approximate the normal cumulative distribution function [17]. We now flip this around, dropping the item index i since all items receive the same treatment. Point estimates of s are entered into the model as non-stochastic data and we estimate . We know that α is centered at 1.749 because s was tuned with that assumption. Hence, we use a prior (truncated at zero). This prior worked well for all models reported here. The information about scale or discriminations, which are two sides of the same coin, is partitioned into a fixed constant s and stochastic parameter α.
2.8. Correlation model
We use a non-centered parameterization that isolates correlation parameters [16, p. 255]. Worths where I dimension correlation matrix Cholesky factor , and are element-wise . Conceptually, we would prefer a uniform prior for the correlation matrix, but Stan often runs into trouble with exactly uniform priors. The correlation prior is fairly uniform with a slight preference toward zero polychoric correlations [18]. This correlation prior worked well for all models reported here, but can be increased if divergences are observed.
2.9. Factor model
The factor model (Equation (4)) demands considerable finesse to implement with a non-centered parameterization [16, p. 255]. Let factor scores be element-wise . When there is more than one factor () then is an F dimensional correlation matrix Choleskey factor and . Otherwise, when there is a single factor (), . The correlation prior is fairly uniform with a slight preference toward zero polychoric correlations [18]. Factor loadings are element-wise expressed as proportion . The prior worked well for all models reported here, but can be increased to if divergences are observed. Conceptually, we would prefer uniform priors for the correlation matrix and factor loadings , but Stan often runs into trouble with exactly uniform priors.
The second part of the factor model (Equation (4)) cannot use an element-wise prior because this would be inconsistent with the parameterization of λ η (i.e., scale multiplied by location). To remain consistent, we decompose ϵ into vector direction and scale , both priors applied element-wise. Scalar vector products form by for with an index of ⋅ selecting the whole vector.
Factor loadings alone are not interpretable since the total variance is not constrained to 1.0 during sampling; also, η must be taken into account. In lieu of factor loadings, λ η vectors are standardized into signed factor proportions for all , [cf. 19, Equation 2]. For identification, the first items with nonzero factor proportions are set positive and the sign of the remaining proportions are determined by the relative vector direction. Despite the priors, which attenuate factor proportions, Heywood cases can still arise where a factor accounts for practically all of the variance [cf. 20]. To stabilize sampling, a prior is placed on logit transformed proportions for all items i which load on factor f. The standard deviation of 1.2 for this prior still permitted absolute factor proportions near 1.0 while avoiding divergences.
2.10. Model fit assessment
Once observed data are fitted, how can we tell whether the model fits well? Posterior predictive checking is one way to assess whether the model is a good fit [21, p. 143]. Observed data should look similar to data generated with the fitted model, for some definition of similar. One way to measure similarity is to tabulate responses between object pairs where and apply the goodness of fit test where H is the number of response options. The problem with this approach is that the test requires a minimum frequency of five per expected cell. Some datasets may partially satisfy this requirement, but a frustrating case would be 25 objects and 1200 round-robin comparisons, in which case none of the object pairs could be evaluated.
Due to the troublesome minimum cell frequency requirement, we instead recommend leave-one-out cross-validation. The naïve approach of re-fitting the model over-and-over with each observation left out would be extremely time consuming. However, per-observation statistics can be efficiently approximated using Pareto-smoothed importance sampling [22]. A Pareto shape parameter k is assigned to each observation. Recommended thresholds guide the interpretation of k. Data with are plausible with respect to the posterior. Data with are possible outliers. When then these data are quite unexpected with respect to the posterior. Finally, any values signal that the model is such a poor fit to the data that the model's predictive density could not be estimated.
3. Simulation studies
3.1. Preliminaries
Simulation studies are often used to validate that a statistical model can accurately recover point estimates of data generating parameters along with accurate estimates of the precision of these recovered parameters. Here we address these questions, and also the selection of which objects to compare, a facet of paired comparison data that is usually unmodelled or regarded as exogenous. If specimens from two sets of objects are never compared then we can only rank within the sets, not between them. Hence, the choice of which objects to compare is germane to the study of our statistical model performance.
A recently acquired dataset prompted the development of the paired comparison factor model. This dataset compared physical activities (i.e., objects) on certain criteria. Sometimes the question of which objects to compare is decided in advance. Round-robin comparisons are the simplest approach, but the number of pairings grows in proportion to number of objects squared, . Another scheme is the single-elimination tournament; the loser of each match-up is not given the opportunity to compete again. Pairings might also be selected by an adaptive testing algorithm [e.g., 23]. When our data were collected, participants themselves decided which physical activities to compare. Many object pairs were not compared. Therefore, we begin with two studies to examine the effect of pairing choice and sample size on worth estimates. It is likely that these questions have already been addressed in prior literature, but we re-examine them here briefly since multi-item models critically depend on single item models.
3.1.1. Sample size by connectivity
We look at the accuracy of latent worth recovery for different numbers of objects and different connectivity regimes. A graph is induced if we regard objects as vertices and paired comparisons as undirected edges. Graphs were generated for two conditions, round-robin and two level, for 15 to 100 objects. A two level graph is generated as follows. Initially, to ensure that all vertices are connected, edges are added from the first vertex to all the other vertices. Thereafter, pairs of edge vertices are drawn from discretized and distributions. The intuition is that the edges will tend to connect a small subset of vertices near the root of the tree to leaf vertices. These vertex connections are similar to the pairs that you might observe in a single-elimination tournament, but with more continuous control over edge non-uniformity. Fig. 2 exhibits example graphs with 15 objects each. Here, two level graph shape parameters were set to 0.64 and 0.24, approximating the distribution of pairings found in our physical activities data.
Figure 2.
Round-robin (left) and two level graph with shape parameters 0.64 and 0.24 (right).
Data with the sample size (i.e., number of edges) set to 300 + 5 times the number of objects were simulated with discrimination , scale , and two thresholds Δ at 0.8 and 1.6. These parameters produced roughly equal proportions of responses, that is, data from which latent worths should be easy to recover. In the parameter recovery phase, worths μ, thresholds Δ, and discrimination α were estimated; worths were simulated as standard normally distributed so there was no need to estimate s. Five Monte Carlo trials were conducted per condition. Both graph configurations performed about the same for up to 30 objects (Fig. 3). For 35 or more objects, a two level graph offered more information than round-robin.
Figure 3.
Mean correlation between true μtrue and recovered mean point estimates of worths μ by round-robin (solid red) and two level graph (dashed blue). Whiskers show maximum and minimum correlation.
3.1.2. Effect of non-uniformity
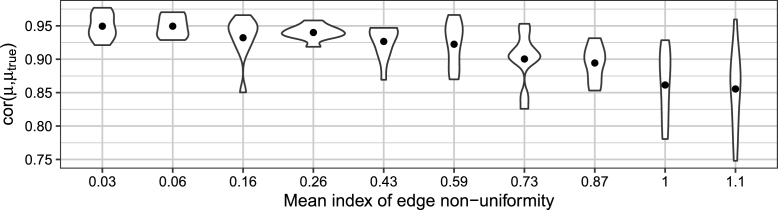
In the previous study, we considered two level graphs with shape parameters 0.64 and 0.24. To provide more information about latent worth recovery performance, we consider two level graphs with shapes and for with 10 Monte Carlo trials per condition. Data generation and recovery of item parameters were the same as in the previous study. Simulations involved about 26 objects with 390 paired comparisons.
As a data cleaning step, vertices (i.e., objects) with fewer than 11 edges and not connected to 2 or more different vertices were excluded. For example, if object A was compared to at least two other objects, B and C, then A was retained. The rationale is that, although little may be learned about A, there may be a transitive relationship, such as , by which the model can infer that . After data cleaning, 91% of the trials had 25 or more objects and no trial had fewer than 21 objects. Non-uniformity was approximated by application of Kullback-Leibler divergence (Equation (B.1)) to counts of how many times each vertex was involved in an edge. Fig. 4 shows the results. In comparison, our physical activities dataset had a non-uniformity index of 0.3.
Figure 4.
Distribution of correlation between true μtrue and recovered mean point estimates of worths μ by non-uniformity.
3.2. Model validation
Evidence from our single item studies suggest that point estimates of latent worths can be recovered with reasonable accuracy in a variety of conditions. However, we have not examined the accuracy of per-parameter marginal posterior distributions, often summarized as standard errors. Simulation-based calibration was originally developed to check the accuracy of inference algorithms [24]. However, the same method can also be used to calibrate models [25]. The core idea of simulation-based calibration is that averaging the posterior distributions fit from observations simulated from the prior predictive distribution will always recover the prior, . Using this idea, we simulate one parameter from the prior distribution , generate data , sample R parameters from these data , and then compute the number of posterior samples larger than the prior sample . We repeat this process L times to obtain rank statistics, displayed as a histogram. The process works similarly when θ is a vector and produces per-parameter histograms.
Non-uniform histogram appearance indicates that simulations are incorrect or our model is inconsistent. We sort histograms by a non-uniformity index (Equation (B.1)) and visually inspect the least uniform histograms by parameter family. To aid in interpretation, a shaded envelope is superimposed over the plot to show 99% of the variation expected from a uniform histogram.
3.2.1. Common conditions for next studies
To avoid repetition, specifications common to the following simulation-based calibration studies are reported here. Parameter histograms were produced with draws from the prior predictive distribution with samples per chain. Object pairings were generated using a random two level graph with shape parameters 0.64 and 0.24. For data generation, item discrimination , and two thresholds and . Scale s was set to 1; since worths μ were simulated as standard normally distributed, there was no need to estimate scale s. For parameter recovery, the priors given in Section 2 were used.
3.2.2. Simulation-based calibration studies
The single item model was calibrated with data generated for 25 objects and 400 comparisons. Maximum non-uniformity (Equation (B.1)) was 0.34 and visual inspection revealed no suspicious patterns. The data generating prior for the thresholds (e.g., for ) did not match the parameter recovery prior on the raw threshold proportions ι (see Section 2.5). However, no distortion in the marginal posteriors was evident.
The correlation model was calibrated with data generated for 50 objects, 500 comparisons, and 3 items. The data generating prior for the correlation matrix was the same as the parameter recovery prior (i.e., from Section 2.8). Maximum non-uniformity (Equation (B.1)) was 0.43. Thresholds exhibited some faint bias; estimated item thresholds were slightly larger than simulated true values (Fig. 5). That we find some bias in the thresholds here is not surprising considering the mismatch in distribution between data generation and parameter recovery. In contrast, both discrimination α and correlation parameters did not exhibit any visually striking non-uniformity.
Figure 5.
Representative simulation-based calibration histograms of parameter families from the correlation model.
A single factor model was calibrated with data generated for 50 objects, 500 comparisons, and 4 items. Signed factor proportions were simulated from a logistic transformed normal,
| (5) |
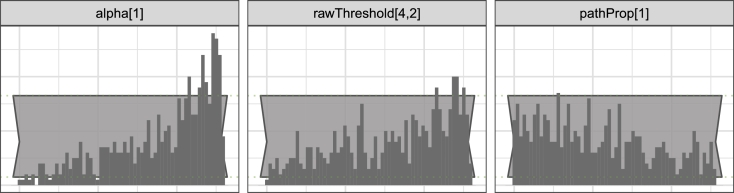
with . Maximum non-uniformity (Equation (B.1)) was 0.54. Discrimination α exhibited pronounced bias; estimated α were larger than simulated true values (Fig. 7). This distortion is due to per-item worth μ distributions tending to have a variance of less than 1.0. Smaller absolute scores are favored by the prior; we could not contrive how to fix the total variance to 1.0 without inviting divergences or other sampling problems. As seen in pathProp[1], factor proportions were slightly biased toward zero, possibly because data were simulated neglecting the priors. The slight threshold bias found in the correlation model is present here as well.
Figure 7.
Representative simulation-based calibration histograms for families of parameters from the single factor model.
A two factor model was calibrated with data generated for 50 objects, 500 comparisons, and 6 items. Signed factor proportions were simulated from a logistic transformed normal (Equation (5)) with and 0.5 for the first and second factors, respectively, with factor loading pattern shown in Fig. 6. Data were generated with factor correlation matrix , the same distribution as the parameter recovery prior (Section 2.9). Maximum non-uniformity (Equation (B.1)) was 0.57. Both the discrimination α and threshold parameters exhibited approximately the same severity of bias as found in the single factor model. In addition, the factor correlation parameter psi[1] may have exhibited faint overdispersion (Fig. 8).
Figure 6.
Path diagram for two factor model. Per-item unique variance were not shown.
Figure 8.
Representative simulation-based calibration histograms for families of parameters from the two factor model.
3.3. Summary
First we examined the accuracy of point estimates by sample size and connectivity. Thereafter, we evaluated the accuracy of the marginal posterior distributions of the parameters. Both point estimates and marginal posterior were recovered with adequate precision. Source code for all simulations is available at https://osf.io/23adh.
4. Application
4.1. Ranking physical activities
Flow is a psychological state, also known as optimal experience, where a person is fully immersed and focused on the task at hand [26]. While flow has been vigorously studied since the 1970s, the primary focus of this body of research has been on the person who experiences flow. There was even an early suggestion that “activity and experience are ultimately independent of each other” [27, p. 85]. However, it is now generally recognized that the activity does matter and some work has begun to examine the interaction between activity and flow [e.g., 28].
We suspected that activities have latent flow propensities. It may be easier to enter into flow while playing golf than while running on a treadmill, averaging across participants. For people who are primarily interested in the experience of flow rather than pursuit of a specific activity, what information can we provide to guide activity selection?
4.2. Method
4.2.1. Measure
We adapted flow-related items to a paired activity comparison format. Our items were based on the Flow State Scale-2 and Dispositional Flow Scale-2 measures [29], supplemented with items inspired by [30].
4.2.2. Procedure
Participants submitted two activities of their choice using free-form input. These activities were substituted into P1 and P2 placeholders in item templates. For example, Item predict prompted, “How predictable is the action?” with response options:
is much more predictable than
.
is somewhat more predictable than
.
Both offer roughly equal predictability.
is somewhat more predictable than
.
is much more predictable than
.
If the participant selected running and golf then the item was rendered as
is much more predictable than
.
is somewhat more predictable than
.
Both offer roughly equal predictability.
is somewhat more predictable than
.
is much more predictable than
.
A somewhat more response was scored 1 or -1 and much more scored 2 or -2. A tie (i.e., roughly equal) was scored as zero. Participants were asked to respond to 16 items.
4.3. Results
Across all 1015 participants, 87 physical activities were named. Hence, this study can be regarded as an incomplete design because each participant only compared two of these 87 activities. Excluding 57 missing responses, this amounted to 16183 observations. We analyzed these data using functions provided by the pcFactorStan package. Raw data and line-by-line R code for the same analysis is available as part of the pcFactorStan manual. Here we briefly report the highlights.
A graph is induced if we regard activities as vertices and paired comparisons as undirected edges. Following the recommended data cleaning procedure, we excluded vertices not part of the largest connected component [31]. Focusing on the remaining vertices, we excluded those connected by fewer than 11 edges and not connected to 2 or more different vertices. These data cleaning steps are built into pcFactorStan. Data reduced to 993 participants who compared 61 physical activities (15832 observations). The connectivity graph of these comparisons obtained a non-uniformity index (Equation (B.1)) of 0.3. We estimated the scale s for each item with the default settings (i.e., ). Two items, goal1 and feedback1, obtain a small scale and were excluded from further analyses. Remaining scale point estimates s ranged from 0.26 to 0.71 with a median of 0.46.
The correlation model was fit to the remaining 14 items. Median polychoric correlations between items are exhibited in Fig. 9. Correlations with an 80% interval crossing zero are omitted. Based on this plot and theoretical considerations, we decided to exclude Items spont, control, evaluated, and waiting from the factor model. We acknowledge that this decision may seem ad hoc; due to space constraints, we could not include the complete rationale for why these items, and not others, were excluded. A detailed justification will be provided in a forthcoming substantive article. Fig. 10 exhibits item response curves (Equation (2)) for the retained items. We plot response curves from the correlation model and not the factor model because the factor model is expected to recover biased discrimination α estimates (see Section 3.2.2). The differing x-axes show how the scale s parameter zooms in or out on the standardized worth scores. Since somewhat responses were rarely the most likely choice, the addition of another response category, such as expansion to a 4-point symmetric scale, is unlikely to improve measurement efficiency [32].
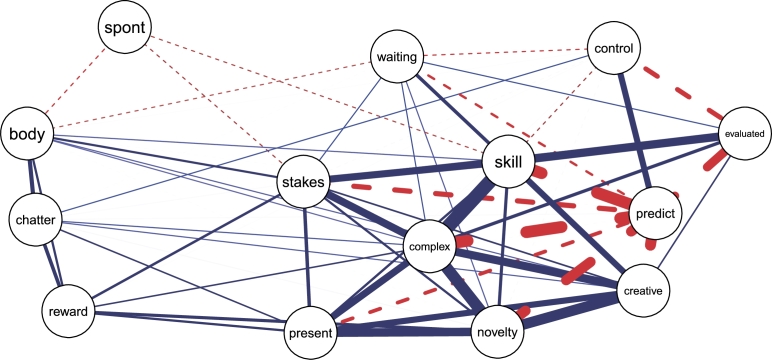
Figure 9.
Visualization of the item polychoric correlation matrix. Blue solid edges indicate positive correlations and red dashed edges indicate negative correlations. Edge thickness is proportional to absolute correlation magnitude.
Figure 10.
Posterior distribution of item response curves conditional on the difference in latent worth (Equation (2)). Responses curve probability peaks from left to right are much more, somewhat more, equal, somewhat less, and much less.
A single factor model was fit to the remaining items. Once sampling was complete, the loo package was used to screen for outliers. All Pareto shape parameters k were less than 0.5, indicating adequate fit [22]. Another way to assess model fit is to examine the residual correlation matrix. If the factor model fits well then residual correlations should be indistinguishable from zero. Fig. 11 suggests that there is room for improvement. For example, Item chatter might be refined since it is implicated in two residual correlations.
Figure 11.
Mean residual correlations with 80% intervals that do not cross zero.
Signed factor proportions are exhibited in Fig. 12. The two weakest items here, chatter and body, are also afflicted by residual correlations (Fig. 11). Factor scores are exhibited in Fig. 13, excluding activities with a sample size of 10 or less. Martial arts, climbing, and snow skiing were estimated to have the highest flow propensities while elliptical and walking were estimated to have the lowest.
Figure 12.
Mean signed proportion of variance accounted for by latent flow propensity factor with 80% uncertainty intervals.
Figure 13.
Mean flow propensity factor scores for activities connected by 11 or more edges with 80% uncertainty intervals.
5. Discussion
Paired comparison models have been in use for about a century, but mainly to rank a single object facet. Here we introduce an exploratory factor model for multiple indicator paired comparison data. We start with the item response model and discuss identification issues. Correctness of the model specifications is demonstrated by simulation. Thereafter, a real-world dataset is analyzed.
The models described here are vanilla, bare-bones versions that would benefit from more modeling options. For example, it is often desirable to investigate measurement invariance [33], [34]. This capability is a planned addition to the pcFactorStan package, to permit multiple groups with some parameters constrained equal across groups. In addition, it may be useful to allow structural equation modeling [e.g., 35], object covariates, and judge-specific effects [36], [37]. Of course the use of paired comparison items does not preclude other types of measurement. We anticipate models that incorporate both relative and absolute judgments simultaneously.
Our item model (Equation (2)) is fairly insensitive to the difference between data indicating that objects have equal worth and contradictory data such as . Prior work has used the degree of transitivity violation as a diagnostic indicator [38]. Moreover, in some contexts, violations of transitivity may be intrinsic to the data generating process such as a home team advantage for soccer matches [39]. We leave more nuanced handling of measurement error to future work.
The paired comparison factor model opens up new opportunities for measurement. Paired comparisons may be easier for participants to respond to [40] and exhibit more reliability than ratings of single objects [41]. One domain where a factor model might profitably be employed is in the assessment of pain. Pain is thought to be a multidimensional construct with physiologic, sensory, affective, cognitive, behavioral, and sociocultural facets [42]. However, attempts to measure pain with paired comparisons have employed unidimensional models [43], [44], [45].
The difficulty of interpretation is sometimes cited as a cost to more complex models [46]. However, complex processes demand complex models [47] and an effort to improve model fit might yield insight into overlooked nuances of the data generating process. Given the relative simplicity of the models described here, additional complexity seems more likely to hone interpretation rather than hinder it.
Declarations
Author contribution statement
J.N. Pritikin: Conceived and designed the analysis; Analyzed and interpreted the data; Contributed analysis tools or data; Wrote the paper.
Funding statement
This work was supported by National Institutes of Health (R01-DA018673) and Center for Information Technology (US) (R25- DA026119).
Competing interest statement
The authors declare no conflict of interest.
Additional information
Supplementary content related to this article has been published online at https://doi.org/10.1016/j.heliyon.2020.e04821.
No additional information is available for this paper.
Footnotes
This research was supported in part by National Institute of Health grants R01-DA018673 and R25-DA026119 (PI Neale).
Supplementary material
The following Supplementary material is associated with this article:
Supporting material about Stan's model fitting diagnostics and details of our index of uniformity.
References
- 1.Spearman C. “General Intelligence,” objectively determined and measured. Am. J. Psychol. 1904;15(2):201–292. [Google Scholar]
- 2.Bradley R.A., Terry M.E. Rank analysis of incomplete block designs: I. The method of paired comparisons. Biometrika. 1952;39(3/4):324–345. [Google Scholar]
- 3.Davidson R.R., Bradley R.A. Multivariate paired comparisons: the extension of a univariate model and associated estimation and test procedures. Biometrika. 1969;56(1):81–95. [Google Scholar]
- 4.Maydeu-Olivares A., Böckenholt U. Structural equation modeling of paired-comparison and ranking data. Psychol. Methods. 2005;10(3):285. doi: 10.1037/1082-989X.10.3.285. [DOI] [PubMed] [Google Scholar]
- 5.Cheung M.W.-L. Recovering preipsative information from additive ipsatized data: a factor score approach. Educ. Psychol. Meas. 2006;66(4):565–588. [Google Scholar]
- 6.King L.M., Hunter J.E., Schmidt F.L. Halo in a multidimensional forced-choice performance evaluation scale. J. Appl. Psychol. 1980;65(5):507. [Google Scholar]
- 7.Brown A., Maydeu-Olivares A. Item response modeling of forced-choice questionnaires. Educ. Psychol. Meas. 2011;71(3):460–502. [Google Scholar]
- 8.Carpenter B., Gelman A., Hoffman M., Lee D., Goodrich B., Betancourt M., Brubaker M.A., Guo J., Li P., Riddell A. Stan: a probabilistic programming language. J. Stat. Softw. 2017;76(1):1–32. doi: 10.18637/jss.v076.i01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Thurstone L.L. A law of comparative judgment. Psychol. Rev. 1927;34(4):273. [Google Scholar]
- 10.Samejima F. Estimation of latent ability using a response pattern of graded scores. Psychometrika. 1969;34(1):1–97. [Google Scholar]
- 11.Baker F.B., Kim S.H. 2nd edition. CRC Press; 2004. Item Response Theory: Parameter Estimation Techniques. [Google Scholar]
- 12.Furr D.C. 2017. edstan: Stan Models for Item Response Theory.https://CRAN.R-project.org/package=edstan r package version 1.0.6. [Google Scholar]
- 13.Olsson U. Maximum likelihood estimation of the polychoric correlation coefficient. Psychometrika. 1979;44(4):443–460. [Google Scholar]
- 14.Gelman A. Parameterization and Bayesian modeling. J. Am. Stat. Assoc. 2004;99(466):537–545. [Google Scholar]
- 15.Ghosh J., Dunson D.B. Default prior distributions and efficient posterior computation in Bayesian factor analysis. J. Comput. Graph. Stat. 2009;18(2):306–320. doi: 10.1198/jcgs.2009.07145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Stan Development Team . 2019. Stan User's Guide 2.19.http://mc-stan.org/ [Google Scholar]
- 17.Savalei V. Logistic approximation to the normal: the KL rationale. Psychometrika. 2006;71(4):763–767. [Google Scholar]
- 18.Lewandowski D., Kurowicka D., Joe H. Generating random correlation matrices based on vines and extended onion method. J. Multivar. Anal. 2009;100(9):1989–2001. [Google Scholar]
- 19.Gelman A., Goodrich B., Gabry J., Vehtari A. R-squared for Bayesian regression models. Am. Stat. 2019;73(3):307–309. [Google Scholar]
- 20.Martin J.K., McDonald R.P. Bayesian estimation in unrestricted factor analysis: a treatment for Heywood cases. Psychometrika. 1975;40(4):505–517. [Google Scholar]
- 21.Gelman A., Carlin J.B., Stern H.S., Dunson D.B., Vehtari A., Rubin D.B. 3rd edition. CRC Press; 2013. Bayesian Data Analysis. [Google Scholar]
- 22.Vehtari A., Gelman A., Gabry J. Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Stat. Comput. 2017;27(5):1413–1432. [Google Scholar]
- 23.Wainer H., Dorans N.J., Flaugher R., Green B.F., Mislevy R.J. Routledge; 2000. Computerized Adaptive Testing: A Primer. [Google Scholar]
- 24.Talts S., Betancourt M., Simpson D., Vehtari A., Gelman A. Validating Bayesian inference algorithms with simulation-based calibration. 2018. arXiv:1804.06788
- 25.Betancourt M. Probabilistic modeling and statistical inference. 2019. https://betanalpha.github.io/assets/case_studies/modeling_and_inference.html Retrieved July 15, 2019 from.
- 26.Csikszentmihaly M. 1975. Beyond Boredom and Anxiety: Experiencing Flow in Work and Play. [Google Scholar]
- 27.Csikszentmihalyi M., Csikszentmihalyi I.S. Cambridge University Press; 1988. Optimal Experience: Psychological Studies of Flow in Consciousness. [Google Scholar]
- 28.Schmidt J.A., Shernoff D.J., Csikszentmihalyi M. Applications of Flow in Human Development and Education. Springer; 2014. Individual and situational factors related to the experience of flow in adolescence; pp. 379–405. [Google Scholar]
- 29.Jackson S.A., Eklund R.C. Assessing flow in physical activity: the flow state scale–2 and dispositional flow scale–2. J. Sport Exerc. Psychol. 2002;24(2):133–150. [Google Scholar]
- 30.Kotler S. Houghton Mifflin Harcourt; 2014. The Rise of Superman: Decoding the Science of Ultimate Human Performance. [Google Scholar]
- 31.Hopcroft J., Tarjan R. Algorithm 447: efficient algorithms for graph manipulation. Commun. ACM. 1973;16(6):372–378. [Google Scholar]
- 32.K.M. Schmidt, More is not better: rescoring combinations for lengthy rating scales, paper presented at the 2010 International Conference on Measurement (Sep. 2010).
- 33.Verhagen A.J., Fox J.P. Bayesian tests of measurement invariance. Br. J. Math. Stat. Psychol. 2013;66(3):383–401. doi: 10.1111/j.2044-8317.2012.02059.x. [DOI] [PubMed] [Google Scholar]
- 34.Verhagen A.J., Levy R., Millsap R.E., Fox J.-P. Evaluating evidence for invariant items: a Bayes factor applied to testing measurement invariance in IRT models. J. Math. Psychol. 2016;72:171–182. [Google Scholar]
- 35.Muthén B., Asparouhov T. Bayesian structural equation modeling: a more flexible representation of substantive theory. Psychol. Methods. 2012;17(3):313–335. doi: 10.1037/a0026802. [DOI] [PubMed] [Google Scholar]
- 36.Tsai R.-C., Böckenholt U. Two-level linear paired comparison models: estimation and identifiability issues. Math. Soc. Sci. 2002;43(3):429–449. [Google Scholar]
- 37.Schauberger G., Tutz G. BTLLasso: a common framework and software package for the inclusion and selection of covariates in Bradley-Terry models. J. Stat. Softw. 2019;88(9):1–29. [Google Scholar]
- 38.Mazzuchi T.A., Linzey W.G., Bruning A. A paired comparison experiment for gathering expert judgment for an aircraft wiring risk assessment. Reliab. Eng. Syst. Saf. 2008;93(5):722–731. [Google Scholar]
- 39.Cattelan M. Models for paired comparison data: a review with emphasis on dependent data. Stat. Sci. 2012;27(3):412–433. [Google Scholar]
- 40.Graus M.P., Willemsen M.C. Proceedings of the 9th ACM Conference on Recommender Systems. ACM; 2015. Improving the user experience during cold start through choice-based preference elicitation; pp. 273–276. [Google Scholar]
- 41.Jones N., Brun A., Boyer A. Proceedings of the 2011 IEEE/WIC/ACM International Conferences on Web Intelligence and Intelligent Agent Technology. vol. 1. IEEE Computer Society; 2011. Comparisons instead of ratings: towards more stable preferences; pp. 451–456. [Google Scholar]
- 42.McGuire D.B. Comprehensive and multidimensional assessment and measurement of pain. J. Pain Symp. Manag. 1992;7(5):312–319. doi: 10.1016/0885-3924(92)90064-o. [DOI] [PubMed] [Google Scholar]
- 43.Snow A.L., Weber J.B., O'Malley K.J., Cody M., Beck C., Bruera E., Ashton C., Kunik M.E. NOPPAIN: a nursing assistant-administered pain assessment instrument for use in dementia. Dement. Geriatr. Cogn. Disord. 2004;17(3):240–246. doi: 10.1159/000076446. [DOI] [PubMed] [Google Scholar]
- 44.Matthews J.N.S., Morris K.P. An application of Bradley-Terry-type models to the measurement of pain. J. R. Stat. Soc., Ser. C, Appl. Stat. 1995;44(2):243–255. [Google Scholar]
- 45.Morris K.P., Hughes C., Hardy S.P., Matthews J.N.S., Coulthard M.G. Pain after subcutaneous injection of recombinant human erythropoietin: does emla cream help? Nephrol. Dial. Transplant. 1994;9(9):1299–1301. [PubMed] [Google Scholar]
- 46.Vehtari A. Parsimonious principle vs integration over all uncertainties. 2018. https://statmodeling.stat.columbia.edu/2018/07/26/parsimonious-principle-vs-integration-uncertainties/ Retrieved July 5, 2019 from.
- 47.Rasmussen C.E., Ghahramani Z. Advances in Neural Information Processing Systems. 2001. Occam's razor; pp. 294–300. [Google Scholar]
Further reading
- 49.Betancourt M. Diagnosing suboptimal cotangent disintegrations in Hamiltonian Monte Carlo. 2016. arXiv:1604.00695 arXiv e-prints.
- 50.Stan Development Team . 2018. RStan: The R Interface to Stan.http://mc-stan.org/ r package version 2.18.2. [Google Scholar]
- 51.Vehtari A., Gelman A., Simpson D., Carpenter B., Bürkner P.-C. Rank-normalization, folding, and localization: an improved for assessing convergence of MCMC. 2019. arXiv:1903.08008 arXiv e-prints.
- 52.Marhuenda Y., Morales D., Pardo M. A comparison of uniformity tests. Statistics. 2005;39(4):315–327. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting material about Stan's model fitting diagnostics and details of our index of uniformity.