Chemical Exchange

Abstract

The phenomenon of chemical or conformational exchange in NMR spectroscopy has enabled detailed characterization of time-dependent aspects of biomolecular function, including folding, molecular recognition, allostery, and catalysis, on time scales from μs-s. Importantly, NMR methods based on a variety of spin relaxation parameters have been developed that provide quantitative information on interconversion kinetics, thermodynamic properties, and structural features of molecular states populated to a fraction of a percent at equilibrium and otherwise unobservable by other NMR approaches. The ongoing development of more sophisticated experimental techniques and the necessity to apply these methods to larger and more complex molecular systems engenders a corresponding need for theoretical advances describing such techniques and facilitating data analysis in applications. The present Review surveys current aspects of the theory of chemical exchange, as utilized in ZZ-exchange; Hahn and Carr-Purcell-Meiboom-Gill (CPMG) spin-echo; and R_1ρ, chemical exchange saturation transfer (CEST), and dark state saturation transfer (DEST) spin-locking experiments. The Review emphasizes theoretical results for kinetic topologies with more than two interconverting states, both to obtain compact analytical forms suitable for data analysis and to establish conditions for distinguishability between alternative kinetic schemes.

1. Introduction

Knowledge about the dynamics of proteins and nucleic acids can assist in understanding and modulating their functions. A significant part of research in structural biology is devoted to exploration of the conformations of biomolecules. Each conformation corresponds to a specific energetic state; the equilibrium populations of various conformations depend on their conformational energies. “Conformational dynamics” describes the nature and distribution of various conformations of a given biomolecule. Equilibrium between populations is established and maintained by kinetic processes, which correspond to paths between the individual conformational states. For two conformations 1 and 2 with populations p₁ and p₂, the corresponding rate constants for conversion between the state satisfy p₂/p₁ = k₁₂/k₂₁. The sum of all populations is unity and does not contain any temporal information; the magnitudes of the rate constants is not defined by the energetic states of the conformational ensembles. The sum k₂₁ + k₁₂ contains temporal information and is defined by the energy barriers along the path connecting the two states. This kinetic information adds the dimension of time to the description of a biomolecule (Ban, Smith, de Groot, Griesinger, & Lee, 2017), which would define the term “dynamics” in a narrower sense. This simple example can be extended to arbitrary numbers of conformational or chemical states.

Dynamic processes in biomolecules occur over a wide range of time scales. This review focuses on NMR methods to study kinetic processes in the μs-s range, which include major conformational changes, molecular recognition, folding and allosteric events. Such phenomenal are generally classified as “chemical exchange” or “conformational exchange” in NMR spectroscopy. Chemical exchange in the μs-ms range is characterized by CPMG and R_1ρ relaxation dispersion and related methods, such as CEST and DEST. Slower chemical exchange in the 10²-10³ ms range, limited by longitudinal relaxation, is characterized by ZZ-exchange or EXSY methods (Farrow, Zhang, Forman-Kay, & Kay, 1995; Furukawa, Konuma, Yanaka, & Sugase, 2016; Montelione & Wagner, 1989; A. G. Palmer, 2014). Faster processes in the ps-ns range mostly can be attributed to more local intramolecular motions. A number of other NMR techniques are used to study these processes, including determination of order parameters, correlation times, residual dipolar couplings, chemical shifts, and cross-correlated relaxation (Charlier, Cousin, & Ferrage, 2016; Kovermann, Rogne, & Wolf-Watz, 2016; A. G. Palmer, 2004; Salmon & Blackledge, 2015). The kinetics of processes too slow for application of the above methods can be studied with real-time NMR spectroscopy (Meier & Ernst, 1979; Rennella & Brutscher, 2013; Wagner et al., 1985).

The kinetics of protein folding occurs over a large range of timescales and protein folding therefore is an ideal problem for application of NMR spectroscopy (Meinhold & Wright, 2011; Zhuravleva & Korzhnev, 2017). Unfolded states of stably folded proteins are closely related to the ensembles of states populated by intrinsically disordered proteins, for which specialized NMR techniques have been developed (Brutscher et al., 2015; Dyson & Wright, 2004; Salvi, Abyzov, & Blackledge, 2017). NMR is an ensemble method uniquely providing multiple types of data that can be highly resolved in many different customized ways. Temperature, pressure, and solution conditions can be changed as physical parameters to alter the energetic landscapes of proteins to study folding kinetics (Roche, Royer, & Roumestand, 2017; Tugarinov, Libich, Meyer, Roche, & Clore, 2015). NMR spectroscopy is usually thought of an equilibrium method (Ban et al., 2017); however, it can be combined with transient methods in order to study protein folding intermediates. Rapid mixing (Fazelinia, Xu, Cheng, & Roder, 2014; Manoharan, Furtig, Jaschke, & Schwalbe, 2009; Roder, Elove, & Englander, 1988; Udgaonkar & Baldwin, 1988), light activation (Nash et al., 2011; Rubinstenn et al., 1999), and most recently pressure-jump (Charlier, Courtney, Alderson, Anfinrud, & Bax, 2018; Furtig et al., 2007; Kremer et al., 2011) methods, classical physical chemistry techniques, have been adapted to NMR spectroscopy. Relaxation dispersion NMR has been applied to study folding intermediates of SH3 domains (Roche et al., 2017; Tollinger, Skrynnikov, Mulder, Forman-Kay, & Kay, 2001; Tugarinov et al., 2015), PBX-homeodomain (Farber, Slager, & Mittermaier, 2012), villin headpiece (Grey et al., 2006; Tang, Grey, McKnight, Palmer, & Raleigh, 2006), the FF domain from HYPA/FBP11 (Korzhnev, Religa, Lundstrom, Fersht, & Kay, 2007), and apo-myoglobin (Dyson & Wright, 2017; Meinhold & Wright, 2011). While amyloid disease and misfolding is mostly studied by other techniques, including solid-state NMR (Chiti & Dobson, 2006), examples for systems that have been studied by solution NMR relaxation dispersion include human ADA2h (Pustovalova, Kukic, Vendruscolo, & Korzhnev, 2015), beta2-microglobulin (Franco, Gil-Caballero, Ayala, Favier, & Brutscher, 2017), amyloid β protofibril interactions (Fawzi, Libich, Ying, Tugarinov, & Clore, 2014), and transthyretin misfolding(Lim, Dyson, Kelly, & Wright, 2013).

For intramolecular μs-ms dynamics, circumscribed structural features causing the exchange process can be frequently identified. These include as examples disulfide bond isomerization in basic pancreatic trypsin inhibitor (Grey, Wang, & Palmer, 2003) and altered coordination of a Zn ion by cysteine sulfides (Deshmukh, Tugarinov, Appella, & Clore, 2018). For FGFR kinase 2, a major drug target, the ability of gain-of function cancer mutant K659E to modulate μs-ms dynamics of the DFG motif and surrounding residues has been revealed by CPMG relaxation dispersion (Chen et al., 2017). Differences in flexibility between S. aureus wild-type DHFR and the methicillin-resistant S1 DHFR mutant were identified by linebroadening and CPMG relaxation dispersion (Sahasrabudhe et al., 2017). The ability of an external allosteric agent to influence internal dynamic processes was demonstrated for imidazole glycerol phosphatase synthase (Lisi et al., 2016) and for dihydrofolate reductase (Oyen et al., 2017).

Due to extended search interactions between protein and ligands, intermolecular processes can occur on intermediate or slow timescales. Examples the initial formation of an X-dimer in the E-Cadherin dimerization process (Y. Li et al., 2013), GB1(A34F) dimerization (Jee, Ishima, & Gronenborn, 2008), formation of a complex between the intrinsically disordered protein MKK4 and MAPK p38α (Delaforge et al., 2018), profilin self-assembly (Rennella, Sekhar, & Kay, 2017), and amyloid β protofibril interactions (Fawzi et al., 2014).

Chemical exchange methods pioneered in applications to proteins increasingly are being extended to investigations of kinetic processes in nucleic acids(Xue et al., 2015). The bases of the experimental methods are unchanged, but the different spin systems and topologies must be considered in optimization of these methods for nucleic acids. For example, rapid imino hydrogen exchange with solvent in nucleic acids makes the imino ¹H and ¹⁵N spins in nucleic aids less suitable than the protein ¹H^N and ¹⁵N amide spins in proteins as probes of chemical exchange and RNA completely lacks methyl groups, which also are powerful probes in proteins. Recent applications include a series of relaxation dispersion studies of base-pair rearrangement in DNA by Al-Hashimi and coworkers, and detailed characterization of the fluoride riboswitch by Zhang and coworkers (Kimsey et al., 2018; Szymanski, Kimsey, & Al-Hashimi, 2017; Zhao, Guffy, Williams, & Zhang, 2017).

Two-site exchange is the paradigmatic example of the effects of kinetic processes on NMR phenomena and this simple system allows derivation of exact or nearly exact theoretical descriptions. As consequence of both the theory and methods available, most experimental investigations of chemical exchange have utilized the 2-site model to interpret experimental data. Beyond the 2-site assumption, the majority of established N-site processes is based on 3-site linear kinetic schemes. Examples have been established in the area of protein folding (Farber et al., 2012; Grey et al., 2006; Tang et al., 2006; Tugarinov et al., 2015) as well as intermolecular processes (Rennella et al., 2017). Kinetically more complex models have been rarely studied by relaxation dispersion to date. Deshmukh and coworkers have suggested a 4-site star scheme for binding kinetics in HIV-1 protease - Gag interactions (Deshmukh, Tugarinov, Louis, & Clore, 2017) and a triangular scheme for the coordination of a zinc ion by thioester groups in NCp7 (Deshmukh, Ghirlando, & Clore, 2014). A quadratic scheme has been used for the folding of a FynSH3 triple mutant with the chaperonin GroEL (Libich, Tugarinov, & Clore, 2015). A recent study on Watson-Crick mismatches in nucleic acids features R_1ρ data that was conclusively described a triangular scheme, but not a 4-site star scheme (Kimsey et al., 2018). Relatively few research groups have generated the majority of examples for N-site exchange probed by relaxation dispersion. This suggests that the main reason for the limited number of examples are practical difficulties to record or process the data, rather than rarity of interesting biological processes. The possibility of N-site (N > 2) exchange is being raised in some studies, warranting further research once appropriate methods are available (Jee et al., 2008). Intramolecular dynamic processes as well as an intramolecular strand-swapping have been identified in separate classical cadherin subtypes (Y. Li et al., 2013; Miloushev et al., 2008). A combination of both phenomena might occur in some cadherin proteins, yielding an N-site exchange situation. Four-site exchange processes have been suggested for unfolding of carbonic anhydrase (Uversky & Ptitsyn, 1996). A theoretical study exploring the possibility to model synthetic data with a 4-site scheme exposed the computational challenges associated with numerical approaches to efficiently fit data, but also highlighted how coupled allostery could give rise to N-site exchange (P. Li, Martins, & Rosen, 2011). One candidate for this type of N-site exchange is the cSH2 domain in phospholipase Cγ1, for which a dynamic allosteric network involving a combination of faster and slower exchange processes was associated with the variable binding of an intramolecular proline-rich, long flexible linker, or to an externally supplied peptide ligand (Koss, Bunney, et al., 2018). A number of exchange processes of different timescales is also qualitatively observed in an NMR study of the β-adrenergic receptor, illustrating that N-site exchange is very frequent but still not easily quantified (Solt et al., 2017).

Evaluation of complex exchange phenomena in large proteins is facilitated by increasingly powerful experimental methods that can be applied to protein side chains. In addition to methyl groups (Gill & Palmer, 2011; Korzhnev, Kloiber, Kanelis, Tugarinov, & Kay, 2004; Skrynnikov, Mulder, Hon, Dahlquist, & Kay, 2001; Tugarinov, Sprangers, & Kay, 2004; Weininger et al., 2013), chemical exchange can be probed in a number of other side chains (Mackenzie & Hansen, 2018; Weininger, Brath, Modig, Teilum, & Akke, 2014). The extraction of structural features from minor conformations using relaxation dispersion experiments is tightly coupled to the ability to extract structural information from chemical shifts (Robustelli, Stafford, & Palmer, 2012), which renders dispersion experiments for nuclei other than ¹⁵N or ¹H particularly relevant (Gopalan, Hansen, & Vallurupalli, 2018; Hansen, Vallurupalli, Lundstrom, Neudecker, & Kay, 2008; Korzhnev, Religa, Banachewicz, Fersht, & Kay, 2010). Relaxation dispersion experiments can also yield RDCs (Hansen, Vallurupalli, & Kay, 2008b; Igumenova, Brath, Akke, & Palmer, 2007), CSAs (Vallurupalli, Hansen, & Kay, 2008a), or information about side chain conformations (Baldwin, Hansen, Vallurupalli, & Kay, 2009; Hansen, Neudecker, Vallurupalli, Mulder, & Kay, 2010), which also can be used in structure calculations (Gopalan et al., 2018; Vallurupalli, Hansen, & Kay, 2008b).

This review begins by outlining theoretical approaches for characterizing chemical exchange phenomena, with an emphasis on extensions from 2 to N-site kinetic topologies. General approximations have recently been obtained for N-site exchange in both CPMG and R_1ρ experiments that are valid for most experimentally accessible time scales (Koss, Rance, & Palmer, 2017, 2018). These results are used to examine conditions under which various N-site kinetic schemes can be distinguished by CPMG or R_1ρ experiments. The review concludes by discussing key aspects of the main experimental methods applied to proteins and nucleic acids, but is not intended as a comprehensive reference to the myriad of experimental techniques available. Other reviews of chemical exchange cover, among other aspects, the theoretical basis (Farber & Mittermaier, 2015; A. G. Palmer, 2014, 2016; Vallurupalli, Sekhar, Yuwen, & Kay, 2017; Xue et al., 2015), the history (A. G. Palmer, 2014, 2016; Sauerwein & Hansen, 2015; Vallurupalli et al., 2017), applications (Farber & Mittermaier, 2015; Lisi & Loria, 2016; Osawa, Takeuchi, Ueda, Nishida, & Shimada, 2012; A. G. Palmer, 2016; Sauerwein & Hansen, 2015), practical considerations (Gopalan et al., 2018; Ishima, 2014; Kempf & Loria, 2004; Walinda, Morimoto, & Sugase, 2018a, 2018b; Xue et al., 2015), comprehensive overview of existing experiments (Sauerwein & Hansen, 2015; Vallurupalli et al., 2017; Walinda et al., 2018b), and special topics, including CEST (Vallurupalli et al., 2017), R_1ρ (Francesca Massi & Peng, 2018; A. G. Palmer & Massi, 2006), high-power relaxation dispersion (Ban et al., 2017), applications to nucleic acids (Xue et al., 2015), and structure determination from relaxation dispersion(Gopalan et al., 2018).

2. Theory

The effects of chemical or conformational exchange kinetic process on NMR observables are described by the stochastic Liouville equation:

$$\frac{d}{dt}\langle \widehat{B}\rangle \left(t\right)=\left\{\widehat{L}+\widehat{R}+\widehat{K}\right\}\langle \widehat{B}\rangle \left(t\right)-\widehat{R}{\langle \widehat{B}\rangle }_0$$ (1)

In Eq. 1, $\langle \widehat{B}\rangle \left(t\right)={\left[\langle {\widehat{B}}_1\rangle \left(t\right)\langle {\widehat{B}}_2\rangle \left(t\right)\cdots \langle {\widehat{B}}_N\rangle \left(t\right)\right]}^T$, N is the number of interconverting sites or species (containing the spin of interest), $\langle {\widehat{B}}_k\rangle \left(t\right)$ is a M × 1 column vector containing the time-dependent amplitudes of the M basis operators B_m for the Liouville space for the nth species, the elements of $\langle {\widehat{B}}_n\rangle \left(t\right)$ are defined by $\langle {\widehat{B}}_{km}\rangle \left(t\right)=\langle B_m\mid {\sigma }_n\left(t\right)\rangle$ for m = 1,…,M, σ_n(t) is the density operator for the nth state, and ${\langle \widehat{B}\rangle }_0$ is defined in similar fashion using the equilibrium density operator. The matrix $\widehat{L}$ is block diagonal with elements ${\widehat{L}}_{nj}={\delta }_{nj}{L}_n$, in which L_n is the M × M matrix for coherent evolution for the nth state (containing chemical shifts, scalar couplings, and radiofrequency fields, for example), the matrix $\widehat{R}$ is block diagonal with elements ${\widehat{R}}_{nj}={\delta }_{nj}{R}_n$, in which R_n is the M × M matrix for relaxation the nth state from processes other than chemical exchange (dipole-dipole, chemical shift anisotropy, and quadrupole relaxation, for example). The exchange matrix $\widehat{K}=K\otimes I_M$, in which I_M is an M × M identity matrix and K is an N × N kinetic matrix with elements K_ij = k_ji, k_ji is the (pseudo-) first-order rate constant for transition from state j to state i for i ≠ j and

$$K_{ii}=-\sum _{\begin{array}{c}j=1\\ j\ne i\end{array}}^N{k}_{ij}$$ (2)

The second term on the right hand side of Eq. 1 ensures that relaxation processes return the spin system to equilibrium or steady state at long times. Equation 1 is valid if the system is at chemical equilibrium and the transitions exchange coherences or populations between states, but do not change the coherences or populations themselves.

Equation 1 has a formal solution given by:

$$\langle \widehat{B}\rangle \left(t\right)=e^{\{\widehat{L}+\widehat{R}+\widehat{K}\}t}\left(\langle \widehat{B}\rangle \left(0\right)+{\{\widehat{L}+\widehat{R}+\widehat{K}\}}^{-1}\widehat{R}{\langle \widehat{B}\rangle }_0\right)-{\{\widehat{L}+\widehat{R}+\widehat{K}\}}^{-1}\widehat{R}{\langle \widehat{B}\rangle }_0$$ (3)

and clearly this expression can be evaluated numerically for any number of sites and basis operators. The amplitude of the mth basis operator in the nth state is obtained as

$$\langle B_{mn}\rangle \left(t\right)=\left({\left[0,\dots ,{\delta }_{nj},\dots ,0\right]}_N\otimes {\left[0,\dots ,{\delta }_{mk},\dots ,0\right]}_M\right)\langle \widehat{B}\rangle \left(t\right)$$ (4)

in which [0,…,δ_jk,…,0]_V is an V × 1 row vector. As noted by Allerhand and Thiele, the kinetic matrix K can be symmetrized by a matrix S with elements $S_{nj}={\delta }_{ij}{p}_n^{-1/2}$, in which p_n is the population of the n^th site, which can simplify analytic or numerical calculations (Allerhand & Thiele, 1966).

Many NMR experiments are designed so that the signal of interest s(T), proportional to a particular basis operator or function of basis operators, has simple functional dependence on a relaxation delay, T. for example, if the signal decay for s(T)∝<B_mn>(T) is monoexponential, then relaxation rate constant for the mth basis operator constant is defined as:

$$R_{mn}=\frac{-1}{T}\text{log}\left[\frac{s\left(T\right)}{s\left(0\right)}\right]=\frac{-1}{T}\text{log}\left[\frac{\langle B_{mn}\rangle \left(T\right)}{\langle B_{mn}\rangle \left(0\right)}\right]$$ (5)

This equation also can be used to define an effective (T-dependent) relaxation rate constant for a multi-exponential decay process. Analytic expressions for relaxation rate constants R_nm′ generally have been obtained either by calculation of the evolution of the average magnetization (and then using Eq. 5) or by calculation of the eigenvalues of $\widehat{L}+\widehat{R}+\widehat{K}$ (Abergel & Palmer, 2004). Exact results are available only for cases in which the product MN is small (≤ 4, but more often 2) or in the limits of very fast or very slow kinetic processes. Approximate expressions applicable to all kinetic rate scales and topologies have been obtained for both the average magnetization and eigenvalue approaches. Analytical (if MN ≤ 4) or numerical eigenvalues (for any MN) can be obtained from the roots of the characteristic equation (Koss et al., 2017; Koss, Rance, et al., 2018):

$$f\left(\lambda \right)=\left|\lambda E-(\widehat{L}+\widehat{R}+\widehat{K})\right|$$ (6)

Approximate roots of Eq. 6 frequently provide simplified expressions. The n^th Newton-Raphson and Halley (linearized Laguerre) approximations are, respectively:

$${\lambda }_n={\lambda }_{n-1}-\frac{f\left({\lambda }_{n-1}\right)}{f^{\prime }\left({\lambda }_{n-1}\right)}={\lambda }_{n-1}+\frac{1}{Tr\left\{{\left({\lambda }_{n-1}E-(\widehat{L}+\widehat{R}+\widehat{K})\right)}^{-1}\right\}}$$ (7)

$$\begin{gathered} {\lambda }_n={\lambda }_{n-1}-\frac{2f\left({\lambda }_{n-1}\right)f^{\prime }\left({\lambda }_{n-1}\right)}{2f^{\prime }\left({\lambda }_{n-1}\right)-f\left({\lambda }_{n-1}\right)f^{″}\left({\lambda }_{n-1}\right)} \\ ={\lambda }_{n-1}+\frac{2Tr\left\{{\left(H\left({\mathit{\tau }}_{cp}\right)-{\lambda }_{n-1}E\right)}^{-1}\right\}}{Tr{\left\{{\left(H\left({\mathit{\tau }}_{cp}\right)-{\lambda }_{n-1}E\right)}^{-1}\right\}}^2+Tr\left\{{\left(H\left({\mathit{\tau }}_{cp}\right)-{\lambda }_{n-1}E\right)}^{-2}\right\}} \end{gathered}$$ (8)

with λ₀ = 0. If the variation in R_n is modest, the effects of $\widehat{R}$ are given to first order by:

$${\lambda }_n={\lambda }_n^0+\frac{Tr\left\{{(\widehat{L}+\widehat{K})}^{-1}\widehat{R}\right\}}{Tr\left\{{(\widehat{L}+\widehat{K})}^{-1}\right\}}={\lambda }_n^0+R_{eff}$$ (9)

in which λ_n⁰ is calculated using Eqs. 6, 7, or 8 assuming $\widehat{R}=0$. A sufficient condition for accuracy of approximations of either type is that that the equilibrium population of one state is much larger than for the other N −1 states. The dominant state is normally denoted as state 1. If site 1 is not dominant, then another sufficient condition is that kinetic exchange amongst the states 2, …, N is fast. The above expressions frequently yield compact algebraic expressions that are also sufficiently accurate for analysis of experimental data; the present Review will emphasize results obtained using the first-order Newton-Raphson and Halley approaches, but both more accurate, but more complex (Koss et al., 2017; Koss, Rance, et al., 2018), and less accurate, but simpler (Trott & Palmer, 2004), expressions have been described. The recently developed geometric approximation approach, in which numerical solutions to Eq. 3 are pre-calculated and stored as a library of response surfaces, is an efficient alternative to “on-the-fly” numerical calculations and to the theoretical approximations that the focus of the present Review (Chao & Byrd, 2016, 2017).

2.1. Free Precession

Free precession of transverse magnetization provides a simple example of the application of the above theoretical description. In this situation, M = 1, $\widehat{B}\left(t\right)={[\langle M_1^{+}\rangle \left(t\right)\langle M_2^{+}\rangle \left(t\right)\cdots \langle M_N^{+}\rangle \left(t\right)]}^T$, L_n = iΩ_n, Ω_n is the resonance offset of a nuclear spin in the nth state, R_n = −R_2n, and R_2n is the transverse relaxation rate constant for a nuclear spin in the nth state. For N = 2 states, Eq. 1 becomes:

$$\begin{gathered} \frac{d}{dt}\left[\begin{array}{c}\langle M_1^{+}\rangle \left(t\right)\\ \langle M_2^{+}\rangle \left(t\right)\end{array}\right]=\{\begin{array}{c}\left[\begin{array}{cc}i{\Omega }_1& 0\\ 0& i{\Omega }_2\end{array}\right]+\left[\begin{array}{cc}-R_{21}& 0\\ 0& -R_{22}\end{array}\right]+\left[\begin{array}{cc}-k_{12}& k_{21}\\ k_{12}& -k_{21}\end{array}\right]\}\left[\begin{array}{c}\langle M_1^{+}\rangle \left(t\right)\\ \langle M_2^{+}\rangle \left(t\right)\end{array}\right]\end{array} \\ =\left[\begin{array}{cc}i{\Omega }_1-R_{21}-k_{12}& k_{21}\\ k_{12}& i{\Omega }_2-R_{22}-k_{21}\end{array}\right]\left[\begin{array}{c}\langle M_1^{+}\rangle \left(t\right)\\ \langle M_2^{+}\rangle \left(t\right)\end{array}\right] \end{gathered}$$ (10)

This equation is the Bloch-McConnell equation for transverse magnetization undergoing 2-site jumps. In this case, the two eigenvalues of the relaxation rate matrix can be obtained exactly. The desired smaller of the two relaxation rate constants is given by the negative of the real part of the eigenvalue:

$${\lambda }_1=\frac{1}{2}\left\{i\left({\Omega }_1+{\Omega }_2\right)-\left(R_{21}+R_{22}\right)-k_{ex}+{\left[{\left(k_{ex}+\Delta R_{21}-i\Delta {\omega }_{21}\right)}^2-4p_b\left(\Delta R_{21}-i\Delta {\omega }_{21}\right)k_{ex}\right]}^{1/2}\right\}$$ (11)

in which p_n is the equilibrium population of the nth site, Δω_ij =Ω_i−Ω_j, ΔR_n1=R_2n−R₂₁, and k_ex = k₁₂ + k₂₁. In this case, the first-order Newton-Raphson estimate of the eigenvalue yield the estimated rate constant

$$\begin{gathered} R_2=R_{21}+p_2{k}_{ex}\left\{\frac{\Delta {\omega }_{21}^2+k_{ex}\Delta R_{21}+\Delta R_{21}^2}{\Delta {\omega }_{21}^2+{\left(\Delta R_{21}+k_{ex}\right)}^2}\right\} \\ \approx R_{21}+p_2{k}_{ex}\left[\frac{\Delta {\omega }_{21}^2+k_{ex}\Delta R_{21}}{\Delta {\omega }_{21}^2+k_{ex}^2}\right] \end{gathered}$$ (12)

in which the second line results from the first-order treatment of ΔR₂₁. The exact and first-order approximate values of R₂ are compared in Figure 1. The Halley approximation is extremely accurate for a 2-state system and results are not shown for clarity. First-order approximations are accurate when exchange is relatively slow (k_ex/|Δω₂₁| < 1) or relatively fast (k_ex/|Δω₂₁| >> 1); higher order approximations are required for high accuracy in the intermediate exchange regime (k_ex/|Δω₂₁| ~ 1). Allerhand and Theile defined C-type or R-type exchange depending upon whether the effects of differences in resonance frequencies or differences in relaxation rate constants, respectively, between sites have a dominant effect. In either limiting case, Δω₂₁ → ∞ or ΔR₂₁ → ∞, R₂ → R₂₁ + p₂k_ex = k₁₂.

Figure 1.

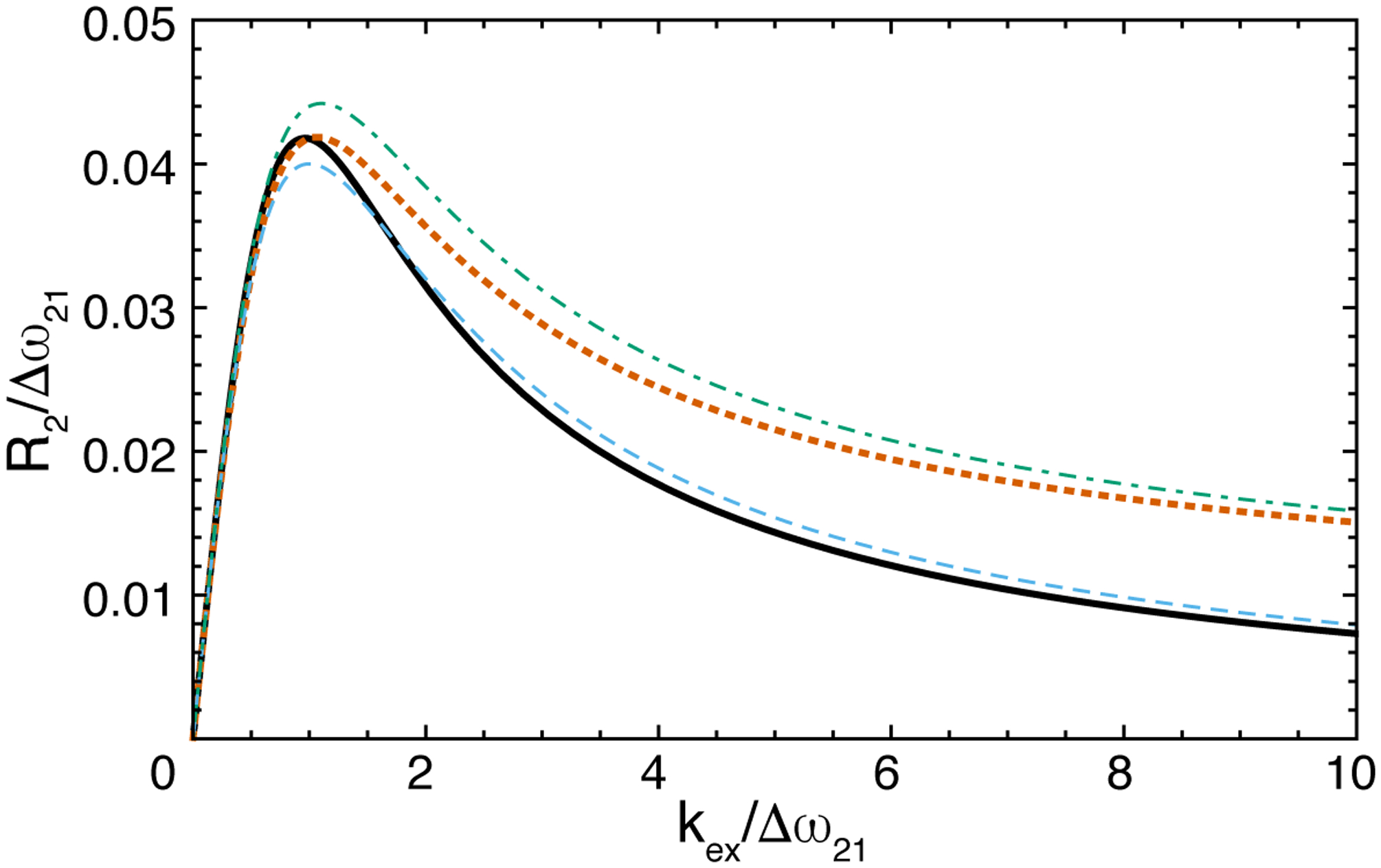
Free-precession transverse relaxation rate constant for 2-site chemical exchange with p₂ = 0.08 and R₂₁ = 0. R₂ obtained from (black, solid) exact eigenvalue and (blue, dashed) first-order approximation assuming ΔR₂₁ = 0. R₂ obrtained from (orange, dotted) exact eigenvalue and (green, dash-dotted) first-order approximation ΔR₂₁/Δω₂₁ = 0.1.

2.2. Carr-Purcell-Meiboom-Gill Relaxation

The CPMG experiment consists of m repetitions of the pulse sequence element:

$${\tau }_{cp}-{180}^{°}-2{\tau }_{cp}-{180}^{°}-{\tau }_{cp}$$ (13)

applied to transverse magnetization. The effect of ideal 180° pulses is to invert the signs of Ω_i.

Thus, evolution of magnetization through the CPMG sequence becomes:

$$M^{+}\left(T\right)=M^{+}\left(4m{\tau }_{cp}\right)={\left[\text{exp}\left\{\Lambda {\tau }_{cp}\right\}\text{exp}\left\{2{\Lambda }^{*}{\tau }_{cp}\right\}\text{exp}\left\{\Lambda {\tau }_{cp}\right\}\right]}^m{M}^{+}\left(0\right)$$ (14)

in which the asterisk indicates complex conjugation, $\Lambda =\widehat{L}+\widehat{R}+\widehat{K}$, and other variables are defined as for the case of free-precession. For 2-site exchange, the Carver-Richards equation gives the relaxation rate constant as (Carver & Richards, 1969):

$$R_{\mathit{\text{cpmg}}}\left({\tau }_{cp}\right)=\frac{1}{2}\left(R_{21}+R_{22}+k_{ex}-\frac{1}{2{\tau }_{cp}}{\text{cosh}}^{-1}\left[D_{+}\text{cosh}\left({\eta }_{+}\right)-D_{-}\text{cos}\left({\eta }_{-}\right)\right]\right)$$ (15)

in which,

$$\begin{gathered} D_{\pm }=\frac{1}{2}\left[\pm 1+\frac{\psi +2\Delta {\omega }^2}{{\left({\psi }^2+{\zeta }^2\right)}^{1/2}}\right] \\ {\eta }_{\pm }=\sqrt{2}{\tau }_{cp}{\left[\pm \psi +{\left({\psi }^2+{\zeta }^2\right)}^{1/2}\right]}^{1/2} \\ \psi ={\left(R_{21}-R_{22}-p_1{k}_{ex}+p_2{k}_{ex}\right)}^2-\Delta {\omega }^2+4p_1{p}_2{k}_{ex}^2 \\ \zeta =2\Delta \omega \left(R_{21}-R_{22}-p_1{k}_{ex}+p_2{k}_{ex}\right) \end{gathered}$$

The Carver-Richards equation for 2-site exchange of single-quantum coherence has been extended to multiple-quantum relaxation (Korzhnev et al., 2004).

In order to provide additional insight for N-site exchange, Koss and coworkers have shown that M(t) obeys a coarse-grained differential equation (Koss, Rance, et al., 2018):

$$\frac{d{M}^{+}\left(T\right)}{dT}=\left(\frac{1}{4{\tau }_{cp}}{e}^{{\Lambda }_{{\tau }_{cp}}}H\left({\tau }_{cp}\right)e^{-\Lambda {\tau }_{cp}}\right)M^{+}(T)$$ (16)

with an average Liouvillian matrix H(τ_cp) defined as:

$$H\left({\tau }_{cp}\right)=\text{log}\left(\text{exp}\left\{2{\Lambda }^{*}{\tau }_{cp}\right\}\text{exp}\left\{2\Lambda {\tau }_{cp}\right\}\right)$$ (17)

The matrix logarithm is determined to high accuracy by Padé approximation. For example, four such approximations are:

$$\begin{gathered} H_{10}\left({\tau }_{cp}\right)\approx -E+Z\left({\tau }_{cp}\right)=-\left(E-\text{exp}\left\{2{\widehat{\widehat{L}}}^{*}{\tau }_{cp}\right\}\text{exp}\left\{2\widehat{\widehat{L}}{\tau }_{cp}\right\}\right) \\ {H}_{11}\left({\tau }_{cp}\right)\approx 2\left\{-E+Z\left({\tau }_{cp}\right)\right\}{\left\{E+Z\left({\tau }_{cp}\right)\right\}}^{-1} \\ {H}_{22}\left({\tau }_{cp}\right)\approx 3\left\{-E+Z^2\left({\tau }_{cp}\right)\right\}{\left\{E+4Z\left({\tau }_{cp}\right)+Z^2\left({\tau }_{cp}\right)\right\}}^{-1} \\ {H}_{33}\left({\tau }_{cp}\right)\approx \frac{1}{3}\left\{-11E-27Z\left({\tau }_{cp}\right)+27Z^2\left({\tau }_{cp}\right)+11Z^3\left({\tau }_{cp}\right)\right\}{\left\{E+9Z\left({\tau }_{cp}\right)+9Z^2\left({\tau }_{cp}\right)+Z^3\left({\tau }_{cp}\right)\right\}}^{-1} \end{gathered}$$ (18)

in which Z(τ_cp)=exp{2Λ*τ_cp}exp{2Λτ_cp} and the subscripts in the expressions H_jk(τ_cp) give the highest order power in the numerator and denominator polynomials in Z(τ_cp). The CPMG relaxation rate constant R_cpmg(τ_cp) then is obtained from the largest (least negative) eigenvalue of the average Liouvillian H(τ_cp) / (4τ_cp), because the eigenvalues are unaffected by the similarity transformation in Eq. 16.

The Cayley-Hamilton theorem allows an arbitrary Padé approximation H_jk(τ_cp) and its inverse to be expressed as:

$$H_{jk}\left({\tau }_{cp}\right)=\epsilon \left(\sum _{n=0}^{N-1}{b}_n{Z}^n\left({\tau }_{cp}\right)\right){\left(\sum _{n=0}^{N-1}{c}_n{Z}^n\left({\tau }_{cp}\right)\right)}^{-1}=\epsilon \sum _{n=0}^{N-1}{a}_n{Z}^n\left({\tau }_{cp}\right)$$ (19)

in which the coefficients, a_n, b_n, c_n, and ε depend on {TrZ(τ_cp), … TrZ^N−1(τ_cp)} and |Z(τ_cp)|. The determinant has the simple form:

$$\left|Z\left({\tau }_{cp}\right)\right|=\text{exp}\left[4{\tau }_{cp}Tr\left\{\widehat{R}+\widehat{K}\right\}\right]$$ (20)

so the main computational effort is determining the traces {TrZ(τ_cp), … TrZ^N−1(τ_cp)} The coefficients a_n depend on b_n, c_n, and ε, but not on the exact functional form of these parameters. Once the representation using b_n, c_n, and ε has been transformed to the representation using a_n, then the resulting expressions can be used with any set of b_n, c_n, and ε. Consequently, the use of higher-order Padé approximations is not computationally prohibitive. In addition, the inverse H⁻¹(τ_cp), needed for application of the eigenvalue approximations, is obtained simply by replacing ε by 1/ε and exchanging b_n and c_n.

Application of these equations for 3-site exchange are presented in the Appendix. Low-order Padé approximations frequently yield compact analytical expressions. For example, using H₁₁(τ_cp) for 3-site exchange,

$$R_{\mathit{\text{cpmg}}}\left({\tau }_{cp}\right)=R_{21}+\frac{1-\left|Z\left({\tau }_{cp}\right)\right|-TrZ\left({\tau }_{cp}\right)+\left\{{Tr}^{2}Z\left({\tau }_{cp}\right)-Tr{Z}^2\left({\tau }_{cp}\right)\right\}/2}{4{\tau }_{cp}\left(3+3\left|Z\left({\tau }_{cp}\right)\right|-TrZ\left({\tau }_{cp}\right)-\left\{{Tr}^{2}Z\left({\tau }_{cp}\right)-Tr{Z}^2\left({\tau }_{cp}\right)\right\}/2\right)}$$ (21)

in which Z(τ_cp) is calculated using $\mathbf{\Lambda }=\left(\widehat{L}-L_1\right)+\left(\widehat{R}-R_1\right)+\widehat{K}$ and $\widehat{K}$ is assumed to be symmetrized (vide supra).

If chemical exchange is slow, (k_ij + k_ji < |Δω_ij|/10), then Koss and coworkers showed that H₁₀(τ_cp) is given by (Koss, Rance, et al., 2018):

$$H_{10}{\left({\tau }_{cp}\right)}_{ij}/\left(4{\tau }_{cp}\right)=\left\{\begin{array}{cc}\sqrt{k_{ij}{k}_{ji}}\text{sinc}\left[\Delta {\omega }_{ij}{\tau }_{cp}\right]\text{exp}\left[-i\Delta {\omega }_{ij}{\tau }_{cp}\right]& i>j\\ K_{ii}-\Delta R_{i1}& i=j\\ \sqrt{k_{ij}{k}_{ji}}\text{sinc}\left[\Delta {\omega }_{ij}{\tau }_{cp}\right]\text{exp}\left[i\Delta {\omega }_{ji}{\tau }_{cp}\right]& i<j\end{array}\right\}$$ (22)

For N = 2,

$$H_{10}\left({\mathit{\tau }}_{cp}\right)/\left(4{\mathit{\tau }}_{cp}\right)=\left[\begin{array}{cc}-k_{12}& \sqrt{k_{12}{k}_{21}}\text{sinc}\left(\Delta {\omega }_{21}{\tau }_{cp}\right)\text{exp}\left(i\Delta {\omega }_{21}{\mathit{\tau }}_{cp}\right)\\ \sqrt{k_{12}{k}_{21}}\text{sinc}\left(\Delta {\omega }_{21}{\mathit{\tau }}_{cp}\right)\text{exp}\left(-i\Delta {\omega }_{21}{\mathit{\tau }}_{cp}\right)& -k_{21}-\Delta R_{21}\end{array}\right]$$ (23)

A further simplification of this equation is obtained by applying another similarity transformation:

$$U=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}\text{exp}\left(-i\Delta {\omega }_{21}{\tau }_{cp}/2\right)& \text{exp}\left(i\Delta {\omega }_{21}{\tau }_{cp}/2\right)\\ -\text{exp}\left(-i\Delta {\omega }_{21}{\tau }_{cp}/2\right)& \text{exp}\left(i\Delta {\omega }_{21}{\tau }_{cp}/2\right)\end{array}\right]$$ (24)

which yields:

$$U{H}_{10}\left({\mathit{\tau }}_{cp}\right)U^{-1}/\left(4{\mathit{\tau }}_{cp}\right)=\frac{1}{2}\left[\begin{array}{cc}2\sqrt{k_{12}{k}_{21}}\text{sinc}\left(\Delta {\omega }_{21}{\mathit{\tau }}_{cp}\right)-k_{ex}-\Delta R_{21}& \left(p_1-p_2\right)k_{ex}+\Delta R_{21}\\ \left(p_1-p_2\right)k_{ex}+\Delta R_{21}& -2\sqrt{k_{12}{k}_{21}}\text{sinc}\left(\Delta {\omega }_{21}{\mathit{\tau }}_{cp}\right)-k_{ex}-\Delta R_{21}\end{array}\right]$$ (25)

This equation illustrates an analogy between the CPMG experiment and the chemical exchange formalism presented above, in which

$$\begin{gathered} \widehat{L}=\sqrt{k_{12}{k}_{21}}\text{sinc}\left(\Delta {\omega }_{21}{\mathit{\tau }}_{cp}\right)\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right] \\ \widehat{R}=\frac{\Delta R_{21}}{2}\left[\begin{array}{cc}-1& 1\\ 1& -1\end{array}\right] \\ \widehat{K}=\frac{k_{ex}}{2}\left[\begin{array}{cc}-1& p_1-p_2\\ p_1-p_2& -1\end{array}\right] \end{gathered}$$ (26)

The relaxation rate constant obtained from the above equation is:

$$\begin{gathered} R_{\mathit{\text{cpmg}}}\left({\tau }_{cp}\right)=R_{21}+\frac{1}{2}\left\{k_{ex}+\Delta R_{21}-{\left[4p_1{p}_2{k}_{ex}^2{\text{sinc}}^2\left(\Delta {\omega }_{12}{\tau }_{cp}\right)+{\left\{\left(p_1-p_2\right)k_{ex}+\Delta R_{21}\right\}}^2\right]}^{1/2}\right\} \\ \approx R_{21}+\frac{p_1{p}_2{k}_{ex}^2\left[1-{\text{sinc}}^2\left(\Delta {\omega }_{21}{\tau }_{cp}\right)\right]+p_2{k}_{ex}\Delta R_{21}}{k_{ex}+\Delta R_{21}} \end{gathered}$$ (27)

in which the second line is the first-order approximation of the eigenvalue. For 3-sites in a linear topology B-A-C, in which the population p₁ >> p₂, p₃ (1, 2, and 3 denote sites A, B, and C), the first-order approximation to the relaxation rate constant is:

$$R_{\mathit{\text{cpmg}}}\left({\mathit{\tau }}_{cp}\right)=R_{21}+\left[\frac{B_0-k_{12}{k}_{21}\left(k_{31}+\Delta R_{31}\right){\text{sinc}}^2\left(\Delta {\omega }_{21}{\mathit{\tau }}_{cp}\right)-k_{13}{k}_{31}\left(k_{21}+\Delta R_{21}\right){\text{sinc}}^2\left(\Delta {\omega }_{31}{\mathit{\tau }}_{cp}\right)}{B_1+k_{12}{k}_{21}{\text{sinc}}^2\left(\Delta {\omega }_{21}{\mathit{\tau }}_{cp}\right)+k_{13}{k}_{31}{\text{sinc}}^2\left(\Delta {\omega }_{31}{\mathit{\tau }}_{cp}\right)}\right]$$ (28)

in which B₀ = (k₁₂+k₁₃)(k₂₁+ΔR₂₁)(k₃₁+ΔR₃₁) and B₁ = (k₂₁+ΔR₂₁)(k₃₁+ΔR₃₁) + (k₁₂+k₁₃) (k₂₁+k₃₁+ΔR₂₁+ΔR₃₁). Expressions for other kinetic schemes have been presented by Koss and co-workers (Koss, Rance, et al., 2018). The above equations demonstrate the main effect of R-type relaxation for the CPMG experiment: ΔR₂₁ becomes important only if k₂₁ is not >> | ΔR₂₁|. Essentially, the difference in relaxation rates must be large enough that relaxation happens efficiently within the lifetime of sites 2,…, N.

The approximations obtained above for 2-site exchange using the exact eigenvalue of H³³(τ_cp) and a second-order approximation to the eigenvalue of the slow exchange Liouvillian (Eq. 8) are compared to the Carver-Richards equation in Figure 2. The H³³(τ_cp) approximation is extremely accurate over all time scales, while the slow exchange result is accurate when k_ex < |Δω_AB|/10.

Figure 2.

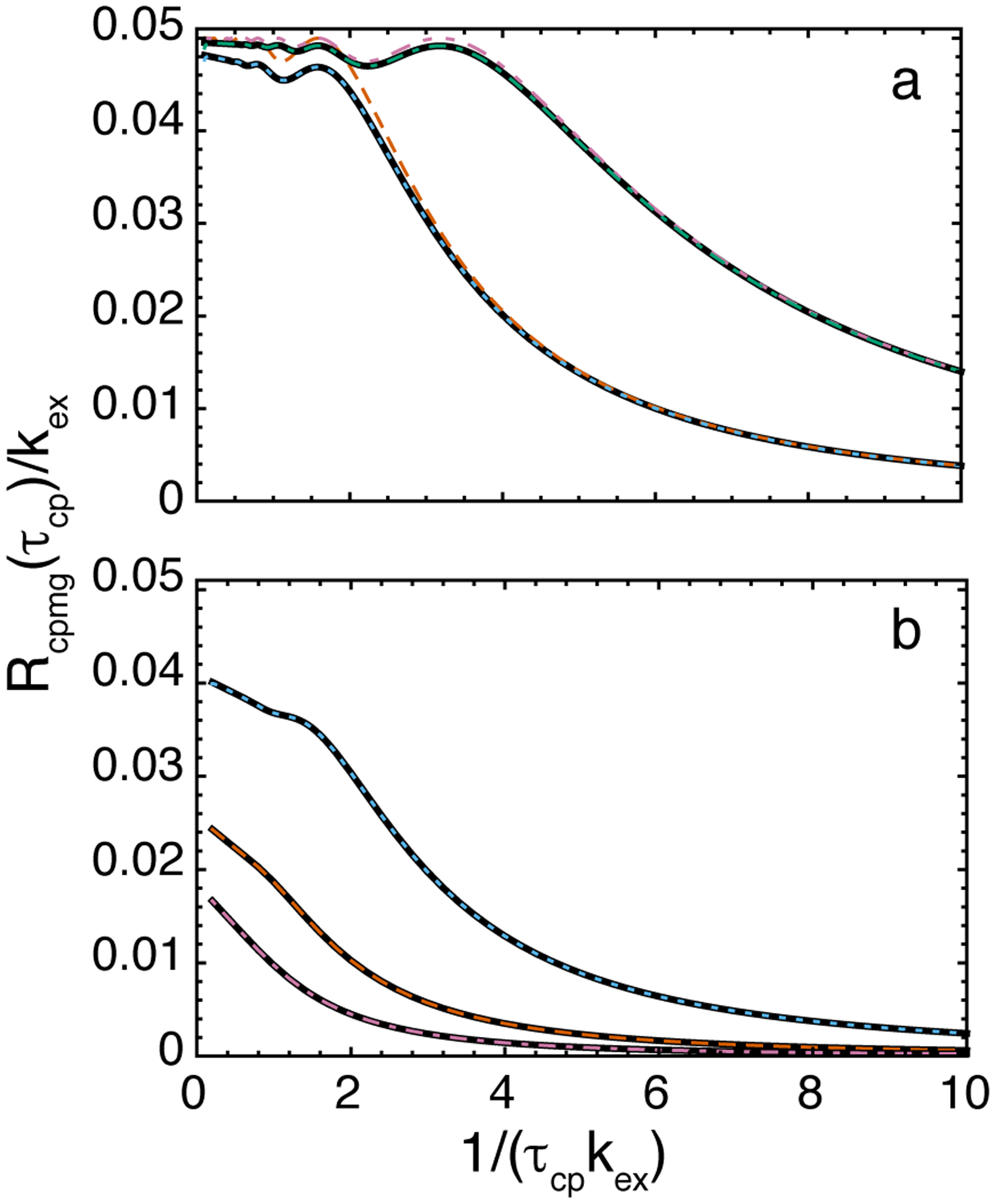
CPMG relaxation dispersion curves for 2-site chemical exchange for p₂ = 0.05, and R₂₂ = R₂₁ = 0. (a) Δω₂₁ /k_ex = 5: (black solid lower curve) Carver-Richards equation, (blue, dotted) exact eigenvalue of H₃₃(τ_cp), (orange, dashed), second-order slow exchange equation. Δω₂₁ /k_ex = 10: (black, solid, upper curve) Carver-Richards equation, (blue, dash-dotted) exact eigenvalue of H₃₃(τ_cp) , (reddish-purple, dash-dot-dotted), second-order slow exchange equation. (b) Δω₂₁ /k_ex = 2: (black, solid, lower curve) Carver-Richards equation, (blue, dotted) exact eigenvalue of H₃₃(τ_cp) ; Δω₂₁ /k_ex = 1: (black, solid, middle curve) Carver-Richards equation, (orange, dashed) exact eigenvalue of H₃₃(τ_cp) ; Δω₂₁ /k_ex = 0.2: (black, solid, lower curve) Carver-Richards equation, (reddish-purple, dash-dotted) exact eigenvalue of H₃₃(τ_cp) ; curves for Δω₂₁ /k_ex = 0.2 have been multiplied by 10 for clarify.

The above approximations for 3-site triangular exchange are illustrated in the left panel of Figure 3. In the given example, k_ex > |Δω_AB|/10 for all sites and the slow exchange approximations for H₁₀ (Eq. 22) are not expected to be accurate. Approximations based on the exact matrix exponential (Eq. 17) are more appropriate, even though the second-order approximation based on Eq. 21 also gives a satisfactory fit in this case. As shown in the Figure, Padé approximations of increasing accuracy can greatly enhance accuracy, provided that the eigenvalue approximation also is sufficiently accurate. The right panel of Fig. 3 illustrates CPMG dispersion curves for 4-site exchange with various kinetic schemes. In most cases shown here, a second-order eigenvalue approximation is sufficient to fit the exact solution; however, for the star scheme, a second-order (Halley’s method) eigenvalue approximation was required to fit data at large τ_cp; these more complex approximations are recommended if data are available at very large τ_cp and if a wide parameter space is being considered (for validity of the single eigenvalue approximation vide infra). The examples of 4-site exchange examples in Fig. 3 also illustrate that the CPMG curve is influenced less by exchange processes between minor sites at large values of τ_cp, while those processes become more influential at smaller τ_cp (Koss et al, 2018).

Figure 3.

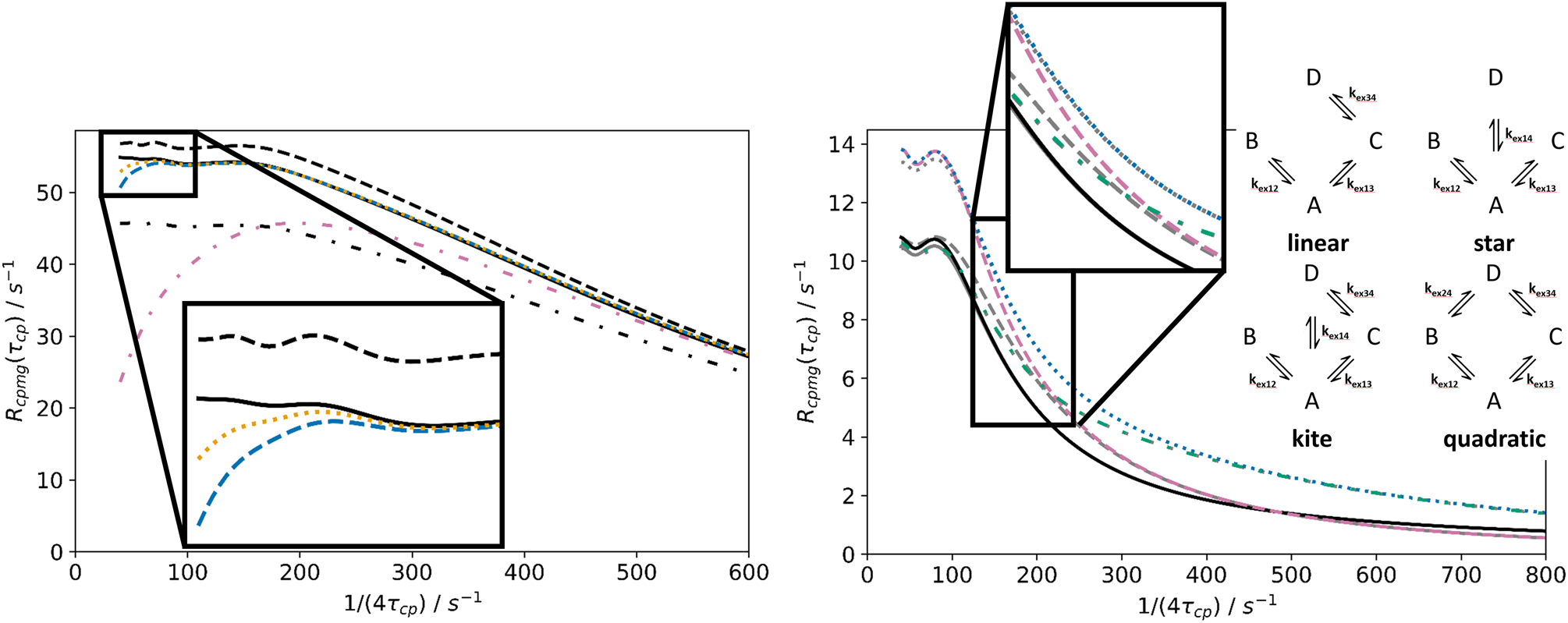
Approximations for N-site kinetic schemes in CPMG experiments. Left: 3-site triangular exchange (see Fig. 6 for the respective R_1ρ figure). (Solid, black) Exact solution; (not black) H_nn(τ_cp) approximations, eigenvalue approximated to second order (Halley’s method), with (reddish-purple, dashed-dotted) n = 1, (blue, dashed) n = 2; (orange, dotted) n = 3; (black, not solid) slow exchange approximations from matrix exponential series truncation, with eigenvalue approximation of order k, with (dashed-dotted) k = 1; (dashed) k = 2 (Halley’s method). Parameters (in analogy to parameters in Fig. 1, Koss et. al. 2018): k₁₂ + k₂₁ = 200 s⁻¹; k₁₃ + k₃₁ = 300 s⁻¹; k₂₃ + k₃₂ = 600 s⁻¹; Δω_AB = 1800 s⁻¹; Δω_AC = −2600 s⁻¹; p_A = 0.85; p_B = 0.08; p_C = 0.07. Right: CPMG curves can help to differentiate between various 4-site schemes. A schematic illustration of 4-site schemes is shown within the figure. Exact solutions (not grey), H_nn(τ_cp) approximations with n = 2 (grey) for CPMG curves for a variety of four-site schemes: kite (blue, dotted), star (reddish-purple, dashed), quadratic (green, dashed-dotted) and linear (black, solid). Eigenvalue approximations to first order almost overlap with the exact solutions, except for the star scheme; however, a second-order eigenvalue approximation (Halley’s formula) gives a perfect overlap in this case. Parameters: k₁₂ + k₂₁ = 200 s⁻¹; k₁₃ + k₃₁ = 20 s⁻¹; k₁₄ + k₄₁ = 70 s⁻¹; k₂₄ + k₄₂ = 400 s⁻¹; k₃₄ + k₄₃ = 150 s⁻¹; Δω_AB = 1000 s⁻¹; Δω_AC = −2900 s⁻¹; Δω_AD = 1100 s_–1; p_A = 0.88; p_B = 0.05; p_C = 0.03; p_D = 0.04.

Relaxation rate constants defined as the least negative eigenvalue of H(τ_cp) or by Eq. 5 differ because if T = 4mτ_cp is not sufficiently long, then contributions to the magnetization decay from other eigenvalues will not have been damped to zero. The effective relaxation rate constant obtained form Eq. 5 will then contains a T-dependent contribution from the residual multi-exponential components of the magnetization decay. This situation arises in particular if exchange is slow and the population of site 1 is not dominant. Baldwin has derived an expression for 2-site CPMG relaxation based on Eq. 5 that provides a correction the Carver-Richards equation, which is itself the negative of the largest (least negative) eigenvalue of H(τ_cp) (Baldwin, 2014). A more formal (without reduction to explicit algebraic form) derivation of the effective relaxation rate constant derived from Eq. 5 for the N-site CPMG experiment is given in the Appendix.

Both the results of Baldwin and those presented in the Appendix (Eq. A14 and A15) show that the difference between the two estimates of the relaxation rate constant depends upon 1/T = 1/(4mτ_cp). Thus these results support the use of constant relaxation time CPMG experimental methods. This correction to the Carver-Richards equation also accounts for different behavior in the slow exchange limit of Eq. 27 (for ΔR₂₁ = 1) and the expression obtained by Tollinger and coworkers (Tollinger et al., 2001):

$$R_{\mathit{\text{cpmg}}}\left({\tau }_{cp}\right)=R_{21}+p_1{k}_{ex}\left[1-{\text{sinc}}^2\left(\Delta {\omega }_{21}{\tau }_{cp}\right)\right]$$

Figure 4 compares the Carver-Richards equation (Eq. 15) with various expressions that estimate R_cpmg(τ_cp) based on more than a single eigenvalue. “Exact” R_cpmg(τ_cp) rate constants were defined by a monoexponential fit to simulated multiexponential decays. Equation 29 reproduces the exact results best at extremely slow exchange (Fig. 4, left panel); for slow or intermediate exchange, the Carver-Richards equation and Eq 27 are more appropriate. Baldwin’s result for 2-site schemes, and equivalently the correction for N-site exchange (Eq. A14), give the effective R_cpmg(τ_cp) rates for experiments with constant T and analyzed as in Eq. 5. These R_cpmg(τ_cp) values fall between the results for Eq. 15 and 29. For exchange which is not too slow (Fig. 4, right panel), simpler approximations for this correction factor to Eq. 15 can be used (Eqs. A16, A17).

Figure 4.

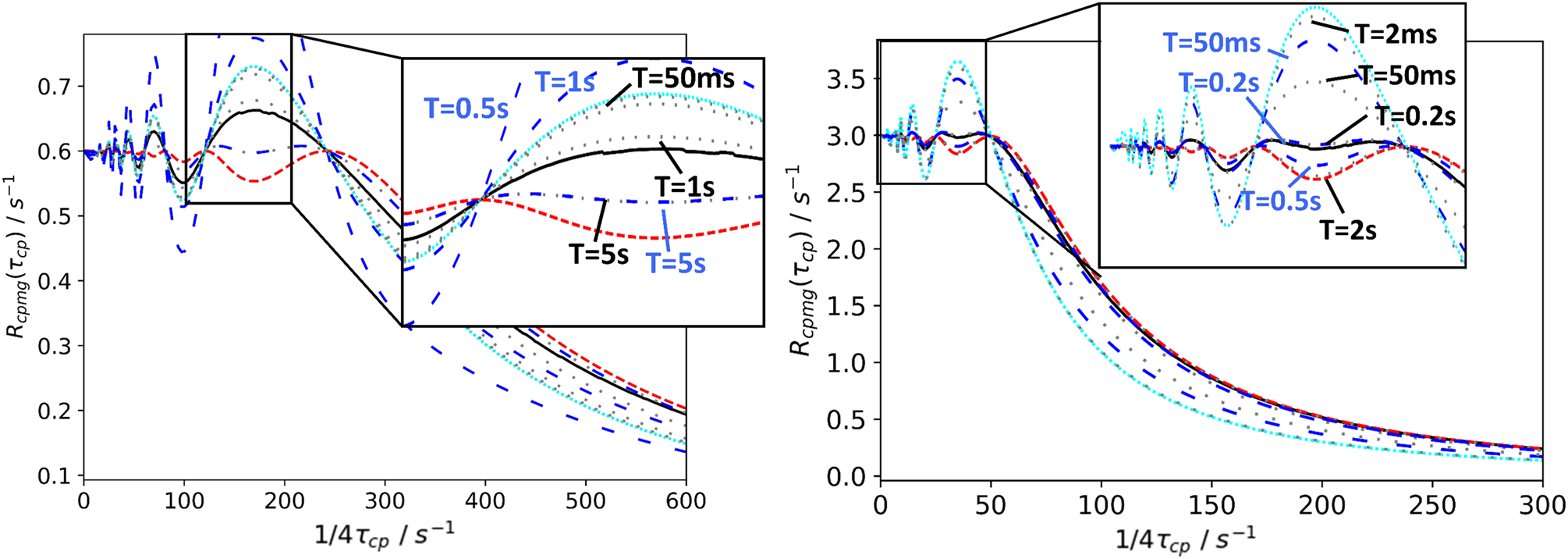
Exact solutions two-site CPMG experiments for R_cpmg obtained from more than one eigenvalue, and/or at constant T. (Solid black) Exact solution, calculated from multiexponential decays from two eigenvalues of H_nn(τ_cp). R_cpmg was extracted from monoexponential fits to the decays, by evenly sampling the curve along the magnetization axis; (red, dense-dashed) Carver- Richards equation / single eigenvalue exact solution; (cyan, dense-dotted) Eq. 29 (Tollinger et al., 2001) for extremely slow exchange; (gray, sparse-dotted) exact solutions for various constant T, based on Eq. A14, equivalent to Baldwin’s expressions (Baldwin, 2014); (blue, sparse-dashed) approximations for constant T expressions (Eq. A16). Left panel: T = {0.05 s, 0.2 s, 0.5s, 1 s, 5s}; labels in figure. Parameters, equivalent to Tollinger et al.: k₁₂ + k₂₁ =2 s⁻¹; Δω_AB = 6 ppm for ¹⁵N at 800 MHz (¹H frequency); p_A = 0.7; p_B = 0.3. Right panel: (dotted) T = {0.002 s, 0.05 s, 0.2 s, 0.5 s, 2 s}; labels in figure. Parameters: k₁₂ + k₂₁ = 30 s⁻¹; Δω_AB/(2π) = 100 Hz; p_A = 0.9; p_B = 0.1.

2.3. Rotating-Frame Relaxation

The above formalism is particularly powerful for spin-locking experiments, including R_1ρ, CEST, and DEST, because the dimensions of the evolution matrix are 3N × 3N and even for 2-site exchange exact analytical results cannot be obtained. For N-sites,

$$L_n=\left[\begin{array}{ccc}0& -{\Omega }_n& 0\\ {\Omega }_n& 0& -{\omega }_1\\ 0& {\omega }_1& 0\end{array}\right]R_n=\left[\begin{array}{ccc}-R_{2n}& 0& 0\\ 0& -R_{2n}& 0\\ 0& 0& -R_{1n}\end{array}\right]$$ (29)

in which the spin-locking field is assumed to have x-phase and amplitude ω₁ and resonance offsets are relative to the frequency of the spin-locking radiofrequency field, ω_rf. The relaxation rate constant R_1ρ is the relaxation rate constant for magnetization spin-locked along the effective field (R_2ρ relaxation of magnetization orthogonal to the effective field has been discussed by Garwood and co-workers (Mangia, Traaseth, Veglia, Garwood, & Michaeli, 2010; Michaeli, Sorce, Idiyatullin, Ugurbil, & Garwood, 2004; Traaseth et al., 2012)). The R_1ρ relaxation rate constant is obtained as the largest (least negative) eigenvalue of the evolution matrix, as discussed above. For N = 2 sites and assuming R₁ = R₂ and p₁ >> p₂, the first-order approximation to the eigenvalue gives (Trott & Palmer, 2002):

$$\begin{gathered} R_{1\rho }={\overline{R}}_1{\text{cos}}^2\theta +{\overline{R}}_2{\text{sin}}^2\theta +\frac{{\text{sin}}^2\theta p_1{p}_2\Delta {\omega }_{21}^2{k}_{ex}}{{\omega }_A^2{\omega }_B^2/{\omega }_e^2+k_{ex}^2} \\ \approx {\overline{R}}_1{\text{cos}}^2\theta +{\overline{R}}_2{\text{sin}}^2\theta +\frac{{\text{sin}}^2\theta p_1{p}_2\Delta {\omega }_{21}^2{k}_{ex}}{{\Omega }_2^2+{\omega }_1^2+k_{ex}^2} \end{gathered}$$ (30)

in which ${\overline{R}}_1$ and ${\overline{R}}_2$ are the population-average relaxation rate constants in the absence of exchange $\text{tan}\theta ={\omega }_1/\overline{\Omega }$, $\overline{\Omega }$ is the population-average resonance offset, ${\omega }_n^2={\Omega }_n^2+{\omega }_1^2$, and ${\omega }_e^2={\overline{\Omega }}^2+{\omega }_1^2$. The second line is obtained if p₁ is sufficiently large that ω_A² ≈ ω_B². This equation demonstrates the main advantage of spin-locking experiments compared with lineshape analysis and CPMG experiments: the relaxation rate constant depends on the resonance offset in the B site (site 2), even if the population of that site is so low that the resonance signal is not directly observable. In contrast, as shown by the Carver-Richards equation (Eq. 15), the CPMG experiment depends only on Δω₂₁² and hence provides information on the magnitude of the resonance frequency difference between sites, but not on the absolute sign (vide supra).

The above equation has been extended both to higher order of approximation and to include differences in relaxation rates R₂₁ and R₂₂ between sites (differences between R₁₁ and R₁₂ are generally small enough to be ignored). In the former case, the second-order result is (Miloushev & Palmer, 2005):

$$\begin{array}{r}\hfill R_{1\rho }={\overline{R}}_1{\text{cos}}^2\theta +{\overline{R}}_2{\text{sin}}^2\theta +\frac{{\text{sin}}^2\theta p_1{p}_2\Delta {\omega }_{21}^2{k}_{ex}}{{\omega }_A^2{\omega }_B^2/{\omega }_e^2+k_{ex}^2+{\text{sin}}^2\theta p_1{p}_2\Delta {\omega }_{21}^2\left\{1+\frac{2k_{ex}^2(p_1{\omega }_A^2+p_2{\omega }_B^2}{{\omega }_A^2{\omega }_B^2+{\omega }_e^2{k}_{ex}^2}\right\}}\end{array}$$ (31)

The latter case has been treated to first order by Baldwin and Kay (Baldwin & Kay, 2013); the resulting equation is lengthy and not reproduced herein. The expression obtained from Eq. 8:

$$R_{1\rho }=R_{11}{\text{cos}}^2\theta +R_{21}{\text{sin}}^2\theta +{\text{sin}}^2\theta \frac{p_1{p}_2\Delta {\omega }_{21}^2{k}_{ex}}{{\omega }_A^2{\omega }_B^2/{\omega }_e^2+k_{ex}^2}+{\text{sin}}^2\theta \left\{\frac{\left(R_{21}-R_{11}\right)\left(p_2{\omega }_A^2{\omega }_e^2+p_1{\omega }_B^2{\omega }_e^2-{\omega }_A^2{\omega }_B^2\right)}{{\omega }_A^2{\omega }_B^2+{\omega }_e^2{k}_{ex}^2}+\frac{\Delta R_{21}{p}_2\left(k_{ex}^2+{\omega }_A^2\right)}{{\omega }_A^2{\omega }_B^2/{\omega }_e^2+k_{ex}^2}\right\}$$ (32)

is more compact, but less accurate. This expression is easily obtained by noting that:

$$-\widehat{R}=R_{11}E+\mathit{\text{Diag}}\left[R_{21}-R_{11},R_{21}-R_{11},0,R_{21}-R_{11},R_{21}-R_{11},0\right]+\mathit{\text{Diag}}\left[0,0,0,R_{22}-R_{21},R_{22}-R_{21},0\right]$$ (33)

in which Diag[ ] is a diagonal matrix and performing the matrix manipulations term by term. The first term in the brackets of Eq. 32 corrects for the different effective fields for spins in the two states, which makes a contribution even if ΔR₂₁ = 0, and the second term corrects for ΔR₂₁ ≠ 0. If ΔR₂₁ = 0, this equation reduces to Eq. 30 if p₁ >> p₂ or exchange is in the fast limit. As for the CPMG experiment, ΔR₂₁ becomes important only if k₂₁ is not >> | ΔR₂₁|.

The behavior of the above expressions for R_1ρ relaxation for 2-site exchange are illustrated in Figure 5. In contrast to the CPMG experiment, in which only τ_cp can be varied, R_1ρ relaxation is altered by changing both ω₁ and ω_rf. Even in relatively fast exchange, the asymmetry in the profile of R_1ρ relaxation rate constants for values of ω_rf upfield or downfield of the observable resonance is significant and allows determination of Ω₂ (Bothe, Stein, & Al-Hashimi, 2014; Kimsey, Petzold, Sathyamoorthy, Stein, & Al-Hashimi, 2015).

Figure 5.

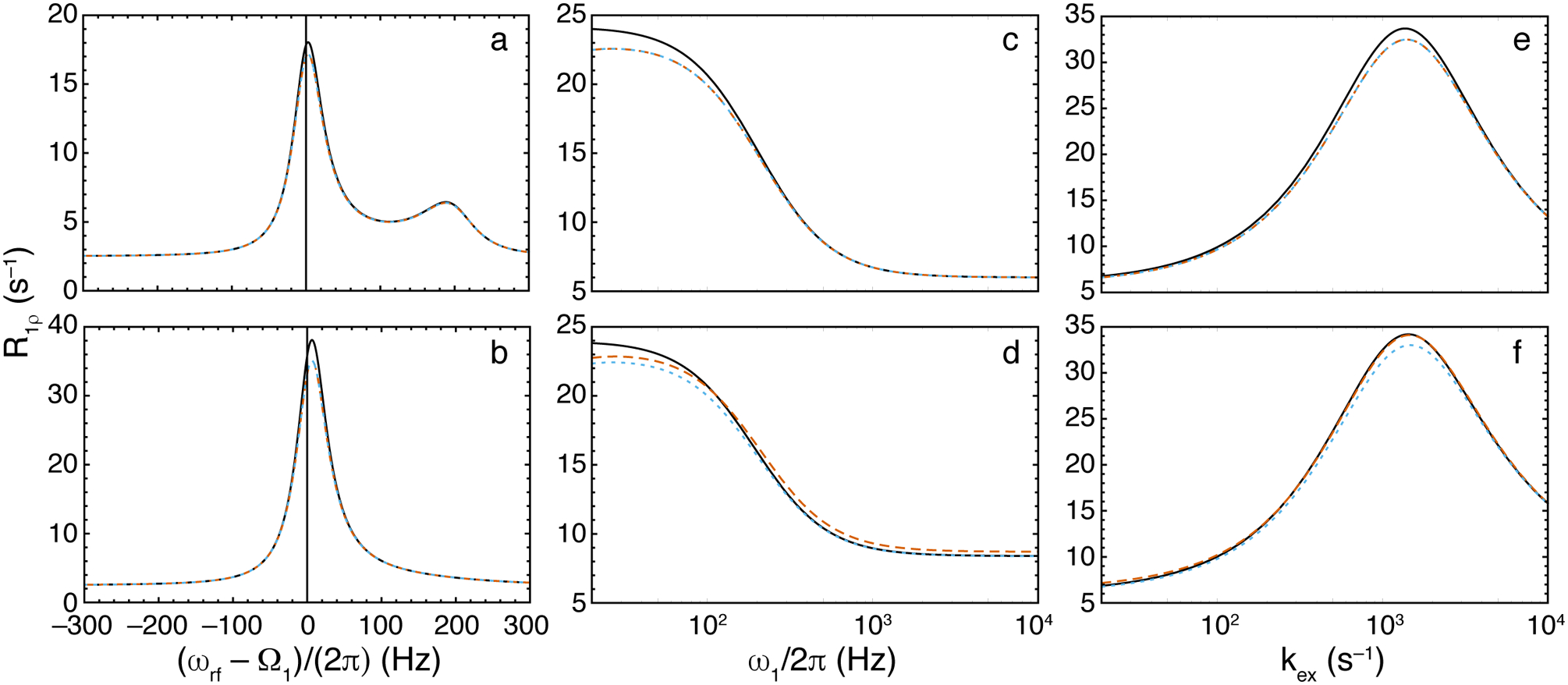
R_1ρ relaxation dispersion curves for 2-site chemical exchange. (black, solid) Numerical eigenvalue, (orange, dashed), Trott-Palmer expression, Eq. 30, (blue, dotted), Eq. 32. Parameters common to all calculations are ω₂₁/(2π) = 200 Hz, p₂ = 0.05, and R₁₁ = R₁₂ = 2.5 s⁻¹. Other parameters are (a) k_ex = 250 s⁻¹, ω₁/(2π) = 25 Hz, R₂₁ = R₂₂ = 6 s⁻¹; (b) as in (a) except k_ex = 1200; (c) ω_rf/(2π) = 0 Hz, k_ex = 400 s⁻¹, R₂₁ = R₂₂ = 6 s⁻¹; (d) as in (c) except R₂₂ = 60 s⁻¹; (e) ω_rf/(2π) = 0 Hz, ω₁/(2π) = 100 Hz, R₂₁ = R₂₂ = 6 s⁻¹; and (f) as in (e), except R₂₂ = 60 s⁻¹.

Koss and coworkers have illustrated results for 3- and 4-site kinetic schemes (Koss et al., 2017). The simplest N-site cases (N > 2) are linear topologies, because the 3N × 3N characteristic equations can be reduced to 3 × 3 matrix polynomials of leading order N. Using this approach, the linear B-A-C scheme has a first-order approximation:

$$\begin{gathered} R_{1\rho }=\frac{-1}{Tr\left\{Y^{-1}X\right\}} \\ X=L_B^{\prime }{L}_A^{\prime }+L_A^{\prime }{L}_C^{\prime }+L_B^{\prime }{L}_C^{\prime }-\left(k_{12}{k}_{21}+k_{13}{k}_{31}\right)I \\ Y=L_B^{\prime }{L}_A^{\prime }{L}_C^{\prime }-k_{13}{k}_{31}{L}_B^{\prime }-k_{12}{k}_{21}{L}_C^{\prime } \end{gathered}$$ (34)

in which $L_n^{\prime }=L_n+K_{nn}\otimes I_3$. The above expression does not include the contribution from relaxation other than chemical exchange. The effects of relaxation can be treated by incorporating the relaxation matrix R_n into $L_n^{\prime }$, approximated as , ${\overline{R}}_1{\text{cos}}^2\theta +{\overline{R}}_2{\text{sin}}^2\theta$ or calculated to first order as in Eq. 9.

Higher-order Newton-Raphson approximations based on the full 3N × 3N matrices L+K+R give results of arbitrary accuracy, which is useful when reduction to N × N matrices schemes is difficult. The examples shown in Figure 6 demonstrate that for complex kinetic schemes (triangular, kite), a second-order Halley approximation for the eigenvalue is applicable to the practically relevant parameter space, and in many cases superior to the approximations of the Woodbury type reported previously (Koss et al., 2017).

Figure 6.

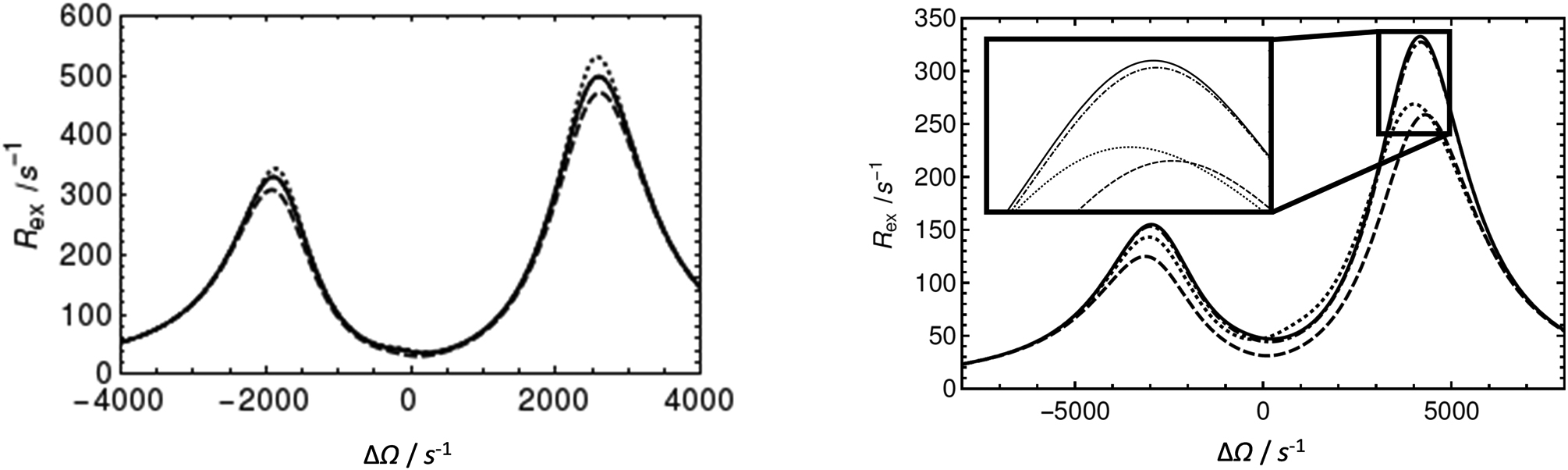
Approximations for N-site kinetic schemes for the R_ex contribution in R_1ρ experiments. (Solid) Numerical calculation of R_ex=−λ/sin2θ from the least negative real eigenvalue of the 12 × 12 evolution matrix, (dashed) calculation from the first order approximation from Eq. 11 in Koss et al., 2017, (dotted) calculation from the Woodbury approximation from Eq. 50 in Koss et al., 2017, (dashed-dotted) calculation from the new second-order eigenvalue (Halley) approximation from Eq. 27 in this paper and Eq. 11 in Koss et al, 2017. This (dashed-dotted) approximation overlaps almost perfectly with the numerical solution. Left: Approximations for the triangular scheme (see Fig. 3 for the respective CPMG figure). k₁₂ + k₂₁ = 200 s⁻¹; k₁₃ + k₃₁ = 300 s⁻¹; k₂₃ + k₃₂ = 600 s⁻¹; Δω_AB = 1800 s⁻¹; Δω_AC = −2600 s⁻¹; p_A = 0.85; p_B = 0.08; p_C = 0.07. Right: Approximations for the 4-site kite scheme. The insets exemplify regions in which the results of the calculations differ. Parameters used for all calculations were used for all calculations were ω₁ = 1250 s⁻¹; k₁₂ + k₂₁ = 140 s⁻¹, k₁₃ + k₃₁ = 350 s⁻¹, k₃₄ + k₄₃ = 700 s⁻¹ and k₁₄ + k₄₁ = 350 s⁻¹, Ω_B − Ω_A = −850 s⁻¹, Ω_C − Ω_A = 2550 s⁻¹, and Ω_D − Ω_A = −4250 s⁻¹. p_A = 0.79, p_B = 0.08, p_C = 0.06, p_D = 0.07.

3. Experimental Techniques and Examples

A large number of variations of NMR experimental methods for investigation of chemical exchange in proteins and nucleic acids have been reported. Many of these experiments have been developed to account for particular isotopic labeling patterns or spin topologies. The following sections address issues that arise in application of the above theoretical results when analyzing experimental data, rather than discussing particular pulse sequences; for the latter, see recent reviews (Francesca Massi & Peng, 2018; A. G. Palmer, 2014; A. G. Palmer, 3rd, Grey, & Wang, 2005; Sauerwein & Hansen, 2015; Vallurupalli et al., 2017; Walinda et al., 2018b). Practical experimental guidelines have been discussed in other reviews (Ishima, 2014; Kempf & Loria, 2004; Francesca Massi & Peng, 2018; Walinda et al., 2018a, 2018b; Xue et al., 2015).

3.1. ZZ-exchange

If chemical exchange is slow enough and populations of minor sites large enough that the resonances for minor sites are observable, then chemical exchange rate constants are conveniently obtained using ZZ-exchange experiments. These experiments are the analogues to the ¹H NOESY experiments, but have the advantage of lacking numerous confounding NOE cross peaks. In proteins, for example, ¹⁵N ZZ-exchange experiments are devoid of ¹⁵N-¹⁵N NOE cross-peaks owing to the low magnetogyric ratio of the ¹⁵N nucleus and the long distance between ¹⁵N atoms. ZZ-exchange experiment for uniformly ¹³C labeled molecules may contain ¹³C-¹³C NOE cross peaks, usually between directly bonded atoms. Pulse sequences have been described in which the chemical exchange occurs between longitudinal magnetization (Farrow et al., 1995; Hwang & Kay, 2005; H. Wang et al., 2002), longitudinal two-spin order (Montelione & Wagner, 1989; Sprangers, Gribun, Hwang, Houry, & Kay, 2005), and single transition operators (Y. Li & Palmer, 2009), and in which detection of the signal utilizes HSQC, TROSY-detection (Hwang & Kay, 2005; Sahu, Clore, & Iwahara, 2007; Sprangers et al., 2005), and TROSY-selection (Y. Li & Palmer, 2009) methods.

For 2-site exchange,

$$\begin{gathered} \frac{d}{dt}\left[\begin{array}{l}\langle M_{z1}\rangle \left(t\right)\hfill \\ \langle M_{z2}\rangle \left(t\right)\hfill \end{array}\right]=\left\{\left[\begin{array}{cc}-R_{11}& 0\\ 0& -R_{12}\end{array}\right]+\left[\begin{array}{cc}-k_{12}& k_{21}\\ k_{12}& -k_{21}\end{array}\right]\right\}\left[\begin{array}{c}\langle M_{z1}\rangle \left(t\right)\\ \langle M_{z2}\rangle \left(t\right)\end{array}\right] \\ =\left[\begin{array}{cc}-R_{21}-k_{12}& k_{21}\\ k_{12}& -R_{22}-k_{21}\end{array}\right]\left[\begin{array}{c}\langle M_{z1}\rangle \left(t\right)\\ \langle M_{z2}\rangle \left(t\right)\end{array}\right] \end{gathered}$$ (35)

The above equation is written for z-magnetization, but as noted ZZ-exchange experiments can be based on other components of the density operator, such as longitudinal two-spin order. The integrated solution to this equation is:

$$\left[\begin{array}{c}\langle M_{z1}\rangle \left(t\right)\\ \langle M_{z2}\rangle \left(t\right)\end{array}\right]=\left[\begin{array}{cc}{a}_{11}\left(t\right)& a_{12}\left(t\right)\\ a_{21}\left(t\right)& a_{22}\left(t\right)\end{array}\right]\left[\begin{array}{c}\langle M_{z1}\rangle \left(0\right)\\ \langle M_{z2}\rangle \left(0\right)\end{array}\right]$$ (36)

in which the eigenvalues of the evolution matrix are:

$${\lambda }_{\pm }=\frac{1}{2}\left\{R_{11}+R_{12}+k_{12}+k_{21}\pm {\left[{\left(k_{12}-k_{21}+R_{11}-R_{12}\right)}^2-4k_{12}{k}_{21}\right]}^{1/2}\right\}$$ (37)

and the mixing coefficients are given by:

$$\begin{gathered} a_{11}\left(t\right)=\frac{1}{2}\left[\left(1-\frac{k_{12}-k_{21}+R_{11}-R_{12}}{{\lambda }_{+}-{\lambda }_{-}}\right)\text{exp}\left(-{\lambda }_{-}t\right)+\left(1+\frac{k_{12}-k_{21}+R_{11}-R_{12}}{{\lambda }_{+}-{\lambda }_{-}}\right)\text{exp}\left(-{\lambda }_{+}t\right)\right] \\ {a}_{22}\left(t\right)=\frac{1}{2}\left[\left(1+\frac{k_{12}-k_{21}+R_{11}-R_{12}}{{\lambda }_{+}-{\lambda }_{-}}\right)\text{exp}\left(-{\lambda }_{-}t\right)+\left(1-\frac{k_{12}-k_{21}+R_{11}-R_{12}}{{\lambda }_{+}-{\lambda }_{-}}\right)\text{exp}\left(-{\lambda }_{+}t\right)\right] \\ {a}_{12}\left(t\right)=\frac{k_{21}}{{\lambda }_{+}-{\lambda }_{-}}\left[\text{exp}\left(-{\lambda }_{-}t\right)-\text{exp}\left(-{\lambda }_{+}t\right)\right] \\ {a}_{21}\left(t\right)=\frac{k_{12}}{{\lambda }_{+}-{\lambda }_{-}}\left[\text{exp}\left(-{\lambda }_{-}t\right)-\text{exp}\left(-{\lambda }_{+}t\right)\right] \end{gathered}$$ (38)

In a conventional two-dimensional ZZ-exchange experiment, t₁ frequency labeling occurs prior to the mixing time t, resulting in two auto-peaks and two cross-peaks for each exchanging spin. The integrated auto- and cross-peak amplitudes resulting from this experiment are given by I_jk(t) = a_jk(t) M_zk(0).

Direct global fitting of the time dependence of the two auto- and cross-peak intensities (measured as peak heights) is prone to systematic errors from the effects of differential relaxation during parts of the experiment other than the relation delay, t, particularly the t₂ acquisition period. Miloushev and coworkers proposed a simplified analysis (Miloushev et al., 2008):

$$\Xi \left(t\right)=\frac{I_{12}\left(t\right)I_{21}\left(t\right)}{I_{11}\left(t\right)I_{22}\left(t\right)-I_{12}\left(t\right)I_{21}\left(t\right)}\approx k_{12}{k}_{21}{t}^2$$ (39)

that is insensitive to such effects. In addition, this equation is independent of moderate differences between R₁₁ and R₁₂, does not require iterative curve-fitting, and is easily used in a global analysis of multiple spins subject to the same exchange process, because the right-hand-side depends only on the exchange rate constants. In order to obtain k₁₂ and k₂₁ individually, the equilibrium constant K_eq = k₁₂/k₂₁ must be known independently or measured from integrated peak volumes using the HSQC₀ approach of Markley and coworkers (Hu, Westler, & Markley, 2011). In an alternative method, Kloiber and coworkers noted that if a second experiment is recorded in which the mixing period is moved prior to the t₁ period, then only auto-peaks are observed with amplitudes given by I_j(t) = [a_jj(t) + a_jk(t)]M_zk(0). A global analysis of the time dependence of I₁₁(t) and I₂₂(t), I₁(t), and I₂(t) allows determination of k₁₂, k₂₁, R₁₁, and R₁₂.(Kloiber, Spitzer, Grutsch, Kreutz, & Tollinger, 2011) This approach also is robust against variations in relaxation during the t₂ acquisition period. For time delays from ~0 to ~0.5/(k₁₂+k₂₁), simulations, such as those shown in Figure 7, suggest that the two methods have similar precisions (although the second approach requires acquiring two spectra at each mixing time). Which approach is optimal in a given situation then depends on whether both I₁₂(t) and I₂₁(t) cross-peaks are resolved in the ZZ-exchange spectra for a suitable number of spins, which is required for the convenient global analysis offered by the approach of Miloushev and coworkers.

Figure 7.

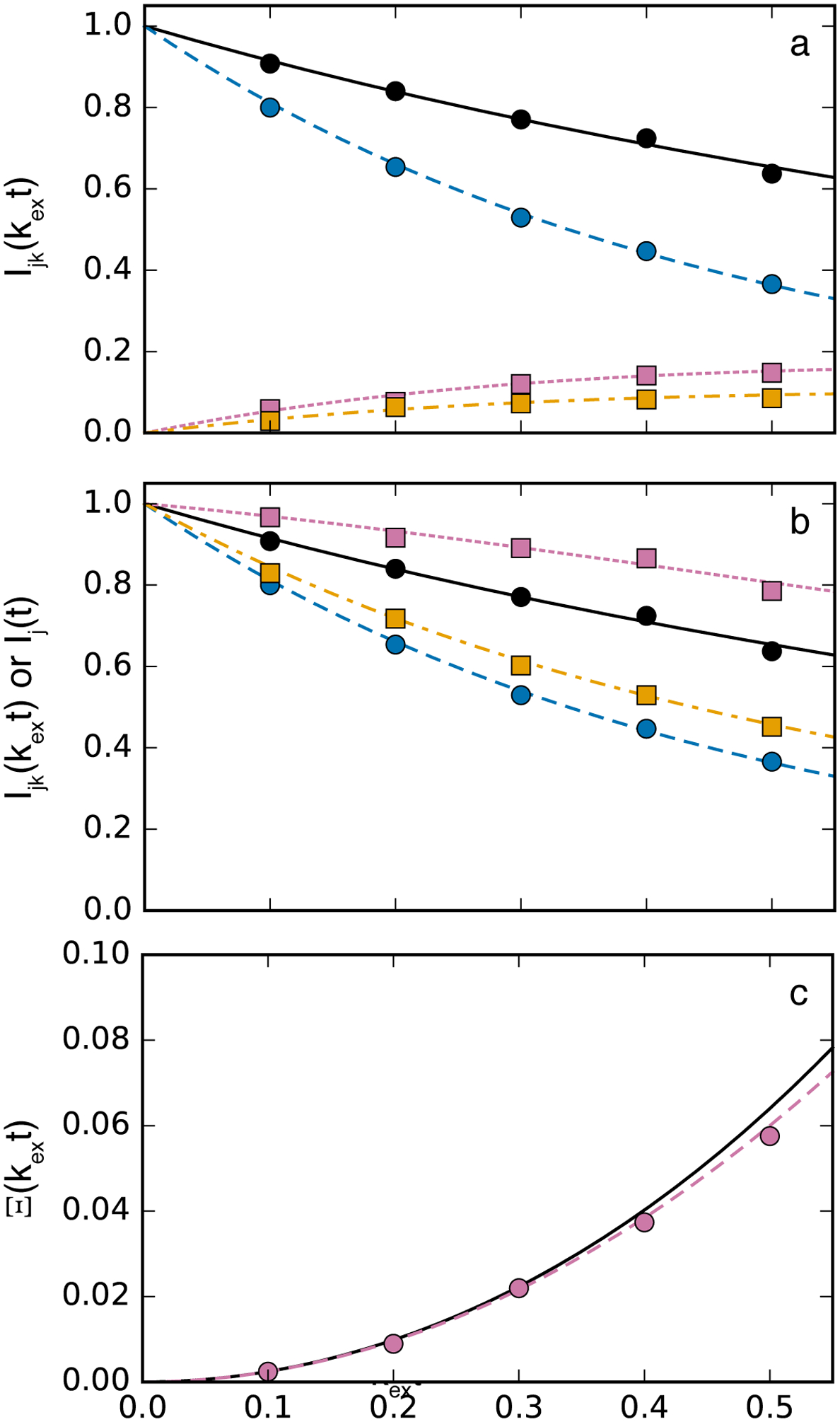
ZZ-exchange relaxation. (top) Normalized amplitudes (black, solid) I₁₁(t), (blue, dashed), I₂₂(t), (reddish-purple, dotted) I₁₂(t), and (orange, dash-dotted) I₂₁(t). (middle) Normalized amplitudes (black, solid) I₁₁(t), (blue, dashed), I₂₂(t), (reddish-purple, dotted) I₁(t), and (orange, dash-dotted) I₂(t). (bottom) Ξ(T) with (black, solid) calculated from best fit values from the analysis of the middle figure and (reddish-purple, dotted) calculated from Eq. 39. Circles, with same color coding as lines, show one of the simulated data sets and lines are calculated from best fit values. Simulations used R₁₁/k_ex = 0.5, R₁₂/k_ex = 1.5, p₁ = 0.6, p₂ = 0.4. Five hundred simulations were performed assuming a standard deviation for amplitudes of 0.01.

A recent example of the use of the ¹H-¹⁵N ZZ-exchange experiment investigated folding kinetics of autonomously folding protein domains derived from the ribosomal protein L9 using high-pressure NMR spectroscopy (Zhang et al., 2016). Figure 8 shows results for three residues in the C-terminal domain of the I98A mutant of L9. As in the original work, data for individual peak intensities shown in Fig. 8a–c were fit simultaneously using Eq. 38 to give individual kinetic rate constants for each residue. Figure 8d shows the global analysis of data for the three residues using Eq. 39 to obtain k₁₂k₂₁. The simplicity of the global analysis is evident. However, as shown, only data at shorter mixing times should be used in the global analysis; at long values of T, the denominator in Eq. 39 approaches 0 and uncertainties in Ξ(T) are amplified.

Figure 8.

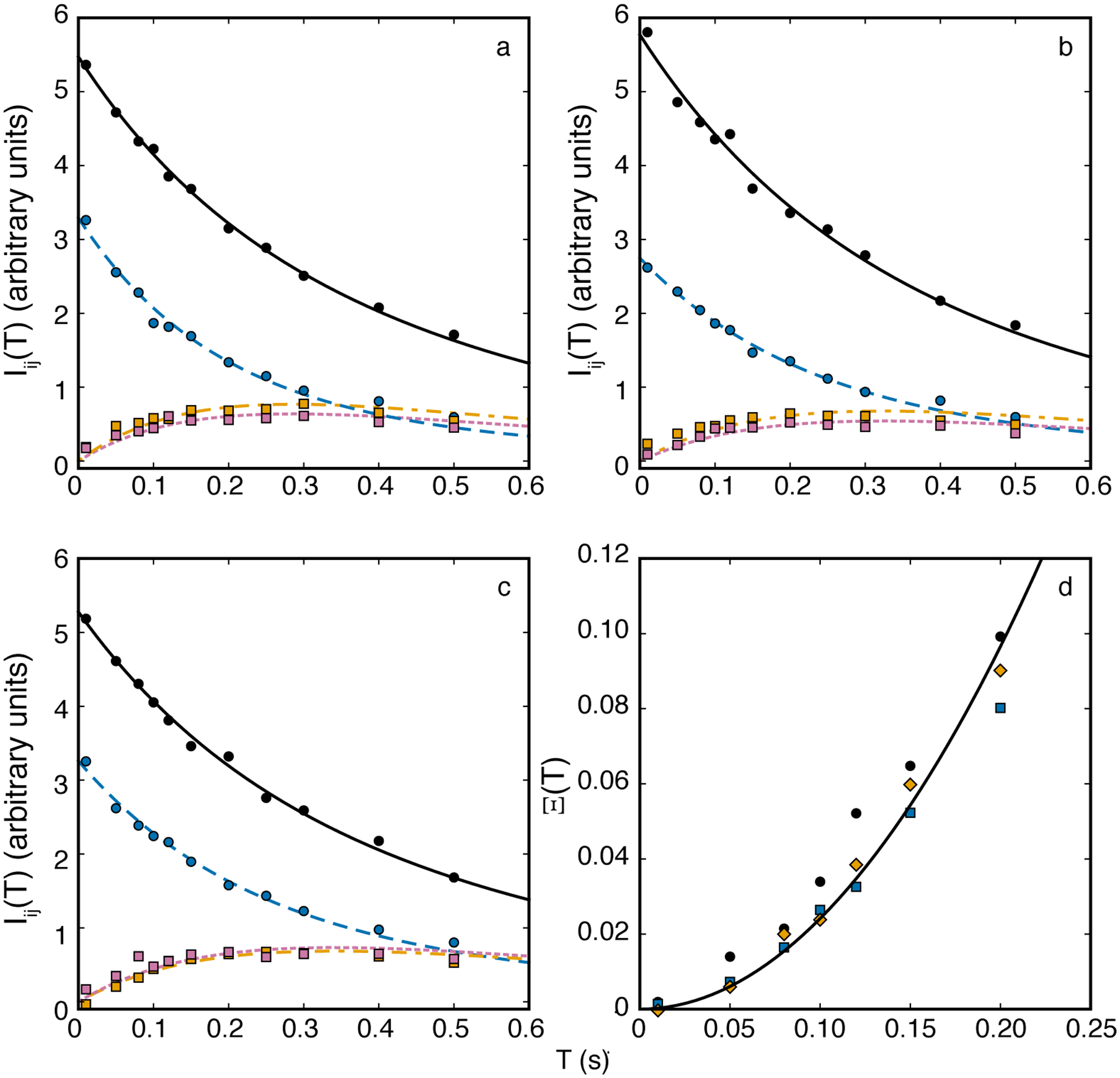
ZZ-exchange spectroscopy for the C-terminal domain of the I98A mutant of L9 protein for residues (a) 70, (b) 71, and (c) 72 at a static pressure of 300 bar. Solid lines in each panel are fits of the auto-peaks for (black, solid, circles) folded and (blue, dashed, circles) unfolded states and two cross peaks for (reddish-purple, dotted, squares) folded → unfolded and (orange, dashed, squares) unfolded → folded states using Eq. 38. (d) Global fit of Ξ(T) for residues (black) 70, (blue) 71, and (orange) 72 fit to Eq. 39. The fitted value of k₁₂k₂₁ = 2.08 ± 0.16 in (d) agrees well with the average value 2.16 ± 0.23 obtained from the fits in (a-c). Data were obtained from Zhang et al (Zhang et al., 2016).

3.2. Hahn-Echo, CPMG and R_1ρ Experiments

Hahn-echo relaxation experiments measure the transverse relaxation rate constant from a spectrum recorded with one or two spin-echo periods, in which the total time T is as long as feasible (consistent with sensitivity) to mimic the free-precession relaxation rate constant. In the simplest approach, a second spectrum is recorded in which the spin-echo periods are omitted. The relaxation rate constant is obtained from the ratio of signal intensities in the two experiments, I(T)/I(0), using Eq. 5. As shown in Figure 9, numerical simulations for a single spin echo, compared with the exact free-precession R₂ (given by the real part of Eq. 11) show that the Hahn-echo experiment closely approximates the free-precession relaxation rate constant if exchange is fast (k_ex/Δω₂₁ > 4) or T is sufficiently long (T greater than ~10/Δω₂₁). Differential relaxation, in which R₂₂ ≠ R₂₁ improves agreement between the exact eigenvalue and the Hahn-echo result (not shown).

Figure 9.

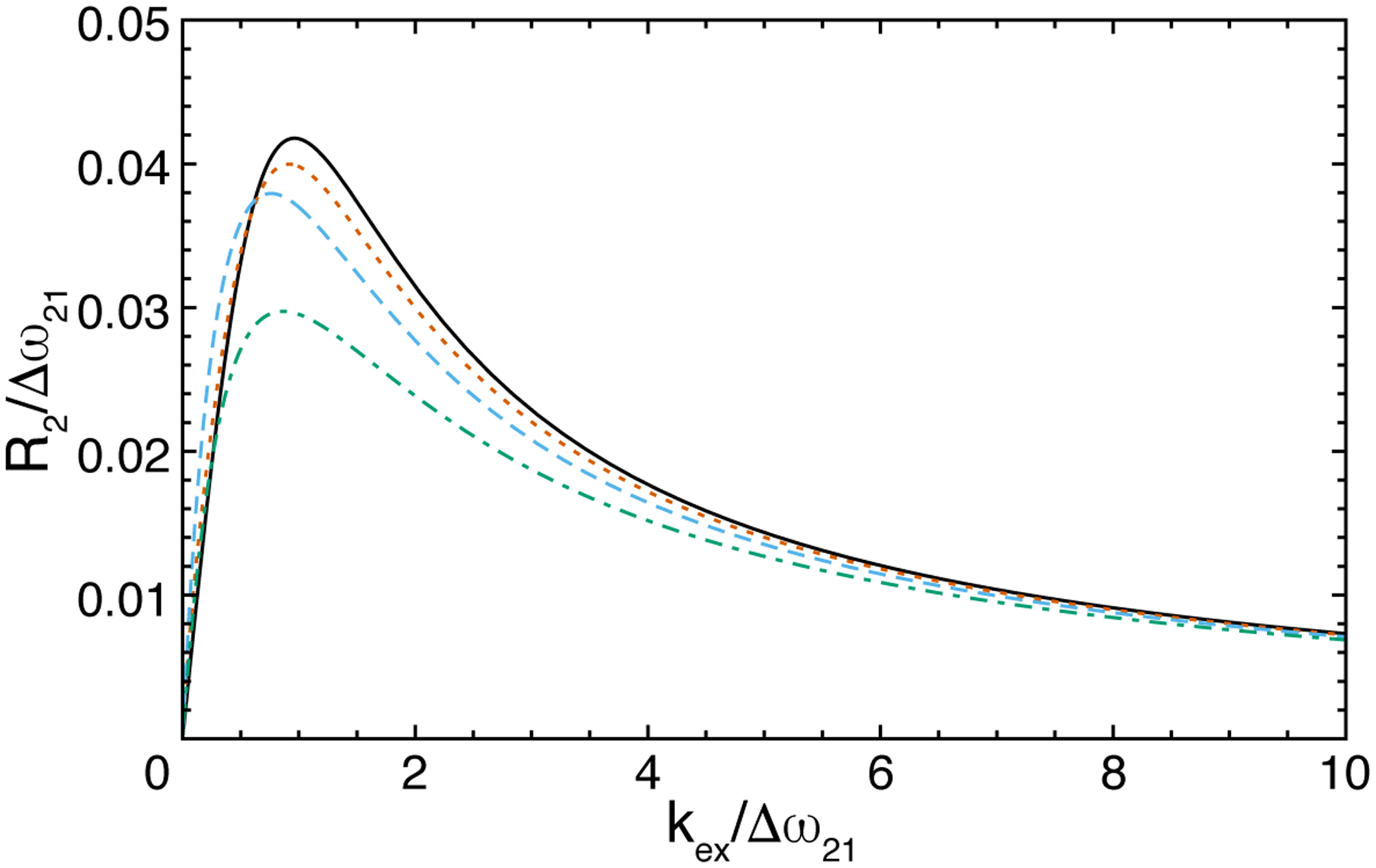
Hahn-echo transverse relaxation rate constant for 2-site chemical exchange with p₂ = 0.08 and R₂₁ = R₂₂ = 0. (black, solid) Exact R₂ given as the real part of eigenvalue for free-precession (Eq. 11) and Hahn-echo for single spin-echo with total time (blue, dashed) t = 25/Δω₂₁, (orange, dotted) t = 10/Δω₂₁, and (green, dash-dotted) t = 5/Δω₂₁.

A number of Hahn-echo experimental methods have been described in the literature. Examples include the ¹H-¹⁵N TROSY Hahn-echo (C. Wang, Rance, & Palmer, 2003), ¹³C^α Hahn-echo (O’Connell et al., 2009), and the ¹³CH₃ methyl zero-quantum TROSY Hahn-echo experiments (Gill & Palmer, 2011; Ollerenshaw, Tugarinov, Skrynnikov, & Kay, 2005; Tugarinov et al., 2004). In particular, the ¹³CH₃ methyl zero-quantum TROSY Hahn-echo experiment recently has been applied to characterization of chemical exchange in the DNA-repair enzyme AlkB (Gill & Palmer, 2011) and in G_α proteins (Toyama et al., 2017).

The CPMG experiment depends on acquisition of a relaxation dispersion curve in which the relaxation rate constants for spins of interest are measured as functions of τ_cp. In coupled spin systems, the evolution of scalar coupling interactions also varies as τ_cp is changed. This results in deleterious τ_cp-dependent averaging of relaxation rate constants of in-phase and anti-phase magnetization. The first solution to this difficulty was the relaxation-compensated CPMG experiment, in which in-phase and anti-phase magnetization components are interchanged halfway through the CPMG pulse train in order to exactly average the in-phase and anti-phase relaxation rate constants, rendering the average independent of τ_cp (Loria, Rance, & Palmer, 1999a). Since the original description of the relaxation-compensated ¹⁵N CPMG experiment, numerous variants have been developed for applications to a variety of spin systems in both proteins and nucleic acids (Sauerwein & Hansen, 2015; Walinda et al., 2018b). The second solution to this difficulty employs spin-decoupling methods to prevent evolution of the scalar coupling. Decoupling must be carefully executed to avoid interfering with proper refocusing of the CPMG spin echoes, but has the advantage of avoiding averaging between in-phase and anti-phase magnetization (Hansen, Vallurupalli, & Kay, 2008a) TROSY(Loria, Rance, & Palmer, 1999b) and BEST-TROSY (Franco et al., 2017) versions of this experiment that improve sensitivity also have been reported.

Only chemical exchange on a time scale covered by the τ_cp range of the CPMG experiment can be detected. For slow exchange, τ_cp therefore has to be large. For large τ_cp, oscillations in the CPMG curve can be observed for slow exchange. Tollinger et al. have found that the oscillations can be described by a functional form depending on sinc(Δω₂₁τ_cp) for very slow exchange (Eq 2 in (Tollinger et al., 2001)). Recently, Koss and coworkers derived analytical expressions for slow N-site exchange (N ≥ 2) that include sinc²(Δω_ijτ_cp) terms (Eqs. 27 and 28 for example) (Koss, Rance, et al., 2018). These expressions approximate the dominant single eigenvalue of the average magnetization evolution matrix; higher-order eigenvalue eigenvalue approximations yield results which are very similar to those obtained from the Carver-Richards equation (for N = 2). The maxima for sinc(Δω₂₁τ_cp) and sinc2(Δω₂₁τ_cp), are identical, at τ_cp = nπ/|Δω₂₁|; the integral for both functions (0 < τ_cp < ∞) is π/2. The sinc(Δω₂₁τ_cp) functional dependence describes oscillations in the dispersion profile better for very slow exchange and very large minor populations (Tollinger et al., 2001); in these special cases, exchange cannot be described using the dominant single eigenvalue. For slow-to-intermediate exchange or smaller minor site populations, the sinc²(Δω₂₁τ_cp) functional dependence gives more accurate results. Analysis of the oscillatory region might be useful to distinguish kinetic schemes: For two-site exchange, sinc²(Δω₂₁τ_cp) (or sinc(Δω₂₁τ_cp)) depends on Δω₂₁τ_cp and directly describes the oscillations, while N-site (N > 2) exchange gives more complex oscillatory patterns. For kinetic schemes with increasing complexity, approximations based on a single dominant eigenvalue become more reliable because the single-eigenvalue model only become invalid for large τcp when the number of sites connected to the major site is 1 or 2, in combination with exclusively very slow exchange, including very slow exchange between minor sites. CPMG data at large τ_cp can be obtained be obtained either by increasing T without changing the number of CPMG cycles, which reduces sensitivity, or by reducing the number of CPMG cycles during a given T. Relaxation-compensated CPMG experiments, however, require a minimum number of 2 cycles. CPMG experiments using ¹H continuous wave decoupling during the relaxation element can be used to overcome this problem by maintaining in-phase magnetization throughout the relaxation delay (Hansen, Vallurupalli, et al., 2008a).

A drawback of the CPMG experiment is that only the magnitude and not the sign of Δω_n1 is obtained from analysis of CPMG relaxation dispersion curves. This disadvantage of the CPMG experiment, compared to the R_1ρ experiment, is offset by the number of available experimental methods and relative ease of CPMG methods. For 2-site exchange, Kay and coworkers have shown that differences in F₁ resonance frequencies between HSQC and HMQC experiments are indicative of the sign of chemical shift difference between states, provided exchange is not too fast (Skrynnikov, Dahlquist, & Kay, 2002). Thus, this technique is an important complement to ¹⁵N and ¹³C CPMG experiments.

As described above, the main strength of R_1ρ measurements over other approaches for characterizing chemical exchange when ZZ-exchange measurements are not feasible, compared with Hahn-echo and CPMG methods, is the sensitivity of the R_1ρ relaxation rate constant to the resonance frequencies of otherwise unobservable sparsely populated states. In many cases, experimental methods for R_1ρ measurements are similar to those used for CPMG relaxation dispersion studies, except that the CPMG pulse train is replaced by a spin-locking sequence, which in the simplest case is continuous-wave radiofrequency field, but might be phase-modulated or applied as an adiabatic sweep. Particular experimental methods differ in how the desired spin magnetization is aligned with the effective field in the rotating frame and in how the effects of scalar coupling interactions are treated. As for other experiments, TROSY and non-TROSY versions of many sequences have been reported (Francesca Massi & Peng, 2018). More recently, R_1ρ measurements for methyl groups (Weininger et al., 2013) or aromatic side chains (Weininger et al., 2014) have come into focus, as well as experiments to characterize slow dynamics in nucleic acids (Xue et al., 2015; Zhao, Hansen, & Zhang, 2014).

3.3. CEST and DEST

As originally described by Allerhand and Thiele, the limiting effect of chemical exchange on spin relaxation can be described as C-type or R-type, depending on whether the differences in chemical shifts or relaxation rates between states dominates (Allerhand & Thiele, 1966). These two cases have been exemplified in modern CEST (Bouvignies & Kay, 2012; Vallurupalli, Bouvignies, & Kay, 2012) and DEST (Fawzi, Ying, Ghirlando, Torchia, & Clore, 2011) experiments, respectively. Both experiments record changes in resonance signal intensities as functions of the resonance offset and amplitude of a spin-locking radiofrequency field. As such, both CEST and DEST experiments can be considered as variants of the general R_1ρ experiment and are described by the same theory as described above for R_1ρ relaxation (A. G. Palmer, 2014; Zhao et al., 2014). Methods for improving the time efficiency of CEST experiments have been developed that use multi-site excitation with DANTE (Yuwen, Kay, & Bouvignies, 2018) or appropriately designed shaped pulses (Leninger, Marsiglia, Jerschow, & Traaseth, 2018). For ¹H-CEST experiments, a longitudinal relaxation optimized sequence has been developed (Yuwen & Kay, 2017).

More specifically, CEST or DEST experiment measures I(T)/I(0) for values of the resonance frequency of the radiofrequency field, ω_rf, stepped through the spectral region of interest, and usually repeated for at least two values of ω₁. As a consequence of the above considerations, the observed intensity signal in the CEST or DEST experiments is:

$$I\left(T\right)/I\left(0\right)={\text{cos}}^2\theta \text{exp}\left(-T\cdot R_{1\rho }\right)$$ (40)

in which T is the length of the irradiation period. In contrast to conventional R_1ρ experiments, the spin magnetization is not rotated to the tilted reference frame prior T and back to the rotating after T. Thus, in Eq. 40, one factor of cosθ results from projection of the initial longitudinal magnetization onto the tilted reference frame (this factor rapidly approaches unity for weak radiofrequency fields off-resonance with respect to the population-average chemical shift) and a second factor of cosθ results from projection of the magnetization locked along the direction of the effective field during T back onto the z-axis after the end of the irradiation period T (transverse magnetization after the irradiation period is dephased by a z-filter gradient pulse). This analysis does not consider the contribution near resonance from evolution of magnetization components orthogonal to the tilted z-axis; for long irradiation times used in CEST and DEST experiments, these components dephase owing to R_2ρ relaxation. An alternative, equally valid, approach treats CEST and DEST experiments as modifications of the classic saturation transfer method introduced by Hoffman and Forsén (Forsén & Hoffman, 1963). In this approach, data analysis requires curve-fitting by numerical integration of the Bloch-McConnell equations, for example Eq. 1 with parameters defined in Eq. 29, rather than direct application of the analytical expression Eq. 40.

In support of the above interpretation, Figure 10 illustrates the approach of the evolving magnetization towards the state described by Eq. 40. Large oscillations arising from magnetization components orthogonal to the effective field are observed when the spin-locking field is on-resonance with the major state (Fig. 10b). The magnetization decays toward zero through a combination of R_1ρ and R_2ρ processes, while B₁ inhomogeneity accelerates the damping process. Off-resonance from the major state, the contribution of orthogonal magnetization is reduced (Fig. 10a and c). Importantly, the effects of orthogonal magnetization are reduced on-resonance with the minor state (Figure 10d). In the example shown, T ≥ 0.25 s assures that Eq. 40 is applicable. The effects of B₁ inhomogeneity are reduced off-resonance from the major state, when resonance offset dominates ω₁, but become more significant as ω₁ is increased. Thus, R_2ρ relaxation contributes to damping of orthogonal magnetization components in the “transient regime” (unless B₁ inhomogeneity or ω₁ is large), but once these components decay to zero at times T commonly employed in practice, Eq. 40 is accurate description of the CEST profile.

Figure 10.

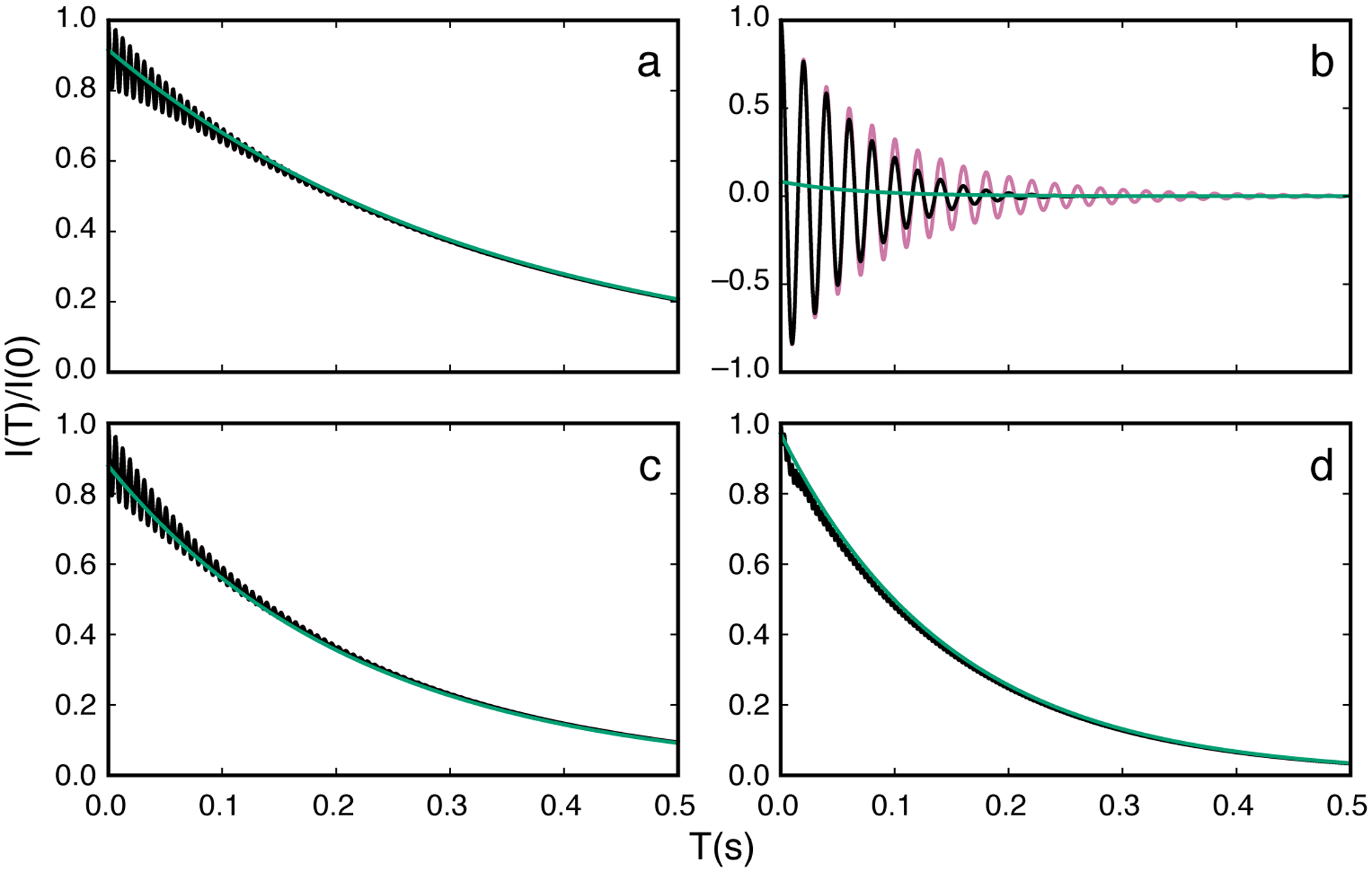
Time evolution of magnetization in CEST experiments. Parameters used for calculations were Δω₂₁/2π = 200 Hz, ω₁/2π = 50 Hz, k_ex = 100 s⁻¹, R₁₁ = R₁₂ = 2.0 s⁻¹, R₂₁ = R₂₂ = 20 s⁻¹, and T = 0.3 s. (reddish-purple or gray, oscillating) Numerical integration of the Bloch-McConnell equations for the nominal value of ω₁, (black, oscillating) numerical integration of the Bloch-McConnell equations for a Gaussian distribution of spin-lock field strengths centered on the nominal value of ω₁ with a standard deviation of 3%, and (green or light gray) Eq. 40 using a numerical eigenvalue of L+K+R. Panels show decay curves for ω_rf/2π = (a) −100 Hz, (b) 0 Hz (on-resonance with major state), (c) 100 Hz, and (d) 200 Hz (on-resonance with minor state).

Equation 40 assumes that either spin-spin interactions are decoupled, or the applied radiofrequency field has amplitude ω₁ >> πJ, in which J is the scalar coupling constant. If these conditions are not satisfied, then each multiplet component in the irradiated spin system experiences a different resonance offset, and hence different relaxation decay profile. This situation has been investigated for R_1ρ relaxation by Igumenova and Palmer and for CEST by Zhou and Yang (Igumenova et al., 2007; Zhou & Yang, 2014). In the simplest case of an IS spin system in which the S spin is irradiated,

$$\begin{gathered} I_{\alpha }\left(T\right)/I_{\alpha }\left(0\right)={\text{cos}}^2{\theta }_{\alpha }\text{exp}\left(-T\cdot R_{1p}^{\alpha }\right) \\ {I}_{\beta }\left(T\right)/I_{\beta }\left(0\right)={\text{cos}}^2{\theta }_{\beta }\text{exp}\left(-T\cdot R_{1\rho }^{\beta }\right) \end{gathered}$$ (41)

In these expressions “α” refers to the S spin magnetization for which the coupling partner is in the α spin state (and similarly for “β”). The offset frequencies used to calculate the tilt angle and effective fields becomes Ω_i ± πJ, depending on the sign of the scalar coupling and whether the α or β spin states were being considered. The resulting CEST profiles then depend on whether coupled or decoupled in-phase magnetization is detected, as in an HSQC or HMQC experiment, or a single multiplet component is detected, as in a TROSY-selected experiment. Note that decoupling or spin-state selection may be infeasible for homonuclear scalar coupling interactions. Simulations of these cases are shown in Figure 11. In addition, as discussed by Igumenova and Palmer, in the spin-locked tilted frames of reference, cross-relaxation between these magnetization components can occur (Igumenova & Palmer, 2006). The cross relaxation rate constant is dominated by dipole-dipole interactions with remote spins. Thus, cross-relaxation is reduced in molecules in which remote sites are highly deuterated.

Figure 11.

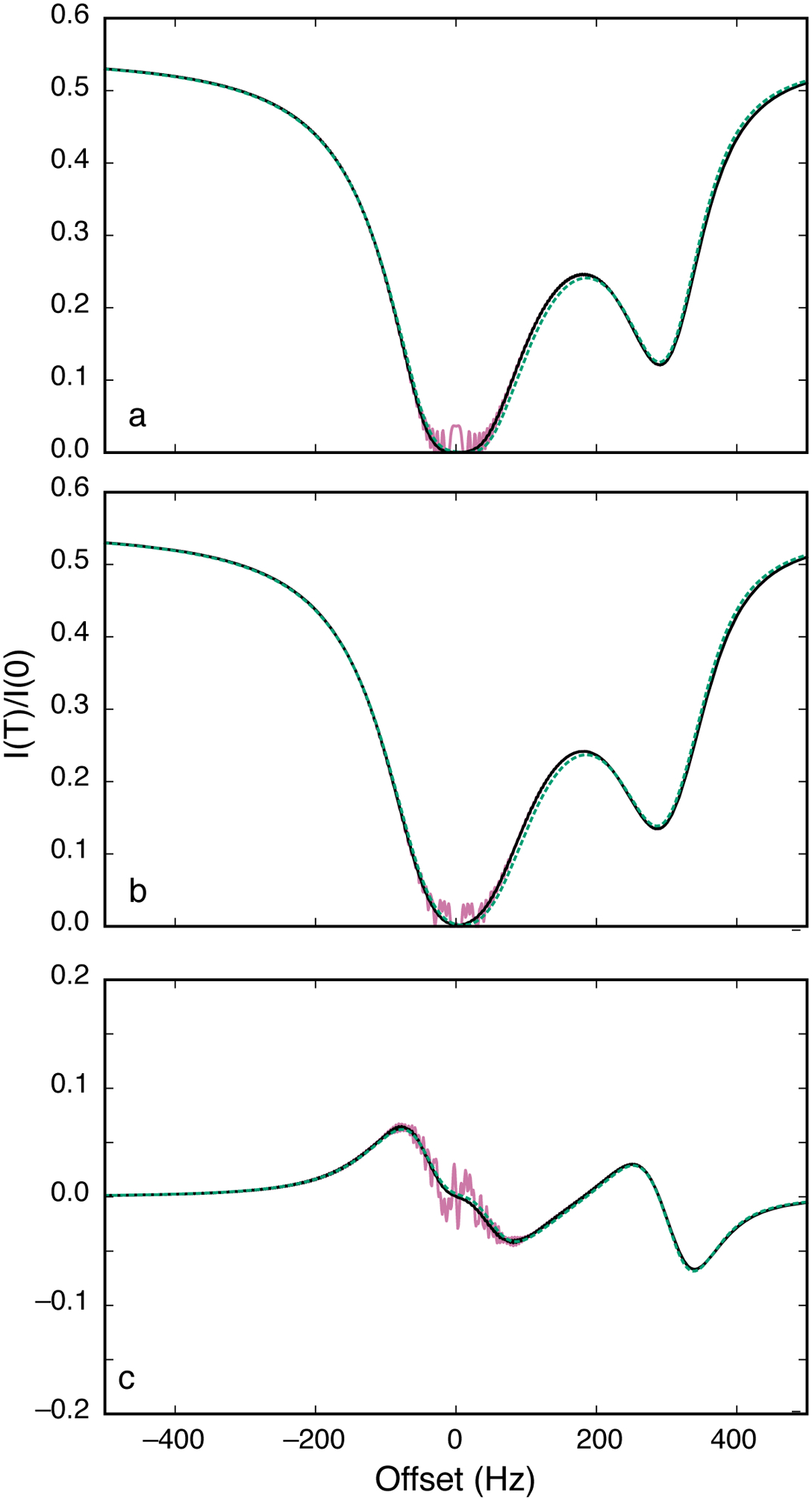
CEST profiles. Parameters used for calculations were Δω₂₁/2π = 300 Hz, ω₁/2π = 50 Hz, k_ex = 100 s⁻¹, R₁₁ = R₁₂ = 2.0 s⁻¹, R₂₁ = R₂₂ = 20 s⁻¹, T = 0.3 s, and J = 33 Hz. (reddish-purple or grey, solid) Numerical integration of the Bloch-McConnell equations for the nominal value of ω₁, (black, solid) numerical integration of the Bloch-McConnell equations for a Gaussian distribution of spin-lock field strengths centered on the nominal value of ω₁ with a standard deviation of 3%, and (green, dotted) Eq. 40 using a numerical eigenvalue of L+K+R. (a) Results are calculated (a) detection of total longitudinal magnetization with decoupling of scalar coupling interactions during T (using Eq. 40) (b) detection of total longitudinal magnetization with no decoupling of scalar coupling interaction during T (using Eq. 42) and (c) detection of longitudinal two-spin order without decoupling of scalar coupling constants (using Eq. 42).

The conceptual simplicity of the CEST experiment can be complicated further by effects other than chemical exchange. As a prominent example, conventional ¹H CEST experiments contain contributions from ¹H-¹H dipole-dipole cross relaxation as well as the effects of the desired chemical exchange phenomena. Yuwen and Kay have described an elegant approach to suppress the artifacts from ¹H-¹H dipole-dipole cross relaxation for amide and methyl groups that makes use of the difference between R_1ρ^α and R_1ρ^β (Yuwen, Sekhar, & Kay, 2017). When the amplitude of the ¹H radiofrequency field used for CEST irradiation satisfies ω₁ < πJ_XH, then ¹H components of the density operator in which the attached heteronuclear spin is in the α or β state are differentially affected by exchange during T, as shown by Eq. 41. As a result, longitudinal two-spin order, 2I_zS_z, is created during T. Subsequently, this two-spin order, rather than z-magnetization as in conventional CEST experiments, is selected and detected. The resulting spectra yield CEST profiles free of dipole-dipole artifacts, because dipole-dipole cross relaxation cannot generate two-spin order. CSA-dipole cross-correlated relaxation does lead to build-up of two-spin order, and can be eliminated by a more complex irradiation scheme, as shown by Yuwen and Kay, but appear to be negligible in practice. An example CEST profile arising from this approach is shown in Fig. 11c.

Equation 32 or the expression obtained by Baldwin and Kay both are accurate for the CEST experiment, provided that ΔR₂₁ is not large (Baldwin & Kay, 2013). However, the DEST experiment relies on ΔR₂₁ >> 0, as for a protein or other molecule interacting with a very large particle, such as a fibril. Equation 32, which is first-order ΔR₂₁, is inaccurate in this limit. The expression obtained by Baldwin and Kay remains accurate, as does the simple result obtained from perturbation theory:

$$\begin{gathered} R_{1\rho }=R_{11}{\text{cos}}^2\theta +R_{21}{\text{sin}}^2\theta +{\text{sin}}^2\theta k_{12}\frac{\left\{\Delta {\omega }_{21}^2+{\left(\Delta R_{21}\right)}^2\right\}{k}_{21}+\Delta R_{21}\left({\omega }_A^2+k_{21}^2\right)}{k_{21}\left\{{\omega }_B^2+{\left(k_{21}+\Delta R_{21}\right)}^2\right\}+\Delta R_{21}{\omega }_1^2} \\ =R_{11}{\text{cos}}^2\theta +R_{21}{\text{sin}}^2\theta +{\text{sin}}^2\theta k_{12} \end{gathered}$$ (42)

in which the second line is obtained as ΔR₂₁ → ∞. In this limit, nearly instantaneous relaxation of spins in site 2 prevents back transfer of magnetization from site 2 to site 1; essentially, the two sites become non-secular in the sense of relaxation theory (vide supra). This result is identical to the the result obtained for C-type exchange if Δω₂₁ → ∞. In addition, if ΔR₂₁ >> Δω₂₁, then Eq. 41 becomes insensitive to C-type exchange and relaxation dispersion arises from R-type relaxation only. Thus, if ΔR₂₁ > 0, chemical exchange can be characterized by R_1ρ relaxation dispersion even if Δω₂₁ = 0 (Yuwen, Brady, & Kay, 2018). Examples of DEST profiles calculated using the above expressions or by numerical integration of the Bloch-McConnell equations (Eq. 1 with parameters as defined in Eq. 29) are shown in Figure 12. The R_1ρ-based approach is seen to be highly accurate in describing the DEST experiment as well as the CEST experiment.

Figure 12.

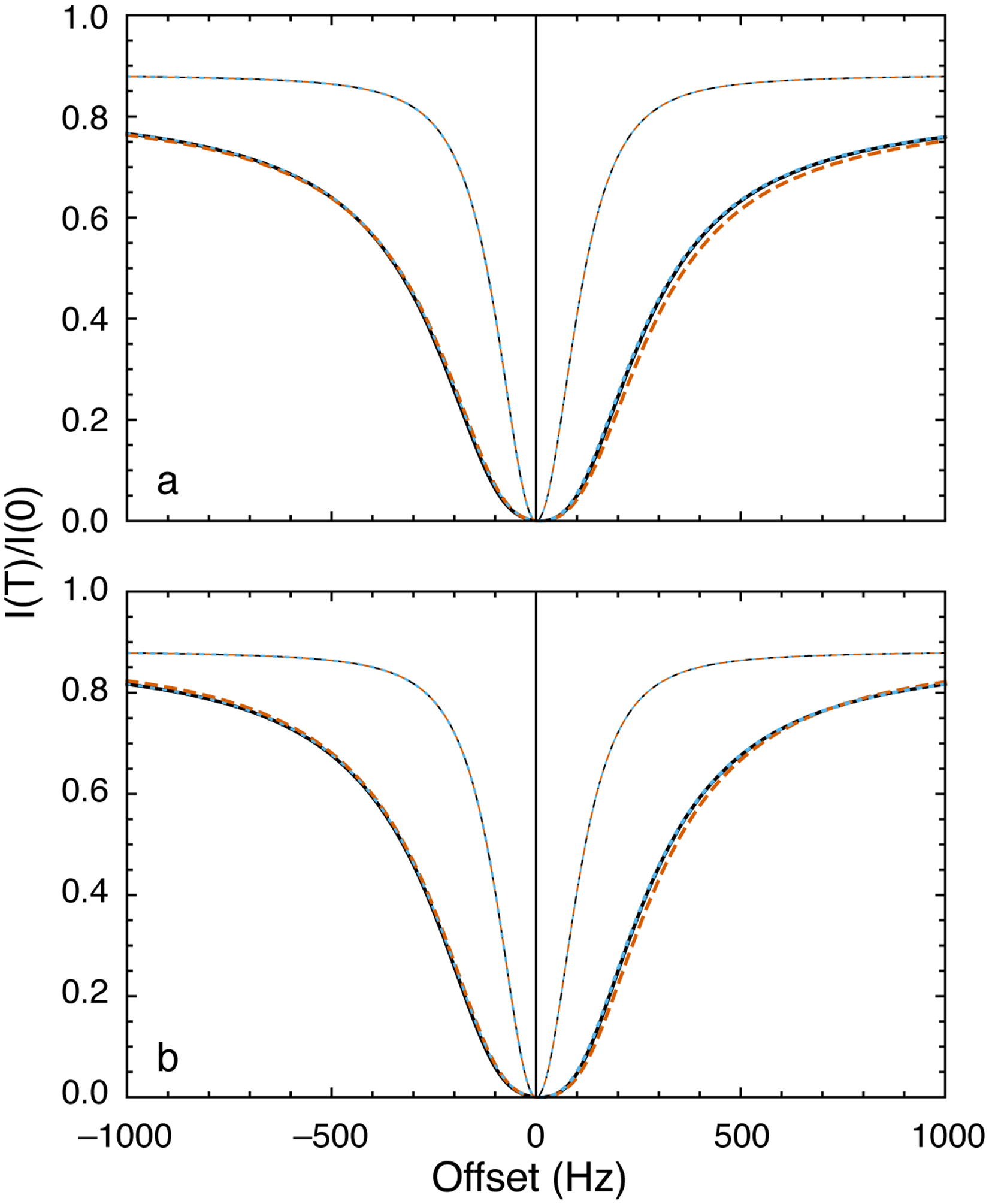
DEST profiles. (a) Parameters used for calculations were Δω₂₁/2π = 200 Hz, ω₁/2π = 200 Hz, k_ex = 1200 s⁻¹, R₁₁ = R₁₂ = 2.5 s⁻¹, R₂₁ = 6 s⁻¹, and ΔR₂₁ = 20,000 s⁻¹. Thick lines show calculations for p₂ = 0.05 and thin lines show calculations for p₂ → 0. (black, solid) Numerical integration of the Bloch-McConnell equations, (blue, dotted) Baldwin-Kay equation,(Baldwin & Kay, 2013) and (orange, dashed) Eqs. 40 and 42. (b) Results are calculated with ΔR₂₁ = 200,000 s⁻¹ and other parameters as in (a). Lines are drawn as in (a) except that the dashed orange line is the limit of Eq. 42 as as ΔR₂₁ → ∞.

Zhang and coworkers have reported a very complete comparison of ZZ-exchange, R_1ρ, and CEST methods applied to the fluoride riboswitch (Zhao et al., 2014). The CEST data were originally analyzed by numerical integration of the Bloch-McConnell equations. The ¹³C CEST data reported for the C8 position of guanine 8 of the riboswitch are shown in Figure 13a. The solid lines show the fit to Eqs. 40 and 42 to highlight the facility of the above interpretation of the CEST experiment. The data analysis using Eqs. 40 and 42 (or the combination of Eqs. 40 and 32) is more efficient than integration of the Bloch-McConnell equations. Of course, R_1ρ can be calculated from the CEST data by inversion of Eq. 40 and a graph of the results obtained by this approach are shown in Figure 13b. The R_1ρ data obtained independently also are shown in Fig. 13c for comparison. The overall profiles are similar, but quantitative differences arise because the initial magnetization in the R_1ρ experiment was selected as the magnetization of the dominant state, as opposed to the CEST experiment, in which the initial magnetization was proportional to the equilibrium magnetization (Xue et al., 2015; Zhao et al., 2014).

Figure 13.

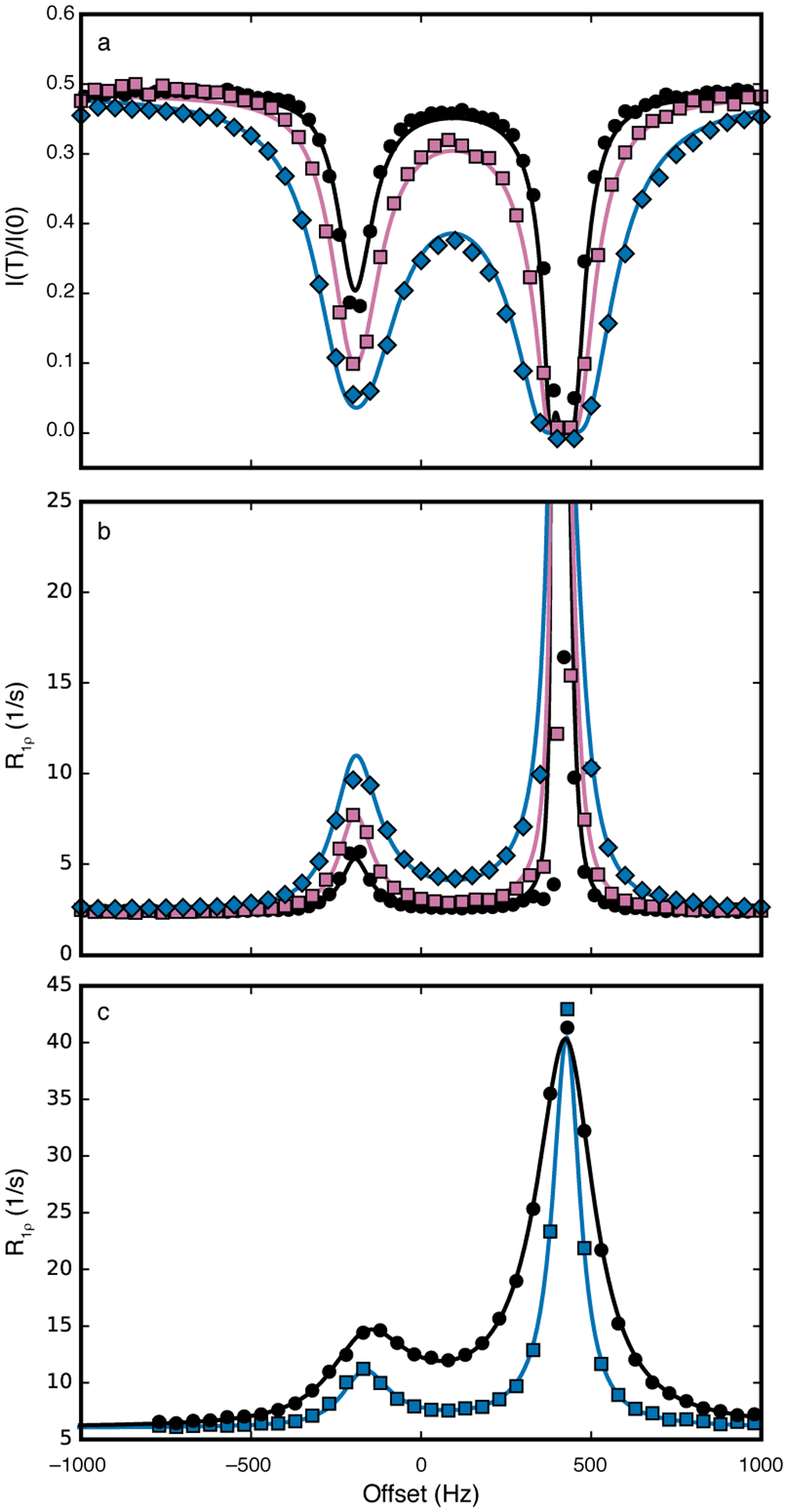
¹³C CEST profiles and R_1ρ dispersion for the C-8 position of Guanine 8 in the fluoride riboswitch. (a) Data were recorded for ω₁/2π = (black, circles) 17.7 Hz, (reddish-purple, squares) 27.9 Hz, and (blue, diamonds) 48.2 Hz. Solid lines represent fits to Eqs 40 and 42. (b) CEST data shown in (a) were converted to R_1ρ values using Eq. 40. Solid lines are calculated from Eq. 42 using fitted parameters from (a). Color scheme as in (a). (c) R_1ρ relaxation dispersion measured using ω₁/2π = (blue, squares) 48.2 Hz and (black, circles) 102.4 Hz. Solid lines are fit with Eq. 42. Data were obtained from Zhao, et al. (Zhao et al., 2014).

3.4. Determination of R_ex from relaxation dispersion experiments

In many situations, differentiating between the effects on relaxation rates or linewidths from chemical exchange, R_ex, and other relaxation mechanisms, such as dipole-dipole and CSA interactions, R₀, is of interest. Thus, a given relaxation rate constant, R, might be partitioned as:

$$\begin{gathered} {\text{R}}_{ex}=R-R_0 \\ =R(\omega \to 0)-R(\omega \to \infty ) \end{gathered}$$ (43)

in which ω = ω_e for R_1ρ -type experiments and 1/(4τ_cp) for CPMG-type experiments. Thus, relaxation experiments generally do not directly measure the exchange contribution to relaxation, R_ex, because dipole-dipole and CSA relaxation processes, R_1j and R_2j, also contribute to spin relaxation through R₀ (vide supra). Because R or R(ω → 0) usually can be approximated in a relatively straightforward manner, as in a Hahn-echo experiment, R₀ or R(ω → ∞) must be measured separately to obtain R_ex. Information on R₀ or R(ω → ∞) also can usefully constrain fitting algorithms for relaxation dispersion data (Grey et al., 2006; O’Connell et al., 2009).

One way to estimate R₀ involves extrapolation of relaxation data that have been recorded at different field strengths to B₀ = 0 (Millet, Loria, Kroenke, Pons, & Palmer, 2000). For example, the static magnetic field dependence of Hahn-echo relaxation rate constants, provided CSA values are available, allows separation of chemical exchange, dipole-dipole, and CSA contributions to relaxation (O’Connell et al., 2009; Phan, Boyd, & Campbell, 1996; Toyama et al., 2017). A second approach estimates the desired R₀ from a relaxation rate constant, such as a cross-correlation relaxation rate constant, that is insensitive to chemical exchange effects but has a similar dependence on other relaxation mechanisms (Kroenke, Loria, Lee, Rance, & Palmer, 1998; F. Massi, Wang, & Palmer, 2006).

Chemical exchange effects also can be suppressed in a reference relaxation dispersion experiment performed very high spin-lock power in R_1ρ experiments or very small τ_cp in CPMG experiments to obtain R(ω → ∞). The realization that modern cryogenically cooled probeheads can withstand 6.4 kHz ¹⁵N-spin lock fields with durations of 20 ms has led to the development of high-power relaxation dispersion experiments, which facilitate determination of R₂₀ (Ban et al., 2017). Thus, the spin-lock based HEROINE experiment can be used as a reference for constant-time relaxation-compensated CPMG experiments (Ban et al., 2013). An analogous approach has been reported for multi-quantum Hahn-Echo experiments (Toyama, Osawa, Yokogawa, & Shimada, 2016). A related approach, suited as a reference experiment for in-phase magnetization relaxation dispersion experiments, has been developed previously by Hansen et al. to obtain exchange-free values R₂ from a linear combination of relaxation rate constants for a specific set of longitudinal and spin-locked ¹H-¹⁵N coherences (Hansen et al., 2007). R₂₀ also can be determined from CPMG by setting τ_cp to be sufficiently small. However, when the duty cycle (ratio of 180° pulsing time to τ_cp) is more than 1/10, as rough approximation, evolution during the pulses may become relevant and complicates data analysis. Reddy et al. have demonstrated in the “extreme CPMG” experiment that R_cpmg(τ_cp) estimates can be obtained at a CPMG frequency of up to 1/(τ_cp) = 6.4 kHz for ¹⁵N nuclei, which is essentially equivalent to τ_cp → 0 (Reddy et al., 2018); an intensive cooling regime is required to protect sample and probe from overheating in this limit. Such a “windowless” extreme-CPMG experiment is equivalent to an R_1ρ experiment with phase jumps (due to the x,x,y,−y phase cycle). Simulations show that relaxation rates are, however, not dramatically changed in comparison to a phase cycle with x-phases only (equivalent to a continuous wave spin-lock). “Extreme-CPMG” experiments can cover a broad chemical shift range, while R_1ρ experiments have the advantage of avoiding complicated evolution of magnetization during 180° pulses, either due to pulse imperfections or phase changes from pulse to pulse.

3.5. Choosing appropriate relaxation dispersion experiments

The complexity of the kinetic schemes and the large number of parameters for N-site kinetic models might suggest that available data would be insufficient to characterize 4-site models like the kite or the quadratic scheme. However, CPMG and R_1ρ/CEST experiments yield an enormous amount of data. First, the static magnetic field B₀ can be varied in all of these experiments (and indeed is essential even for 2-site exchange) (Millet et al., 2000). In addition, these experiments typically simultaneously record data for a number of spins with different chemical shifts. For CPMG experiments, theoretical calculations illustrated in Figure 14 suggest that various 2- and 3-site models often can be distinguished as long as data are recorded at two different B₀ fields, and as long as data for a sufficient number of spins (preferably > 15) are analyzed (Koss, Rance, et al., 2018). For R_1ρ/CEST experiments, data should be recorded preferably at 2 different B₀ fields and at two ω₁ fields. In an R_1ρ experiment, theoretical calculations suggest that a combination of spins with different shifts, in the given example five, can be sufficient to drastically enhance distinguishability between two- and three-site (triangular/BAC) models for a wide range of parameters (Figure 15). Interestingly, a combination of a small and large ω₁ fields generally performs well, but in particular also for cases in which exchange between sites A and B and between sites A and C is slow, but between minor sites B and C is fast. Based on these simulations, complicated N-site schemes may be distinguishable, for example by the combination of the following experiments, all at two different B₀ fields: CEST experiments for at least 3 spins, and an R_1ρ experiment at a higher ω₁ field (to complement the CEST data); additional CPMG data can also be useful in many cases.

Figure 14:

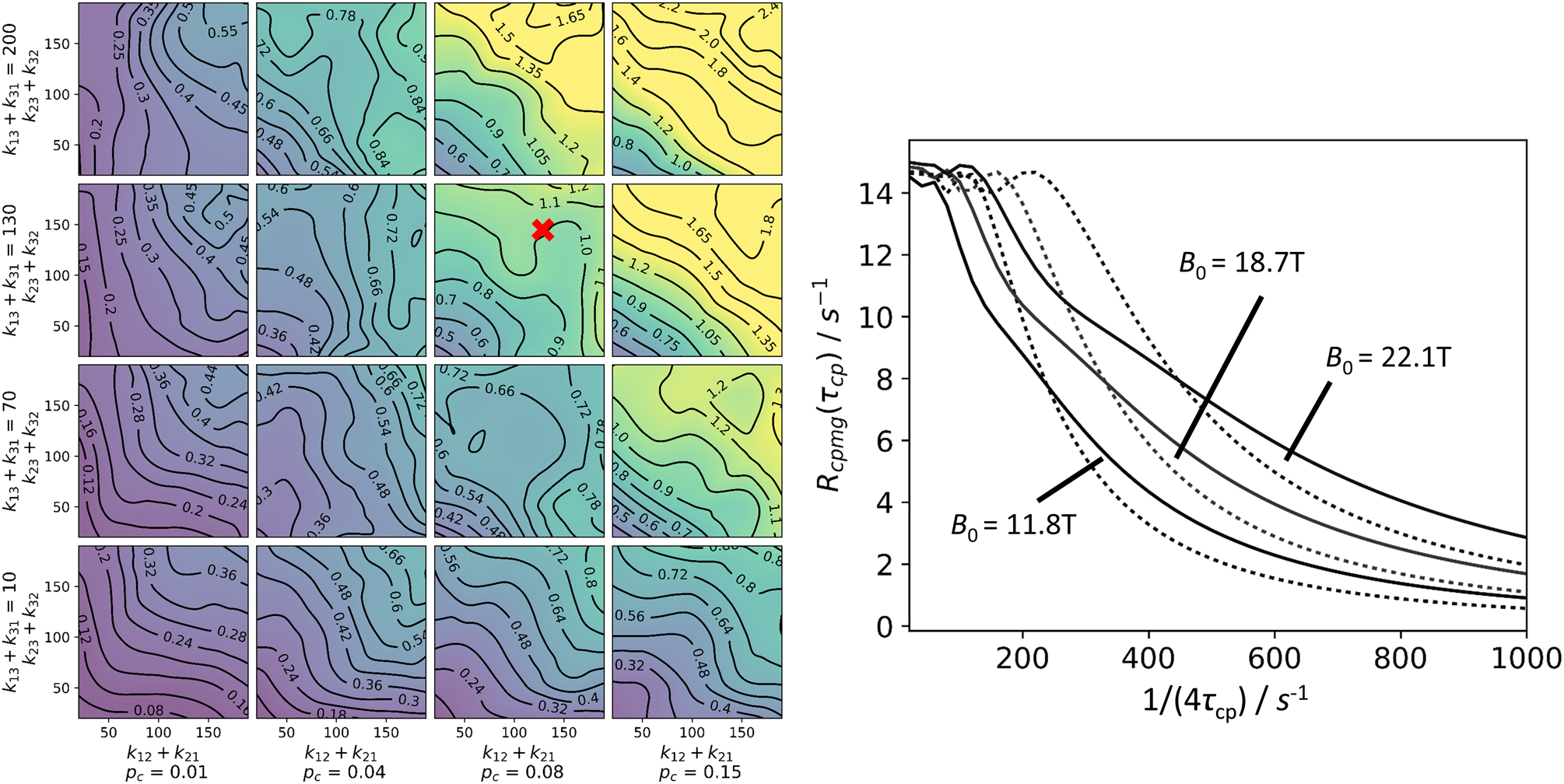
Distinguishability of the triangular kinetic scheme from the two-state model for CPMG experiments. Left: General conditions for distinguishability between triangular and linear schemes. In each of the 16 subpanels, 25 points with different values of k₁₂/k₂₃ were analyzed by globally fitting synthetic three-state curves to a two-state model, with a 1/(4τ_cp) range 20–1000 s⁻¹. For each point, 20 RMS values, comparing the synthetic and the fitted data set, were obtained. For the global fitting procedure, a set of 3 × 32 CPMG curves was used, with 32 randomized Δω_AB (700–2000 s⁻¹ at 11.7 T) and Δω_AC(±700–2000 s⁻¹), and with 3 magnetic fields (11.7 T, 18.7 T, 22.2 T). The median, which was obtained from the 20 RMS values, is shown. p_b was set to 0.04. To aid in convergence, some variables were constrained between upper and lower bounds during fitting: p_b between 0.005 and 0.25; k₁₂ + k₂₁ between 10 s⁻¹ and 400 s⁻¹; Δω_AB between 450 s⁻¹ and 2500 s⁻¹. Right: Example plot for fits of synthetic triangular data to a two-state model (slow exchange approximations from truncation of the matrix exponential series, with eigenvalue approximation of 2^nd order, Halley’s method), point of interest labeled in left panel. (solid) Synthetic triangular scheme data; (dotted) best fits. In this global fit, 32 randomized spin sets (see left panel) were used; plots are shown for a single spin set, Δω_AB (1892 s⁻¹) and Δω_AC(−722 s⁻¹), at three magnetic fields, as indicated in the figure. Other parameters: k₁₂ + k₂₁ = 100 s⁻¹; k₁₃ + k₃₁ = 130 s⁻¹; k₂₃ + k₃₂ = 150 s⁻¹; p_A = 0.88; p_B = 0.04; p_C = 0.08. The RMS deviation in this example is 1.38 s⁻¹for the 1/(4τ_cp) region 20–300 s⁻¹.

Figure 15.

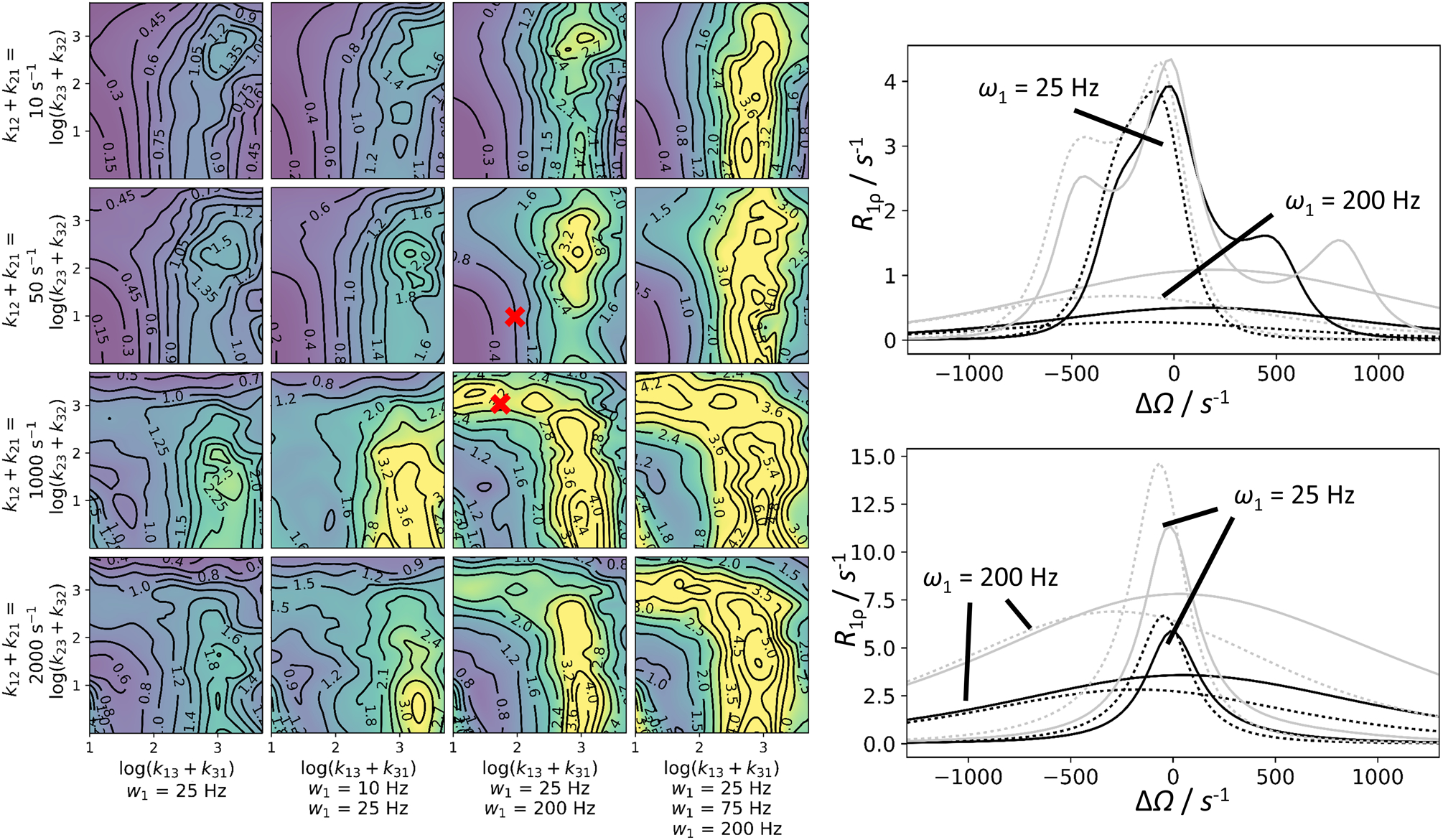
Distinguishability of the 3-state linear and triangular kinetic scheme from the two-state model in R_1ρ experiments. Left panel: General conditions for distinguishability. Each subpanel has been created from 90 data points; each corresponds to the median of 20 separately calculated RMS values. For each RMS value, five sets of spins with randomly generated chemical shifts Δω_AB (200–800 s⁻¹ at 11.7 T) and Δω_AC (±200–800 s⁻¹) were included. In addition, two B₀ fields (11.7 T, 18.7 T) and various combinations of one to three ω₁ fields (see figure) were used. This yielded 10 to 30 numerically generated R_1ρ curves for three sites. These curves were globally fit to a two-site model (ΔΩ range: −1300 to 1300 s⁻¹). The RMS for each of the synthetic and fitted curve combinations was calculated. The results are shown in the contour plot. The points from which the sample fits in the right panels were generated are marked. Multiple parameters are shown in the plot, other parameters are: p_B = 0.05; p_C = 0.02. To aid in convergence, some variables were constrained between upper and lower bounds during fitting: p_B between 0.005 and 0.23; k₁₂ + k₂₁ between 5 s⁻¹ and 7000 s⁻¹; Δω_AB between 100 s⁻¹ and 1200 s⁻¹. Right panel: Example curves corresponding to various kinetic situations marked in the right panel (top: k₁₂ + k₂₁ = 50 s⁻¹; k₁₃ + k₃₁ = 100 s⁻¹; k₂₃ + k₃₂ = 10 s⁻¹; ω₁/(2π) = 25 and 200 Hz; bottom: k₁₂ + k₂₁ = 1000 s⁻¹; k₁₃ + k₃₁ = 50 s⁻¹; k₂₃ + k₃₂= 1000 s⁻¹; ω₁/(2π) = 25 and 200 Hz). Numerical three-state solutions (solid lines) are shown alongside the best two-state fits (dotted lines). The fits result from global fits of 20 curves: five spins (in plot only shown: Δω_AB = 536 s⁻¹; Δω_AC = −312 s⁻¹); B₀ = 11.7 T, black; B₀ = 18.7 T, grey; ω₁/(2π) = 50 Hz and 200 Hz, as indicated in the figure. The RMS deviation for the given examples are 0.74 s⁻¹ (top) and 3.48 s⁻¹ (bottom).

Conclusion

The 2-site model in which a molecule or system of molecules interconverts reversibly between two states at chemical equilibrium is powerful in descriptions of chemical exchange in NMR spectroscopy (and other areas of biophysics) because it is analytically tractable, allowing both qualitative insight and facile data analysis. More complex biological systems are becoming accessible to NMR spectroscopy, for example due to techniques focusing on the side chains of large proteins, or embedment of membrane proteins into nanodiscs. In those systems, multiple states may interconvert on multiple timescales. The complexity of the resulting Bloch-McConnell or stochastic Liouville equations obscures insight and complicates data analysis. The examples surveyed in this review illustrate theoretical advances leading to improved experimental methods, formulations facilitating global analysis of experimental data for improved power, and analytical approximations generalizing the simple 2-site model to arbitrary kinetic schemes.

Abbreviations

CEST

Chemical exchange saturation transfer

CPMG

Carr-Purcell-Meiboom-Gill

DEST

Dark state exchange saturation transfer

Appendix

A.1. Cayley-Hamilton theorem

The Cayley-Hamilton theorem states that a matrix A satisfies its own characteristic equation. Thus, for a 2 ×2 matrix,

$$A^2-ATrA+E\left|A\right|=0$$ (A1)

in which 0 is the zero matrix. Any matrix equation containing powers of A > 1 can be reduced by repeated use of the above expression. For example,

$$\begin{gathered} H_{22}\left({\tau }_{cp}\right)\approx 3\left\{-E+Z^2\left({\tau }_{cp}\right)\right\}{\left\{E+4Z\left({\tau }_{cp}\right)+Z^2\left({\tau }_{cp}\right)\right\}}^{-1} \\ =3\left\{-E+Z\left({\tau }_{cp}\right)TrZ\left({\tau }_{cp}\right)-E\mid Z\left({\tau }_{cp}\right)\right\}{\left\{(E+4Z\left({\tau }_{cp}\right)+Z\left({\tau }_{cp}\right)TrZ\left({\tau }_{cp}\right)-E\left|Z\left({\tau }_{cp}\right)\right|\right\}}^{-1} \\ =3\left\{-\left(1+\left|Z\left({\tau }_{cp}\right)\right|\right)E+Z\left({\tau }_{cp}\right)TrZ\left({\tau }_{cp}\right)\right\}{\left\{\left(1-\mid Z\left({\tau }_{cp}\right)\right)E+\left(4+TrZ\left({\tau }_{cp}\right)\right)Z\left({\tau }_{cp}\right)\right\}}^{-1} \end{gathered}$$ (A2)

which has the form of Eq. 19:

$$H_{22}\left({\tau }_{cp}\right)\approx \epsilon \left\{E+b_{1}Z\left({\tau }_{cp}\right)\right\}{\left\{E+c_{1}Z\left({\tau }_{cp}\right)\right\}}^{-1}$$ (A3)

with

$$\begin{gathered} \epsilon =-3\frac{1+\left|Z\left({\tau }_{cp}\right)\right|}{1-\left|Z\left({\tau }_{cp}\right)\right|} \\ {b}_1=\frac{-TrZ\left({\tau }_{cp}\right)}{1+\left|Z\left({\tau }_{cp}\right)\right|} \\ {c}_1=\frac{4+TrZ\left({\tau }_{cp}\right)}{1-\left|Z\left({\tau }_{cp}\right)\right|} \end{gathered}$$ (A4)

The equation

$$\left\{E+b_{1}Z\left({\tau }_{cp}\right)\right\}{\left\{E+c_{1}Z\left({\tau }_{cp}\right)\right\}}^{-1}=a_{0}E+a_{1}Z\left({\tau }_{cp}\right)$$ (A5)

is formally solved for a₀ and a₁ by diagonalizing Z(τ_cp) (this matrix is Hermitian and consequently has real eigenvalues) to obtain the algebraic equations:

$$\left[\begin{array}{c}\frac{1+b_1{\Lambda }_1}{1+c_1{\Lambda }_1}\\ \frac{1+b_1{\Lambda }_2}{1+c_1{\Lambda }_2}\end{array}\right]=\left[\begin{array}{cc}1& {\Lambda }_1\\ 1& {\Lambda }_2\end{array}\right]\left[\begin{array}{c}{a}_0\\ a_1\end{array}\right]$$ (A6)

in which Λ_n is an eigenvalue of Z(τ_cp). The solution to this equation gives:

$$\begin{gathered} a_0=\frac{1+c_1\left({\Lambda }_1+{\Lambda }_2\right)+b_1{c}_1{\Lambda }_1{\Lambda }_2}{1+c_1\left({\Lambda }_1+{\Lambda }_2\right)+c_1^2{\Lambda }_1{\Lambda }_2}=\frac{1+c_{1}TrZ\left({\tau }_{cp}\right)+b_1{c}_1|Z\left({\tau }_{cp}\right)|}{1+c_{1}TrZ\left({\tau }_{cp}\right)+c_1^2\left|Z\left({\tau }_{cp}\right)\right|} \\ {a}_1=\frac{b_1-c_1}{1+c_1\left({\Lambda }_1+{\Lambda }_2\right)+c_1^2{\Lambda }_1{\Lambda }_2}=\frac{b_1-c_1}{1+c_{1}TrZ\left({\tau }_{cp}\right)+c_1^2|Z\left({\tau }_{cp}\right)|} \end{gathered}$$ (A7)

in which the relationships between the eigenvalues, the trace and determinant have been used. This expression can be used with any Padé approximation to the Liouvillian for 2-site exchange. Using the above example,

$$H_{22}\left({\tau }_{cp}\right)=3\frac{\left\{-1+TrZ\left({\tau }_{cp}\right)\left(4+TrZ\left({\tau }_{cp}\right)\right)+{\left|Z\left({\tau }_{cp}\right)\right|}^2\right\}E+2\left\{2+TrZ\left({\tau }_{cp}\right)+2\left|Z\left({\tau }_{cp}\right)\right|\right\}Z\left({\tau }_{cp}\right)}{1+TrZ\left({\tau }_{cp}\right)\left(4+TrZ\left({\tau }_{cp}\right)\right)+2\left|Z\left({\tau }_{cp}\right)\right|\left(7+2TrZ\left({\tau }_{cp}\right)\right)+{\left|Z\left({\tau }_{cp}\right)\right|}^2}$$ (A8)

As noted in the text, this approach allows the inverse matrix to be easily obtained as:

$$H_{22}^{-1}\left({\tau }_{cp}\right)=\frac{\left\{-1+T{r}^{2}Z\left({\tau }_{cp}\right)+4TrZ\left({\tau }_{cp}\right)\left|Z\left({\tau }_{cp}\right)\right|+{\left|Z\left({\tau }_{cp}\right)\right|}^2\right\}E-2\left\{2+TrZ\left({\tau }_{cp}\right)+2\left|Z\left({\tau }_{cp}\right)\right|\right\}Z\left({\tau }_{cp}\right)}{3\left\{1+\left|Z\left({\tau }_{cp}\right)\right|-TrZ\left({\tau }_{cp}\right)\right\}\left\{1+\left|Z\left({\tau }_{cp}\right)\right|+TrZ\left({\tau }_{cp}\right)\right\}}$$ (A9)

and the lowest-order approximation to the relaxation rate constant is given by:

$$R_{\mathit{\text{cpmg}}}\left({\tau }_{cp}\right)=R_{21}+\frac{3\left\{1+\left|Z\left({\tau }_{cp}\right)\right|-TrZ\left({\tau }_{cp}\right)\right\}\left\{1+\left|Z\left({\tau }_{cp}\right)\right|+TrZ\left({\tau }_{cp}\right)\right\}}{8{\tau }_{cp}\left\{1-{\left|Z\left({\tau }_{cp}\right)\right|}^2-2\left|Z\left({\tau }_{cp}\right)\right|TrZ\left({\tau }_{cp}\right)+2TrZ\left({\tau }_{cp}\right)\right\}}$$ (A10)

For 3-site exchange, the evolution matrices have dimensions 3 ×3 and the Cayley-Hamilton theorem is:

$$A^3-A^{2}TrA+\frac{1}{2}A\left(T{r}^{2}A-Tr{A}^2\right)-E\left|A\right|=0$$ (A11)

The same approach as outlined for 2-site exchange, but more complicated algebraically, allows the Hamiltonian H₁₁(t_cp) to be expressed using a_n = d_n/D with:

$$\begin{gathered} D=1+\frac{c_2^2}{4}{\left(T{r}^{2}Z-T{r}^2{Z}^2\right)}^2+\left(\frac{c_1{c}_2}{2}TrZ+\frac{c_1^2}{2}\right)\left(T{r}^{2}Z-Tr{Z}^2\right)+c_{1}TrZ+c_{2}Tr{Z}^2+\left|Z\right|(c_1^3-3c_1{c}_2+\left(c_1^2-2c_2\right)c_{2}TrZ+\frac{c_1{c}_2^2}{2}\left(T{r}^{2}Z-Tr{Z}^2\right)+c_2^3|Z{|}^2 \\ {d}_0=1+\frac{c_2^2}{4}{\left(T{r}^{2}Z-T{r}^2{Z}^2\right)}^2+\left(\frac{c_1{c}_2}{2}TrZ+\frac{c_1^2}{2}\right)\left(T{r}^{2}Z-Tr{Z}^2\right)+c_{1}TrZ+c_{2}Tr{Z}^2+\left|Z\right|(-b_2{c}_1+b_1\left(c_1^2-c_2\right)-c_1{c}_2-\left(b_2-b_1{c}_1+c_2\right)c_{2}TrZ+\frac{b_1{c}_2^2}{2}\left(T{r}^{2}Z-Tr{Z}^2\right)+b_2{c}_2^2|Z{|}^2 \\ {d}_1=b_1-c_1+\left(\frac{b_2-c_2}{2}{c}_{2}TrZ+\frac{b_2{c}_1}{2}\right)\left(T{r}^{2}Z-Tr{Z}^2\right)+c_1\left(b_1-c_1\right)TrZ+\frac{b_1-2c_1}{2}{c}_{2}T{r}^{2}Z+\frac{b_1{c}_2}{2}Tr{Z}^2+\left|Z\right|\left(b_2\left(c_1^2-c_2\right)+c_2\left(c_2-b_1{c}_1\right)+\left(b_2{c}_1-b_1{c}_2\right)c_{2}TrZ\right) \\ {d}_2=b_2-b_1{c}_1+c_1^2-c_2+\frac{c_2-b_2}{2}{c}_2\left(T{r}^{2}Z-Tr{Z}^2\right)+c_2\left(c_1-b_1\right)TrZ+\left|Z\right|\left(b_1{c}_2-b_2{c}_1\right) \end{gathered}$$ (A12)

A.2. Effective relaxation rate constant in CPMG experiments

A formal solution for N-state CPMG obtained from Eq. 14 is (with detection of the major species):

$$\begin{gathered} \langle M^{+}\rangle \left(4m{\tau }_{cp}\right)/\langle M^{+}\rangle \left(0\right)=\left[\begin{array}{cccc}{p}_1^{-1}& 0& \cdots & 0\end{array}\right]S{\left\{e^{(L+R+K){\tau }_{cp}}{e}^{\left(L^{*}+R+K\right)2{\tau }_{cp}}{e}^{(L+R+K){\tau }_{cp}}\right\}}^m{S}^{-1}\left[\begin{array}{c}{p}_1\\ ⋮\\ p_N\end{array}\right] \\ =p_1^{-1/2}\langle {\delta }_{1n}\left|{\left\{e^{(L+R+K){\tau }_{cp}}{e}^{\left(L^{*}+R+K\right)2{\tau }_{cp}}{e}^{(L+R+K){\tau }_{cp}}\right\}}^m\right|p^{1/2}\rangle \\ =p_1^{-1/2}\langle {\delta }_{1n}\left|e^{(L+R+K){\tau }_{cp}}{\left\{e^{\left(L^{*}+R+K\right)2{\tau }_{cp}}{e}^{(L+R+K)2{\tau }_{cp}}\right\}}^m{e}^{-(L+R+K){\tau }_{cp}}\right|p^{1/2}\rangle \\ =p_1^{-1/2}\langle {\delta }_{1n}\left|e^{(L+R+K){\tau }_{cp}}{e}^{H4m{\tau }_{cp}}{e}^{-(L+R+K){\tau }_{cp}}\right|p^{1/2}\rangle \\ =p_1^{-1/2}\langle {\delta }_{1n}\left|e^{(L+R+K){\tau }_{cp}}{e}^{H4m{\tau }_{cp}}{e}^{-(L+R+K){\tau }_{cp}}\right|p^{1/2}\rangle \\ =p_1^{-1/2}\sum _{j=1}^N\langle {\delta }_{1n}\left|e^{(L+R+K){\tau }_{cp}}\right|{\psi }_j\rangle \langle {\psi }_j\left|e^{-(L+R+K){\tau }_{cp}}\right|p^{1/2}\rangle e^{{\Lambda }_{j}4m{\tau }_{cp}} \\ =p_1^{-1/2}\sum _{i=1}^N\sum _{j=1}^N\sum _{k=1}^N\langle {\delta }_{1n}\mid u_i\rangle \langle u_i\mid {\psi }_j\rangle \langle {\psi }_j\mid u_k\rangle \langle u_k\mid p^{1/2}\rangle e^{{\Lambda }_{j}4m_{{\tau }_{cp}}}{e}^{\left({\lambda }_i-{\lambda }_k\right){\tau }_{cp}} \end{gathered}$$ (A13)

in which <δ_1n| is a 1 × N vector with values δ_1n for n = {1,..,N}; S is diagonal with $S_{\text{ii}}=p_k^{12}$;|u_j> and {λ_j} are the eigenvectors and eigenvalues of (symmetrized) evolution matrix $\widehat{L}+\widehat{R}+\widehat{K}$, in which |u_j> is the jth column of U and < u_j| is the the jth row of U⁻¹; |ψ_j> and Λ_j are the eigenvectors and eigenvalues of the symmetrized average Liouvillian H(τ_cp), in which <ψ_j| is the complex transpose of $\left|{\psi }_j>;<p^{1/2}\right|=\left[p_1^{1/2}{p}_2^{1/2}\right]$; and H(τ_cp) is defined in Eq. 17.

From Eq. 5, an effective relaxation rate constant is defined as:

$$\begin{gathered} R_{cpmg}\left({\tau }_{cp}\right)=\frac{-1}{4m{\tau }_{cp}}\log \left[\frac{\langle M^{+}\rangle \left(4m{\tau }_{cp}\right)}{\langle M^{+}\rangle (0)}\right] \\ =\frac{-1}{4m{\tau }_{cp}}\log \left[p^{-1/2}\sum _{i=1}^N\sum _{j=1}^N\sum _{k=1}^N\langle {\delta }_{1n}\mid u_i\rangle \langle u_i\mid {\psi }_j\rangle \langle {\psi }_j\mid u_k\rangle \langle u_k\mid p^{1/2}\rangle e^{{\Lambda }_{j}4m{\tau }_{cp}}{e}^{\left({\lambda }_i-{\lambda }_k\right){\tau }_{cp}}\right] \\ =\frac{-1}{4m{\tau }_{cp}}\log \left[p^{-1/2}{e}^{{\Lambda }_{1}4n{\tau }_{cp}}\sum _{i=1}^N\sum _{j=1}^N\sum _{k=1}^N\langle {\delta }_{1n}\mid u_i\rangle \langle u_i\mid {\psi }_j\rangle \langle {\psi }_j\mid u_k\rangle \langle u_k\mid p^{1/2}\rangle e^{\left({\Lambda }_j-{\Lambda }_1\right)4m{\tau }_{cp}}{e}^{\left({\lambda }_i-{\lambda }_k\right){\tau }_{cp}}\right] \\ =-{\Lambda }_1-\frac{1}{4m{\tau }_{cp}}\log \left[p^{-1/2}\sum _{i=1}^N\sum _{j=1}^N\sum _{k=1}^N\langle {\delta }_{1n}\mid u_i\rangle \langle u_i\mid {\psi }_j\rangle \langle {\psi }_j\mid u_k\rangle \langle u_k\mid p^{1/2}\rangle e^{\left({\Lambda }_j-{\Lambda }_1\right)4m{\tau }_{cp}}{e}^{\left({\lambda }_i-{\lambda }_k\right){\tau }_{cp}}\right] \\ =-{\Lambda }_1-\frac{1}{4m{\tau }_{cp}}\log \left[\sum _{j=1}^N\sum _{k=1}^N\sum _{l=1}^N\langle u_k\left|\widehat{p}\right|u_i\rangle \langle u_i\left|{\Psi }_j\right|u_k\rangle e^{\left({\Lambda }_j-{\Lambda }_1\right)4m{\tau }_{cp}}{e}^{\left({\lambda }_i-{\lambda }_k\right){\tau }_{cp}}\right] \\ =-\left({\Lambda }_1+R_{corr}\right) \end{gathered}$$ (A14)

in which

$$\begin{gathered} \widehat{p}=p_1^{-1/2}|p^{1/2}\rangle \langle {\delta }_{1n}| \\ {\Psi }_j=|{\psi }_j\rangle \langle {\psi }_j| \end{gathered}$$ (A15)

and ${\widehat{p}}_{n,j}={\delta }_{1j}{\left(p_n/p_1\right)}^{1/2}$. On the last line of the above equations, Λ₁ is the least-negative eigenvalue of H(τ_cp), which is approximated as described in Section 2.2, and R_corr gives the difference between the eigenvalue estimate of the relaxation rate constant and the effective relaxation rate constant obtained from Eq. 5.

The matrix H(τ_cp) is Hermitian, so the eigenvalues Λ_j are real and the factors exp[(Λ_j−Λ₁)4mτ_cp] are pure exponential decays. The eigenvalues λ_i are complex and the factors exp[(λ_i−λ_k)τ_cp] are oscillatory. These contribute significantly when τ_cp is long (or exchange is very slow). If T = 4nτ_cp is sufficiently long, as is usually the case if significant magnetization decay occurs during T, then |(Λ₂ − Λ₁)|4mτ_cp >> 1, exp[(Λ_j−Λ₁)4mτ_cp]→0 and the j > 1 terms vanish:

$$\begin{gathered} R_{\mathit{\text{corr}}}=\frac{1}{4m{\tau }_{cp}}\text{log}\left[\sum _{j=1}^N\sum _{k=1}^N\sum _{l=1}^N\langle u_k\left|\widehat{p}\right|u_i\rangle \langle u_i\left|{\Psi }_j\right|u_k\rangle e^{\left({\Lambda }_j-{\Lambda }_1\right)4m{\tau }_{cp}}{e}^{\left({\lambda }_i-{\lambda }_k\right){\tau }_{cp}}\right] \\ \approx \frac{1}{4m{\tau }_{cp}}\text{log}\left[\sum _{k=1}^N\sum _{l=1}^N\langle u_k\left|\widehat{p}\right|u_i\rangle \langle u_i\left|{\Psi }_1\right|u_k\rangle e^{\left({\lambda }_i-{\lambda }_k\right){\tau }_{c_p}}\right] \end{gathered}$$ (A16)

In addition, if the correction is small, then the logarithm can be expanded to first-order:

$$R_{\text{corr}}\approx \frac{-1}{4m{\tau }_{cp}}\left[1-\sum _{k=1}^N\sum _{l=1}^N\langle u_k\left|\widehat{p}\right|u_i\rangle \langle u_i\left|{\Psi }_1\right|u_k\rangle e^{\left({\lambda }_i-{\lambda }_k\right){\tau }_{cp}}\right]$$ (A17)

The correction term R_corr vanishes as T = 4nτ_cp becomes large. The correction term also will vanish as p_n→0 for n > 1, or exchange becomes fast.

The eigenvalues and eigenvectors of $\widehat{L}+\widehat{R}+\widehat{K}$ are obtained at low computational cost by standard methods. If the approximations of Eqs. A16 or A17 are appropriate, the eigenvector ψ₁ can be estimated efficiently by inverse iteration:

$$\begin{gathered} z^{(m+1)}={\left(H\left({\tau }_{cp}\right)-{\Lambda }_1^{0}E\right)}^{-1}{\psi }_1^{\left(m\right)} \\ {\psi }_1^{(m+1)}=Z^{(m+1)}/\Vert Z^{(m+1)}{\Vert }_{\infty } \end{gathered}$$ (A18)

with z⁽⁰⁾ = [0 … 1]^T and the approximate largest (least negative) eigenvalue of H(τ_cp), Λ₁⁰, as described in Section 2.2, Numerical calculations suggest that ψ₁⁽²⁾ or ψ₁⁽³⁾ are sufficiently accurate. Note that for N = 2, the eigenvalue Λ₁ and the eigenvector ψ₁ can be calculated exactly, leading to the result reported by Baldwin (Baldwin, 2014). Additional considerations arising from detection when exchange occurs on the intermediate time scale also have been discussed by Baldwin.