Abstract
Preferential crystallization (PC) is a powerful method to separate the enantiomers of chiral molecules that crystallize as conglomerates. The kinetically controlled separation method works in a typically narrow metastable zone. Currently, there are no simple models available that allow estimating the productivity of PC and, thus, the comparison with rivalling resolution techniques. In this Article, we suggest a simple shortcut model (SCM) capable of describing the main features of batch-wise operated PC using three ordinary differential equations originating from the mass balance of the target enantiomer and solvent in the liquid and solid phases. Compared to population balance models, the basis of the SCM is the assumption that the crystals for each enantiomer have the same size, which increases continuously from prespecified initial values. The goal of the model is to describe the initial period of the batch, during which the purity is within the specification required. It is accepted that after reaching this border, the precision of predictions can drop. This Article also illustrates a simple strategy how to parametrize the model based on a few experimental runs of PC. At first, for demonstration purposes, theoretical transients generated using the more rigorous PBE model is analyzed using SCM considering the separation of the enantiomers of dl-threonine. Subsequently, results of an experimental study with the enantiomers of asparagine monohydrate are presented to validate the shortcut model, which is seen as a new valuable tool to quantify more rapidly the productivity of PC and to further promote this elegant technique capable to resolve enantiomers of conglomerate forming chiral systems.
Short abstract
A simplified model is proposed to estimate the productivity of preferential crystallization of conglomerates using only two ODEs and relatively easy to find parameters. The goal of the model is to describe the essential initial period of a batch process, during which high product purity is achievable.
1. Introduction
Each enantiomer of a pair has usually different pharmacological activity. Therefore, the production of pure chiral molecules is essential. In the past few decades, the number of enantiopure chiral drugs in the market has strongly increased and in 2015 more than 94% of the chiral drug-like compounds approved by the US Food and Drug Administration (FDA) were single enantiomers.1 Enantiopurity can be achieved by two main approaches: asymmetric synthesis or nonselective synthesis followed by chiral resolution.2 Although very attractive, efficient and cost-effective routes for asymmetric synthesis providing the required purity are often not available.3 Consequently, a great effort has been done to develop separation techniques to obtain pure enantiomers. Many methods have been successfully applied for this purpose, for instance chromatography,4−6 chiral membranes7,8 and crystallization.9,10 The later one is an attractive process since it provides solid product, which is, frequently, the desired form for pharmaceuticals. Furthermore, in industrial applications it is beneficial to implement the chiral resolution early in the production route rather than in the final API.
Direct selective crystallization starting from the racemic mixture is possible only if both enantiomers crystallize separately. These systems are called conglomerates, and their racemate consist of a mechanical mixture of both enantiomers. In contrast, racemic compound forming systems crystallize, as 50:50 mixture, in a heterochiral crystal lattice. Chiral resolution of such systems using crystallization is possible but requires previous enantiomeric enrichment.11,12 In this study, we focus on the resolution of conglomerate forming systems using preferential crystallization (PC). This is a kinetically driven process suitable to separate conglomerates.9,13,14 It is carried out by adding homochiral seeds of the target enantiomer to a supersaturated racemic solution. The process is operated in a metastable zone, where the seeded crystals will grow preferentially for its given surface area. The crystallization of the counter enantiomer will be kinetically inhibited for a certain period—later in this work nominated as stop time. Eventually crystals of the nontarget molecule crystallize and purity is compromised. If the system is let to reach equilibrium, the solid phase becomes racemic with slight excess of the target enantiomer because of the added seed crystals. To ensure purity requirements, PC has to be designed in a way of avoiding crystallization of the counter enantiomer. Several process configurations in both batch and continuous mode have been studied with this purpose, for example, coupled crystallizers,15−18 coupling crystallizers with dissolution (CPC-D),19,20 mixed suspension mixed product removal crystallizers (MSMPR),21−23 and fluidized bed crystallization.24,25 Comparative performance of liquid exchange PC processes was recently published by Majumder and Nagy.10 A racemization reaction using a catalyst can also be implemented to avoid crystallization of the counter enantiomer.26,27
To model crystallization processes and other particulate processes, population balance models (PBM)28,29 are extensively applied. They were used also to describe and optimize preferential crystallization.30,31 Hereby, the dynamic behavior of PC is described by two population balance equations, one for each enantiomer, and their respective mass balances. PBM incorporate the various mechanisms involved in PC, for example, growth, nucleation, breakage, and agglomeration, and predicts the particle size distribution for each discrete time point. Models for each mechanism can be found in literature,28 but they often require many parameters which are difficult to predict or to determine. Despite large efforts toward quantification of crystallization kinetics,32−34 a significant number of experiments is required to determine the process parameters. Furthermore, solving PBM requires efficient tools for discretization of the equations. Therefore, there is still a lack of simple tools to quickly access key performance parameters (KPIs), such as productivity, purity, and yield for process design.
Prior to exploiting mathematical modeling, solid–liquid equilibria provide crucial information for designing a crystallization process. Solubility isotherms are commonly represented in a ternary phase diagram (TPD). Although TPDs represent the thermodynamic conditions, a kinetically time-dependent state can also be taken from the diagram. As described by Jacques et al.,13 the metastable solubility limiting PC is characterized by prolongations of the solubility isotherms beyond equilibrium. This metastable solubility defines a pseudo-equilibrium state that controls the behavior of the system for a certain period of time. The distances between a current composition and the extended solubility curves form the driving forces for crystallization.35,36
In this Article, we propose a simple shortcut model (SCM) to assess productivity of batch preferential crystallization based on mass balances and metastable solubilities calculated from the TPD. The model is applied to isothermal PC of conglomerates. In the next section, the assumptions of the model are explained and a strategy to estimate its parameters from a minimum number of experiments is proposed. The model is then evaluated based on two case studies considering one anhydrous and one solvate crystalline phase. The first analysis is based on transients generated with a classical population balance model. For the second case, the results of an experimental study using the proposed strategy are used to validate the model. Productivity calculations for each case are presented to demonstrate the strength of the shortcut model. Finally, based on experimental results, for the second case study, we propose an extension of the model to include temperature effects.
2. Theory: Mathematical Model
Population balance models (PBM) are widely used to describe and to optimize crystallization-based processes.28,29 For a general, ideally mixed batch process with one internal coordinate, the population balance is given by eq 1
| 1 |
where f represents the population number density of the particles of enantiomers of size L, S is the supersaturation, G is the growth rate of the particles, B is the birth rate of new particles due to nucleation, attrition, and agglomeration, and D is the death rate due to dissolution, attrition, and agglomeration.
The PBM must be complemented by a liquid phase balance. This needs to be coupled with eq 1, and they can be solved, for instance, by using a high resolution finite volume method and by applying model reduction techniques, such as the method of moments. The population balance model also requires previous determination of model parameters for the different kinetic processes involved, for example, growth, primary and secondary nucleation, breakage, attrition, etc. Many studies have been dedicated to reduce computational and experimental efforts and facilitate implementation and efficient usage of the PBM,32−34 but it is still considered labor intensive. PBM generates particle size distribution of solid phase, which is not necessarily required for all process evaluations. Therefore, for initial process design, it is attractive to reduce the complexity of the model used. In the following sections, we propose a shortcut model that requires a minimum number of experiments to implement and offers a rather quick analysis of process performance.
2.1. Shortcut Model of PC
The shortcut model (SCM) for batch preferential crystallization introduced in this work exploits the principle of “total mass transfer”, which causes mass depletion of the liquid phase and mass build-up of the solid phase during the process. The following assumptions are made in order to derive the model:
-
(1)
Nucleation and growth rates are lumped and jointly cause liquid-phase mass depletion and solid-phase mass build up, and no distinction is made between process steps of mass transfer and surface integration.
-
(2)
All crystals of one enantiomer are spheres of identical increasing size.
-
(3)
Very small particles of the counter-enantiomer below a contamination threshold are assumed to be initially present along with seeds of the preferred enantiomer.
-
(4)
A stop time for the process (tstop) is used to activate “growth” of the particles of the counter enantiomer. This is the start of solid phase contamination.
-
(5)
No aggregation and breakage take place.
-
(6)
The total number of crystals in the beginning of the process is equal to the number of crystals at the end of the process.
-
(7)
Simple power rate laws are used to describe the mass exchange between the phases.
-
(8)
Driving forces respect metastable solubility limits in the 3-phase region of the ternary phase diagram.
-
(9)
There is no epitaxy between the crystals of the opposite enantiomer.
A ternary system with preferred enantiomer (index 1) and its antipode (index 2) dissolved in a corresponding solvent or solvent system (index 3) is balanced with the shortcut model. The drops of the masses of the solutes in the liquid phase correspond to the total solid mass gains during the batch PC process. The changes in the masses of the liquid (mi) and solid phase (mSi related to the solid density ρS and volume of solid phases VSi) are quantified assuming an effective overall mass transfer rate (GBeff) caused by growth and nucleation of particles.
For the liquid and solid phases of the two enantiomer holds
| 2 |
| 3 |
The overall rate of the mass transfer between the liquid and solid phases is described in the SCM for each enantiomer i using the following equation:
| 4 |
The effective rate GBieff is characterized by three terms (eq 4): an effective mass transfer (or effective crystallization rate) constant keff; the total surface area of all crystals, where Ni is the total number of spherical particles of radius Ri; and a driving force term, dependent on supersaturation Si and effective order neff. The two lumped kinetic parameters keff and neff are assumed to be identical for both enantiomers.
The driving force for PC is generated by the different concentrations between the current process state and the equilibrium state. The quantification of the driving force exploits the supersaturation Si, which is conveniently expressed as a mass fraction ratio (eqs 5 and 6).
| 5 |
| 6 |
The supersaturation of each enantiomer i changes according to the depletion in concentration of the liquid phase during crystallization. A key issue in quantifying PC, both within a more detailed PBM and the shortcut model suggested here, is the correct formulation of the supersaturations. The saturation mass fractions wsat,i are determined based on solubility data described in the ternary phase diagram (TPD).13,35,36Figure 1 illustrates TPDs for the system of enantiomers 1 and 2 (or solvates 1′ and 2′) and the solvent 3. The lines AB and CB are the solubility curves at the crystallization temperature for target and counter enantiomer, respectively. The solubility ratio (wα) between the racemic composition (w12) at point B and that of pure enantiomer (w1) at point A is defined in eq 7. This equation could be similarly written for composition of antipode (w2) at point C. For ideal systems, solubility of the racemate is double of solubility of the pure enantiomer and, hence, wα = 2.
| 7 |
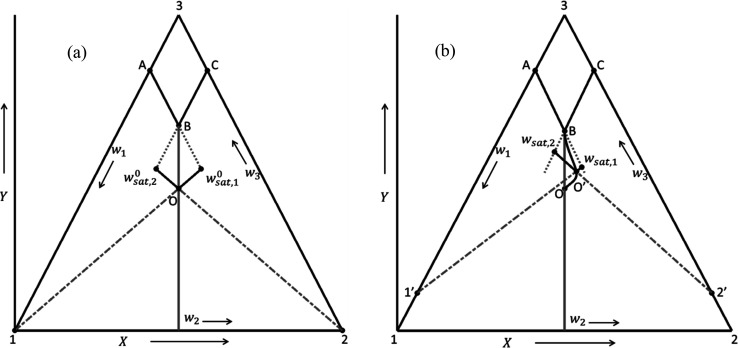
Figure 1.
Ternary phase diagrams of conglomerates illustrating calculations of driving forces used in the SCM demonstrated (a) at starting point O (lines Owsat,10 and Owsat,2) and (b) for solvated systems, at any process point O′ (lines O′wsat,1 and O′wsat,2). Points 1′ and 2′ are the respective solvated compounds of preferred and counter enantiomers. The driving force correspondent to each enantiomer at each time t is calculated from the intersection between the line connecting pure phase corner (1, 2, 1′, or 2′) and current state O′ (dash-dotted lines) and the metastable solubility (dotted lines).13,35,36
In Figure 1, O is the starting point of PC and its concentration is given by the racemate solubility at the saturation temperature. Saturation mass fractions for the preferred enantiomer can be obtained at starting composition (Figure 1a) or at any time (e.g., PC progress curve OB in Figure 1b) by calculating the intersection point of the prolongation of the solubility isotherm (e.g., line AB for preferred enantiomer) and the line connecting the time dependent current liquid phase composition (O′) with the corresponding pure enantiomer (points (a) 1 or (b) 1′). Similarly, the current saturation mass fraction can be calculated for the counter enantiomer.
The approach described can be applied for systems forming anhydrous
or solvate crystals (Figure 1a and b, respectively) and be extended to systems characterized
by curved solubility isotherms (not showed here). This requires to
respect the following transformations:37,38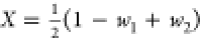 and
and 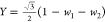 , and vice versa
, and vice versa 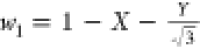 ,
, 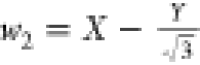 , and
, and 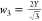 , which can be derived
using geometric consideration
of an equilateral triangle placed in the Cartesian plane as depicted
in Figure 1.
, which can be derived
using geometric consideration
of an equilateral triangle placed in the Cartesian plane as depicted
in Figure 1.
Equations 2–4 combined form a system of ordinary differential equations (ODEs) capable of describing the transients of the two enantiomers in the liquid and solid phases. These equations are rearranged for spherical particles of uniform radius Ri, providing eqs 8–12.
| 8 |
| 9 |
| 10 |
| 11 |
| 12 |
An important element of the model is the counter enantiomer contamination factor F2
| 13 |
This contamination factor F2 is used in eqs 9, 10, and 12 to introduce the stop time and to activate crystallization of the unwanted enantiomer. As described in the model assumptions 3 and 4, nuclei of the counter enantiomer are present since the start of the process but remain inactive until tstop. Therefore, a successful batch PC process should be stopped at tstop to avoid undesired depletion in purity and contamination of product. Eq 10 is the mass balance of the solvent for cases when a solvate (or hydrate) is formed. The changes of solvent mass in liquid phase depends on the crystallization of each enantiomer and is dependent on the ratio between the molar mass of solid solvate MS and that of the nonsolvate enantiomer Mi (i ∈ {1,2}). For product purity specification defined at 100%, only the three ODEs eqs 8, 10, and 11 are necessary to describe the initial period of PC until stop time. This is the time interval applied in this work to estimate parameters and model the process. eq 9 and 12 are helpful to illustrate how the process trends continue, but without the intention to match real systems. Thus, F2 can be seen as a “switch parameter”, which increases the number of equations required to approximate the dynamics of solid phase contamination for purity < 100%.
To solve the set of ODEs the following initial conditions for both solid and liquid phase are necessary.
| 14 |
| 15 |
| 16 |
The initial conditions of the liquid phase for all compounds (eq 14) are calculated from the initial solution composition. The initial mass of solid particles of target compound is the seed mass (mseeds) introduced in eq 15. The initial radius of solid target enantiomer R10 can be calculated from the average size of experimentally determined seed mass distributions. The total number of particles is assumed to be constant during the process, and it is calculated from the initial conditions as the total solid mass divided by the mass of one single particle:
| 17 |
The initial conditions for the solid phase of target enantiomer depend on experimental conditions. Nevertheless, the initial conditions for the solid phase of counter enantiomer rely on assumptions. The initial particle size R20 should be a very small quantity. We used 0.01 nm, which is even below the single unit cell or zero-dimensional crystal structure. This value effects the predicted concentration trajectories only beyond the stop time tstop. To complete the SCM, we suggest as an easy approach to set N2 to be equal to the number of particles of the target enantiomer N10, that is,
| 18 |
Strong simplifications were made to result in minimum number of equations that could still describe isothermal PC with good approximation. To reduce the number of crystallization kinetic parameters, the particulate system was assumed to be of monodispersed spheres, and all kinetic terms were lumped in the keff, as described in assumptions 1 and 2. It is well-known that nucleation plays an important role in PC. To account for this phenomenon without the strong support of nucleation theory, assumptions 3, 4, and 6 were made. The parameter tstop, along with the contamination factor F2, were introduced to border the system of equations. PC is driven by supersaturation, which was introduced via a power law function (assumptions 7 and 8), which depends only on effective order neff and Si (calculated from the TPD and depicted in Figure 1).
Another solution technique is the Method of Moments (MoM) which describes PC by using at least five differential equations. It can take into account not only growth and nucleation but also agglomeration and breakage.39 It requires several kinetic submodels with at least two parameters and a respective set of experiments to parametrize the equations for each mechanism. On the other hand, our shortcut model is more reduced and describes PC by only two or three differential equations with relatively easy to find parameters.
2.2. Implementation, Illustration, and Exploitation of the Shortcut Model
The differential equations (eqs 8–12) with the initial conditions (eqs 14–18) can be solved simultaneously in MATLAB40 using, for example, solver ode15s. Parameters needed for the simulation are m10, m2, m30, mseeds, R1, R20, ρS, wsat,1, and wsat,20. The solution of the ODE equations providing the transients of m1, m2, m3, R1, and R2 can be subsequently used to evaluate the process characteristics, for instance, enantiomeric excess, productivity.
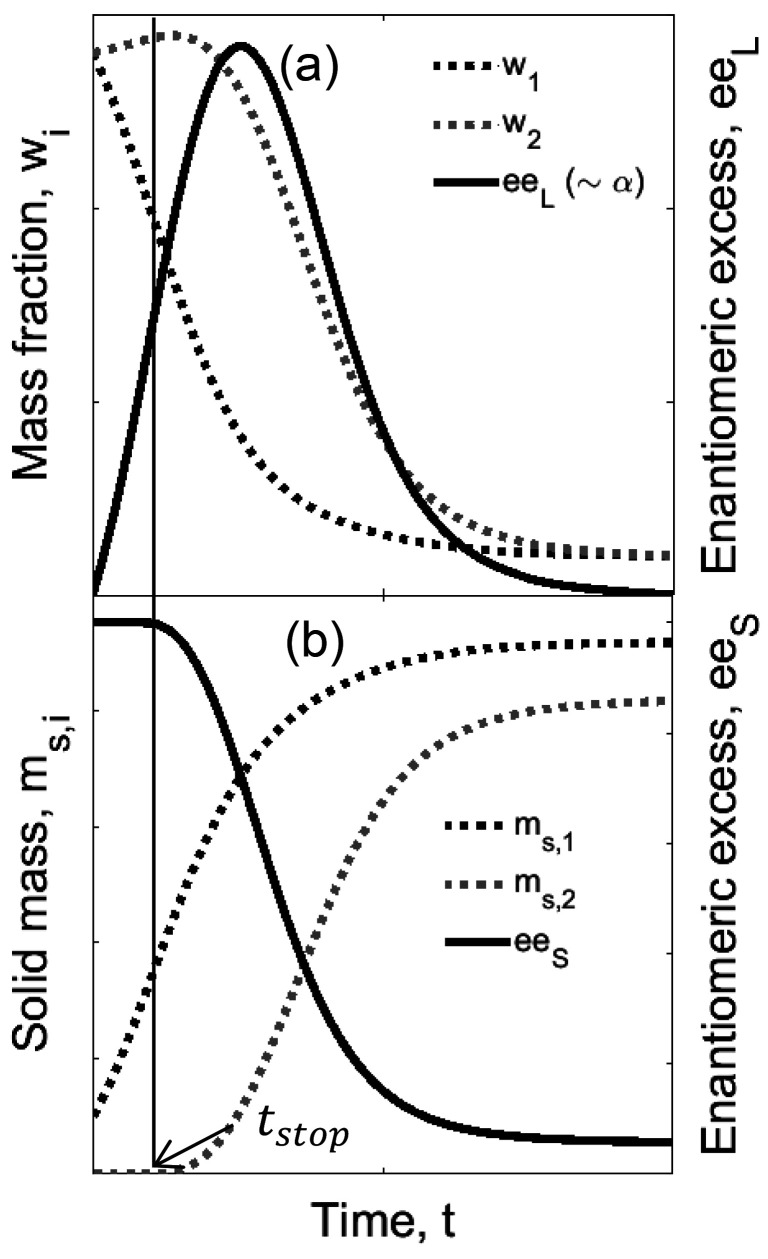
Figure 2 shows illustrative results of the shortcut model. The concentration of the seeded enantiomer in the liquid phase decreases immediately after the start of the process. The mass of the counter enantiomer in the liquid phase remains constant, and its concentration slightly increases (Figure 2a). This is a result of the reduction in the total mass of the liquid phase due to crystallization of the target enantiomer (and of solvent in the case of formation of solvate). When stop time is finally reached (see section 2.3.1), crystallization of the nontarget compound takes place. At this point, the very small particles of enantiomer 2, so far inactive, start growing. Consequently, the concentration of the counter enantiomer in the liquid phase drops and its solid mass increases until equilibrium is reached (Figure 2b). The evolution of enantiomeric excess (ee) is calculated from the mass fraction concentrations according to eq 19. An ee can be calculated for both liquid (eeL) and solid (eeS) phases, as shown in Figure 2.
| 19 |
Figure 2.
Qualitative description of preferential crystallization using the shortcut model: Evolution of (a) mass fractions and enantiomeric excess in the liquid phase eeL (directly proportional to optical rotation α) and (b) solid masses and enantiomeric excess eeS in the solid phase. In the SCM, “nuclei” of the counter enantiomer are virtually present since the start of PC but stay on hold until the process reaches the stop time tstop.
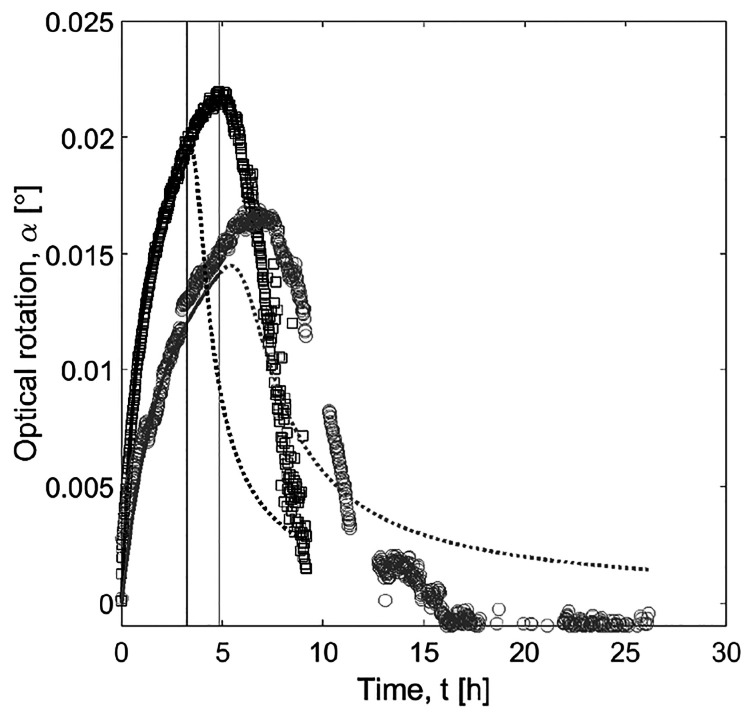
In a batch isothermal PC process, the liquid phase eeL starts at zero, since it is racemic, reaches a maximum, and depletes again following the crystallization of component 2. The solid phase eeS reflects the product purity and also drops after the stop time is reached.
To validate the model and estimate SCM kinetic parameters, it is necessary to have experimental results that give information on the time progress of PC. We propose the use of a polarimeter with online measurements of optical rotation. It can be easily implemented and calibrated with the relation
| 20 |
where α is the optical rotation and kα is a temperature dependent calibration parameter. When eqs 19 and 20 are combined, the polarimetric signal can also be expressed as function of the enantiomeric excess of the mother liquor and the total solute concentration as follows:
| 21 |
The optical rotation of isothermal batch preferential crystallization has similar time profile as the enantiomeric excess of the liquid phase as shown in Figure 2a. When the calibration factor (kα) is known, the model can be used to simulate the progress of optical rotation and to compare model and experimental results.
Another important parameter used further to correlate model and experimental data is the initial supersaturation. Since the initial solution is racemic, S10 = S2 = S0, and it is defined from eq 5 as
| 22 |
One of the main goals of the described simplified SCM is to quickly access process performance parameters. Productivity of PC is essential to evaluate performance and compare the process with different alternative processes. It is defined as the mass of produced enantiomer harvested per batch time and per unit volume of the solution, which is given by the expression
| 23 |
where tdead is an additional time needed for preparation and cleaning and VL is the volume of the liquid phase in the crystallizer.
2.3. Estimation of the Essential Parameters of SCM
To parametrize and apply the model, preliminary knowledge regarding solubility and width of metastable zone (MSZ) in the range of potential application are necessary. Then, as shown in eqs 8–12, the SCM has three main additional parameters: stop time (tstop), effective crystallization rate constant (keff), and effective order of crystallization (neff). They have to be determined with the help of experimental data.
To obtain the free model parameters a minimum of three experiments with successful PC are required. In this work, the three experiments were performed by changing the initial supersaturation (Si0), while keeping the seeding strategy (i.e., mass and size) and crystallization temperature (Tcryst) constant. It will be shown that this allows parametrizing correlations for estimating tstop and keff. During the experiments, the changes in optical rotation α over time were measured with an online polarimeter.
In summary, we propose the following strategies for estimating the free parameters of the SCM:
-
(1)
Calibrate a polarimeter to determine kα(T).
-
(2)
Perform experiments I, II, and III for three different initial supersaturations (SI0, SII, SIII0 at the same Tcryst using the same seed amounts of the same sizes) and record the profiles of optical rotation αI(t), αII(t), and αIII(t).
-
(3)
For each of the three experiments: find αmax, calculate Xα × αmax and determine tstop (see below, Figure 3 and section 2.3.1).
-
(4)
Apply the SCM to simulate the initial part of the three experiments using eqs 8, 10, and 11, that is, generating αtheoI[0,tstopI], αtheoII[0,tstopII], and αtheoIII[0,tstopIII].
-
(5)
Estimate the three free parameters by minimizing the error between simulation and experiments, that is, various sets of neff, kIeff(SI), kIIeff(SII), kIIIeff(SIII) (see objective function eq 24).
-
(6)
Correlate the three determined tstop values with the initial supersaturations S0 (section 2.3.3).
-
(7)
Correlate the three determined keff values with the initial supersaturations S0 (section 2.3.3).
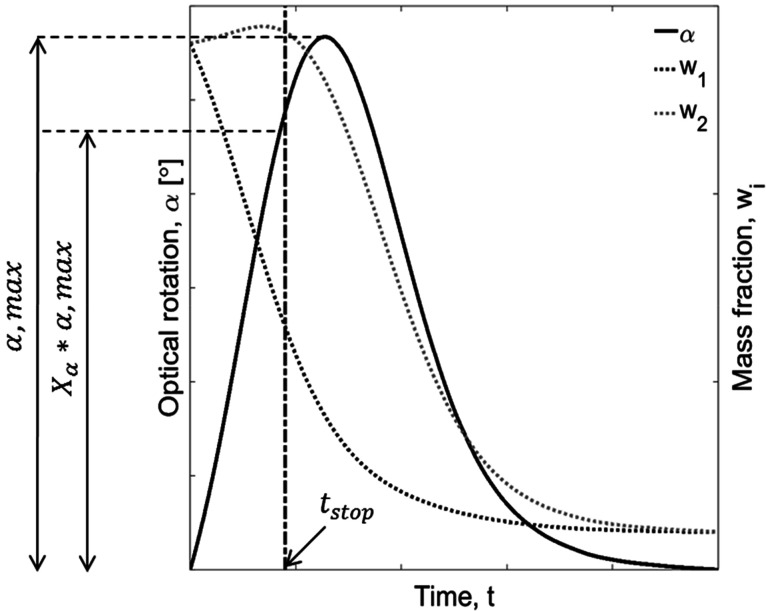
Figure 3.
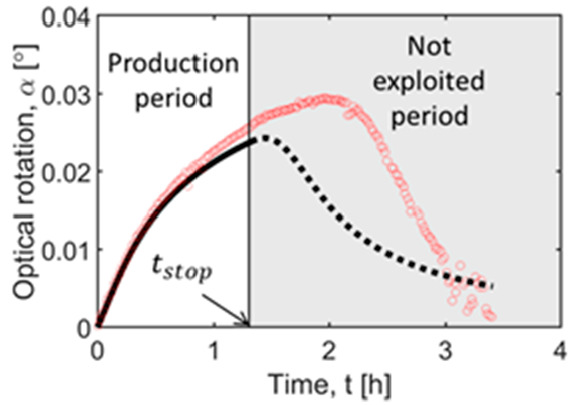
Illustration of estimation of stop time tstop. The operation window for PC lies in the interval between t = 0 and the drop in solid product caused by crystallization of the counter enantiomer. The factor Xα = 90% of the maximum optical rotation αmax is chosen to ensure product purity.
For optimal execution of these strategies, step 2 could be split into two parts: perform one experiment and, based on its results and the specifications of the compound or process studied, define the next subsequent initial conditions (e.g., higher or lower initial supersaturation).
To further increase the range of applicability of the model, additional experiments with different initial solid phase areas are to be performed.
2.3.1. Stop Time
The stop time (tstop) is the time until which the crystallization of the counter enantiomer is assumed to be inactive. It defines the time window for the production of the preferred enantiomer. As mentioned above, simulations using SCM concern and intend to predict only this region. In the systems of ODE forming the SCM, tstop is implemented via a discrete contamination factor F2. After nucleation of the counter enantiomer, the optical rotation reaches a maximum until it drops toward zero, when equilibrium is reached. However, it is difficult to provide a precise time at which the nucleation of counter enantiomer starts. Therefore, to have a safer window to harvest the product, it is proposed to stop the process before it reaches the maximum enantiomeric excess of liquid phase. In this study, the value of stop time is estimated by the time required to reach Xα = 90% of the maximum polarimetric signal αmax (Figure 3). It is well-known that nucleation and, thus, stop time is a characteristic of a given setup.41 Hence, it is also dependent on the scale of the process. Thus, it would be more beneficial to perform the experiments in the scale later used for production. If this is not feasible, an additional uncertainty has to be accepted.
2.3.2. Effective Rate Constant and Order of Crystallization
The effective crystallization rate constant (keff) is the rate constant that determines the amount of solid that crystallizes. It accounts for overall mass transfer due to both nucleation and growth. The effective order of crystallization kinetics (neff) is the hypothetical order of the driving force of the overall mass transfer process. In the SCM, neff is assumed to be independent of initial supersaturation and to be a constant value for a specific system. Both parameters, keff and neff, should be estimated simultaneously based on experimental results.
There are several ways to estimate model parameters. The algorithm for finding the parameters proposed here exploits a loop of two minimizations. The objective function that was minimized is defined in eq 24. A set of four parameters is optimized simultaneously, namely, neff and the three keff for experiments I, II, and III, that is, kIeff, kII, kIIIeff. For each experiment, the polarimetric signals αexp(t) and αtheo(t) are calculated using eq 20. To estimate the parameters, the data values of αexp and αtheo are used only until tstop. High-resolution scanning over the four parameters was performed to minimize the errors between αexp and αtheo.
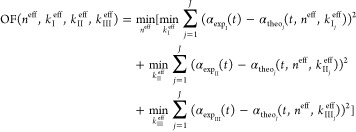 |
24 |
2.3.3. Correlation of tstop and keff with Initial Supersaturation S0
Stop time (tstop) and effective crystallization rate constant (keff) are clearly a function of temperature and supersaturation and depend on these values at each instant of time. For the sake of simplification, we propose correlating first these two parameters only with initial supersaturation. The set of experiments performed to evaluate model and correlation parameters is carried out at the same crystallization temperature. The possible inclusion of temperature will be addressed in the end of this paper.
Lower values of supersaturation are expected to generate higher stop time and vice versa. The limiting conditions for tstop are given in eq 25.
| 25 |
A simple empirical model to calculate tstop as a function of supersaturation is given by eq 26. Least square curve fitting of the linearized form of this equation can be used to determine the correlation parameters (at, bt).
| 26 |
In contrast, keff may depend on S0 in various ways, since it lumps several effects causing the mass transfer between the phases. Therefore, a more flexible dependence on initial supersaturation is required. We selected a log–log distribution with three parameters ak, bk, and ck as given by eq 27. No crystallization should happen if the system is not supersaturated, that is, S0 = 1, keff = 0. The MATLAB40 fmincon function was used to determine ak, bk, and ck from the results of three experiments with three different supersaturations.
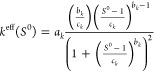 |
27 |
3. Experiments
Results of two case studies are presented in this work to demonstrate the applicability of the SCM. Investigated were (1) d-/l-threonine in water and (2) d-/l-asparagine monohydrate in water. In both cases, the l enantiomer was considered to be the target molecule. For the first case, simulated “experiments” were generated using an available fully parametrized population balance model. Real experiments described in the following subsections were performed with the system d-/l-asparagine monohydrate in water for case study 2. Detailed solubility data and information on the metastable zone for threonine42,43 and asparagine26,35,44 were published. Both compounds present near ideal solubility behavior. For threonine, the solubility was assumed to be perfectly ideal; therefore, wα = 2 (eq 7). For asparagine monohydrate, wα = 2.07 was calculated from available solubility equation35 in the temperature range of application. Experimental conditions for the two cases are described in Table 1.
Table 1. Summary of Experimental Conditions for Case Studies 1 and 2a.
| case study | experiment | w10 [102 g g–1] | wsat,10 [102 g g–1] | S0 | Tcryst [°C] | Tsat [°C] |
|---|---|---|---|---|---|---|
| 1b: threonine in water | I(1) | 8.10 | 7.40 | 1.09 | 18 | 24.5 |
| II(1) | 8.39 | 7.40 | 1.14 | 18 | 27.5 | |
| III(1) | 8.71 | 7.40 | 1.17 | 18 | 30.5 | |
| IV(1) | 8.88 | 7.40 | 1.20 | 18 | 33 | |
| V(1) | 10.14 | 7.40 | 1.37 | 18 | 44 | |
| 2c: asparagine monohydrate in water | I(2) | 4.56 | 3.68 | 1.24 | 30 | 35 |
| II(2) | 4.95 | 3.68 | 1.34 | 30 | 37 | |
| III(2) | 5.57 | 3.68 | 1.51 | 30 | 40 | |
| IV(2) | 3.68 | 2.93 | 1.26 | 25 | 30 |
Experiments I(1)–III(1) and I(2)–III(2) were used for parameter estimation. Experiments IV(1) and V(1) were used to validate the range of application of the model and experiment IV(2) to study the influence of temperature in SCM parameters. In case study 1, mseeds = 1 g and VL = 0.5 L, and in case study 2, mseeds = 0.2 g, VL = 0.2 l. w10 = initial conc. of target enantiomer (solubility at Tsat); wsat,1 was calculated from the TPD (Figure 1) using wα. The initial solution was always racemic (w10 = w12(Tsat)/2).
Experiments simulated with PBM.45
3.1. Materials
dl-Asparagine monohydrate (purity ≥ 99%) was supplied from Sigma-Aldrich Chemie GmbH, Steinheim, Germany. Ultrapure water (Millipore, Milli-Q Advantage A10) was used as solvent. l-Asparagine monohydrate (purity ≥ 99%) purchased from Acros Organics (Thermo Fisher Scientific, Geel, Belgium) was used to prepare enantiopure seed crystals.
3.2. Experimental Setup and Procedures
It is now possible and instructive to observe many process variables, for instance, total and individual concentrations, particle sizes, and distribution and solution densities. When developing this shortcut model, our goal was as to design experiments requiring only simple set up and analytics. Thus, we propose the use of only a polarimeter to track the process changes. A pair of enantiomers has specific rotation of opposite signs but equal in magnitude. The net signal measured by the polarimeter is proportional to the difference in concentration of both enantiomers as in eq 20. kα is the calibration parameter determined experimentally, which is constant for fixed temperature, wavelength, and length of measurement cell. As explained above, recorded optical rotation time profiles can be used to compare model with experimental results and to optimize parameters for SCM.
Experiments were carried out in a double vessel crystallizer of maximum volume VL = 0.2 L equipped with a Pt-100 sensor for temperature control. This scale was seemed sufficient for the purpose of this study. The solution was continuously agitated at 280 rpm using an overhead stirrer (Heidolph RZR 1, Heidolph Instruments GmbH & CO. KG, Schwabach, Germany) with 3-blade impeller (Heidolph PR 30). Online monitoring of the experiments was obtained by pumping crystal free solution through a polarimeter (MCP 500 Modular Circular Polarimeter, Anton Paar, Graz, Austria; length of cuvette 100 mm, volume of cuvette 2.0 mL, wavelength 365 nm). The flow rate of the peristaltic pump (Heidolph PD 5201 SP Quick, Heidolph Instruments GmbH & Co. KG, Schwabach, Germany) was 20 mL/min. Sintered glass filters were used to prevent crystal removal and the stream was thermostatted above the saturation temperature to avoid nucleation. For each experiment, the initially supersaturated solution (at respective Tsat) was filtrated to ensure complete dissolution and transferred to the reactor. The mother liquor was then cooled down to the crystallization temperature.
After reaching Tcryst, the solution was seeded in all three experiments identically with mseeds = 0.2 g of l-asparagine monohydrate carefully sieved to the fraction 90–125 μm. In the shortcut model, the mean size is identified as the particle diameter, therefore R10 = 53.7 μm.
4. Results and Discussion
In this section, SCM predictions are compared to experimental results for the two cases studies. For case study 1, theoretical profiles were generated with the PBM.45 In case study 2, experiments were performed with a hydrate compound, which required modifications in the driving force calculations (Figure 1) and the additional use of the mass balance for the solvent (eq 10).
4.1. Case Study 1: d-/l-Threonine in Water
We exploited a detailed population balance model with previously published crystallization kinetics45 to generate three simulated “experiments”. The PBM kinetic parameters are shown in Table A1 in Appendix. The detailed model equations and a full parameter list are found in ref (45).
Table A1. Kinetic Parameters for Population Balance Model of System d-/l-Threonine in Watera.
| kinetics | symbol | value | unit |
|---|---|---|---|
| growth | kg,0 | 1.32 × 1010 | m h–1 hng |
| EAg | 76.1 | kJ mol–1 | |
| g | 1.5 | ||
| secondary nucleation | kbsec,0 | 4.46 × 1024 | h–1 (m3)−nμ3 |
| bsec | 4.33 | ||
| nμ3b | 0.83 | ||
| primary nucleation | kbprim1 | 4.45 × 10–2 | h–1 K–1 m7 kg–(7/3) |
| kbprim2 | 4.65 × 10–4 | ||
| Aprim | 1.88 × 104 | (m2)−nμ2 | |
| nμ2c | 1.68 |
Other parameters and model equations given in ref (45).
Exponents of primary nucleation empirical kinetics.
Exponents of the secondary nucleation empirical kinetics.
4.1.1. Parameter Estimation
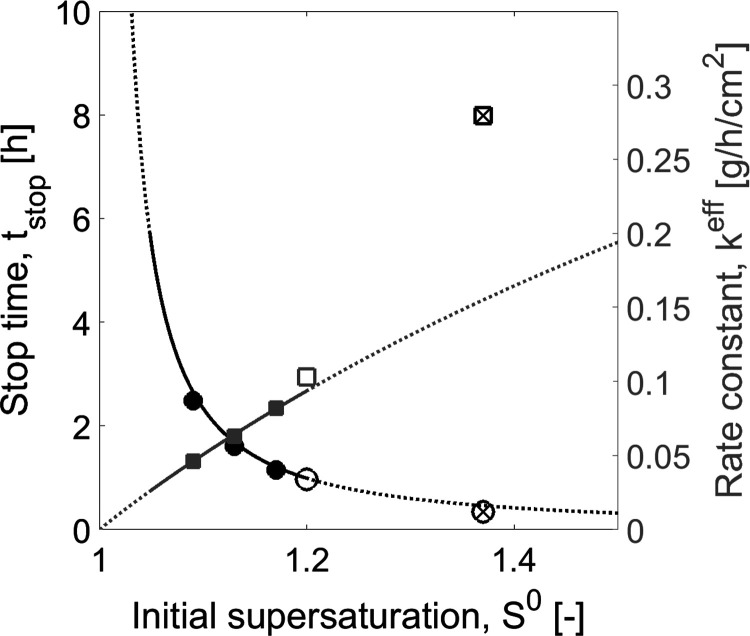
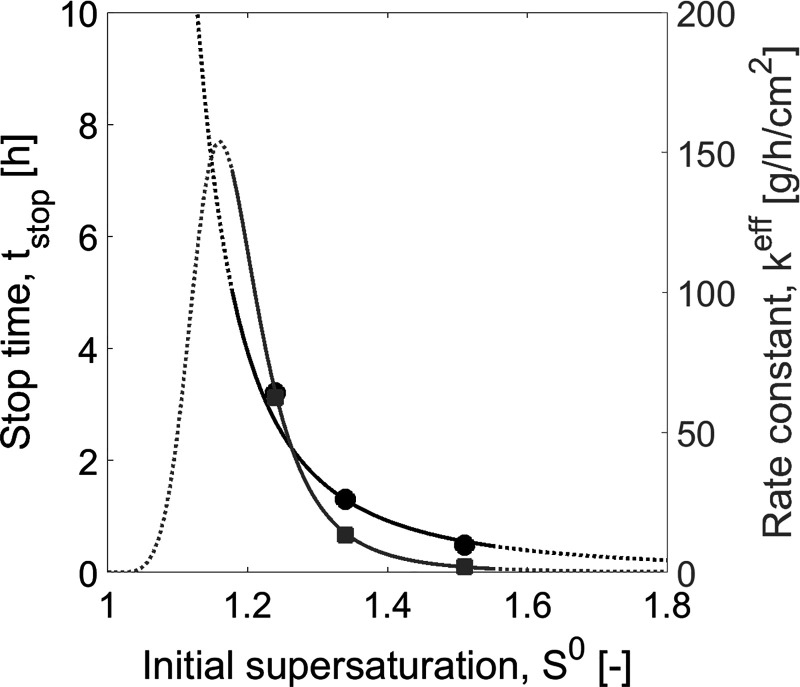
Three experiments were generated for different initial supersaturation. The crystallization temperature Tcryst was kept constant at 18 °C. Three supersaturations were produced by different Tsat and hence different initial saturation concentrations. The results of “experiments” I(1)–III(1) in Table 1 were applied to estimate tstop and keff. The output of this analysis is presented in Figures 4 and 5. Additional simulated “experiments” IV(1) and V(1) were generated for validation, and they will be discussed later in this work. The methodology to estimate the free parameters of SCM described in section 2.3 was followed. The corresponding parameters are shown in Table 2, and the correlations are depicted in Figure 4. As expected, tstop decreases with increasing S0 because a higher initial driving force for crystallization causes earlier primary nucleation of the nontarget enantiomer. Since the order of crystallization kinetics, neff, was identified to be close to unity, neff = 1 was used in the SCM. This simplifies the minimization for parameter estimation, since only the effective crystallization rate constant needs to be fitted for each experiment independently. The values of keff were correlated with initial supersaturation using eq 27. All estimated parameters are found in Table 2. Results showed that the effective crystallization rate increases proportionally to initial supersaturation in the range covered by the “experiments”, which also verifies the assumption of neff = 1 and the linear dependence on supersaturation.
Figure 4.
Case study 1: Correlation of SCM parameters tstop and keff as a function of initial supersaturation S0. Curves: Correlation functions (eq 26 and 27). Symbols: PBM simulated “experiments” (Table 1, experiments I(1)–III(1)). Black line and circles: Stop time tstop. Gray line and squares: Effective rate constant keff. Empty and crossed symbols: Additional PBM experiments used for validation for S0 close to limit and outside the width of MSZ (Table 1, experiments IV(1) and V(1)), respectively. Solid lines: Range of application of the SCM until MSZ. Tcryst = 18 °C and mseeds = 1.0 g for all “PBM experiments”.
Figure 5.
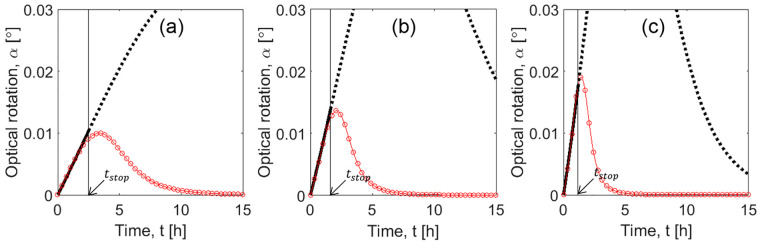
Case study 1: Comparison between SCM simulations and “experiments”. PC profiles were generated with PBM (red line and circles) for different initial supersaturations S0: (a) 1.09, (b) 1.13, and (c) 1.17 (conditions described in Table 1, experiments I(1)–III(1)). Solid black curves: SCM results until tstop, indicated with an arrow. Dotted curves: Extrapolation of SCM beyond stop time. Tcryst = 18 °C and mseeds = 1.0 g for all PBM experiments.
Table 2. Shortcut Model Parameters for Case Study 1: Simulated Experiments with the d-/l-Threonine System in Watera.
4.1.2. Illustration and Validation
The comparison between transients predicted by the PBM and the SCM is shown in Figure 5. SCM presents a very good agreement with PBM during the time frame of interest, when crystallization of the counter enantiomer is avoided and product purity is preserved. As expected, simulations beyond tstop, depicted in dotted curves, show larger deviations. Only data until tstop were used to optimize the model parameters of the shortcut model.
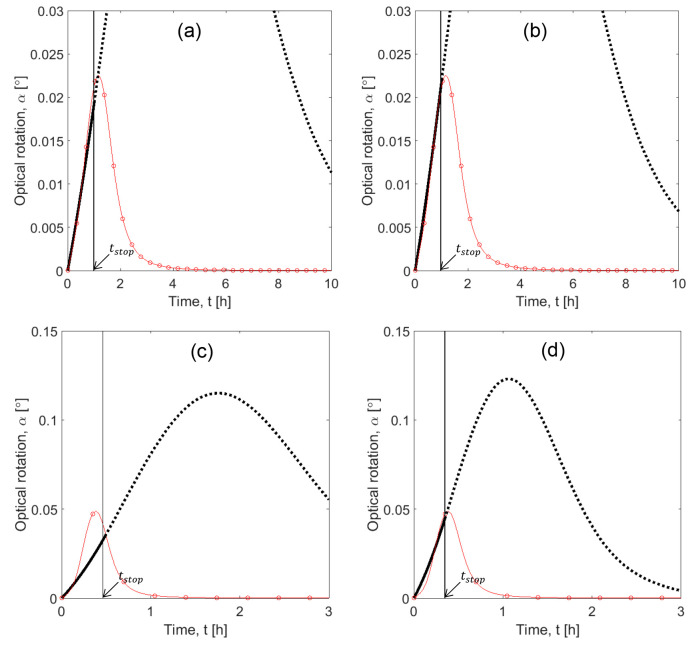
Two additional PBM simulated experiments were generated to evaluate the range of applicability of the correlations. The process conditions are given in Table 1, as experiments IV(1) and V(1). Results of experiment IV(1) (empty symbols in Figure 4) showed a good match between PBM simulated experiment and the SCM correlation functions. This validates the extension of applicability of the correlation to slightly higher values of initial supersaturation. Results of experiment V(1) (crossed symbols in Figure 4) were in larger disagreement with SCM correlations, which is in particular pronounced for the value of effective rate constant keff. These results can also be seen in the time profiles plotted in Figure 6a and c. The model fits well to the “experiments” when the correlations are not used and the parameters are estimated directly by new fit of the SCM to PBM generated transients (Figure 6b and d). It is important to note that the hypothetical experiment V(1) was only successful because it was simulated with the population balance model. It is known that, for threonine, initial supersaturations higher than 1.2 the process exceeds the metastable zone (MSZ) width42 and results in primary nucleation of the counter enantiomer. For experiment V(1), S0 was taken 1.37, which is already beyond this MSZ limit.
Figure 6.
Case study 1: Range of application of SCM. Comparison of SCM results with additional “experiments”. PC profiles were generated with PBM (red line and circles). Simulations for supersaturations S0 = 1.20 in panels a and b (Table 1, experiment IV(1)) and S0 = 1.37 in panels c and d (Table 1, experiment V(1)). SCM plots, in panels a and c, parameters previously estimated (Table 2) and, in panels b and d, parameters estimated by new fit. Solid black curve: SCM. Dotted curves: Extrapolation of SCM beyond tstop. Tcryst = 18 °C and mseeds = 1.0 g for all PBM experiments.
4.1.3. Evaluation of Productivity
To illustrate the potential of the model, SCM was further used to estimate the effect of seed mass on productivity for a range of initial supersaturations. The dead time (tdead in eq 23) between two batches was assumed to be 1 h. The results were depicted in Figure 7. The mass of seeds was evaluated relative to the maximum theoretical product mass (mmax) that can be possibly achieved thermodynamically in order to have comparable results. mmax depends on the solubility of the compound at the initial and the saturation states, as expressed in eq 28. The range of seed mass was set between 1 and 10% of the maximum theoretical product.
| 28 |
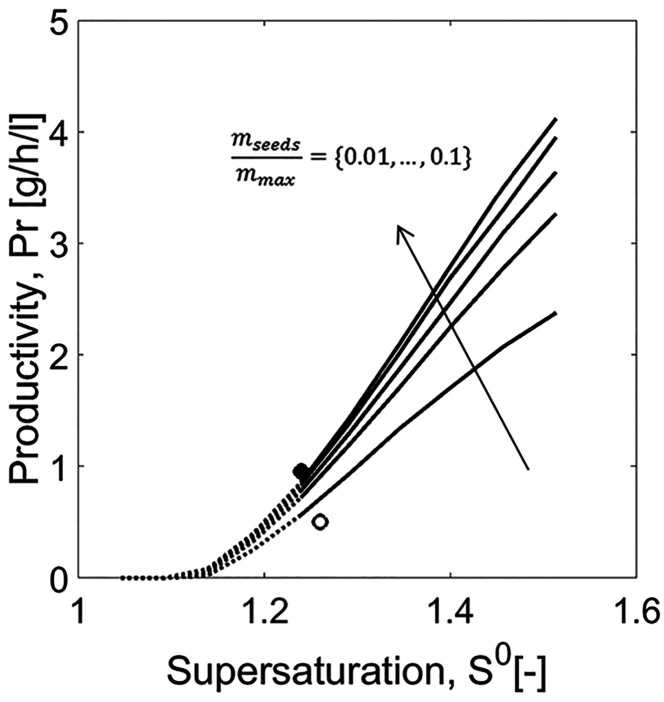
Figure 7.
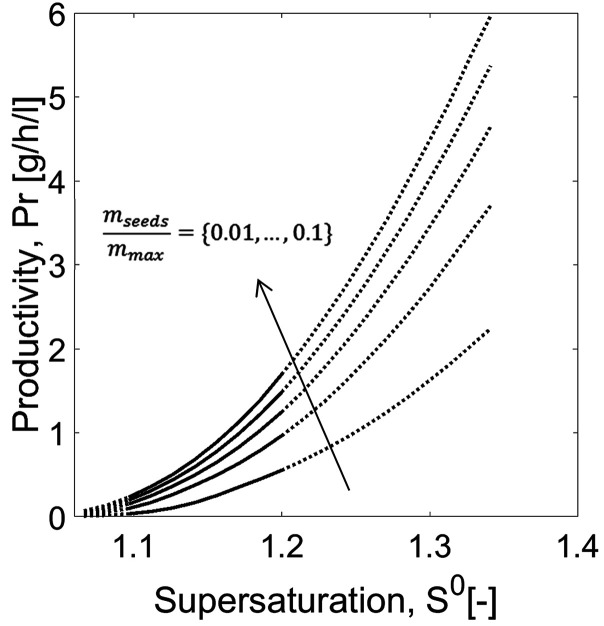
Case study 1: Productivity estimated using SCM (eq 23) and impact of seed mass. Solid curves: Range of application of SCM within the experimental conditions studied; its lower limits are delimited by the range of S0 studied in the “experiments” and its upper limits are bound by the width of MSZ (dotted curves). Tcryst = 18 °C and mseeds/mmax = 0.010, 0.032, 0.055, 0.077, and 0.100.
As expected, higher productivity can be achieved by increasing the ratio mseed/mmax. To design a cost-effective process, it is recommended that we evaluate the trade-off between higher investment in seeds, gain in productivity, and loss in process robustness, since the faster is the depletion in concentration, the higher the probability of uncontrollable fast nucleation. The profiles in Figure 7 also show that productivity increases with higher S0. Nevertheless, here, there is a limitation when designing PC since relatively high initial supersaturations are difficult to execute in practice. Clearly the width of the metastable zone plays an important role in this kinetically driven process. This property is a characteristic of the specific compound and process conditions. In Figure 7, the dashed curves for initial supersaturations beyond 1.2 indicate the MSZ limits of threonine.42,43 There is a higher probability of primary nucleation by exceeding this empirical range, thereby compromising product purity and hindering process predictability. Productivity can only be evaluated on the range of the experiments used for parameter estimation. In the present case study, all process transients used for parameter estimation have been generated for a similar crystallization temperature. Hence, the limit of the metastable zone is a constant. To evaluate the process at other temperature, additional experimental data would be necessary. In this interval, the productivity of PC for resolving the enantiomers of threonine in a batch mode lies between Pr = 0.2 and 2.0 g h–1 L–1 (eq 23).
In this calculation, we assume that the tstop is not a function of mseeds. This is apparently only valid in limited range of deviation from the reference experiment. This is a very crude assumption and can be easily relaxed provided additional experimental data are available varying either the initial crystal radius or the initial crystal numbers or both. This deeper analysis is outside the scope of this Article.
4.2. Case Study 2: d-/l-Asparagine Monohydrate in Water
To further validate the model, experiments were performed with asparagine monohydrate. Since this compound forms a hydrate, the respective ternary phase diagram was taken into consideration for calculation of driving forces, as presented in Figure 1b. Moreover, eq 10 has an important contribution since it accounts for transport of solvent molecules from the liquid to the solid phase.
4.2.1. Parameter Estimation
Figure 8 depicts the stop time over initial supersaturation for experiments I(2)–III(2) (Table 1). As expected and noticed in case 1, the higher the initial supersaturation values, the lower the stop time. Eq 26 was used to correlate tstop and S0. The resulting parameters are shown in Table 3. The table also presents the estimated values of effective crystallization order and effective rate constant. Contrary to the previous case, neff is much greater than 1. This implies deviation from linearity regarding supersaturation, which is also seen on the correlation of the effective rate to initial supersaturation (gray curves in Figures 4 and 8). Also differently from results found in the previous case, the effective crystallization rate constant for asparagine decreases with increasing initial supersaturation within the studied range. keff versus S0 has a more complex profile than the linear one observed for the threonine case. For this case, all four parameters (neff, kIeff, kII, kIIIeff) are fitted together, and neff is estimated as a compromise considering all experimental results. The success of the correlations shows the capability of the model to account for more complex nonlinear kinetics.
Figure 8.
Case study 2: Correlation of SCM parameters tstop and keff as a function of initial supersaturation S0. Solid symbols: Experimental data (Table 1, experiments I(2)–III(2)). Lines: Correlation functions (eq 26 and 27). Stop time tstop: Black curves and circles. Effective rate constant keff: Gray curves and squares. Solid lines define the range of application of the SCM. Tcryst = 30 °C and mseeds = 0.2 g for all experiments.
Table 3. Shortcut Model Parameters for Case Study 2, System d-/l-Asparagine Monohydrate in Watera.
| parameter | experimentb | value | unit |
|---|---|---|---|
| kα | 0.048 | g g–1 | |
| tstop | I(2) | 3.14 | h |
| II(2) | 1.37 | h | |
| III(2) | 0.48 | h | |
| neff | 6.10 | ||
| keff | I(2) | 62.3 | g h–1 cm–2 |
| II(2) | 13.4 | g h–1 cm–2 | |
| III(2) | 1.97 | g h–1 cm–2 | |
| at | 0.095 | h | |
| bt | 2.46 | ||
| ak | 20.8 | g h–1 cm–2 | |
| bk | 4.41 | ||
| ck | 0.17 |
4.2.2. Validation
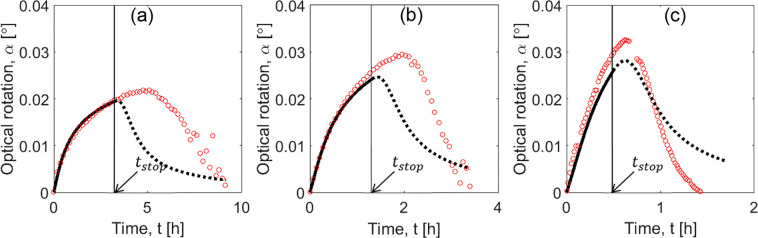
Figure 9 shows the comparison between experiments with asparagine monohydrate and SCM simulations. Here again the dotted lines are the extrapolation of the shortcut model after the stop time and includes the eqs 9 and 12 in the model. They are showed as reference and do not intend to fit experimental data. For the region of interest, there is a good match between experiments and simulation with a rather conservative estimation of the transient profile for higher values of S0. This implies slight underestimation of productivity, which is rather positive for process design. Profile a, with lower value of initial supersaturation, resulted in a better fitting between model and experiment. This difference in fitting among profiles a–c is partly because all parameters, reaction rates kIeff, kII, and kIIIeff and order neff, are optimized simultaneously (eq 24).
Figure 9.
Case study 2: Comparison between SCM simulations and experiments. Red circles: Experimental profiles for S0: (a) 1.24, (b) 1.34, and (c) 1.51 (conditions described in Table 1, experiments I(2)–III(2)). Solid black curve: SCM results until tstop, indicated with an arrow. Dotted lines: Extrapolation of SCM beyond stop time shown for illustration. Tcryst = 30 °C and mseeds = 0.2 g for all experiments.
4.2.3. Evaluation of Productivity
Results of productivity of PC to resolve asparagine monohydrate as estimated with SCM for different initial supersaturation are depicted in Figure 10. As for the previous case study, the effect of normalized seed mass was evaluated. The productivity trends are similar to the ones of threonine demonstrated in Figure 7: productivity increases by increasing mass of seeds or initial supersaturation. For similar values of initial supersaturation threonine achieves higher productivity values. Nevertheless, for asparagine higher values of initial supersaturation can be generated because of its solubility and metastable zone limits. Considering the respective temperature range studied of each compound, threonine is more strongly limited by the metastable solubility (Figure 7). Such high S0 conditions as the ones used in asparagine experiments are unlikely to work for threonine. The limits of the MSZ of asparagine monohydrate at Tcryst = 30 °C lie beyond initial supersaturation values of 1.5.44 The productivity range achieved for asparagine monohydrate at Tcryst = 30 °C is Pr = 0.5–4.0 g h–1 L–1.
Figure 10.
Case study 2: Productivity estimated using SCM and impact of seed mass. Solid curves: Range of application of SCM within the experimental conditions studied. Dotted lines delimit the lower S0 investigated in the experiments. Tcryst = 30 °C and mseeds/mmax = 0.010, 0.032, 0.055, 0.077, and 0.100. Full and empty circles indicate estimated productivity at Tcryst = 30 °C (experiment I(2)) and 25 °C (experiment IV(2)), respectively.
4.2.4. Including Temperature Effects in the SCM
So far, three experiments and simulations presented were isothermal batch PC with similar crystallization temperature, namely 18 °C for threonine and 30 °C for asparagine monohydrate. The proposed correlations for tstop (eq 26) and keff (eq 27) are a function of initial supersaturation only. For process conditions, where Tcryst is different, the effective rate and the stop time will also depend on temperature.
To evaluate the effect of temperature in the parameters of the SCM, an additional PC experiment was performed at a lower crystallization temperature. Its conditions were described in number IV(2), Table 1. This is an extra experiment to those primarily suggested in step 2 of section 2.3. On the basis of solubility data, the experimental conditions were chosen with S0 = 1.26, comparable to S0 = 1.24 of experiment I(2), but with a lower crystallization temperature Tcryst = 25 °C. In both cases, the ΔT = Tsat – Tcryst was equal to 5 K. Therefore, we assumed that the values of initial supersaturation were similar enough so that the influence of this parameter would be neglected and temperature effects could be assessed. The experimental profiles and simulations of experiments I(2) and IV(2) are depicted in Figure 11. SCM plot (solid and dotted curves) is identical to the one showed in Figure 9a for experiment I(2). For experiment IV(2), tstop was calculated as showed in section 2.3.1, and keff was estimated from the experimental data again using the MATLAB40 fmincon function. The values are indicated in Table 4. As expected, for similar values of initial supersaturation, the process with higher Tcryst presented higher keff and lower tstop. The effective rate constant for experiment I(2) was almost three times higher than experiment IV(2), while at this condition the process took a bit more than half the time to reach tstop.
Figure 11.
Case study 2: Impact of crystallization temperature in SCM parameters. Black squares: Experiment I(2), S0 = 1.24, Tcryst = 30 °C. Gray circles: Experiments IV(2), S0 = 1.26, Tcryst = 25 °C. Solid curves: SCM simulations until tstop. Dotted curves: extrapolations of these predictions beyond tstop.
Table 4. Shortcut Model Parameters for System d-/l-Asparagine Monohydrate in Watera.
| parameter | experimentb | value | unit |
|---|---|---|---|
| tstop | I(2) | 3.14 | h |
| IV(2) | 4.85 | h | |
| keff | I(2) | 62.3 | g h–1 cm–2 |
| IV(2) | 16.3 | g h–1 cm–2 | |
| Eeff | 201 | kJ mol–1 | |
| k0eff | 3.27 × 1036 | g h–1 cm–2 |
To account for the influence of temperature in the effective rate constant, we propose to extend the correlation given in eq 27 according to Arrhenius law as follows:
| 29 |
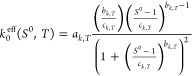 |
30 |
Note that ak,T, bk,T, ck,T ≠ ak, bk, ck from eq 27, since the parameters in eq 30 are also temperature dependent. The values of effective activation energy Eeff and prefactor k0eff were calculated using eq 29 with keff and Tcryst from experiments I(2) and IV(2). The results can be seen in Table 4. To further evaluate the correlation parameters, as well as to assess quantitatively temperature dependency in tstop, a minimum of three experiments in a range of Tcryst would be required. The goal of performing experiment IV(2) was to have an indication on the trends of parameters behavior for different crystallization temperatures. These effects will not be discussed in detail in this work. However, productivity for experiment I(2) and IV(2) was evaluated for the comparison of the two processes and they are indicated in Figure 10. The correspondent values are Pr = 0.95 g L–1 h–1 for experiment I(2) (solid circle) and Pr = 0.50 g L–1 h–1 for experiment IV(2) (empty circle). For processes with similar initial supersaturation S0, the crystallization rate increases with increase in the crystallization temperature Tcryst, which results in higher productivity.
5. Outlook
The SCM provides relative rapid access to key performance parameters of PC, as demonstrated in this work for productivity. This allows comparing PC with other possible enantioselective resolutions, for example, Viedma ripening46−49 and preparative chromatography.2 Previously, only PBM has been used for such analysis. In ref (48), the authors showed a model-based study for comparison between PC and Viedma ripening in continuous mode. A reduced model was developed for simulating the ripening process. Chromatography is reported to achieve productivities of 1–15 kg of pure enantiomer per kg stationary phase per day.50 To the best of our knowledge, such a profound comparison has not been reported yet.
Another aspect that could be treated in future work is the fact that SCM can be extended beyond isothermal batch PC for more complex process alternatives, such as batch coupled crystallizers, continuous PC and its variants, and also PC of compound-forming systems.
6. Conclusions
This Article presents a shortcut model (SCM) capable of quantifying the process of preferential crystallization (PC) of enantiomers that crystallize as conglomerates using just two (or three in case of solvates) ordinary differential equations and three easy to estimate model parameters. Previous knowledge regarding solubility and the width of metastable zones of the compounds of interest are needed. The correct formulation of supersaturations is essential for describing PC, which was demonstrated here and applied in the SCM using characteristic points in the ternary phase diagrams for both nonsolvate and solvate systems. Other requirements for application of SCM are results of at least three PC resolution experiments varying in particular in the initial supersaturation. Further model refinement requires additional experiments varying the crystallization temperature and the characteristics of the seeds used. The SCM exploits as free parameters a stop time, an effective rate constant, and an effective order of crystallization. The model allows estimating optimal performance criteria as productivities and yields. We demonstrated and validated for two case studies a simple procedure how to identify these free parameters. Initial supersaturation and seed masses were identified as the essential parameters to achieve higher productivities. The possibility to include temperature as another degree of freedom was indicated.
The success of the simplified model was only possible because PC is a relatively simple process, which includes mainly growth and nucleation. It allows in the period of interest applying a single rate constant (keff). For other more complicated crystallization processes, which might involve additional mechanisms (as agglomeration, breakage, etc.) more assumptions and parameters will be necessary to predict process productivity. Similarly, scaling-up to industrial production requires understanding of other features that will affect productivity and the parameters of the SCM would need to be eventually adjusted. A clear limitation of the shortcut model is the fact that it cannot predict the crystal size distribution and higher moments are not conserved. Nevertheless, the model is seen as a useful tool to evaluate the productivity of PC and to compare it with other rivaling techniques.
Acknowledgments
This research received funding as part of the CORE project (October 2016–September 2020) from the European Union Horizon 2020 research and innovation under Marie Sklodowska Curie Grant Agreement No. 722456 CORE ITN.
Glossary
Notation
- ak
parameter of correlation of keff(S0) [g h–1 cm–2]
- ak,T
parameter of correlation of keff(S0,T) [g h–1 cm–2]
- at
parameter of correlation of tstop [h]
- bk
parameter of correlation of keff(S0)
- bk,T
parameter of correlation of keff(S0,T)
- bt
parameter of correlation of tstop
- ck
parameter of correlation of keff(S0)
- ck,T
parameter of correlation of keff(S0,T)
- D
dissolution rate in PBM [cm h–1]
- ee
enantiomeric excess
- eeL
enantiomeric excess of liquid phase
- eeS
enantiomeric excess of solid phase
- Eeff
effective activation energy [kJ mol–1]
- f
number density function [no. cm–1]
- F2
counter enantiomer contamination factor
- GBeff
effective overall mass transfer rate [g h–1]
- i
index of target and counter enantiomers (1, 2) or solvent (3)
- j
index of iteration of keff optimization
- J
number of guesses of keff for optimization
- keff
effective crystallization rate constant, parameter of SCM [g h–1 cm–2]
- k0eff
parameter of correlation of keff(S0,T) [g h–1 cm–2]
- kα
calibration parameter of polarimeter [g g–1 deg–1]
- L
coordinate of particles in PBM [cm]
- m
mass of liquid phase [g]
- mmax
maximum theoretical product mass [g]
- mS
mass of solid phase [g]
- mseeds
mass of seeds [g]
- mtot
total mass of liquid phase [g]
- m0
initial mass of liquid phase [g]
- mS0
initial mass of solid phase [g]
- Mi
molar mass of nonsolvate enantiomer [g mol–1]
- MS
molar mass of solid phase [g mol–1]
- neff
effective order of crystallization kinetics
- N
number of particles
- OF
objective function
- Pr
productivity [g h–1 L–1]
- R
radius of particles [cm]
- Rg
universal gas constant [J mol–1 K–1]
- R0
initial radius of particles [cm]
- S
supersaturation
- S0
initial supersaturation
- t
time [h]
- tdead
dead time or idle time during PC process [h]
- tstop
stop time, parameter of SCM [h]
- T
temperature [°C]
- Tcryst
crystallization temperature [°C]
- Tsat
saturation temperature [°C]
- VL
volume of liquid phase [cm3]
- VS
volume of solid phase [cm3]
- w0
initial mass fraction [g g–1]
- w
mass fraction [g g–1]
- wsat
saturation mass fraction [g g–1]
- w12
saturation mass fraction of racemate [g g–1]
- wα
solubility ratio
- X
Cartesian coordinate
- Xα
fraction of αmax for estimation of tstop [%]
- Y
Cartesian coordinate
- α
optical rotation [deg]
- αexp
experimental values of optical rotation [deg]
- αmax
maximum optical rotation reached during batch PC [deg]
- αtheo
theoretical values of optical rotation simulated with SCM [deg]
- ρs
density of solid phase [g cm–3]
Variables Used in Case Study 1 for Population Balance Model (see Ref (45))
- Aprim
PBM coefficient of heterogeneous contribution (prim. nucleation) [m–2nμ2]
- bsec
PBM power law exponent (sec. nucleation)
- B
PBM nucleation rate [no. h–1]
- EAg
PBM activation energy of growth kinetics [J mol–1]
- g
PBM power law exponent of growth kinetics
- G
PBM growth rate [cm h–1]
- kbprim1
PBM pre-exponential coefficient (prim. nucleation) [h–1 K–1 m7 kg–7/3]
- kbprim2
PBM exponential coefficient (prim. nucleation)
- kbsec0
PBM pre-exponential coefficient (sec. nucleation) [h–1m–3nμ3]
- kg0
PBM pre-exponential coefficient (growth) [m h–1 hgn]
- ng
PBM exponent of stirrer speed correlation (growth)
- nμ2
PBM exponent of second moment in correlation for primary nucleation
- nμ3
PBM exponent of third moment in correlation for secondary nucleation
Appendix
The PBM was used to generate simulated experiments to evaluate a shortcut model in case study 1. The main estimated parameters are here summarized in Table A1. Other constants and technical details can be found in Eicke’s work.45
The authors declare no competing financial interest.
This paper was originally published ASAP on August 14, 2019. Due to a production error, the last term of eq 10 was incorrect. The revised version was reposted on August 15, 2019.
References
- Calcaterra A.; D’Acquarica I. The market of chiral drugs: Chiral switches versus de novo enantiomerically pure compounds. J. Pharm. Biomed. Anal. 2018, 147, 323–340. 10.1016/j.jpba.2017.07.008. [DOI] [PubMed] [Google Scholar]
- Lorenz H.; Seidel-Morgenstern A. Processes To Separate Enantiomers. Angew. Chem., Int. Ed. 2014, 53 (5), 1218–1250. 10.1002/anie.201302823. [DOI] [PubMed] [Google Scholar]
- Lovette M. A. Chiral control of enantiomers through crystallization: Moving from ternary phase diagrams to design spaces. AIChE J. 2018, 64 (9), 3323–3331. 10.1002/aic.16202. [DOI] [Google Scholar]
- Juza M.; Mazzotti M.; Morbidelli M. Simulated moving-bed chromatography and its application to chirotechnology. Trends Biotechnol. 2000, 18 (3), 108–118. 10.1016/S0167-7799(99)01419-5. [DOI] [PubMed] [Google Scholar]
- Lorenz H.; Sheehan P.; Seidel-Morgenstern A. Coupling of simulated moving bed chromatography and fractional crystallisation for efficient enantioseparation. Journal of Chromatography A 2001, 908 (1), 201–214. 10.1016/S0021-9673(00)00992-4. [DOI] [PubMed] [Google Scholar]
- Wrzosek K.; García Rivera M. A.; Bettenbrock K.; Seidel-Morgenstern A. Racemization of undesired enantiomers: Immobilization of mandelate racemase and application in a fixed bed reactor. Biotechnol. J. 2016, 11 (4), 453–463. 10.1002/biot.201500494. [DOI] [PubMed] [Google Scholar]
- Afonso C. A. M.; Crespo J. G. Recent Advances in Chiral Resolution through Membrane-Based Approaches. Angew. Chem., Int. Ed. 2004, 43 (40), 5293–5295. 10.1002/anie.200460037. [DOI] [PubMed] [Google Scholar]
- Xie R.; Chu L.-Y.; Deng J.-G. Membranes and membrane processes for chiral resolution. Chem. Soc. Rev. 2008, 37 (6), 1243–1263. 10.1039/b713350b. [DOI] [PubMed] [Google Scholar]
- Coquerel G.Preferential crystallization. In Novel Optical Resolution Technologies; Springer, 2006; pp 1–51. [Google Scholar]
- Majumder A.; Nagy Z. A comparative study of coupled preferential crystallizers for the efficient resolution of conglomerate-forming enantiomers. Pharmaceutics 2017, 9 (4), 55. 10.3390/pharmaceutics9040055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenz H.; Polenske D.; Seidel-Morgenstern A. Application of preferential crystallization to resolve racemic compounds in a hybrid process. Chirality 2006, 18 (10), 828–840. 10.1002/chir.20327. [DOI] [PubMed] [Google Scholar]
- von Langermann J.; Kaspereit M.; Shakeri M.; Lorenz H.; Hedberg M.; Jones M. J.; Larson K.; Herschend B. r.; Arnell R.; Temmel E.; et al. Design of an integrated process of chromatography, crystallization and racemization for the resolution of 2′, 6′-pipecoloxylidide (PPX). Org. Process Res. Dev. 2012, 16 (2), 343–352. 10.1021/op200268h. [DOI] [Google Scholar]
- Jacques J.; Collet A.; Wilen S., Enantiomers, Racemates and Resolution; Krieger Publishing Company: Malabar, FL, 1994. [Google Scholar]
- Levilain G.; Coquerel G. Pitfalls and rewards of preferential crystallization. CrystEngComm 2010, 12 (7), 1983–1992. 10.1039/c001895c. [DOI] [Google Scholar]
- Elsner M. P.; Ziomek G.; Seidel-Morgenstern A. Simultaneous preferential crystallization in a coupled batch operation mode. Part II: Experimental study and model refinement. Chem. Eng. Sci. 2011, 66 (6), 1269–1284. 10.1016/j.ces.2010.12.035. [DOI] [Google Scholar]
- Elsner M. P.; Ziomek G.; Seidel-Morgenstern A. Efficient separation of enantiomers by preferential crystallization in two coupled vessels. AIChE J. 2009, 55 (3), 640–649. 10.1002/aic.11719. [DOI] [Google Scholar]
- Hein J. E.; Cao B. H.; van der Meijden M. W.; Leeman M.; Kellogg R. M. Resolution of omeprazole using coupled preferential crystallization: efficient separation of a nonracemizable conglomerate salt under near-equilibrium conditions. Org. Process Res. Dev. 2013, 17 (6), 946–950. 10.1021/op400081c. [DOI] [Google Scholar]
- Chaaban J. H.; Dam-Johansen K.; Skovby T.; Kiil S. Separation of enantiomers by continuous preferential crystallization: Experimental realization using a coupled crystallizer configuration. Org. Process Res. Dev. 2013, 17 (8), 1010–1020. 10.1021/op400087g. [DOI] [Google Scholar]
- Eicke M. J.; Levilain G.; Seidel-Morgenstern A. Efficient resolution of enantiomers by coupling preferential crystallization and dissolution. Part 2: A parametric simulation study to identify suitable process conditions. Cryst. Growth Des. 2013, 13 (4), 1638–1648. 10.1021/cg3018503. [DOI] [Google Scholar]
- Levilain G.; Eicke M. J.; Seidel-Morgenstern A. Efficient resolution of enantiomers by coupling preferential crystallization and dissolution. Part 1: Experimental proof of principle. Cryst. Growth Des. 2012, 12 (11), 5396–5401. 10.1021/cg3009943. [DOI] [Google Scholar]
- Galan K.; Eicke M. J.; Elsner M. P.; Lorenz H.; Seidel-Morgenstern A. Continuous preferential crystallization of chiral molecules in single and coupled mixed-suspension mixed-product-removal crystallizers. Cryst. Growth Des. 2015, 15 (4), 1808–1818. 10.1021/cg501854g. [DOI] [Google Scholar]
- Kóllges T.; Vetter T. Model-based analysis of continuous crystallization/reaction processes separating conglomerate forming enantiomers. Cryst. Growth Des. 2017, 17 (1), 233–247. 10.1021/acs.cgd.6b01487. [DOI] [Google Scholar]
- Vetter T.; Burcham C. L.; Doherty M. F. Separation of conglomerate forming enantiomers using a novel continuous preferential crystallization process. AIChE J. 2015, 61 (9), 2810–2823. 10.1002/aic.14934. [DOI] [Google Scholar]
- Tung H.-H.; Paul E. L.; Midler M.; McCauley J. A.. Crystallization of Organic Compounds: An Industrial Perspective; John Wiley & Sons, 2009. [Google Scholar]
- Binev D.; Seidel-Morgenstern A.; Lorenz H. Continuous separation of isomers in fluidized bed crystallizers. Cryst. Growth Des. 2016, 16 (3), 1409–1419. 10.1021/acs.cgd.5b01513. [DOI] [Google Scholar]
- Petruševska-Seebach K.Overcoming Yield Limitations when Resolving Racemates by Combination of Crystallization And, Or Chromatography with Racemization; Docupoint-Verlag, 2012. [Google Scholar]
- Wuerges K.; Petruševska-Seebach K.; Elsner M. P.; Lütz S. Enzyme-assisted physicochemical enantioseparation processes—Part III: Overcoming yield limitations by dynamic kinetic resolution of asparagine via preferential crystallization and enzymatic racemization. Biotechnol. Bioeng. 2009, 104 (6), 1235–1239. 10.1002/bit.22498. [DOI] [PubMed] [Google Scholar]
- Randolph A. D.; Larson M. A.. Theory of Particulate Processes: Analysis and Techniques of Continuous Crystallization, 2nd ed.; Academic Press: New York, 1988. [Google Scholar]
- Ramkrishna D.Population Balances: Theory and Applications to Particulate Systems in Engineering; Elsevier, 2000. [Google Scholar]
- Elsner M. P.; Menéndez D. F.; Muslera E. A.; Seidel-Morgenstern A. Experimental study and simplified mathematical description of preferential crystallization. Chirality 2005, 17 (S1), S183–S195. 10.1002/chir.20135. [DOI] [PubMed] [Google Scholar]
- Qamar S.; Galan K.; Elsner M. P.; Hussain I.; Seidel-Morgenstern A. Theoretical investigation of simultaneous continuous preferential crystallization in a coupled mode. Chem. Eng. Sci. 2013, 98, 25–39. 10.1016/j.ces.2013.05.010. [DOI] [Google Scholar]
- Nagy Z. K.; Fevotte G.; Kramer H.; Simon L. L. Recent advances in the monitoring, modelling and control of crystallization systems. Chem. Eng. Res. Des. 2013, 91 (10), 1903–1922. 10.1016/j.cherd.2013.07.018. [DOI] [Google Scholar]
- Temmel E.; Eicke M.; Lorenz H.; Seidel-Morgenstern A. A short-cut method for the quantification of crystallization kinetics. 2. Experimental application. Cryst. Growth Des. 2016, 16 (12), 6756–6768. 10.1021/acs.cgd.6b00789. [DOI] [Google Scholar]
- Temmel E.; Eisenschmidt H.; Lorenz H.; Sundmacher K.; Seidel-Morgenstern A. A short-cut method for the quantification of crystallization kinetics. 1. Method development. Cryst. Growth Des. 2016, 16 (12), 6743–6755. 10.1021/acs.cgd.6b00787. [DOI] [Google Scholar]
- Temmel E.; Gánsch J.; Lorenz H.; Seidel-Morgenstern A. Measurement and evaluation of the crystallization kinetics of L-asparagine monohydrate in the ternary L-/D-asparagine/water system. Cryst. Growth Des. 2018, 18 (12), 7504–7517. 10.1021/acs.cgd.8b01322. [DOI] [Google Scholar]
- Coquerel G. Solubility of chiral species as function of the enantiomeric excess. J. Pharm. Pharmacol. 2015, 67 (6), 869–878. 10.1111/jphp.12395. [DOI] [PubMed] [Google Scholar]
- Shimura T.; Kemp A. I. Tetrahedral plot diagram: A geometrical solution for quaternary systems. Am. Mineral. 2015, 100 (11–12), 2545–2547. 10.2138/am-2015-5371. [DOI] [Google Scholar]
- Temmel E.; Müller U.; Grawe D.; Eilers R.; Lorenz H.; Seidel-Morgenstern A. Equilibrium model of a continuous crystallization process for separation of substances exhibiting solid solutions. Chem. Eng. Technol. 2012, 35 (6), 980–985. 10.1002/ceat.201200002. [DOI] [Google Scholar]
- Qamar S.; Mukhtar S.; Ali Q.; Seidel-Morgenstern A. A Gaussian quadrature method for solving batch crystallization models. AIChE J. 2011, 57 (1), 149–159. 10.1002/aic.12264. [DOI] [Google Scholar]
- Mathworks M., MATLAB and Statistics Toolbox Release; The MathWorks, Inc.: Natick, MA, 2017. [Google Scholar]
- Mersmann A.Crystallization Technology Handbook; CRC Press, 2001. [Google Scholar]
- Lorenz H.; Perlberg A.; Sapoundjiev D.; Elsner M. P.; Seidel-Morgenstern A. Crystallization of enantiomers. Chem. Eng. Process. 2006, 45 (10), 863–873. 10.1016/j.cep.2005.11.013. [DOI] [Google Scholar]
- Sapoundjiev D.; Lorenz H.; Seidel-Morgenstern A. Solubility of chiral threonine species in water/ethanol mixtures. J. Chem. Eng. Data 2006, 51 (5), 1562–1566. 10.1021/je060053h. [DOI] [Google Scholar]
- Petruševska-Seebach K.; Seidel-Morgenstern A.; Elsner M. P. Preferential crystallization of L-asparagine in water. Cryst. Growth Des. 2011, 11 (6), 2149–2163. 10.1021/cg101408e. [DOI] [Google Scholar]
- Eicke M.Process Strategies for Batch Preferential Crystallization; PhD Thesis, Otto-von-Guericke University, Shaker Verlag, Aachen, 2016. [Google Scholar]
- Viedma C. Chiral symmetry breaking during crystallization: complete chiral purity induced by nonlinear autocatalysis and recycling. Phys. Rev. Lett. 2005, 94 (6), 065504. 10.1103/PhysRevLett.94.065504. [DOI] [PubMed] [Google Scholar]
- Noorduin W. L.; van Enckevort W. J.; Meekes H.; Kaptein B.; Kellogg R. M.; Tully J. C.; McBride J. M.; Vlieg E. The driving mechanism behind attrition-enhanced deracemization. Angew. Chem., Int. Ed. 2010, 49 (45), 8435–8438. 10.1002/anie.201002036. [DOI] [PubMed] [Google Scholar]
- Kóllges T.; Vetter T. Design and performance assessment of continuous crystallization processes resolving racemic conglomerates. Cryst. Growth Des. 2018, 18 (3), 1686–1696. 10.1021/acs.cgd.7b01618. [DOI] [Google Scholar]
- Breveglieri F.; Maggioni G. M.; Mazzotti M. Deracemization of NMPA via Temperature Cycles. Cryst. Growth Des. 2018, 18 (3), 1873–1881. 10.1021/acs.cgd.7b01746. [DOI] [Google Scholar]
- Blehaut J.; Franco P.; Zhang T.; Lang E.; Valery E.; Marcoux J.-F. 9.17 Industrial Applications of Chiral Chromatography. Comprehensive Chirality 2012, 400–456. 10.1016/B978-0-08-095167-6.00920-4. [DOI] [Google Scholar]