Automated Raman Spectral Preprocessing of Bone and Other Musculoskeletal Tissues

Abstract

Raman spectroscopy of bone is complicated by fluorescence background and spectral contributions from other tissues. Full utilization of Raman spectroscopy in bone studies requires rapid and accurate calibration and preprocessing methods. We have taken a step-wise approach to optimize and automate calibrations, preprocessing and background correction. Improvements to manual spike removal, white light correction, software image rotation and slit image curvature correction are described. Our approach is concisely described with a minimum of mathematical detail.

1. INTRODUCTION

Raman spectroscopy of biological samples has been established as a method to examine tissues, cells and biological fluids in the spectroscopy laboratory.^1–4 In the Morris laboratory, Raman spectroscopy is used to examine musculoskeletal tissues.^5–10 The application of Raman spectroscopy to musculoskeletal tissues requires increasingly complex experimental procedures for analyzing the resulting data. Many software routines have been developed in the Morris lab for preprocessing and analysis of Raman spectra of bone. Preprocessing steps include: cosmic ray removal, correction for slit curvature, correction for the quantum efficiency of the detector, and calibration of the wavelength axis. Principal components analysis, factor analysis or band target entropy minimization (BTEM) have been used to extract important Raman features, which include band intensity or band width.¹¹ These routines are effective in preprocessing and extracting Raman data. However, the conventional approach to the analysis of Raman data is time-intensive, requires multiple software programs, and is subjective. As Raman imaging modalities and multi-point probes become more widely used, labor-intensive data processing routines will become impractical. Recent technological advances, including intensified detectors and fiber optic systems, have the potential to expand the utility of Raman spectroscopy in the biomedical field. As Raman spectroscopy becomes more useful in clinics and hospital laboratories, the concept of how spectral data is processed and interpreted must be reconsidered for a non-specialist user.

In our case, the recovery of Raman spectra from bone in vivo is complicated by light scattering (which decreases the efficiency of Raman collection), fluorescence, absorption (and heating from the excitation laser) and overlapping spectral features. Similar spectral interference can be observed when collecting Raman spectra of tissue sections, cell or tissue cultures, and biological fluids. For both novice users and experienced spectroscopists, the correct application of preprocessing methods is critical to extracting the best possible information from a spectrum. For example, accurate calculations of band intensity ratios used to describe bone tissue health are affected by the baseline-correction step.

In vivo Raman spectroscopy is limited by both experimental and data processing barriers.^12–17 The two fundamental problems are in detecting adequate Raman signal and discrimination of the Raman signal from the complex fluorescence background. Various methods such as surface-enhanced Raman spectroscopy (SERS) and coherent anti-Stokes Raman spectroscopy (CARS) are used to enhance Raman scattering, however these methods have limited applicability for in vivo measurements. SERS is not routinely used in vivo because it requires the insertion of a suitable substrate. The coherent nature of CARS, combined with optical scattering of skin, limits CARS measurement to within 1 mm of the skin surface. As a result, normal Raman scattering is currently the only practical means for performing in vivo Raman spectroscopy. The measured Raman signal can also be increased by increasing the excitation power, or by improving the collection efficiency. Power densities also cause local heating, and excitation light must be limited to safe exposure levels. Collection efficiency can be improved by optical clearing, improving collection optics, or using better detectors. Again, these experimental methods are limited by the practicality of current technologies in terms of both cost and time. Both temporal methods and spatial methods can be used to reject fluorescence.^18,19 Temporal methods are complicated by light diffusion in tissue and cost prohibitive. Spatial methods are again hampered by scattering. Excitation and Raman scattered light diffuse and heterogeneity is decreased.

Enhancement of data preprocessing measures offers a simpler path toward improving in vivo Raman spectroscopy. Simple data processing methods have been developed which improve our ability to use Raman spectral information and reduce the time required to process the data. Several examples of helpful data processing methods include: derivative minimization for fitting spectral components,²⁰ iteratively modified polynomial baseline fitting,¹⁶ and abscissa error detection.²¹

In this paper, we report a step-wise approach toward optimizing and automating calibrations for an imaging Raman spectrometer, and automation of the spectral data preprocessing and background correction. We include spike removal, dichroic transmission, white light and dark current correction, slit image curvature correction, wavelength calibration against atomic emission spectra, and calibration of the laser wavelength against Raman standards. An extra step has been incorporated to correct for image rotation, which corrects for minor misalignment of the detector to the dispersion axis of the grating. This step reduces the complexity of the background correction polynomial by several polynomial orders. These preprocessing steps reduce the variance in extracted band features including band area, height, and width with minimal user intervention. This methodology is especially useful for multi-day or longer experimental sequences which generate large numbers of spectra. Ex vivo spectral measurements of bone are used to illustrate the usefulness of our new approach.

2. METHODOLOGY

2.1. Raman Spectroscopy Instrumentation

Raman imaging data was collected in this study using an axial-transmissive spectrograph (Holospec VPT f1.8, Kaiser Optical Systems Inc., Ann Arbor, MI, USA) equipped with an Andor camera (DU401-BR-DD, Andor Technology, Belfast, Ireland) with a Peltier-cooled charge-coupled device (CCD). The excitation source for the Raman spectra was an Invictus 785 laser (785nm, 450mW, Kaiser Optical Systems Inc.). The excitation laser is shaped into a line using two spherical lenses to select the magnification, and one cylindrical lens between them to form the laser beam into a line shape. The excitation laser line and Raman scattered light are coupled into a Nikon microscope (Eclipse ME600, Nikon Instruments Inc., Melville, NY, USA) through an optical port above the objectives. Prior to entering the microscope the excitation laser line and Raman spectral collection paths are made coaxial using a dichroic filter (LPD01-785RS-25, Semrock, Rochester, NY, USA) mounted in a 1” Flipper mount (Model 9891, New Focus, San Jose, CA). The microscope stage was fitted with a motorized stage (ProScan II, Prior Scientific, Rockland, MA, USA) to enable automated Raman pushbroom imaging along the X- and Y-axes.

2.2. Image Acquisition, Conversion and Loading

Prior to analysis of any samples, several calibration spectral were recorded. Calibration images of neon and a white-light are initially recorded from the Holospec Calibration Accessory (HCA, Kaiser Optical Sytems Inc.). A simple flip-down of the dichroic allows collection of a white-light image without the dichroic mirror. This action allows us to compensate for imperfections in the dichroic filter. A Raman image of Teflon® is then recorded. Dark images (with an opaque tape blocking the spectrograph slit) are recorded for each of the acquisition times (including for each Raman image acquisition time later used in the microscopic imaging).

Once the sample is correctly positioned, spectral images are recorded using vendor-supplied software (Andor MCD, Andor Technology) to record the initial camera output images as ‘.SIF’ fries. Files are then converted to ‘.ASC’ (ASCII) format using the vendor-supplied software. All subsequent data-manipulation is performed in MATLAB (version 7.6, The MathWorks Inc., Natick, MA, USA). The images are loaded into MATLAB through a function written in-house allowing multi-frame images to be efficiently loaded into a 3-dimensional array for hyperspectral image processing. Individually acquired 2-dimensional frames can also be stacked into 3-dimensional arrays in this way to group the data and simplify handling steps by ensuring that all spectral images are processed identically.

3. RESULTS AND DISCUSSION

Unprocessed images have several undesirable features which hamper analysis of the observed Raman signal. Undesirable features include non-uniform background signals, wavelength-dependent gain, noise, sample fluorescence, slit image curvature, as well as hot-pixels and cosmic-ray hits (commonly referred to as spikes). Most of these features can be easily corrected, such as background offsets, and wavelength-dependent gain (flat-field correction). Other features, such as tissue fluorescence background and cosmic-rays hits are quite challenging to automatically correct.

3.1. Cosmic-Ray ‘Spike’ Correction

Cosmic ray hits (environmental radiation) must first be removed from all image frames. Typical cosmic ray signals in our system have intensities of 500-3000 counts and also affect adjacent pixels. Several cosmic ray signals accumulated over one hundred 10 second acquisitions are shown in Figure 1a. The nature of these cosmic rays has been nebulous, and a commonly accepted principle is that cosmic ray signals are due to high-energy particles. Recent studies have suggested that permanent defects in sensitive CCD’s may arise during air-transport, because of reduced atmospheric shielding of high-energy inter-stellar particles (such as neutrons) at high elevations.²² At lower altitudes, radioactive trace components in glass and semiconductor materials emit radiation and cause both permanent damage (from alpha radiation) and transient spikes (from beta and gamma radiation) in CCD sensors.²² Several methods have been proposed to remove cosmic rays.^23–29 A method known as “upper-bound spectrum”, or UBS, is a straight-forward algorithm that corrects for spikes in multi-frame images.²⁷ In UBS, pixel signals affected by cosmic rays can be located because they have much greater intensity than surrounding pixels. Other cosmic ray correction methods include image filters (median filters, Laplacian edge detection, smoothing filters, derivatives), and spectral outlier detection.²⁵

Figure 1.

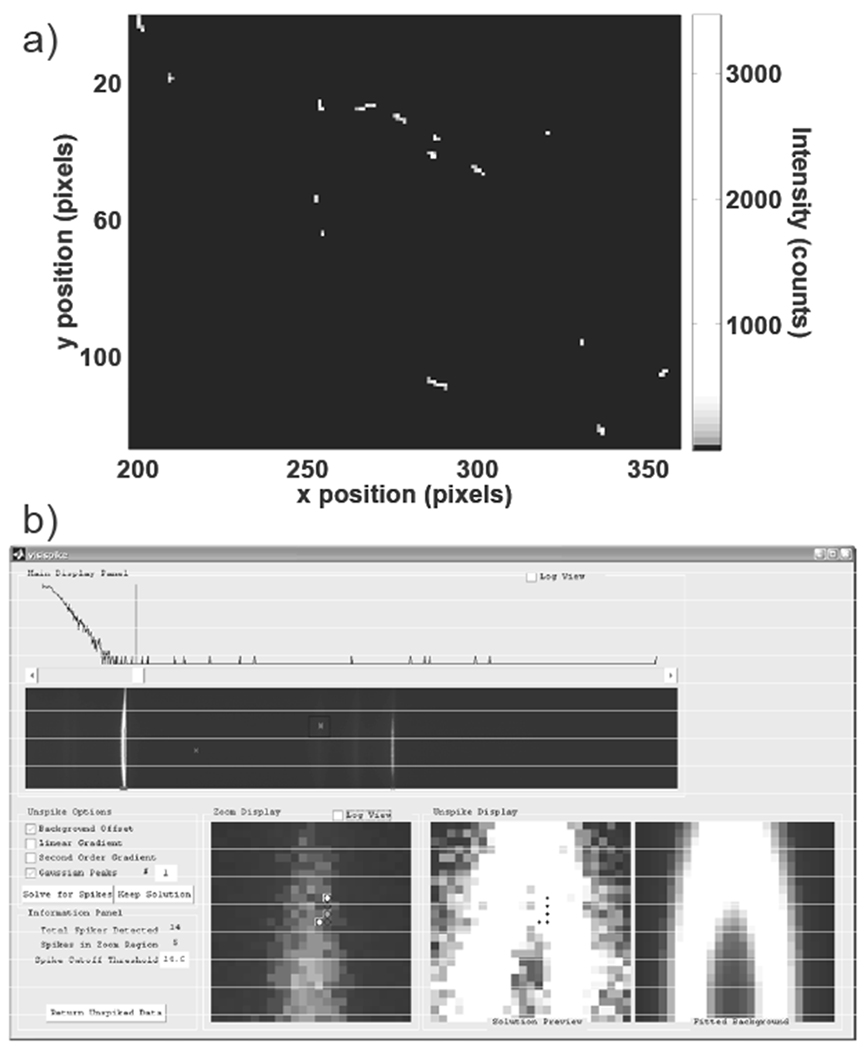
Example of cosmic ray spikes and VisiSpike correction program interface. In a), a portion of the cosmic ray signals accumulated over one hundred 10 second dark exposures are shown. Cosmic ray signals vary substantially in position, morphology, and intensity. In b), the VisiSpike program is shown. In the upper portion of the window the spectral image and a histogram with accompanying slider for highlighting signals exceeding the threshold are shown. At the bottom a zoomed view of the region of interest with potential spike pixels marked for replacement in the bottom left, the estimated background signal at bottom right, and the zoom region with the spike pixels interpolated in the bottom middle. On the left are options for various 2D background fitting functions. The user has the option to correct for spikes using a combination of 2D constant offset, linear, exponential, and Gaussian functions.

In Raman spectroscopy of tissue several factors complicate and prevent the acquisition of replicate spectra. Complicating factors include temporal changes in the sample composition (particularly in vivo), photo-bleaching, thermal damage, and sample motion. Filtering methods are efficient for detecting and replacing spikes in images, however an automated filter may erroneously identify a sharp Raman band as a spike and remove that valid spectral feature. We developed a custom data processing program to indicate and facilitate removal of cosmic ray spikes using a MATLAB function called VisiSpike A median filter is used to automatically highlight regions affected by cosmic rays. The user selects and corrects for cosmic ray signals using one of several pre-defined functions to interpolate the missing region from the surrounding image. The interface for the VisiSpike program is shown in Figure 1b, with subregions corresponding to the original image, identified spikes, and the fitted background. Although the VisiSpike program requires more user-intervention than an automated filter, we have found that VisiSpike method precisely removes spikes and estimates the true signal for affected regions.

3.2. White/Dark Correction

Background offset signals are corrected by subtracting the dark images acquired with the spectrograph entrance blocked. Flat-field correction was applied by normalizing all images to a white halogen light calibration image. We observed nonlinear transmission in our older dichroic filters. White-light spectra measured through an older dichroic and a newer dichroic were compared against spectra from the white-light source placed directly at the spectrograph entrance slit, as shown in Figure 2a. The reference dichroic spectra supplied with the two filters are shown in Figure 2b for comparison. Some oscillations previously attributed to complexity in the fluorescence background signal were likely a result of the dichroic filter transmission efficiency. After replacement of our older dichroic filter, the apparent background complexity was decreased. Differences between the older and newer filters are attributed to the number of discrete layers in the filters, where the newer filter is composed of hundreds of discrete layers rather than just a few. To minimize any residual interference due to the dichroic filter transmission function, we now normalize the white light calibration image to a white light calibration image acquired when the dichroic is flipped down in its mount, removing the filter from the optical path. Because the dichroic filter is mounted in a Flipper mount, the filter can be reproducibly moved into and out of the optical path. A pixel-by-pixel correction for the dichroic and wavelength dependent camera gain was applied using the following equation: $I_2=\frac{\text{max}\left(wdc-dark\right)}{\left(wdc-dark\right)}\cdot \frac{\left(wnd-dark\right)}{\left(wdc-dark\right)}\cdot \left(I_1-dark\right)$ where I₂ is the corrected pixel intensity, wnd is the white image with the dichroic filter removed from the optical path, wdc is the white image with the dichroic filter in the optical path, dark is the dark image, and I₁, is the initial spike-corrected data image.

Figure 2.

Transmission of white light through dichroic filters, in a) measured transmission of HCA white light source, in b) transmission spectrum specified by the vendors. Spectra shown in a) were measured on different dates with slightly different system alignments; however the relative efficiency is indicative of the performance differences expected according to the transmission efficiencies shown in b). In a) the reference white is lower in intensity than the intensity transmitted through the Semrock dichroic, this is an artifact of both the normalization and slight changes in the optical path between the dates when these spectra were acquired.

3.3. Image Rotation and Slit-image Curvature

While examining recorded spectral images during extended calibration checks, we observed that rows in the camera detector were not perfectly aligned to the spectrograph dispersion axis. This rotation is in addition to the commonly observed issue of slit-image curvature. Using broadband (white) illumination with point-source illumination or masked patterns with sharp edges (such as USAF 1951 imaging bar targets), the dispersion angle of the spectra over the CCD was determined. In the system described above, this was determined to be approximately −0.69 degrees through linear fitting of the pixel boundaries between the bright and dark points in the recorded image at the far ends of the CCD. While this angle is quite small, it leads to spectra being dispersed over several adjacent rows in the recorded images. The CCD alignment to the spectrograph was subsequently improved, and the rotation angle was reduced to 0.12 degrees. With the ~1 m long lever this corresponds to a 2 mm displacement from the optimal position. Some groups use micrometer stages attached to the CCD to adjust rotation. At the ~6 cm camera radius, the position would need to be adjusted to within 7 μm to exceed this accuracy. Subsequent to the physical adjustment of the camera rotation, we still found that correction for the image rotation improved the spectral background. In theory, a camera-grating rotational misalignment of even 0.07 degrees would still lead to unnecessary row-overlap (assuming a dispersion region of 815 columns). To obtain optimal experimental results, compensation for rotation is necessary in data preprocessing for Raman imaging.

Several factors obscure the effects of rotational misalignment. First, the detector is much wider than it is tall, and the spectra are only tilted by a small angle. Additionally, background intensities in the low wavenumber region of the image are typically much more intense than background intensities in the high wavenumber region, therefore image contrast in the high wavenumber region is low. Images are commonly truncated to the laser-illuminated region of the CCD, and the horizontal dark regions which would provide great contrast are typically not displayed in raw or preprocessed data. Finally, the slit image curvature correction step partially masks the rotation in the preprocessed images, by interpolating along the rows and smoothing any sudden baseline changes.

We identified two potential sources of rotation misalignment, where the grating, the CCD, or both are not perfectly aligned to the slit. One of these effects has been described as leading to a ‘twisted image’, where the slit and camera are properly aligned, but the dispersion axis is not.²⁸ It is difficult to distinguish ‘twisting’ from the case where the slit, dispersion axis and CCD are all slightly out of alignment, in which the spectral bands should also be rotated slightly with respect to the dispersion axis. However, owing to the significant difference between the vertical and horizontal dimensions of the CCD, the rotation along the spectral axis is less than a full pixel except in extreme cases (where the slit is at an angle of more than 0.5 degrees to the grating). Hence an image ‘rotation’ will appear to be identical to ‘twisting’ provided that the rotation causes less than one full pixel shift along the shorter axis. In the case described above, we have a CCD at a 0.12 degree rotation, with 815 illuminated columns and 128 rows. From theory we expect a vertical shift of 1.71 pixels along the run of the horizontal axis (observable), while the horizontal shift along the vertical axis is only 0.27 pixels which is much less than the shift due to slit-image curvature.

We developed two software methods for correcting rotation and slit image curvature. The first correction method incorporates the MATLAB imrotate function with a subsequent slit-image curvature correction developed in-house. The second correction method consists of applying an image registration operation, which simultaneously corrects both rotation and curvature (MATLAB image-processing toolbox function imtransform). The image registration method is described in greater detail below. Only one of these two correction methods should be applied. Because the image registration method replaces two discrete steps which both use interpolation, we expect that better results will be obtained with the image registration method.

3.4. Image Registration

We applied image registration correction to compensate for imperfections in the imaging optics. We have used registration software commonly employed for correction of photographic images. For image registration to be used in Raman imaging, the dispersion properties of the spectrograph must be mapped. From this mapping, control points in the imperfectly aligned image are linked to their ideal placement. Control points can be determined either automatically, or by selecting them manually. To automatically map the dispersion, we used combinations of white light transmission images of a bar target pattern (USAF 1951) and a neon calibration spectrum to determine horizontal lines along the dispersion axis, and vertical lines of constant wavelength. Control points are set as the intersection of lines with constant dispersion or spatial position. Other spatial masks, such as Ronchi rulings or fiber optic arrays, may prove more convenient for projecting alternating stripes of high and low intensity to map the dispersion axis. Through software the intersection points between the edges of the bright/dark bar patterns and the atomic emission lines were used to determine control points corresponding to known constant wavelength and known constant spatial values. From the imperfect and corresponding ideal control points, an image registration filter was created. Spectral images are corrected for both rotation and curvature in a single step using this image transformation filter. The primary concern with this method is that the transform function uses various interpolation methods (such as bilinear and bicubic) which will affect the spatial and wavelength resolution as well as image noise.

Raman imaging test data taken with the −0.68 degree image rotation was examined using either the rotation or image registration corrections. Intensity-corrected data from a Raman cross-section of intact equine metacarpal bone is shown in Figure 3. The misalignment in the rotation of the initial image in Figure 3a has been highlighted with a dotted horizontal line and accentuated by displaying the image with an aspect ratio of 1:4.8 rather than the true aspect ratio of 1:6.4. Rotation and transformation corrected images are shown in Figure 3b and 3c. Differences between 3b and 3c are not obvious in this view, however slit-image curvature is not yet corrected in 3b. Without some form of rotation correction, spatially-distinct spectra are concatenated along a single camera row.

Figure 3.

Raman images of intensity versus spatial position (vertical) and wavelength (horizontal). In a), the initial image is shown with a horizontal line accentuating the image rotation, in b), the image is shown after rotation correction, and in c), the image is shown after image transformation.

To illustrate the overlap of the spatially distinct spectra, the intensities of individual image rows must be examined further. Spectral intensities from several camera rows are shown in Figure 4 (five rows from the bright central band in Figure 3 have been plotted). The most apparent difference between the three plots is the background. The background appears to be high-order polynomial biological fluorescence in 4a, but is reduced to a simple linear background in 4b and 4c. An example of the polynomial background fitting for these cases is shown in Figure 5. In Figure 5a the initial image is fitted with a fourth order polynomial, while the registration-corrected image was fitted to a linear background, as shown in 5b. Rotation and transformation conections can reduce the polynomial complexity of biological spectral backgrounds in Raman imaging by several polynomial orders.

Figure 4.

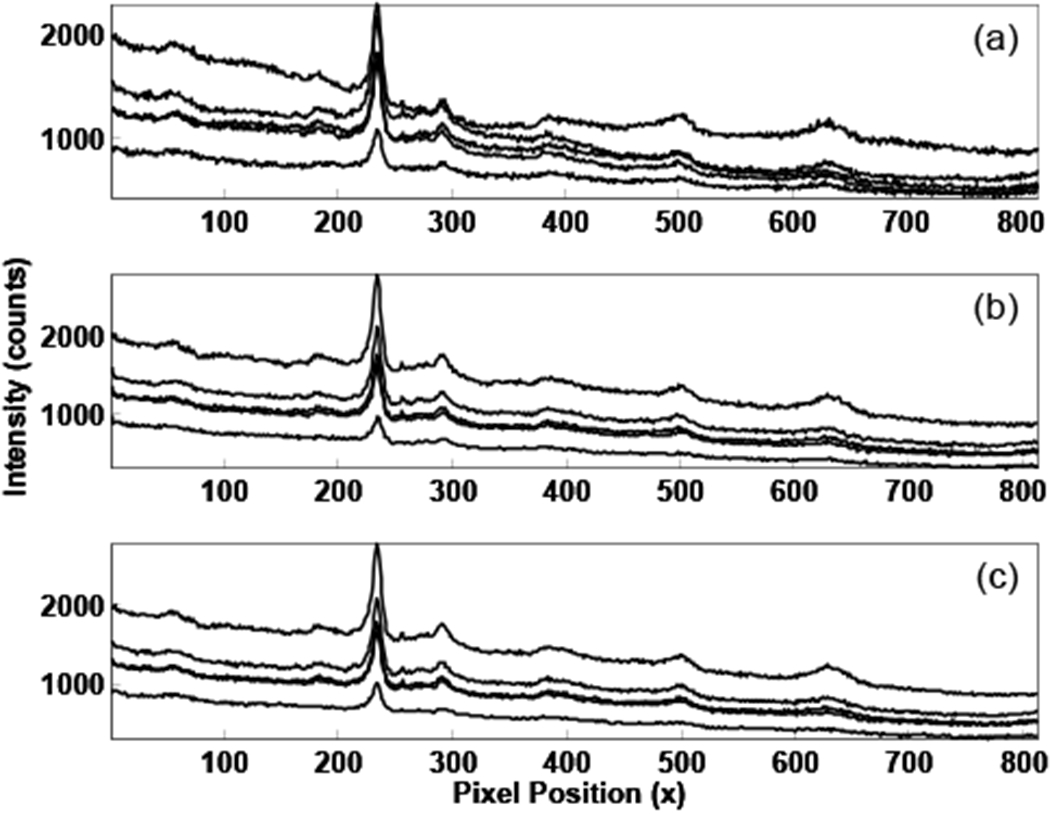
Spectra corresponding to the brightest band in Figure 3. In a), spectra from the initial image, in b), spectra after rotation correction, and in c), spectra after image transformation.

Figure 5.

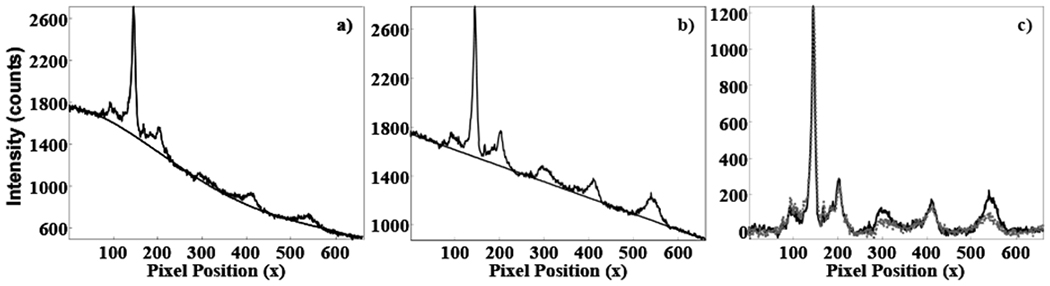
Spectra with polynomials fitted to the baseline. In a), a spectrum from the initial image is fitted with a fourth order polynomial, b), a spectrum from the registration corrected image is fitted with a first order polynomial, in c) spectra from a and b are shown after baseline subtraction. In c) the initial spectrum is plotted as a grey dashed line, while the registration corrected spectrum is plotted as a solid black line.

Increases in background complexity can be due to the concatenation of spectra from distinct spatial positions with different excitation power, sample composition, or differences in background fluorescence. This difference in background complexity and the concatenation of spectra from distinct spatial positions deleteriously affects important analytical parameters such as ratios of Raman band intensity. In Figure 5c, the baseline-subtracted spectra from Figures 5a and 5b are shown overlaid. The plotted spectra have not been normalized, but the phosphate ν₁ (~ pixel 130) intensities in both spectra are almost identical because they have been taken from the same row in the image. Substantial differences exist between the initial and registration-corrected spectra, particularly in the carbonate ν₁ to phosphate ν₁ and phosphate ν₁ to amide I ratios.

To demonstrate the differences between the initial and corrected images, the mean and standard deviation of the band-intensity ratios across the image are shown in Table 1. While the mean values for the band intensity ratios differ by less than 11% for both bands, standard deviations across the image are reduced by 60% for the phosphate ν₁ to amide I ratio, and by 46% for the carbonate ν₁ to phosphate ν₁ ratio. Plotting the band intensity ratios for each component versus spatial position, the trends across the spatial positions were similar in the unconected and registered images, but with much greater variance in the uncorrected image.

Table 1.

Influence of image registration on band intensity ratio in a Raman image.

Band Intensity Ratio	Initial Image (mean and std. dev.)	Registered Image (mean and std. dev.)	% Difference
Carbonate ν1 to Phosphate ν1 (1068 cm−1 / 958 cm−1)	0.226 ± 0.035	0.224 ± 0.019	0.9 ± 45.7 %
Phosphate ν1 to Amide I (958 cm−1 / 1650 cm−1)	11.78 ± 6.88	10.52 ± 2.79	10.7 ± 59.5 %

The significant differences presented here apply only to cases where the data is being used for imaging purposes, or if only a portion of the illuminated CCD (binning) is being used to collect spectra. We have found that when spectra are summed over all the rows in the CCD to produce one integrated spectrum, the initial, rotated and registered CCD images are nearly identical. A summed spectrum is the normal output from most commercial Raman instruments, which by default uses the information from the entire illuminated region to generate one high quality spectrum. As a result, the single-spectrum output from commercial instruments will be insignificantly affected by rotation. Likewise, when the mean spectrum is calculated from a subregion of the image, rotation aligmnent has a negligible effect on the mean spectrum, provided that the entire illuminated region of the CCD is integrated. If the illuminated region is instead divided into multiple binning’ regions, or some portion of the illuminated region is not considered, the summed spectrum may vary considerably according to the rotation.

3.5. Fluorescence Background Removal

Three background removal methods are currently in use in our lab. The first is a traditional user-operated spline baseline removal in GRAMS. The spline baseline removal method is highly reproducible for a particular expert user, but is not feasible for large data sets or hyperspectral imaging. An automated method was adapted from the polynomial baseline fitting routine described by Lieber and Mahadevan-Jansen.¹⁶ In unusual circumstances we observed difficulties with automated polynomial fitting, particularly when using high order polynomials, if the edges of the spectrum are not at the baseline, or if the baseline has a large concave curvature. Under these rare conditions, portions of the baseline are estimated below the actual baseline in early algorithm iterations and subsequent fits estimate the baseline poorly.

Another automated method uses polynomial fitting to preselected regions of baseline where no Raman signal is observed. The preselected background region method was used for the baseline fitting shown in Figure 5. We found that automated polynomial fitting methods to background-correct large data sets are quick and consistent, though the results are not always optimal. Problems with polynomial fitting were reduced with application of image rotation or registration corrections prior to baseline correction.

4. CONCLUSIONS

The automated methods outlined in this manuscript have greatly reduced the time required for preprocessing our spectral data, while simultaneously reducing the variance. Matlab code for the functions described above will be made accessible through the Morris group web site (http://www.umich.edu/~morgroup/).