Abstract
Progress in the development of GPU-accelerated free energy simulation software has enabled practical applications on complex biological systems and fueled efforts to develop more accurate and robust predictive methods. In particular, this work reexamines concerted (a.k.a., one-step or unified) alchemical transformations commonly used in the prediction of hydration and relative binding free energies (RBFEs). We first classify several known challenges in these calculations into three categories: endpoint catastrophes, particle collapse, and large gradient-jumps. While endpoint catastrophes have long been addressed using softcore potentials, the remaining two problems occur much more sporadically and can result in either numerical instability (i.e. complete failure of a simulation) or inconsistent estimation (i.e. stochastic convergence to an incorrect result). The particle collapse problem stems from an imbalance in short-range electrostatic and repulsive interactions and can, in principle, be solved by appropriately balancing the respective softcore parameters. However, the large gradient-jump problem itself arises from the sensitivity of the free energy to large values of the softcore parameters, as might be used in trying to solve the particle collapse issue. Often no satisfactory compromise exists with the existing softcore potential form. As a framework for solving these problems, we developed a new family of smoothstep softcore (SSC) potentials motivated by an analysis of the derivatives along the alchemical path. The smoothstep polynomials generalize the monomial functions that are used in most implementations and provide an additional path-dependent smoothing parameter. The effectiveness of this approach is demonstrated on simple, yet pathological cases that illustrate the three problems outlined. With appropriate parameter selection we find that a second-order SSC(2) potential does at least as well as the conventional approach and provides a vast improvement in terms of consistency across all cases. Lastly, we compare the concerted SSC(2) approach against the gold-standard stepwise (a.k.a., decoupled or multi-step) scheme over a large set of RBFE calculations as might be encountered in drug discovery.
Graphical Abstract
Introduction
Recent progress and improvements in computer hardware, simulation software, and free energy methods,1-12 especially the development of highly efficient and cost-effective GPU accelerated free energy calculations,12-18 have significantly extended the accessible timescales of computer simulations and scope of applications. In addition to ongoing challenges of developing more accurate force fields and efficient sampling methods, there is need to improve our ability to optimally set up alchemical free energy calculations.19-32
The setup problem refers to not only how to create the relevant necessary input files but also the proper simulation protocols and parameters that will yield the best results for a given system of interest. In alchemical free energy simulations, one of the most difficult but pivotal technical issues is the choice of the alchemical path connecting the two real states (i.e., connecting the two thermodynamic endpoints). While the free energy difference between two states is independent of the path that connects them in the regime of complete conformational sampling, in practical calculations of complex systems, the choice of the alchemical transformation path is critical to obtain stable, converged results with affordable sampling.
One of the first major obstacles that was encountered in simple concerted (a.k.a., one-step or unified) linear alchemical transformations was the ”endpoint catastrophe”.33-39 Numerical singularity or instability occurs when evaluating ensembles generated with one Hamiltonian using the potential energy at other points along the alchemical pathway (as required to obtain thermodynamic derivatives or perturbations) for which there is poor phase space overlap. The most severe case occurs with linear interpolation of two real state endpoints, where the difference between the real state potential energy functions is required to evaluate the thermodynamic derivative or exponentiated energy difference.34-36 Since different atoms in the two states can be artificially superimposed in such a transformation, this can lead to energy differences or thermodynamic derivatives that are unstably large in magnitude, and even singular. The singularity arises due to “hard” (i.e., inverse power law form of the interaction potential at short distances) exchange repulsions and/or Coulombic interactions between atoms in the core transformation region that unphysically overlap.35,40
There are two general approaches to address the endpoint catastrophe. The first is the use of “softcore potentials” with separation-shifted scaling,36,38 short-range switching,39 or capping the short-range interactions.41,42 The second is to use non-linear mixing of the endpoint potentials.33-35,37,43 Nowadays combinations of these two approaches are most often utilized.38,42,43 A formalism for minimal variance path based on the standard form of softcore potentials has also been reported.44,45 These have been successful strategies to formally address the classical endpoint catastrophe, as defined in the present context.
Nonetheless, with the use of softcore potentials to address the endpoint catastrophe, there remains two other major problems in concerted transformations that can result in numerical instabilities and poor statistical results.39 The first is the “particle collapse” problem that stems from an imbalance of softcore Coulomb attraction and exchange repulsions, and can lead to artificial minima where particles from the two transforming states are on top of one another. The second is the “large gradient-jump” problem that arises from sensitivity of the free energy to large values of the softcore parameters sometimes required to balance the softcore Coulomb and exchange interactions.
An alternate strategy to circumvent the “particle collapse” and “large gradient-jump” problems altogether is to avoid use of a concerted transformation, and instead use a “stepwise” approach, sometimes referred to as “multi-step” or “split” procedures,46 in which the electrostatic and Lennard-Jones (LJ) interactions are handled in separate steps in the alchemical transformation. An example of a stepwise “decharge-vdW-recharge” strategy would be as follows:
Step 1: decharge the mutating atoms in the initial state (with LJ and other parameters fixed at their initial state values) so that there will be no electrostatic interactions that can lead to an imbalance in the next step. Note, during this step, all interactions including electrostatics from the final state are turned off.
Step 2: with all the mutating atoms in both the initial and final states turned off (i.e., “decharged”), transform the LJ parameters, including r−12 exchange repulsions, from the initial state to the final state, along with any additional bonded parameters.
Step 3: re-charge the mutating atoms (with LJ and other parameters fixed at their final state values) to their final state values.
While stepwise approaches have been demonstrated to be quite robust, they have several disadvantages. First, the procedure is more tedious to set up and can be sensitive to the choice of atoms in the decharge/recharge region, in some cases leading to intermediate states that have significantly different net charge. Second, the procedure is more computationally intensive as it requires more steps, each with different sampling requirements and statistical error estimates. And third, the procedure is not well suited for advanced λ-schedule optimization and enhanced sampling schemes, such as λ dynamics,47-50 Hamiltonian replica exchange methods,51-55 adaptive biasing48,56,57 or self-adjusted mixture sampling58,59 methods. Consequently, it is of practical interest to work toward a more robust and efficient solution for concerted alchemical transformations.
In this work, we present methods for improved “concerted” alchemical free energy transformations of complex biomolecular systems. The remainder of the paper is outlined as follows: The Theory section develops the mathematical model framework, provides definitions of the three main problems commonly encountered in concerted transformations, and presents a systematic set of formulas to facilitate their discussion. We then formulate a new smooth softcore potential using smoothstep functions of variable order P that we designate “SSC(P)”. In the Results section, we demonstrate how the SSC(2) potential with optimized parameters is able to overcome all problematic cases of concerted alchemical transformations we have yet encountered. We demonstrate the robustness of the SSC(2) potential compared to a conventional widely used softcore potential for a broad range of hydration free energy and relative binding free energy (RBFE) calculations. Results are compared to benchmark quality “stepwise” (decharge-vdW-recharge) free energy calculations. The Discussion places the work into broader context, while the Conclusion summarizes the main points of the paper and identifies future research directions. The methods presented here have been originally implemented as a modified enhancement of the GPU-accelerated free energy methods in AMBER18,17 which have recently been extensively validated,60 and now are in the recent AMBER20 release.61
Theory
One can formulate the computation of relative free energies from equilibrium simulations using a thermodynamic perturbation (TP)62 (sometimes referred to as “free energy perturbation”) or thermodynamic integration (TI),63,64 or through non-equilibrium ensemble simulations using the Jarzynski equality and its equation variations.65-70 In the present work, we focus on equilibrium methods, and formulate the problem in the TI framework. Nonetheless, the fundamental barriers to progress that we address herein are not specific to the TI method, as we show through numerical examples, the new methods presented here are equally transferable to TP methods with Bennett Acceptance Ratio (BAR) analysis and its multistate variant (MBAR).71-75
Thermodynamic Integration with Original AMBER Softcore Potentials
The free energy is a state function, and thus the free energy difference between thermodynamic states is independent of the path that connects them (assuming fully converged sampling along the path). Computationally, however, the choice of this pathway is most often of immense importance, since for non-trivial problems, statistical sampling is required not just at the end states, but along the pathway itself.
Consider the transformation of a system of N particles in an initial state “0” characterized by potential energy function U0(q), where q represents the degrees of freedom of the system (e.g., Cartesian positions of each particle along with any system variables), to a final state “1” characterized by potential energy function U1(q) having the same degrees of freedom. Let us define a thermodynamic parameter λ that smoothly connects these states through a λ-dependent potential U(q; λ) such that U(q; 0) = U0(q) and U(q; 1) = U1(q). In this case, the change in free energy ΔG0→1 = G1 − G0 can be determined through the thermodynamic integration formula
| (1) |
where the second sum indicates numerical integration over M quadrature points (λk, for k = 1, ⋯ M) with associated weights wk. We now discuss specific ways in which the U(q; λ) can be constructed. The simplest way to establish a thermodynamic connection is to use a linear interpolation between states, which we will designate as UL(q; λ):
| (2) |
where ΔU(q) = U1(q) − U0(q). The simple linear alchemical transformation pathway has the thermodynamic derivative
| (3) |
Hence, the common energy components that are identical between U1(q) and U0(q) need not be explicitly considered as the corresponding difference is zero. As has been well established and is discussed in more detail below, however, the linear alchemical transformation pathway leads to practical problems that can be partially overcome by the use of so-called “softcore” potentials. These potentials, in the present context and the discussion that follows, apply only to non-bonded (i.e., LJ and electrostatic) interactions within the non-bonded cut-off.36,38 All other components of the energy are achieved here through the conventional linear transformation pathway, although other non-linear pathways are also possible through parameter interpolation.16 Here we define the original softcore potential transformation pathway38 in AMBER as
| (4) |
where . Note that, after adding the softcore modification, the original λ-independent end state Hamiltonians U0(q) and U1(q) now become λ-dependent and , respectively. The corresponding thermodynamic derivative is given by
| (5) |
In the current AMBER implementation, a nonbonded cut-off is defined and the softcore potentials are applied as correction terms to the original non-bonded LJ and electrostatic interactions between the softcore region atoms and other non-softcore atoms within the nonbonded cut-off. As a result, when utilizing the particle-mesh Ewald method (PME),76 only the direct space term evaluated within the nonbonded cut-off is affected by the softcore potentials. Details are described in the Supporting Information.
There have been many different proposed softcore potential forms that modify, or “soften”, the nonbonded interactions. In the discussion below of specific interaction potentials, we simplify the presentation by only showing the softcore potential corresponding to one end state. It should be reminded that the total system potential energy at a particular λ value should contain weighted contributions from both end state potentials as is Eqn. 4.
The LJ and electrostatic interactions for a set of interacting point particles i and j separated by a distance rij are given by
| (6) |
and
| (7) |
where σij and ϵij are the pairwise van der Waals contact distance and well depth, respectively, and qi and qj are the partial charges of particles i and j.
The Cartesian derivatives of these energies are straight forward as ∇iU(rij) = (rij/rij)(∂U/drij) = −∇jU(rij), where the derivatives with respect to rij are given by
| (8) |
and
| (9) |
These derivatives are programmed in molecular simulation software codes in order to derive the normal electrostatic and van der Waals forces on particles. In order to “soften” these pairwise interactions with particles contained within the selected softcore region, one can modify the effective interaction distance by introducing a parametric form for separation-shifted scaling with an adjustable parameter. A commonly used form of these modifications is36,38
| (10) |
and
| (11) |
where n and m are positive integers and α and β are adjustable positive semidefinite parameters for the LJ and electrostatic softcore interactions, respectively, with values of zero corresponding to no softcore modification for any λ value. In several molecular simulation software suites, including the default in AMBER, the values of n = 6 and m = 2 are used, although other values have also been suggested.38 Note that for positive values of α and β parameters and λ values between 0 and 1, the effective interaction distances satisfy the conditions
| (12) |
| (13) |
where the equality holds only for the real state endpoint λ=0. This results in a “softening” of the LJ and electrostatic interactions with increasing values of α and β parameters, respectively, particularly at short range where they are largest in magnitude. From these modified effective interaction distances, the LJ and electrostatic softcore potentials can be defined as
| (14) |
and
| (15) |
The thermodynamic derivatives with respect to λ can be obtained using the chain relation as
| (16) |
where
| (17) |
and
| (18) |
where
| (19) |
Problems with Original AMBER Softcore Potentials and Their Underlying Causes
The field of free energy methods is vast, and yet there currently exists no commonly accepted and consistently used terminology that enables discussion of certain classes of problems that can occur when performing free energy simulations. Here we define the main problems that we have encountered regarding the alchemical transformation path in free energy simulations and have endeavored to overcome in the current work. Further, we distinguish the problems themselves, which manifest as observed symptoms in the simulations, from their underlying origins (causes), which we relate mathematically to the equations, in order to motivate their solutions.
There are three main problems related to the alchemical path and associated softcore potential that can commonly occur in free energy simulations, and in particular with so-called “concerted transformations” that involve simultaneous changes in both non-bonded LJ and electrostatic terms. We will refer to these as the endpoint catastrophe, the particle collapse problem, and the large gradient-jump problem. We now discuss each of these in more detail, including defining the symptoms of each problem, highlighting their underlying causes, and outlining solutions.
1. Endpoint catastrophe:
Definition: With linear alchemical transformations, the sharp divergence (and sometimes singularity) of the free energy difference or the thermodynamic derivative at the thermodynamic endpoints (λ values near 0 and 1).
Cause: endpoint catastrophes are due to poor phase space overlap. The endpoint catastrophe is a well known problem often encountered with simple linear alchemical transformations where the total potential is defined as the linear combinations of the end state potentials, and occurs when the λ value approaches a real state endpoint where the potential energy of one real state endpoint needs to be evaluated with the conformational ensemble generated from the other real state endpoint, and can result in unphysical atom-atom overlap and thermodynamic derivatives. Equation (3) shows that the required thermodynamic derivative involves a difference between real state endpoint potentials (i.e., ΔU(q)) for all λ points, even if this difference is unstably large. Formally, the endpoint catastrophe can occur not only at the endpoints of an alchemical transformation, but any point that produces the symptoms as described above.
Solution: the endpoint catastrophe can be avoided by the use of original AMBER softcore potentials. Formally, the endpoint catastrophe can be avoided by use of the softcore potentials presented in Equation (4), with particular sensitivity to the α parameter that tunes the “softness” of the LJ terms, including the short-ranged repulsive potential. Larger β and especially α values thus tend to have the greatest affect in alleviating the endpoint catastrophe.
2. Particle collapse:
Definition: With softcore potentials, the artificial superposition of particles at intermediate values of λ that can lead to large amplitude fluctuations or phase transition behavior along the λ dimension.42
Cause: particle collapse results from an imbalance of Coulomb attraction and exchange repulsions that favors atomic overlap. While softcore potentials formally eliminate singularities at the endpoints, they can also lead to the creation of new artificial minima mostly commonly at very small interaction distances (r → 0, but possibly at other locations for complex interactions) if the short-range exchange repulsion terms of the softcore LJ potential is not sufficient to overcome the softcore Coulomb attractions of oppositely charged particles.38,39 This could cause unwanted alchemical traps, or even phase transition-like behavior, along the λ dimension, resulting in unstable, unconverged numerical results.
Solution: the Coulomb-Exchange imbalance problem can be overcome by adjustment (decrease) of the α/β softcore parameter ratio, and/or modification of the softcore potential functional form. In order to avoid Coulomb-Exchange imbalance, the softcore exchange repulsions need to be made “harder” (smaller α value) and/or the softcore Coulomb interactions need to be made “softer” (larger β value). While this adjustment is somewhat system-dependent, as will be illustrated below, certain combinations appear to be remarkably robust for a variety of transformations in different environments for a range of protein-ligand systems.
3. Large gradient-jump:
Definition: With softcore potentials, the sensitivity of the free energy for large values of the softcore parameters can lead to spurious jumps in the free energy near the thermodynamic endpoints.
Cause: large jumps in free energy can result from sensitivity of the thermodynamic derivatives (gradient) to certain softcore parameter values near the real state endpoints. This is particularly manifested when large β values are required to adjust the α/β softcore parameter ratio to solve the Coulomb-Exchange imbalance problem. This can result in a dramatic increase in the terms in Equation (5) involving λ derivatives of and at the λ=1 and 0 endpoints, respectively. Equations (17) and (19) show that the thermodynamic derivatives for the softcore LJ and Coulomb interactions are roughly linear in the parameters α and β, respectively, particularly for λ values near the real state endpoints where energy changes are typically largest and nonlinear.39
Solution: the large gradient-jump problem can be solved by formulating a more sophisticated smooth softcore potential with derivatives that vanish at the endpoints. We formulate a family of smooth softcore potentials that use smoothstep weighting functions with favorable endpoint derivative properties with the intent of developing and testing a robust softcore framework that can be used for efficient concerted transformations.
With proper choice of α and β softcore parameters, together with an appropriately smooth weighting function (see below), we find a solution across all the above problems for a wide range of alchemical transformations, including several severe problematic test cases.
Formulation of a family of smoothstep softcore potentials for robust concerted alchemical transformations
We consider a family of smoothstep functions, SP (λ), of orders P (P = 0, 1, 2, ⋯) and defined as the polynomial functions (up to P = 4 shown):
and
| (20) |
The smoothstep functions are monotonically increasing functions that have the desirable endpoint values:
| (21) |
and derivative properties
| (22) |
From these smoothstep functions, we create a family of smooth softcore potentials for nonbonded LJ and electrostatic interactions involving atoms in the softcore region by replacing λ with SP(λ) in Equations (4) and (5) to obtain:
| (23) |
with thermodynamic derivatives
| (24) |
where, following from Equation (5), we have
| (25) |
Note that Equation (23) for USSC(P) (q; λ) is identical to Equation (4) for USC(q; λ) with the latter having λ argument replaced by SP(λ). Further, note that USSC(0) (q; λ) (P = 0 family member), is identical to USC(q; λ). Thus the original softcore potential is contained as the lowest order member of the smoothstep softcore potential family described here. However, this is the only member of the family that does not have derivative values that vanish at the boundaries (λ=0 and 1), but rather has a constant value of 1 over the range of λ. As we will demonstrate below, other higher-order members of the family have numerical properties that are more well-behaved, and in particular the S2 family member, with appropriate choice of α and β values overcomes all problematic cases of concerted transformations.
As mentioned earlier, the smoothstep softcore potential introduced here is only applied to nonbonded LJ and electrostatic interactions between atoms in the softcore region and atoms in the non-softcore region within the cutoff. To be consistent, the smoothstep combination scheme of potentials (the prefactors 1 − SP(λ) and SP(λ) in Equation (23)) is applied to not only the above softcore terms but also to the corresponding the long-range analytic dispersion ” tail” corrections77 beyond the cut-off, and 1-4 scaled non-bonded terms. Other components of the λ-dependent potential energy without softcore potential correction, and their thermodynamic derivatives do not use the smoothstep functions but use the original linear combination scheme. These terms include the PME reciprocal space term (including the ”self-energy” and net charge correction), bonded terms, and restraint terms.
Methods
Simulation setup and protocols
A modified version of AMBER18 with the proposed SSC(P) scheme implementation, now in AMBER20,61 was employed for all simulations. All simulations were performed with the recently implemented GPU-TI modules14,17 built against the CUDA 10.1 GPU library and run on various GPU workstations and servers equipped with NVIDIA GTX 1080TI, RTX 2080 TI, Titan V, and V100 GPUs. Results reported were created with the single precision calculation/flexible precision accumulation (SPFP) model.78
The setups and protocols for AMBER standard GPU-accelerated TI simulations14,17 are employed. The AMBER ff14SB force field79 is used for standard amino acids and GAFF80 with the AM1-BCC charges81,82 for molecules without AMBER parameters. The TIP3P water model83 is utilized. The parmed module of AMBER18 is used to prepare the topology files for TI calculations. The SHAKE algorithm84,85 is used to constrain bonds between heavy atoms and hydrogens, except in the mutating parts, where no SHAKE is applied. Long-range electrostatic interactions are treated by the particle-mesh Ewald method (PME).76 A cut-off of 10 Å for the model systems (see below sections) and the hydration free energy calculations, and 8 Å for RBFEs, is used for non-bonded interactions, including the direct space terms of the PME method and particles interacting through softcore potentials. The Ewald error tolerance is set to 10−5 and the Ewald coefficient is automatically set according to the error tolerance and non-bonded cut-off. The model systems are simulated with the NVT ensemble at 300K while the hydration free energy and the RBFE simulations are performed with the NPT ensemble regulated at 1.0 atm at 298K. Detailed setups and protocols for individual systems can be found in the Supporting Information.
Results
Here we develop a P-order smoothstep softcore potential, SSC(P), to overcome problems inherent in concerted transformations with the conventional softcore potential38 currently used in many molecular simulation packages. While many values of P have been explored in this work, P=2 (second order) was found to have the most reliable performance and hence will be the focus in the following results and discussion. Nevertheless, higher orders of P may be useful for specific scenarios not encountered in this work and therefore this variable has been retained for the user to adjust, with P=2 being the default in AMBER20. We begin by examining a select set of alchemical transformations in solution that represent edge cases to illustrate the origin of the endpoint catastrophe, particle collapse, and large gradient-jump problems, and how these problems can be overcome by use of the SSC(2) with optimized parameters. We first demonstrate below how SSC(2) can robustly handle concerted alchemical transformations for a variety of absolute and relative hydration free energies of molecules in comparison with benchmark stepwise (decharge-vdW-recharge) transformations. Next we consider a more complex set of alchemical transformations involving protein-ligand binding that represent edge cases where the conventional softcore potential fails (sometimes dramatically) for concerted transformations, and demonstrate that the SSC(2) potential overcomes these problems. Finally, we demonstrate that the SSC(2) potential can reproduce benchmark stepwise transformations for a broad range of RBFEs of ligand sets for eight protein targets.
Illustration of problems using original AMBER softcore potentials and proposed solutions
In this section, we examine a set of simple edge cases that illustrate the endpoint catastrophe, particle collapse and large gradient-jump problems, and go on to propose a solution using a new second-order smoothstep softcore potential, SSC(2), with optimized parameters. The test cases involving absolute and relative hydration free energies (gas phase part of the cycle is not considered in these illustrations) are as follows: The first test case involves calculation of the absolute hydration free energy of 3,4-diphenyltoluene (denoted as the DPT/0), a bulky fairly hydrophobic system, which will be made to vanish in solution. The second test case is the absolute hydration free energy of a Na+ ion (denoted Na+/0), a small charged system that will introduce new issues when made to vanish in solution. The third test system is the relative hydration free energy of two Factor Xa ligands,14,86 L51c and L51h, involving the transformation L51c → L51h in solution (denoted as L51c/h), involving migration of charge from one region of the ligand to another.
Results of the original AMBER softcore potentials:
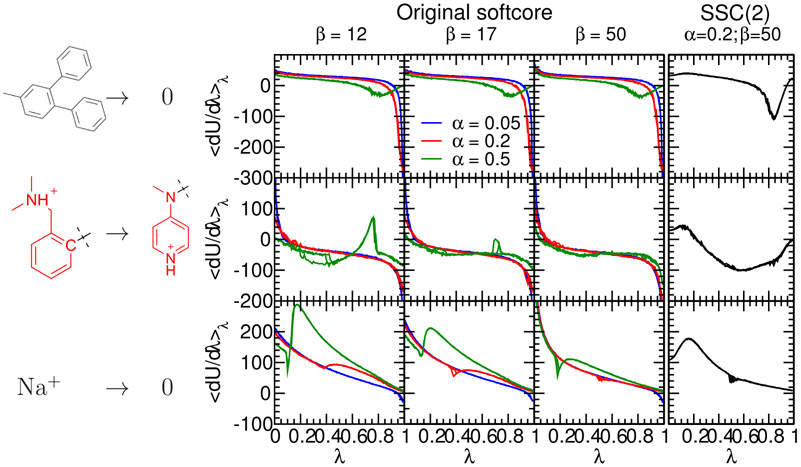
Figure 1 shows the ⟨∂U/∂λ⟩λ vs. λ plots for alchemical free energy simulations of these test systems using the one-step concerted scheme and different α and β softcore parameters. The DPT/0 (upper panels), L51c/h (middle panels), and Na+/0 (lower panels) transformations are shown in solution. The original AMBER softcore potential form of Equation (4) is used, or equivalently the zeroth order smoothstep softcore function, SSC(0), of Equation (23), in the results shown in the first three left columns while the results from the proposed smoothstep softcore potential SSC(2) are shown in the rightmost column. In Equation (25), one could also apply the smooth step function only to the weights of the Hamiltonians, i.e., only replace λ with SP(λ) in the pre-factors of Equation (25), not the λ function argument within the softcore potentials. This “midway” scheme applied to the weights only reduces the end-point catastrophe but does not eliminate the large gradient jump problem, and is compared with the original softcore scheme and SSC(2) with different α/β parameters in Figure S4 of the Supporting Information.
Figure 1:
The ⟨∂U/∂λ⟩λ vs. λ plots for alchemical simulations of three molecular systems using the one-step concerted scheme : the absolute hydration free energies for diphenyl toluene (upper rows, denoted as DPT/0) and single Na+ ion (lower rows, denoted as Na+/0), and the relative hydration free energy simulations for the Factor Xa ligand L51c to L51h mutation (middle rows, denoted as L51c/h). The L51c ligand has 65 atoms and L51h 58 atoms. The red-colored atoms shown are the defined softcore regions, i.e., the unique atoms for the individual ligands. The atoms common to both ligands are not shown except the connecting carbon shown in black.
The left three columns show the result using the original AMBER softcore potentials. These three columns show different β values (Å2), and different colored curves correspond to different α values (unitless).
The rightmost column shows the results from the proposed smoothstep softcore potential SSC(2) with the optimal softcore parameters (α=0.2, β=50 Å2). Each curve represents one 101-window (total 5 ns) TI simulation and there are four simulations for each condition. Note that the endpoint and the large gradient-jump problems with the original softcore potentials near λ=0 and 1 are absent in the results with the SSC(2) smoothstep softcore potentials. The particle collapse problem shown in L51c/h around λ=0.2 to 0.4 and 0.7 to 0.8, and in Na+/0 around λ=0.2 with the original softcore potential, disappears with the SSC(2) smoothstep softcore potentials.
Consider first the leftmost panels in Figure 1, corresponding to a β value of 12 Å2, which is the default value in AMBER18. For this value of β, with small α values (0.05 and 0.2), the endpoint “catastrophe” is formally averted, but its effects are still clearly prevalent for DPT/0 (large negative ⟨∂U/∂λ⟩λ at λ=1) and L51c/h (large positive ⟨∂U/∂λ⟩λ at λ=0 and large negative at λ=1), whereas it is much less apparent for Na+/0 which involves much smaller steric annihilation.
Softening the repulsive potential by using a larger value of α (0.5), reduces the problems at the endpoints, but leads to other issues at intermediate states. Specifically, for L51c/h the profiles are not smooth for λ values between 0.2 and 0.4, and λ ~ 0.8, and for Na+/0 for λ ~ 0.2. The origin of this irregularity is the particle collapse problem, where at some intermediate λ values, the softened exchange repulsions (large α) can no longer counterbalance the attractive softcore Coulomb attractions of oppositely charged particles, causing them to collapse on top of one another, and leading to sampling issues.
This imbalance can be reduced by increasing the value of β, as is indicated by the second leftmost (β=17 Å2) and third leftmost (β=50 Å2) columns of panels in Figure 1, which softens the electrostatic interactions. With β set to 17 Å2, the ⟨∂U/∂λ⟩λ curve for L51c/h is much improved relative to β=12 Å2, particularly for the α values of 0.05 and 0.2. In the case of Na+/0, the strong electrostatic interactions require a β value of 50 Å2 to achieve stable (smooth) ⟨∂U/∂λ⟩λ curves for α values of 0.05 and 0.2.
However, the large value of β required to address the particle collapse problem also has the effect of leading to much larger values of ⟨dU/dλ⟩λ that arise from the derivative (gradient) term in Equation (19) that is scaled by β. In the Na+/0 transformation, this manifests as a dramatic rise in ⟨dU/dλ⟩λ at λ=0 for larger β values. This is the large gradient-jump problem, which has also been discussed by others.39
At this point, we conclude that the default softcore potential parameters α/β in AMBER18, 0.5/12Å2, are useful to adequately address the “endpoint catastrophe” for the edge cases considered here, but have considerable susceptibility to the “particle collapse” problem. The particle collapse problem can be addressed by reducing α to harden the short-ranged repulsions of the softcore LJ potential, and increasing β to soften the electrostatic interactions. Nonetheless, with this strategy for choice of α and β, using the conventional linear softcore scheme of Equation (4), it does not appear possible to simultaneously address the endpoint catastrophe, particle collapse, and large gradient-jump problems, arising from small values of α and large values of β, respectively.
Development of a second-order smoothstep softcore potential
We now consider an alternative smoothstep softcore function, which employs a second-order smoothstep function, SSC(2), as described in Equation (23). This form of the softcore potential was tested and demonstrated to concerve energy as well as the regular GPU-accelerated MD of the real state endpoint and not exacerbate energy drift. The rightmost column of Figure 1 shows the ⟨∂U/∂λ⟩λ vs. λ plots for alchemical free energy simulations of the same systems as Figure 1, but with the SSC(2) softcore potential as opposed to the original AMBER softcore potential. To be clear, only results with with re-optimized softcore parameters (α=0.2, β=50 Å2) are shown here. The results using the SSC(2) potential with other combinations of α/β can be found in Figure S5 of Supporting Information.
The first thing that is apparent is that the behavior at all of the λ=0 and 1 endpoints have greatly improved. This is because the derivatives of the smoothstep function vanish at the endpoints, making the first term in brackets in Equation (24) also go to zero at λ=0 and 1. In fact, it is clear from Equation (24) that the conventional thermodynamic derivative of the softcore potential is multiplied by a term that involves the derivative of the smoothstep function, which is zero at the endpoints for all orders greater than zero (in which case the derivative is unity). This also has the consequence that the “large gradient-jump” problem due to large values of β at the endpoints is also mitigated.
The use of the smoothstep function is not guaranteed to resolve the particle collapse problem for all possible cases. The particle collapse problem, in its most general form, arises from the creation of new artificial minima along the λ alchemical progress coordinate. It is therefore possible that use of the smoothstep softcore, for a particular set of α/β softcore parameters, in some cases may only shift the artificial minima to different regions of the q, λ space. Nonetheless, what the smoothstep function does allow is the stable adjustment of the α/β softcore parameters so as to mitigate particle collapse without the adverse consequences of the endpoint and large gradient-jump problems that occur when the conventional softcore potential is used (see Figures S4 and S5 in the Supporting Information). Note that, from Equation (25), the total softcore contributions to ⟨∂U/∂λ⟩λ will be exactly zero at the end points, but the ⟨∂U/∂λ⟩λ results shown in Figure 1 are not zero because of other interactions terms, which currently are not treated with the proposed SSC scheme.
For α/β values of 0.2/50 Å2, all of the edge cases examined here appear quite stable. Higher order smoothstep functions approach the endpoints more gradually and smoothly, as a consequence of having a steeper slope in the transition between 0 and 1 in the intermediate λ values (Figure S4 of Supporting Information). Comparison of smoothstep functions of different orders indicated a good balance between these properties was to use a second-order smoothstep function (see Supporting Information for details). In the remainder of the paper, we will use the SSC(2) potential together with α/β values of 0.2/50 Å2 to test and validate against a broad range of hydration free energy and RBFE calculations. Comparison will be made with the original AMBER softcore potential with default α/β values of 0.5/12 Å2. These methods have recently been extensively validated60 in AMBER18 and the new AMBER20 release.61
Hydration free energies of small organic molecules
Here we examine absolute and relative hydration free energies of a series of small organic molecules that have been recently employed to verify the reproducibility of free energy calculations across different molecular simulation software packages.87 The purpose is to verify that the SSC(2) potential, with parameters adjusted by consideration of the edge cases in the previous section, is robust in reproducing results from the stepwise scheme. Table 1 lists the free energy values for alchemical transformations representing the absolute (de)hydration free energies for 9 organic molecules as well as several relative hydration free energies. Results from simulations of concerted transformations with the original AMBER softcore potential and 2nd-order smoothstep softcore potential, SSC(2) with the set, are compared with reference calculations using the stepwise approach with original AMBER softcore potential and BAR71 analysis. Free energy simulations with the original AMBER softcore potential used the parameters α = 0.5 and β = 12Å2 that are the default in AMBER18, and simulations with the SSC(2) potential used the parameters α = 0.2 and β = 50Å2 developed and tested here that are the default in AMBER20. In most cases, the differences between the free energy values with respect to the reference results, designated as Δ in the table, are comparable to or less than the error estimates of the results themselves. A minor exception occurs for the absolute dehydration free energy of methanol (3.78 kcal/mol) which is slightly overestimated with both the original AMBER softcore potential and SSC(2) by 0.06–0.07 kcal/mol. The largest deviation with respect to the reference values occurs for the methanol → ethane transformation which is overestimated by 0.68 kcal/mol with the original AMBER softcore potential, whereas SSC(2) agrees closely (0.02 kcal/mol). The only instance where SSC(2) performs statistically more poorly than the original AMBER softcore potential is for the 7-CPI → 2-CPI transformation, which is overestimated by 0.15 kcal/mol with SSC(2) whereas the original AMBER softcore potential is closer to the reference result (0.04 kcal/mol). Overall, the error estimates for SSC(2) appear very slightly larger than the original AMBER softcore potential, and overall the results are quite comparable, except in the instances of the edge cases where SSC(2) provides accurate results whereas the original AMBER softcore potential fails.
Table 1:
Comparison of relative hydration free energiesa obtained by stepwise and concerted protocols with the original AMBER softcore potentials (labeled as “Original”) and with the proposed second-order smoothstep function (labeled as SSC(2)).
| Transformation | stepwise | concerted | |||
|---|---|---|---|---|---|
| Original | Original | Δb | SSC(2) | Δb | |
| methane → 0 | −2.34(02) | −2.34(02) | 0.00 | −2.36(03) | 0.02 |
| methanol → 0 | 3.78(02) | 3.84(03) | 0.06 | 3.85(04) | 0.07 |
| ethane → 0 | −2.51(02) | −2.54(03) | 0.03 | −2.54(04) | 0.03 |
| toluene → 0 | 0.84(04) | 0.80(04) | 0.04 | 0.82(07) | 0.02 |
| neopentane → 0 | −2.66(04) | −2.67(07) | 0.01 | −2.69(06) | 0.03 |
| 2-methylfuran → 0 | 0.57(03) | 0.56(04) | 0.01 | 0.56(06) | 0.01 |
| 2-methylindole → 0 | 6.25(04) | 6.26(04) | 0.01 | 6.22(08) | 0.03 |
| 2-cyclopentanylindole → 0 | 6.59(05) | 6.56(05) | 0.03 | 6.55(09) | 0.04 |
| 7-cyclopentanylindole → 0 | 6.85(06) | 6.78(05) | 0.07 | 6.73(10) | 0.12 |
| Avg. Δ | 0.03 | 0.04 | |||
| methane → ethane | 0.07(06) | 0.07(08) | 0.00 | 0.04(08) | 0.03 |
| methanol → methane | 6.19(06) | 6.26(07) | 0.07 | 6.21(07) | 0.02 |
| methanol → ethane | 6.19(04) | 6.87(06) | 0.68 | 6.21(04) | 0.02 |
| toluene → methane | 3.23(07) | 3.24(09) | 0.01 | 3.25(10) | 0.02 |
| methane → neopentanec | 0.07(14) | 0.00(18) | 0.07 | −0.01(18) | 0.08 |
| methane → neopentaned | 0.23(07) | 0.20(10) | 0.03 | 0.21(10) | 0.02 |
| 2-methylfuran → methane | 2.90(07) | 2.95(09) | 0.05 | 2.95(10) | 0.05 |
| 2-methylindole → methane | 8.66(07) | 8.74(10) | 0.08 | 8.66(12) | 0.00 |
| 7-CPIe → 2-CPIf | 0.04(11) | 0.08(14) | 0.04 | 0.19(16) | 0.15 |
| Avg. Δ | 0.11 | 0.04 | |||
All free energy results were ΔΔG obtained by TI, except that the data from the stepwise scheme with traditional softcore potential are obtained by BAR. Free energy simulations with the original AMBER softcore potential used the parameters α = 0.5 and β = 12Å2 that are the default in AMBER18, and simulations with the SSC(2) potential used the parameters α = 0.2 and β = 50Å2 developed and tested here that are the default in AMBER20. The upper rows show the absolute hydration ΔΔG values while the lower rows show the relative hydration ΔΔG values. Both are obtained by ΔΔG = ΔGaq - ΔGgas.
Use the results from stepwise scheme, traditional softcore potential with BAR as the reference to show the errors with respect to the reference.
Central mapping.
Terminal mapping.
7-cyclopentanylindole.
2-cyclopentanylindole.
RBFE calculation of 8 published protein systems
In this section we examine more complex cases of RBFE on a series of previously studied drug targets.88 This set (defined as the Wang et al. dataset) covers eight protein systems and 314 ligand mutations and has been widely used as a benchmark test set for tractable RBFE calculations without significant conformational changes or other challenging scenarios such as changes in tautomer/ionization states or buried waters. We first examine two systems that demonstrate significant edge cases where the original AMBER softcore potential fails, whereas the SSC(2) potential is shown to be accurate. Next we examine the six additional protein-ligand systems to demonstrate the SSC(2) is also robust.
Results of the two problematic protein targets: PTP1B and p38
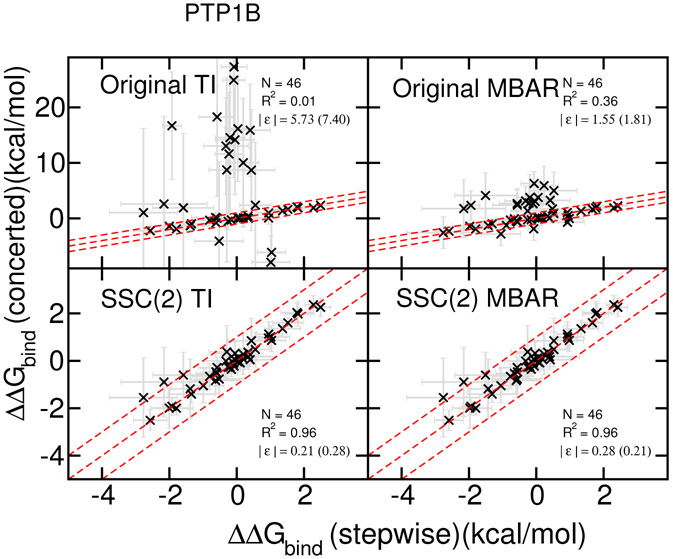
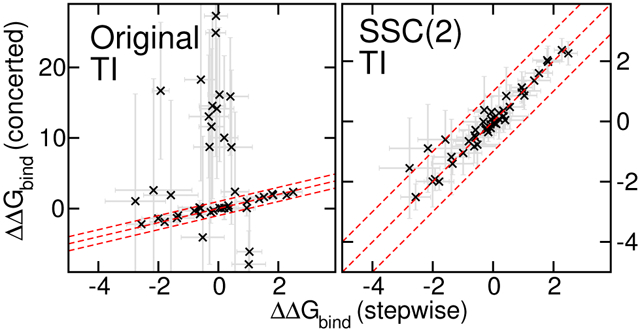
Out of the Wang et al. dataset, two protein targets (PTP1B and p38) demonstrated significant edge cases where the conventional softcore potential with default parameters was observed to fail. The RBFE predictions for PTP1B ligands are plotted in Figure 2, comparing the stepwise scheme (x-axis) and the concerted scheme (y-axis). The upper two panels show the results for the original softcore potential parameter set analyzed by TI (left panels) and MBAR (right panels). The lower two panels show the corresponding results for the SSC(2) smoothstep softcore potential. It is clear that the original AMBER softcore potential produces several prominent outlier points with respect to the stepwise scheme. These outliers are exacerbated for the TI results, which are more sensitive to the integration of thermodynamic derivatives. Nonetheless, the MBAR results are clearly problematic with the original softcore potential. With the use of the SSC(2) smoothstep softcore potential, the RBFE results agree with those of the stepwise scheme to within statistical error estimates, and the TI and MBAR results are virtually identical.
Figure 2:
RBFE results for PTP1B ligands:
Upper panels: simulations results with the original AMBER softcore potential parameter set and the linear combination of the softcore potentials, analyzed by TI (left panels) and MBAR (right panels).
Lower panels: simulations results with the proposed second order smoothstep function SSC(2) and the softcore potential parameter set (α=0.2, β=50 Å2), analyzed by TI (left panels) and MBAR (right panels). Plots show the the comparison between the stepwise scheme (x-axis) and the concerted scheme (y-axis). The dashed red lines indicate the region of ±1.0 kcal/mol difference. The calculated ∣ϵ∣’s are positive definite values and not normally distributed, hence their standard deviations (shown in parentheses) should not be interpretted as indicative of data range.
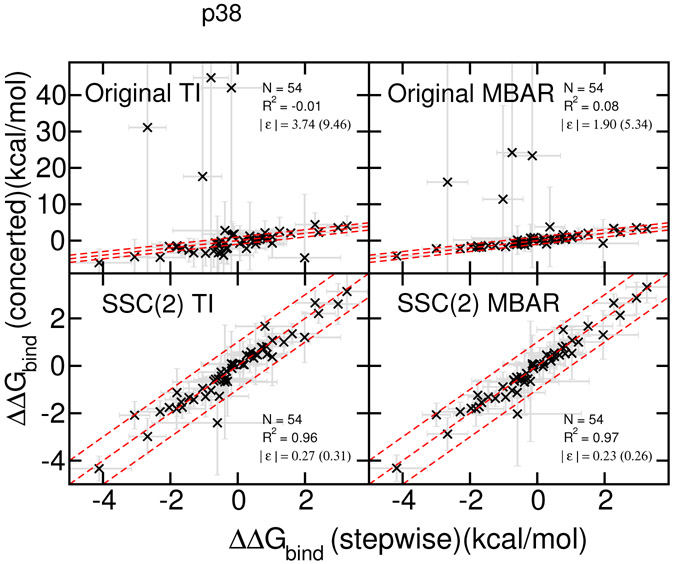
Analogous results for p38 ligands are plotted in Figure 3. Again, with the original AMBER softcore potential, both TI and MBAR produce several outlier points that vary dramatically from the reference results computed with the stepwise scheme. With the SSC(2) smoothstep softcore potential, results are in close agreement (within statistical error estimates, typically less than 1 kcal/mol) of the reference values. Further, the TI and MBAR results are almost indistinguishable. Hence, it appears that the SSC(2) smoothstep softcore potential can successfully overcome limitations of the original AMBER softcore potential for the problematic edge cases considered here, where the main causes are the particle collapse problem according to the curves (see typical problematic curves in Supporting Information).
Figure 3:
RBFE results for p38 ligands:
Upper panels: simulations results with the original AMBER softcore potential parameter set and the linear combination of the softcore potentials, analyzed by TI (left panels) and MBAR (right panels).
Lower panels: simulations results with the proposed second order smoothstep function SSC(2) and the softcore potential parameter set (α=0.2, β=50 Å2), analyzed by TI (left panels) and MBAR (right panels). Plots show the the comparison between the stepwise scheme (x-axis) and the concerted scheme (y-axis). The dashed red lines indicate the region of ±1.0 kcal/mol difference. The calculated ∣ϵ∣’s are positive definite values and not normally distributed, hence their standard deviations (shown in parentheses) should not be interpretted as indicative of data range.
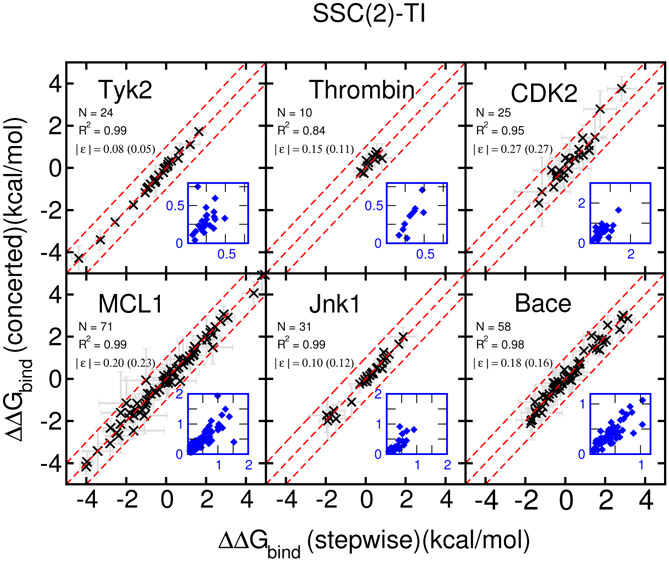
Results of the six well-behaved protein targets:
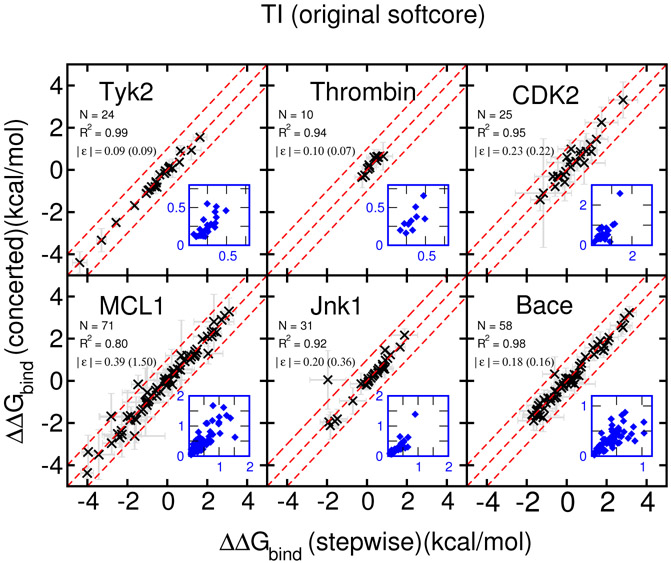
The RBFE results for the remaining 6 targets of the Wang et al. dataset using the concerted scheme are shown in Figure 4 for the original AMBER softcore scheme and the Figure 5 proposed SSC(2) scheme, respectively. Plots show the comparison between the stepwise scheme (x-axis) and the reported concerted scheme (y-axis). The dashed red lines indicate the region of ±1.0 kcal/mol difference. The corresponding standard deviations are plotted as gray error bars and also shown in the small blue plots.
Figure 4:
The results (y-axis) of RBFE for 6 targets of the Wang et al. dataset using the concerted scheme and the AMBER original softcore potential with default parameters (α=0.5, β=12 Å2) are compared with corresponding values with the stepwise scheme (x-axis). The dashed red lines indicate the region of ±1.0 kcal/mol difference. The corresponding standard deviations are plotted as gray error bars and also shown in the small blue inset plots. The calculated ∣ϵ∣’s are positive definite values and not normally distributed, hence their standard deviations (shown in parentheses) should not be interpretted as indicative of data range.
Figure 5:
The results (y-axis) of RBFE for 6 targets of the Wang et al. dataset using the concerted scheme and the SSC(2) smoothstep softcore potential (α=0.2, β=50 Å2) are compared with corresponding values with the stepwise scheme (x-axis). The dashed red lines indicate the region of ±1.0 kcal/mol difference. The corresponding standard deviations are plotted as gray error bars and also shown in the small blue inset plots. The calculated ∣ϵ∣’s are positive definite values and not normally distributed, hence their standard deviations (shown in parentheses) should not be interpretted as indicative of data range.
The original AMBER softcore scheme results (Figure 4) for these six targets indicate that the concerted scheme produces virtually the same RBFE (within 1.0 kcal/mol) results compared to the stepwise scheme, except one outlier in the Jnk1 case and one in the MCL1 case (which is out of range on the plot with a ΔΔG = 13.46 resulting from an unstable particle collapse problem shown in Fig. S1 in Supporting Information). The standard deviations from the concerted and the stepwise schemes are also roughly similar and correlated. The proposed SSC(2) scheme results (Figure 5) are qualitatively similar, except the outliers of Jnk1 and MCL1 now are eliminated. Nevertheless, comparing the correlation coefficients (R2), the proposed SSC(2) scheme delivers better results for MCL1 (0.80 vs. 0.99) and Jnk1 (0.92 vs. 0.99). The same trend can be found in the regression errors as well in MCL1 (original:0.39 vs. SSC(2):0.20 kcal/mol). For the thrombin case, the agreement with the stepwise protocol is worse for SSC(2) in terms of R2 (original:0.94 vs. SSC(2):0.84). In both protocols, the regression errors are less than 0.15 kcal/mol with only 10 data points.
Hence, for these six targets the proposed SSC(2) scheme performs at least as well as the original AMBER softcore approach and they produces virtually the same RBFE (within 1.0 kcal/mol) results compared to the stepwise scheme, except few points near or on the 1.0 kcal/mol error lines, which all have large errors in both the concerted and the stepwise schemes. This might imply that other hidden issues besides the softcore potentials need to be further investigated.
Discussion
Although it is one of the most pivotal decisions in setting up a free energy simulations, the choice of alchemical pathway essentially remains an unsolved issue. For many transformations, existing softcore potential implementations are stable and lead to numerically satisfactory results. However, many seemingly benign transformations can sporadically and/or unexpectedly become unstable with no obvious indication as to the underlying issue. To be clear, this is a separate problem from the standard simulation issues of adequate statistical sampling and accurate force field modeling. Indeed, the issue is considerably more fundamental since a numerically unstable algorithm can neither sample exhaustively nor correctly characterize even a “perfect” physical model. The previous sections showed several examples where these failures occur using the standard softcore implementation in AMBER. Although we do not present specific evidence here, we feel that the data provides a reasonable indication that other related implementations would likely lead to similar failures on at least some of these examples. Regardless, the SSC(2) potential resolves the issues in nearly all instances, except when overall certainty is precluded by a system that is challenging for other reasons (e.g. slow degrees of freedom or high variability). Even so, this is still an absence of evidence that SSC(2) fails and not evidence that SSC(2) does not fail – there may indeed be situations where the issues outlined here are not resolved by SSC(2). Hence, as a community it is important to continue to build up benchmark datasets and to document their known pathologies.
The choice of α/β inevitably impacts the behavior of the softcore potentials significantly. As already demonstrated and discussed in the Results section, the proposed SSC(2) scheme does not necessary make the corresponding softcore function better for every set of α/β. Instead, the proposed SSC(2) scheme eliminates the end point catastrophe and mitigates the large-jump gradient problem, and hence provides a more stable platform for selecting the best α/β to reduce the particle collapse problems and other possible irregularities of the softcore function potentials. In the present work, we demonstrated that α=0.2 and β = 50 Å2 perform reasonably well for all cases we tested. Nevertheless, this parameter set is not perfect for all cases, e.g., as in the case of Na+/0, the ⟨∂U/∂λ⟩λ curve is still not very smooth at λ ≈ 0.5 due to minor effect of particle collapse. In fact, in some cases of the Tyk2 and MCL1 datasets the proposed approach yields larger standard deviations compared to the original protocol (see Section 3 of Supporting Information). This suggests that further exploration of the form of the softcore potential and optimization of parameters therein may lead to even more stable and robust concerted alchemical pathways. In this sense, it is the hope that the smoothstep softcore potential introduced here is a valuable step forward.
Other authors have also considered alchemical path selection in detail. Most notably, this has been done in the context of non-equilibrium schemes where the path implies a time-dependent protocol.89,90 Indeed, there has recently been renewed interest in this approach for ligand binding calculations due to its focus on explicit bound/unbound states.91 However, this technique is not considered here and it is not obvious that the developments here would transfer. This is because the success of non-equilibrium methods seem to be more strongly conditioned on fluctuations at the endpoints, both in terms of their magnitude and timescale.92 While this is essentially the same as the endpoint catastrophe, the current approach is also concerned with discontinuities along the path, as these are more central in TI. Similar in spirit, but slightly different in details, is closely related work first introduced by Hritz and Oostenbrink93 in the context of replica exchange molecular dynamics using softcore potentials, and described in further detail by Riniker and co-workers94 where the use of thrid-order polynomials enable different λ-dependency (referred to a “individual Lambdas”) for calculation of relative free energies. The form of the softcore potential also has been shown to have impact on the ability to predict λ derivatives at non-simulated points in extended thermodynamic integration methods.95 Shirts and co-workers have considered the problem of finding a minimum variance path in equilibrium alchemical schemes and found that the fluctuations at intermediate states (especially the timescales thereof) are of critical importance.44,45 It has been proposed to overcome the end-point catastrophe through a capped form of softcore potential by Buelens and Grubmüller,41 and Pal and Gallicchio.42 Recently, Pal and Gallicchio proposed a general design strategy of the alchemical pathways.42
Besides the various softcore potential forms and alchemical path selections, there are theoretical and technical issues that need be taken into consideration, such as the treatment of the non-bonded40 interactions within the softcore region and the bonded interactions across the common core/softcore boundary.43,96,97 While this topic is beyond the scope of the present work, the solutions to these issues have been recently implemented and extensively validated and tested in AMBER18,60 fixing some long-standing problems with previous versions, along with the presented SSC scheme developed here and implemented as the default in the AMBER20 release.61
The stepwise scheme has been widely thought to be the most stable procedure for performing TI calculations. The results here show that employing the smoothstep softcore potential, TI calculations can be performed in a single concerted transformation without a loss of precision compared to the stepwise scheme. Hence the smoothstep potential should be the choice in situations where concerted simulations are preferred.
The calculations shown in this paper mainly utilized the thermodynamic integration method. Nonetheless, our data suggests that many of the pathological problems discussed in the context of TI are also problematic for other free energy approaches such as thermodynamic perturbation62 with BAR71 or MBAR75 analysis. Our results of PTP1B and p38 (Figures 2 and 3) demonstrate that the SSC(2) potential also eliminates the observed problems that occur with thermodynamic perturbation methods with MBAR analysis, and converge to the same result as TI.
Furthermore, the proposed SSC(2) scheme is well suited for advanced λ-scheduling optimization and enhanced sampling schemes in the λ-space where a single-pass concerted λ transformation is desirable, including λ dynamics,47-50 Hamiltonian replica exchange methods,51-55 adaptive biasing,48,56,57 or self-adjusted mixture sampling58,59 methods. We are actively investigating possible incorporation of the proposed SSC(2) potential with these techniques.
Conclusion
In conclusion, we propose a novel second-order smoothstep softcore potential, SSC(2), to overcome the endpoint catastrophe, particle collapse, and large gradient-jump problems routinely encountered in alchemical free energy simulations using concerted transformations. These problems stem from poor phase space overlap, imbalance of Coulomb attraction and exchange-repulsion, and thermodynamic derivative terms in the softcore potential that lead to sensitivity to softcore α and particularly β parameters. The SSC(2) smoothstep softcore potential with α=0.2 and β=50 Å2 has been demonstrated to overcome these problems for a broad set of alchemical transformations used in the calculation of hydration free energies and RBFEs. The key characteristic of the smoothstep softcore function is that the weights used in the alchemical transformation have derivatives that vanish at the transformation endpoints (λ=0 and 1), and enable smooth adjustment of the λ-dependent terms in the potential. This in turn allows Coulomb attraction and exchange-repulsions to be rebalanced so as to avoid introduction of artificial minima where a particle in the softcore region can collapse on a neighboring particle at intermediate λ states. Results are examined for edge cases where the original AMBER softcore potential is observed to fail, and the SSC(2) smoothstep softcore potential is shown to remain accurate. The SSC(2) potential is further tested against a broad set of hydration free energy and RBFEs for the JACS dataset containing 314 ligand mutations and spanning 8 protein targets. The SCC(2) potential developed here is demonstrated to be highly robust, leading to precise free energy values for all the systems considered here. The SSC(2) potential has the advantage that it can be used in concerted transformations with less computational effort than the stepwise scheme, and is better suited for enhanced sampling methods with more advanced, adaptive λ scheduling requirements.
Supplementary Material
Acknowledgement
The authors are grateful for financial support provided by the National Institutes of Health (No. GM107485 to DMY). Computational resources were provided by the Office of Advanced Research Computing (OARC) at Rutgers, The State University of New Jersey, the National Institutes of Health under Grant No. S10OD012346, the Blue Waters sustained-petascale computing project (NSF OCI 07-25070, PRAC OCI-1515572), and by the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number No. ACI-1548562.98 This work used the XSEDE resource COMET and COMET GPU at SDSC through allocation TG-CHE190067. We gratefully acknowledge the support of the NVIDIA Corporation with the donation of several Pascal, Volta, and Turing GPUs and the GPU-time of a GPU-cluster where the reported benchmark results were performed.
Footnotes
Additional information including: the direct space implementation of the electrostatic interaction, the simulation setup and protocols, representative curves, the plots of the smooth step functions of different orders and their derivatives, comparison of the original softcore and SSC(2) functions with different values of α and β, and results of smoothstep functions with different orders, are described in the Supporting Information. This information is available free of charge via the Internet at https://pubs.acs.org/
References
- (1).Stone JE; Phillips JC; Freddolino PL; Hardy DJ; Trabuco LG; Schulten K Accelerating molecular modeling applications with graphics processors. J. Comput. Chem 2007, 28, 2618–2640. [DOI] [PubMed] [Google Scholar]
- (2).Anderson JA; Lorenz CD; Travesset A General purpose molecular dynamics simulations fully implemented on graphics processing units. J. Comput. Phys 2008, 227, 5342–5359. [Google Scholar]
- (3).Hardy DJ; Stone JE; Schulten K Multilevel Summation of Electrostatic Potentials Using Graphics Processing Units. Parallel Computing 2009, 35, 164–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Harvey MJ; Giupponi G; Fabritiis GD ACEMD: Accelerating Biomolecular Dynamics in the Microsecond Time Scale. J. Chem. Theory Comput 2009, 5, 1632–1639. [DOI] [PubMed] [Google Scholar]
- (5).Harvey MJ; De Fabritiis G An Implementation of the Smooth Particle Mesh Ewald Method on GPU Hardware. J. Chem. Theory Comput 2009, 5, 2371–2377. [DOI] [PubMed] [Google Scholar]
- (6).Stone JE; Hardy DJ; Ufimtsev IS; Schulten K GPU-accelerated molecular modeling coming of age. J. Mol. Graphics Model 2010, 29, 116–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Farber RM Topical perspective on massive threading and parallelism. J. Mol. Graphics Model 2011, 30, 82–89. [DOI] [PubMed] [Google Scholar]
- (8).Göetz A; Williamson MJ; Xu D; Poole D; Le Grand S; Walker RC Routine microsecond molecular dynamics simulations with AMBER on GPUs. 1. Generalized Born. J. Chem. Theory Comput 2012, 8, 1542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Eastman P et al. OpenMM 4: A Reusable, Extensible, Hardware Independent Library for High Performance Molecular Simulation. J. Chem. Theory Comput 2013, 9, 461–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Salomon-Ferrer R; Götz AW; Poole D; Le Grand S; Walker RC Routine microsecond molecular dynamics simulations with AMBER on GPUs. 2. Explicit solvent Particle Mesh Ewald. J. Chem. Theory Comput 2013, 9, 3878–3888. [DOI] [PubMed] [Google Scholar]
- (11).Chipot C Frontiers in free-energy calculations of biological systems. WIREs Comput. Mol. Sci 2014, 4, 71–89. [Google Scholar]
- (12).Eastman P; Swails J; Chodera JD; McGibbon RT; Zhao Y; Beauchamp KA; Wang L-P; Simmonett AC; Harrigan MP; Stern CD; Wiewiora RP; Brooks BR; Pande VS OpenMM 7: Rapid development of high performance algorithms for molecular dynamics. PLoS Comput. Biol 2017, 13, 1005659–1005659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Abel R; Wang L; Harder ED; Berne BJ; Friesner RA Advancing Drug Discovery through Enhanced Free Energy Calculations. Acc. Chem. Res 2017, 50, 1625–1632. [DOI] [PubMed] [Google Scholar]
- (14).Lee T-S; Hu Y; Sherborne B; Guo Z; York DM Toward Fast and Accurate Binding Affinity Prediction with pmemdGTI: An Efficient Implementation of GPU-Accelerated Thermodynamic Integration. J. Chem. Theory Comput 2017, 13, 3077–3084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Mermelstein DJ; Lin C; Nelson G; Kretsch R; McCammon JA; Walker RC Fast and flexible gpu accelerated binding free energy calculations within the amber molecular dynamics package. J. Comput. Chem 2018, 39, 1354–1358. [DOI] [PubMed] [Google Scholar]
- (16).Giese TJ; York DM A GPU-Accelerated Parameter Interpolation Thermodynamic Integration Free Energy Method. J. Chem. Theory Comput 2018, 14, 1564–1582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Lee T-S; Cerutti DS; Mermelstein D; Lin C; LeGrand S; Giese TJ; Roitberg A; Case DA; Walker RC; York DM GPU-Accelerated Molecular Dynamics and Free Energy Methods in Amber18: Performance Enhancements and New Features. J. Chem. Inf. Model 2018, 58, 2043–2050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Song LF; Lee T-S; Zhu C; York DM; Merz KM Jr. Using AMBER18 for Relative Free Energy Calculations. J. Chem. Inf. Model 2019, 59, 3128–3135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Chipot C, Pohorille A, Eds. Free Energy Calculations: Theory and Applications in Chemistry and Biology; Springer Series in Chemical Physics; Springer: New York, 2007; Vol. 86. [Google Scholar]
- (20).Jorgensen WL Efficient drug lead discovery and optimization. Acc. Chem. Res 2009, 42, 724–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Mobley DL; Dill KA Binding of Small-Molecule Ligands to Proteins: What You See Is Not Always What You Get. Structure 2009, 17, 489–498, 0969-2126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Christ C; Mark A; van Gunsteren W Basic Ingredients of Free Energy Calculations: A Review. J. Comput. Chem 2010, 31, 1569–1582. [DOI] [PubMed] [Google Scholar]
- (23).Foloppe N; Hubbard R Towards Predictive Ligand Design With Free-Energy Based Computational Methods? Curr. Med. Chem 2006, 13, 3583–3608. [DOI] [PubMed] [Google Scholar]
- (24).Pohorille A; Jarzynski C; Chipot C Good Practices in Free-Energy Calculations. J. Phys. Chem. B 2010, 114, 10235–10253. [DOI] [PubMed] [Google Scholar]
- (25).Michel J; Essex JW Prediction of protein-ligand binding affinity by free energy simulations: assumptions, pitfalls and expectations. J. Comput.-Aided Mol. Des 2010, 24, 639–658. [DOI] [PubMed] [Google Scholar]
- (26).Gallicchio E; Levy RM Advances in all atom sampling methods for modeling protein-ligand binding affinities. Curr. Opin. Struct. Biol 2011, 21, 161–166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Chodera J; Mobley D; Shirts M; Dixon R; Branson K; Pande V Alchemical free energy methods for drug discovery: progress and challenges. Curr. Opin. Struct. Biol 2011, 21, 150–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Mobley DL; Klimovich PV Perspective: Alchemical free energy calculations for drug discovery. J. Chem. Phys 2012, 137, 230901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Gumbart JC; Roux B; Chipot C Standard Binding Free Energies from Computer Simulations: What Is the Best Strategy? J. Chem. Theory Comput 2013, 9, 794–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Hansen N; van Gunsteren WF Practical Aspects of Free-Energy Calculations: A Review. J. Chem. Theory Comput 2014, 10, 2632–2647. [DOI] [PubMed] [Google Scholar]
- (31).Cournia Z; Allen B; Sherman W Relative Binding Free Energy Calculations in Drug Discovery: Recent Advances and Practical Considerations. J. Chem. Inf. Model 2017, 57, 2911–2937. [DOI] [PubMed] [Google Scholar]
- (32).de Ruiter A; Oostenbrink C Advances in the calculation of binding free energies. Curr. Opin. Struct. Biol 2020, 61, 207–212. [DOI] [PubMed] [Google Scholar]
- (33).Mezei M Polynomial path for the calculation of liquid state free energies from computer simulations tested on liquid water. J. Comput. Chem 1992, 13, 651–656. [Google Scholar]
- (34).Resat H; Mezei M Studies on free energy calculations. I. Thermodynamic integration using a polynomial path. J. Chem. Phys 1993, 99, 6052–6061. [Google Scholar]
- (35).Simonson T Free energy of particle insertion. Mol. Phys 1993, 80, 441–447. [Google Scholar]
- (36).Beutler TC; Mark AE; van Schaik René C. and Gerber Paul R. and van Gunsteren Wilfred F., Avoiding singularities and numerical instabilities in free energy calculations based on molecular simulations. Chem. Phys. Lett 1994, 222, 529–539. [Google Scholar]
- (37).Steinbrecher T; Mobley DL; Case DA Nonlinear scaling schemes for Lennard-Jones interactions in free energy calculations. J. Chem. Phys 2007, 127, 214108. [DOI] [PubMed] [Google Scholar]
- (38).Steinbrecher T; Joung I; Case DA Soft-Core Potentials in Thermodynamic Integration: Comparing One- and Two-Step Transformations. J. Comput. Chem 2011, 32, 3253–3263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Gapsys V; Seeliger D; de Groot BL New Soft-Core Potential Function for Molecular Dynamics Based Alchemical Free Energy Calculations. J. Chem. Theory Comput 2012, 8, 2373–2382. [DOI] [PubMed] [Google Scholar]
- (40).Gapsys V; Khabiri M; de Groot BL; Freddolino PL Comment on “Deficiencies in Molecular Dynamics Simulation-Based Prediction of Protein-DNA Binding Free Energy Landscapes”. J. Phys. Chem. B 2020, 124, 1115–1123, PMID: 29741907. [DOI] [PubMed] [Google Scholar]
- (41).Buelens FP; Grubmüller H Linear-scaling soft-core scheme for alchemical free energy calculations. J. Comput. Chem 2012, 33, 25–33. [DOI] [PubMed] [Google Scholar]
- (42).Pal RK; Gallicchio E Perturbation potentials to overcome order/disorder transitions in alchemical binding free energy calculations. J. Chem. Phys 2019, 151, 124116. [DOI] [PubMed] [Google Scholar]
- (43).Jiang W; Chipot C; Roux B Computing Relative Binding Affinity of Ligands to Receptor: An Effective Hybrid Single-Dual-Topology Free-Energy Perturbation Approach in NAMD. J. Chem. Inf. Model 2019, 59, 3794–3802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Pham TT; Shirts MR Identifying low variance pathways for free energy calculations of molecular transformations in solution phase. J. Chem. Phys 2011, 135, 034114. [DOI] [PubMed] [Google Scholar]
- (45).Pham TT; Shirts MR Optimal pairwise and non-pairwise alchemical pathways for free energy calculations of molecular transformation in solution phase. J. Chem. Phys 2012, 136, 124120. [DOI] [PubMed] [Google Scholar]
- (46).Klimovich PV; Shirts MR; Mobley DL Guidelines for the analysis of free energy calculations. J. Comput.-Aided Mol. Des 2015, 29, 397–411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Ding X; Vilseck JZ; Hayes RL; Brooks CL Gibbs Sampler-Based λ-Dynamics and Rao-Blackwell Estimator for Alchemical Free Energy Calculation. J. Chem. Theory Comput 2017, 13, 2501–2510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Hayes RL; Armacost KA; Vilseck JZ; Brooks CL Adaptive Landscape Flattening Accelerates Sampling of Alchemical Space in Multisite λ Dynamics. J. Phys. Chem. B 2017, 121, 3626–3635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Guo Z; Brooks CL Rapid Screening of Binding Affinities: Application of the λ-Dynamics Method to a Trypsin-Inhibitor System. J. Am. Chem. Soc 1998, 120, 1920–1921. [Google Scholar]
- (50).Guo Z; Brooks CL III; Kong X Efficient and Flexible Algorithm for Free Energy Calculations Using the λ-Dynamics Approach. J. Phys. Chem. B 1998, 102, 2032–2036. [Google Scholar]
- (51).Jiang W; Roux B Free energy perturbation Hamiltonian replica-exchange molecular dynamics (FEP/H-REMD) for absolute ligand binding free energy calculations. J. Chem. Theory Comput 2010, 6, 2559–2565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Arrar M; de Oliveira CAF; Fajer M; Sinko W; McCammon JA w-REXAMD: A Hamiltonian replica exchange approach to improve free energy calculations for systems with kinetically trapped conformations. J. Chem. Theory Comput 2013, 9, 18–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Itoh SG; Okumura H Hamiltonian replica-permutation method and its applications to an alanine dipeptide and amyloid-β(29-42) peptides. J. Comput. Chem 2013, 34, 2493–2497. [DOI] [PubMed] [Google Scholar]
- (54).Armacost KA; Goh GB; Brooks CL Biasing Potential Replica Exchange Multisite λ-Dynamics for Efficient Free Energy Calculations. J. Chem. Theory Comput 2015, 11, 1267–1277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Yang M; Huang J; MacKerell AD Jr. Enhanced Conformational Sampling Using Replica Exchange with Concurrent Solute Scaling and Hamiltonian Biasing Realized in One Dimension. J. Chem. Theory Comput 2015, 11, 2855–2867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (56).Babin V; Roland C; Sagui C Adaptively biased molecular dynamics for free energy calculations. J. Chem. Phys 2008, 128, 134101. [DOI] [PubMed] [Google Scholar]
- (57).Darve E; Rodríguez-Gómez D; Pohorille A Adaptive biasing force method for scalar and vector free energy calculations. J. Chem. Phys 2008, 128, 144120. [DOI] [PubMed] [Google Scholar]
- (58).Carlson DE; Stinson P; Pakman A; Paninski L Proceedings of the 33rd International Conference on Machine Learning; ICML’16; JMLR.org: New York, NY, USA, 2016; Vol. 48; pp 2896–2905. [Google Scholar]
- (59).Tan Z Optimally Adjusted Mixture Sampling and Locally Weighted Histogram Analysis. J. Comput. Graph. Stat 2017, 26, 54–65. [Google Scholar]
- (60).Tsai H-C; Tao Y; Lee T-S; Merz KM Jr.; York DM Validation of Free Energy Methods in AMBER. J. Chem. Inf. Model 2020, in press, 0–0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (61).Case DA et al. AMBER 20. University of California, San Francisco: San Francisco, CA, 2020. [Google Scholar]
- (62).Zwanzig RW High-temperature equation of state by a perturbation method. I. Non-polar gases. J. Chem. Phys 1954, 22, 1420–1426. [Google Scholar]
- (63).Kirkwood JG Statistical mechanics of fluid mixtures. J. Chem. Phys 1935, 3, 300–313. [Google Scholar]
- (64).Straatsma TP; Berendsen HJ Free energy of ionic hydration: Analysis of a thermodynamic integration technique to evaluate free energy differences by molecular dynamics simulations. J. Chem. Phys 1988, 89, 5876–5886. [Google Scholar]
- (65).Jarzynski C Nonequilibrium equality for free energy differences. Phys. Rev. Lett 1997, 78, 2690–2693. [Google Scholar]
- (66).Crooks GE Path-ensemble averages in systems driven far from equilibrium. Phys. Rev. E 2000, 61, 2361–2366. [Google Scholar]
- (67).Boresch S; Woodcock HL Convergence of single-step free energy perturbation. Mol. Phys 2017, 115, 1200–1213. [Google Scholar]
- (68).Gapsys V; Michielssens S; Peters JH; de Groot BL; Leonov H Calculation of binding free energies. Methods Mol. Biol 2015, 1215, 173–209. [DOI] [PubMed] [Google Scholar]
- (69).Jeong D; Andricioaei I Reconstructing equilibrium entropy and enthalpy profiles from non-equilibrium pulling. J. Chem. Phys 2013, 138, 114110. [DOI] [PubMed] [Google Scholar]
- (70).Wei D; Song Y; Wang F A simple molecular mechanics potential for μm scale graphene simulations from the adaptive force matching method. J. Chem. Phys 2011, 134, 184704. [DOI] [PubMed] [Google Scholar]
- (71).Bennett CH Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys 1976, 22, 245–268. [Google Scholar]
- (72).Torrie GM; Valleau JP Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys 1977, 23, 187–199. [Google Scholar]
- (73).Lu N; Kofke DA Accuracy of free-energy perturbation calculations in molecular simulation. I. Modeling. J. Chem. Phys 2001, 114, 7303–7311. [Google Scholar]
- (74).Shirts MR; Pande VS Comparison of efficiency and bias of free energies computed by exponential averaging, the Bennett acceptance ratio, and thermodynamic integration. J Chem Phys 2005, 122, 144107. [DOI] [PubMed] [Google Scholar]
- (75).Shirts MR; Chodera JD Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys 2008, 129, 124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (76).Darden T; York D; Pedersen L Particle mesh Ewald: An N log(N) method for Ewald sums in large systems. J. Chem. Phys 1993, 98, 10089–10092. [Google Scholar]
- (77).in’t Veld P. j.; Ismail AE; Grest GS Application of Ewald summations to long-range dispersion forces. J. Chem. Phys 2007, 127, 144711. [DOI] [PubMed] [Google Scholar]
- (78).Le Grand S; Göetz AW; Walker RC SPFP: Speed without compromise-A mixed precision model for GPU accelerated molecular dynamics simulations. Comput. Phys. Commun 2013, 184, 374–380. [Google Scholar]
- (79).Maier JA; Martinez C; Kasavajhala K; Wickstrom L; Hauser KE; Simmerling C ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput 2015, 11, 3696–3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (80).Wang J; Wolf RM; Caldwell JW; Kollman PA; Case DA Development and testing of a general amber force field. J. Comput. Chem 2004, 25, 1157–1174. [DOI] [PubMed] [Google Scholar]
- (81).Jakalian A; Jack DB; Bayly CI Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. parameterization and validation. J. Comput. Chem 2002, 23, 1623–1641. [DOI] [PubMed] [Google Scholar]
- (82).Jakalian A; Bush BL; Jack DB; Bayly CI Fast, efficient generation of high-qualigy atomic charges. AM1-BCC model: I. method. J. Comput. Chem 2000, 21, 132–146. [DOI] [PubMed] [Google Scholar]
- (83).Jorgensen WL; Chandrasekhar J; Madura JD; Impey RW; Klein ML Comparison of simple potential functions for simulating liquid water. J. Chem. Phys 1983, 79, 926–935. [Google Scholar]
- (84).Ryckaert JP; Ciccotti G; Berendsen HJC Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes. J. Comput. Phys 1977, 23, 327–341. [Google Scholar]
- (85).Miyamoto S; Kollman PA SETTLE: An analytic version of the SHAKE and RATTLE algorithms for rigid water models. J. Comput. Chem 1992, 13, 952–962. [Google Scholar]
- (86).Lee Y-K; Parks DJ; Lu T; Thieu TV; Markotan T; Pan W; McComsey DF; Milkiewicz KL; Crysler CS; Ninan N; Abad MC; Giardino EC; Maryanoff BE; Damiano BP; Player MR 7-fluoroindazoles as potent and selective inhibitors of factor Xa. J. Med. Chem 2008, 51, 282–297. [DOI] [PubMed] [Google Scholar]
- (87).Loeffler HH; Bosisio S; Duarte Ramos Matos G; Suh D; Roux B; Mobley DL; Michel J Reproducibility of Free Energy Calculations across Different Molecular Simulation Software Packages. J. Chem. Theory Comput 2018, 14, 5567–5582. [DOI] [PubMed] [Google Scholar]
- (88).Wang L et al. Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field. J. Am. Chem. Soc 2015, 137, 2695–2703. [DOI] [PubMed] [Google Scholar]
- (89).Suh D; Radak BK; Chipot C; Roux B Enhanced configurational sampling with hybrid non-equilibrium molecular dynamics-Monte Carlo propagator. J. Chem. Phys 2018, 148, 14101. [DOI] [PubMed] [Google Scholar]
- (90).Chen Y; Roux B Enhanced Sampling of an Atomic Model with Hybrid Nonequilibrium Molecular Dynamics-Monte Carlo Simulations Guided by a Coarse-Grained Model. J. Chem. Theory Comput 2015, 11, 3572–3583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (91).Gapsys V; Pérez-Benito L; Aldeghi M; Seeliger D; van Vlijmen H; Tresadern G; de Groot BL Large scale relative protein ligand binding affinities using nonequilibrium alchemy. Chem. Sci 2020, 11, 1140–1152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (92).Radak BK; Roux B Efficiency in nonequilibrium molecular dynamics Monte Carlo simulations. J. Chem. Phys 2016, 145, 134109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (93).Hritz J; Oostenbrink C Hamiltonian replica exchange molecular dynamics using softcore interactions. J. Chem. Phys 2008, 128, 144121. [DOI] [PubMed] [Google Scholar]
- (94).Riniker S; Christ CD; Hansen HS; Hünenberger PH; Oostenbrink C; Steiner D; van Gunsteren WF Calculation of relative free energies for ligand-protein binding, solvation, and conformational transitions using the GROMOS software. J. Phys. Chem. B 2011, 115, 13570–13577. [DOI] [PubMed] [Google Scholar]
- (95).Ruiter A. d.; Oostenbrink C Extended Thermodynamic Integration: Efficient Prediction of Lambda Derivatives at Nonsimulated Points. J. Chem. Theory Comput 2016, 12, 4476–4486. [DOI] [PubMed] [Google Scholar]
- (96).Boresch S; Karplus M The Role of Bonded Terms in Free Energy Simulations:1. Theoretical Analysis. J. Phys. Chem. A 1999, 103, 103–118. [Google Scholar]
- (97).Boresch S; Karplus M The Role of Bonded Terms in Free Energy Simulations:2. Calculation of Their Influence on Free Energy Differences of Solvation. J. Phys. Chem. A 1999, 103, 119–136. [Google Scholar]
- (98).Towns J; Cockerill T; Dahan M; Foster I; Gaither K; Grimshaw A; Hazlewood V; Lathrop S; Lifka D; Peterson GD; Roskies R; Scott JR; Wilkins-Diehr N XSEDE: Accelerating Scientific Discovery. Comput. Sci. Eng 2014, 16, 62–74. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.