Understanding Time-Dependent Surface-Enhanced Raman Scattering from Gold Nanosphere Aggregates Using Collision Theory

Abstract

Aggregates or clusters of primary metal nanoparticles in solution are one of the most widely used platforms for surface-enhanced Raman scattering (SERS) measurements because these nanostructures induce strong electric fields or hot spots between nanoparticles and as a result, SERS signals. While SERS signals are observed to vary with time, the impact of cluster formation mechanisms on SERS activity has been less studied. Herein, variations in time-dependent SERS signals from gold nanosphere clusters and aggregates are considered both experimentally and theoretically. An excess of the Raman reporter molecule, 2-naphthalenethiol, is added to induce rapid monolayer formation on the nanoparticles. In this diffusion-limited regime, clusters form as loosely packed fractals and the ligands help control nanoparticle separation distances once clusters form. By systematically varying gold nanosphere concentration and diameter, the reaction kinetics and dynamics associated with cluster formation can be studied. Dynamic light scattering (DLS), localized surface plasmon resonance (LSPR) spectroscopy, and SERS reveal that aggregates form reproducibly in the diffusion-limited regime and follow a self-limiting cluster size model. The rate of cluster formation during this same reaction window is explained using interaction pair potential calculations and collision theory. Diffusion-limited reaction conditions are limited by sedimentation only if sedimentation velocities exceed diffusion velocities of the clusters or via plasmon damping through radiation or scattering losses. These radiative loses are only significant when the extinction magnitude near the excitation wavelength exceeds 1.5. By evaluating these responses as a function of both nanosphere radius and concentration, time-dependent SERS signals are revealed to follow collision theory and be predictable when both nanosphere concentration and size are considered.

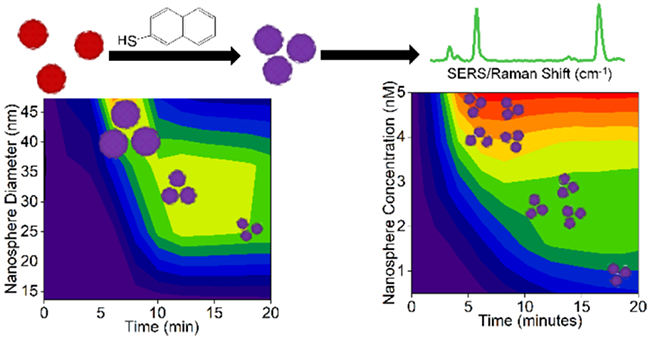
Graphical Abstract

INTRODUCTION

Surface-enhanced Raman scattering (SERS) measurements have been shown to be highly sensitive to trace amounts of target molecules through the enhancement of vibrational modes by plasmonic nanoparticles. One of the mostly widely used SERS substrates are solution-phase aggregates or clusters of primary metal nanoparticles.^1–5 Clusters are used because of the strong electric fields, or hot spots, that are generated at the junction of the plasmonic nanostructures.^3,6–8

Conventionally, clusters form when repulsive interactions between objects are minimized relative to attractive forces. Aggregation, induced upon nanoparticle collisions, occurs because of the high surface energies and significant short-range attractive interaction potentials that are present between nanostructures. Clusters form if the attractive interactions are stronger than repulsive forces.^9,10 Repulsive potentials between nanoparticles can be modulated by changing the protonation states of surface-stabilizing agents using pH,^11–13 increasing solution ionic strength,^14–16 or replacing charged stabilizing agents by neutral molecules.^17–20 While self-assembled monolayers (SAMs) of ligands can reduce the impact of these short-range screening effects, nanoparticle clusters can form and often do so as fractals.^9,21,22

The SERS magnitude of adsorbates on clusters are influenced by inter-nanoparticle distances^3,6,23 and cluster size.²⁴ For instance, SERS intensities have been shown to increase as inter-nanoparticle distances decrease to ~2 nm.^25,26 This effect is directly correlated to electric field strength and is limited by quantum tunneling at shorter distances. In addition, the number of primary nanoparticles per cluster also influences observed SERS signals.^1,27,28 Initially, SERS signals increase as clusters grow because the electric field strength between nanoparticles increases. Additional cluster growth, however, leads to plasmon damping through radiation or scattering losses.^1,24 As such, SERS signals arising from nanoparticle aggregation promote excellent signal-to-noise ratios for identification of molecules, but quantification is generally limited.

Previously, the mechanisms associated with cluster formation were both modeled^1,10,29 and experimentally evaluated.^3,4,9,18,29 Both thermodynamics (i.e., nanoparticle concentration, analyte concentration, initial nanoparticle surface chemistry, and solution parameters) and kinetics (i.e., nanoparticle functionalization and collision rates) were shown to influence the dynamics of formation and geometries of the resulting clusters. Both reaction-limited and diffusion-limited cluster growth mechanisms were observed for colloidal nanomaterials.^1,30,31 Clusters that formed under reaction-limited conditions were shown to depend on the kinetics of monolayer formation (i.e., when surface modification is limited by the number of molecules present in solution or flux to a surface).^1,32 As such, resulting clusters were heterogeneous in size and contained closely spaced primary nanoparticles with a packing density of ~64%, a value consistent with random packing.³³ In contrast, clusters formed under diffusion-limited conditions were composed of primary nanoparticles coated with a relatively higher SAM density that formed prior to cluster formation.^1,31,32 Thus, resulting clusters were largely more homogeneous and contained more loosely packed primary nanoparticles versus those formed under reaction-limited conditions. As a result, primary nanoparticles exhibited a packing density of ~4–5% of the total cluster volume.³¹

Herein, we investigate how the kinetics and dynamics associated with cluster formation under diffusion-limited conditions influence time-dependent SERS responses. In so doing, temporal responses commonly observed in SERS measurements using solution-phase nanoparticles can be understood. Namely, we systematically evaluate how primary gold nanosphere concentration and diameter influence the reaction rate associated with cluster formation and resulting SERS signals. To aid in forming clusters under diffusion-limited conditions, an excess of the reporter molecule, 2-naphthalenethiol (2-NT) is used. 2-NT readily forms a covalent bond to the gold surface, providing a steric barrier on the metal surface to reduce quantum tunneling between nanoparticles and producing strong SERS signals. Interaction pair potential energies from DLVO theory and kinetic energies from collision theory are used to understand both the dynamics and kinetics associated with cluster formation. These processes are experimentally monitored using dynamic light scattering (DLS) and selected flocculation area analysis of localized surface plasmon resonance (LSPR) spectra. This study reveals that time-dependent SERS responses are directly correlated to the dynamics of cluster formation but limited by both sedimentation and plasmonic losses because of scattering and reabsorption. As such, guidance is provided that describes how parameters such as nanoparticle concentration and size influence SERS measurements when a relatively high concentration or excess of a tight binding analyte is added to solution-phase nanoparticles.

MATERIALS AND METHODS

Materials.

Gold(III) chloride trihydrate (HAuCl₄·3H₂O), sodium chloride (NaCl), and 2-NT (99%) were purchased from Sigma Aldrich (St. Louis, MO). All other chemicals were purchased from Fisher Scientific (Pittsburgh, PA) and used as received. Ultrapure water (18.2 MΩ·cm⁻¹) was obtained from a Nanopure System from Barnstead (Dubuque, IA) and used for all samples. All glassware were cleaned with aqua regia (3:1 HCl/HNO₃), rinsed thoroughly with water, and oven-dried before use.

Gold Nanosphere Synthesis.

Gold nanospheres were synthesized using a standard citrate reduction method and grown via previously established methods.^34–36 Briefly, 100 mL of 1.0 mM HAuCl₄·3H₂O was refluxed and stirred for 15 min using a reflux condenser. Next, 10 mL of 39 mM trisodium citrate was added quickly, the solution was stirred, and then cooled for 10 and 15 min, respectively. The resulting seed nanoparticle diameters were 13.6 (±1.1) nm (N = 185) as determined by transmission electron microscopy (TEM). Next, these nanoparticles were grown through a seeded growth method.³⁶ An 18.75 mL aliquot of the seed nanoparticles was diluted by adding 168.75 mL of water and stirred at room temperature. Aliquots of a 1 M citrate stock (10.36 μL) and 1.565 mL of a 0.2 M stock hydroxylamine hydrochloride solution were added to the seeds and then stirred for 5 min. Finally, 1.875 mL of a 1% HAuCl₄·3H₂O solution was quickly added to the reaction flask and stirred for 5 h. The resulting nanoparticles exhibited diameters of 27.7 (±2.9) nm (N = 134).

Subsequently, these ~28 nm diameter nanospheres served as seeds for a third nanoparticle sample. First, 150 mL of water was added to 50 mL of the gold nanoparticles (d = 27.7 nm) and stirred. Next, 76.64 μL and 1.124 mL of 1 M citrate and 0.2 M hydroxylamine hydrochloride solutions, respectively, were added and stirred for 5 min. Next, 2 mL of 1% HAuCl₄·3H₂O was quickly added and stirred for 5 h. These nanoparticles exhibited diameters of 47.3 (±5.3) nm (N = 102). After synthesis, all nanoparticles were centrifuged for 30 min three times (7000, 1269, and 496g for 13.6, 27.7, and 47.3 nm nanospheres, respectively) and then resuspended in 1 mM citrate until use. TEM images of synthesized nanoparticles are shown in Figure 1. A JEOL 1230 TEM and formvar/carbon-coated TEM grids were used. Image Pro was used to determine average nanoparticle diameters. Extinction coefficients (ε at the λ_max) facilitated nanosphere concentration determination and were 2.73 × 10⁸, 2.78 × 10⁹, and 1.86 × 10¹⁰ cm⁻¹ M⁻¹ for the 13.6, 27.7, and 47.3 nm diameter nanoparticles, respectively.³⁷

Figure 1.

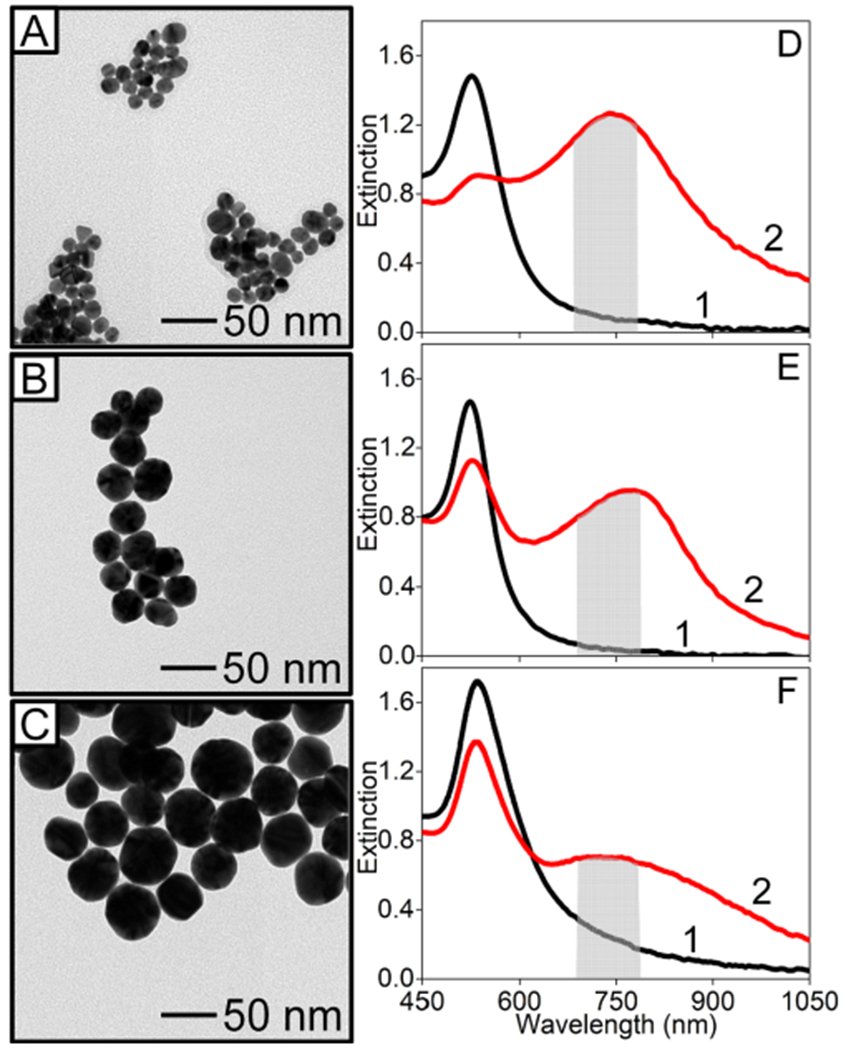
Representative TEM images of Au nanospheres with diameters (d) of (A) 13.6 (±1.1) nm (N = 185), (B) 27.7 (±2.9) nm (N = 134), and (C) 47.3 (±5.3) nm (N = 102), where N = the number of measurements. Representative LSPR spectra of (D) 5 nM (d = 13.6 nm), (E) 0.5 nM (d = 27.7 nm), and (F) 0.1 nM (d = 47.3 nM) gold nanospheres (1) before and (2) after adding an excess of 2-NT (equilibrated for 15 min). Integrated area ranges used to indicate clustering is shaded.

Sample Preparation, Simultaneous Extinction and SERS Spectroscopies, and DLS Measurements.

Solutions ranging in concentration from 0–7, 0–1, and 0–1 nM for the 13.6, 27.7, and 47.3 nm diameter nanospheres, respectively, were prepared by diluting the samples in 1 mM citrate. After 2-NT addition, samples were vortexed for 10 s and then placed on a VWR Minishaker plate (380 RPM). Both extinction (10 s intervals) and SERS (20 s intervals) spectra were collected simultaneously using a modified sample holder as a function of time for 1 h using a BW-Tec UV–vis iTrometer (pathlength = 0.5 cm) and iRaman (excitation wavelength (λ_ex) = 785 nm), respectively. An excess of 2-NT was added to the nanoparticle solution to ensure surface saturation, assuming a 2-NT packing density of 4.1 × 10¹⁴ molecules/cm².¹⁷ Final 2-NT concentrations ranged from ~2.5 to 40 μM for the lowest–highest nanosphere concentrations, respectively.

Waterfall plots for time-dependent LSPR and SERS data were generated using Origin Pro. Random XYZ and Renka-Cline matrix conversion methods were used to generate 3D plots (11 columns × 5 rows and 11 columns × 4 rows, respectively). Experimental parameters were as follows: λ_ex = 785 nm, laser power (P) = 83.3 mW, power density of ~1500 mW/cm², and integration time (t_int) = 10 s for LSPR and 20 s for SERS. Each SERS spectrum containing 2-NT was treated by subtracting a blank spectrum that contained nanoparticles only. Flocculation areas were calculated using integrated areas from 670 to 770 nm in LSPR spectra, as shown in Figure 1D–F. Reaction and diffusion-limited regimes in time-dependent LSPR and SERS spectral changes were determined from zero values in their second derivatives.

DLS measurements were collected using a disposable cuvette and a Malvern Zetasizer (25 °C) that was configured in a backscattering geometry (173°). A polystyrene latex reference with a refractive index of 1.590 and an absorption of 0.01 was used. Water was registered at 25 °C with a density of 0.8872 and a refractive index of 1.330. Initial hydrodynamic diameters were calculated before and then every ~2 min after the addition of 2-NT for a total of 45–60 min.

Zeta Potential.

Nanoparticle surface potential was estimated from electrophoretic mobilities collected at 25 °C using a Malvern Zetasizer (Worcestershire, UK). The mobility of 1 nM gold nanospheres in 1 mM citrate was measured before and after incubation with 13 μM 2-NT. Ionic strength was calculated assuming a citrate concentration of 1 mM. All solutions were vortexed for 10 s and equilibrated at room temperature for 15 min prior to measurement. The zeta potential was calculated using Henry’s equation, measured mobilities, and ionic strength.³⁸ Gold nanospheres before and after incubation with excess 2-NT possessed zeta potentials of −49.9 (±0.4) and −12.0 (±0.6) mV, respectively.

Conventional and Extended Derjaguin–Landau–Verwey–Overbeek (DLVO and xDLVO) Theory.

Attractive and repulsive interactions were modeled using DLVO theory. The attractive van der Waals interaction potential (Φ_VDW) of two identical particles with a given radius (r) was calculated as follows³⁹

$$\begin{gathered} {\Phi }_{{}_{\text{VDW}}}=\frac{V_{\text{vdw}}}{k_{\text{B}}T} \\ =-\frac{A}{6}[\frac{2r^2}{s^2+4rs}+\frac{2r^2}{s^2+4rs+4r^2} \\ +\text{ln}\left(\frac{s^2+4r{s}^2}{s^2+4rs+4r^2}\right)] \end{gathered}$$ (1)

where s is the separation distance, and A is the size-dependent Hamaker constant (3.7, 3.4, and 3.1 × 10⁻¹⁹ J, for diameters 13.6, 27.7, and 47.3 nm, respectively¹⁰). The electrostatic interaction potential (Φ_EL) depends on the relative magnitude between Debye length (κ⁻¹) and particle radius.⁴⁰ When κ⁻¹ is less than 5r

$${\Phi }_{\text{EL}}=\frac{V_{\text{ele}}}{k_{\text{B}}T}=\frac{2\pi {\epsilon }_0\epsilon {\psi }_0{}^{2}r}{k_{\text{B}}T}\text{ln}\left(1+e^{-\kappa s}\right)$$ (2)

and when κ⁻¹ is greater than 5r

$${\Phi }_{\text{EL}}=\frac{V_{\text{ele}}}{k_{\text{B}}T}=\frac{4\pi {\epsilon }_0\epsilon Y^2{r}^2{k}_{\text{B}}T}{e^2}\frac{{\text{e}}^{-\kappa s}}{s+2r}$$ (3)

where

$$\begin{array}{l}Y=\frac{8\tanh \left(\frac{e{\psi }_0}{4k_{\text{B}}T}\right)}{1+{\left[1-\frac{2\kappa r+1}{{\left(\kappa r+1\right)}^2}+{\tanh }^2\left(\frac{e{\psi }_0}{4k_{B}T}\right)\right]}^{1/2}};\\ {\begin{array}{cc}{\psi }_0=\xi \left(1+\frac{1}{\kappa r}\right)\cdot \exp \left(1\right),& {\kappa }^{-1}=\left(\sqrt{\frac{2e^2{N}_{\text{A}}I}{\epsilon {\epsilon }_0{k}_{\text{B}}T}}\right)\end{array}}^{-1}\end{array}$$ (4)

ψ₀ is the surface potential, ξ is the zeta potential, e is the elementary charge, ε is the relative permittivity of water (78.54), ε₀ is the electric permittivity of free space, R is the gas constant, I is ionic strength (5 mM), and N_A is Avogadro’s number.

Upon 2-NT addition, both osmotic (Φ_osm) and elastic (Φ_elas) repulsive interaction potentials, which defend on monolayer thickness (t), were also included.^10,41 The monolayer thickness was determined using an extended molecular length of 0.93 nm⁴² and a 30° tilt angle.⁴² At large separation distances (s > 2t), Φ_osm(s) = 0. When t ≤ s ≤ 2t

$$\frac{{\Phi }_{\text{osm}}\left(s\right)}{k_{\text{B}}T}=\frac{4\pi a{N}_{\text{A}}}{{\upsilon }_1}{\varphi }_{\text{P}}{}^2\left(\frac{1}{2}-\chi \right){\left(t-\frac{s}{2}\right)}^2$$ (5)

where υ₁ is the molar volume of the solvent, χ is the Flory–Huggins interaction parameter (0.45 for a well-ordered monolayer),⁴³ and φ_P is the volume fraction of the ligand.

When s < t, ligand interactions cause elastic deformation and compression of ligand tails.^41,43 Thus, Φ_osm(s) and Φ_elas(s) are included as follows

$$\frac{{\Phi }_{\text{osm}}\left(s\right)}{k_{\text{B}}T}=\frac{4\pi a{N}_{\text{A}}}{{\upsilon }_1}{\varphi }_{\text{P}}{}^2\left(\frac{1}{2}-\chi \right)\left[t^2\left(\frac{s}{2t}-\frac{1}{4}-\ln \left(\frac{s}{t}\right)\right)\right]$$ (6)

$$\frac{{\Phi }_{\text{elas}}\left(s\right)}{k_{\text{B}}T}=\left(\frac{2\pi a{N}_{\text{A}}}{M_{\text{W}}}{\varphi }_{\text{P}}{t}^2{\rho }_{\text{d}}\right)\left(\left(\frac{s}{t}\right)\text{ln}\left(\frac{s}{t}{\left(\frac{3-\frac{s}{t}}{2}\right)}^2\right)\right)-6\ln \left(\frac{3-\frac{s}{t}}{2}\right)+3\left(1-\frac{s}{t}\right)$$ (7)

where M_w (160.24 g/mol) and ρ_d (1.22 g/cm³) are the molecular weight and density of pure 2-NT, respectively. The total interaction potential between a nanoparticle pair is the sum of all relevant interaction potentials.

Kinetic energy was calculated using collision theory. First, the Brownian motion of nanoparticles¹⁰ was determined by calculating the root-mean-square velocity

$$\langle v\rangle ={\left(\frac{8k_{\text{B}}T}{\pi \mu }\right)}^{0.5}$$ (8)

where k_B is the Boltzmann constant, T is the temperature, and μ is the reduced mass of the two objects. Next, the total number of collisions

$$z=4\pi r^2\langle v\rangle N\cdot t$$ (9)

between two nanoparticles was estimated (N is the number of nanoparticles and t is the duration time). Finally, the kinetic energy (KE_min) required for nanoparticle clusters to form was estimated from the probability that one inelastic collision would occur when

$$\frac{1}{z}={\text{e}}^{-{\text{KE}}_{\text{min}}/k_{\text{B}}T}\text{or}{\text{KE}}_{\text{min}}=-\ln \left(\frac{1}{z}\right)$$ (10)

RESULTS AND DISCUSSION

Dynamics and Kinetics of Cluster Formation.

The dynamics of cluster formation depends on the potential energy associated with the primary nanoparticles upon collision. Conventionally, experimentally relevant interaction potentials can be estimated for a pair of objects using DLVO and xDLVO theories¹⁰ coupled with collision theory. To estimate the attractive van der Waals interactions, a previously determined size-dependent Hamaker constant¹⁰ is used, while the electrostatic interaction potential arises from the nanoparticle surface potential [−49.5 (±0.4 mV)]. The sum of these two parameters leads to a total interaction potential that depends on separation distance. An example of these potentials is shown in Figure 2A for 13.6 nm gold nanospheres immersed in an aqueous solution with an ionic strength of 5 mM and a citrate concentration of 1 mM at 20 °C. The energy difference between the maximum energy versus that at long separation distances results in a potential energy barrier (V_max) of 56/k_BT, thereby suggesting these nanoparticles resist aggregation for long periods of time.

Figure 2.

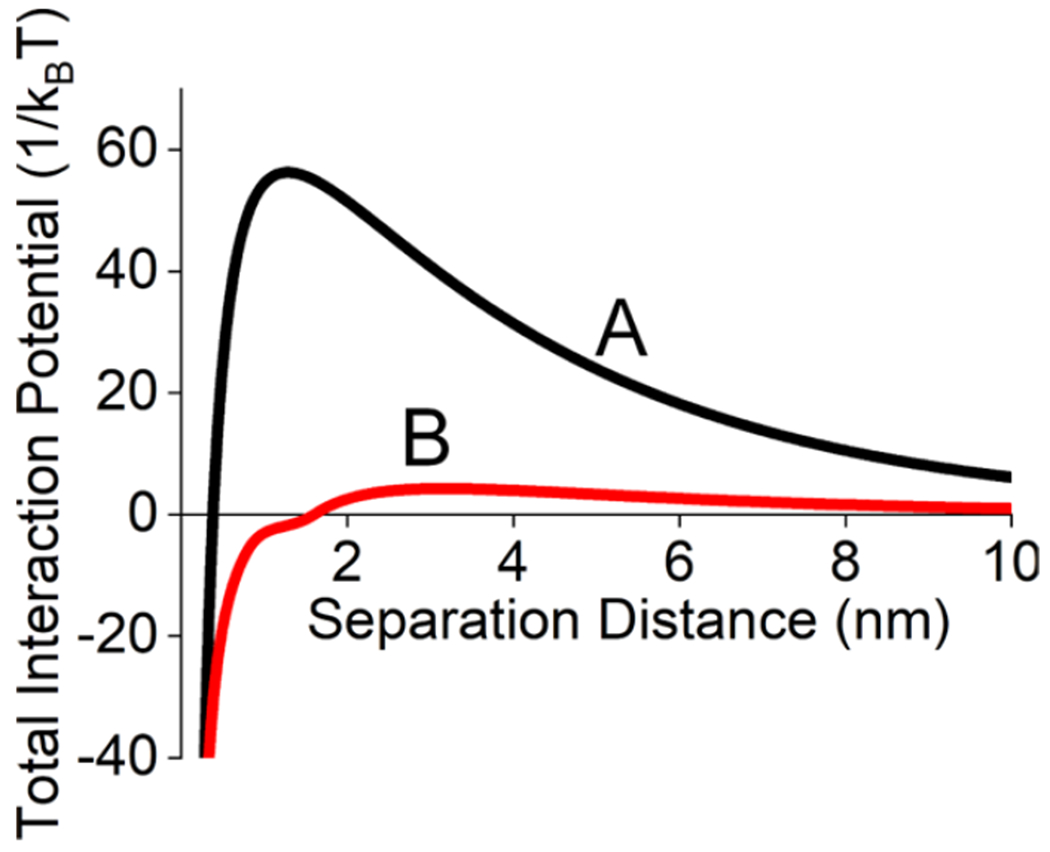
Total interaction pair potential between 13.6 nm gold nanospheres calculated using xDLVO theory (A) without and (B) with a 2-NT monolayer. Values used for modeling include the following: r = 6.8 nm, Hamaker constant = 3.7 × 10⁻¹⁹ J, zeta potential = −49.9 and −12 mV for A and B, ionic strength = 5 mM, molecular weight of ligand = 160.24 g/mol, density of pure ligand = 1.22 g/cm³, SAM packing density = 4.1 × 10¹⁴ molecules/cm², and SAM thickness = 0.93 nm × sin(60°) = 0.80₅ nm.

Upon 2-NT modification, SAM formation induces both repulsive elastic and osmotic potentials, and the electrostatic repulsive interaction potential decreases because the surface potential reduces in magnitude to −12.0 (±0.6) mV. As a result, V_max decreases to ~4/k_BT (Figure 2B). When kinetic energy exceeds this interaction potential energy, gold clusters are more likely to form upon nanostructure collision rather than respond elastically. The adsorption of 2-NT proceeds with increasing time. Thus, the probability of cluster formation increases as a monolayer forms because V_max decreases. Clusters that form in this time window follow a reaction-limited process as cluster formation depends on the rapid adsorption of 2-NT. Once a sufficient SAM layer has formed, diffusion-limited conditions where spectroscopic changes depend on cluster formation rather than surface modification are likely. For example, the nanoparticles in a 5 nM gold nanosphere solution (d = 13.6 nm) collide ~800 times per second with a kinetic energy of 6.7/k_BT. Because potential energy is ~8 times larger than the kinetic energy prior to 2-NT adsorption, the collisions have a low probability of resulting in cluster formation. The potential energy drops to less than the kinetic energy once a monolayer has formed. This leads to the onset of diffusion-limited cluster formation.

Previously and for a given nanoparticle concentration, reaction-limited and diffusion-limited regimes were shown to occur at low and high analyte concentrations, respectively.²² Relevant to the present study, the kinetics of cluster formation from SAM-functionalized nanospheres depends on the local medium and relative motion of the objects. Assuming two identical particles, A and B, where particle B moves with respect to particle A, collisions arise at a critical distance (r_AB) resulting in a cluster (A–B). This process can be described as an irreversible reaction: A + B → A – B because V_max is small. As such, the reaction rate (ρ) associated with cluster formation is as follows⁴⁴

$$\rho =4\pi r_{\text{AB}}{D}_{\text{AB}}{C}_{\text{B}}{C}_{\text{A}}$$ (11)

where D_AB is the diffusion coefficient of the cluster A–B (=D_A + D_B), and C_A and C_B are the concentrations of A and B, respectively. Upon substituting these parameters into the Stokes–Einstein equation,⁴⁵ the reaction rate (eq 11) becomes

$$\rho =4\pi r_{\text{AB}}\frac{k_{\text{B}}T}{3\pi \eta }\left(\frac{1}{r_{\text{H,A}}}+\frac{1}{r_{\text{H,B}}}\right)C_{\text{A}}{C}_{\text{B}}=\frac{4k_{\text{B}}T}{3\eta }{r}_{\text{AB}}\frac{2}{r_{\text{H}}}{C}_{\text{A}}{C}_{\text{B}}$$ (12)

where r_H is the hydrodynamic radius of the nanoparticles. Under diffusion-limited conditions, primary nanoparticles tend to collide inelastically with existing clusters rather than with other primary nanoparticles. Assuming A to be a primary nanoparticle and B to be a cluster whose concentration remains ~constant, eq 12 becomes pseudo-first order with respect to C_nanoparticle and exhibits a rate constant (k, molecule/s) of $\frac{8k_{\text{B}}T}{3\eta }\frac{r_{\text{AB}}}{r_{\text{H}}}{C}_{\text{cluster}}$. This indicates that the rate constant associated with cluster growth depends on primary nanosphere concentration and the radius of the nanostructures. As a result, the kinetics of cluster formation should correlate with collision frequency and have correlated effects on LSPR and SERS in the diffusion-limited regime (vide infra).

Impact of Cluster Formation on LSPR and SERS Responses.

When clusters form, average inter-nanoparticle distances decrease leading to the formation of strong electric fields between nanoparticles.^1,3,7,25 The magnitude of resulting SERS enhancements depends on inter-nanoparticle distance, a parameter that is difficult to control for clusters that form in solution. To combat this, 2-NT is used, and time-dependent LSPR and SERS data are simultaneously monitored so that impacts on the dynamics and kinetics of cluster formation can be ascertained. Because different regions of LSPR spectra are sensitive to both local refractive index changes and cluster formation, selected flocculation area analysis can be used for correlation to cluster formation dynamics and kinetics.

To monitor the time-dependent formation of clusters under both reaction and diffusion-limited reaction conditions, an excess of 2-NT is added to 5 nM gold nanospheres (d = 13.6 nm). Three-dimensional (3D) waterfall maps associated with time-dependent LSPR and SERS spectra for 5 nM gold nanospheres (d = 13.6 nm) before and after addition of excess 2-NT are shown in Figure 3A,B, respectively. Three observations are noted. First, the dipole resonance associated with primary nanoparticles, centered at ~520 nm, redshifts slightly and decreases in magnitude with increasing time. Second, a new extinction band associated with electromagnetic coupling between clusters of nanospheres is observed at longer wavelengths (~720 nm). Finally, all vibrational mode intensities associated with 2-NT (assignments found in Table S1) vary with time, and the most intense mode at 1067 cm⁻¹ (combination mode associated with ring breathing + in-plane C–H bending + ring stretching) is representative of the time-dependent spectral changes observed for all vibrational modes.

Figure 3.

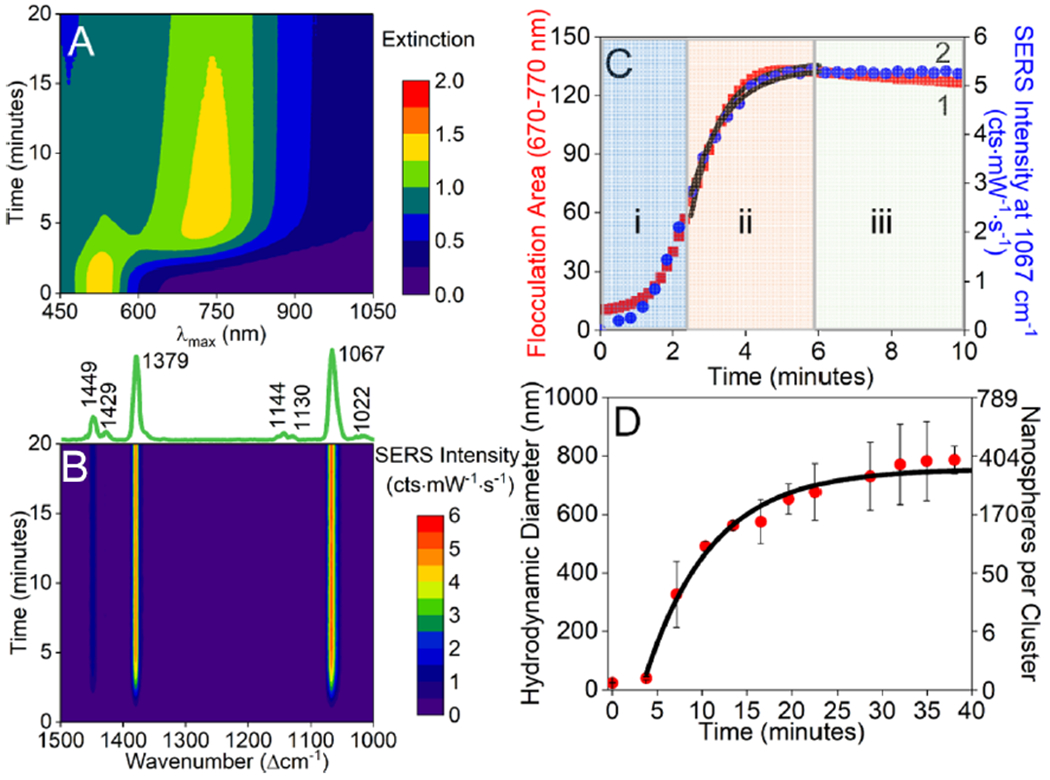
Waterfall maps of time-dependent (A) LSPR and (B) SERS spectra of 5 nM gold nanospheres (d = 13.6 nm) before and after addition of 27.0 μM 2-NT. SERS experimental conditions: λ_ex = 785 nm, t_int = 20 s, P = 83.3 mW. Detailed assignments for all SERS bands can be found in Table S1 in Supporting Information. (C) Time-dependent (1) LSPR flocculation area analysis (from 670 to 770 nm) and (2) SERS intensity of the 1067 cm⁻¹ band. Zones i, ii, and iii represent kinetics driven by SAM formation, cluster formation, and other processes, respectively. Data in zone ii were fit using eq 13. (D) Time-dependent hydrodynamic diameter associated with 5 nM gold nanospheres (d = 13.6 nm) after the addition of 27.0 μM 2-NT. The black solid line illustrates the self-limiting cluster model. The right y axis represents calculated values for the number of nanospheres per cluster.

Figure 3C compares time-dependent SERS signals to the low-energy plasmon signal (integrated area from 670 to 770 nm). Initially, both data sets reveal a short ~2.5 min lag time, a window in which reaction-limited conditions (zone i) and rapid SAM formation occur. As such, both LSPR and SERS responses follow reaction-limited kinetics²² (S = S₀e^kt where S₀ is the initial signal, S is the time-dependent signal, and k is the rate constant). Resulting rate constants for the two spectroscopic methods are similar and vary from 1.68 (±0.10) to 1.07 (±0.29) min⁻¹, respectively. As surface modification proceeds, diffusion-limited reaction conditions begin to govern dynamics and because the interaction pair potential between nanoparticles decreases, clusters form (zone ii). Upon reaching diffusion-limited conditions, both LSPR and SERS responses increase rapidly with increasing incubation time, a response consistent with the self-limiting cluster model,⁴⁶ and rate constants associated with cluster formation can be extracted by calculating the time-dependent cluster size (d_t) as follows

$$d_t=d_{\max }-\left(d_{\max }-d_0\right){\text{e}}^{-kt}$$ (13)

where d₀ is the primary nanoparticle diameter and k is the first-order growth rate constant. Rate constants are extracted from the data collected between 2.5 and 6 min in Figure 3C.

This analysis reveals cluster formation rate constants of 1.1 (±0.1) (LSPR) and 0.9 (±0.1) (SERS) min⁻¹, indicating similar dependencies on cluster growth formation for the two techniques. The rate constant for data collected in this same regime using DLS (Figure 3D) is slightly larger at 1.58 min⁻¹. This is reasonable given DLS measurements are less influenced by plasmonic losses than the other two spectroscopic measurements. The diffusion-limited regime ends at ~6 min. LSPR and SERS data collected during the third postdiffusion limited regime (zone iii) are influenced by processes such as sedimentation and optical losses. As shown in Figure 3C, the LSPR signal slowly decays with longer incubation times, while SERS signals do not significantly change. This behavior can be understood in terms of impacts of cluster sedimentation on the measurements and as a result, a decrease in the optical cross section of the clusters in the light path. It should be noted that LSPR and SERS data are collected at the top and middle of the sample cuvette, respectively. As such, LSPR data are more influenced by sedimentation than SERS.⁴⁶

To extract impacts of sedimentation, relative values of diffusion (v_D) and sedimentation velocities (v_sed) of relevant clusters⁴⁷ are calculated. Initially, diffusion velocity is the dominant mechanism driving cluster motion and is described as follows

$$v_{\text{D}}=\frac{2k_{\text{B}}T}{3\pi \eta x{d}_{\text{h}}}$$ (14)

where x is the net displacement of a cluster. Later, sedimentation velocity drives motion and is described as follows

$$v_{\text{s}}=\frac{2g\left({\rho }_{\text{Au}}-{\rho }_{\text{m}}\right)d_{\text{h}}{}^2}{9\eta }$$ (15)

where g is the gravitational constant (9.8 m/s²), ρ_Au is the density of gold in the clusters (1.77 × 10⁴ kg/m³), ρ_m is the density of the medium (1000 kg/m³), η is the viscosity of the medium (8.9 × 10⁻⁴ kg/m·s), and d_h is the hydrodynamic cluster diameter (m). When the hydrodynamic diameters of the objects are equal (~325 nm as shown in Figure S1), sedimentation influences cluster motion (primary nanosphere d = 13.6 nm). As indicated in the LSPR flocculation area analysis, this occurs after ~6 min (Figure 3C–1).

Of the three techniques, DLS remains the most effective way of quantifying the average cluster size⁴⁸ and as a result, number of primary nanostructures per cluster. To do this, time-dependent hydrodynamic diameters are shown in Figure 3D along with analysis using the self-limiting cluster model. A maximum cluster size (i.e., self-limiting cluster diameter, d_max) of 760 ± 40 nm is revealed from this analysis. Because clusters are three-dimensional and change in size rapidly with time, microscopic methods such as TEM provided limited information regarding the number of primary nanoparticles per cluster. As such, a theoretical approach is utilized to do so where we use a hydrated primary nanoparticle diameter of 38.5 (±3.0) nm (from DLS) and assume an average packing density of 4.5%.³¹ These values are included as a second y-axis in Figure 3D and reveal that ~340 primary nanoparticles are present in each cluster upon reaching the average self-limiting cluster size. Furthermore, we can estimate the number of primary nanoparticles present at the end of diffusion-limited kinetic regime (t = 6 min). Using the self-limiting cluster model, each cluster contains ~3 primary nanoparticles (i.e., nanospheres). Of note, the separation distance between primary nanospheres is limited by ~2 times the SAM thickness or ~1.6 nm (~2 × 0.81 nm for 2-NT on gold).¹⁰ While the number of nanoparticles per cluster continues to increase, the ensemble-averaged SERS signal does not dramatically change, a result consistent with previous reports that suggest SERS enhancements are largest for dimers and trimers and that radiative and scattering losses occur for larger clusters.²³

Manipulating Kinetics of Cluster Formation Using Primary Nanosphere Concentration and Diameter.

Previously, SERS intensity was shown to depend on the number of nanospheres per cluster.^1,23 As clusters grow from one to a few nanoparticles per cluster, increasing electric field strength with minimal losses causes the SERS intensity to increase. Larger clusters, however, exhibit diminished SERS signals because of plasmon damping,²⁴ other radiative losses, and sedimentation when solution-phase nanostructures are used. Because both primary nanoparticle concentration and diameter influence these phenomena, we explore these effects as a function of primary nanosphere size and concentration. In all cases, photothermal effects have been minimized by continuously mixing the samples in a high thermal conductivity medium (i.e., water, 0.56 W/m/K). This is supported by similar rate constants measured using DLS, LSPR, and SERS. This is significant given the power densities used in SERS exceeds 2–3 mW/cm², where photothermal effects become noticeable.^49,50

First, we investigate how primary nanosphere concentration influences cluster formation and as a result, LSPR responses and SERS activity. To do so, gold nanospheres with an average diameter of 13.6 (±1.1) nm and concentrations ranging from 0.5 to 5.0 nM are used. Above 5 nM, reabsorption significantly biased the measurements; therefore, they were not included in this analysis. In all cases, an excess of 2-NT is added. Both LSPR and SERS spectra are collected so that time-dependent trends in the reaction-limited and diffusion-limited regimes could be studied. These data are summarized in Figure 4A/4C,4B/4D for LSPR and SERS, respectively. Flocculation areas and SERS intensities are plotted versus time.

Figure 4.

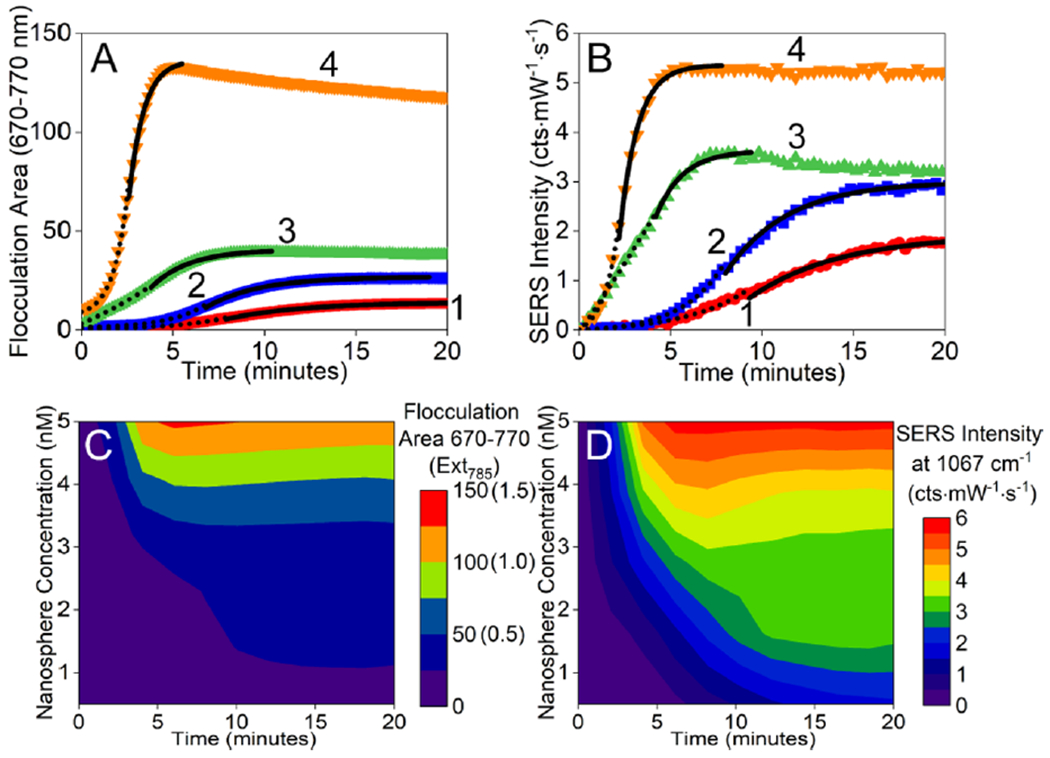
(A) Time-dependent flocculation area calculated from LSPR spectra upon adding excess 2-NT to (1) 0.5, (2) 1, (3) 3, and (4) 5 nM 13.6 nm gold nanospheres. (B) Time-dependent SERS intensity of the 1067 cm-1 band upon adding excess 2-NT to (1) 0.5, (2) 1, (3) 3, and (4) 5 nM 13.6 nm gold nanospheres. The dotted and solid lines represent analysis of reaction-limited and diffusion-limited regimes, respectively. Waterfall maps of (C) LSPR flocculation area 670–770 nm (and extinction at 785 nm) and (D) SERS intensity at 1067 cm⁻¹ as a function of time and nanoparticle concentration. Same data collection parameters used in Figure 3 unless noted.

Several trends are noted. First, the window in which reaction-limited kinetics occur, as indicated from LSPR flocculation analysis, decreases from 8.0 to 2.5 min with increasing nanosphere concentration (Figure 4A). A similar result is observed with SERS where these same values range from 9.3 to 2.2 min (Figure 4B). Because the adsorption rate of 2-NT onto gold is independent of nanosphere concentration, this variation in time is likely governed by both collision frequency, which depends on nanosphere concentration, as well as interaction pair potential energy, which decreases with increasing surface modification. As nanosphere concentration increases from 0.5 to 5 nM, the total number of collisions per second increases by an order of magnitude (from 80 to 800 collisions/s, eq 9), but these collisions are occurring at the same time when ligand density increases, which causes the interaction pair potential energy to decrease. As a result, the time reaction-limited conditions are observed decreasing with increasing nanosphere concentration. Second, increasing nanosphere concentration from 0.5 to 5 nM causes the window in which diffusion-limited kinetics to decrease by 10.5 (13.6 to 3.1 min) and 13.4 min (19.0 to 5.6 min) for LSPR and SERS, respectively. These ranges are noted in Figure 4A,B as solid lines and were determined using the self-limiting size cluster model. While values differ slightly between the two spectroscopic methods, a decrease in the diffusion-limited time window with increasing nanoparticle concentration is reasonable given their dependence on collision frequency. Third and related to the previous observation, the rate at which clusters form increases from 0.29 (±0.08) to 1.13 (±0.10) min⁻¹ when nanosphere concentration increases from 0.5 to 5.0 nM. Only data collected in the diffusion-limited time regime were used to quantify these differences. These values, which are calculated using the self-limiting cluster size model and LSPR data, are similar to those extracted from SERS data (0.24 (±0.05) to 0.85 (±0.14) min⁻¹). Slight differences in magnitude can be attributed to variations in extinction coefficients for growing clusters (LSPR) and the magnitude of electric fields that influence the overall SERS signal.

Three-dimensional waterfall plots for both LSPR flocculation area (Figure 4C) and SERS intensity (Figure 4D) reveal correlated effects as a function of nanosphere concentration and time. Two similarities are noted. First and when considering low nanosphere concentrations, both spectroscopic signals increase and then saturate with increasing time. This observation can be explained using collision theory and relative energy differences between the kinetic energy associated with particle motion and the potential energy as quantified using xDLVO theory. From eq 12, the rate constant of cluster formation depends on particle concentration, which is directly related to collision frequency if kinetic energy exceeds potential energy (V_max). Consequently, clusters form and grow. This leads to an increase in both LSPR flocculation area and SERS signals. It should be noted that cluster sedimentation is most apparent for only the highest nanoparticle concentration studied. This occurs only when the sedimentation velocity of clusters exceeds that of cluster diffusion (see Figure S2 for DLS confirmation). Second, when nanosphere concentration exceeds ~3.5 nM, both spectroscopic signals reach a maximum and then decay slightly. This decay occurs after the diffusion-limited regime, where plasmonic losses and/or sedimentation influence systematic spectroscopic responses. It should be noted that the SERS signal only minimally degrades. This is likely because smaller clusters contribute the most to ensemble averaged measurements,²³ and these small clusters grow but remain stably suspended in solution for the duration of the measurement.

The impact of nanosphere size, another parameter that should influence collision frequency, cluster formation, and SERS, is shown in Figure 5. Object size becomes important as collision frequency depends on the collisional cross-sectional area associated with objects in solution. As the diameter increases, both cross-sectional area and reduced mass increase while diffusion velocity decreases. Upon combining eqs 8 and 9, the relationship between collision frequency and cluster size can be developed as follows

$$\text{frequency}\alpha 4\pi r^2{\left(\frac{8k_{\text{B}}T}{\pi \mu }\right)}^{0.5}=4\pi r^2{\left(\frac{8k_{\text{B}}T}{\pi \rho \frac{4}{3}\pi r^3}\right)}^{0.5}\alpha r^{0.5}$$ (16)

As such, increases in kinetic energy scale with the square root of cluster radius. Similar effects are also expected when the size (i.e., diameter) of gold nanospheres is varied but concentration is maintained.

Figure 5.

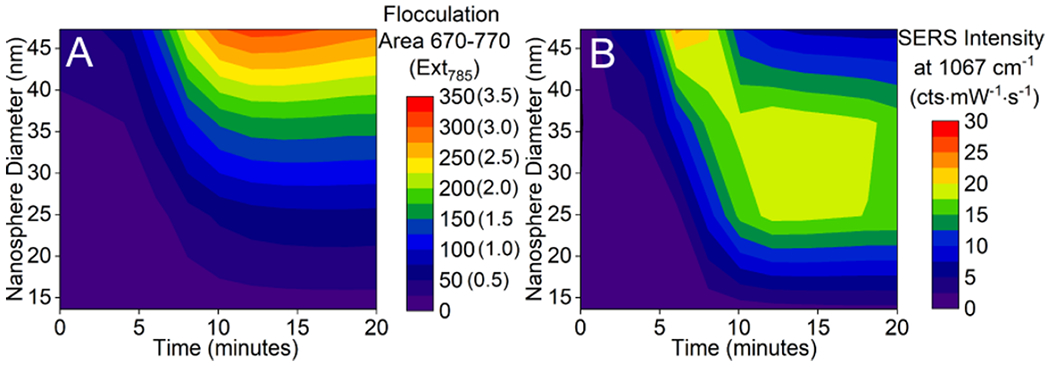
Waterfall plots of time-dependent (A) LSPR flocculation area from 670 to 770 nm (and extinction at 785 nm) and (B) SERS intensity at 1067 cm⁻¹ as a function of nanosphere diameter. Same data collection parameters are used in Figure 3 unless noted.

To evaluate these effects, 0.5 nM gold nanospheres with diameters ranging from 13.6 to 47.3 nm are incubated with an excess of 2-NT, and correlated LSPR and SERS spectra are collected (Figures S3, S4, and S5). Time-dependent trends in flocculation area (integrated area from 670 to 770 nm) or extinction magnitude at the SERS excitation wavelength (785 nm) and SERS intensity (example shown for 1067 cm⁻¹) are shown in Figure 5A,B, respectively. These waterfall plots clearly demonstrate that variations in primary nanoparticle diameter have different kinetic effects on LSPR and SERS responses. To understand these differences, we first evaluate plasmonic effects. In general, flocculation area increases with increasing nanosphere diameter, a response that correlates with variations in extinction cross section.⁵¹ Losses from sedimentation and reabsorption or scattering are apparent when primary nanosphere diameter exceeds ~30 nm.

Similar trends are observed in the correlated LSPR and SERS results for the smallest nanospheres only as these responses depend solely on the number of primary nanoparticles per cluster. The SERS responses from larger primary nanospheres and their resulting clusters are also impacted by plasmon damping through radiation or scattering losses. For instance, SERS responses for 27.7 nm gold nanospheres initially increase and correlate with the number of clusters present in solution and/or cluster formation. After ~12 min, SERS signals saturate and then begin to decrease. Using DLS (Figure S6A), the number of primary nanostructures per cluster at 12 min is ~2–3. After 12 min, the extinction magnitude at the excitation wavelength exceeds 1.5; therefore, we attribute the decrease in SERS signal with longer times to radiation or scattering losses. As the primary nanoparticle diameter increases, the time to reach a maximized SERS signal decreases. This is most apparent for the largest primary nanoparticles studied (d = 47.3 nm). As with the smaller nanospheres, a maximum signal is observed when the number of primary particles per cluster is ~2—3 (per DLS, Figure S6B). After longer incubation times, effects from both sedimentation and plasmonic losses are likely. This is indicated from a decrease in flocculation area as well as extinction magnitude, which well exceeds 1.5 at the excitation wavelength.

Experimental rate constants of cluster formation obtained from LSPR and SERS increase from 0.29 (±0.08) to 0.42 (±0.07) min⁻¹ and from 0.24 (±0.05) to 0.53 (±0.01) min⁻¹, respectively, as primary nanosphere diameter increases. These values are obtained using the self-limiting cluster formation model in the diffusion-limited regime (Figure S7). It is important to note that the rapid kinetics of cluster formation from large versus small primary nanoparticles is predicted from collision theory. While diffusion coefficients for the primary nanoparticles decrease with increasing dimension, collisions still occur rapidly (~150 collisions/s vs ~80 collisions/s for the largest and smallest nanostructure studied, respectively). Consequently, cluster formation increases in probability as object size increases assuming the kinetic energy associated with a collision is greater than the interaction pair potential energy.

CONCLUSIONS

In summary, the dynamics and kinetics of cluster formation from gold nanospheres were evaluated using DLS, LSPR, and SERS spectroscopies as well as modeled using xDLVO and collision theories. Growth rates associated with cluster formation influenced each spectroscopic technique. By adding an excess of the ligand, 2-naphthalenethiol, monolayer formation occurred rapidly and clusters subsequently formed under diffusion-limited conditions with loosely packed fractal geometries. Two major conclusions are noted. First, cluster formation followed the self-limiting cluster model. As such, rate constants associated with cluster formation could be quantified. These values were directly related to both nanosphere concentration and size. Increasing nanosphere concentration caused the rate of cluster formation to increase and decreased the time required for maximum SERS enhancements. These variations were attributed to an increase in collision frequency. Increasing nanosphere diameter exhibited similar effects. Second, DLS, LSPR, and SERS data revealed similar kinetics during the diffusion-limited cluster growth regime. DLS measurements facilitated the extraction of cluster size, while LSPR and SERS showed dependencies on sedimentation and plasmonic losses, respectively. In all cases, collision frequency during cluster formation was shown to affect time-dependent SERS responses. It should be noted that primary nanoparticle diffusion coefficients played only a minor role in the time-dependent spectroscopic changes. As such, these variables should be considered when balancing SERS enhancements and reproducibility when clusters are used as SERS substrates and an excess of molecules are added relative to available binding sites.