Sex-specific growth, shape, and their impacts on the life history of a long-lived vertebrate

Abstract

Background:

Individual growth rates both comprise and determine life-history phenotypes. Despite decades of interest in understanding the relationship between individual growth and life history, chelonian longevity has limited our ability to robustly estimate individual growth curves that span the life of both sexes.

Questions:

(1) Do patterns of growth in size and shape differ between the sexes of the painted turtle, Chrysemys picta? (2) Does individual variation in size and shape affect female reproductive effort?

Methods:

Using 30 years of field data on shell morphology of a single population of painted turtles, we used principal components analysis to summarize multivariate size and shape. We assessed the ability of three non-linear growth models – the logistic, Gompertz, and von Bertalanffy – to predict size-at-age and used model comparison to justify sex-specific model fits. We correlated age-specific size and shape of females with their reproductive efforts.

Results:

Model comparison supported separate fits of the von Bertalanffy growth function for each sex; non-overlapping confidence intervals imply differences in sex-specific asymptotic size, but not growth rate. Higher-order axes of variation in shell morphology described significant sexual dimorphism in shell shape related to the sphericity and curviness of the shell. Shell sphericity of females covaried with clutch size, mean egg mass, and total clutch mass. Irrespective of shell morphology, we found evidence of an egg number versus egg mass trade-off. Yet, females who matured at a larger size produced greater reproductive efforts.

INTRODUCTION

A long-standing assumption in life-history theory is that larger individuals should have higher fitness than smaller individuals, provided that the advantages of being large are not outweighed by fitness costs (Charlesworth, 1994). Adult body size often positively relates to components of reproductive success such as clutch size, birth weight, and maturation time (reviewed in Roff, 1992). Thus, all things equal, individuals are expected to quickly attain a large size, mature early, and begin reproducing as soon as their development allows. Our ability to test this assumption in long-lived organisms has been hampered by their longevity and the need for long-term studies of such species (Clutton-Brock and Sheldon, 2010). Moreover, our understanding of the life histories of long-lived species in general, and the trajectories of age-specific vital rates, is limited by insufficient knowledge of individual growth rates and therefore the relationship between an individual’s size and age. This is particularly true for species with indeterminate growth that are followed with capture-mark-recapture protocols. In such species, understanding how size, age, growth, maturation, reproduction, and survival relate to each other, and how these relationships differ between the sexes requires sustained observational effort across the lifespan of individuals.

An added complexity to understanding the relationship between body size and fitness is that animals with indeterminate growth may continue growing over their lifespans, or at least well past maturation, which further impacts the size–fitness relationship. An ecological model organism for testing the assumption that bigger is better, and testing whether the relationship differs between the sexes, can be found in painted turtles (Chrysemys picta). Painted turtles live to about 25 years, experience non-linear, indeterminate growth (Congdon et al., 2013), and have long been studied for their size, growth, and survival during the juvenile stage (e.g. Pearse, 1923; Paitz et al., 2007). Juveniles grow rapidly, but growth slows as maturity is reached and continues at a fraction of previous rates for the remainder of a turtle’s life (e.g. Wilbur, 1975). However, turtles also exhibit plasticity in growth parameters (e.g. age and size at maturity) in response to predatory and anthropogenic pressures (Spencer et al., 2006; Spencer and Janzen, 2010). And, despite the absence of sex chromosomes, male and female painted turtles mature at different ages [e.g. 4 years for males and 5–7 years for females (Schwanz et al., 2010; Spencer and Janzen, 2010)] and express many sexually dimorphic traits throughout their lifetime. Studies of early-life effects of body size (and therefore growth) have suggested that larger individuals have higher probability of survival (e.g. Brodie and Janzen, 1996; Paitz et al., 2007; Janzen and Warner, 2009; Mitchell et al., 2013) and may mature earlier (Roosenberg and Kelley, 1996). Thus, many models have been used to predict growth of turtles, including the logistic, Gompertz, and von Bertalanffy growth functions (e.g. Wilbur, 1975; Rickard et al., 1989; Frazer et al., 1991). Application of these models is typical for many animal species to inform population management (see Ogle, 2016a), but can also be used to parameterize quantitative genetic models for the study of life-history evolution and the inheritance of body size, growth, and fitness (sensu Gomulkiewicz et al., 2018).

To assist in filling this gap in our knowledge of growth, size, age, and fitness in a long-lived species, we ask here the question of how these traits (growth, size, age, and reproduction) impact fitness in a long-term study of painted turtles as a model ectothermic vertebrate. We have three specific goals under the overarching theme of how growth impacts fitness: (1) to test for significant variation in sex-specific growth in size and shape in a long-lived species; (2) to test for impacts of age-specific size and shape variation on female reproductive effort (our proxy for fitness) to better understand targets of natural selection on the life histories of longevous vertebrates; and (3) to highlight the value of long-term field studies by leveraging 30 years of intensive mark-recapture and repeated fitness measures, and making these data publicly available.

METHODS

Field site and data collection

Our data have been collected over 30 years, using capture-mark-recapture in a single population of painted turtles inhabiting the backwaters of the Mississippi River near Thomson Causeway Recreation Area (TCRA) in Thomson, IL, USA (‘all turtles’, Table 1). Females were captured while nesting terrestrially and turtles of both sexes were captured with aquatic traps in the adjacent slough. Individuals were marked by filing or drilling unique combinations of the marginal scutes (Cagle, 1939). For each capture, straight measurements of the carapace length (SCL), carapace width (SCW), plastron length (PL), and plastron width (PW) were taken using digital callipers and recorded to the nearest millimetre. Curved measurements of carapace length (CCL) and carapace width (CCW) were taken with a cloth tape measure and also recorded to the nearest millimetre.

Table 1.

Summary statistics for the capture-mark-recapture dataset and the four partitions used to analyse size, shape, and female reproductive effort

Dataset	No. of females	No. of males	Figures(s)	Table(s)
All turtles	1681	1273	—	—
Observed-age1	446	145	1, 2	2, 3, 4, 5, 6, 7
Post-maturation2	824	858	3, 4, 5	3, 4, 8
Nesting females	1140	—	7	3, 4, 9
Primiparous females	38	—	—	3, 4, 10, 11

¹Includes all capture records with a known age.

²Includes all capture records where PC1 exceeded the estimated asymptotic size.

Observed age was assigned using the number of ridges (i.e. growth rings) on the pectoral scutes, which are laid down annually. Growth ring counts are a reliable method of ageing painted turtles into young adulthood (reviewed in Wilson et al., 2003). In this population, males and females achieve maturity at different ages: 5–7 years for females and 3–5 years for males (Schwanz et al., 2010); and growth rings are visible up to 8–10 years. Primiparity was assigned sensu Warner et al. (2016). From a single observation of young (known) age, we assigned age to the remainder of an individual’s capture records. In this way, we identified 140 males of known age, with an average of 1.2 records per individual, and 446 females of known age, with an average of 3.6 records per individual (‘observed-age’ dataset, Table 1). The ‘observed-age’ dataset was used to model growth and to test for the effects of sex and age on body shape and size. Using estimates of size-at-maturity from the ‘observed-age’ dataset, we also categorized ‘all turtles’ as pre or post maturation regardless of having an observed age (‘post-maturation’ dataset, Table 1), thus providing a larger sample size to power tests of sex-specific differences in adult shape (see ‘Analysis of shape’, below).

To estimate female reproductive effort, nests were immediately excavated following oviposition. Eggs were counted and weighed to the nearest milligram and any damage to eggs was indicated prior to replacing the clutch in the nest. The female reproductive dataset was used in two different ways. First, regardless of known age, capture records from all nesting females (‘nesting females’ dataset, Table 1) were used to evaluate patterns of covariation in size, shape, and reproductive effort. To more explicitly evaluate age-specific effects of variation in shell size and shape, we also focused on a subset of nesting females for which we had: (1) reproductive records at primiparity, (2) at least two additional years of reproductive records, and (3) a minimum inter-nesting interval of 2 years (‘primiparous females’ dataset, Table 1). This dataset includes females with the most complete and contiguous estimates of reproductive effort.

Principal components analysis

For all datasets listed in Table 1, we centred and log-transformed the six, highly correlated morphological measurements (see Table 2). To ensure that different subsetting of ‘all turtles’ did not affect the orthogonality of the principal components, we independently calculated the principal components for each subset. For all datasets, because the morphological measures were similarly scaled, we calculated principal components using the covariance matrix. For all analyses, the first principal component (PC1) explained at least 81.4% of the variation in shell morphology (Table 3). Furthermore, all six measures loaded similarly onto PC1 (Table 4), justifying its use as a single measure of multivariate size for modelling growth. To assist in the biological interpretation of principal components, we compared congruence of their explanatory power, as well as the rotations and loadings of shell morphology measures among the different datasets (Tables 3 and 4). Finally, we plotted relevant lower-dimensional contrasts to aid interpretation of higher principal components (Figs. 3, 4).

Table 2.

Pearson’s correlation matrix for six measurements of the painted turtle shell from ‘observed-age’ turtles

	CCL	CCW	SCL	SCW	PL	PW
CCL	1.00
CCW	0.97	1.00
SCL	0.99	0.96	1.00
SCW	0.95	0.96	0.96	1.00
PL	0.98	0.96	0.99	0.96	1.00
PW	0.95	0.94	0.96	0.96	0.96	1.00

Note: All variables were log-transformed and correlations were significant at P < 0.001. These correlations are representative of those found across all datasets listed in Table 1 and used for analysis of size and shape. CCL = curved carapace length, CCW = curved carapace width, SCL = straight carapace length, SCW = straight carapace width, PL = plastron length, PW = plastron width.

Table 3.

The percent variance explained by the first three principal components of all datasets

Dataset	Trait	% variance explained
Observed-age	PC1 (size)	97.2
	PC2 (sphericity)	1.1
	PC3 (curvature)	0.9
Post-maturation	PC1 (size)	94.6
	PC2 (sphericity)	2.2
	PC3 (curvature)	1.6
Nesting females	PC1 (size)	87.1
	PC2 (sphericity)	5.5
	PC3 (curvature)	4.0
Primiparous females	PC1 (size)	81.4
	PC2 (sphericity)	8.5
	PC3 (curvature)	5.6

Table 4.

Principal components analysis of all turtles with known age. Loading of predictors onto the first three principal components

Dataset	Trait	PC1 (size)	PC2 (sphericity)	PC3 (curvature)
Observed-age	CCL	−0.43	0.43	0.08
	CCW	−0.43	−0.25	0.80
	SCL	−0.43	0.37	−0.15
	SCW	−0.34	−0.54	−0.04
	PL	−0.44	0.29	−0.23
	PW	−0.36	−0.49	−0.54
Post-maturation	CCL	−0.40	−0.45	0.15
	CCW	−0.50	0.41	0.71
	SCL	−0.38	−0.45	−0.07
	SCW	−0.36	0.43	−0.24
	PL	−0.42	−0.34	−0.18
	PW	−0.37	0.36	−0.61
Nesting females	CCL	−0.43	0.42	−0.01
	CCW	−0.45	−0.12	−0.83
	SCL	−0.42	0.35	0.19
	SCW	−0.37	−0.52	0.04
	PL	−0.42	0.29	0.33
	PW	−0.35	−0.58	0.41
Primiparous females	CCL	−0.51	0.46	−0.32
	CCW	−0.51	−0.60	−0.51
	SCL	−0.46	0.31	0.08
	SCW	−0.28	−0.48	0.41
	PL	−0.39	0.27	0.40
	PW	−0.22	−0.19	0.54

Note: CCL = curved carapace length, CCW = curved carapace width, SCL = straight carapace length, SCW = straight carapace width, PL = plastron length, PW = plastron width.

Fig. 3.

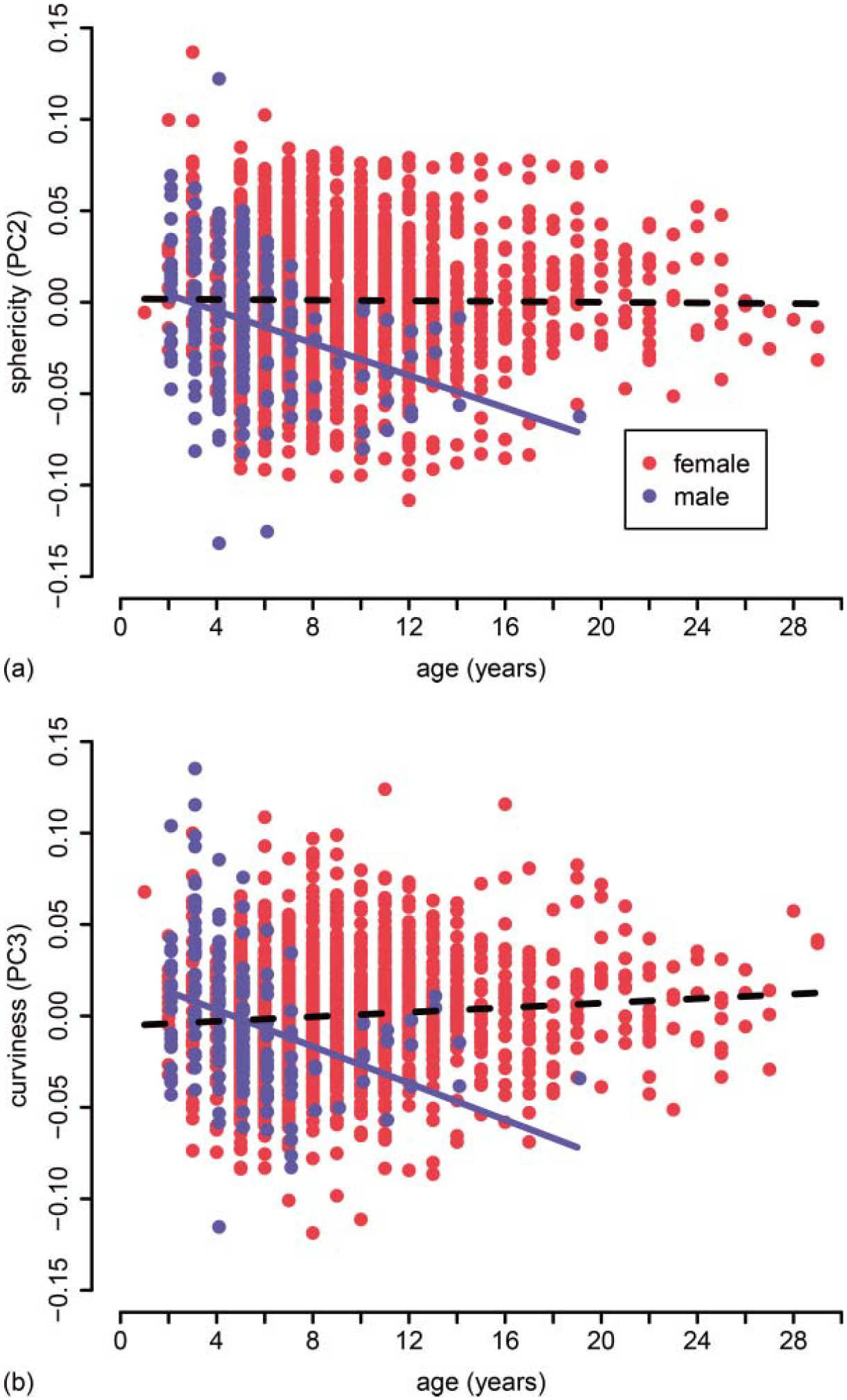
Relative shell sphericity (PC2, a) and shell curvature (PC3, b) decrease with age in males (blue dots and line), but not females (red dots and dashed line). Solid lines indicate significant slopes.

Fig. 4.

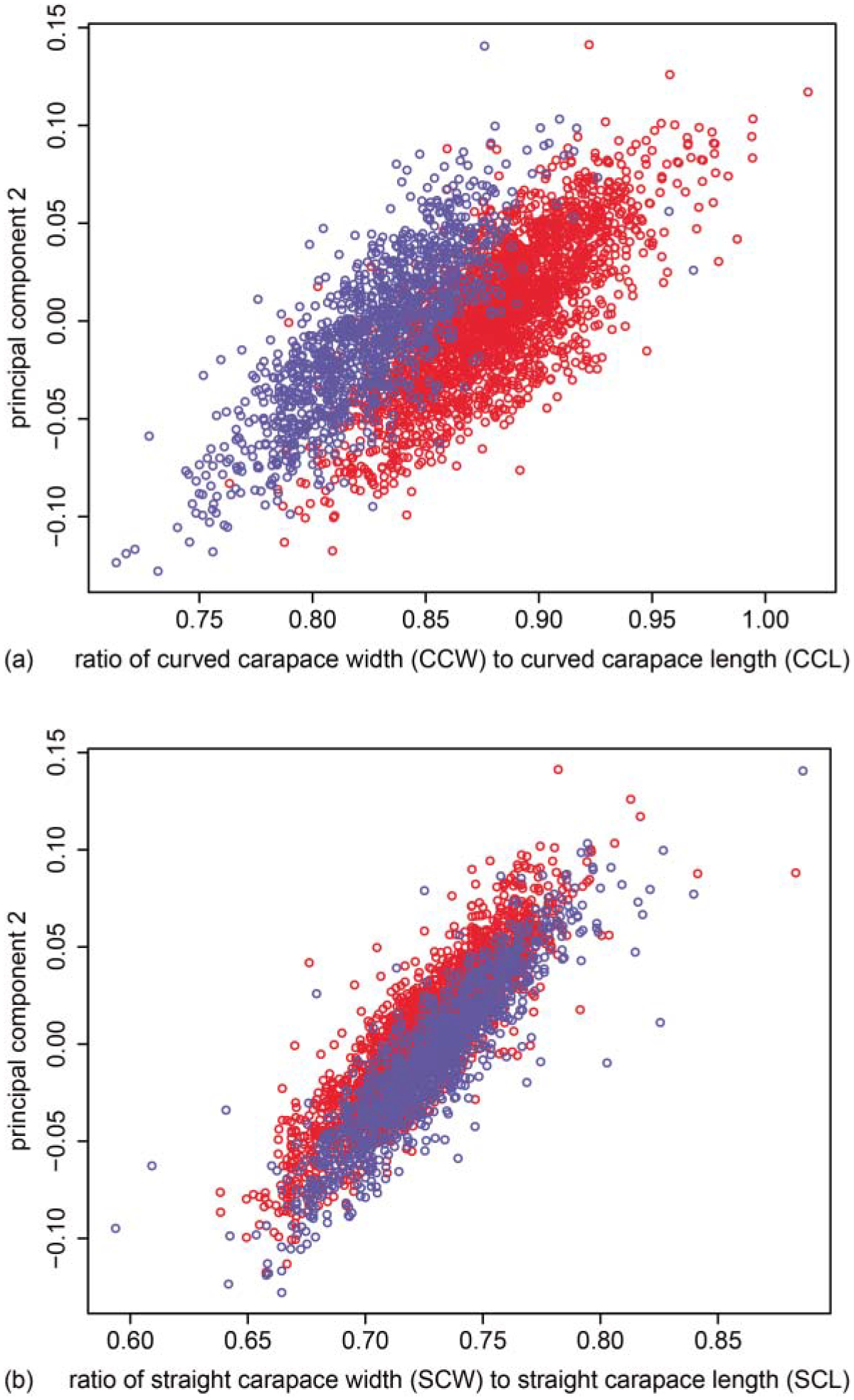
PC2 summarizes the contrast between the relative length of the shell and the relative width of the shell. (a) PC2 was highly correlated (r = 0.68, P < 0.001) with a measure of the relative curved width of the shell along the dorsoventral axis (CCW/CCL) in adult female (red) and male (blue) painted turtles. Note that the non-overlapping distribution of PC2 (y-axis) among the sexes likely underlies the sex-specific effects reported for PC2 in Table 7. (b) PC2 was also highly correlated (r = 0.87, P < 0.001) with a measure of the relative straight width of the shell (SCW/SCL) along the anterior-posterior axis, indicative of the multiple dimensions of shape summarized by PC2, but not a distinguishing factor among the sexes.

Growth modelling of observed-age turtles

A mean-length analysis of growth for ages 0–29 years (‘observed-age’ dataset; Fig. 1) indicated that, although male and female turtles hatch at similar size and grow at similar rates, females continue their exponential growth phase longer and attain larger adult sizes than males. This sex-specific pattern of growth suggested that our modelling of individual growth should be done separately by sex. Thus, we modelled individual growth using the Fisheries Stock Assessment (FSA) package in R (Ogle, 2016b). This package provided a convenient framework to fit non-linear growth functions and perform model comparisons using the Akaike Information Criterion (AIC). Three asymptotic growth models – logistic, Gompertz, and von Bertalanffy – were tested for their ability to predict multivariate size at age. Each model was fit separately to subsets of males and females from the ‘observed-age’ dataset and their fits compared using AIC (Table 5). To improve model fits, we estimated size at age zero as the mean hatchling size of a complementary dataset comprised of 12,161 hatchling observations from 1989 to 2016. We used mean hatchling measures because they have low morphological variation and, because of this minimal variation, curved measurements were not taken, precluding generation of individual hatchling PCs. Our single estimate of hatchling size (PC1) anchored growth models at the start of the exponential juvenile growth phase.

Fig. 1.

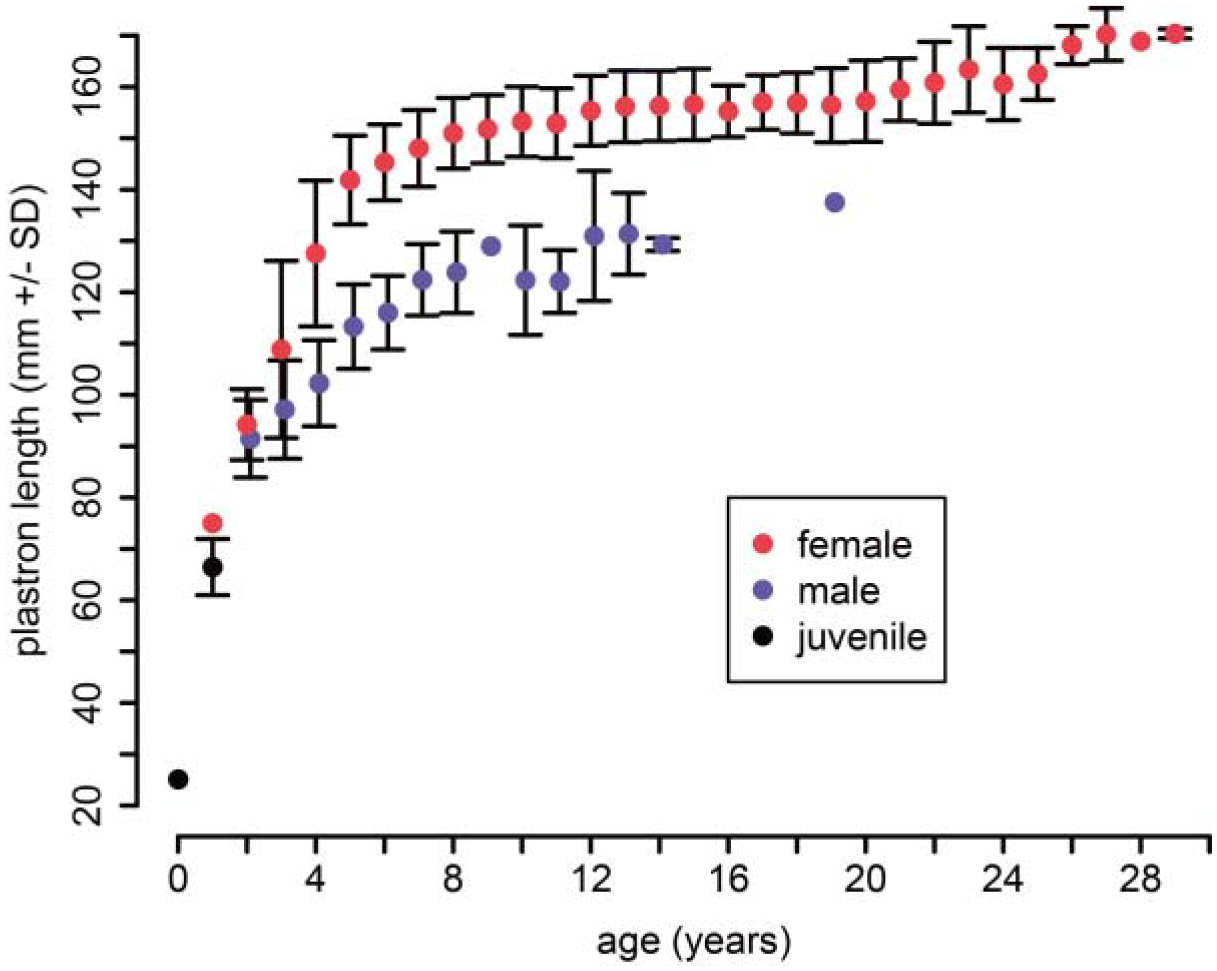
Mean plastron length at age for juvenile (black), female (red), and male (blue) painted turtles of known age.

Table 5.

Bootstrapped summary statistics for model comparisons of male and female growth curves using the Akaike Information Criterion (AIC)

Sex	Growth function	Residual df	Residual deviance	ΔAIC	Weight
Female	von Bertalanffy	444	11.26	0	1
	Gompertz	444	12.39	42.65	0
	Logistic	444	13.32	75.03	0
Males	von Bertalanffy	143	5.97	0	1
	Gompertz	143	6.90	22.13	0
	Logistic	143	7.66	37.67	0

Note: Three different growth functions were compared by separately fitting models to the same 20 independent samplings of male and female datasets from ‘observed-age’ turtles.

Although our data represent one of the most comprehensive capture-mark-recapture studies of freshwater turtles, few records spanned more than 3 years, particularly for males, and there were few records of individuals younger than age 3 (n = 13 females, 19 males at age 2; n = 1 female, 0 males less than age 2). This deficit limited the inference of sex-specific growth that could be made by modelling individual growth curves (e.g. using mixed-effects models with individual as a random effect). To circumvent these issues, we employed a bootstrap approach to modelling individual growth that was analogous to population re-sampling (Ogle, 2016b). Specifically, we controlled for repeated measures by subsampling one record from each individual of ‘observed age’ with replacement 20 times to form 20 subsamples of equal size. The three alternative growth models were then fit to the 20 subsamples using nls. We took the mean AIC values and weights for each growth model for model comparison (Table 5). For the best-supported model, we bootstrapped parameter estimates and errors (Table 6) by averaging estimates from the 20 subsets for each sex. We used the Taylor-series expansion method in the R package propagate to estimate error in our model predictions and the nlsTools package to generate confidence intervals on the model coefficients. For bootstrapped coefficient estimates, we took non-overlapping confidence intervals as support for sex-specific modelling (Table 6). We then plotted the model predictions (Fig. 2) to verify fit with the size-at-age data (Fig. 1). Finally, to verify the appropriateness of using our multivariate estimate of size (i.e. PC1) for growth modelling, we also generated univariate models of growth (using PL or SCL) and compared quasi-R² values calculated as the squared correlation between the fitted and observed values of each model. We found that growth models using PC1 consistently performed equally well in explaining variance in growth (mean quasi-R² = 0.67 for PC1, PL or SCL), while offering the advantages of describing growth in multiple dimensions and the ability to analyse orthogonal axes of variation (i.e. shape).

Table 6.

Bootstrapped coefficients of the von Bertalanffy growth model for female and male ‘observed-age’ turtles

Sex	Coefficient	Mean estimate (± 95% CI)
Female	L inf	4.10 (0.07)*
	K	0.55 (0.07)
	t 0	−0.15 (0.28)
Male	L inf	3.47 (0.11)*
	K	0.75 (0.18)
	t 0	−0.12 (0.34)

Note: Estimates of the mean maximum PC1 (L_inf) were significantly higher for females, while estimates of the growth constant (K) and age at length zero (t₀) did not differ between the sexes. Principal components and the estimate of L_inf are unitless. Asterisks indicate non-overlapping 95% confidence intervals.

Fig. 2.

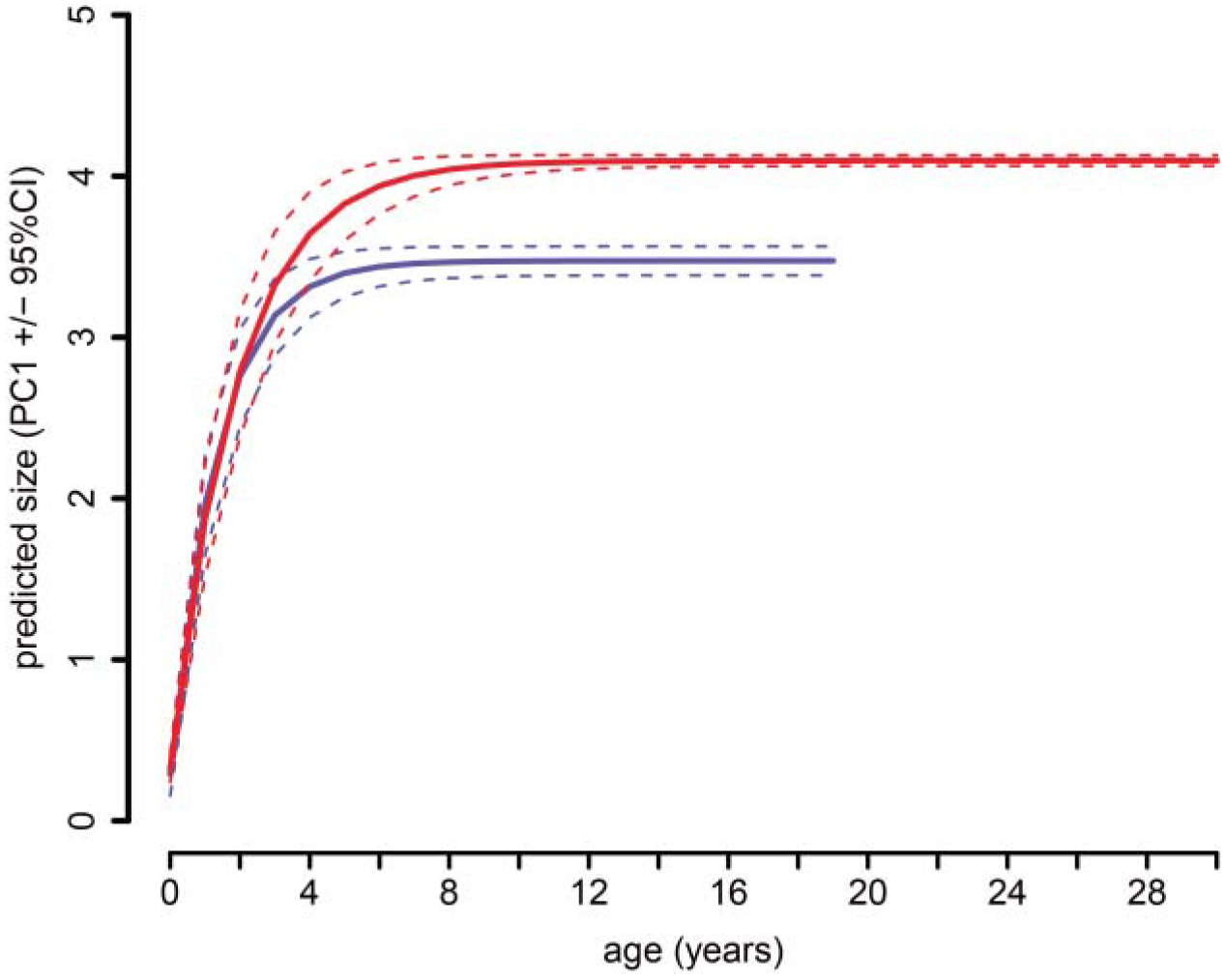
von Bertalanffy growth model predictions of size (PC1) at age using bootstrapped model coefficients (Table 5) show that the predicted size at maturity (i.e. L_inf) of female painted turtles (red) is significantly larger than that of males (blue). The maximum observed age was 19 years for males versus 29 years for females.

Analysis of shape

To evaluate sexual dimorphism of shape, we first tested for sex- and age-specific variation in shape of the ‘observed-age’ turtles using linear mixed-effects regression models. For each principal component, we fit ‘sex’, ‘age’, and their interaction as fixed effects and controlled for repeated measures by allowing random intercepts for each ‘individual turtle ID’. We evaluated the significance of model terms using analysis of deviance and Type II Wald χ² tests. We then used the mean asymptotic size for each sex (L_inf, Table 5) as estimated from the ‘observed-age’ individuals to define a larger subset of adults for statistical analysis of shape (‘post-maturation’ dataset, Table 1). The ‘post-maturation’ dataset contains all individuals inside the asymptotic growth phase, eliminating variation in shell morphology due to exponential juvenile growth. Using this size criterion, we were able to add 378 mature females and 713 mature males of unknown age, but post-asymptotic growth, thus minimizing variation in shell morphology due to individual growth. We tested for sexual dimorphism in shape with the ‘post-maturation’ dataset in a similar manner as above, using linear mixed-effect regression models and Type II Wald χ² tests for significance, except we could only use this dataset to test for the effect of ‘sex’. All statistical analyses were performed in R v. 3.2.1 (R Core Team, 2015).

Analysis of reproductive effort

To investigate potential causes and consequences of sexual dimorphism in size and shape, we examined their relation to female reproductive effort. We summarized female reproductive effort as mean individual egg mass, total clutch size, and total clutch mass (the sum of intact egg mass + the number of damaged eggs * mean egg mass of the clutch) at each reproductive bout. The number of damaged eggs per clutch was minimal (median = 0), but egg damage was frequent enough across the study to require this correction. For all females with reproductive data (‘nesting females’), we examined the relationship between clutch size and total clutch mass with a linear mixed-effect regression model. Similarly, we analysed the effect of size (PC1) and shape (PC2, PC3) on female reproductive effort using linear mixed-effects regression models, controlling for repeated measures by allowing random intercepts for each ‘individual turtle ID’. We again calculated significant effects using Type II Wald χ² tests.

To further address questions related to age-, size-, and shape-specific trade-offs in reproduction, we focused on a set of females (n = 38 individuals) with both nesting data at primiparity and at least three more nests in subsequent years with no more than two years in between nesting events. We also focused only on first clutches (n = 351 total nesting events). This ‘primiparous female’ subset facilitated testing hypotheses regarding potential trade-offs in reproduction related to variation in size (and shape) at maturity, and we employed the same mixed-model regression framework described above.

RESULTS

For the ‘observed-age’ turtles, Pearson’s correlation matrix showed highly significant pairwise correlations between all shell measurements (r > 0.95, P < 0.001, Table 2), and the first principal component explained 97% of the variation in shell morphology (Table 3). Concordance among loadings of the six traits onto PC1 also indicated that this major axis of variation describes multivariate size (Table 4). Model comparisons of three non-linear growth functions (i.e. logistic, Gompertz, and von Bertalanffy) describing the relationship between PC1 and age supported the use of the von Bertalanffy growth function for each sex (Table 5). In terms of absolute fit, the mean quasi-R² of the von Bertalanffy models was 0.77 for females and 0.72 for males. Bootstrapped estimates of the von Bertalanffy growth coefficients revealed that females attained a larger mean maximum length (L_inf), corresponding to a plastron length of 152 mm for females and 122 mm for males. However, estimates of the growth constant (K) and age at length zero (t₀) did not differ significantly between the sexes (Table 6). These patterns indicate that young females grow at similar rates to young males, but continue growing for longer durations, thus reaching larger asymptotic sizes. Using the ‘observed-age’ turtles, we also detected significant sex- and sex-by-age effects on shell shape (PC2 and PC3, Table 7; Fig. 3). We discuss the biological interpretation of shell shape variables (PC2 and PC3) below.

Table 7.

Mixed linear model analysis of the effects of sex and age on principal components of ‘observed-age’ turtles confirms significant sex-by-age effects on size (PC1) and shell shape (PC2, PC3)

	PC1 (size)		PC2 (sphericity)		PC3 (curvature)
Factor	χ2-value	P-value	χ2-value	P-value	χ2-value	P-value
Sex	920	<0.001	5.95	0.01	1.35	0.24
Age	858	<0.001	17.5	<0.001	0.14	0.71
Sex-by-age	151	<0.001	59.6	<0.001	50.1	<0.001

Note: Sex-by-age effects on shape are illustrated in Fig. 3.

After describing changes in size and shape with age using the ‘observed-age’ turtles, we used our estimates of asymptotic size (L_inf) for each sex to subset our data and focus on adults, irrespective of known age. Subsetting ‘all turtles’ based on estimates of asymptotic size eliminated individuals experiencing exponential growth and allowed us to include data from turtles of unknown age, but of sufficient size such that we could confidently determine they were mature adults. The correlation matrices and the resulting principal components using the ‘observed-age’ and ‘post-maturation’ datasets were qualitatively similar (Tables 3 and 4), except PC2 and PC3 from the ‘post-maturation’ and ‘nesting females’ subsets explained successively more of the total variance in shell morphology (1.1% vs. 2.2% vs. 5.5% and 0.9% vs. 1.6% vs. 4.0%, respectively, Table 3).

Interpretation of higher-order principal components in adult turtles

PC2 consistently represented a contrast between the three measures of length and the three measures of width (Table 4). As PC2 increased, the oblongness of the shell increased (Fig. 4). Since PC2 describes relative width versus length in multiple dimensions, it may be best described as representing shell sphericity. Male and female distributions of PC2 overlap (Fig. 4a) but PC2 significantly differs by sex (Table 8), as females achieved a higher degree of sphericity (i.e. a width greater than 90% of length). PC2 was not well related to shell curvature as represented by the ratio of CCW to PW (r = 0.03, P = 0.1), but because SCL and CCL loaded similarly onto PC2, it is possible that PC2 includes some information regarding curvature of the shell (i.e. a curvier turtle is more spherical and less flat). In other words, PC2 represents the trade-off (i.e. negative covariance) between relative curved width and relative straight length. A high PC2 indicates high curviness of the shell along the dorsoventral plane and a relatively rounded shell along the anterior-posterior plane (most painted turtle shells are oblong). Given the negative relationship between relative straight length and relative curved width (Fig. 4), a turtle shell can either be curvy or oblong – not both.

Table 8.

Mixed linear model analysis of the effects of sex on higher principal components of ‘post-maturation’ turtles confirms significant sexual dimorphism in adult turtle shell sphericity (PC2) and shell curvature (PC3)

	PC2 (sphericity)		PC3 (curvature)
Factor	χ2-value	P-value	χ2-value	P-value
Sex	34.81	<0.001	9.54	0.002

Note: Models included individual turtle ID as a random effect to account for repeated measures.

PC3 represented a contrast between curved measures and straight measures, more specifically between CCW and PW (Table 4). Higher PC3 scores correlate with highly curved carapaces along the dorsoventral axis relative to the plastron width – possibly related to the depth of the shell or thickness of the bridge (Fig. 5). Unlike with PC3 from the ‘observed-age’ dataset (Table 7), there was a significant main effect of sex on shell curvature (PC3) of the ‘post-maturation’ turtles (Table 8). The lack of a main effect of sex on PC3 in the ‘observed-age’ turtles may have been obscured by the interaction of sex and age (see Fig. 3). Our biological interpretations of how PC2 and PC3 represent variation in shell shape are further illustrated in Fig. 6.

Fig. 5.

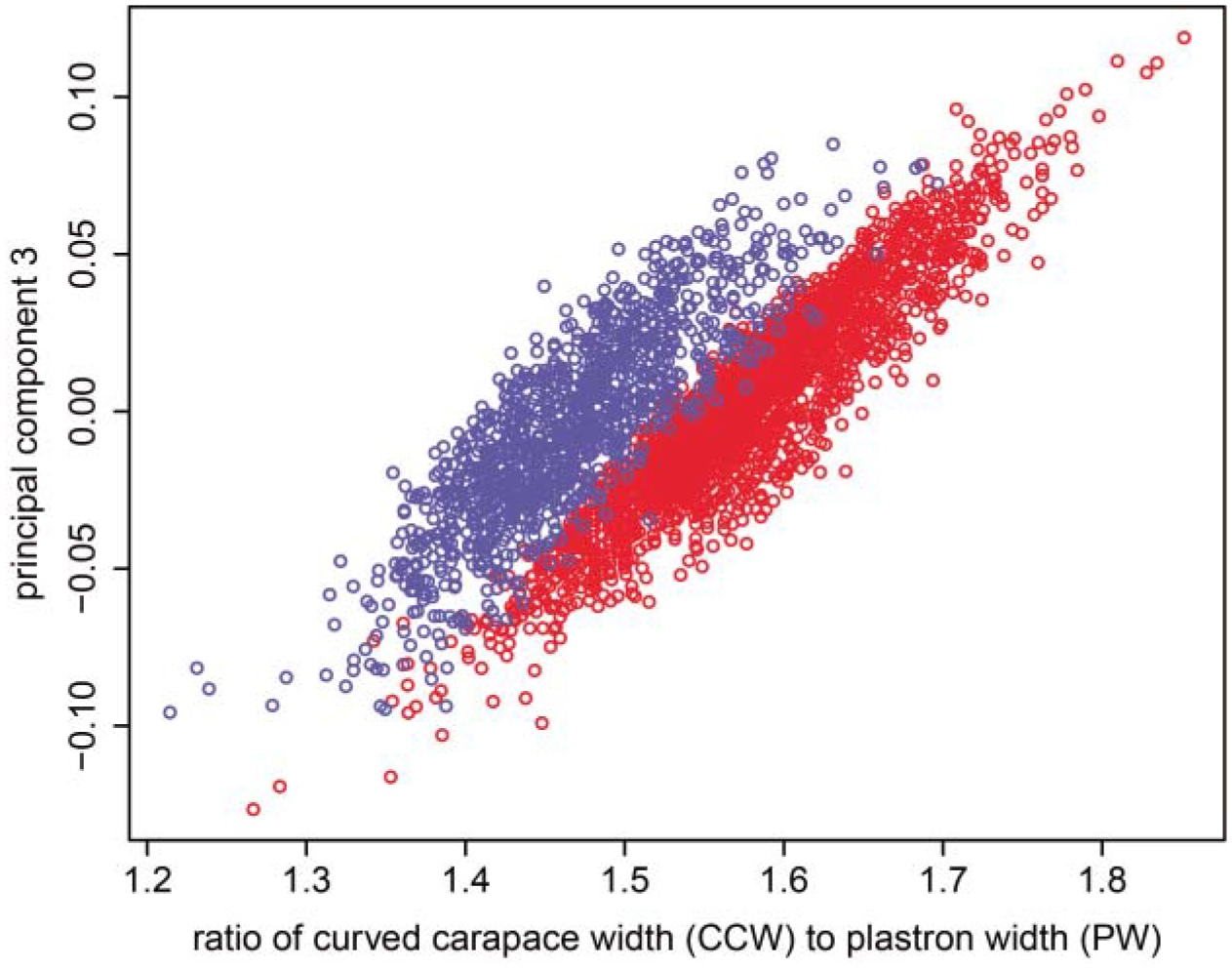
As seen by its relationship to the ratio of curved carapace width to plastron width (CCW/PW; r = 0.78, P < 0.001), PC3 represents a measure of relative shell curvature. Only females (red dots) achieve the highest shell curvature and lowest PC3 values.

Fig. 6.

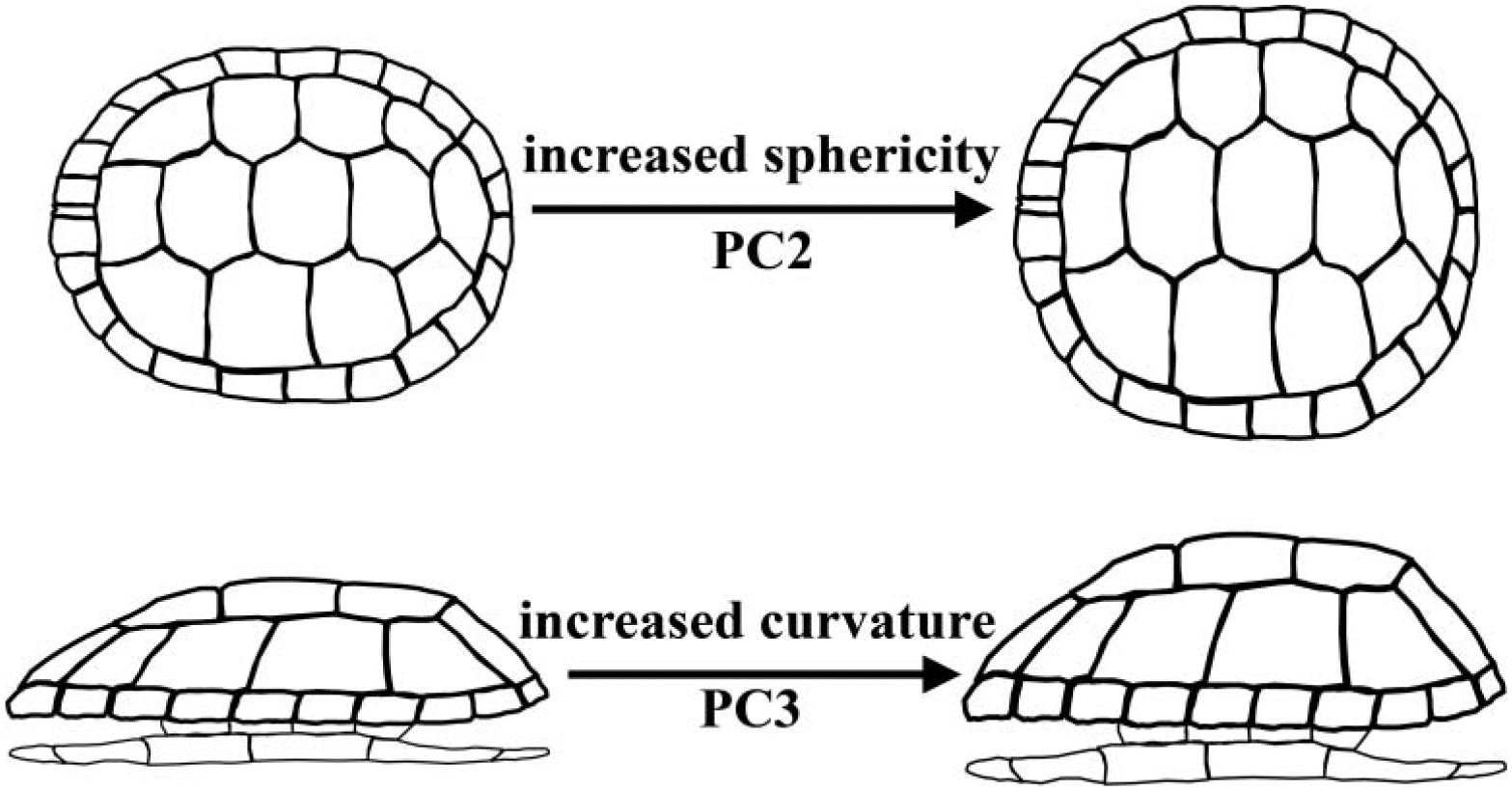
Illustration summarizing the two major axes of variation in shell shape. PC2 represents differences in shell sphericity. Note that while the illustration necessarily depicts a two-dimensional difference in shell roundness, PC2 describes three-dimensional variation in shell roundness (i.e. sphericity). PC3 represents a difference in the curvature or domedness of the shell.

Covariates of female reproductive effort

For all reproductive females measured (i.e. ‘nesting females’, Table 1), mean egg mass was negatively correlated with clutch size (P < 0.001, Fig. 7). To test for covariation in nesting female shape and reproductive output, we performed mixed-model linear regressions of the effects of adult PC1, PC2, and PC3 on clutch size, mean egg mass, and total clutch mass. Intercepts were allowed to vary randomly by ‘individual turtle ID’ in these models to control for repeated measures. When considering ‘nesting females’, we found that all measures of reproductive effort were positively correlated with shell size (PC1), but had no relation to shell curviness (PC3). Whereas clutch size and total clutch mass were negatively related to shell sphericity (PC2), mean egg mass increased with shell sphericity (Table 9).

Fig. 7.

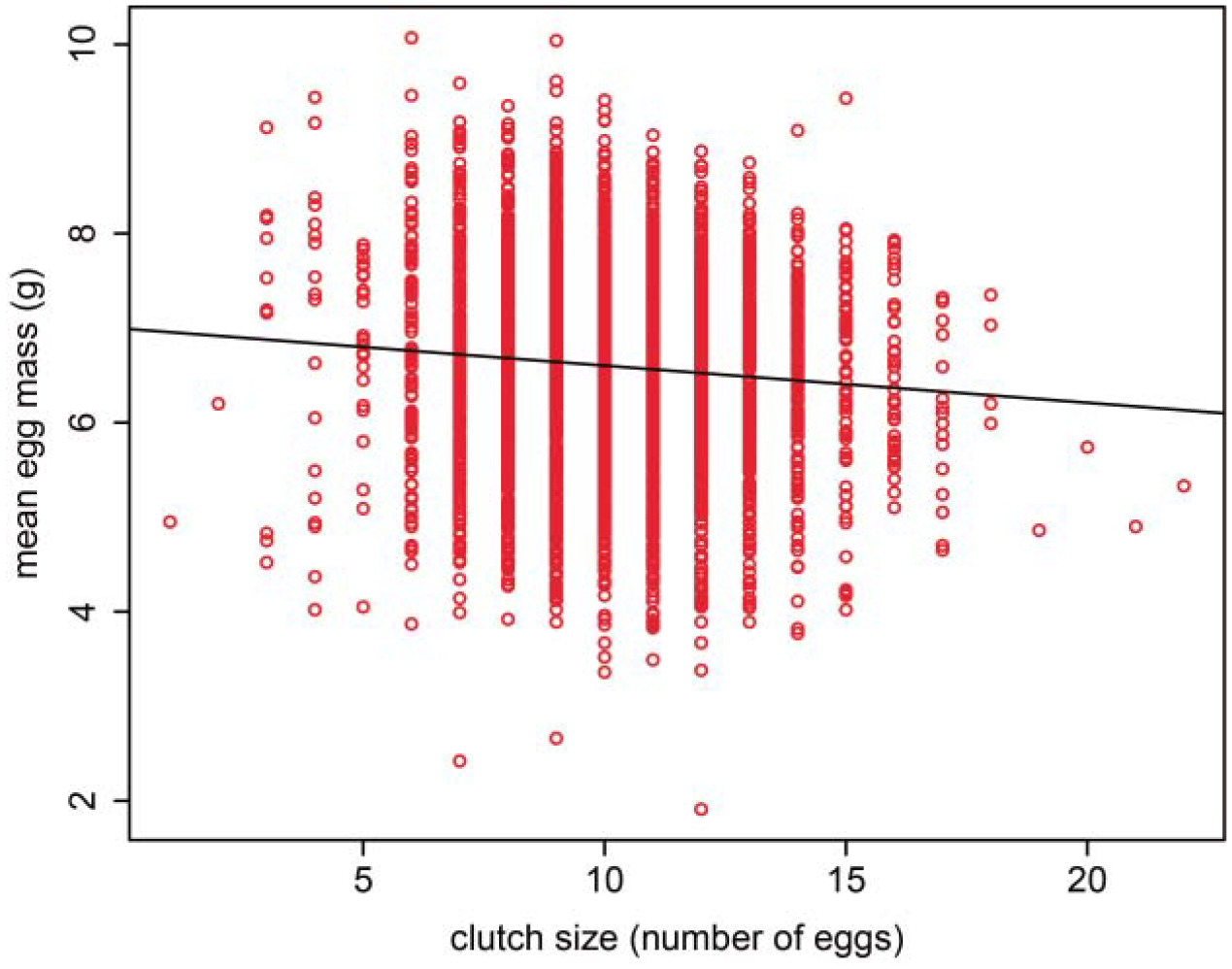
The trade-off between egg size (mean egg mass of a clutch) and egg number (clutch size) for ‘all nesting females’.

Table 9.

Mixed linear model analysis of the effects of shell size (PC1) and shape (PC2 and PC3) on three aspects of female reproductive effort (‘nesting females’)

	Clutch size		Total clutch mass		Mean egg mass
Factor	χ2-value	P-value	χ2-value	P-value	χ2-value	P-value
PC1	554	<0.001	2935	<0.001	2477	<0.001
PC2	8.07	0.005	11.1	<0.001	3.55	0.05
PC3	0.15	0.70	2.07	0.15	0.18	0.67

Note: Size and sphericity, but not curviness, significantly affected all measures of female reproductive output. Models included individual turtle ID as a random effect.

In a similar repeated-measures framework, all measures of reproductive effort for the subset ‘primiparous females’ depended positively on size (PC1), but only mean egg mass and total egg mass varied positively with maternal age. As with the ‘nesting females’, one measure of shell shape (sphericity, PC2), but not shell curvature (PC3, Table 10), negatively affected female reproductive effort as measured by clutch size and total clutch mass. For the same ‘primiparous females’ subset, size-at-maturity (PC1) positively affected lifetime reproductive effort as estimated by total clutch mass and mean egg mass, but not clutch size. Shape-at-maturity had no substantive effect on any measure of lifetime reproductive effort (Table 11).

Table 10.

Mixed linear model analysis of the effects of age and shell morphology (size PC1, or shape PC2 and PC3) on female reproduction

	Clutch size		Total clutch mass		Mean egg mass
Factor	χ2-value	P-value	χ2-value	P-value	χ2-value	P-value
PC1	1.97	0.16	4.76	0.03	12.8	<0.001
PC2	13.1	<0.001	64.3	<0.001	110.2	<0.001
PC3	7.60	0.006	4.72	0.03	0.56	0.45

Note: Data are from a subset of ‘primiparous females’ with nearly contiguous nesting records (n = 38 individuals). Models include individual turtle ID as a random effect.

Table 11.

Mixed linear model analysis of the effects of size-at-maturity (PC1) and shape-at-maturity (PC2, sphericity; PC3; curvature) on female reproductive effort

	Clutch size		Total clutch mass		Mean egg mass
Factor	χ2-value	P-value	χ2-value	P-value	χ2-value	P-value
PC1-at-maturity	3.36	0.07	19.3	<0.001	8.84	0.003
PC2-at-maturity	2.27	0.13	2.30	0.13	0.02	0.88
PC3-at-maturity	2.78	0.10	2.27	0.13	0.23	0.63

Note: Data are from a subset of ‘primiparious females’ with contiguous nesting records (n = 38 individuals with 368 total nesting records). Models include individual turtle ID as a random effect.

DISCUSSION

We found support for sex-specific modelling of multivariate growth using the von Bertalanffy growth function. The Gompertz growth model deviates from the logistic growth function by allowing an asymmetric inflection point (Berger, 1981), potentially better reflecting natural growth rates (e.g. Nahashon et al., 2006). The von Bertalanffy model contains no such inflection point, instead assuming that there is, from the onset, linear exponential growth over a period of time that levels off post maturation. This lack of a fixed inflection point likely fits better to data, such as ours, that contain a highly linear juvenile growth phase. Bootstrapping of male and female coefficients for the von Bertalanffy model revealed significantly different asymptotic sizes, supporting the hypothesis that the sexes were better modelled separately. However, despite evidence that females grow faster in some populations of snapping turtles (Armstrong and Brooks, 2013) and painted turtles (Janzen and Morjan, 2002; Dolph, 2017), we did not find strong support for sex-specific differences in growth rate in our population (i.e. K). This discrepancy is unlikely due to our incorporation of multiple measures of size, as univariate modelling of size also showed equivalent growth rates (Table 12).

Table 12.

Bootstrapped coefficients of the von Bertalanffy growth model for female and male ‘observed-age’ turtles

Sex	Coefficient	Mean estimate (± 95% CI)
Female	L inf	157 (3.93)*
	K	0.39 (0.07)
	t 0	−0.31 (0.54)
Male	L inf	128 (11.1)*
	K	0.33 (0.17)
	t 0	−1.38 (1.53)

Note: Estimates of the mean maximum plastron length (L_inf) were significantly higher for females, while estimates of the growth constant (K) and age at length zero (t₀) did not differ between the sexes. Asterisks indicate non-overlapping confidence intervals.

In addition to sex-specific differences in the duration of growth (but not growth rate), we demonstrated that shell shape depends on sex and age. Female shape does not covary with age, whereas males tend to decrease sphericity and shell curvature – likely via non-isometric increases to the length of the shell. This pattern is consistent with the action of sex-specific hormones determining sex-specific shell shape starting after sexual differentiation, concurrently with sexual maturation, and potentially continuing to influence growth for several years post maturation (e.g. Lerner and Mason, 2001; Crews, 2003).

Overall, our results demonstrate the value of accounting for multidimensional growth. While geometric-morphometric techniques have been used successfully to support phenomena such as ecomorphological variation of turtle shells (Rivera, 2008) and sexual dimorphism of hatchling or adult shell shape (Valenzuela et al., 2004; Vega and Stayton, 2011), we show that even a modest number of orthogonal measures can complement analyses of growth. Shell growth and shape differences may relate to variation in sex-specific life-history trade-offs, but male reproductive data would be needed to confirm their evolutionary significance.

Female life-history trade-offs

Because of the lack of sex chromosomes and apparent lack of sex-determining loci, sexual dimorphism in most turtles must come from differential expression of the genome. Sex differences in growth rates pre and post maturation may indicate different resolutions of competing demands for somatic versus reproductive growth. Also, sexual dimorphism in shell sphericity could be related to sex-specific reproductive demands – although, if true, it is interesting that we saw consistent decomposition of variation in shell shape both between and within the sexes and that the distributions of these major axes of shape variation are largely overlapping between the sexes. Females, but not males, likely benefit from the increased capacity a curved shell provides for egg storage (Vitt and Congdon, 1978) – and yet, if anything, adult male shell shape is more constrained, possibly indicating that their more purely aquatic lifestyle constrains male shell shape (sensu Jolicoeur and Mosimann, 1960).

Our findings confirm several aspects of previous reports on life-history traits of turtles (e.g. Congdon and Gibbons, 1985), including low variation in relative clutch mass (clutch mass/body size) where larger females have greater reproductive efforts. There is evidence of egg-size versus egg-number trade-offs in painted turtles (Rowe, 1994), but some studies have failed to detect a trade-off (Congdon and Gibbons, 1985; Spencer and Janzen, 2010). Here, we found a negative relationship between egg size and clutch size consistent with optimal egg-size theory.

As in previous studies, clutch size did not depend strongly on mother’s age (e.g. Bowden et al., 2004). Rather, young females laid relatively small eggs amounting to smaller total clutch masses. Furthermore, neither size-at-maturity nor shape-at-maturity significantly influenced clutch size – as might have been expected if the size of the pelvic aperture or the caudal gap height constrained reproductive effort (sensu Congdon and Gibbons, 1987). Together these patterns suggest an age-dependent optimal egg size, with a significant role for physiological constraints (e.g. hormone titre) on early-lifetime reproductive effort in place of or in addition to morphological constraints from the shell (Bowden et al., 2004). Size-at-maturity did positively relate to reproductive effort in terms of egg mass and total clutch mass, but not clutch size. This is consistent with a recent study on covariance of size and reproduction in the common snapping turtle, which found no evidence for growth versus reproduction trade-offs (Armstrong et al., 2018). Furthermore, multiple studies of painted turtles report that bigger offspring are better – larger eggs have better hatching success and produce larger hatchlings (Janzen and Warner, 2009), and larger hatchlings have better overwintering success (Mitchell et al., 2013), better nest-to-water migration survival (Paitz et al., 2007), and better early-lifetime survivorship in captivity up to age 4 years (Brodie and Janzen, 1996). Together, these results suggest a clear direction for natural selection on body size with multiple factors associated with fitness and collinear with body size.

The usefulness of long-term data

Understanding both the proximate and ultimate mechanisms of life-history variation in longevous species requires long-term data. Detailed knowledge of non-human species lags behind, but is required to power the comparative studies that will contextualize interspecific variation in the life history of vertebrates and provide insights into their evolution. We are just now able to test some of the most important aspects of life-history theory in painted turtles.