Accessing Covid19 epidemic outbreak in Tamilnadu and the impact of lockdown through epidemiological models and dynamic systems

Highlights

• •Impact of lockdown and social distancing in Tamilnadu through epidemiological models.
• •Accessing district wise clustered spread merged with lockdown and social distancing.
• •Identifying key drivers for rapid reproductive rate through Epidemiological models.
• •Impact of comorbidity conditions in clustered population with specific Gender and Age.

Abstract

Despite having a small footprint origin, COVID-19 has expanded its clutches to being a global pandemic with severe consequences threatening the survival of the human species. Despite international communities closing their corridors to reduce the exponential spread of the coronavirus. The need to study the patterns of transmission and spread gains utmost importance at the grass-root level of the social structure. To determine the impact of lockdown and social distancing in Tamilnadu through epidemiological models in forecasting the “effective reproductive number” (R₀) determining the significance in transmission rate in Tamilnadu after first Covid19 case confirmation on March 07, 2020. Utilizing web scraping techniques to extract data from different online sources to determine the probable transmission rate in Tamilnadu from the rest of the Indian states. Comparing the different epidemiological models (SIR, SIER) in forecasting and assessing the current and future spread of COVID-19. R₀ value has a high spike in densely populated districts with the probable flattening of the curve due to lockdown and the rapid rise after the relaxation of lockdown. As of June 03, 2020, there were 25,872 confirmed cases and 208 deaths in Tamilnadu after two and a half months of lockdown with minimal exceptions. As on June 03, 2020, the information published online by the Tamilnadu state government the fatality is at 1.8% (208/11345 = 1.8%) spread with those aged (0–12) at 1437 and 13–60 at 21,899 and 60+ at 2536 the risk of symptomatic infection increases with age and comorbid conditions.

1. Introduction

The thrust of this global Pandemic is disrupting the natural flow of human existence via COVID-19 of the “common cold” coronavirus family, its existing versions of a severe acute respiratory syndrome (SARS) (2001–2003), and middle east respiratory syndrome (MERS) (2012–2015). SARS-CoV and covid19 spread from infected civets and bats, while MERS-CoV originated from dromedary camels resulting in an epidemic as corroborated by scientific research. This paper intends to provide a detailed view of the different mathematical models in predicting the rife of covid19. Modeling a detailed view in determining the spread of covid19 taking into account the influences of provincial factors, thereby providing a fundamental understanding through quantitative and qualitative inferences during these uncertain times. The model utilizes population dynamics and conditional dependencies such as new cases, deaths, social distancing, and herd immunity over a stipulated time-period to simulate probable outcomes. The social stigma determines the rate of spread and is specific to the region and religious practices and different structure congregation of the masses. A thorough study of different epidemiological models is presented in the subsequent section and the comparative analysis of the various factors and socio-economic needs that influence the model’s capabilities in determining the spread of the epidemic.

2. Related works

The epidemiological model provides a system to define and determine interventions based on statistics of collected data and predicting the probability of determining the development prevention and control of diseases. Epidemiology models are classified into respective categories based on the chance variations (stochastic & deterministic), time (continuous & discrete intervals), space (spatial & non-spatial), and population (homogenous & heterogenous) to predict the dispersion of diseases [7]. The factors governing the spread are infectious agents, modes of transmission, susceptibility, and immunity [4]. The different modes of transmission are

• i).person → person,
• ii).person → environment/ environment → person,
• iii).reservoir → vector/vector → person,
• iv).reservoir → person

The case fatality rate (CFR) is highly variable and increases with severe respiratory symptoms in adults with comorbid conditions [3] . There present scenario specified in this paper is currently no specific vaccine available for covid19, despite quarantines and lockdowns imposed. The authors also specify a need to accelerate protocols to rapid point of care diagnostic testing and effective personal care in preventing the transmission and spread of the disease.

The authors provide a time dependent model more adaptive than the existing models but with a way of further improving the results and predictions by taking into account the disease propagation probabilities and transmission rates [5].

2.1. Acquiring data

The portals and dashboard created by WHO [12].) and Tamilnadu government [11] from which data is acquired through open data initiative in both local and global scope are as follows,

• • https://stopcorona.tn.gov.in/daily-bulletin/
• • https://covid19.who.int/
• • https://www.mohfw.gov.in/index.html
• • https://nhmtn.maps.arcgis.com/apps/opsdashboard/index.html
• • https://covid19.who.int/

2.2. Retrieving the data

• •Download data in the form of excel sheets, text, and json files.
• •Use specific API’s for accessing dashboard [11] of covid19.
• •Utilize a language library(python) designed for covid19.

3. Different mathematical models for infectious diseases

The Reed-Frost Theory [1] represents Soper’s equation as follows

$$C_{t+1}=S_t(1-q^{C_t})$$ (1)

The proposed equation (1) helps in determining the cases in successive time periods. Where $C_t$ → number of cases, t → time and $q^{C_t}$ → probability of an individual with no contact with $C_t$, $1-q^{C_t}$→probability of an individual having contact with $C_t$.

The Reed-Frost Theory [1] states that

$$E(C_{t+1})=O(S_t)(1-q^{O(C_t)})$$ (2)

and

$$E\left(S_{t+1}\right)=O\left(S_t\right)-E(C_{t+1})$$ (3)

For a population of A and B, the theory states in equation (4) that individual is not infected from cases in population B

$$q^{C_t^A}.Q^{C_t^B}$$ (4)

But is infected from any one of the cases in either of population A or B

$$1-q^{C_t^A}.Q^{C_t^B}$$ (5)

The cases infected from the population A in time t + 1 is

$${C_{t+1}}^A=S_t^A\left(1-q^{C_t^A}.Q^{C_t^B}\right)$$ (6)

The cases infected from the population B in time t + 1 is

$${C_{t+1}}^B=S_t^B\left(1-q^{C_t^B}.Q^{C_t^A}\right)$$ (7)

Both equations (6), (7) determined the introduction of cases into the population, which forms the initial spread for epidemics.

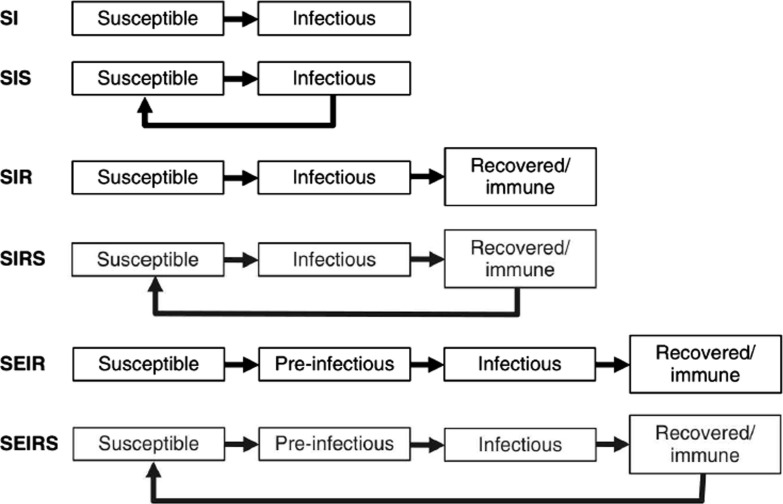
The compartmental structure of different epidemiological models SI, SIS, SIR, SIRS, SEI, SEIS, SEIR, SEIRS, MSEIR, MSEIRS, are represented in Fig. 1 .

Fig. 1.

Common Structure for infectious diseases models.

3.1. Compartmental models

The dynamics of covid19 are mapped into a compartmental model that generates the mean-field approximations to ensemble or population dynamics

four latent factors determine the distributions

• (i).Location

The transmission probability

$$P\left({\mathit{loc}}_{i+1}=work\right|{\mathit{loc}}_t=home,{\mathit{clin}}_t={\mathit{asymptotic}}_t)=\theta {(1-P_{\mathit{infected}}^{\mathit{inf}})}^{{\theta }_{\mathit{sde}}}$$ (8)

where ${\theta }_{\mathit{sde}}$ → social distancing component

Further classification of location into four factors as

$$p^{\mathit{loc}}=[P_{\mathit{home}}^{\mathit{loc}},P_{\mathit{work}}^{\mathit{loc}},P_{\mathit{CCU}}^{\mathit{loc}},P_{\mathit{morgue}}^{\mathit{loc}}]$$ (9)

where home→ $P_{\mathit{home}}^{\mathit{loc}}$,work → $P_{\mathit{work}}^{\mathit{loc}},$CCU→ $P_{\mathit{CCU}}^{\mathit{loc}}$,morgue→ $P_{\mathit{morgue}}^{\mathit{loc}}$

• (ii).Infection status

$$p^{\mathit{inf}}=[P_{\mathit{susceptible}}^{\mathit{inf}},P_{\mathit{infected}}^{\mathit{inf}},P_{\mathit{infectious}}^{\mathit{inf}},P_{\mathit{immune}}^{\mathit{inf}}]$$ (10)

• (iii).Clinical status

$$p^{\mathit{clin}}=[P_{\mathit{asymptomatic}}^{\mathit{clin}},P_{\mathit{symptomatic}}^{\mathit{clin}},P_{\mathit{ADRS}}^{\mathit{clin}},P_{\mathit{deceased}}^{\mathit{clin}}]$$ (11)

• (iv).Diagnostic and testing

$$p^{\mathit{test}}=[P_{\mathit{untested}}^{\mathit{test}},P_{\mathit{waiting}}^{\mathit{test}},P_{\mathit{positive}}^{\mathit{test}},P_{\mathit{negative}}^{\mathit{test}}]$$ (12)

the master equation for the dynamic part of the dynamic casual model is

$$p_{t+1}=T(\theta ,p_t)p_t$$ (13)

Which supports active reproduction number or rate R

$$R={\theta }_{\mathit{trn}}·P_{\mathit{susceptible}}^{\mathit{inf}}·\left(P_{\mathit{home}}^{\mathit{loc}|infectious}{\theta }_{\mathit{Rin}}+P_{\mathit{work}}^{\mathit{loc}|infectious}{\theta }_{\mathit{Rou}}\right)·{\tau }_{\mathit{con}}$$ (14)

The population of infectious is denoted as $P^{\mathit{infectious}}$ and the local population infected is denoted as $P^{\left(loc|infectious\right)}.$

3.2. Case fatality rate (CFR)

$$\mathrm{C}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{f}\mathrm{a}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}(\mathrm{C}\mathrm{F}\mathrm{R})=\frac{\mathrm{N}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{p}\mathrm{e}\mathrm{o}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{e}\mathrm{d}}{\mathrm{N}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{p}\mathrm{e}\mathrm{o}\mathrm{p}\mathrm{l}\mathrm{e}\mathrm{i}\mathrm{n}\mathrm{f}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}}$$ (15)

The reproductive number (R₀) called “R naught” defines the average number of secondary infections caused by an infected individual introduced into an uninfected population. The range of$R_0$ > 1 signifies an epidemic while$R_0$ < 1 defines the disease as eliminated.

$$R_0=Days\ast Suceptiblepeople\ast chanceofinfection$$ (16)

Impact of the interventions in the spread of covid19

3.3. Intercontinental & interstate transmission

There has been a high spread from the interstate and intercontinental travelers to Tamilnadu state. Air & rail travel has eased the transmission and spread of the covid19 diseases in rural and urban districts of Tamilnadu. The statistics are as follows

A total number of 2,10,538 passengers were screened at Tamilnadu airports in Chennai, Madurai Trichy, and Coimbatore.

3.4. Clustered community spread

To measure the clustered spread of covid19 is to determine the geolocation of the infected individual as the individual is entering into the community with zero infected individuals [13]. In order to measure the intensity of the spread, each individual is measured as the centroid of the cluster [9]. The dependent features are the age, embarking source, and destination vectors [4]. The specific clusters identified in Tamilnadu are that of the Delhi cluster, Koyambedu cluster [10]. The data defined with that of the cluster is as shown in the table

3.5. Demographic models [7]

The age-structured epidemiological models are differential equations specific to the changing size and age structure of a population over time. These models work on continuous age and age groups as partial and ordinary differential equations. The continuous age model is determined with a partial differential equation for the population growth.

A demographic model with Continuous Age

$$\frac{\partial U}{\partial a}+\frac{\partial U}{\partial t}=-d(a)U$$ (17)

Let $U\left(a,t\right)\to totalpopulationsagedistribution$, $t\to noofindividualodtime$, $\left[a_1,a_2\right]\to ageintervel$, $U\left(a,t\right)\to integralfrom{a}_{1}to{a}_2$

$$B\left(t\right)=U\left(0,t\right)=\underset{0}{\stackrel{\infty }{\int }}f\left(a\right)U\left(a,t\right)da$$ (18)

This population model called the Lotka -Mckendrick Model [2].

The classic Kermack-Mckendrik model

$$\lambda \left(t\right)={\int }_0^{\theta }{\lambda }_o\left(\theta \right)i\left(\theta ,t\right)d\theta$$ (19)

where

$${\lambda }_0\left(\theta \right)=\frac{c(\theta )\chi (\theta )}{N}$$ (20)

These class-age-structured model equations are

$$\left\{\begin{array}{c}i)S^{\prime }\left(t\right)=-\lambda \left(t\right)S\left(t\right),\\ \mathit{ii})i_t\left(\theta ,t\right)+i_{\theta }\left(\theta ,t\right)+\gamma \left(\theta \right)i\left(\theta ,t\right)=0,\\ \mathit{iii})i\left(\theta ,t\right)=\lambda \left(t\right)S\left(t\right),\\ \mathit{iv})R^{\prime }\left(t\right)=\underset{0}{\overset{{\theta }_{†}}{\int }}\gamma \left(\theta \right)i\left(\theta ,t\right)d\theta ,\end{array}\right)$$ (21)

The initial population age distribution epidemiological model assumes that there is a steady age distribution in the total population size.

$$U\left(a,t\right)=\rho e^{\mathit{qt}}{e}^{-D\left(a\right)-qa}with\rho =\frac{1}{{\int }_o^{\infty }{e}^{-D\left(a\right)-qa}da}$$ (22)

A demographic model with Age groups

$$N_i\left(t\right)={\int }_{a_{i-1}}^{a_i}U(a,t)da=e^{\mathit{qt}}{\int }_{a_{i-1}}^{a_i}A\left(a\right)da=e^{\mathit{qt}}{P}_i$$ (23)

4. The impact of lockdown

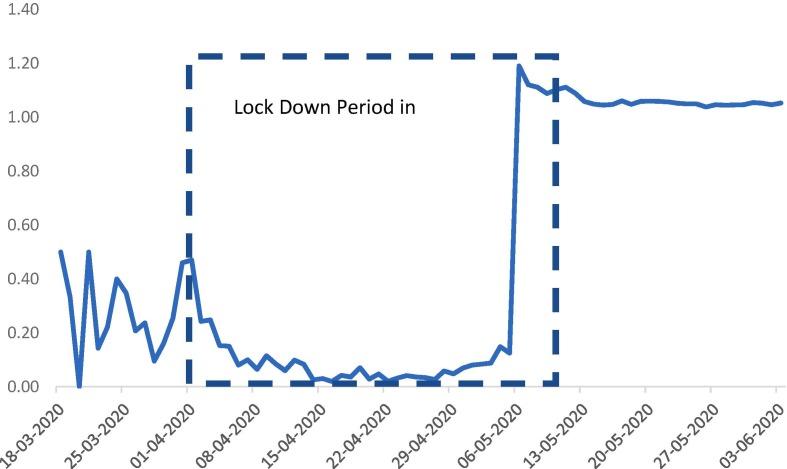
The government of India and the state of Tamilnadu implemented lockdown for four periods as lockdown 1.0–4.0 from March till May and further extending with leniency. This lockdown has reduced the rapid spread of covid19 through social distancing, reducing fatalities. The three main transmission modes through physical contact, respiratory droplets $<5\mu m$ through sneezing or coughing, indirect contact with surfaces handled by an infected person.

The impact of lockdown in different stages of transmission is

Stage 1: Travel History

In this stage, the probability transmission is from traveling individuals from different geographical locations, the sources are highly identifiable, and isolation is high. The isolated individuals infect a small cluster of the surrounding, thereby creating sporadic pockets of infection.

$$p^{\mathit{travel}}=[p_{\mathit{air}}^{\mathit{travel}},p_{\mathit{rail}}^{\mathit{travel}}{,p}_{\mathit{ship}}^{\mathit{travel}},p_{\mathit{road}}^{\mathit{travel}}]$$ (24)

where $p_{\mathit{air}}^{\mathit{travel}}\to$ travel from international communities, $p_{\mathit{rail}}^{\mathit{travel}}\to$travel between local communities, $p_{\mathit{ship}}^{\mathit{travel}}\to$travel from isolated communities, $p_{\mathit{road}}^{\mathit{travel}}\to$travel between local states and neighboring countries

Stage 2: Local Transmission

In this stage, the source from where the individual travelled is identifiable, traced, and isolated. The individuals isolated become carriers infecting households and family.

$$p^{\mathit{local}trans}=[p_{\mathit{air}}^{\mathit{local}trans},p_{\mathit{rail}}^{\mathit{local}trans}{,p}_{\mathit{ship}}^{\mathit{local}trans},p_{\mathit{road}}^{\mathit{local}trans}]$$ (25)

Individual identified within the local cluster $p^{\mathit{local}trans}$.

Stage 3: Community Transmission

In this stage, the source is not identifiable, and vast masses of people are infected. The infection spreads through random patterns where random members start to get infected.

$$p^{\mathit{community}}=[p_{\mathit{local}}^{\mathit{travel}},p_{\mathit{international}}^{\mathit{travel}}{,p}_{\mathit{state}}^{\mathit{travel}},p_{\mathit{district}}^{\mathit{travel}}]$$ (26)

$P^{\mathit{travel}}\to$ denotes the travel of the individual from state, district, international locations.

Stage 4: Epidemic

In this stage, the spread becomes an epidemic with a large number of infected people and an increase in the number of deaths. After a while, the community starts to develop immunity to this specific strain of the virus, thereby reducing transmission and death eventually. There is also a possibility of the virus mutating generating a second wave.

$$p^{\mathit{epic}}=\left[p_{\mathit{local}}^{\mathit{epic}},p_{\mathit{cluster}}^{\mathit{epic}}{,p}_{\mathit{household}}^{\mathit{epic}},p_{\mathit{untracable}}^{\mathit{epic}}\right]$$ (27)

$$p_{\mathit{cluster}}^{\mathit{epic}}\to individualinfectedfromthecluster{,p}_{\mathit{household}}^{\mathit{epic}}\to individualinfectedfromhousehold,p_{\mathit{untracable}}^{\mathit{epic}}\to individualinfectedfromuntraceblesource$$

The mapping of transmission of covid19 is done through contact tracing, thereby isolating individuals infected by the epidemic at different epicentres of the society denoted by $P^{\mathit{epic}}$.

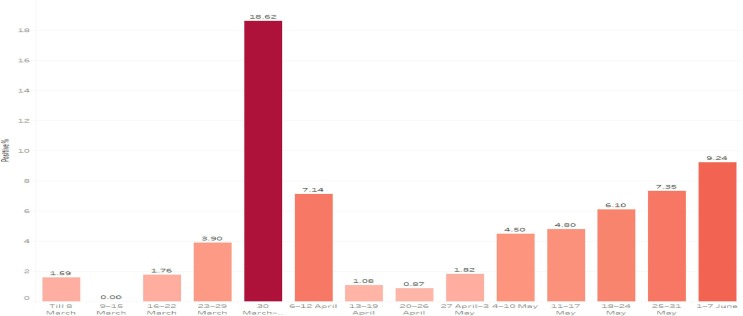
Lockdown reduced the spread of covid19 in Tamilnadu as represented in dotted lines in the figure below (see Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 7, Fig. 8, Fig. 9, Fig. 10, Fig. 11, Fig. 12, Fig. 13 and Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7 ).

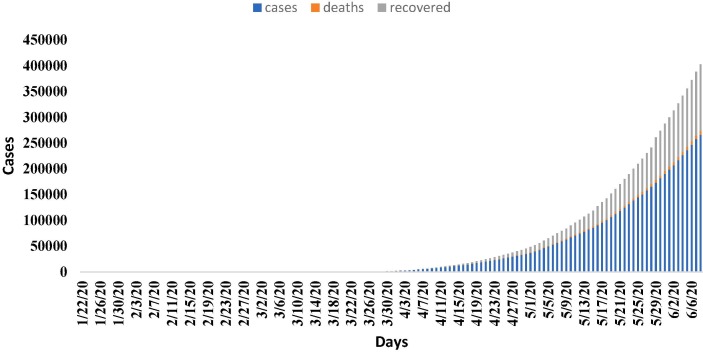
Fig. 2.

Tamilnadu Covid19 Statistics.

Fig. 3.

Impact of Lockdown in Tamilnadu.

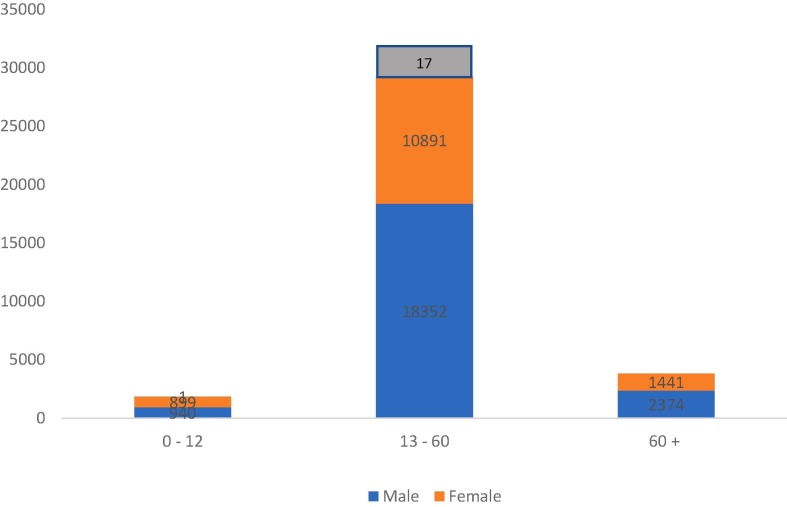
Fig. 4.

Age/Gender Statistics Covid19 Tamilnadu.

Fig. 5.

Age/Gender Statistics Coivd19 Tamilnadu 20/08/2020.

Fig. 6.

India Covid19 status.

Fig. 7.

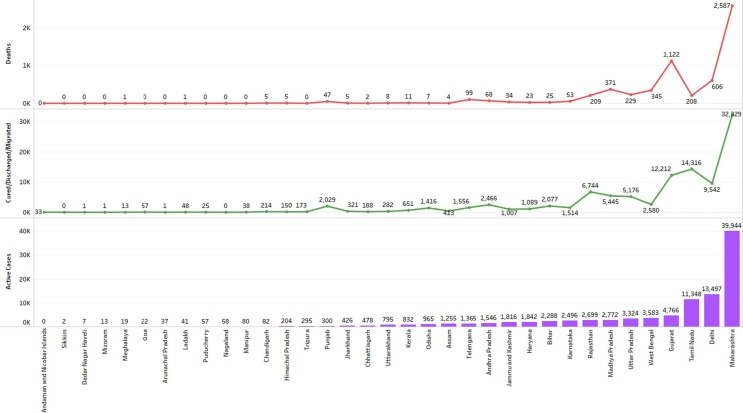
Active Case Details of Covid19 Pandemic in Indian states.

Fig. 8.

Tamilnadu District wise Covid-19.

Fig. 9.

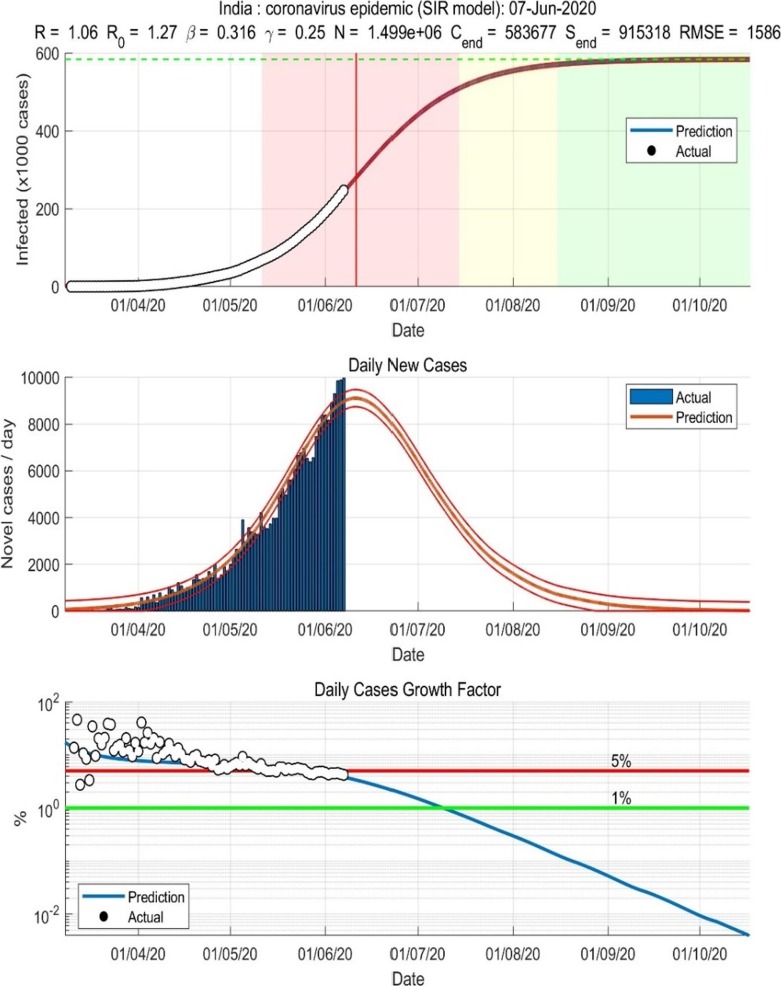
India Covid19 SIR Model on 07/06/2020.

Fig. 10.

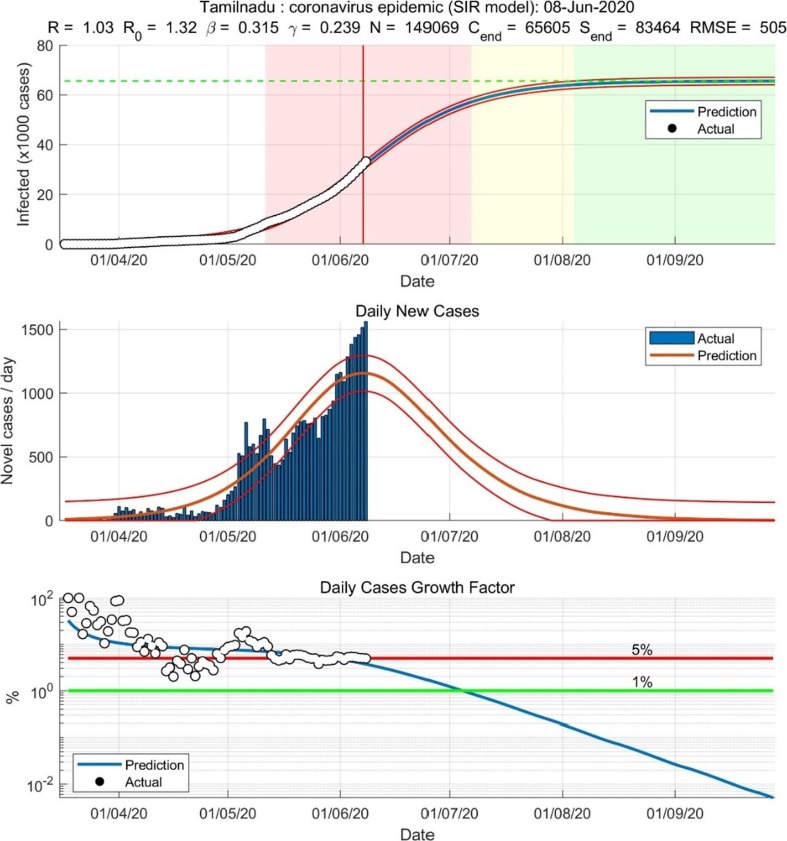
Tamilnadu coronavirus epidemic (SIR Model) on 08/06/2020.

Fig. 11.

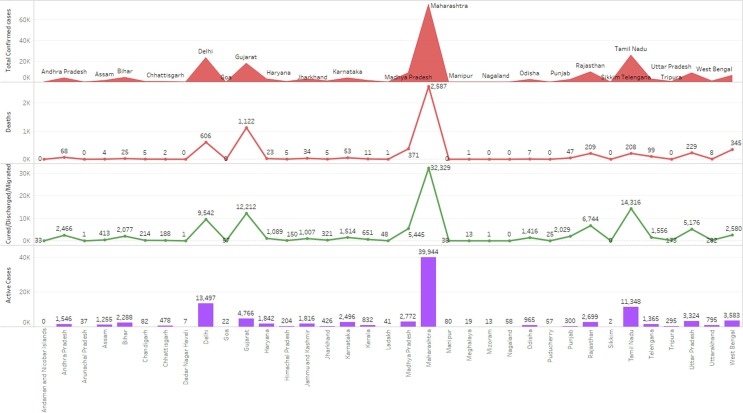
Combined statistics of Indian states covid19 cases.

Fig. 12.

Combined cases cluster statistics of Indian states.

Fig. 13.

Covid19 Testing Statistics.

Table 1.

Surveillance of Passengers at Seaport.

SI. No	Sea Port	No. of Ships arrived	No. of Passengers screened	No. Positive
1	Chennai	1	161	0
2	Thoothukudi	2	1385	5
	Total	3	1546	5

Table 2.

Surveillance of Passengers at Airport.

Sl. No.	Airport	No. of Flights arrived	No. of Passengers	No. Positive
1	Chennai	459	31,381	23
2	Coimbatore	75	8447	33
3	Madurai	62	4171	25
4	Trichy	27	1644	4
Total		623	45,643	85

Table 3.

Surveillance and Quarantine of International Passengers.

Date	Total screened passengers	Passengers completed 28 days quarantine	Passengers under home quarantine
01–04-2020	2,10,538	4070	77,330
02–04-2020	2,10,538	4070	86,342
03–04-2020	2,10,538	5080	90,412
04–04-2020	2,10,538	5315	90,541
05–04-2020	2,10,538	10,814	90,824
06–04-2020	2,10,538	19,060	72,791
07–04-2020	2,10,538	27,416	66,430
08–04-2020	2,10,538	32,075	60,739
09–04-2020	2,10,538	32,896	59,918

Table 4.

Tamilnadu District wise Covid19 Statistics as on 01/06/2020.

Sl.	District	Total	Discharged	Active Cases	Death
No		Positive Cases
1	Ariyalur	365	355	10	0
2	Chengalpattu	1177	610	555	11#
3	Chennai	14,802	7891	6781	129*
4	Coimbatore	146	144	0	1*
5	Cuddalore	461	420	40	1
6	Dharmapuri	8	5	3	0
7	Dindigul	139	122	16	1
8	Erode	72	70	1	1
9	Kallakurichi	246	111	135	0
10	Kancheepuram	407	232	173	2
11	Kanyakumari	67	32	34	1
12	Karur	81	76	5	0
13	Krishnagiri	28	20	8	0
14	Madurai	269	164	102	3
15	Nagapattinam	60	51	9	0
16	Namakkal	78	77	0	1
17	Nilgiris	14	14	0	0
18	Perambalur	141	139	2	0
19	Pudukottai	26	16	10	0
20	Ramanathapuram	84	38	45	1
21	Ranipet	98	84	14	0
22	Salem	176	53	123	0
23	Sivagangai	33	28	5	0
24	Tenkasi	86	63	23	0
25	Thanjavur	89	77	12	0
26	Theni	109	86	21	2
27	Thirupathur	32	28	4	0
28	Thiruvallur	948	603	334	11
29	Thiruvannamalai	419	144	273	2
30	Thiruvarur	47	33	14	0
31	Thoothukudi	226	135	89	2
32	Tirunelveli	352	211	140	1
33	Tiruppur	114	114	0	0
34	Trichy	88	70	18	0
35	Vellore	43	34	8	1
36	Villupuram	346	318	26	2
37	Virudhunagar	123	58	65	0
Grand Total		22,333	12,757	9400	173

Table 5.

Tamilnadu State Covid19 SIR Model Calculations.

S. No.	Date	Day/Time	S	I	R	S + I + R
1	07-May-20	0	13.5741	0.5739	0.2524	14.4004
2	08-May-20	0.125	13.5393	0.5924	0.1901	14.4468
3	09-May-20	0.25	13.5029	0.6228	0.1962	14.5719
4	10-May-20	0.375	13.4646	0.6546	0.2026	14.6968
5	11-May-20	0.5	13.4245	0.6879	0.2093	14.8217
6	12-May-20	0.625	13.2149	0.8619	0.245	14.9468
7	13-May-20	0.75	12.9574	1.0749	0.2895	15.0718
8	14-May-20	0.875	12.6441	1.3328	0.3449	15.1968
9	15-May-20	1	12.2676	1.6409	0.4133	15.3218
10	16-May-20	1.125	11.6715	2.1243	0.526	15.4468
11	17-May-20	1.25	10.9478	2.7032	0.6709	15.5719
12	18-May-20	1.375	10.0994	3.3691	0.8533	15.6968
13	19-May-20	1.5	9.1452	4.0988	1.0778	15.8218
14	20-May-20	1.625	7.8782	5.0285	1.4151	15.9468
15	21-May-20	1.75	6.5898	5.9123	1.8197	16.0718
16	22-May-20	1.875	5.3651	6.6715	2.2852	16.1968
17	23-May-20	2	4.2712	7.2499	2.8007	16.3218
18	24-May-20	2.125	3.1908	7.6691	3.4619	16.4468
19	25-May-20	2.25	2.3537	7.82	4.1481	16.5718
20	26-May-20	2.375	1.7299	7.7534	4.8386	16.6969
21	27-May-20	2.5	1.2809	7.5252	5.5157	16.8218
22	28-May-20	2.625	1.0308	7.284	6.007	16.9468
23	29-May-20	2.75	0.8358	7.005	6.481	17.0718
24	30-May-20	2.875	0.6832	6.7027	6.9359	17.1968
25	31-May-20	3	0.5636	6.388	7.3703	17.3219
26	01-Jun-20	3.125	0.4695	6.0689	7.7834	17.4468
27	02-Jun-20	5.75	0.3948	5.7516	8.1754	20.0718
28	03-Jun-20	5.875	0.3351	5.4401	8.5466	20.1968
29	04-Jun-20	6	0.2869	5.1375	8.8974	20.3218
30	05-Jun-20	6.125	0.2401	4.7813	9.3004	20.4468
31	06-Jun-20	6.25	0.2035	4.4432	9.6751	20.5718

Table 6.

Attack Rate & Doubling time for high-risk groups.

	Ro = 1.5		R0 = 2.5		R0 = 3.5
Infectious function	Flat	peaked	Flat	peaked	Flat	peaked
Case on day 0	1	3	2	9	15	67
Case on day 10	6	124	67	690	29	309
Case on day 20	234	911	411	1075	309	969
Case on day 30	969	1520	1242	1821	1937	2757
Case on day 40	1596	2323	1755	4058	3023	6535
Case on day 50	2526	7204	5409	10,108	8718	13,967
Cases on day 60	8002	13,191	9674	15,512	14,753	22,333
Doubling time (days)	10	20	8	15	6	8
Eventual attack rate (%)	75%		85%		95%

Table 7.

Rate of Susceptible, infectious and recovered at a specified time interval.

	0 days	40 days	60 days	90 days
Susceptible individuals as on March 24 2020	126,370	1379	7219	17,179
Infected individuals as on May 20 2020	10	3023	22,333	36,841
Recovered individuals as on June 10 2020	0	13,191	5882	19,333
S + R + I	126,380	17,593	35,434	73,353

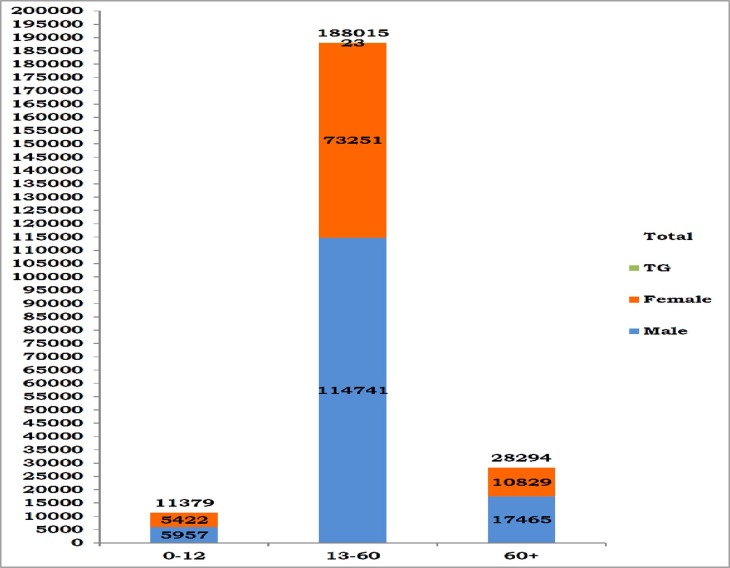
The figure below describes the age/gender wise impact of covid19 in Tamilnadu. The figure also represents seventeen transgender individuals infected by covid19. This impact of the demographic models with continuous age as represented by equation (18)

The growth factor = $\frac{\mathrm{\Delta }{N}_d}{\mathrm{\Delta }{N}_d-1}$

$$\frac{\partial N}{\partial t}=c(1-N/populationsize)N$$

The attack rate

It’s the measure of transmission and transmissibility.

$$\mathit{AR}=\frac{\mathit{cases}}{\mathit{populationsize}}$$ (28)

The attack rate contributes to the different cycles and the modes of the transmission of covid19. The implication depends on the population cluster size and the number of infected cases.

Secondary attack rate

$$\mathrm{S}\mathrm{A}\mathrm{R}=\frac{I-1}{N-1}$$

The SAR is the infectability rate of the individuals already infected by covid19 and recovered. The SAR contributes to the identification of the whether recovered patients are immunized for lifetime or for a few months.

Susceptible exposed attack rate

$$\mathrm{S}\mathrm{E}\mathrm{A}\mathrm{R}=\frac{\mathit{potential}infection}{\mathit{risk}ofinfectionongenrationoftransmission}$$

• $N_d$ = number of cases on a given day

• E = Average number of people infected through exposure each day

• P = probability of each exposure becoming an infection

$${\mathrm{\Delta }N}_d=\mathrm{E}.\mathrm{p}.N_d$$

$$N_{d+1}=N_d+E.p.N_d$$

$$N_{d+1}=\left(1+E.p\right)N_d$$

5. The simple model of contagion

The infected person enters the population and transmits to each person with probability p. k the number of people re-infected while being contagious for transmission of secondary infections [8].

$R_0$ = p.(k) the average number of secondary infections.

On the nth step the average number of infected people $R_0^n={\left(p\left(k\right)\right)}^n$

• $R_0>$1, the average grows geometrically as$R_0^n$

• $R_0<$1, the average shrinks geometrically as $R_0^n$

• When n$\to t$, geometric growth $\to$exponential growth

• $R_0=1$ $\to$ determines the threshold of infection for the new host population

5.1. SI model

$$S\to I$$

$$S\left(t\right)+I\left(t\right)=N$$

$\beta$ – transmission /infection rate, number of transmitting contacts per unit time, $T_c=\frac{1}{\beta }$ time between transmitting contact [6].

5.2. Infection equation

$$I\left(t+\delta t\right)=I\left(t\right)+\frac{\beta S\left(t\right)}{N}I\left(t\right)\delta t$$

$$\frac{dI\left(t\right)}{\mathit{dt}}=\frac{\beta S\left(t\right)}{N}I(t)$$

$$\frac{di\left(t\right)}{\mathit{dt}}=\beta s\left(t\right)i\left(t\right)$$

$$s\left(t\right)+i\left(t\right)=1$$

The differential equation is $i\left(t=0\right){=i}_0$

$$\frac{di\left(t\right)}{\mathit{dt}}=\beta \left(1-i\left(t\right)\right)i\left(t\right)$$

The logistic growth functions

$$i\left(t\right)=\frac{i_0}{i_0+{\left(1-i_0\right)}^{e^{-\beta t}}}$$

5.3. SIS model

S $\to$I $\to$S

$$S\left(t\right)+I\left(t\right)=N$$

$\beta$– infection rate, $\gamma$– recovery rate, $T_r\frac{1}{\gamma }\to$ average time to recovery

Infections equations

$$\frac{\mathit{ds}}{\mathit{dt}}=-\beta si+\gamma i$$

$$\frac{\mathit{di}}{\mathit{dt}}=\beta si-\gamma i$$

$$s+i=1$$

Differential equation i (t = 0) =$i_0$

$$\frac{\mathit{di}}{\mathit{dt}}=(\beta -\gamma -i)i$$

$$i\left(t\right)=\frac{\left(1-\frac{\gamma }{\beta }\right)C}{C}+e^{{\left(\beta -\gamma \right)}^t}$$

where $C=\frac{\beta i_0}{\beta }-\gamma -\beta i_0$ if $\beta >\gamma$, i(t) $\to (1-\frac{\gamma }{\mathit{beta}})$, $\beta <\gamma ,i\left(t\right)=i_0{e}^{{\left(\beta -\gamma \right)}^t}\to 0$

5.4. SIR model

$$S\to I\to R$$

$$S\left(t\right)+I\left(t\right)+R\left(t\right)=N$$

$$\beta -infectionrate,\gamma -recoveryrate$$

$$\frac{\mathit{ds}}{\mathit{dt}}=-\beta si$$

$$\frac{\mathit{di}}{\mathit{dt}}=\beta si-\gamma i$$

$$\frac{\mathit{dr}}{\mathit{dt}}=\gamma i$$

$$s+i+r=1$$

$$t=\frac{1}{\gamma }{\int }_0^r\frac{\mathit{dr}}{1-r-s_0{e}^{(}-\frac{\beta }{\gamma }r)}$$

$r_{\infty }-$ the total size of the outbreak

Epidemic threshold

$$R_0>1\beta >\gamma ,r_{\infty }=const>0$$

$$R_0<1,\beta <\gamma ,r_{\infty }\to 0$$

5.5. Basic reproduction number

$$R_0=\frac{\beta }{\gamma }=\frac{T_r}{T_c}$$

The average number of people infected before recovery is

$$R_0=E\left[\beta r\right]=\beta {\int }_0^{\infty }\gamma \tau e^{-\gamma \tau }d\tau =\beta /\gamma$$

5.6. SIER model

$$\frac{\mathit{ds}}{\mathit{dt}}=-aSI-dSE$$

$$\frac{\mathit{dE}}{\mathit{dt}}=-aSI-CE+dSE$$

$$\frac{\mathit{dC}}{\mathit{dt}}=CE-bI$$

$$\frac{\mathit{dr}}{\mathit{dt}}=bI$$

Let $\mu$ be birth and death rate,

$$\frac{\mathit{dy}}{\mathit{dx}}=-\mu S$$

$$\frac{\mathit{dy}}{\mathit{dx}}=$$

The probabilistic model process through different nodes as infected and recovered [14].

5.7. Node infection

$$p_{\mathit{inf}}\approx \beta s_i\left(t\right)\sum _{j\in N(i)}^{}{x}_j\left(t\right)\delta t$$

5.8. Node recovery

$$p_{\mathit{rec}}=\gamma X_i\left(t\right)\delta t$$

6. Results and discussions

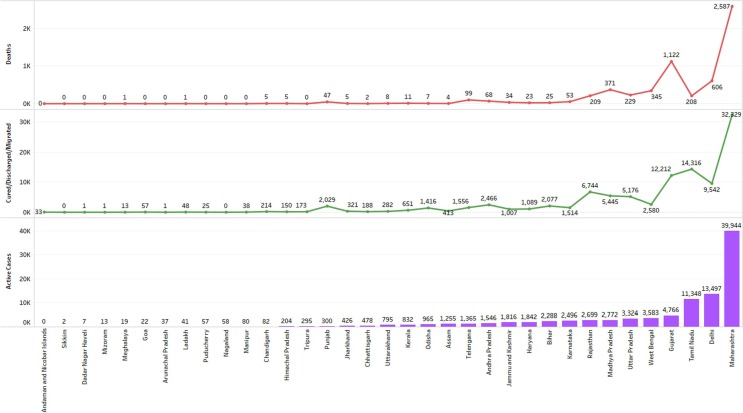
The figure below shows Indian state/UT wise details of Active cases of covid19 Pandemic in India till June 04.

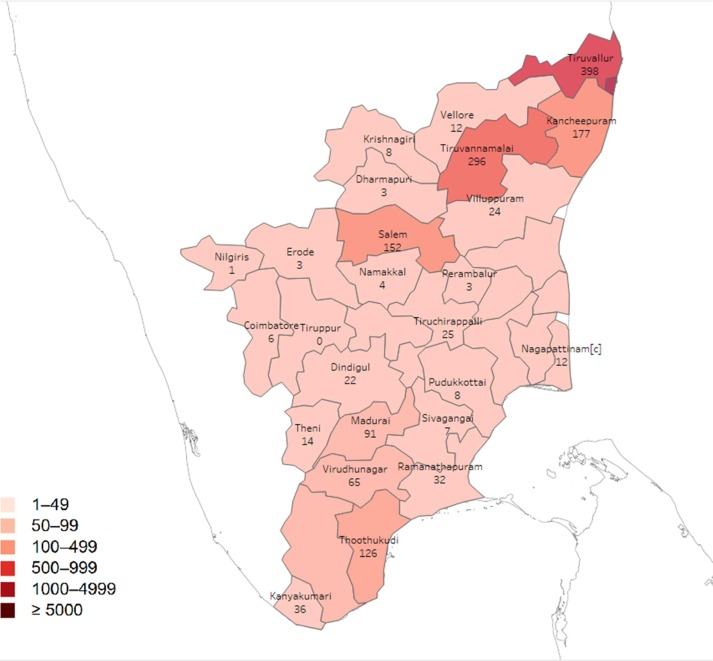
In this proposed study of covid19 infection in Tamilnadu, the dataset consists of cases district wise till 31 may 2020 is used. The status of individual district details is extracted from the Health & family welfare department government of Tamilnadu. The district-wise details of the covid19 status displayed in the sample table.

The different statistical measure models have evolved to predict the transmission of infectious viruses/ bacteria. The different measures taken into account depends on the geographical structure, climatic condition, and region-specific human practices. The infectious pathogens follow specific traits while infecting and spreading from host to host, creating a life cycle. The transmission rate and intensity may vary between interspecies transmission and human transmission, depending on whether the transmission is direct or intermediary. The infection rate is very low at the initial transmission between interspecies, while there is an exponential increase in human transmission.

6.1. Tamilnadu state Covid19 (SIR Model)

The study of Covid19 spread in Tamilnadu from May 07, 2020, within a population of 5,93,189 on June 10, 2020, with a positive confirmed case of 34,914 and the death toll of 307 with active cases at 16279.

The initial value of populations represented a $S_0=13.57410$, $I_0$ = 0.56340, $R_0$ = 0.18430

The recovery rate is calculated as

$$r=\frac{\mathit{infected}populationofTamilnaduon10June2020}{\mathit{susceptible}populationofTamilnadu}$$ (29)

$$=\frac{34914}{593189}$$

$$r=0.05764435$$

$$\frac{1}{a}=14incubationdaysinIndia$$

$$a=\frac{1}{14}=0.0714$$

$$\delta t=0.125$$

$$S_1=s_0-r$$

$$S_1=13.57410-(0.03156x0.56340x13.27410x0.125)$$

$$S_1=14.54014$$

$$I_1=I_0+\left(r_0{I}_0{s}_s-\alpha I_0\right)\delta t$$

$$S_1=0.56340+(0.3156x0.56340x13.57410-0.07143x0.56340)x0.4107)$$

$$S_1=0.591698$$

$$R_1=R_0+\alpha I_0\delta t$$

$$R_1=0.18430+0.074143x0.56340x0.1407$$

$$R_1=0.188996$$

$$N_d=1384$$

$$E=394.4103$$

$$P=1-\frac{1348}{72147030}$$

$$=0.99$$

$$N_{d+1}=394.4103x0.99x1348$$

$$=5,40,405.216648$$

The transmission of infection from infected to the susceptible persons is at 5,40,405. The recovery rate and the comorbidity rate of the covid19 varies predominantly as the geographical and climatic changes influence the spread. The attack rate and the susceptibility rate rapidly increase due to the adaption of the virus strain pertaining to the individual’s genetic morphology. The susceptible individuals are isolated with the impact of lockdown reducing the susceptibility rate of covid19.

6.2. Doubling time

The time the infectious disease doubles in number with $N_0$ as the initial number of infected cases

$T_d$ doubling period of the cases and $N_t$ the initial number of infected cases at time t.

$$N\left(t\right)=N_0{2}^{\frac{t}{T_{\left(d\right)}}}$$ (30)

The initial time and the doubling time taken to reproduce is reduced to seven days as the spread of the infection amplifies with the different strains and clusters of infection. The peak period of the infection is gradually increased as the imposition of the lockdown reduces the transmission cycle of covid19.

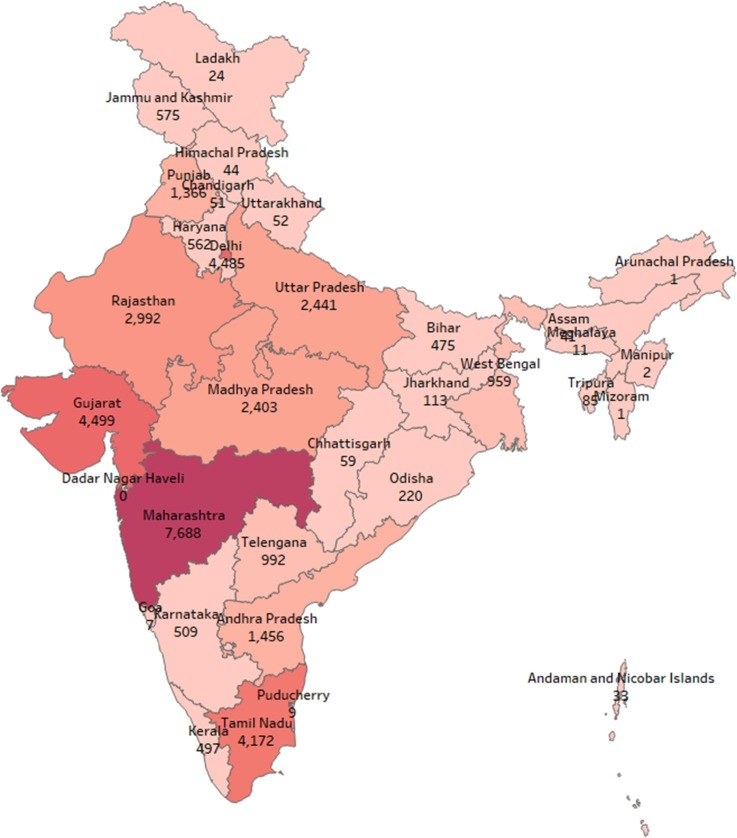
This model represents the SIR epidemic Model for Indian states with different geographical regions. The data is collected for a period of two and a half months and pre-processed to remove the missing and noisy data [13], [14]. The transformation from raw data to geospatial data is possible through QGIS, and mapping the shapefiles created through ArcGIS [5], [6], [7], [8], [9], [10], [11], [12]. A sample of the mapped data is, as shown in Fig. 13.

The Daily Testing statistics of the covid19 per lakh population in Tamilnadu is at 865 as on 15-06-2020 with the number of persons tested is at 6,42,201, and the number of samples tested is at 7,10,599. The daily testing statistics of the covid19 per lakh population in Tamilnadu is at 3760 as on 08–08-2020 with the number of persons tested is at 29,75,657.

7. Conclusion

Based on the data provided by the government of Tamilnadu, the SIR model, compared with the other compartmental model’s project, the outbreak will peak at the end of June and will start decreasing towards the end of August. Based on this model and the different parameters like the lockdown and the social distancing and applying face mask has postponed the infectious rate of transmission through May 2020 to June 2020. The proposed model compares the age/ gender wise social distancing to be for comparison through the dynamic models. The model specifies Doubling time and the attack rate at which the infection spreads. The inclusion of Tamilnadu State district wise rate of attack is necessary to determine the rate of spread of Covid19 at the district, town, and village panchayat levels. The flattening of the curve is ascertained by the end of August in Tamilnadu as the R₀ values are at an inflection point where the curve attains the period of a downtrend as the herd immunity increases as social distancing and personal protection becomes a daily ritual.

The estimated values of the data should be interpreted with caution as the data may vary based on the climatic condition, geographical variations and frequential history of susceptibility to infectious diseases. The important findings are to impose lockdowns that supress the transmission of the diseases, and isolate individuals with comorbidity. The covid19 $R_0$ value varies considerably for different models and moreover the reinfection rate of the already infected is unknown and the future impact of subsequent fatalities are unknown.

The mathematical numerical analysis conducted in the paper is more adaptive than the traditional models. The model can be extended to study the infective rate and the asymptotic infectious rate by including both the infected and the asymptotic undetected individuals. The model can be extended to other states characterized by similar geographic and climatic conditions and a closer reproductive rate $R_0$.

CRediT authorship contribution statement

Sukumar Rajendran: Conceptualization, Methodology, Software, Data curation, Visualization, Investigation. Prabhu Jayagopal: Supervision, Validation.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Biographies

Mr. Sukumar R received his Master of Engineering with specialization in Computer Science and Engineering from Anna University, Chennai, Tamilnadu, India and he received his B.Tech degree with specialization in Information Technology degree from Arulmigu Meenakshi Amman College of engineering affiliated to Madras University in 2004 located in Kanchipuram, Tamilnadu India. Now he is pursuing his PhD in Vellore Institute Technology, Vellore, Tamilnadu, India. His research interests are Natural Language Processing, Privacy, and Machine Learning.

Dr. Prabhu J received his Ph.D. (Computer science and Engineering) and Master of Computer Science and Engineering from Satyabhama University, Chennai, Tamil Nadu, India and he received his B.Tech degree from the Department of Information Technology, Vellore Engineering College, Affiliated to Madras University in 2004 located at Vellore, Tamil Nadu, India. He worked as an Assistant Professor in various Engineering colleges for more than 13 years. Now he is working as an Associate Professor in the Department of Software Systems and Engineering, School of Information Technology and Engineering, Vellore Institute Technology, Vellore, Tamil Nadu, India. His research interests are software testing, Software Quality Assurance, and big data.