Skip to main content
PMC home page
Elsevier - PMC COVID-19 Collection logoLink to Elsevier - PMC COVID-19 Collection
. 2020 Sep 17;760:138006. doi: 10.1016/j.cplett.2020.138006

Structural parameters and electronic properties of 2D carbon allotrope: Graphene with a kagome lattice structure

B Sarikavak-Lisesivdin a,b, SB Lisesivdin a,b,⁎, E Ozbay c,d,e, F Jelezko b,f
PMCID: PMC7494512  PMID: 32958962

Graphical abstract

graphic file with name ga1_lrg.jpg

Open in a new tab

Keywords: Two-dimensional material, Carbon allotrope, Density functional theory, Kagome lattice

Highlights

  • •

    Structure parameters and electronic properties of graphene with kagome lattice structure is calculated.

  • •

    Various XC and dispersion correction methods are used and similar results are obtained.

  • •

    Pristine graphene with kagome lattice structure shows very small magnetic properties.

  • •

    A kagome flat-band structure is observed near the EF.

  • •

    High DOS at flat-band is mostly consisting of pz orbital and also dxz and dyz orbital contributions.

Abstract

In this paper, the electronic properties of a carbon allotrope, graphene with a kagome lattice structure, are investigated. Spin-polarized density functional theory (DFT) calculations with Grimme dispersion corrections were done. Bond lengths, electronic band structure, and projected density of states were calculated. Electronic band structure calculations show kagome flat-band formation with higher d-orbital contributed bonding behavior than the pristine graphene structure. The structural parameters and electronic band results of this 2D carbon allotrope show wider possible usage in many applications from desalination membranes to possible high-temperature superconductors.

1. Introduction

Because of its unique properties and possible promising applications, graphene has attracted an important amount of attention both experimentally and theoretically since its first experimental isolation and characterization reported by Novoselov et al. [1]. With the triggered interest in graphene, searching for different carbon nanomaterials, graphene-derivatives and allotropes have also gained huge interest [2], [3]. These new carbon materials have superior mechanical, electronic, and thermal features, which makes them implemented in many applications of semiconductor devices, such as electronic components [4], and gas sensors [5]. In addition to these small device applications, new carbon materials, especially graphene and graphene oxide with pores, are proposed to be used as a nanofiltration membrane for desalination, drinking water production, water reuse and wastewater treatment applications [6], [7]. Also, on reusable or single-use personal protective equipment (PPE) or filters in air purification and air-conditioning devices, coated with modified nanomaterials like graphene or graphene-oxide with pores can enhance the repellent SARS-CoV-2 or similar viruses [8]. With the COVID-19 outbreak, it is well understood that the usage of enhanced filters is necessarily required to prevent aerosol transmission even in daily life.

The variety of proposed and implemented applications with new carbon materials also motivates the studies on new two-dimensional (2D) carbon allotropes. Some of the novel theoretical 2D allotrope studies including radialene [9], pentaheptite [10], haeckelites [11], graphdiyne [12], biphenylene [13], T-carbon [14], T graphene [15], net W and C carbon structures [16], graphenylene [17], pentahexoctite [18], penta-graphene [19], alpha-graphyne [20], twin-graphene [21], THD-graphene [22], DHP-graphene [23], tetrahexcarbon [24], net Y carbon [25] and D-Carbon [26] can be listed with respect to their date of report. In addition to these theoretical studies, T-carbon was experimentally observed as T-carbon nanowires in Zhang et al.’s study in 2017 [27]. And in 2018, D-Carbon was suggested to be experimentally possible due to satisfactorily match of previously unexplained X-Ray Diffraction (XRD) peak of a measured chimney or detonation soot [28], [29] powder to calculated D-carbon XRD peaks [26].

With these recent signs of progress and possible future developments in experimental studies of new carbon allotropes, the electronic properties of the carbon allotrope with a kagome lattice [30], [31], [32], and kagome-like 2D metamaterials [33] took attention recently. In this study, the electronic properties and the structural parameters of graphene with a kagome lattice structure are investigated with implementing the density functional theory (DFT) method.

2. Computational details

Our DFT calculations are carried out using the Atomistic Toolkit (ATK) software v.2017.2 [34]. Spin-polarized generalized gradient approximation (SGGA) was used for exchange-correlation (XC) functional and the double-ζ (DZ) orbital basis set is adopted. For SGGA calculations, Perdew, Burke, and Ernzerhof (PBE) [35] functionals were used purely and also with Grimme D2 dispersion correction. For further calculations, RPBE functional [36] was used with Grimme D3 dispersion correction.

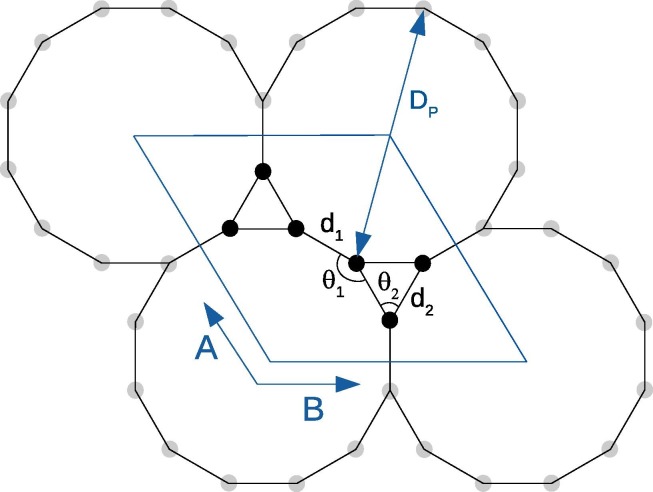
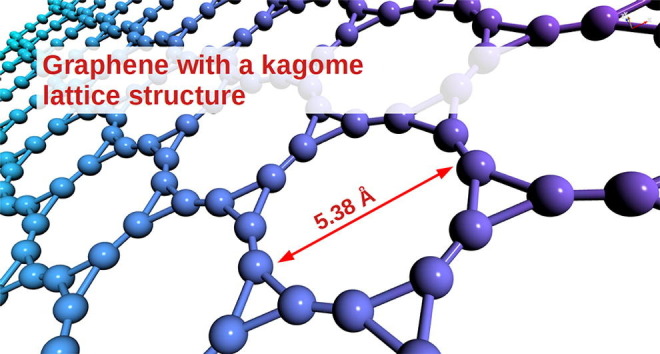
Fig. 1 (a) and (b) show the structure of the investigated structure’s unit cell. The unit cell consists of 6 identical carbon atoms. All carbon atoms have a similar bonding scheme with 3 bonds like graphene. One of the mentioned bonds is represented with d1 and the other two bonds are identical and represented as d2 in Fig. 1. Bonds with d2 length resulted in a cyclopropatriene-like (CP-like) structures [37] with triangular gaps between dodecagonal structures. From a different point of view, a CP-like structure is bonding with three neighbor CP-like structures and the dodecagonal structures with Dp diameter wide “gaps” occur. In this study, the “gap” represents this wide space inside the dodecagonal structures. The equilateral triangular structure of CP-like structures requires the bond angles of 60° between carbon-carbon with a covalent bond nature. The cut-off energy is used as 600 Ryd and Monkhorst-Pack k-point grid is chosen as 10 × 10 × 1 to sample Brillouin zone energy calculations. The two layers are separated with a 15 Å vacuum space, therefore the whole structure is accepted to be a two-dimensional structure. For the geometrical optimization, the maximum force on each atom is set to be smaller than 0.005 eV/Å.

Fig. 1.

Fig. 1

Open in a new tab

Unit cell of graphene with a kagome lattice structure. All six carbon atoms are equivalent and are connected to other atoms with one d1-long and two d2-long bonds.

3. Results and discussion

The optimized structural parameters for the investigated structure with SGGA methods are summarized in Table 1 . The C-C bond length between CP-like structures (d1 ~ 1.36 Å) exhibits a featured characteristic of the double bond. The C-C bonds of CP-like structure (d1 ~ 1.43 Å) represent similarity with sp2-sp or sp2 bonding. However, unconventional bent bond angles of 60° and 150° raise questions for explaining the bonds with known hybridizations (trigonal sp2 or sp2-sp5 doublets) [38] and needs a better explanation. Also, bent bonds are known to result in the possibility of high chemical reactivity [39]. The calculated bond angles are not given in Table 1, because of obtaining perfect 60° and 150° for all three methods. The diameter of the dodecagon pores is also calculated and listed in Table 1. As can be seen from table 1, the pore diameter is found smaller with the SGGA-PBE method. All methods result ~5.38 Å of diameter, which is a suitable value for a salt filtration application. The salt rejection ability of a graphene-like membrane is known to decrease with an increase in pore size [7]. The study of Cohen-Tanugi and Grossman shows that most salt ions can pass through graphene with pores of diameter above 5.5 Å [40]. Therefore, the pore diameter of graphene-like 2D carbon allotropes should be below this value to successfully filter Na+ and Cl− ions from water, where graphene with a kagome lattice structure fulfills this requirement and also have a very high porosity value of ~97%. With the possible experimental proof in the future, graphene membranes with a kagome lattice structure having a very high porosity value may open the possibility of the low pressure or passive desalination applications and also can be used on reusable or single-use PPE or on filters in air purification and air-conditioning devices to prevent virus transmission. Graphene is already suggested as single flakes and sheet with defects in these applications and with the possible experimental confirmation of graphene with kagome lattice structure, there will be no need for introducing defects in the structure for increasing selective permeability.

Table 1.

Optimized lattice constant (a), bond length (d), and pore diameter (DP) values for dodecagon holes for the investigated structure for SGGA-PBE, SGGA-PBE with Grimme D2 correction, and SGGA-RPBE with Grimme D3 correction methods.

Method a (Å) d1 (Å) d2 (Å) DP (Å)
SGGA-PBE 5.2085 1.3559 1.4305 5.3817
SGGA-PBE with Grimme D2 5.2086 1.3554 1.4304 5.3821
SGGA-RPBE with Grimme D3 5.2087 1.3567 1.4299 5.3829
Open in a new tab

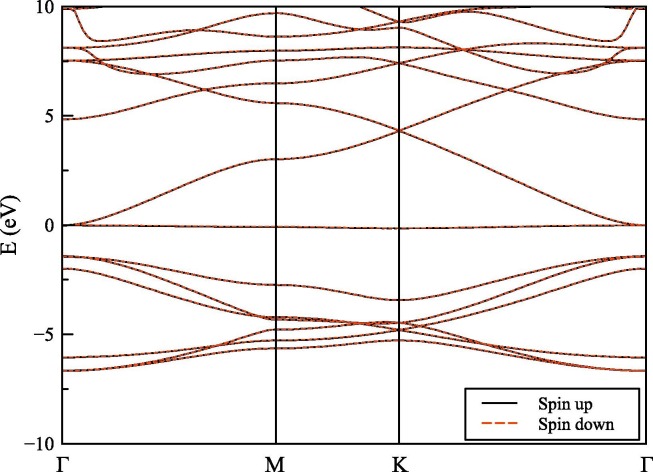
Fig. 2 shows the spin-dependent electronic band structure of the graphene with a kagome lattice structure. Band structure in the figure is calculated with SGGA-PBE. However, other methods gave similar results and will be discussed shortly after. As seen in Fig. 2, the band structure has a similar behavior for spin-up and spin-down electrons. Therefore, it is seen that the non-interacting pristine graphene with a kagome lattice structure shows a very small magnetic nature as the pristine graphene sheet. However, it is already shown that the DFT calculations of graphene with a kagome lattice structure with doping by reducing the density of valence electrons (hole doping) makes the flat-band partially filled [30]. This type of doping can be done with the electrostatic gating, and it is highly known that graphene has a similar behavior [41]. This type of doping results in a ferromagnetic flat-band formation where it is possible to explore new exotic phases by tuning the filling factor of the flat-band. There is a graphene-like linear band formation at K-point. However, it is not located at the Fermi level (EF). Also, it is clear that the kagome flat-bands emerge around the EF [30]. This kagome flat-bands are important because the electrons are confined in a very narrow energy interval with a huge number of density of states (DOS) which may be related with Wigner-crystallization [30], [42], flat-band ferromagnetism [43], fractional quantum Hall states [44] and a possibility of a high-temperature-superconductivity [45].

Fig. 2.

Fig. 2

Open in a new tab

The spin-dependent electronic band structure of the investigated structure was calculated with SGGA-PBE functional.

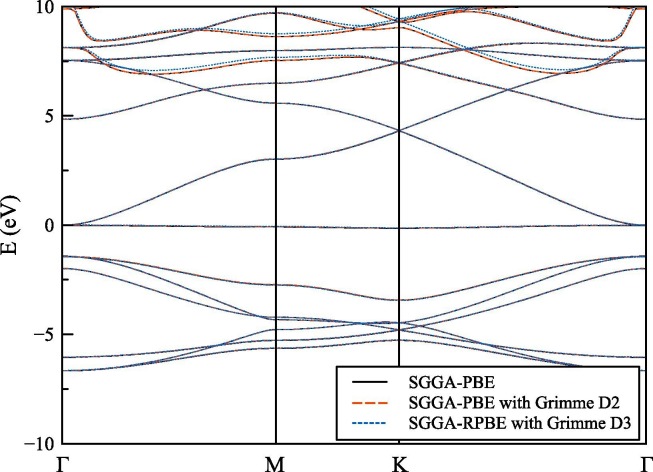
In Fig. 3 , electronic band structure calculation for structure for SGGA-PBE, SGGA-PBE with Grimme D2 dispersion correction, and SGGA-RPBE with Grimme D3 dispersion correction methods for only spin-up states were shown. Band structures of spin-down states are similar and not shown in the figure for clarity. As can be seen from the figure, SGGA-PBE with Grimme D2 dispersion correction results are similar to legacy SGGA-PBE calculations show high similarity among the all investigated momentum and energy space. Energy values for SGGA-RPBE with Grimme D3 dispersion correction method is seemed to be shifted further away from the EF. SGGA-PBE method is providing adequate results with a lower computational cost for the pristine graphene with a kagome lattice structure. The similarity of SGGA-PBE with Grimme D2 dispersion correction method and for SGGA-RPBE with Grimme D3 correction method results with legacy SGGA-PBE calculation results can be expected because of there is a large 15 Å vacuum space over a single layer structure where van der Waals interactions are not playing a significant role in the overall structure. In fact, showing these similarities also confirms that our results belong to an isolated single layer system.

Fig. 3.

Fig. 3

Open in a new tab

Electronic band structure calculation for structure for SGGA-PBE, SGGA-PBE with Grimme D2 dispersion correction, and SGGA-RPBE with Grimme D3 dispersion correction methods. For clarity, only spin up states were shown.

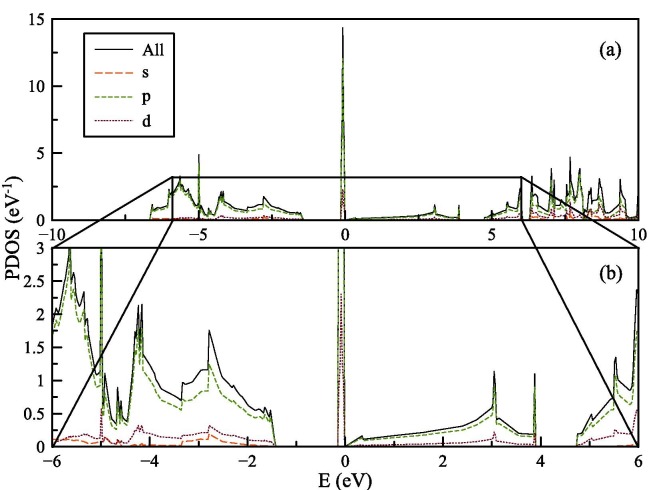
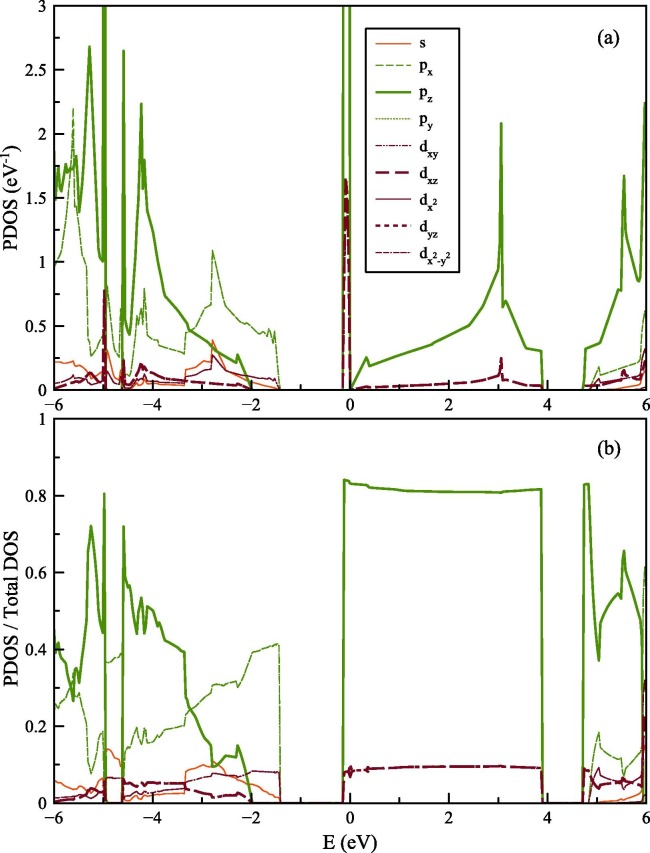
In Fig. 4 (a) and (b), the projected density of states (PDOS), which are calculated with SGGA-PBE functional, are shown for only spin-up states. As pointed before, the values of spin-down states are similar and not shown in the figure for clarity. High numbers of states are observed at kagome flat-band located at the EF. In the near vicinity of EF, only states of p and d orbitals are found.

Fig. 4.

Fig. 4

Open in a new tab

(a) PDOS for graphene with graphene with kagome lattice structure, (b) details of the PDOS between −6 and 6 eV.

To understand the nature of the bonds in the graphene with a kagome lattice structure, DOS is projected onto orbitals of carbon atoms for SGGA-PBE calculations as shown in Fig. 5 (a). The main peak at the EF is mostly consisting of electronic states of the pz orbital (l = 1, ml = 0). The main peak at the EF is also consisting of electronic states of dxz and dyz orbitals (l = 2, ml = ±1). pz do hybridize with dxz and dyz orbitals, forming together the π band [46]. The contribution of dxz and dyz orbitals to the total electronic states at EF is more significant in graphene with a kagome lattice structure than the pristine graphene structure. With the same calculation parameters, the each d-orbital's states near to Dirac point in pristine graphene structure are found to be 7% of total pz + dxz + dyz states. However, in graphene with a kagome lattice structure, the each d-orbital's states at EF is found to be 9% as can be seen in Fig. 5 (b). From Fig. 5 (b) the long-range unvarying π bonding (pz hybrid with dxz and dyz orbitals) behavior can be observed between 0 and 4 eV and also can be observed in the near vicinity of Dirac point which is located at 4.31 eV. It is important to point that the density of states with dxz and dyz orbitals follows in shape that of p z, which results the long-range unvarying π bonding mentioned above. The similarity of the shape of density of states of dxz and dyz orbitals to the pz, is found to in agreement with Gmitra et al.’s study for the pristine Graphene [47].

Fig. 5.

Fig. 5

Open in a new tab

(a) PDOS onto orbitals of carbon atoms in Graphene with Kagome lattice structure (b) Normalized PDOS onto orbitals concerning total DOS.

4. Conclusion

In this study, structural parameters and the electronic band structure of graphene with kagome lattice structure is theoretically studied. Spin-polarized DFT calculations were done with SGGA-PBE, SGGA-PBE with Grimme D2 correction, and SGGA-RPBE with Grimme D3 correction methods. All methods resulted in similar bond lengths and similar electronic band structure and density of state distributions. A kagome flat-band structure is observed near the EF and high number of electronic states at this kagome flat-band is mostly consisting of pz orbital and also dxz and dyz orbital contributions with a π bonding behavior. Also, d-orbital contribution near K-point in graphene with a kagome lattice structure is found to be larger than the related contribution observed in the pristine graphene. The reason for the high contribution of d-orbital states between 0 and 4 eV needs more quantitative investigation that the plane-wave approach can be utilized in addition to the already implemented linear combination of the atomic orbitals approach. This 2D carbon allotrope, which has a novel electronic structure, can be a promising structure for many possible electronic device applications or it may be used mechanically in desalination applications because of suitable pore size and density of dodecagons in its structure.

CRediT authorship contribution statement

B. Sarikavak-Lisesivdin: Conceptualization, Formal analysis, Methodology, Writing - original draft. S.B. Lisesivdin: Visualization, Writing - original draft. E. Ozbay: Software, Project administration, Supervision. F. Jelezko: Resources, Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

S.B.L. was supported in part by the Distinguished Young Scientist Award of the Turkish Academy of Sciences (TUBA-GEBIP 2016). E.O. acknowledges partial support from the Turkish Academy of Sciences.

References

  • 1.Novoselov K.S., Geim A.K., Morozov S.V., Jiang D., Zhang Y., Dubonos S.V., Grigorieva I.V., Firsov A.A. Electric field effect in atomically thin carbon films. Science. 2004;306:666–669. doi: 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
  • 2.Hirsch A. The era of carbon allotropes. Nat. Mater. 2010;9:868–871. doi: 10.1038/nmat2885. [DOI] [PubMed] [Google Scholar]
  • 3.Georgakilas V., Perman J.A., Tucek J., Zboril R. Broad family of carbon nanoallotropes: classification, chemistry, and applications of fullerenes, carbon dots, nanotubes, graphene, nanodiamonds, and combined superstructures. Chem. Rev. 2015;115:4744–4822. doi: 10.1021/cr500304f. [DOI] [PubMed] [Google Scholar]
  • 4.Li G., Yang J., Yang W., Wang F., Wang Y., Wang W., Liu L. Label-free multidimensional information acquisition from optogenetically engineered cells using a graphene transistor. Nanoscale. 2018;10:2285–2290. doi: 10.1039/c7nr07264c. [DOI] [PubMed] [Google Scholar]
  • 5.Yoon H.J., Yang J.H., Zhou Z., Yang S.S., Cheng M.M.C. Carbon dioxide gas sensor using a graphene sheet. Sens. Actuat. B-Chem. 2011;157:310–313. [Google Scholar]
  • 6.Surwade S.P., Smirnov S.N., Vlassiouk I.V., Unocic R.R., Veith G.M., Dai S., Mahurin S.M. Water desalination using nanoporous single-layer graphene. Nat. Nanotechnol. 2015;10:459–464. doi: 10.1038/nnano.2015.37. [DOI] [PubMed] [Google Scholar]
  • 7.Anand A., Unnikrishnan B., Mao J.-Y., Lin H.-J., Huang C.-C. Graphene-based nanofiltration membranes for improving salt rejection, water flux and antifouling–a review. Desalination. 2018;429:119–133. [Google Scholar]
  • 8.Raghav P.K., Mohanty S. Are graphene and graphene-derived products capable of preventing COVID-19 infection? Med. Hypotheses. 2020;144:110031. doi: 10.1016/j.mehy.2020.110031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Boldi A.M., Diederich F. Expanded radialenes: a novel class of cross-conjugated macrocycles. Angew. Chem. Int. Ed. 1994;33:468–471. [Google Scholar]
  • 10.Crespi V.H., Benedict L.X., Cohen M.L., Louie S.G. Prediction of a pure-carbon planar covalent metal. Phys. Rev. B. 1996;53:R13303. doi: 10.1103/physrevb.53.r13303. [DOI] [PubMed] [Google Scholar]
  • 11.Terrones H., Terrones M., Hernández E., Grobert N., Charlier J.C., Ajayan P.M. New metallic allotropes of planar and tubular carbon. Phys. Rev. Lett. 2000;84:1716–1719. doi: 10.1103/PhysRevLett.84.1716. [DOI] [PubMed] [Google Scholar]
  • 12.Li G., Li Y., Liu H., Guo Y., Li Y., Zhu D. Architecture of graphdiyne nanoscale films. Chem. Commun. 2010;46:3256–3258. doi: 10.1039/b922733d. [DOI] [PubMed] [Google Scholar]
  • 13.Hudspeth M.A., Whitman B.W., Barone V., Peralta J.E. Electronic properties of the biphenylene sheet and its one-dimensional derivatives. ACS Nano. 2010;4:4565–4570. doi: 10.1021/nn100758h. [DOI] [PubMed] [Google Scholar]
  • 14.Sheng X.-L., Yan Q.-B., Ye F., Zheng Q.-R., Su G. T-carbon: a novel carbon allotrope. Phys. Rev. Lett. 2011;106:155703. doi: 10.1103/PhysRevLett.106.155703. [DOI] [PubMed] [Google Scholar]
  • 15.Liu Y., Wang G., Huang Q., Guo L., Chen X. Structural and electronic properties of graphene: a two-dimensional carbon allotrope with tetrarings. Phys. Rev. Lett. 2012;108:225505. doi: 10.1103/PhysRevLett.108.225505. [DOI] [PubMed] [Google Scholar]
  • 16.Wang X.-Q., Li H.-D., Wang J.-T. Prediction of a new two-dimensional metallic carbon allotrope. Phys. Chem. Chem. Phys. 2013;15:2024–2030. doi: 10.1039/c2cp43070c. [DOI] [PubMed] [Google Scholar]
  • 17.Song Q., Wang B., Deng K., Feng X., Wagner M., Gale J.D., Müllen K., Zhi L. Graphenylene, a unique two-dimensional carbon network with nondelocalized cyclohexatriene units. J. Mater. Chem. C. 2013;1:38–41. [Google Scholar]
  • 18.Sharma B.R., Manjanath A., Singh A.K. pentahexoctite: a new two-dimensional allotrope of carbon. Sci. Rep. 2014;4:7164. doi: 10.1038/srep07164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Zhang S., Zhou J., Wang Q., Chen X., Kawazoe Y., Jena P. Penta-graphene: a new carbon allotrope. Proc. Natl. Acad. Sci. USA. 2015;112:2372–2377. doi: 10.1073/pnas.1416591112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Qin X., Liu Y., Chi B., Zhao X., Li X. Origins of Dirac cones and parity dependent electronic structures of α-graphyne derivatives and silagraphynes. Nanoscale. 2016;8:15223–15232. doi: 10.1039/c6nr03603a. [DOI] [PubMed] [Google Scholar]
  • 21.Jiang J.-W., Leng J., Li J., Guo Z., Chang T., Guo X., Zhang T. Twin graphene: a novel two-dimensional semiconducting carbon allotrope. Carbon. 2017;118:370–375. [Google Scholar]
  • 22.Xu X., Jiang B., Guo Y., Cai Y. THD-graphene used for a selective gas detector. Mater. Chem. Phys. 2017;200:50–56. [Google Scholar]
  • 23.Cai Y., Guo Y., Jiang B., Lv Y. Encapsulation of cathode in lithium-sulfur batteries with a novel two-dimensional carbon allotrope: DHP-graphene. Sci. Rep. 2017;7:14948. doi: 10.1038/s41598-017-15010-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Ram B., Mizuseki H. Tetrahexcarbon: a two-dimensional allotrope of carbon. Carbon. 2018;137:266–273. [Google Scholar]
  • 25.Rong J., Dong H., Feng J., Wang X., Zhang Y., Yu X., Zhan Z. Planar metallic carbon allotrope from graphene-like nanoribbons. Carbon. 2018;135:21–28. [Google Scholar]
  • 26.Fan D., Lu S., Golov A.A., Kabanov A.A., Hu X. D-carbon: ab initio study of a novel carbon allotrope. J. Chem. Phys. 2018;149:114702. doi: 10.1063/1.5037380. [DOI] [PubMed] [Google Scholar]
  • 27.Zhang J., Wang R., Zhu X., Pan A., Han C., Li X., Zhao D., Ma C., Wang W., Su H., Niu C. Pseudo-topotactic conversion of carbon nanotubes to T-carbon nanowires under picosecond laser irradiation in methanol. Nature Commun. 2017;8:683. doi: 10.1038/s41467-017-00817-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Chen P., Huang F., Yun S. Characterization of the condensed carbon in detonation soot. Carbon. 2003;41:2093–2099. [Google Scholar]
  • 29.Pantea D., Brochu S., Thiboutot S., Ampleman G., Scholz G. A morphological investigation of soot produced by the detonation of munitions. Chemosphere. 2006;65:821–831. doi: 10.1016/j.chemosphere.2006.03.027. [DOI] [PubMed] [Google Scholar]
  • 30.Chen Y., Xu S., Xie Y., Zhong C., Wu C., Zhang S.B. Ferromagnetism and Wigner crystallization in kagome graphene and related structures. Phys. Rev. B. 2018;98:035135. [Google Scholar]
  • 31.Li Z., Xie Y., Chen Y. Three-dimensional Kagome graphene networks and their topological properties. Comput. Mater. Sci. 2020;173:109406. [Google Scholar]
  • 32.Zhou J., Xie Y., Zhang S., Chen Y. Critical topological nodal points and nodal lines/rings in Kagome graphene. Phys. Chem. Chem. Phys. 2020;22:8713–8718. doi: 10.1039/d0cp00190b. [DOI] [PubMed] [Google Scholar]
  • 33.Liu D., Kim E., Weck P.F., Tománek D. Strain-controlled magnetic ordering in 2D carbon metamaterials. Carbon. 2020;161:219–223. [Google Scholar]
  • 34.Smidstrup S., Markussen T., Vancraeyveld P., Wellendorff J., Schneider J., Gunst T., Verstichel B., Stradi D., Khomyakov P.A., Vej-Hansen U.G., Lee M.-E., Chill S.T., Rasmussen F., Penazzi G., Corsetti F., Ojanperä A., Jensen K., Palsgaard M.L.N., Martinez U., Blom A., Brandbyge M., Stokbro K. QuantumATK: an integrated platform of electronic and atomic-scale modelling tools. J. Phys.: Condens. Matter. 2020;32:015901. doi: 10.1088/1361-648X/ab4007. [DOI] [PubMed] [Google Scholar]
  • 35.Perdew J.P., Burke K., Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  • 36.Hammer B., Hansen L.B., Nørskov J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B. 1999;59:7413. [Google Scholar]
  • 37.Rogers D.W., McLafferty F. G2 ab initio calculations of the enthalpies of formation of C3 hydrocarbons. J. Phys. Chem. 1995;99:1375–1376. [Google Scholar]
  • 38.Bernett W.A. A unified theory of bonding for cyclopropanes. J. Chem. Edu. 1967;44:17–23. [Google Scholar]
  • 39.Lukina M.Y. Structure and reactivity of cyclopropane and its derivatives. Rus. Chem. Rev. 1962;31:419–438. [Google Scholar]
  • 40.Cohen-Tanugi D., Grossman J.C. Water desalination across nanoporous graphene. Nano Lett. 2012;12:3602–3608. doi: 10.1021/nl3012853. [DOI] [PubMed] [Google Scholar]
  • 41.Liu X., Oostinga J.B., Morpurgo A.F., Vandersypen L.M. Electrostatic confinement of electrons in graphene nanoribbons. Phys. Rev. B. 2009;80:121407. [Google Scholar]
  • 42.Wu C., Das Sarma S. px,y-orbital counterpart of graphene: cold atoms in the honeycomb optical lattice. Phys. Rev. B. 2008;77:235107. [Google Scholar]
  • 43.Tasaki H. From Nagaoka's ferromagnetism to flat-band ferromagnetism and beyond: an introduction to ferromagnetism in the Hubbard model. Prog. Theo. Phys. 1998;99:489. [Google Scholar]
  • 44.Neupert T., Santos L., Chamon C., Mudry C. Fractional quantum Hall states at zero magnetic field. Phys. Rev. Lett. 2011;106 doi: 10.1103/PhysRevLett.106.236804. [DOI] [PubMed] [Google Scholar]
  • 45.Miyahara S., Kusuta S., Furukawa N. BCS theory on a flat band lattice. Physica C. 2007;460:1145. [Google Scholar]
  • 46.Konschuh S., Gmitra M., Fabian J. Tight-binding theory of the spin-orbit coupling in graphene. Phys. Rev. B. 2010;82 [Google Scholar]
  • 47.Gmitra M., Konschuh S., Ertler C., Ambrosch-Draxl C., Fabian J. Band-structure topologies of graphene: spin-orbit coupling effects from first principles. Phys. Rev. B. 2009;80 [Google Scholar]

Articles from Chemical Physics Letters are provided here courtesy of Elsevier

RESOURCES