Which bilinguals reverse language dominance and why?

Abstract

When naming pictures in mixed-language blocks, bilinguals sometimes exhibit reversed language dominance effects. These have been attributed to proactive inhibitory control of the dominant language, or adaptation of language-specific selection thresholds. Even though reversed dominance arguably provides the most striking evidence of inhibition, few studies have focused on when and why this effect occurs. We investigated this topic in a large data set (>400 bilinguals) using a continuous and objective measure of language dominance. We found larger reversed language dominance effects in more (vs. less) balanced bilinguals in mixed-language blocks. However, after taking into account standard language dominance effects in single-language blocks, the extent to which dominance effects changed across block types was actually significantly smaller for more balanced bilinguals, which is in line with the inhibitory control account. Interestingly, dominance reversal was not associated with increased overall speed in the mixed-language block. Thus, dominance reversal is more likely in balanced bilinguals not because they are better at applying proactive control, but because they are more likely to overshoot when the goal is to make both languages about equally accessible – and overall, unbalanced bilinguals apply more proactive control than balanced bilinguals to facilitate picture naming in mixed-language blocks.

Introduction

Bilinguals rely on multiple language control mechanisms, likely applied at multiple different processing levels, to enable them to produce words in the appropriate language and to minimize cross-language interference during bilingual language production. A striking signature of language control, which is sometimes found when bilinguals name pictures in mixed-language blocks, consists of worse performance in the dominant language than in the nondominant language (e.g., Christoffels, Firk, & Schiller, 2007; Costa & Santesteban, 2004; Gollan & Ferreira, 2009; Heikoop, Declerck, Los, & Koch, 2016; Kleinman & Gollan, 2018; Verhoef, Roelofs, & Chwilla, 2009; for a review, see Declerck, 2020). This so-called reversed language dominance effect is referred to as “reversed” because the dominance pattern is the opposite of what is typically observed in single-language blocks.

Reversed dominance is most often explained in terms of proactive inhibition of the dominant language, to improve performance in the mixed-language blocks (e.g., Christoffels et al., 2007; Declerck, 2020; Gollan & Ferreira, 2009; Kleinman & Gollan, 2018). This inhibition is the result of a top-down control process that aims to resolve any anticipated language interference (for a review, see Declerck, 2020). Based on this inhibitory account, bilinguals with similar proficiency levels in their two languages, i.e. balanced bilinguals, should need little to no inhibition, since they have relatively similar language proficiency across both languages. Meanwhile, less balanced bilinguals, who start out with a larger disparity between languages, should benefit more from proactive inhibition of the dominant language. On this basis, less balanced bilinguals might be expected to show larger reversed dominance effects (or, similarly, be more likely to show reversed dominance effects of any size) than balanced bilinguals, especially if determining how much inhibition to apply or actually applying that inhibition is a noisy (imperfect) process.

However, this does not seem to be in line with the literature, which – if anything – suggests the opposite. While some studies that examined performance in mixed-language blocks with unbalanced bilinguals reported reversed dominance effects (e.g., Heikoop et al., 2016; Liu, Timmer, Jiao, Yuan, & Wang, 2019; Peeters & Dijkstra, 2018), others did not (e.g., Jackson, Swainson, Cunnington, & Jackson, 2001; Ma, Li, & Guo, 2016; Meuter & Allport, 1999; Wang, Kuhl, Chen, & Dong, 2009). Instead, highly proficient (and likely more balanced) bilinguals are the ones who tend to show reversed dominance effects more reliably (e.g., Bonfieni, Branigan, Pickering, & Sorace, 2019; Costa & Santesteban, 2004; Costa, Santesteban, & Ivanova, 2006; de Bruin, Samuel, & Duñabeitia, 2018; Martin et al., 2013; however, see Declerck, Thoma, Koch, & Philipp, 2015). For example, Costa and Santesteban (2004) found reversed language dominance in highly balanced bilinguals across four experiments. The same bilinguals also exhibited symmetrical (i.e., equally sized) switch costs in the two languages, thereby not exhibiting a different commonly cited marker of inhibitory control (asymmetrical switch costs, in which switch costs are larger in the dominant than the nondominant language; Meuter & Allport, 1999). Since reversed dominance was observed with highly balanced bilinguals but asymmetrical switch costs were not, the authors proposed a different account of reversed dominance effects that does not rely on inhibitory control. They proposed that reversed dominance is caused by a control mechanism that develops only in proficient bilinguals: the ability to set different selection thresholds for each language, with a higher threshold for the dominant than for the nondominant language in mixed language blocks. In turn, this would mean that only very balanced bilinguals would be able to show a reversed dominance effect.

Here too, however, not all the evidence points in this direction. While Korean-speaking learners of Spanish did not exhibit reversed dominance in Costa and Santesteban (2004), Catalan-speaking learners of Spanish who were not proficient in Spanish did exhibit reversed dominance effects (in addition to showing asymmetrical switch costs). As indicated above, other studies also found reversed dominance with unbalanced bilinguals (e.g., Heikoop et al., 2016; Liu et al., 2019; Peeters & Dijkstra, 2018). Additionally, Costa et al. (2006) found reversed dominance in multilinguals switching between any combinations of their top-three most proficient languages, but no reversed dominance when switching between the dominant language and a newly acquired language. The latter finding is inconsistent with the proposal that highly proficient bilinguals develop different control mechanisms (which can then be applied to any known languages), and instead suggests that the proficiency level of the weaker language determines whether or not dominance reverses. Note, however, that the participants in this study learned the words of the new language just prior to the language-switching task. Costa and colleagues concluded that because these newly created lexical representations were not well established, bilinguals could not apply a language-specific selection mechanism to lower their selection threshold, resulting in reversed language dominance. Another study by Santesteban and Costa (2016) directly compared less and more proficient bilinguals, and found no difference in the extent to which dominance was reversed in the two groups (for a similar result, see Costa & Santesteban, 2004). This result seems inconsistent with both accounts of reversed dominance effects discussed so far.

A separate and equally important question that might shed additional light on the question of which bilinguals reverse dominance is: Why does language dominance reverse? One possibility is that dominance reversal reflects a special option that only develops with proficient bilingualism, in which adjusting of the selection thresholds makes nondominant language production substantially more efficient over dominant language production (with the benefit outweighing the cost). If this is the case, then overall performance (i.e., average reaction time) in mixed-language blocks should be faster in bilinguals who reverse dominance relative to those who do not (or cannot; Costa & Santesteban, 2004). However, an alternative possibility is that bilinguals’ intended goal was to make the two languages about equally accessible in mixed-language blocks, and that full dominance reversal is an incidental unintended outcome – an “overshooting” effect (Gollan & Ferreira, 2009). These two claims can be investigated by asking which language dominance pattern results in the most efficient performance in mixed-language blocks. If reversed dominance effects are associated with more efficient mixed-language performance, this would support the proposal that reversed dominance happens not by accident but is in fact intended (as in the language-specific selection threshold account). However, if reversed dominance is not associated with more efficient performance, this would suggest that bilinguals do not have access to the exact amount of inhibition that should be applied to the dominant language to maximize performance. Such a finding would be consistent with “overshooting” proposal, and inconsistent with any form of explanation that assumes that more balanced bilinguals have better or different control mechanisms.

The overshooting account requires an elaboration of the inhibition account of reversed dominance effects. Instead of intending to reverse dominance, bilinguals might aim to make both languages about equally accessible in the mixed-language blocks. Highly balanced bilinguals would show larger reversed language dominance effects, not because they apply different control mechanisms, but because their two languages start out being more similarly accessible. Hence, much less inhibition would be required for balanced bilinguals to show a reversed dominance effect than unbalanced bilinguals. In addition, a further assumption is needed to explain why being close to the line means that balanced bilinguals are more likely to cross it. For example, it may be more difficult to determine exactly how much inhibition to apply, or it may be more difficult to apply exactly the determined amount, when only a small quantity of inhibition is needed. If either quantity were consistently rounded up, then balanced bilinguals would show larger reversed dominance effects than unbalanced bilinguals.

Finally, by related logic, it might be possible to shed light on yet another alternative explanation of reversed dominance effects: that it reflects proactive activation of the nondominant language, rather than inhibition of the dominant language (Branzi et al., 2014; Declerck et al., 2015; Philipp, Gade, & Koch, 2007; Verhoef et al., 2009). This account is very similar to the inhibition account, with the main difference being that instead of proactively inhibiting the dominant language, instead it is assumed that the nondominant language is proactively activated throughout mixed-language blocks. Such an account seems less feasible because precisely those bilinguals who would need to activate the nondominant language the most (i.e., unbalanced bilinguals) would also seem the least able to do so (there are hard limits on the extent to which inaccessible representations can be intentionally activated; if there were no such limits, then becoming proficient in a second language would be easy; for discussion, see Gollan & Goldrick, 2018). By contrast, more proficient bilinguals might more easily be able to activate representations in a (slightly) nondominant language as those representations would still be highly accessible. Thus, much like the assumption of different selection thresholds for each language, this account also predicts that more balanced bilinguals should be more likely to exhibit reversed dominance.

In the current study, we investigated the relationship between the reversed dominance effect and relative proficiency of the two languages, and if reversed dominance leads to more efficient performance in mixed-language blocks. Unlike in prior research, we investigated this question within a single population of bilinguals on a continuum by using an objective measure to determine the extent to which the two languages differed in proficiency level (cf. Gollan, Weissberger, Runnqvist, Montoya, & Cera, 2012). To this end, we used an existing data set with a very large number of Spanish-English bilinguals (> 400 participants), in which we previously reported that inhibition of the dominant language accumulates throughout the mixed-language block (resulting in dominance reversal by the end of the testing block; Kleinman & Gollan, 2018).

In our reanalysis of these data, we hypothesized that if the amount of inhibition applied depends directly on the extent to which the dominant language is dominant over the nondominant language, then – relative to balanced bilinguals – less balanced bilinguals might exhibit larger reversed dominance effects in a mixed-language block. This would in turn lead to a larger change in dominance effects across block types; i.e., more change relative to balanced bilinguals in the extent of language dominance effects across single- versus mixed-language blocks. On the other hand, according to the language-specific selection threshold account, only more balanced bilinguals should exhibit reversed dominance effects, and the relationship between proficiency and dominance reversal should not be linear so much as a step function (emerging at a particular high level of proficiency). Finally, we examined which profile of dominance effect (reversed dominance vs. “normal” dominance) is associated with maximally efficient performance in the mixed-language blocks, as this could shed light on why reversed dominance effects emerge.

Method

Participants

A total of 416 Spanish-English bilinguals, originally tested for Kleinman and Gollan (2016, 2018), recruited at the University of California, San Diego, participated for course credit, not counting two participants who were excluded due to technical errors. Two additional participants were excluded due to missing language proficiency scores, which was assessed using the Multilingual Naming Test (MINT; Gollan et al., 2012). This is one of the few objective tests specifically designed to measure how balanced bilinguals are, and has been validated with different types of healthy and patient bilinguals (Sheng, Lu, & Gollan, 2014; Gollan et al., 2012; Ivanova, Salmon, & Gollan, 2013; Tomoschuk, Ferreira, & Gollan, 2019). In this test, bilinguals attempted to name 68 pictures presented in order of increasing difficulty in each language. Bilinguals who scored higher in English than in Spanish, and if they got the same score in both languages (n=3), were classified as English-dominant (91.6%), while the smaller number of remaining bilinguals were classified as Spanish-dominant. A Bilingual Index Score (cf. Gollan et al., 2012) was calculated by dividing the score of the nondominant language by the score of the dominant language. Bilingual Index Scores ranged from 27% to 100%, with higher scores indicating more balanced bilingualism (and 100% representing bilinguals who named exactly the same number of pictures correctly in English and Spanish; for more details on the bilinguals’ language background, see Kleinman & Gollan, 2016, 2018).

Materials, task, and procedure

Across all participants, 20 unique pictures were used (see Appendix for an overview of the names in English and Spanish). Each participant saw 9 of these pictures 12 times in each block. Most participants (n=286) named a single set of 9 pictures in every block, whereas the rest named different (non-overlapping) sets of 9 pictures in each block.

All participants completed a mixed-language block, which had 50% English and 50% Spanish trials. The switch rate was 33% for 286 participants and 50% for the remaining 128 participants. Additionally, the same picture was never presented on consecutive trials, and there were no more than four consecutive switch trials and no more than five consecutive repetition trials. The 286 participants also completed two single-language blocks in which they named the same pictures as in the mixed-language block. Finally, all participants were also presented with another mixed-language block in which they could (with some restrictions) choose which language to use to name each picture; however, since this block was not within the focus of the current study, it will not be further discussed (for more details, see Kleinman & Gollan, 2016). Block order was counterbalanced across participants. Each block consisted of 109 trials (one practice trial followed by 108 critical trials) and was preceded by a practice block (12 trials).

Trials started with a fixation cross that was replaced after 350 ms by a blank screen. After 150 ms, a language cue appeared, while after another 250 ms the picture appeared below the language cue. Both the language cue and the picture stayed on the screen until either the participant responded or 3000 ms elapsed (whichever came first). Finally, there was an inter-trial interval of 850 ms.

Data analyses

Across all included participants, 44,712 trials were collected in the mixed-language block. Trials with response errors or voice key errors, or which were faster than 250 ms or slower than 3000 ms, were classified as error trials and excluded from RT analyses of the mixed-language block (8.1% total).

The RT data were analyzed using linear mixed-effects regression modeling (lme4 v. 1.1–21; Baayen, Davidson, & Bates, 2008), and denominator degrees of freedom were estimated via the Sattherthwaite approximation (lmerTest v. 3.1–0; Kuznetsova, Brockhoff, & Christensen, 2017). Fixed effects comprised Language Dominance (Nondominant = −0.5; Dominant = +0.5), Bilingual Index Score (represented as a proportion and mean-centered), and their interaction. For this model and all other models reported below, we followed the same three-step strategy: (1) We fit a model with a maximal random effects structure: random intercepts, all within-factor random slopes and their interactions, and correlations between random slopes. If this model did not converge, (2) we removed correlations between random slopes. If the resulting model still did not converge, (3) we identified random slopes accounting for less than 1% of the variance of their associated random factors, then removed all such slopes simultaneously (Bates, Kliegl, Vasishth, & Baayen, 2015). Relative to step 2, step 3 never changed the significance of any fixed effect, but always resulted in convergence. Error data (where reported below, mainly to rule out the existence of speed-accuracy tradeoffs) were analyzed using generalized linear mixed-effects modeling, with the same contrast codings and model-fitting strategies as above.

Trial-level data and analysis scripts are publicly available at https://osf.io/f35v4/.

Results

Overall, bilinguals responded equally quickly in the two languages in the mixed-language block, as there was no main effect of Language Dominance, b = 0.43, SE = 9.79, t(17.8) = 0.04, p = .966. So, dominance was not reversed. Balanced and unbalanced bilinguals responded about equally quickly, as there was no main effect of Bilingual Index Score, b = 14.1, SE = 44.1, t(308) = 0.32, p = .750. However, there was an interaction between Language Dominance and Bilingual Index Score, b = −89.1, SE = 39.8, t(15.3) = −2.24, p = .041, such that more balanced bilinguals exhibited a greater difference between response times in the two languages – specifically, they exhibited a stronger reversal of language dominance than less balanced bilinguals (see Figure 1a).¹ This same interaction was statistically significant in the error rates as well, b = −3.72, SE = 1.04, z = −3.58, p < .001, such that less balanced bilinguals produced more errors in the nondominant language than in the dominant language whereas more balanced bilinguals produced about the same number of errors in each language (see Figure S1a in the Supplementary Material). More generally, participants’ mean RTs in the mixed-language block were positively correlated with their mean error rates in that block, r(412) = 0.23, p < .001, and their dominance effects in RTs were uncorrelated with their dominance effects in error rates, r(412) = 0.05, p = .314, indicating that there was no speed-accuracy tradeoff either overall or between languages.

Figure 1.

Language dominance effects (nondominant-language RT – dominant-language RT) as a function of Bilingual Index Score, both (a) in the mixed-language block only, for all bilinguals who completed it (n=414); and (b) in the mixed- and single-language blocks, for all bilinguals who completed both (n=286). Note that bilinguals who did both block types are contributing the same mixed-language block data to both panels. The Bilingual Index Score equals the MINT score in the nondominant language divided by the MINT score in the dominant language, multiplied by 100. Bilinguals with reversed dominance effects are represented by points below the dashed Y=0 line. Error ribbons = 95% confidence intervals.

Next, we considered whether the finding of greater dominance reversal in more balanced bilinguals would survive a control for starting point. That is, since the two languages are more similarly accessible in balanced than in unbalanced bilinguals, it is necessary to control for these different baselines before bilinguals implemented proactive language control. Balanced bilinguals would need to apply less proactive language control than unbalanced bilinguals to exhibit reversed dominance in mixed-language blocks. To examine whether the extent of dominance reversal is modulated by degree of dominance in single-language blocks, we used language dominance effects in single-language blocks as a baseline, and asked if controlling for this factor would modulate dominance reversal in mixed-language blocks (for a similar idea, see Declerck, 2020) across bilinguals varying in Bilingual Index Score. This analysis was restricted to data from bilinguals who completed single-language blocks in addition to a mixed-language block (n=286). Across these participants, 61,776 trials were collected in single-language blocks, of which 3.3% were excluded from analysis (exclusion criteria were the same as for the mixed-language block). The maximal model included the same fixed and random factors as the model reported above, as well as the factor Block Type (Single-Language = −0.5; Cued = +0.5) and its interactions with all other fixed and random effects.

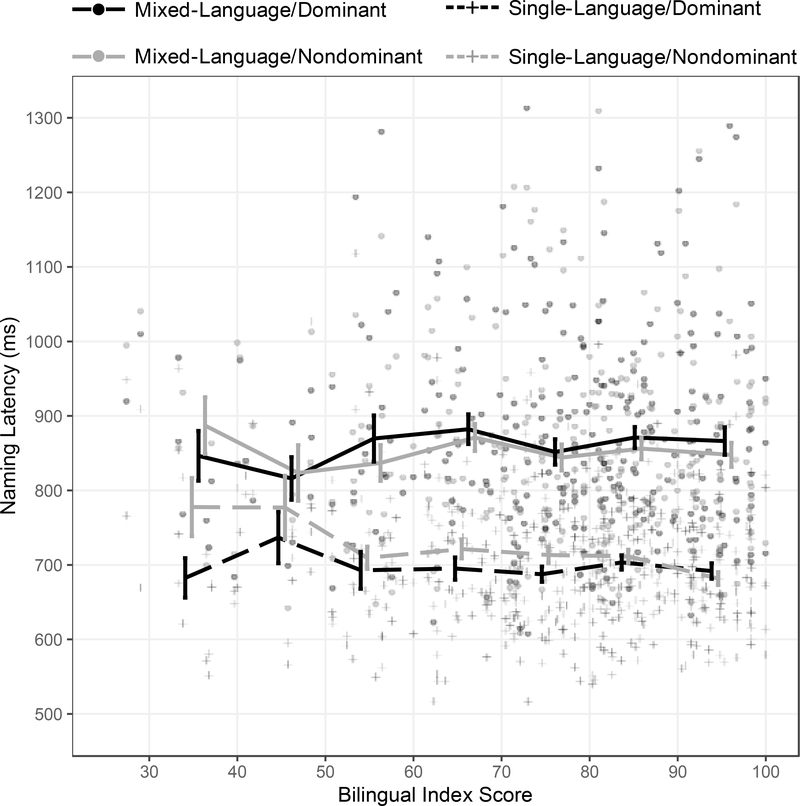
As reported for the larger set of bilinguals, in this subset of bilinguals, those with more balanced index scores reversed dominance more than less balanced bilinguals, a significant interaction between Language Dominance and Bilingual Index Score, b = −86.9, SE = 30.4, t(33.6) = −2.86, p = .007. Balanced bilinguals responded marginally slower than unbalanced bilinguals especially in mixed-language blocks, a marginally significant interaction between Block Type and Bilingual Index Score, b = 68.4, SE = 35.2, t(150) = 1.94, p = .054. Crucially, more balanced bilinguals exhibited a smaller change than less balanced bilinguals in the magnitude of language dominance effects when comparing single- to mixed-language blocks, a significant three-way interaction between Block Type, Language Dominance, and Bilingual Index Score, b = 75.2, SE = 35.3, t(50.5) = 2.13, p = .038. This interaction is shown in Figure 1b, while Figure 2 shows performance in the dominant vs. the nondominant languages in different conditions separately. The three-way interaction was statistically significant in the error rates as well, b = 1.53, SE = 0.77, z = 1.99, p = .046 (see Figure S1b and S2 in the Supplementary Material). These data reveal that less balanced bilinguals reduced their language dominance effects – both in RTs and in error rates – to a greater degree from single- to mixed-language blocks than more balanced bilinguals.²

Figure 2.

Picture naming latencies in each block (mixed- vs. single-language) and language (dominant vs. nondominant) as a function of Bilingual Index Score, for all bilinguals who completed both block types (n=286). The Bilingual Index Score equals the MINT score in the nondominant language divided by the MINT score in the dominant language, multiplied by 100. Lines show mean latencies for bilinguals in each 10% score bin (<= 40%, 41–50%, 51–60%, … 91–100%; ns from 8 to 76). Error bars = 1 SEM.

Surprisingly, Figure 1b also shows that some bilinguals exhibited reversed language dominance even in the single-language blocks. Such bilinguals might have idiosyncratically varying dominance profiles for the small number of pictures tested in single-language blocks (the magnitude of language dominance effects can vary with different measures of performance; Bedore et al., 2013). However, note too that some bilinguals completed the mixed-language block prior to single-language blocks, and thus whatever process instigates reversed language dominance effects could have persisted into the following single-language blocks (Christoffels, Ganushchak, & La Heij, 2016). As balanced bilinguals showed larger reversed dominance effects in the mixed-language block, persistence of control processes between blocks could have led to a smaller between-block difference in dominance effects for those bilinguals – exactly the pattern of data described by the 3-way interaction. To address this concern, we conducted the same analysis only for the small number of bilinguals (n=48) who completed both single-language blocks before any mixed-language blocks, as (due to block order) language mixing could not have impacted their single-language block performance. The 3-way interaction remained significant, b = 270.3, SE = 111.5, t(41.9) = 2.43, p = .020, indicating that this potential confound cannot account for the observed pattern.

Finally, we investigated the relationship between dominance effects and overall speed in the mixed-language block (though see below for a discussion of the statistical limitations of such an analysis). If reversed dominance were increasingly associated with faster ability to accurately name pictures in the mixed-language block, we should have found a positive correlation such that increasingly normal dominance effects would be associated with slower naming latencies. However, as shown in Figure 3, the best-fitting line for this comparison is not a straight line, but rather a U-shape with maximally efficient performance tending towards small standard dominance effects, or relatively equal accessibility of naming responses in the two languages. When considering mixed-language block data for all bilinguals, there was a significant negative linear component, t(411) = −3.64, p < .001, and a significant positive quadratic component as well, t(411) = 5.83, p < .001, indicating that – in addition to the U-shape – increasingly normal dominance effects in RTs were associated with faster naming latencies. The relationship between participants’ dominance effects in RTs and mean error rates across languages was also quadratic, t(411) = 2.39, p = .017 (see Figure S3 in the Supplementary Material), indicating that more extreme dominance effects in RTs (both extreme standard dominance effects and extreme reversed dominance effects) were associated with higher error rates. Thus, this quadratic relationship does not reflect a speed-accuracy tradeoff.

Figure 3.

Picture naming latencies in the mixed-language block averaged across language (dominant and nondominant) as a function of language dominance effect (nondominant RT – dominant RT), for all bilinguals who completed the mixed-language block (n=414). Error ribbon = 95% confidence interval.

Given this U-shaped relationship, we can ask another question: What range of dominance effects was associated with most efficient overall performance? To estimate the variance of the point at which the curve reached its minimum (i.e., the level and direction of dominance score that yielded maximal efficiency in the mixed-language block), we performed a bootstrap analysis by resampling participants at random with replacement from the data, re-fitting the curve, and obtaining the coordinates of the minimum point 10,000 times, then used the resulting distribution to estimate the confidence interval. The minimum was at 18.0 ms (95% CI = [−3.7, +40.2] ms). As the confidence interval around the estimate includes zero, we cannot conclude that bilinguals with standard dominance effects were more efficient overall than bilinguals who were equally fast in both languages. However, what seems most critical is the fact that dominance was clearly not reversed for those who were maximally efficient, as reversed dominance effects greater than about 4 ms were outside the confidence interval. This fits the “overshoot” hypothesis better than any hypothesis that implies special control mechanisms in balanced bilinguals, and more efficient performance in mixed-language blocks with reversed language dominance.

It is important to note that an analysis like the one described above and presented in Figure 3 has a particular statistical limitation, and its conclusion should be qualified accordingly. Specifically, we used data from the same two variables (mean RTs in the mixed-language block for the dominant and nondominant languages) to compute both the independent variable (dominance effects; the difference between them) and the dependent variable (mean naming latency across languages; their average) used in a regression. We found that the best-fit curve had a significantly negative linear component, indicating that bilinguals with more standard dominance effects had faster naming latencies overall. However, the sign (and significance) of this linear component is entirely determined by the relative standard deviations (or variances) of the mean dominant- and nondominant-language RTs – in fact, a simple correlation between them is formally equivalent to the procedure for testing the equality of variance between correlated samples (Lee, 1992; Pitman, 1939). In the mixed-language block in our dataset, mean dominant-language RTs were somewhat more variable across bilinguals (SD=145 ms) than mean nondominant-language RTs (SD=133 ms)³. Our large sample size (n=414) ensured that the deviation of this ratio (145/133=1.09) from 1.00 was statistically significant.

Although this means that the linear component cannot be interpreted separately from the relative variances of each language, we wish to stress two points. First, there was no indication that the interpretation of the quadratic component was affected in the same way. Simulations with our sample size and correlational structure showed that although the variance ratio was almost perfectly correlated with the t-value of the linear component across a range of ratios (r² = 0.97), this relationship did not hold for the quadratic component (r² = 0.00). Accordingly, we believe that the U-shaped relationship we describe is robust to differences in variance between languages. Second, we think that the significantly larger variance of dominant-language RTs represents signal rather than noise. That difference cannot be trivially reduced to differences in mean RTs (which positively correlate with standard deviation RTs): The main effect of language was non-significant in the overall analysis, and the ratio of mean dominant RTs (M=885 ms) to mean nondominant RTs (M=871 ms) was close to 1.00 (885/871=1.02) and less than the ratio of the SDs (1.09). Furthermore, the direction of the effect strikes us as counterintuitive, as we would expect language proficiency across bilinguals to vary more for the nondominant language than the dominant language (the reverse of what we found). Accordingly, it seems possible that variance was greater for dominant-language RTs because bilinguals vary in the amount of inhibition they apply to the dominant language. (For further evidence along these lines, see Footnote 4.)

Discussion

In the current study, we examined the connection between the reversed language dominance effect and the objectively measured relative proficiency level of bilinguals’ two languages. The first analysis (n=414 bilinguals) showed a significant and positive correlation between more balanced proficiency level and reversed dominance. However, this result was qualified by the results of a second analysis (n=286 bilinguals who completed both single-language and mixed-language blocks), which revealed that unbalanced bilinguals exhibited the largest change in the size of language dominance effects when comparing single- versus mixed-language blocks (see Figure 1b and Figure 2; for similar findings with non-linguistic inhibitory control tasks, see Anthony & Blumenfeld, 2019; Goral, Campanelli, & Spiro, 2015). Finally, a third analysis demonstrated that reversed dominance was not associated with maximal efficiency; instead, small but normal language dominance effects were associated with fastest ability to name pictures in the mixed-language block (though these were not statistically distinguishable from balanced naming times i.e., a language dominance effect of zero ms).

Inhibition Best Accounts for Reversed Dominance Effects

Our finding that unbalanced bilinguals exhibit the greatest change in the magnitude of language dominance effects across block types fits a central claim of the Inhibitory Control Model (Green, 1998; Abutalebi & Green, 2007). On this view, unbalanced bilinguals need to exert more effort to switch back and forth between languages, as they have to work harder to inhibit the dominant language to make both languages about equally accessible in mixed-language blocks (e.g., Gollan & Ferreira, 2009). By contrast, relatively balanced bilinguals, who start out with both languages already being about equally accessible, need to implement less inhibition of the dominant language to enable efficient performance in mixed-language blocks. This makes sense, since unbalanced bilinguals’ initial proficiency levels are very skewed towards the dominant language, whereas that is less the case for more balanced bilinguals. Thus, more balanced bilinguals do not use a different control process than less balanced bilinguals; instead they use the same process, but are more likely to “overshoot” and reverse dominance because of pre-existing differences in relative accessibility of the two languages. The language-specific language threshold account (Costa & Santesteban, 2004), on the other hand, cannot explain why unbalanced bilinguals would exhibit the greatest change in the size of dominance effects across blocks, and the activation account suffers similar problems. As such, our analyses favor the inhibition account over all other explanations of reversed dominance effects.⁵

It should be noted that while we had a large pool of bilinguals, few of these bilinguals were on the low end of the L2 proficiency spectrum. However, we do not believe that this impacted our central conclusions. The language-specific selection threshold account assumes that language dominance should not reverse for unbalanced bilinguals since these bilinguals would not be able to use language-specific selection thresholds, regardless of whether they had low or intermediate L2 proficiency. The inhibition account would predict that any differences between unbalanced bilinguals with intermediate L2 proficiency and balanced bilinguals would simply be larger when comparing unbalanced bilinguals with low L2 proficiency and balanced bilinguals, since the unbalanced bilinguals with low L2 proficiency should require more proactive L1 inhibition. Hence, if anything, we would expect to have found a larger effect if the participant pool had included more bilinguals with low L2 proficiency.

Why Do Bilinguals Reverse Language Dominance in Mixed-Language Blocks?

An assumption inherent to the language-specific selection threshold account is that reversed language dominance is a better approach – an ability that only develops in highly proficient bilinguals (Costa & Santesteban, 2004; Costa et al., 2006). It follows that overall performance in mixed-language blocks should be optimized when dominance is reversed. Yet, that was not the case in our study. When considering data from all bilinguals, the relationship between mixed-language dominance effects and overall efficiency in the mixed-language block exhibited a U-shape such that larger language dominance effects (whether reversed or normal) were associated with slower overall naming latencies (than no dominance effects), and thus decreased overall efficiency, in mixed-language blocks.

This finding seems decidedly inconsistent with any form of explanation that associates reversed dominance effects with elite control abilities that develop only in highly proficient bilinguals. It also seems inconsistent with our finding that some relatively less balanced bilinguals nevertheless did exhibit reversed language dominance effects (see Figure 1a). This result seems more difficult to explain given that less balanced bilinguals should have difficulty activating the nondominant language. The inhibition account has an easier time explaining this finding if the ability to apply proactive inhibition of the dominant language is or can be at least partially independent of language proficiency. Importantly, Green’s (1998) original proposal assumed that inhibitory control at the lexical level is reactive in proportion to the relative degree of activation of the two languages at the lexical level, but also that bilinguals have a second independent proactive (or global) control process. Our results further imply that proactive inhibition is not necessarily always proportional to the relative degree of activation of the two languages. Given our previous report that dominance reversed increasingly over the course of a mixed-language block (Kleinman & Gollan, 2018), we must further assume that balanced and unbalanced bilinguals increase application of inhibitory control throughout the block to the same degree.

This could provide a partial answer to another question raised by our results: If dominance reversal does not lead to more efficient performance in mixed-language blocks, then why do a substantial number of bilinguals “overshoot” with their proactive language control to the point that performance is better in their nondominant language? Here we consider three speculative explanations to this thus-far unanswered question. First, it is possible that bilinguals are not aware of what would be the most optimal dominance profile for mixing efficiently (though there is some evidence that bilinguals can be explicitly instructed on how to switch languages cost-free; Kleinman & Gollan, 2016). Also, optimal dominance could depend on the type of items included in the block (which bilinguals also cannot anticipate, at least not in advance).

Second, bilinguals may not have access to the precise amount of inhibition that would be needed to optimize performance. On this view, proactive control need not always be exactly proportional to the relative activation of the two languages (though note that to some degree it must be proportional since unbalanced bilinguals did inhibit significantly more than balanced bilinguals). This second possibility might seem challenged by asymmetrical switch costs, in which bilinguals show larger costs of switching into L1 than into L2 (e.g., Gollan, Kleinman, & Wierenga, 2014; Kirk, Kempe, Scott-Brown, Philipp, & Declerck, 2018; Meuter & Allport, 1999; see also Green, 1998). This asymmetry is generally assumed to reflect the application of inhibition in proportion to the level of activation that interferes with intended language selection (though not all evidence is along these lines, see Footnote 1 and Declerck & Philipp, 2015). But such effects could be explained by reactive inhibition arising at the lexical level. Similarly, block order effects, which typically affect only the dominant language, could pose some challenges to this claim (Branzi et al., 2014; Guo, Liu, Chen, & Li, 2013; Misra et al., 2012; Van Assche et al., 2013; Wodniecka, Szewczyk, Kałamała, Mandera, & Durlik, 2020; for a review see Declerck, 2020). However, not all measures of bilingual inhibitory control provide evidence for proportional inhibition (e.g., n-2 language repetition costs; e.g., Declerck & Philipp, 2018; Guo et al., 2013; Philipp et al., 2007). It is possible that proactive control sometimes is, and in other situations is not, proportionally applied based on the relative accessibility of the two languages, and there may also be differences between how proactive control is applied during mixed-language blocks versus what survives across blocks (when bilinguals return to speaking only the dominant language).

A final possibility is that bilinguals prepare for a ‘worst-case scenario’. Put differently, they apply enough inhibition so that even highly activated dominant-language words are not selected by mistake. In turn, when bilinguals encounter dominant-language words that are not highly activated, they will inhibit these words too much. This will not result in overall similar accessibility of the two languages, but rather in a reversed dominance pattern.

Conclusion

While some aspects of reversed language dominance remain a mystery, the current analyses show that relative accessibility of the two languages is a critical factor that determines whether dominance will be reversed or not. Relative to unbalanced bilinguals, more balanced bilinguals are more likely to exhibit dominance reversal because even a small amount of inhibition of the dominant language is more likely to get them reversed. On average, unbalanced bilinguals actually apply more inhibition than balanced bilinguals when mixing languages; thus, what makes balanced bilinguals qualify as “elite bilinguals” in this context is not that they exhibit reversed dominance, but rather that they need to apply less inhibition to mix languages efficiently. A broader implication is that proactive control seems to be at least partially blind (or indifferent) either to the precise amount of inhibition needed to reach an optimal level, or to what will be the optimal level of relative accessibility of the two languages to enable mixing most efficiently (or both). The implications of this conclusion could be quite far-reaching if they apply to proactive control in general (linguistic and not) and awaits further investigation to reveal what factors motivate and facilitate proactive control in various contexts.