Characterizing and predicting cortical evoked responses to direct electrical stimulation of the human brain

Abstract

Background:

Direct electrical stimulation of the human brain has been used to successfully treat several neurological disorders, but the precise effects of stimulation on neural activity are poorly understood. Characterizing the neural response to stimulation, however, could allow clinicians and researchers to more accurately predict neural responses, which could in turn lead to more effective stimulation for treatment and to fundamental knowledge regarding neural function.

Objective:

Here we use a linear systems approach in order to characterize the response to electrical stimulation across cortical locations and then to predict the responses to novel inputs.

Methods:

We use intracranial electrodes to directly stimulate the human brain with single pulses of stimulation using amplitudes drawn from a random distribution. Based on the evoked responses, we generate a simple model capturing the characteristic response to stimulation at each cortical site.

Results:

We find that the variable dynamics of the evoked response across cortical locations can be captured using the same simple architecture, a linear time-invariant system that operates separately on positive and negative input pulses of stimulation. We demonstrate that characterizing the response to stimulation using this simple and tractable model of evoked responses enables us to predict the responses to subsequent stimulation with single pulses with novel amplitudes, and the compound response to stimulation with multiple pulses.

Conclusion:

Our data suggest that characterizing the response to stimulation in an approximately linear manner can provide a powerful and principled approach for predicting the response to direct electrical stimulation.

Introduction

Clinicians and researchers have been directly stimulating the human brain with electrical current for decades in order to address a variety of neurological disorders and to gain insight into the neural circuits that govern function and behavior [1, 2]. Yet despite this vast experience, precisely how electrical stimulation affects neural circuitry and neuronal activity in the human brain remains unclear [2, 3]. Direct electrical stimulation depolarizes membrane potentials, leading to neural responses both locally and in distant neural structures through activation of axons underlying the stimulation site [4–6]. The distal effects of stimulation are complex and involve direct activation of orthodromic, and to a lesser extent antidromic, propagation pathways to the target site as well as indirect activation of local circuits within those target regions [7, 8].

These complex local and distal effects have therefore made it difficult to anticipate and predict the neural responses to stimulation. This has consequently presented a challenge for accurately interpreting the behavioral effects of electrical stimulation when used routinely for clinical purposes or for research. Stimulation can result in positive responses, such as evoked phosphenes or motor movements [9, 10], but stimulation can also induce negative responses such as in speech arrest [11]. Similarly, stimulation can have variable effects on higher order cognitive functions such as memory [12–14]. Stimulation at a single site can even promote both positive and negative responses, likely depending on the broader regions that are connected to and therefore targeted by activation of the stimulation site [2, 11, 15]. These effects of stimulation suggest that there is a need to well characterize the responses to stimulation across broader brain regions.

There are clear benefits to well characterizing the effects of stimulation on neural activity. First, bettter understanding of the effects of stimulation could allow clinicians and researchers to more accurately predict neural responses. This in turn could lead to developing more effective stimulation algorithms for treating neurological disorders that are more adaptive to the individual patient, that require less power, and that produce fewer side effects. Second, characterizing the effects of stimulation may provide fundamental knowledge regarding neural function. By directly manipulating neural responses in a controlled manner, stimulation may be used to provide insight into neural structure and connectivity between different brain regions and to investigate the causal role of neural activity on behavior. Direct stimulation with individual current pulses that result in cortical evoked potentials has been successfully used, for example, to map connections between brain regions [16–18].

Here, we demonstrate that by directly delivering single pulses of electrical stimulation to the human brain with amplitudes drawn from a random distribution, we can characterize and subsequently predict the responses in other brain regions to stimulation at a given site. Although the dynamics of the evoked response to stimulation are governed by the variable interconnections between each brain region and the stimulation site, we find that the responses in each brain region can be characterized using the same simple architecture - a linear time-invariant system that operates separately on positive and negative input pulses of stimulation. Characterizing the responses to stimulation using this simple and tractable model enables us to accurately predict the response to subsequent stimulation using individual pulses with novel amplitudes, and the compound response to stimulation using combinations of multiple pulses. Our results therefore suggest that the complex mechanisms that underlie the effects of stimulation of one site on another can be captured in an approximately linear manner. Moreover, our results suggest an approach for building more complex electrical stimuli and anticipating the responses to stimulation in other brain regions.

Material and Methods

Ten individuals (8 male; 32.5 ± 0.9 years) with drug resistant epilepsy underwent a surgical procedure in which subdural platinum recording contacts (3 mm exposed diameter; PMT Corporation, Chanhassan MN) were implanted on the cortical surface. In all cases, placement of the contacts was determined by the clinical team in order to best localize epileptogenic regions for resection. Data were collected at the Clinical Center at the National Institutes of Health (NIH; Bethesda, MD). The research protocol was approved by the Institutional Review Board, and informed consent was obtained from all participants in the study. All data are reported as mean ± SEM unless otherwise noted.

In order to characterize the responses to electrical stimulation, we applied individual biphasic pulses to a pair of neighboring electrodes while recording the intracranial EEG (iEEG; Nihon Kohden Inc., Irvine CA) responses in the remaining electrodes in each participant. For each individual pulse, we used a stimulation amplitude that was randomly drawn from a uniform distribution of amplitudes between approximately 8 and −8 mA (Fig. 1C). We presented trials of single pulses of electrical stimulation in two experimental sessions while capturing iEEG recordings in each participant (Fig. 1F). In each session, trials were separated by approximately one second, resulting in a stimulation frequency of approximately 1 Hz. We used the first session, which we refer to as training, in order to generate a tractable model that characterizes how each recording site responds to stimulation at each stimulation site. During the second session, which we refer to as testing, we used trials of individual pulses, consisting of novel stimulation amplitudes also drawn randomly from the same distribution, and trials containing multiple pulses to test how well the identified model can predict the evoked response to novel stimulation.

Figure 1. Evoked Responses to Single Pulse Stimulation.

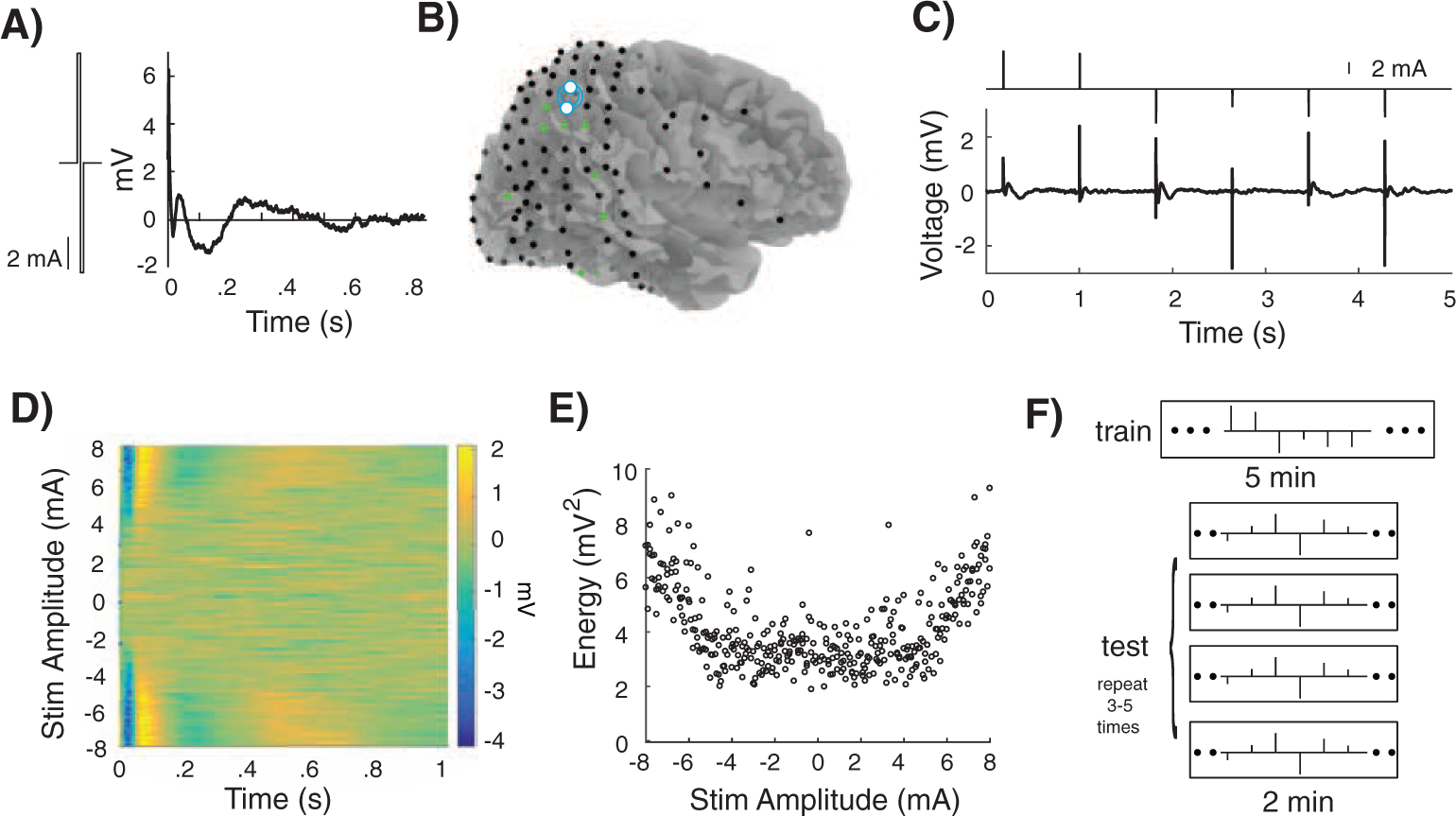
A) Example stimulation pulse and evoked response recorded in a single electrode. B) In an example participant, stimulation was delivered at one bipolar cortical site (white). Only a subset of electrode (green) are responsive. C) Stimulation consisted of stimulation pulses with amplitudes drawn from a white noise distribution. A single electrode exhibits evoked responses to the pulses that appear modulated by stimulation amplitude. D) For a single responsive electrode, responses to all stimulation amplitudes over time showed consistently timed, symmetric response to high amplitude current stimulation. E) For this same electrode, the energy of the evoked response was also symmetric with stimulation amplitude and increases with greater magnitude of stimulation. F) Stimulation pulses were delivered to each participant for five minutes of training at a single cortical location. During testing, a series of pulses with novel amplitudes was delivered for two minutes at the same location. The test series of pulses was repeated 3–5 times in each participant.

We identified every electrode that was responsive to stimulation (Supplementary Fig. S1). For each responsive electrode, we constructed a model that characterizes the evoked response to stimulation at the stimulation site by examining the evoked responses to the input sequence of pulses presented during the five-minute training session (see Suppplementary Material and Methods). Each model had an identical architecture, comprised of a linear system with impulse responses, h⁺[t] and h⁻[t], that separately operate on positive and negative input pulses, respectively. Hence, given an input, x[t], our model estimates a predicted output, $\widehat{y}[t]=\mathcal{H}\{x[t]\}$ by separately convolving the positive and negative input pulses with the impulse responses, h⁺[t] and h⁻[t], respectively:

$$\widehat{y}[t]=\mathcal{H}\{x[t]\}=\sum _{\tau =0}^L{h}^{+}[\tau ]f^{+}(x[t-\tau ])+\sum _{\tau =0}^L{h}^{-}[\tau ]f^{-}(x[t-\tau ]),$$

where f⁺(x) and f⁻(x) are rectifiers that select positive and negative pulses, respectively, and where each impulse response is of finite duration, L. The model $\mathcal{H}$ is therefore fully parametrized by the two finite impulse responses, h⁺[t] and h⁻[t].

Using the derived impulses responses, h⁺[t] and h⁻[t], we then estimated a predicted output, ŷ[t], to the pulses presented during the testing experimental session. We computed the prediction error between ŷ[t] and the observed output y[t] by calculating the mean squared error (MSE) directly on the differences between their time series (see Supplementary Material and Methods).

Data availability

Processed data and MATLAB code used for analysis is available upon request.

Results

We collected intracranial EEG (iEEG) data from ten participants with drug resistant epilepsy who were being monitored for seizures with surgically implanted subdural electrodes. We recorded iEEG signals at every electrode while delivering biphasic current pulses to one site in the brain (Fig. 1A; Material and Methods). At each stimulation site, we used bipolar stimulation across two adjacent electrode contacts (Fig. 1B). We delivered one pulse approximately once per second, with the amplitude of each pulse drawn randomly from a uniform distribution of amplitudes between 8 mA and −8 mA (Fig. 1C). We considered the presentation of each individual stimulation pulse, followed by its inter-stimulus interval, a single stimulation trial. The stimulation amplitude of each pulse in each trial defines both phases of the biphasic pulse such that stimulation using a positive (negative) current amplitude resulted in an initial positive (negative) deflection followed by an equally sized negative (positive) deflection. The series of stimulation amplitudes has the characteristics of a white noise input since the amplitudes are uncorrelated and have zero mean.

At each unique stimulation site (n = 12 across participants), we delivered a five minute training session consisting of trials in which one pulse was delivered at the beginning of each trial, and with each trial and therefore each pulse delivered approximately once every second, resulting in a stimulation frequency of approximately 1 Hz. We examined the evoked responses captured on the iEEG traces at every other electrode to every trial of single pulse stimulation during training (Fig. 1D). In many example electrodes, stimulation resulted in an evoked response that appeared to increase in magnitude with stimulation amplitude (Fig. 1E). We often observed this increase in the evoked response to both positive and negative stimulation. Based on the average evoked response to all stimulation trials, we determined whether each electrode in each participant was responsive to stimulation (Material and Methods; Fig. 1B; Supplementary Figs. S1 and S2). We examined only the electrodes that exhibited an average evoked response to stimulation that met our criteria for responsiveness in subsequent analyses (52 total responsive electrodes, 4.3 ± 1.42 electrodes, corresponding to 5.02 ± 1.7%, per participant; for analyses of remaining electrodes, see Supplementary Figures).

At each stimulation site, we subsequently presented a two-minute test series containing trials of individual pulses, with each trial and therefore each pulse also delivered with a stimulation frequency of approximately 1 Hz. The trials used in the test series were comprised of individual pulses with novel stimulation amplitudes also drawn from a uniform distribution of amplitudes between 8 mA and −8 mA (Fig. 1F). Our initial goal was to determine whether we could use the evoked responses captured during training to generate a simple linear model capable of predicting the responses to novel individual pulses of stimuli during testing. We reasoned that if we could generate such a model, we could then use the same linear model to predict the compound response to multiple pulses delivered in quick succession.

Consistent Responses Across Time

One requirement for being able to successfully predict responses to direct cortical stimulation is that the response to the same stimulus should be consistent across time, or time-invariant. We examined this by repeating the two-minute test series of trials of single pulses between three and five times in each participant (Material and Methods). We observed that the evoked responses to the same pulses were indeed consistent (Fig. 2A). To quantify this consistency, we computed the average response across all but the first repetition of the same two-minute test series of trials of pulses and examined how well that average response trace could be used to predict the responses observed during the first presentation of the test series of trials (Fig. 2A). We used the residual difference between that average response trace and the response observed during the first presentation of the same trials of pulses to compute the mean squared error (MSE; Material and Methods). This measure, the MSE between the predicted and observed trace, reflects the extent to which the brain’s response to stimulation is consistent across time. Across responsive electrodes, we found that the average MSE was 0.024 ± 0.003mV² (Fig. 2B). We also computed the average response across all but the final repetition, and similarly found that the MSE between the predicted and observed trace in that final repetition was 0.027 ± 0.003mV².

Figure 2. Responses to Repeated Stimulation.

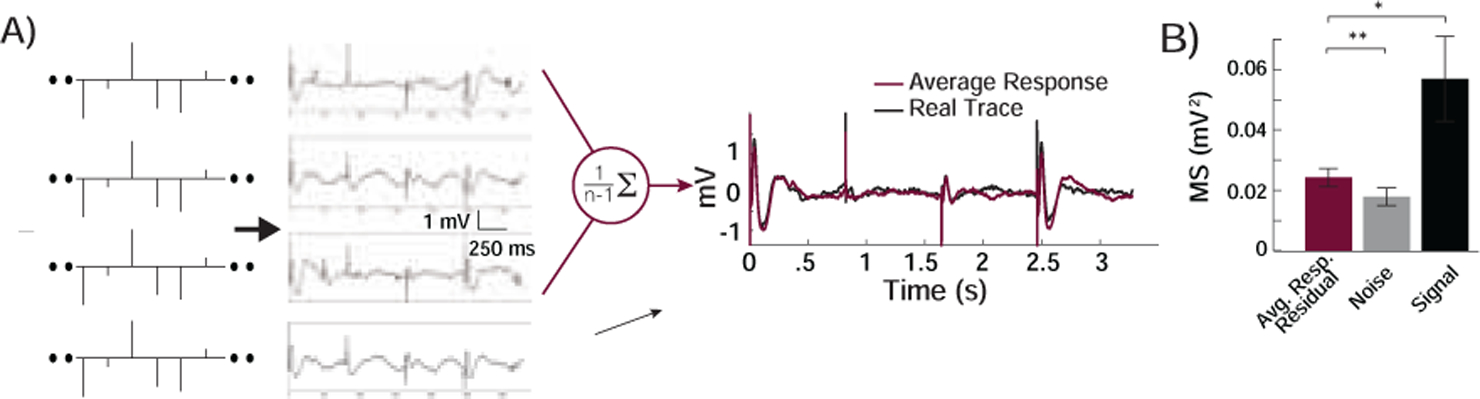
A) We repeated the two-minute series of testing pulses three to five times in each participant. The responses at a typical recording electrode were consistent. Using all repetitions excluding the first one, we averaged the responses to create a predicted response based on the average. We compared this average response to the actual response observed during the first repetition. B) The MSE between the average response and the first repetition (Average Response Residual) was significantly smaller than the mean of squares of the signal, which is equivalent to the error if our predicted response were the mean value of zero (MS_signal, Signal), but was higher than the variance of the baseline noise activity (MS_noise, Noise). **, p < .01; *, p < .05; paired t-test.

We compared this MSE to the mean of the squares of each electrode’s evoked response observed during the first presentation of the two-minute test series of trials, which is proportional to the energy of the evoked trace. This is equivalent to the MSE that would arise had we predicted a response that was the mean value of the recorded trace, which was zero, for all time points, and is the upper limit of any measure of MSE since this would represent the error we would observe had we made no prediction. We refer to this upper bound as MS_signal. Any meaningful predictions would necessarily have to result in a residual error that is lower than this upper bound. The MSE between the prediction using the average response and the observed response during that first repetition was significantly less than MS_signal across all responsive electrodes (0.024 ± 0.003mV² versus 0.057±0.014mV², t(51) = −2.65, p = .011, paired t-test; Fig. 2B; Supplementary Fig. S3). Similarly, the MSE between the prediction using the average response and the observed response during the final repetition was significantly less than MS_signal across all responsive electrodes (0.027 ± 0.003mV² versus 0.060 ± 0.014mV², t(51) = −2.70, p = .009, paired t-test). Hence, the average response across multiple repetitions of the same series of trials of test pulses can be used to predict a significant portion of the response observed in a repeated presentation of that same series of trials of pulses.

We also compared the MSE between the predicted and observed response to the mean of the squares of each electrode’s baseline activity at rest, which is proportional to that electrode’s baseline energy. This is the lower limit of any measure of MSE, given a baseline level of noise on each electrode, and is the best level of error one can achieve with any prediction. We refer to this value as the MS_noise. The MSE of the prediction was significantly larger than this lower limit, MS_noise (0.024±0.003mV² versus 0.018±0.003mV², t(51) = 4.95, p < .001). Together, these data suggest that the evoked responses to stimulation are relatively, but not strictly, consistent across time.

Prediction of Single Pulse Responses

We were interested in characterizing the response to stimulation across all recording sites in a simple and tractable model that can be used to predict future responses. For each responsive electrode, we therefore constructed a model with an identical architecture. Each model characterized the response to stimulation using a linear impulse response that separately operates upon positive and negative stimulation pulses based on the observation that both positive and negative stimulation amplitudes often evoked similar responses (Material and Methods). The input to each model is therefore a static nonlinear rectification that selects for positive or negative stimulation pulses, respectively (Fig. 3A). Although we observed in some electrodes that the magnitude of the evoked responses could be different depending on whether stimulation was applied with a positive or negative pulse (Supplementary Fig. S2C), we set the gain for this nonlinear rectification to be the same for both positive and negative inputs. Because the evoked responses to stimulation appeared to scale with stimulation amplitude for each polarity of stimulation and were relatively consistent across time, the rectification is then followed by a linear time-invariant (LTI) operator.

Figure 3. Linear System Model Predicts the Responses to Single Pulses.

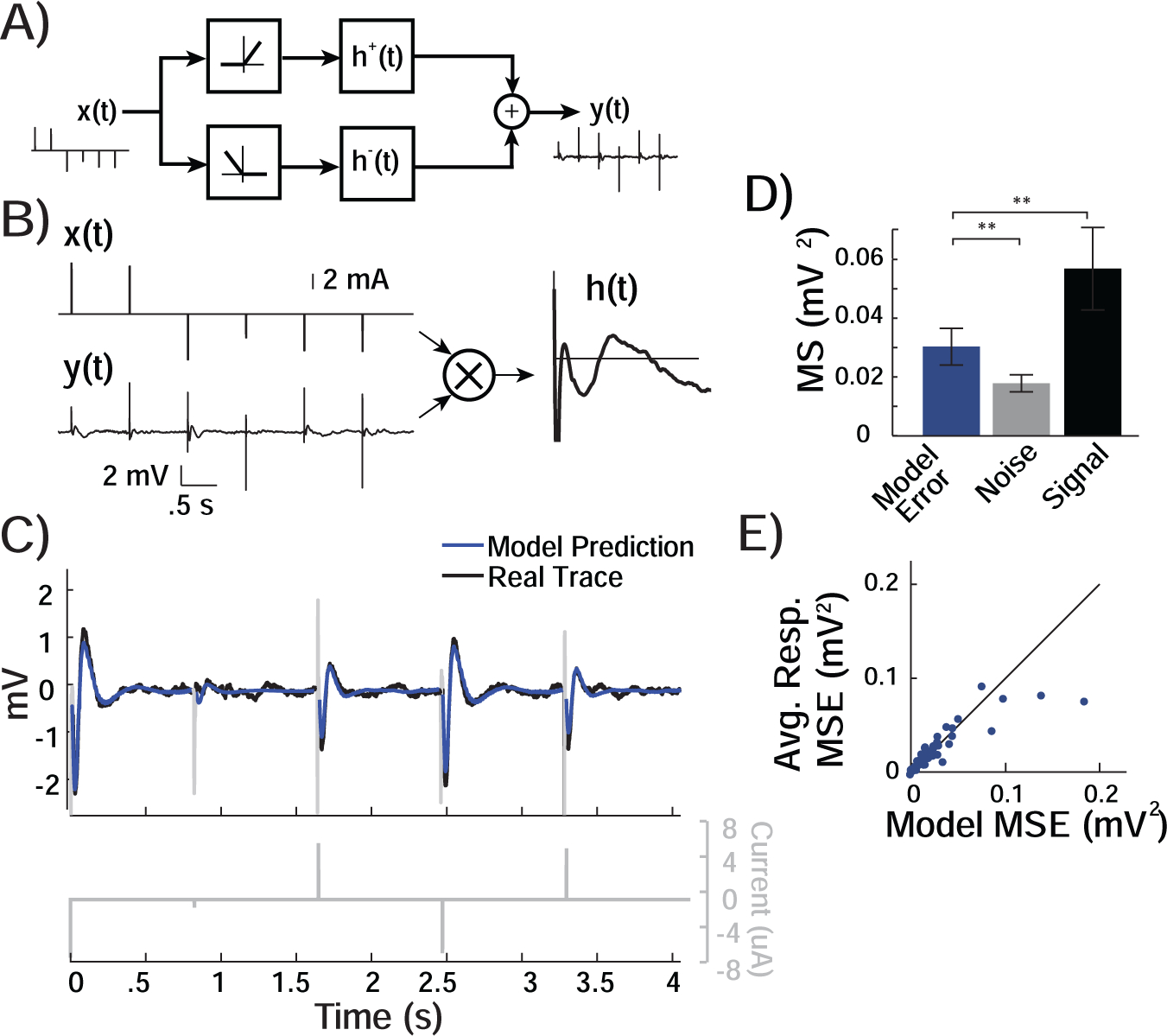
A) When constructing the simple model characterizing the response to stimulation, we divided each training series of pulses, x[t], into positive and negative pulses because the responses to stimulation appeared symmetric. We therefore modeled the system as a nonlinear rectification followed by a separate impulse response, h⁺[t] and h⁻[t] for positive and negative pulses, that together produce the output y[t]. B) Cross-correlating the input x[t] of stimulation pulses with the recorded output, y[t], generates the first order kernel, or impulse response h[t], of the system for each recorded electrode. C) For each recorded electrode, we can convolve any new input x[t] with the derived model to generate a prediction, ŷ[t] of the evoked response. The model prediction appears to match the actual evoked response, y[t], to the novel series of pulses. D) Across responsive electrodes, the MSE between the predicted and recorded response (Model Error) was significantly lower than the mean of squares of the signal, which is equivalent to the MSE if the predicted response were the mean value of zero, (MS_signal, Signal). The residual error was higher than the mean of squares of the baseline activity, which is the lowest possible level of MSE that is attainable (MS_noise, Noise). The model prediction reduced the error from its maximum value to its minimum possible value by 69.7 ± 12.1% across responsive electrodes. **, p < .01; paired t-test. E) The MSE for each responsive electrode using the model prediction was similar to the MSE derived using the prediction based on the average response. Each point represents a single responsive electrode.

A feature of the LTI operator is that we can derive the characteristic response to stimulation, or the impulse response, simply by minimizing the mean square error between the prediction any model would make and the observed evoked responses captured during the five minute training session (Fig. 3A,B). We therefore used the evoked responses to the five minute training session to derive the impulse response, h[t], which fully characterizes the relation between an idealized input pulse at every cortical stimulation site and the anticipated response at every recording electrode site. Because we characterize the response to stimulation by separately processing positive and negative stimulation inputs, we derived a separate impulse response for positive and negative stimulation, h⁺[t] and h⁻[t] respectively, at every recording site (Fig. 3A).

We tested if we could use the simple models we generated that characterize the response to stimulation during training in order to predict the evoked response to the novel trials of single pulses presented during testing (Fig. 1F). One of the key assumptions in constructing a model using an LTI system is that the response amplitudes scale linearly with stimulation input. Examining the responses predicted by an impulse response function that operates upon single pulse inputs with different stimulation amplitudes, and comparing the predicted responses to the responses observed during testing allows us to directly investigate this assumption. Using the derived impulse responses for each responsive electrode, we generated a predicted response, ŷ[t], to the pulses presented during testing and that were comprised of novel stimulation amplitudes (Fig. 3C). As with the predictions based on the average response, we computed the MSE between the predicted output, ŷ[t], and the observed output, y[t]. We compared this measure of error to the upper and lower bounds of error, MS_signal and MS_noise respectively. Across all responsive electrodes, the MSE using the predicted response, ŷ[t], was significantly less than MS_signal of the recorded response, y[t] (0.03 ± 0.006mV² versus 0.057 ± 0.014mV², t(51) = −3.28, p = .0019, paired t-test; Fig. 3D), but significantly greater than the lower bound, MS_noise (0.03 ± 0.006mV² versus 0.018 ± 0.003mV², t(51) = 3.28, p = .0019, paired t-test; Supplementary Fig. S4A). We found that this level of MSE of the predicted response was consistent when we examined all trials of different stimulation amplitudes, although the trials with the most negative stimulation amplitude exhibited slightly larger MSE (Supplementary Fig. S4B). In addition, we found that only approximately ten training trials were required in order to generate a linear model that was capable of predicting the evoked responses with a similar level of MSE as the model generated using all of the training trials (Supplementary Fig. S4C).

For every electrode, we quantified the percentage by which any prediction, ŷ[t] reduced the error from the upper to lower bounds (Material and Methods). Given the baseline noise, the best prediction would reduce the error from the upper limit, MS_signal, proportional to the energy of the evoked response, to the minimum level, MS_noise, proportional to the energy of the noise, by 100%. Across responsive electrodes, we found that our predictions reduced the MSE by an average of 69.7±12.1%. Our model that separately rectifies positive and negative inputs before processing them with a linear time-invariant operator can therefore predict a significant component of the evoked response to a novel input.

We then compared how well the prediction based on the derived impulse responses for each brain region compared to the prediction based on the average responses. The MSE computed using the predicted response, ŷ[t], approximately matched the MSE computed using the average of the repetitions for every responsive electrode (Fig. 3E; t(51) = 1.38, p = 0.173, paired t-test; Supplementary Fig. S4A). The similar levels of residual error suggest that our constructed model can predict responses to single pulses with novel input amplitudes with errors that are likely related to the consistency of the responses over time.

One concern with a predictive model that generates evoked responses that scale linearly with stimulation amplitude is that the observed evoked responses are not strictly linear (Fig. 1E). To confirm the predictive ability of our simple linear model, we therefore constructed a second model in which the initial rectification is replaced by a quadratic fit to the observed increases in signal energy that occur with increasing stimulation amplitude (Supplementary Fig. S4D). The input to this model is therefore a static nonlinear quadratic that operates on the input stimulation pulse amplitude, which is then followed by the linear time-invariant operator. We again calculated the MSE of the predicted output of this model when compared to the observed response during the testing session. Across all responsive electrodes, the MSE using the predicted response, ŷ[t], was significantly less than the upper bound of error, MS_signal, of the recorded response, y[t] (0.029 ± 0.006mV² versus 0.057 ± 0.014mV², t(51) = −3.36, p = .0015, paired t-test), but significantly greater than the lower bound, MS_noise (0.029 ± 0.006mV² versus 0.018 ± 0.003mV², t(51) = 3.06, p = .0036, paired t-test; Supplementary Fig. S4D). The MSE of the predicted output using the quadratic input was not significantly different from the MSE using the linear model, suggesting that a linear model can account for much of the predicted response despite the apparent non-linear nature of the evoked response.

Prediction of Responses to Multiple Pulses

We were interested in whether characterizing the response to individual pulses of stimulation can also enable us to predict the compound response to combinations of multiple pulses. In this case, if multiple pulses are delivered before the response to any one pulse has time to return to rest, then the predicted response to these multiple pulses should simply be the superposition of the predicted responses to the individual pulses. This would suggest that this simple linear model operating separately on positive and negative stimulation pulses could be used to predict the responses to more complex patterns of electrical stimulation. To test this, in five participants who had a total of 22 responsive electrodes (4.4±2.2 electrodes per participant), we delivered a series of trials during the experimental testing session in which some trials contained two to seven consecutive pulses. During these trials with multiple pulses, we presented each pulse within 20 to 50 ms of the previous pulse (Material and Methods). Hence, although each trial of stimulation was delivered approximately once every second, resulting in an overall stimulation frequency of approximately 1 Hz, within the trials with multiple pulses the stimulation frequency was not fixed. Within each trial with multiple pulses, any response evoked by the first pulse of this train of pulses would still contribute to the observed response when the second pulse was presented. In a typical example, the evoked responses to multiple consecutive stimulation pulses can be predicted by the model derived for this recording electrode (Fig. 4A).

Figure 4. Predicting Responses to Multiple Pulses.

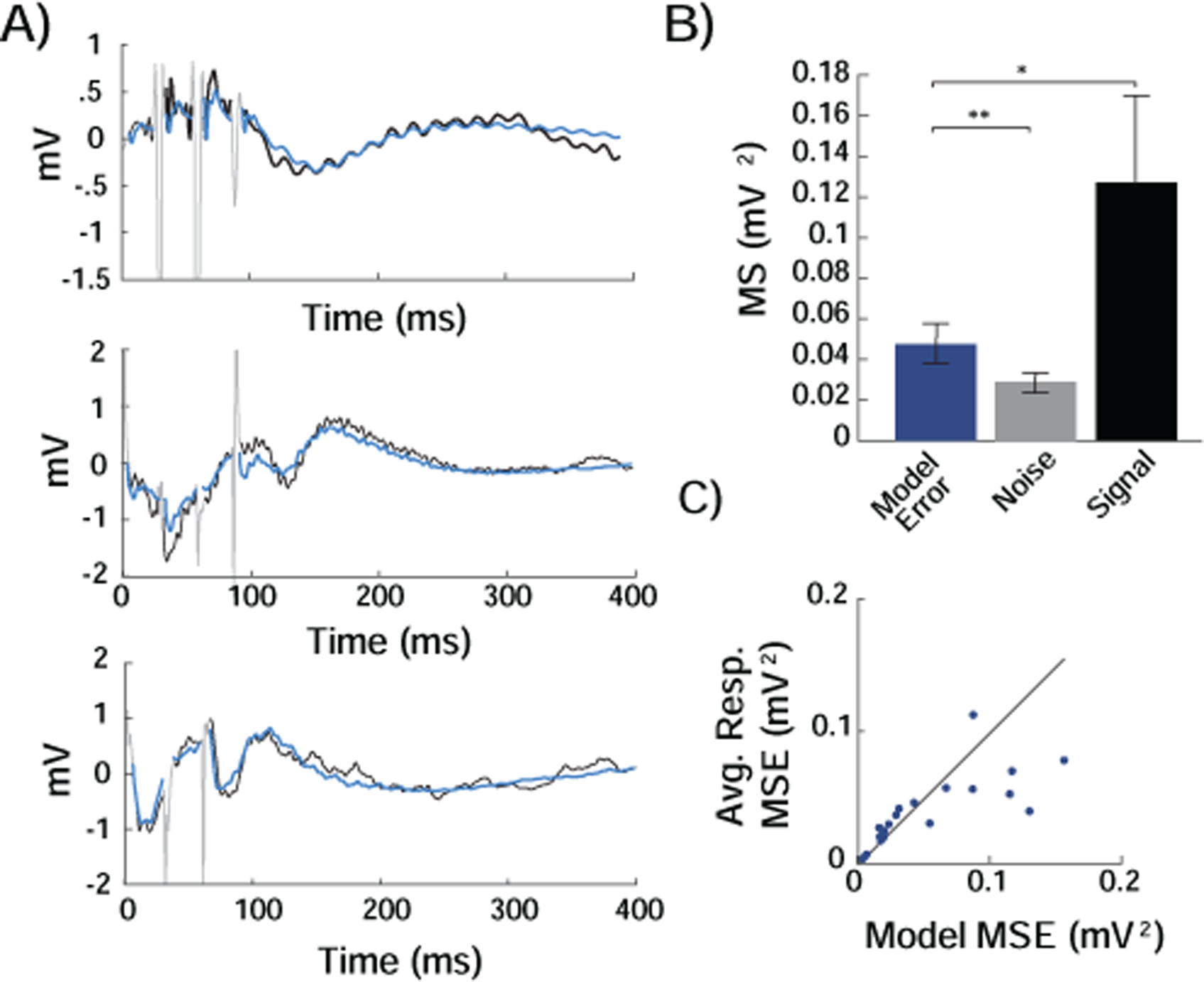
A) In a subset of participants, each trial during testing contained between two to seven pulses in quick succession (grey; three example trials shown). Using the derived model, we predicted the evoked response in a single electrode to the multiple pulses in different trials. The correspondence between the predicted response (blue) and the recorded response (black) suggests that predicting the response to multiple pulses can be attained through superposition. B) Across responsive electrodes, the MSE between the model prediction and the recorded responses to multiple pulses (Model Error) was significantly lower than the mean of squares of the signal, which is equivalent to the MSE if the predicted responses were the mean value of zero, (MS_signal, Signal). The model prediction reduced the error for predicting multiple pulses from its maximum value to its minimum possible value (MS_noise, Noise) by 88.6 ± 22.9% across responsive electrodes. **, p < .01; *, p < .05; paired t-test. C) The MSE for each responsive electrode using the model prediction of the response to multiple pulses was similar to the MSE using the prediction based on the average response. Each point represents a single responsive electrode.

We tested how well the predictions using the impulse responses derived for each electrode during training were able to predict the responses to multiple pulses presented during the two minute testing session. Across all responsive electrodes, the MSE using the predicted ŷ[t] was significantly less than the upper bound of error, MS_signal, of the recorded output, y[t] (0.048 ± 0.010 mV² versus 0.128 ± 0.041 mV², t(21) = −2.31, p = .031, paired t-test; Fig. 4B; Supplementary Fig. S5). We also compared the MSE of the prediction to the mean of squares of the baseline activity, MS_noise, which represents the lower limit of error that can be achieved with any prediction (0.048 ± 0.010 mV² versus 0.029 ± 0.005 mV², t(21) = 2.86, p = .0093). When predicting the response to multiple pulses, the predictions reduced the error by an average of 88.6 ± 22.9%.

As above, we also repeated the series of trials containing multiple pulses several times in order to compare the prediction of evoked responses using the model to the prediction we would obtain based on the average of several repetitions (Fig. 4C). In most cases, the model prediction matched the prediction using the average response. Across all responsive electrodes, the model prediction did not have a MSE that was significantly different than the MSE we found when using the average responses to predict the evoked response (0.048 ± 0.010 mV² versus 0.037 ± 0.006 mV², t(21) = 1.65, p = 0.11; Supplementary Fig. S5). Together, these data suggest that characterizing the response to stimulation using a linear impulse response that separately operates upon positive and negative inputs can predict the responses to multiple pulses, and suggest that the responses to more complex patterns of direct cortical stimulation can be estimated in an approximately linear manner.

Discussion

Our results demonstrate that by examining the responses to individual pulses with amplitudes drawn from a random distribution, we can characterize and subsequently predict the response to electrical stimulation across different brain regions. The evoked response in each electrode can be characterized using the same architecture, comprised of a linear system that separately operates on positive and negative input pulses. The information captured in these simple and tractable models has two important implications. First, characterizing neural responses to stimulation in this manner presents a powerful tool for predicting the future response to novel patterns of stimulation. Second, the features of each response may provide insight into underlying neural function and the structures and pathways connecting one region with another.

Direct stimulation of the brain has been utilized for several decades, but stimulation parameters generally have not been well explored even when applied to new disorders or patient populations [2]. In some of the most widely used and successful clinical applications, such as deep brain stimulation for movement disorders [23] or direct cortical stimulation mapping [11] for example, widely adopted stimulation parameters have largely been passed down based on previous studies or historical data. Stimulation often involves continuous or intermittent bursts of identical square wave pulses, and the main parameters that are manipulated relate to the location, frequency, amplitude, and width of the stimulating pulses.

Deviations from such standard stimulation algorithms, whether to improve treatment or to expand stimulation to new disorders or patient populations [24], rarely occur, largely because modeling and understanding all of the factors that underlie the various effects of stimulation has proven to be challenging [2, 3]. There are several reasons for this. Brain structures are interconnected in complex ways, and how information is propagated across this distributed network of neural circuits is still an active area of research [25, 26]. The fundamental units responsible for processing information within these networks, the neurons, are also complex, with electrophysiological dynamics that depend on neuron type, neuron location, interconnections with other neurons, and extra- and intracellular environments. Stimulation can affect these dynamics by changing the extracellular environment, which in turn can impact the activity of each neuron, ultimately leading to a network effect [27]. The underlying mechanisms for how this occurs are not fully understood. Finally, developing mechanistic and detailed models that can reliably take into account all of these complexities and predict neural responses to stimulation requires substantial data captured during stimulation from in vivo recordings of an entire neural circuit within an individual. These experiments are difficult to perform and must be done with care. Researchers have attempted to create realistic biophysical models that explicitly capture these dynamics, but these models are often high dimensional and nonlinear [28], and thus not tractable nor amenable, for example, to the design of closed-loop stimulation strategies that must operate in real time.

By characterizing the responses to stimulation using a simple and tractable model, however, and by demonstrating that these responses approximately add linearly, our data raise the possibility of addressing this challenge. Importantly, this approach solely relies upon the responses to stimulation itself and makes no assumptions about the underlying neurons or fibers of passage. Instead, we treat the brain as we would any other system whose inner mechanisms are relatively unknown but for which the inputs and outputs can be well controlled and described. We derive the relationship between stimulation and response based on the evoked responses to pulses of electrical stimulation. This approach builds upon previous work using single pulse electrical stimulation to investigate the evoked cortical responses [16–18, 29]. In this case, however, we use a random series of stimulation inputs with amplitudes that are temporally uncorrelated, an approach that has been successful in the study of mammalian vision in which random input pulses of light have been used to characterize how the retina and other higher order circuits process visual information [30, 31], as well as to characterize the effects of electrical stimulation on neural activity in the retina [32]. We use direct cortical stimulation with implanted electrodes to derive these responses here, but this approach is generalizable to any neuromodulation technology, including non-invasive stimulation modalities such as TMS or tDCS.

A relatively less explored, but equally important, use of direct stimulation is in providing fundamental knowledge regarding the function, structure, and connections of the human brain. A common criticism of many studies investigating the neural mechanisms of behavior is that any inferences that are drawn between neural activity and cognitive function are only correlative [33]. Predicting the effects of stimulation can offer the possibility of controlling its effects, and therefore an opportunity to answer this criticism by evoking neural activity in a precise manner and demonstrating the causal role played by such activity on behavior. This approach could complement existing studies of single pulse stimulation and the resulting cortical evoked potentials that have already been used to infer the presence of causal connections between brain regions [17, 18]. Interestingly, how these evoked potentials differ between brain regions has also not been well explored. Future studies could investigate how the features of the response models described here, such as the size, shape, and latency of the linear component, may distinguish the neural architecture and connections between one region and another [25, 26].

Our goal here was to determine whether, by capturing evoked responses to individual stimulation pulses with different amplitudes, we could build a simple model to predict future responses to novel inputs. This approach was premised on a starting assumption that the brain and the response to stimulation can be reasonably approximated as a linear system with responses that are consistent, reproducible, scalable, and that can be combined. The responses that we observe to repeated series of individual pulses suggest that the effects of stimulation are relatively time invariant. Because the dynamics of brain activity are variable and therefore hard to predict, observing consistent responses to stimulation across time is a necessary requirement in order to predict any future response to direct cortical stimulation. Moreover, the evoked activity that our simple model could predict in response to single pulses suggest that the response amplitudes scale linearly with stimulation. If the effects of stimulation are scalable and can be linearly combined, then the responses to multiple individual pulses should reflect the superposition of the responses to individual pulses. We found that using the impulse response to predict the response to multiple pulses can significantly reduce the error in predicting the observed data, providing additional evidence that the assumption of linearity is a reasonable first approximation.

It is clear, however, from the observed evoked responses that the responses to stimulation have a component that is nonlinear. At the very minimum, the response to positive and negative stimulation have similar directions, suggesting an initial rectification of the stimulation input. Such a rectification suggests that perhaps only one phase of the stimulation pulse has modulatory effects on the underlying neural structures. In addition, we find that the derived predictions do not perfectly capture all of the deflections observed in the actual responses to novel inputs. This may be related to nonlinear effects of stimulation that are not captured in our analyses, or that may result from more temporally overlapping responses to higher frequency stimulation. Moreover, we specifically focused on the large evoked response observed during the first 300 ms following stimulation. These responses are dominated by a low frequency component that largely returns to baseline by that time. Although our data suggest that these responses can be reasonably captured using a linear approach, they do not address the extent to which higher frequency smaller amplitude signals that may also be present in the evoked response can be characterized and predicted.

Our data also do not take into account the nonlinearities that may arise when stimulating at multiple locations simultaneously. More sophisticated approaches have been invoked to explore such nonlinearities when characterizing the neural responses to visual inputs [34]. Examining the responses to multielectrode stimulation would be a natural extension of this work, and similar approaches as those use here could help elucidate higher order spatial interactions related to electrical stimulation. In addition, because of stimulation artifacts, we are unable to characterize the response at the actual site of stimulation. This may be addressed through better recording amplifiers that are capable of capturing evoked responses even in the same electrode used for stimulation.

In our analysis, we used the average evoked response at each electrode to identify whether that electrode is responsive to stimulation. Our criteria for determining responsiveness was that the average evoked response should have the characteristic biphasic morphology observed in previous studies of cortico-cortical evoked potentials [16–18], and that the energy of the average evoked response exceeds a given threshold. As expected, predictions were better for those electrodes that were identified as responsive. However, the distinction between responsive and non-responsive electrodes is somewhat arbitrary, and the threshold we choose could fall at any point along a spectrum. The choice of threshold reflects the tolerance for including or excluding electrodes based on a different signal to noise ratio in their response to stimulation. In practice, stimulation at one site likely results in effects at many more electrodes than those we have identified as responsive. Hence, a more general approach for predicting responses that is agnostic to whether an individual electrode is responsive would likely exhibit variable performance in predicting the evoked responses. Reducing the threshold for inclusion may identify a larger set of responsive electrodes, but the reduced signal to noise ratio of their responses may compromise the predictive ability of the response models associated with those newly included electrodes.

Finally, our results suggest that the predictions derived using a simple linear model match the predictions one could make by using the average response to a repeated series of stimuli. An important distinction, however, between using the average response to repeated stimulation to predict future responses and using the linear model is that the latter does not require multiple stimulation sessions to accurately predict future responses. From a practical standpoint, our data therefore suggest that a single and relatively short training session is sufficient for generating a linear model that is capable of predicting the future response to novel stimulation inputs, therefore providing a principled approach for designing and anticipating the responses to different stimulation paradigms.

Conclusion

Our analyses here focus on capturing the responses to stimulation in multiple brain regions when stimulating at an individual site. Our results suggest that the neural responses to direct electrical stimulation are approximately linear and consistent across time, and can therefore be predictable. Characterizing the responses to stimulation in this manner may therefore may provide an important tool for advancing our ability to directly stimulate the human brain in a principled manner.

Highlights.

• Cortical evoked responses can be characterized by a linear system.

• Generated linear models predict the responses to individual stimulation pulses.

• Models also predict the responses to combinations of stimulation pulses.

• This offers an approach for predicting responses to more complex stimulation.