Abstract
Fast Fourier transform (FFT)-based protein ligand docking together with parallel simulated annealing for both rigid and flexible receptor docking are implemented on graphical processing unit (GPU) accelerated platforms to significantly enhance the throughput of the CDOCKER and flexible CDOCKER — the docking algorithms in the CHARMM program for biomolecule modeling. The FFT-based approach for docking, first applied in protein-protein docking to efficiently search for the binding position and orientation of proteins, is adapted here to search ligand translational and rotational spaces given a ligand conformation in protein-ligand docking. Running on GPUs, our implementation of FFT docking in CDOCKER achieves a 15,000 fold speedup in the ligand translational and rotational space search in protein-ligand docking problems. With this significant speedup it becomes practical to exhaustively search ligand translational and rotational space when docking a rigid ligand into a protein receptor. We demonstrate in this paper that this provides an efficient way to calculate an upper bound for docking accuracy in the assessment of scoring functions for protein-ligand docking, which can be useful for improving scoring functions. The parallel molecular dynamics (MD) simulated annealing, also running on GPUs, aims to accelerate the search algorithm in CDOCKER by running MD simulated annealing in parallel on GPUs. When utilized as part of the general CDOCKER docking protocol, acceleration in excess of 20 times is achieved. With this acceleration, we demonstrate that the performance of CDOCKER for re-docking is significantly improved compared with three other popular protein-ligand docking programs on two widely used protein ligand complex datasets — the Astex diverse set and the SB2012 test set. The flexible CDOCKER is similarly improved by the parallel MD simulated annealing on GPUs. Based on the results presented here, we suggest that the accelerated CDOCKER platform provides a highly competitive docking engine for both rigid-receptor and flexible-receptor docking studies, and will further facilitate continued improvement in the physics-based scoring function employed in CDOCKER docking studies.
Graphical Abstract

1. INTRODUCTION
Protein-ligand docking methods aim to predict how ligands bind with a target protein, i.e., binding poses of ligands and their binding affinities.1 They are widely employed in drug discovery processes to virtually screen libraries of a large number of small molecules to search for hit compounds that could provide a basis for the development of novel small molecule therapeutics.2 Multiple off-the-shelf protein-ligand docking programs, either commercial or free, are available for use,3 such as CDOCKER,4 Autodock,5 Autodock Vina,6 DOCK,7 and Glide.8,9 Most protein-ligand docking programs consist of two essential components — a scoring function for the assessment and ranking of ligand-binding poses and a search algorithm that facilitates the search for and discovery of those low free energy binding poses.4 The scoring function quantifies the fit between a ligand’s binding pose and the protein receptor and is expected to be able to differentiate the correct binding pose from incorrect ones through the assertion that the correct binding pose has the best score. When used to predict binding affinities, the scoring function is also expected to approximate the binding free energy between ligands and target proteins. The search algorithm is utilized to sample potential ligand binding poses and identify the binding pose with the best score. Because the scoring functions used in protein-ligand docking programs are not convex functions and typically have multiple local minima, heuristic search algorithms such as genetic algorithms and simulated annealing are often used in search for optimal binding poses.4,6
CDOCKER,4 a CHARMM10 module for protein-ligand docking, is one of the protein-ligand docking programs that are widely used in both academia and industry for drug discovery. It uses the interaction energies between proteins and ligands calculated with the CHARMM force field10 for proteins and the CGenFF force field11 for ligands as its scoring function. To search for the lowest energy pose of ligands, CDOCKER utilizes molecular dynamics (MD) based simulated annealing followed by energy minimization. In the MD based simulated annealing, MD is used to simulate the dynamics of protein-ligand interaction and the temperature of the MD first increases to a high value and then slowly decreases. As the temperature of the MD decreases, ligands are expected to adopt low energy poses. The resulting ligand poses from simulated annealing are further optimized by energy minimization. As the MD-based simulated annealing is a heuristic search approach, it is not guaranteed that the ligand will converge to the lowest energy pose in each trial of MD-based simulated annealing. To increase the chance that the lowest energy pose of the ligand is identified, multiple trials of simulated annealing are employed. In each trial, the ligand is first initialized with a random conformation,12 a random orientation, and a random position within the binding pocket before going through the MD-based simulated annealing and energy minimization. After the energy minimization, the resulting poses, one from each trial, are ranked by their energies that include the intra-interaction energy of the ligand and the interaction energy between the ligand and the protein. The pose with the lowest energy is predicted to be the binding pose. In a typical application of CDOCKER, a large number of ligands need to be docked with a protein. Therefore, the docking procedure has to run fast enough to make the method practical. To accelerate the docking procedure and help search for the lowest energy pose of ligands, CDOCKER utilizes a cubic grid representation of the binding pocket and soft-core potentials,1,4 respectively, both of which will be described in detail in following sections.
In this paper two new features — fast Fourier transform (FFT)13 docking and parallel MD simulated annealing — are added to CDOCKER to further accelerate the search algorithm in CDOCKER. Both features are implemented such that they can take advantage of the parallel computing power of graphical processing units (GPUs). In addition, the original CDOCKER routine used for computing protein grid potentials is also updated such that it can run on GPUs.
2. METHODS
2.1. Accelerated routine for computing soft-core grid potentials
In CDOCKER’s docking protocol, most of the computational time is spent on calculating forces on ligand atoms and the ligand’s interaction energy with the protein for a large number of ligand poses. To accelerate the force and energy calculation, a cubic grid representation of the binding pocket is used. Specifically, the binding pocket inside a protein is discretized onto a cubic grid (Figure 1A). Probe atoms are placed on each of the grid points and their interaction energies with the protein are saved in a lookup table. Then the interaction energy of a ligand atom with the protein can be rapidly calculated by looking up values in the tables, instead of explicitly calculating its interaction with all of the protein atoms. When a ligand atom’s position is not on any grid points, its interaction energy with protein atoms is calculated using a trilinear interpolation of the energy values on the eight grid points of the cell which contains the ligand atom. The force acted by protein atoms on a ligand atom is approximated using the local energy gradient. To accurately approximate the interaction energy between different ligand atoms and a protein, multiple grids are needed and calculated based on the protein. One of the grids is for computing the electrostatic interaction energy and the remaining grids are for computing the van der Waals interaction energy for ligand atoms with different atom types. In total, 26 grid potentials are computed based on the structure of the protein receptor in CDOCKER.
Figure 1:
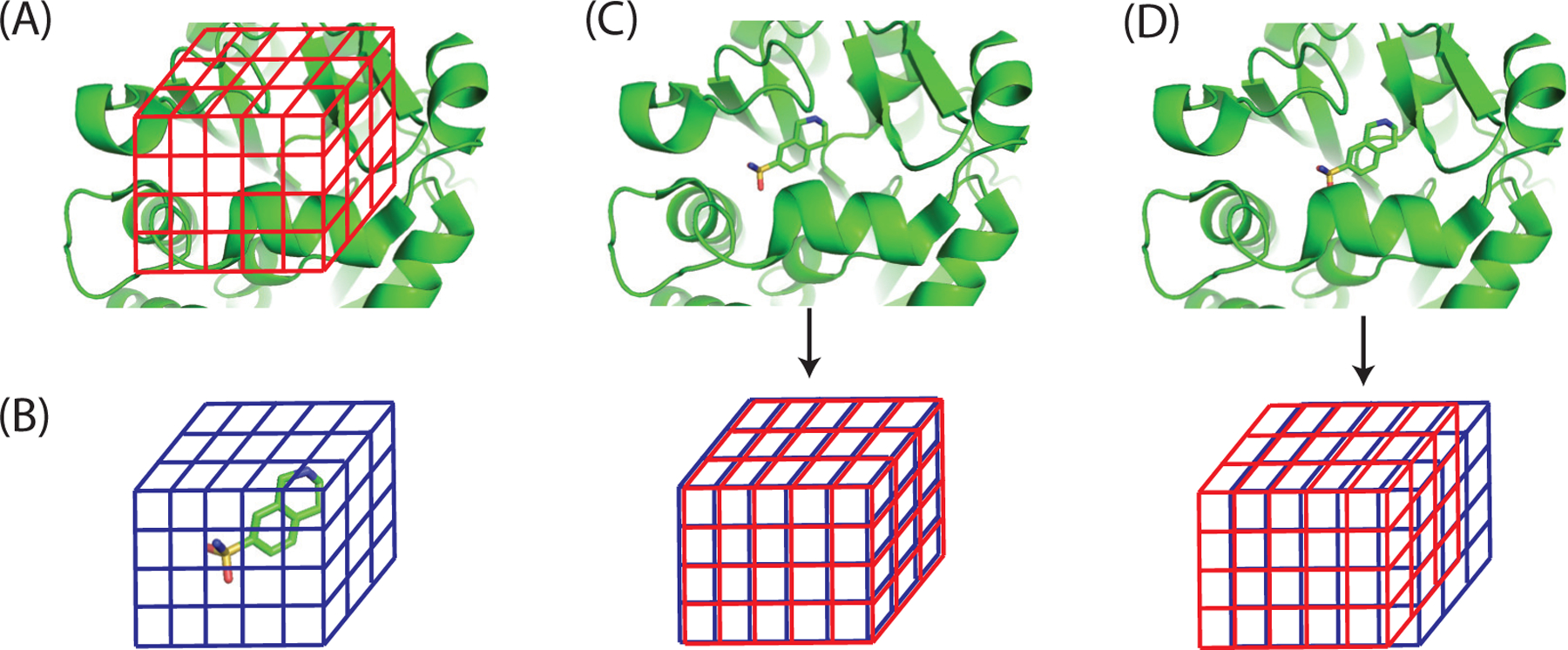
The electrostatic interaction energy between proteins and ligands can be calculated as a cross correlation function between the protein electrostatic potential grid and the ligand charge grid. (A) The binding pocket in the protein is discretized into a cubic grid with equally spaced grid points. (B) Charges of ligand atoms are distributed onto a cubic grid which has the same spacing and the same number of grid points as the potential grid in (A). (C,D) As the ligand translates within the binding pocket by multiple units of the spacing distance, the electrostatic interaction energy can be approximated using a cross correlation function Uelec(i, j, k) between the protein potential grid (red grids) and the ligand charge grid (blue grids). (C) and (D) correspond to the cases Uelec(0, 0, 0) and Uelec(1, 0, 0), respectively.
Soft-core potentials in CDOCKER are used to smooth the energy landscape, which can help the MD-based simulated annealing search escape from local minima and identify the ligand pose with the lowest energy. Specifically, when using soft-core potentials, the van der Waals, electrostatic attractive, and electrostatic repulsive energies are approximated using the formula:
| (1) |
where is the regular interaction energy; Emax is a parameter controlling the “softness” of the potential; Given Emax, a and b are automatically determined using the condition that the energy and the force calculated using Eq. 1 have to be equal to that calculate using the regular formula at the switch distance where .
In the previous version of CDOCKER, the routine for computing soft-core grid potentials for the protein receptor can only run on central processing units (CPUs), which can be slow due to the large number of grid points and protein atoms. For instance, to compute 26 grid potentials, each of which has 43×43×43 lattice points, for a target protein of 8757 atoms, the number of float point operation is on the order of 43×43×43×26×8, 757 = 18, 102, 312, 774. It took 2,100 seconds for the previous implementation running on a CPU(Intel® Xeon® Processor E5520) to compute these grid potentials. Here, we added a parallel implementation of the routine such that it can calculate the soft-core grid potentials on GPUs. To do the same computation, it only takes 2.5 seconds for the new implementation running on a CPU (NVIDIA® GEFORCE® GTX 1080). Therefore, our new implementation on GPUs is more than 800 times faster than the previous implementation on CPUs. The details of the new implementation on GPUs are included in the Supporting Information.
2.2. Fast Fourier transform docking
The FFT approach for docking was first used in rigid protein-protein docking.14 In this approach, proteins are represented as three dimensional grids such that the surface complementarity of two proteins can be formulated as the correlation function between two grids.14 Calculating the correlation function between two grids can be greatly accelerated using the FFT algorithm.15 Since its first use in protein-protein docking,14 the FFT approach has been extended and improved in several aspects. In addition to the original potential term representing protein shape complementarity,14 potential terms representing desolvation and electrostatic interactions were added into the scoring function16–18 to more accurately model the physical interaction between proteins. Moreover, the FFT approach was further accelerated by using spherical polar Fourier correlations19–21 and GPUs.22,23 With these extensions and improvements, the FFT approach has been widely adopted in multiple protein-protein docking programs.18,20,24
In contrast to FFT’s wide application in protein-protein docking, its application in protein-ligand docking is largely unexplored.25 One difficulty in adopting the FFT approach for protein-ligand docking is to represent the scoring function as a correlation function between grids, because the scoring function used in protein-ligand docking is often more complicated than that in protein-protein docking. In addition, the FFT approach assumes both protein and ligand are rigid bodies, whereas, in protein-ligand docking, at least the ligand needs to be modeled as flexible. Therefore multiple FFTs are required to search the ligand’s conformation space. This in turn requires a fast implementation of the FFT for it to be practical. Otherwise running multiple FFTs will take too much time.
Here we investigated the use of the FFT approach for protein-ligand docking in the context of CDOCKER where the CHARMM force field10,11 is used as the scoring function. The interaction energy, including electrostatic and van der Waals energy, between proteins and ligands is represented as the sum of multiple correlation functions between multiple pairs of grids and the calculation of correlation functions is accelerated using FFTs. Moreover, calculating multiple FFTs is further accelerated using GPUs.
2.2.1. Representing the non-bonded interaction energy between proteins and ligands as correlation functions between grids.
In order to use the FFT approach for protein-ligand docking, the interaction energy between a protein and a ligand needs to be expressed as a set of correlation functions between grids. Because CDOCKER uses the CHARMM force field10,11 as its scoring function, the interaction energy between proteins and ligands includes electrostatic and van der Waals interactions terms.4
The electrostatic interaction energy between proteins and ligands is calculated as
| (2) |
where L and P are collections of ligand atoms and protein atoms, respectively; qi and qj are atom partial charges; ri and rj are atom coordinates. is the protein electrostatic potential at position ri. As Eq. (2) shows, the electrostatic interaction energy between protein and ligand atoms can be calculated as an inner-product between the ligand charge vector qL = (qi)i∈L and the protein electrostatic potential vector Velec = (Velec(ri))i∈L. However, the protein electrostatic potential vector Velec still depends on the positions of the ligand atoms that are not known in advance. To get rid of this dependency, grid representations are used for both the protein electrostatic potential and the charges of ligand atoms (Fig. 1). Specifically, the binding pocket of a protein is discretized using a 3 dimensional grid and protein electrostatic potentials at all the grid points are calculated and saved in a lookup table (Fig. 1A). The protein electrostatic potential at the grid point (l, m, n) is represented as . Because the protein electrostatic potential is calculated only at the grid points, in order to calculate the electrostatic interaction energy between proteins and ligands, the partial charges of ligand atoms are also distributed onto a three dimensional grid (Fig. 1B) in a trilinear manner. The aggregated charge at the grid point (l, m, n) is represented as Qgrid(l, m, n). Then the electrostatic interaction energy between protein atoms and ligand atoms can be approximated using the inner-product of protein electrostatic potential grid and ligand charge grid (Fig. 1C):
| (3) |
where Nx, Ny, and Nz are the numbers of grid points along the X, Y, and Z directions, respectively. Moreover, when the ligand is translated within the binding pocket by i, j, and k grid spacing units in the X, Y , and Z directions, respectively, the electrostatic potential energy between the protein and ligand can be similarly approximated using (Fig. 1D):
| (4) |
where is extended into a periodic grid, i.e., . As shown in Eq. 4, as the ligand moves within the binding pocket by distances of multiple units of grid spacing in each direction, the electrostatic interaction energy between the protein and ligand can be approximated as a cross correlation function between the protein electrostatic potential grid and the ligand charge grid Qgrid. An advantage of using the grid representation, as in Eq. 4, over that in Eq. 2 is that is independent of the ligand and can be calculated with only the protein. Similarly, grid Qgrid is independent of the protein and can be calculated with only the ligand.
The van der Waals interaction energy between proteins and ligands is calculated using the Lennard-Jones potential:
| (5) |
where , , ϵi, and ϵj are parameters of the Lennard-Jones potential and are parts of the CHARMM force field;
| (6) |
Eq. 5 for the van der Waals energy is similar to that in Eq. 2, except that depends on both ligand coordinates ri and parameters , whereas Velec(ri) only depends on ligand coordinates ri. Because of this difference, the approach used to represent the electrostatic energy between proteins and ligands as a cross correlation function between a pair of grids can not be directly applied to the van der Waals interaction. In the CHARMM force field, parameters rmin of ligand atoms depend on their atom types and the total number of atom types is finite. Therefore, there are only a finite number of possible values for rmin. Taking advantage of this fact, we can group the terms in Eq. 5 based on the value of rmin:
| (7) |
where Rmin is the set of possible values of rmin for ligand atoms and is the set of ligand atoms that have the parameter of rmin. The individual van der Waals energy corresponding to rmin is , which is similar to the Eq. 2 and can be calculated as a cross correlation function between grids using the same approach used for calculating the electrostatic energy. Therefore, the total van der Waals interaction energy can be approximated as the sum of multiple correlation functions between multiple pairs of grids.
2.2.2. Calculating cross correlation functions between grids using FFTs in parallel on GPUs.
Based on the convolution theorem,15 the cross correlation function for the electrostatic energy in Eq. 4 can be calculated by applying a Fourier transform and an inverse Fourier transform successively on both sides of the equation, i.e.,
| (8) |
The FFT algorithm is utilized to efficiently calculate both the Fourier transform and the inverse Fourier transform operations. In contrast to the naive algorithm which requires number of operations to calculate the cross correlation function, the FFT algorithm only needs number of operations. Similarly, the FFT algorithm can also be used to calculate the van der Waals interaction energy in Eq. 7. Although the FFT algorithm can significantly accelerate the calculation of cross correlation functions, one cross correlation function can only provide interaction energies between a proteins and a ligand as the ligand translates within the binding pocket with a fixed conformation and a fixed orientation. In other words, FFTs only accelerate the search of the ligand translational space. However, in protein-ligand docking where at least the ligand is modeled as flexible, the interaction energies need to be calculated for different conformations and orientations of the ligand, in addition to different positions. Therefore, multiple FFTs, each for one particular conformation and orientation of the ligand, are needed in protein-ligand docking. To accelerate this calculation, multiple FFTs are run on GPUs in a batch mode to take advantage of the pipelined parallel computing power of GPUs.26
2.3. Parallel MD-based simulated annealing with GPUs
One of the advances in using MD simulations to study both chemical and biological systems has been the utilization of GPUs.27–30 Compared with CPUs, the parallel computing power of GPUs enables us to run MD simulations orders of magnitude faster and simulate longer timescale dynamics of chemical and biological systems, which makes MD suitable to study processes that were not accessible before.27–30 Although GPUs have been widely employed in running MD simulations of large chemical and biological systems, they are rarely used to accelerate protein-ligand docking methods. Here we investigated the utilization of GPU computing to accelerate CDOCKER for protein-ligand docking by running MD-based simulated annealing of multiple copies of ligands and any included flexible receptor regions in parallel on one GPU.
Because protein-ligand interaction energy landscapes have many local minima and the MD-based simulated annealing is a heuristic search method, multiple trials of simulated annealing have to be employed to search for the lowest energy pose. As the number of trials increases, the docking accuracy usually improves until it reaches a plateau. In addition, in a typical application, CDOCKER needs to dock a large number of ligands with a protein. Therefore, accelerating multiple trials of MD-based simulated annealing can help CDOCKER to dock a large number of ligands in a limited time while maintaining docking accuracy. Because trials of MD-based simulated annealing are independent, one way to accelerate the calculation is to run them in parallel with multiple processors. In the existing implementation of CDOCKER, multiple trials of MD-based simulated annealing can be run in parallel with multiple CPUs. Here we introduce a new feature into CDOCKER to enable it to run multiple trials of MD-based simulated annealing simultaneously on GPUs.
As there are already implementations of MD engines running on GPUs, instead of writing a new MD engine specifically for running multiple trials of MD-based simulated annealing on GPUs, we utilize the existing GPU-enabled MD engine that is part of the CHARMM/OpenMM interface.31 To utilize the MD engine from OpenMM for our purpose, we make a customized system consisting of multiple copies of a ligand and any included flexible receptor regions and one copy of the potential grids of the protein. Atoms in each copy of the ligand and the flexible receptor group interact with atoms in the same copy and the potential grids, but do not interact with atoms in all other copies of flexible groups. Therefore, although the system includes multiple copies of the flexible atoms, these copies are independent from each other and the dynamics of each copy is the same as if there is just one copy. Running one trial of MD-based simulated annealing with this customized system on GPUs is equivalent to running multiple trials of simulated annealing using the previous implementation on CPUs.
The parallel MD-based simulated annealing with GPUs is implemented for both rigid receptor and flexible receptor docking.1 In rigid receptor docking, protein grid potentials are computed using all protein atoms and the customized OpenMM system consists of multiple copies of ligand atoms. In flexible receptor docking, side chains of multiple amino acids near the binding pocket are modeled as flexible regions. The protein atoms of these flexible side chains are modeled similarly as ligand atoms, except that they are attached to fixed protein backbone atoms through bonded interaction. These protein atoms of flexible side chains are excluded when computing protein grid potentials and the customized OpenMM system consists of multiple copies of both ligand atoms and atoms in flexible side chains. More detailed information on flexible receptor docking in CDOCKER is available in the original paper describing flexible CDOCKER.1
3. RESULTS
3.1. Benchmark datasets and computational details
Three sets of protein-ligand complexes are used as benchmark datasets to evaluate the protein-ligand docking methods just described. The Astex diverse set32 and the SB2012 set33 are used for evaluating rigid receptor docking. The SEQ17 dataset34 is used for evaluating flexible receptor docking. The Astex diverse set contains 85 diverse high-resolution protein-ligand complexes and has been widely used for benchmarking different protein-ligand docking methods.32 In this study, 70 of the 85 protein-ligand complexes that do not include cofactors are used. Compared to the Astex diverse set, the SB2012 set33 is a much larger set of protein-ligand complexes. It contains 1043 protein-ligand complexes, out of which the 1003 complexes that do not have cofactors and can be typed using CGenFF35 are used in this study. The 1003 protein-ligand complexes from the SB2012 set overlap with 69 out of 70 complexes from the Astex diverse set. Protein-ligand complexes with cofactors are excluded because force field parameters of the cofactors are not readily available in the CHARMM force field. Unlike protein-ligand docking methods that use empirical scoring functions, CDOCKER uses physical interaction energies based on the all-atom CHARMM force field. Cofactors have to be parameterized based on the CHARMM force field in order to be included in docking. Because not all cofactors in the benchmark datasets can be accurately parameterized using CGenFF, we excluded all protein-ligand complexes with cofactors such that the complexes in the benchmark datasets are more consistent and the docking accuracy is not affected by the errors introduced in the parameterization of cofactors. The SEQ17 dataset, which was originally used to benchmark the flexible receptor docking method AutodockFR,34 contains 17 pairs of apo-holo structures. These 17 systems were selected to represent a wide range of receptors.
The MD-based simulated annealing in CDOCKER is conducted over several stages and different stages use protein grid potentials with different softness, i.e., grid potentials calculated using different Emax (Eq. 1). Three sets of values for the parameter Emax are used for rigid receptor docking and they are summarized in Table 1. The stages of simulated annealing for rigid receptor docking are as follows. Using the soft-core grid potential I, the ligand is heated up from 300K to 700K over 3000 MD integration steps with a step size of 1.5 femtoseconds and then cooled down from 700K to 300K over 14000 steps. Then using the soft-core grid potential II, the ligand is further cooled down from 500K to 300K over 7000 steps and then from 400K to 50K over 3000 steps. Final, the ligand is minimized using the soft-core grid potential III for 200 steps.
Table 1:
Soft-core potentials used in rigid receptor docking
| name | E* max (vdw) | E* max (att) | E* max (rep) |
|---|---|---|---|
| soft-core potential I | 0.6 | −0.4 | 8.0 |
| soft-core potential II | 3.0 | −20.0 | 40.0 |
| soft-core potential III | 100 | −100 | 100 |
Emax(vdw), Emax(att) and Emax(rep) in the unit of kcal/mol are parameters for the van der Waals, electrostatic attractive, and electrostatic repulsive interactions, respectively.
Similar stages of MD-based simulated annealing are used in flexible receptor docking except that soft-core grid potentials with different softness are used. Specifically, the soft-core grid potential I is changed and is adopted from the flexible docking protocol outlined by Gagnon et al.1 to prevent ligands from leaving the binding pocket during the initial searching and heating stages of simulated annealing. The soft-core potential III is designed to give a more native-like energy landscape. Since there are more explicit atoms involved in flexible receptor docking, these values are larger than those used for rigid receptor docking. Detailed values for the softness parameter Emax used in flexible receptor docking are summarized in Table 2. More details on simulate annealing procedures are available in the CHARMM scripts included in the Supporting Information.
Table 2:
Soft-core potentials used in flexible receptor docking
| name | E* max (vdw) | E* max (att) | E* max (rep) |
|---|---|---|---|
| soft-core potential I | 15.0 | −120.0 | −2.0 |
| soft-core potential III | 10000 | −10000 | 10000 |
Emax(vdw), Emax(att) and Emax(rep) in the unit of kcal/mol are parameters for the van der Waals, electrostatic attractive, and electrostatic repulsive interactions, respectively.
3.2. Fast Fourier transform docking
3.2.1. Energy calculation acceleration with FFTs and GPUs
When a ligand has a fixed conformation and a fixed orientation, its interaction energy with a protein as the ligand translates on grid points can be represented as the cross correlation function between grids and both FFTs and GPUs are used to accelerate the calculation of these cross correlation functions. To see the extent to which FFTs and GPUs can accelerate the calculation, we applied the FFT approach to a test example utilizing the protein-ligand complex 1G9V(PDB ID). The ligand in 1G9V has dimensions of 5.8Å × 14.5Å × 8.5Å in the X, Y, and Z directions, respectively. With a grid spacing distance of 0.5Å, the ligand grid has 13 × 30 × 18 points. The binding pocket is defined as a cubic box with a dimension of 29.5Å, and the protein potential grid with the same grid spacing distance as the ligand grid has 60 grid points in all three directions. Therefore, within the binding pocket, the ligand has 59, 220 = 47 × 30 × 42 possible positions. The interaction energy between the protein and the ligand for all possible positions of the ligand are calculated using three methods: the naive method, which explicitly calculates the interaction energy for each position on a CPU, FFTs running on a CPU, and FFTs running on a GPU. The wall times used by the three methods are summarized in Table 3. Compared with the naive method, the FFT approach with CPUs accelerates the calculation by more than 100 times and running FFTs on GPUs in a batch mode further accelerates the calculation by 140 fold. Overall, compared with the naive method, the speedup of using both FFTs and GPUs is about 15,000 fold.
Table 3:
Wall time used by the three methods: the naive method looping through all positions on a CPU, FFTs (CPU), and FFTs (GPU) to calculate interaction energies between the protein and the ligand in 1G9V for the ligand’s 59,220 positions.
The CPU is an Intel Xeon Processor E5645 2.4GHz;
The GPU is a NVIDIA GeForce GTX 1080;
Multiple FFTs run in parallel on GPUs in a batch mode. The wall time is calculated as the wall time used to run one batch of FFTs divided by the batch size which is 100.
3.2.2. Scoring function accuracy: identifying ligand native orientations and positions.
With the acceleration from both FFTs and GPUs for calculating the interaction energy between ligands and proteins, it becomes feasible to systematically search ligand orientations and positions in a reasonable computation time. This, in turn, enables us to investigate the scoring function’s accuracy in terms of identifying native orientations and positions given the conformations of both the ligand and the protein. Using the Astex diverse set and the SB2012 set as test sets, we applied the FFT-based approach with GPUs to rigidly dock ligands onto proteins using the native conformations of ligands and proteins. To systematically search the orientation and translation space of ligands, 100,000 randomly sampled orientations of each ligand are used. For each orientation, the ligand’s translational space is uniformly covered by a three dimensional grid with a grid spacing distance of 05Å. The docked pose of a ligand is chosen to be the lowest energy pose among the poses with all possible combinations of sampled orientations and translations.
For both test sets, the docking accuracy first increases as the number of randomly sampled ligand orientations increases and reaches a plateau when 100,000 random orientations are used (Fig. 2A). Here the docking accuracy is defined as the percentage of protein-ligand complexes in the benchmark datasets for which the root mean square deviation (RMSD) of the docked pose is within 2.0Å with respect to the native pose. Because the lowest energy pose is not necessarily within 2.0Å to the native pose for all the protein-ligand complexes in the benchmark datasets, the accuracy on the Y axis does not reach 100%. The plateau occurs at a docking accuracy of about 66.34% and 66.22% for the Astex diverse set and the SB2012 set, respectively. (Fig. 2B). When the native orientation is included, in addition to the 100,000 random orientations, the docking accuracy increases to about 67.75% and 67.63% for the Astex diverse set and the SB2012 set, respectively. (Fig. 2B). It is notable that this small difference suggests that the use of 100,000 rotational samples is sufficiently dense to cover the rotational space. The docking accuracy at the plateau, which is around 68%, represents the accuracy of the CHARMM force field in identifying the native orientations and positions of ligands assuming the native conformations of ligands are given. This accuracy should be an upper bound of the CHARMM force field’s accuracy in identifying native ligand poses, which includes the native conformations in addition to the native orientations and positions. Although the size of the SB2012 set is more than ten times larger than the Astex diverse set, the results on the two sets are quite similar. The good agreement between different benchmark datasets suggests that the physics-based scoring function used in CDOCKER is potentially transferable among a large variety of protein ligand complexes.
Figure 2:
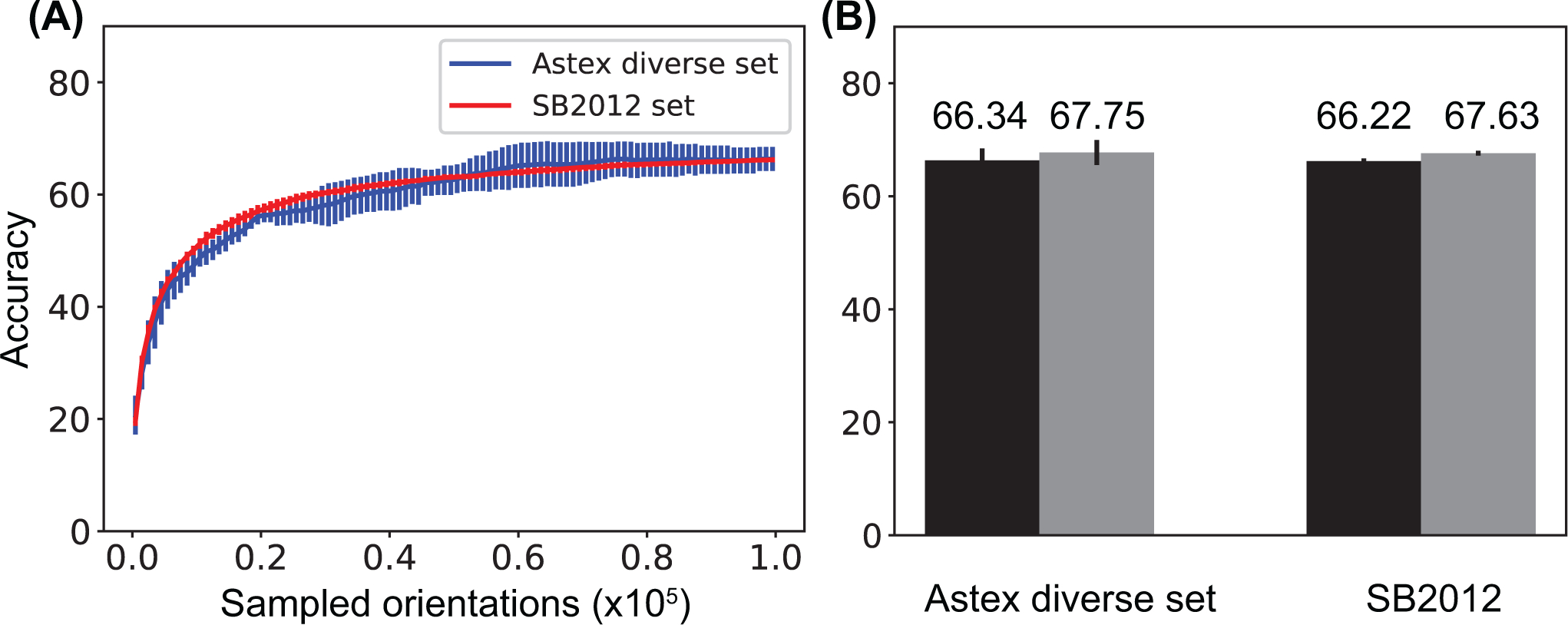
Docking accuracy of the FFT approach for docking rigid ligands onto rigid proteins with the native conformations of both ligands and proteins using the Astex diverse set and the SB2012 set. (A) Docking accuracy increases as the number of randomly sampled orientations increases. The error bars are estimated using 10 independent repeats. (B) Docking accuracy when 100,000 randomly sampled orientations are used (black) and when 100,000 randomly sampled orientations plus the native orientation are used (grey).
We note that the above FFT-based rigid docking approach could be generalized to permit ligand conformational space to be sampled. This would involve first sampling a suitable ensemble of ligand conformations36 and then carrying out the rotational/translational sampling to identify the lowest energy conformation using GPU-accelerated FFTs. This protocol can readily be implemented using CHARMM scripting language.10 However, we instead pursue in the following integration of ligand (and possibly receptor side chain) sampling into an MD simulated annealing scheme as employed in CDOCKER4 and flexible CDOCKER.1
3.3. Parallel MD-based simulated annealing with GPUs
3.3.1. GPU accelerated parallel simulated annealing significantly accelerates CDOCKER
Compared with the original CDOCKER running serially on CPUs, the speedup of the parallel MD-based simulated annealing with GPUs is shown in Table 4. For the protein-ligand pairs in the Astex diverse set, when 100 and 500 docking trials are used, the average wall time used by the original CDOCKER with CPUs are 338.4 and 1692.0 seconds, respectively. In contrast, the average wall time used by the parallel MD-based simulated annealing with GPUs are 30.8 and 85.5 seconds, respectively, which is about 10 fold and 20 fold faster. The speedup becomes even larger when the number of trials increases, because the wall time used by the original CDOCKER on CPUs is proportional to the number of trials.
Table 4:
Acceleration of parallel MD-based simulated annealing with GPUs compared with the original CDOCKER with CPUs on the Astex diverse set.
| CDOCKER with CPUs | CDOCKER with parallel MD-based simulated annealing with GPUs | |
|---|---|---|
| accuracya | 0.623 ± 0.023 | 0.631 ± 0.029 |
| wall timeb (seconds) | 338.4 | 30.8 |
| wall timec (seconds) | 1692.0 | 85.5 |
The accuracy when 100 trials are used; The ligand native conformation is used as the starting conformation; The uncertainty is estimated using 10 independent repeats.
The wall time used when 100 trials are used;
The wall time used when 500 trials are used.
3.3.2. Comparison with other protein-ligand docking programs for rigid receptor docking.
The accelerated CDOCKER is compared with three other widely used protein-ligand docking programs: Autodock, Autodock Vina, and DOCK. The computational details for setting up docking in all the docking programs presented here are included in the Supporting Information. To make a fair comparison between different protein-ligand docking programs, same settings are used for all docking programs whenever it is possible. For instance, for a protein-ligand complex, the docking grid box with the same position and size is used in all programs. The docking accuracy is calculated as the percentage of protein-ligand complexes in benchmark datasets for which the RMSD of the docked pose is less than 2.0Å with respect to the native pose.
The re-docking results on the Astex diverse set and the SB2012 set are shown in Table 5 and Table 6, respectively. With the acceleration achieved by the parallel MD-based simulated annealing with GPUs in CDOCKER, the average wall time required by CDOCKER for docking one protein-ligand complex is either faster than or on par with other programs. For CDOCKER, Autodock, and Autodock Vina, the docking accuracy one obtains depends on whether the ligands’ native conformation or a random conformation is used as the starting conformation: all of these approaches perform better when the ligand native conformation is used as the starting conformation. Starting with ligands’ native conformation makes the conformational search easier and the docking accuracies higher than those corresponding to using random starting conformations. Because the DOCK program uses the “anchor and grow” search method,7 its accuracy does not depend on the starting conformation.
Table 5:
Docking accuracy of multiple protein-ligand docking programs on the Astex diverse set.
| CDOCKERd | Autodock v4.2.6 | Autodock Vinae | Autodock Vinaf | DOCK v6.7 | |
|---|---|---|---|---|---|
| accuracy (nativea) | 0.664 (± 0.022g) | 0.600 (± 0.020) | 0.701 (±0.019) | 0.710 (± 0.009) | 0.639 (± 0.016) |
| accuracy (randomb) | 0.537 (±0.021) | 0.530 (±0.029) | 0.633 (±0.014) | 0.623 (±0.011) | |
| wall time (sec)c | 85.5 | 279.6 | 82.3 | 202.9 | 50.0 |
Ligand native conformations are used as starting conformations.
Ligand random conformations are used as starting conformations.
CDOCKER is run on a GPU (NVIDIA GeForce GTX 980). All the other docking programs use one CPU (Intel Xeon Processor E5645 2.4GHz).
500 trials are used in CDOCKER.
exhaustiveness = 8.
exhaustiveness = 20.
All uncertainties are estimated using 10 independent repeats.
Table 6:
Docking accuracy of multiple protein-ligand docking programs on the SB2012 set.
| CDOCKERc | Autodock v4.2.6 | Autodock Vinad | Autodock Vinae | DOCK v6.7 | |
|---|---|---|---|---|---|
| accuracy(nativea) | 0.569 (± 0.006f) | 0.477 (± 0.009) | 0.631 (±0.004) | 0.642 (± 0.005) | 0.553 (±0.005) |
| accuracy (randomb) | 0.429 (± 0.007) | 0.418 (±0.004) | 0.532 (±0.004) | 0.547 (±0.004) |
Ligand native conformations are used as starting conformations.
Ligand random conformations are used as starting conformations.
500 trials are used in CDOCKER.
exhaustiveness = 8.
exhaustiveness = 20.
All uncertainties are estimated using 10 independent repeats.
Based on the results from the Astex diverse set, when ligand random conformations are used as starting conformations, DOCK and Autodock Vina have similar and higher docking accuracy. Autodock has the lowest docking accuracy and CDOCKER is in between. Increasing the parameter that controls the searching exhaustiveness in Autodock Vina from 8 to 20 proportionally increases the run time, but it does not change its docking accuracy significantly. Compared with the results on the Astex diverse set (Table 5), the relative performance of the protein-ligand docking programs on the SB2012 set is the same in terms of docking accuracy (Table 6). However, for all of the programs, the docking accuracy is lower on the SB2012 set (Table 6). Although the Astex diverse set contains a diverse set of protein-ligand complexes, the number of protein-ligand complexes in the set is relatively small. Because the SB2012 dataset contains more than an order of magnitude more protein-ligand complexes, the performance on the SB2012 set should be a more objective measure of the protein-ligand docking programs’ docking accuracy. The lower docking accuracy on the SB2012 set for all the tested protein-ligand docking programs can be attributed to either search algorithms or scoring functions or both. This suggests that more efforts are required to further improve search algorithms and scoring functions including both physics based score functions used in CDOCKER and DOCK and empirical scoring functions used in Autodock and Autodock Vina. We note that the docking accuracies of both Autodock Vina and DOCK reported in this study are quite different from those reported in previous studies.6,7,37 This is because of the fact, as shown in this study, that the docking accuracy of a protein-ligand docking program can vary significantly depending on ligand starting conformation and benchmark dataset.
3.3.3. Benchmarking flexible receptor docking
The implementation of parallel simulated annealing on GPUs also significantly accelerates the flexible receptor docking in CDOCKER. To test both the docking accuracy and speed of flexible receptor docking in CDOCKER after the acceleration, we used the SEQ17 set which contains 17 pairs of apo-holo structures and represents a subset of the SEQ dataset which comprises ligand-receptor complexes that can be successfully docked using AutoDock (RMSD < 2.0 Å) with rigid re-docking.34 These 17 systems were selected to represent a wide range of receptors. For each of 17 apo-protein structures, there is at least one amino acid side chain around the binding pocket whose conformation in the holo structure is different from that in the apo structure by at least 2.5 Å (RMSD). Therefore, there would be at least one severe clash between ligand atoms and the receptor side chain if the ligand native conformation from the protein-ligand complex is directly fit onto the apo structure. In what follows, we evaluate the overall performance (accuracy and speed) of flexible CDOCKER for flexible receptor docking using this dataset and compare it with AutodockFR.34
In preparing each system for flexible receptor docking, the apo structure is superposed on the corresponding holo structure. The criteria used for selecting flexible side chains is the same as that used in AutoDockFR, except that in flexible CDOCKER the heavy atoms beyond Cα are considered to be flexible, whereas the heavy atoms beyond Cβ are set to be flexible in AutoDockFR.34 The RMSD cutoff for native-like pose is set to be 2.5 Å to be consistent with the evaluation criteria used by AutoDockFR.34 We performed 10 repeated calculations, each of which consists of 500 trials of both flexible CDOCKER and the rigid CDOCKER.
The docking results on the SEQ17 set are shown in Table 7. In each repeat, we first computed the searching accuracy. A searching success is defined as at least one native-like docking pose is identified among the docked poses from 500 trials of docking. The searching accuracy for rigid CDOCKER is 36.47% ± 5.41% when the apo structure is used as the receptor and 95.88% ± 2.84% when the holo structure is used. In contrast, for flexible CDOCKER, the search accuracies are 95.29% ± 2.48% and 80.00% ± 6.90% when the apo structures and the holo structure are used as receptors, respectively (Table 7). Therefore, flexible CDOCKER has a higher searching accuracy than rigid CDOCKER when the receptor binding pocket has a conformational change upon binding with ligands.
Table 7:
Docking accuracy of SEQ17 dataset using flexible CDOCKER
| Receptor Structure | Searching Accuracy | Ranking Accuracy |
|---|---|---|
| Holo | 95.29% ± 2.48% | 78.82% ± 4.96% |
| Apo | 80.00% ± 6.90% | 57.06% ± 3.97% |
To further assess the accuracy of flexible CDOCKER for this set, we considered the following scoring accuracy. The docked poses from 500 trials of docking are clustered using a K-means clustering algorithm from the MMTSB toolset (cluster.pl)38 based on ligand heavy atoms with a RMSD cutoff of 2.0 Å. If the number of docked poses in a cluster is less than 10, then the cluster is discarded. This allows us to remove those less populated docking poses that are frequently away from the binding pocket. Then the minimum energy pose of each cluster is selected and ranked based on the scoring function. A scoring success is defined as at least one of the cluster representatives is a native-like pose.34 The scoring accuracy of flexible docking in CDOCKER is about 57.06% when apo structures are used as receptors (Table 7) and the corresponding scoring accuracy of AutodockFR is 70.6%34 which is higher than CDOCKER. However, as mentioned before, the SEQ17 dataset is intentionally designed to only include protein-ligand complexes that can be correctly re-docked (RMSD < 2 Å) using the Autodock. If we do the same filtering process for CDOCKER, i.e., exclude protein-ligand complexes that can not be re-docked using CDOCKER, which include 3PTE and 2A78, the scoring accuracy of flexible docking in CDOCKER becomes 68.82%±3.97%, which is similar to the accuracy achieved by the AutodockFR.
In high-throughput virtual screening where a large number of ligands need to be docked, the major barrier for the use of flexible receptor docking is its speed. For flexible CDOCKER with parallel simulated annealing running on a GPU (NVIDIA® GEFORCE® GTX 1080), the average wall time required for one protein-ligand complex is about one hour. In contrast, AutodockFR running on a CPU (Intel® Xeon® Processor E5520) requires on average 50 × 8.5 = 425 hours for one protein-ligand complex:34 it takes 8.5 hours for AutodockFR to run one round of genetic algorithm and 50 rounds of genetic algorithms are required. Therefore, our flexible CDOCKER based on parallel MD-based simulated annealing on GPUs greatly reduces the amount of time required while maintaining similar docking accuracy for flexible receptor docking.
4. CONCLUSIONS AND DISCUSSIONS
Two new features — fast Fourier transform (FFT) docking and parallel MD-based simulated annealing — are implemented and added to the protein-ligand docking program CDOCKER in CHARMM. The FFT docking not only utilizes the acceleration provided by FFTs but also employs the parallel computing power of GPUs. Overall, FFT docking with GPUs accelerates the search of ligand positions and orientations by as much as 15,000 fold. With the significant speedup achieved by FFT docking on GPUs, it becomes practical to exhaustively search the translation and rotation space of ligands when docking a rigid ligand into a binding pocket. Although FFT docking alone can not solve the protein-ligand docking problem in which ligands are flexible, the FFT docking can be used to quickly calculate an upper bound of the docking accuracy that can be achieved by a scoring function. This in turn can provide insights into the problems of current scoring functions and help improve the scoring function. In addition, because FFT docking with GPUs can efficiently calculate protein ligand interaction energies for an almost exhaustive list of positions and orientations given a ligand conformation, FFT docking could also be used to explicitly calculate the partition function corresponding to a ligand’s translational and rotational space. This can be combined with existing scoring functions in protein-ligand docking to more accurately estimate protein-ligand binding affinities. A similar idea has been investigated by Nguyen et. al.39
The parallel MD-based simulated annealing with GPUs enables CDOCKER to run about 20 times faster when 500 trials of simulated annealing are used. The speedup becomes even larger when more trials of simulated annealing are employed. With this acceleration, the speed of CDOCKER is on par with or faster than several other popular protein-ligand docking programs tested in this study. In addition, the parallel MD-based simulated annealing on GPUs also enables flexible CDOCKER to achieve significant speed advantages while maintaining similar accuracy for flexible receptor docking. We note that these additions to the CDOCKER and flexible CDOCKER modules described in this paper are part of the c43a1 development version of CHARMM and will be released for general use in the near feature.
Supplementary Material
Acknowledgement
This work is supported by grants from the NIH (GM037554 and GM107233)
Footnotes
Supporting Information Available
The supporting information is included in SI.pdf. This material is available free of charge via the Internet at http://pubs.acs.org/.
References
- (1).Gagnon JK; Law SM; Brooks CL III Flexible CDOCKER: Development and application of a pseudo-explicit structure-based docking method within CHARMM. J. Comput. Chem 2016, 37, 753–762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Jorgensen WL The Many Roles of Computation in Drug Discovery. Science 2004, 303, 1813–1818. [DOI] [PubMed] [Google Scholar]
- (3).Sousa SF; Fernandes PA; Ramos MJ Protein–ligand docking: current status and future challenges. Proteins: Struct., Funct., Bioinf 2006, 65, 15–26. [DOI] [PubMed] [Google Scholar]
- (4).Wu G; Robertson DH; Brooks CL III; Vieth M Detailed analysis of grid-based molecular docking: A case study of CDOCKER?A CHARMm-based MD docking algorithm. J. Comput. Chem 2003, 24, 1549–1562. [DOI] [PubMed] [Google Scholar]
- (5).Goodsell DS; Morris GM; Olson AJ Automated docking of flexible ligands: applications of AutoDock. J. Mol. Recognit 1996, 9, 1–5. [DOI] [PubMed] [Google Scholar]
- (6).Trott O; Olson AJ AutoDock Vina: improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem 2010, 31, 455–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Allen WJ; Balius TE; Mukherjee S; Brozell SR; Moustakas DT; Lang PT; Case DA; Kuntz ID; Rizzo RC DOCK 6: impact of new features and current docking performance. J. Comput. Chem 2015, 36, 1132–1156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Friesner RA; Banks JL; Murphy RB; Halgren TA; Klicic JJ; Mainz DT; Repasky MP; Knoll EH; Shelley M; Perry JK; Shaw DE; Francis P; Shenkin PS Glide:? A New Approach for Rapid, Accurate Docking and Scoring. 1. Method and Assessment of Docking Accuracy. J. Med. Chem 2004, 47, 1739–1749. [DOI] [PubMed] [Google Scholar]
- (9).Halgren TA; Murphy RB; Friesner RA; Beard HS; Frye LL; Pollard WT; Banks JL Glide: a new approach for rapid, accurate docking and scoring. 2. Enrichment factors in database screening. J. Med. Chem 2004, 47, 1750–1759. [DOI] [PubMed] [Google Scholar]
- (10).Brooks BR; Brooks CL; Mackerell AD; Nilsson L; Petrella RJ; Roux B; Won Y; Archontis G; Bartels C; Boresch S; Caflisch A; Caves L; Cui Q; Dinner AR; Feig M; Fischer S; Gao J; Hodoscek M; Im W; Kuczera K; Lazaridis T; Ma J; Ovchinnikov V; Paci E; Pastor RW; Post CB; Pu JZ; Schaefer M; Tidor B; Venable RM; Woodcock HL; Wu X; Yang W; York DM; Karplus M CHARMM: The biomolecular simulation program. J. Comput. Chem 2009, 30, 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Vanommeslaeghe K; Hatcher E; Acharya C; Kundu S; Zhong S; Shim J; Darian E; Guvench O; Lopes P; Vorobyov I; Mackerell AD CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem 2010, 31, 671–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).O’Boyle NM; Banck M; James CA; Morley C; Vandermeersch T; Hutchison GR Open Babel: An open chemical toolbox. J. Cheminformatics 2011, 3, 33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Brigham EO; Brigham EO The fast Fourier transform and its applications; prentice Hall; Englewood Cliffs, NJ, 1988; Vol. 448. [Google Scholar]
- (14).Katchalski-Katzir E; Shariv I; Eisenstein M; Friesem AA; Aflalo C; Vakser IA Molecular surface recognition: determination of geometric fit between proteins and their ligands by correlation techniques. Proc. Natl. Acad. Sci. U.S.A 1992, 89, 2195–2199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Bracewell RN; Bracewell RN The Fourier transform and its applications; McGraw-Hill; New York, 1986; Vol. 31999. [Google Scholar]
- (16).Gabb HA; Jackson RM; Sternberg MJ Modelling protein docking using shape complementarity, electrostatics and biochemical information1. J. Mol. Biol 1997, 272, 106–120. [DOI] [PubMed] [Google Scholar]
- (17).Mandell JG; Roberts VA; Pique ME; Kotlovyi V; Mitchell JC; Nelson E; Tsigelny I; Ten Eyck LF Protein docking using continuum electrostatics and geometric fit. Protein Eng. Des. Sel 2001, 14, 105–113. [DOI] [PubMed] [Google Scholar]
- (18).Chen R; Li L; Weng Z ZDOCK: an initial-stage protein-docking algorithm. Proteins: Struct., Funct., Bioinf 2003, 52, 80–87. [DOI] [PubMed] [Google Scholar]
- (19).Ritchie DW; Kozakov D; Vajda S Accelerating and focusing protein–protein docking correlations using multi-dimensional rotational FFT generating functions. Bioinformatics 2008, 24, 1865–1873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Garzon JI; Lopéz-Blanco JR; Pons C; Kovacs J; Abagyan R; Fernandez-Recio J; Chacon P FRODOCK: a new approach for fast rotational protein–protein docking. Bioinformatics 2009, 25, 2544–2551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Padhorny D; Kazennov A; Zerbe BS; Porter KA; Xia B; Mottarella SE; Kholodov Y; Ritchie DW; Vajda S; Kozakov D Protein–protein docking by fast generalized Fourier transforms on 5D rotational manifolds. Proc. Natl. Acad. Sci. U.S.A 2016, 113, E4286–E4293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Ritchie DW; Venkatraman V Ultra-fast FFT protein docking on graphics processors. Bioinformatics 2010, 26, 2398–2405. [DOI] [PubMed] [Google Scholar]
- (23).Sukhwani B; Herbordt MC GPU acceleration of a production molecular docking code. Proceedings of 2nd Workshop on General Purpose Processing on Graphics Processing Units 2009; pp 19–27. [Google Scholar]
- (24).Kozakov D; Brenke R; Comeau SR; Vajda S PIPER: an FFT-based protein docking program with pairwise potentials. Proteins: Struct., Funct., Bioinf 2006, 65, 392–406. [DOI] [PubMed] [Google Scholar]
- (25).Padhorny D; Hall DR; Mirzaei H; Mamonov AB; Moghadasi M; Alekseenko A; Beglov D; Kozakov D Protein–ligand docking using FFT based sampling: D3R case study. J. Comput.-Aided Mol. Des 2018, 32, 225–230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Nvidia, C. CUFFT library 2010. [Google Scholar]
- (27).Salomon-Ferrer R; Götz AW; Poole D; Le Grand S; Walker RC Routine microsecond molecular dynamics simulations with AMBER on GPUs. 2. Explicit solvent particle mesh Ewald. J. Chem. Theory Comput 2013, 9, 3878–3888. [DOI] [PubMed] [Google Scholar]
- (28).Stone JE; Hardy DJ; Ufimtsev IS; Schulten K GPU-accelerated molecular modeling coming of age. J. Mol. Graphics Modell 2010, 29, 116–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Hynninen A-P; Crowley MF New faster CHARMM molecular dynamics engine. J. Comput. Chem 2014, 35, 406–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Eastman P; Friedrichs MS; Chodera JD; Radmer RJ; Bruns CM; Ku JP; Beauchamp KA; Lane TJ; Wang L-P; Shukla D; Tye T; Houston M; Stich T; Klein C; Shirts MR; Pande VS OpenMM 4: A Reusable, Extensible, Hardware Independent Library for High Performance Molecular Simulation. J. Chem. Theory Comput 2012, 9, 461–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Eastman P; Swails J; Chodera JD; McGibbon RT; Zhao Y; Beauchamp KA; Wang LP; Simmonett AC; Harrigan MP; Stern CD; Wiewiora RP; Brooks BR; Pande VS OpenMM 7: Rapid development of high performance algorithms for molecular dynamics. PLOS Comput. Biol 2017, [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).Hartshorn MJ; Verdonk ML; Chessari G; Brewerton SC; Mooij WT; Mortenson PN; Murray CW Diverse, high-quality test set for the validation of protein-ligand docking performance. J. Med. Chem 2007, 50, 726–741. [DOI] [PubMed] [Google Scholar]
- (33).Mukherjee S; Balius TE; Rizzo RC Docking validation resources: protein family and ligand flexibility experiments. J. Chem. Inf. Model 2010, 50, 1986–2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Ravindranath PA; Forli S; Goodsell DS; Olson AJ; Sanner MF AutoDockFR: advances in protein-ligand docking with explicitly specified binding site flexibility. PLOS Comput. Biol 2015, 11, e1004586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Vanommeslaeghe K; Hatcher E; Acharya C; Kundu S; Zhong S; Shim J; Darian E; Guvench O; Lopes P; Vorobyov I; Mackerell AD CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem 2010, 31, 671–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Vieth M; Hirst JD; Brooks CL Do active site conformations of small ligands correspond to low free-energy solution structures? J. Comput.-Aided Mol. Des 1998, 12, 563–572. [DOI] [PubMed] [Google Scholar]
- (37).Gaillard T Evaluation of AutoDock and AutoDock Vina on the CASF-2013 benchmark. J. Chem. Inf. Model 2018, 58, 1697–1706. [DOI] [PubMed] [Google Scholar]
- (38).Feig M; Karanicolas J; Brooks CL III MMTSB Tool Set: enhanced sampling and multiscale modeling methods for applications in structural biology. J. Mol. Graphics Modell 2004, 22, 377–395. [DOI] [PubMed] [Google Scholar]
- (39).Nguyen TH; Zhou H-X; Minh DD Using the fast fourier transform in binding free energy calculations. J. Comput. Chem 2018, 39, 621–636. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


