Improvement of Performance of Cardiac SPECT Camera Using Curved Detectors With Pinholes

Abstract

SPECT is primarily used in the clinic for cardiac myocardial perfusion imaging. However, for SPECT, sensitivity is impaired due to the need for collimation. System resolution FWHM is poor as well (~ 1 cm). In this work the resolution of a curved detector was theoretically derived. The advantage of a curved detector over a flat detector with pinhole collimation was demonstrated for cardiac applications using theoretical derivations as well as a ray-tracing voxel-based forward projector. For the flat detector using parameters close to what was expected for the new multi-pinhole GE Discovery system, it is shown that using a paraboloid detector one may obtain a better system resolution (about 29% better on the average), keeping same pinhole opening. Alternately, sensitivity gains of as much as 2.25 may be obtained, for similar resolutions as a flat detector by just using a different pinhole with higher hole-diameter.

I. Introduction

SPECT remains an important technique for assessing myocardial perfusion. However SPECT in general suffers from low sensitivity because of the necessity for collimation. New designs have emerged with 5–8 times the sensitivity of the standard gamma cameras currently used in the clinic for estimating myocardial perfusion [1]–[8]. Very innovative designs by Funk et al. [1] and UFC (ultra-fast-camera, the precursors to the Discovery system) from GE [2]–[5] use multiple pinholes. For an overview of the technologies, see Slomka [9]. Most of these designs choose a region of interest around the heart. We briefly touch upon the key design points for some of these new systems, to the extent data analysis is available.

Erlandsson et al. [6] and Gambhir [7] analyzed the DSPECT system which uses 9 flat CZT detectors with parallel-hole collimation arranged in a configuration conforming to the shape of the patient’s chest. Each of the 9 detector blocks rotates around its central axis and is also translated to give a complete tomographic sampling [6], [7], [9]. Higher sensitive, worse resolution collimators are used compared to the LEHR used in a standard cardiac acquisition. Hence the geometric resolution was expected to be worse by more than a factor of 2 [7]. However, using collimator resolution compensation in iterative OSEM reconstruction, the resolution degradation with respect to a standard system was entirely compensated for [7]. The planar sensitivity improvement compared to standard GE (Infinia) acquisition was 5.5 times, and for tomographic reconstruction, the improvement was 4.6–7.9 times for the heart region [6]. The acquisition times reported in [7] for clinical studies were 5.5 times faster compared to standard system (2 min for DSPECT versus 11 min for conventional). The CZT-based system can be used for dual-isotope molecular imaging [6]. The Digirad Cardiac 3XPo has 2–3 heads of dimensions 21.2 × 15.8 cm which can move in and out. The C-SPECT platform is based on a large stationary C-shaped detector and collimator assembly, which surrounds a patient sitting upright on a smart-chair [8]. Another system, CardiArc, uses a slit aperture moving over horizontal vanes (effectively achieving slit-slat collimation) over a curved-shaped detector. The CardiArc was designed with semi-conductor CZT as well as crystal NaI detectors [10]. Clinical images displayed on the CardiArc website pertain to the CZT design [10]. The acquisition time reported by the company is 2 min [10]. The resolution is 3.6 mm at 82 mm depth of source from aperture.

Pinhole collimation is used in the Discovery System (formerly also known as Ultra-Fast Cardiac SPECT Camera) from GE [2]–[5]. The advantages of this particular kind of pinhole design are that there are no moving parts, thus reducing manufacturing and servicing costs. The UFC system also uses CZT detectors. Initial UFC performance reports indicate rest and stress acquisition times of 5 and 3 min compared to 12.5 and 10 min for GE Ventri Camera [3] for an anthropomorphic phantom. In [2] the sensitivity is observed to be 3 times the clinical system.

Funk et al. [1] used a multi-pinhole system attached to a NaI crystal detector. Detailed measurements and simulations were done on point sources and an anthropomorphic phantom. Their measurements were compared to parallel-collimation using LEGP (low energy general purpose collimators) and from those measurements it was predicted by simulation that the system would provide sensitivity improvement factor of 5 over the standard parallel-LEHR that is typically used for myocardial perfusion clinical studies for similar resolution. Further they did simulation studies with the NCAT phantom using a single-view, 2-view and 4-view of the 9-pinhole system and found that 4-views (with 36 pinholes) were adequate for artifact-free reconstruction.

The small-animal imaging literature is rich with fine-resolution and/or fast acquisition system designs [11]–[25]. In [13] a SPECT/CT system is described. For the SPECT part, there are 4 rotating detector heads (with pinhole or parallel collimators) which may be operated in pairs to implement a unique half-cone geometry, reducing the acquisition time compared to a full-cone-beam geometry. Use of a multiplexed coded aperture system with pinholes projecting into overlapping detector areas also results in more efficient coverage of detector space [23], leading to an increase in system sensitivity [14], [15]. However, the multiplexing may degrade the system matrix and may introduce problems in tomographic image reconstruction [15]. In [16]–[18] a high performance SPECT system with a stationary configuration of pinholes focused on a small object is described. In [21] and [22] performance of a triple-detector SPECT system with 2 pinholes per detector is described. Recently curved detectors have been used in pinhole SPECT for small animal imaging with the purpose of reducing parallax effect on resolution by collecting light from fiber optics bundles placed normal to the curved detector surface [25]. For human cardiac applications, due to dimensions involved and higher sensitivity requirements, the collimator hole plays a greater role than the intrinsic parallax effect at the detector in resolution considerations. Furthermore, improving the magnification improves both aspects of resolution, namely the collimator aspect as well as the intrinsic detector resolution (which includes the parallax effect).

In this work the author proposed a novel method to improve sensitivity (and/or resolution) over flat-detector-with-pinhole-collimator designs by using appropriately curved detectors fitted to pinholes in a configuration, as shown in Fig. 1. Each pinhole has a curved detector attached to it (an example in Fig. 2), lending improved magnification over a flat-detector connected to the same pinhole, if one keeps the same pinhole diameter, thus if the surface is chosen rightly, improving the resolution over the flat-detector. Then resolution and sensitivity may be traded off by increasing the pinhole diameter for the curved-detector system to obtain increased sensitivity for similar resolution as the flat-detector-system. This enables one to choose to improve resolution and/or sensitivity with the same compactness. It is pointed out that the resolution versus sensitivity trade-off only involves a different pinhole diameter, thus it may be possible to choose a higher/lower sensitive pinhole as the case requires. For example one may wish to choose a higher pinhole diameter for a bigger patient while opting for higher resolution for average sized patients, for the same curved detector. As described in [26], for human Cardiac application, the pinholes are arranged in a stationary configuration arranged in sectors conforming to the body contour where in each sector, they are focused on a region in the heart (see Fig. 1). For example, the pinholes may possibly be arranged in three different surfaces (sections of three spheres with same radius but different centers) around the heart region of the torso.

Fig. 1.

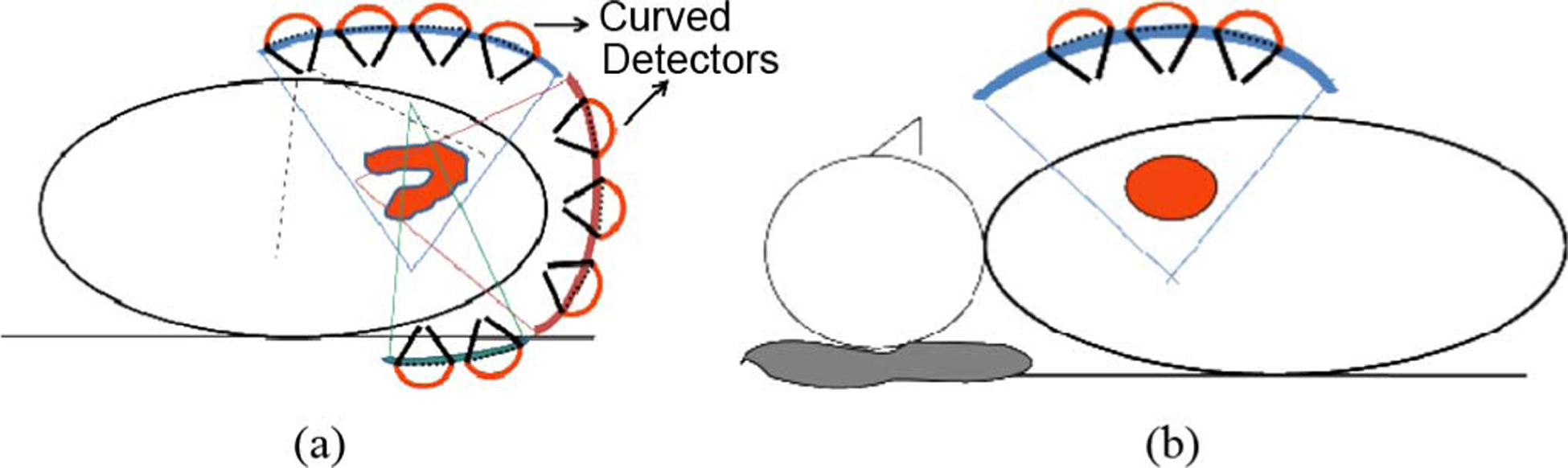
Pinholes on a stationary configuration for Cardiac application. (a) Three sectors on a transverse view. (b) One of the sectors along longitudinal axis. Diagram not to relative scale.

Fig. 2.

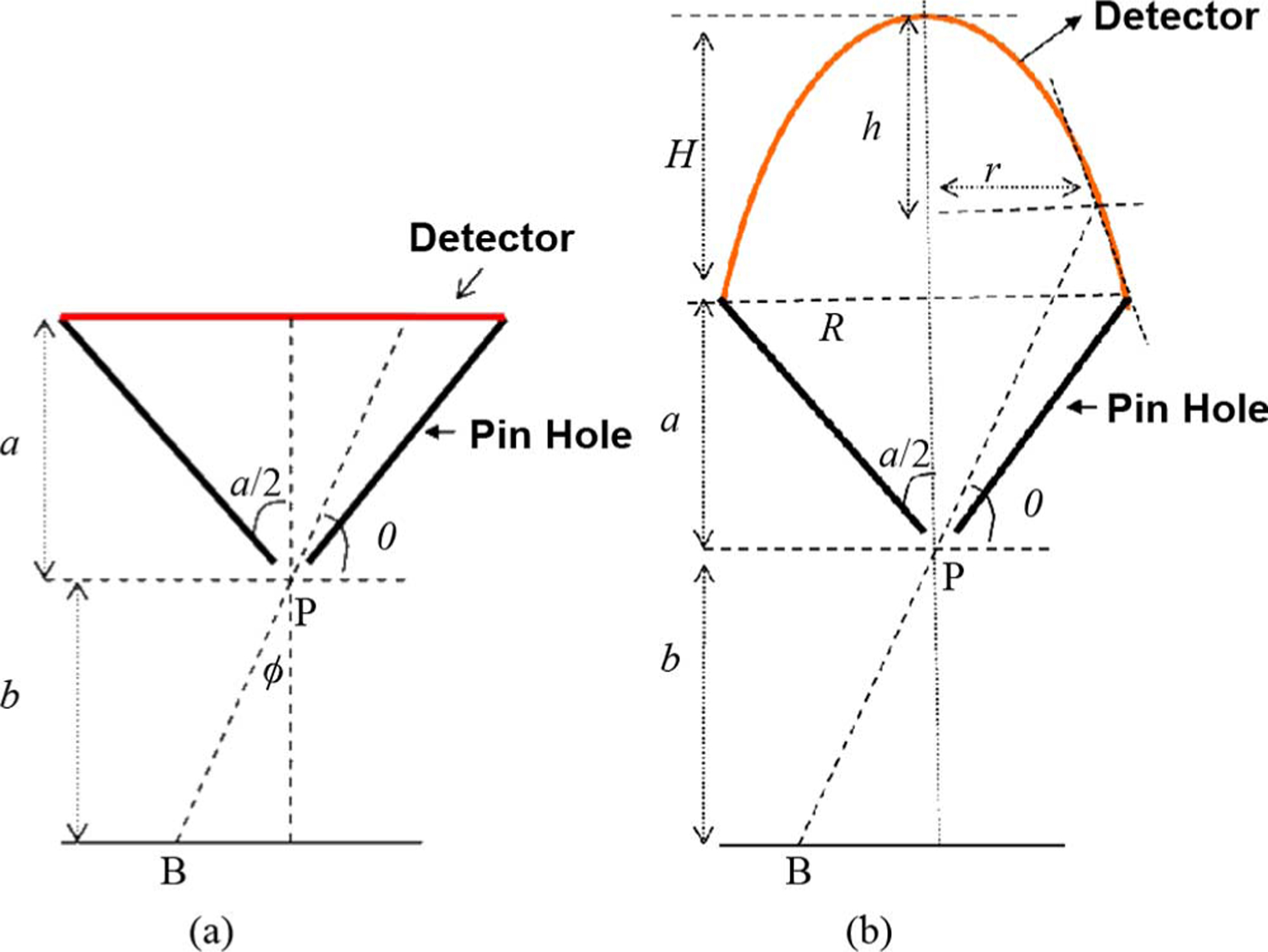
Profile of (a) flat and (b) paraboloid. Diagrams are not to relative scale.

It is possible to improve detector resolution by choosing a higher focal distance “a” (from pinhole to flat detector) for a flat surfaced detector. But for packing factor considerations, curved detector on same base radius is more efficient. This is illustrated in Fig. 3. For example considering the flat detector system in Fig. 3(a) (called “hypothetical” base flat detector), one can attempt to improve performance by replacing the base flat detector by curved detector on the same base radius [Fig. 3(a)] or use larger flat detectors further back [Fig. 3(b)]. Note that the depth of interest below pinhole and the acceptance angle is fixed and guided by application requirement. One can then see that the larger flat detectors would require some extra “dead”-space relative to Fig. 3(a) with the curved or original flat detectors. Thus lesser detectors can be packed when using larger flat detectors for a geometry such as Fig. 1. Lessor detector may mean reconstruction artifacts and/or less sensitivity. These aspects are investigated in more details in this study.

Fig. 3.

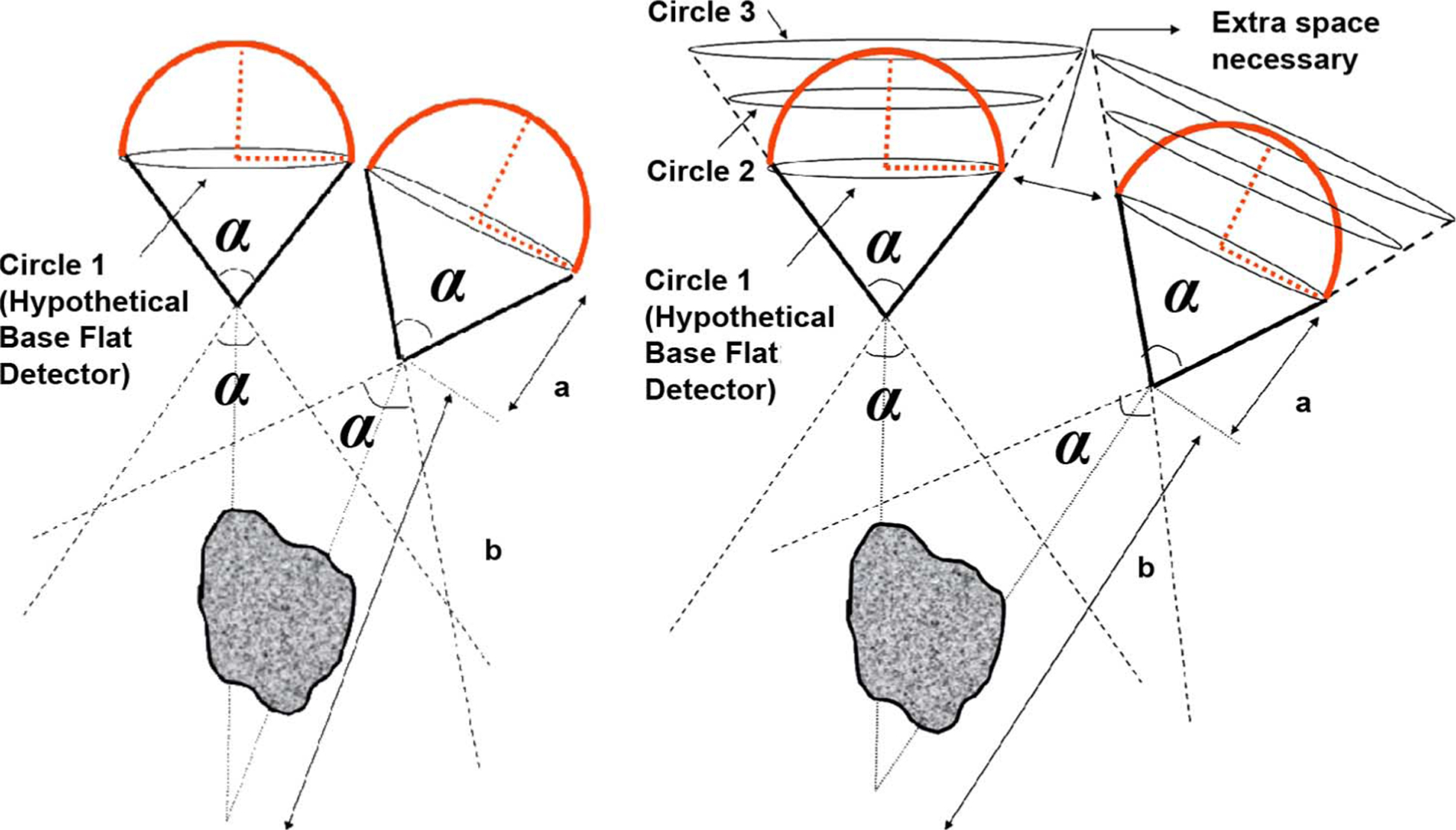
(a) Curved-detectors with pinholes focused on a region of interest distance b from pinhole. (b) For the same a and b parameters and acceptance angle α of the pinhole, we show (hypothetical) flat detectors at different locations (Circle 1, 2, 3) for comparison. Instead of the curved detectors on the base-plane shown in case (a) if the detector was a larger flat one at the tangential plane on the tip, indicated by Circle 3 (or at Circle 2 with the same surface area as the curved-detector), extra space would be necessary to pack them into the same configuration focused at distance b in object space, resulting in relatively less number of pinholes.

The improvement in curving the detector reduces as the focal length of the base flat detector system (that it is compared to) increases. As a quick preview, see the last row of Table II, Sensitivity Improvement Ratio (SIR) of using a curved detector instead of using a flat detector drops from 2.25 to 1.49 when the focal length of the flat detector is varied from a = 60 mm to a = 120 mm. Note that for this comparison, for each case the pinhole diameter is changed between the flat and the curved units so that the flat and curved detectors have same resolution at depth of 15 cm. This issue is particularly important for an isolated detector with a pinhole collimator. But in a configuration of multiple flat-detector-with-pinhole-collimator units in the system, arranged in a stationary geometry around the object for Cardiac SPECT (such as in Fig. 1), it is necessary to limit to smaller base focal lengths of about 60 mm (as calculated in this paper, summarized in Table II for a flat detector). This is because the system has to satisfy the criterion of non-truncation of object for each and every pinhole, as well as have adequate number of detector-pinhole units for purpose of reconstruction. At this necessarily de-magnified end of the spectrum, curving the detector has higher value in improving the resolution without compromising sensitivity (or vice versa).

TABLE II.

Field of View (FOV) and No. of Pinholes (Nx, Nz) for Different Focus Distances for Flat Detector. To Calculate the no. of Pinholes, it is Assumed That the Pinholes are all Placed on a Sphere Of Radius 200 mm (i.e., all Pinholes Point to a Co-Center 200 mm Below Their Axis). the SIR is the Sensitivity Improvement for a Curved Detector After opening d0 Such That Resolution is Same as Flat at 15 cm

a (mm)	60.0	70.0	70.0	80.0	80.0	90.0	90.0	100.0	100.0	110.0	110.0	120.0	120.0
W1 (mm)	80.0	90.0	100.0	90.0	110.0	100.0	120.0	100.0	140.0	100.0	150.0	110.0	166.0
W2 (mm)	60.8	68.4	76.0	68.4	83.6	76.0	91.2	76.0	106.4	76.0	114.0	83.60	126.16
Nz	9	8	8	9	7	8	7	8	7	9	6	8	6
Nx	3	3	2	3	2	3	2	3	2	3	2	3	2
FOV15cm	200.0	192.84	214.29	168.75	206.25	166.67	200.00	150.0	210.0	136.36	204.55	137.5	207.50
α1 (deg)	67.38	65.47	71.07	58.72	69.02	58.11	67.38	53.13	69.98	48.89	68.57	49.25	69.34
α2 (deg)	53.74	52.08	56.99	46.29	55.17	45.78	53.74	41.61	56.03	38.11	54.78	38.41	55.46
d0 (mm)	3.86	3.86	3.86	3.86	3.86	3.86	3.86	3.86	3.86	3.86	3.86	3.86	3.86
deff 1 (mm)	4.08	4.07	4.10	4.05	4.09	4.04	4.08	4.03	4.09	4.01	4.09	4.01	4.09
deff 2 (mm)	4.03	4.02	4.04	4.00	4.03	4.00	4.03	3.99	4.04	3.98	4.03	3.98	4.03
SIR	2.25	2.03	2.03	1.85	1.86	1.73	1.73	1.63	1.63	1.55	1.55	1.48	1.49

Thus in this work, the author investigates a Funk et al. like system with a = 120 mm and a GE-like system with a = 60 mm. The resolution is derived for the paraboloid detector, shown in the Appendix. These derivations were reported earlier (along with that of cone and sphere) in a conference record [26]. In [26] we showed that the sensitivity improvement of the paraboloid-detector design on each pinhole was more than that with a conical or a spherical detector. Hence in this paper, only the numerical and simulation results with paraboloid detector are shown.

In this work a voxel-based ray-simulator for a pinhole on a flat and on a curved detector (reported in a second conference record [27]) was also reported. The author’s implementation is modular with input detectors that can be of any surface shape in three dimensions (including a flat detector). Influence of the pinhole was modeled so far, the detector resolution modeling for the curved detector is subject of further research. The forward modeling was compared with the appropriate theory.

II. Methods

In this section, first the resolution on a curved detector was derived. Then an implementation of a ray-based forward model, independent of theory, was described. However there are some differences in the effects taken into account in the two methods as will be clarified.

For a flat detector on a pinhole, the system resolution squared at depth below the pinhole is given by [28], [29]

$${\text{Res\_flat}}^{\text{2}}\text{=}{\left(\text{1+}\frac{b}{a}\right)}^{\text{2}}{d}^{\text{2}}\text{+}{\left(\frac{b}{a}\right)}^{\text{2}}{R}_I^{\text{2}}$$ (1)

where is the distance from pinhole to detector, d = effective diameter of the pinhole opening, R_I is the detector resolution, which in general is dependent on the incident angle at the detector (and therefore the angle of the ray). It is observed that the system resolution depends on the pinhole opening, the intrinsic detector resolution and the magnification at depth b given by a/b. For the SPECT cardiac application the pinhole diameter is the primary contributor to resolution degradation. For example for a flat detector with a = 6 cm, b = 15 cm, pinhole diameter of approximately 4 mm, and approximate detector resolution (ignoring parallax effects) of R_I = 3.2 mm, contribution of the pinhole diameter to squared resolution is d² (b/a + 1)² = 196 mm² and the contribution of the detector resolution is ${(b/a)}^2{R}_I^2=64{\text{mm}}^2$. For the curved detector the detector resolution depends on the surface design and the data-read off and is a topic of investigation by itself. This is subject of ongoing and future research. However, for our theoretical calculations we approximate the detector resolution by a constant independent of ray-angle, in (1). For now the parallax is ignored, but it is noted that the parallax effect (present both for the flat and the curved detectors) would also be reduced somewhat by the magnification factor improvement for curved detector as opposed to the flat detector. The d in (1) is in general different from the geometric opening d₀, depending on if penetration through the septa is modeled or not. In our theoretical frame-work, we do model the penetration to a first standard approximation, given by [29]

$$d=\sqrt{d_0\left(d_0+2{\mu }^{-1}\text{tan}\frac{\alpha }{2}\right)}$$ (2)

where d₀ is the actual physical hole-diameter and μ = 29.44 cm⁻¹ is the linear attenuation coefficient of lead at 140 keV. Note that a more accurate model [30]–[32] would show that the effective pinhole diameter also depends on ray-angle.

The detector resolution is not included, in the forward-model ray-tracing implementation. Thus, when comparing the forward model and theory, this term is taken out of the theoretical formula for fairness in comparison. The penetration (a very small effect) is not implemented in the forward model, so only the geometric pinhole opening was considered for the theory when comparing the two methods.

Thus to summarize, for the pure theoretical derivations and plots, detector resolution is modeled to a constant approximation and penetration is approximated by (2), but for the experimental and theory comparisons, only the pinhole-geometric effect is considered.

A. Theoretical Average Resolution for a Paraboloid Detector on a Pinhole

For the resolution considerations on a non-flat surface, the magnification changes with ray-angle. The expressions for the average resolution may be derived by finding the magnification as a function of ray-angle and integrating the square-of-the-resolution function over the surface and normalizing by the surface area and then taking the square root thereof. The main technique is to either represent the resolution function as a function of the surface variables, or represent the surface variables in terms of the ray-angle θ (wrt horizontal), shown in Fig. 2. The average squared resolution over the surface of the paraboloid with height H and base radius R [see Fig. 2(b)], placed on a pinhole with parameters a, b, was derived in details in Appendix A, taking the ratio of squared resolution integrated across the surface divided by the surface area.

Briefly the equations were derived by modifying the well-established formula for system resolution at depth b for a pinhole on a flat-detector in (1) and incorporating the angle-dependent magnification in the resolution expression. The ratio reduces to that of two line integrals, given as follows:

$${\text{Res}}_{av}^2=\frac{\underset{0}{\overset{H}{\int }}\left[{\left(1+\frac{b}{a+H-h}\right)}^2{d}^2+{\left(\frac{b}{a+H-h}\right)}^2{R}_I^2\right]\frac{{\left(R^4+4R^{2}Hh\right)}^{1/2}}{2H}dh}{\underset{0}{\overset{H}{\int }}\frac{{\left(R^4+4R^{2}Hh\right)}^{1/2}}{2H}dh}.$$ (3)

Equation (3) can be obtained in closed form in terms of the radius and height R and H of the paraboloid and the a and b of the pinhole collimator, however we chose to calculate it computationally for simplicity.

Square root of (3) was used to obtain our system resolution for two sets of system designs, one with a larger base-focal distance a = 12 cm and another with a more de-magnified base-focus of a = 6 cm. Base focal distance refers to the distance of the pinhole opening to the base of the curved detector. These systems were compared to flat detectors at their bases (BFD).

To compare with our forward projector simulations different points located in a line at depth b, going radially outwards from central axis were considered. For each point, the corresponding θ was derived and the height h was calculated [see Fig. 2(b) and (A1) in the Appendix]. Furthermore, since the projector does not have penetration or detector resolution modeled, just the effect of the pinhole was considered, i.e., the focus was on just the first term in (A1)

$$\text{Expected\_Res\_curved\_at\_depth\_b =}\left(1+\frac{b}{a+H-h}\right)d_0$$ (4)

where d₀ is the physical diameter of the pinhole. For each point (θ) there would be a different h.

For the flat detector the expected resolution will be simply

$$\text{Expected\_Res\_flat\_at\_depth\_b }=\left(1+\frac{b}{a}\right)d_0=\left(\frac{a+b}{a}\right)d_0.$$ (5)

For the flat detector, at the detector the resolution will be given by

$$\text{Expected\_Res\_flat\_at\_detector}=\left(\frac{a+b}{b}\right)d_0.$$ (6)

When the averages are compared, the detector term was eliminated in (3) and the average squared resolution was used for the pinhole (ph) only:

$${\text{Res}}_{\text{avph}}^2=\frac{\underset{0}{\overset{H}{\int }}\left[{\left(1+\frac{b}{a+H-h}\right)}^2{d}_0^2\right]\frac{{\left(R^4+4R^{2}Hh\right)}^{1/2}}{2H}dh}{\underset{0}{\overset{H}{\int }}\frac{{\left(R^4+4R^{2}Hh\right)}^{1/2}}{2H}dh}.$$ (7)

B. Voxel-Based Ray-Tracing Simulations

The author implemented a ray-tracing based forward projector of the pinhole for a general detector (which is assumed to be a surface in 3-D). A volume-mask of the detector was created with ones only on the surface. This volume may, thus, be any mathematically generated curved surface or a flat surface (in which case the height dimension of the volume is one). The number of rays is determined by the size of the circular pinhole, sampled in two directions. For each point in object, a ray is traced to each of the pinhole samples and then extended through the pinhole into the detector volume mask. As soon as the ray hits the first detector point the process is stopped and the counts accumulated at the detector point. The sensitivity is related to the pinhole opening diameter and the angulation of the ray wrt the pinhole. Once inside the pinhole the counts are simply detected by the detector, whether flat or curved. For each ray the solid angle at the aperture is accounted for by

$$G(B,P)\propto \frac{d_0^2\text{cos}\varphi }{4\pi |B-P{|}^2}=\frac{d_0^2\text{sin}\theta }{4\pi |B-P{|}^2}$$

where G(B, P)is the geometric factor taking into account the inclination of the rays wrt to the normal to the plane of the pinhole, ϕ or the angle with the aperture plane itself, θ = π/2 − ϕ [see Fig. 2(a) or Fig. 2(b)] which is loosely called the ray angle here. B and P are the source and the pinhole points in 3-D. This essentially amounts to the factor $G(B,P)\propto d_0^2{\text{sin}}^3\theta /4\pi b^2$ where b is the vertical distance of the viewing plane from the pinhole. The sensitivity is computed by summing the point-spread function.

When simulating different pinhole openings, the sampling resolution of the pinhole is kept constant. Therefore, the number of rays is proportional to area of pinhole, or $n{o}_{-}o{f}_{-}\mathit{\text{rays}}\propto d_0^2$. When the measured sensitivity via ray-tracing is compared to the expected value, one can then simply compare to

$$G(B,P)\propto \frac{d_0^2}{4\pi b^2}{\text{sin}}^3\theta \propto \frac{no.\_of\_\mathit{\text{rays}}}{4\pi b^2}{\text{sin}}^3\theta .$$ (8)

The rays are back-traced through the center of the pinhole to view the object in a viewing plane at specified depth. Gaussian interpolator has been optimally used for projection/back-projection in iterative reconstruction [33], [34]. The Gaussian interpolation method used in [34] was adapted here for the back-tracing. A narrow 2-D Gaussian interpolator (sigma = 0.5 pixel, window = ± − 3 pixels, and a 65 sample representation) was used to interpolate onto the viewing plane (of resolution 2 mm). Since the effective resolution of this Gaussian appears in approximate quadrature with the PSFs measured, it has a small fraction of mm effect on the FWHM (only about 0.2–0.3 mm) and hence it is ignored when computing the resolution measurements.

Care is taken to ensure the detector representation is without gaps, so as not to loose counts from any ray. It is also noted that a voxelized representation of a surface (such as was used here) would be only approximate for a curved surface such as a paraboloid and the surface may not be just one-voxel thick everywhere. The ray propagation is stopped as soon as it hits the detector, thus the stopped ray is essentially accumulating the counts at the inner surface of the detector. The detector sampling is important, particularly the ratio of the detector sample size to the pinhole size.

As mentioned before, the detector resolution and the septa-penetration effects are not explicitly modeled here in the ray-tracing.

C. Choice of (Base) Focal-Length and Number of Pinholes

For the GE Discovery system or the system considered here (unlike the Funk et al. system [1]), one design requirement is that there are no moving pinholes, all the pinholes should acquire simultaneously.

For a given focus distance a, for our stationary geometry there are two conflicting requirements: no truncation for any pinhole (i.e., use large acceptance angle, and hence detector) and adequate number of pinholes in each sector such that enough independent views are obtained.

The best pinhole distribution in 3-D is an investigation by itself and outside the scope of this work, but heuristically the number of pinholes which are placed directly above the heart in the main central arc about the z- (superior-inferior) direction is most important as these will have the best sensitivity and least attenuation. Furthermore the pinholes in the third arc at the back of the torso in Fig. 1(a) would not contribute a great deal as they would have larger distance from heart (hence lower sensitivity) and more attenuation. The author’s preliminary investigations show that at least 8 pinholes in the central arc cross-product with at least 3 pinholes along the longitudinal direction are adequate [35], [36]. One can further subsample (reject) pinholes that are in the not in the central-arc. But it is best to pack as many pinholes as possible within the central arc directly above the heart but using the extent of only two of the three sub-arcs shown in Fig. 1(a).

To find the best focal distance and acceptance angle (or relatedly detector size) for a flat-detector system given our application and a stationary geometry a rudimentary investigation was done by changing the acceptance angle for a given focus a = 120 m (Table I) and repeating for different focal distances a = 60 mm to a = 120 mm (Table II). To calculate the number of pinholes, they are assumed to be on a single spherical surface, i.e., the two arcs considered in Fig. 1(a) are assumed to have the same center, pointed 200 mm from their pinholes. The resulting number of pinhole are calculated as explained by (B1a) in Appendix B. The results are tabulated in Table I. In the table (Table I), W₁, W₂ are the detector widths in two directions, N_Z, N_X are the number of pinholes that can be accommodated around the Z-axis (SI-axis) and the X-axis (RL-axis), FOV15 cm is the field of view at 15 cm depth, α₁ and α₂ are the acceptance angles for the given focus and detector widths in the two directions. Table I also includes the effective diameter openings deff₁ and deff₂ (based on α₁ and α₂) for an example geometric opening d₀ = 3.86 mm to show the small differences due to penetration effects at different acceptance angles. Nine designs were looked into, increasing the width W₁ in steps of 10 mm from 80 mm. The last one uses the parameters from Funk et al. design [1].

TABLE I.

Field of View (FOV) and No. Of Pinholes (Nx, Nz) for Different Flat Detector Sizes (Thus Acceptance Angles) for a = 120 mm. To Calculate the no. Of Pinholes, it is Assumed That the Pinholes are All Placed on a Sphere of Radius 200 mm (i.e., All Pinholes Point to a Co-Center 200 mm Below Their Axis)

	Design 1	Design2	Design3	Design4	Design5	Design6	Design7	Design8	Design9
W1 (mm)	80.0	90.0	100.0	110.0	120.0	130.0	140.0	150.0	166.0
W2 (mm)	60.8	68.4	76.0	83.6	91.20	98.80	106.4	114.0	126.16
Nz	11	10	9	8	8	7	7	7	6
Nx	3	3	3	3	2	2	2	2	2
FOV15cm (mm)	100.0	112.5	125.0	137.5	150.0	162.5	175.0	187.5	207.5
α1 (deg)	36.89	41.11	45.24	49.25	53.13	56.89	60.51	64.01	69.34
α2 (deg)	28.43	31.82	35.14	38.41	41.61	44.75	47.82	50.82	55.46
d0 (mm)	3.860	3.860	3.860	3.860	3.860	3.860	3.860	3.860	3.860
deff 1 (mm)	3.97	3.99	4.00	4.01	4.03	4.04	4.05	4.07	4.09
deff 2 (mm)	3.95	3.96	3.97	3.98	3.99	4.00	4.01	4.02	4.03

The long-axis of the heart is around 16–17 cm. Allowing for big patients in a practical clinical system with allowances for placement errors, ideally the FOV at 15 cm should be 20 cm. The three important design parameters Nz, Nx and FOV15 cm are highlighted. In Table I, the Design9 has the original dimensions given in Funk et al., where 3 × 3 pinholes are packed into 500 mm × 380 mm for each view. Thus one would get a detector size approximately 166 mm × 126 mm, which would yield too few pinholes for reconstruction in our stationary geometry. If the bigger side of the detector is reduced to 150 mm, 140 mm, etc., going up the table, keeping the aspect ratio same, the number of pinholes do not rise fast enough, until we are as low as 110 mm (Design 4). But for this case, there would be severe truncation as the field of view is only 13.8 cm at a depth of 15 cm. As mentioned, one needs at least 20 cm FOV at 15 cm to accommodate different patients for a good clinical design.

Thus one can see that for no design at a = 120 mm are both the conditions satisfied: FOV at least 200 mm and (Nz, Nx) at least (8,3) within our constrained geometry.

The excellent and very original idea behind Funk et al.’s design works very well for their system, where if understood correctly, the detector-setup would be rotated to get 4 views (with 9 pinholes each). However for a stationary geometry such as described here (Fig. 1), for a = 12 cm, one would have in-adequate number of pinholes or truncation, and a more de-magnified focal distance would be necessary. One could potentially move the pinholes away and accommodate bigger flat detectors but that defeats the purpose because of sensitivity loss with 1/b².

Thus the analysis was repeated for a = 60 to 120 in steps of 10 mm. Instead of adding a new table for each focus, Table II lists just the conditions where at least one of the conditions [(Nz, Nx) =(8,3) or FOV => 20cm] is just about satisfied for the focus distance. When the condition on (Nz,Nx) is satisfied for multiple detector sizes for the focus, the one with the higher FOV was reported. Similarly when FOV is satisfied for multiple settings, we report the one with highest number of pinholes. Thus for focus distance 70 mm there are two columns, one where (Nz,Nx) = (8,3) where FOV is 19.3 cm, and another column where FOV is 21.4 cm (but Nx= 2).

Note that only by reducing the focal distance to as low as a = 60 mm, both the conditions (Nz,Nx) >= (8,3) and FOV >=20cm was satisfied at the same time.

Table II also includes the effective diameter openings deff₁ and deff₂ for d₀ = 3.86 mmThe final row also include sensitivity improvement ratio (or SIR) if one placed a paraboloid detector (on a base-diameter W₁) and opened the pinhole diameter d₀ until the average resolution based on theory equaled that of the flat base system (again based on W₁) at a distance of 15 cm from pinhole. These are discussed in more details in the Results section.

III. Results

A. Theoretical Simulations of Resolution and Sensitivity for a Paraboloid

The theoretical results of average resolution for the paraboloid in (3) were shown here in Figs. 4 and 5. For these results (Figs. 4 and 5) as mentioned before the detector resolution is included to a constant and the penetration is approximated by (2). As noted before, the parameters a, α and the depth b at which the pinholes are pointed at are guided by the physiology imaged. Two cases were chosen to test. Case 1 is similar to the design of Funk et al., shown as Design 1 in Table I. For simplicity the bigger of the acceptance angle was chosen. Thus a = 12 cm, the pinholes are pointed at depth b = 20 cm from the pinhole and the acceptance angle of α = 69.34 deg. However as shown in Table I (Design 9) this design would not have adequate pinholes for a stationary geometry. Hence another design was also chosen, Case 2, with smaller a = 6 cm, with an acceptance angle of α = 67.38 deg. This is shown in column 1, in Table II to be a good design in that the number pinholes are adequate and the FOV is ample. These parameters are expected to be closer to that of the GE Discovery system. For either design the paraboloid height above the base was kept at H = 12 cm. For this Case 2, choice of the base hole-diameter (on the flat-detector-pinhole system), due to the smaller a, is difficult. The hole-diameter if chosen to match the LEHR is very small, about 2 mm which is unrealistically small for this application, as it would affect the sensitivity. The base-line hole-diameter is chosen to be 3.86 mm again to be consistent with Case 1. The effective diameter (Case 2) is 4.08 mm.

Fig. 4.

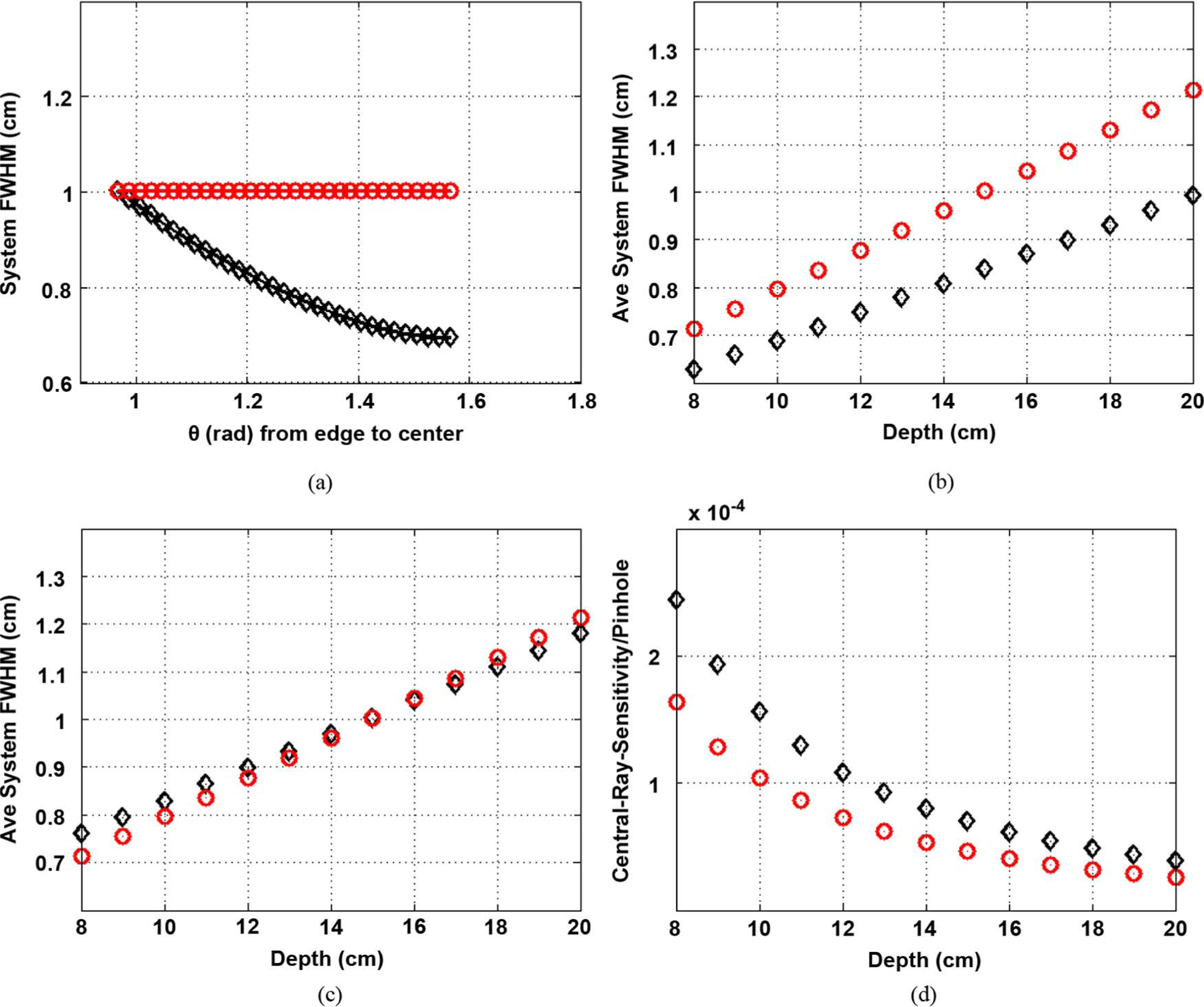
Comparison with Funk et al. like design (a = 12 cm). In the plots, “o” marks the base-plane-flat-detector BFD, diamond-marks the paraboloid-detector. Paraboloid height set at H = 12 cm. (a) FWHM profiles for BFD and paraboloid with respect to ray angle θ (angle wrt horizontal) with pinhole geometric diameter 3.86 mm. (b) Average FWHM versus Depth, for same hole-dia hence same sensitivity. Note BFD resolution = LEHR’s (0.8 cm) at depth 10 cm. (c) Average FWHM versus Depth for resolution of curved detectors matched to BFD at 15 cm. (d) Central-ray sensitivity for each pinhole for case (c) Sensitivity improvement ratio is 1.49 per pinhole. (a) At 15 cm. (b) (c) Res = BFD at 15 cm. (d) Res = BFD at 15 cm.

Fig. 5.

Comparison with GE-like design (a = 6 cm). In the plots, “o” marks the base-plane-flat-detector BFD, diamond marks the paraboloid-detector. Paraboloid height set at H = 12 cm. (a) FWHM profiles for BFD and paraboloid with respect to ray angle θ (angle wrt horizontal) with pinhole geometric diameter 3.86 mm. (b) Average FWHM versus Depth, for same hole-dia hence same sensitivity. (c) Average FWHM versus Depth for resolution of curved detectors matched to BFD at 15 cm, with pinhole opening at 5.85 mm (effective 6.12 mm). (d) Central-ray sensitivity for each pinhole for case (c). Sensitivity improvement ratio is 2.25 per pinhole. (a) At 15 cm. (b), (c) Res = BFD at 15 cm. (d) Res = BFD at 15 cm.

For the first case, the sensitivity improvement per pinhole was found to be 1.49 times the base-flat-detector pinholes. For the second case the sensitivity improvement per pinhole was as much as 2.25. The results are shown in plots in Figs. 4 and 5, respectively. These calculations include an approximate constant for the detector resolution, as in (3). The plots are explained below.

For each case, a higher-resolution design and higher sensitivity design was shown. In the higher-resolution design, the FWHM-profile across the face of the detector at depth of 15 cm is shown first, for the curved detector and the flat-detector at its base (BFD). Then the average FWHM across depth is compared for flat and curved detector for same pinhole-diameter (similar sensitivity). The average is calculated from (3). Finally a higher-sensitivity design is shown, where the pinhole-opening diameter is increased for the curved detector unit until the resolution matches that of the base flat detector (BFD) at 15 cm depth (depth of interest). Then the increased sensitivity (due to increased pinhole-opening) is estimated. Strictly speaking this SIR is for each pinhole-detector unit. However since the curved detector and flat-detector at its base have the same compactness (same extent of radius or base-radius), the number of pinholes is assumed to be the same for the two systems considered. Thus the SIR would apply to the whole system sensitivity.

Additionally tests were done by changing the focal distance from a = 60 mm to a = 120 mm and finding the sensitivity improvement ratio of using curved versus flat (SIR) at similar resolution.

Finally, for Case 2 above (GE-like system), the starting pinhole-opening diameter d₀was varied to test how the SIR changes with this parameter.

1). Case 1. Focal Distance a = 12 cm:

Higher-Resolution Design:

For Case 1, Fig. 4(a)–(b), the hole-diameter is chosen such that the resolution of BFD is that of LEHR (0.8 cm) at 10 cm depth. This pinhole diameter is 3.86 mm, the effective diameter being 4.09 mm. In Fig. 4(a) from the FWHM profile it can be seen that while the BFD resolution is held flat across the face at 1 cm (at 15 cm depth), the paraboloid-detector resolution goes from being equal to that of BFD at the extreme end to 0.694 cm or about ~ 30% less (i.e., improved) at the center. In Fig. 4(b), as expected, the resolution with the curved detector compared with BFD is lower (better) and the improvement increases with depth. Since hole-diameters are the same, the sensitivities will be the same for the two. The average resolution over depth of 8–20 cm drops from 0.96 cm for the BFD to about 0.81 cm for the paraboloid, or about a 16% improvement.

High-Sensitivity Design:

Increasing the pinhole-diameter of the curved-detector unit from 3.9 mm to 4.8 mm (effective diameter 5.0) would make the resolution match the resolution of the BFD at 15 cm, see Fig. 4(c). The sensitivity increased by a factor of 1.49 per-pinhole (based on square of effective diameter ratios), throughout the depth of interest for the curved over the BFD [Fig. 4(d)]. In Fig. 4(d), even though the absolute sensitivity is lowered with depth for each of curved-detector and BFD, as expected due to the sensitivity falling off as 1/depth², the improvement ratio remains the same across depth (due to different hole-diameters). Thus if one kept the number of pinholes of the two systems the same, one would get a 49% improvement over Funk et al.’s design without compromising resolution significantly. The resolution of the two systems remains similar in the depth of interest. In particular, the resolution of the paraboloid-detector case at depth 10 cm is about 0.83 cm which is close to that of LEHR (0.8 cm).

2). Case 2. Focal Distance a = 6 cm:

Higher Resolution Design:

For Case 2, in Fig. 5(a), the FWHM profile shows the BFD resolution remains constant at 1.64 cm (at 15 cm depth), the paraboloid-detector resolution goes from being equal to that of BFD at the extreme end to approximately 0.8 cm (or lowered by half, thus improved overall). For Fig. 5(b), the average resolution over depth of 8–20 cm drops from 1.55 cm for he BFD to about 1.10 cm for the paraboloid, or about a 29% improvement.

High-Sensitivity Design:

For Fig. 5(c)–(d), when we increased the hole-diameter to match the resolution of the BFD at 15 cm, the pinhole is about 5.85 mm (or effectively 6.122 mm). But the sensitivity increased by a factor of 2.25 per pinhole (based on square of effective diameter ratios, or (6.12/4.08)², throughout the depth of interest for the curved detector over the BFD [Fig. 5(d)]. The resolution of the curved-detector pinhole is close to that of the BFD throughout the depth of interest see Fig. 5(c). And at depths larger than 15 cm the curved detector at 5.85 mm opening has a slightly lower (better) resolution on the average than the flat detector with pinhole at 3.86 mm, while the reverse holds at depths below 15 cm.

3). Sensitivity Improvement Ratio of Curved Versus Flat for Different Base Focal Distance:

The SIR for paraboloid over flat detectors was calculated when the focal distance a was varied as in Table II. These are obtained [as done for Fig. 4(c)–(d) or Fig. 5(c)–(d)] by placing a paraboloid detector (on a base-diameter W₁) and opened the pinhole diameter until the average resolution [based on theory (3), with constant detector model and penetration model (2)] equaled that of the flat base system (again based on W₁) at a distance of 15 cm from pinhole. The sensitivity improvement ratio goes from 2.25 at a =60 mm to 1.49 for a = 120 mm. At a = 70 mm the sensitivity improvement is about 2.03. (Note to conserve space these results were placed in Table II.)

4). Sensitivity Improvement Ratio of Curved Detector Versus Flat Detector for Different Pinhole Diameters:

For the GE-like system (Case 2 above with the focus at a = 60 mm) the pinhole size was varied around the 3.86 mm diameter, to find the sensitivity improvement ratio with paraboloid detector as opposed to the base flat-detector, keeping the average resolution [based on (2)] of the paraboloid and flat systems matched closely, at depth of 15 cm. For pinhole diameters of the flat detector system at 3 mm and 5 mm (effective diameters 3.22 mm and 5.22 mm, respectively), to match the resolution at depth of interest (15 cm), the diameter of the paraboloid-detector system could be, respectively, opened to 4.84 mm (effective diameter 5.06 mm) and 7.4 mm (effective diameter 7.59 mm). Thus sensitivity improvement ratios (based on effective diameter squared) are 2.47 and 2.11 for starting pinhole-diameters of the flat-detector-system d₀ at 3 mm, and 5 mm, respectively. Therefore the factor of 2 or more advantage of paraboloid-detector-system over the flat-detector-system sustains for this range of the pinhole diameters.

B. Ray-Tracing and Theoretical Comparisons

The parameters for Case 2 were chosen for Case 2 simulations. This is because as per Table II, this is a practically useful clinical design for our configuration. Thus a = 60 mm and the diameter of the flat-detector (or base of the curved detector) to be 80 mm. The acceptance angle is approximately 67.38 deg. While the exact GE Discovery system parameters were not known, but these values are expected similar, given the human cardiac geometry. For the paraboloid detector, the height was H = 120 mm.

The resolution and sensitivity of flat detector was compared with that of the paraboloid detector with the geometric pinhole opening diameters at 3.86 mm and 5.85 mm, the starting diameters used for Case 2 for the theoretical simulations in previous section. The detector resolution or penetration effects are not included in the forward model. The resolution for 5 points were measured, placed 20 mm apart starting from the center to 80 mm at depth b = 150 mm. The resolution is measured at the detector (when possible) as well as at a viewing plane (where counts are back-traced onto via the center of pinhole) which is also kept at depth of 150 mm.

The pinhole is sampled at 0.02 mm in two directions. In sub-sequent relevant plots, all the points were displayed in a single mesh or image, but it is emphasized that each point was obtained individually and the PSF measured independently.

The FWHM calculation is prone to noise if it is just based on horizontal or vertical width of half-max spot (or the average of the two). Because the circular pinhole is projected onto square pixels of detector plane (for flat detector) or the plane back-traced to, the measurement of FWHM has to be done carefully. To calculate it robustly, a same area circle is fitted to the half-max spot and the diameter of the circle is reported.

The FWHM results at the detector for the flat-detector system with 3.86 mm pinhole, the measured sensitivity factor was identical to the expected (8) in this noise-less simulation, since every ray’s contribution (weighted by the solid-angle-factor) is accumulated. The FWHM closely approximates the expected FWHM to within fraction of mm.

The points, back-traced onto the viewing plane at 15 cm depth, is shown in Fig. 6. A slightest drop in sensitivity (only about ~2%) is seen but this can be perhaps attributed to the fact that the Gaussian interpolator nearly sums to 1 but not exactly. The projector and the expected resolutions match with RMS error of 0.16 mm, and a maximum difference of 0.3 mm.

Fig. 6.

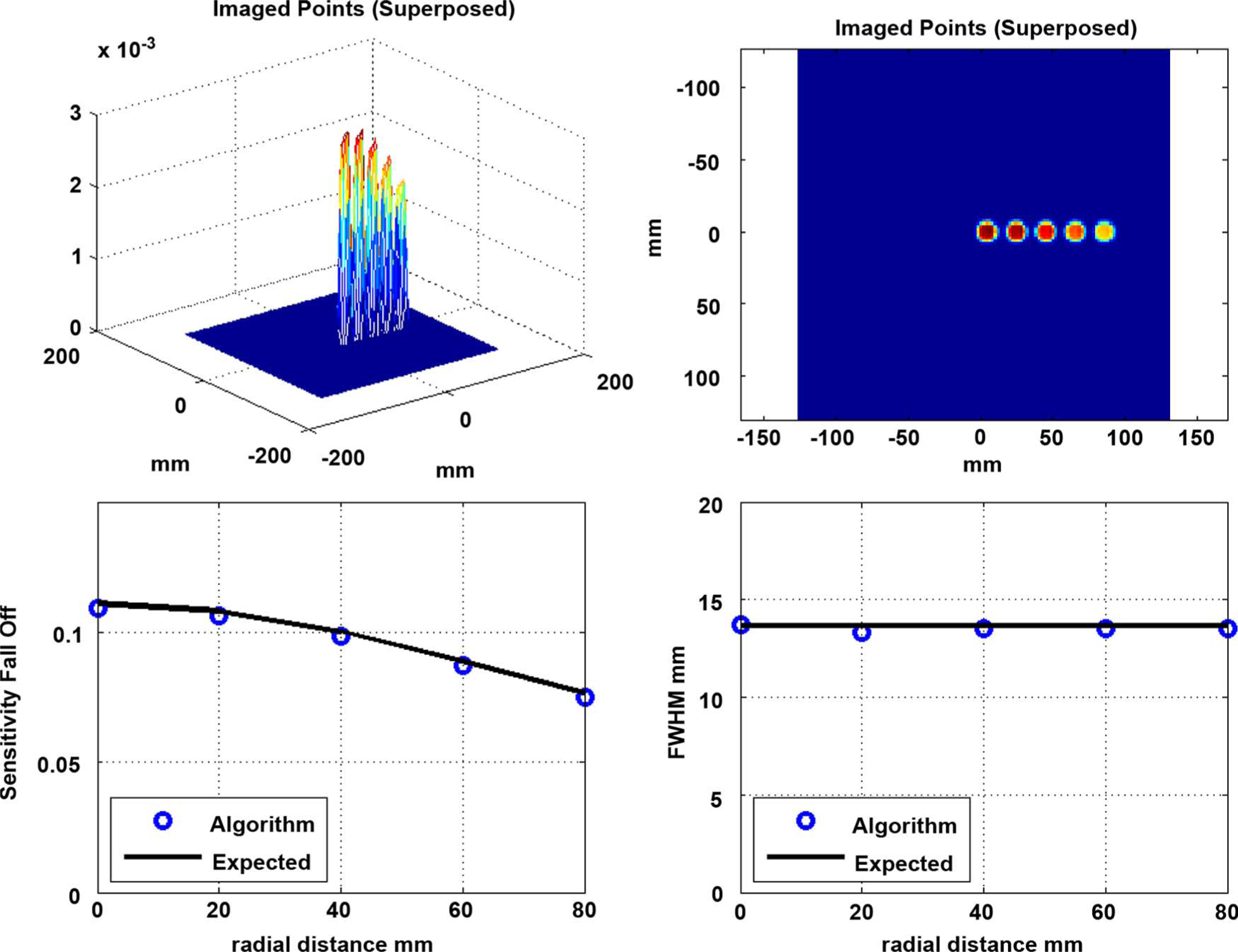
Flat Detector, at the ViewPlane at 150 mm (pinhole 3.86 mm dia, a = 60 mm): (Top Left) Mesh-plot of Point Spread Functions (PSF) of 5 points, (Top Right) Image of the five points superposed, (Bottom Left) Sensitivity Fall-off Factor measured (sum of each of the PSF) versus expected, (Bottom Right) Measured versus expected Full-Width-Half-Max in mm.

For the same 3.86 mm pinhole paraboloid-detector system, the sensitivity is again indistinguishable from expected since all rays are accumulated in the simulations. Since it is difficult to measure the FWHM of the PSF on the curved surfaces, those measurements were not attempted. The points are shown back-traced on the viewing plane (via pinhole center) in the next figures.

In Figs. 7 and 8, the resolution is close to the expected values. For Fig. 7, smaller pinhole, the root mean squared error is 0.56 mm and the maximum deviation from expected is 0.77 mm. For the bigger pinhole (Fig. 8) the projector-based FWHM numbers match the expected to within root mean square error of 0.41 mm and maximum deviation of 0.66 mm. The sensitivity is again a small percentage (~ 2%) off between the detector and viewing plane and this may again be attributed to the interpolator.

Fig. 7.

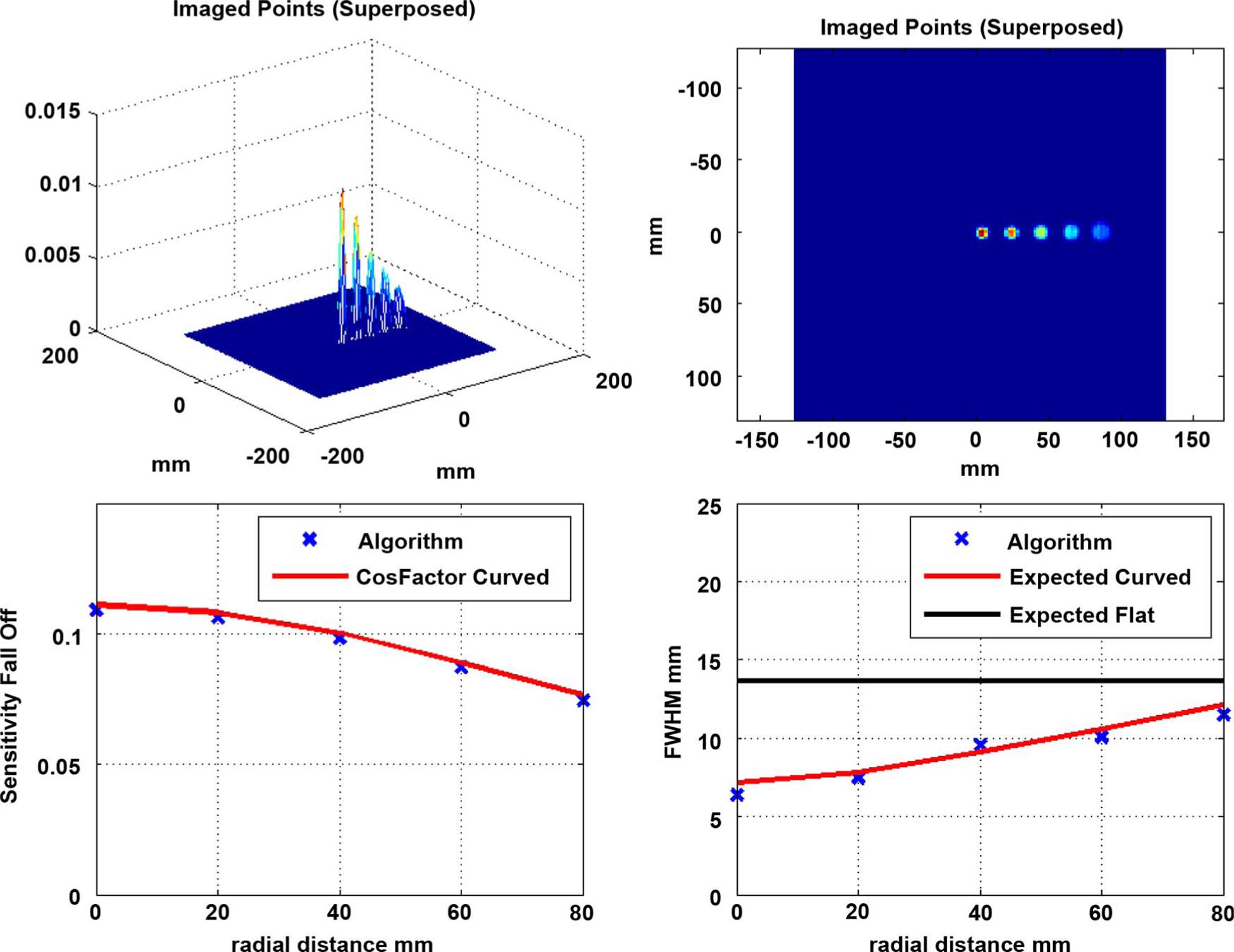
Paraboloid Detector, at the ViewPlane at 150 mm (pinhole 3.86 mm, a = 60 mm, H = 120 mm): (Top Left) Mesh-plot of Point Spread Functions (PSF) of 5 points superposed, (Top Right) Image of the five points, (Bottom Left) Sensitivity Fall-off Factor measured (sum of each of the PSF) versus expected, (Bottom Right) Measured versus expected Full-Width-Half-Max in mm.

Fig. 8.

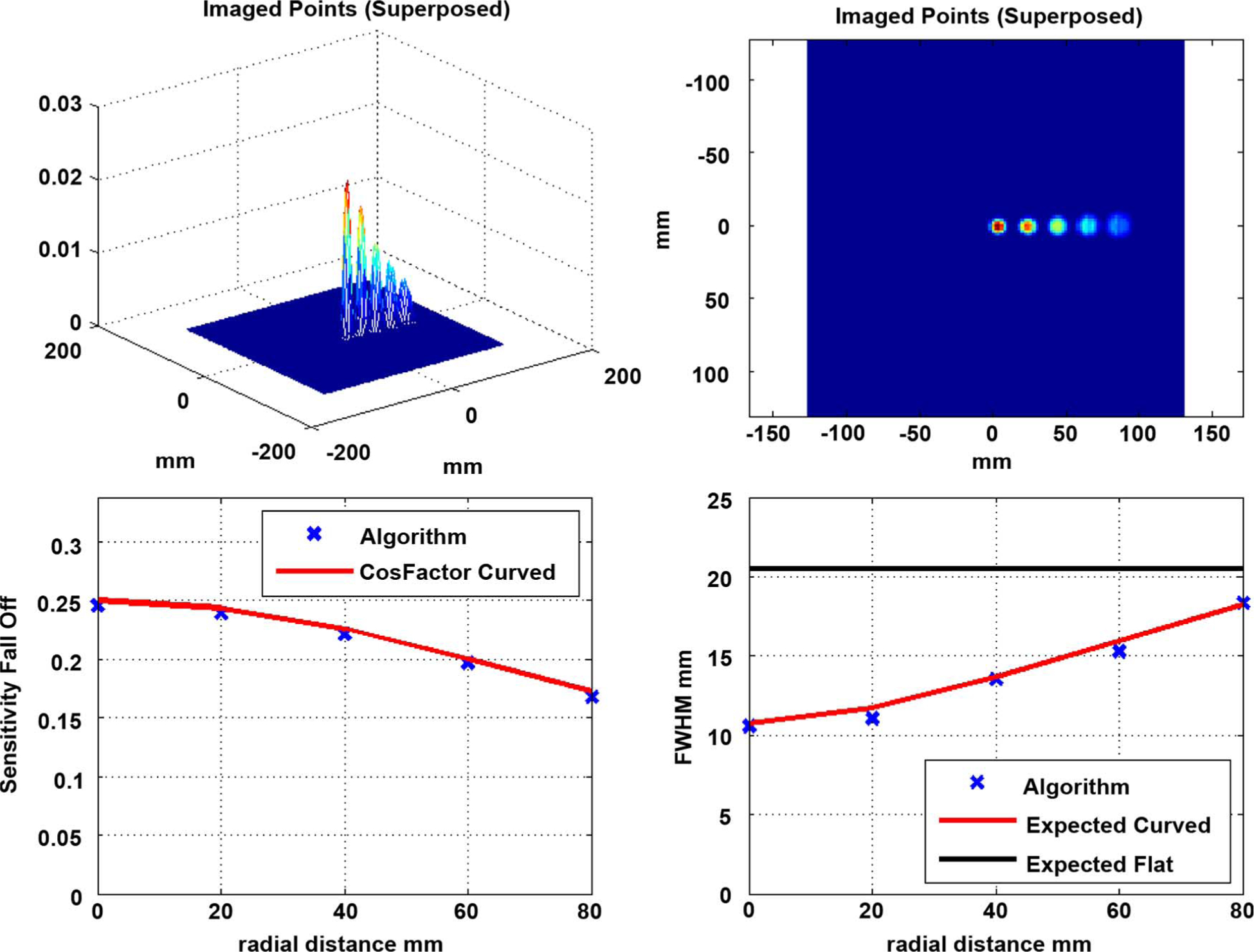
Paraboloid Detector, at the ViewPlane at 150 mm (pinhole 5.85 mm, a = 60 mm, H = 120 mm): (Top Left) Mesh-plot of Point Spread Functions (PSF) of 5 points superposed, (Top Right) Image of the five points, (Bottom Left) Sensitivity Fall-off Factor measured (sum of each of the PSF) versus expected, (Bottom Right) Measured versus expected Full-Width-Half-Max in mm.

Key Result:

Comparing the image points in Figs. 6 and 7 one can see that for same diameter opening (equivalent sensitivity) one can obtain a better resolution with paraboloid detector. The average of FWHM obtained via ray-tracing is 9.01 mm for paraboloid detector (Fig. 7) while for the flat one it is 13.54 mm. Thus with the curved detector we obtain a resolution better by 33% via ray-tracing simulation. As a comparison, note that the theoretical gain (without detector resolution considerations) between Figs. 7 and 6 is from 9.36 mm to 13.65 or a slightly smaller, 31% gain expected.

Alternately one may trade off some of the resolution advantages with sensitivity and can go to a higher diameter (Fig. 8) and get a 2.25 times sensitivity at comparable average resolution (~ 13.6 mm).

In the future, the resolution recovery within an iterative reconstruction frame-work will be investigated.

IV. Discussion

It is noted that the very first equation (proposed by Anger) is somewhat approximate and assumes that the pinhole response and the detector response are Gaussians and therefore the resulting resolution is in quadrature. However, in reality the circular pinhole is more like a circ-function and a more realistic model might be a circ-function as the pinhole-effect convolved with a Gaussian as the detector-blur. This would suggest a reduction of the theoretical FWHM values (for either curved or flat detector system) in Figs. 4 and 5. When comparing the forward ray-tracing simulator with theory without the detector resolution however, effectively a Circ-function on was used (4)–(6).

In forward simulator, the depth of interaction or detector intrinsic resolution (which partly depend on detector design and read-off) were not simulated as yet and is a subject of further detailed investigation. However, the detector resolution was included approximately (as a constant) in the theoretical results in Figs. 4 and 5. The sensitivity improvement of the paraboloid detector over flat was similar with/without detector resolution included. Specifically, for the low-magnification design (a = 6 cm, Fig. 5), for the full-theoretical case (with a constant detector resolution and approximate penetration model included) the improvement was 2.25 times sensitivity or 29% resolution improvement (Results Section A, Case 2) of curved over flat-detector. For Results in Section B, without detector resolution or penetration included the improvement was similar (2.25 times sensitivity or 31% resolution theoretically). The difference in theoretical resolution with and without detector-resolution/penetration is only 2%. This can be understood upon realizing that the detector resolution, when included, is also subject to the magnification improvement due to curved detector, though not exactly in the same way as pinhole diameter [see (1) and (3)].

Another factor affecting the sensitivity/resolution is the pinhole penetration, which changes with the ray-angle with respect to the pinhole central axis. Here this penetration effect was not considered to the fullest. More accurate models [than (2)] are explained in [30] and [31]. These effects were studied in detail by Williams et al., 2003 [32] for a planar array as well as a curved array of detectors pointed towards the pinhole. In their investigations for a small animal imaging system ([32, p. 1567, Fig. 9]), the FWHM reduced monotonically with ray-angle (angle wrt the pinhole axis) while the planar array results show an increase with angle (after a certain angle). Note the trend with angle (and not relative values) are important—since (as is explained in the paper) the magnification for curved-array used was lower (1.3 versus 2) for the flat-array, due to physical limitations and so for central axis the FWHM was different for two system.

Both the curved and the flat detectors will have varying intrinsic resolution due to parallax error (due to non-alignment of surface normal with the pinhole), since the incident angle is varying across the face. However it is important to point out that the increased magnification for the curved detector will again help reduce the effect of the parallax effect just as it did for the pinhole aspect. The parallax effect and a correction strategy is being investigated in more details using GATE.

Rigorous investigations are underway to find the optimal detector surface that will minimize the FWMH on the average, considering the magnification, the detector intrinsic resolution, the depth of interaction effect (theoretical equations given in [37]) and last but not least, the pinhole penetration and the appropriate convolution. Many of these effects which vary with the ray-angle, and the incident angle at the detector and will guide the optimal shape.

At the high values of FWHM achieved compared to LEHR for the de-magnified pinhole-system (a = 6 cm), obviously resolution recovery will be necessary to obtain comparative or better resolution than the clinical LEHR systems, for a flat or a curved detector system. While it is not known exactly how the comparisons will turn out after resolution recovery, one would expect the inherent advantages of the curved detector compared to a base flat detector to sustain. This is because improvement after resolution recovery is in proportion to improvements in design parameters as far as resolution is concerned. That is, in general a system with intrinsically better system resolution will show pro-portionally better improvement of resolution, with and without resolution recovery [17]–[21].

Last but not least, while this initial analysis shows that curved detector has some definite resolution/sensitivity advantages for a multi-pinhole system in a compact space, and an optimal surface is to be found, an important issue is that of the manufacturing expense of a curved-detector system. Indeed system would be more expensive than a base-flat detector system. Approximations of curved detectors where one uses flat strips (pyramidal or trapezoidal) are being investigated using GATE. The increase in detector material for the case of a paraboloid detector (height H=12 cm, base radius R=4 cm) versus its base circular flat detector would be a factor of 4 times. This certainly makes use of CZTs for detector material prohibitively costly. However with CsI or NaI materials our collaborators and our group are looking to design a mid-range ($300–$400 K) system with a factor of 2.25 improved in sensitivity or a ~ 29% better resolution over a GE-like flat-detector system.

V. Conclusion and Future Work

In this work the theoretical resolutions of curved detectors (paraboloid, cone and semi-sphere) set on a pinhole was approximately derived. The advantages of a paraboloid detector over a flat detector using ray-tracing simulations were demonstrated and compared to independently-obtained theoretical derivations. It is shown that for a curved detector one may obtain sensitivity gains as much as 2.25 for similar resolutions as a flat detector by opening the pinhole or one could obtain a better system resolution (29% better on the average) by keeping the same pinhole opening. The flat detector parameter values are expected to be close to that of the new GE system. In our forward model, only pinhole PSF was modeled so far. Ongoing and future software work includes modeling the detector resolution, DOI effects and penetration effects within the forward model and compensating for the pinhole-resolution effects in an MLEM reconstruction algorithm. Our group is also investigating different curved detector performances against flat detector with pinhole collimation using GEANT4 software. The parallax effect and a correction strategy is being investigated and evaluated. Finally we are investigating an optimized surface to minimize the FWHM. Last but not least, along with collaborators our group is also looking at inexpensive ways to build a curved detector for this multi-pinhole Cardiac SPECT application.

Appendix

Derivation of Average System Resolution in Curved Surfaces:

The average squared resolution is obtained by integrating the squared resolution over the surface and then dividing by the surface area. In what follows, the derivation is shown for paraboloid. For those for cone and sphere, refer to conference record [26].

Paraboloid:

The average squared resolution over the surface of the paraboloid with height H and base radius R [see Fig. 2(b)], placed on a pinhole with parameters a, b, was derived as follows. The derivation is started by modifying the well-established formula for system resolution at depth θ for a pinhole on a flat-detector in (1) and incorporating the angle-dependent magnification in the resolution expression. The angle b is the angle a ray makes with the horizontal. The new inverse magnification is the ratio PB/PM, where the line-segments PB and PM can be straightforwardly related to the surface parameters H and R and the ray angle θ as shown in (2):

$$\begin{gathered} {\text{Res}}^2(\theta )=\left[{\left(1+\frac{\frac{b}{\text{sin}(\theta )}}{\frac{(a+H-h)}{\text{sin}(\theta )}}\right)}^2{d}^2+{\left(\frac{\frac{b}{\text{sin}(\theta )}}{\frac{(a+H-h)}{\text{sin}(\theta )}}\right)}^2{R}_I^2\right] \\ =\left[{\left(1+\frac{b}{a+H-h}\right)}^2{d}^2+{\left(\frac{b}{a+H-h}\right)}^2{R}_I^2\right]. \end{gathered}$$ (A1)

Here h is the height [from the inverted paraboloid, see Fig. 2(b)] at which the ray at angle θ intersected the surface, given by

$$h=\left[(a+H)+\left(\frac{R^2{\text{tan}}^2\theta }{2H}\right)\right]-\sqrt{{\left((a+H)+\frac{R^2{\text{tan}}^2\theta }{2H}\right)}^2-{(a+H)}^2}.$$ (A1a)

Going one step further, one can integrate the resolution squared function over the paraboloid surface and divi by the surface area to obtain the average resolution, as given by

$$\begin{gathered} {\text{Res}}_{\text{av}}^2=\left[\frac{\int {\text{Res}}^2(\theta )dA}{\int dA}\right] \\ =\frac{\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{H}{\int }}{\text{Res}}^2(\theta )\frac{{\left(R^4+4R^{2}Hh\right)}^{1/2}}{2H}dhd\varphi }{\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{H}{\int }}\frac{{\left(R^4+4R^{2}Hh\right)}^{1/2}}{2H}dhd\varphi } \\ =\frac{2\pi \underset{0}{\overset{H}{\int }}{\text{Res}}^2(\theta )\frac{{\left(R^4+4R^{2}Hh\right)}^{1/2}}{2H}dh}{2\pi \underset{0}{\overset{H}{\int }}\frac{{\left(R^4+4R^{2}Hh\right)}^{1/2}}{2H}dh} \end{gathered}$$ (A2)

$$=\frac{\underset{0}{\overset{H}{\int }}\left[{\left(1+\frac{b}{a+H-h}\right)}^2{d}^2+{\left(\frac{b}{a+H-h}\right)}^2{R}_I^2\right]\frac{{\left(R^4+4R^{2}Hh\right)}^{1/2}}{2H}dh}{\underset{0}{\overset{H}{\int }}\frac{{\left(R^4+4R^{2}Hh\right)}^{1/2}}{2H}dh}.$$ (A3)

The steps use the surface element relation for a paraboloid surface, given by dA = (R⁴ + 4R²Hh)^1/2 /2H dhdϕ where the variable ϕ is the angle of rotation about the axis. The surface is generated by taking the curve in one-quadrant and rotating about the axis by 2π. Thus the integral over dϕ simply yields a 2π factor, (A2), which maybe then cancelled from the numerator and denominator, as shown in (A3). It can be verified that the surface area of paraboloid is given by the integral in the denominator of (A2)–(A3) can be obtained in closed form in terms of the radius and height R and H of the paraboloid and the a and b of the pinhole collimator, however we chose to calculate it computationally for simplicity. The system resolution is then the square root of (A3).

Derivation of Number of Pinholes:

Referring to Fig. 1, the pinholes are arranged in surfaces around the torso. To adapt to the patients’ body contour, the geometry is divided into three regions, as illustrated in the transverse cross-section of the body in Fig. 1(a). In Fig. 1(b) we show one of the cross-sectional sectors of the surface in the axial direction. The two dimensional surface spanned by the corresponding arcs in the transverse and axial directions will accommodate a two-dimensional array of detector-pinhole pairs over the body contour around region of interest. The detector bases for each pinhole-detector-pair are aligned along the sectors. From practical considerations, some buffer is necessary when calculating the number of pinholes to be accommodated. The number of pinholes accommodated in the geometrical configuration can be roughly calculated by

$$N\approx \frac{{\varphi }_{t1}}{\Delta {\varphi }_{t1}}\times \frac{{\varphi }_{a1}}{\Delta {\varphi }_{a1}}+\frac{{\varphi }_{t2}}{\Delta {\varphi }_{t2}}\times \frac{{\varphi }_{a2}}{\Delta {\varphi }_{a2}}+\frac{{\varphi }_{t3}}{\Delta {\varphi }_{t3}}\times \frac{{\varphi }_{a3}}{\Delta {\varphi }_{a3}}$$ (B1)

where ϕ_ti and ϕ_ai for i =1, 2, 3 are the arc lengths in the three sector along the transverse and axial directions, Δϕ_ti and Δϕ_ai are the angular extents required to accommodate for each pinhole, after allowing for a small, fixed buffer. Each sector is independent (part of different spherical surfaces in general). Thus the number of pinholes in each sector cross-product ϕ_ti/Δϕ_ti × ϕ_ai/Δϕ_ai is given approximately by the cross-product, and then they are added together to yield the total number of pinholes.

The Δϕ_ti = 2 tan⁻¹ [R_ti/B + a] where R_ti is half the base extent of the detector (for base flat-detector) with some small fixed buffer-space included. The parameter B is the depth at which all the pinholes are focused at, and a is the focal distance. A similar expression holds on the longitudinal direction for Δϕ_ai.

For Tables I and II, we combined (co-centered) sectors 1 and 2 into a single sphere and eliminated the arc behind the torso. So our number of pinholes simplified as

$$N\approx \frac{{\varphi }_t}{\Delta {\varphi }_t}\times \frac{{\varphi }_a}{\Delta {\varphi }_a}$$ (B1a)

and Δϕ_t = 2 tan⁻¹ [R_t/B + a] That is, it is R_t = W₁/2 + buffer_t and similarly Δϕ_a is based on R_a = W₂/2 + buffer_a. We chose the total arcs in the two directions as ϕ_t = π and ϕ_a = 0.3π + Δϕ_a. B = 200 mm and a is a test parameter in the table. The fixed buffers in transverse and axial directions are chosen as 10 mm and (in accordance to aspect ratio), 7.6 mm, respectively.