Base and Covariate Population Pharmacokinetic Analyses of Dupilumab Using Phase 3 Data

Abstract

Population pharmacokinetic base and covariate models were developed to study functional dupilumab for regulatory submissions, using data from healthy volunteers and patients with moderate‐to‐severe atopic dermatitis (AD) receiving intravenous or subcutaneous doses. Sixteen studies were pooled (N = 2115; 202 healthy volunteers, 1913 AD patients). The best model was a 2‐compartment model with linear and Michaelis‐Menten elimination and 3 transit compartments describing absorption. A stepwise approach to model building, with some parameters estimated using mostly rich data and subsequently fixed, was used to avoid adverse effects of sparse data and a steep target‐mediated phase on pharmacokinetic parameters, which require rich sampling for proper estimation. Parameterization of models in terms of rates was a useful alternative to the parameterization in terms of clearances, allowing for a reduced number of covariates while providing accurate predictions. While antidrug antibodies, albumin, race, body mass index, and Eczema Area and Severity Index score were statistically significant covariates, only body weight had a notable effect on central volume, explaining interindividual variability. The model adequately described dupilumab pharmacokinetics in phase 3 trials.

Atopic dermatitis (AD) is a chronic, predominantly type 2–driven inflammatory skin disease with eczematous lesions and intense pruritus.1 The pathophysiology of AD is influenced by a complex interplay between genetic and environmental factors.2 There is evidence suggesting that impaired skin‐barrier function in patients with AD may allow for transcutaneous penetration of allergens, triggering a robust type 2–mediated immune response, immunoglobulin E–mediated inflammation (not always present), susceptibility to cutaneous infections, and chronic pruritus substantially impairing the quality of life of AD patients.2, 3

Dupilumab is a fully human, VelocImmune‐derived monoclonal antibody,4, 5 blocking the shared receptor component for interleukin (IL)‐4 and IL‐13, cytokines that are key drivers of type 2 diseases such as AD, asthma, allergic rhinitis, and food allergies, which are often associated as comorbidities.6 The binding of dupilumab to human IL‐4 receptor alpha (IL‐4Rα) results in blockade of the functions of IL‐4 and IL‐13 signal transduction.7, 8, 9, 10, 11, 12

The pharmacokinetics (PK) of dupilumab are typical for a human immunoglobulin G4 monoclonal antibody, with distribution, linear, and target‐mediated phases after intravenous (IV) administration and absorption, linear, and target‐mediated phases following subcutaneous (SC) dosing.13 As is frequently observed with monoclonal antibodies, the PK of dupilumab are substantially nonlinear due to target‐mediated clearance. Dupilumab has a steep target‐mediated phase, which is assumed to be due to the presence of the target receptor on the surface of circulating mononuclear blood cells.14 The metabolic pathway of dupilumab has not yet been characterized; however, as dupilumab is a monoclonal immunoglobulin G4 antibody, it is expected to be degraded into small peptides and amino acids via catabolic pathways in the same manner as endogenous immunoglobulin G.15 Furthermore, no meaningful effects of dupilumab have been found on the PK of the cytochrome P450 (CYP) substrates, suggesting that IL‐4/IL‐13 signaling has no significant effect on the activity of CYP3A4, CYP2C19, CYP2C9, CYP1A2, or CYP2D6.16

Dupilumab is approved for SC administration for the treatment of patients aged ≥12 years in the United States with moderate to severe AD inadequately controlled with topical prescription therapies or when those therapies are not advisable, in Japan for the treatment of adult patients with AD not adequately controlled with existing therapies, and for use in patients aged ≥12 years with moderate to severe AD who are candidates for systemic therapy in the European Union. Dupilumab is also approved for certain patients with other type 2 inflammatory diseases, including asthma and chronic rhinosinusitis with nasal polyps, in multiple countries. The approved dosing regimen in adults is a 300 mg every 2 weeks SC regimen. Dupilumab demonstrated efficacy and an acceptable safety profile in early‐phase and phase 3 clinical trials in adults and adolescents with moderate to severe AD,7, 10, 11, 12, 17, 18, 19, 20 asthma,8, 21, 22 chronic rhinosinusitis with nasal polyps,23, 24 and eosinophilic esophagitis.25 Dupilumab is also under development as a potential novel treatment in pediatric populations with asthma (NCT02948959) and food allergy (NCT03682770).

The aim of this analysis was to perform a population PK analysis for regulatory submissions using data from 16 dupilumab phase 1 to 3 trials in healthy volunteers and patients with moderate to severe AD who received IV or SC doses.

Methods

Study Design and Population

A population PK analysis was performed, including data from trials described in Table S1.7, 9, 10, 11, 12, 26, 27 The studies presented here were performed in accordance with Good Clinical Practice guidelines and adhered to the Declaration of Helsinki. The study protocols and procedures were approved by the appropriate institutional review boards and ethics committees at each study site. All participants provided written informed consent before any study procedure was undertaken.

Overall, 16 studies were pooled for population PK analyses; 2041 of 2115 participants on active treatment and 18 243 of 20 809 samples were included in the analyses (most excluded samples were collected before the first dose). All data set creation and analyses followed US Food and Drug Administration guidelines.

Assay Methodology

The quantitation of functional dupilumab was performed using a validated enzyme‐linked immunosorbent assay,13 with a lower limit of quantification (LLOQ) of 0.078 mg/L in undiluted human serum. Concentrations of functional dupilumab (ie, dupilumab not bound to cell receptors and with at least 1 arm free for binding) were measured. In this functional assay, dupilumab was used as the assay standard, and human IL‐4Rα served as the capture reagent. The assay does not detect dupilumab when both binding sites are occupied by soluble IL‐4Rα, or when at least one site is bound to membrane‐bound IL‐4Rα.

Unlike the total assay format, which can make the target‐mediated phase look linear and nonlinearity less evident, the functional assay format used made nonlinearity more transparent. Two versions of the dupilumab functional assay used during drug development were cross validated.

Anti‐dupilumab antibodies (ADAs) were assessed in serum samples using a validated electrochemiluminescence bridging immunoassay. The method involved 3 steps for the evaluation of ADAs in serum samples: screening, confirmation, and titer determination. The screening assay identified potentially positive samples; samples that were positive in the screening assay were then analyzed in the confirmation (drug specificity) assay. Samples were considered negative for ADAs if either the screening or confirmation tests were negative; samples that were positive in the confirmation assay were considered to be positive for ADAs. A titration assay was then used to determine the ADA titer.

The functional dupilumab and ADA assays used in these analyses had passed multiple regulatory reviews during the regulatory submissions.

Population PK Analysis

While this manuscript does not propose new methods of population PK analysis, it suggests a combination of existing methods, allowing the analysis to account for a steep target‐mediated phase when data are sparse; the target‐mediated phase is the terminal phase when target‐mediated clearance dominates linear clearance, decreasing the half‐life over time. One of the goals of this article is to present the methodology and results of the phase 3 population PK analysis conducted for regulatory submission, rather than develop a new structural model. The structural model used in this analysis was only slightly advanced by the addition of transit compartments to the previously published model, which supported early clinical development.13 Transit compartments allowed for more physiological characterization of the absorption phase. Importantly, and in contrast with our previous analysis,13 the models described in this manuscript were developed for regulatory submission rather than for exploratory analyses or developmental simulations; the modeling methodology was advanced toward an analysis of a large phase 3 sparse data set, in which a broad variety of covariates were explored and parameterization of the model, in terms of clearance and elimination rates, was compared between models. In addition, the study addresses modeling issues associated with sparsity of data in the presence of target‐mediated clearance.

The population PK of dupilumab was conducted using Monolix version 2016R1 (LIXOFT, Antony, France) and NONMEM Version 7.3 (ICON Development Solutions, Dublin, Ireland). Parameterization of the model in terms of rates was chosen to reduce correlations between PK parameters, avoid repetitive covariates, and minimize potential overparameterization.13 A sensitivity analysis using clearance instead of rates was provided to demonstrate the accuracy of the results of the primary covariate model.

The strategy was to estimate some parameters using mostly rich data from early clinical studies, and subsequently fix them when phase 3 data were analyzed. This stepwise approach to modeling was used due to the substantially nonlinear PK of dupilumab and the availability of sparse (primarily trough) concentrations reaching beta phase in phase 3 trials, which cannot inform the model about many parameters. Beta half‐life represents the half‐life during the linear elimination phase, which is also called beta phase when the target‐mediated clearance is saturated, and has negligible impact on this half‐life. Combining small rich and large sparse data sets in the presence of a steep target‐mediated phase led to instability of parameters that require rich data for assessment. However, this issue was not observed when rich and small sparse data sets were combined.13

Four models were developed using the stepwise approach; the structure of the models was the same (Figure 1), while the number of fixed parameters, the number of parameters with implemented between‐subject variability, and the number of studies were different. Four studies were used in Model 1 (R668‐AS‐0907, TDU12265, PKM14161, and R668‐AD‐1117). The goal was to obtain good estimates of PK parameters that primarily required data from studies with rich sampling schedules. Twelve studies (phase 1 through phase 2b) were analyzed using Model 2 (R668‐AS‐0907, PKM12350, PKM14161, PKM14271, TDU12265, R668‐AD‐0914, R668‐AD‐1026, R668‐AD‐1117, R668‐AD‐1121, R668‐AD‐1021, R668‐AD‐1307, and R668‐AD‐1314). The primary goal was to understand whether target‐mediated clearance is different between healthy volunteers and patients with AD. The secondary goals were to (1) understand the behavior of the model when values below the limit of quantitation (BLQ) are excluded, (2) understand the behavior of the model when parameters that became unstable with an increasing proportion of sparse data were fixed, (3) use the test population (normal volunteers vs patients with AD) and assay as covariates in the model. Models 3 and 4 were the primary base and primary covariate models, respectively. Only 3 pivotal phase 3 studies were used in this analysis (R668‐AD‐1334, R668‐AD‐1416, and R668‐AD‐1224) to inform regulatory submissions about exposure and covariates.

Figure 1.

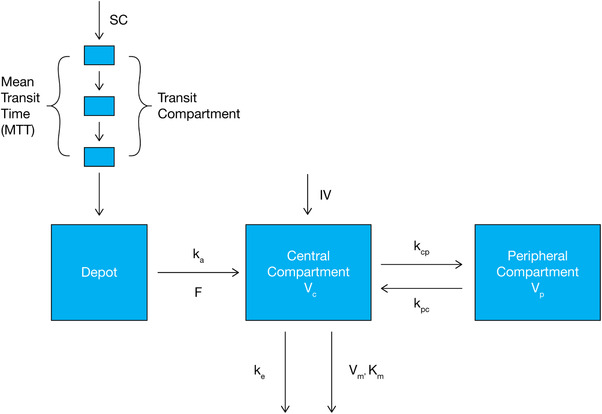
Structural representation of model with parallel Michaelis‐Menten and linear elimination of dupilumab. F, bioavailability; IV, intravenous; k_cp, central‐to‐peripheral rate; k_pc, peripheral‐to‐central rate; k_a, absorption rate; k_e, elimination rate; K_m, Michaelis–Menten constant; SC, subcutaneous; V_c, central volume of distribution; V_m, maximum target‐mediated rate of elimination; V_p, peripheral volume.

Except for the central volume (V_c), elimination rate (k_e), omega (ω, standard deviation [SD] of between‐subject variability), sigma (σ, SD of measurement error), and covariate effects, parameters in Models 3 and 4 were fixed to values estimated from the phase 1 and 2 data. Weight was included as a covariate in all models, since it is well established that it is an important and statistically significant covariate of V_c for monoclonal antibody (mAb) PK.13, 28

Forward inclusion and backward elimination were applied to build both the base and covariate models. A parameter remained in the model when the addition of the covariate resulted in α ≤0.01 and removal of the covariate resulted in α ≤0.001.

A multiplicative model was used to test for continuous covariates:

$$Y({\lambda }_{\mathrm{i}})=Y·{\left[\frac{{\lambda }_{\mathrm{i}}}{\mathrm{Central}\mathrm{value}({\lambda }_{\mathrm{i}})}\right]}^{\theta }$$

where Y(λ_i) is a population PK parameter adjusted for the covariate, λ_i is an individual value of the covariate, i is a subject number, Y is a population PK parameter at median or another selected level of covariate called central value, and θ is a parameter describing an effect of the covariate on the population PK parameter.

The following multiplicative model was used to test for dichotomous covariates:

$$\mathrm{Y}\left({\lambda }_i\right)=\mathrm{Y}·{\mathrm{e}}^{\theta ·{\lambda }_i}$$

where Y is a population PK parameter when λ_i = 0; λ_i is equal to 0 or 1.

The following variables were tested as potential model covariates: body mass index (BMI), version of dupilumab assay, sex, age, race, population (healthy volunteers vs patients with AD), predicted creatinine clearance, aspartate aminotransferase, alanine aminotransferase, alkaline phosphatase, albumin, antidrug antibodies (ADAs) at any time, and Eczema Area and Severity Index (EASI).29 The test of assay as a covariate was a precautionary step, to confirm the results of the assay cross validation.

The objective function in the model is a mathematical equation describing the model fit that requires optimization. Under some conditions, an estimated objective function value (OFV) allows for testing the statistical significance of difference between models. When a large variability in the OFV did not allow for statistical tests, the decision about statistical significance was made using bootstrap confidence intervals (CIs) for population PK parameters; the bootstrap approach was applied to test only for impact of the dupilumab functional assay and population. The results of the Wald test, which were also not affected by variability of OFV, were used to confirm results of the statistical tests (log‐likelihood test and/or bootstrapping).

Response variables for the covariate analysis primarily included V_c and k_e. As phase 3 observations were primarily at concentrations at which linear clearance (CL) predominates, only the impact of population was tested on the maximum target‐mediated rate of elimination (V_m) using early‐phase data and bootstrapping.

The stability of the base and covariate models was evaluated based on comparison of the primary and sensitivity analyses, random changes in initial parameters, condition numbers, and bootstrap results.

The validation of the models was performed using different approaches, including the bootstrap method, visual predictive checks, validation of early exploratory versions of the model using later‐stage data as external data sets, and comparison of estimated PK parameters with those published for mAbs.28 In addition, several sensitivity analyses were conducted. For example, all early‐ and late‐phase studies were combined in the model, CL instead of elimination rate was tested as a response variable, and/or excluded observations were used in the model.

BLQ values were used in the analysis to better characterize the nonlinear elimination phase.13 The most frequently used Beal M3 method30 was used to incorporate BLQ observations in the objective function. Stochastic approximation expectation–maximization and importance sampling methods were used to estimate PK parameters.

Results

An initial strategy for the primary base and covariate models was to combine data from clinical trials with both rich and sparse sampling and to estimate population PK parameters. This led to several challenges.

First, it appeared that having a large portion of sparse data (particularly in the presence of steep target‐mediated phase) adversely affected the estimation of some PK parameters; central‐to‐peripheral rate (k_cp), peripheral‐to‐central rate (k_pc), mean transit time (MTT), absorption rate (k_a), and bioavailability (F) could only be properly estimated using rich data or rich data in combination with a small or moderate portion of sparse data. The listed parameters had large standard errors or even became unstable when large sparse data sets were added.

Second, predominantly trough levels in the beta phase (when the nonlinear clearance was essentially saturated) were available in phase 3 studies, suggesting that only 1 compartment linear model can be properly identified if only phase 3 data are used in the analysis. As the early clinical data clearly indicated the presence of the peripheral compartment and target‐mediated clearance, such a model was inconsistent with known biology and appeared to be inadequate to make meaningful predictions. Therefore, using phase 3 data alone was not a useful option.

Third, while parameters in some variants of the model were stable (eg, Model 2), estimates of the OFV had wide variability, making it impossible to obtain meaningful P values based on the OFV (likelihood ratio test). This increased variability was due to the use of sparse data and the marked nonlinearity of the target‐mediated phase, with a terminal slope approaching minus infinity as concentrations approached the LLOQ. As a result, small changes in PK parameters caused large changes in ratios of observed to predicted values, and consequently in the OFV.

Fourth, while the presence of BLQ values in the analysis allowed for appropriate estimates of parameters describing nonlinear kinetics and characterization of target‐mediated phase (nonlinear elimination rate of dupilumab [V_m] and the concentration of dupilumab [K_m] that enables the achievement of half V_m), it also led to an increase in OFV variability and affected the stability of some parameters when large sparse data sets were added.

To address the challenges listed above, the approach of this analysis was first to estimate parameters using mainly rich data from early clinical trials with BLQ values in the analysis, and subsequently to fix some of these parameters in the analysis of phase 3 data. This approach allows for the use of OFV, and consequently the likelihood‐ratio test, to study covariates. An alternative to the likelihood‐ratio test while testing covariates was the bootstrap CIs, but this was not a computationally feasible approach to testing all covariates. Another option was to exclude BLQ values from an analysis of rich data (Model 1) and use subsequent models predicting a less steep target‐mediated phase, with less physiologically meaningful parameters characterizing the target‐mediated phase, and with pure predictions of frequency of BLQ observations and concentrations during the target‐mediated phase.

It appeared that the BLQ values used in the analysis of dupilumab provided essential information about the target‐mediated phase. The BLQ observations were informative, as few low quantifiable concentrations were available to characterize the target‐mediated phase. Proper characterization of the target‐mediated phase using BLQ values can be essential for pharmacodynamic (PD) modeling, as half‐maximal effective concentration can occur during this phase. Also, BLQ values during the absorption phase are essential to estimating MTT and subsequently obtaining better estimates of intercompartmental rates (k_cp and k_pc) when IV and SC data are combined. Due to the large amounts of sparse data integrated, the use of BLQ values increased variability in the OFV. The large variability in OFV can be explained as follows: due to the steep target‐mediated phase, the OFV was hypersensitive to small changes in some PK parameters in some patients. This happened because the target‐mediated phase was a close‐to‐vertical line, and small changes in time caused extreme fold changes in predicted PK concentrations, which consequently affected the OFV. Therefore, BLQ values were used only when rich data, together with a small proportion of sparse data, were analyzed; then, some parameters were fixed and BLQs were excluded when additional sparse data were integrated or when only sparse data were analyzed. As parameters that can be affected by exclusion of the BLQ values were fixed, exclusion had no meaningful impact on the remaining parameters.

Using BLQ values had 2 disadvantages. First, the computational time of modeling and the complexity of the model development increased. Second, a singularity caused by the steep target‐mediated phase became apparent and influential, and had to be addressed. This singularity did not reveal itself when BLQ values were excluded from the analysis; rather, the model without BLQ values predicted a less steep target‐mediated phase, increasing both V_m and K_m. A less rigorous approach of excluding BLQ values can be used when the task is limited to covariate model building. Nevertheless, as V_m can be affected by exclusion of the BLQs from the data, this approach should be exercised carefully when a meaningful value of V_m is needed, when covariates of V_m have to be identified, or when the PK model is the basis for PK/PD analysis.

The final structural model is presented in Figure 1. It is a 2‐compartment PK model, implementing parallel linear and Michaelis‐Menten elimination and a transit compartment model of lag time.

Estimates of population PK parameters are presented in Table 1 for 4 major steps of the modeling. Covariates other than weight are excluded from Table 1, as they are presented in Table 3. All PK parameters, including standard deviations of characterizing between‐subject variability in PK parameters and standard deviation of residual errors, as well as bootstrap CIs, are presented in Tables S2 through S4. Abbreviations of PK parameters are defined in Figure 1, Tables 1, 2, 3, and Tables S2‐S4.

Table 1.

Population PK Parameters and Bootstrap Confidence Intervals for Initial Models Based on Rich and Sparse Data (Models 1 and 2)

	Parameter Estimate (SE)
Parameter Name	Model 1 Estimates All Parameters	Model 2 Confirms Vm	Model 3 Base Model	Model 4 Covariate Model
PK parameter
Vc (L)	2.48 (0.0481)	2.54 (0.021)	2.76 (0.021)	2.74 (0.021)
ke (1/d)	0.0534 (0.000387)	0.0550 (0.000831)	0.0448 (0.000490)	0.0477 (0.00078)
kcp (1/d)	0.213 (0.0286)	0.211 (fixed)	0.211 (fixed)	0.211 (fixed)
kpc (1/d)	…	0.310 (fixed)	0.310 (fixed)	0.310 (fixed)
Mpc (1/d)	0.686 (0.00986)	…	…	…
ka (1/d)	0.256 (0.00696)	0.309 (0.00942)	0.306 (fixed)	0.306 (fixed)
MTT (d)	0.105 (0.0100)	0.105 (fixed)	0.105 (fixed)	0.105 (fixed)
Vm (mg/L/d)	1.07 (0.0279)	1.07 (0.0162)	1.07 (fixed)	1.07 (fixed)
Km (mg/L)	0.01 (fixed)	0.01 (fixed)	0.01 (fixed)	0.01 (fixed)
F (unitless)	0.643 (0.00914)	0.642 (fixed)	0.642 (fixed)	0.642 (fixed)
Impact of weight
Vc ∼ weight	0.711 (0.0161)	0.803 (0.0322)	0.919 (0.027)	0.817 (0.031)
Derived PK parameters
CL (L/d)	0.132	0.140	0.124	0.131
kpc	0.310	…	…	…

CL, clearance; F, bioavailability; k_a, absorption rate; k_cp, central‐to‐peripheral rate; k_e, elimination rate; K_m, Michaelis–Menten constant; k_pc, peripheral‐to‐central rate; MTT, mean transit time; PK, pharmacokinetics; SE, standard error; V_c, central volume of distribution; V_m, maximum target‐mediated rate of elimination.

M_pc is ratio of k_cp and k_pc (M_pc = k_cp/k_pc); parameterization of the model in terms of M_pc and k_cp and in terms of k_cp and k_pc led to almost identical results and the latter parameterization was used in the subsequent models.

Table 3.

Parameterizations of Covariate Model Using Clearance

	Population Estimates
	Model 4A Parameterized Using Linear CL		Model 4 Parameterized Using ke
Parameters	Estimate (SE)	P Values	Estimate (SE)	P Values
PK parameter
Vc (L)	2.73 (0.022)	…	2.74 (0.021)	…
ke (1/d)	0.0476a	…	0.0477 (0.00078)	…
CL (L/d)	0.130 (0.002)	…	0.131a	…
Covariates
Vc ∼ weight	0.811 (0.035)	<10−10	0.817 (0.031)	<10−10
Vc ∼ albumin	−0.550 (0.096)	10−8	−0.653 (0.072)	<10−10
CL ∼ weight	0.806 (0.074)	<10−10	…	…
CL ∼ albumin	−0.800 (0.110)	<10−10	…	…
CL ∼ BMI	0.372 (0.086)	1.5  × 10−5	…	…
CL ∼ EASI	0.140 (0.021)	<10−10	…	…
CL ∼ race (white)	−0.118 (0.018)	<10−10	…	…
ke ∼ BMI	…	…	0.368 (0.053)	<10−10
ke ∼ EASI	…	…	0.143 (0.021)	<10−10
ke ∼ race (white)	…	…	−0.123 (0.018)	<10−10
Information criteria
Bayesian information criteria	70 699.71		70 688.53

BMI, body mass index; CL, clearance; EASI, Eczema Area and Severity Index; k_e, elimination rate; SE, standard error; V_c, central volume of distribution.

^aThese parameters were derived using estimated population pharmacokinetic parameters.

Table 2.

Population PK Parameters and Bootstrap Confidence Intervals for Covariate Coefficients (Model 2)

Covariate Name	Population Estimate of Covariate Coefficient	Bootstrap Median (90%CI)	Bootstrap Median (95%CI)	Bootstrap Median (99%CI)
Vm ∼ population	0.967	0.972 (0.915, 1.02)	0.972 (0.896, 1.03)	0.972 (0.876, 1.05)
Vc ∼ assay	0.964	0.960 (0.935, 0.990)	0.960 (0.931, 0.995)	0.960 (0.919, 1.01)

CI, confidence interval; PK, pharmacokinetics; V_c, central volume; V_m, maximum target‐mediated rate of elimination.

Healthy volunteers were coded as 0 and AD patients as 1. The early and later versions of the functional dupilumab assay were coded as 0 and 1, respectively.

The number of fixed PK parameters changed from 1 in Model 1 to 5 in Model 2 (Table 1), and to 7 in Models 3 and 4 (Table 1). Model 1 was based on data from 4 phase 1 and 2 trials: 3 trials with rich data and 1 trial with sparse data (sparse data were added to provide additional information about the beta phase). Model 2 was based on 12 trials from phase 1 through phase 2b. Models 3 and 4 were based on data from phase 3 studies only. Estimated PK parameters in all models were similar. The structure of all models was the same. Beta half‐life, calculated using parameters of the covariate model, was 25.4 days. The linear CL was calculated as V₂ × k_e.

The transit compartments and removal of some sparse data differentiate Model 1 from an earlier published model.13 As removal of transit compartments from the model led to biased estimates of k_cp and k_pc upon comparison with estimates based on IV data alone and with the biased estimate of k_a, the transit compartment model was needed to account for lag time and ensure that these parameters have biologically informative values. The number of transit compartments was changed from 0 to 9. Based on the OFV, 3 transit compartments were selected; fewer compartments led to a large, statistically significant increase in OFV, and there was no meaningful advantage in using additional compartments.

Values for K_m and σ_add in Model 1 were fixed as described elsewhere.13 Estimates of shrinkage in the SD of random effects (etas or η) for V_c, k_e, V_m, k_a, and MTT, were 10.4%, 25.2%, 22.9%, 23.2%, and 54.9% respectively, demonstrating that the data were informative in relation not only to population but also to individual parameters.

In Model 2, we fixed k_cp, k_pc, F, and MTT in addition to K_m. BLQ values were excluded from the analysis to reduce variability in the OFV, which increased due to the addition of sparse AD data; this was permissible, as parameters that can be affected by such exclusion were fixed, and the exclusion had no meaningful impact on the remaining parameters.

First, it was found in Model 2 that the addition of large data sets with sparse samples increased variability in the OFV, even when BLQ values were removed. Based on 20 Monolix model runs of Model 2 using the “convergence assessment” tool, the difference between the highest and lowest OFV values was 14.9, which was unsuitable for the calculation of P values. Keeping the BLQ values in the analysis exacerbated the OFV variability. Nevertheless, the model demonstrated very stable convergence of population PK parameters to the same values. Second, it was found that the parameters estimated in the model (including V_m) were similar to those estimated using mostly rich data. Third, the bootstrap CIs decreased, indicating more precise estimates. Overall, Model 2 replicated the estimates obtained with Model 1 and demonstrated excellent stability. Thus, it appeared proper to apply Model 2 to test covariates using bootstrapping CIs and/or standard errors of covariate coefficients (Wald test).

The data in Model 2 included 2 populations (patients with AD and healthy volunteers) and were based on 2 cross‐validated versions of the dupilumab functional assay. As combining rich data and phase 3 sparse data led to a large variability in OFV and in V_m, and phase 3 data alone included only AD population and data generated from one assay, Model 2 was used to test these 2 covariates. The results of the tests based on 200 bootstraps, which were indifferent to the variability in the OFV when a model is stable, are presented in Table 2. In this table, CIs are presented at significance levels of 0.1, 0.05, and 0.01. The median bootstrap estimates were very similar to the population estimates. Since the prespecified P value for inclusion was 0.01, neither population nor assay entered the model as a covariate. Healthy volunteers had slightly higher V_m; the difference was not statistically significant. For both covariates, the differences between the subgroups were very small (0.967‐fold and 0.964‐fold changes for population and assay, respectively). This was consistent with the results of cross validation of the dupilumab functional assays and with early clinical findings, in which a model based only on the first‐in‐human study in healthy volunteers accurately predicted dupilumab concentrations in studies of patients with AD.13 The remaining covariates were evaluated using covariate Model 4 applied to phase 3 data only.

Base Model 3 was developed to address the PK of dupilumab only in patients in the phase 3 trials. The following parameters were fixed: k_cp, k_pc, k_a, MTT, V_m, K_m, and F (Table 3). Fixing these parameters ensured the stability of the model and a low variability in OFV and, therefore, allowed for conventional likelihood ratio tests of covariates based on comparison of OFVs. Interindividual variability was implemented in V_c and k_e. The results of Wald and log‐likelihood tests were consistent.

The primary base model (Model 3) demonstrated excellent stability. Shrinkage in SD of etas for k_e and V_c was 22% and 19%, respectively.

Covariate Model 4 was developed to explain sources of variability in the PK of dupilumab only in patients from the phase 3 studies. While ADA, albumin, race, BMI, and EASI score were statistically significant covariates, only weight had a notable effect on the V_c, explaining interindividual variability. Diagnostic plots for Model 4 are provided in Figures 2 and 3 and show a good model fit.

Figure 2.

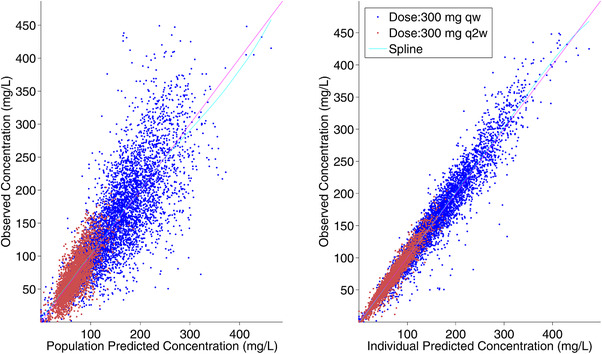
Observed vs predicted dupilumab concentrations for primary covariate model (Model 4). Unit line and spline are provided in the figure. qw, weekly; q2w, every 2 weeks.

Figure 3.

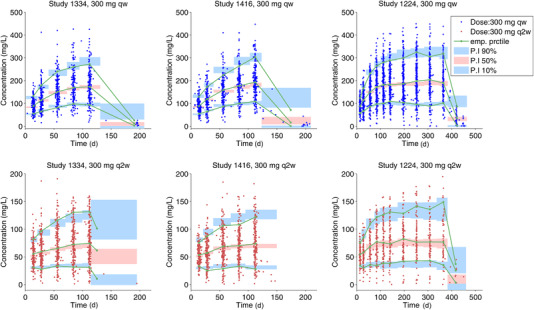
Visual predictive check of dupilumab concentrations by study and treatment regimen—primary covariate model (Model 4). PI, predicted interval; qw, weekly; q2w, every 2 weeks.

A sensitivity analysis in which linear CL instead of k_e is a response variable is presented in Table 3. The fixed PK parameters are the same as in the base and covariate models (Table 1) and are excluded from this table. In this analysis, weight and albumin are significant covariates of not only V_c but also CL, presumably because CL = k_e  × V_c. This analysis confirms the robustness of results obtained with the primary covariate model. Parameterization of the covariate model in terms of rates required fewer covariates (Tables 3 and S4) and yielded higher Bayesian information criteria (BIC). BIC is a criterion for model selection in which the model with the lowest BIC is preferred.

In Figure 4, linear, nonlinear, and total clearance are presented vs concentration of functional dupilumab. An example of simulation‐based predictions of treatment with following maintenance therapies is presented in Figure 5.

Figure 4.

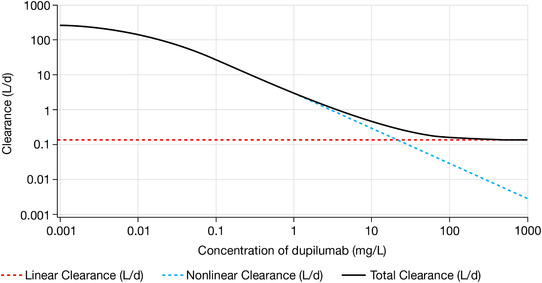
Plot of the dependence of clearance on serum dupilumab concentrations.

Figure 5.

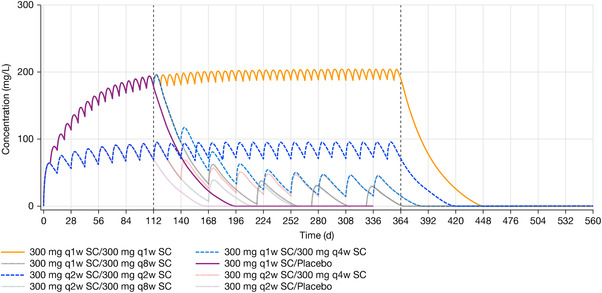
Median of simulated concentration of functional dupilumab over time by treatment. SC, subcutaneous; q1w, every week; q2w, every 2 weeks; q4w, every 4 weeks; q8w, every 8 weeks.

Discussion

The provided population PK analysis results were used for exposure‐response analysis and subsequently for regulatory submissions and responses. The model was also used to simulate exposure (area under the plasma concentration–time curve, maximum concentration, and trough concentration) after the first dose and at steady state for regulatory responses. The simulated exposure metrics were further used as benchmarks to select pediatric doses and ensure that pediatric exposure did not exceed that in adults.

The BLQ values used in the analysis of phase 1 and 2 data provided essential information about the target‐mediated phase, allowing for proper estimation of the nonlinear elimination rate of dupilumab (V_m) and the concentration of dupilumab (K_m) half that enables the achievement of V_m. The stepwise approach to covariate model building, with some parameters fixed, was useful to account for the steep target‐mediated phase and avoid an adverse effect of sparse data on PK parameters, which require rich sampling for proper estimation. The reasons PK parameters rely on a small and rich portion of the data to become unstable when the ratio of subjects with rich data to subjects with sparse data is very small are (1) the global minimum in the OFV becomes less pronounced in relation to parameters that rely on a small rich subsample; and (2) variability in the OFV increases in the presence of a singularity introduced by the steep target‐mediated clearance, making it difficult or impossible to find the global minimum for such parameters, while stability of the parameters that can be estimated using large sparse data is unaffected by this variability in the OFV.

It appears that the high variability of OFV can be misinterpreted as instability in a model such as Model 2. While instability of a model can lead to high variability in the OFV, this variability does not necessarily indicate instability. When an OFV has low or no sensitivity to a PK parameter it leads to a high standard error of the estimate or to instability of the model, respectively. When the opposite happens (ie, an OFV is hypersensitive to a PK parameter), a steep target‐mediated phase can lead to increased variability in the OFV, even when the model is stable. The stability of Model 2 with high variability in OFV was tested and confirmed.

Due to substantially nonlinear kinetics, beta half‐life and linear clearance cannot be used to predict time to a concentration of interest. Predictions based on modeling should be used. As half‐life substantially changes over time during the terminal target‐mediated phase of elimination, no meaningful terminal half‐life can be calculated, and no such half‐life was provided to regulatory agencies. A plot of population‐predicted instantaneous half‐life vs time is presented in Figure S1, demonstrating the extent to which half‐life changes over time and eventually decreases to zero.

The impact of ADAs on k_e was small and not clinically significant; this was consistent with an observation of low frequency of ADAs and that ADAs are mostly transient. A typical scenario was when ADAs were observed at week 4 and then disappeared (data not shown). As ADAs cannot be directly compared across different products due to different procedures, chemicals, equipment, and assays, the impact of ADAs is not presented.

When associations between both weight and BMI with both V_c and k_e were tested, only the associations between weight and V_c and between BMI and k_e remained significant. It was hypothesized that the association of BMI and k_e may reflect an impact of obesity and/or body composition on the catabolic rate of mAbs, but this hypothesis requires additional exploration.

While only accounting for the impact of weight on V_c had a notable effect explaining interindividual variability in the data, this association did not warrant a dose adjustment because the therapeutic index of dupilumab is wide7, 10, 11 and variability in weight only partially explains variability in the data.

The parameters of the model specified using CL instead of k_e were very similar to those of the primary covariate model (Table 3); values of covariate parameters, that reflect an association between linear CL and covariates, were similar to those that reflect an association between k_e and corresponding covariates. The impact of weight on CL was essentially the same as the impact of weight on V_c. Nevertheless, when CL was used in the model instead of k_e, the number of covariates increased from 6 to 8, and BIC worsened from 70 688.53 to 70 699.71. For example, both weight and BMI were covariates of CL, as CL is a product of V_c and k_e. BIC (which is a preferable criterion for model selection under some broad conditions31) suggests superiority of the parameterization in terms of rates for covariate exploration. If the model is further reparameterized in terms of intercompartmental clearance (Q) and peripheral volume (V_p) instead of k_cp and k_pc, covariates affecting V_c may also be associated with Q and V_p. Therefore, the number of covariates may further increase, which can complicate interpretation and adversely affect the convergence, stability, and BIC of the model. Parameterization of the model in terms of rates allowed to obtain “clean” covariate analysis results with all Wald P values for included covariates being below 10^–10 (Table 3). Thus, the parameterization of covariate model, in terms of rates, can potentially be a useful alternative to the parameterization in terms of clearances and V_p, as it reduces the number of covariates and may allow for a more mechanistic interpretation of the covariate impact.

The developed Models 1, 2, and 3 can be used to predict concentrations of dupilumab for new doses and dosing regimens, design new studies, and extrapolate the impact of weight in different patient populations; it appeared that these models provide very similar predictions. Model 1 was used to estimate PK parameters that require rich data. Model 2 was used for population PK/PD modeling, with BLQ values added to the analysis. Base Model 3 was a step toward developing covariate Model 4. Finally, Model 4 was “fit for purpose” to estimate the impact of covariates.

Maximal total clearance was substantially higher than linear clearance, which explains the steep target‐mediated phase (Figure 4).

The simulation example in Figure 5 shows the median of simulated concentrations. The median in this figure was close to population predictions, but deviated from the means at low concentrations. For example, it takes approximately 3 months longer to approach the mean than the median LLOQ level in the 300 mg every week treatment group; when median concentration approaches the LLOQ, mean concentration is still approximately 10 mg/L. However, as dupilumab was well tolerated, such differences may not be critical.

Conclusions

A 2‐compartment PK model implementing parallel linear and Michaelis‐Menten elimination and a transit compartment model of absorption lag time adequately described the PK of dupilumab in phase 3 clinical trials. The BLQ values used in the analysis of phase 1 and 2 data provided essential information for proper characterization of the target‐mediated phase in phase 3 clinical trials. While ADAs, albumin, race, BMI, and EASI score were statistically significant covariates, only body weight had a notable effect on V_c, explaining interindividual variability. The impact of weight on V_c did not warrant a dose adjustment because the therapeutic index of dupilumab is wide,7, 10, 11 and variability in weight only partially explains variability in the data. A stepwise approach to model building with some parameters estimated using mostly rich data and subsequently fixed was used to account for a steep target‐mediated phase and avoid an adverse effect of large sparse data sets on PK parameters, which require rich sampling for proper estimation. Finally, the parameterization of models in terms of rates can potentially be a useful alternative to the parameterization in terms of clearances, allowing for a reduced number of covariates and more mechanistic interpretation of a covariate impact.

Conflicts of Interest

P.K., J.D.D., M.A., B.S., N.M.H.G., M.A.K., and A.T.D. are employees and shareholders of Regeneron Pharmaceuticals, Inc. R.R. was an employee and shareholder of Regeneron Pharmaceuticals, Inc. at the time of study conduct. G.P. and M.L. were employees of Sanofi at the time of study conduct and held stock and/or stock options in the company.

Funding

Research was sponsored by Sanofi and Regeneron Pharmaceuticals, Inc.

Author Contributions

P.K. wrote the first draft of the manuscript. P.K., J.D.D., M.A., B.S., N.M.H.G., G.P., and A.T.D. designed the research; P.K., M.L., R.R., M.A., and M.A.K. performed the research; P.K. analyzed the data. All authors reviewed and approved the final version of the manuscript.

Supporting information

Table S1. Summary of Dosing and PK Sampling Study Design^a

Table S2. Population PK Parameters and Bootstrap Confidence Intervals for Initial Models Based on Rich and Sparse Data (Models 1 and 2)

Table S3. Population PK Parameters and Bootstrap Confidence Intervals for Primary Base and Primary Covariate Models Based on Phase 3 Data

Table S4. Parameterizations of Covariate Model Using Clearance

Figure S1. Population‐predicted instantaneous half‐life and concentration of functional dupilumab vs time after single IV dose of 24 mg/kg. A large hypothetical dose of 24 mg/kg was simulated to achieve maximal half‐life close to the beta half‐life.