Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Aug 5;20(9):6372–6380. doi: 10.1021/acs.nanolett.0c01955

Large Damping-Like Spin–Orbit Torque in a 2D Conductive 1T-TaS2 Monolayer

Sajid Husain †, Xin Chen ‡, Rahul Gupta †, Nilamani Behera †, Prabhat Kumar , Tomas Edvinsson †, F García-Sánchez §, Rimantas Brucas †, Sujeet Chaudhary ○, Biplab Sanyal ‡, Peter Svedlindh †,*, Ankit Kumar †,*
PMCID: PMC7496736  PMID: 32786947

Abstract

graphic file with name nl0c01955_0006.jpg

A damping-like spin-orbit torque (SOT) is a prerequisite for ultralow-power spin logic devices. Here, we report on the damping-like SOT in just one monolayer of the conducting transition-metal dichalcogenide (TMD) TaS2 interfaced with a NiFe (Py) ferromagnetic layer. The charge-spin conversion efficiency is found to be 0.25 ± 0.03 in TaS2(0.88)/Py(7), and the spin Hall conductivity 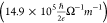Inline graphic is found to be superior to values reported for other TMDs. We also observed sizable field-like torque in this heterostructure. The origin of this large damping-like SOT can be found in the interfacial properties of the TaS2/Py heterostructure, and the experimental findings are complemented by the results from density functional theory calculations. It is envisioned that the interplay between interfacial spin–orbit coupling and crystal symmetry yielding large damping-like SOT. The dominance of damping-like torque demonstrated in our study provides a promising path for designing the next-generation conducting TMD-based low-powered quantum memory devices.

Keywords: Transition-metal dichalcogenide, Damping-like torque, Spin-torque ferromagnetic resonance, Planar Hall effect

Spin–orbit torques (SOTs) induced by spin currents are prerequisite to controlling the magnetization (m) in next-generation nonvolatile three-terminal memory devices,1−3 spin-torque nano-oscillators for microwave-assisted switching and neuromorphic computing.4 SOT-based magnetic memories are considered to be more reliable by utilizing low energy induced switching of the magnetization in contrast to the low endurance and low speed of two-terminal spin-transfer torque (STT)-based random access memories. A spin current with spin polarization vector σ generated by the spin Hall effect (SHE) and/or the Rashba–Edelstein effect (REE) in the presence of high spin–orbit coupling (SOC) in a material may give rise to two types of SOTs, damping-like (τDL = m × (m × σ)) and field-like (τFL = m × σ) torques, and have been reported for a number of heavy metals (HMs).3,5−8 In contrast to STT devices where the spin polarization of the charge current passing through the free layer enforce the switching of the magnetization, the physical origin of SOTs is the transfer of spin and orbital angular momenta through exchange interaction process,8 the latter via contributions mainly from different d orbitals.9 The SOT in HMs is reported to be a bulk-like phenomenon, which requires the thickness of the HM layer to be larger than its spin diffusion length in order to produce appreciable torque.10 However, it is difficult to control the crystallinity of the HM in the low thickness regime. Recently, very large SOT has been reported in topological insulators (TIs),11,12 but the topological surface states are quenched if the TI is deposited next to a metallic ferromagnet and hence a ferromagnetic insulator is required to render high SOTs,13 which implies industrial compatibility issues.14

To overcome the bulk-like effect in HMs, with perceived industrial compatibility, two-dimensional transition-metal dichalcogenides (2D-TMDs) were proposed a few years ago for spintronic applications.15−18 By replacing the HMs with TMDs, one can anticipate two positive outcomes for spin devices. First, a pure spin current can be produced by just a monolayer thick TMD without any bulk-like effect. Second, being a layered material, it is possible to realize smooth surfaces with atomic-scale flatness, i.e., in the Ångström scale. Although there are few reports on the observation of SOTs in TMDs,18,19 they are, however, encountered with the problem of a dominating field-like torque due to their semiconducting nature.16,12 The SOC in TMDs/FM at the interface can also give Dzyaloshinkii–Moriya interaction (DMI),20 which can generate chiral structures such as skyrmions. The surface quality of TMD exfoliated films grown by chemical vapor deposition is also compromised due to high roughness and strain.21,22 TMD films produced in this way exhibit inhomogeneity and are thus not suitable for spintronic device applications. Thus, we are forced to face two challenges to realize the requirement of dominating damping-like torques in TMDs. One is to grow large-area TMDs directly on SiO2 substrates and concomitantly to provide large damping-like torques by using conducting TMD/ferromagnet bilayers. Keeping in mind the growth problem of conducting TMDs, the 1T-tantalum-disulfide (TaS2) system is yet to be explored, which can be easily fabricated by the sputtering technique along with the distinctive plasma sulphurization process. The prefix 1T in 1T-TaS2 refers to 1 layer per trigonal (T) unit cell. Being conducting with high SOC,23 the 1T-TaS2 system also possesses exotic temperature-dependent properties, owing to several charge density wave (CDW) transitions,24 thus contributing with the rich physics of CDWs to the field of SOTs. Previously, researchers have reported the growth of TaS2 by various methods,24−26 which is yet to be explored for spin–orbitronics.

Here, we report a dominating damping-like torque in conducting TaS2/Py bilayer heterostructures. The high-quality large-area TaS2 monolayers have been prepared by ion-beam sputtering combined with plasma-assisted sulfurization (see methods and materials for details in Supporting Information S1). The SOTs were measured by using spin-torque ferromagnetic resonance (ST-FMR) and angle-dependent planar Hall effect (PHE) measurements. First-principles calculations based on density functional theory envisage the possible source of the damping-like torque in the TaS2/Py heterostructures. Micromagnetic simulations corroborate the experimental results.

Results

Monolayer Characteristics

Figure 1 shows the transmission electron microscopy (TEM) cross-sectional image of the TaS2(1 ML)/Py(7)/Al(3) heterostructure. The thickness of the individual layers is found to be similar to the nominal ones. Notably, the thickness of the TaS2 layer is found to be equivalent to one monolayer, which is around ∼0.88 nm. In the left inset, the large-scale TEM image shows a uniform film and sharp interface of TaS2 in contact with the Py layer. Elemental mapping of the stack (inset) also supports the uniform growth of all layers in the stack (see Supporting Information, S14). It also confirms that our ferromagnet layer shows less affinity to sulfur because metals having a large affinity to sulfur can degrade the 2D characteristics of TMDs.27Figure 1b shows the room-temperature Raman spectra recorded on a single-layer TaS2 film using two different lasers. Strong fundamental peaks are observed at 305 and 231 cm–1, corresponding to the 1T-TaS2 phase.28 The uniformity of the film can be seen in the Raman mapping as recorded around the most intense Raman peak (shown in the inset). Elemental analysis has been performed by X-ray photoelectron spectroscopy (XPS) as presented in Figure 1c,d for Ta and S, respectively. Observed peaks are deconvoluted into the two spin–orbit split peaks, which confirms the TaS2 formation without residual phases.29,30 We also observed a finite shift around 1.5 ± 0.9 eV for the Ta(4f7/2) orbital peak position in TaS2 in comparison to the metal Ta,31 which indicates a large spin-orbit splitting in TaS2. Further, surface topography and step height scans were also recorded using atomic force microscopy and confirm the monolayer thickness and the smooth interface with Ångström scale flatness of the TaS2 layer (see Supporting Information, S4).

Figure 1.

Figure 1

Open in a new tab

(a) High-resolution cross-sectional TEM image of the TaS2(0.88)/Py(7)/Al(3) heterostructure. Insets: (left) low-magnification cross-sectional image; (right) elemental EDX mapping of the trilayer sample. (b) Raman spectra recorded using two lasers (532 and 785 nm) and mapping (10 × 10 μm2) in an inset on single-layer TaS2 using a 785 nm laser. (c, d) XPS spectra of Ta and S recorded on a single-layer TaS2 sample.

ST-FMR Measurements

The magnitude of the SOT efficiency governed by the spin-torque efficiency (θS) was measured using ST-FMR. The applied field makes an angle of 45° with respect to the current as shown in Figure 2a (scanning electron microscopic (SEM) image of the device). An SEM image with the measurement circuit is shown in Figure 2b. A schematic of the torques acting on the magnetization due to the microwave current IRF is shown in Figure 2c. The ST-FMR measurements were performed in a field-sweep mode in the frequency range of 5–16 GHz. We have used a lock-in detection technique with an IRF current frequency modulation of 1000 Hz at 9 dB microwave power (see Supporting Information, S7).

Figure 2.

Figure 2

Open in a new tab

(a) Scanning electron microscopic (SEM) image of the TaS2(0.88)/Py(7) device. (b) High-magnification SEM image (area indicated by a square in panel a showing the ST-FMR measurement circuit). (c) Layer schematic shown with torques acting on the magnetization. (d) ST-FMR spectra recorded at various frequencies in the range of 5–16 GHz. Inset, ST-FMR spectra at 12 GHz recorded in opposite magnetic field directions. (e) ST-FMR spectrum (recorded at 15 GHz) fitted separately with symmetric and antisymmetric Lorentzian unctions. (f, g) Line width and resonance field versus frequency plots, respectively.

The rf current generates an Oersted field as well as spin–orbit torques in the presence of the magnetic field and acts as torques on the magnetization. The IRF-induced torque acting on the Py layer generates a sustained precession of the magnetization, which mixes with the anisotropic magnetoresistance and spin Hall magnetoresistance creating a dc-mixing voltage Vmix. This rectified mixing voltage provides the information on the material parameters and torques acting on the magnetization, which is written as32Vmix = V0(Sfs + Afa). Here, V0 is the amplitude of the mixing voltage, and fs and fa are symmetric and antisymmetric Lorentzian functions, respectively. S = ℏJrf/2eμ0MStPy and 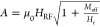Inline graphic are symmetric and antisymmetric weight factors, respectively, where μ0, e, tPy, Jrf, MS, HRF, Hr, and Meff are the magnetic permeability in free space, electronic charge, thickness of ferromagnet layer, rf-current density, saturation magnetization, microwave field, resonance field, and effective magnetization, respectively.

Figure 2d shows the ST-FMR spectra together with fits using the equation for Vmix, which give the line-shape parameters. The ST-FMR spectra for positive and negative magnetic field scans are shown in the inset (at 12 GHz). It is to be noted that the peak changes its sign on changing the direction of the external magnetic field, indicating a damping-like torque τDL and ruling out the possibility of a dominating Oersted field generated torque (τFL). The symmetric and antisymmetric amplitudes have been separately fitted to the spectra; an example for the spectrum recorded at 15 GHz is shown in Figure 2e. The effective damping (αeff) of the TaS2(0.88)/Py(7) bilayer is evaluated by fitting the μ0ΔH versus f data (as shown in Figure 2f) using the equation, μ0ΔH = μ0ΔH0 + 2αeffω/γ, where μ0ΔH0 is the line width contribution from inhomogeneity in the magnetic film, ω (=2πf) is the microwave frequency, and γ/2π (28.8 GHz/T) is the magnetogyric ratio. From the fitting, the values of effective damping are found to be 0.0067 ± 0.0007. The inhomogeneous line width is found to be 0.20 ± 0.02 mT, which is quite small and indicative of a smooth and clean interface of the Py/TaS2 heterostructure. Further, μ0Meff and the anisotropy field (μ0HK) values have been calculated by fitting the f versus μ0Hr data to the Kittel equation, f = μ0γ/2π[(Hr + HK)(Hr + HK + Meff)]1/2, yielding 0.902 ± 0.004 T and 1.8 ± 0.4 mT, respectively. The values of μ0Ms of TaS2(0.88)/Py(7) are measured using a QD-MPMS setup and found to be 1.00 ± 0.02 T (see Supporting Information, S5), which is consistent with the μ0Meff value extracted from the ST-FMR results considering the out-of-plane anisotropy field contribution to the effective magnetization.

From the line-shape parameters, the value of the spin-torque efficiency θS is evaluated using the standard line-shape analysis method33 and found to be 0.023 ± 0.01. However, in this method, it is assumed that the symmetric component is purely from a damping-like torque, disregarding a possible contribution from spin pumping due to the inverse spin Hall effect (ISHE) and can, therefore, yield erroneous values for the SOT efficiency.34−36 Concomitantly, the antisymmetric component is considered as an Oersted field generated torque component, but it is again a naive approximation.35 Moreover, the line-shape analysis also shows a frequency dependency,33 which may lead to the wrong estimation of the effective spin-torque efficiency. Hence, to determine a reliable value of the effective spin-torque efficiency and evidence of damping-like torque, we use the so-called damping modulation scheme by applying a dc during the ST-FMR measurement, where spin pumping due to the ISHE and field-like contributions are insignificant.

Current Induced Modulation/Changes of Effective Damping in the TaS2(0.88)/Py(7) Device

In this method, the dc-induced nonequilibrium spin accumulation at the interface, resulting due to the SHE in TaS2, acts as a torque on the Py magnetization, resulting in a change of the effective damping as described by33,35

graphic file with name nl0c01955_m003.jpg

The effective spin-torque efficiency using the dc-induced change of the damping is defined as the ratio of spin to charge current density: 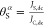Inline graphic. Here, 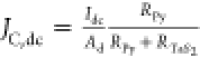Inline graphic, where RPy, RTaS2, and Ad are the resistances of permalloy and TaS2, respectively, and the cross-sectional area of the device. φ is the angle between the magnetization and the applied field, which is 45° in our case. Figure 3a shows the change/modulation of effective damping as a function of the dc (Idc). For comparison, the δαeff values are plotted for the two directions of the magnetic field scan. The corresponding changes of μ0ΔH with dc, i.e., δμ0ΔH, are shown in Figure 3b. The slopes of the δαeff versus Idc curves for the two field directions are almost equal, which confirm that the damping-like torque acting on the magnetization in our TaS2/Py bilayer is due to the SHE generated spin current. The damping values are reversed on current polarity reversal. This reversal is also observed when reversing the magnetic field direction. Therefore, the spin Seebeck and anomalous Nernst effect induced modulation of the damping can be ruled out in our measurements. The slope of the change in αeff with dc (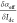Inline graphic) is 2.17 ± 0.21 × 10–4/mA and 1.95 ± 0.17 × 10–4/mA for positive and negative applied fields, respectively. Using the measured resistances of Py (225 Ω) TaS2 (952 Ω) (see Supporting Information, S8) in the equation for JC,dc, the θSα value is found to be 0.25 ± 0.03. Within the experimental uncertainty, the values of the spin-torque efficiency are the same for both positive and negative field scans. The obtained value is better than the values reported for other TMDs.37,20,38 The intercept with the current axis is known as the critical current density for auto-oscillations and estimated to be 5.13 × 1010 A/m.2 ST-FMR measurements were also performed on a controlled Ta(0.9)/Py(7) device, which shows a weak signal-to-noise ratio (see Figure S11). We further measured the efficiency of various Py thicknesses with a fixed TaS2 layer (see Supporting Information, S10b). The spin Hall conductivity (SHC) (σS = σdc × θS) is found to be 14.9 × 105Inline graphic (Ω–m)−1, using σdc = 5.9 × 106 (Ω–m)−1 of TaS2 and θSα = 0.25. The SHC value is ∼10 times smaller than the value reported for the TI Bi0.9Sb0.1/MnGa,12 100 times larger than for the field-like torque-dominated semiconducting TMDs MoSe2 and WS2,19 conducting TMD NbSe217 and comparable to that of the Pd1–xPtx alloy.39 TIs suffer from issues related to industrial compatibility,14 while HMs and alloys have limitations with respect to the spin diffusion length due to the spin relaxation being controlled by the Elliot–Yafet40 and D’yakonov–Perel’41 scattering mechanisms. The conducting TMD 1T-TaS2 investigated in this work is an industrial compatible material and is easy to fabricate for SOT devices and therefore avoid such limitations. Moreover, 1T-TaS2 provides rich physics due to its inherent property of CDW fluctuations, where electrons collectively may carry a charge current in a highly correlated fashion.

Figure 3.

Figure 3

Open in a new tab

(a) dc-induced changes of effective damping in the TaS2(0.88)/Py(7) bilayer for positive and negative field directions. (b) dc-induced line width changes for positive and negative magnetic fields. (c) Line width versus frequency. (d) ST-FMR spectra recorded at 10 GHz and (e) frequency versus resonance field measured at +0.8 mA and −0.8 mA dc applied to the device in a positive magnetic field.

The dc-induced changes of the effective damping can also be seen in the μ0ΔH versus f results shown in Figure 3c for positive and negative direct currents. The current distribution in the heterostructure was evaluated, and it was found that 19% of the current is flowing through the TaS2(0.88) layer (see Supporting Information, S8). Consequently, the Oersted field μ0HOe in the TaS2(0.88) layer is found to be ∼0.012 mT/mA, which is very small, and it is, therefore, concluded that the field-like torque contribution generated by dc passing through the TaS2 layer can be neglected. The ST-FMR spectra and resonance field plots shown for two currents in Figure 3d,e, respectively, show no change during a current polarity reversal, which is indicative of negligible field-like torque contributions. However, a small field-like torque contribution can arise from the unavoidable interface symmetry breaking,42,43 which is discussed in Supporting Information, S10a.

We validate the dc-induced damping-like torque in the TaS2(0.88)/Py(7) device by means of magnetization in the in-plane field scan in two opposite current directions, which yield the opposite hysteresis formation, discussed in Supporting Information, S12. The magnetization switching indicates the presence of dominating damping-like torque in TaS2(0.88)/Py(7). The Hall voltage hysteresis was also recorded using a Hall bar structure as is shown in Supporting Information, S11d. Further, using micromagnetic simulations, the switching of the in-plane magnetization for different current amplitudes has also been studied (see Supporting Information, Figure S13).

Angle-Dependent Planar Hall Effect (PHE) for SOTs

Planar Hall effect (PHE) measurements have received much attention for characterizing the SOTs in the in-plane magnetized systems.44−46Figure 4a shows a scanning electron microscope (SEM) image of the Hall device used for PHE measurements. A schematic of the measurement circuit has been added to the image. In the planar Hall measurement, the sample is rotated 360° at fixed dc. The vector representation of the PHE is shown in Figure 4b, where φ is the angle between the current direction and the applied field, and θ is the angle between the current direction and the magnetization vector. The theoretical background of the PHE is discussed in Supporting Information, S11a. Figure 4c shows the PHE signal (RH) versus φ recorded for two direct currents of the same magnitude but of opposite polarity. A magnetic field of 0.4 T was used for the measurements, which was enough for suppressing the field-like torque contribution. The PHE measured at different magnetic fields and currents are discussed in the Supporting Information, S11a. The difference between the curves (RDH) is plotted as a function of φ in Figure 4d, which embraces the dominance of the damping-like torque. The RDH versus φ curve was fitted using eq S12 with HFL and HSO as fitting parameters. The HSO field determines the amount of damping-like torque acting on the ferromagnetic layer. The value is found to be 1 Oe per 1010 A/m,2 from which the spin-torque efficiency (ζS) has been obtained by using the expression, 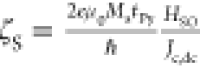Inline graphic. The field-like contribution HFL has been found to be negligibly small. The dc density Jc can be calculated by considering the dimensions of the device and the conductivity values at a dc value of 4.5 mA, yielding a dc density of 5 × 1010 A/m.2 Using the thickness and saturation magnetization, ζS is found to be 0.19 ± 0.01, which is comparable to the value obtained using the ST-FMR analysis. We have also measured the Py thickness-dependent efficiency (see Supporting Information, S11b). For comparison, we have measured the angle-dependent PHE on the Ta(0.9)/Py(7) reference sample, which shows a very weak signal-to-noise ratio (see Supporting Information, S11c). Therefore, it is confirmed without a doubt that a monolayer of 1T-TaS2 produces a damping-like torque acting on the Py magnetization.

Figure 4.

Figure 4

Open in a new tab

(a) SEM image of the TaS2(0.88)/Py(7) Hall bar (100 × 20 μm2) device together with a schematic of the circuit used for planar Hall effect measurements. The angle φ (θ) is the in-plane angle between the magnetic field (magnetization) and the current direction in the device. (b) Vector components of the applied field H, magnetization, and the fields generated by SOTs. (c) Planar Hall effect signal recorded for two directions of the dc (magnitude = 5 × 1010 A/m2) in the presence of an in-plane magnetic field of 0.4 T. (d) Plot of the Hall resistance difference observed for two current directions versus angle φ.

Discussion

It is to be pointed that the possibility of a finite field-like torque contribution is not ruled out (see Figure S10a) in this work, which is reasonable and cannot be disentangled in SOT-based systems.42,43,47 There has been no clear evaluation of the critical current density and spin-torque efficiency in previously reported results for TMD/FM heterostructures.17−19 The quantitative estimation of the SHC and auto-oscillations current density in our TaS2/Py hold valuable information for several spintronic applications. Evidently, the interface of our TaS2/Py bilayer, as confirmed by cross-sectional TEM and supported by parameters extracted from X-ray reflectivity measurements, is clean in contrast to other works using exfoliated sheets and nonuniform growth where extrinsic contributions from strain and defect-related issues17,48,38 reduce the charge-spin conversion efficiency. First-principles calculations based on the density functional theory (DFT) reveal the role of SOC for lifting the degeneracy in the band structure of TaS2/Py. Figure 5 shows the energy band structures without and with the inclusion of SOC for both pristine TaS2 and TaS2/Py systems. A detailed discussion of the structural and electronic properties is presented in Supporting Information, S2. For pristine TaS2, the effects of SOC are clearly observed at Γ and K points (see the expanded views). Specifically, at the Γ point, the degenerate dxz and dyz bands are split due to SOC. It should be noted that this degeneracy is already lifted by the lower symmetry present at the interface between TaS2 and Py due to the distorted atomic structures. On top of that, further splitting occurs due to the presence of SOC. Therefore, one can conclude that a sizable redistribution of band structure and hence the splitting of states due to the interface occurs, which becomes responsible for prominent damping-like torque. Moreover, a low-symmetry-induced out-of-plane unconventional torque,49 which mimics the out-of-plane Rashba-like or field like torque, can also be present in this heterostructure (see Supporting Information, S10a). To highlight the contribution from different d orbitals, we show in Figure 5d the orbital projected DOSs of Ta in pristine TaS2 and also for the TaS2/Py bilayer. Moreover, the projected DOSs of d orbitals of Fe and Ni in Py are shown to reveal features of hybridization. As our energy range of interest is in the vicinity of the Fermi level, we will consider the electronic states within that energy range. It is observed that in the pristine material, dxy, dz2, and dxz are the orbitals of interest. However, for the bilayer, the dz2 orbital for both spin channels is quite prominent at the Fermi level and its vicinity. Moreover, for the spin-down channel, hybridization between the dz2 orbitals of Ta and Ni is seen for the spin-down channel.

Figure 5.

Figure 5

Open in a new tab

(a) Unit cell and Brillouin zone of pristine TaS2. Both top and side views of the hexagonal unit cell are shown. (b) Band structure of pristine TaS2 with and without spin–orbit coupling (SOC) (middle panel), expanded view of a part of the band structure (encircled) at the Γ point without and with SOC (left panel) and the same but at the K point (right panel). (c) Top and side views of the unit cell of TaS2/Py illustrating the optimized geometry. In the lower panel, the BZ is shown. (d) (left) Projected densities of states (DOSs) for different d orbital symmetries of Ta for pristine TaS2 and (right) spin-polarized projected DOSs for the TaS2/Py system, where the d orbitals of Ta, Fe, and Ni are shown.

In conclusion, the damping-like spin-torque efficiency has been carefully investigated in the one monolayer of TaS2 using ST-FMR and PHE measurements. Employing effective damping modulation or changes with dc, the effective spin-torque efficiency is found to be 0.25 ± 0.03 in TaS2 (1 ML)/Py(7). Angle-dependent PHE measurements verify the spin-torque efficiency and clearly reveal the dominance of damping-like torque in our 1 ML TaS2/Py bilayers. Further, the microscopic origin of the observed dominance of damping-like torque has been substantiated by DFT calculations. The observation of a dominating damping-like torque in just one monolayer provides a path for how to use TaS2 in future spin–orbitronic devices.

Acknowledgments

The Swedish Research Council (VR) supports this work (2017-03799). Authors thank Seda Ullusoy for SEM imaging. We thank Cheuk-Wai Tai for providing cross-sectional TEM measurements. D. M. Polishchuk and V. Korenivski, Nanostructure Physics, Royal Institute of Technology, Stockholm, Sweden are gratefully acknowledged for providing the Ta/Py reference sample.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.0c01955.

  • Full growth and characterization details, density functional theory, crystal structure and thickness analysis, atomic force microscopy, magnetization measurements, angular dependent FMR for in-plane anisotropy measurement, power calibration for ST-FMR measurement, resistivity measurement and current distribution, RF-current measurement in TaS2(0.88)/Py(7) device, field-like contributions in TaS2(1 ML)/Py(tPy), Py thickness-dependent damping modulation using ST-FMR, current modulation in Ta(0.9)/Py(7), planar Hall effect (PHE) for spin-orbit torques, Py thickness-dependent SOT using PHE, comparison between Py, Ta/Py, and TaS2/Py, magnetization switching in the presence of in-plane field at constant dc, micromagnetic modeling, and elemental mapping using STEM (PDF)

The authors declare no competing financial interest.

Due to a production error, this paper was published on August 17, 2020, with the incorrect version of the Supporting Information. The corrected version was reposted on August 19, 2020.

Supplementary Material

nl0c01955_si_001.pdf (1.9MB, pdf)

References

  1. Emori S.; Bauer U.; Ahn S.-M.; Martinez E.; Beach G. S. D. Current-Driven Dynamics of Chiral Ferromagnetic Domain Walls. Nat. Mater. 2013, 12, 611–616. 10.1038/nmat3675. [DOI] [PubMed] [Google Scholar]
  2. Safeer C. K.; Jué E.; Lopez A.; Buda-Prejbeanu L.; Auffret S.; Pizzini S.; Boulle O.; Miron I. M.; Gaudin G. Spin-Orbit Torque Magnetization Switching Controlled by Geometry. Nat. Nanotechnol. 2016, 11 (2), 143–146. 10.1038/nnano.2015.252. [DOI] [PubMed] [Google Scholar]
  3. Garello K.; Miron I. M.; Avci C. O.; Freimuth F.; Mokrousov Y.; Blügel S.; Auffret S.; Boulle O.; Gaudin G.; Gambardella P. Symmetry and Magnitude of Spin-Orbit Torques in Ferromagnetic Heterostructures. Nat. Nanotechnol. 2013, 8 (8), 587–593. 10.1038/nnano.2013.145. [DOI] [PubMed] [Google Scholar]
  4. Chen T.; Dumas R. K.; Eklund A.; Muduli P. K.; Houshang A.; Awad A. A.; Dürrenfeld P.; Malm B. G.; Rusu A.; Akerman J. Spin-Torque and Spin-Hall Nano-Oscillators. Proc. IEEE 2016, 104 (10), 1919–1945. 10.1109/JPROC.2016.2554518. [DOI] [Google Scholar]
  5. Kim J.; Sinha J.; Hayashi M.; Yamanouchi M.; Fukami S.; Suzuki T.; Mitani S.; Ohno H. Layer Thickness Dependence of the Current-Induced Effective Field Vector in Ta|CoFeB|MgO. Nat. Mater. 2013, 12 (3), 240–245. 10.1038/nmat3522. [DOI] [PubMed] [Google Scholar]
  6. Zhang W.; Han W.; Jiang X.; Yang S.-H.; S. P. Parkin S. Role of Transparency of Platinum–Ferromagnet Interfaces in Determining the Intrinsic Magnitude of the Spin Hall Effect. Nat. Phys. 2015, 11 (6), 496–502. 10.1038/nphys3304. [DOI] [Google Scholar]
  7. Kurebayashi H.; Sinova J.; Fang D.; Irvine A. C.; Skinner T. D.; Wunderlich J.; Novák V.; Campion R. P.; Gallagher B. L.; Vehstedt E. K.; et al. An Antidamping Spin-Orbit Torque Originating from the Berry Curvature. Nat. Nanotechnol. 2014, 9 (3), 211–217. 10.1038/nnano.2014.15. [DOI] [PubMed] [Google Scholar]
  8. Manchon A.; Železný J.; Miron I. M.; Jungwirth T.; Sinova J.; Thiaville A.; Garello K.; Gambardella P. Current-Induced Spin-Orbit Torques in Ferromagnetic and Antiferromagnetic Systems. Rev. Mod. Phys. 2019, 91, 035004. 10.1103/RevModPhys.91.035004. [DOI] [Google Scholar]
  9. Mahfouzi F.; Mishra R.; Chang P. H.; Yang H.; Kioussis N. Microscopic Origin of Spin-Orbit Torque in Ferromagnetic Heterostructures: A First-Principles Approach. Phys. Rev. B: Condens. Matter Mater. Phys. 2020, 101 (6), 060405(R) 10.1103/PhysRevB.101.060405. [DOI] [Google Scholar]
  10. Berger A. J.; Edwards E. R. J.; Nembach H. T.; Karis O.; Weiler M.; Silva T. J. Determination of the Spin Hall Effect and the Spin Diffusion Length of Pt from Self-Consistent Fitting of Damping Enhancement and Inverse Spin-Orbit Torque Measurements. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 98 (2), 024402. 10.1103/PhysRevB.98.024402. [DOI] [Google Scholar]
  11. Mellnik A. R.; Lee J. S.; Richardella A.; Grab J. L.; Mintun P. J.; Fischer M. H.; Vaezi A.; Manchon A.; Kim E. A.; Samarth N.; et al. Spin-Transfer Torque Generated by a Topological Insulator. Nature 2014, 511 (7510), 449–451. 10.1038/nature13534. [DOI] [PubMed] [Google Scholar]
  12. Khang N. H. D.; Ueda Y.; Hai P. N. A Conductive Topological Insulator with Large Spin Hall Effect for Ultralow Power Spin–Orbit Torque Switching. Nat. Mater. 2018, 17 (9), 808–813. 10.1038/s41563-018-0137-y. [DOI] [PubMed] [Google Scholar]
  13. Li P.; Kally J.; Zhang S. S. L.; Pillsbury T.; Ding J.; Csaba G.; Ding J.; Jiang J. S.; Liu Y.; Sinclair R.; et al. Magnetization Switching Using Topological Surface States. Sci. Adv. 2019, 5 (8), eaaw3415 10.1126/sciadv.aaw3415. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Pai C. F. Switching by Topological Insulators. Nat. Mater. 2018, 17 (9), 755–757. 10.1038/s41563-018-0146-x. [DOI] [PubMed] [Google Scholar]
  15. Feng Y. P.; Shen L.; Yang M.; Wang A.; Zeng M.; Wu Q.; Chintalapati S.; Chang C. R. Prospects of Spintronics Based on 2D Materials. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2017, 7, e1313. 10.1002/wcms.1313. [DOI] [Google Scholar]
  16. Husain S.; Kumar A.; Kumar P.; Kumar A.; Barwal V.; Behera N.; Choudhary S.; Svedlindh P.; Chaudhary S. Spin Pumping in the Heusler Alloy C O2FeAl/Mo S2 Heterostructure: Ferromagnetic Resonance Experiment and Theory. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 98 (18), 180404(R) 10.1103/PhysRevB.98.180404. [DOI] [Google Scholar]
  17. Guimarães M. H. D.; Stiehl G. M.; MacNeill D.; Reynolds N. D.; Ralph D. C. Spin-Orbit Torques in NbSe2/Permalloy Bilayers. Nano Lett. 2018, 18 (2), 1311–1316. 10.1021/acs.nanolett.7b04993. [DOI] [PubMed] [Google Scholar]
  18. Lv W.; Jia Z.; Wang B.; Lu Y.; Luo X.; Zhang B.; Zeng Z.; Liu Z. Electric-Field Control of Spin-Orbit Torques in WS2/Permalloy Bilayers. ACS Appl. Mater. Interfaces 2018, 10 (3), 2843–2849. 10.1021/acsami.7b16919. [DOI] [PubMed] [Google Scholar]
  19. Shao Q.; Yu G.; Lan Y. W.; Shi Y.; Li M. Y.; Zheng C.; Zhu X.; Li L. J.; Amiri P. K.; Wang K. L. Strong Rashba-Edelstein Effect-Induced Spin-Orbit Torques in Monolayer Transition Metal Dichalcogenide/Ferromagnet Bilayers. Nano Lett. 2016, 16 (12), 7514–7520. 10.1021/acs.nanolett.6b03300. [DOI] [PubMed] [Google Scholar]
  20. Shi S.; Liang S.; Zhu Z.; Cai K.; Pollard S. D.; Wang Y.; Wang J.; Wang Q.; He P.; Yu J.; et al. All-Electric Magnetization Switching and Dzyaloshinskii–Moriya Interaction in WTe2/Ferromagnet Heterostructures. Nat. Nanotechnol. 2019, 14 (10), 945–949. 10.1038/s41565-019-0525-8. [DOI] [PubMed] [Google Scholar]
  21. You J.; Hossain M. D.; Luo Z. Synthesis of 2D Transition Metal Dichalcogenides by Chemical Vapor Deposition with Controlled Layer Number and Morphology. Nano Converg 2018, 5 (1), 26. 10.1186/s40580-018-0158-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Yun S. J.; Chae S. H.; Kim H.; Park J. C.; Park J. H.; Han G. H.; Lee J. S.; Kim S. M.; Oh H. M.; Seok J.; et al. Synthesis of Centimeter-Scale Monolayer Tungsten Disulfide Film on Gold Foils. ACS Nano 2015, 9 (5), 5510–5519. 10.1021/acsnano.5b01529. [DOI] [PubMed] [Google Scholar]
  23. Sanders C. E.; Dendzik M.; Ngankeu A. S.; Eich A.; Bruix A.; Bianchi M.; Miwa J. A.; Hammer B.; Khajetoorians A. A.; Hofmann P. Crystalline and Electronic Structure of Single-Layer TaS2. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 94 (8), 1–5. 10.1103/PhysRevB.94.081404. [DOI] [Google Scholar]
  24. Wang X.; Liu H.; Wu J.; Lin J.; He W.; Wang H.; Shi X.; Suenaga K.; Xie L. Chemical Growth of 1T-TaS 2 Monolayer and Thin Films: Robust Charge Density Wave Transitions and High Bolometric Responsivity. Adv. Mater. 2018, 30 (38), 1800074. 10.1002/adma.201800074. [DOI] [PubMed] [Google Scholar]
  25. Navarro-Moratalla E.; Island J. O.; Manãs-Valero S.; Pinilla-Cienfuegos E.; Castellanos-Gomez A.; Quereda J.; Rubio-Bollinger G.; Chirolli L.; Silva-Guillén J. A.; Agraït N.; et al. Enhanced Superconductivity in Atomically Thin TaS 2. Nat. Commun. 2016, 7, 11043. 10.1038/ncomms11043. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Fu W.; Chen Y.; Lin J.; Wang X.; Zeng Q.; Zhou J.; Zheng L.; Wang H.; He Y.; He H.; et al. Controlled Synthesis of Atomically Thin 1T-TaS2 for Tunable Charge Density Wave Phase Transitions. Chem. Mater. 2016, 28 (21), 7613–7618. 10.1021/acs.chemmater.6b02334. [DOI] [Google Scholar]
  27. Wu R. J.; Udyavara S.; Ma R.; Wang Y.; Chhowalla M.; Birol T.; Koester S. J.; Neurock M.; Mkhoyan K. A. Visualizing the Metal-MoS 2 Contacts in Two-Dimensional Field-Effect Transistors with Atomic Resolution. Phys. Rev. Mater. 2019, 3, 111001. 10.1103/PhysRevMaterials.3.111001. [DOI] [Google Scholar]
  28. Hirata T.; Ohuchi F. S. Temperature Dependence of the Raman Spectra of 1T-TaS2. Solid State Commun. 2001, 117 (6), 361–364. 10.1016/S0038-1098(00)00468-3. [DOI] [Google Scholar]
  29. Tison Y.; Martinez H.; Baraille I.; Loudet M.; Gonbeau D. X-Ray Photoelectron Spectroscopy and Scanning Tunneling Microscopy Investigations of the Solid Solutions TixTa1-XS 2 (0 ≤ x ≤ 1). Surf. Sci. 2004, 563 (1–3), 83–98. 10.1016/j.susc.2004.05.134. [DOI] [Google Scholar]
  30. Zeng Z.; Tan C.; Huang X.; Bao S.; Zhang H. Growth of Noble Metal Nanoparticles on Single- Layer TiS2 and TaS2 Nanosheets for Hydrogen Evolution Reaction. Energy Environ. Sci. 2014, 7 (2), 797–803. 10.1039/C3EE42620C. [DOI] [Google Scholar]
  31. XPS Interpretation of Tantalum. https://xpssimplified.com/elements/tantalum.php (accessed June 22, 2020). [Google Scholar]
  32. Kumar A.; Akansel S.; Stopfel H.; Fazlali M.; Åkerman J.; Brucas R.; Svedlindh P. Spin Transfer Torque Ferromagnetic Resonance Induced Spin Pumping in the Fe/Pd Bilayer System. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 95, 064406. 10.1103/PhysRevB.95.064406. [DOI] [Google Scholar]
  33. Liu L.; Moriyama T.; Ralph D. C.; Buhrman R. A. Spin-Torque Ferromagnetic Resonance Induced by the Spin Hall Effect. Phys. Rev. Lett. 2011, 106 (3), 036601. 10.1103/PhysRevLett.106.036601. [DOI] [PubMed] [Google Scholar]
  34. Tserkovnyak Y.; Brataas A.; Bauer G. E. W. Enhanced Gilbert Damping in Thin Ferromagnetic Films. Phys. Rev. Lett. 2002, 88 (11), 117601. 10.1103/PhysRevLett.88.117601. [DOI] [PubMed] [Google Scholar]
  35. Demasius K. U.; Phung T.; Zhang W.; Hughes B. P.; Yang S. H.; Kellock A.; Han W.; Pushp A.; Parkin S. S. P. Enhanced Spin-Orbit Torques by Oxygen Incorporation in Tungsten Films. Nat. Commun. 2016, 7, 10644. 10.1038/ncomms10644. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Saitoh E.; Ueda M.; Miyajima H.; Tatara G. Conversion of Spin Current into Charge Current at Room Temperature: Inverse Spin-Hall Effect. Appl. Phys. Lett. 2006, 88 (18), 182509. 10.1063/1.2199473. [DOI] [Google Scholar]
  37. Zhao B.; Khokhriakov D.; Zhang Y.; Fu H.; Karpiak B.; Hoque A.; Xu X.; Jiang Y.; Yan B.; Dash S. P. Observation of Charge to Spin Conversion in Weyl Semimetal WTe 2 at Room Temperature. Phys. Rev. Res. 2020, 2 (1), 013286. 10.1103/PhysRevResearch.2.013286. [DOI] [Google Scholar]
  38. Xu H.; Wei J.; Zhou H.; Feng J.; Xu T.; Du H.; He C.; Huang Y.; Zhang J.; Liu Y.; Wu H.-C.; Guo C.; Wang X.; Guang Y.; Wei H.; Peng Y.; Jiang W.; Yu G.; Han X.; et al. High Spin Hall Conductivity in Large-Area Type-II Dirac Semimetal PtTe 2. Adv. Mater. 2020, 32, 2000513. 10.1002/adma.202000513. [DOI] [PubMed] [Google Scholar]
  39. Zhu L.; Sobotkiewich K.; Ma X.; Li X.; Ralph D. C.; Buhrman R. A. Strong Damping-Like Spin-Orbit Torque and Tunable Dzyaloshinskii–Moriya Interaction Generated by Low-Resistivity Pd 1–x Pt x Alloys. Adv. Funct. Mater. 2019, 29 (16), 1805822. 10.1002/adfm.201805822. [DOI] [Google Scholar]
  40. Zimmermann B.; Mavropoulos P.; Heers S.; Long N. H.; Blügel S.; Mokrousov Y. Anisotropy of Spin Relaxation in Metals. Phys. Rev. Lett. 2012, 109 (23), 236603. 10.1103/PhysRevLett.109.236603. [DOI] [PubMed] [Google Scholar]
  41. Long N. H.; Mavropoulos P.; Bauer D. S. G.; Zimmermann B.; Mokrousov Y.; Blügel S. Strong Spin-Orbit Fields and Dyakonov-Perel Spin Dephasing in Supported Metallic Films. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 94 (18), 180406(R) 10.1103/PhysRevB.94.180406. [DOI] [Google Scholar]
  42. Amin V. P.; Stiles M. D. Spin Transport at Interfaces with Spin-Orbit Coupling: Formalism. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 94 (10), 104419. 10.1103/PhysRevB.94.104419. [DOI] [Google Scholar]
  43. Amin V. P.; Stiles M. D. Spin Transport at Interfaces with Spin-Orbit Coupling: Phenomenology. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 94 (10), 104420. 10.1103/PhysRevB.94.104420. [DOI] [Google Scholar]
  44. Fan X.; Wu J.; Chen Y.; Jerry M. J.; Zhang H.; Xiao J. Q. Observation of the Nonlocal Spin-Orbital Effective Field. Nat. Commun. 2013, 4, 1799. 10.1038/ncomms2709. [DOI] [PubMed] [Google Scholar]
  45. Dc M.; Grassi R.; Chen J. Y.; Jamali M.; Reifsnyder Hickey D.; Zhang D.; Zhao Z.; Li H.; Quarterman P.; Lv Y.; et al. Room-Temperature High Spin–Orbit Torque Due to Quantum Confinement in Sputtered BixSe(1–x) Films. Nat. Mater. 2018, 17 (9), 800–807. 10.1038/s41563-018-0136-z. [DOI] [PubMed] [Google Scholar]
  46. Kawaguchi M.; Shimamura K.; Fukami S.; Matsukura F.; Ohno H.; Moriyama T.; Chiba D.; Ono T. Current-Induced Effective Fields Detected by Magnetotrasport Measurements. Appl. Phys. Express 2013, 6 (11), 113002. 10.7567/APEX.6.113002. [DOI] [Google Scholar]
  47. Kim K. W.; Lee K. J.; Sinova J.; Lee H. W.; Stiles M. D. Spin-Orbit Torques from Interfacial Spin-Orbit Coupling for Various Interfaces. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96 (10), 104438. 10.1103/PhysRevB.96.104438. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Zibouche N.; Kuc A.; Musfeldt J.; Heine T. Transition-Metal Dichalcogenides for Spintronic Applications. Ann. Phys. 2014, 526 (9–10), 395–401. 10.1002/andp.201400137. [DOI] [Google Scholar]
  49. Zhao B.; Karpiak B.; Khokhriakov D.; Hoque A. M.; Xu X.; Jiang Y.; Dash S. P.. Edelstein Effect in Type-II Weyl Semimetal WTe2 up to Room Temperature. 2019, 1910.06225, arXive. https://arxiv.org/abs/1910.06225 (accessed June 22, 2020). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl0c01955_si_001.pdf (1.9MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES