T₂ relaxation‐time mapping in healthy and diseased skeletal muscle using extended phase graph algorithms

Abstract

Purpose

Multi‐echo spin‐echo (MSE) transverse relaxometry mapping using multi‐component models is used to study disease activity in neuromuscular disease by assessing the T₂ of the myocytic component (T_2water). Current extended phase graph algorithms are not optimized for fat fractions above 50% and the effects of inaccuracies in the T_2fat calibration remain unexplored. Hence, we aimed to improve the performance of extended phase graph fitting methods over a large range of fat fractions, by including the slice‐selection flip angle profile, a through‐plane chemical‐shift displacement correction, and optimized calibration of T_2fat.

Methods

Simulation experiments were used to study the influence of the slice flip‐angle profile with chemical‐shift and T_2fat estimations. Next, in vivo data from four neuromuscular disease cohorts were studied for different T_2fat calibration methods and T_2water estimations.

Results

Excluding slice flip‐angle profiles or chemical‐shift displacement resulted in a bias in T_2water up to 10 ms. Furthermore, a wrongly calibrated T_2fat caused a bias of up to 4 ms in T_2water. For the in vivo data, one‐component calibration led to a lower T_2fat compared with a two‐component method, and T_2water decreased with increasing fat fractions.

Conclusion

In vivo data showed a decline in T_2water for increasing fat fractions, which has important implications for clinical studies, especially in multicenter settings. We recommend using an extended phase graph–based model for fitting T_2water from MSE sequences with two‐component T_2fat calibration. Moreover, we recommend including the slice flip‐angle profile in the model with correction for through‐plane chemical‐shift displacements.

1. INTRODUCTION

Quantitative MRI shows promising results as a biomarker in the follow‐up of disease progression in neuromuscular diseases (NMDs). ¹ In these diseases, inflammation and progressive fat replacement of muscle tissue are major histological hallmarks. Although imaging of the fat fraction using MRI or MRS is used to assess disease progression, transverse relaxometry mapping or T₂ relaxation‐time mapping has been applied as an MRI marker for disease activity. ² , ³ , ⁴

Quantitative measurements of T₂ relaxation times are commonly performed using T2prep sequences, ⁵ multi‐acquisition single‐TE spin‐echo sequences, IDEAL‐CPMG (iterative decomposition of water and fat with echo asymmetry and least‐squares estimation and Carr‐Purcell‐Meiboom‐Gill), ⁶ MRS, ⁷ or multi‐spin‐echo (MSE) sequences. ⁸ Acquisition times for multi‐acquisition sequences are longer ⁹ (typical acquisition time: 10 minutes) compared with MSE sequences (typical acquisition time: 3 minutes) and more sensitive to motion artifacts, whereas MRS can only give information for a single muscle. Therefore, MSE is commonly used, as it allows for fast scans with a large FOV. ⁸ To measure the T₂ relaxation time from a MSE sequence, a mono‐exponential decay can be fitted to the signal intensity as a function of TE. However, this combined T₂ relaxation time, also defined as the “global T₂ relaxation time,” ¹⁰ represents the combined relaxation of all different components, including the T₂ relaxation time of water and fat. In the presence of fat replacement, which is often the case in NMD, this combined T₂ is primarily affected by the fat signal, which has a relatively long T₂ relaxation time, masking the more subtle changes in T₂ due to the other changes in muscle tissue. ¹¹ Therefore, in NMD it is preferred to separate the signal into different components for water (T_2water) and fat (T_2fat), where the T₂ of the myocytic component (T_2water) has been proposed as a more accurate biomarker for disease activity. ¹⁰

Assessment of T_2water using MSE has been performed using various approaches including fat suppression and modeling. Fat suppression has the advantage that it is available on all scanners; however, it is sensitive to field inhomogeneities and is often unable to suppress the entire fat spectrum. ¹² , ¹³ As an alternative, different modeling approaches have been proposed to separate the contribution of the water and fat signal. Originally, bi‐exponential ¹⁴ or tri‐exponential ¹⁵ , ¹⁶ methods were introduced to separate both contributions to the signal at the successive TEs. However, these models assume a perfect mono‐exponential decay for the components, which is generally not observed in vivo. One important deviation from this perfect mono‐exponential decay are stimulated echoes that result in an oscillation of the measured signal. ¹⁷ , ¹⁸ This oscillation results in an overestimation of the T₂, when estimated using an exponential model. As a result, the accuracy and reproducibility of these exponential models are limited. ¹¹

To overcome these limitations, which are caused primarily by deviations from the assumed Hahn echo sequence due to, for example, a lower B₁, fitting using extended phase graphs (EPGs) ¹⁹ has been proposed. The EPG concept is a tool for describing the magnetization response in multipulse MR sequences, using a Fourier‐based magnetization description. Similar to exponential models, a two‐component EPG model can be used to account for the fat signal, which has been shown to yield T_2water values in the range of the gold‐standard MRS, and which is largely independent of fat fractions up to 50% in several NMDs. ²⁰ , ²¹ However, there are still several aspects that are not taken into account in the currently used EPG analyses.

First, current analyses do not report T_2water values above a fat fraction of about 50%, ¹¹ whereas in muscular dystrophies fat fractions above 50% are not an exception, ⁴ thereby limiting the applicability of the method. Second, the effect of inaccuracies in the estimation of T_2fat remain unexplored. Determination of the T_2fat from MSE sequences is challenging, as the spectral components of fat each have different T₂ relaxation times that, due to J‐coupling, also depend on the echo spacing. ²² , ²³ , ²⁴ The current EPG implementations calibrate the T₂ relaxation time of the fat component using subcutaneous fat, ¹⁶ thereby assuming that the T_2fat in muscle is similar to subcutaneous fat. However, subcutaneous fat contains on average only 90% fat and 10% water, ²⁵ rather than 100% fat. Third, the spatial variation of the flip angle across the slice is not taken into account. ¹¹ Because of the limited duration of the RF pulses, the excitation and refocusing pulses do not provide a homogeneous flip angle across the excited slice. This is especially the case in T₂ mapping using MSE, as short RF pulses are applied to facilitate short echo spacings. ¹⁷ , ¹⁸ Fourth and finally, the chemical‐shift displacement between water and fat in the slice direction has to be taken into account. When the slice‐selection gradient of the excitation pulse is different from the slice‐selection gradient of the refocusing pulse, the flip‐angle profiles are not aligned for the protons in fat. Therefore, the fat protons experience a different refocusing than the water protons, resulting in different strength of the stimulated echoes of the fat signal.

In the present work, we aim to improve the performance of EPG fitting methods to determine T_2water in muscles of different NMDs with a large range of fat fractions by studying the effect of the incorporation of the flip‐angle profile with a chemical‐shift displacement in the slice direction and the assumptions for the calibration of the T_2fat. We present the importance of including slice flip‐angle profiles with a chemical‐shift displacement in the slice direction and correct calibration methods for the T₂ of the fat component. Furthermore, we show the performance of the model in four clinical cohorts, which show a gradual decline in T_2water for increasing fat fractions.

2. METHODS

A signal model based on extended phase graphs, including a slice flip‐angle profile with a chemical shift between water and fat, was used to fit the MSE signal. The fit was performed using a dictionary fitting method as proposed by Marty et al. ¹¹ The performance of this model was studied in simulation experiments. The influence of the slice flip‐angle profile with the chemical shift and the influence of the assumed T_2fat were studied in simulations 1 and 2, respectively. Using in vivo data from four patient cohorts, we performed two additional experiments. In experiment 1 the performance of different calibration methods for the T_2fat was examined, and in experiment 2 the model was applied to the data, to study the performance and the outcome parameters. All analyses were performed in MATLAB 2016a (The MathWorks, Natick, MA).

2.1. Extended phase graph model

The model used for the MSE signal simulation consists of a water and a fat signal simulated with EPGs, ¹⁹ including the T₁, the T₂, and the B₁. The slice flip‐angle profiles of the RF pulses were calculated using Bloch equations at 30 samples along the slice flip‐angle profile (3× slice thickness). ¹⁷ , ¹⁸ Slice‐angle profiles for a B₁ of 70%, 100%, and 130% are shown in Figure 1A, respectively, for the water signal, the fat signal, and the combined signal.

FIGURE 1.

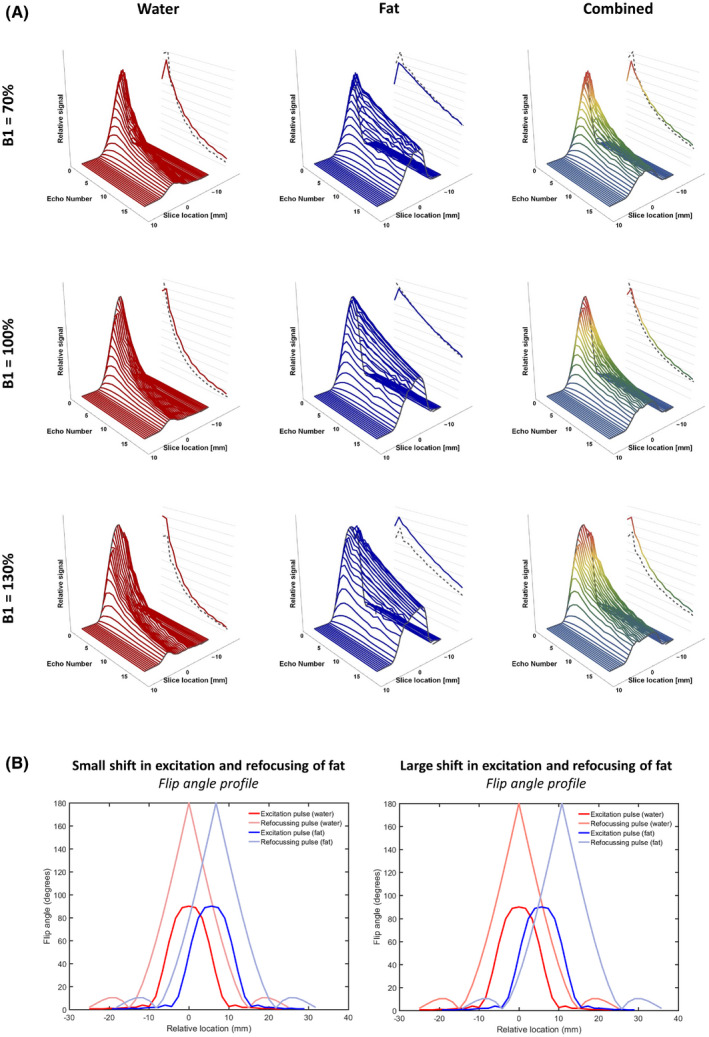
A, Signal profiles for a B₁ of 70%, 100%, and 130%, from left to right. Noticeable is the asymmetry around a B₁ of 100%. The right dotted line in each signal profile represents the signal in the center of the slice, and the right colored line depicts the final signal after averaging all signal contributions. B, Example flip‐angle profile of the pulses throughout the slice. The left side shows an example of a flip‐angle profile with a minor shift (1.1 mm) between the excitation and refocusing pulse as experienced by the fat, and the right side shows an example of a major shift (5.1 mm)

Because the slice‐selection gradients can differ between the excitation and refocusing pulses, the slice flip‐angle profiles are not aligned for the protons in fat (Figure 1B). This chemical‐shift artifact was incorporated in the model for the fat signal, by shifting the fat signal in the slice direction according to

$$\mathrm{\Delta }\mathbf{L}=\frac{1}{\mathbf{\gamma }\ast \mathbf{G}}\ast \mathrm{\Delta }\mathbf{f}\ast {\mathbf{B}}_0,$$

where ΔL is the shift in location in meters, γ is the Larmor frequency in hertz/Tesla, G is the gradient strength in Tesla/meters, Δf is the chemical shift between water and fat in hertz/Tesla, and B₀ is the field strength of the scanner in Tesla.

2.2. Fitting of MSE signal

The measured signal vector $\mathit{S}$ with size $N_{\mathit{echo}}$ (number of echoes) can be approximated using a bicomponent EPG model in which the modeled signal vector $\widehat{S}$ can be defined as

$$\widehat{S}=w{\mathit{S}}_{\mathit{water}}+f{\mathit{S}}_{\mathit{fat}}=\left[\begin{array}{cc}{\mathit{S}}_{\mathit{water}}& {\mathit{S}}_{\mathit{fat}}\end{array}\right]\left[\begin{array}{c}w\\ f\end{array}\right],$$

where $w$ and $f$ are the water and fat signal amplitudes. The signal at each echo of the water and fat component are ${\mathit{S}}_{\mathit{water}}$ and ${\mathit{S}}_{\mathit{fat}}$, respectively, and are defined as

$${\mathit{S}}_{\mathit{water}}=\sum _{m=1}^{M}EPG\left(T_{1wat},T_{2wat},B1,\mathrm{\Delta }TE,N_{\mathit{echo}},{\mathit{\alpha }}_{\mathit{ex}}^m,{\mathit{\alpha }}_{\mathit{ref}}^m\right)$$

$${\mathit{S}}_{\mathit{fat}}=\sum _{m=1}^{M}EPG\left(T_{1fat},T_{2fat},B1,\mathrm{\Delta }TE,N_{\mathit{echo}},{\mathit{\alpha }}_{\mathit{ex}}^m,{\mathit{\alpha }}_{\mathit{ref}}^m\right),$$

where ${\mathit{\alpha }}_{\mathit{ex}}$ and ${\mathit{\alpha }}_{\mathit{ref}}$ are the flip‐angle profiles along the slice direction of the excitation and refocusing pulses, respectively, and $M$ is the number of samples along the slice profile.

The signal was fitted using a dictionary‐based method. The precalculated dictionary contains a range of values for T_2fat, T_2water and B₁. The T₂ parameters ranged between boundaries based on literature values (T_2fat: 120‐200 ms with 2‐ms steps and T_2water: 10‐60 ms with 1‐ms steps), and the B₁ value ranged between 50% and 140% (with 2% steps), as the incorporation of the flip‐angle profile breaks the B₁ symmetry around 100% for the excitation pulse (Figure 1A). ¹⁸ The $i$th dictionary EPG signals ${\mathit{d}}_{\mathit{water}}^i$ and ${\mathit{d}}_{\mathit{fat}}^i$ with $\mathit{T}{2}_{\mathit{wat}}^i$ and $\mathit{B}{1}^i$ are defined as

$${\mathit{d}}_{\mathit{water}}^i=\sum _{m=1}^{M}EPG\left(T_{1wat},\mathit{T}{2}_{\mathit{wat}}^i,\mathit{B}{1}^i,\mathrm{\Delta }TE,N_{\mathit{echo}},{\mathit{\alpha }}_{\mathit{ex}}^m,{\mathit{\alpha }}_{\mathit{ref}}^m\right)$$

$${\mathit{d}}_{\mathit{fat}}^i=\sum _{m=1}^{M}EPG\left(T_{1fat},T_{2fat},\mathit{B}{1}^i,\mathrm{\Delta }TE,N_{\mathit{echo}},{\mathit{\alpha }}_{\mathit{ex}}^m,{\mathit{\alpha }}_{\mathit{ref}}^m\right).$$

For each dictionary value of $\mathit{T}{2}_{\mathit{wat}}^i$ and $\mathit{B}{1}^i$, the water and fat amplitudes ${\mathit{w}}^i$ and ${\mathit{f}}^i$ and the modeled signal ${\widehat{S}}^{\mathit{i}}$ at the $i$th dictionary index are estimated using a matrix formulation of the multiple regression model:

$$\left[\begin{array}{c}{\mathit{w}}^i\\ {\mathit{f}}^i\end{array}\right]={\left[\begin{array}{c}{\mathit{d}}_{\mathit{water}}^i\\ {\mathit{d}}_{\mathit{fat}}^i\end{array}\right]}^{-1}S$$

$${\widehat{S}}^{\mathit{i}}=\left[\begin{array}{cc}{\mathit{d}}_{\mathit{water}}^i& {\mathit{d}}_{\mathit{fat}}^i\end{array}\right]\left[\begin{array}{c}{\mathit{w}}^i\\ {\mathit{f}}^i\end{array}\right].$$

The optimal dictionary values ${\mathit{T}}_{2,wat}^i$ ${\mathit{B}}_1^i$ and the corresponding amplitudes of the water and fat signal ${\mathit{w}}^i$ and ${\mathit{f}}^i$ are determined by minimizing the Euclidian norm:

$$\text{argmin}\mathit{S}-{\widehat{S}}_2^i.$$

To include a water fraction $g$ ( $0\le g\le 1$) with $T_{1,watfat}$ and $T_{2,watfat}$ in the dictionary fat signal, ${\mathit{d}}_{\mathit{fat}}^i$ was defined as

$${\mathit{d}}_{\mathit{fat}}^i=\sum _{m=1}^M\left(1-g\right)EPG\left(T_{1fat},T_{2fat},\mathit{B}{1}^i,\mathrm{\Delta }TE,N_{\mathit{echo}},{\mathit{\alpha }}_{\mathit{ex}}^m,{\mathit{\alpha }}_{\mathit{ref}}^m\right)+gEPG\left(T_{1watfat},T_{2watfat},\mathit{B}{1}^i,\mathrm{\Delta }TE,N_{\mathit{echo}},{\mathit{\alpha }}_{\mathit{ex}}^m,{\mathit{\alpha }}_{\mathit{ref}}^m\right).$$

2.3. Simulation experiments

To assess the incorporation of the slice flip‐angle profile, the chemical shift of the slice profile between water and fat, and the effect of the assumed T_2fat, the MSE signal evolution was simulated using EPG assuming a known slice flip‐angle profile (Figure 1). In the simulations the T_2water was fixed at 30 ms, B₁ and fat fractions were randomized between the possible boundaries (B₁, 50%‐140%; and fat fraction, 0%‐100%), and the T_2fat was modeled with Gaussian distribution (mean of 150 ms and SD of 10 ms). The T_1water and T_1fat were fixed on 1400 ms and 365 ms, respectively. Two simulation experiments as described subsequently were performed: one to investigate the effect of slice flip‐angle profiles, and one to investigate the effect of using wrongly calibrated T_2fat.

2.4. Simulation 1: Effect of the slice flip‐angle profile

We conducted two simulations to study the effect of incorporating the flip‐angle profile and the chemical shift of the slice profile between water and fat signals on the estimated T_2water. In simulation 1A, the data were simulated assuming the full‐slice flip‐angle profile, and fitting was done with and without assuming the full‐slice flip‐angle profile. Next, in simulation 1B, data were simulated assuming using the full‐slice flip‐angle profile with a large and a small chemical shift between water and fat slice profiles. The simulated data were fitted with and without accounting for the chemical shift. The used slice flip‐angle profiles for the small and large chemical shift are shown in Figure 1.

2.5. Simulation 2: Effect of T_2fat

To study the effect of wrongly calibrated T_2fat on the estimated T_2water, we conducted a simulation in which a full‐slice flip‐angle profile and chemical shift was incorporated. In simulation 2, data were simulated with T_2fat = 150 ± 10 ms. Next, the data were fitted with a correct, an overestimated, and an underestimated T_2fat of 150 ms, 180 ms, and 120 ms, respectively.

2.6. In vivo experiments

2.6.1. Study populations and MR scans

To study the effect of T₂ calibration methods in vivo, we used data from four different clinical cohorts that contained MSE data of both patients and healthy controls. The four cohorts contained data from 92 patients and 56 healthy controls. These data sets were acquired in the context of four clinical studies and will be used for methodological purposes in the current work. ²⁶ , ²⁷ , ²⁸ , ²⁹ The Medical Ethics Review Committee of the Leiden University Medical Center and the University Medical Center Utrecht approved the studies, and all patients or parents provided written informed consent before study participation.

All patients were scanned on a 3T Philips MRI system (Philips Healthcare, Best, The Netherlands). The first cohort (cohort 1) consisted of 18 nonambulant patients with Duchenne muscular dystrophy (DMD) (17.1 ± 5.1 years, range 9‐24 years) and 11 age‐matched healthy controls (14.7 ± 4.0 years, range 10‐25 years) from the Leiden University Medical Center. ²⁹ In this cohort, upper‐arm scans had been acquired. The second cohort (cohort 2) consisted of 22 patients with DMD (9.3 ± 3.1 years, range 5‐16 years, 16 ambulant and 6 nonambulant) and 12 age‐matched healthy controls (9.7 ± 2.9 years, range 5‐14 years) from the Leiden University Medical Center. ²⁸ The third cohort (cohort 3) consisted of 23 patients with Becker muscular dystrophy (BMD) (42.7 ± 13.6 years, range 18‐67 years, all ambulant) and 13 age‐matched healthy controls (43.0 ± 13.7 years, range 21‐63 years), also from the Leiden University Medical Center. ²⁶ In both cohorts 2 and 3, lower‐leg scans had been acquired. The fourth and final cohort (cohort 4) consisted of 29 patients with spinal muscular atrophy (SMA) (29.6 ± 18.0 years, range 17‐71 years, 48% male, 14 patients with SMA type 2 and 15 patients with SMA type 3) and 20 age‐matched healthy controls (37.9 ± 12.8 years, range 17‐71 years, 40% male) from the University Medical Center Utrecht. ²⁷ In this cohort, upper‐leg scans had been acquired. In each data set, regions of interest were manually drawn on five slices that consisted of the entire cross‐sectional muscle compartment without the bone and subcutaneous fat (Figure 2). The sequence parameters for each cohort are listed in Table 1.

FIGURE 2.

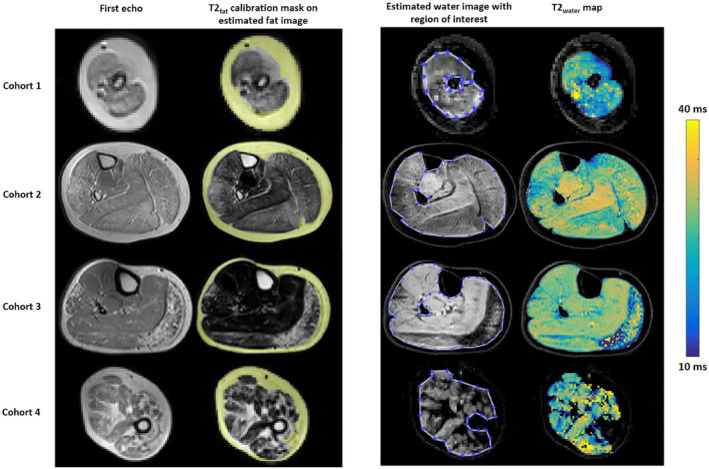
Example raw data and maps from 1 patient in all four cohorts. Left to right: the signal for the first echo, the estimated fat map with the T_2fat calibration mask, the estimated water map with the region of interest, and the T_2water map

TABLE 1.

Acquisition and pulse parameters for the four cohorts

	Cohort 1 (DMD: n = 18; HC: n = 11)	Cohort 2 (DMD: n = 22; HC: n = 12)	Cohort 3 (BMD: n = 23; HC: n = 13)	Cohort 4 (SMA: n = 29; HC: n = 20)
Anatomical location	Upper arm	Lower leg	Lower leg	Upper leg
Sequence parameters
First TE	8.0 ms	8.0 ms	8.0 ms	7.6 ms
Time between echoes	8.0 ms	8.0 ms	8.0 ms	7.6 ms
Number of echoes	17	17	17	17
TR	3000 ms	3000 ms	3000 ms	4598 ms
Slice thickness	10 mm	10 mm	10 mm	6 mm
Slice gap	20 mm	20 mm	20 mm	0 mm
Slices	5	5	5	13
Resolution	2.0 × 2.0 mm	1.6 × 1.6 mm	1.6 × 1.6 mm	3.0 × 3.0 mm
ΔChemical shift*	0.1 mm	1.1 mm	1.1 mm	0.9 mm
Excitation pulse
Bandwidth	1000 Hz	1000 Hz	1000 Hz	768 Hz
Gradient strength	1.78 mT/m	1.78 mT/m	1.78 mT/m	2.28 mT/m
Refocusing pulse
Bandwidth	632 Hz	632 Hz	632 Hz	486 Hz
Gradient strength	1.80 mT/m	1.48 mT/m	1.48 mT/m	1.90 mT/m

Cohort 1 included Duchenne’s muscular dystrophy patients and healthy controls; cohort 2 included Duchenne’s muscular dystrophy patients and healthy controls; cohort 3 included Becker muscular dystrophy patients and healthy controls; and cohort 4 included spinal muscular atrophy patients and healthy controls.

Abbreviations: BMD, Becker muscular dystrophy; DMD, Duchenne’s muscular dystrophy; HC, healthy control; SMA, spinal muscular atrophy.

^*Chemical‐shift displacement difference in slice direction between excitation and refocusing pulse for fat.

With the data of these cohorts, we performed two experiments as described subsequently. The first experiment aimed to compare three different T_2fat calibration methods using voxels from the subcutaneous fat. The second experiment evaluated the effect of these fat calibration methods on the T_2water estimation.

2.6.2. Calibration of T_2fat

The T_2fatwas calibrated on subcutaneous fat using a fat mask based on the last echo in the echo sequence. ¹⁶ The mask was determined by thresholding the last echo in the MSE sequence with the mean signal intensity (Figure 2). The signal was fitted for each voxel using the library method described previously, fixing the T_2water and the water/fat quantities as described subsequently. The T_2fat was obtained by averaging all fitted voxels in the fat mask.

2.6.3. Experiment 1: In vivo calibration of T_2fat

The T_2fat of the subcutaneous fat was estimated using three different methods. The first, method A, assumed one fat component with a 100% fat fraction. The second, method B, estimated T_2fat using a fixed fat fraction of 90% (based on literature values ³⁰ ) and a water component of 10%, in which both relaxation times are fitted in the model. In the third and last method, method C, calibration was done using a fixed fat fraction of 90% and a fixed T_2water in the fat of 20 ms, to stabilize the fit with low water signal.

2.6.4. Experiment 2: In vivo T₂ estimation

To study the performance of the different methods of calibration, we compared the outcome parameter T_2water for 5 slices of the patient cohorts using method A, B and C as described above. In summary, with method A the T_2fat is calibrated assuming one fat component (fat fraction 100%), with method B the calibration is performed using a fixed fat fraction of 90% and a 10% water‐fraction with a fitted T_2water and with method C the calibration is done using a fixed fat fraction of 90% and a 10% water‐fraction with T_2water of 20 ms. In the last two methods, fitting is performed with the calibrated T_2fat that also includes a 10% water component with the calibrated T_2water and a T_2water of 20 ms, respectively. Example T_2water maps are shown in Figure 2.

2.6.5. Statistics

For the simulation experiments, the relation between simulated fat fractions and fitted T_2water values and fitted fat fractions was obtained using locally weighted scatterplot smoothing regression. A linear regression analysis was performed, and the slope and intercept were reported. The voxels that were fitted with boundary values (T_2water shorter than 10 ms and longer than 60 ms) were excluded from statistical analysis and depicted in red in the figures. For the calibration experiment (experiment 1), smoothed histograms were generated for all calibrated values. Average T_2water values among different calibration methods were compared using paired t‐tests. The T_2fat values within the different calibrations were compared using a Kruskal‐Wallis test with post‐hoc comparison using Bonferroni correction. For the in vivo fitting experiment (experiment 2), locally weighted scatterplot smoothing regression was used to assess the relation between T_2water and fat fractions.

3. RESULTS

3.1. Simulation 1: Effect of the slice flip‐angle profile

In simulation 1A, data were simulated assuming the slice flip‐angle profile and fitted with and without taking the flip‐angle profile into account. The results of the fit are depicted in Figure 3. Without incorporation of the flip‐angle profile, the results show an overestimation of T_2water, with a median of 40 ms (5th‐95th percentile: 34‐57 ms) and with many voxels on the dictionary boundaries (30%). The results also show an underestimation of the fitted fat fraction for the entire range of values (intercept: −2.26%, slope: 0.87). However, fitting with incorporation of the flip‐angle profile resulted in a median T_2water of 30 ms (5th‐95th percentile: 26‐35 ms), and only 1.5% of fits were on dictionary boundaries. The correlation between the simulated and fitted fat fraction show an intercept of 0.3% and a slope of 0.99.

FIGURE 3.

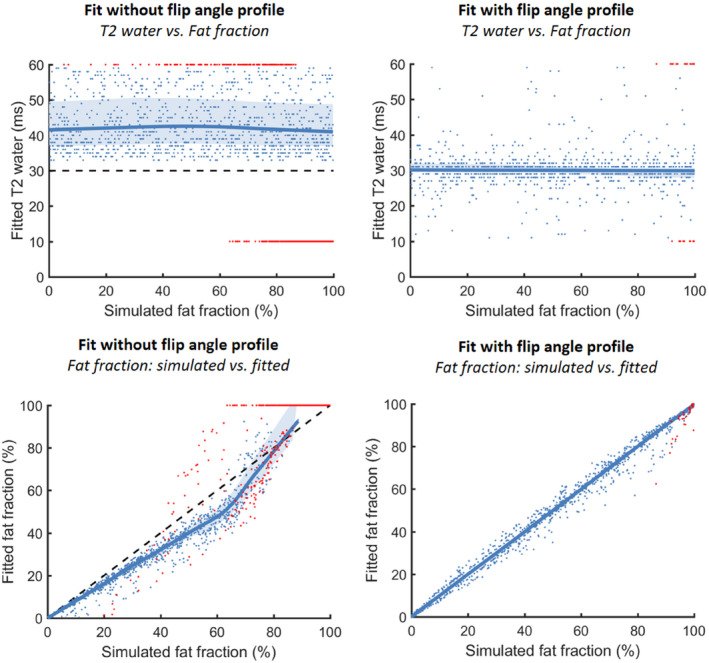
Simulation 1A shows the relationship between the simulated fat fraction and the fitted T_2water for simulation without incorporation of the flip‐angle profile (T_2water: median: 40 ms [34‐57 ms], on dictionary boundaries: 30%) and fitted by incorporating the flip‐angle profile (top row) (T_2water: median: 30 ms [26‐35 ms], on dictionary boundaries: 1.5%). In the bottom row, the relation between the simulated fat fraction and the fitted fat fraction is shown without and with the flip‐angle profile. The values fitted on dictionary boundaries are depicted in red, and the correctly fitted values are depicted in blue. A reference line is shown at a T_2water of 30 ms, and a unity line is shown for the fat fractions

In simulation 1B, data were simulated assuming a small and a large chemical shift between water and fat, and fitting with and without assuming the chemical shift (Figure 1B). The results for the fits simulated and fitted with the small and large chemical shift are comparable (T_2water: median: 30 ms [5th‐95th percentile: 26‐35 ms], on dictionary boundaries: 1.5%; and fat fraction: intercept: 0.3%, slope: 0.99), and show no underestimation or overestimation of the T_2water and the fat fraction (Figure 4). However, when the chemical shift is not included in the analysis, T_2water was overestimated with a median of 32 ms (5th‐95th percentile: 28‐51 ms) and 34 ms (5th‐95th percentile: 30‐53 ms) for the small and large chemical shift, respectively. The fat fraction is globally underestimated, and the fit is increasingly unstable for higher fat fractions (small shift: intercept, 0.72%; slope, 0.92; and high shift: intercept, −1.28%; slope: 0.79).

FIGURE 4.

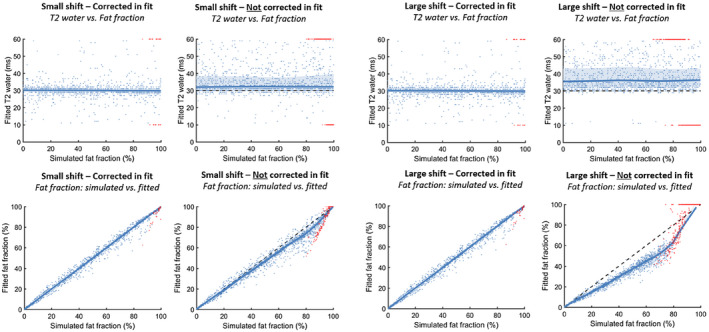
Simulation 2 shows the effect of simulating data with a chemical shift in the location of the pulses and fitting it with or without incorporating the chemical shift of the slice. The four figures on top show the simulation with a small shift (T_2water: median: 32 ms (28‐51 ms), on dictionary boundaries: 6.8%; and fat fraction: intercept: 0.72%, slope: 0.92), and the four figures on bottom show the simulation with a large shift (T_2water: median: 34 ms (30‐53 ms), on dictionary boundaries: 22%; and fat fraction: intercept: −1.28%, slope: 0.79). The values fitted on dictionary boundaries are depicted in red, and the correctly fitted values are depicted in blue. A reference line is shown at a T_2water of 30 ms, and a unity line is shown for the fat fractions

3.2. Simulation experiment 2: Influence of the T₂fat

In simulation 2A, data were simulated with a known T_2fat and fitted with an underestimated, correct, and overestimated T_2fat (Figure 5). A baseline was established by fitting the values with an average T_2fat, with the median of the T_2water at 30 ms (5th‐95th percentile: 23‐38 ms) with 4% of voxels on the dictionary boundaries and no apparent error in the fitted fat fraction (intercept: 0.6%, slope: 1.0). With an underestimation of the T_2fat, the T_2water is underestimated and the fat fraction is overestimated, and the fit is more unstable (T_2water: median: 26 ms (5th‐95th percentile: 14‐30 ms), on dictionary boundaries: 26%; and fat fraction: intercept: 2.71%, slope: 1.11). With an overestimation of the T_2fat, the T_2water is overestimated and the fat fraction is underestimated (T_2water: median: 33 ms (5th‐95th percentile: 30‐51 ms), on dictionary boundaries: 9%; and fat fraction: intercept: 0.32%, slope: 0.84).

FIGURE 5.

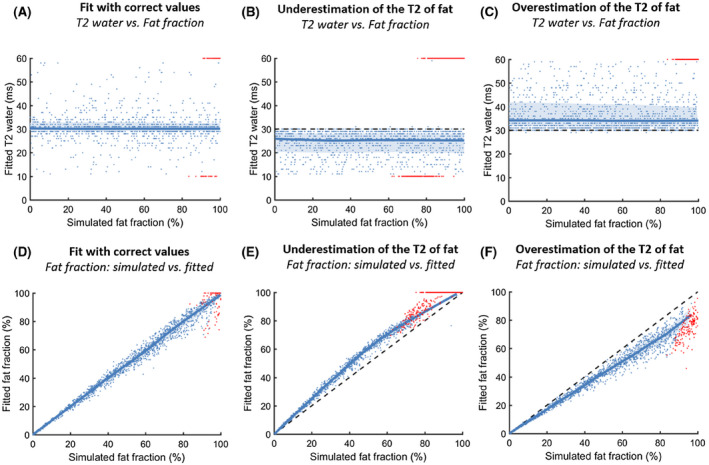
Simulation 2 shows the effect of fitting simulated data with different assumed T_2fat values. A, Top row shows the T_2water for assuming the correct T_2fat (T_2water: median: 30 ms [23‐38 ms], on dictionary boundaries: 4%. B, Underestimation of T_2fat (T_2water: median: 26 ms [14‐30 ms], on dictionary boundaries: 26%. C, Overestimation of T_2fat (T_2water: median: 33 ms [30‐51 ms], on dictionary boundaries: 9%). D‐F, Relationship between the simulated fat fraction and fitted fat fraction. The values fitted on dictionary boundaries are depicted in red, and the correctly fitted values are depicted in blue. A reference line is shown at a T_2water of 30 ms, and a unity line is shown for the fat fractions

3.3. Experiment 1: In vivo calibration of T_2fat

The T_2fat values for the three described methods to calibrate the T_2fat are depicted as smoothed histograms in Figure 6, separated for all four clinical cohorts. In method A, in which the calibration was done assuming one fat component (fat fraction = 100%), a median T_2fat of 137 ms, 132 ms, 131 ms, and 144 ms was found for cohorts 1 to 4, respectively. The T_2fat differed significantly between cohorts (P < .001), except between cohorts 2 and 3, which were acquired with the same sequence. Using method B, the calibration was done using a fixed fat fraction of 90% and a fixed water component of 10%, of which both the relaxation times were fitted. This method results in a median T_2fat of 149 ms, 141 ms, 140 ms and 158 ms, which again differed significantly (P < .001), except between cohorts 2 and 3. The water component had a median T_2water of approximately 27 ms, 24 ms, 24 ms, and 22 ms for cohorts 1 to 4. The histogram for cohort 1 shows that a portion of the values are over 30 ms, possibly representing the T_2water of muscle. In the last experiment (method C), the calibration was performed using a fixed fat fraction of 90% and a T_2water component in the fat of 20 ms. This method results in a median T_2fat of 150 ms, 142 ms, 140 ms, and 159 ms for cohorts 1 to 4, respectively, which is similar to the results of experiment 1B (also statistically different among all cohorts except cohorts 2 and 3, P < .001).

FIGURE 6.

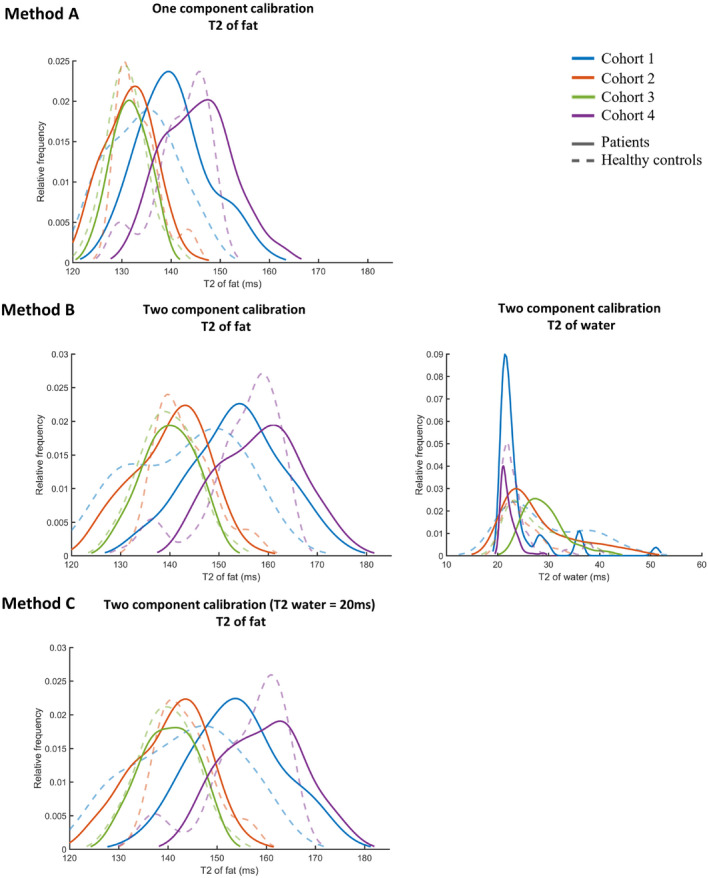
Outcome of the calibration of the T_2fat on subcutaneous fat for methods A, B, and C. The values for the patients in the cohorts are shown as a solid line, and the values for the healthy controls are shown as a dashed line. Method A with one‐component calibration leads to a lower T_2fat (137 ms, 132 ms, 131 ms, and 144 ms for cohorts 1‐4, respectively) than method B with two‐component calibration (149 ms, 141 ms, 140 ms, and 158 ms for cohorts 1‐4, respectively). The calibrated T_2fat is comparable for method B without a fixed T_2water and method C with a fixed T_2water (150 ms, 142 ms, 140 ms, and 159 ms for cohorts 1‐4, respectively)

The one‐component fitting model leads to a lower T_2fat compared with the two‐component fitting model. Notable is the difference of approximately 10 ms in median T_2fat among the cohorts for all methods, except for cohorts 2 and 3, which have similar T_2fat values. Comparing methods B and C appears to result in similar T_2fat values.

For cohort 1 there was a difference in T_2fat for the two‐component calibrations between the healthy controls and patients, explaining the difference in the histograms with methods B and C. In this cohort, the average calibrated T_2fat was 139 ms for healthy controls and 155 ms for the patients in cohort 1 (DMD arm scans), whereas for the other cohorts the histograms of the healthy controls and patient overlap. For example, for cohort 3 (BMD leg scans), the average calibrated T_2fat was 140 ms for both the healthy controls and the patients with BMD.

3.4. Experiment 2: In vivo T₂ estimation

The T_2water values differed less than 1 ms between methods B and C for all patients (mean difference 0.7 ms, P < .001, paired t‐test). Method B resulted in unphysiologically high T_2water values of the fat component (above 35 ms) in healthy controls, showing that this calibration method is less stable. Therefore, method C was used to compare one‐component versus two‐component calibrations. The average T_2water for healthy controls was comparable between these two methods of calibration. The T_2water was 27.4 ms, 28.8 ms, 28.7 ms, and 28.5 ms for the one‐component calibration and 27.5 ms, 29.2 ms, 29.2 ms, and 29.2 ms for the two‐component calibration for cohorts 1 to 4, respectively. For the patients, the T_2water in the one‐component calibration is lower (P < .001, paired t‐test) than the two‐component calibration. The T_2water was 19.6 ms, 25.5 ms, 26.6 ms, and 20.6 ms for the one‐component calibration, and 24.0 ms, 28.8 ms, 27.7 ms, and 27.1 ms for the two‐component calibration, for cohorts 1 to 4. The fat fractions were higher in patients than in healthy controls (Table 2).

TABLE 2.

Average T_2water and fat fractions (+ SDs) for the four cohorts, divided into healthy controls and patients

Cohort		One‐component calibration		Two‐component calibration
		Fat fraction	T2water	Fat fraction	T2water
1. DMD arm	Healthy controls	4.7% ± 1.7%	27.4 ± 1.0 ms	4.9% ± 1.7%	27.5 ± 1.0 ms
	DMD patients	55.8% ± 15.0%	19.6 ± 4.7 ms	62.0% ± 10.4%	24.0 ± 2.2 ms
2. DMD leg	Healthy controls	9.2% ± 3.7%	28.8 ± 0.6 ms	9.9% ± 3.0%	29.2 ± 0.6 ms
	DMD patients	39.0% ± 22.6%	25.5 ± 4.9 ms	41.4% ± 24.2%	28.8 ± 3.9 ms
3. BMD	Healthy controls	11.9% ± 2.5%	28.8 ± 0.7 ms	14.7% ± 9.1%	29.2 ± 0.7 ms
	BMD patients	29.1% ± 17.2%	27.0 ± 2.9 ms	30.1% ± 18.5%	27.8 ± 2.2 ms
4. SMA	Healthy controls	17.3% ± 7.2%	28.5 ± 0.7 ms	18.1% ± 6.9%	29.2 ± 0.7 ms
	SMA patients	84.1% ± 19.4%	20.6 ± 4.2 ms	86.3% ± 24.7%	27.1 ± 3.4 ms

The results are shown for the one‐component calibration (method A) and the two‐component calibration (method C). Regions of interest included the entire muscle compartment without the bone and subcutaneous fat.

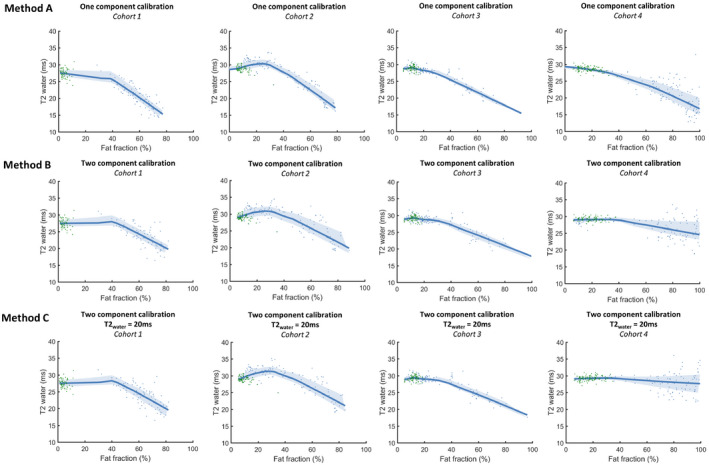
In Figure 7 the relation between fat fraction and T_2water is shown for each cohort and the three calibration methods. Using the one‐component calibration method, with increasing fat fraction the T_2water decreases for all cohorts. With the two‐component calibrations, the negative correlation between T_2water and fat fractions is reduced in cohorts 1 to 3 (DMD and BMD cohorts), especially in the fat fraction range of less than 50%, and absent in cohort 4 (SMA cohort).

FIGURE 7.

Association between the fat fraction and the T₂ of the water component in vivo in four cohorts (cohorts 1‐4 from left to right) for the two calibration methods: A (top row), B (middle row), and C (bottom row). Healthy controls are depicted in green, and patients are depicted in blue. Values are shown for each of the five slices per individual

4. DISCUSSION

Multi‐echo spin‐echo transverse relaxometry mapping using multicomponent models are used to study disease activity in neuromuscular disease. Recently, an EPG model has been introduced to obtain separate T₂ values for water and fat, accounting for B₁ and stimulated echoes. ¹¹ We improved this model and showed the importance of including slice flip‐angle profiles with a chemical‐shift displacement in the slice direction. Different calibration methods for the T₂ of the fat component showed that the assumption of the T₂ of the fat component has a large influence on the estimation of T_2water. Finally, we studied the performance of the model in four clinical cohorts, which showed a gradual decline in T_2water for increasing fat fractions.

Our simulations showed that, not including the slice flip‐angle profile introduced an overestimation of the T_2water up to 10 ms and an underestimation of the fat fraction up to 20%. Accordingly, without accounting for the flip‐angle slice profile the calibrated T_2fat is also overestimated. Including the flip‐angle profile also improved the stability of the fit in higher fat fractions, with fewer voxels reaching the dictionary boundaries. With better‐defined slice profiles, which can be obtained by increasing the RF duration, this effect can likely be reduced. Additionally, simulations showed the importance of including the slice profile chemical shift in EPG simulations for the fat signal, when the gradient strength of the slice‐selection gradient differs for the excitation and refocusing pulse. The water fat shift in the slice‐encoding direction is larger at high field, with thin slices and with large differences between the slice‐encoding gradients of the excitation and refocusing RF pulses. Including the flip‐angle profile and its chemical shift makes T_2water values comparable between different sequences and different MRI systems, improving comparison between cohorts in literature and in multicenter trials. These simulations show that it is essential to be aware of the sequence used in clinical studies, especially in the context of multicenter studies in which exact sequence parameters between MR systems and/or vendors are likely different.

The assumption of the T₂ of the fat component has a large influence of the estimation of T_2water. Assuming one general T_2fat without specific calibration is not recommended, as the T₂ of the fat component can differ for different scanners and sequences due to J‐coupling. ²² The T_2fat can automatically be calibrated on the subcutaneous fat as a reference for fatty tissue. From in vivo studies ³⁰ and Dixon scans of subcutaneous fat, we know that the fat fraction in subcutaneous fat is about 90%. Our simulations show that the T_2fat is underestimated by approximately 10 ms when using a one‐component model for fat calibration. Therefore, performing a two‐component fit improves the accuracy of the estimated T_2fat, and therefore the accuracy of the estimated T_2water and fat fraction.

In the in vivo data we studied, the calibrated T_2fat differed between sequences, which could be explained by differences in scan and sequence parameters. The TE, slice thickness, and profiles all influence J‐coupling of fat protons, which might result in different apparent T_2fat values. Additionally, between subjects within the same cohort there was a variation in the T_2fat, possibly reflecting differences in composition of subcutaneous fat between subjects and MRI acquisition parameters like B₁. For cohort 1 with upper‐arm scans of DMD patients and healthy controls, there was a difference in the calibrated T_2fat between healthy controls and patients (Figure 6). This can probably be attributed to partial‐volume effects, as the thickness of the subcutaneous fat is covered by a relatively sparse number of voxels in the arms due to the low resolution of these scans, and the subcutaneous fat in the arm only covered two to four voxels in most healthy controls. To allow accurate and robust calibration of T_2fat it is essential that there are enough pure subcutaneous fat voxels, preferably equally distributed over slices and in regions with varying B₁. As such, basing the calibration on a small manual region is not recommended.

The in vivo analyses of four cohorts, with healthy controls and patients with different neuromuscular diseases, was performed with the two proposed calibration methods. Assuming the subcutaneous fat to be one component of only fat, we saw a gradual decline in the T_2water with increasing fat fractions for all cohorts. Assuming subcutaneous fat to consist of 90% fat and 10% water, the decline in T_2water for higher fat fractions decreased for DMD and BMD, and was even absent in the SMA cohort (cohort 4). The decrease of T_2water with increase of fat fraction in our cohorts is consistent with the T_2water measured with the gold‐standard spectroscopy in patients due to other neuromuscular disease with fatty replacement. ³¹ Spectroscopy‐based T_2water measurements are typically performed using voxel localization containing both muscle and intramuscular fat. Therefore, similar to the model here, spectroscopy‐based T_2water estimations are likely biased toward lower T_2water as well, with increasing contributions of the water component of fat, which has a lower T_2water compared with muscle.

Although the scope of this work was methodological optimization of multicomponent MSE fitting, data from the two‐component fitting method can be used to look at clinical differences (Figure 7; method C). The dependence of T_2water on the fat fraction was different in the SMA cohort compared with the DMD and BMD cohorts. This may be explained by differences in pathophysiology between SMA and dystrophinopathies (DMD/BMD). SMA is a disease characterized by muscle atrophy, presumably caused by the effects of denervation secondary to motor neuron degeneration, in addition to some fat replacement of muscle tissue. ³² In BMD and DMD, pathophysiology is primarily characterized by replacement of muscle tissue by fat and endomysial fibrosis, of which the latter can reach up to 35% of muscle biopsy areas in histological studies. ³³ The T_2water of fibrotic tissue is below 10 ms, ³⁴ , ³⁵ possibly explaining the T_2water decrease in severely affected DMD and BMD individuals with high amounts of fat replacement. Alternatively, susceptibility differences between muscle water and fat have also been mentioned as explanations. ³¹ However, to fully explain this difference, further work is needed.

There are some limitations of the used model. We assumed that the fat in tissue contributes to the signal as one mono‐exponential component. However, fat contains several components with different relaxation times and J‐coupling interactions. ²² These J‐coupling effects influence the signal in a complex matter by stimulated echoes, possibly causing the relaxation to deviate from pure mono‐exponential behavior. Furthermore, we assume a fixed water fraction in the fat calibration, and for fitting stability for this fraction we fixed the T₂ relaxation of this water component to 20 ms. The assumption of a fixed T_2water for the water component in fat resulted in the most stable fit for all investigated cohorts, even though the calibration method with a two‐component calibration in fat shows a 0.7‐ms difference in T_2water. In addition, in our final recommended model (C), the assumptions of an approximate 10% fat contribution and a water T₂ in fat of about 20 ms are supported by previous work. ³⁰ , ³⁶ In future work in different cohorts, the T_2water of the fat component could be included in the fit and the stability of that model could be studied. Additionally, for the calibration of T_2fat, we assume that the fatty replacement in muscle tissue has the same composition and relaxation parameters as subcutaneous fat. However, differences exist in the composition of different fat tissues. ²⁵ More research is needed to quantify the composition of fat that infiltrates the muscle in neuromuscular diseases to mitigate potential biases due to these assumptions.

5. CONCLUSIONS

We recommend using an EPG‐based model for fitting T_2water from the MSE signal with calibration of T_2fat assuming two components. Moreover, we recommend including the slice flip‐angle profile in the model, which includes chemical‐shift displacements. In vivo data showed a gradual decline in T_2water for increasing fat fractions, with important implications for clinical studies using T_2water as an outcome parameter. Using these recommendations, T_2water measurements will be more reliable and will allow for better comparison of values between centers and diseases.

Keene KR, Beenakker J‐WM, Hooijmans MT, et al. T₂ relaxation‐time mapping in healthy and diseased skeletal muscle using extended phase graph algorithms. Magn Reson Med. 2020;84:2656–2670. 10.1002/mrm.28290

DATA AVAILABILITY STATEMENT

The used MATLAB scripts and one example data set presented in this article will be made available at the request of a qualified investigator. Requests should be made to K. R. Keene (k.r.keene@lumc.nl). A Mathematica version of the fitting algorithm is available at Github (https://github.com/mfroeling/QMRITools).