Magnetic Sedimentation Velocities and Equilibria in Dilute Aqueous Ferrofluids

Abstract

Dilute ferrofluids have important applications in the separation of materials via magnetic levitation. However, dilute ferrofluids pose an additional challenge compared to concentrated ones. Migration of the magnetic nanoparticles toward a magnet is not well counteracted by a buildup of an osmotic pressure gradient, and consequently, homogeneity of the fluid is gradually lost. Here, we investigate this phenomenon by measuring and numerically modeling time-dependent concentration profiles in aqueous ferrofluids in the field of a neodymium magnet and at 10 T in a Bitter magnet. The numerical model incorporates magnetic, frictional, and osmotic forces on the particles and takes into account the polydispersity of the particles and the spatial dependence of the magnetic field. The magnetic sedimentation rate in our most stable ferrofluids can be understood in terms of the magnetophoresis of separate nanoparticles, a best-case scenario when it comes to applications.

Introduction

Ferrofluids are liquid dispersions of superparamagnetic nanoparticles, dispersions that combine properties of liquids and magnets.¹ Many applications, from loudspeakers to rotary seals,²⁻⁵ require ferrofluids with a high volume fraction of the magnetic nanoparticles. The concentration of such ferrofluids remains relatively homogeneous in external fields because magnetic sedimentation is rapidly balanced by back-diffusion of the particles.^6,7 In dilute ferrofluids, however, sedimentation proceeds much longer before the equilibrium between sedimentation and diffusion is approached, and by then much of the magnetic material has settled toward the magnet. Dilute ferrofluids have applications in the separation of materials via magnetic levitation in magnetohydrostatic separators, for instance, in the separation of diamonds,⁸ minerals,⁹ waste metals,¹⁰ and plant seeds.¹¹ Moreover, waste plastics can be separated into different fractions in a single continuous processing step via magnetic density separation.¹² Sedimentation is a clear drawback of dilute ferrofluids since it renders their magnetic density separation performance time dependent. Nevertheless, the sedimentation rate can be kept as low as possible by using small magnetic nanoparticles and by preventing aggregation.¹³

The presence of aggregates is detrimental to the performance of the ferrofluid because they sediment much more rapidly than single particles. Sedimentation is driven by forces that scale with particle volume,¹⁴⁻¹⁷ whereas the frictional force on a colloidal particle, Stokes drag, scales with particle diameter, resulting in sedimentation rates that increase quadratically with particle size, assuming spherical particle shape.¹⁸ In magnetic fields, sedimentation can be further accelerated by the magnetically induced growth of aggregates. This does not occur for sufficiently small and separate nanoparticles. For instance, when two magnetic iron oxide particles in the 5—10 nm range collide with each other, they experience a magnetic coupling energy that is smaller than the thermal energy. However, for larger particles or magnetically aligned aggregates of magnetic nanoparticles, the magnetic coupling energy is much stronger. This can lead to the formation of large dipolar structures that sediment rapidly.¹⁹ On this basis, we recently demonstrated that colloidal stability at fields of up to 10 T can be predicted from the magnetic coupling energy and colloidal concentration.²⁰

Experimentally, the magnetic sedimentation of nanoparticles has been studied in different ways, using, for instance, optical transmission,^21,22 magnetic detection,^23,24 and density measurements.²⁵ Not only sedimentation rates were determined, but also sedimentation equilibrium profiles, to deduce the size distribution of polydisperse particles²¹ or the interactions of monodisperse particles.²⁶ To our knowledge, experimental time-dependent concentration profiles in magnetic fields have not yet been compared to theoretical calculations. This is, however, what is needed to validate a model that can predict how the concentration of magnetic materials will evolve in time in an installation for magnetic density separation on an industrial scale.

In this work, a model is presented that describes time-dependent concentration profiles of polydisperse ferrofluids in inhomogeneous magnetic fields. The model’s validity is evaluated through comparison with experimental data, obtained at different magnetic field strengths and gradients. The studied dispersions are two model ferrofluids, with reportedly good colloidal stability, and, for comparison, two commercial ferrofluids with somewhat lower stability. Finally, time-dependent profiles are calculated for sedimentation across distances typical for the industrial separation of plastics via magnetic density separation.

Theory

In our experiments, the main measured quantities are the saturation magnetization of the sample and a time- and height-dependent measure of the nanoparticle volume fraction. For this reason, we present the experimental time-dependent concentration profiles as a height-dependent saturation magnetization. For comparison, theoretical time-dependent profiles of the saturation magnetization are calculated as follows.

A log-normal distribution of nanoparticle size is assumed.²⁶ The probability of finding a particle of diameter D is defined in formula 1.

1

Here, D̃ is the median diameter and 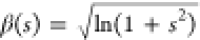, with s the standard deviation divided by the average diameter. Equation 1 gives the distribution of the number density, which is converted into a distribution of the volume fraction by calculating the median particle volume from the median diameter.²⁷ Time-dependent concentration profiles are calculated for each particle size separately and added together, with weights corresponding to the overall volume fraction of particles of each size. This assumes a lack of interactions between the particles, in line with the relatively dilute concentrations accessible in our measurements. By considering our sedimenting objects to be separate spheres, we also neglect the presence of aggregates of nanoparticles that stay together for chemical reasons, aggregates whose total magnetic moment is determined by its constituent nanoparticles and which have a different shape and density than separate nanoparticles.

In the numerical calculations, space is discretized in bins of height Δh, where Δh is defined as the total height of the liquid column divided by the number of bins. The transfer of particles between bins is calculated according to the average velocity of particles in a bin, which results from a balance of forces on the particles:

2

where F_mag, F_g, F_osm, and F_fric are the magnetic, gravitational, osmotic, and frictional forces, respectively. The average magnetic force on a particle is found by multiplying the magnetic field gradient at height h by the magnetic moment μ_np of the nanoparticle:²⁸

3

where L(B(h)) is the average degree of magnetic alignment of magnetic particles with the external field and dB(h)/dh is the magnetic field gradient. To find the dipole moment of the particles, the volume of the particle is multiplied by the bulk magnetization m_s of the material:

4

where D is the diameter of the nanoparticle. The average degree of alignment of magnetic moments to the external field is described by the Langevin function L(B):²⁹

5

where k_BT is the thermal energy of a particle.

In principle, the gravitational force on a particle can be calculated from Δρ, the mass density difference between the nanoparticle and the solvent, and g, the gravitational acceleration:

6

However, the gravitational force will be neglected, since it is smaller than the magnetic force by 2 orders of magnitude (Δρ·g ≪ m_s·L(B(h))·dB/dh).

For the osmotic force that counteracts magnetophoresis, the local osmotic pressure is assumed to be that of an ideal solution, neglecting any interactions between the particles:

7

Here, c(h) is the particle number concentration and dc(h)/dh is the number concentration gradient, calculated from the concentrations in neighboring bins, each of height Δh.

For the frictional force, the Stokes drag on a spherical particle is assumed:³⁰

8

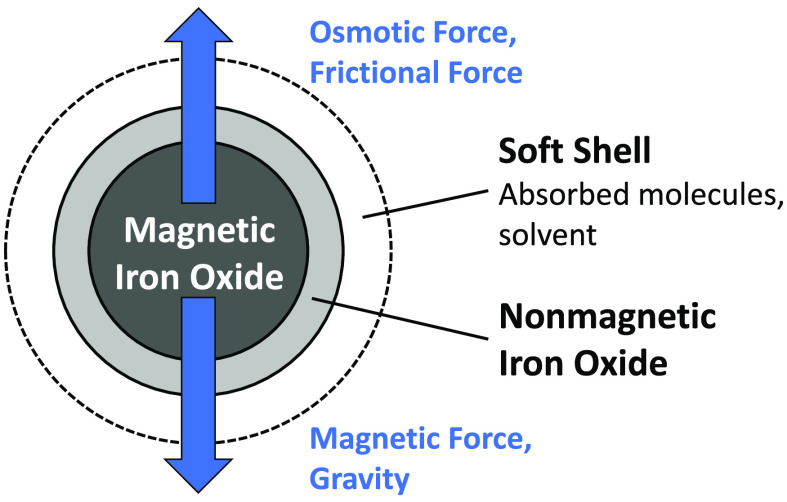
where η is the viscosity of the solvent, v the average velocity of the particles, and D_h the hydrodynamic diameter. Note that the hydrodynamic diameter D_h is treated separately from the magnetic core diameter D, allowing for the modeling of a shell of nonmagnetic material—such as a surfactant—around the magnetic core. An expression for the average velocity of all particles in a bin at height h is found by combining and rewriting eqs 2, 3, 7, and 8:

9

Time-dependent concentration profiles are computed numerically by starting from a homogeneous concentration profile and computing the change Δc(h) in number concentration resulting from transfer between neighboring segments in discrete time steps Δt:

10

Equation 10 is first calculated for every elevation before the calculated numbers of particles are transferred at once, resulting in a new concentration profile. Since the outermost bins can only exchange particles toward one side, particles cannot flow out of the system, and the total number of particles remains constant throughout the simulation.

The saturation magnetization profile of the polydisperse system at time t is obtained by summation of the profiles for each particle size, from a minimum value D_min to a maximum value D_max, taking into account the number concentrations c_D(h) of particles of diameter D at each height h, as well as the particle volumes and bulk magnetization of the material:

11

Here, m_sat is the concentration expressed as a saturation magnetization, calculated for direct comparison with the experimental data. A diameter step size ΔD = 1 nm is used.

The equilibrium concentration profile obtained after prolonged sedimentation can also be computed directly, without tracking profiles during time-dependent sedimentation. At equilibrium, for each particle size, the magnetic and osmotic forces (eqs 3 and 7) are equal at every height:

12

The equilibrium profile is obtained by first calculating the relative number concentrations of particles with diameter D in each bin according to eq 12, after which the total profile is scaled to agree with the total number of particles of diameter D in the system. Equation 11 is finally used to find the equilibrium profile for the entire system. By fitting this theoretical profile to the experimental equilibrium profile, a median particle size and standard deviation (eq 1) are found that we use to compute time-dependent concentration profiles that are consistent with the equilibrium profile.

Experimental Section

Ferrofluid Preparation

Maghemite (γ-Fe₂O₃) nanoparticles were prepared by coprecipitation of Fe(II) and Fe(III) salts, following a variation on the protocols by Massart and Dubois.^31,32 Iron chloride salts of p.a. grade were obtained from Sigma-Aldrich. All other chemicals, also of p.a. grade, were obtained from Merck. Water used in this protocol was Milli-Q water. In short, 5.19 g of FeCl₃·6H₂O and 1.92 g of FeCl₂·4H₂O were dissolved in 130 mL of water, and 3.0 g of NaOH in 20 mL of water was added rapidly under heavy stirring. After 5 min of stirring, the precipitate was gathered using a hand-held magnet, and the supernatant was poured off. The sediment was redispersed in 24 mL of 2 M HNO₃, and 3.42 g of FeCl₃·6H₂O in 36 mL of water was added, after which the suspension was refluxed at 90 °C for 1 h. After refluxing, particles were gathered by hand-held magnet, the supernatant was poured off, and the particles were redispersed in 2 M HNO₃. This washing step was repeated twice. Here, the batch was split into two equal parts: (1) part of the sediment (batch PPEG) was redispersed in 2 mL of 30 mg/mL poly(ethylene glycol) monophosphate (M_w = 2000 g/mol) and (2) the remainder of the particles (batch Citrate) was redispersed in 8 mL of 375 mM trisodium citrate and refluxed at 90 °C for 20 min. After cooling down, particles were precipitated by the addition of acetone and transferred to a 10 mM NaCl solution. Particles were washed with 10 mM NaCl four times to a final volume of 2 mL.

Two commercial ferrofluids of undisclosed precise composition (sterically stabilized magnetic iron oxide in water) were also used in the experiments. One ferrofluid, labeled FT, was produced by FerroTec (Santa Clara, USA) for Urban Mining Corporation (Rotterdam, The Netherlands) for use in magnetic density separation. The other ferrofluid, labeled UMC, was produced by Urban Mining Corporation.

Surfactant Preparation

Poly(ethylene glycol) monophosphate (M_w = 2000 g/mol) was synthesized following a variation on published protocols.³³⁻³⁵ To a solution of 5 g of poly(ethylene glycol) methyl ether (M_w = 2000 g/mol) in 7.5 mL of THF, 0.41 g of POCl₃ was added under stirring. The solution was stirred overnight, after which the reaction was stopped by the addition of 5 mL of water. THF and water were evaporated at reduced pressure. The product was purified by dissolving it in 5 mL of CHCl₃ and running it through a column (40 mm diameter, approximately 15 cm height) filled with silica particles (mesh size 200–425). The eluent was a mixture of CHCl₃ and methanol, where the volume fraction of methanol was linearly increased from 0 to 3.5%. Upon reaching 3.5% volume fraction of methanol, the column was flushed with 10% methanol solution. Collected fractions were analyzed by TLC plates using the Dragendorff reagent³⁶ as indicator, which stains all poly(ethylene glycol) compounds. All fractions containing poly(ethylene glycol) compounds were analyzed by ¹H and ³¹P NMR, after which the fractions containing poly(ethylene glycol) monophosphate were collected and the solvent was evaporated under reduced pressure. The final product was dissolved in water to a final concentration of 30 mg/mL.

Sample Characterization

Magnetic characterization was done by vibrating sample magnetometry using a Microsense EZ-9. Measurements were performed up to 1.5 T on weighed samples containing approximately 60 μL in a plastic cup. Magnetization curves were used to fit log-normal particle magnetic size distributions.³⁷

Transmission electron microscopy was done using a Tecnai 10 at 100 kV. For size distributions from TEM images, at least 120 particles were measured for each sample.

Analytical centrifugation experiments were performed on a Beckman Coulter ProteomeLab XL-I analytical ultracentrifuge. A sample of ferrofluid was diluted to an iron oxide volume fraction of approximately 1 × 10^–4 with 10 mM NaCl in water and was put in a cell with 3 mm optical path length. Absorbance was measured at a wavelength of 376 nm against a reference cell containing 10 mM NaCl in water. The experiment was performed at a rotational rate of 16 000 rpm at 20 °C (20 000 g at 7.0 cm from the rotor axis). In order to obtain a distribution of sedimentation coefficients, scans were analyzed using Sedfit software version 16.1c, fitting a continuous c(s) distribution model, where c is the concentration and s is the sedimentation coefficient (see the Supporting Information). In the fitting, the bottom was kept at a fixed value, and the meniscus, the frictional coefficient, and the baseline were floated.

Dynamic light scattering measurements were performed on a Malvern Instruments Zetasizer Nano ZS using a 633 nm laser at 20 °C. Scattered light was collected at an angle of 173°. For each measurement, 15 runs of 10 s each were performed, and reported values are the average of 20 measurements. Samples were diluted to an iron oxide volume fraction of approximately 1 × 10^–5.

Magnet Characterization

Sedimentation experiments were carried out in well-characterized magnetic fields. Calibration data of the Bitter magnet used for high-field measurements are publicly available from the HFML Web site.³⁸ The calibration data for the Bitter magnet are obtained by setting a constant current (typically 10 kA) through the magnet and measuring the field as a function of height using a Hall probe. Subsequently, the Hall probe is fixed in the field center, and the magnetic field is measured as a function of current. Calibration measurements for the low-field permanent magnet setup, containing cylindrical neodymium magnets of 30 mm thickness and 45 mm diameter (Supermagnete GmbH), were performed using a Lakeshore 421 Gaussmeter, fixing a MMT-6J04-VR probe to a cathetometer with micrometer-sensitive digital readout of the height and taking into account the precise position of the Hall effect sensor inside the probe. Measurements show excellent agreement with theoretical predictions for the magnetic field along the axial direction of a cylindrical permanent magnet.³⁹ Magnetic field profiles for both setups are shown in Figure 1.

Figure 1.

(a) Magnetic field as a function of height inside the bore of the 30 T Bitter magnet used in this research. Field is expressed in units of B₀, the magnetic field in the center of the magnet, which is adjustable from 0 to 30 T. Height is defined relative to the center of the field. The inset shows a schematic of the measurements setup with the sample in red; vertical sample position is adjustable within the bore of the magnet. Sample liquid column height: 1 mm. (b) Magnetic field as a function of height for a cylindrical magnet of 30 mm thickness and 45 mm diameter. The solid line represents theoretical field, and the marks indicate measurements done on five magnets.³⁹ The inset shows a schematic of the measurements setup, with the sample indicated in red. Sample liquid column height: 10 mm.

Sedimentation Experiments

Low-field sedimentation experiments were done in polycarbonate cuvettes with a cross section of 2 mm by 9 mm filled to 10 mm height, closed by a cap to prevent evaporation. Cuvettes were placed on the mentioned neodymium magnets. The position of samples with respect to the magnets was controlled precisely by a custom-built magnet holder with a cutout for sample placement.

Measurements of concentration profiles in the low-field setup were done ex situ, using a LUMiReader X-ray (LUM, Berlin, Germany). Concentration profiles were calculated from X-ray absorbance, which scales linearly with concentration. This was confirmed by separate calibration experiments for all ferrofluids. Samples were carefully taken from the magnet and placed in the LUMiReader X-ray, where X-ray transmission profiles were measured at 17.48 keV with a spatial resolution on the order of 100 μm. Each measurement typically took 11 scans. After measurements, samples were carefully placed back on the magnets. In order to check for disturbances in the concentration profiles due to movement of the sample, all low-field measurements were performed as duplicate or triplicate experiments. All low-field sedimentation experiments were performed at 20 °C.

High-field sedimentation experiments were performed at the High Field Magnet Laboratory in Nijmegen.³⁸ Samples were placed in the bore of a 30 T Bitter magnet using a custom-made sample holder, adjustable in height. The temperature was kept at 25 °C using a Julabo FP-50 HE refrigerated/heating circulator. By changing the position of the samples with respect to the center of the magnetic field and the current through the magnet, magnetic field strength and gradient could be separately adjusted. Up to seven capillaries at a time were positioned horizontally in the sample holder. Rectangular capillaries with internal cross section of 50 μm × 1 mm were used, positioned such that the sedimentation took place over a total height of 1 mm. Using optical imaging, the sedimentation was followed in situ. Concentration profiles were calculated from optical attenuation in the green channel of the CCD camera. Calibration experiments were performed for all ferrofluids.

Numerical Calculations

Simulations were performed using a range of values for simulation parameters Δt and Δh. Final values for Δt and Δh were chosen such that decreasing them by a factor of 2 influenced the calculated concentrations by less than 1%. At higher values of Δt and Δh than used to calculate the figures in the next section, computational artifacts led to diverging results (negative concentrations and loss of continuity of the concentration profiles). At the finally chosen values of Δt and Δh, the computation time was limited to approximately 4 h on a personal computer with an Intel Core i5-6400 processor. In the section on Sedimentation Rates, for the low-field simulations, Δt was 200 ms and Δh was 20 μm, whereas for the high-field experiments simulations, Δt was 10 ms and Δh was 10 μm. In the section Prediction of Magnetic Sedimentation on an Industrial Scale, Δt was 5 s and Δh was 1 mm.

Results and Discussion

In this section, size distributions of the particles will first be presented, as determined in three different ways: magnetometry, electron microscopy, and sedimentation equilibrium profiles. Then, time-dependent sedimentation measurements will be reported and compared with numerical calculations, and complementary analytical centrifugation and light-scattering measurements will be discussed as well. Finally, the physical model will be applied to predict sedimentation on the length scale of an industrial installation for magnetic density separation.

Particle Size Distributions

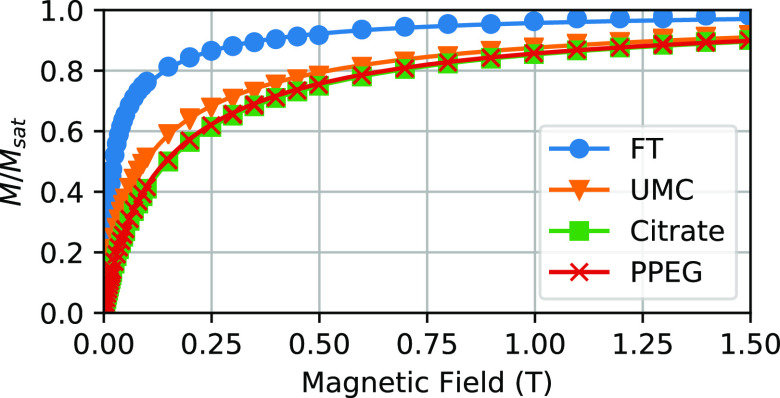
The magnetization curves (Figure 2) displayed no hysteresis, confirming the presence of superparamagnetic particles. Size distributions were obtained by fitting according to eqs 1 and 5. The volume magnetization of the material used to calculate magnetic size distributions was 430 kA/m for the homemade maghemite particles.⁴⁰ For the commercial particles, we concluded from magnetometry, infrared spectroscopy, and density measurements with a pycnometer that they probably consisted largely of magnetite, whose volume magnetization is 480 kA/m.⁴¹

Figure 2.

Magnetization curves for the tested ferrofluids, scaled to saturation magnetization. No hysteresis was observed, and for clarity, only the positive part of the measured curves is shown.

All samples were analyzed by TEM; see typical images in Figure 3. Particles in all ferrofluid samples here have irregular shapes, although the aspect ratio of the particles is close to 1. The size analysis of the commercial systems from TEM images was hindered by the presence of excess surfactant. In all samples, the size distribution was found to be log-normal, as expected for coprecipitated maghemite ferrofluids.⁷

Figure 3.

Typical TEM images for (a) citrate ferrofluid, (b) PPEG ferrofluid, (c) FT ferrofluid, and (d) UMC ferrofluid. Scale bars represent 50 nm in all images.

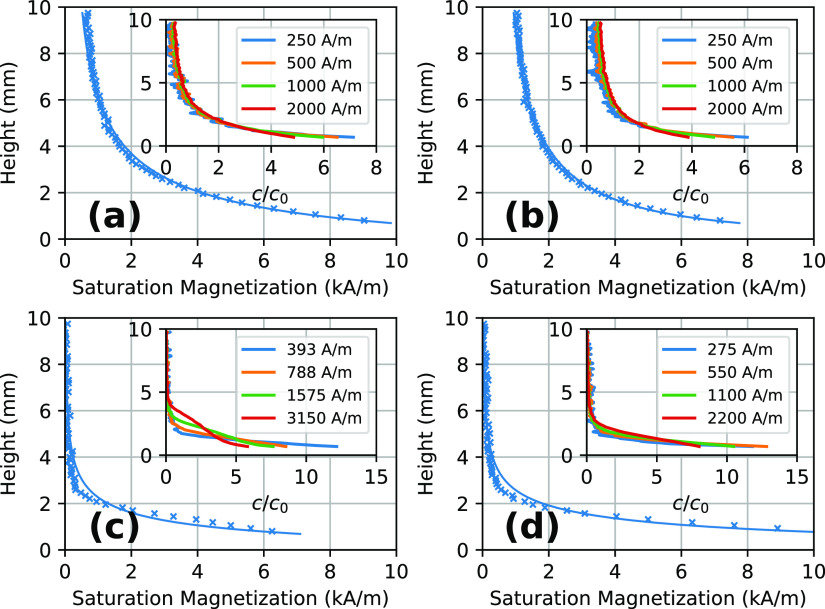
Equilibrium concentration profiles in the low-field sedimentation setup were typically obtained after 200 h of equilibration. In the approach presented in the Theory section, particle interactions are neglected, which implies that there should be no effect of initial concentration on the shape of the equilibrium profile. Sedimentation experiments were performed for a range of initial concentrations, and a selection of the results is shown in Figure 4. Each plotted profile represents the average of duplicate or triplicate measurements on different samples of the same fluids. No significant differences were found between multiple experiments with similar initial conditions.

Figure 4.

Equilibrium concentration profiles in the low-field setup as measured (crosses) and fitted according to eqs 1 and 12 (full lines). Concentration is expressed as a saturation magnetization since the raw data consists of saturation magnetizations of the entire samples, plus height-dependent absorbance data that scale with the volume of magnetic material. Concentration profiles are (a) citrate ferrofluid with initial saturation magnetization 2000 A/m, (b) PPEG ferrofluid with initial saturation magnetization 2000 A/m, (c) FT ferrofluid with initial saturation magnetization 788 A/m, and (d) UMC ferrofluid with initial saturation magnetization 1100 A/m. Insets show measured equilibrium concentration profiles for a range of concentrations c, scaled to their initial concentration c₀. Height is defined relative to the surface of the magnet.

Particle size distributions were calculated by fitting equilibrium concentration profiles to log-normal particle size distributions (see the Theory section, in particular eqs 1, 11, and 12). For the PPEG and citrate ferrofluids, the measurements with the highest initial concentration were used, as they provide the best signal-to-noise ratio. Since the equilibrium profiles for the FT fluid show a concentration dependence, the most dilute sample was used for the fitting. For the UMC fluid, the sample with saturation magnetization of 1100 A/m was used for fitting. These samples were chosen because the effects of particle interactions are expected to decrease with lower concentration.

The particle size distributions found by the three methods agree fairly well with each other in the case of the citrate and PPEG ferrofluids (Figure 5 and Table 1). The particle size as measured by TEM is larger than that obtained by magnetic methods since the particle contains a magnetic core and a layer of nonmagnetic iron oxide.^{27,32,42−44} From the X-ray absorbance of our samples, compared to their saturation magnetizations and literature values for the mass attenuation coefficients and densities of maghemite and water,^45,46 the maghemite particles have an average bulk magnetization of 229 kA/m; see the Supporting Information. This corresponds to a nonmagnetic iron oxide shell of about 0.5 nm, in line with earlier results⁷ and the conclusion drawn from comparing size distributions from TEM and VSM.

Figure 5.

Volume-weighted particle size distributions as found by TEM analysis (blue histograms), VSM analysis (dashed red lines), and the sedimentation equilibrium fit (solid black lines) for (a) citrate ferrofluid, (b) PPEG ferrofluid, (c) FT ferrofluid, and (d) UMC ferrofluid. Parts of this figure were previously published in a different form in ref (20).

Table 1. Overview of Volume-Weighted Particle Size Distributions Found by VSM Measurements, TEM Images, and Magnetic Sedimentation Experiments (Average Sizes and Standard Deviations).

sample	VSM (nm)	TEM (nm)	sedimentation (nm)
citrate	6.0 ± 2.5	6.6 ± 1.5	6.9 ± 1.8
PPEG	6.1 ± 2.6	7.5 ± 1.9	5.8 ± 2.1
FT	10.5 ± 5.8	14.0 ± 3.5	9.1 ± 1.8
UMC	6.7 ± 3.5	8.1 ± 2.1	9.6 ± 1.9

In the case of the FT and UMC fluids (Figure 4), the fitted concentration profiles deviate from the measured concentration profiles, and more discrepancy is found between the particle size distributions from sedimentation equilibrium analysis and data from the other methods. In the case of the FT fluid, the largest particles seen by TEM disappear from the sedimentation equilibrium profile, particles that presumably aggregated and rapidly sedimented beyond the experimentally accessible concentration range. In the case of the UMC fluid, the entities detected in the equilibrium profile show agreement with the particle sizes determined by TEM, but they are significantly larger than those found by VSM, possibly indicating small aggregates or multidomain particles.

It is noted that when the sample is removed from the magnet after sedimentation equilibrium has been obtained on a magnet, diffusion slowly causes the sample to revert to its initial homogeneous profile; see the Supporting Information.

Sedimentation Rates

Concentration profiles were measured at several times during the sedimentation process (Figure 6). However, due to the ex situ nature of the analysis in the low-field sedimentation experiments, concentrations profiles could be measured only once every several hours (Figure 6a). In the high-field setup (Figure 6c), depending on the experiments, measurements were taken in situ at intervals of a few seconds.

Figure 6.

(a) Selection of measured concentration profiles for the citrate ferrofluid (initial concentration 2000 A/m) as measured with the low-field setup using X-ray transmission. Profiles shown are averages of measurements on three samples. Shown profiles were measured at 0, 3, 19, 43, 67, and 163 h. (b) Simulated concentration profiles at the same time points using the particle size distribution obtained by fitting the equilibrium concentration profile, with a 3 nm nonmagnetic shell (see the Theory section). (c) Selection of measured concentration profiles for the citrate ferrofluid (initial concentration 2200 A/m) as measured in the high-field setup at 10 and 100 T/m using optical transmission. Shown profiles were measured at 0, 5, 10, 30, 60, and 90 min. (d) Simulated concentration profiles using the same particle size distribution as in panel (b). Profiles are shown at the same time points as in panel (c). Parts of this figure were previously published in a different form in ref (20).

Since there is no sharply defined sedimentation front to be monitored, we describe the average sedimentation velocity of the particles in a different way. For each measured profile, the concentration-weighted average particle height is calculated using eq 13, with h_max and h_min the outermost points of the measured profile:

13

Here, c(h) is the concentration as a function of height.

The rate at which the average particle height changes is an average sedimentation velocity of all particles in the system. This average velocity starts at a maximum, decreasing as the system tends toward a sedimentation–diffusion equilibrium. This is shown for a selection of experiments in Figure 7.

Figure 7.

(a) Concentration-weighted average particle height in the low-field setup plotted as a function of time for the four ferrofluids. (b) Concentration-weighted average particle height in the high-field setup plotted as a function of time; the latter experiments were performed using the citrate ferrofluid in a magnetic field of 10 T, with different magnetic field gradients. Symbols represent measurements; lines represent simulations on the basis of size distributions from sedimentation equilibrium profiles plus, in the case of the PPEG and citrate fluids, a nonmagnetic shell of 3 nm in thickness.

Although this representation of the data is less informative than plotting full concentration profiles, it does provide a clear indication of both the magnitude and the time scale at which sedimentation occurs. Using the approach presented in the Theory section, concentration profiles were simulated. The particle size distribution found from the magnetic sedimentation equilibrium profile was used for the magnetic size of the particles, and the hydrodynamic radius was varied to fit the measured data. The hydrodynamic radius was taken as the magnetic radius plus an additional shell of fixed thickness, independent of the magnetic radius; see below.

The calculations for the UMC ferrofluid show agreement with experimental data (Figure 7a) if the simulations are performed without a shell around the particles, even though these particles are likely to have a stabilizing layer. Apparently, even though the equilibrium concentration profile was not fitted well, the calculated effective particle size distribution does give a good description of the sedimentation rate.

For the FT ferrofluid, sedimentation in experiments is faster than that in simulations. The simulations were performed without a shell around the particles, which is unlikely to be the case for this ferrofluid. For simulations performed with a shell, the deviation between simulated and experimental results grows larger. The largest deviation between simulations and experiments is in the initial part of the experiment, pointing to the presence of aggregates and field-induced structures.

The size distribution, magnetic moment, and sedimentation coefficient of such aggregates are not well described by our simple magnetic sedimentation model, which assumes a single population of separate dipolar spheres. The commercial samples probably contain more than one population of particles: separate nanoparticles, small chemical clusters of field-independent size, and larger magnetically growing clusters. The cluster size probably does not have a log-normal distribution. Moreover, the magnetic moment of an aggregate is a function of magnetic field strength, close to zero in zero field because of the random orientations of the nanoparticle magnetic moments, in contrast to the constant magnetic moment of a single superparamagnetic particle. Furthermore, the aggregates have a somewhat open, ramified structure and therefore a frictional coefficient that is higher than for a compact sphere containing the same amount of iron oxide.

Hydrodynamic Size Determination

For the PPEG and the citrate ferrofluids, the simulated sedimentation behavior agrees quantitatively with the experimental data when a shell thickness of 3 nm is assumed, both the time-dependent average heights (Figure 7) and the time-dependent profiles (Figures 6b and 6d). Since a compact physical shell of 3 nm thickness is unlikely for citrate-stabilized particles, considering the small size of the stabilizer molecules, we attribute this to a combination of a thin shell and a friction factor that is higher than that of a sphere. The shell around a particle is likely to consist of a layer of nonmagnetic iron oxide near the surface and a layer of stabilizing organic material. The friction factor of nonspherical particles is known to be different from that of spheres.⁴⁷ A cube, for instance, has an approximately 8% lower terminal velocity than a sphere of equal volume.⁴⁸

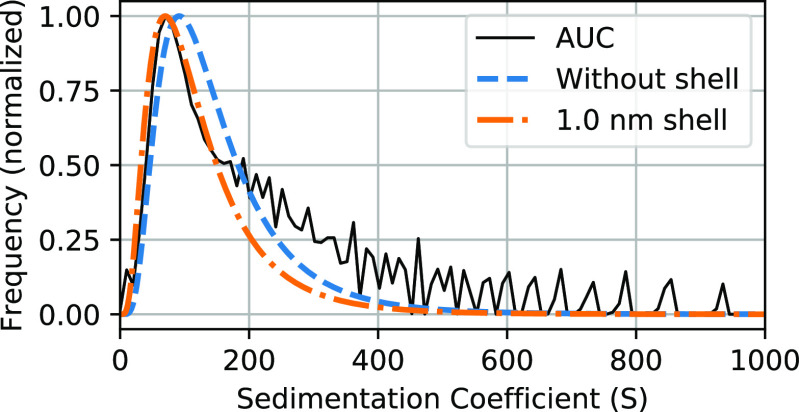
From analytical centrifugation, the hydrodynamic diameter of the citrate-stabilized maghemite particles in the absence of magnetic field is only about 2 nm larger than the iron oxide core (including nonmagnetic iron oxide layer); see Figure 8 (and the Supporting Information for further details). The thickness of the hydrodynamic shell found with this method is thus 1.0 nm, which is in line with values of 0.7–1.0 nm found by AFM for citrate layers on flat gold substrates and XPS analysis on gold nanoparticles,^49,50 where the citrate groups form a layer that is thicker than a single citrate group; it is unknown to us whether this also applies to citrate adsorption on iron oxide nanocrystals.

Figure 8.

Distribution of the sedimentation coefficient of the nanoparticles obtained by analytical ultracentrifugation (solid black line), compared to distributions calculated from the core size found by TEM without a shell (blue dashed line) or with a shell of 1.0 nm thickness (orange dashed line).

The hydrodynamic size of the citrate-stabilized particles was also examined using dynamic light scattering; see the Supporting Information. However, for such small particles, this technique often results in larger sizes than expected, which is often attributed to the presence of the adsorbed stabilizing molecules,⁵¹ but in our case, where we find an average diameter of 12.7 nm, such an explanation does not seem sufficient. Both the magnetic sedimentation equilibria and hydrodynamic sizes from AUC clearly indicate the presence of single particles not much larger than the iron oxide core. Optical inhomogeneity and the distinction between scattering particle size and hydrodynamic size should be taken into account, but this is likely to introduce more model dependence of the results. Moreover, values reported by DLS are dependent on scattering angle and concentration of nanoparticles.^52,53

In summary of the information on hydrodynamic size, obtained from magnetic sedimentation, DLS, and AUC, the three techniques do not agree with each other quantitatively. It is puzzling that the citrate-stabilized particles, which do not form dipolar structures in external field (Figure 5a, SE) because of insufficient magnetic coupling energy,²⁰ sediment more slowly in magnetic fields than expected from their physical size. If sedimentation had been more rapid than expected, this could have been ascribed to cooperative magnetophoresis, with the formation of field-induced structures that are more strongly accelerated than single particles in the magnetic gradient. A possible clue pointing to the origin of the discrepancy is the following trend: the experimental hydrodynamic size seems to decrease with increasing field-driven velocity v, with maximum size found in DLS (v ∼ 0.05 nm/s in normal gravity), intermediate size in magnetophoresis (v ∼ 0.1 μm/s), and minimum size in AUC (v ∼ 2 μm/s). This might suggest that field-driven motion of the particles causes a change in their average orientation or a deformation of the soft layer of citrate and solvent molecules at their surface, in ways that decrease friction. However, this is speculative, and the quantitative results also depend on the different practical limitations and operating assumptions of the three techniques, for instance, concerning the optical properties of the particles (see the Supporting Information, DLS).

Prediction of Magnetic Sedimentation on an Industrial Scale

The presented model was tested experimentally on a millimeter scale, but it can also be used to predict sedimentation across larger distances. In a magnetic density separation setup on an industrial scale, magnetic field gradients might typically be on the order of 10 T/m across several tens of centimeters. A simulation of the sedimentation of particles in our citrate ferrofluid was performed for a sample height of 20 cm and an exponentially decaying magnetic field of 4 T at the bottom of the fluid and going down to 0.54 T at 20 cm height (Figure 9a).

Figure 9.

(a) Height-dependent profiles of magnetic field strength and gradient as used for the simulation in panels (b) and (c). The magnetic field starts at 4 T and decays exponentially with a factor e every 10 cm across an experimental space of 20 cm. (b) Selection of concentration profiles as found by a simulation for the magnetic field shown in panel (a). The particle size distribution of the citrate ferrofluid was used. (c) Effective density profile as experienced by a millimeter-sized nonmagnetic particle across the experimental space over time. The initial ferrofluid concentration was set at a saturation magnetization of 500 A/m.

Simulated concentration profiles are shown in Figure 9b. Remarkably, once sedimentation starts, the concentration profile goes through a maximum in the upper half of the system. Since we assume an exponential field profile, not only field strength and its first derivative—field gradient—increase toward the magnet, but also the second derivative of field strength. As a result, the magnetic force increases rapidly in the vicinity of the magnet, and particles are removed toward the bottom in a zone that becomes depleted of particles. Much farther from the magnet, in the top quarter of Figure 9b, the situation resembles more closely the situation in our laboratory-scale experiments, with a field gradient that is not strongly height-dependent; there, the concentration gradually increases toward the magnet as particles of different sizes sediment more slowly at more or less constant rates.

The calculated profiles of the apparent density (Figure 9c) present the height dependence of ρ_liquid + M dB/dh, where ρ_liquid is the mass density of the ferrofluid, M is the magnetization of the ferrofluid, and dB/dh is the magnetic field gradient. Nonmagnetic particles that are much larger than the magnetic nanoparticles experience this apparent density.⁵⁴ The formation of a dense sediment at the bottom of the experimental space starts right away, but in the first 100 h, most of the effective density profile remains largely unchanged. In some ways, a ferrofluid with nanoparticles in the size range of 5–10 nm diameter dispersed as single particles is a best case scenario since sedimentation will be much faster with larger particles or aggregates. However, our calculations do not take into account convection, which may cause homogenization of the fluid and therefore mitigate the effects of sedimentation. No convective flow was observed in our laboratory-scale experiments, but in industrial magnetic density separation, motion of the nonmagnetic millimeter-sized particles as well as temperature gradients will unavoidably cause convection. For industrial separation of materials using dilute magnetic fluids, magnetic sedimentation may well be a manageable problem, as long as aggregation of the magnetic nanoparticles can be prevented.

Conclusions

Particle size distributions of dilute polydisperse ferrofluids were deduced from equilibrium concentration profiles measured in well-characterized magnetic fields. On the basis of these size distributions, time-dependent concentration profiles were calculated. In the case of ferrofluids with particles in the 5–10 nm diameter range without aggregation, sedimentation rates agree quantitatively with the presented theory, although questions remain about the precise origin of the hydrodynamic size, friction factor, or diffusion coefficient of the particles. The same theoretical model is applicable to other stable ferrofluids in other experimental geometries and on other length scales. Magnetic sedimentation in dilute ferrofluids cannot be prevented because of the weak osmotic pressures in such systems. However, sedimentation is slow, and possibly a bit of convection may suffice to keep the ferrofluid much more homogeneous during applications than predicted by the presented model.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.0c06795.

• Additional experimental results for the citrate-stabilized ferrofluids: back-diffusion after removal of the magnet; analytical ultracentrifugation; bulk magnetization from saturation magnetization and X-ray absorbance; dynamic light scattering (PDF)

The authors declare no competing financial interest.