Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Dec 12;59(1):548–554. doi: 10.1021/acs.inorgchem.9b02834

Cs3Cu4In2Cl13 Nanocrystals: A Perovskite-Related Structure with Inorganic Clusters at A Sites

Roman Kaiukov †,§, Guilherme Almeida †, Sergio Marras ‡, Zhiya Dang †, Dmitry Baranov †, Urko Petralanda †, Ivan Infante †,∥,*, Enrico Mugnaioli ⊥, Andrea Griesi ⊥,#, Luca De Trizio †,*, Mauro Gemmi ⊥,*, Liberato Manna †,*
PMCID: PMC7497414  PMID: 31829568

Abstract

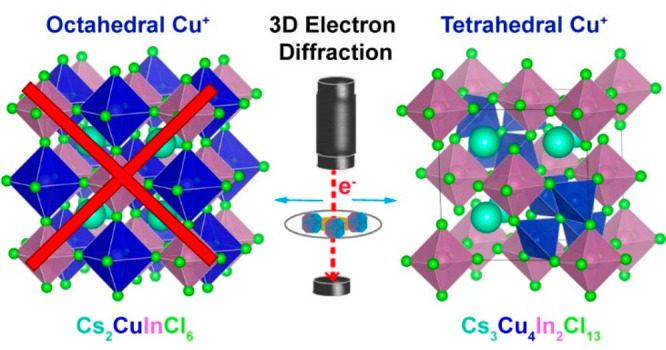
graphic file with name ic9b02834_0006.jpg

An effort to synthesize the Cu(I) variant of a lead-free double perovskite isostructural with Cs2AgInCl6 resulted in the formation of Cs3Cu4In2Cl13 nanocrystals with an unusual structure, as revealed by single-nanocrystal three-dimensional electron diffraction. These nanocrystals adopt a A2BX6 structure (K2PtCl6 type, termed vacancy ordered perovskite) with tetrahedrally coordinated Cu(I) ions. In the structure, 25% of the A sites are occupied by [Cu4Cl]3+ clusters (75% by Cs+), and the B sites are occupied by In3+. Such a Cs3Cu4In2Cl13 compound prepared at the nanoscale is not known in the bulk and is an example of a multinary metal halide with inorganic cluster cations residing in A sites. The stability of the compound was supported by density functional theory calculations that also revealed that its bandgap is direct but parity forbidden. The existence of the Cs3Cu4In2Cl13 structure demonstrates that small inorganic cluster cations can occupy A sites in multinary metal halides.

Short abstract

We report the synthesis of Cs3Cu4In2Cl13 nanocrystals with a vacancy ordered A2BX6 perovskite structure, in which Cu(I) ions are tetrahedrally coordinated. In this new structure (determined by single-nanocrystal three-dimensional electron diffraction), 25% of the A sites are occupied by [Cu4Cl]3+ clusters (75% by Cs+), while the B sites are occupied by In3+. Such a compound, not known in the bulk, is the first case of a perovskite-related structure with inorganic cluster cations residing in A sites.

Introduction

Perovskites (ABX3) and perovskite-related compounds are some of the most chemically diverse crystal structures with many possible substitutions at A and/or B sites, as demonstrated in oxide systems.1−3 Similarly, multinary metal halides are very versatile: many types of substitutions are known to be possible at the B sites (e.g., double and vacancy ordered perovskites)4−6 and A sites [can be filled with both atomic (inorganic) and molecular organic cations].7−9 However, substitutions at the A site in multinary metal halides are mostly limited to monovalent cations (cesium, methylammonium, formamidinium, etc.),10 with rare examples of divalent organic cations, such as piperazine-1,4-diium (C4H12N42+) and a few others.11−14

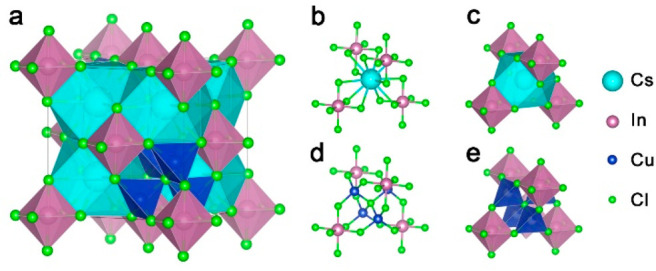
In our efforts to explore new metal halide materials, we have discovered a novel perovskite-related structure with a general formula Cs3Cu4In2Cl13, in the form of colloidal nanocrystals (NCs). The structure of these NCs was determined using three-dimensional electron diffraction (3D ED) on single NCs in combination with powder X-ray diffraction (XRD), as is discussed in detail below. One way to describe Cs3Cu4In2Cl13 is to relate it to a vacancy (□) ordered perovskite [A2BX6 type, (Cs3,Cu4Cl)(In2,□2)Cl12] in which 25% of the A sites are occupied by [Cu4Cl]3+ clusters and the remaining 75% by Cs+, while the B sites are occupied by In3+ ions. In this structure, Cu(I) is tetrahedrally coordinated, with each Cu(I) ion surrounded by three chloride anions belonging to three neighboring [InCl6]3– octahedra, and with a fourth chloride anion sitting at the center of the A site that would be otherwise occupied by a Cs+ ion (Scheme 1). Although substitutions at the A site with atomic and/or molecular organic cations are common, the reported structure further expands the possible variants by demonstrating that small inorganic cluster cations ([Cu4Cl]+) can occupy A sites, as well. While previous theoretical works have shown that Cs2CuInCl6 double perovskites with octahedrally coordinated Cu(I) at one of the B sites are unlikely to exist,15 our density functional theory (DFT) calculations indicate that the Cs3Cu4In2Cl13 structure is stable. Electronic structure calculations unveiled a strong charge-transfer character as [Cu4Cl]3+ and [InCl6]3– clusters are electronically disconnected and align in a type II arrangement, resulting in a semiconductor with a parity forbidden bandgap of 2.4 eV (∼2.9 eV from the experiment).

Scheme 1. (a) Unit Cell of the Cs3Cu4In2Cl13 Structure and Details of (b and c) the Cs+ Site and (d and e) the Corresponding Site with the Cs+ Ion Being Replaced by a (Cu4Cl)3+ Cluster, with Ball-and-Stick and Polyhedral Representations, Respectively.

Scheme 1

Open in a new tab

Experimental Section

Chemicals

Cu(I) acetate (97%), In(III) acetate (99.99%), Cs carbonate (Cs2CO3, reagent plus 99%), oleic acid (OA, 90% technical grade), benzoyl chloride (98%), dioctyl ether (99%), and anhydrous toluene (99.8%) were purchased from Sigma-Aldrich. Oleylamine (OLAm, 80–90%) was purchased from Acros Organics. All chemicals were used without further purification.

Synthesis of Cs–Cu–In–Cl NCs

A 1 M cesium oleate stock solution was prepared by mixing 1.63 g of cesium carbonate with 10 mL of oleic acid in a three-neck flask under a nitrogen flux. The mixture was heated to 100 °C and kept at that value for 10 min, after which the temperature was increased to 120 °C and kept at that value for 1 h (the mixture usually became clear after being heated at 120 °C for 40 min). The solution was cooled to room temperature, and it was then mixed with 30 mL of acetone, which led to the precipitation of cesium oleate. The precipitate was washed five times with 30 mL of acetone and then dried in air at room temperature for 24 h. In a typical synthesis of Cs–Cu–In–Cl NCs, 0.12 mmol of cesium oleate (50 mg), 0.23 mmol of indium(III) acetate (68 mg), 0.22 mmol of copper(I) acetate (28 mg), 1 mL of oleic acid, and 4 mL of dioctyl ether were loaded in a three-neck flask and degassed under vacuum for 5 min at room temperature. The mixture, still under vacuum, was heated to 115 °C and kept at that temperature for 10 min during which it became clear and slightly greenish. The atmosphere was then switched to nitrogen, and the solution was heated to 145 °C at a rate of 30 °C/min. After the temperature had reached 145 °C, 0.3 mL of degassed oleylamine was swiftly injected, and the mixture changed its color to deep bluish. Following this, 2.58 mmol of benzoyl chloride (0.3 mL) was injected into the flask, and the solution became turbid and dark brown in color. After 4 min, the synthesis was quenched by immersing the flask in an ice–water bath. Once at room temperature, the final solution was centrifuged at 5500 rpm for 5 min and the supernatant was discarded, while the precipitate was redispersed in 30 mL of anhydrous toluene. The NCs were cleaned by repeated cycles (five in total) of centrifugation followed by redispersion in anhydrous toluene. The final NC solution was stored in a N2-filled glovebox for further characterization.

Optical Absorption Spectroscopy

Absorption spectra from NC films were recorded using a Cary5000 spectrophotometer equipped with an integrating sphere. The samples were prepared by drop-casting a concentrated suspension on a quartz glass slide.

Transmission Electron Microscopy (TEM) Analysis

Low-resolution TEM images were acquired on a JEOL JEM-1011 microscope equipped with a thermionic gun at an accelerating voltage of 100 kV. The samples were prepared by drop-casting diluted NC suspensions onto 200 mesh carbon-coated copper grids. High-resolution (HR) TEM, high-angle annular dark field (HAADF) scanning TEM (STEM), and energy dispersive X-ray spectroscopy (EDS) characterizations were performed using an image-corrected JEOL JEM2200FS microscope operating at 200 kV and equipped with a Bruker Quantax 400 EDS system. The samples were prepared by drop-casting the NC solution onto ultrathin carbon/holey carbon-coated 400 mesh gold grids.

Scanning Electron Microscopy (SEM)

The samples were drop-cast on Si wafers and then placed in a vacuum for 30 min. No coating procedures were performed as the samples were already conductive. The analysis was performed using a SEM JEOL JSM-7500LA microscope equipped with a cold field-emission gun, operating at a 15 kV acceleration voltage. Energy dispersive spectroscopy (EDS, Oxford instrument, X-Max, 80 mm2) was used to evaluate the elemental ratios. All experiments were performed at an 8 mm working distance, a 15 kV acceleration voltage, and a 15 sweep count for each sample.

Powder X-ray Diffraction (XRD) and Rietveld Analysis

X-ray diffraction analysis was performed on a Rigaku SmartLab system, equipped with a 9 kW rotating Cu anode working at 40 kV and 150 mA and a D/teX Ultra one-dimensional silicon strip detector. XRD samples were prepared by grinding dried NCs into a powder. The measurements were carried out in air at room temperature using a zero diffraction silicon substrate. The Rietveld refinement was performed with the GSAS software.16 The refined parameters were as follows: 16 coefficients of a Chebyshev polynomial curve for background modeling, five profile parameters of a pseudo-Voigt profile function (GU, GV, GW, LX, and LY), the scale factor, the zero shift, the unit cell parameters, the atomic coordinates, the partial occupancies of the (Cs, Cl) and Cu sites, and the isotropic thermal parameters of all of the atoms (for a total of 31 parameters). The Cu occupancies and the Cl occupancy of the Cu4Cl cluster at the Cs site were constrained to be equal.

3D Electron Diffraction Experiments and Analysis

3D ED data17,18 were collected on a Zeiss Libra transmission electron microscope operating at 120 kV and equipped with a LaB6 source and a Bruker EDS detector XFlash6T-60 instrument. 3D ED acquisitions were performed in STEM mode after defocusing the beam to have a pseudoparallel illumination of the sample. A beam size of ∼150 nm in diameter was obtained by inserting a 5 μm C2 condenser aperture. An extremely mild illumination was adopted to avoid any alteration or amorphization of the sample and to slow the accumulation of organic contaminants during the 3D ED experiment. 3D ED data were taken from nine nanoparticles by working in continuous-rotation mode19 or in discrete steps of 1° with a processing beam20 obtained with a Nanomegas Digistar P1000 device. Tilt ranges were ≤120°. The camera length was 180 mm, with a theoretical resolution limit of 0.75 Å. ED data were recorded by an ASI Timepix detector, able to record the arrival of single electrons and deliver a pattern that is virtually background-free. Data were analyzed using ADT3D21 and PETS22 for cell and space group determination. Intensity integration for structure determination and final least-squares refinement were performed with PETS using standard integration and interpolation options. The ab initio structure solution was achieved independently from two data sets collected on nanoparticles, using direct methods implemented in SIR2014.23 The least-squares refinement was performed using SHELXL24 without any restraints or constraints. For both the ab initio structure determination and the structure refinement, data were treated with the kinematical approximation (Ihkl proportional to F2hkl), using scattering factors for electrons that are present in the SIR2014 database.

DFT Calculations

Band structure calculations were performed using the BAND package, within the Amsterdam Modeling Suite (ADF),25,26 which employs Slater type orbitals and numerical atomic orbitals (NAOs) as basis sets.27 The exchange-correlation potential was approximated by the hybrid HSE06 exchange-correlation functional28 to attain a good accuracy in the band structure calculations. The employed basis set was a triple ζ augmented by one polarization function (TZP) for Cs, In, and Cu and a double ζ (DZP) for Cl. Due to the light elements involved, no spin–orbit coupling was included in the calculations. Inner electrons were kept relaxed. We used a k mesh grid of 3 × 3 × 3 for the Brillouin zone integration. All atomic positions and lattice parameters were relaxed until forces were <0.001 Hartree/Å. For thermodynamic stability calculations, we used the Quantum Espresso code,29 employing the DFT/PBESol exchange-correlation functional.30 Core electrons were replaced by ultrasoft pseudopotentials.31 We considered monoclinic space group (SG) No. 12 for InCl3, cubic SG No. 216 for CuCl, cubic SG No. 221 for CsCl, orthorhombic SG No. 62 for Cs3Cu2Cl5, trigonal SG No. 167 for Cs3In2Cl9, and cubic SG No. 224 for Cs3Cu4In2Cl13. All cells and atomic positions were relaxed below 0.002 eV/Å. We used a kinetic energy cutoff of 35 Ry in all cases, and 4 × 3 × 4, 5 × 5 × 5, 8 × 8 × 8, 4 × 4 × 3, 3 × 3 × 2, and 4 × 4 × 4 k grids were selected for the structures listed above, respectively.

Results and Discussion

Synthesis and Characterization of the NCs

The preparation of Cs–Cu–In–Cl NCs was possible via our recently developed benzoyl halide hot-injection route,32 which allows for the synthesis of complex metal halides starting from separate metal and halide precursors. Briefly, metal carboxylates [i.e., Cu(ac), In(ac)3, and Cs oleate powder] were dissolved in dioctyl ether in the presence of oleic acid at 115 °C under vacuum (10 min) forming a slightly green transparent solution. After the degassing step, the atmosphere was switched to nitrogen, and the temperature was increased to 145 °C. At this point, OLAm was swiftly injected, followed by benzoyl chloride, which caused the nucleation and growth of the NCs (see Experimental Section for details). After the cleaning steps, the product consisted of a light yellow precipitate.

Elemental analysis (performed via SEM- and STEM-EDS) indicated a composition of Cs3.0Cu4.2In2.0Cl12.8 (see Table S1). In particular, STEM-EDS characterization revealed that Cs, Cu, In, and Cl elements were uniformly distributed throughout the NCs (Figure S1). TEM analysis revealed that the product was made of NCs having different shapes, such as cubes, truncated cubes, and octahedral and triangular prisms, with sizes ranging from 20 to 60 nm (Figure 1a). HRTEM images from any of these NC shapes [see a representative NC in Figure 1b with its corresponding fast Fourier transform (FFT) reported in Figure S2] were always consistent with a perovskite-related lattice. As these NCs did not form stable colloidal dispersions [the suspensions were milky/white (see the inset of Figure 1c)], we measured their absorbance spectrum in the form of a thin film prepared by drop-casting the NC suspension on a quartz substrate. The NCs featured an absorbance onset at ∼400 nm (Figure 1c), indicative of a wide bandgap semiconductor. X-ray photoelectron spectroscopy (XPS) analysis revealed an oxidation state of +1 for Cs, +3 for In, and +1 for Cu (Figure 1d and Figure S3). Indeed, the position of the Cu 2p3/2 peak (at a binding energy of 932.0 ± 0.2 eV), together with that of the Cu LMM Auger peak (at a kinetic energy of 915.2 ± 0.2 eV), corresponding to a modified Auger parameter of 1847.2 eV, is in agreement with reports on Cu(I) compounds (Figure 1d).33,34 Moreover, the absence of typical Cu(II) satellites in the binding energy range of 940–950 eV is a further proof of the absence of Cu(II) species.34

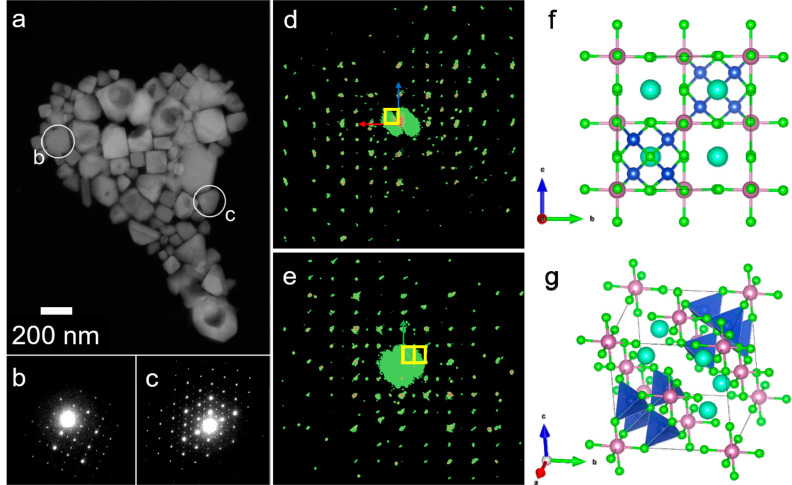
Figure 1.

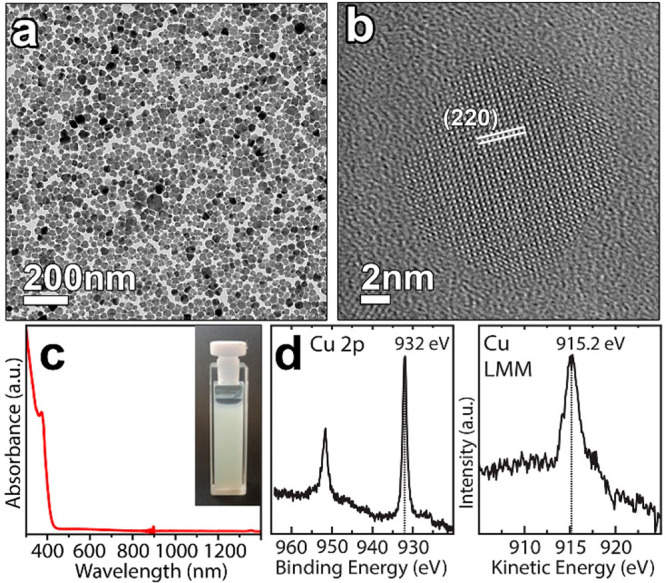
Figure 1

Open in a new tab

(a) Low-resolution and (b) high-resolution transmission electron micrographs of Cs3Cu4In2Cl13 NCs. The lattice planes were indexed considering a double perovskite structure (Fm3̅m; a = 10.48 Å). (c) Absorbance spectrum of the Cs3Cu4In2Cl13 NCs film. The inset shows the NC dispersion in toluene. (d) Selected regions of the X-ray photoelectron and Auger spectra of Cs3Cu4In2Cl13 NCs confirming the +1 oxidation state of copper.

The powder XRD peak positions of the NCs (Figure S4a) produced a reasonable match with a simulated powder XRD pattern of a hypothetical Cs2CuInCl6 double perovskite structure (space group Fm3̅m) with a lattice parameter of 10.48 Å in which Cu+ ions are octahedrally coordinated to Cl anions (Figure S4b). Still, the experimental peak intensities were different from the calculated ones, and, additionally, there were minor reflections that remained unmatched. This evidence suggested the presence of impurity phases or a deviation from the ideal structure of the double perovskite.

To disentangle the crystal structure of these NCs, we employed 3D electron diffraction (ED) analysis. To prepare NC samples of larger sizes, compatible with this technique, we carried out the synthesis at a higher temperature (175 °C), while keeping all of the other parameters constant. This new sample featured a powder XRD pattern that was almost identical to that obtained by working at 145 °C (Figure S5) and a very similar elemental composition (see Table S2). A representative HAADF-STEM image of this sample evidenced that the NCs could have two quite distinct habits (Figure 2a): the smaller NCs had a cubic shape with size of approximately 50–100 nm, while the larger ones had a platelet shape with a triangular or hexagonal cross section. The sizes of this second NC family ranged from 100 to 200 nm. Intermediate morphologies were also seen, with NCs characterized by corners and acute features that break the otherwise cubic habit (Figure S6). According to the 3D ED analysis, the cube-shaped particles had a metrically cubic cell with a lattice parameter of 10.5(2) Å, in apparent agreement with powder XRD results. All strong reflections were consistent with a face-centered cubic cell, but additional weak reflections appeared in positions that should be extinct due to the lattice centering (Figure 2d,e). It is worth pointing out that these additional reflections cannot be produced by dynamical scattering, as it could be expected for axial and planar extinctions. Their presence definitely points to a primitive lattice, which is in fact geometrically consistent with the minor reflections observed in the powder XRD pattern. The presence of the extinction rule 0kl: k + l = 2n pointed to extinction symbol “Pn – −” consistent with either space group Pn3̅ (201) or space group Pn3̅m (224).

Figure 2.

Figure 2

Open in a new tab

(a) HAADF-STEM image of an aggregate of NCs showing both cubic and triangular shapes. Cavities in the crystals are due to electron beam damage. (b) Diffraction pattern collected on a cube-shaped NC at a 0° tilt close to the [100] zone axis. (c) Diffraction pattern collected on a triangle-shaped NC at a 0° tilt close to the [111] zone axis. (d) Projection of the 3D ED diffraction volume along (100). The reciprocal unit cell is colored yellow. (e) Projection of the 3D ED diffraction volume along (110). The reciprocal unit cell is colored yellow. (f) Cs3Cu4In2Cl13 ordered structure viewed along [100]. (g) Diagonal view of the Cs3Cu4In2Cl13 ordered structure.

All attempts to determine the structure in the cubic symmetry failed. Instead, the ab initio structure determination by direct methods converged rapidly to a model when the symmetry was relaxed to the orthorhombic space group Pnnn (48) (Table S4). The structure can be described as a pseudoperovskite ABCl3, in which six of the eight A sites of the unit cell are occupied by Cs+ ions, while the remaining two sites are occupied by [Cu4Cl]3+ clusters, the latter aligned along one of the cubic [111] diagonals (see Figure 2f,g). In this structure, half of the octahedral sites are occupied by In3+ ions and half by vacancies. The model is also consistent with a cubic Pn3̅m symmetry, however with small distortions of the coordination polyhedra. Therefore, we carried out a least-squares refinement in both space groups Pnnn and Pn3̅m. To check for the presence of disorder, we allowed partial Cs/Cl occupancies for all A sites and we inserted four tetrahedrally coordinated Cu atoms around all A sites. Both refinements converged with similar agreement factors (R1cubic = 33% vs R1ortho = 31%). Additionally, in both models, the refinement converged toward a fully ordered model, with the sites along the diagonal parallel to the 3-fold axis fully occupied by [Cu4Cl]3+ clusters and the other six A sites fully occupied by Cs. Therefore, the formula can be conveniently rewritten as (Cs3,Cu4Cl)(In2,□2)Cl12, in agreement with the expected stoichiometry. To find the best approximation to the real structure, we then performed DFT calculations. We relaxed the geometry of the orthorhombic Pnnn structure and discovered that it did not exhibit an energy minimum; on the contrary, the structure relaxed to a cubic Pn3̅m space group. The combination of all of these data led us to assign the Pn3̅m space group to the Cs3Cu4In2Cl13 structure.

The high R values of the refinement and the anomalous peak height of the central Cl atom of the [Cu4Cl]3+ cluster in the potential map of the ab initio solution attest to the presence of a certain degree of disorder in the structure. Disorder in the [Cu4Cl]3+ distribution results in small merohedral twinned domains. When Cs+ and [Cu4Cl]3+ ions arrange in a fully disordered fashion, the structure can be described by a face-centered cubic model with partial occupancies. We observe evidence of disorder already for 3D ED data collected on a single NC of <100 nm. Therefore, this mechanism acts at a scale of a few cell repetitions, and even a single NC is better addressed as a crystalline assembly with a dominant coherent volume neighbored by more disordered areas. This is not an unusual situation for nanocrystalline materials, as shown by a number of recent works employing the 3D ED technique.35−38

Larger pseudotriangular and pseudohexagonal platelet particles exhibit the same primitive cubic cell. In addition, extra reflections appeared parallel to one of the ⟨111⟩* directions, which correspond to one of the main diagonals of the cubic cell (Figure S7). These extra reflections can be described by the nonmerohedric twin law:

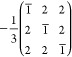graphic file with name ic9b02834_m001.jpg

This additional twinning, typical of face-centered structures, represents, in fact, a rotation of 180° around the main diagonal of the cubic cell. This twinning also mimics a mirror plane (111) that does not exist in an ordered domain. Remarkably, cubic and triangular/hexagonal NCs expose different crystallographic facets. The cube-shaped NCs always expose pseudocubic {100} facets, while the main facet of triangular/hexagonal platelets is the pseudocubic {111} one (Figure 2b,c).

The primitive cubic model explains the non-indexed weak peaks in the powder XRD pattern (inset of Figure 3a). However, a good Rietveld refinement could be achieved only by considering a completely disordered model in space group Fm3̅m, where each of the eight Cs sites in the unit cell was partially occupied by a (Cu4Cl)3+ cluster with a probability of 0.25 (Figure 3a) (see also Table S5 for further details). The discrepancy between 3D ED and powder XRD is likely due to the disorder that dampens specific classes of reflections. The single particles sampled by 3D ED may have a significant fraction of ordered and coherent areas, giving a solution only in the ordered primitive cubic model. However, the structural solution retains the trace of disorder through a higher potential peak of the Cl atom substituting Cs. For a comparison, Figure S4 groups together the following XRD patterns: (a) the experimental pattern of the NCs synthesized at 145 °C, (b) the simulated pattern by considering a Cs2CuInCl6 double perovskite (space group Fm3̅m) structure with a lattice parameter of 10.48 Å, (c) the Rietveld refinement of the Fm3̅m disordered model of the Cs3Cu4In2Cl13 structure, and (d) the simulated pattern from the primitive cubic Cs3Cu4In2Cl13 structure belonging to the Pn3̅m space group.

Figure 3.

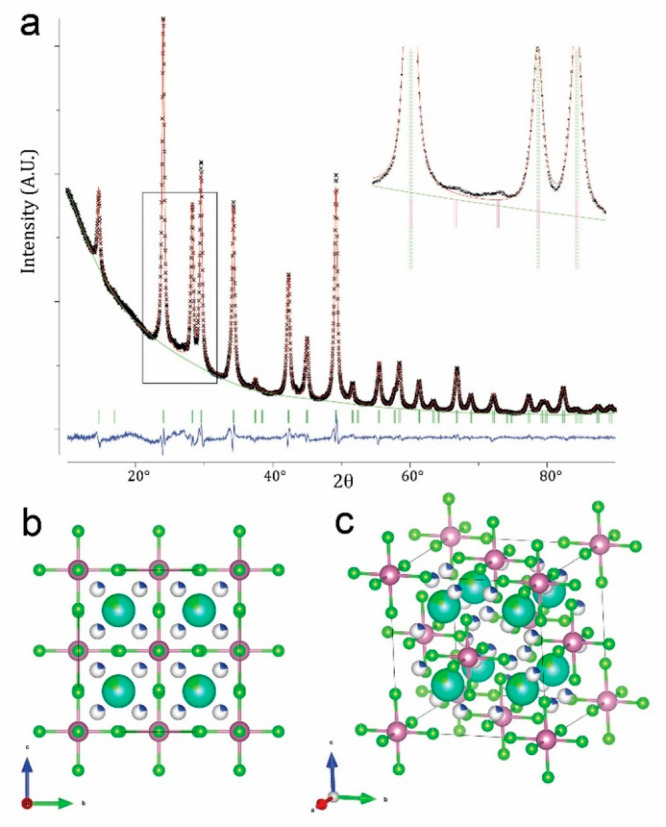
Figure 3

Open in a new tab

(a) Rietveld refinement of the Fm3̅m disordered model of the Cs3Cu4In2Cl13 structure. The inset is a magnified view of the region of the fit corresponding to the rectangular box, in which the peak positions of the disordered face-centered cubic model and those of the ordered primitive cubic model are displayed through dashed green lines and solid red ticks, respectively. (b) Cs3Cu4In2Cl13 disordered structure viewed along the [100] axis. (c) Same structure in a tilted view.

To understand the optical properties of these NCs, we performed DFT calculations. In Figure 4a, we report the computed band structure on the experimental primitive cubic unit cell with space group Pn3̅m and Cs3Cu4In2Cl13 stoichiometry. Here, the two [Cu4Cl]3+ tetrahedral units are placed along the diagonal of the cube, maintaining a center of inversion inside the cell. This type of configuration is helpful in assigning the band parity and thus the probability of a transition between bands. The inspection of the band structure, computed at the DFT/HSE06 level of theory, indicates that the bandgap is direct and of ∼2.0 eV, albeit with a parity forbidden transition [the Tauc plot analysis of the absorption spectrum is consistent with a direct parity forbidden bandgap of ∼2.9 eV (see Figure S8)]. Of particular interest is the fact that the valence band (VB) is divided in two well-separated blocks: (i) a set of high-energy states at the VB edge that belongs to the 3d orbitals of Cu mixed with the Cl 3p orbitals (see the orbital plots at the bottom left of Figure 4b) and (ii) another set, at lower energies, composed by the mixed contribution of In 4d orbitals with the 3p orbitals of Cl ions, i.e., the [InCl6]3– octahedra (Figure 4b, bottom right). In both cases, the bands are rather flat, indicating that tetrahedra and octahedra are, at least in the VB, electronically disconnected, and the effect of periodic replication along the highest symmetry points is basically negligible. Similarly, the conduction band (CB) presents also two blocks of bands. At the CB edge, we find states that are mostly composed by In 5s and Cl 3p orbitals, with some contribution from the Cu 4s orbitals (Figure 4b, top right). The bands are more dispersive than in the VB, suggesting that the [Cu4Cl]3+ units help to connect electronically the In-based octahedra. At higher energies, we find bands mostly composed by Cu 4s orbitals mixed with the 3p orbitals of Cl and, to a minor extent, the 4s orbitals of In.

Figure 4.

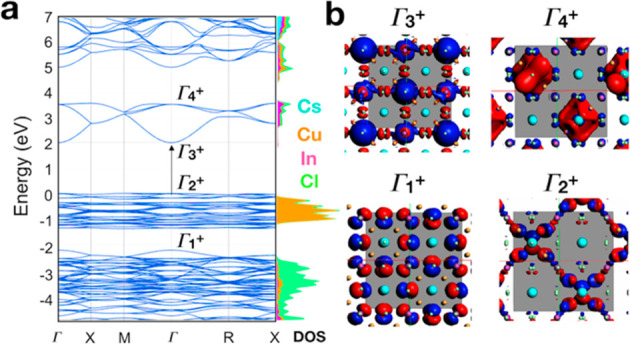
Figure 4

Open in a new tab

(a) Band structure of the primitive cubic Cs3Cu4In2Cl13 belonging to the Pn3̅m space group computed at the DFT/HSE06 level of theory. On the right side is shown the cumulative projected density of states on each atom type. Color code: black for Cs, orange for In, blue and Cu, and red for Cl. (b) Orbital plot computed at the γ point for the highest (in the VB) and the lowest (in the CB) states of each block.

Overall, we can make the following observation: both Cu+ and In3+ have similar electronic configurations, with the n + 1 orbitals empty and the nd occupied. This suggests that all transitions are of the s → d type, and thus parity forbidden and with expected weak oscillator strengths. The same parity transitions are present for all blocks described above. For these reasons, it is difficult to establish with high certainty the exact absorption onset, in both the theory and experimental measurements: the former presents inaccuracies, intrinsic to all DFT methodologies, in the estimation of the bandgap; for the latter, the lack of a photoluminescence emission is not providing any helpful hint. The strong absorption at 400 nm, which is observed in the experimental spectrum, can indeed stem from a dense number of high-lying excitations with weak oscillator strengths, probably occurring within the InCl6 or [Cu4Cl]3+ units. Finally, we have also computed the thermodynamic stability of Cs3Cu4In2Cl13 by assessing the enthalpy of decomposition into a different combination of phase-separated materials, all relaxed in their most stable structural configurations. The inspection of Table 1 shows that the Cs3Cu4In2Cl13 system, which presents a DFT relaxed cubic cell of 10.3 Å in length, is the most stable one for all possible decomposition pathways.

Table 1. Decomposition Enthalpies (millielectronvolts per atom) Computed at the DFT/PBESol Level of Theory.

decomposition mechanism ΔHd (meV/atom)
Cs3Cu4In2Cl13 → 4CuCl + 2InCl3 + 3CsCl 83.2
Cs3Cu4In2Cl13 → Cs3Cu2Cl5 + 2InCl3 + 2CuCl 57.5
Cs3Cu4In2Cl13 → Cs3In2Cl9 + 4CuCl 23.5
Open in a new tab

Conclusions

Colloidal Cs3Cu4In2Cl13 NCs with a peculiar structure were synthesized by a benzoyl chloride-based hot-injection approach. The structure, which is not known in the bulk, was characterized by means of powder XRD and single nanocrystal 3D electron diffraction analyses. The structure can be described as a vacancy ordered perovskite-like (A2BX6 type) in which 25% of the A sites are occupied by [Cu4Cl]3+ clusters and only one-half of the octahedral sites are occupied by In3+ ions. In that structure, Cu(I) ions adopt tetrahedral coordination instead of an octahedral one as could be expected from a hypothetical Cu(I) double perovskite. Two different twin systems, which induce disorder in the occupancy of A sites, were detected already in ∼100 nm nanoparticles. According to DFT calculations, this structure is stable and has a direct but parity forbidden bandgap, in agreement with the experimental data that showed the absence of any PL emission from the NCs. Our results indicate that Cu(I) ions in perovskite-related structures do not occupy octahedral sites and prefer instead to cluster and adopt tetrahedral coordination. The existence of this structure demonstrates that small inorganic cluster cations can occupy A sites in perovskite-related structures, paving the way for a new class of materials.

Acknowledgments

The authors thank Anatolii Polovitsyn for his help in developing the synthesis, Mirko Prato for the XPS analysis, and Simone Lauciello for carrying out the SEM-EDS measurements. The authors also acknowledge funding from the programme for research and Innovation Horizon 2020 (2014–2020) under the Marie Skłodowska-Curie Grant Agreement COMPASS 691185. The work of D.B. was supported by the European Union’s Horizon 2020 research and innovation programme under Marie Sklodowska-Curie Grant 794560 (RETAIN). I.I. acknowledges the Dutch NWO for financial support under the Vidi scheme (Grant 723.013.002).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.9b02834.

  • Elemental analyses, XPS spectra, XRD patterns, STEM-EDS maps, dark field STEM images, 3D ED refinement, electron diffraction patterns of a single and a twinned nanocrystal, and details of Rietveld refinement (PDF)

Accession Codes

CCDC 1955351 and 1955353 contain the supplementary crystallographic data for this paper. These data can be obtained free of charge via www.ccdc.cam.ac.uk/data_request/cif, or by emailing data_request@ccdc.cam.ac.uk, or by contacting The Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; fax: +44 1223 336033.

The authors declare no competing financial interest.

Supplementary Material

ic9b02834_si_001.pdf (1.1MB, pdf)

References

  1. Aleksandrov K. S.; Beznosikov V. V. Hierarchies of perovskite-like crystals. Phys. Solid State 1997, 39 (5), 695–715. 10.1134/1.1130120. [DOI] [Google Scholar]
  2. Bhalla A. S.; Guo R.; Roy R. The perovskite structure—a review of its role in ceramic science and technology. Mater. Res. Innovations 2000, 4 (1), 3–26. 10.1007/s100190000062. [DOI] [Google Scholar]
  3. Davies P. K.; Wu H.; Borisevich A. Y.; Molodetsky I. E.; Farber L. Crystal Chemistry of Complex Perovskites: New Cation-Ordered Dielectric Oxides. Annu. Rev. Mater. Res. 2008, 38 (1), 369–401. 10.1146/annurev.matsci.37.052506.084356. [DOI] [Google Scholar]
  4. Igbari F.; Wang Z.-K.; Liao L.-S. Progress of Lead-Free Halide Double Perovskites. Adv. Energy Mater. 2019, 9 (12), 1803150. 10.1002/aenm.201803150. [DOI] [Google Scholar]
  5. Maughan A. E.; Ganose A. M.; Scanlon D. O.; Neilson J. R. Perspectives and Design Principles of Vacancy-Ordered Double Perovskite Halide Semiconductors. Chem. Mater. 2019, 31 (4), 1184–1195. 10.1021/acs.chemmater.8b05036. [DOI] [Google Scholar]
  6. Khalfin S.; Bekenstein Y. Advances in lead-free double perovskite nanocrystals, engineering band-gaps and enhancing stability through composition tunability. Nanoscale 2019, 11 (18), 8665–8679. 10.1039/C9NR01031A. [DOI] [PubMed] [Google Scholar]
  7. Saparov B.; Mitzi D. B. Organic–Inorganic Perovskites: Structural Versatility for Functional Materials Design. Chem. Rev. 2016, 116 (7), 4558–4596. 10.1021/acs.chemrev.5b00715. [DOI] [PubMed] [Google Scholar]
  8. Li W.; Wang Z.; Deschler F.; Gao S.; Friend R. H.; Cheetham A. K. Chemically diverse and multifunctional hybrid organic-inorganic perovskites. Nat. Rev. Mater. 2017, 2 (3), 16099. 10.1038/natrevmats.2016.99. [DOI] [Google Scholar]
  9. Ono L. K.; Juarez-Perez E. J.; Qi Y. Progress on Perovskite Materials and Solar Cells with Mixed Cations and Halide Anions. ACS Appl. Mater. Interfaces 2017, 9 (36), 30197–30246. 10.1021/acsami.7b06001. [DOI] [PubMed] [Google Scholar]
  10. Wang Z.; Shi Z.; Li T.; Chen Y.; Huang W. Stability of Perovskite Solar Cells: A Prospective on the Substitution of the A Cation and X Anion. Angew. Chem., Int. Ed. 2017, 56 (5), 1190–1212. 10.1002/anie.201603694. [DOI] [PubMed] [Google Scholar]
  11. Paton L. A.; Harrison W. T. A. Structural Diversity in Non-Layered Hybrid Perovskites of the RMCl3 Family. Angew. Chem., Int. Ed. 2010, 49 (42), 7684–7687. 10.1002/anie.201003541. [DOI] [PubMed] [Google Scholar]
  12. Chen X.-G.; Gao J.-X.; Hua X.-N.; Liao W.-Q. Three-dimensional organic-inorganic hybrid sodium halide perovskite: C4H12N2·NaI3 and a hydrogen-bonded supramolecular three-dimensional network in 3C4H12N2·NaI4·3I·H2O. Acta Crystallogr., Sect. C: Struct. Chem. 2018, 74 (6), 728–733. 10.1107/S2053229618006885. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ferrandin S.; Slawin A. M. Z.; Harrison W. T. A. Syntheses and crystal structures of a new family of hybrid perovskites: C5H14N2·ABr3·0.5H2O (A = K, Rb, Cs). Acta Crystallographica, Section E: Crystallographic Communications 2019, 75 (8), 1243–1248. 10.1107/S2056989019010338. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gebhardt J.; Rappe A. M. Mix and Match: Organic and Inorganic Ions in the Perovskite Lattice. Adv. Mater. 2018, 31 (47), 1802697–10.1002/adma.201802697. [DOI] [PubMed] [Google Scholar]
  15. Xiao Z.; Du K.-Z.; Meng W.; Mitzi D. B.; Yan Y. Chemical Origin of the Stability Difference between Copper(I)- and Silver(I)-Based Halide Double Perovskites. Angew. Chem., Int. Ed. 2017, 56 (40), 12107–12111. 10.1002/anie.201705113. [DOI] [PubMed] [Google Scholar]
  16. Larson A.; Von Dreele R.. General Structure Analysis System (GSAS); Los Alamos National Laboratory, 2000; pp 86–748. [Google Scholar]
  17. Yun Y.; Zou X.; Hovmoller S.; Wan W. Three-dimensional electron diffraction as a complementary technique to powder X-ray diffraction for phase identification and structure solution of powders. IUCrJ 2015, 2 (2), 267–282. 10.1107/S2052252514028188. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gemmi M.; Mugnaioli E.; Gorelik T. E.; Kolb U.; Palatinus L.; Boullay P.; Hovmöller S.; Abrahams J. P. 3D Electron Diffraction: The Nanocrystallography Revolution. ACS Cent. Sci. 2019, 5, 1315–1329. 10.1021/acscentsci.9b00394. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gemmi M.; La Placa M. G. I.; Galanis A. S.; Rauch E. F.; Nicolopoulos S. Fast electron diffraction tomography. J. Appl. Crystallogr. 2015, 48 (3), 718–727. 10.1107/S1600576715004604. [DOI] [Google Scholar]
  20. Mugnaioli E.; Gorelik T.; Kolb U. “Ab initio” structure solution from electron diffraction data obtained by a combination of automated diffraction tomography and precession technique. Ultramicroscopy 2009, 109 (6), 758–765. 10.1016/j.ultramic.2009.01.011. [DOI] [PubMed] [Google Scholar]
  21. Kolb U.; Mugnaioli E.; Gorelik T. E. Automated electron diffraction tomography – a new tool for nano crystal structure analysis. Cryst. Res. Technol. 2011, 46 (6), 542–554. 10.1002/crat.201100036. [DOI] [Google Scholar]
  22. Palatinus L.; Petricek V.; Correa C. A. Structure refinement using precession electron diffraction tomography and dynamical diffraction: theory and implementation. Acta Crystallogr., Sect. A: Found. Adv. 2015, 71 (2), 235–244. 10.1107/S2053273315001266. [DOI] [PubMed] [Google Scholar]
  23. Burla M. C.; Caliandro R.; Carrozzini B.; Cascarano G. L.; Cuocci C.; Giacovazzo C.; Mallamo M.; Mazzone A.; Polidori G. Crystal structure determination and refinement via SIR2014. J. Appl. Crystallogr. 2015, 48 (1), 306–309. 10.1107/S1600576715001132. [DOI] [Google Scholar]
  24. Sheldrick G. A short history of SHELX. Acta Crystallogr., Sect. A: Found. Crystallogr. 2008, 64 (1), 112–122. 10.1107/S0108767307043930. [DOI] [PubMed] [Google Scholar]
  25. Quapp W.; Hirsch M.; Heidrich D. Bifurcation of reaction pathways: the set of valley ridge inflection points of a simple three-dimensional potential energy surface. Theor. Chem. Acc. 1998, 100 (5), 285–299. 10.1007/s002140050389. [DOI] [Google Scholar]
  26. te Velde G.; Bickelhaupt F. M.; Baerends E. J.; Fonseca Guerra C.; van Gisbergen S. J. A.; Snijders J. G.; Ziegler T. Chemistry with ADF. J. Comput. Chem. 2001, 22 (9), 931–967. 10.1002/jcc.1056. [DOI] [Google Scholar]
  27. Van Lenthe E.; Baerends E. J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003, 24 (9), 1142–1156. 10.1002/jcc.10255. [DOI] [PubMed] [Google Scholar]
  28. Heyd J.; Scuseria G. E.; Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118 (18), 8207–8215. 10.1063/1.1564060. [DOI] [Google Scholar]
  29. Giannozzi P.; Baroni S.; Bonini N.; Calandra M.; Car R.; Cavazzoni C.; Ceresoli D.; Chiarotti G. L.; Cococcioni M.; Dabo I.; Dal Corso A.; de Gironcoli S.; Fabris S.; Fratesi G.; Gebauer R.; Gerstmann U.; Gougoussis C.; Kokalj A.; Lazzeri M.; Martin-Samos L.; Marzari N.; Mauri F.; Mazzarello R.; Paolini S.; Pasquarello A.; Paulatto L.; Sbraccia C.; Scandolo S.; Sclauzero G.; Seitsonen A. P.; Smogunov A.; Umari P.; Wentzcovitch R. M. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys.: Condens. Matter 2009, 21 (39), 395502. 10.1088/0953-8984/21/39/395502. [DOI] [PubMed] [Google Scholar]
  30. Perdew J. P.; Ruzsinszky A.; Csonka G. I.; Vydrov O. A.; Scuseria G. E.; Constantin L. A.; Zhou X.; Burke K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100 (13), 136406. 10.1103/PhysRevLett.100.136406. [DOI] [PubMed] [Google Scholar]
  31. Garrity K. F.; Bennett J. W.; Rabe K. M.; Vanderbilt D. Pseudopotentials for high-throughput DFT calculations. Comput. Mater. Sci. 2014, 81, 446–452. 10.1016/j.commatsci.2013.08.053. [DOI] [Google Scholar]
  32. Imran M.; Caligiuri V.; Wang M.; Goldoni L.; Prato M.; Krahne R.; De Trizio L.; Manna L. Benzoyl Halides as Alternative Precursors for the Colloidal Synthesis of Lead-Based Halide Perovskite Nanocrystals. J. Am. Chem. Soc. 2018, 140 (7), 2656–2664. 10.1021/jacs.7b13477. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Vasquez R. P. CuCl by XPS. Surf. Sci. Spectra 1993, 2 (2), 138–143. 10.1116/1.1247732. [DOI] [Google Scholar]
  34. Biesinger M. C. Advanced analysis of copper X-ray photoelectron spectra. Surf. Interface Anal. 2017, 49 (13), 1325–1334. 10.1002/sia.6239. [DOI] [Google Scholar]
  35. Neagu A.; Tai C.-W. Local disorder in Na0.5Bi0.5TiO3-piezoceramic determined by 3D electron diffuse scattering. Sci. Rep. 2017, 7 (1), 12519. 10.1038/s41598-017-12801-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Rozhdestvenskaya I. V.; Mugnaioli E.; Schowalter M.; Schmidt M. U.; Czank M.; Depmeier W.; Rosenauer A. The structure of denisovite, a fibrous nanocrystalline polytypic disordered ‘very complex’ silicate, studied by a synergistic multi-disciplinary approach employing methods of electron crystallography and X-ray powder diffraction. IUCrJ 2017, 4 (3), 223–242. 10.1107/S2052252517002585. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Zhao H.; Krysiak Y.; Hoffmann K.; Barton B.; Molina-Luna L.; Neder R. B.; Kleebe H.-J.; Gesing T. M.; Schneider H.; Fischer R. X.; Kolb U. Elucidating structural order and disorder phenomena in mullite-type Al4B2O9 by automated electron diffraction tomography. J. Solid State Chem. 2017, 249, 114–123. 10.1016/j.jssc.2017.02.023. [DOI] [Google Scholar]
  38. Mugnaioli E.; Gorelik T. E. Structure analysis of materials at the order-disorder borderline using three-dimensional electron diffraction. Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater. 2019, 75 (4), 550–563. 10.1107/S2052520619007339. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ic9b02834_si_001.pdf (1.1MB, pdf)

Articles from Inorganic Chemistry are provided here courtesy of American Chemical Society

RESOURCES