Impact of the Prevalence of Cognitive Impairment on the Accuracy of the Montreal Cognitive Assessment

Supplemental Digital Content is available in the text.

Objectives:

The focus of this study is the classification accuracy of the Montreal Cognitive Assessment (MoCA) for the detection of cognitive impairment (CI). Classification accuracy can be low when the prevalence of CI is either high or low in a clinical sample. A more robust result can be expected when avoiding the range of test scores within which most classification errors are expected, with adequate predictive values for more clinical settings.

Methods:

The classification methods have been applied to the MoCA data of 5019 patients in the Uniform Data Set of the University of Washington’s National Alzheimer’s Coordinating Center, to which 30 Alzheimer Disease Centers (ADCs) contributed.

Results:

The ADCs show sample prevalence of CI varying from 0.22 to 0.87. Applying an optimal cutoff score of 23, the MoCA showed for only 3 of 30 ADCs both a positive predictive value (PPV) and a negative predictive value (NPV) ≥0.8, and in 18 cases, a PPV ≥0.8 and for 13 an NPV ≥0.8. Overall, the test scores between 22 and 25 have low odds of true against false decisions of 1.14 and contains 55.3% of all errors when applying the optimal dichotomous cut-point. Excluding the range 22 to 25 offers higher classification accuracies for the samples of the individual ADCs. Sixteen of 30 ADCs showed both NPV and PPV ≥0.8, 25 show a PPV ≥0.8, and 21 show an NPV ≥0.8.

Conclusion:

In comparison to a dichotomous threshold, considering the most error-prone test scores as uncertain enables a classification that offers adequate classification accuracies in a larger number of clinical settings.

INTRODUCTION AND OBJECTIVE

In general, prevalence is a difficult issue to handle when screening patients for cognitive impairment (CI). If the prevalence is low, then it is easy to incorrectly classify patients without CI and when the prevalence is high, it is easy to misclassify the patients who have CI.

For most tests, a single cutoff score is proposed. In most cases, such a dichotomous cutoff score is based on the quality indices sensitivity and specificity. These indices provide information about the proportion of correctly diagnosed patients when given knowledge about the true status of the patient. Obviously, this latter piece of information is not available when screening a new patient.1 Although sensitivity and specificity are useful to indicate the accuracy of the test, both indicators cannot be used for the interpretation of the results of individual patients whose true status is unknown. Predictive values give the answers required when screening: they provide probabilities for the presence of the disease, given the obtained test result.1 Predictive values consequently provide information about the accuracy of the classification. A positive predictive value (PPV) or a negative predictive value (NPV) provides a clear interpretation for the individual patient: it indicates the probability of correct classification, given the test result.

The independence of prevalence is considered an important advantage of sensitivity and specificity: when samples with and without the targeted disease are randomly drawn from the same population, there is no relation between sensitivity and specificity and sample prevalence. For this reason, the accuracy indices sensitivity and specificity are used for the determination of a cutoff score. In the case of the Montreal Cognitive Assessment (MoCA), Nasreddine et al2 chose for the balance between sensitivity and specificity for the determination of the cutoff score, resulting in a threshold of 25, with scores of 25 and lower used for the identification of possible CI. In their validation study, the sensitivity associated with that threshold was 0.9 for the correct identification of 94 patients diagnosed with Mild Cognitive Impairment (MCI), whereas specificity was 0.87 for 90 healthy elderly controls with no CI.

Due to their dependence on prevalence, predictive values are seldom considered as indicators of test accuracy. They are, however, valid indicators of the proportion of correctly classified patients, given the test result.1 Commonly, when applying a single cutoff score, the PPV of the MoCA indicates the proportion correctly classified patients with CI, and NPV the proportion correctly classified patients without CI. The values of the NPV and PPV can differ considerably with prevalence.

Although the MoCA is generally considered one of the best instruments for screening patients for possible CI,3–5 there is a discussion about the proposed cutoff score. Furthermore, this cutoff score is suboptimal in comparison with the optimal cutoff score that optimizes the Youden index.6,7 The optimized Youden index provides a cutoff score that maximizes the sum of sensitivity and specificity and minimizes the total amount of classification errors. Several statisticians have pointed to the fact that different clinical samples can hardly be considered as taken from a single population.8,9 When the clinical samples are taken from populations with a different mix of patients, that is, having a different spectrum bias,10 different values for sensitivity and specificity can be expected. In that case, it can be expected that the values of sensitivity and specificity are not independent of prevalence.8,9

Different studies have led to different proposed cutoff scores. Freitas et al3 proposed a cutoff score of 17 for the optimal distinction of patients with and without Alzheimer disease. Damian et al6 proposed an optimal threshold of 26 for screening in primary care, but for testing in memory disorders clinics, a lower threshold was proposed. Davis et al7 found that in 4 studies that used the recommended threshold score of 26 or over for the indication of normal cognition (NC), the MoCA had high sensitivity of ≥0.94, but low specificity of ≤0.60. They suggested a threshold >26 for optimal diagnostic accuracy in dementia to improve the specificity of the test.

Dealing with the differences in clinical samples is a complicated issue.8,9 Proposals to provide detailed information on the clinical and demographic characteristics of the study sample and inclusion and exclusion criteria9,11,12 are most sensible. The downside of this approach is that when clinical centers must decide whether the results of a specific study are relevant for their practice, they must compare their selection of patients with the selection made in the study. Such a comparison can be difficult to make, as selections for study purposes can be very different from the selections that occur in practice.

In this study, the data of 5019 patients are used. Data have been contributed by 30 Alzheimer Disease Centers (ADCs) to the Uniform Data Set (UDS), collected by the University of Washington’s National Alzheimer’s Coordinating Center.13,14 The case-mix of patients with and without CI who were referred to these centers is highly variable, which allows us to compare the accuracies of the MoCA as an indicator of the presence of CI for these clinical samples. First, the usefulness of the application of a single cutoff score is evaluated for each of the 30 ADCs. Second, a 3-way classification is proposed, which uses a class of uncertain test scores to indicate the group of patients for whom the presence of CI is the most difficult to determine. The method is described in the Methods section, whereas details of this method are described in Supplemental File A (Supplemental Digital Content 1, http://links.lww.com/WAD/A257). Because this class of uncertain test scores is the most prone to error, it contains a surplus of errors. The 3-way classification is expected to allow better classification accuracy as it allows for avoiding this abundance of errors. The 3-way classification is therefore expected to be applicable in a larger number of clinical centers compared with the more commonly used dichotomous classification.

METHODS

Data Set

The data used are part of the UDS, collected by the University of Washington’s National Alzheimer’s Coordinating Center (NACC), and have been described extensively.13,14 The MoCA data used in this study have been collected in the period from March 2015 to August 2018. The start date of version 3 of the UDS, which includes the MoCA, was March 2015. The first assessment of each patient has been used. Participants come from 30 American ADCs, who contributed the MoCA data of a total of 5531 patients. Consent is obtained at each individual ADC. It is required that all eligible ADC research participants be evaluated with the UDS protocol. The UDS is administered as a standard instrument and complete data collection is expected for each patient annually.15 Some of the ADCs contributed a relatively small number of participants. One of the ADC was funded only recently. Other ADCs have enrolled a few new participants since version 3 of the UDS was implemented.

The patient’s cognitive status is determined at every visit: NC, cognitively impaired, but not fulfilling the criteria for MCI, MCI, and Dementia. The global score of the Clinical Dementia Rating (CDR) Dementia Staging Instrument16,17 is calculated using the defined scoring algorithm. This score is useful for characterizing a patient’s level of CI/dementia, with score 0 indicating NC functioning.

Gold Standard

The patients with and without CI are defined with their cognitive status and the global CDR at their first visit to the ADC. Following Weintraub et al,18 the norm group is defined with a cognitive status of NC and a global CDR score of 0, whereas the other patients are defined as having minor or serious CI (a cognitive status other than NC and CDR>0). Patients who have received an ambiguous assessment (CDR>0 and a cognitive status of NC, or a CDR of 0, and a cognitive status other than NC) have been excluded (n=512). Following Weintraub et al,18 participants in the norm group who achieved low scores on the MoCA were not removed from the analyses as the patient’s status was not defined by the test. This resulted in a healthy norm group of size 2379 and a group with a varying level of CI of 2640. The prevalence of CI is 0.53.

Optimal Cutoff Score and Uncertain Test Scores

The optimal cutoff score that optimizes the sum of sensitivity and specificity19 and minimizes the sum of the errors is 23. Uncertain test scores are defined as a range of test scores that have about equal densities in the 2 distributions of patients with and without the targeted disease. How much uncertainty can be allowed is open for discussion. This range of test scores is typically found around the point of intersection of the 2 distributions of patients with and without the targeted impairment.20–22 The point of intersection is equal to the Youden threshold.23 Standardized predictive values24,25 are most suitable for the determination of uncertain test scores. In this paper, standardized NPV or standardized PPV <0.667 (odds of true against false decision probabilities lower than two to one) are used for defining test scores that are too uncertain for making a classification concerning the presence of CI. This led to the range of test scores 22 to 25. As this uncertain interval is related to the Youden threshold, this optimal dichotomous threshold is used for comparison. Other dichotomous thresholds that do not minimize the sum of errors lead to higher rates of the sum of errors. Details of the methods to obtain these cutoff scores are provided in Supplemental File A (Supplemental Digital Content 1, http://links.lww.com/WAD/A257).

Statistical Methods

PPV and NPV are used for evaluating the obtained classification accuracies. Although predictive values are widely used, the details of the methods are relevant and described in Supplemental File A (Supplemental Digital Content 1, http://links.lww.com/WAD/A257). Due to the classification in >2 classes, there are minor differences with the common dichotomous classification. Also, for the test accuracies, the values of sensitivity and specificity are presented. An implementation of the statistical methods will be made available as the function RPV in the package Uncertain Interval20 for the R statistical language.26

RESULTS

The mixed densities of the 2 distributions of all patients with and without CI are shown in Figure 1. The patients with CI form the left distribution (blanc) and the norm group form the distribution to the right (black). The area under the curve of the receiver operating characteristics is 0.89. Applying the cutoff score of 25 and lower for the positive classification of CI results in sensitivity=0.89, specificity=0.67, NPV=0.85, and PPV=0.75. The optimal threshold that maximizes the Youden Index is test score 23, with test scores ≤23 indicating the presence of CI. This results in sensitivity=0.77; specificity=0.86; NPV=0.77; and PPV=0.86. Figure 1 shows how several lower scores (almost) uniquely define the presence of CI, whereas the higher scores always represent a mix of patients with and without CI. As a result, Figure 1 shows that when using the MoCA, the correct classification of patients with CI is easier than correct classification of patients without CI.

FIGURE 1.

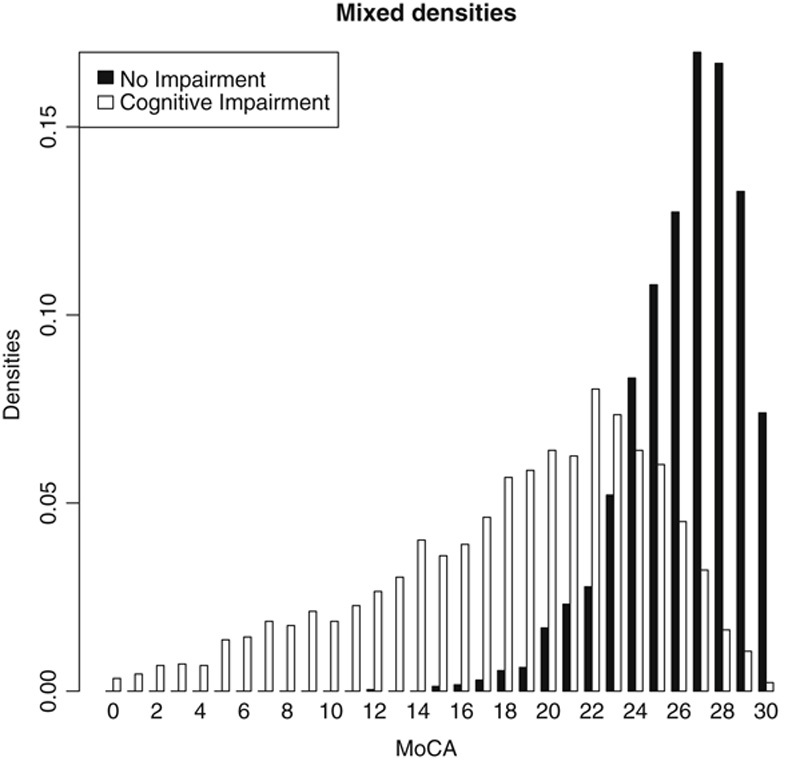
Distributions of 5019 patients with and without cognitive impairment. MoCA indicates the Montreal Cognitive Assessment.

The graphics of the mixed frequencies and densities of all 30 individual ADCs are displayed in Supplemental File B (Supplemental Digital Content 2, http://links.lww.com/WAD/A258). These graphs show that the MoCA results of the ADCs can have deviations, such as an unexpected missing score and truncated test scores. These aberrations occur particularly when the number of observed patients is low. The plots also show the individual optimal thresholds (using the optimized Youden index) for each of the ADCs. These differ considerably, ranging from 19 to 26.

Table 1 shows the results for each of the 30 ADCs when the optimal cutoff score (maximized Youden index) of 23 is applied, with scores 23 and lower to indicate CI.

TABLE 1.

MoCA Test and Classification Accuracies for 30 Different ADCs When Applying the Optimal Threshold of 23

	Prevalence	N0	N1	Sp	Se	NPV	PPV
1	0.216	91	25	0.912	0.76	0.933	0.704
2	0.223	94	27	0.830	0.741	0.918	0.556
3	0.283	198	78	0.909	0.91	0.963	0.798
4	0.293	256	106	0.879	0.774	0.904	0.726
5	0.298	139	59	0.921	0.712	0.883	0.792
6	0.325	129	62	0.899	0.806	0.906	0.794
7	0.330	77	38	0.844	0.711	0.855	0.692
8	0.364	49	28	1.000	0.464	0.766	1.000
9	0.369	123	72	0.675	0.889	0.912	0.615
10	0.371	107	63	0.897	0.794	0.881	0.820
11	0.373	151	90	0.775	0.744	0.836	0.663
12	0.375	70	42	0.914	0.500	0.753	0.778
13	0.429	20	15	0.600	0.867	0.857	0.619
14	0.450	105	86	0.762	0.756	0.792	0.722
15	0.465	76	66	0.829	0.909	0.913	0.822
16	0.478	93	85	0.903	0.812	0.840	0.885
17	0.543	37	44	0.919	0.500	0.607	0.880
18	0.561	43	55	1.000	0.691	0.717	1.000
19	0.620	68	111	0.882	0.847	0.779	0.922
20	0.620	30	49	0.900	0.755	0.692	0.925
21	0.622	96	158	0.740	0.816	0.710	0.838
22	0.635	38	66	0.895	0.773	0.694	0.927
23	0.733	40	110	0.950	0.791	0.623	0.978
24	0.737	31	87	0.903	0.701	0.519	0.953
25	0.762	35	112	0.771	0.902	0.711	0.927
26	0.765	43	140	0.907	0.586	0.402	0.953
27	0.821	63	288	0.889	0.781	0.471	0.970
28	0.825	7	33	1.000	0.455	0.280	1.000
29	0.849	21	118	0.810	0.669	0.304	0.952
30	0.870	49	327	0.959	0.847	0.485	0.993

N₀, N₁: sizes of the samples of patients without and with CI.

ADCs indicates Alzheimer Disease Centers; CI, cognitive impairment; MoCA, Montreal Cognitive Assessment; NPV, negative predictive value; PPV, positive predictive value; Se, sensitivity; Sp, specificity.

The prevalence of CI varies widely from 0.216 to 0.87. Table 1 shows that the test accuracies specificity and sensitivity differ considerably, from 0.60 to 1.0 and from 0.45 to 0.91, respectively. The mean sensitivity is 0.74 and the mean specificity is 0.87. There is some correlation between prevalence and specificity (Pearson correlation r=0.16) and between prevalence and sensitivity (r=−0.10). Relatively low and high values for sensitivity are found for ADCs with both low and high prevalence and the same can be observed for specificity. Although there is no high correlation with prevalence, the values for sensitivity and specificity of the individual ADCs clearly differ from the values obtained in the overall file and especially the values for sensitivity can be very low (numbers 8, 12, 17, 18, 26, 28, and 29 show undesirable low sensitivity<0.7, whereas 9 and 13 show specificity<0.7). Leaving out these 10 ADCs reduces the correlations with prevalence slightly to −0.09 (sensitivity) and 0.06 (specificity). Using a higher threshold of 25 changes in this situation: a higher threshold increases sensitivity (number 8 lower 0.7) and lowers specificity (2, 4, 7, 9, 11, 13, 14, 15, 16, 19, 21, 24, and 29<0.7). The use of such a suboptimal threshold also increases the total number of misclassifications overall.

The obtained NPV for a negative classification (scores>23) varies considerably from 0.28 to 0.96, whereas PPV for a positive classification varies from 0.55 to 1.0. There is a strong correlation with prevalence. High values are found for NPV when the prevalence is low and low values when the prevalence is high (Pearson r=−0.89). The reverse is true for PPV (r=0.77).

When classifying with the MoCA using this single threshold, the test qualities (sensitivity and specificity), but especially the values of the correct positive and negative classifications (NPV and PPV), vary between different ADCs. If a predictive value of 0.8 is considered as a lower limit for positive or negative classification, 13 of 30 ADCs show an adequate negative predictive value and 18 show a sufficient positive predictive value, whereas only 3 ADCs show both a positive and a negative predictive value ≥0.8 (10, 15, and 16).

When a dichotomous cutoff score of 25 is used, the results are comparable (not shown). Unsurprisingly, values are generally higher for sensitivity (mean 0.88) and lower for specificity (mean 0.69) compared with the lower optimal cutoff score. Twenty-one of the 30 ADCs shows an NPV ≥0.8 and 13 a PPV ≥0.8, but only 4 of the ADCs have both NPV and PPV ≥0.8.

When applying the Uncertain Interval method (Supplemental File A, Supplemental Digital Content 1, http://links.lww.com/WAD/A257) with odds of a correct classification as 2 against 1, the minimum level of both standardized NPV and standardized PPV is 0.667. The obtained results for the total sample are shown in Table 2. The row “Correct classifications” represents the common NPV and PPV for the negative and positive classifications (NPV=0.85; PPV=0.922).

TABLE 2.

Obtained Results, Using Standardized Predictive Values and Trichotomization With Classification Odds of 2

	Negative Classifications	Uncertain	Positive Classifications
Scores	26-30	22-25	0-21
N	1877	1379	1763
Total sample	0.374	0.275	0.351
Correct classifications	0.850	—	0.922
True negative status	0.671	0.271	0.058
True positive status	0.106	0.278	0.616
Realized odds	5.7	1.14	11.8

The scores in the range 22 to 25 lead to odds of 1.14 (true positive over true negative). Such a value close to 1 indicates that it is difficult to base classifications on that range of scores. Although 27.5% of all test scores are found in that range, 55.3% of all errors are in that range when the optimal cutoff score of 23 is applied. When using another, non-optimal dichotomous cutoff score, this percentage of errors will be even larger. For instance, when using cutoff score 25 (score 25 and less indicate CI), 60.6% of all errors are found in the range 22 to 25.

Positive classifications on the basis of scores 0 to 21 are far less error prone, with realized odds of 11.8, with a 92.2% rate of correct classifications. Making correct negative classifications on the basis of the MoCA scores 26 to 30 is slightly more difficult than making positive classifications with an 85% rate of correct classifications. Because the same range of scores is used for negative classifications, as proposed by Nasreddine et al2 (test result>25 indicate CI), accuracy results are equal: specificity is 0.671 and NPV is 0.85. In comparison with the dichotomous cutoff score of 25, the rate of positive classifications when the true status is positive (sensitivity=0.616) is lower. The reason for this is that for the calculation, uncertain scores are considered as unambiguous errors which consideration is hardly realistic.

Table 3 shows the accuracy results for the 30 ADCs when the range of uncertain test scores is not used for an explicit positive or negative classification. In comparison with Table 1, the values for both NPV and PPV are higher (mean NPV=0.82; mean PPV=0.90). The results for specificity and sensitivity in Table 3 are relatively lower compared with Table 1. The reason for this is that for their calculation, the uncertain test scores are considered as unambiguous errors. The indices sensitivity and specificity are meant for a dichotomous classification and are cumbersome to apply when using a 3-way classification.

TABLE 3.

Realized Results for Trichotomization, With Test Scores 22 to 25 Considered as Uncertain

	Prevalence	N0	N1	Sp	Se	NPV	PPV
1	0.216	91	25	0.725	0.600	0.957	0.938
2	0.223	94	27	0.628	0.444	0.967	0.545
3	0.283	198	78	0.717	0.692	0.993	0.885
4	0.293	256	106	0.656	0.623	0.908	0.868
5	0.298	139	59	0.748	0.508	0.929	0.811
6	0.325	129	62	0.721	0.581	0.912	0.923
7	0.330	77	38	0.636	0.632	0.891	0.857
8	0.364	49	28	0.980	0.286	0.814	1.000
9	0.369	123	72	0.504	0.694	0.984	0.735
10	0.371	107	63	0.701	0.603	0.938	0.927
11	0.373	151	90	0.543	0.589	0.891	0.736
12	0.375	70	42	0.729	0.357	0.836	0.882
13	0.429	20	15	0.400	0.867	1.000	0.684
14	0.450	105	86	0.505	0.570	0.898	0.790
15	0.465	76	66	0.553	0.667	0.933	0.936
16	0.478	93	85	0.570	0.659	0.898	0.949
17	0.543	37	44	0.838	0.341	0.738	1.000
18	0.561	43	55	0.884	0.582	0.826	1.000
19	0.620	68	111	0.574	0.766	0.907	0.955
20	0.620	30	49	0.767	0.653	0.767	0.970
21	0.622	96	158	0.615	0.715	0.819	0.904
22	0.635	38	66	0.737	0.712	0.824	1.000
23	0.733	40	110	0.800	0.645	0.744	0.986
24	0.737	31	87	0.613	0.494	0.633	0.977
25	0.762	35	112	0.743	0.741	0.963	0.954
26	0.765	43	140	0.767	0.436	0.541	0.968
27	0.821	63	288	0.873	0.597	0.611	0.983
28	0.825	7	33	0.857	0.364	0.500	1.000
29	0.849	21	118	0.429	0.508	0.346	0.984
30	0.870	49	327	0.878	0.722	0.632	1.000

N₀, N₁: sizes of the samples of patients without and with CI.

NPV indicates negative predictive value; PPV, positive predictive value; Se, sensitivity; Sp, specificity.

If a lower limit of 0.8 is considered sufficient for positive and negative classifications, the NPV for the range of test scores 26 and higher are for 21 ADCs ≥0.8. For ADC 1 to 16, 18, 19, 21, 22, and 25, the NPV is ≥0.8. A PPV ≥0.8 is found for 25 of the ADCs, with the exception of 2, 9, 11, 13, and 14. Sixteen ADCs show ≥0.8 for both NPV and PPV values.

The Pearson correlations between prevalence and NPV and PPV are 0.85 and 0.69, respectively. Although their absolute values are slightly less than when applying a single cutoff score, they are still considerable.

CONCLUSIONS AND DISCUSSION

When the handling of uncertain or inconclusive test results is considered as an important subject that is not adequately addressed by standard dichotomization approaches, then the adaptation to a middle range of uncertain test scores offers several advantages. The lower and upper ranges of test scores can lead more quickly to the line of action required for patients with and without CI. The middle range of uncertain test scores should lead to more restraint. The trichotomization with 2 thresholds is simple to apply and provides therefore a more cautious procedure than a simple yes/no dichotomous classification.

It should be clear that it is not intended to abandon patients with uncertain test scores in any way. Uncertain test scores should lead to more cautious action. Other tests should be applied, when these other tests can reduce the considerable uncertainty about the true status of the patient. Another possibility is awaiting the further developments of the patient by either active surveillance or watchful waiting. Recognizing the uncertainty of the classification and awaiting further developments is considered best practice in some fields27,28 and it may prevent overdiagnosis.

Various methods that have been proposed earlier for the determination of uncertain test scores29–33 have not found broad acceptance. The proposed method for the determination of the trichotomous thresholds has as an advantage over earlier proposals that it is clearly related to the dichotomous optimal threshold,19 which is widely accepted. Although the problem of comparing tests and their distributions can be approached in many different ways, the use of the well-known predictive values may ease the adaptation to the proposed method. Also, the availability of open-source software as an R package20,26 may be an attractive feature for test developers. Simulation results21,22 have shown that a range around the dichotomous optimal threshold identifies the most error prone test scores more efficiently than alternative methods for trichotomization.

The 30 ADCs showed a wide variety in the mix of their patients with CI, with prevalence ranging from 0.216 to 0.87. The test accuracy of the MoCA seems to be adequate for the majority of ADCs, largely independent of whether the prevalence of CI is high or low. However, there are a few ADCs where the MoCA shows insufficient test accuracies. This deserves further attention.

As is expected, the accuracies of the classifications are greatly dependent on the prevalence and can offer insufficient values for negative classifications of CI when prevalence is high and insufficient values for positive classifications when prevalence is low. Although the MoCA is one of the best screening instruments available, the application of a single cutoff score is a rather coarse approach for ADCs that vary considerably in the mix of patients they receive with and without CI. In most cases, at least one of the predictive values becomes insufficiently high, causing the number of misclassified patients to become too high.

The results of this study demonstrate the usefulness of a method to detect the most error-prone range of test scores. Avoiding these uncertain test scores allows for a more robust classification that can be applied in a considerably larger number of ADCs compared with a dichotomous classification. It results in adequate classification accuracies for most of the clinical centers, although it only slightly reduces the effects of prevalence on the obtained predictive values.

The best reason for the identification of the range of uncertain test scores is that patients with a test score within that range are about equally likely to be classified with or without CI. In the data set, 27.5% of all patients received such an uncertain test score, but when the optimal cutoff score is applied, 55.3% of all erroneous classifications would have been found in this range. Clearly, this is the most error-prone range of test scores. Further testing or awaiting further developments can increase the certainty of the presence or absence of CI. The strategy to avoid these classification errors results in better values for the test’s PPV and NPV compared with the application of the dichotomous optimal cut-point of 23. Simply changing this single cut-point to a higher value improves the sensitivity, but lowers the specificity of the test and does not decrease the number of classification errors.

This study considers the MoCA as the start of a decision process. The proposed method is targeted at reducing random classification errors, but systematic differences between ADC patients can also be relevant. The application of a 3-way classification diminishes the relevance of prevalence. However, prevalence remains a relevant factor. This study has not looked at other relevant predictors, such as relevant covariates or specific underlying diseases. Relevant differences may arise through disease-related covariates. For instance, education is often considered a protective factor against CI. However, the required norms for either well-educated or low-skilled patients may vary considerably.34,35 Other covariates that are unrelated to the disease may influence patients’ testing behavior. Hearing and vision impairments influence the results obtained with the MoCA.36 It is also well-known that CI test results are different for patients with different underlying diseases, such as Alzheimer3 and Parkinson disease.37 Stratification of patients on a variety of relevant predictors is a complex task and although it may further enhance classification accuracy, it is not easily applied in primary care. Nevertheless, systematic differences between samples remain a relevant topic for future research and more so for identifying groups for which the test accuracies are insufficient.

The distinction between cognitively impaired and healthy participants has been based on the concordant results of the global CDR and the clinical status, both of which were available for all patients. Defining a gold standard for CI, especially when the impairment is mild, remains a fundamental challenge.38 Hopefully, future research will allow for an even better distinction.

Supplementary Material

Supplemental Digital Content is available for this article. Direct URL citations appear in the printed text and are provided in the HTML and PDF versions of this article on the journal's website, www.alzheimerjournal.com.