Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Feb 14;124(10):1941–1948. doi: 10.1021/acs.jpcb.0c00770

Analysis of Brightness of a Single Fluorophore for Quantitative Characterization of Biochemical Reactions

Krzysztof Bielec 1, Grzegorz Bubak 1, Tomasz Kalwarczyk 1, Robert Holyst 1,*
PMCID: PMC7497653  PMID: 32059107

Abstract

graphic file with name jp0c00770_0009.jpg

Intrinsic molecular brightness (MB) is a number of emitted photons per second per molecule. When a substrate labeled by a fluorophore and a second unlabeled substrate form a complex in solution, the MB of the fluorophore changes. Here we use this change to determine the equilibrium constant (K) for the formation of the complex at pM concentrations. To illustrate this method, we used a reaction of DNA hybridization, where only one of the strands was fluorescently labeled. We determined K at the substrate concentrations from 80 pM to 30 nM. We validated this method against Förster resonance energy transfer (FRET). This method is much simpler than FRET as it requires only one fluorophore in the complex with a very small (a f̃ew percent) change in MB.

Introduction

Investigation of noncovalent complex-forming reactions is essential for understanding and eventually controlling biochemical processes in living systems.1−4 Most of the known pharmaceuticals rely on such complexes with specific components (e.g., enzymes or receptors).5−8 The equilibrium constant (K) of the reactions allows one to predict the stability of these complexes at various concentrations of substrates. Among various methods for K determination, only fluorescent-based methods are sensitive enough to measure K in solutions of low concentrations (<1 nM) and small volume (<1 μL).9−15 These techniques are fluorescence correlation spectroscopy (FCS), fluorescence titration (FLT), two-color coincidence detection (TCCD) and Förster resonance energy transfer (FRET).16−23 To determine K by FCS, the fluorescent substrate and formed complex must differ significantly in diffusion coefficients.24 This requirement can be omitted by using fluorescence cross-correlation spectroscopy (FCCS), although it involves multicomponent diffusional analysis and labeling with more than one fluorophore.25 FLT measures complex formation by observing changes of absorption and emission spectra (i.e., shift of maximum, shape, intensity) at different ratios of substrates. A major problem with TCCD is that it can be performed only at subnanomolar concentrations and the acquisition time is rather long (i.e., tens of minutes)22,23,26 The last method used directly in living cells—FRET—became a general technique in biochemical measurements as it combines substrate sensitivity at picomolar concentrations, nanoliter sample volume, and a short time of data acquisition (in order of seconds).27−30 However, FRET requires to label two substrates with two different dyes (donor and acceptor of energy) and confine them in close proximity within the complex (<10 nm). These requirements are often challenging to control due to availability of binding sites for fluorophore on the biomolecule, size of donor/acceptor probes and their reactivity.31 Recently, protein induced fluorescence enhancement (PIFE) has been proposed as a method to study unlabeled proteins bound to DNA.32−34 In the PIFE method, fluorescent dye (typically Cy3) is attached to immobilized double stranded DNA.35,36 The fluorescent intensity enhancement upon binding of a protein to DNA enables protein detection and its movement.

We employed molecular brightness (MB) analysis irrespective to the direction of change. Our objective was to quantitatively characterize formation of other type of noncovalent complexes beyond DNA–protein systems without the limitation of using specific dye and immobilization methods. As a model reaction, we chose hybridization of complementary DNA oligonucleotides where only one strand is labeled. DNA pairs, although with both labeled strands, were previously used to evaluate association/dissociation kinetics while demonstrating the alternating-laser excitation method by Kapanidis et al.30 This advancement allowed sorting a signal from each fluorophore and reduce the background-noise level. Taking advantage of this technical improvements, we develop the method based on the analysis of changes in MB of a single fluorophore, and it still retains all the advantages of FRET. The changes in local environment can quench or enhance fluorophore MB due to effects such as noncovalent interactions between the substrates, charge transfer, steric shielding, changes in dissipation of energy in different solvents, photoisomerization rate, changing HOMO–LUMO gap due to the change of temperature, or even a combination of those effects.38−43 This fact was used to develop viscosity sensors and ion concentration indicators, as well as to study complicated processes such as protein activation and tRNA translocation.44−49 In our approach to measure K, instead of collecting emission spectra, we record changes of the number of emitted photons per second upon complex formation; see Figure 1. We performed a series of titration experiments resulting in the changes of MB. We applied the method for concentration of DNA strands down to 80 pM. We estimated K even for a pair where changes in MB were as small as 5% difference in the intrinsic MB of fluorophore. By using FRET as a benchmark, we confirmed the reliability of the brightness-based method for determination of K.

Figure 1.

Figure 1

Open in a new tab

Principle of brightness changes analysis method for the determination of the equilibrium constants. (a) As a model complex-forming reaction we investigated fluorescently single-labeled complementary oligonucleotides. (b) With the use of TCSPC, we record a countrate of photons for substrate alone and after hybridization. (c) FCS measurements were conducted as a supporting technique for background correction and initial MB estimation. The FCS analysis alone is not sufficient for K determination due to overlapping autocorrelation curves of donor-only and formed complex with inseparable fluorescent fractions. The ratio between diffusion coefficients of the substrate (155 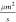Inline graphic) and the complex (144 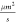Inline graphic) is much lower than 1.6. Thus, it does not meet the requirement for fraction separation.37 (d) Illustrative representation of fluorescence titration experiment with a fixed concentration of one substrate. (e) Changes of photon countrate upon complex formation.

Materials and Methods

Brightness Method for Equilibrium Constant Determination

Figure 1 schematically illustrates the brightness method for K determination. The total number of emitted photons is proportional to the time of signal acquisition t and the concentration CA of the fluorophore excited inside the focal volume V0. The average number of photons emitted per unit time defines the countrate, χ0:

graphic file with name jp0c00770_m001.jpg 1

As a model reaction we consider a formation of complex AB according to A + B ⇌ AB, where A is the labeled oligonucleoide strand and B is the nonfluorescent complementary strand. In this reaction, the only fluorescent components in a solution are A and AB. Therefore, eq 1 takes the form:

graphic file with name jp0c00770_m002.jpg 2

When complex AB is formed, the intrinsic brightness of fluorophore, α, changes to γ. In eq 2, CAeq and CAB are equilibrium concentrations of reagents in the mixture, related by the equation 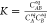Inline graphic. Because CA = CAeq + CAB and CB = CBeq + CAB we get the relation:

graphic file with name jp0c00770_m004.jpg 3

Equation 3 is analytically solved to determine the equilibrium concentration of complex CABeq. CAB is the function of three experimentally known variables, CABeq = f(CA,CB,K) = 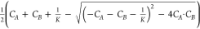Inline graphic.

Finally, the eq 2 is rewritten as

graphic file with name jp0c00770_m006.jpg 4

Equation 4 depends on parameters which we obtain experimentally: (1) the confocal volume V0 is defined during calibration of setup under chosen detection conditions; (2) both α and initial concentration CA of fluorescent substrate are determined in one FCS experiment according to eq 1; (3) the last γ brightness is evaluated in experiment where the second substrate B is in excess compared to concentration CA or vice versa. As the ratio 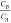Inline graphic of reagents increases, function χ as a function of CB begins to resemble a binding isotherm, Figure 1e. The workflowchart of brightness analysis method and details of FCS measurements are presented in the Supporting Information.

Oligonucleotide Pairs

Oligonucleotide strands were purchased from IBA GmbH, Germany and used without further purification. The custom-synthesized 13-mer strands were labeled with ATTO dyes at either 5′ or 3′ ends and named as indicated in Figure 3. The designed sequence prevents hairpin formation or secondary binding. Purification of oligonucleotides was performed by the manufacturer using the IBA Premium PAGE method. The strands were bought lyophilized. We resuspended them in Tris EDTA (TE) buffer to obtain a stock concentration of 100 μM, aliquoted and stored at −20 °C. Experimental concentrations of oligonucleotides were obtained by diluting stock solutions in 20 mM phosphate buffer (PB), pH = 7.4. Mixtures of complementary strands were incubated at 25 °C. The time of incubation depends on the sample concentrations—the lower the concentration, the longer the incubation time. The details are described elsewhere.50

Figure 3.

Figure 3

Open in a new tab

Schematic representation of the studied pairs. Complementary strands are labeled with ATTO488 (donor) and ATTO647N (acceptor) dyes.

Time-Correlated Single-Photon Counting Setup

All FCS, FRET and brightness measurements were performed using an inverted confocal microscope Nikon EZ-C1 setup equipped with a water immersion Nikon PlanApo 60x objective (NA = 1.2). The Nikon confocal unit was equipped with PicoQuant LSM upgrade system including PicoHarp 300 TCSPC module combined with two single-photon avalanche photodiodes (SPAD), by PerkinElmer Optoelectronics and Micro Photon Devices (Milan, Italy). Wavelength filters and dichroic mirrors placed in front of the detector were manufactured by Chroma (USA). We used two pulsed diode lasers 485 and 636 nm (PicoQuant GmbH, Germany). Lasers excitations pulses were controlled by the Sepia II laser controller (PicoQuant GmbH) together with the SymPhoTime 64 software. System details including filters and excitation pulse scheme are described in Figure S1.

Photodamaging of dyes was prevented by two factors (see Supporting Information section S1): first, no single dye was directly irradiated for prolonged periods of time (as it is a case in most imaging-based experiments), due to the fast diffusion of the probes (D = 155 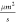Inline graphic); second, the dyes on average were illuminated by 55 μW (laser power measured before entering the objective) over time tD = 64 μs, the time of diffusion across a focal volume. Before each experimental session the laser power was measured by a PM100 power meter (Thorlabs, USA) and set at a constant value for whole measurements. Lab-Tek 8-Chambered cover-glass (Thermo Fisher Scientific, USA) was used as sample container. Focal volume was set at distance of 10 μm from the edge of the cover-glass. The temperature was maintained at 25 ± 0.5 °C within an isolating box enclosure with the temperature controller (OkoLab, Italy). Both FCS and TCSPC measurements were performed using the same confocal system.

FRET Analysis

We performed control FRET experiments (see Figure 2) to determine hybridization equilibrium constants K on oligonucleotide pairs with donor and acceptor dyes either on the same end (3′488/647N) of the formed complex or on the opposite sides (488/647N), Figure 3. We determined the average equilibrium constant for the broad range of concentrations. We found K equal to (3.5 ± 1.9) × 109 M–1 and (1.1 ± 0.5) × 109 M–1 for 3′488/647N and 488/647N pairs at 25 °C, 20 mM PB (pH = 7.4) buffer, respectively. This value is in a good agreement with the results of our previous work for the similar pair reaction at different ionic strength.50

Figure 2.

Figure 2

Open in a new tab

Example of FRET efficiency analysis of the sample where concentration of donor strand CA = 2 nM: (a) histograms for series of samples in different ratio Inline graphic binned with 100 ms interval for double labeled oligonucleotide pairs on the same sides (3′488/647N, top panel) and on the opposite sides (488/647N, bottom panel); (b) determination of equilibrium constant for a given pair. The analysis is described in detail in the Supporting Information.

Results and Discussion

Equilibrium Constant Determination Performed on Double Labeled Oligonucleotide Pairs

To test the MB method, we analyzed data obtained during FRET experiments on double labeled DNA pairs. We analyzed photons recorded upon blue excitation pulse for both red and blue channels. We performed an FCS analysis to determine the brightness of each component of the reaction after background correction. From brightness analysis, we observed increasing intensity in the red channel and a decrease in blue one, which was in good agreement with the energy transfer mechanism. Our analytical approach is presented in Figure 4.

Figure 4.

Figure 4

Open in a new tab

Labeled oligonucleotides before and after hybridization, excited in blue laser focal volume. The fluorescence photons emitted by the complex are visible in blue and red channels. (a) In the blue channel, the sample with donor only has the background-corrected countrate proportional to brightness and initial concentration of oligonucleotides. After the addition of acceptor-labeled strand, sample begins to reach the equilibrium. A complex possesses lower brightness due to energy transfer between strands, therefore overall countrate is decreased. (b) In the red channel analysis, due to the spectral properties of donor-strand, brightness is close to the background signal. After hybridization, transferred energy can be emitted as photons by acceptor molecule and hence complex brightness is increased. The scheme is not drawn to scale.

Recorded data points of countrate in a function of concentration follow the binding isotherm behavior as shown in Figure 5. To obtain K these data points were fitted with eq 4 for both red and blue channels. We performed analysis even at a concentration of around 100 pM, Figure 5a. The concentration-averaged values of K are shown in Table 1. The average equilibrium constants obtained by MB-based method from all experimental series for 3′488/647N and 488/647N labeling pairs are (3.4 ± 1.1) × 109 and (1.2 ± 0.8) × 109 M–1. These values are in good agreement with K determined by FRET analysis.

Figure 5.

Figure 5

Open in a new tab

Double labeled oligonucleotide pairs analyzed by changes of molecular brightness. The molecular brightness is measured as a function of countrate. It is observed either by an increase in the recorded number of photons in the red channel or a decrease in the blue one.

Table 1. Equilibrium Constants K Determined by FRET and BRIGHTNESS method for Double Labeled Pairs of Oligonucleotides.

  K × 109 M–1
    brightness method
  FRET blue channel red channel
3′488/647N 3.5 ± 1.9 2.9 ± 0.9 3.9 ± 1.1
488/647N 1.1 ± 0.5 0.9 ± 0.7 1.4 ± 0.9
Open in a new tab

Determination of DNA Hybridization Equilibrium Constants Using Only One Labeled Oligonculeotide Strand

Once the brightness methodology was verified, we moved from conventional donor–acceptor pair by replacing one of the complementary ATTO-dye labeled strand with a nonlabeled one, as shown in Figure 3. This implicates that, upon excitation, the energy can no longer be transferred, as stated in the FRET theorem. We performed measurements on a similar range of concentrations as in previous experiments. Results for both pairs are presented in Figure 6. Through the countrate analysis, we observed that ATTO488 (blue) labeled pair upon complex formation increases its MB by 22%. The change in fluorophore brightness enables us to fit eq 4 even at the picomolar regime (79 pM estimated by fitting). On the other hand, the ATTO647N (red) brightness was less influenced by the hybridization of DNA strands, which resulted in a decrease of only 5% regardless of the initial value. Due to such spectral behavior and limited detectors sensitivity, the equilibrium constant can be estimated for concentrations of ATTO647N labeled strand bigger than 10 nM. During the fitting we estimated average equilibrium constants for both pairs equals to (1.11 ± 0.9) × 109 and (0.9 ± 0.4) × 109 M–1, for 3′488/NN and NN/647N pairs, respectively. The MB changes showed that single labeled pairs have the same values of K as 488/647N pair (two labels at the opposite sides of the complex). The comparison of equilibrium constants obtained for four differently labeled pairs of oligonucleotides are shown in Figure 8. Having proofed the brightness approach to determine the equilibrium constant when unlabeled oligonucleotides are used, we also anticipate that this method could be used to study reactions in living cells. It can be especially useful, where other techniques like FCS3 or FRET51 cannot be used due to several reasons: not significant differences in diffusion coefficients or low FRET efficiency upon complex formation as well as difficulties in attaching fluorophores to biomolecules of interest. In contrast to FRET, TCCD, and FCCS, in our approach, only one of the substrates needs to be fluorescent. This can simplify measurements in living cells by introducing a fluorescent substrate (e.g., GFP labeled protein) via genetic modifications and controlling a ratio of second substrate by cell medium composition, microinjections, physical triggers, or vice versa.

Figure 6.

Figure 6

Open in a new tab

Exemplary results of the brightness analysis method for single labeled oligonucleotide pairs. By fixing the concentration of the labeled strand, we were able to observe equilibrium states at each CB just by a local change of an environment around each dye. (a) The ATTO488-labeled strand upon complex formation increased molecular brightness by 22%. (b) As a second case where ATTO647N was used as labeling fluorophore, its molecular brightness decreased by only 5%.

Figure 8.

Figure 8

Open in a new tab

Comparison of equilibrium constants obtained from brightness method for all experimental oligonucleotide pairs. Box-whisker plots represent the distributions of equilibrium constants for double labeled and single labeled pairs. The boxes show the first (Q1) and third quartiles (Q3) whereas the whiskers show the minimum and maximal values (excluding outliers). The medians and averages are shown according to the figure legend.

Experimental Errors

Molecular brightness analysis is based on recording the changes of the single photon emission at different concentration ratio, 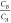Inline graphic. We wanted to estimate how experimental errors (especially during preparation of samples) may affect the determination of K. Therefore, the Equation 4 should be transformed from χ(CA, CB, K) to K(CA, CB, χ). Then, the error of K determination, σ(K), is calculated through the total differential approximation to estimate the total/maximum experimental error; see eq 5.

graphic file with name jp0c00770_m010.jpg 5

However, eq 4 contains the implicit function, f(CA,CB,K) which makes impossible to analytically solve σ(K). To estimate the error of K we performed Monte Carlo simulations. We set the program to use one of previously measured and fitted data series for pair 3′488/NN. The molecular brightness α and γ were estimated in separate sets of measurements with the error of around 1%; therefore, we use them as a constant values. The molecular brightness ratio was set to 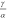Inline graphic=1.23. Through the analysis of a data series for a given CA concentration, we estimated average error for substrate concentration σ(CB) and countrate σ(χ) as 15% and 5% respectively.

In order to determine the error of σ(K), we draw the error values from the normal distribution of σ(CB) and σ(χ). We applied them for the entire data series, see Figure 7a. We solve eq 4 ten thousand times (N = 10000) for each generated series. All of the obtained CA and K fitted values were averaged with calculated error through standard deviation.

Figure 7.

Figure 7

Open in a new tab

σ(K) estimation based on randomly generated experimental errors by Monte Carlo simulations.

The fitting values for nonmodified data series were CA = 6.31 ± 0.01 nM and K = (1.06 ± 0.71) × 109 M–1. Through the simulations we obtained K value equal to (1.15 ± 0.67) × 109; see Figure 7b. These results are in good agreement with the averaged errors obtained experimentally (1.11 ± 0.9) × 109. The σ(χ) is related to the instrumental characteristics of the detector, i.e., noise level, dead time, sensitivity at given wavelength of collected photon, and proper filtration of the background. The lower the concentration the higher the σ(χ) is. By increasing the number of data points for given 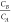Inline graphic the impact of experimental and instrumental error can be reduced. However, after our analysis we would like to underline that the critical attention should be paid toward correct preparation of solutions CA and CB.

Explanation of the Differences in K Values for Single and Double Labeled Pairs

The observed change of the MB of a single fluorophore upon complex formation can be attributed to the known effect of DNA–DNA noncovalent π–π stacking.52 Upon hybridization, parallelly arranged base pairs interfere with the HOMO–LUMO gap of dyes by changing local electron density, which cause either lowering or increasing the gap distance. The common sensitive part responsible for changes of MB upon fluctuation of local environment are delocalized electrons in chromophore aromatic structure. Such effects are observed in many examples of commercially available dyes, i.e., SYBR, DAPI, YOYO, or even the anticancer drug doxorubicin.21,53,54 The comparison of differences in K values among all four oligonucleotide pairs (two double and two single labeled) shows that there is an additional attraction between dyes themselves in the case of the 3′488/647N pair. The pair 3′488/647N showed three times higher K than other pairs. This effect is most probably related to the π–π stacking of ATTO dyes aromatic groups located at the same end of the formed complex. The binding energy calculated as the difference in Gibbs free energy is about ΔG = −2.75 kJ·M–1. This value is bigger than energy of thermal fluctuations in the system kBT = |2.48| kJ·M–1 at 25 °C. The obtained ΔG value is in good agreement with stacking energy between polyaromatic groups.55

The results from single labeled pairs experiments are used here to discuss the complexity of energy transfer in double labeled pairs with ATTO488 and ATTO647N dyes. Three competing effects overlaps in the double labeled system. First is energy transfer according to the FRET theorem. In the close distance (<10 nm) two fluorophores of specific spectral properties exchange the energy depending on the separating distance between them. From the FRET analysis the pair 488/647N (opposite ends) has 34% of energy transfer upon complex formation. It means that, out of 100 photons absorbed by donor 34 are transferred and observed in red channel. Figure 5b shows inequality of photons transfer (60 photons decrease in blue, and 290 increase in red channel). Second, upon the hybridization of DNA duplex ATTO488 increases MB by 22% (extra 130 according to initial 580). Those values sum up to 190 and after correction by factor γ are equal to 263 photons. Lastly, a 5% decrease of MB by ATTO647N upon hybridization might facilitate energy transfer, which should fills the missing 30 photons. This suggests that additional MB changes by each fluorophore in any double labeled system for the FRET measurements may affect estimated FRETMAX.56,57 Such effects need to be considered during the design and analysis of experiments where FRET is used.

Conclusions

In summary, we present the applicability of molecular brightness analysis for determination of the equilibrium constants K in noncovalent complex-forming reactions (A + B ⇌ AB), down to picomolar concentrations. To estimate K, we record the changes of MB upon the complex formation where only one substrate is fluorescently labeled. We apply this analysis providing that the fluorophore changes its MB upon complex formation irrespective to the direction of change (increase or decrease of MB). The K can be estimated in reactions where complexation changes MB by as low as 5% with respect to the initial MB of a substrate.

We demonstrated that commercially available ATTO488 and ATTO647N dyes change brightness upon DNA hybrydization sufficiently to determine K. We assume that also increase of MB of a cyanine dye (e.g., Cy3), as upon protein binding, could be employed for brightness analysis of reactions where a substrate binds in the vicinity of the fluorophore.38 It was demonstrated for several fluorophores that their inherent fluorescence changes by order of magnitudes when a DNA is attached (e.g., YOYO, SYBR). This effect may allow K determination at picomolar concentration regimes. At this stage, it is difficult to judge how other dyes will be useful in brightness analyses. We expect that our method can be enhanced by synthesizing novel fluorophores with higher sensitivity. The values of K estimated on the same pairs obtained by FRET and our method, show no significant differences. This method can be applied not only for oligonucleotide-based technologies like PCR, fluorescence in-situ hybridization (FISH), and gene editing but also for determining the interactions of chemical compounds characterized by low internal brightness. We expect that this method is adaptable to any microscope system including super resolution techniques, i.e., TIRF and STED.

Acknowledgments

This work was supported by the National Science Centre, Poland within the grant Maestro UMO-2016/22/A/ST4/00017.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.0c00770.

  • Results mentioned in the main text in a tabular form as well as concentration working regime analysis, fluorescence correlation spectroscopy measurements, FRET and FCS analysis, workflowchart of the brightness-based method, details on setting the laser power, and oligonucleotide complexes emission spectra (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp0c00770_si_001.pdf (2.3MB, pdf)

References

  1. Hu C.-D.; Chinenov Y.; Kerppola T. K. Visualization of interactions among bZIP and Rel family proteins in living cells using bimolecular fluorescence complementation. Mol. Cell 2002, 9, 789–798. 10.1016/S1097-2765(02)00496-3. [DOI] [PubMed] [Google Scholar]
  2. Van Rood J. v.; Van Leeuwen A.; Ploem J. Simultaneous detection of two cell populations by two-colour fluorescence and application to the recognition of B-cell determinants. Nature 1976, 262, 795. 10.1038/262795a0. [DOI] [PubMed] [Google Scholar]
  3. Kwapiszewska K.; Kalwarczyk T.; Michalska B.; Szczepański K.; Szymański J.; Patalas-Krawczyk P.; Andryszewski T.; Iwan M.; Duszyński J.; Hołyst R. Determination of oligomerization state of Drp1 protein in living cells at nanomolar concentrations. Sci. Rep. 2019, 9, 5906. 10.1038/s41598-019-42418-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Tsvetanova N. G.; Irannejad R.; von Zastrow M. G. protein-coupled receptor (GPCR) signaling via heterotrimeric G proteins from endosomes. J. Biol. Chem. 2015, 290, 6689–6696. 10.1074/jbc.R114.617951. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Gilli P.; Ferretti V.; Gilli G.; Borea P. A. Enthalpy-entropy compensation in drug-receptor binding. J. Phys. Chem. 1994, 98, 1515–1518. 10.1021/j100056a024. [DOI] [Google Scholar]
  6. De Lean A.; Stadel J.; Lefkowitz R. A ternary complex model explains the agonist-specific binding properties of the adenylate cyclase-coupled beta-adrenergic receptor. J. Biol. Chem. 1980, 255, 7108–7117. [PubMed] [Google Scholar]
  7. Lu H.; Tonge P. J. Drug–target residence time: critical information for lead optimization. Curr. Opin. Chem. Biol. 2010, 14, 467–474. 10.1016/j.cbpa.2010.06.176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Rehman S. U.; Sarwar T.; Husain M. A.; Ishqi H. M.; Tabish M. Studying non-covalent drug–DNA interactions. Arch. Biochem. Biophys. 2015, 576, 49–60. 10.1016/j.abb.2015.03.024. [DOI] [PubMed] [Google Scholar]
  9. Olaru A.; Bala C.; Jaffrezic-Renault N.; Aboul-Enein H. Y. Surface plasmon resonance (SPR) biosensors in pharmaceutical analysis. Crit. Rev. Anal. Chem. 2015, 45, 97–105. 10.1080/10408347.2014.881250. [DOI] [PubMed] [Google Scholar]
  10. Pérez-Arnáiz C.; Busto N.; Leal J. M.; García B. New microsecond intramolecular reactions of human telomeric DNA in solution. RSC Adv. 2016, 6, 39204–39208. 10.1039/C6RA04203A. [DOI] [Google Scholar]
  11. Liu Y.; Yu X.; Zhao R.; Shangguan D.-H.; Bo Z.; Liu G. Real time kinetic analysis of the interaction between immunoglobulin G and histidine using quartz crystal microbalance biosensor in solution. Biosens. Bioelectron. 2003, 18, 1419–1427. 10.1016/S0956-5663(03)00090-3. [DOI] [PubMed] [Google Scholar]
  12. Rao B.; Buttlaire D.; Cohn M. 31P NMR studies of the arginine kinase reaction. Equilibrium constants and exchange rates at stoichiometric enzyme concentration. J. Biol. Chem. 1976, 251, 6981–6986. [PubMed] [Google Scholar]
  13. Fielding L. NMR methods for the determination of protein-ligand dissociation constants. Curr. Top. Med. Chem. 2003, 3, 39–53. 10.2174/1568026033392705. [DOI] [PubMed] [Google Scholar]
  14. Garbett N. C.; Ragazzon P. A.; Chaires J. B. Circular dichroism to determine binding mode and affinity of ligand–DNA interactions. Nat. Protoc. 2007, 2, 3166. 10.1038/nprot.2007.475. [DOI] [PubMed] [Google Scholar]
  15. Jelesarov I.; Bosshard H. R. Isothermal titration calorimetry and differential scanning calorimetry as complementary tools to investigate the energetics of biomolecular recognition. J. Mol. Recognit. 1999, 12, 3–18. . [DOI] [PubMed] [Google Scholar]
  16. Zhang X.; Poniewierski A.; Sozański K.; Zhou Y.; Brzozowska-Elliott A.; Holyst R. Fluorescence correlation spectroscopy for multiple-site equilibrium binding: a case of doxorubicin–DNA interaction. Phys. Chem. Chem. Phys. 2019, 21, 1572–1577. 10.1039/C8CP06752J. [DOI] [PubMed] [Google Scholar]
  17. Moor N. A.; Vasil’eva I. A.; Anarbaev R. O.; Antson A. A.; Lavrik O. I. Quantitative characterization of protein–protein complexes involved in base excision DNA repair. Nucleic Acids Res. 2015, 43, 6009–6022. 10.1093/nar/gkv569. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gelfand C. A.; Plum G. E.; Mielewczyk S.; Remeta D. P.; Breslauer K. J. A quantitative method for evaluating the stabilities of nucleic acids. Proc. Natl. Acad. Sci. U. S. A. 1999, 96, 6113–6118. 10.1073/pnas.96.11.6113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Lynch I.; Dawson K. A. Protein-nanoparticle interactions. Nano Today 2008, 3, 40–47. 10.1016/S1748-0132(08)70014-8. [DOI] [Google Scholar]
  20. Airoldi M.; Barone G.; Gennaro G.; Giuliani A. M.; Giustini M. Interaction of doxorubicin with polynucleotides. A spectroscopic study. Biochemistry 2014, 53, 2197–2207. 10.1021/bi401687v. [DOI] [PubMed] [Google Scholar]
  21. Perez-Arnaiz C.; Busto N.; Leal J. M.; Garcia B. New insights into the mechanism of the DNA/doxorubicin interaction. J. Phys. Chem. B 2014, 118, 1288–1295. 10.1021/jp411429g. [DOI] [PubMed] [Google Scholar]
  22. Orte A.; Birkett N. R.; Clarke R. W.; Devlin G. L.; Dobson C. M.; Klenerman D. Direct characterization of amyloidogenic oligomers by single-molecule fluorescence. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 14424–14429. 10.1073/pnas.0803086105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Orte A.; Clarke R.; Balasubramanian S.; Klenerman D. Determination of the fraction and stoichiometry of femtomolar levels of biomolecular complexes in an excess of monomer using single-molecule, two-color coincidence detection. Anal. Chem. 2006, 78, 7707–7715. 10.1021/ac061122y. [DOI] [PubMed] [Google Scholar]
  24. Zhang X.; Sisamakis E.; Sozanski K.; Holyst R. Nanoscopic approach to quantification of equilibrium and rate constants of complex formation at single-molecule level. J. Phys. Chem. Lett. 2017, 8, 5785–5791. 10.1021/acs.jpclett.7b02742. [DOI] [PubMed] [Google Scholar]
  25. Schwille P.; Meyer-Almes F.-J.; Rigler R. Dual-color fluorescence cross-correlation spectroscopy for multicomponent diffusional analysis in solution. Biophys. J. 1997, 72, 1878–1886. 10.1016/S0006-3495(97)78833-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Höfig H.; Yukhnovets O.; Remes C.; Kempf N.; Katranidis A.; Kempe D.; Fitter J. Brightness-gated two-color coincidence detection unravels two distinct mechanisms in bacterial protein translation initiation. Communications biology 2019, 2, 1–8. 10.1038/s42003-019-0709-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Cao L.; Cheng L.; Zhang Z.; Wang Y.; Zhang X.; Chen H.; Liu B.; Zhang S.; Kong J. Visual and high-throughput detection of cancer cells using a graphene oxide-based FRET aptasensing microfluidic chip. Lab Chip 2012, 12, 4864–4869. 10.1039/c2lc40564d. [DOI] [PubMed] [Google Scholar]
  28. Zhang C.-y.; Johnson L. W. Microfluidic control of fluorescence resonance energy transfer: breaking the FRET limit. Angew. Chem., Int. Ed. 2007, 46, 3482–3485. 10.1002/anie.200604861. [DOI] [PubMed] [Google Scholar]
  29. Phillip Y.; Kiss V.; Schreiber G. Protein-binding dynamics imaged in a living cell. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 1461–1466. 10.1073/pnas.1112171109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Kapanidis A. N.; Lee N. K.; Laurence T. A.; Doose S.; Margeat E.; Weiss S. Fluorescence-aided molecule sorting: analysis of structure and interactions by alternating-laser excitation of single molecules. Proc. Natl. Acad. Sci. U. S. A. 2004, 101, 8936–8941. 10.1073/pnas.0401690101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Medintz I. L.; Hildebrandt N.. FRET-Förster resonance energy transfer: from theory to applications; John Wiley & Sons: 2013. [Google Scholar]
  32. Hwang H.; Kim H.; Myong S. Protein induced fluorescence enhancement as a single molecule assay with short distance sensitivity. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 7414–7418. 10.1073/pnas.1017672108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Ploetz E.; Lerner E.; Husada F.; Roelfs M.; Chung S.; Hohlbein J.; Weiss S.; Cordes T. Forster resonance energy transfer and protein-induced fluorescence enhancement as synergetic multi-scale molecular rulers. Sci. Rep. 2016, 6, 33257. 10.1038/srep33257. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lerner E.; Ploetz E.; Hohlbein J.; Cordes T.; Weiss S. A Quantitative Theoretical Framework For Protein-Induced Fluorescence Enhancement–Forster-Type Resonance Energy Transfer (PIFE-FRET). J. Phys. Chem. B 2016, 120, 6401–6410. 10.1021/acs.jpcb.6b03692. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Hwang H.; Myong S. Protein induced fluorescence enhancement (PIFE) for probing protein–nucleic acid interactions. Chem. Soc. Rev. 2014, 43, 1221–1229. 10.1039/C3CS60201J. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Valuchova S.; Fulnecek J.; Petrov A. P.; Tripsianes K.; Riha K. A rapid method for detecting protein-nucleic acid interactions by protein induced fluorescence enhancement. Sci. Rep. 2016, 6, 39653. 10.1038/srep39653. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Meseth U.; Wohland T.; Rigler R.; Vogel H. Resolution of fluorescence correlation measurements. Biophys. J. 1999, 76, 1619–1631. 10.1016/S0006-3495(99)77321-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Stennett E. M.; Ciuba M. A.; Lin S.; Levitus M. Demystifying PIFE: The photophysics behind the protein-induced fluorescence enhancement phenomenon in Cy3. J. Phys. Chem. Lett. 2015, 6, 1819–1823. 10.1021/acs.jpclett.5b00613. [DOI] [PubMed] [Google Scholar]
  39. Rachofsky E. L.; Osman R.; Ross J. A. Probing structure and dynamics of DNA with 2-aminopurine: effects of local environment on fluorescence. Biochemistry 2001, 40, 946–956. 10.1021/bi001664o. [DOI] [PubMed] [Google Scholar]
  40. Dos Remedios C. G.; Moens P. D. Fluorescence resonance energy transfer spectroscopy is a reliable” ruler” for measuring structural changes in proteins: Dispelling the problem of the unknown orientation factor. J. Struct. Biol. 1995, 115, 175–185. 10.1006/jsbi.1995.1042. [DOI] [PubMed] [Google Scholar]
  41. Marras S. A.; Kramer F. R.; Tyagi S. Efficiencies of fluorescence resonance energy transfer and contact-mediated quenching in oligonucleotide probes. Nucleic acids research 2002, 30, 122e–122e. 10.1093/nar/gnf121. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Castello F.; Casares S.; Ruedas-Rama M. J.; Orte A. The first step of amyloidogenic aggregation. J. Phys. Chem. B 2015, 119, 8260–8267. 10.1021/acs.jpcb.5b01957. [DOI] [PubMed] [Google Scholar]
  43. Lakowicz J. R.Principles of fluorescence spectroscopy; Springer Science & Business Media: 2013. [Google Scholar]
  44. Kotlikoff M. I. Genetically encoded Ca2+ indicators: using genetics and molecular design to understand complex physiology. J. Physiol. 2007, 578, 55–67. 10.1113/jphysiol.2006.120212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Renard D.; Lefebvre J.; Griffin M.; Griffin W. Effects of pH and salt environment on the association of β-lactoglobulin revealed by intrinsic fluorescence studies. Int. J. Biol. Macromol. 1998, 22, 41–49. 10.1016/S0141-8130(97)00086-X. [DOI] [PubMed] [Google Scholar]
  46. Minta A.; Kao J.; Tsien R. Y. Fluorescent indicators for cytosolic calcium based on rhodamine and fluorescein chromophores. J. Biol. Chem. 1989, 264, 8171–8178. [PubMed] [Google Scholar]
  47. Lamichhane R.; Liu J. J.; Pljevaljcic G.; White K. L.; van der Schans E.; Katritch V.; Stevens R. C.; Wüthrich K.; Millar D. P. Single-molecule view of basal activity and activation mechanisms of the G protein-coupled receptor β2AR. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, 14254–14259. 10.1073/pnas.1519626112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Munro J. B.; Wasserman M. R.; Altman R. B.; Wang L.; Blanchard S. C. Correlated conformational events in EF-G and the ribosome regulate translocation. Nat. Struct. Mol. Biol. 2010, 17, 1470. 10.1038/nsmb.1925. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Pan D.; Kirillov S. V.; Cooperman B. S. Kinetically competent intermediates in the translocation step of protein synthesis. Mol. Cell 2007, 25, 519–529. 10.1016/j.molcel.2007.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Bielec K.; Sozanski K.; Seynen M.; Dziekan Z.; ten Wolde P. R.; Holyst R. Kinetics and equilibrium constants of oligonucleotides at low concentrations. Hybridization and melting study. Phys. Chem. Chem. Phys. 2019, 21, 10798–10807. 10.1039/C9CP01295H. [DOI] [PubMed] [Google Scholar]
  51. Chen W.; Avezov E.; Schlachter S. C.; Gielen F.; Laine R. F.; Harding H. P.; Hollfelder F.; Ron D.; Kaminski C. F. A method to quantify FRET stoichiometry with phasor plot analysis and acceptor lifetime ingrowth. Biophys. J. 2015, 108, 999–1002. 10.1016/j.bpj.2015.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Matta C. F.; Castillo N.; Boyd R. J. Extended weak bonding interactions in DNA: π-stacking (base- base), base- backbone, and backbone- backbone interactions. J. Phys. Chem. B 2006, 110, 563–578. 10.1021/jp054986g. [DOI] [PubMed] [Google Scholar]
  53. Wang L.; Pyle J. R.; Cimatu K. L.; Chen J. Ultrafast transient absorption spectra of photoexcited YOYO-1 molecules call for additional investigations of their fluorescence quenching mechanism. J. Photochem. Photobiol., A 2018, 367, 411–419. 10.1016/j.jphotochem.2018.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Dragan A.; Pavlovic R.; McGivney J.; Casas-Finet J.; Bishop E.; Strouse R.; Schenerman M.; Geddes C. SYBR Green I: fluorescence properties and interaction with DNA. J. Fluoresc. 2012, 22, 1189–1199. 10.1007/s10895-012-1059-8. [DOI] [PubMed] [Google Scholar]
  55. Silva N. J.; Machado F. B.; Lischka H.; Aquino A. J. π–π stacking between polyaromatic hydrocarbon sheets beyond dispersion interactions. Phys. Chem. Chem. Phys. 2016, 18, 22300–22310. 10.1039/C6CP03749F. [DOI] [PubMed] [Google Scholar]
  56. Roy R.; Hohng S.; Ha T. A practical guide to single-molecule FRET. Nat. Methods 2008, 5, 507. 10.1038/nmeth.1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. McCann J. J.; Choi U. B.; Zheng L.; Weninger K.; Bowen M. E. Optimizing methods to recover absolute FRET efficiency from immobilized single molecules. Biophys. J. 2010, 99, 961–970. 10.1016/j.bpj.2010.04.063. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp0c00770_si_001.pdf (2.3MB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES