Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Aug 19;5(9):2972–2978. doi: 10.1021/acsenergylett.0c01410

Reduction of the Lattice Thermal Conductivity of Polymer Semiconductors by Molecular Doping

Osnat Zapata-Arteaga †, Aleksandr Perevedentsev †, Sara Marina ‡, Jaime Martin ‡,§, Juan Sebastián Reparaz †,*, Mariano Campoy-Quiles †,*
PMCID: PMC7497712  PMID: 32953988

Abstract

graphic file with name nz0c01410_0004.jpg

Here we show that molecular doping of polymer thermoelectrics increases the electrical conductivity while reducing the thermal conductivity. A high-throughput methodology based on annealing and doping gradients within individual films is employed to self-consistently analyze and correlate electrical and thermal characteristics for the equivalent of >100 samples. We focus on the benchmark material system poly(2,5-bis(3-alkylthiophen-2-yl)thieno[3,2-b]thiophene) (PBTTT) doped with molecular acceptor 2,3,5,6-tetrafluoro-7,7,8,8-tetracyanoquinodimethane (F4TCNQ). The thermal conductivity of neat PBTTT films is dominated by the degree of crystallinity, with thermal percolation observed for annealing temperatures >170 °C. Upon doping the samples with a relatively low amount of F4TCNQ (anion content <1 mol %), the thermal conductivity exhibits a two-fold reduction without compromising the crystalline quality, which resembles the effect of alloy scattering observed in several inorganic systems. The analysis of the relation between thermal and electrical conductivities shows that thermal transport is dominated by a doping-induced reduced lattice contribution.

Organic semiconductors are promising candidates for ubiquitous molecular electronics and energy harvesting due to their low cost, abundance of constituent elements, and amenability to scalable low-temperature processing. The use of doping to vary the electrical conductivity by several orders of magnitude1−5 has emerged as a key enabler for a wide range of organic-semiconductor-based devices including transistors, light-emitting diodes, and, in particular, thermoelectric generators.6,7 In the concept of thermoelectricity, heat flux is converted to electrical power with an efficiency that scales with the figure of merit (ZT), which is related to both electrical (σ) and thermal (κ) conductivities as ZT ∝ σκ–1. Whereas the majority of recent reports have explored doping-induced electrical conductivity as the principal parameter for optimizing the characteristics of thermoelectric materials, comparatively few studies have investigated the simultaneous impact on thermal conductivity.8,9 Even fewer studies have attempted to unravel the “Gordian knot” of inter-related electrical and thermal conductivities as well as the inevitable dependence of both on the semicrystalline microstructure of the organic semiconductor.10

More particularly, the previously mentioned inter-relation arises from the fact that in electrically conductive systems the total thermal conductivity, κ, is given by the sum of electronic (κe) and lattice (κlatt) contributions. For metals and highly doped semiconductors, κe is proportional to the electrical conductivity following the Wiedemann–Franz law, κe = σLT, where L is the Lorenz number and T is the temperature.11 Although in such materials the electrical and vibrational contributions to ZT are inevitably coupled, it cannot be concluded that this relation also holds for doped organic semiconductors. In fact, several studies for PEDOT:PSS, PEDOT:Tos, and doped polyacetylene suggest that the correlation between σ and κ is not yet fully understood.12−15 Furthermore, a recent theoretical work based on Monte Carlo simulations questioned the validity of the Wiedemann–Franz law in conducting polymers.16 One of the reasons leading to this ambiguity is, perhaps, that there are few reports that simultaneously address electrical and thermal conduction.13,17

Here we present a comprehensive study of electrical and thermal characteristics of poly(2,5-bis(3-alkylthiophen-2-yl)-thieno[3,2-b]-thiophene) (PBTTT) films doped with 2,3,5,6-tetrafluoro-7,7,8,8-tetracyanoquinodimethane (F4TCNQ). For this purpose, we employed a novel high-throughput methodology based on doping gradients and analysis using high-spatial-resolution noncontact optical methods, which yielded thermal and electrical conductivity data for the equivalent of >100 samples with different doping levels while avoiding uncertainties from sample-to-sample variation. We show that the key finding is that the presence of a low doping level (hereafter expressed as the molar ratio of F4TCNQ anion per PBTTT monomer, MRD) within PBTTT films leads to a reduction in thermal conductivity, resembling a similar effect that arises from the alloy scattering observed in other materials. By studying the relation between the thermal and the electrical conductivity, we also demonstrate that the effective lattice thermal conductivity decreases by doping within the Wiedemann–Franz framework.

To study the thermal and electrical conductivity of the PBTTT films as a function of the F4TCNQ anion amount, we have developed a novel fabrication process based on the concept of annealing18−20 and doping gradients.21 The “baseline” samples comprised PBTTT films (thickness ≈ 160 nm) deposited onto 75 mm long conventional glass substrates by blade-coating. (See the Supporting Information for fabrication details.) Thereafter, two types of samples were fabricated by postprocessing: (i) neat (that is, undoped) PBTTT films, which were annealed at spatially varying temperatures using a Kofler bench, and (ii) PBTTT films (160 nm) with a spatially varying MRD of up to 0.23. The latter were fabricated by, first, homogeneous vapor-phase doping of “baseline” samples, followed by thermal annealing using the Kofler bench (temperatures spanning 130–200 °C), which induced spatially varying degrees of dedoping according to the local temperature set by the Kofler bench.21 Whereas both samples (i) and (ii) were used to study the role of the dopant in determining the overall thermal conductivity, sample (ii) was used to address the electrical characteristics. Because thermal and electrical conductivities were both studied using contactless optical methods, the doping level variation is considered to be negligible within the laser spot (typical radius of probed region <5 μm; spatial variation of MRD < 0.004 mm–1). An additional set of samples with a homogeneous doping level was specifically fabricated for the grazing-incidence wide-angle X-ray scattering (GIWAXS) analysis to correlate the microstructures of the samples with their electrical and thermal properties.

Figure 1a,d presents absorption spectra of films as a function of the annealing temperature: 70–200 °C for the neat sample (i) and 130–200 °C for doped sample (ii), respectively. The spectra for the neat sample (i) exhibit two bands around 530 nm (A0–1) and 630 nm (A0–0) belonging to the disordered polymer and crystalline fractions, respectively.22 The intensity ratio between these bands is related to the free exciton bandwidth (W) and is considered to be an indicator of the degree of crystallinity, whereby a smaller W implies a higher conjugation length and interchain order.22−24 (See Figure S3a.) As the annealing temperature increases, W gradually decreases (100 → 50 meV), indicating that the annealing process increases the degree of crystallinity within the polymer film, in agreement with the observations of refs (25) and (26). In the case of the doped sample (ii), we identify integer charge transfer (ICT) between PBTTT and F4TCNQ by the appearance of three subgap transitions that belong to the radical anion of the F4TCNQ*– (A1, A2, and A3; see Figure 1d).18,27,28 By fitting these features as well as those of the neutral polymer, the doping level across the gradient of the film can be estimated23,28,29 (Figure S3b).

Figure 1.

Figure 1

Open in a new tab

(a) Absorption spectra of a PBTTT film featuring a gradient of the degree of crystallinity induced by annealing on a temperature gradient. Data are normalized by the A0–1 transition. (b) Thermal conductivity as a function of the free exciton bandwidth, W, for the annealed PBTTT film; the inset shows the data for W = 40–50 meV. (c) Schematic illustration of the microstructure of a neat PBTTT film for different annealing temperatures, which is rationalized in terms of a series or parallel thermal resistor model. (d) Absorption spectra for a PBTTT film with a gradient of doping. (e) Thermal conductivity (left ordinate) as a function of the estimated doping level (green line is a fit to the data) and the fitted free exciton bandwidth as a function of the doping level (orange line, right ordinate). (f) Schematic illustration of the microstructure of a doped PBTTT film for different dedoping temperatures along a proposed a resistor model.

The thermal conductivity of both samples is shown in Figure 1b,e. To address the influence of the degree of crystallinity of the PBTTT films upon their thermal conductivity, we plot the thermal conductivity as a function of W for the neat sample (i) in Figure 1b, as obtained from the analysis of the corresponding absorption spectra. It is interesting to note that the thermal conductivity of the neat sample exhibits an abrupt increase from ∼0.3 to ∼0.7 W m–1 K–1, which corresponds to a rather small change in the exciton bandwidth (∼50 meV) for annealing temperatures above ∼170 °C. We ascribe this to the occurrence of thermal percolation; that is, as the annealing temperature increases, PBTTT crystallites grow larger25,30 within the films, which yields a substantial increase in thermal conductivity when the crystals are thermally interconnected. These observations are also consistent with the appearance of a “terraced” phase in PBTTT, as reported elsewhere,26,30 and with our atomic force microscopy measurements. (See Figure 2 and Figure S4 for more details.) Figure 1c shows a schematic illustration of the influence of the annealing process on the crystalline microstructure of PBTTT films. We propose an equivalent thermal resistance circuit that behaves as follows: For low annealing temperatures, the thermal transport is dominated by the thermal resistance between crystals, which can be modeled by a series resistance model. However, as the annealing temperature increases, the size of the crystals grows until thermal percolation is established, which is then represented by a parallel resistor geometry. We note, however, that this is our current working hypothesis, as we do not have access to the exact crystalline/amorphous ratio that will be necessary to quantitatively describe the observed behavior through available models, such as effective medium, percolation theory, or the rule of mixtures, among others.8,31,32

Figure 2.

Figure 2

Open in a new tab

GIWAXS patterns for (a) out-of-plane (h00) and (b) in-plane (0k0) integrations. Data are shown for a neat as-deposited PBTTT film and the same film following annealing at T = 100 and 180 °C (as indicated). Also shown are the data for a film annealed at T = 180 °C and subsequently doped and the same film following dedoping. Data are offset for clarity; vertical markers are guides to the eye for peak shifts relative to the data for the neat PBTTT annealed at T = 180 °C.

The effect of doping on the overall thermal conductivity is shown in Figure 1e. In this case, the thermal conductivity is plotted as a function of the estimated doping level present in the PBTTT thin films, which is obtained via the previously described analysis (Figure 1d). Interestingly, the thermal conductivity remains essentially constant at ∼0.35 W m–1 K–1 for an MRD greater than ∼0.01, with the few points falling out of the trend attributed to dopant aggregates on the film surface.21 (See Figure S6 for more details.) Below this value, the thermal conductivity of the films approaches the value obtained for the neat sample (i) at high annealing temperatures. The latter is expected given that the doped sample (ii) was precrystallized by annealing at 180 °C prior to doping, and thus its crystalline structure before the doping process matches that obtained for the neat sample (i) at annealing temperatures >170 °C. Surprisingly, a relatively low MRD (<0.01) already induces a two-fold decrease in the thermal conductivity. This resembles the effect of alloy scattering, as observed in inorganic materials.33−37 Furthermore, as shown in Figure 1e, the exciton bandwidth remains constant (∼40 meV) across the entire range of the doping level, which suggests that the crystalline quality of the PBTTT thin film does not deteriorate following the doping process. In fact, the simultaneous observation of a small exciton bandwidth and a small thermal conductivity can be rationalized by considering that the dopant is probably located within PBTTT crystals. Figure 1f displays a schematic illustration of the microstructure of doped samples. In this case, the microstructure of the samples before the doping process is dictated by the initial annealing process. Further doping increases the thermal resistance between crystalline domains, thus leading to a smaller average thermal conductivity of the films. The present observations suggest that the primary thermal transport mechanism in this system is given by the lattice and not by the free electrons arising from doping.

To get further insights into the mechanisms controlling the thermal conductivity, we have performed a detailed structural analysis of the samples by means of GIWAXS. Figure 2a,b shows the evolution of the (h00) and (0k0) crystalline planes associated with the lamellar packing and π–π stacking in PBTTT, respectively.18,25,27,38−40 For the case of the neat samples, two main observations should be highlighted. As the annealing temperature increases, the width of the out-of-plane diffraction peaks (Figure 2a) progressively narrows, thus indicating an improved ordering of the lamellar packing.25,41 This observation is consistent with the corresponding evolution of the exciton bandwidth and thermal conductivity (Figure 1a,b respectively); that is, as the annealing temperature increases, the exciton bandwidth decreases, leading to the observed two-fold increase in the thermal conductivity. We note that typically, an increased degree of crystallinity or crystal coherence length is responsible for higher thermal conductivities. On the contrary, the peak attributed to π–π stacked planes along the in-plane integration, that is, the (010) reflection shown in Figure 2b, shifts toward lower scattering vectors, Q. This suggests that increasing the annealing temperatures gradually leads to an expansion of the lattice in the (010) direction by ∼0.01 nm. No appreciable effect on the thermal conductivity is expected for this rather small lattice distortion.

After the doping process was conducted on the sample annealed at 180 °C, more significant changes in both crystalline planes were observed. In the out-of-plane direction, all peaks shift toward shorter scattering vectors, indicating an expansion of the lamella by ∼0.24 nm and simultaneously introducing some disorder relative to the pristine film, as seen in Figure S7. In the in-plane direction, the (010) scattering peak exhibits the opposite behavior; that is, it contracts by ∼0.01 nm and induces a relative broadening of the (003) scattering peak compared with that annealed at 180 °C. This behavior suggests that the dopant induces a certain uniaxial strain on the PBTTT microcrystals, which is compensated by the distortion of the lattice, as given by its Poisson ratio. Strikingly, after the dedoping process, all diffraction peaks from both crystalline planes shift to, essentially, their original position. This is consistent with the increase in the thermal conductivity observed for MRD < 0.01, demonstrating that in the doped samples, thermal transport is dominated by the physical presence of the dopant.

To evaluate this point further, we investigated the thermal properties of a different polymer, PTB7-Th, mixed with F4TCNQ. Reassuringly, we observed a similar evolution of thermal conductivity with the doping level (cf. Figure S8 and Figure 1e) as for the PBTTT case. These experiments suggest that the alloying effect constitutes a general behavior for polymers and molecular dopants (not just a particular effect associated with dopants inhibiting a particular phase in PBTTT). Moreover, this experiment also indicates that the effect is associated with the physical presence of the dopant; the reduction of thermal conductivity cannot be ascribed to electronic interactions such as the formation of the charge-transfer complex because PTB7-Th is not effectively doped by F4TCNQ due to the unfavorable energy level alignment.

Finally, we study the relationship between thermal and electrical conductivity to test the applicability of the Wiedemann–Franz law. We have already shown in Figure 1e that the thermal conductivity of PBTTT films is independent, to a large extent, of the MRD for values >0.01. The local electrical conductivity is estimated using an indirect analysis based on spectroscopic Raman mapping, previously shown to be effective for spatially mapping conductivity in PBTTT doped with the Lewis acid tris(pentafluorophenyl)borane.42,43 The method relies on there being continuous variation of the intensity ratio rR of the ∼1393 and ∼1493 cm–1 Raman peaks of PBTTT with electrical conductivity (that is, the MRD). Hence, by obtaining the “calibration” data of rR as a function of electrical conductivity for reference samples (see the Methods in the Supporting Information), the local electrical conductivity was estimated across the entire sample along the doping gradient.

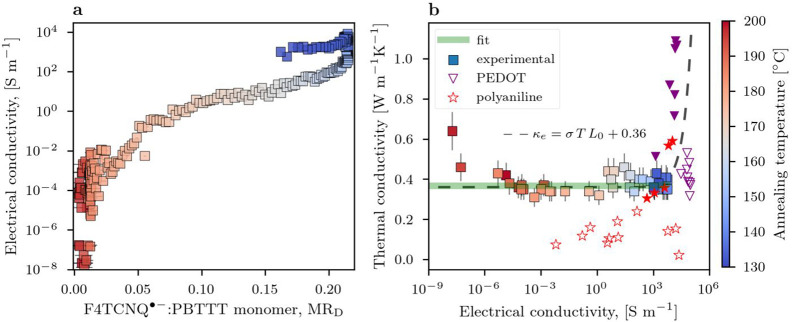
Electrical conductivity as a function of the F4TCNQ molar fraction is shown in Figure 3a. We note that a rather small (MRD < 0.03) doping level already increases the electrical conductivity by several orders of magnitude, finally saturating at σ ≈ 103 S m–1 and reaching values as high as 6800 S m–1. These values are in reasonable agreement with those reported for similar materials and processing.18,40Figure 3b shows the thermal conductivity as a function of the electrical conductivity for PBTTT films. We have also included the observations of refs (17, 44, and 13) in two conducting polymers for comparison, that is, PEDOT and PANI. Our data were modeled using the expression κexp = κlatt + σL0T, where the second term accounts for the electronic contribution according to the Wiedemann–Franz law (κe = σLT), and using the Sommerfeld value (L0) as an approximation for the Lorenz number. The fit suggests a lattice contribution of 0.36 W m–1 K–1, which is much smaller than that of the undoped polymer. This, again, provides evidence that the presence of the dopants reduces the thermal conductivity. Indeed, the deviations observed for the lower electrical conductivity values arise from the higher thermal conductivity exhibited by the neat PBTTT samples, as shown by the previously described analysis (Figure 1). Judging by the compiled data for different systems, the electronic contribution to the overall thermal conductivity becomes apparent only at very high electrical conductivities.

Figure 3.

Figure 3

Open in a new tab

(a) Estimated electrical conductivity as a function of the doping level. (b) Thermal conductivity as a function of electrical conductivity. The green line is a fit of the experimental data using κexp = κlatt + σL0T. The black curve is a model of κexp = κlatt + σL0T using κlatt from the fit (0.36 W m–1 K–1) and L0 = 2.44 × 10–9 V2 K–2. Also shown for comparison are literature data for polyaniline doped with hydrochloric acid (solid stars)17 and with a set of distinct acids (open stars).44 Also shown for comparison is PEDOT doped with tosylate or PSS supported on a substrate (open triangles) and suspended on a microdevice (solid triangles).13

In conclusion, we have shown that the thermal conductivity of PBTTT thin films can be tailored between 0.3 and 0.7 W m–1 K–1 by increasing the annealing temperature, which originates from the formation of percolating crystals within the films. Furthermore, the addition of small doping levels (MRD < 0.01) is sufficient to reduce the thermal conductivity to a minimum of 0.38 W m–1 K–1. This effect resembles the observation in alloy systems, where thermal transport is dominated by disorder. Studying the relation between the thermal and electrical conductivity, we also show that the electronic contribution to the overall thermal conductivity is negligible up to electrical conductivities greater than σ ≈ 6.8 × 103 S m–1.

Acknowledgments

We acknowledge financial support from the Spanish Ministry of Science and Innovation through projects PGC2018-095411-B-I00 and MAT2017-90024-P (TANGENTS)-EI/FEDER, UE projects; the Generalitat de Catalunya through grants 2017SGR488 and AGAUR 2018 PROD 00191; and from the European Research Council (ERC) under grant agreement no. 648901. O.Z.-A. acknowledges CONACYT-SENER for his Ph.D. scholarship (no. 472571). J.M. thanks MCIU for the Ramón y Cajal contract and grant PGC2018-094620-A-I00. We thank Dr. Agustín Mihi for the access to and support with the FTIR equipment. We acknowledge the technical and human support provided by SGIker of UPV/EHU and European funding (ERDF and ESF). We thank Andrés Gómez Rodríguez from the Scanning Probe Microscopy Laboratory (ICMAB-CSIC) for a set of AFM measurements. We acknowledge support of the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsenergylett.0c01410.

  • Materials and sample fabrication methods, calculation of the dopant content, calculation of the free exciton bandwidth, determination of electrical conductivity from Raman measurements, frequency domain thermoreflectance description, GIWAXS 2D patterns, and atomic force microscopy data (PDF)

The authors declare no competing financial interest.

Supplementary Material

nz0c01410_si_001.pdf (1.4MB, pdf)

References

  1. Harada K.; Sumino M.; Adachi C.; Tanaka S.; Miyazaki K. Improved Thermoelectric Performance of Organic Thin-Film Elements Utilizing a Bilayer Structure of Pentacene and 2,3,5,6-Tetrafluoro-7,7,8,8- Tetracyanoquinodimethane (F4 -TCNQ). Appl. Phys. Lett. 2010, 96 (25), 253304. 10.1063/1.3456394. [DOI] [Google Scholar]
  2. Yim K. H.; Whiting G. L.; Murphy C. E.; Halls J. J. M.; Burroughes J. H.; Friend R. H.; Kim J. S. Controlling Electrical Properties of Conjugated Polymers via a Solution-Based p-Type Doping. Adv. Mater. 2008, 20 (17), 3319–3324. 10.1002/adma.200800735. [DOI] [Google Scholar]
  3. Patel S. N.; Glaudell A. M.; Kiefer D.; Chabinyc M. L. Increasing the Thermoelectric Power Factor of a Semiconducting Polymer by Doping from the Vapor Phase. ACS Macro Lett. 2016, 5 (3), 268–272. 10.1021/acsmacrolett.5b00887. [DOI] [PubMed] [Google Scholar]
  4. Salzmann I.; Heimel G.; Oehzelt M.; Winkler S.; Koch N. Molecular Electrical Doping of Organic Semiconductors: Fundamental Mechanisms and Emerging Dopant Design Rules. Acc. Chem. Res. 2016, 49 (3), 370–378. 10.1021/acs.accounts.5b00438. [DOI] [PubMed] [Google Scholar]
  5. Hyder M. N.; Kavian R.; Sultana Z.; Saetia K.; Chen P.-Y.; Lee S. W.; Shao-Horn Y.; Hammond P. T. Vacuum-Assisted Layer-by-Layer Nanocomposites for Self-Standing 3D Mesoporous Electrodes. Chem. Mater. 2014, 26 (18), 5310–5318. 10.1021/cm502328h. [DOI] [Google Scholar]
  6. Russ B.; Glaudell A.; Urban J. J.; Chabinyc M. L.; Segalman R. A. Organic Thermoelectric Materials for Energy Harvesting and Temperature Control. Nat. Rev. Mater. 2016, 1 (10), 16050. 10.1038/natrevmats.2016.50. [DOI] [Google Scholar]
  7. Wang H.; Yu C. Organic Thermoelectrics: Materials Preparation, Performance Optimization, and Device Integration. Joule 2019, 3 (1), 53–80. 10.1016/j.joule.2018.10.012. [DOI] [Google Scholar]
  8. Campoy-Quiles M. Will Organic Thermoelectrics Get Hot? Philos. Trans. R. Soc. A Math. Philos. Trans. R. Soc., A 2019, 377 (2152), 20180352. 10.1098/rsta.2018.0352. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Russ B.; Glaudell A.; Urban J. J.; Chabinyc M. L.; Segalman R. A. Organic Thermoelectric Materials for Energy Harvesting and Temperature Control. Nat. Rev. Mater. 2016, 1 (10), 16050. 10.1038/natrevmats.2016.50. [DOI] [Google Scholar]
  10. Boudouris B. W.; Yee S. Structure, Properties and Applications of Thermoelectric Polymers. J. Appl. Polym. Sci. 2017, 134 (3), 44456. 10.1002/app.44456. [DOI] [Google Scholar]
  11. Scheunemann D.; Kemerink M. Non-Wiedemann-Franz Behavior of the Thermal Conductivity of Organic Semiconductors. Phys. Rev. B: Condens. Matter Mater. Phys. 2020, 101 (7), 075206. 10.1103/PhysRevB.101.075206. [DOI] [Google Scholar]
  12. Kim G. H.; Shao L.; Zhang K.; Pipe K. P. Engineered Doping of Organic Semiconductors for Enhanced Thermoelectric Efficiency. Nat. Mater. 2013, 12 (8), 719–723. 10.1038/nmat3635. [DOI] [PubMed] [Google Scholar]
  13. Weathers A.; Khan Z. U.; Brooke R.; Evans D.; Pettes M. T.; Andreasen J. W.; Crispin X.; Shi L. Significant Electronic Thermal Transport in the Conducting Polymer Poly(3,4-Ethylenedioxythiophene). Adv. Mater. 2015, 27 (12), 2101–2106. 10.1002/adma.201404738. [DOI] [PubMed] [Google Scholar]
  14. Liu J.; Wang X.; Li D.; Coates N. E.; Segalman R. A.; Cahill D. G. Thermal Conductivity and Elastic Constants of PEDOT:PSS with High Electrical Conductivity. Macromolecules 2015, 48 (3), 585–591. 10.1021/ma502099t. [DOI] [Google Scholar]
  15. Upadhyaya M.; Boyle C. J.; Venkataraman D.; Aksamija Z. Effects of Disorder on Thermoelectric Properties of Semiconducting Polymers. Sci. Rep. 2019, 9 (1), 5820. 10.1038/s41598-019-42265-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Scheunemann D.; Kemerink M. Non-Wiedemann-Franz Behavior of the Thermal Conductivity of Organic Semiconductors. Phys. Rev. B: Condens. Matter Mater. Phys. 2020, 101 (7), 075206. 10.1103/PhysRevB.101.075206. [DOI] [Google Scholar]
  17. Yoon H.; Jung B. S.; Lee H. Correlation between Electrical Conductivity, Thermal Conductivity, and ESR Intensity of Polyaniline. Synth. Met. 1991, 41 (1–2), 699–702. 10.1016/0379-6779(91)91162-4. [DOI] [Google Scholar]
  18. Kang K.; Watanabe S.; Broch K.; Sepe A.; Brown A.; Nasrallah I.; Nikolka M.; Fei Z.; Heeney M.; Matsumoto D.; Marumoto K.; Tanaka H.; Kuroda S.; Sirringhaus H. 2D Coherent Charge Transport in Highly Ordered Conducting Polymers Doped by Solid State Diffusion. Nat. Mater. 2016, 15 (8), 896–902. 10.1038/nmat4634. [DOI] [PubMed] [Google Scholar]
  19. Hase H.; O’Neill K.; Frisch J.; Opitz A.; Koch N.; Salzmann I. Unraveling the Microstructure of Molecularly Doped Poly(3-Hexylthiophene) by Thermally Induced Dedoping. J. Phys. Chem. C 2018, 122 (45), 25893–25899. 10.1021/acs.jpcc.8b08591. [DOI] [Google Scholar]
  20. Root S. E.; Alkhadra M. A.; Rodriquez D.; Printz A. D.; Lipomi D. J. Measuring the Glass Transition Temperature of Conjugated Polymer Films with Ultraviolet-Visible Spectroscopy. Chem. Mater. 2017, 29 (7), 2646–2654. 10.1021/acs.chemmater.7b00242. [DOI] [Google Scholar]
  21. Zapata-Arteaga O.; Dörling B.; Perevedentsev A.; Martín J.; Reparaz J. S.; Campoy-Quiles M. Closing the Stability-Performance Gap in Organic Thermoelectrics by Adjusting the Partial to Integer Charge Transfer Ratio. Macromolecules 2020, 53 (2), 609–620. 10.1021/acs.macromol.9b02263. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Clark J.; Chang J. F.; Spano F. C.; Friend R. H.; Silva C. Determining Exciton Bandwidth and Film Microstructure in Polythiophene Films Using Linear Absorption Spectroscopy. Appl. Phys. Lett. 2009, 94 (16), 163306. 10.1063/1.3110904. [DOI] [Google Scholar]
  23. Lim E.; Glaudell A. M.; Miller R.; Chabinyc M. L. The Role of Ordering on the Thermoelectric Properties of Blends of Regioregular and Regiorandom Poly(3-hexylthiophene). Adv. Electron. Mater. 2019, 5 (11), 1800915. 10.1002/aelm.201800915. [DOI] [Google Scholar]
  24. Crossland E. J. W.; Rahimi K.; Reiter G.; Steiner U.; Ludwigs S. Systematic Control of Nucleation Density in Poly(3-Hexylthiophene) Thin Films. Adv. Funct. Mater. 2011, 21 (3), 518–524. 10.1002/adfm.201001682. [DOI] [Google Scholar]
  25. McCulloch I.; Heeney M.; Bailey C.; Genevicius K.; MacDonald I.; Shkunov M.; Sparrowe D.; Tierney S.; Wagner R.; Zhang W.; Chabinyc M. L.; Kline R. J.; McGehee M. D.; Toney M. F. Liquid-Crystalline Semiconducting Polymers with High Charge-Carrier Mobility. Nat. Mater. 2006, 5 (4), 328–333. 10.1038/nmat1612. [DOI] [PubMed] [Google Scholar]
  26. DeLongchamp D. M.; Kline R. J.; Jung Y.; Germack D. S.; Lin E. K.; Moad A. J.; Richter L. J.; Toney M. F.; Heeney M.; McCulloch I. Controlling the Orientation of Terraced Nanoscale “Ribbons” of a Poly(Thiophene) Semiconductor. ACS Nano 2009, 3 (4), 780–787. 10.1021/nn800574f. [DOI] [PubMed] [Google Scholar]
  27. Cochran J. E.; Junk M. J. N.; Glaudell A. M.; Miller P. L.; Cowart J. S.; Toney M. F.; Hawker C. J.; Chmelka B. F.; Chabinyc M. L. Molecular Interactions and Ordering in Electrically Doped Polymers: Blends of PBTTT and F 4 TCNQ. Macromolecules 2014, 47 (19), 6836–6846. 10.1021/ma501547h. [DOI] [Google Scholar]
  28. Wang C.; Duong D. T.; Vandewal K.; Rivnay J.; Salleo A. Optical Measurement of Doping Efficiency in Poly(3-Hexylthiophene) Solutions and Thin Films. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91 (8), 085205. 10.1103/PhysRevB.91.085205. [DOI] [Google Scholar]
  29. Hamidi-Sakr A.; Biniek L.; Bantignies J.-L.; Maurin D.; Herrmann L.; Leclerc N.; Lévêque P.; Vijayakumar V.; Zimmermann N.; Brinkmann M. A Versatile Method to Fabricate Highly In-Plane Aligned Conducting Polymer Films with Anisotropic Charge Transport and Thermoelectric Properties: The Key Role of Alkyl Side Chain Layers on the Doping Mechanism. Adv. Funct. Mater. 2017, 27 (25), 1700173. 10.1002/adfm.201700173. [DOI] [Google Scholar]
  30. DeLongchamp D. M.; Kline R. J.; Jung Y.; Lin E. K.; Fischer D. A.; Gundlach D. J.; Cotts S. K.; Moad A. J.; Richter L. J.; Toney M. F.; Heeney M.; McCulloch I. Molecular Basis of Mesophase Ordering in a Thiophene-Based Copolymer. Macromolecules 2008, 41 (15), 5709–5715. 10.1021/ma800440f. [DOI] [Google Scholar]
  31. Bergman D. J.; Levy O. Thermoelectric Properties of a Composite Medium. J. Appl. Phys. 1991, 70 (11), 6821–6833. 10.1063/1.349830. [DOI] [Google Scholar]
  32. Straley J. P. Thermoelectric Properties of Inhomogeneous Materials. J. Phys. D: Appl. Phys. 1981, 14 (11), 2101–2105. 10.1088/0022-3727/14/11/017. [DOI] [Google Scholar]
  33. Lee Y.; Pak A. J.; Hwang G. S. What Is the Thermal Conductivity Limit of Silicon Germanium Alloys?. Phys. Chem. Chem. Phys. 2016, 18 (29), 19544–19548. 10.1039/C6CP04388G. [DOI] [PubMed] [Google Scholar]
  34. Tong T.; Fu D.; Levander A. X.; Schaff W. J.; Pantha B. N.; Lu N.; Liu B.; Ferguson I.; Zhang R.; Lin J. Y.; Jiang H. X.; Wu J.; Cahill D. G. Suppression of Thermal Conductivity in InxGa1-XN Alloys by Nanometer-Scale Disorder. Appl. Phys. Lett. 2013, 102 (12), 121906. 10.1063/1.4798838. [DOI] [Google Scholar]
  35. Xie H.; Wang H.; Fu C.; Liu Y.; Snyder G. J.; Zhao X.; Zhu T. The Intrinsic Disorder Related Alloy Scattering in ZrNiSn Half-Heusler Thermoelectric Materials. Sci. Rep. 2015, 4 (1), 6888. 10.1038/srep06888. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Li J.; Chen Z.; Zhang X.; Yu H.; Wu Z.; Xie H.; Chen Y.; Pei Y. Simultaneous Optimization of Carrier Concentration and Alloy Scattering for Ultrahigh Performance GeTe Thermoelectrics. Adv. Sci. 2017, 4 (12), 1700341. 10.1002/advs.201700341. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Lee Y. H.; Oh J.; Lee S.-S.; Kim H.; Son J. G. Highly Ordered Nanoconfinement Effect from Evaporation-Induced Self-Assembly of Block Copolymers on In Situ Polymerized PEDOT:Tos. ACS Macro Lett. 2017, 6 (4), 386–392. 10.1021/acsmacrolett.7b00137. [DOI] [PubMed] [Google Scholar]
  38. Chabinyc M. L.; Toney M. F.; Kline R. J.; McCulloch I.; Heeney M. X-Ray Scattering Study of Thin Films of Poly(2,5-Bis(3-Alkylthiophen-2-Yl) Thieno[3,2-b]Thiophene). J. Am. Chem. Soc. 2007, 129 (11), 3226–3237. 10.1021/ja0670714. [DOI] [PubMed] [Google Scholar]
  39. DeLongchamp D. M.; Kline R. J.; Lin E. K.; Fischer D. A.; Richter L. J.; Lucas L. A.; Heeney M.; McCulloch I.; Northrup J. E. High Carrier Mobility Polythiophene Thin Films: Structure Determination by Experiment and Theory. Adv. Mater. 2007, 19 (6), 833–837. 10.1002/adma.200602651. [DOI] [Google Scholar]
  40. Patel S. N.; Glaudell A. M.; Peterson K. A.; Thomas E. M.; O’Hara K. A.; Lim E.; Chabinyc M. L. Morphology Controls the Thermoelectric Power Factor of a Doped Semiconducting Polymer. Sci. Adv. 2017, 3 (6), e1700434 10.1126/sciadv.1700434. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Rivnay J.; Noriega R.; Kline R. J.; Salleo A.; Toney M. F. Quantitative Analysis of Lattice Disorder and Crystallite Size in Organic Semiconductor Thin Films. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 84 (4), 045203. 10.1103/PhysRevB.84.045203. [DOI] [Google Scholar]
  42. Kang K.; Schott S.; Venkateshvaran D.; Broch K.; Schweicher G.; Harkin D.; Jellett C.; Nielsen C. B.; McCulloch I.; Sirringhaus H. Investigation of the Thermoelectric Response in Conducting Polymers Doped by Solid-State Diffusion. Mater. Today Phys. 2019, 8, 112–122. 10.1016/j.mtphys.2019.02.004. [DOI] [Google Scholar]
  43. Perevedentsev A.; Campoy-Quiles M. Rapid and High-Resolution Patterning of Microstructure and Composition in Organic Semiconductors Using ‘Molecular Gates’. Nat. Commun. 2020, 11 (1), 3610. 10.1038/s41467-020-17361-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Yan H.; Sada N.; Toshima N. Thermal Transporting Properties of Electrically Conductive Polyaniline Films as Organic Thermoelectric Materials. J. Therm. Anal. Calorim. 2002, 69 (3), 881–887. 10.1023/A:1020612123826. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nz0c01410_si_001.pdf (1.4MB, pdf)

Articles from ACS Energy Letters are provided here courtesy of American Chemical Society

RESOURCES