Identification of Proton Populations in Cherts as Natural Analogues of Pure Silica Materials by Means of Low Field NMR

Abstract

Recent theories about the sources of silica in bedded and nodular cherts do not fit the origin of cherts from the Kraków–Częstochowa Upland. Since siliceous sponges as a single source of silica is questionable, assumptions about additional sources have to be verified. In order to do so, three samples of nodular cherts and one representative sample of bedded chert were studied by means of ¹H LF-NMR 1D and 2D relaxometry and complementary geochemical methods. The results were compared with the literature and standard silica materials which helped to identify five types of ¹H signal. The very distinct 1D-T₂ spectra of the dried samples indicated the existence of closed pores which, after comprehensive analysis, were identified as inclusions filled with different types of siliceous materials. Saturation revealed the differences between nodular and bedded cherts that were visible mainly in the amount and size of open porosity. The principal component analysis of NMR parameters showed the excellent separation of these two groups of samples and this is well visible on the biplots. Additionally, the estimated pore size distribution revealed that the total porosity of around 2% consisted primarily of mesopores (2–50 nm in diameter) and macropores (diameter >50 nm). In bedded cherts, open porosity is dominated by macropores, while the share of mesopores and macropores is similar in nodular cherts.

1. Introduction

Cherts are a type of sedimentary, nonporous, highly siliceous rocks composed of quartz. Silicon in cherts may occur in various forms, such as silica or silanols (in the magnetic resonance nomenclature Q₄ or Q₃, Q₂, Q₁, Q₀, where an index corresponds to the number of oxygen atoms).¹ Two forms of cherts exist, nodular (concretions) or bedded, and their origin is sometimes problematic to discern. However, the differentiation of cherts is important from the geological, archeological²⁻⁵ and petrological⁶ point of view. The origin of both the chert nodules and the bedded cherts in the Fanerozoic sediments has attracted the attention of many authors. Generally, these rocks are interpreted as the products of synsedimentary, or early- to late-diagenetic, or epigenetic processes (see, e.g., refs (7−32)). One of the regions of the occurrence of cherts is the Kraków-Częstochowa Upland (KCU). The KCU is located in southern Poland and is a part of the Silesian-Kraków Homocline—the regional tectonic unit built up of the Triassic, Jurassic and Cretaceous sediments deposited unconformably onto the Precambrian and Paleozoic formations, and transected by the major the Kraków-Lubliniec Fault Zone.³³ Various assumptions as to the origin of silica in bedded and nodular cherts have been made. The assumption that siliceous skeletons of sponges were the main source of silica for chert nodules forming horizons in biostrome-like Oxfordian bedded limestones has already been presented in the literature.³⁴⁻³⁷ However, the origin of silica in bedded cherts hosted in calciturbidites from the Oxfordian/Kimmeridgian turn has only been discussed in a single publication by Matyszkiewicz,³⁸ who suggested the accumulations of radiolarians abruptly buried in sediments by density flows as the source of silica, in accordance with the model after Bustillo and Ruiz-Ortiz.³⁰ Recently, the concept of siliceous sponges skeletons as practically the sole source of silica for chert nodules hosted in the Upper Jurassic microbial-sponge megafacies of the KCU (as a part of the Tethyan northern margin) has been questioned due to three facts: (i) the lack of a clear correlation between the abundance of siliceous sponges in bedded limestones³⁹⁻⁴¹ and the accumulations of chert nodules, which only occasionally form horizons in the Middle Oxfordian bedded, biostrome-like limestones,^35,42 (ii) the occurrence of chert nodules within the calciturbidites from the Oxfordian/Kimmeridgian turn, whereas the share of siliceous sponges in in situ sediments of that age is lower than in the Middle Oxfordian sediments and while radiolarians are present in marly sediments overlying the calciturbidites,^38,42 and (iii) the just documented, multistage silicification of the Upper Jurassic neptunian dykes cutting through these sediments.⁴³ These facts imply the contribution of additional sources of silica related to the appearance of radiolarians, as well as the periodic transfer of hydrothermal solutions along deep fracture zones generated by an extensional tectonic regime. The occurrence of chert nodules and bedded cherts in calciturbidites from the Oxfordian/Kimmeridgian turn cannot be related exclusively to the presence of Hexactinellida sponges since these organisms formed rather limited accumulations in that part of the stratigraphic column. However, these sediments contained radiolarians which may have provided a potential source of silica for bedded cherts.^24,30,38,44

Apart from the full mineralogical and petrographic characterization supported by specialized analytical methods, the genetic concepts of cherts should be confronted with a comprehensive sedimentological, paleontological and tectonic characterization. In the literature, we may encounter numerous reports about research on their identification and characterization by means of instrumental methods ranging from infrared spectroscopy (IR),^45,46 X-ray diffraction (XRD),⁴⁷ emission and atomic absorption spectroscopy,⁴⁸ and energy-dispersive X-ray fluorescence (EDXRF)⁴⁹ to neutron activation analysis (NAA).⁵⁰ The development of nuclear magnetic resonance (NMR) techniques over the last 50 years has meant that NMR has been applied as an alternative method for geological purposes. Due to the high abundance of silicon and their crystal structure, solid state NMR (magic angle spinning NMR, MAS NMR) has been widely used for the study of cherts.⁵¹ In contrast to other sedimentary rocks, such as sandstones or shales, cherts have been poorly analyzed by proton nuclear magnetic resonance (¹H NMR). We propose ¹H low field NMR as a nondestructive tool for distinguishing cherts of different types or with varying provenances. Low field NMR is commonly used for the investigation of sandstones, shales, and carbonates, and it can also be applicable for studies on cherts as it has a number of advantages. Primarily, it is noninvasive and nondestructive to rock core samples, and thus, the analysis is repeatable. Second, we obtain a signal from the water (protons) present in several forms, including microporosity free water, adsorbed water or even protons in the crystal lattice. These types of “water” have very short relaxation times due to their strong interactions with adsorbent surface or bonding. Also, every magnetic susceptibility difference causes the induction of internal gradients that arise in higher magnetic fields and distort the interpretation of obtained data. A low field helps to overcome these problems, because we can attain low values of echo time and operate at a low magnetic field strength. This enables us to register short relaxation times and, when the difference between susceptibilities of water and rock matrix is small and pores are nanometric, ignore the diffusion impact from internal gradients (which we will show in the work), respectively.

Silicon is present in various forms in geology, but also, due to its wide range of properties, in technology. Many silica structures, such as mesopores, nanotubes, silicagels, silicate glass, and cherts, have been investigated by NMR. Results show that different proton populations are possible to identify in these materials. ¹H low field NMR relaxometry revealed that in MCM-41 and SBA-15 mesopores, three water populations can be seen and they are associated with inner bulk water, surface water and OH groups.⁵²T₁ and T₂ relaxation times measurements in low field enabled adsorbed water to be distinguished on the surface of silica nanotubes which helped to estimate the number of functional groups with which a nanotube can bond.⁵³ Relaxation times and diffusion coefficients also enabled three types of water to be detected in silica gels that were related to free water and the first and second layer of water.⁵⁴ Protons from OH groups and molecular H₂O demarcation by ¹H wide-line and MAS NMR experiments helped to determine water content in hydrous silicate glass that alters in the presence of specific cations and changes the physical properties of the glass.⁵⁵ It is also possible to investigate the chemical properties of silica. T₁ and T₂ distributions from ¹H MAS NMR of nonporous silica yielded information about molecular dynamics and interactions of fluid particles with the adsorbent’s surface (different relaxation times for subsequent layers of water, cross-polarization).⁵⁶ These colloidal silica particles can be used as a model of water- or 1-heptanol-bearing rocks. NMR spectroscopy (²⁹Si MAS NMR) also helped to trace the depolymerization process of amorphous silica due to ASR (alkali silica reaction) reaction on the grounds of dominant peak location (the Q₄ peak disappeared and a Q₃, Q₂ or Q₁ peak appeared).⁵⁷ The same experiment allowed the identification of protons associated with silanol (Q₃) on the surface of structural defects in flints and the estimation of water and OH protons content that can change the physical and chemical properties of rocks.⁵¹

In this work, ¹H-LF-NMR is applied for the first time to chert studies. This technique allowed us to characterize the differences in porosity (including size and distribution of pore spaces) of chert nodules and bedded cherts.

2. Materials and Methods

2.1. Characterization of Samples

Four chert core samples from different places from the KCU are the subject of the study, and in the paper, we distinguish between them by using the form AKi, where i = 1, 2, 3, 4 is the number of a sample. The samples vary in color. Samples of nodular and bedded cherts were studied in thin sections and examined using a scanning electron microscope (SEM). In the description of samples, a classification after Folk and Pittman⁵⁸ has been used. It was assumed that the limit of the diameter for distinguishing between quartz and microquartz is 20 μm. Within the microquartz there are equant and fibrous quartz types. Microflamboyant quartz (flamboyant lutecite after Folk and Pittman⁵⁸ or quartz with flamboyant spectral extinction after Chowns and Elkins⁵⁹) has a fabric which is between the equant and fibrous quartz types.

The AK1 sample is the typical bedded chert, forming regular, flat, or lens-shaped horizons up to 1.2 m in length and 0.5 m thick with distinguished zonation. It occurs in calciturbidites,³⁸ characterized by the excellent sorting of carbonate grains within the Bouma sequence. The groundmass of the cherts is mainly composed of microcrystalline quartz. In the SEM view, it is a dense, nonporous mass. Rare relicts of bioclasts are filled with megaquartz. Chalcedonic and opal aggregates are absent.

The AK2–4 samples are nodular cherts forming irregular, flat or regular lens shaped nodules up to 20 cm in diameter. The groundmasses of the cherts are mainly composed of opal-CT, but microcrystalline quartz and chalcedony also occur. Inside the cherts, microflamboyant quartz aggregates cutting the fossils were also found. The textures of the host rock are recognizable, especially in the outermost parts of cherts, and are composed of wackestone or packstone. Carbonate fossils are replaced by megaquartz, and quartzine and chalcedony occur as a cement.

2.2. Chemical Composition of Samples

The geochemical analyses were carried out at the Activation Laboratories Ltd. (Actlabs) in Ancaster in Canada. The major element in the composition was analyzed using fusion-inductively coupled plasma (FUS-ICP). Samples are prepared and analyzed in a batch system. Each batch contains a method reagent blank, certified reference material and 17% replicates. Samples are mixed with a flux of lithium metaborate and lithium tetraborate and fused in an induction furnace. The molten melt is immediately poured into a solution of 5% nitric acid containing an internal standard and mixed continuously until completely dissolved (about 30 min). The samples are run for major oxides on a combination simultaneous/sequential Thermo Jarrell-Ash ENVIRO II ICP. Results are shown in Table 1.

Table 1. Chemical Composition (Major Elements) of the Samples Obtained from FUS-ICP Analysis.

major elements	SiO2 (%)	Al2O3 (%)	Fe2O3(T) (%)	MnO (%)	MgO (%)	CaO (%)	Na2O (%)	K2O (%)	TiO2 (%)	P2O5 (%)	LOI (%)	total (%)
AK1	98.44	0.13	0.92	0.01	0.01	0.08	0.04	0.03	0.00	<0.01	0.39	100.1
AK2	98.26	0.10	1.26	0.01	0.02	0.14	0.05	0.04	0.01	0.01	0.92	100.8
AK3	98.20	0.13	1.37	0.01	0.01	0.09	0.05	0.04	0.02	<0.01	0.67	100.6
AK4	97.93	0.14	1.45	0.014	0.02	0.08	0.06	0.05	0.01	<0.01	1.04	100.8

2.3. NMR Experiments

NMR experiments were carried out using a Magritek Rock Core Analyzer (Aachen, Germany) spectrometer with a 0.05 T (2 MHz) magnetic field. Inversion Recovery (IR) and Carr–Purcell–Meiboom–Gill (CPMG) sequences were applied to obtain 1D-T₁, 1D-T₂ and T₁–T₂ maps. The schemes of the applied sequences are shown in Figure 1. 1D distributions were calculated using Inverse Laplace Transform (ILT), Hanson and Lawson method, while T₁–T₂ correlation maps used the FISTA algorithm. Table 2 shows the protocol used in each experiment.

Figure 1.

Schemes of sequences used in the experiments: (A) 1D-T₁, inversion recovery free induction decay (IR-FID); (B) 1D-T₂, CPMG with N echoes; (C) 2D T₁–T₂ correlation experiment that delivered T₁–T₂ maps.

Table 2. Protocols Applied in the Experiments^a.

Experiment name	IE-delay (ms)	TE = 2τ (μs)	NoS	NoE	min delay (ms)	max delay (ms)	min τ (ms)	max τ (ms)
1D-T1	5000	–	24	–	0.05	5000	–	–
1D-T2	1500	60	512	10000	–	–	–	–
T1–T2	1500	60	128	10000	–	–	0.1	5000

^aIE-delay is an inter-experiment delay, i.e., time between subsequent scans, NoS is the number of scans, NoE is the number of echoes, min./max. delay is the minimum/maximum time between 180 and 90 pulses in IR sequence, min./max. τ is minimum/maximum time between 90 and 180 pulses in CPMG sequence.

All of the experiments were performed for three saturation states of rock core samples: native (N), dry (D), and saturated (S). Native samples were measured and then dried for 12 h in 200 °C in vacuum conditions. Dry samples were measured and then saturated with water in vacuum conditions. The saturated samples were wrapped tightly in plastic foil in order to prevent the evaporation of water prior to measuring. 1D-T₁ and 1D-T₂ distributions of signal coming from hydrogen species in the samples in three saturation states (N, D, S) delivered relaxation times (peaks locations) and relative contributions (peaks integrals) of each hydrogen population. Additionally, we subtracted raw data from the measurements of saturated and dry samples and obtained differential data (SD). Peaks in the 1D-T₂ distributions were numbered Ni, Di, Si, and SDi, while in the 1D-T₁ ni, di, si, sdi, where i = 1, 2, 3, 4, and 5 is the number of a peak beginning from the left side on a time axis and corresponds to a given time range, Ri. It should be noted that for 1D-T₁ distribution, lowercase was applied to highlight the fact that D1 and d1 do not necessarily come from the same hydrogen population. The integrals of peaks were called I₁ and I₂ for peaks concerning 1D-T₁, 1D-T₂ distributions, respectively. In addition, we determined the total porosity, ϕ, and logarythmic means of T₁ and T₂ distributions called T₁lm and T₂lm, respectively. Peaks in the T₁–T₂ maps were matched to those from 1D-T₂ distributions and marked with the same number.

2.4. Principal Component Analysis (PCA)

The 1D data was analyzed qualitatively by using PCA in PQStat software. PCA is a procedure that enables the transformation of a set of correlated variables to another set of new variables, called Principal Components (PCs), that are no longer linearly correlated. This transformation usually leads to the reduction of variables and simplifies the process of finding samples that have similar features.

The original variables in the PCA were relaxational parameters, i.e. T₁, T₂, I₁, I₂ of peaks Ni, Di, Si, SDi, ni, di, si, and sdi. PCA transforms this relaxational data into new variables, PCs, which the original variables have a certain contributions in. The number of PCs is always less or equal to the number of original variables, and the transformation ensures that the first PC explains the largest percentage of the total variance of the data. In our case, the number of PCs was equal to 3, however, the first two PCs, PC 1 and PC 2, explained the satisfactory percentage of the total variance and results of the analysis for these two PCs will be presented on the biplots. For a more detailed description of the PCA, the reader is referred to Supporting Information.

2.5. Pore Size Distribution (PSD)

In porous systems, the T₂ relaxation time determined experimentally is dependent on three components:⁶⁰

1

where a is a constant dependent on fluid type, η is viscosity (Pa·s), T_K is temperature (°C), ρ₂ is the surface relaxivity of the pore walls (m/s), 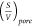is the surface-to-volume ratio of a pore (m^–1), D is diffusion coefficient (m²/s), γ is gyromagnetic ratio (MHz/T), G is magnetic field gradient (T/m) and TE is echo time (s).

PSD was estimated based on T₂ distributions of saturated samples. The calculations were conducted assuming cylindrical pore geometry, for which

2

where d is a pore diameter (m). Surface relaxivity for a given sample in the second component in (1) is assumed to be ρ_2 Sample=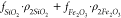, which is a sum weighted by the fractions of SiO₂ and Fe₂O₃ showed in the Table 1, where 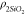=0.18 μm/s is a mean value of surface relaxivities for pure silica materials MCM-41 and SBA-15 reported by Krzyżak and Habina⁵² and 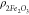is the additional contribution from Fe₂O₃ to surface relaxivity calculated from the relationship proposed in ref (61). In practice, the surface relaxivity is dominated by the impact of iron(III) oxide. We can assume that magnetic field gradient results from differences between magnetic susceptibilities, Δχ, of water and a matrix of samples,

3

where 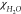is a magnetic susceptibility of water equal to −9.02 × 10^–6 and χ_Sample is a magnetic susceptibility of a sample. χ_Sample value was calculated as a sum of 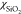and 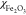weighted by their fractions in a given sample. The volume magnetic susceptibility of SiO₂ was assumed to be equal to −10.55 × 10^–6, while 500 × 10^–662 for iron(III) oxide. In pore of size d, the induced gradient is

4

where B₀ is a magnetic field induction (T) and in our case B₀ = 0.05 T. Substituting for (2) and (4) in (1), and introducing 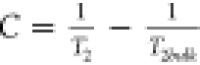and 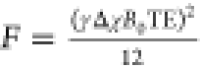, we obtain the quadratic equation for d:

5

which has two roots

6

Only positive roots will be considered. The diameter of a pore for a given time step was calculated assuming T_2 bulk = 2.2 s.

In the second approach, typically assumed to be valid for small B₀ and short echo time, TE,^60,63 the diffusional component in (1) was omitted and a pore size was calculated as

7

The amplitude of the PSD consists of a normalized amplitude in the time step from the 1D-T₂ distribution.

3. Results and Discussion

3.1. 1D Distributions

Different types of porosity were estimated from the T₂ distributions shown in Figure 2. The total recorded porosity value for dry samples ranges from 0.65% for AK2 to 1.31% for AK3 and AK4. For the native state, we observe an increase in porosity by 0.3–0.4% on average, and in most cases the maintenance or slight decrease in T₂lm: from 2.1 to 2.2 ms for AK1, and from 1.2 to 1.4 ms for AK2 and AK4. Only for AK3 there is a clear decrease of T₂lm from 1.2 to 0.7 ms. In the saturated state we observe a further increase in porosity, the largest for AK1 by 1.2% to the maximum observed value of 2.32%. A further decrease in the T₂lm value to 0.5–0.6 ms was also recorded, with the exception of AK1, where we noticed a clear increase in value to 3.2 ms (Table 3).

Figure 2.

1D-T₂ and 1D-T₁ distributions for different saturation states of samples: (A) T₂ dry state; (B) T₁ dry state; (C) T₂ native state; (D) T₁ native state; (E) T₂ saturated state; (F) T₁ saturated state; (G) T₂ differential distribution of saturated and dry states; (H) T₁ differential distribution of saturated and dry states. The numeration of peaks was taken from the left to the right side of a distribution. It should be noted that for 1D-T₁ distribution, lowercase was applied to highlight the fact that, e.g., D1 and d1 do not necessarily come from the same hydrogen population. The corresponding T₁ and T₂ times for the population should be taken from T₁–T₂ maps.

Table 3. Coordinates of Peaks from 1D-T₂ Distributions Shown in Figure 2, Parts A, C, E, and G^a.

^aPeaks were located in the five regions, for which T₂ was consecutively one order larger, and numbered from 1 to 5, from the left to the right side of the distributions. In addition to the number, the peaks have a letter that corresponds to the saturation state for which the distributions were obtained: dry, D, native, N, saturated, S and for differential data of saturated and dry samples, SD. The last two columns consist of T₂ logarithmic means (T₂lm) and total porosities (ϕ) calculated from 1D-T₂ distributions for the samples in each saturation state.

T₂ experiments revealed very similar distributions for all samples, with peak coordinates virtually coinciding (Table 3; coordinates of peaks from 1D-T₁ distributions are shown in the Table S1). Each peak number, i (ranging from 1 to 5), represents the same region regardless of saturation state. In the distributions of dry and native samples (Figure 2A,C) four different peaks (i = 2–5) can be seen. After saturation, we can additionally distinguish another peak S1 with the shortest T₂ time, in the order of 0.06–0.1 ms (Figure 2E). The least significant peak, with i = 5, that has the highest T₂ does not occur for AK3. Peaks D2–D5 are slightly shifted toward shorter T₂ times with respect to N2–N5. Sample AK1 distinguishes itself in the saturated state. Since it was not possible to separate modes to five peaks, we observe trimodal distribution. Figure 2G shows distributions of differential data of saturated and dry samples, which reveals areas where water migrates after saturation. The most significant contribution can be observed for the SD1 and SD2 having maxima between 0.06 and 0.1 ms and 0.4–1 ms, respectively. These peaks are very distinct and almost coincide for all samples, except for AK1. In addition, SD3 and SD4 appear and cover for most samples, however, they have a negligible contribution to the T₂ distribution.

Thus, based on the obtained T₂ distributions, we made a fairly obvious division into 5 hydrogen signal regions R1–R5. The regions are characterized by the maxima of peaks that are in the following ranges: 0.05–0.2 ms (R1), 0.2–2 ms (R2), 2–12 ms (R3), 18–40 ms (R4), and 90–300 ms (R5).

T₁ distributions provide complementary information (see Figure 2, parts B, D, F, and H). The connection of the peaks with those from the T₂ distributions is possible after taking into account the data from the T₁–T₂ maps.

3.2. T₁-T₂ Maps

The T₁–T₂ maps correlate T₁ and T₂ times observed in 1D experiments, enabling a better assessment of relaxation centers. The association of the T₁/T₂ ratio with the T₂ relaxation time provides important information about the strength of hydrogen bonding and its source. The recorded T₁/T₂ values, depend on the region, R (R1–R5), and the degree of water saturation, and range from ∼2 to nearly 300 (Table 4). This suggests the existence of water confined tightly in the pores, as well as very strongly bound and the existence of a signal from OH groups.

Table 4. Coordinates of the Peaks from T₁–T₂ Correlation Maps for Different Saturation States^a.

^aT₂ and T₁ are transverse and longitudinal relaxation times, respectively, and T₁/T₂ is the T₁ to T₂ ratio; if a given peak does not occur on the map, it is marked by a dark gray cell.

The T₁–T₂ correlation maps of dried samples (Figure 3) revealed four distinct peaks that are shown in Table 4. The peaks D1 and D2 are usually combined in one averaged spot (seen as D1 or D2), except for the AK4 sample, where five peaks are visible on the map. D1 did not occur on the 1D-T₂ distributions at all. It is likely that D2 on 1D-T₂ distributions represents the average of D1 and D2 from the map (see for example T₂ times of D1 and D2 for AK4 in Table 4, their average is very similar to the T₂ of D2 from the 1D experiments, Table 3). For the native state, associated with a higher degree of water saturation, we observe a pattern of N1–N5 spots similar to the dried samples, with a tendency to average or overlap in areas of N1 and N2 (Figure 4). The impact of the further increase of water saturation visible on the maps of saturated samples (Figure 5) indicates that chert rock core samples are able to absorb water, causing an increase in porosity by 0.4–1.2% (Table 3). Regions that are reflected by peak 2 on the maps are refilled with water, which we observe as the appearance of S2 or an increase in its amplitude. Hydrogen populations reflected by peaks 4 and 5 also absorb water, mainly in the case of AK1 (Figure 5A), which additional averaging of signals associated with peaks S4 and S5 occur for.

Figure 3.

T₁–T₂ correlation maps of dry samples: (A) AK1; (B) AK2; (C) AK3; (D) AK4. Peaks are numbered according to the location in the T₂ time domain, while the letter “D” corresponds to the abbreviation of the Dry state. Additionally, the projections of the maps on the two time domains (T₁ and T₂) are shown.

Figure 4.

T₁–T₂ correlation maps of native samples: (A) AK1; (B) AK2; (C) AK3; (D) AK4. Peaks are numbered according to the location in the T₂ time domain, while the letter “N” corresponds to the abbreviation of the native state. Additionally, the projections of the maps on the two time domains (T₁ and T₂) are shown.

Figure 5.

T₁–T₂ correlation maps of saturated samples: (A) AK1; (B) AK2; (C) AK3; (D) AK4. Peaks are numbered according to the location in the T₂ time domain, while the letter “S” corresponds to the abbreviation of the saturated state. Additionally, the projections of the maps on the two time domains (T₁ and T₂) have been shown.

Differential maps of saturated and dried samples (Figure 6) additionally help in the interpretation of maps for different saturation states and deliver information about open porosity. Saturation effects for AK2–AK4 samples are seen mainly in regions R1 and R2 (SD1 and SD2), and for AK1 in R4. On these maps, peaks lie close to the red-dotted line and have T₁/T₂ equal to 11–24 for SD2 and 1.3–6.7 for SD3. Only AK4 (Figure 6D) absorbs water in bigger spaces reflected by SD4, which has T₁/T₂ = 2.1 and corresponds to poorly bound water in the pores. Differential maps, especially for AK2 (Figure 6B) and AK3 (Figure 6C), show a trail for very short T₂s, which extends to the wide range of T₁. This is probably related to the formation of new OH groups (this kind of pattern on the maps for the observed T₂ times is characteristic to hydroxyls).

Figure 6.

T₁–T₂ correlation maps of differential data of saturated and dry samples: (A) AK1; (B) AK2; (C) AK3; (D) AK4. Peaks are numbered according to the location in the T₂ time domain, while the letters “SD” correspond to the abbreviation of the differential data from saturated and dry state. Additionally, the projections of the maps on the two time domains (T₁ and T₂) are shown.

After the initial characterization of samples based on 1D and 2D experiments, the following chapters will discuss the issue of porosity distribution and its types.

3.3. Estimation of Pore Size Distribution in Cherts

As demonstrated in ref (60), at low B₀ and for short value of echo time in the CPMG measurement, PSD can usually be calculated from eq 7, and in practice, it is dominated by surface relaxation. This approach has been repeatedly verified, but rather on rock cores which have much larger pore diameters^60,63 in comparison to the cherts examined in our study. That is why we decided to analyze the possible impact of diffusion on PSD for cores with a large population of pores having diameters of several nanometers. For comparison, both eqs 1 and 7 were applied.

The diffusion coefficient D was estimated based on theoretical⁶⁴⁻⁶⁶ and experimental^54,67,68 results. According to these, the D of water confined in silica nanopores varies strongly for pore size between 0.7 and 4 nm (Table 5). Below and above this range it is almost constant and equal to 0.45 × 10^–10 (the most strongly bound first water monolayer) and 2.3 × 10^–9 m²/s (bulk water), respectively. The obtained PSD’s based on the T₂ distributions of saturated and dried samples as well as their difference are shown in Figure 7. At the same time, they correspond to the total, closed and open porosity distribution, respectively. The influence of diffusion and induced gradients on PSDs is additionally shown for a few pore diameters in Table 5. In general, noticeable changes are visible in the range of 1–10 nm. The effect of gradients outside this range is negligible. As we can see in our case, PSDs are completely dominated by the influence of surface relaxivity. However, as we show in theoretical considerations for an identical PSD system, in the absence of iron(III) oxide or its negligible amount, the dependence on diffusion would be significant if one does not account for the decrease of the diffusion coefficient of water confined in nanopores (Figure S1 in Supporting Information). Although in our case (diffusion coefficient that is smaller for nanometer pores, small differences between volume magnetic susceptibilities of water and sample) the use of a linear relationship (eq 7) for PSD estimation is sufficient in practice.

Table 5. Comparison of Pore Sizes Determined Using Two Approaches—with and without Diffusional Component in Equation 1^a.

^aDiffusion coefficients D for exemplary, theoretical pore sizes, d_t, are shown.

Figure 7.

PSD calculated based on T₂ distributions of saturated (A) and dry (B) samples and differential data of saturated and dry samples (C), which corresponds to the total (A), closed (B), and open (C) porosity, respectively. Pore size was determined from eq 6 assuming that samples are composed of SiO₂ and Fe₂O₃, and that diffusion coefficient D is influenced by the size of confinement up to d = 10 nm, for which D is equal to the diffusion coefficient of a bulk water.

3.4. Porosity in Cherts

As mentioned in subsection 3.2, T₁–T₂Maps, the T₁/T₂ parameter reflects the strength of hydrogen bonding.⁶⁹ Combining 1D and 2D data, we can assume that in the R1 region is a signal from OH groups and water, while in the R2–R5 regions, the source is water in various pore systems. Although we also note high T₁/T₂ values in the R3 region, taking into account the results of other researchers,^52,70,71 we are inclined to ascribe to the thesis that the hydrogen population in R3 comes from water that is strongly bound to the surface rather than chemically bound hydrogen. In the study of water adsorbed on silica gel, two hydrogen relaxation centers were recorded. The first, strongly bound to the surface, with a T₂ of 0.06–0.2 ms and T₁/T₂ ≈ 400–500, assigned to OH in silanol^52,71 and the second, less strongly, with a T₂ of 1–6 ms and T₁/T₂ ≈ 4–100.^52,70,71 In our case, this suggests the existence of water bound on silica surface with a very high roughness. The above considerations regarding the sources of proton signals are supported by recent reports describing the processes of hydroxylation of quartz surfaces as well as the creation of preferred hydrogen bonds.^72,73

Based on the PSDs (Figure 7), we can conclude that total porosity consists primarily of mesoporosity (R1–R2) and macroporosity (R3–R5) (according to IUPAC classification). We can also extract trace amounts of microporosity (R1) and a clear signal (R1) for very short T₂ (0.05–0.1 ms) and very high T₁/T₂ (>200), as mentioned corresponding to compounds containing hydroxyl groups.

The total porosity, which varies from 1.08 to 2.32% depending on the sample, can be divided into closed and open. Closed porosity (0.65–1.31%) is composed of inclusions perfectly visible on T₂ distributions registered for rock cores in the “dry” state. During the drying process (12 h at 200 °C in a vacuum) we got rid of both physically and chemically bound water, therefore the observed signals (D2–D5) come from water in inclusions. Open porosity (0.4–1.2%), revealed in the saturation process, is located in different regions. In the case of AK1 (bedded chert) we observe the largest increase in total porosity (1.2%), associated with an increase of T₂lm (from 2.2 to 3.2 ms), in a very wide range from R1 to R4 and four maxima: SD1, SD2, SD3, and SD4, which correspond to the dominance of macropores (Figures 2G and 6A). In the case of nodular cherts (AK2–4), the signals in areas R1 and R2 (SD1, SD2) dominate, with a simultaneous decrease in the T₂lm values from 1.2 to 1.4 ms to 0.55–0.65 ms, which corresponds to the formation of open porosity by microporosity, a few nanometer mesoporosity and newly formed hydroxyl groups (Figure 2G, 6B-D). Table 6 sums up the values of different types of porosities.

Table 6. Different Types of Porosities Determined Based on the PSDs of Saturated (Microporosity, ϕ_micro, Mesoporosity, ϕ_meso, Macroporosity, ϕ_macro, Total Porosity), Dry (Closed Porosity), and Differential Data of Saturated and Dry Samples (Open Porosity).

		porosity value (%)
porosity type	pore size range	AK1	AK2	AK3	AK4
microporosity, ϕmicro	<2 nm	0.02	0.02	0.02	0.02
mesoporosity, ϕmeso	2–50 nm	0.63	0.53	0.92	0.95
macroporosity, ϕmacro	50–280 nm	0.44	0.27	0.69	0.52
	0.280–1.4 μm	0.92	0.21	0.31	0.38
	1.4–4 μm	0.32	0.05	0.05	0.10
	4–40 μm	0.009	0	0	0.007
	0–40 μm (total ϕmacro)	1.691	0.531	1.056	1.015
total porosity	0–40 μm	2.34	1.08	1.99	1.98
closed porosity	0–40 μm	1.22	0.65	1.31	1.31
open porosity	0–40 μm	1.2 ± 0.1	0.44 ± 0.09	1.0 ± 0.2	0.7 ± 0.1

We provide further information on the PSD of chert cores by comparing them with model porous systems built of pure silica particles with mesoporosity in the following sections.

3.5. Standards of Mesoporous Systems Made up of Silica

Considering that the studied cherts consist of up to 98% of silica, it is reasonable to analyze them in comparison to standard porous systems structured from SiO₂, assuming that magnetic impurities will have a fine or identifiable impact on a signal. Such standards can be, for example, synthetic systems MCM-41 and SBA-15, made from pure silica with a 100 nm to 1–2 μm particles size. The particles contain pores with diameters equal to 3–4 nm and 8–10 nm for MCM-41 and SBA-15, respectively. These kind of standards were studied by LF-NMR in regard to their relaxational properties (T₁, T₂ relaxation times, T₁–T₂ maps) for different water content.⁵² A signal was detected for water volume, ranging from a value that exceeded the calculated pore volume several times, to a value lower than required for the total surface of all pores to be covered by a single layer of water. These extreme water contents correspond to the different relaxation mechanisms that dominate the signal, i.e. interparticle water relaxation and intraparticle surface relaxation associated with dipolar coupling effects among water molecules and/or between water molecules and OH groups. T₁ and T₂ distributions and T₁–T₂ maps presented in ref (52) revealed significant changes when decreasing water content evincing the domination of bulk, surface and chemically bound water (OH groups) in the signal. It is worth noticing that, despite the information provided by the producer that both MCM-41 and SBA-15 are pure silica samples, T₁/T₂ ratios reflecting the desorption energy, i.e. the bonding energy with the surface,⁶⁹ are much higher for SBA-15 even though it has larger pores compared to MCM-41. It is probably connected with different surface roughness and associated with the existence of stronger interactions between hydrogen atoms and the surface.⁶⁹ Results from the study on MCM-41 and SBA-15 which are relevant to this paper are shown in Table 7, while for further details the reader is referred to ref (52).

Table 7. Values of T₂, T₁ Times and T₁/T₂ Ratios for the Different Hydrogen Populations in the Reference Silica Porous Systems: MCM-41 and SBA-15 (Based on Reference (52)).

	T2 (ms)
sample	OH groups	surface water	filled pores	overfilled pores
MCM-41	0.06	1.4	5.8	6–31.4
SBA-15	0.05	2	8.6	9–65.1

	T1 (ms)
sample	OH groups	surface water	filled pores	overfilled pores
MCM-41	25–30	10.4	25.6	26–94
SBA-15	20–25	175	678	679–1835

	T1/T2
sample	OH groups	surface water	filled pores	overfilled pores
MCM-41	400–500	7.4	4.4	4.3–3
SBA-15	400–500	87.5	78.8	75.4–28.2

3.6. Comparison of Chert Rock Core Samples with Standard Systems

Studies on pure silica systems deliver valuable information for the interpretation of results from the measurements conducted on the chert rock core samples. A first glance at the T₂ times (Table 3 and 4) and T₁/T₂ (Table 4) ratios from the experiments on cherts suggests that the studied systems are constructed from silica particles with a mesoporous structure. Moreover, dry chert rock core samples are characterized by distinct T₁ and T₂ distributions with four coinciding modes. On the basis of this observation, it is possible that samples contain inclusions, in which different amount of water and silica occur (the reasoning is explained in section 3.7 Inclusions in Cherts). High, but different, T₁/T₂ ratios suggest the strong bonding of water in mesopores that have surfaces with different roughness and/or content of paramagnetic compounds. Of particular interest is the fact that T₂ distributions are very similar for all of the samples, despite that they have different origin (two sampling sites). This might be evidence of potentially similar conditions of rock formation. After saturation, a new peak (S1, Figure 2C) appears in the region of T₂ = 60–100 μs, which, according to the literature, together with high T₁/T₂ (of an order of several hundred; Table 4) corresponds to OH groups. It is especially visible in Figure 2D, which shows the distribution of differential data of saturated and dry samples. Peak S1/SD1 is associated with a signal probably originating from SiOH that forms after saturation in the open porosity of the crystal lattice. On the same distribution (Figure 2D) we can see the rise of the signal in the range of 1 ms marked as SD2. In relation to T₁/T₂ = 20–30 we can suspect that this signal comes from water bonded to the surface of open mesopores characterized by roughness (after comparison with standards) between MCM-41 and SBA-15. It is likely that water forms a H-bonding with surface silanols and gives rise to this peak in such a form. A similar T₂ was observed for the surface water in pure silica pores (Table 7).⁵² Peaks S1/SD1 and S2/SD2, despite having different amplitudes depending on the sample number, occur for all of them. For AK1, the more visible differences appear for peaks SD3 and SD4. A significant rise of T₂ signal in the range of 5–30 ms, with practically no signal in this region for other samples having been observed (Figure 2E, G). This indicates that open porosity in the rock core sample appeared in the form of slits in the microcrystalline quartz. Thus, except for the mesoporous water signal, we can observe a signal originating from water in pores that have larger diameters, located between crystallites. This situation is similar to the overfilled pores state of standard systems (Table 7).

3.7. Inclusions in Cherts

Distinct, regular T₂ distributions of chert rock core samples, after heating in 200 °C and vacuum, clearly indicate closed inclusions. It is very interesting that regardless of the core sample (i.e., sampling site), we observe four aligned peaks (Figure 2A). Due to the fact that inclusion size is stochastic and would impact T₂ time in the same manner (T₂ scales with the pore size), the occurrence of four identically localized peaks has to be triggered by something else. The most plausible explanation seems to be that the inclusions are filled with different proportions of silica and water which leads to different T₂ and T₁/T₂ values. This statement is based on the previous studies on MCM-41 and SBA-15 (Table 7),⁵² since the T₂ (Table 3 and 4) and T₁/T₂ (Table 4) obtained in this work suggest a similar situation. Additionally, four clearly separated peaks that align for all the samples of different types of chert (Figure 2A) suggests that different formation conditions (temperature, pressure, and the composition and origin of the fluid), rather than origin, were responsible for this mutual feature. The above statements lead to the model describing inclusions (Figure 8 and Table 8). It should be noted that for the system of natural nanometric inorganic pores, we recorded water signals characterized by unusually high T₁/T₂ values.^74,75 In the case of inclusions, it is even up to 100. In contrast, for open pores the ratio is of the order of 20. This suggests the existence of the structures shown schematically in Figure 8 and Table 8.

Figure 8.

Schematic model of inclusions. Inclusions may differ in the type of silica as well as its quantity and water solution content.

Table 8. Average Values of T₂ and T₁/T₂ from Tables 3 and 4^a.

inclusion	T2 (ms)	d (nm)	T1/T2	roughness
1	0.45	36	22	comparable to SBA-15
2	4.8	3.9 × 102	109	greater than SBA-15
3	24.5	1.9 × 103	10	between MCM-41 and SBA-15
4	108	9.1 × 103	2.5	comparable to MCM-41

^aThe estimated value of the pore diameter, d, is the average apparent porosity for various mixtures of silica particles and water. The roughness, which is reflected by the T₁/T₂ ratio, is compared with the standards MCM-41 and SBA-15 from the Table 7.

3.8. Differentiation between Bedded and Nodular Cherts

Figure 9 shows biplots for different saturation states obtained from PCA. The first two PCs make the coordinate system, and axes labels include a percentage of a total variance that is explained by the particular PC. Vectors on the biplots are rather divided into groups which have different colors. Table S2 shows original variables that are incorporated into each coloristic group. As we can see, sample AK1 stands out for each saturation state, but for the saturated state (Figure 9C) or differential data (Figure 9D) there is a clear division of samples into two coherent groups. For these two states, AK1 has the minimal value of PC 1, which indicates that original variables that have the highest contribution to this PC differentiate this sample.

Figure 9.

Biplots from PCA: (A) dry samples data; (B) native samples data; (C) saturated samples data; (D) differential data of saturated and dry samples. Vectors reflect the load of original variables into PCs and are divided into coloristic groups (the contents of each group are shown in Table S2).

The results of the PCA analysis correspond well with the observations of T₂ distributions and T₁–T₂ maps. AK1 is always characterized by the highest T₁lm and T₂lm, which indicates that the distributions are shifted toward higher T₂s that result from the biggest pores among the samples. Additionally, it has the highest porosity independently on saturation state. The most noticeable difference is the type of pores that saturates most preferably. For AK2-AK4 we observed a significant increase in the signal from OH-groups and mesoporosity, while for AK1 this was from macropores.

3.9. Summary

• T₂ distributions and T₁–T₂ maps revealed that cherts contain protons associated with hydroxyl groups (R1: T₂ ∼ 0.06–0.2 ms) and molecular water (R2–R5: T₂ > 0.4–2 ms) with total porosity varying from 1.08 to 2.32%.

• PSDs, determined based on the T₂ distributions, indicate that the rock core samples contain a wide range of pores size, including mainly mesopores (R1–R2: T₂< 2 ms) and macropores (R3–R5: T₂> 2 ms) with a very low content of micropores (R1: T₂ < 0.03 ms).

• Very distinct peaks on the T₂ distributions and the T₁–T₂ maps in the dry state of the samples revealed the existence of the kind of closed porosity (0.65–1.31%) associated with inclusions possibly filled with different amounts of silica particles and water.

• Types of inclusions are characterized by a large diversity of T₁/T₂ and T₂ parameters, which is probably associated with various geological processes accompanying their formation.

• The registered open porosity (0.4–1.2%) is composed of a considerable volume of macropores in bedded cherts and mesopores in nodular cherts and, in addition, a visible increase in the signal from the newly formed OH groups (probably in silanols) in both cases.

• Existence of unusually high T₁/T₂ values (inclusions: up to ∼100, open pores: ∼20) for water in inorganic nanometric pores suggests the occurrence of pores that may differ in the type of silica as well as its quantity and water solution content (Figure 8, Table 8).

• PCA helped to distinguish AK1 (bedded chert) from others, yielding a set of variables which differentiate the sample the most.

• Finally, LF-NMR relaxometry in the three saturation states delivers a complete and sufficient set of information, based on which bedded and nodular cherts can be distinguished.

4. Conclusions

The analysis of natural inorganic porous systems showed that we were dealing with samples that have porosity at the level of 1–2%, consisting of several clear hydrogen signal sources. A significant part of the pore volume was inaccessible and were considered to be inclusions. Depending on chert type, different pore types were saturated. Bedded chert seems to have bigger pores in a fairly wide range and hence higher porosity than nodular cherts. Therefore, saturation leads to the filling of a considerable number of macropores in bedded cherts and mesopores in nodular ones and, in addition, a visible increase in the signal from the newly formed OH groups in both cases. Moreover untypical for inorganic pores high values of T₁/T₂ factor equal to ∼100 and ∼20 was registered for T₂ in the range of several and over a dozen milliseconds, respectively. The identification of pore types was possible due to the chemical analysis of the elemental composition of rock core samples, which revealed that they consist of at least 98% pure silica. With this information it was possible to compare them with standard models built from pure silica, MCM-41 and SBA-15, as well as making an estimation of PSD using its relationship with 1D-T₂ distribution. The analysis of PSD showed that for samples containing Fe₂O₃, the influence of diffusion on transverse magnetization decay is negligible. Hence, PSD can be sufficiently accurately determined from the linear relationship between pore size and surface relaxation time. In addition, the performed experiments delivered a sufficient set of variables for PCA, which turned out to be the right tool for the clear division of cherts into two groups. This means that the differences between the parameters obtained from relaxometry for bedded and nodular cherts were statistically significant. The outcomes indicate the possible use of the LF-NMR method for the noninvasive and effective distinction of cherts types expected by geologists, archeologists, and petrographers.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.9b11790.

• Principal component analysis—theory and interpretation method; coordinates of peaks from 1D-T₁ distributions (Table S1); original variables that were considered in the PCA (Table S2); and pore size distribution (PSD) determined from 1D-T₂ distributions of saturated samples, assuming that they are composed of 100% SiO₂ (Figure S1) (PDF)

Author Present Address

^§ AGH University of Science and Technology, al. Mickiewicza 30, 30–059, Krakow, Polan

The authors declare no competing financial interest.