SUMMARY
Searching for food, friends, and mates often begins with an airborne scent. Importantly, odor concentration rises with physical proximity to an odorous source, suggesting a framework for orienting within olfactory landscapes to optimize behavior. Here, we created a two-dimensional odor space composed purely of odor stimuli to model how a navigator encounters smells in a natural environment. We show that human subjects can learn to navigate in olfactory space and form predictions of to-be-encountered smells. During navigation, fMRI responses in entorhinal cortex and ventromedial prefrontal cortex take the form of grid-like representations with hexagonal periodicity and entorhinal grid strength scaled with behavioral performance across subjects. The identification of olfactory grid-like codes with 6-fold symmetry highlights a unique neural mechanism by which odor information can be assembled into spatially navigable cognitive maps, optimizing orientation, and path finding toward an odor source.
In Brief
Grid cells in entorhinal cortex underlie spatial orientation and path finding. Bao et al. show that entorhinal grid-like codes with behavioral relevance emerge when humans mentally navigate an olfactory landscape, highlighting potential neural mechanisms for locating odor sources in odiferous environments.
INTRODUCTION
A key function of sensory systems is to optimize one’s physical proximity to distant objects. Sensory cues are essential for guiding animals closer to appetitive sources and further from aversive sources. Through exploration and experience, animals can adaptively learn to harness the sensory properties of their environments, enabling them not only to locate salient positions in space but also to plan and predict the most efficient route to those positions. Across different sensory modalities, the olfactory system is uniquely suited for achieving these goals.
The sense of smell is fundamentally a predictive sense. Each sniff represents an olfactory snapshot at a specific time and place and simultaneously represents a prediction of what odor is likely to be encountered on the next sniff, at the next time and place (Jacobs, 2012). The sense of smell is also a distance sense, as airborne odors can defy physical boundaries and the absence of light in ways that visual information cannot, providing a means of identifying and tracking remote sources (Gire et al., 2016). Finally, there is a relative physical constancy of an odor source, given that a lingering imprint of the odor is typically rooted at a fixed position in the environment. These features endow the olfactory system with a keen capacity for using chemical cues to navigate physical spaces. Curiously, studies examining the behavioral and neural underpinnings of odor navigation are sparse (Jacobs, 2012). In the animal kingdom, olfactory cues play an indispensable role in navigation, such as foraging in insects (Reinhard et al., 2004), homing behaviors in pigeons (Papi, 1991), and scent tracking in dogs (Thesen et al., 1993). When blindfolded, humans are able to track odors (Porter et al., 2007) and identify the direction of an odor source from distance (Welge-Lussen et al., 2014). However, it is unknown whether humans can navigate a sensory space informed only by odor cues and how the brain might internalize a representation of two-dimensional olfactory space.
Here, we posit a world populated exclusively with odor stimuli to determine whether and how a navigator—with only the luxury of the sense of smell—can traverse an olfactory landscape. Our first step was to design an ecologically plausible landscape of smells that might be naturally encountered in the environment. We took advantage of the fact that odor concentration decreases with distance from its source and that perceived odor intensity monotonically scales with concentration (Conover, 2007; Gire et al., 2016; Jacobs, 2012; Vickers et al., 2001). To this end, we created a two-dimensional plane where x,y coordinates were defined by two different odors (banana and pine) that independently varied in perceived intensity from 0% to 100%, at 20% increments, forming a 6 × 6 space (Figures 1A and 1B). Based on theoretical (Wallraff, 2000) and empirical (Jacobs et al., 2015) data, each position in this two-dimensional space can be derived from the intensity of the two odors, enabling a navigator to extrapolate new information from learned odors, to predict future odor percepts, and, by extension, to predict future locations (Jacobs, 2012).
Figure 1. Experimental Design and Navigation Performance.
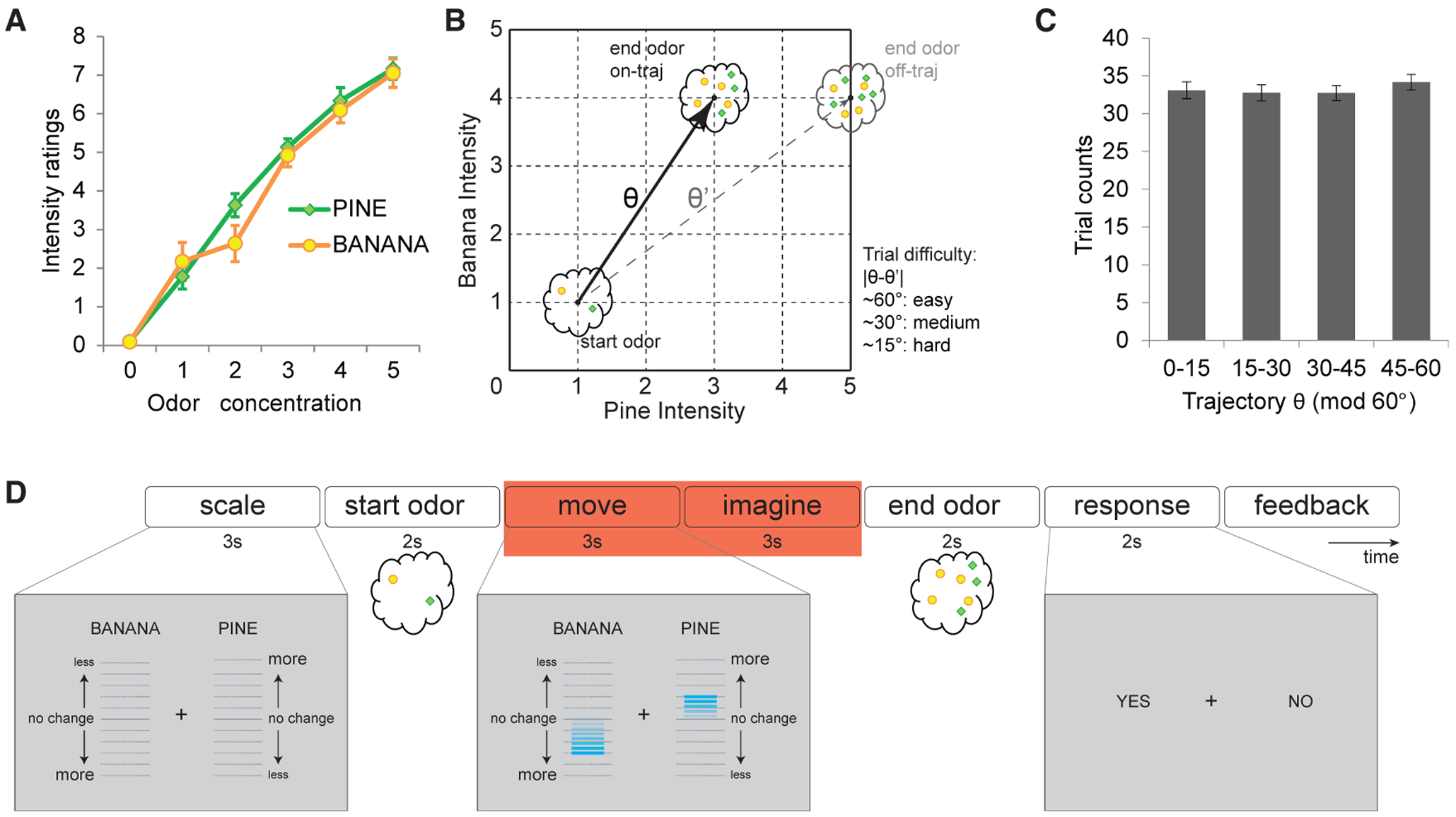
(A) Intensity ratings (mean ± SEM) of pure pine and pure banana odors at different concentrations. As odor concentrations increased stepwise, subjects’ perceived intensity increased stepwise as well (chi-square = 204.93; p < 0.001; Friedman test), but ratings did not differ between the two odors at each intensity step (chi-square = 1.03; p = 0.31; Friedman test).
(B) Conceptual layout of the odor map, in which each coordinate on the odor map corresponds to a unique mixture of the two odors. Trajectory angles were defined by start and end odor positions, and the end odor might appear on (“on-traj”) or off (“off-traj”) the predicted trajectory. There were three difficulty levels according to the difference between on-trajectory θ and off-trajectory θ’. Easy trials: 60° ± 5°; medium trials: 30° ± 5°; hard trials: |θ-θ’| 15° ± 5°.
(C) Trajectory θ was sampled evenly across the 60° cycle, with no difference in sampling frequency across directions (chi-square = 2.22; p = 0.53; Friedman test). Data are mean ± SEM. See also Figure S1.
(D) Timeline of an example trial of the odor prediction task. Red box indicates the time period used for the grid-cell analyses; relative movements of the banana and pine scale bars (compare left and center screenshots in gray) informed subjects how much to expect the intensities of the two odor components to change, who then indicated whether the end odor matched their prediction (right screenshot).
See also Figure S2.
An important feature of our stimulus set was guided by hypotheses about how the brain would encode a mental map of odor space. In rodents, open-field foraging elicits spatially modulated activity in medial entorhinal cortex (ERC), with individual neurons (grid cells) firing at multiple discrete and hexagonally periodic locations in space (Hafting et al., 2005; Stensola et al., 2012). In tiling spatial fields, grid cells provide a neural metric and internalized representation for self-location, route planning, and path integration (Bush et al., 2015). Similarly, humans can navigate virtual (Doeller et al., 2010), visual (Julian et al., 2018; Nau et al., 2018), abstract (Constantinescu et al., 2016), and imagined space (Bellmund et al., 2016; Horner et al., 2016), inferred solely from visual inputs, with single-cell recordings (Jacobs et al., 2013) and fMRI (Doeller et al., 2010) techniques supporting evidence for grid-like representations in ERC as well as medial prefrontal, posterior parietal, and lateral temporal cortices (Constantinescu et al., 2016; Doeller et al., 2010; Jacobs et al., 2013). Therefore, based on our hypothesis that navigation of an odorinformed space would rely on a grid-like coding scheme, we ensured the odor array was optimized to assess grid-like fMRI responses, including sufficient angle resolution to identify hexagonal (6-fold) symmetry and sufficient range to characterize odor trajectories rather than odor identities per se (Figures 1C and S1).
In this study, we asked human subjects to mentally navigate along a trajectory defined by a “start” odor and an “end” odor and to indicate whether their predicted translation corresponded to the veridical end odor. Success on this task requires access to an internalized map of odor space, and our behavioral data revealed above-chance accuracy in orienting within this space. We demonstrate that grid-like representations with hexagonal periodicity emerged in ERC and ventromedial prefrontal cortex (vmPFC) during olfactory navigation, with grid strength in ERC correlating with behavioral performance across subjects. Our findings reveal that two-dimensional arrays of odor intensities, which themselves cannot be topographically encoded as a set of Cartesian coordinates on the olfactory epithelial sheet, nevertheless map onto grid-like scaffolds that can support spatial orientation and route planning within an olfactory space.
RESULTS
Humans Can Mentally Navigate Two-Dimensional Odor Space Defined Purely by Olfactory Stimuli
To encourage mental navigation through odor space, we adapted a task similar to those used in virtual and abstract navigation studies (Bellmund et al., 2016; Constantinescu et al., 2016; Doeller et al., 2010; Horner et al., 2016; Nau et al., 2018). Subjects were provided a start location and a trajectory and then assessed whether their predicted (imagined) endpoint along the trajectory corresponded to the veridical endpoint. Our task was introduced to subjects as an “odor prediction” task, but the latent structure of the map was not revealed until after the experiment. Trajectories were defined using a start odor mixture, along with a visual instruction screen indicating how much the intensities of banana and pine in the mixture would change upon delivery of the end odor (Figures 1B, 1D, and S2). After a 6-s period of mental navigation along the specified trajectory, subjects received the end odor and indicated whether it matched their prediction. On 50% of trials, the end odor was on trajectory, and on 50% of trials, the end odor was off trajectory, varying by 15°–60°. Correct answers would be compatible with successful navigation.
Twenty-five subjects underwent behavioral training on the prediction task for φ days, followed by fMRI scanning on day 5. Two different measures of task performance suggested that subjects internalized mental maps of the odor space. First, prediction accuracy was consistently higher than chance (50%) on training and scan days (Figure 2A), though no significant difference was observed across days (repeated-measures ANOVA; F3.41,81.91 = 1.41; p = 0.24). Second, we used signal detection methods to derive a navigation index, which adjusted for subject-specific olfactory perceptual limits (see STAR Methods). This analysis revealed an effect of training on navigation performance, particularly for easier trials in which the “off-trajectory” end odor was at a larger angle from the instructed trajectory, with a significant performance gain from day 1 to subsequent days (t24 = −2.17; p = 0.04; paired t test; two-tailed; Figure 2B). Collectively, these findings indicate that human subjects can generate predictions of to-be-encountered odors that vary in magnitude across two independent feature dimensions.
Figure 2. Olfactory Navigation Performance.
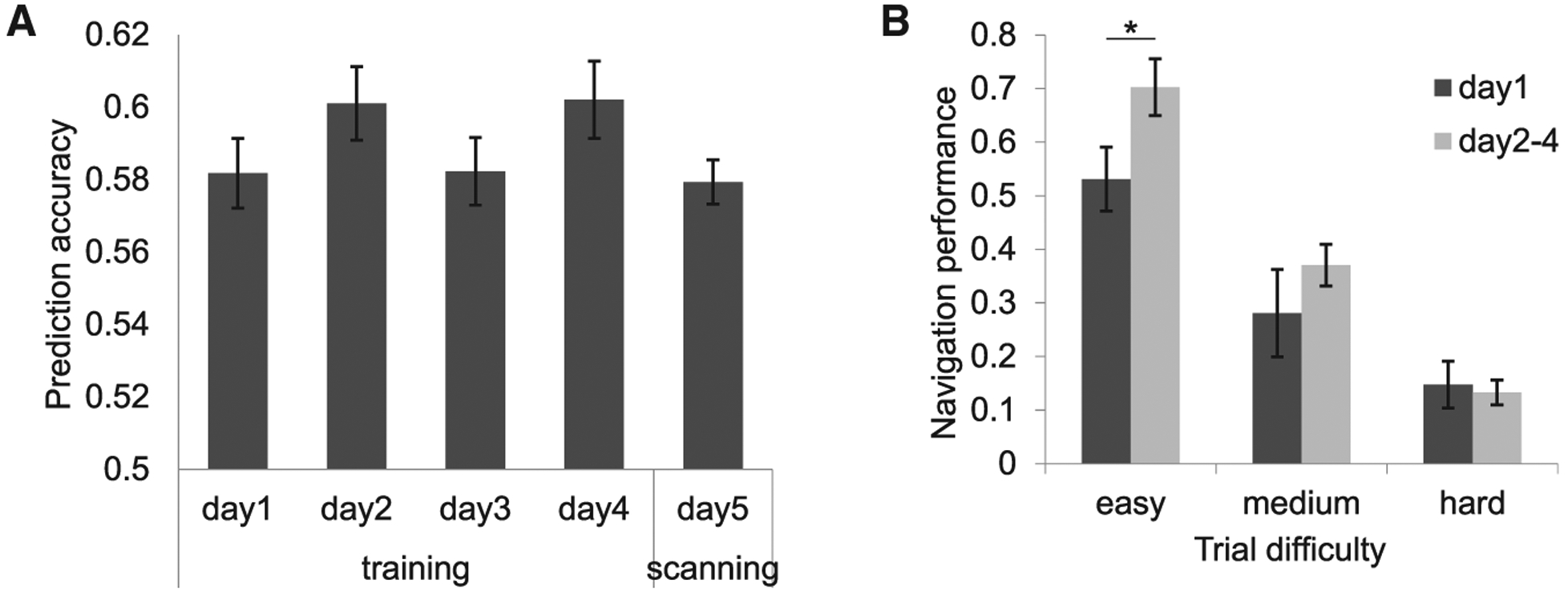
(A) Performance accuracy during φ training days and the following scanning day were consistently and significantly greater than chance (50%; Z > 4.21; p < 0.001; Wilcoxon signed-rank test).
(B) Navigation performance (computed as the prediction d’ adjusted for perceptual discrimination on a subject-wise basis) revealed a significant effect of training, particularly for easy trials (day 1 versus days 2–4; easy trials: t24 = −2.17, *p = 0.04; medium trials: t24 = −1.01, p = 0.32; hard trials: t24 = 0.28, p = 0.78; paired t tests; two-tailed). In this and all figures, statistical tests are one-tailed unless otherwise noted; error bars, ±1 SEM.
Grid-like Representations of Two-Dimensional Odor Space in vmPFC
We next asked whether the human brain uses a grid-like architecture as a metric of odor space. Because most grid cells share a common grid-axis angle in the same animal (Hafting et al., 2005; Sargolini et al., 2006), the group activities of grid cells can be manifested in fMRI signals showing a hexagonal periodicity as a function of moving direction (Figures 3A and 3B). Such profiles have been identified in ERC and medial prefrontal cortex in neuroimaging studies of human navigation (Bellmund et al., 2016; Constantinescu et al., 2016; Doeller et al., 2010; Horner et al., 2016; Julian et al., 2018; Nau et al., 2018). Here, we first searched for regions where fMRI signals were hexagonally modulated by the odor trajectory direction θ during the navigation period (Figure 1D). Using a quadrature filter (effectively, a pair of sine and cosine regressors with 60° periodicities; Doeller et al., 2010; see STAR Methods), we identified the largest cluster in ventromedial prefrontal cortex (vmPFC) (Figure 3C). Notably, within the vmPFC region of interest (ROI) of a given subject, the grid angles of individual voxels were closely aligned to the same angle, a profile that was observed in all but one subject (Figure S3A).
Figure 3. Grid-like Signals during Odor Navigation.
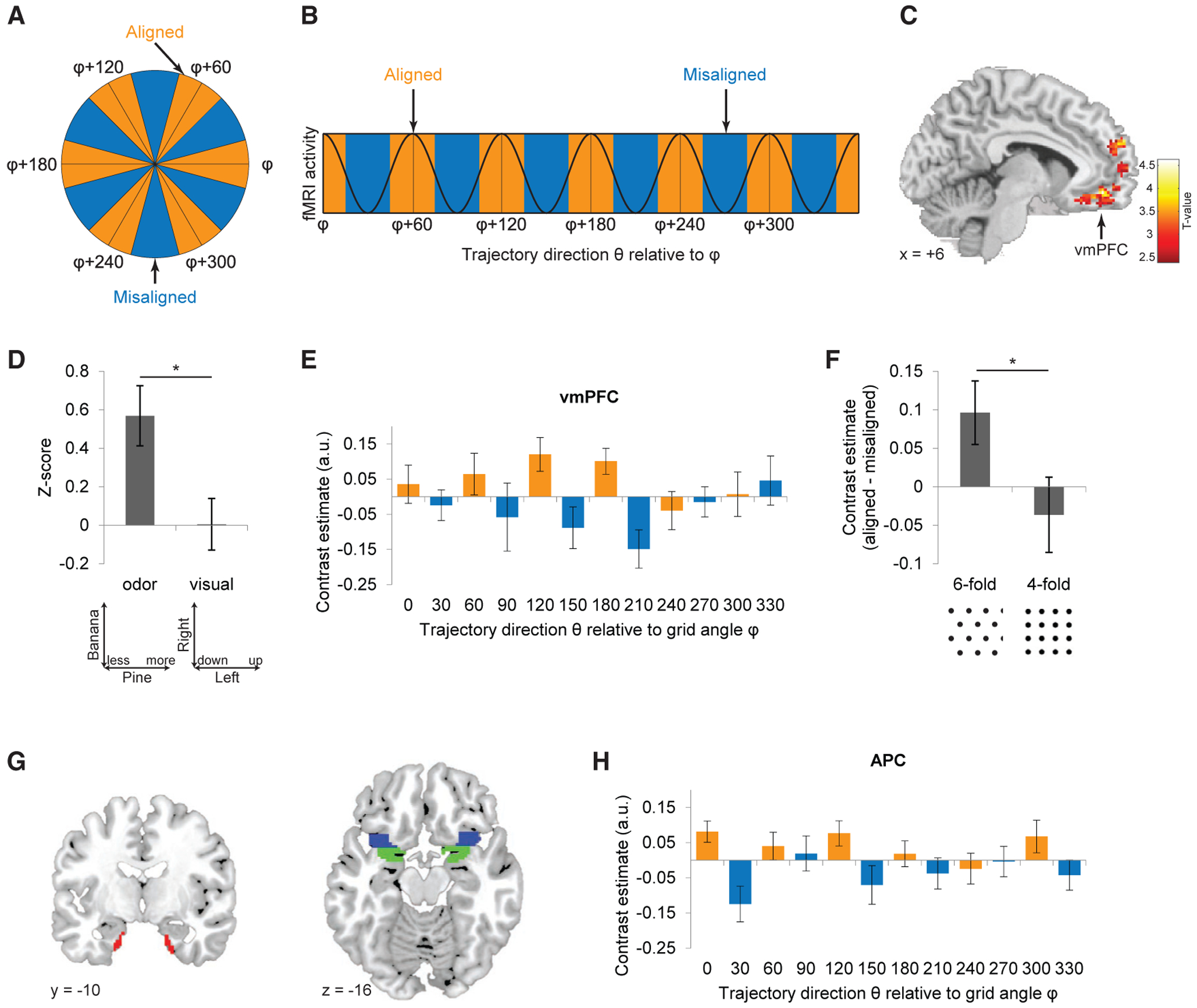
(A and B) Analysis schematic. Given a hexagonal grid field with main axis angle φ, trajectories on the odor map can be binned as aligned or misaligned with φ (A). Grid-like fMRI activity with 60° periodicity would thus be higher for aligned versus misaligned trajectories (angle φ modulo 60° versus angle [φ+30°] modulo 60°) (B).
(C) Hexagonally modulated fMRI signal activity was identified in vmPFC (x = 6, y = 46, z = −10; Montreal Neurological Institute [MNI] coordinate space; Z = 3.87; cluster-level PFWE-corr = 0.0012, cluster-defining threshold p < 0.001; voxel-level Puncorr = 0.000055). Data overlaid on a T1-weighted sagittal brain section are shown (display threshold; p < 0.01 uncorrected).
(D) Hexagonally modulated activity was not elicited in vmPFC in response to trajectories defined by the movement of the visual bars (t24 = 0.037; p = 0.97; two-tailed); the direct comparison of odor versus visual trajectories was significantly different (t24 = 2.65; *p = 0.0070; paired t test). Bar plot shows condition-specific averages of voxels from a 5-mm sphere centered at the vmPFC peak in (C). See also Figure S5.
(E) Cross-validation analysis of the grid-like effect in vmPFC (based on cluster in C; threshold; p < 0.001) reveals grid angle reproducibility across time (aligned > misaligned; t24 = 2.33; p = 0.014). Orange and blue bars, aligned and misaligned to φ.
(F) The grid-like effect in vmPFC was specific for 6-fold, but not 4-fold, periodicity (aligned > misaligned; Z = −0.04; p = 0.97; Wilcoxon signed-rank test), and the difference between 6-fold and 4-fold symmetry was significant (Z = 1.98; p = 0.048; Wilcoxon signed-rank test). See also Figure S4.
(G) Anatomical masks delimiting ROIs in ERC (red), APC (blue), and PPC (green).
(H) The preferred grid angle in vmPFC predicted hexagonally modulated signal in APC (aligned > misaligned; t24 = 3.08; p = 0.0026; α = 0.016; Bonferroni correction for multiple comparisons of three ROIs).
Data are mean ± SEM.
Insofar as the quadrature filter is effectively a functional localizer, this approach is predisposed toward identifying regions with 6-fold symmetry. Therefore, to minimize any analysis bias, we created a new independent anatomical localizer of the vmPFC (5-mm radius), centered at the vmPFC coordinate (6, 44, −10) reported in the grid cell study by Constantinescu et al. (2016). In this way, we could test the strength of vmPFC modulation for the 6-symmetry fold, as well as for other control folds (from 3- to 5-fold). Among all symmetries tested, only the 6-fold model yielded a significant modulatory effect, but not 3-, 4-, or 5-fold models (Figure S4).
Our 6-fold model of odor space included the “movement” period of the task, in which vertical translations of two visual bars informed upcoming changes in odor intensity. To minimize the possibility that the observed grid-like effects could be attributed to visual stimulation, we ensured the positions of the odor columns (“pine” and “banana”) and the axis labels (“more” and “less”) were randomly alternated across trials, dissociating spatial changes in visual features from magnitude changes in odor features. As a formal test that grid-like maps in vmPFC were not driven by visual confounds, we designed a complementary model in which θ was determined by the absolute directions and translations of the visual bars (Figure S5). Visual stimulation had no significant effect on grid-like vmPFC representations, and the emergence of hexagonally modulated activity was specific for odor versus visual trajectory (Figure 3D). Interestingly, a visual model with 4-fold symmetry showed significant modulation of fMRI activity in primary visual cortex (Figure 4), indicating sensitivity to the low-level visual movements of the rating scale bars.
Figure 4. 4-Fold Modulation of fMRI Activity Based on Visual Trajectory in Bilateral V1.
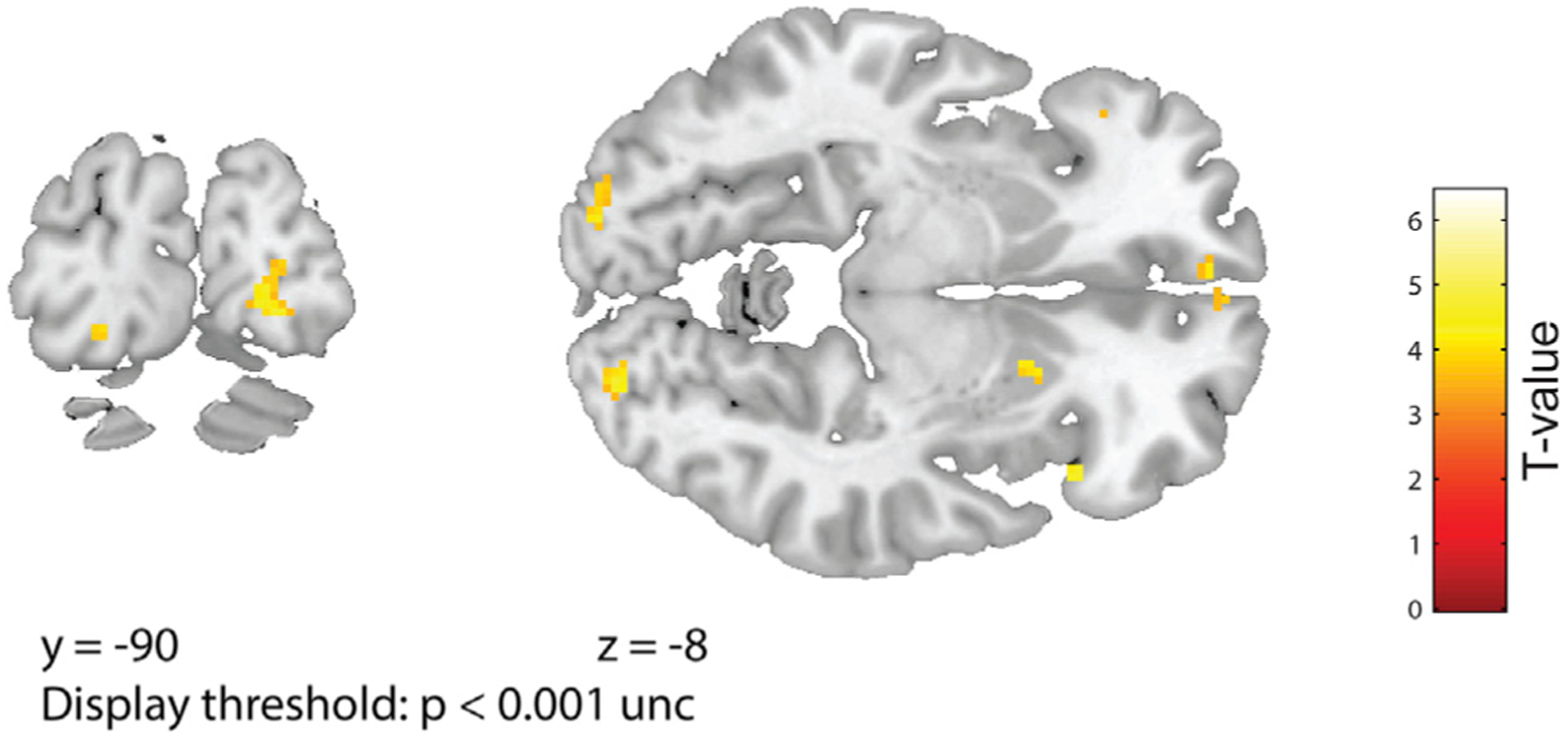
A visual model, based on the up and down vertical movements of the visual bars during the experiment, significantly modulated activity with 4-fold symmetry in bilateral primary visual cortex in left V1 (−20/−88/−14, Z = 3.79; puncorr < 0.0001; small-volume correction [SVC] using an anatomical mask of Brodmann areas 17 and 18: pSVC-corr = 0.003) and in right V1 (22/−90/−8; Z = 3.88; puncorr < 0.0001; pSVC-corr = 0.012). Activations are overlaid on coronal (left) and axial (right) sections of T1 template, at a display threshold of p < 0.001 uncorrected.
Finally, to assess the reproducibility of these effects in vmPFC, we performed a leave-one-out cross-validation analysis to test whether the 6-fold periodic signals conform to a consistent grid-axis angle across time. Using N-1 scan runs, we estimated each subject’s grid angle φ from the vmPFC and reserved the left-out (Nth) run as the test set, which was organized into 12 conditions by binning trials into successive 30° bins relative to φ. The key prediction was that fMRI activity would be higher for trials aligned to φ (0° modulo 60°) than those misaligned (30° modulo 60°). Using this unbiased analysis, we confirmed that the same grid angle was consistently identified in vmPFC (Figure 3E), implying stability of grid angle over the duration of the experiment. This effect was specific to 6-fold symmetry: a control analysis based on a 4-fold periodicity, corresponding to a square grid field, did not elicit significant modulation in vmPFC (Figure 3F).
Grid-like Representations in APC Align with vmPFC Grid Angle
Using the same approach, we tested whether other brain regions might align to the same vmPFC angle (Figure 3G). The demonstration of interregional angle stability would support the idea that a coordinated network of regions—tuned to the same grid angle—helps direct navigation of an odor space. Here, we focused on ERC, based on its prominent role in grid cell coding (Doeller et al., 2010; Hafting et al., 2005), and anterior and posterior piriform cortex (APC and PPC), given that our task centers on exploration of olfactory space (Giessel and Datta, 2014). Of note, mean fMRI signal activity in APC significantly varied in a 6-fold symmetric manner, entrained to the same angle as in vmPFC (Figure 3H). A similar trend was observed in PPC but was not significant (aligned > misaligned; t24 = 2.02; p = 0.027; α = 0.016; Bonferroni correction for multiple comparisons of three ROIs). No hexagonal effect was found in the mean ERC signal (aligned > misaligned; t24 = 0.19; p = 0.42), and the preferred grid angles independently estimated in vmPFC and in ERC were not correlated across subjects (circular correlation r = −0.034; p = 0.86).
Multi-voxel Ensemble Patterns of Olfactory Grid-like Codes in Entorhinal Cortex
Although grid-like coding in ERC was not identified in the above analysis, it is possible that ERC employs a distributed coding scheme during odor navigation (Diehl et al., 2017; Hardcastle et al., 2017), which might be better characterized using multi-voxel pattern-based approaches (Bellmund et al., 2016). Moreover, to the extent that low signal quality in ERC (due to its location in an area of high susceptibility artifact) limits our ability to resolve ERC grid angles using univariate analyses, multi-voxel pattern analysis (MVPA) methods might be more robust to signal dropout in ERC. To this end, we reasoned that, if distributed grid-like representations of odor space exist in ERC, then for each subject, there should be an intrinsic preferred grid angle φ (presumably aligned with vmPFC) with 60° periodicity, such that trial trajectory θ at any 60° equivalent of φ should exhibit greater pattern overlap than with 30° trajectories (Figures 5A and S6). A region-of-interest analysis in ERC (Figure 3G) confirmed this prediction: after aligning trials to φ estimated from vmPFC activity, ensemble pattern similarity in ERC was significantly greater for trial pairs with trajectories aligned to the same 60° periodicity, in comparison to trial pairs in which one of the trajectories was offset by 30° (Figure 5B).
Figure 5. Grid-like Ensemble Activity in Entorhinal Cortex.
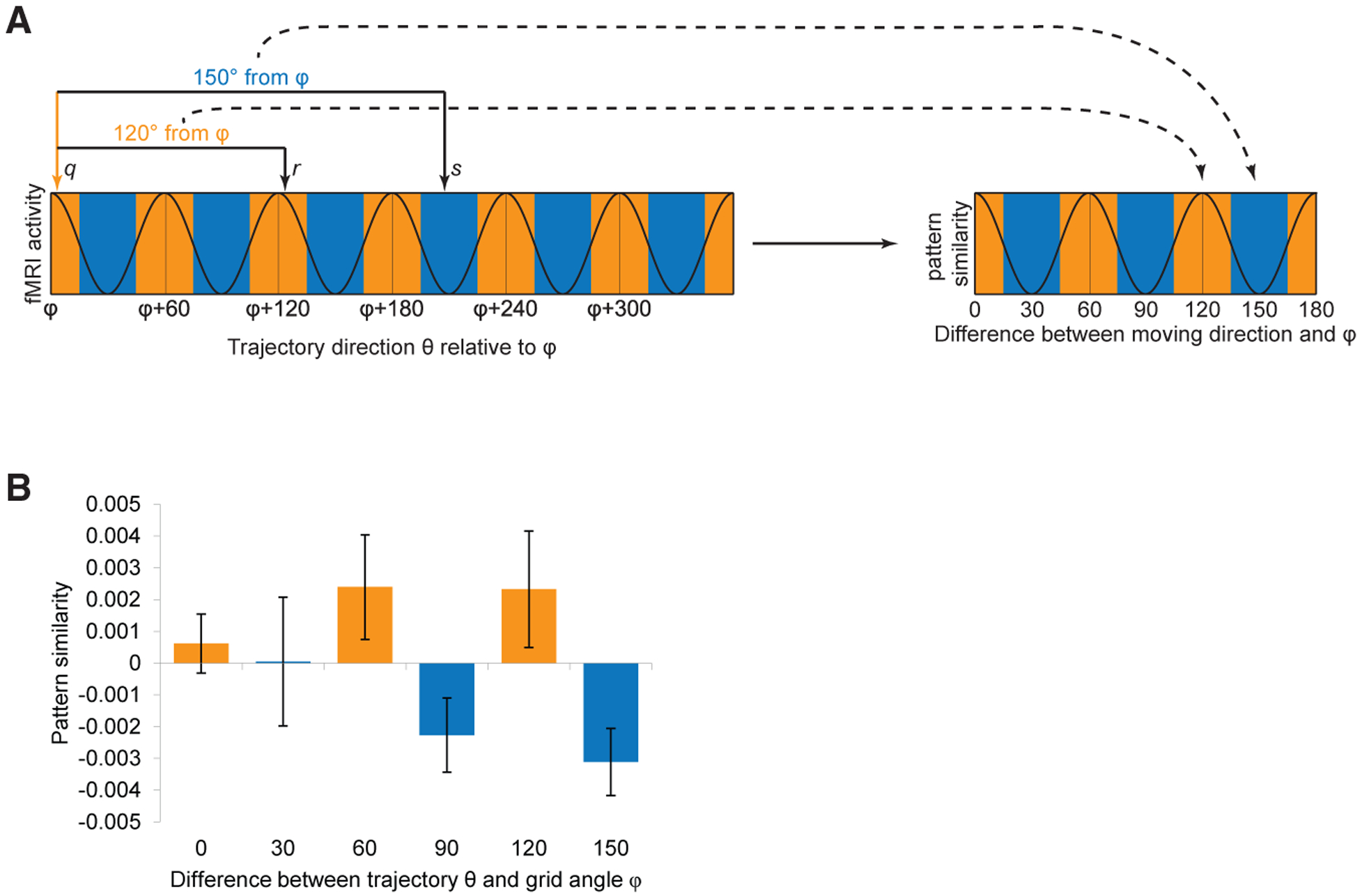
(A) Conceptual schematic for the multi-voxel pattern analysis of grid-like representations in ERC. (Left) Hypothetical fMRI activity in a grid-like system shows hexagonal modulation as a function of trajectory direction θ, where θ is aligned to each subject’s preferred grid angle φ, estimated from vmPFC. If the trajectories of a given pair of trials are aligned at a 60° multiple of φ (e.g., trial q at φ and trial r at φ + 120°), then pattern similarity should be high. Alternatively, if the trajectories of a given trial pair are misaligned with respect to φ (e.g., trial q at φ and trial s at φ + 210°), then pattern similarity should be low. (Right) Linear correlations between trial pairs were estimated, enabling a test of the hypothesis that aligned-aligned patterns (angular difference of 0° mod 60°; orange colors) would elicit greater pattern overlap than aligned-misaligned patterns (angular difference of 30° mod 60°; blue colors). See Figure S6 for details.
(B) Pattern similarity between trajectory pairs in ERC exhibited hexagonally periodic modulation, with greater similarity for pairs aligned to grid angle φ and its 60° multiples (orange versus blue bars; aligned > misaligned; t24 = 2.15; p = 0.021). Data are mean ± SEM.
To test whether this multivariate effect in ERC emerged only in context of 6-fold rotational symmetry, we conducted the same analyses with 3- to 5-fold symmetries. Importantly, we found no evidence of periodic pattern signals in 3-, 4-, or 5-fold control models (Figure 6A). Moreover, a visual model where trajectory directions were determined by visual movements of the scale bars found no significant grid-like coding in ERC patterns (Figure 6B). Interestingly, a complementary whole-brain searchlight analysis did reveal limited evidence for 6-fold multivoxel representations in vmPFC (Figure S7), though these effects were relatively weak and did not survive multiple comparison correction (Z = 2.74; p = 0.003 uncorrected). Finally, to investigate whether olfactory grid-like pattern representations in ERC are capable of supporting behavior, we computed the linear correlation between grid-pattern robustness (aligned versus misaligned) and performance on the odor prediction task. Across subjects, stronger grid-like ensemble activity in ERC was associated with greater ability to predict which odor would be encountered on a specified trajectory (Figure 6C), implicating the potential involvement of this region in orienting an olfactory navigator in two-dimensional odor space.
Figure 6. Grid-like Pattern Representations in ERC Are Specific to 6-Fold Symmetry and to Odor Trajectories, with Grid Angle Aligned to vmPFC.
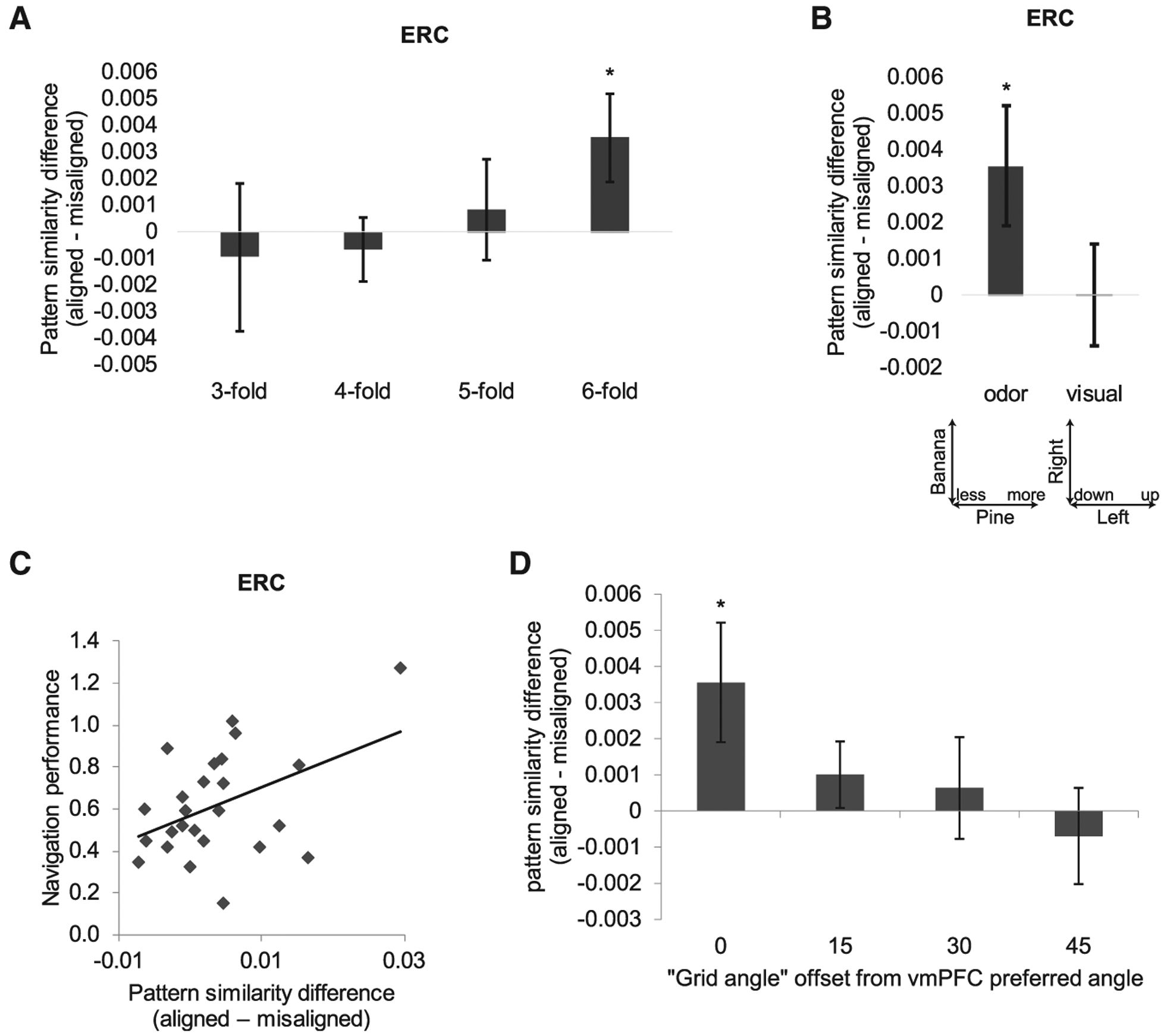
(A) N-fold sinusoidal modulation of ERC pattern similarity was significant with the 6-fold model (aligned > misaligned; t24 = 2.15; p = 0.021), but not with 3-, 4-, or 5-fold models (t24 < 0.43; p > 0.33).
(B) Grid-like pattern representations in ERC were significant for odor trajectories, but not for visual trajectories (aligned > misaligned; t24 = 0.01; p = 0.49).
(C) Strength of grid-like pattern representations in ERC, estimated as the difference between angle-aligned and misaligned conditions, correlated with behavioral performance (“easy” trials) on the odor navigation task across subjects (Pearson’s r = 0.44, p = 0.026, two-tailed; robust regression r = 0.48, p = 0.03).
(D) Grid-like pattern representations in ERC were only significant when the grid angle in ERC was aligned to the vmPFC grid angle φ, but not at 15°, 30°, or 45° offsets from φ (aligned > misaligned; φ + 15°: t24 = 1.09, p = 0.15; φ + 30°: t24 = 0.45, p = 0.33; φ + 45°: t24 = −0.52, p = 0.67).
Data are mean ± SEM.
Our pattern analysis was based on the assumption that the grid angle in ERC was aligned to vmPFC grid angle φ (see STAR Methods). However, it remains possible that any periodic regularity in the ERC signal, irrespective of vmPFC grid angle φ, might still show significant variations between mod 60° and mod 30°. Therefore, we explicitly tested the hypothesis that the pattern-based hexagonal effect in ERC is most robust at vmPFC grid angle φ. Here, the prediction was that, with increasing divergence from φ (estimated in vmPFC), the strength of the correlation difference (between aligned and misaligned pairs) in ERC would progressively decrease. In this analysis, we computed correlations by offsetting the assumed grid angle φ by 15°, 30°, and 45° away from the subject’s preferred vmPFC angle. These results establish that the hexagonal effect is only significant for the vmPFC grid angle φ, but not for the other three conditions (Figure 6D). Moreover, fitting a linear regression across the four conditions revealed that the slope is significantly negative across subjects (t24 = −2.65; p = 0.014).
Olfactory Grid-like Representations in Entorhinal Cortex Are Not Driven by Mere Differences in Stimulus Discriminability or Task Difficulty
The use of angular parameters as regressors in our models of 6-fold symmetry is predicated on the assumption that the olfactory behavioral trials to which subjects were exposed were analogous to navigating on a two-dimensional “arena.” However, it remains possible that the same brain areas would have been uncovered if the data had been analyzed without including any angular parameters. In other words, it would be important to determine whether ERC is reflecting the discriminative abilities of the subjects rather than the spatial structure underlying the odorant combinations. To explore this question, we sorted trials into correct responses (hits + correct rejections) and incorrect responses (misses + false alarms). We then used two different classifier methods to assess whether information about odor discrimination aptitude could be decoded from pattern representations in ERC. First, a correlation analysis between linear vectors of voxel-wise pattern activity demonstrated that within-condition pattern similarities (e.g., “correct” versus correct trial pairs) did not differ from between-condition similarities (e.g., correct versus “incorrect” trial pairs; t24 = 0.046; p = 0.96). Second, a support vector machine (SVM)-decoding analysis showed that classification accuracy (correct or incorrect) for individual trials was not different from 50% chance level (t24 = 0.034; p = 0.97). Together, these data suggest that odor discrimination per se did not influence effects in ERC.
We also inspected three additional potential confounding factors. First, we examined task difficulty. Here, trials were sorted into “hard” versus (“medium” + “easy”) difficulty levels, based on our definition of “difficulty” as the difference between the subject’s mental prediction of the end odor and the actual delivered end odor. The hypothesis is that, on hard trials, reflecting a shorter distance between the imagined endpoint and the actual endpoint (based on delivery of the actual end odor), it would be more difficult to estimate whether the end odor differed from its instructed trajectory. Using classifier models, we found that task difficulty could not be decoded from ERC patterns (correlation analysis: t24 = 1.71, p = 0.10; SVM decoding: t24 = −0.57, p = 0.58). Second, we examined trial distance. We performed a median split of trials based on the distance of the trajectory (from [x1,y1] to [x2,y2]), where further distances between start odor and end odor would presumably be easier to discriminate. Using either correlation analysis or SVM, the factor of distance could not be decoded from ERC patterns (correlation analysis: t24 = 0.33, p = 0.74; SVM decoding: t24 = −0.28, t = 0.78). Finally, we examined the change in the number of odor components. We separated trials based on whether the number of odorants in the start odor differed from the number of odorants in the end odor, e.g., moving from 60% pine and 40% banana to 0% pine and 40% banana. Again, using correlation analysis or SVM, the factor of component change could not be decoded from ERC patterns (correlation analysis: t24 = −0.81, p = 0.43; SVM decoding: t24 = 0.54, p = 0.59).
DISCUSSION
Neural mechanisms addressing the “where” question of human olfaction—that is, how the olfactory system tracks and locates odor sources in an odiferous environment—are poorly understood. Indeed, spatial navigation is a core function of the olfactory system in most animal species, yet a unified model of olfactory navigation, incorporating neurobiological data with a spatially plausible array of odors, is almost completely lacking. In this study, we tested the hypothesis that human subjects, using only the sense of smell, could navigate through a two-dimensional olfactory space. When provided with a start odor location and route (trajectory) instructions, subjects were able to imagine and predict their perceptual translocation in this odor space. Odor navigation was associated with hexagonal grid-like coding in vmPFC, APC, and ERC, with behavioral performance scaling with the robustness of entorhinal responses across subjects. These findings mirror the behavior relevance of grid-like units in navigation of physical and abstract spaces (Constantinescu et al., 2016; Doeller et al., 2010; Kunz et al., 2015) and highlight the idea that the human brain has access to internalized representations of odor mixture arrays to guide spatial orientation and route planning.
Insofar as the two orthogonal axes of our odor space (banana, 0%–100% and pine, 0%–100%) naturally establish angle symmetries of 90°, we tested whether the 6-fold periodicity observed in vmPFC and ERC could not be better accounted for by a 4-fold periodicity. This analysis confirmed that the 6-fold model was significantly stronger than the 4-fold model in both brain regions. Furthermore, by randomizing the visual directions of the odor trajectory and testing a visual model, we eliminated the possibility that grid-like signals were influenced by gaze movement from the visual field (Julian et al., 2018; Killian et al., 2012; Nau et al., 2018). These control tests bring greater confidence to the idea that the human brain can create a 6-fold map out of systematic translations in olfactory perceptual space.
One striking finding is that, when human subjects chart their course through odor space, fMRI-based representations in ERC, vmPFC, and APC are generally aligned to the same grid angle. It is possible that different brain areas utilize hexagonal grid architectures to represent different types of mental maps, but for each of these areas to converge on the same preferred grid angle seems unlikely unless there was direct interareal coordination. Moreover, the few rodent studies testing for hexagonal profiles outside of ERC have only identified grid fields in the presubiculum and parasubiculum (Boccara et al., 2010), though single-neuron recordings from humans have reported grid-like spiking patterns in the cingulate cortex (Jacobs et al., 2013). Thus, a plausible alternative explanation would be that odor navigation engages hexagonally periodic activity in ERC, with feedback projections to vmPFC and APC signaling whether the subject is either on or off trajectory as they traverse through olfactory space. Information about angle alignment could be integrated with action-outcome contingencies in vmPFC to refine behavior and support more sophisticated cognitive maps (Schiller et al., 2015; Wikenheiser and Schoenbaum, 2016) and with olfactory information in APC to tag or strengthen a set of odor representations associated with the current trajectory.
Whether our findings are a manifestation of abstract conceptual spaces more broadly, especially for a region such as vmPFC, cannot be ruled out here (Constantinescu et al., 2016). However, the identification of grid-like representations in APC reasonably implies that there is something “olfactory” being endowed upon this network, rather than being a pure (modality-free) abstract space. In future work, we could test the hypothesis that a grid-like code of odor space is not observed when the start and end odors are navigationally irrelevant, for example, using a task in which subjects simply indicate whether the second odor is stronger or weaker in intensity than the first odor.
In this study, grid-like representations of olfactory space in ERC were identified in the form of multivoxel patterns instead of mean univariate signals. In turn, a pattern-based hexagonal profile was not found in vmPFC (aligned > misaligned; t24 = 0.33; p = 0.37). We suspect that the discordance between the MVPA and the standard (univariate) analyses is because each analysis is sensitive to different types of signals: MVPA is sensitive to signals that vary across voxels, whereas univariate analysis is sensitive to mean activation that is consistent across subjects. To this point, the absence of a multivoxel effect in vmPFC could be due to low variability across voxels, whereas a pattern-based effect in ERC only emerges if there is substantial variation across voxels. To test this hypothesis, we compared cross-voxel variance for the raw fMRI time series between vmPFC and ERC (see STAR Methods). Supporting our prediction, we found that voxel-wise variability was significantly lower in vmPFC than in ERC (Figure S8), implying that fundamental signal differences between the two brain regions account for why grid-like codes in vmPFC and ERC were uncovered using different analysis approaches.
An inverse question can also be posed: why was the quadrature filter unable to identify 6-fold (univariate) effects in ERC? One possible explanation is that fMRI signal quality (temporal signal-to-noise ratio [tSNR]) is relatively weak in ERC, consistent with its position in an area of higher MRI signal artifact. Therefore, to examine whether lower overall ERC signal quality—in a given subject—tends to be associated with weaker ERC grid-like effects, we tested the hypothesis that, across subjects, ERC voxels with weaker tSNR would also have lower 6-fold effects based on the use of the quadrature filter (see STAR Methods). This analysis revealed a marginally positive effect across subjects (Fisher Z-transformed R = 0.032 ± 0.025; Wilcoxon signed rank test, Z = 1.61, p = 0.053, one-tailed), suggesting that a stronger univariate hexagonal effect is more likely to be found in ERC voxels with better signal quality. As such, our ability to identify univariate grid-like effects in ERC may be principally limited by tSNR in this region.
Aside from potential differences in signal quality between ERC and vmPFC, it is also possible that grid-like representations in ERC are fundamentally different for olfactory spaces, as opposed to visual spaces and abstract relational spaces. Such differences could arise from the fact that, in rodents at least, olfactory inputs predominantly converge on the lateral ERC, whereas visual and spatially modulated inputs converge on the medial ERC (Kerr et al., 2007; Witter et al., 2017). Assuming that a similar dichotomy exists in the human ERC, it is plausible that neural representations of two-dimensional odor space are associated with grid angles, spacing, and phase that are qualitatively distinct, such that MVPA methods are more sensitive for identifying olfactory grid-like representations.
The identification of olfactory grid-like neural representations has important implications for understanding how animals navigate through odor space. It has been suggested that odor concentration differences across sequential sniffs and odor timing differences at each nostril can be useful cues for tracking an olfactory source (Catania, 2013; Gire et al., 2016; Porter et al., 2007; Rajan et al., 2006). However, neither of these models is sufficient for encoding the full relational details among elements in an odorous environment. Our data highlight a novel mechanism by which the brain can construct a cognitive map of odor space. Having access to such a map would enable animals to plan how to navigate through an olfactory terrain and to select a route that optimizes their physical proximity to odor objects. The utility of olfactory cognitive maps is ideal for environments where odor sources are spatially and temporally anchored to a landscape, such as fruit trees, watering holes, and nesting sites, but given that grid cell fields can re-map to a new set of physical features (Diehl et al., 2017; Fyhn et al., 2007; Marozzi et al., 2015), olfactory maps may also be effective in less stationary environments.
Our experimental paradigm is the first to use odors exclusively as metric cues (including distance and direction) to study the neural foundations of human spatial navigation. As a reductionist model, we show that grid-like representations can be assembled from an array of odor mixtures, but in theory, each individual olfactory mixture can signify a unique “place” in two-dimensional odor space. In the rodent literature, an interplay between hippocampal place fields and entorhinal grid cells is thought to enhance and stabilize place cell activity (Hales et al., 2014; Langston et al., 2010; Wills et al., 2010) and may provide a mechanism for associating episodes, position, and velocities to predict future locations (Bush et al., 2014; Rennó-Costa and Tort, 2017; Sanders et al., 2015). Indeed, a computational simulation of spatial navigation showed that an artificial agent with a “grid network” incorporated into the system learns more efficiently than a control agent with only “place cells” available (Banino et al., 2018). The extent to which discrete odor mixtures can be represented as place fields in human hippocampus, and how place cells shape the emergence of grid fields, will be important questions for future work.
STAR★METHODS
CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Xiaojun Bao (xiaojunbao2011@u.northwestern.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Twenty-five participants (22 women, aged 18–37, mean age 24.3 years) completed this study. They reported to be right-handed nonsmokers with no history of significant medical illness, psychiatric disorder, or olfactory dysfunction. Fifty-two participants (40 women, age range: 18–39) gave informed consent as approved by the Northwestern University Institutional Review Board. All subjects participated in an initial screening session on day 0, which comprised an odor intensity rating task and an odor discrimination task. Thirty-four subjects who reached 70% accuracy on the odor discrimination task entered four consecutive days of behavioral training with an odor prediction task on days 1–4. Twenty-five of them who reached 60% on at least one training day then took part in an fMRI scan with the same prediction task on day 5.
METHOD DETAILS
Odor stimuli and delivery
Two monomolecular odorants, β-pinene (pine smell) and isoamyl acetate (banana smell) were diluted in mineral oil and matched for intensity. Odors were delivered using a custom-built air-dilution olfactometer. In the odor intensity rating task, subjects rated each pure odorant at 6 different levels of air-diluted concentrations (0%, 14.5%, 19.5%, 27%, 36.5%, and 50%). In the odor discrimination and odor prediction tasks, the two odorants, at each of the 6 concentrations, were combined into 36 different pine-banana mixtures. Each mixture represented a location in a 6 × 6 2-D odor space. Clean (odorless) or odorized air was directed toward subjects via Teflon tubing at a rate of 4L/min. Subjects were cued to sniff for the odors upon viewing instructions on a computer screen.
Odor intensity rating and odor discrimination task
On the screening day, subjects first rated 6 concentrations (3 trials per concentration) of pure pine odorant and pure banana odorant on a linear visual analog scale (anchors “not detectable” and “extremely strong,” from 0–10). Next, they performed an odor discrimination task with the pine-banana mixtures. In the discrimination task, subjects were cued to smell two odor mixtures consecutively, and were prompted to respond whether the second odor has “more pine (or banana)” or “less pine (or banana),” compared to the first odor. During half of the trials (72 in total) they were asked to focus on discriminating pine, and the other half of trials on discriminating banana. They did not know which component they would be asked about until the choice options appeared on the screen after the second odor. The stimulus set was drawn from the “hard” trials used in the odor prediction task (see below), to ensure that subjects can perceptually discriminate between on-trajectory and off-trajectory odors spaced only 15° away from each other.
Odor prediction task
On training days 1–4 and the scanning day 5, subjects performed an odor prediction task. This task was designed to be analogous to those in virtual spatial navigation (Constantinescu et al., 2016; Doeller et al., 2010). The basic idea was that subjects would first smell an initial “start” odor, then mentally navigate to an “end” odor based on instructive visual cues, and finally smell a second odor, reporting whether it corresponded to their mental prediction. Subjects were familiarized on the task with a set of 16 practice trials prior to training day 1.
At the start of a trial, subjects viewed a screen display showing two vertically oriented scale bars, one labeled “PINE” and the other labeled “BANANA” (Figure 1D, timeline 0–3 s). Verbal labels were placed alongside the scales: “no change” at the midpoint, and “more” and “less” at the endpoints of the scales. The labels “more” and “less” referred to the amounts of intensity change to be expected from the first sniff (first odor) to the second sniff (second odor). After viewing the scale, subjects were cued to smell an initial “start” odor (timeline 3–5 s) and instructed to pay attention to the intensities of pine and banana components in the mixture. The next part of the task was designed to encourage mental navigation in the odor space, whereby instructive cues in the visual scale bars specified the movement trajectories for a given trial. First, two bars appeared at the midpoints of each scale (“no change”), and subjects watched these bars move up and/or down along the two scales for 3 s (timeline 5–8 s), indicating proportional changes of the two odor components (in relation to the initial start odor). The further that each bar moved away from the midpoint, the more the respective odor component would be expected to change. In an imagination phase of the task, the same screen remained for another 3 s (timeline 8–11 s) as subjects actively imagined what the end odor would smell like, based on the start odor and the movements of the bars. Finally, subjects were cued to smell a second (end) odor (timeline 11–13 s), and pressed a button indicating whether they thought the end odor was on-trajectory (“YES”) or off-trajectory (“NO”). Half of the end odors were on-trajectory and half were off-trajectory. Among off-trajectory odors, there were three “difficulty levels”: easy, medium, and hard. The direction of the off-trajectory was 60° ± 5° away from the on-trajectory in easy trials, 30 ± 5° in medium trials, and 15° ± 5° in hard trials. Subjects received feedback after their response. Another 8 s passed before the next trial began. There were 72 trials per training day, and 4–6 fMRI runs (24 trials per run) on the scanning day.
Our definition of “trial difficulty” referred to the moment after completion of the imagination phase of the trial, when subjects are presented with actual odor 2 (end odor) and need to decide whether this odor corresponded to their imagined trajectory. This is the point at which a given trial could be considered easy, medium, or hard in difficulty: easy trials were those where the actual odor 2 appeared at a 60° offset away from the imagined trajectory (and thus was more discriminable); medium trials, at a 30° offset; and hard trials, at a 15° offset. In terms of the trial structure of the task, subjects were first asked to imagine their perceptual trajectory from odor 1 (start odor) to odor 2 (end odor). In this way, during the imagination period of the trial, any given trajectory was no more “easy” or “difficult” for the subjects than other trajectories, and thus each movement direction was sampled with the same difficulty. Of course, there were exceptions, including trials where the translation from odor 1 to odor 2 involved moving in only one of the two cardinal axes (e.g., 20% pine and 40% banana to 20% pine/80% banana), or trials involving shorter translation distances. Follow-up analyses of task difficulty can be found in the Results section, “Olfactory grid-like representations in entorhinal cortex are not driven by mere differences in stimulus discriminability or task difficulty.”
Note, across trials, the “more” and “less” labels randomly switched between top and bottom positions, and the “PINE” and “BANANA” labels randomly alternated between left and right sides of the visual display. With this randomization, imagined movement within the 2-dimensional odor space could be dissociated from mere visual cues and directional translations of the scale bars and labels.
Odor navigation index
The performance accuracy of the prediction task depended on two factors: subjects’ ability to make fine perceptual discriminations between pairs of closely related odor mixtures, and their memory ability to navigate to the designated location on the odor map. The former sets the upper limit of their prediction accuracy, and the latter is what we would like to capture. It is important to note that performance accuracy is intrinsically limited by the subjects’ ability to make fine perceptual discriminations between pairs of closely related odor mixtures (where average discrimination accuracy across subjects was 77%). This means that even if subjects can perfectly navigate through the odor space, their performance (on average) will be at a ceiling level of 77% due to their intrinsic limitations in discrimination acuity. Therefore, we adjusted the prediction performance by the discrimination performance to derive an odor navigation measure. We calculated the sensitivity index d’ of discrimination and prediction tasks to account for response bias (Macmillan and Creelman, 1990). The odor navigation index was computed as prediction d’ divided by discrimination d’.
Respiratory recording and analysis
During scanning, breathing activity was monitored using an MRI-compatible respiration transducer for MRI (BIOPAC Systems) affixed around subjects’ torso and recorded using PowerLab (ADInstruments). Breathing traces from each run were smoothed with a low-pass FIR filter (cutoff frequency at 2 Hz) and scaled to have a mean of 0 and standard deviation of 1 (Howard et al., 2016). The cued sniff waveforms were extracted from each trial. Inhalation duration and volume were computed and used as nuisance regressors in statistical modeling of the fMRI data (see below).
fMRI acquisition
Gradient-echo T2*-weighted echo-planar images (EPI) were acquired on a Siemens 3T Prisma scanner with the following parameters: repetition time (TR) = 2000 ms, echo time (TE) = 22 ms, flip angle = 80°, matrix size = 104 3 98 voxels, field of view (FoV) = 208 mm, voxel size = 2 × 2 × 2 mm3, 58 slices per volume. The slice angle was set 15° relative to the anterior-posterior commissure line to minimize signal dropout in the basal frontal areas of the brain (Deichmann et al., 2003; Weiskopf et al., 2006). In addition, a field map with dual echo-time images was acquired for geometric distortion correction of the EPI functional scans, with the following parameters: TR = 555 ms, TE1 = 4.92 ms, TE2 = 7.38 ms, flip angle = 50°, FoV = 208 mm, voxel size = 2 × 2 × 2 mm3. A 0.8 × 0.8 × 0.8 mm3 T1-weighted structural MRI scan was also obtained to facilitate normalization of EPIs into standard space and to define piriform cortex and entorhinal cortex ROI.
Image pre-processing
fMRI data were pre-processed with SPM12 software (https://www.fil.ion.ucl.ac.uk/spm12/) in MATLAB. Functional images were spatially realigned to the first image in the time series, and were corrected for movement-related variance based on the field map and movement-by-distortion interactions using the Unwarp tool in SPM (Andersson et al., 2001; Hutton et al., 2002). The T1 structural image was co-registered to the mean aligned functional image, and underwent segmentation and spatial normalization to MNI space. Realigned functional images were normalized using the transformation parameters derived from the structural image normalization. Finally, the normalized functional images were smoothed with a 6mm full-width half-maximum Gaussian kernel. For multivariate pattern analysis of the entorhinal cortex, as well as for the whole-brain searchlight analysis, images were smoothed with a 2mm kernel.
Univariate analysis in whole brain
After pre-processing, we modeled fMRI time series using a set of general linear models (GLMs). All models included regressors for the main effects of the movement-and-imagination period (red box in Figure 1C), parametric modulators of this period (see below), start odor and end odor periods, the response event, and nuisance regressors to account for head movement and differential sniff sizes. All main regressors were convolved with the canonical hemodynamic response function (HRF) in SPM. Nuisance regressors included the following: six movement parameters derived from spatial realignment, their squares, derivatives, and squares of derivatives (24 in total), within-volume slice variance and odd-versus-even slice differences, their derivatives and squares (to account for within-scan motion), breathing trace, trial-by-trial sniff volume and duration convolved with HRF and orthogonalized with the sniff events.
Additional regressors were included when needed to model individual volumes that exhibited excessive head motion. An individual volume was defined as “excessive” head motion if one of 10 motion-correction parameters exceeded 6 SD (of the mean) from one volume to the next volume. Such volumes were excluded by modeling these events as nuisance regressors in the GLM. On average, 12 volumes (range, 4–57) were excluded from each subject, out of a total of 2,100 fMRI volumes (350 volumes per session, 6 sessions) acquired during the experiment. Note, for two subjects, one entire session was excluded from fMRI analysis because more than 30 volumes from a single session (about 9% of the session) were identified as having excessive head motion. Data were high-pass filtered at 1/128 Hz, and temporal autocorrelation was adjusted using an AR(1) process.
GLM1: functional localizer for hexagonal modulation
See Figure 3C. GLM1 was used as the first step to localize brain areas that showed the strongest hexagonal modulation. This analysis searched for brain areas where fMRI activity profiles fit a waveform of cos(6(θ-φ)), where θ is the movement trajectory direction on each trial, φ is the hypothetical axis angle of the grid field, and the factor 6 gives a 6-fold periodicity. According to the angle difference formula for cosine:
the cosine term on the left side of the equation (a sinusoid with angle modulation) can be decomposed into two amplitude-modulated sinusoids, cos6θ and sin6θ. Therefore, we created two parametric modulators for the regressor of the movement-and-imagination period (Doeller et al., 2010): cos(6θ) and sin(6θ). We used an F-test to search for brain areas where the linear combination of the two parameter estimates (βcos and βsin) produced the largest amplitude. We transformed the F-statistic to a Z-statistic in each subject (Hughett, 2007), and performed a 1-sample t test across the group. To test an alternative 4-fold periodicity corresponding to a square grid, we included parametric modulators of both 4-fold and 6-fold in the same GLM.
Note that the main purpose of GLM1 was to serve as a functional localizer to identify brain regions for subsequent cross-validation analysis (GLM2; see next section). However, statistical analyses of hexagonally modulated vmPFC activity in Figures 3C and 3D (derived from GLM1) should be interpreted with care. As discussed in Constantinescu et al. (2016), because of temporal autocorrelations that naturally occur in fMRI time-series data, within-subject variance at the first level of analysis can be underestimated. As such, analysis of variance (ANOVA) models to estimate six-fold symmetry can lead to an overestimation of the F-statistic at the first level, which in turn will lead to an inflated Z-score, biasing the group-level effect. Given that a direct comparison of odor versus visual trajectories (Figure 3D), both of which shared the same autocorrelation structure, revealed significant effects, we believe that statistical overestimation was not a problem. Nevertheless, these considerations formed part of our rationale for conducting cross-validation analyses (GLM2) to obtain unbiased estimates of group-wise effects.
GLM2: iterative cross-validation analysis in vmPFC
See Figure 3E. To test whether the 6-fold symmetry was robust and reproducible in vmPFC, we performed a leave-one-run-out cross-validation analysis. Each subject completed 4–6 scanning runs. First, per subject, we performed GLM1 on all but one scanning run of the data (“training data”), and estimated grid angle φ for each voxel within the vmPFC ROI (cluster threshold, p < 0.001). To this end, we averaged the parametric modulator estimates (betas; β) across all voxels in the ROI, then calculated φ as the angular coordinate mapped from Cartesian coordinates (βcos, βsin), divided by 6 (Doeller et al., 2010). We then performed a new GLM2 on the left-out run of the data (“test data”). In GLM2, we aligned the trajectory direction θ to each individual subject’s grid angle φ, and separated all directions into 12 bins of every 30° around the unit circle. We created 12 regressors for trials that belonged to each bin. At the group level, we extracted the 12 parameter estimates from the vmPFC ROI, and tested whether the resulting betas of aligned directions (0° mod 60°) were higher than misaligned directions (30° mod 60°). In the control analysis of 4-fold periodicity, we used the same approaches as above, but estimated φ with factor 4 and separated all conditions into 8 bins of every 45°.
GLM3: interregional consistency angle
See Figure 3H. This analysis was similar to GLM2, except that the grid angle φ was estimated from all runs from the vmPFC ROI. Of note, there was no consistency of the preferred grid angle φ across subjects (Figure S3B). After modeling 12 trajectory directions, we extracted the parameter estimates from anatomically defined ROIs of entorhinal cortex (ERC), anterior piriform cortex (APC), and posterior piriform cortex (PPC). We used an ERC mask in MNI space available online from a study using high-resolution 7-T MRI (Maass et al., 2015). APC and PPC were manually outlined with reference to a human brain atlas (Mai et al., 1997) using MRIcron software (https://www.mccauslandcenter.sc.edu/mricro/mricron/). For each of the ROIs, we tested whether trials with directions aligned to vmPFC φ evoked higher activities than ones with misaligned directions.
Multi-voxel pattern analysis in entorhinal cortex
See Figure 5B. MVPA offers greater sensitivity to capture distributed signals in the brain compared to traditional univariate approaches (Norman et al., 2006), which is particularly important in ERC, a brain region that is susceptible for distortion and signal drop-out in fMRI recordings. For this analysis, a trial-by-trial GLM was specified for the movement-and-imagination period of each trial separately from 2mm smoothed functional images. To account fully for all variables in the task, the model also included onset times for the start odor, the end odor, and the button response. Nuisance regressors were the same as those included in the univariate analyses. Following GLM estimation, we extracted single-trial β pattern vectors in each subject from each and every voxel within the ERC ROI (Figure 3G). One important aspect of this analysis was to realign individual trials according to their trajectory direction θ with respect to each subject’s preferred grid angle φ in vmPFC. By defining each individual’s own grid angle φ, rather than relying on angle-free MVPA methods, this approach can optimize sensitivity for identifying a 6-fold periodic signal from ERC pattern correlations between trials separated by 60° increments.
The MVPA procedure involved (a) estimating each subject’s grid angle (φ) from vmPFC; (b) using φ as a reference angle for determining whether the trajectory angle (θ) for a given trial was aligned to φ (at mod 60°); (c) using MVPA to obtain the linear pattern correlation between all pairs of aligned trials (at φ mod 60°), as well as between all pairs of aligned and misaligned trials (at φ mod 30°); and finally (d) testing the pattern difference in ERC between aligned and misaligned conditions. In this way, trials that were aligned to the ERC grid angle would exhibit higher pattern similarity than trials that were phase-misaligned (Figure S6). Importantly, we only considered pattern correlations where (at least) one of the trials is aligned to grid angle φ (at mod 60°). This way we excluded those comparisons where both trials were misaligned to φ, in which case both patterns would be low-signal high-noise.
Whole-brain MVPA searchlight analysis
A complementary searchlight-based multivoxel pattern analysis was conducted on normalized, 2mm-smoothed whole-brain images using the same method above. A radius of 2.45 voxels was used as the search sphere, and the resulting aligned versus misaligned pattern difference maps were smoothed with a 6mm Gaussian kernel prior to group comparison.
Comparing cross-voxel variance between vmPFC and ERC
To test the spatial variability in vmPFC and ERC, the raw data from the full time-series in vmPFC and ERC were each averaged across time to obtain an average raw response for each voxel. We then computed the variance across voxels, separately for vmPFC and ERC, on a subject-by-subject basis. By comparing cross-voxel variances between vmPFC and ERC, we found a similar pattern of results: voxel-wise variability was significantly lower in vmPFC than ERC (Wilcoxon sign rank test, Z = −3.81, p < 0.001).
Comparing fMRI signal quality between vmPFC and ERC
To clarify why the quadrature filter was unable to identify 6-fold (univariate) effects in ERC, we tested whether temporal signal-to-noise (tSNR) is a limiting factor in detecting grid-like representations in this region. The hypothesis was that subjects with weaker tSNR in ERC would also exhibit lower 6-fold effects in ERC. Specifically, for each subject, we computed the tSNR value (signal quality) for each voxel in ERC. Next, a 6-fold effect size (grid signal magnitude) was computed for each ERC voxel. These voxel-wise 6-fold effects were based on the univariate quadrature measure in each ERC voxel. We then computed the linear correlation between tSNR and the 6-fold effect across voxels, yielding one r value for each subject. Finally, we tested whether the correlation was significantly different from zero at the group level.
QUANTIFICATION AND STATISTICAL ANALYSIS
Error bars throughout figures are shown as mean ± SEM across subjects (n = 25). In figures showing the contrast of aligned versus misaligned conditions with 60° periodicity, bar plots were mean-corrected within subjects. The significance threshold was set at p < 0.05 one-tailed for testing brain areas showing effects of aligned > misaligned directions, as well as testing 6-fold > 4-fold periodicity, based on our directional hypotheses (Julian et al., 2018). Grid-angle distribution was tested for the Rayleigh test of circular non-uniformity using CircStat within MATLAB (Berens, 2009). Significance threshold was otherwise set at p < 0.05 two-tailed. Non-parametric tests were used in cases where normality was violated based on Lilliefors test.
In the correlation plot (Figure 6C) between navigation performance and grid-like coding in ERC, one data point exceeded 3 SD on the x axis. Therefore, we also used robust regression, a statistical technique that is relatively insensitive to the presence of outliers by accordingly down-weighting each observation point in the data by its deviation from the mean (Wager et al., 2005). According to a robust regression analysis (robustfit function in MATLAB), the correlation between navigation performance and ERC pattern strength remained significant (r = 0.48, p = 0.03). By comparison, the correlation between navigation performance and grid-like coding strength were not significant in vmPFC (r = 0.18, p = 0.38) or APC (r = 0.22, p = 0.28).
DATA AND SOFTWARE AVAILABILITY
Software used in the present study is listed in Key Resources Table.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Software and Algorithms | ||
| MATLAB R2015b | MathWorks | https://www.mathworks.com/ |
| SPM12 | The Wellcome Trust Centre for Neuroimaging | https://www.fil.ion.ucl.ac.uk/spm/software/spm12/ |
| f2z.m | Hughett, 2007 | https://www.jstatsoft.org/article/view/v023c01 |
| CircStat | Berens, 2009 | http://bethgelab.org/software/circstat/ |
Supplementary Material
Highlights.
How the human brain supports navigation in an odorous landscape is poorly understood
Subjects learn to orient within a 2D intensity space defined by two different odors
Odor navigation elicits grid-cell-like activity in prefrontal and entorhinal cortices
Findings suggest a mechanism by which the brain constructs olfactory cognitive maps
ACKNOWLEDGMENTS
We thank Tim Behrens and Alexandra Constantinescu at the University of Oxford and Russell Epstein at the University of Pennsylvania for helpful discussions. This work was supported by National Institute on Deafness and Other Communication Disorders (NIDCD) grant R01DC010014 to J.A.G.
Footnotes
SUPPLEMENTAL INFORMATION
Supplemental Information can be found online at https://doi.org/10.1016/j.neuron.2019.03.034.
DECLARATION OF INTERESTS
The authors declare no competing interests.
REFERENCES
- Andersson JL, Hutton C, Ashburner J, Turner R, and Friston K (2001). Modeling geometric deformations in EPI time series. Neuroimage 13, 903–919. [DOI] [PubMed] [Google Scholar]
- Banino A, Barry C, Uria B, Blundell C, Lillicrap T, Mirowski P, Pritzel A, Chadwick MJ, Degris T, Modayil J, et al. (2018). Vector-based navigation using grid-like representations in artificial agents. Nature 557, 429–433. [DOI] [PubMed] [Google Scholar]
- Bellmund JL, Deuker L, Navarro Schröder T, and Doeller CF (2016). Grid-cell representations in mental simulation. eLife 5, e17089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berens P (2009). CircStat: a MATLAB toolbox for circular statistics. J. Stat. Softw 31, 1–21. [Google Scholar]
- Boccara CN, Sargolini F, Thoresen VH, Solstad T, Witter MP, Moser EI, and Moser MB (2010). Grid cells in pre- and parasubiculum. Nat. Neurosci 13, 987–994. [DOI] [PubMed] [Google Scholar]
- Bush D, Barry C, and Burgess N (2014). What do grid cells contribute to place cell firing? Trends Neurosci. 37, 136–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bush D, Barry C, Manson D, and Burgess N (2015). Using grid cells for navigation. Neuron 87, 507–520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catania KC (2013). Stereo and serial sniffing guide navigation to an odour source in a mammal. Nat. Commun 4, 1441. [DOI] [PubMed] [Google Scholar]
- Conover MR (2007). Predator-Prey Dynamics: The Role of Olfaction (CRC Press; ). [Google Scholar]
- Constantinescu AO, O’Reilly JX, and Behrens TEJ (2016). Organizing conceptual knowledge in humans with a gridlike code. Science 352, 1464–1468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deichmann R, Gottfried JA, Hutton C, and Turner R (2003). Optimized EPI for fMRI studies of the orbitofrontal cortex. Neuroimage 19, 430–441. [DOI] [PubMed] [Google Scholar]
- Diehl GW, Hon OJ, Leutgeb S, and Leutgeb JK (2017). Grid and nongrid cells in medial entorhinal cortex represent spatial location and environmental features with complementary coding schemes. Neuron 94, 83–92.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doeller CF, Barry C, and Burgess N (2010). Evidence for grid cells in a human memory network. Nature 463, 657–661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fyhn M, Hafting T, Treves A, Moser MB, and Moser EI (2007). Hippocampal remapping and grid realignment in entorhinal cortex. Nature 446, 190–194. [DOI] [PubMed] [Google Scholar]
- Giessel AJ, and Datta SR (2014). Olfactory maps, circuits and computations. Curr. Opin. Neurobiol 24, 120–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gire DH, Kapoor V, Arrighi-Allisan A, Seminara A, and Murthy VN (2016). Mice develop efficient strategies for foraging and navigation using complex natural stimuli. Curr. Biol 26, 1261–1273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hafting T, Fyhn M, Molden S, Moser MB, and Moser EI (2005). Microstructure of a spatial map in the entorhinal cortex. Nature 436, 801–806. [DOI] [PubMed] [Google Scholar]
- Hales JB, Schlesiger MI, Leutgeb JK, Squire LR, Leutgeb S, and Clark RE (2014). Medial entorhinal cortex lesions only partially disrupt hippocampal place cells and hippocampus-dependent place memory. Cell Rep. 9, 893–901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardcastle K, Maheswaranathan N, Ganguli S, and Giocomo LM (2017). A multiplexed, heterogeneous, and adaptive code for navigation in medial entorhinal cortex. Neuron 94, 375–387.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horner AJ, Bisby JA, Zotow E, Bush D, and Burgess N (2016). Grid-like processing of imagined navigation. Curr. Biol 26, 842–847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard JD, Kahnt T, and Gottfried JA (2016). Converging prefrontal pathways support associative and perceptual features of conditioned stimuli. Nat. Commun 7, 11546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughett P (2007). Accurate computation of the F-to-z and t-to-z transforms for large arguments. J. Stat. Softw 23, 1–5. [Google Scholar]
- Hutton C, Bork A, Josephs O, Deichmann R, Ashburner J, and Turner R (2002). Image distortion correction in fMRI: a quantitative evaluation. Neuroimage 16, 217–240. [DOI] [PubMed] [Google Scholar]
- Jacobs LF (2012). From chemotaxis to the cognitive map: the function of olfaction. Proc. Natl. Acad. Sci. USA 109 (Suppl 1 ), 10693–10700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobs J, Weidemann CT, Miller JF, Solway A, Burke JF, Wei XX, Suthana N, Sperling MR, Sharan AD, Fried I, and Kahana MJ (2013). Direct recordings of grid-like neuronal activity in human spatial navigation. Nat. Neurosci 16, 1188–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobs LF, Arter J, Cook A, and Sulloway FJ (2015). Olfactory orientation and navigation in humans. PLoS ONE 10, e0129387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Julian JB, Keinath AT, Frazzetta G, and Epstein RA (2018). Human entorhinal cortex represents visual space using a boundary-anchored grid. Nat. Neurosci 21, 191–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerr KM, Agster KL, Furtak SC, and Burwell RD (2007). Functional neuroanatomy of the parahippocampal region: the lateral and medial entorhinal areas. Hippocampus 17, 697–708. [DOI] [PubMed] [Google Scholar]
- Killian NJ, Jutras MJ, and Buffalo EA (2012). A map of visual space in the primate entorhinal cortex. Nature 491, 761–764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kunz L, Schröder TN, Lee H, Montag C, Lachmann B, Sariyska R, Reuter M, Stirnberg R, Stöcker T, Messing-Floeter PC, et al. (2015). Reduced grid-cell-like representations in adults at genetic risk for Alzheimer’s disease. Science 350, 430–433. [DOI] [PubMed] [Google Scholar]
- Langston RF, Ainge JA, Couey JJ, Canto CB, Bjerknes TL, Witter MP, Moser EI, and Moser MB (2010). Development of the spatial representation system in the rat. Science 328, 1576–1580. [DOI] [PubMed] [Google Scholar]
- Maass A, Berron D, Libby LA, Ranganath C, and Düzel E (2015). Functional subregions of the human entorhinal cortex. eLife 4, e06426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macmillan NA, and Creelman CD (1990). Response bias: characteristics of detection theory, threshold theory, and “nonparametric” indexes. Psychol. Bull 107, 401–413. [Google Scholar]
- Mai JK, Assheuer J, and Paxinos G (1997). Atlas of the Human Brain (Academic Press; ). [Google Scholar]
- Marozzi E, Ginzberg LL, Alenda A, and Jeffery KJ (2015). Purely translational realignment in grid cell firing patterns following nonmetric context change. Cereb. Cortex 25, 4619–4627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nau M, Navarro Schröder T, Bellmund JLS, and Doeller CF (2018). Hexadirectional coding of visual space in human entorhinal cortex. Nat. Neurosci 21, 188–190. [DOI] [PubMed] [Google Scholar]
- Norman KA, Polyn SM, Detre GJ, and Haxby JV (2006). Beyond mindreading: multi-voxel pattern analysis of fMRI data. Trends Cogn. Sci 10, 424–430. [DOI] [PubMed] [Google Scholar]
- Papi F (1991). Orientation in birds. Olfactory navigation. EXS 60, 52–85. [PubMed] [Google Scholar]
- Porter J, Craven B, Khan RM, Chang SJ, Kang I, Judkewitz B, Volpe J, Settles G, and Sobel N (2007). Mechanisms of scent-tracking in humans. Nat. Neurosci 10, 27–29. [DOI] [PubMed] [Google Scholar]
- Rajan R, Clement JP, and Bhalla US (2006). Rats smell in stereo. Science 311, 666–670. [DOI] [PubMed] [Google Scholar]
- Reinhard J, Srinivasan MV, and Zhang S (2004). Olfaction: scent-triggered navigation in honeybees. Nature 427, 411. [DOI] [PubMed] [Google Scholar]
- Rennó-Costa C, and Tort ABL (2017). Place and grid cells in a loop: implications for memory function and spatial coding. J. Neurosci 37, 8062–8076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanders H, Rennó-Costa C, Idiart M, and Lisman J (2015). Grid cells and place cells: an integrated view of their navigational and memory function. Trends Neurosci. 38, 763–775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sargolini F, Fyhn M, Hafting T, McNaughton BL, Witter MP, Moser MB, and Moser EI (2006). Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science 312, 758–762. [DOI] [PubMed] [Google Scholar]
- Schiller D, Eichenbaum H, Buffalo EA, Davachi L, Foster DJ, Leutgeb S, and Ranganath C (2015). Memory and space: towards an understanding of the cognitive map. J. Neurosci 35, 13904–13911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stensola H, Stensola T, Solstad T, Frøland K, Moser MB, and Moser EI (2012). The entorhinal grid map is discretized. Nature 492, 72–78. [DOI] [PubMed] [Google Scholar]
- Thesen A, Steen JB, and Døving KB (1993). Behaviour of dogs during olfactory tracking. J. Exp. Biol 180, 247–251. [DOI] [PubMed] [Google Scholar]
- Vickers NJ, Christensen TA, Baker TC, and Hildebrand JG (2001). Odour-plume dynamics influence the brain’s olfactory code. Nature 410, 466–470. [DOI] [PubMed] [Google Scholar]
- Wager TD, Keller MC, Lacey SC, and Jonides J (2005). Increased sensitivity in neuroimaging analyses using robust regression. Neuroimage 26, 99–113. [DOI] [PubMed] [Google Scholar]
- Wallraff HG (2000). Simulated navigation based on observed gradients of atmospheric trace gases (Models on pigeon homing, part 3). J. Theor. Biol 205, 133–145. [DOI] [PubMed] [Google Scholar]
- Weiskopf N, Hutton C, Josephs O, and Deichmann R (2006). Optimal EPI parameters for reduction of susceptibility-induced BOLD sensitivity losses: a whole-brain analysis at 3 T and 1.5 T. Neuroimage 33, 493–504. [DOI] [PubMed] [Google Scholar]
- Welge-Lussen A, Looser GL, Westermann B, and Hummel T (2014). Olfactory source localization in the open field using one or both nostrils. Rhinology 52, 41–47. [DOI] [PubMed] [Google Scholar]
- Wikenheiser AM, and Schoenbaum G (2016). Over the river, through the woods: cognitive maps in the hippocampus and orbitofrontal cortex. Nat. Rev. Neurosci 17, 513–523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wills TJ, Cacucci F, Burgess N, and O’Keefe J (2010). Development of the hippocampal cognitive map in preweanling rats. Science 328, 1573–1576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witter MP, Doan TP, Jacobsen B, Nilssen ES, and Ohara S (2017). Architecture of the entorhinal cortex a review of entorhinal anatomy in rodents with some comparative notes. Front. Syst. Neurosci 11, 46. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Software used in the present study is listed in Key Resources Table.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Software and Algorithms | ||
| MATLAB R2015b | MathWorks | https://www.mathworks.com/ |
| SPM12 | The Wellcome Trust Centre for Neuroimaging | https://www.fil.ion.ucl.ac.uk/spm/software/spm12/ |
| f2z.m | Hughett, 2007 | https://www.jstatsoft.org/article/view/v023c01 |
| CircStat | Berens, 2009 | http://bethgelab.org/software/circstat/ |


