A CD-based mapping method for combining multiple related parameters from heterogeneous intervention trials

Abstract

Effect size can differ as a function of the elapsed time since treatment or as a function of other key covariates, such as sex or age. In evidence synthesis, a better understanding of the precise conditions under which treatment does work or does not work well has been highly valued. With increasingly accessible individual patient or participant data (IPD), more precise and informative inference can be within our reach. However, simultaneously combining multiple related parameters across heterogeneous studies is challenging because each parameter from each study has a specific interpretation within the context of the study and other covariates in the model. This paper proposes a novel mapping method to combine study-specific estimates of multiple related parameters across heterogeneous studies, which ensures valid inference at all inference levels by combining sample-dependent functions known as Confidence Distributions (CD). We describe the “CD-based mapping method” and provide a data application example for a multivariate random-effects meta-analysis model. We estimated up to 13 study-specific regression parameters for each of 14 individual studies using IPD in the first step, and subsequently combined the study-specific vectors of parameters, yielding a full vector of hyperparameters in the second step of meta-analysis. Sensitivity analysis indicated that the CD-based mapping method is robust to model misspecification. This novel approach to multi-parameter synthesis provides a reasonable methodological solution when combining complex evidence using IPD.

1. INTRODUCTION

Meta-analysis is a well-established statistical procedure for quantitatively synthesizing evidence from independent studies [43]. In recent years, meta-analysis has increasingly been discussed as an important research method to strengthen statistical inference [25]. Compared to traditional, standard meta-analysis of aggregate data (AD), meta-analysis of individual patient or participant data (IPD) in a one-step or two-step approach [49] or in a one-step, simultaneous “integrative data analysis” (IDA) of IPD [8, 24] represents a major innovation, which can expand the scope of evidence synthesis and produce clinically most meaningful results. When IPD are available, the same model can be applied across all studies, ensuring that the combined data have the same interpretation. In addition, it is possible to address more complex research questions with more appropriate and sophisticated models. Overall, meta-analysis of IPD provides unparalleled flexibility for analysts. At the same time, it is challenging to combine IPD from heterogeneous trials because they differ in key study features, including designs, populations, measures, or settings [20, 53]. For example, with respect to different measures, a commonly used screening equipment in medical settings may not always be available in other locations. Furthermore, longitudinal clinical trials included in a meta-analysis typically differ in their study duration and follow-up frequency and period [32, 57]. It is also not uncommon that binary or categorical covariates may not have any variability either by design (e.g., a study of all women) or naturally in a data set [11, 33]. Any one of these situations can pose significant estimation challenges for an IPD meta-analysis because they essentially represent study-level missing data. Typically, IPD meta-analysis applications have included a subset of studies that have all covariates or used a simpler model with a fewer number of covariates, either of which essentially deletes partially available data (i.e., listwise deletion) and represents an important loss of information, precision, power, and generalizability.

We propose a new information combination method that combines confidence distributions, hereon called the “CD-based approach” [59]. A confidence distribution (CD) is a sample-dependent distribution function that contains information about confidence intervals of a parameter of interest at all levels. It can be referred to as a confidence density if presented in a density function form [34]. This new method has been demonstrated as a powerful inference tool in connection with meta-analysis [6, 34, 60, 62]. The current study extends the CD-based approach to a multivariate random-effects meta-analysis model, which is based on more reasonable assumptions but computationally more challenging, compared with a multivariate fixed-effects meta-analysis model [34]. The current work, which explicitly accommodates heterogeneous designs and partial information, also provides a more general framework than the existing model [63] for random-effects meta-analysis models.

To implement the CD-based approach, we utilize a “two-step” IPD meta-analysis approach [54]. We proceed as follows. First, we identify an underlying “full” model for all studies included in a meta-analysis and conduct separate analyses for each study to obtain study-specific parameter estimates. Second, we identify appropriate connections between the expectation of study-specific vectors of parameters and the hyperparameters of the full model via appropriately identified “mapping” matrices. We subsequently estimate all hyperparameters of the full model in a multivariate random-effects meta-analysis model. Upon obtaining all hyperparameters, we can flexibly derive any relevant population-level inferences as needed (e.g., different treatment effect sizes for men vs. women).

The rest of this paper has four main sections. Section 2 discusses the data set that motivated the CD-based mapping method. Section 3 introduces the method in greater detail. Section 4 presents the findings, including those from sensitivity analyses. We conclude this paper with discussion in Section 5.

2. MOTIVATING DATA

The current study was motivated by Project INTEGRATE [37]. Project INTEGRATE obtained de-identified, item-level IPD from 24 trials through a network of interested collaborators. All trials tested the efficacy of brief motivational interventions (BMIs) to reduce excessive alcohol use and prevent harm among college students. Typical BMIs are brief, and provide personalized feedback on alcohol use and alcohol-related problems, as well as general educational information on alcohol.

2.1. Intervention and control groups

IPD for the current analysis come from 7,996 participants from 14 trials at baseline after excluding studies featuring a single intervention (i.e., no comparison group) or unique interventions, resulting in 10 stand-alone, personalized feedback intervention (“PF”) groups; eight in-person motivational intervention with personalized normative feedback profile (“MI + PF”) groups; and 13 no-treatment control (“Control”) groups. Note that studies 13 and 14 were originally independent trials but were subsequently collapsed (designated as study 13/14), given their similarities in study design characteristics and small samples. In addition, no systematic differences existed across intervention groups at baseline for studies 13 and 14. Tables 1 and 2, as well as Figure 1, provide an overview of all studies and descriptive statistics. With the exception of one study (study 1), all remaining 13 studies had a control group. Eleven of the 13 studies had an assessment-only control group, and the remaining two studies (studies 18 and 20) had a control group who received a single page information sheet containing very limited, generally-written information about alcohol use (e.g., alcohol has no nutritional value; space your drinks). Based on the quantitative content analysis of all intervention materials across groups, we determined that the exposure for the latter two groups was essentially the same as what other 11 control groups received [40, 45].

Table 1.

Baseline and follow-up assessment schedule by study

	Time in months (0 = baseline)
Study	0	1	2	3	4	5	6	7	8	9	10	11	12
1	X				X								X
2	X		X				X
8a	X												X
8b	X												X
8c	X												X
9	X			X			X
10.1	X												X
11	X		X		X
12	X	X		X			X
13/14	X			X			X			X
18	X	X					X
20	X												X
21	X			X			X						X
22	X										X

Notes. “X” indicates that baseline or follow-up outcome data exist at that time.

Table 2.

Means, standard deviations in parentheses, and percentages of the variables by study

	Variable
Study	Man	White	First-year	PBS	AlcProb
1	60%	73%	62%	1.06(0.79)	0.21(0.72)
2	71%	69%	63%	1.01(0.84)	−0.60(0.72)
8a	33%	87%	50%	0.55(0.85)	−0.08(0.97)
8b	41%	62%	47%	0.57(0.89)	−0.11(1.00)
8c	38%	83%	36%	0.46(0.91)	0.02(0.94)
9	38%	73%	100%	0.42(0.77)	0.75(0.71)
10.1	46%	84%	100%	-	1.03(0.76)
11	59%	64%	100%	-	−0.82(0.95)
12	47%	93%	3%	−0.46(0.92)	0.39(0.60)
13/14	38%	95%	26%	-	1.08(0.51)
18	25%	89%	33%	0.49(0.88)	−0.17(0.96)
20	52%	84%	78%	-	0.62(0.83)
21	36%	85%	42%	0.36(0.92)	0.89(0.77)
22	43%	87%	100%	0.38(0.89)	−0.18(0.90)

Notes. Man (coded 1; 0 = woman), White (coded 1; non-White = 0), First-year (coded 1; 0 = non first-year). PBS = Estimated latent trait (θ) scores at baseline for utilizing protective behavioral strategies. AlcProb = Estimated latent trait scores at baseline for alcohol-related problems. “−” indicate that the variable was not assessed. The presented descriptive statistics were obtained from the entire study sample.

Figure 1.

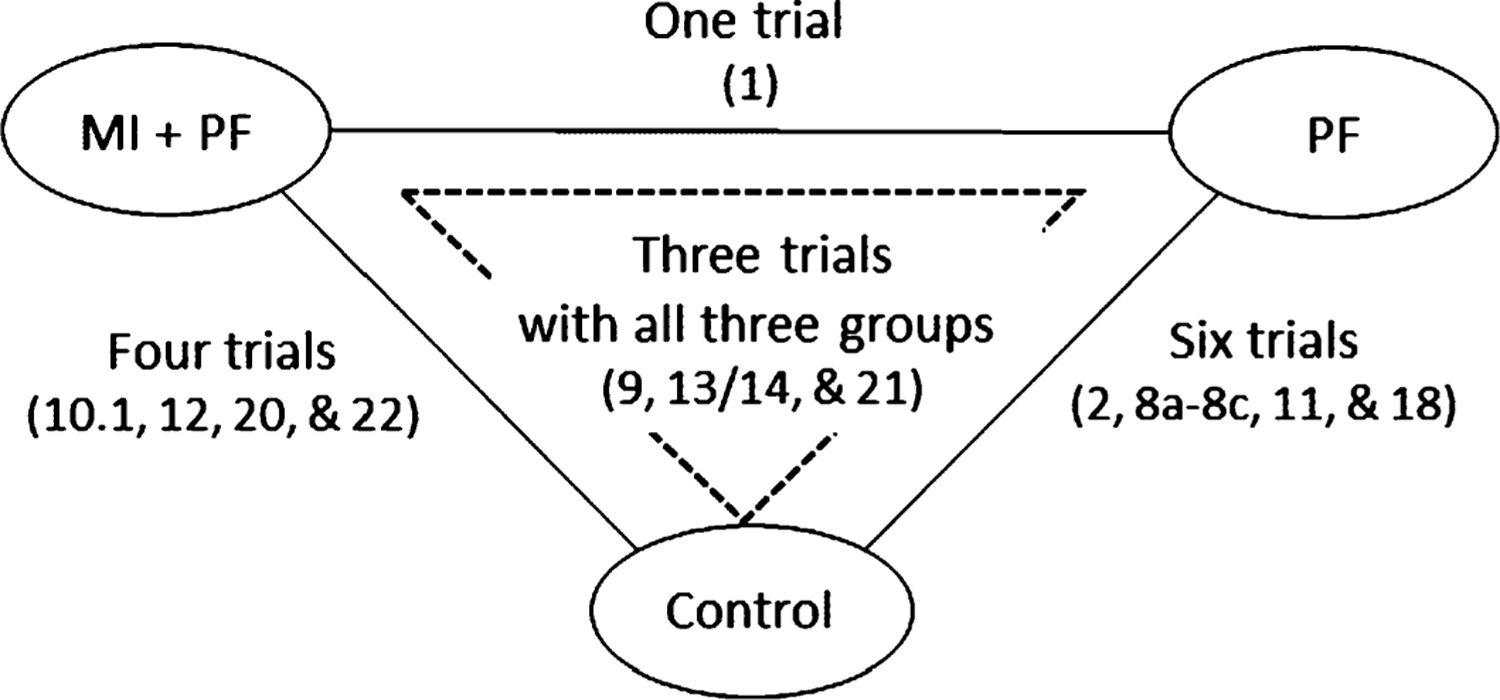
A diagram of the evidence network (numbers in parenthesis indicate studies).

2.2. Measures

We focus on alcohol-related problems (e.g., neglecting responsibilities; friends and relatives avoiding you) as the outcome variable of the current analysis. Because this outcome variable was assessed differently across studies (i.e., slightly differently worded items, different referent time frames, and response options), they could not be directly pooled. Therefore, we previously utilized a 2-parameter logistic item response theory (2-PL IRT) model to derive latent trait scores (called theta [θ] scores) in a separate hierarchical, multi-unidimensional IRT analysis using the Markov chain Monte Carlo algorithms that we specifically developed and validated for Project INTEGRATE [23]. Latent trait scores from IRT models can be interpreted with direct reference to item parameters, and are independent of which items that participants were tested on or who else was tested together [12]. IRT models are widely used in educational test settings to estimate latent trait (e.g., ability or severity) scores and increasingly utilized also for psychological and medical research [18]. The latent trait scores for one’s tendency to adopt protective behavioral strategies prior to, during, and after drinking to protect oneself from experiencing negative consequences from drinking [36], such as setting limits or alternating drinks, were estimated using a generalized partial credit IRT model [41] to accommodate polytomous responses [23, 37, 39]. The latent trait scores are estimated based on the assumption that the distribution follows a standard normal (i.e., an expected population mean of 0).

2.3. Motivating challenges

Example 1. Heterogeneity in study interventions. Figure 1 shows that there are up to three intervention arms in data. However, only three studies (studies 9, 13/14, and 21) have all three intervention groups, providing direct comparative evidence between three pairs of groups. The remaining 11 studies are two-arm trials, of which one did not have a control (study 1). The challenge that arises is how to draw valid inference regarding relative effectiveness of two competing interventions (i.e., “MI + PF” vs. “PF”) from the perspective of network meta-analysis [35], despite that we have (1) one missing treatment arm for 11 studies and (2) one study (i.e., study 1) without a control group. The latter condition results in several unique study-specific parameters, which require a “blueprint” directing how they can be related to study-specific parameters of other studies, and to their corresponding hyperparameters of the full model.

Example 2. Heterogeneity in the assessment of covariates. Studies 9, 10.1, 11, and 22 recruited exclusively first-year students. In these studies, study-specific parameters for first-year student status (coded 1 = first-year; 0 = other) are not estimable and cannot be linked directly to their counterpart from other studies or to the corresponding full model hyperparameter because the intercept parameters from these four studies would indicate the mean outcome level for their first-year students, assuming all study-specific covariates in the model are held constant (e.g., constrained to zero) within studies. In contrast, study-specific intercept parameters from the remaining 10 studies would reflect the mean outcome level of the students in 2nd year and above (i.e., referent demographic group) when all other covariates are held constant within studies. Therefore, the interpretation of the study-specific intercept parameters differs between studies due to the study design difference. Ignoring the study design difference would mean that the combined hyperparameter estimate for the intercept would be biased and/or not interpretable.

If one were to drop this covariate, the four studies with all first-year students would be retained in the analysis. However, first-year college students have higher levels of alcohol-related problems, compared with students in the second year and beyond. Due to their high risk status, the studies with only first-year students may have specific intervention content and different intervention effect sizes, compared with other studies that provide the same intervention for students across all years in college. If we exclude the studies that recruited exclusively first-year students, then resulting inferences would suffer from reduced power. Therefore, either option-excluding the covariate or the studies-can result in non-negligible loss of information and biased inference in a typical meta-analysis. Clearly, there is a need to properly separate the effect of interest from potential confounding effects when simultaneously combining multiple related parameters from heterogeneous studies.

Example 3. Availability of follow-up assessments. Some studies had a single post-intervention follow-up assessment, whereas others had at least two follow-up assessments within 12 months post intervention (see Table 1). Such between-study design differences can cause study-level missing data under certain full models. For example, if a true full model has a quadratic functional form, then it would require at least three data points over time to fit linear and quadratic terms in a longitudinal model. One may choose a simpler model that does not correctly reflect true change processes. Alternatively, one may limit the analysis to a subset of studies with a sufficient number of follow-up assessments. Neither option is optimal.

Note that the motivating challenges illustrated above do not represent a missing data problem within individual studies. However, when data from independently conducted studies are pooled in a meta-analysis, any between-study design heterogeneity, including differences in the number of treatment arms, comparison or control group, and lack of variability in covariates, can lead to a challenge in estimation and interpretation. In other words, study-specific parameters need to be made equivalent via “mapping” so that each study-specific parameter can be validly linked to the corresponding hyperparameter(s) of the full model. A multivariate CD-based approach provides a novel method, which incorporates mapping matrices in the estimation, for a multivariate fixed-effects or random-effects meta-analysis model.

3. METHODS

3.1. A mapping method with a CD-based meta-analysis approach

Consider k independent studies each with n_i observations for i = 1, ⋯ , k. First, we formulate a full model as a generalized linear mixed model. We assume a random-intercept model with a total of p − 1 covariates across k studies:

$$g\left(E\left(y_{ijt}\mid {\beta }_{di},u_{ij0}\right)\right)={\beta }_{0i}+{\beta }_{1i}{x}_{1ijt}+{\beta }_{2i}{x}_{2ijt}+{\beta }_{3i}{x}_{3ijt}+\cdots +{\beta }_{(p-1)i}{x}_{(p-1)ijt}+u_{ij0},$$

where g(·) is the link function, E(·) denotes expectation, and β_i = (β_0i, β_1i, β_2i, … , β_(p−1)i)^T represents a study-specific parameter vector. y_ijt indicates the outcome for participant j in study i at time t, and x_dijt is value of the d^th covariate for participant j in study i at time t, where β_di indicates the coefficient associated with the d^th covariate for study i with d = 0, ⋯ , p − 1. The term u_ij0 indicates a participant-specific random intercept effect. The link function is an identity link for a linear model with a continuous outcome. Other link functions can be specified depending on the distribution of outcomes [62].

The full model for the motivating example at the participant level is:

$$E\left(y_{ijt}\mid {\beta }_{di},u_{ij0}\right)={\beta }_{0i}+{\beta }_{1i}{\text{Man}}_{ijt}+{\beta }_{2i}{\text{White}}_{ijt}+{\beta }_{3i}{\text{First-year}}_{ijt}+{\beta }_{4i}{\text{PBS}}_{ijt}+{\beta }_{5i}{\text{PF}}_{ijt}+{\beta }_{6i}{(\text{MI}+\text{PF})}_{ijt}+{\beta }_{7i}{\text{Month}}_{ijt}+{\beta }_{8i}{\text{Month}}_{ijt}^2+{\beta }_{9i}{(\text{PF}\times \text{Month})}_{ijt}+{\beta }_{10i}{((\text{MI}+\text{PF})\times \text{Month})}_{ijt}+{\beta }_{11i}{\left(\text{PF}\times {\text{Month}}^2\right)}_{ijt}+{\beta }_{12i}{\left((\text{MI}+\text{PF})\times {\text{Month}}^2\right)}_{ijt}+u_{ij0},$$

where the terms Man, White, First-year, PF, and MI + PF are binary indicator variables; PBS and Month are continuous variables; and the rest of the terms are either interaction terms between the aforementioned ones and/or a quadratic form. Table 2 shows the descriptive statistics of all covariates.

Throughout Section 3, we denote b_i as the study-specific estimates of the corresponding Level-1 parameters β_i for study i, E(β_i) as the expectation of the study-specific vector of parameters at Level 1 (with dimension p_i, where p_i ≤ p), and β as the full vector of hyperparameters at Level 2 (with dimension p), respectively. We assume that a study-specific parameter vector β_i follows a multivariate normal distribution with mean β and covariance matrix Σ for a multivariate random-effects meta-analysis model, an extension of its univariate counterpart [43]. As long as the the expectation of study-specific parameters has the same interpretation across studies, we can directly fit the full model (i.e., without any mapping) and obtain the full vector of hyperparameter estimates β and its covariance matrix Σ as follows:

$$\text{ Level }1:b_i\mid {\mathit{\beta }}_i,S_i~{\text{MVN}}_{p_i}\left({\mathit{\beta }}_i,S_i\right)$$

$$\text{ Level }2:{\mathit{\beta }}_i\mid \mathit{\beta },\Sigma ~{\text{MVN}}_{p_i}(\mathit{\beta },\Sigma ),$$

where MVN_pi stands for the multivariate normal distribution with dimension p_i, S_i is the observed covariance matrix for study i, and Σ is the unknown between-study covariance matrix that needs to be estimated. With a set of heterogeneous studies (study i = 1, 2, ⋯ , k) and covariate d = 1, 2, ⋯ , p − 1, we additionally identify and adopt an appropriate study-specific mapping matrix M_i for study i where M_i is a p_i × p matrix, and obtain the full model as follows:

$$\text{ Level }1:b_i\mid {\beta }_i,S_i~{\text{MVN}}_{p_i}\left({\beta }_i,S_i\right)$$

$$\text{ Level }2:{\beta }_i\mid \beta ,\Sigma ~{\text{MVN}}_{p_i}\left(M_i\beta ,M_i\Sigma M_i^T\right).$$

We first obtain b_i for study-specific parameters β_i for study i in the first step. Next, we identify an appropriate mapping matrix M_i for study i and link all study-specific parameters to their corresponding hyperparameters of the full model in the second step. Let M_i be the mapping function for study i that links β_i to β: E(β_i) ≡ M_i (β). In a linear model, the relationship E(β_i) ≡ M_i (β) can typically be simplified to the following linear equation: E(β_i) ≡ M_iβ, where M_i is a p_i × p matrix.

3.2. Mapping matrix to connect study-specific parameters to hyperparameters

As an illustration, we show how to determine an appropriate mapping matrix connecting the study-specific parameter vector β_i to the hyperparameter vector β. Let us assume that we have a model of a continuous response variable y with two continuous covariates x₁ and x₂:

$$E\left(y_{ij}\mid {\beta }_i\right)={\beta }_{0i}+{\beta }_{1i}{x}_{1ij}+{\beta }_{2i}{x}_{2ij},$$

where subscripts i and j index study and participant, respectively. If study i has all the covariates required, then

$$M_i=\left[\begin{array}{lll}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill \end{array}\right].$$

In this case, study-specific parameters can be linked to the population hyperparameter vector directly in a standard multivariate random-effects meta-analysis model [26, 28]. However, consider a situation where β_2i cannot be estimated for study i because x_2i was not assessed by design. If we can assume that x₂ has an expected zero mean, then its average influence on the outcome would be zero, which can be reflected in the following mapping matrix:

$$M_i=\left[\begin{array}{lll}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill \end{array}\right].$$

Consequently, the resulting reduced vector of estimable parameters in this situation for study i (Level-1 parameters) would be E(β_i) = M_iβ = (β₀, β₁)^T.

If x₂ is a binary variable with a constant value (e.g., x_2i = 1) for study i, then β_2i cannot be estimated because there is no variability for that covariate. In this situation, a proper mapping matrix is

$$M_i=\left[\begin{array}{lll}1\hfill & 0\hfill & 1\hfill \\ 0\hfill & 1\hfill & 0\hfill \end{array}\right]$$

and

$$E\left({\beta }_i\right)=M_i\beta ={\left({\beta }_0+{\beta }_2,{\beta }_1\right)}^T.$$

The first term on the right side of the equation above indicates that the expectation of the intercept parameter β_0i cannot be directly linked to the corresponding hyperparameter β₀ of the full model. Rather, the expectation of β_0i, in the context of the full model, is linked to the sum of hyperparameters β₀ and β₂. In contrast, β_1i can be linked directly to its corresponding hyperparameter β₁. Since no variability exists for x₂ for study i, there is no β_2i.

Table 3 shows two mapping matrices for two different studies from the motivating data example. Table 4 shows covariate availability by study for the entire motivating data. Most studies have reduced sets of covariates, requiring mapping matrices. Let us consider a few specific mapping cases in the current study. The first motivating challenge example in Section 2.3 can be illustrated in this specific case (i.e., Mapping Pattern 1 in Table 3). Study 1 tested the efficacy of two BMIs (i.e., “MI + PF” and “PF”) without a no-treatment control group, whereas all other trials were two-arm or three-arm trials with a control group (see Figure 1).

Table 3.

Mapping matrix pattern. The pattern indices here correspond to the numbers shown in the last column in Table 4. Underlined elements indicate how the identity matrix was modified to link study-level parameters to hyperparameters

Covariate	0	1	2	3	4	5	6	7	8	9	10	11	12
Pattern 1 (Study 1)
0. Intercept1	1	0	0	0	0	1	0	0	0	0	0	0	0
1. Man (= 1 vs. woman = 0)	0	1	0	0	0	0	0	0	0	0	0	0	0
2. White (= 1 vs. nonwhite = 0)	0	0	1	0	0	0	0	0	0	0	0	0	0
3. First-year (= 1 vs. other = 0)	0	0	0	1	0	0	0	0	0	0	0	0	0
4. PBS at Baseline	0	0	0	0	1	0	0	0	0	0	0	0	0
5. PF1(= 1 vs. control = 0)	0	0	0	0	0	0	0	0	0	0	0	0	0
6. MI + PF1(= 1 vs. control = 0)	0	0	0	0	0	−1	1	0	0	0	0	0	0
7. LS	0	0	0	0	0	0	0	1	0	0	0	0	0
8. QS	0	0	0	0	0	0	0	0	1	0	0	0	0
9. LS × PF1	0	0	0	0	0	0	0	0	0	0	0	0	0
10. LS × (MI + PF)1	0	0	0	0	0	0	0	0	0	−1	1	0	0
11. QS × PF1	0	0	0	0	0	0	0	0	0	0	0	0	0
12. QS × (MI + PF)1	0	0	0	0	0	0	0	0	0	0	0	−1	1
Pattern 5 (Study 11)
0. Intercept	1	0	0	1	0	0	0	0	0	0	0	0	0
1. Man (= 1 vs. woman = 0)	0	1	0	0	0	0	0	0	0	0	0	0	0
2. White (= 1 vs. nonwhite = 0)	0	0	1	0	0	0	0	0	0	0	0	0	0
3. First-year (= 1 vs. other = 0)	0	0	0	0	0	0	0	0	0	0	0	0	0
4. PBS at Baseline	0	0	0	0	0	0	0	0	0	0	0	0	0
5. PF (= 1 vs. control = 0)	0	0	0	0	0	1	0	0	0	0	0	0	0
6. MI + PF (= 1 vs. control = 0)	0	0	0	0	0	0	0	0	0	0	0	0	0
7. LS	0	0	0	0	0	0	0	1	0	0	0	0	0
8. QS	0	0	0	0	0	0	0	0	1	0	0	0	0
9. LS × PF	0	0	0	0	0	0	0	0	0	1	0	0	0
10. LS × (MI + PF)	0	0	0	0	0	0	0	0	0	0	0	0	0
11. QS × PF	0	0	0	0	0	0	0	0	0	0	0	1	0
12. QS × (MI + PF)	0	0	0	0	0	0	0	0	0	0	0	0	0

Note.

¹indicate that study 1 had two treatment groups.

Table 4.

Estimable covariates for the underlying full model by study and by mapping matrix pattern

Study	N	Covariate position in the full model													Mapping matrix pattern
		0	1	2	3	4	5	6	7	8	9	10	11	12
1+	348	X	X	X	X	X	-	X	X	X	-	X	-	X	1
2	230	X	X	X	X	X	X	-	X	-	X	-	-	-
8a	1486	X	X	X	X	X	X	-	X	-	X	-	-	-	2
8b	2155	X	X	X	X	X	X	-	X	-	X	-	-	-
8c	600	X	X	X	X	X	X	-	X	-	X	-	-	-
9	302	X	X	X	-	X	X	X	X	X	X	X	X	X	3
10.1	348	X	X	X	-	-	-	X	X	-	-	X	-	-	4
11	383	X	X	X	-	-	X	-	X	X	X	-	X	-	5
12	167	X	X	X	X	X	-	X	X	X	-	X	-	X	6
13/14	109	X	X	X	X	-	X	X	X	X	X	X	-	X	7
18	215	X	X	X	X	X	X	-	X	X	X	-	X	-	8
20	928	X	X	X	X	-	-	X	X	-	-	X	-	-	9
21	216	X	X	X	X	X	X	X	X	X	X	X	X	X	10
22	509	X	X	X	-	X	-	X	X	-	-	X	-	-	11

Notes. “X” indicates estimable parameters whereas “−” indicates inestimable parameters. Covariate in the full model are (0) Intercept; (1) Man (= 1 vs. woman = 0); (2) White (= 1 vs. non-white = 0); (3) First-year (= 1 vs. other = 0); (4) PBS (Estimated latent trait (θ) scores for utilizing protective behavioral strategies) at Baseline; (5) PF (stand-alone personalized feedback intervention) (= 1 vs. control = 0); (6) MI + PF (in-person motivational intervention with personalized normative feedback profile) (= 1 vs. control = 0); (7) LS (Linear slope of time in month); (8) QS (Quadratic slope of time in month); (9) LS × PF (vs. control); (10) LS × (MI + PF) (vs. control); (11) QS × PF (vs. control); (12) QS × (MI + PF) (vs. control). N represents sample size at baseline. ⁺= Study 1 did not have a control group, thus, PF served as a comparison group.

In the context of a network meta-analysis [5, 29], the relative intervention benefit between two BMIs − “MI + PF” and “PF” − can be seen as follows: “MI + PF” vs. “PF” = ((MI + PF) − control) − (PF − control) = ((MI + PF) − PF). Therefore, the study-specific parameter of the relative intervention effect from study 1 can provide valuable information as long as its expectation can properly be aligned to match up with the hyperparameters for intervention effects.

To include data from study 1 in our meta-analysis and draw valid inference, we need to identify an appropriate mapping matrix to link E(β_i) to β. A mapping matrix for study 1 can be identified as follows. First, change the diagonal 1s from a 13 × 13 identity matrix into 0s in the 6^th, 10^th, and 12^th rows (numbered as covariates 5, 9, and 11 in Table 3). These three rows correspond to the three hyperparameters comparing PF with control (i.e., PF vs. control; [PF vs. control] × linear growth slope; and [PF vs. control] × quadratic growth slope, respectively). These rows are then removed. Second, change the first row to indicate that the intercept parameter from study 1 describes the study-specific average outcome response of PF, rather than control, in the context of the full model. Therefore, the expectation of the intercept parameter β_0i from study 1 corresponds to the sum of hyperparameters β₀ and β₅ at Level 2 and contributes to their estimation for the full model. Third, change the 8^th and 9^th rows (covariates 7 and 8 in Table 3) to indicate that the linear and quadratic slope parameters from study 1 represents the slope parameters for PF. Finally, contrast “MI + PF” against “PF” when applicable. The study-specific vector of Level-1 parameters for study 1 can be seen as

$${\left({\beta }_{0i},{\beta }_{1i},{\beta }_{2i},{\beta }_{3i},{\beta }_{4i},{\beta }_{6i},{\beta }_{7i},{\beta }_{8i},{\beta }_{10i},{\beta }_{12i}\right)}^T,$$

whose expectation can be linked to the full vector of hyperparameters β at Level 2 as follows:

$$\left(\begin{array}{l}{\beta }_0+{\beta }_5\hfill \\ {\beta }_1\hfill \\ {\beta }_2\hfill \\ {\beta }_3\hfill \\ {\beta }_4\hfill \\ -{\beta }_5+{\beta }_6\hfill \\ {\beta }_7+{\beta }_9\hfill \\ {\beta }_8+{\beta }_{11}\hfill \\ -{\beta }_9+{\beta }_{10}\hfill \\ -{\beta }_{11}+{\beta }_{12}\hfill \end{array}\right).$$

To provide another motivating challenge example (Example 2 in Section 2.3 & Mapping Pattern 5 in Table 3), study 11 exclusively recruited first-year students, did not assess protective behavioral strategies at baseline, and tested the efficacy of PF against a control in a two-arm trial. Therefore, to map the expectation of estimable parameters from study 11 into the full hyperparameter vector, the rows of an identify matrix corresponding to these variables should be modified (Table 3). The first row of the mapping matrix are modified to indicate that the expectation of the intercept parameter from study 11 is the average outcome of first-year students in the context of the full model. The row for PBS can be removed because the estimated PBS trait scores follows a standard normal distribution with an expected population mean of 0. We expect that the omission of this row for missing PBS does not influence the mean model part of the full model, although the variation surrounding the mean may influence the error part of the model. The resulting vector of study-specific parameters for study 11 and its expectation E(β_i) can be linked to β as follows:

$${\left({\beta }_0+{\beta }_3,{\beta }_1,{\beta }_2,{\beta }_5,{\beta }_7,{\beta }_8,{\beta }_9,{\beta }_{11}\right)}^T.$$

A reduced model is analyzed separately and sequentially for each study. At this step, we save study-specific regression parameter estimates, b_i and their covariance matrix, S_i. For studies with partial information, one can obtain estimates of the p_i length parameter vector β_i for study i with p_i ≤ p. All of the study-specific parameters are then linked to the full vector of hyperparameters β of the underlying full model via M_i.

3.3. Estimation of a multivariate random-effects meta-analysis model with mapping matrices

Once we obtain all study-specific parameter estimates and identify their appropriate mapping patterns to the full model, we need to estimate the full vector of hyperparameters, β ≡ (β₀, β₁, β₂, ⋯ , β_p−1)^T. We denote b_i as the study-specific estimates of the corresponding parameters β_i for study i.

To estimate the hyperparameter vector β, one needs to estimate the between-study covariance matrix Σ. In the current study, we used the restricted maximum likelihood (REML) method while using the estimates from the method of moments [3] for starting values to achieve faster convergence. The estimation of Σ can be done by modifying the formula given by Jennrich and Schluchter [30] to incorporate mapping matrices:

$${\widehat{\Sigma }}_{\text{REML}}=\text{arg\hspace{0.17em}}\underset{\mathbf{\Sigma }}{\text{max}}\left\{-\frac{1}{2}\sum _{i=1}^k\text{log}\left|S_i+M_i\Sigma M_i^T\right|-\frac{1}{2}\text{log}\left|\sum _{i=1}^k{M}_i^T{\left(S_i+M_i\mathbf{\Sigma }{M}_i^T\right)}^{-1}{M}_i\right|-\frac{1}{2}\sum _{i=1}^k{\left(b_i-M_i\widehat{\beta }\right)}^T{\left(S_i+M_i\mathbf{\Sigma }{M}_i^T\right)}^{-1}\times \left(b_i-M_i\widehat{\beta }\right)\right\},$$

where

$$\widehat{\beta }={\left(\sum _{i=1}^k{M}_i^T{\left(S_i+M_i\mathbf{\Sigma }{M}_i^T\right)}^{-1}{M}_i\right)}^{-1}\times \left(\sum _{i=1}^k{M}_i^T{\left(S_i+M_i\mathbf{\Sigma }{M}_i^T\right)}^{-1}{M}_i{M}_i^{+}{b}_i\right)$$

and $M_i^{+}$ is the Moore-Penrose generalized inverse of M_i. Once ${\widehat{\Sigma }}_{\text{REML}}$ is estimated, β can be estimated from a combined multivariate normal CD as follows.

First, to accommodate the multivariate nature of β (see [59] for the CD approach for univariate applications), we construct a multivariate normal CD function for β [55]. By definition, H (·) is a multivariate normal CD function for a p×1 vector β, if the projected distribution H_λ (·) on a p×1 vector λ, for any given $\lambda \in {\Re }^p$, is a univariate normal CD for λ^T β.

Second, at the individual study level, assuming that S_i and Σ are known,

$$H_i\left({\theta }_i\right)={\Phi }_{p_i}\left({\left(S_i+M_i\Sigma M_i^T\right)}^{-1/2}\left({\theta }_i-b_i\right)\right)$$

is a corresponding multivariate CD function for study i, where θ_i = E(β_i) = M_iβ and Φ_u(·) is the cumulative distribution function for the standard multivariate normal distribution with u dimension, where u is any dimension. On the conditions that M_i is positive and semidefinite, and that all parameters can be linked via appropriate mapping matrices, a combined multivariate CD function for the population-level hyperparameter vector β has been shown as

$$H^{(c)}(\beta )={\Phi }_p\left({\Sigma }_c^{-1/2}\left(\beta -{\widehat{\beta }}^{(c)}\right)\right),$$

assuming that Σ is known (see Yang et al. [62] for a formal definition). Here, in this definition, because S_i and Σ are known ${\widehat{\beta }}^{(c)}={\left({\sum }_{i=1}^k{W}_i\right)}^{-1}\left({\sum }_{i=1}^k{W}_i{M}_i^{+}{b}_i\right)$ and its covariance matrix ${\Sigma }_c={\left({\sum }_{i=1}^k{W}_i\right)}^{-1}$, where $W_i=M_i^T{\left(S_i+M_i\Sigma M_i^T\right)}^{-1}{M}_i$.

If we plug in the consistent estimator of the variance matrix Σ, then β can be directly estimated from the asymptotic combined multivariate normal CD. In other words, from H^(c) (β):

$${\widehat{\beta }}^{(c)}={\left({\sum }_{i=1}^k{\widehat{W}}_i\right)}^{-1}\left({\sum }_{i=1}^k{\widehat{W}}_i{M}_i^{+}{b}_i\right)$$

for the estimated mean vector and

$${\widehat{\Sigma }}_c={\left({\sum }_{i=1}^k{\widehat{W}}_i\right)}^{-1}$$

for its covariance matrix, where ${\widehat{W}}_i$ is defined as

$${\widehat{W}}_i=M_i^T{\left(S_i+M_i{\widehat{\Sigma }}_{\text{REML}}{M}_i^T\right)}^{-1}{M}_i.$$

Therefore, ${\widehat{\beta }}^{(c)}$ and ${\widehat{\Sigma }}_c$ are CD estimators of β and Σ_c, respectively. Note that we use the sample covariance estimators S_i and ${\widehat{\Sigma }}_{\text{REML}}$ because the combined CD function H^(c) (β) would be an asymptotic multivariate normal CD as long as these estimators are consistent. The CD-based approach yields estimates with several desirable properties (e.g., asymptotically efficient and robust against model misspecification). See the Appendix for more details.

Finally, upon obtaining all estimates of the full model, flexible inference can be made using the combined full model. For example, to interpret decaying intervention effects over time, one can compare estimated outcomes at a given time across intervention groups. To estimate outcomes at specific values of the covariates, the estimated hyperparameters ${\widehat{\beta }}^{(c)}$ from the full model can be used to construct the estimated full model. We can then use the full model to obtain model-based mean ŷ₀ and its variance by plugging in a set of in-sample covariate values x₀ using the following formula:

$${\widehat{y}}_0={\mathit{x}}_0^T{\widehat{\beta }}^{(c)}$$

and

$$\text{var\hspace{0.17em}}\left({\widehat{y}}_0\right)=x_0^T\text{Cov}\left({\widehat{\beta }}^{(c)}\right)x_0.$$

4. DATA EXAMPLE

4.1. Underlying full model specification

Alcohol use trajectories among college students after various interventions typically show a sharp immediate decline, followed by a slow rebound to levels on par with or above the pre-intervention level over time [2, 58] because alcohol use and alcohol-related problems tend to peak during ages 18–24. Therefore, we chose a quadratic growth model and tested it using IPD from several individual studies separately, which supported the appropriateness of the model. We visually examined all available data, tested unconditional growth models, compared their fit indices (e.g., AIC, BIC), and examined growth coefficients and residual plots. To test intervention effects over time, we included interaction terms between time and intervention groups. We included gender, first-year student status, and race (white or otherwise) as demographic covariates. In addition, we conducted a separate analysis within individual studies to see if attrition at follow-ups could be explained by participant-level covariates. Based on this attrition analysis, we discovered that the tendency to use protective behavioral strategies prior to and while drinking, such as setting drinking limits, was related to greater chances for participants to drop out at follow-ups in some of the studies. We subsequently added this covariate to the full model.

All analyses were performed using R (version 3.4.4). The “nlme” R package [44] was used to fit a random-intercept growth model. We developed R codes to identify patterns of estimable covariates and to construct mapping matrices and used the “optimx” package [42] to obtain the REML estimates of the between-study covariance matrix.

4.2. Partial information and mapping matrices

Table 4 shows all 13 coefficients included in the current analysis and their availability by study. Some coefficients could not be estimated because (1) variables were not assessed by study design (e.g., PBS; studies 10.1, 11, 13/14, and 20); (2) the entire sample consisted of only first-year students (studies 9, 10.1, 11, and 22); (3) not all intervention groups were included in original studies (studies 1, 2, 8a, 8b, 8c, 10.1, 11, 12, 18, 20, and 22; see also Figure 1); and (4) only one follow-up assessment was available (i.e., only a linear slope term could be estimated; studies 2, 8a, 8b, 8c, 10.1, 20, and 22; see Table 1). A total of just three covariate coefficients were estimable across all studies (i.e., man vs. woman, white vs. non-white, and a linear slope of time), and only one study (study 21) had the necessary data to estimate all coefficients. There were a total of 11 different mapping matrix patterns. With the exception of study 21, all other studies required mapping matrices with reduced dimensions.

4.3. Estimation and interpretation

The full vector of hyperparameter estimates ${\widehat{\beta }}^{(c)}$ (see Table 5) and its corresponding covariance matrix $\text{Cov}\left({\widehat{\beta }}^{(c)}\right)$ were obtained by applying the estimation procedures described in Section 3. Table 6 shows that the correlation estimates of the regression coefficients derived in the current study were not boundary estimates (i.e., away from ±1), which usually suggests estimation difficulties in certain multivariate meta-analysis models [47]. The estimated full model for the data example at the participant level was:

$$E\left(y_{ijt}\right)=+0.4449+\left(0.0172\times {\text{Man}}_{ijt}\right)+\left(0.0564\times {\text{White}}_{ijt}\right)+\left(0.0403\times {\text{ First-year }}_{ijt}\right)+\left(-0.2825\times {\text{PBS}}_{ijt}\right)+\left(-0.0028\times {\text{PF}}_{ijt}\right)+\left(0.0841\times {(\text{MI}+\text{PF})}_{ijt}\right)+\left(-0.0442\times {\text{ Month }}_{ijt}\right)+\left(0.0041\times {\text{ Month }}_{ijt}^2\right)+\left(0.0006\times {(\text{PF}\times \text{ Month })}_{ijt}\right)+\left(-0.0311\times {((\text{MI}+\text{PF})\times \text{Month})}_{ijt}\right)+\left(-0.0004\times {\left(\text{PF}\times {\text{Month}}^2\right)}_{ijt}\right)+\left(-0.0003\times {\left((\text{MI}+\text{PF})\times {\text{Month}}^2\right)}_{ijt}\right).$$

Table 5.

Combined parameter estimates from the multivariate random-effects meta-analysis

Covariate	Estimate	p value
0. Intercept	0.4449	0.0051
1. Man (=1 vs. woman=0)	0.0172	0.7184
2. White (=1 vs. nonwhite=0)	0.0564	0.1309
3. First-year (=1 vs. other=0)	0.0403	0.1928
4. PBS at Baseline	−0.2825	0.0000
5. PF (=1 vs. control=0)	−0.0028	0.9223
6. MI + PF (=1 vs. control=0)	0.0841	0.1270
7. LS	−0.0442	0.0178
8. QS	0.0041	0.0276
9. LS × PF	0.0006	0.8729
10. LS × (MI + PF)	−0.0311	0.0006
11. QS × PF	−0.0004	0.5774
12. QS × (MI + PF)	−0.0003	0.8314

Notes. PBS = Estimated latent trait (θ) scores for utilizing protective behavioral strategies; PF = stand-alone personalized feedback intervention; MI + PF = in-person motivational intervention with personalized normative feedback profile; LS = Linear slope (time in month); and QS = Quadratic slope (months squared).

Table 6.

Synthesized between-study correlation matrix of the combined parameter estimates

	1	2	3	4	5	6	7	8	9	10	11	12
0	0.23	−0.46	−0.37	−0.39	−0.03	−0.49	0.22	−0.57	0.36	0.20	0.07	0.57
1		−0.32	−0.28	0.12	−0.07	−0.38	0.29	−0.24	0.43	0.54	−0.27	0.03
2			0.32	0.28	0.12	0.07	0.38	0.29	0.24	0.43	−0.03	−0.10
3				−0.06	0.26	0.47	−0.28	0.30	−0.42	−0.41	0.13	−0.13
4					−0.02	−0.11	−0.61	0.71	0.01	−0.21	−0.15	0.05
5						0.27	−0.31	0.24	−0.47	−0.33	0.13	0.13
6							−0.13	0.22	−0.42	−0.51	0.13	−0.24
7								−0.87	−0.29	0.72	0.14	−0.33
8									−0.31	−0.56	−0.13	0.00
9										0.40	−0.37	0.12
10											−0.25	−0.40
11												0.26

Notes. 0 = Intercept, 1 = Man, 2 = White, 3 = First-year, 4 = PBS at baseline, 5 = PF, 6 = MI + PF, 7 = LS, 8 = QS, 9 = LS × PF, 10 = LS × (MI + PF), 11 = QS × PF, and 12 = QS × (MI + PF). PBS = Estimated latent trait (θ) scores for utilizing protective behavioral strategies; PF = stand-alone personalized feedback intervention; MI + PF = in-person motivational intervention with personalized normative feedback profile; LS = Linear slope (time in month); and QS = Quadratic slope (months squared).

Substantively, results indicated that there was a significant interaction between MI + PF and the linear slope of time. To interpret this interaction effect, we calculated model-implied outcome values for all groups based on the estimated full model. Namely, we used in-sample covariate values (i.e., first-year, male, white students, a mean PBS score) and obtained model-implied means for alcohol-related problems and their estimated variances at various time points post intervention. The estimates were derived based on the estimated full model.

Figure 2 shows the expected mean levels for all three groups, which shows a reduction in alcohol-related problems at 6 months, followed by a rebound at 12 months (top). To demonstrate the flexibility of this approach, we plotted monthly estimates of alcohol-related problems up to 12 months post intervention (bottom), which shows the linear and quadratic growth functions for the following three groups: MI + PF, PF, and control. MI + PF showed the best post-intervention trajectory over time, showing a clearer intervention benefit, which was better maintained over time, compared with PF. We further probed this by comparing estimated alcohol-related problems for PF vs. control and for MI + PF vs. control every three months (top) and every month (bottom) for up to 12 months post intervention (Figure 3). Figure 3 (bottom) shows that statistically significant group differences in alcohol-related problems emerged around 5–6 months post intervention (95% confidence intervals are below the dotted horizontal line).

Figure 2.

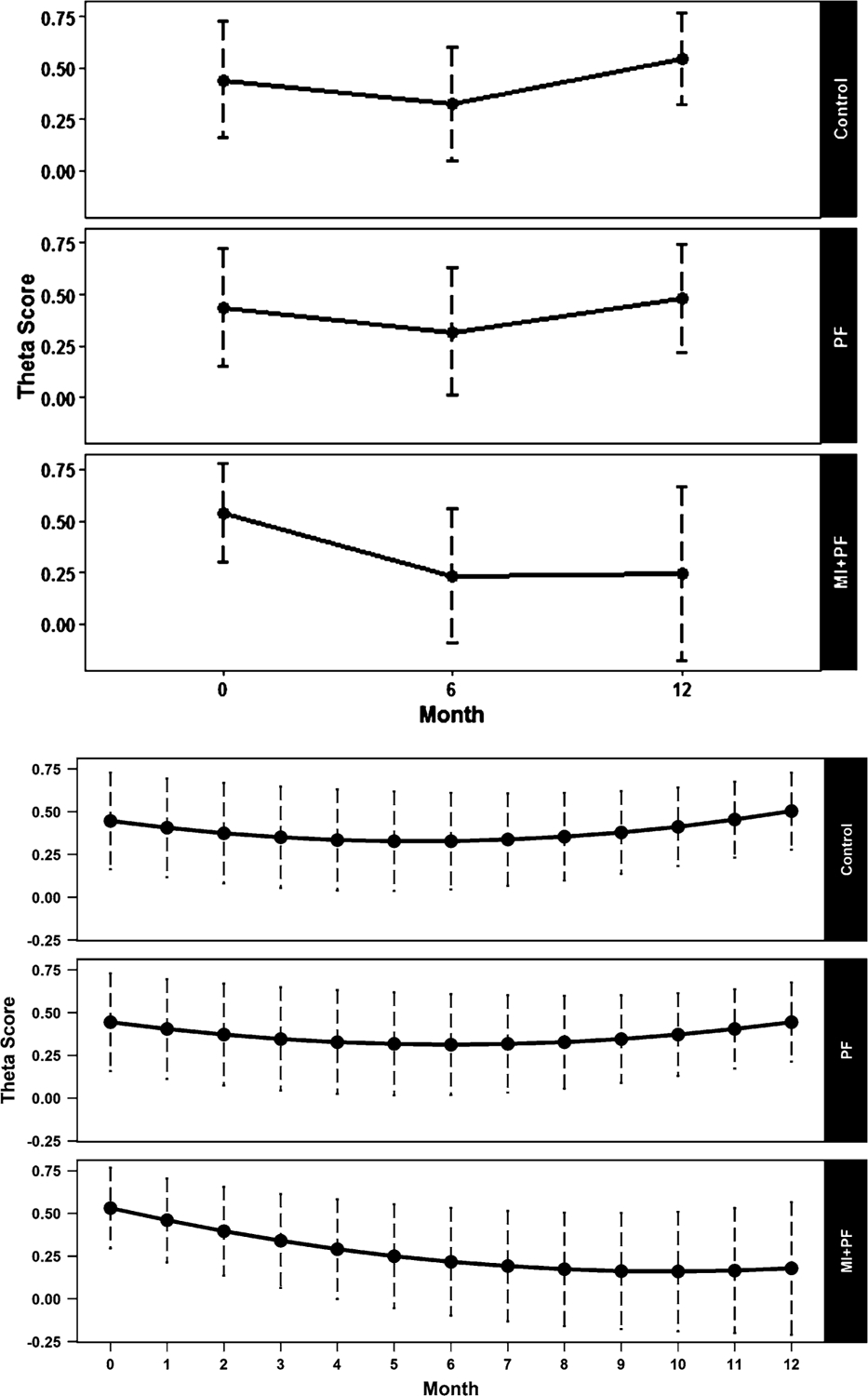
Model-based mean estimates for three different groups using the estimated full model shown in Table 5. The top figure shows estimates at baseline, and 6- and 12-month follow-ups. The bottom figure shows monthly estimates for 12 months post intervention. Theta score = latent trait severity score for alcohol-related problems. PF = stand-alone personalized feedback intervention; MI + PF = in-person motivational intervention with personalized normative feedback profile. Values for covariates were set for White, first-year, male students with a mean PBS score at baseline. Vertical dotted lines indicate 95% confidence intervals.

Figure 3.

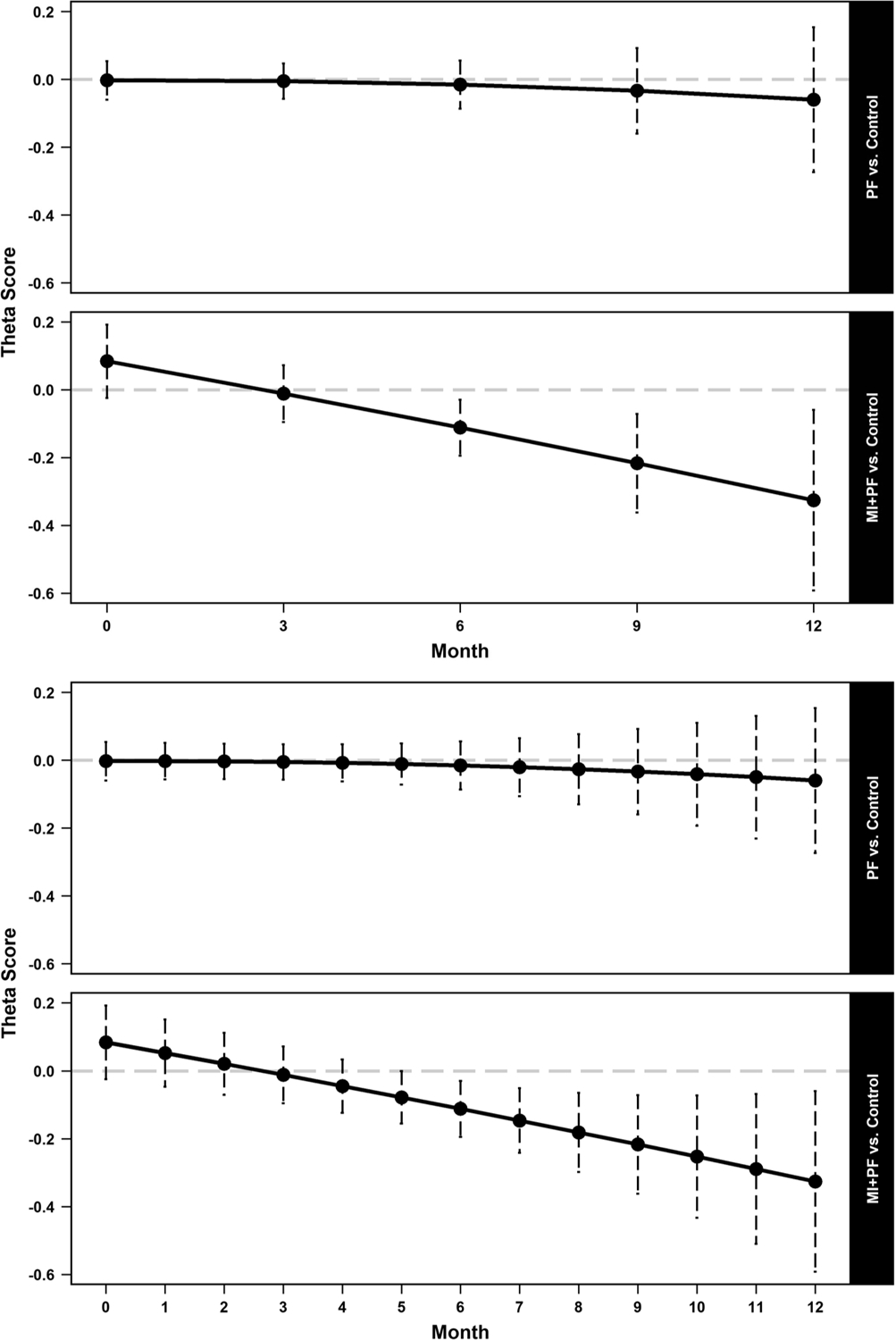
Model-based mean difference estimates of the two intervention groups, compared to control, in alcohol-related problems at baseline and every three months (top), and at baseline and each subsequent month post intervention (bottom). Theta score = latent trait severity score for alcohol-related problems. PF = stand-alone personalized feedback intervention; MI + PF = in-person motivational intervention with personalized normative feedback profile. Vertical dotted lines indicate 95% confidence intervals. A horizontal dashed line at zero indicates no group difference.

4.4. Sensitivity analyses

To examine if the reported results were overly influenced by outlying studies, we conducted a sensitivity analysis by excluding one study at a time and repeating the analysis. Results indicated that while individual regression parameters changed in magnitude to some extent, the overall findings remained largely the same (not shown). In addition, we sequentially removed two different covariates from the analysis at two different steps of the analysis (i.e., when estimating Level-1 parameters in the first step and when estimating Level-2 hyperparameters in the second step) and examined the impact of model misspecification on two key coefficients (i.e., PF × Linear Slope and (PF + MI) × Linear Slope).

Figure 4 shows the results when we removed PBS (top) and first-year student status (bottom) during the second step when hyperparameters were estimated. Figure 5 shows the results when we removed covariates during the first step of the analysis when each covariate was removed from the study-specific analysis (i.e., removed from both Level-1 and Level-2 analyses). Results from both sensitivity analyses suggest that the estimated hyperparameters (shown in filled diamond symbols in Figures 4 and 5) were fairly robust to model misspecification, and that an omitted covariate made little impact on the final estimates, regardless of whether it was a continuous or binary covariate. We also inspected other estimated coefficients and concluded that the derived hyperparameter estimates could be trusted.

Figure 4.

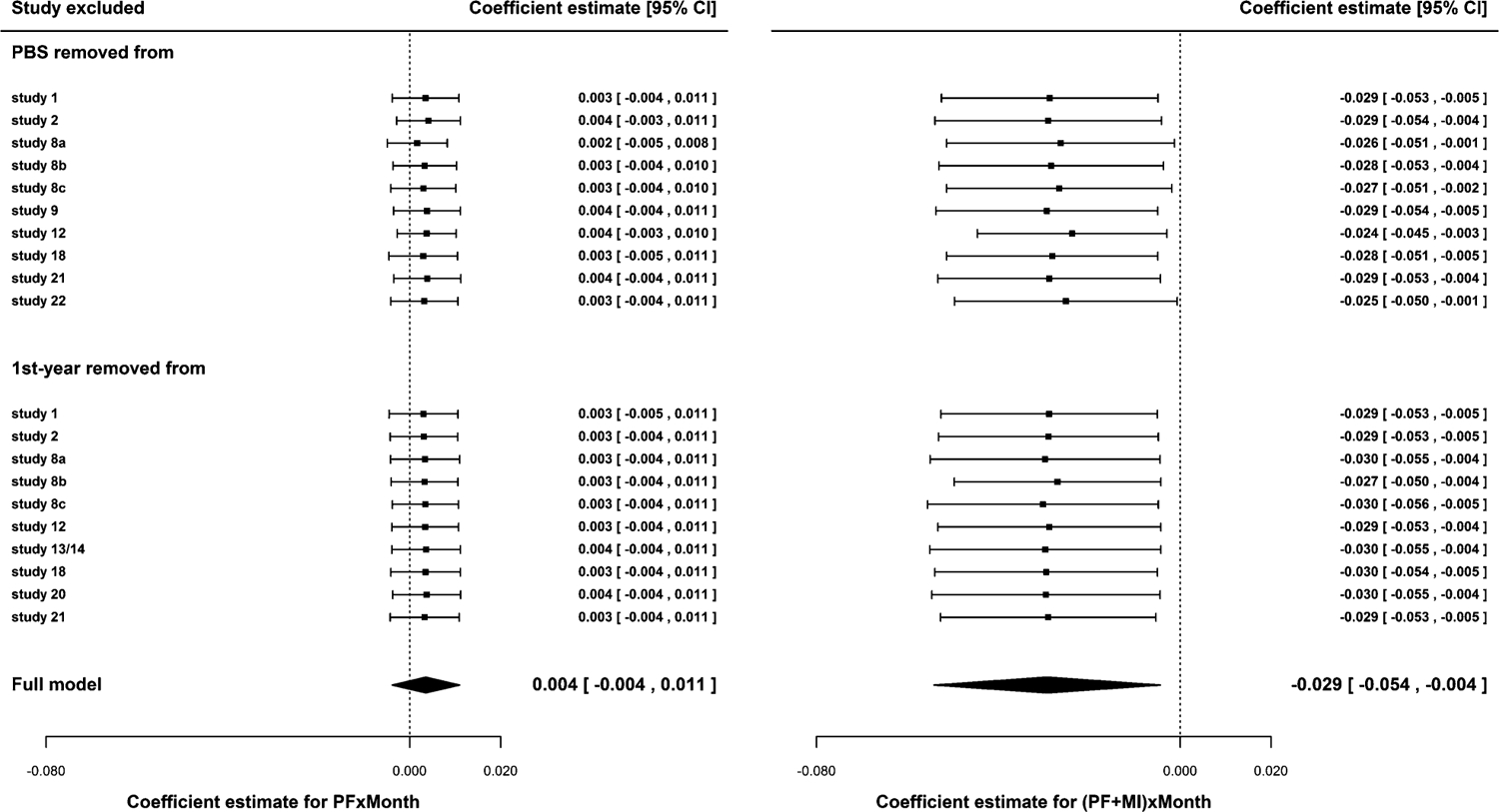
Results from sensitivity analyses where each covariate from each study was treated as systematically missing in the second step. The effects of the exclusion of a continuous covariate (PBS at baseline; top) and a binary covariate (first-year student status; bottom) on the combined estimates of PF × Linear Slope (left) and (MI + PF) × Linear Slope (right) are shown, respectively. Filled diamond symbols indicate the combined estimates from all 14 studies as reported in Table 5. The estimates from sensitivity analyses are shown in filled squares.

Figure 5.

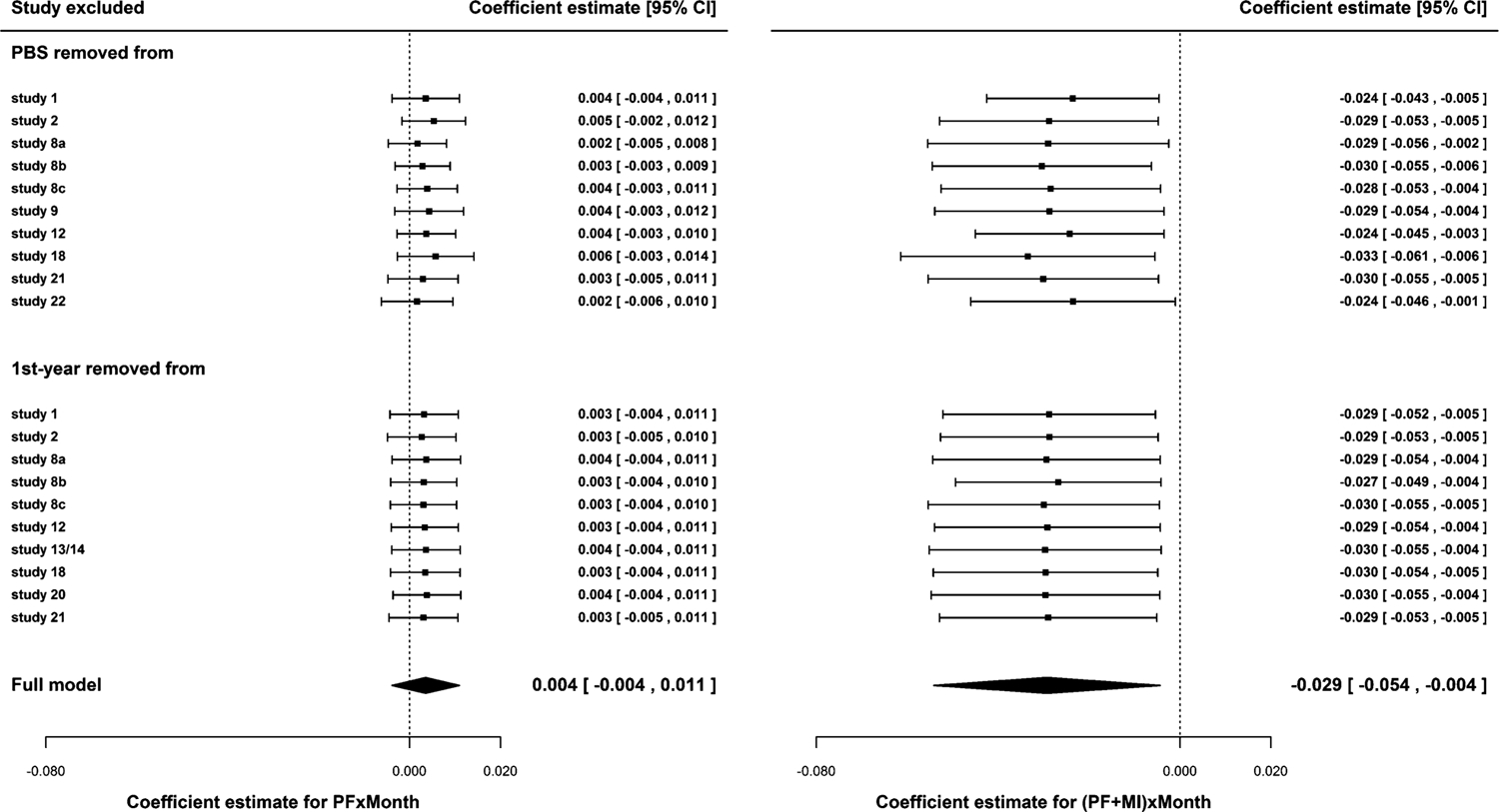
Results from sensitivity analyses where a covariate from each study was sequentially removed throughout the entire analysis. The effects of the exclusion of a continuous covariate (PBS at baseline; top) and a binary covariate (first-year student status; bottom) on the combined estimates of PF × Linear Slope (left) and (MI + PF) × Linear Slope (right) are shown, respectively. Filled diamond symbols indicate the combined estimates from all 14 studies as reported in Table 5. The estimates from sensitivity analyses are shown in filled squares.

5. DISCUSSION

The current study extended the CD-based mapping method to a multivariate random-effects meta-analysis model from the multi-parameter synthesis perspective [1, 16, 17]. We showed that data from heterogeneous trials can be validly accommodated by utilizing the CD concept [59, 60]. The two-step CD-based mapping method differs from the existing methods in the sense that it is aimed at combining the entire full model, which is subsequently used to derive model-based estimates for flexible inference. Broadly speaking, the two-step CD-based mapping method shares some features in common with Bayesian and meta-analytic structural equation modeling (MASEM) [4] approaches in the sense that the CD-based method does not focus on deriving isolated point estimates. Rather, the CD-based mapping method utilizes all available evidence that exist within studies to link to, and estimate, the underlying full model. This method makes fewer assumptions and can be broadly applicable, providing a more general synthesis framework (Table 7).

Table 7.

The premises, assumptions, and challenges of the CD-based mapping method

Premises

The CD-based mapping method can be used for both aggregate data and individual participant data. This method can be applied to both fixed- and random-effects meta-analysis models. Flexible model-based inference, which includes confidence intervals or regions at all levels for all testing questions (i.e., above and beyond a few isolated point estimates), can be obtained. Data can be combined from exploratory studies (e.g., to generate hypothesis testing questions) as well as from confirmatory studies (e.g., large-scale clinical trials).

Assumptions

A full model is assumed to be shared by all studies. Study-level systematic missing data are assumed to be missing at random. Appropriate mapping matrices can be identified for all studies to validly link the expectation of the study-specific parameters to the vector of hyperparameters of the full model. For studies with missing numerical covariates, their population means (e.g., zero) can be reasonably assumed and accommodated in mapping matrices.

Challenges

A true full model may be difficult to identify or justify, especially when combining data from highly heterogeneous studies. Appropriate mapping matrices can be challenging to identify as the dimensions of data (i.e., covariate by study) increase. When item-level IPD are available, an additional analysis may be needed to retrospectively establish a commensurate metric. When individual studies have small samples and the number of studies in a meta-analysis is small, it may be desirable to accommodate uncertainty surrounding covariance estimators.

In the present study, the combined full model had 13 hyperparameter estimates across 11 different estimable patterns of coefficients for 14 trials. To accommodate missing or inestimable covariates and covariates with different meanings across studies, we identified appropriate connections between the expectation of the study-specific parameters and the full model hyperparameters and subsequently, derived the joint distribution of hyperparameters using the multivariate CD-based approach to meta-analysis. This new method may provide the field with a methodological alternative to consider, in connection with methods of aggregating published prediction models [9, 10], dealing with systematic missing data [13, 31, 46, 52], exploring subgroups that may respond differently to an intervention [14, 50], and combining multiple parameter estimates from either AD or IPD [4, 17].

Multivariate meta-analysis, despite its well established rationale and premise, has resulted in a rather small improvement in the statistical properties of individual estimates [26, 56]. In typical multivariate meta-analysis applications, the dimension of combined coefficients has been rather limited, which may help explain the small gain thus far in the literature. The method illustrated in the current paper allows us to make more specific inference based on the full model, which may be helpful for the development of personalized treatment approaches using clinical trial data (i.e., the Precision Medicine Initiative [7]).

In addition, the CD-based mapping method for multivariate meta-analysis explicitly accommodates between-study differences. Consequently, the derived estimates are not confounded with between-study differences. This CD-based method may be helpful when estimating treatment effects for subgroups in data situations where no within-study estimates exist for some of the studies included in a meta-analysis. Riley et al. [48] explored a multivariate meta-analysis extension application, in which different treatment effects were examined separately for each subgroup. However, this approach, as Riley et al. discussed, can result in a confounded treatment effect estimate when one cannot reasonably assume that within-study and between-study covariate interactions are the same. Riley et al. discussed the advantages (e.g., power) and disadvantages (e.g., ecological inference bias and study-level confounding) of combining within-study estimates with between-study estimates of the approach. The method we illustrated in the current study may offer a more favorable solution for this challenge.

Table 7 shows a summarized list of the premises, assumptions, and challenges of the CD-based approach to multivariate meta-analysis. It is flexible and not computationally intensive. Most of the assumptions involved in this CD-based approach are assumed for the existing meta-analysis methods. For example, we assume that the designated full model is a true model for all studies. For a meta-analysis of clinical trials, a true full model is reasonable to assume. We also assume that the pattern of omitted covariates at the study level meets the MAR assumption, which may be quite reasonable for randomized clinical trials [48]. Other assumptions, such as common scales, can be explicitly checked and analyzed when item-level IPD (as opposed to scale-level IPD) are available. In addition, as long as mapping matrices can be identified, this CD-based approach can be used more generally without any restrictions on the distributions of outcome variables or the types of coefficients being combined for a full model. In the current study, we simultaneously combined three different types of related coefficients: the relative intervention benefits (network), informative covariates (regression), and repeated follow-up outcome data (longitudinal).

There are challenges and caveats of the CD-based approach. First, the implementation of this approach using IPD requires considerable time and efforts by a research team with a wide range of complementary expertise and skills. In particular, the necessary identification of an appropriate full model and subsequent mapping matrices can be difficult especially when data dimensions (covariates × study) increase. For randomized controlled trials, the identification of an appropriate full model is more straightforward than observational studies. Nonetheless, it would be beneficial to include domain experts to help identify important factors that may affect outcomes so that full models can be reasonably identified. Despite the best effort, however, if a full model is incorrect or if mapping matrices are incorrect, how robust the method is to model misspecification remains to be more thoroughly studied.

Second, the studies included in a meta-analysis should be sufficiently similar in terms of their methodological and clinical characteristics to justify that data can be combined. Although this assumption is generally required for meta-analysis, it may not be reasonable or desirable in some data applications, depending on its goals. If a comprehensively inclusive meta-analysis is the goal, then creating a subgroup of studies sharing the same full model within the subgroup and developing multiple full models to accommodate other subgroups of studies may be needed.

Third, not all constructs can be directly observed or may share the same interpretation across studies. For example, a death is directly observable and has the same meaning regardless of study membership. Mental health outcomes and correlates, however, are not directly observable but derived, and measured in a number of different ways. In the case of depression, there are more than 280 different depression scales with little item overlap across scales [15]. If there is sufficient overlap in items across studies, items may be linked across studies via shared items and a commensurate metric may be established [38, 23].

Fourth, when the number of studies is small or when individual studies have small samples, it may be necessary to accommodate uncertainty surrounding covariance estimators S_i and ${\widehat{\Sigma }}_{\text{REML}}$. In future meta-analysis studies, this uncertainty may be reflected, for example, by inflating confidence intervals for the REML method [27]. Finally, our previous measurement work to make IPD comparable across studies involved an additional set of assumptions and constraints, which need to be considered when developing appropriate mapping matrices.

Substantively, we found the positive effect of the MI + PF intervention on alcohol-related problems, which is consistent with the previously reported findings [21], despite using a different methodological approach to IPD meta-analysis. Huh et al. estimated a Bayesian three-level model in a “one-step” meta-analysis of IPD [19] (see also Huh et al. [22]). In addition, Huh et al. used a different full model, which specified alcohol-related problem scores at baseline as a covariate. Intervention effects were estimated within studies using posterior distributions. Consequently, studies without their own control group were excluded in the analysis.

Based on the comparison of the one-step approach with the current two-step CD-based approach, albeit indirectly, we reach two conclusions. First, the convergent findings from the two studies increase our confidence in the substantive conclusion that MI + PF has an advantage over PF in terms of reducing alcohol-related problems for college students. Second, the two-step CD-based mapping method approach to IPD multivariate meta-analysis may be better suited to build a “scalable” evidence base, compared to the one-step approach. The term “scalable” applies not only to the number of studies but also to the number of informative covariates that can be examined in a meta-analysis. Instead of imputing study-level missing data, the CD-based approach utilizes information from all available data across studies to provide inference. Given that with increasing data dimensions, between-study heterogeneity increases, it is critical that missing or inestimable data are appropriately handled in IPD meta-analysis. A recent study [51] discussed that accurate imputations of study-level missing data across 19 depression trials were not obtained, which is a critical step needed for conducting one-step IPD meta-analysis or IDA. This has been a major barrier to harmonizing and synthesizing IPD across studies. The CD-based method that we showcased in the present study may be an important new tool for the field of complex research synthesis.

In conclusion, to provide answers to complex questions from available large-scale data, it is critical to account for between-study differences and accommodate study-level missing data. The CD-based method is a promising new approach aimed at promoting large-scale, complex evidence synthesis of IPD for multivariate meta-analysis models.

APPENDIX

Proof of the claims in Section 3.3. First, let us assume that Σ is known. At the individual study level, $b_i~N_{p_i}\left({\theta }_i,S_i+M_i\Sigma M_i^T\right)$, where b_i is a point estimator of θ_i = E(β_i) = M_iβ. By Singh et al. [55], $H_i\left({\theta }_i\right)={\Phi }_{p_i}\left({\left(S_i+M_i\Sigma M_i^T\right)}^{-1/2}\left({\theta }_i-b_i\right)\right)$ is a corresponding multivariate CD function for θ_i, for i = 1, … , k.

Following Xie et al. [60] and Yang et al. [61], we know that combining normal CDs of individual studies can be achieved by a linear combination of normal CDs with weight W_i. In particular, when Σ is known, we have

$${\widehat{\beta }}^{(c)}={\left({\sum }_{i=1}^k{W}_i\right)}^{-1}\left({\sum }_{i=1}^k{W}_i{M}_i^{+}{b}_i\right).$$

Since ${\widehat{\beta }}^{(c)}~N_p\left(\beta ,{\Sigma }_c\right)$, the combined CD function for the regression parameter of interest β is $H^{(c)}(\beta )={\Phi }_p\left({\mathbf{\Sigma }}_c^{-1/2}\left(\beta -{\widehat{\beta }}^{(c)}\right)\right)$. When Σ is not known, we then replace it with a consistent estimator (as k → ∞). This leads to the following asymptotic combined CD: $H^{(c)}(\beta )={\Phi }_p\left({\widehat{\Sigma }}_c^{-1/2}\left(\beta -{\widehat{\beta }}^{(c)}\right)\right)$ as described in Section 3.3.