Models with interactions overestimated heterogeneity of treatment effects and were prone to treatment mistargeting

Abstract

Objectives:

We aimed to compare the performance of different regression modelling approaches for the prediction of heterogeneous treatment effects.

Study Design and Setting:

We simulated trial samples (n=3,600; 80% power for a treatment odds ratio of 0.8) from a superpopulation (N=1.000.000) with 12 binary risk predictors, both without and with 6 true treatment interactions. We assessed predictions of treatment benefit for four regression models: a “risk model” (with a constant effect of treatment assignment) and three “effect models” (including interactions of risk predictors with treatment assignment). Three novel performance measures were evaluated: calibration-for-benefit (i.e. observed versus predicted risk difference in treated versus untreated), discrimination-for-benefit, and prediction error-for-benefit.

Results:

The risk-modeling approach was well-calibrated for benefit while effect models were consistently overfit, even with doubled sample sizes. Penalized regression reduced miscalibration of the effect models considerably. In terms of discrimination and prediction error, the risk-modeling approach was superior in the absence of true treatment effect interactions, while penalized regression was optimal in the presence of true treatment interactions.

Conclusion:

A risk-modeling approach yields models consistently well-calibrated for benefit. Effect-modeling may improve discrimination-for-benefit in the presence of true interactions, but is prone to overfitting. Hence, effect models – including only plausible interactions – should be fitted using penalized regression.

BACKGROUND

The main goal of predictive analyses of heterogeneous treatment effects is to develop models that can be used to predict which of two or more treatments will be better for a particular individual [1]. In prior work, we discuss two broad approaches to regression-based predictive heterogeneity of treatment effects (HTE) analysis: 1) outcome risk modeling (or “risk modeling”) and 2) treatment effect modeling (or “effect modeling”) [2]. Risk modeling is performed “blinded” to treatment assignment, where the treatment effect is examined across risk strata; treatment effect interactions with candidate relative effect modifiers are not explored. This conservative approach is designed to produce honest estimates of treatment effects within groups that differ by their risk of the outcome of interest and therefore by their risk difference (i.e. treatment effect on the clinically important absolute scale). Because risk is a mathematical determinant of treatment effect, it can be used to identify risk groups who differ greatly in their degree of benefit (particularly on the clinically important absolute scale) [3, 4]. Treatment effect modeling, on the other hand, is a more “aggressive” data-driven approach that seeks to explore and/or include potential relative effect modifiers within a predictive model. This approach has the potential to better segregate those patients who benefit from those who do not. Particularly when treatment is associated with some treatment-related harm or burden, these approaches may be useful in targeting treatment to those most likely to benefit.

WHAT IS NEW?

Key findings

• The risk-modeling approach was well-calibrated for benefit in contrast with effect models which were consistently miscalibrated (“overfit”).

• Lasso regression considerably reduced, but did not nullify benefit miscalibration of the effect models.

• In terms of discrimination and prediction error, the risk-modeling approach was superior in the absence, while penalized regression was optimal in the presence of true treatment interactions, respectively.

What this adds to what was known

• Effect models overestimate the heterogeneity of treatment effects considerably, even for large sample sizes.

• Penalized regression prevents overfitting of risk, but still suffers from overfitting of benefit even when the events per variable are high.

What is the implication, and what should change now

• Effect models, including treatment interactions, may lead to treatment mistargeting.

• We recommend the risk-model approach for the analysis of heterogeneity of treatment effects.

• Effect models should only be considered when treatment interactions are plausible, and should always be fitted with penalized regression.

We performed simulations to compare the various approaches to predictive HTE analysis, and to illustrate and quantify some of the problems with overfitting for models used to predict benefit that are not widely appreciated. For risk modeling, we sought to illustrate problems that arise when an endogenous model is developed on the control arm only. While this problem has been shown in previous simulations [5, 6], we sought to use data generated with a substantially different set of assumptions to test the robustness of prior observations, especially those indicating that modeling on the whole trial eliminated the bias induced by modeling only on the control arm.

We also sought to examine how risk modeling compared to several different effect modeling approaches, using both measures of calibration-for-benefit and discrimination-for-benefit—where benefit is defined as the risk-difference. These simulations permitted us to explore how serious the problems of overfitting were when using “conventional” non-penalized maximum likelihood regression for effect modeling in settings that emulate the statistical power likely to be available to explore heterogeneous effects in large clinical trials. Finally, we also sought to examine the ability of penalized regression (i.e. Lasso and Ridge regression) to correct for the overfitting anticipated when “conventional” non-penalized maximum likelihood regression was used for effect modeling.

METHODS

Population

The population consists of 1 million patients equally divided into a control arm and a treatment arm. For each patient, 12 binary baseline characteristics are independently generated with a prevalence of 20% each. The outcomes in the control arm are generated with an average event rate of approximately 25% from a logistic regression model with associations between baseline characteristics and outcomes varying from an odds ratio of 1 to 2 (table 1; “control arm”). The outcomes for patients in the treatment arm were first generated from the same logistic regression model (table 1; “treatment without true interactions”), but including a main treatment effect odds ratio of either 1 (“null”), 0.8 (“moderate”; we considered this the “base case”), or 0.5 (“strong”), respectively. Alternatively, the outcomes for patients in the treatment arm were generated from a logistic regression model in which 6 of the 12 associations between baseline characteristics and outcomes differed from the control arm (table 1; “treatment arm with true interaction”), with relative odds ratios varying from 0.67 to 1.33. The prevalence of true interactions among all possible interactions (50%) is designed to emulate the “prior probability” for confirmatory subgroup analysis, while the prior probability for exploratory subgroup analysis would be considerably lower [7–9]. To analyze the sensitivity of the results to the use of continuous rather than binary baseline characteristics, we repeated the analysis with 12 normally distributed baseline characteristics. We chose the same mean (0.2) and variance (0.16) as for the binary baseline characteristics to obtain similar precision when estimating the effects of baseline characteristics and the effects of their interaction with treatment. To analyze the sensitivity of the results to correlation between baseline characteristics, we repeated the analysis with 12 correlated normally distributed baseline characteristics (correlation coefficients of 0.5).

Table 1. Population (N=1.000.000) characteristics x₁ – x₁₂; outcomes are simulated from a logistic regression model with parameters b_i and bint_i.

For each patient, 12 binary baseline characteristics were independently generated with a prevalence of 20% each. The outcomes of the 500.000 patients in the control arm (average event rate of 25%) are generated from a logistic regression model with associations between baseline characteristics and outcomes according to column 3 (“control arm”). The outcomes for patients in the treatment were first generated from the same logistic regression model (column 4; “treatment arm without true interaction”), but including a main treatment effect odds ratio of either 1 (“null”), 0.8 (“moderate”), or 0.5 (“strong”), respectively. Alternatively the outcomes for patients in the treatment arm were generated from a different logistic regression model (column 6; “treatment arm with interaction”).

	Control arm	Treatment arm without interactions		Treatment arm with interactions
Variable	ORC	ORTR	ORTR / ORC	ORTR	ORTR / ORC
x1	1	1	1	1	1
x2	1	1	1	1	1
x3	1	1	1	1	1
x4	1.2	1.2	1	1.4	1.17
x5	1.2	1.2	1	1.2	1
x6	1.2	1.2	1	1	0.83
x7	1.5	1.5	1	2	1.33
x8	1.5	1.5	1	1.5	1
x9	1.5	1.5	1	1	0.67
x10	2	2	1	2.5	1.25
x11	2	2	1	2	1
x12	2	2	1	1.5	0.75

Clinical example

We illustrate the simulated population with the clinical example of choosing between treatment of patients with complex coronary artery disease with either Coronary Artery Bypass Graft surgery (CABG; “treatment”) or Percutaneous Coronary Intervention (PCI; “control”). Evidence suggests that, on average, treatment with CABG leads to lower mortality than treatment with PCI. Baseline characteristics that are associated with high mortality risk are high SYNTAX score (high anatomical disease complexity), high age, low creatinine clearance, low left ventricular ejection fraction, presence of unprotected left main coronary artery disease, peripheral vascular disease, female sex, COPD, and diabetes mellitus. The simulation scenario without true treatment interaction assumes that these baseline characteristics increase the odds of mortality equally after both treatments, e.g. COPD doubles the odds of mortality, regardless of treatment. The simulation scenario with true treatment interaction assumes that some of the associations between the baseline characteristics and the odds of mortality are different after treatment with CABG and treatment with PCI, e.g. COPD increases the odds of mortality after PCI with 50%, but triples the odds of mortality after CABG.

Samples

A simulation consists of 500 random samples of 3,600 patients (80% power to detect a treatment versus control odds ratio of 0.8) from the population. To study the impact of sample size we alternatively sampled 1,800 patients and 7,200 patients per sample, respectively.

Risk models

In each sample of patients, we fitted a risk model consisting of all of the 12 baseline characteristics. This model was fitted in the patients in the control arm only, as well as in the whole sample, blinded to treatment. For each of these risk models, the predicted risk was calculated for each patient in the sample and in the population. The sample and the population were stratified into quartiles of predicted risk (according to the sample-derived risk model) and the observed absolute treatment benefit (i.e. the event rate of control patients minus the event rate of treated patients) was determined in each risk quartile of the sample and of the population. To compare these approaches (control arm only versus whole trial), within-strata event rates in the population were used to represent “ground truth”. We assessed the ‘calibration for benefit’ of these approaches by examining the observed absolute treatment benefit (i.e. risk difference) in quartiles of predicted risk in in the sample versus that in the population. We present box plots describing the distribution of these values across the 500 samples.

Treatment effect models

In each sample of patients we first fitted:

• 1A model consisting of all of the 12 baseline characteristics and the treatment, assuming a constant relative treatment effect. This approach is equivalent to a risk modeling approach, but with a constant relative effect imposed across risk groups; this was done in order to generate values for predicted benefit – predicted outcome with versus without treatment – so that the approach can be compared to the other effect modeling approaches below.

Then we fitted different treatment effect models in each sample of patients consisting of all of the 12 baseline characteristics and:

• 22 pre-specified treatment interactions with baseline characteristics x₁₀ and x₁₂, corresponding to a parsimonious and non-data-driven approach including only of two “established” relative effect modifiers
• 3treatment interactions with all 12 baseline characteristics.
• 4treatment interactions with all 12 baseline characteristics, using backward selection based on AIC (p=0.157).
• 5treatment interactions with all 12 baseline characteristics, using Lasso regression with minimum mean cross-validated error (referred to as Standard Lasso).
• 6treatment interactions with all 12 baseline characteristics, using Ridge regression with minimum mean cross-validated error (referred to as Standard Ridge).
• 7treatment interactions with all 12 baseline characteristics, using Lasso regression with maximum penalization such that the error is within one standard error of the minimum (Referred to as Strong Lasso).
• 8treatment interactions with all 12 baseline characteristics, using Ridge regression with maximum penalization such that the error is within one standard error of the minimum (Referred to as Strong Ridge).

For each effect model that was fitted in each consecutive sample, the predicted absolute treatment benefit (i.e. predicted risk difference) in the population was calculated as the model’s outcome prediction conditional on assignment to the control arm minus the outcome prediction conditional on assignment to the treatment arm. The population was stratified into quartiles of predicted absolute treatment benefit. In each quartile of the population, we calculated the mean predicted absolute treatment benefit and the observed absolute treatment benefit, i.e. the event rate of control patients minus the event rate of treated patients.

Metrics of model performance

Calibration-for-benefit

A well calibrated sample-based model fit would have good agreement in the population between predicted and observed benefit in quartiles of predicted benefit. We assessed the calibration-for-benefit of each model fit by the difference between predicted absolute treatment benefit and observed absolute treatment benefit in quartiles of predicted absolute benefit of the population. We present box plots of the observed versus predicted treatment benefit in quartiles of predicted benefit for each model describing the distribution of these values across the 500 samples. Because calibration in the second and third quartile of predicted benefit is always excellent, we numerically express calibration by the mean difference between the predicted treatment benefit and the observed treatment benefit in the 2 extreme predicted benefit quartiles (i.e. lowest and highest quartiles) of the population.

Discrimination-for-benefit

A well discriminating sample-based model fit would have a large difference between the observed benefit in the first and fourth predicted benefit quartile of the population. We assessed the discrimination of each model fit by the extreme quartile difference (EQD) of benefit in the population, i.e. the arithmetic difference between the observed absolute benefit in the fourth quartile and the observed absolute benefit in the first quartile of the population. A model that shows a higher EQD in the population is better able to discriminate patients for treatment benefit, i.e. to separate patients with low treatment benefit from those with high treatment benefit.

Prediction error-for-benefit

The simulation settings (table 1) allow the calculation of true individual treatment benefit for each individual patient in the population, which is unidentifiable in real world settings. We were thus able to assess the accuracy of each model’s benefit predictions by the root mean squared error (rMSE), i.e. the root of the mean of the square differences between predicted absolute benefit and true absolute benefit in the population.

RESULTS

Simulated population

The discriminative ability of the true risk model in the control arm of the population was moderate with an area under the receiver operating characteristic curve of 0.66. The event rates in the control arm were 14.7%, 21.2%, 28.9% and 43.3% in true risk quartiles 1–4 respectively. With a main treatment effect odds ratio of 0.8 (the “base case”), these event rates were reduced by absolute treatment benefits of 2.4%, 3.3%, 4.2% and 5.1%, respectively. With a main treatment effect odds ratios of 0.5, these event rates were reduced by absolute treatment benefits of 6.8%, 9.2%, 12.0% and 15.4%, respectively.

Risk models

When the risk model was fitted in the whole sample, the benefit in quartiles of predicted risk in the sample was well calibrated to the ‘true’ benefit in quartiles of predicted risk in the population (figure 1A). This was true regardless of the sample size (Figure A.1A), the treatment effect magnitude and whether the data was generated by a regression model with or without treatment interactions (Figures A.1A and A.2A). In contrast, when the risk model was fitted in only the control patients of the sample, the benefit in quartiles of predicted risk was more heterogeneous in the sample as compared to the population, i.e. the benefit in the first risk quartile was substantially lower in the sample than in the population while the benefit in the fourth risk quartile was substantially higher in the sample than in the population, reflecting differential fit (i.e. overfitting) of the model on the sample control arm compared to the treatment arm. For example, in the base case scenario (treatment odds ratio of 0.8; sample size 3,600; figure 1B), the median benefit in the highest risk fourth quartile (6.5%) of the sample was 30% higher than the median benefit in this quartile (5.1%) of the population. Similarly, the median benefit in the lowest risk first quartile (1.7%) of the sample was 30% lower than the median benefit in this quartile (2.4%) of the population. Even where there was no treatment effect whatsoever (treatment odds ratio of 1; Figures A.1B and A.2B), modeling in the control arm induced a spurious risk-by-treatment effect interaction, which was more often statistically significant (in 9.6% of the samples) than expected under the null condition of no treatment effect interaction (5%). This effect attenuated but persisted even when the sample was very large (n=7,200; Figures A.1B and A.2B), with an event-per-variable (EPV) ratio of 81.

Figure 1. Risk modeling on only the control patients led to an exaggeration of the treatment effect heterogeneity across predicted risk quartiles.

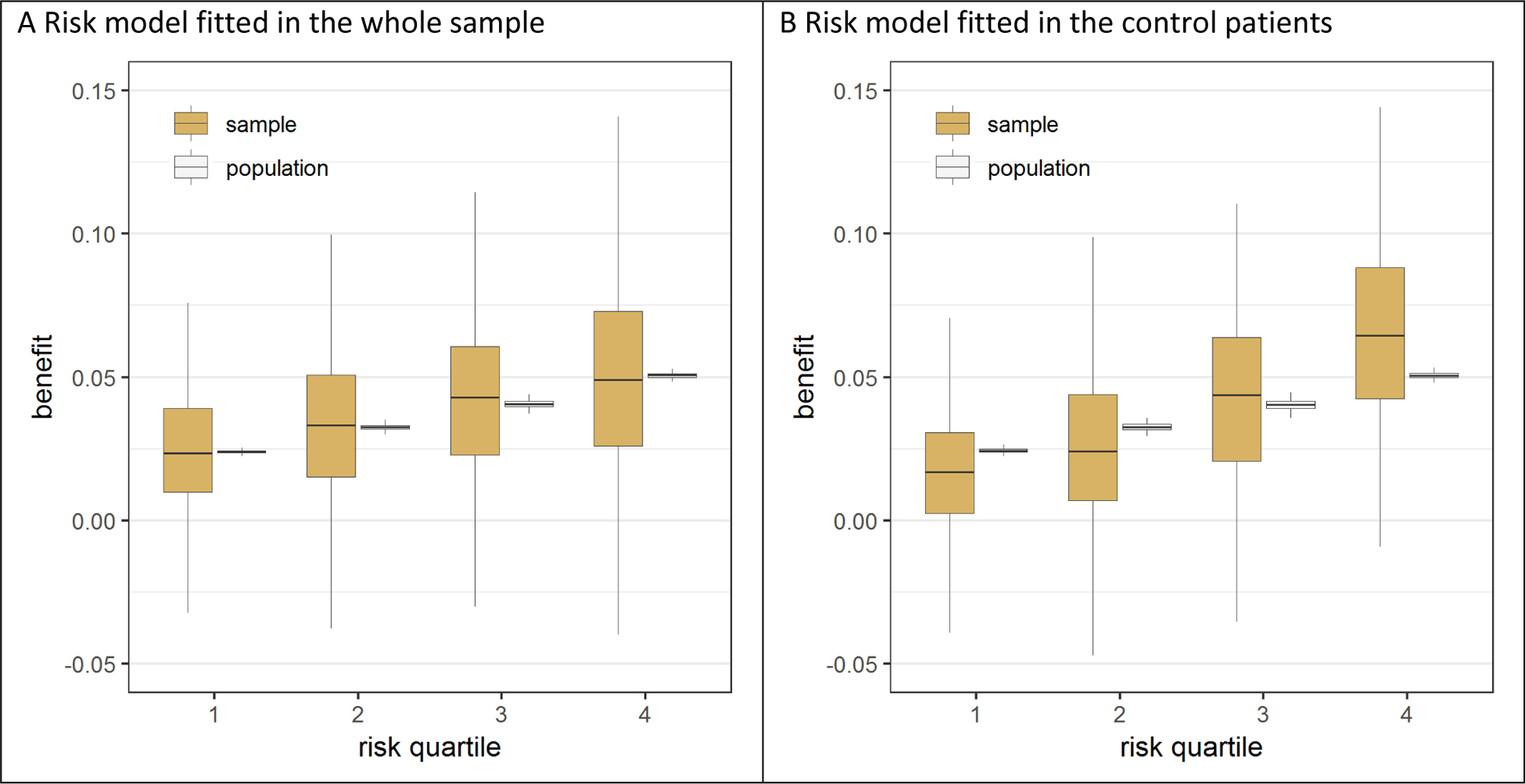
In the base case simulation scenario without true interaction, the risk model was fitted in either the whole sample or in the control patients of the sample. When the model fitted on the whole sample was used for stratification in risk quartiles (panel A), the observed benefit in the sample (brown bars) is an unbiased estimate of the observed benefit in the population (white bars). In contrast, when the model fitted on the control patients was used for stratification in risk quartiles (panel B), the observed benefit in the sample is too heterogeneous across risk quartiles compared to the observed benefit in the population.

Treatment effect models

General

Using backward selection in the base case scenario (treatment odds ratio of 0.8; sample size 3,600), 90% of the true prognostic factors and 48% of the true interactions were kept in the model (true positive), while 29% of the null prognostic factors and 17% of the null interactions were kept in the model (false positive; table A.1). With Lasso regression 95% of the true prognostic factor effects and 75% of the true interaction effects were kept in the model (true positive), while 55% of the null prognostic factor effects and 54% of the null interaction effects were kept in the model (false positive). As expected, for backward selection the true positive rate increased with sample size with a stable false positive rate. For Lasso regression, both the true and the false positive rate increased with sample size, but the effect sizes of the retained variables were shrunk.

Calibration-for-benefit

In the absence of true treatment interactions, the model with a constant relative treatment effect was well calibrated (figure 2A), while all the models that included treatment interactions overfitted treatment benefit (figure 2B, 2C and 2D; figure A.3). In the base case scenario (treatment odds ratio of 0.8; sample size 3,600), the mean difference between predicted and observed benefit (i.e. miscalibration), averaged over the two extreme predicted benefit quartiles, was 6.1% for the model with all interactions (3.8% after backward selection), but was reduced by 60% to 2.5% when that model was fitted with Lasso regression (figure A.3D). For the population generated from the “hard null” assumptions (no treatment effect, no interactions), the models spuriously identified groups with treatment-related harm and benefit. The mean difference between predicted and observed benefit, averaged over the two extreme predicted benefit quartiles, was even larger than in the base case scenario (6.4% for the model with all interactions, 4.4% after backward selection, and 3.0% with Lasso regression; figure A.4).

Figure 2. Effect modeling approaches were seriously overfit and were prone to treatment mistargeting in the absence of true treatment interaction.

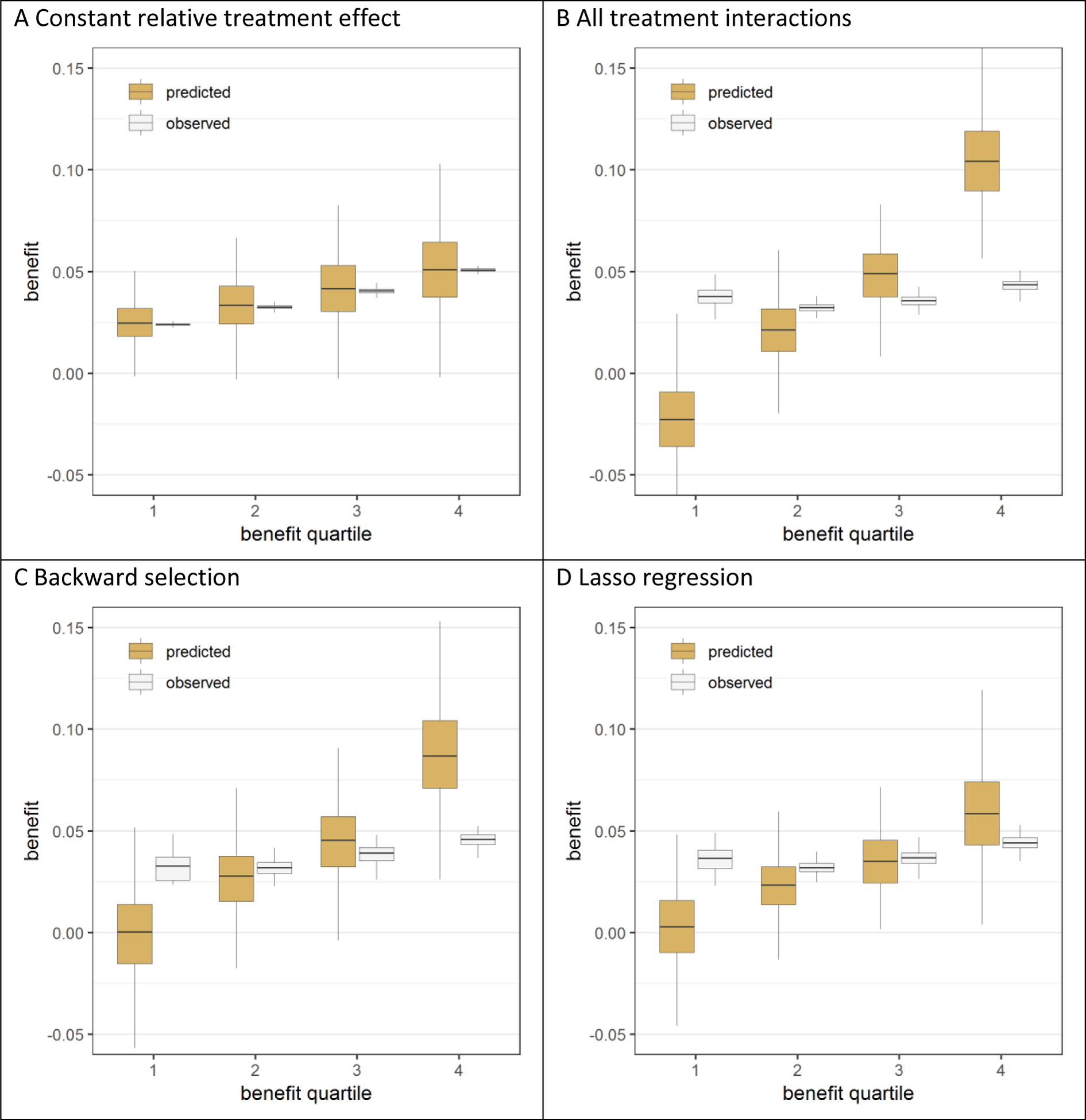
Benefit predictions were based on different models fitted in the samples: a model without treatment interactions (panel A), a model with all treatment interactions (panel B), a model with all treatment interactions using backward selection based on AIC (panel C), and a model with all treatment interactions fitted with Lasso regression (panel D). The agreement between predicted (brown bars) and observed (white bars) benefit in predicted benefit quartiles of the population was better for the risk modeling approach (A) compared to the effect modeling approaches (B-D). Moreover, the risk modeling approach (A) resulted in more heterogeneity of observed benefit, i.e. is better able to distinguish between patients with low and patients with high benefit.

In the presence of true treatment interactions all models overfitted treatment benefit, but to a varying extent (figure 3; figure A.5). Overfitting increased with the number of modeled treatment interactions. In the base case scenario (treatment odds ratio of 0.8; sample size 3,600), the mean difference between predicted and observed benefit, averaged over the two extreme predicted benefit quartiles, was only 0.9% for the model with a constant relative treatment effect and 4.4% for the model with all interactions. Backward selection only slightly reduced the overfitting (3.5% difference). In contrast, Lasso regression considerably reduced, but did not eliminate, the overfitting (1.5% difference), even for the larger sample size (Figures A.6–A.9). Additionally, even when just two “established” predictors were forced into the model without any statistically driven model selection, overfitting for benefit prediction persisted (1.0% difference). Overfitting for the prediction of benefit was relatively much stronger than overfitting for outcome prediction (Figure A.10). Finally, overfitting for the prediction of benefit also persisted even though Lasso regression with minimum mean cross-validated error essentially eliminated miscalibration for outcome prediction (Figure A.11).

Figure 3. Effect modeling approaches were better able to separate patients with differential benefit in the presence of true treatment interaction, but required penalized regression to prevent overfitting.

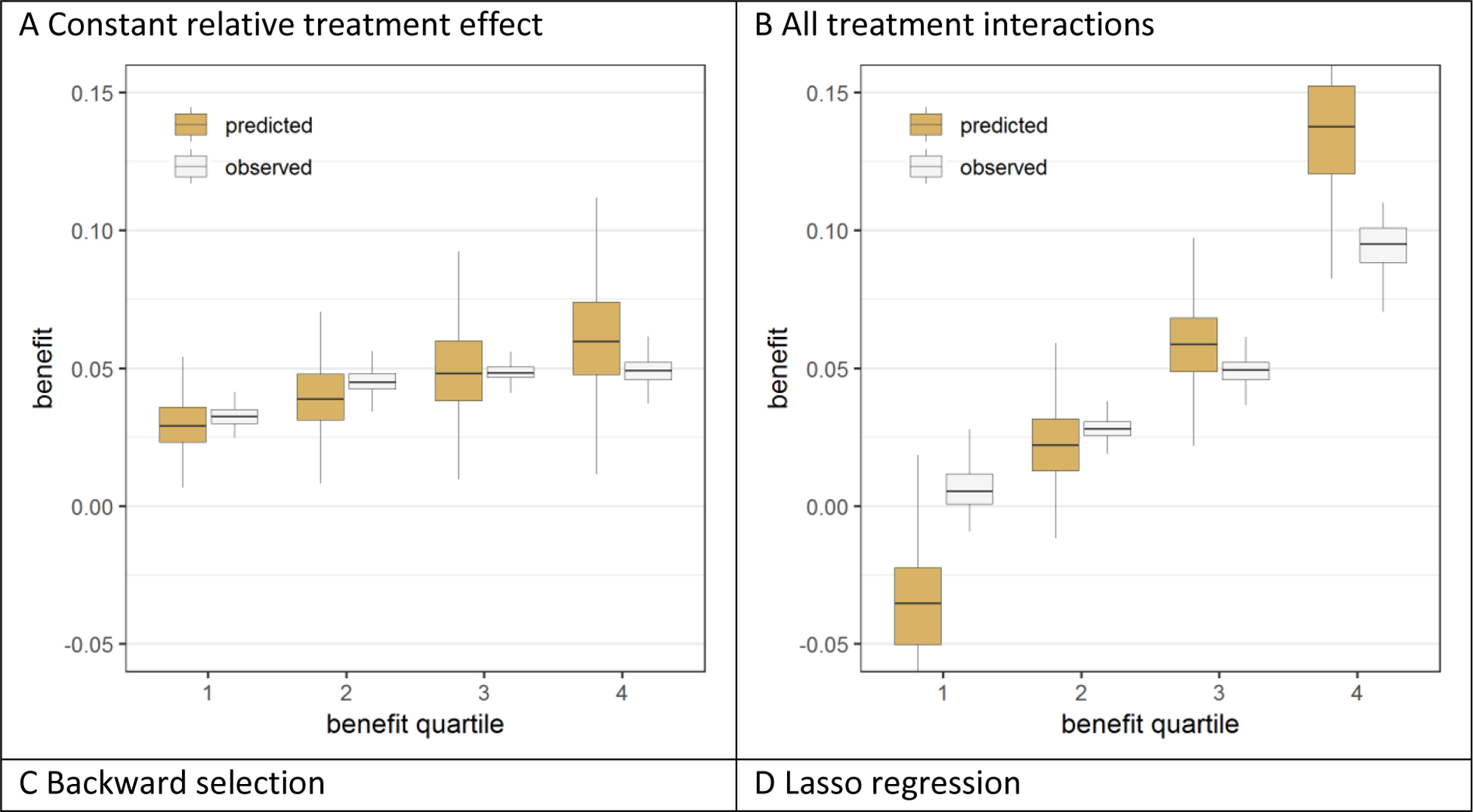
Benefit predictions were based on different models fitted in the samples: a model without treatment interactions (panel A), a model with all treatment interactions (panel B), a model with all treatment interactions using backward selection based on AIC (panel C), and a model with all treatment interactions fitted with Lasso regression (panel D). The agreement between predicted benefit (brown bars) and observed benefit (white bars) in predicted benefit quartiles of the population is better for both the risk modeling approach (A) and the Lasso regression approach (D) compared to the unpenalized effect modeling approaches (B-C). However, the Lasso regression approach (D) resulted in more heterogeneity of observed benefit than the risk modeling approach (A), i.e. is better able to distinguish between patients with low and patients with high benefit.

Models that were fitted with Lasso regression performed consistently better than models that were fitted with Ridge regression, especially in the absence of true treatment interaction (Figures A.7 and A.9). Furthermore, models that were fitted using penalized regression with minimum mean cross-validated error (“Standard Lasso”) consistently outperformed models that were fitted using penalized regression with maximum penalization, such that the error is within one standard error of the minimum (“Strong Lasso”). In the remainder of the results, we will therefore limit the presentation of penalized regression models to Lasso regression with minimum mean cross-validated error (“Standard Lasso”).

Discrimination-for-benefit

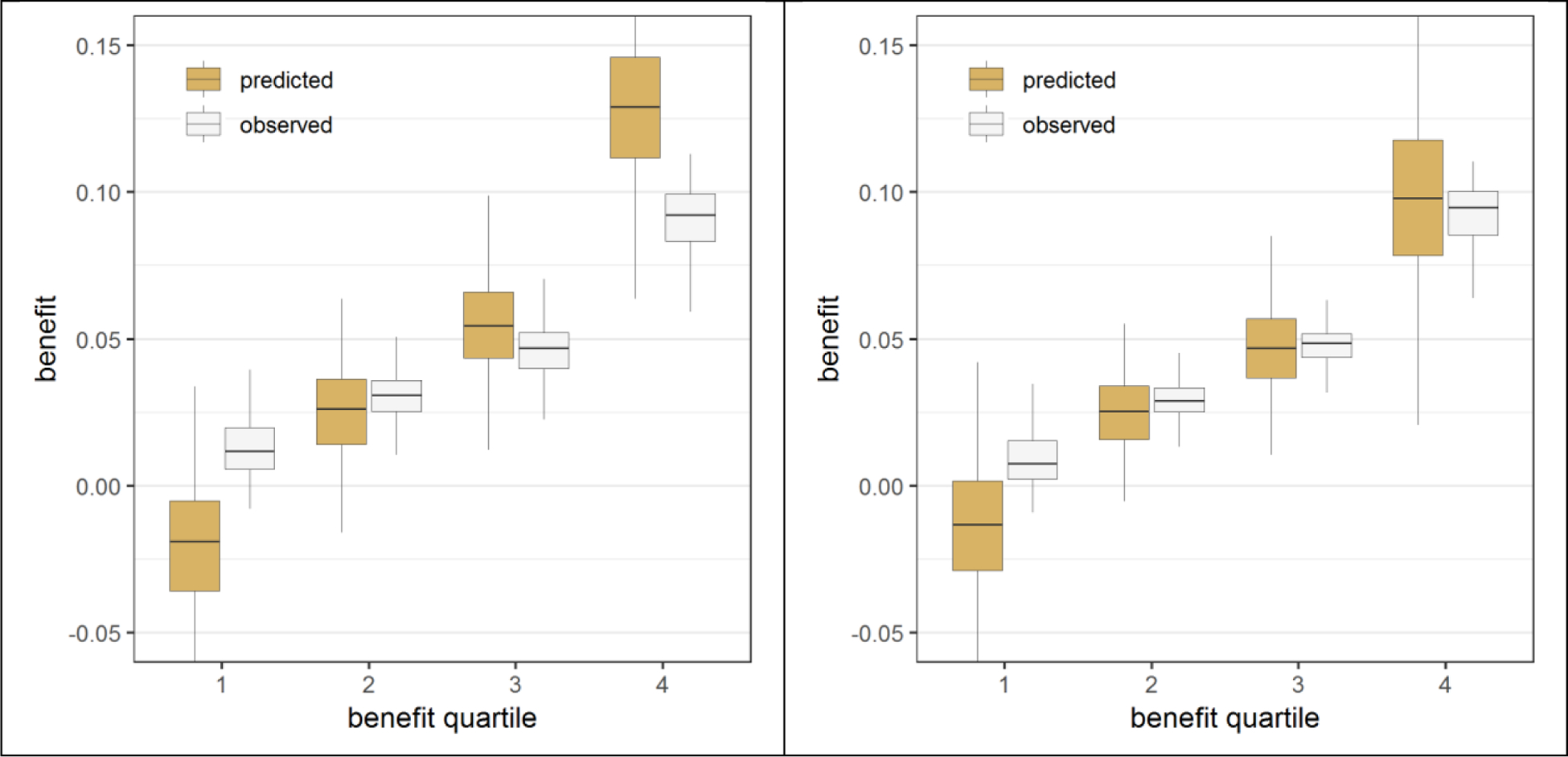
In the absence of true treatment interactions, the extreme quartile difference (EQD) of benefit in the population of the model with the constant relative treatment effect (2.7% in the base case scenario) was almost equal to the potential maximum as defined by the true model (figure 4). This means that we observe 2.7% more absolute treatment benefit in the 25% of patients with the highest compared to the 25% of patients with the lowest predicted benefit according to the model; this corresponds to more than a doubling of the effect size. Despite the fact that models with interaction terms misleadingly appeared to have substantially higher EQDs within the sample (indicating better discrimination for benefit), the population EQD decreased as the number of interactions in the model increased, indicating worse discrimination than risk modelling. Lasso regression moderately improved the population discrimination (0.8% EQD) compared to conventional maximum likelihood regression (0.6% EQD), but did not reach the potential maximum (2.7% EQD), even for the largest sample size (Figure A.12).

Figure 4. The risk modeling approach (Constant relative treatment effect) discriminated best in the absence of true interactions, but left considerable treatment benefit heterogeneity undetected in the presence of true interactions.

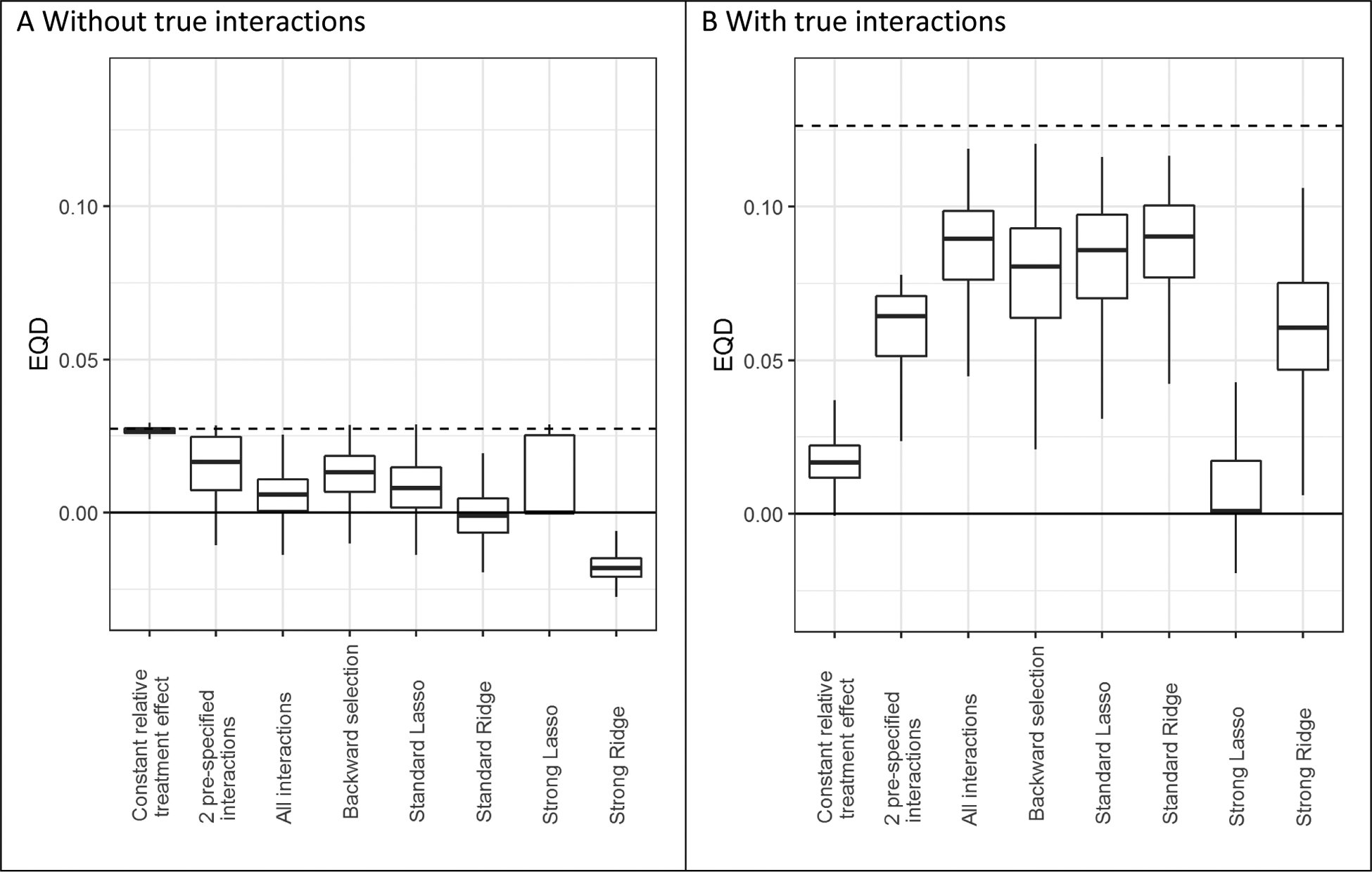
Extreme quartile difference (EQD) represents the difference between the observed benefit in the fourth quartile and the observed benefit in the first quartile of the population in base case simulation scenarios without true interactions (panel A) and with true interactions (panel B). The maximum achievable EQD of the true model is represented by the dashed horizontal lines. In the presence of true interactions (B), penalized regression approaches (Standard Lasso and Standard Ridge) discriminated similarly to unpenalized regression (All interactions).

In the presence of true treatment interactions, the population EQD of the model with a constant relative treatment effect was lowest (1.7% in the base case scenario), representing poor benefit discrimination. In the presence of true treatment interactions, Lasso regression showed very similar discriminative ability compared to conventional maximum likelihood regression (population EQD of 8.6% versus 9.0% in the base case scenario) and somewhat better discriminative ability than backward selection (population EQD of 8.1%). The difference in population EQD between the model with a constant relative treatment effect and other models was limited when the sample size was low (1,800) and the treatment effect was large (OR 0.5; Figure A.12).

Prediction error-for-benefit

In the absence of true treatment interactions, the rMSE of the individual estimated treatment benefits versus the true individual treatment benefits increased with the number of modeled treatment interactions (figure 5). In the base case scenario (treatment odds ratio of 0.8; sample size 3,600), the rMSE was 0.013 for the model with a constant relative treatment effect and 0.053 for the model with all interactions. Lasso regression decreased the rMSE considerably to 0.029, but did not outperform the model with two pre-specified treatment interactions (0.024), even in the largest sample size (Figure A.13).

Figure 5. The risk modeling approach (Constant relative treatment effect) had minimal prediction error in the absence of true interactions, but was outperformed by penalized regression approaches (Standard Lasso or Ridge) in the presence of true interactions.

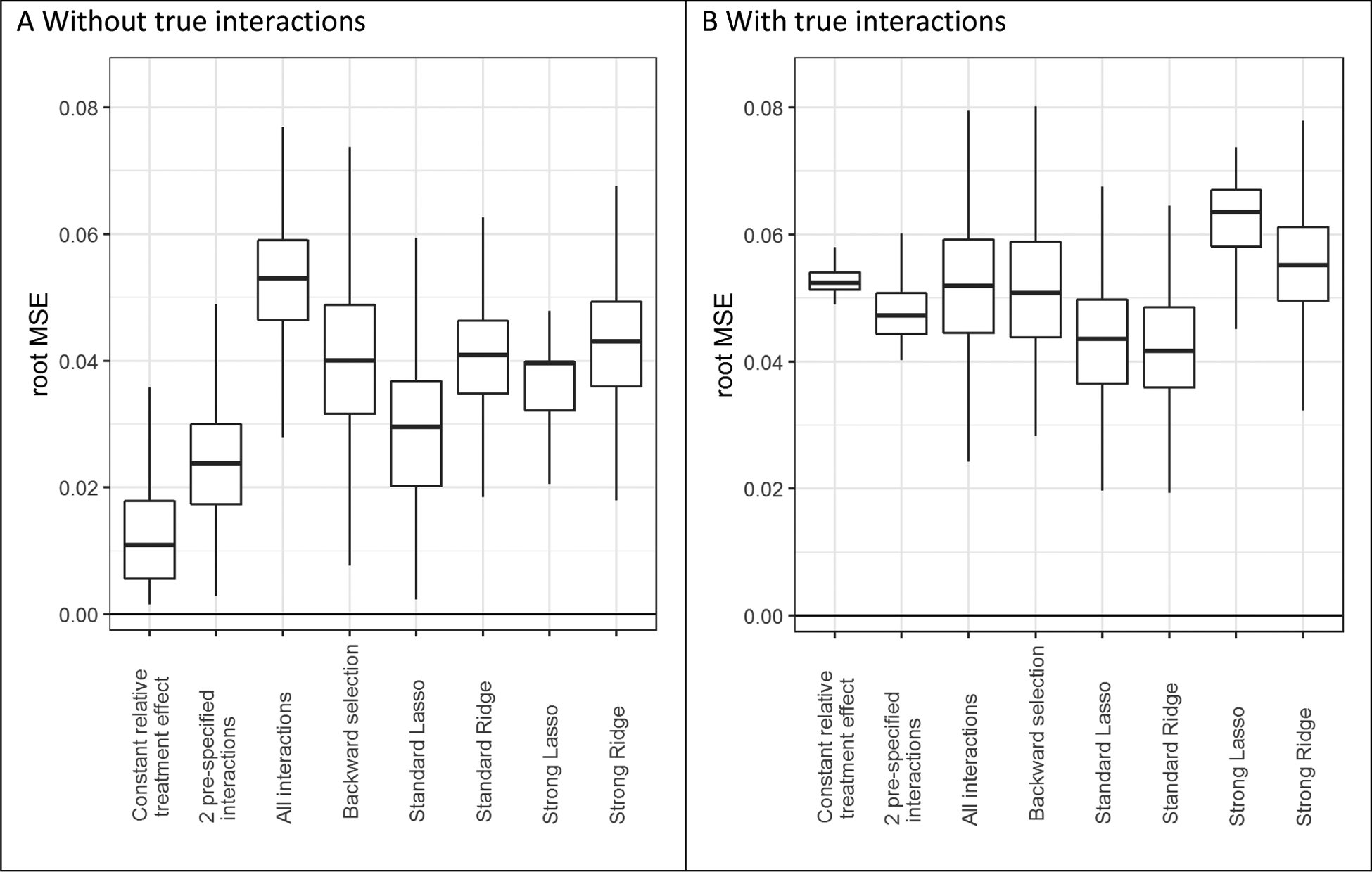
The root mean squared error (rMSE) represents the root of the mean of the square differences between predicted benefit and true benefit in the population for base case simulation scenarios without true interaction (panel A), and with true interaction (panel B).

In the presence of true treatment interactions, (unpenalized) models with interactions only outperformed the model with a constant relative treatment effect with large sample size (n=7,200; Figure A.14). For example, in the base case scenario (treatment odds ratio of 0.8; sample size 3,600), the rMSE was 0.053 for the model with a constant relative treatment effect and 0.052 for the model with all interactions (figure 5). Lasso regression decreased the rMSE considerably (0.043), but moderate sample size (n=3,600) was needed for Lasso to outperform the model without treatment interactions or with two pre-specified treatment interactions.

Sensitivity analyses

When continuous rather than binary baseline characteristics were simulated, the results were much the same (Figures A.15–A.18). When the baseline characteristics were correlated rather than independent, the results were also very similar in the absence of true treatment interactions (Figures A.19; A.21A; A.22.A). In the presence of true treatment interactions however, when baseline characteristics were correlated, the advantage of Lasso regression over a model with a constant relative treatment effect attenuated (Figures A.20; A.21B; A.22.B). Less diversity in the possible combinations of strongly correlated baseline characteristics clearly reduced the additional discriminative ability that can be achieved by treatment interactions with individual baseline characteristics.

DISCUSSION

This simulation exercise illustrates the serious overfitting that can arise when developing models to predict heterogeneous treatment effects in randomized samples. We have shown that overfitting of treatment effect heterogeneity can significantly overestimate (and underestimate) the treatment benefit for a substantial proportion of patients, potentially leading to suboptimal treatment decisions. The magnitude of the miscalibration of predicted benefit when treatment interaction terms are incorporated into a prediction model is relatively much larger than the miscalibration typically observed when stratifying a trial by predicted outcome risk, and potentially much more clinically influential. Standard heuristics used to avoid overfitting models to predict outcome risk (e.g. 10 or 20 outcomes for each variable or interaction term considered [10, 11]) are grossly inadequate to avoid this overfitting. Overfitting for predicted benefit persisted despite approaches that are usually effective for eliminating overfitting for outcome risk (such as penalized regression and a parsimonious non-data-driven approach including only two “established” effect modifiers), and even with large sample sizes.

In the absence of true treatment interactions, a prediction model without treatment interactions – i.e. a risk modelling approach – has superior predictive performance, even for large sample size. Our simulations also confirm a prior study showing that, with a risk modelling approach, modelling on the control arm only induces serious overfitting that can be completely eliminated by modelling on the whole population, blinded to treatment [6]. Even in the absence of any treatment effect and with an event-per-variable (EPV) ratio over 80, modeling in the control arm induced a spurious risk-by-treatment effect interaction. To understand this phenomenon, one can imagine a model fitted only to the noise of the control arm. Using this model, the treatment arm would appear to have a uniform ‘average’ risk, while the control arm would seem well stratified. In such a scenario, high risk patients would erroneously be expected to benefit and low risk patients would erroneously be expected to be harmed by a totally ineffective treatment.

When true interactions are present, risk modeling still provides well-calibrated predictions, although it does not discriminate as well as models including interaction terms. Of the effect modeling approaches compared, Lasso regression proved to be the optimal approach to minimize overfitting of treatment benefit. Interestingly, some overfitting for the prediction of benefit persisted even though Lasso regression leads to excellent calibration of predicted outcome risk in both trial arms, underscoring the importance of using metrics for benefit prediction rather than relying on conventional prediction metrics when validating models that predict benefit.

Intuitively, benefit prediction is more sensitive to miscalibration than risk prediction, because relatively small discrepancies in observed versus predicted outcome rates in the control and treatment arms can add up to large discrepancies in absolute treatment effects (Figures A.10 and A.11). In addition, because the scale of absolute risk difference is generally much smaller than the scale of outcome risk, the error will be comparatively large (i.e. magnified). Further, differences in treatment effects can be extremely consequential for clinical decision making. This can be illustrated most dramatically by the effect models that were developed in samples from the population simulated with the “hard null” assumption (of no treatment effect). With 12 null treatment interactions, statistically significant HTE was found 87% (1-(1–0.157^12)) of the time, an issue that cannot be corrected with even larger sample sizes. Inclusion of more candidate predictors with their potential treatment interactions – for example in a case study of high-dimensional data – would have increased the number of false positive treatment interactions and would presumably have increased the degree of overfitting when predicting benefit. For these reasons, effect modeling should be applied cautiously, particularly in the absence of a well-established overall treatment effect.

Previously published treatment effect models to support decision making in reperfusion therapy for both coronary artery disease and for acute stroke were developed with conventional maximum likelihood estimation [12–14]. This simulation shows that the treatment benefit predictions from these models are likely to be overfit, even when the treatment interactions are clinically and biologically plausible. Assessment of treatment benefit calibration in new settings is required to better understand the validity of these models. Recalibration using penalized regression techniques may improve the ability of these models to predict treatment benefit [15, 16]; this was well-demonstrated in a re-analysis of the SPRINT trial comparing conventional regression to elastic net regularization (an amalgam of Ridge and Lasso) [17]. When tested on a separate but related clinical trial, predictions of benefit generated with conventional regression were virtually useless but those generated with elastic net regularization validated substantially better. Nevertheless, the best approach to penalization is a subject for future research.

In our simulations, models that were fitted with Lasso regression performed consistently better than models that were fitted with Ridge regression, although both were significantly overfit for benefit across most of the simulated scenarios. We hypothesize that Lasso more stringently penalizes null treatment interaction effects. More research is required to better understand the differences between using Lasso or Ridge regression for models that predict treatment benefit, and also to compare these to other (regression- and non-regression-based) approaches used for data-driven benefit prediction [18, 19]. Since penalization reduced the overfitting of benefit predictions, one might anticipate that stronger penalties would further improve benefit predictions. However, models that were fitted using penalized regression with maximum penalization, such that the error is within one standard error of the minimum, performed substantially worse than models that were fitted using penalized regression with minimum mean cross-validated error. The more stringent penalization of these methods seem to overly shrink the average treatment effect, resulting in poor calibration even in the middle quartiles of predicted benefit.

When true interactions are present in the data, discrimination improved with models incorporating interaction terms (i.e. an effect modeling approach always provided superior discrimination to a risk modeling approach). However, the effect modeling approaches were consistently overfit. The trade-off in terms of clinical decision making between the improved discrimination and worse calibration resulting from the more aggressive effect modeling approaches will depend on the specific decisional context of each case. More research is needed to determine those circumstances where the trade-offs are likely to favor these more aggressive approaches. Because these effect modeling approaches can mislead investigators into falsely “discovering” subgroup treatment effects even when no treatment effects exist, and even in large simulated databases, we recommend caution in applying these approaches, pending future research. These approaches might be applied in situations in which there is sufficient randomized data to permit fully external model validation, and in situations with a priori evidence for important treatment interactions.

Benefit prediction approaches are useful in targeting treatment to those patients most likely to benefit, especially when treatment is associated with some treatment-related harm or burden. When we added a constant treatment-related harm – i.e. we added outcomes with a 2.5% event rate in the treatment arm regardless of the risk factors – most of the findings were very similar (data not shown). The additive harm induced some interaction with risk on the relative scale, which the risk modeling approach unsurprisingly could not pick up. However, this led to a slight underfitting of the treatment effect heterogeneity by the risk modeling approach, in contrast with the general finding of overfitting the treatment effect heterogeneity by the effect modeling approaches.

As with all simulations, we were limited in covering the entire relevant space of risk and effect modelling in these simulated clinical trials. We attempted to emulate common scenarios. However, the benefits of the risk modelling approach (compared to a conventional one-sized-fits-all approach) may be limited since the risk-heterogeneity within these simulated trials is relatively modest (c-index = 0.66). We have found extreme quartile risk ratios substantially larger in a recent empirical evaluation [20]. We also note that several aspects of the simulated trial population make it a relatively favourable setting for effect modelling, including the fact that 50% of tested interactions include ‘true’ effects, some true effects were known a priori, and there were abundant outcomes. Nevertheless, our results consistently indicated problematic and resilient overfitting when an effect modelling approach was attempted. Risk modelling, on the other hand, when performed on the whole trial population, yielded well calibrated treatment effects within risk strata, even in the presence of treatment interaction terms that were excluded from the model. We expressed calibration-for-benefit and discrimination-for-benefit of each modelling approach in terms of quartiles of predicted benefit. A more detailed stratification – e.g. into octiles or deciles of predicted benefit – would have emphasized the degree of overfitting through more extreme miscalibration in the lowest and highest strata of predicted benefit. Although calibration-for-benefit and discrimination-for-benefit can also be expressed on a continuous scale, e.g. with a c-statistic and an E-statistic [21, 22], the quartile-based presentation has the advantage of being illustrative for the actual use of these models in clinical practice. Future research could enable more individualized approaches to implementing predictive models in clinical practice.

In conclusion, predicting heterogeneous treatment effects has substantial challenges beyond prediction of outcome risk. A risk-modeling approach yields models consistently well-calibrated for benefit. Effect-modeling may improve discrimination-for-benefit in the presence of true interactions, but are prone to serious overfitting; they should only be considered when important treatment interactions are highly likely. Even under these circumstances, penalized approaches should be favored and external validation remains very important.