Transition-State Vibrational Analysis and Isotope Effects for COMT-Catalyzed Methyl Transfer

Abstract

Isotopic partition-function ratios (IPFRs) computed for transition structures (TSs) of the methyl-transfer reaction catalyzed by catechol O-methyltransferase and modeled by hybrid QM/MM methods are analyzed. The ability of smaller Hessians to reproduce trends in α-³H₃ and ¹⁴C_α IPFRs as obtained using the much larger subset QM/MM Hessians from which they are extracted is investigated critically. A 6-atom-extracted Hessian reproduces perfectly the α-T₃ IPFR values from the full-subset Hessians of all the TSs but not the α-¹⁴CIPFRs. Average AM1/OPLS-AA harmonic frequencies and mean-square amplitudes are presented for the 12 normal modes of the α-CH₃ moiety within the active site of several enzymic transition structures, together with QM/MM potential energy scans along each of these modes to assess the degree of anharmonicity. A novel investigation of ponderal effects upon IPFRs suggests that the value for α-¹⁴C tends toward a limiting minimum whereas that for α-T₃ tends toward a limiting maximum as the mass of the rest of the system increases. The transition vector is dominated by motions of atoms within the donor and acceptor moieties and is very well described as a simple combination of Walden-inversion “umbrella” bending and asymmetric stretching of the SC_α and C_αO bonds. The contribution of atoms of the protein residues Met40, Tyr68, and Asp141 to the transition vector is extremely small. Average valence force constants for the COMT TS show significant differences from early BEBOVIB estimates which were used in support of the compression hypothesis for catalysis. There is no correlation between TS IPFRs and the nonbonded distances for close contacts between the S atom of SAM and Tyr68 or between any of the H atoms of the transferring methyl group and either Met40 or Asp141.

Introduction

The transition state (TS) has been a cornerstone of physical organic chemistry for many years and has provided a useful foundation for discussions of reaction mechanisms in solution and in enzymes. To quote Gandour and Schowen, “Every dynamical problem of biochemistry finds its most elegant and economical statement in terms of [TS] theory. Enzyme catalytic power, for example, derives from the interaction of enzyme and substrate structures in the transition state, so that an understanding of this power must grow from a knowledge of these structures and interactions.”¹ These authors acknowledged that the form of any complete description might need to go beyond “present-day” TS theory, and the concept of the TS has recently been reassessed in the light of developments of computer simulations of chemical reactions in condensed-phase systems,² but the elegance and economy of Schowen’s “fundamentalist” view remains: the entire and sole source of catalytic power is TS stabilization.³ Moreover, from this point of view, details of specific structures and pathways encountered between the reactant state (RS) and TS (as described by so-called “canonical” formulations of enzyme catalysis)³ are unimportant, just as the difference between two thermodynamic functions of state is independent of the path that connects those states.

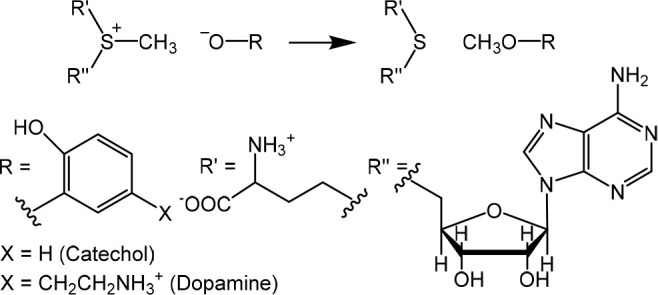
Methyl transfer catalyzed by catechol O-methyltransferase (COMT) is a reaction of considerable topical interest in its own right³⁻⁷ but which has also served as a testbed for ideas about the origins of enzymic catalysis⁸⁻¹⁶ and the role of kinetic isotope effects (KIEs) as probes for reaction mechanism and transition-state (TS) structure.¹⁴⁻¹⁶ The experimental observation of a much more inverse secondary α-deuterium kinetic isotope effect (2° α-D KIE) k(CH₃)/k(CD₃) for methyl transfer (Scheme 1) to catecholate anion from S-adenosyl-l-methionine (SAM), catalyzed by COMT at 37 °C in water,⁸ than for uncatalyzed methyl transfer to methoxide anion from S-methyldibenzothiophenium cation at 25 °C in methanol⁹ was originally interpreted as evidence of compression by the enzyme causing a tighter S_N2 TS than for the nonenzymic reaction.¹⁰ However, hybrid quantum-mechanics/molecular mechanics (QM/MM) calculations reproduced the trend in the 2° α-D₃ KIEs without evidence of compression,^12,13 but more recent experiments for wild-type (WT) and mutant human COMTs were interpreted as fresh evidence in favor of active-site compression (or “compaction”)^14,16 as opposed to an electrostatic explanation.^11,15,20,21

Scheme 1. Methyl Transfer Reactions Catalyzed by COMT.

Computational studies on model systems have employed a variety of techniques. Ab initio QM calculations for (ultra)simple models indicated the validity of compression as a possible stratagem for catalysis^17,18 but could not comment upon the specific case of COMT. Seminal bond-energy/bond-order vibrational analysis (BEBOVIB) calculations provided early support for the compression hypothesis¹⁰ but were always open to concern regarding the fundamental lack of data for TS geometries and force constants.¹⁹ This empirical modeling method uses estimated geometries and valence force constants to compute vibrational frequencies and KIEs for isotopically substituted RS and TS.¹⁰ The HC_αS and HC_αO bending force constants, involving a methyl H atom and either the nucleofuge S or the nucleophile O atom, were significantly larger in the QM/MM TS than in the reactant structure (RS), both in the COMT active site and in solution;^12,13 in contrast, TS bending force constants used in the BEBOVIB modeling were obtained by use of a rule that took the product of the RS force constant (for HC_αS) or the product structure (PS) force constant (for HC_αO) and the appropriate TS bond order (B_CS or B_CO) which always had a value < 1; the TS bending force constants were, therefore, always less than the corresponding RS (or PS) value. In order to calculate an inverse 2° α-D KIE to match that of the enzymic reaction, it was necessary to use larger values for B_CS or B_CO than for the uncatalyzed reaction. The apparently shorter bond lengths for the C_α···S and C_α···O partial bonds in the TS were probably an artifact of the arbitrary rule used to generate TS bending force constants within BEBOVIB.¹⁹

The experimental KIEs reported by Klinman and co-workers^14,16 for methyl transfer catalyzed by WT and mutant COMT are isotope effects upon k_cat/K_m measured under nonsaturating conditions; this implies that the RS is the methyl donor SAM in aqueous solution and that each KIE is determined by the isotopic difference in Gibbs energy of activation between the same RS and each particular TS. In other words, differences between KIEs for different enzyme structures arise purely from differences in their respective TSs.

It is often assumed that trends in KIEs may be related to structural changes in TSs understood in terms of geometries and bond orders,^10,22 but recent computational studies have suggested that changes in the electrostatic environment of a TS^20,21,23,24 or its stabilization by C_αH···O hydrogen-bonding interactions might also be significant.^21,25 As part of a program of investigation into factors underlying 2° KIEs and their meaningful interpretation, the possible contribution of anharmonicity has also been considered, but this has not been found to be significant for equilibrium isotope effects (EIEs).^26,27 The matrix of second derivatives of energy with respect to Cartesian coordinates (the Hessian) plays a key role in the theory of molecular vibrations and of isotope effects, since its mass-weighting and diagonalization leads to the normal modes and associated harmonic frequencies; the same Hessian is used for each isotopologue with different masses as appropriate. QM/MM modeling of EIEs or KIEs based upon the isotopic sensitivity of harmonic frequencies is invariably “supramolecular” in nature, involving a subset Hessian for the RS and TS, rather than “molecular” and involving a Hessian for the entire system.¹⁹ Moreover, modeling of large, flexible systems requires averaging over thermally accessible configurations. How many configurations need to be sampled in order to obtain a reliable mean value for a KIE or EIE depends on how many significant figures are required.²⁷ How large does the subset Hessian need to be? This remains a question of interest and practical importance. Remarkably, it has been found that EIEs for transfer of a carbocation between media of differing polarity may be reproduced by an “atomic” Hessian for a single isotopically substituted atom. However, the values of the force constants in this symmetrical 3 × 3 matrix must accurately reflect the influence of the whole supramolecular environment.²⁴

The purpose of this paper is to investigate how large the subset Hessian needs to be in order to obtain reliable mean KIE values for COMT-catalyzed methyl transfer and to consider the validity of the harmonic approximation. Since it is not our present purpose to offer a definitive computational model to reproduce KIEs and trends in their values for mutant COMTs, our analysis is restricted to consideration of TS isotopic partition function ratios (IPFRs) evaluated using the semiempirical AM1 Hamiltonian within a QM/MM model. The ratio ⟨f_RS⟩/⟨f_TS⟩ of average IPFR values for the reactant state and the transition state yields a KIE, and each IPFR corresponds to the Gibbs-energy stabilization (ΔG = −RT ln f) of a system due to substitution by a heavier isotope: vibrational frequencies are lowered, f is always > 1 and so ΔG < 0. However, because the RS is always free SAM in water, the value of ⟨f_RS⟩ remains constant (for a given temperature and theoretical method); variation between KIE values depends only on the TS IPFRs for rate-determining methyl transfer and not on IPFRs for any other species (such as the Michaelis complex) traversed along the reaction path between RS and TS.

A recent computational study of methyl cation within a model cage of constrained water molecules reported the vibrational analysis of the 12 degrees of freedom of Me⁺ within its cage.²⁸ The 3 translations and 3 rotations of the Me⁺ moiety were treated as harmonic vibrations, whose frequencies were determined by the dimensions of the cage through nonbonding interactions between the “substrate” and the “catalyst”. Here a similar approach is applied to perform vibrational analysis upon the transferring methyl moiety in the COMT-catalyzed reaction 1.

Computational Methods

Initial coordinates were taken from the X-ray crystal structure²⁹ of a COMT/SAM/inhibitor complex; the 3,5-dinitrocatechol inhibitor was replaced by the substrate dopamine (DOP) with the terminal amine protonated and one catechol hydroxyl group deprotonated. The smallest QM region contained SAM and DOP (72 atoms) and was described by AM1, while the remainder of the enzyme and solvating water molecules formed the MM subsystem described by OPLS-AA³⁰ and TIP3P³¹ potentials, respectively (3347 enzyme atoms, Mg²⁺, 5Na⁺, and 15572 water molecules within a cubic box of side 79.5 Å). The fDynamo library^32,33 was used to perform QM/MM potential of mean force (PMF) calculations with respect to the antisymmetric combination of the breaking C···S and forming C···O bond lengths, with harmonic umbrella sampling³⁴ using a force constant of 2500 kJ mol^–1 Å^–2 on the reaction coordinate. Within each overlapping window, an NVT molecular dynamics simulation was performed at 310 K using periodic boundary conditions: 10 ps of relaxation plus 20 ps of production. The PMF is depicted in Figure S1. From the window corresponding to the maximum Helmholtz energy, a representative structure was selected and a 500 ps QM/MM MD simulation was performed, with the system restrained to remain in the transition-state region. The value of the force constant used to restrain the distinguished reaction coordinate was 10 000 kJ mol^–1 Å^–2. From this simulation, structures were selected and were each then refined and characterized as a first-order saddle-point by means of QM/MM methods using a microiterative approach implemented in a modified fDynamo library.

TS optimizations were performed for QM regions of varying size, and in each case the subset Hessian was comprised of the same atoms. In addition to the 72-atom core, amino-acid residues with any atom within a distance of 4, 5, 6, or 7 Å of the transferring methyl C_α atom were included (along with Mg²⁺), resulting in QM regions and Hessians containing 127, 180, 225, and 299 atoms in total, respectively (Figure 1 and Figure S2). Further sets of transition structures were obtained for systems that included only the side chains of those residues within each of the distance-selection criteria. Mass-weighting and diagonalization of these subset Hessians yielded 3N_s nonzero harmonic vibrational frequencies (for an N_s-atomic subset), from which molecular partition functions q and IPFRs (f_TS) were obtained by means of eqs 1–5 as implemented in the UJISO program from the SULISO suite of utilities.^19,35

1

2

3

4

5

Here u_i = hcω_i/k_BT, ω_i is an unscaled harmonic frequency (as a wavenumber/cm^–1), ω₁ is the modulus of the imaginary frequency, T is the absolute temperature, h is Planck’s constant, c is the velocity of light, and k_B is Boltzmann’s constant; quantities pertaining to the heavy isotopologue are denoted by a prime. IM is the isotopic mass factor, equal to 0.007207 and 0.793285 for ³H₃ and ¹⁴C substitutions, respectively; this factor cancels from a KIE (= f_RS/f_TS) since the same factor appears in the IPFR for the reactant state. EX is the excitational factor due to the population of vibrational energy levels with quantum number v > 0, and ZP is the zero-point energy factor. TV is the leading term of the Bell model for tunneling through an inverted parabolic barrier,^36,37 valid for u₁ < 5 (and barrier height <20 k_BT),³⁸ conditions that are amply satisfied at 310 K for the TSs considered here. The overall expression for f_TS (eq 1) includes a quantum correction to the partition function not only for each separable vibrational mode with a real frequency (i.e., zero-point energy) but also for motion in the transition vector with its imaginary frequency (ω₁) which is always first in the ordered list of 3N_s frequencies. All three factors EX, ZP, and TV are quantum corrections to ratios of classical partition functions, not only the one associated with tunneling.

Figure 1.

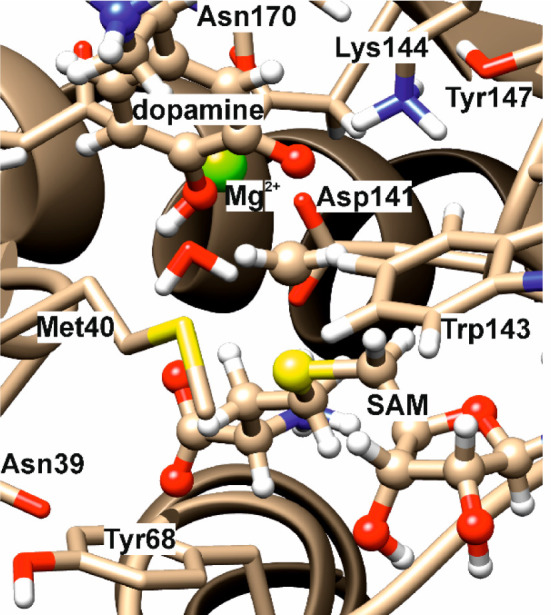
Close-up of active-site region of a representative optimized transition structure for the COMT-catalyzed reaction.

The subset Hessians had dimensions ranging from 216 × 216 to 897 × 897. “Extracted” Hessians were obtained by deletion of all rows and columns except for those belonging to the atoms to be retained (SC_αH₃O, C_αH₃, or C_α), giving smaller matrices which, when mass-weighted and diagonalized in the usual way, yielded either 18, 12, or 3 nonzero eigenvalues and corresponding eigenvectors for 6, 4, or 1 retained atoms, respectively.

This method, in which a larger Hessian is pared back to a smaller one, is not the same as a traditional “cutoff” procedure^39,40 in which an isotope-effect calculation is performed for a model system containing only atoms within a certain number of bonds (typically 2) from the site of isotopic substitution.³⁵ It must be emphasized that the elements of the extracted Hessian (those that remaining after paring back) are evaluated with the environment of the full system, whereas the included elements of a conventional cutoff Hessian would be evaluated in the absence of any environmental influences. However, it can easily be verified that a Hessian determined by (say) numerical differentiation of analytical gradients for a small number of atoms within the environment of a much larger system is identical to one obtained by paring back the larger Hessian computed with the same system.

Vibrational analysis for the four atoms of the transferring methyl group alone involved a transformation of the 4-atom extracted 12 × 12 Hessian from Cartesian coordinates to a nonredundant set of 6 internal coordinates (3 CH stretches, 2 in-plane bends, 1 out-of-plane bend) and 6 external coordinates (3 translations, 3 rotations). This transformation was performed by means of a modified Wilson s-vector method⁴¹ (see the Supporting Information for details). A rigid QM/MM potential-energy scan was performed for incremental displacements of 0.02 Å along the vibrational trajectory (±0.4 Å from the equilibrium position) for each of the 12 vibrational modes, and a least-squares fit to a quadratic function was obtained for each scan, except for that corresponding to the imaginary frequency.

The mean-square amplitude δ_i of a harmonic vibration is given by eq 6.⁴²

6

Results and Discussion

6-Atom Extracted Hessians: α-T₃ IPFRs

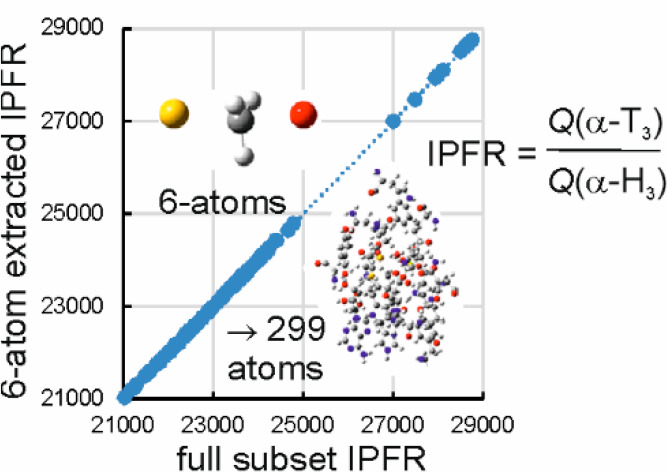
A total of 112 optimized transition structures were considered (Table S1), each possessing a single imaginary frequency corresponding to the transition vector. Elimination of all elements of the computed Hessians, except those associated with the four atoms of the transferring CH₃ group plus the donor S atom of SAM and the acceptor O atom of DOP, yields extracted IPFR values for 3-fold substitution of tritium for protium in the methyl group (α-T₃) which, when plotted against the IPFRs from the full subset Hessians (Figure 2), give an essentially perfect linear correlation: f_6-atom = 1.018f_full – 60 (r² = 0.9997). The magnitudes of the IPFRs are typical for a mass change from 1 to 3 in three positions. Since ΔG = −RT ln(f), an IPFR of 23000 corresponds to a stabilization of about 26 kJ mol^–1 at 310 K; substituting a heavier isotope into a molecule always stabilizes it (ΔG < 0) as real vibrational frequencies are lowered and f is always > 1. (See below for a comment on imaginary frequencies.) Note that a 2° α-T₃ KIE corresponds to a much smaller ΔG because it is proportional to the difference between ln(f) values for RS and TS (KIE = f_RS/f_TS).

Figure 2.

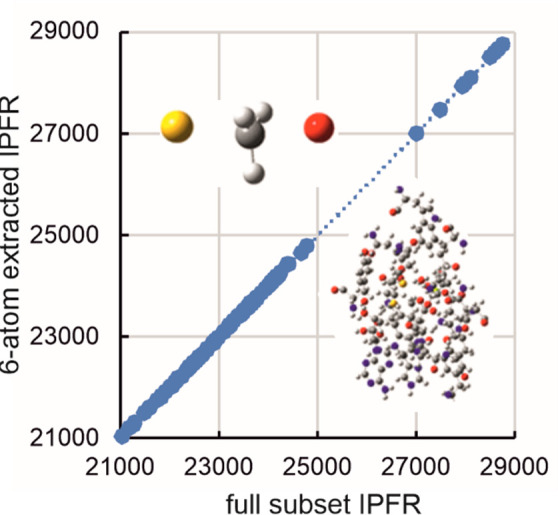
Correlation of α-T₃ IPFRs (310 K) for AM1/OPLS-AA/TIP3P transition structures of COMT-catalyzed methyl transfer: 6-atom extracted Hessian vs full subset Hessian values for between 72 and 299 atoms.

The essentially perfect linear correlation in Figure 2 shows that the origin of variation in IPFR values for systems of any size is entirely due to changes in the isotopic sensitivity of the vibrational frequencies of the extracted 6-atom core. There is evidently a gap in the plot between lower IPFR values (in the range 21000 < f < 25000) and higher values (f > 27000). The higher values are all associated with the smallest QM region (N_s = 72) and would imply larger inverse 2° α-T₃ KIEs than would be predicted for the larger QM regions which all include the Met40 and Asp141 residues as well as Mg²⁺ in the active-site. It may be concluded that it is necessary to include these residues in the QM region in order to obtain the correct isotopic sensitivities for the vibrational modes of the 6-atom core but that the subset Hessian does not need to be any larger. Typically, subset Hessians and QM regions have been chosen to be identical in published isotope-effect calculations using QM/MM methods, but the present result implies that more reliable results could be obtained more efficiently if a larger QM region and a smaller subset Hessian were to be selected. The adequacy of this 6-atom extract for α-T₃ is equivalent to the traditional “2-bond cutoff” rule^39,40 although, as noted above, the elements of the extracted Hessian do depend upon the surrounding environment.

Individual plots of EX, ZP, and TV factors for the 6-atom-extracted versus full-subset Hessians are each linear (Table S2 and Figure S3). The overall IPFR is dominated by the ZP factor (with values in the range from 1.2 × 10⁶ to 1.4 × 10⁶), since the most significant effect of isotopic substitution is upon the high-frequency C_αH vibrational modes. Although small in magnitude, the EX factor (with values in the range from 2.20 to 2.45) is dominated by the six lowest-frequency modes of the 6-atom Hessian, which correspond to librational motions of these atoms within their environment. The TV factor is always very small (with values in the range from 0.9966 to 0.9980); its reciprocal would be the tunneling contribution to a KIE.

4-Atom Extracted Hessians: α-T₃ IPFRs and Vibrational analysis

Sixteen transition structures were selected for further analysis. These were all obtained using QM regions containing residues within 6 or 7 Å from C_α. Furthermore, these structures all possessed interatomic distance S_SAM. . .S_Met40 > 3 Å and angle S_SAM···C_α···S_Met40 > 65°; the AM1 method generated some structures with unrealistically short S_SAM···S_Met40 distances which gave rise to artificially high IPFR values (Table S1, comments, and Figure S5). Elimination of all elements of the computed Hessians, except those associated with the four atoms of the transferring CH₃ group alone, yields extracted α-T₃ IPFR values which, when plotted against the IPFRs from the full subset Hessians, give a good linear correlation (f_4-atom = 1.066f_full – 1121, r² = 0.997); within the range 21000 < f_full < 22500, this line is nearly parallel to that for the 6-atom extracted IPFRs but is offset to slightly higher values. The structural variations in the IPFR values are reproduced well by the Hessian elements for only the four atoms of the transferring methyl, although exclusion of the donor S and acceptor O atoms from the extracted Hessian leads to a small systematic error in the absolute magnitude of the IPFR.

Vibrational analysis of the 12 normal modes allows for assignment of harmonic frequencies for six internal modes (three CH stretches, two in-plane bends, and one out-of-plane bend) and six external modes (three translations and three rotations). Because of the asymmetry of the enzyme active-site environment, the extracted Hessian does not display D_3h symmetry and there are no degeneracies among the vibrational frequencies. The stretching modes are each localized to one of the otherwise indistinguishable CH bonds and their frequencies are labeled simply as “highest”, “medium”, and “lowest”. Similarly, the in-plane (IP) bends are denoted only as “higher” and “lower”. The direction normal to the plane of the methyl group is defined as the z-axis: translation (T_z) in this direction is strongly coupled with out-of-plane bending (OP). Translations (T_x and T_y) in the xy plane and rotations (R_x and R_y) out of this plane are also denoted as “higher” and “lower”, whereas rotation (R_z) about the z-axis is clearly distinguishable (see Figure 3). The average value for each of these frequencies in the protiated form of the 16 transition structures is shown in Table 1, together with its average contribution to the α-T₃ IPFR at 310 K and the average mean-square amplitude ⟨δ⟩₃₁₀ of the harmonic vibration.³⁹ The same method was applied previously to analyze methyl-group vibrations within a constrained cage of water molecules.²⁸

Figure 3.

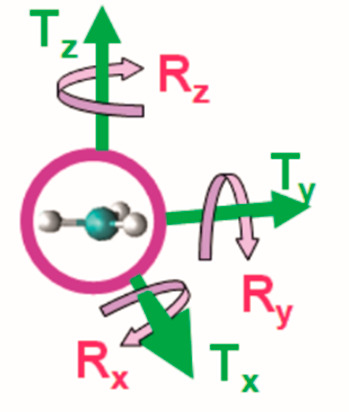
Designation of axes for translational and rotational modes of the transferring methyl group.

Table 1. Average Harmonic Frequencies (as Wavenumbers, ν) and Single Standard Deviations (σ), α-T₃ IPFR Factors (f_T3) with Standard Errors and Mean-Square Amplitudes (δ) at 310 K for 4-Atom Hessians Extracted from Full-Subset AM1/OPLS-AA/TIP3P Hessians for 16 Transition Structures of COMT-Catalyzed Methyl Transfer.

mode		⟨ v ⟩ (cm–1)	⟨fT3 ⟩310	⟨ δ⟩310⟩/Å
1	CH highest	3137 ± 8	9.03 ± 0.02	0.02
2	CH medium	3124 ± 7	9.01 ± 0.02	0.02
3	CH lowest	3097 ± 12	11.71 ± 0.06	0.02
4	IP higher	1339 ± 6	2.044 ± 0.004	0.03
5	IP lower	1304 ± 4	1.976 ± 0.002	0.03
6	OP/Tz	1224 ± 9	1.982 ± 0.004	0.03
7	Rx/Ry higher	1065 ± 5	1.722 ± 0.002	0.03
8	Rx/Ry lower	982 ± 16	1.606 ± 0.006	0.03
9	Tx/Ty higher	273 ± 5	1.0202 ± 0.0002	0.09
10	Tx/Ty lower	238 ± 5	1.0161 ± 0.0002	0.10
11	Rz	164 ± 30	1.016 ± 0.001	0.14
12	Tz/OP	441i ± 20	0.9942 ± 0.0004	0.06

It is clear from the results presented in Table 1 that the three CH stretching modes are responsible for the largest part of the overall IPFR: they contribute a factor of 953 toward the overall value of 22094 (at 310 K), with the three IP and OP bending modes and the six external modes contributing factors of only 8 and 3, respectively. However, it is important to recognize that the external modes should not be neglected for the purpose of calculating the α-T₃ KIE. Although this is not the subject of the present paper, it is worth noting that the respective IPFR contributions of both the internal and external modes of the methyl group in the reactant state must be taken into account, since failure to do so might omit a very significant factor, namely the influence of the environment on all degrees of freedom of this group.

A further comment must be made regarding the IPFR factor < 1 for mode 12, in which translation in the direction perpendicular to the plane of the methyl group is coupled to out-of-plane bending. This mode is associated with an imaginary frequency and corresponds to the transition vector for transfer of the methyl group between the donor and acceptor atoms in the COMT active site. The inverse IPFR factor implies a destabilizing effect of isotopic substitution in each of the transition structures and a higher contribution from this mode to the effective Gibbs energy for the transition state relative to the reactant state. Of course, the tunneling “correction” to a KIE is just the reciprocal of the IPFR for the transition vector with its imaginary frequency: in this case tunneling contributes an average factor of 1.006 at 310 K, favoring the lighter isotopologue in the transition state.

4-Atom Extracted Hessians: Normal-Mode PE Scans

Figure 4 shows rigid potential-energy scans along each of the 12 normal modes from the 4-atom extracted Hessian for the transferring methyl group in the COMT-catalyzed reaction; these were obtained using the AM1/OPLS potential for the whole enzymic TS complex for one of the structures in which the QM region contained residues within 7 Å of C_α. The red circles represent harmonic fits over the range of displacements considered, for which full details are given in the Supporting Information. It is evident that the harmonic approximation is very good for most of the modes, especially for smaller displacements closer to the mean-square amplitudes. Modes 9 and 10 (the T_x/T_y combinations) are essentially harmonic but their potential-energy minima are displaced a little from the geometry of the optimized first-order saddle point for the transition structure selected for this study. The minimum for mode 11 (R_z) is also displaced from the originally optimized structure and is markedly anharmonic. Note that these three modes have the largest calculated mean-square amplitudes, although these are still much smaller than the extent of the displacements considered in the potential-energy scans. Finally, as expected for a transition vector, the scan for mode 12 (the T_z/OP combination) displays a maximum near to the optimized structure and is highly anharmonic over the range ± 0.4 Å. There is a minimum at about −0.29 Å from the maximum: this corresponds to the reactant complex, for which a transition-state C_α···S bond extension of about 0.29 Å was obtained in a previous AM1/OPLS study for this reaction.¹³

Figure 4.

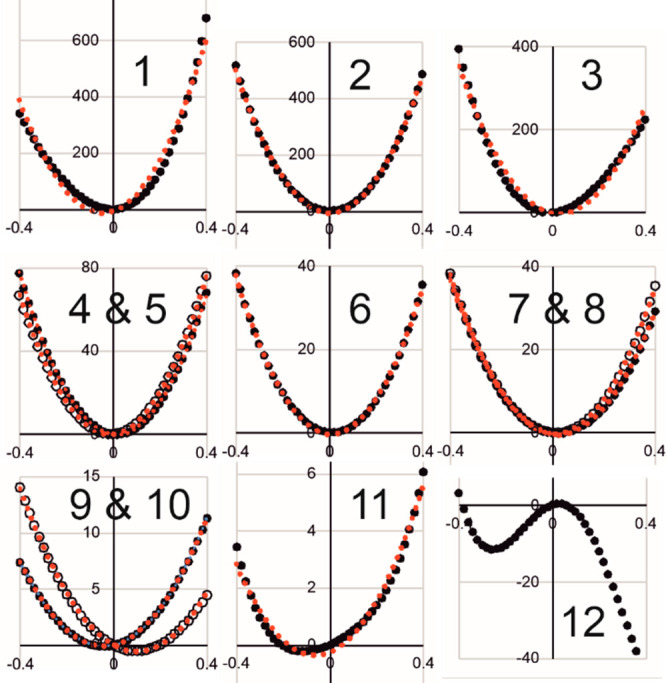
QM/MM potential energy scans along normal modes 1 to 12 (see Table 1) of the 4-atom extracted Hessian in a representative transition structure for COMT-catalyzed methyl transfer. Black ● are AM1/OPLS-AA/TIP3P calculated relative energies (/kJ mol^–1), and red ● denote harmonic fits over the range ± 0.4 Å; black and red ○ have the same meanings but for the higher-frequency mode of a pair.

α-¹⁴C IPFRs from Extracted Hessians

Figure 5 shows plots of extracted IPFR values against full-subset Hessian values for substitution of ¹⁴C for ¹²C in the methyl group of the same 16 transition structures considered above. The number of atoms included in the extracted Hessian is denoted by N_x. Table 2 contains the slopes (m), intercepts (c), and correlation coefficients (r²) for the linear regressions. The 72-atom “core” of SAM + DOP correlates almost perfectly for all structures, with m ≈ 1.0, c ≈ 0.0, and r² ≈ 1.0; the solid black line has unit slope and zero intercept.

Figure 5.

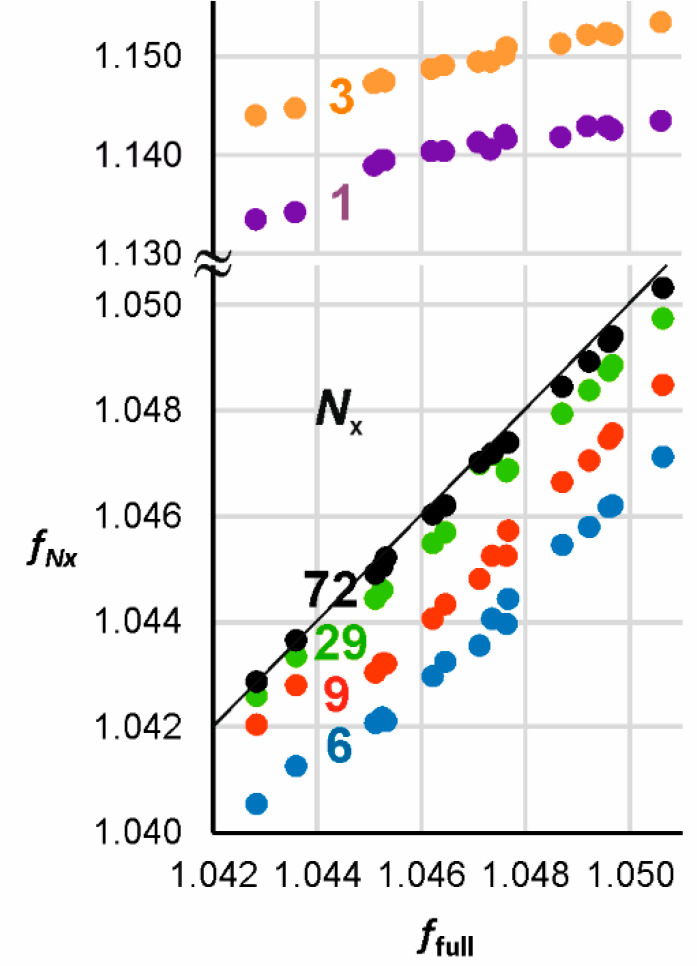
Correlation of α-¹⁴C IPFRs (310 K) for AM1/OPLS-AA/TIP3P transition structures of COMT-catalyzed methyl transfer: N_x-atom extracted Hessian vs full subset Hessian values for 16 transition structures of COMT-catalyzed methyl transfer. Note the change of scale in the vertical axis. The solid black line has unit slope and zero intercept; slopes, intercepts, and correlation coefficients for each value of N_x are presented in Table 2.

Table 2. Slopes (m), Intercepts (c), and Correlation Coefficients (r²) for Linear Regression of IPFRs for N_x-Atom-Extracted Hessians vs Full-Subset AM1/OPLS-AA/TIP3P Hessians for n Transition Structures of COMT-Catalyzed Methyl Transfer at 310 K^a.

Nx	n	m	c	r2	atoms
1	16	1.1875	–0.1029	0.8542	Cα
3	16	1.1963	–0.1031	0.9826	SCαO
	14	1.1014	–0.0036	0.9798	SCαO
6	16	0.8571	0.1464	0.9861	SCαH3O
	14	0.9305	0.0695	0.9927	SCαH3O
9	16	0.8608	0.1438	0.9679	(C)2SCH3OC
	14	0.9939	0.0043	0.9961	(C)2SCH3OC
29	16	0.9206	0.0825	0.9878	(C)2SCH3 + DOP
	14	0.9268	0.0760	0.9787	(C)2SCH3 + DOP
72	16	0.9589	0.0428	0.9993	SAM + DOP

^aNote that correlation coefficients for different sample sizes should not be compared directly.

In view of the success of atomic Hessian analysis in reproducing the trend of EIEs for transfer of a carbocation between media of differing polarity where isotopic substitution is upon a single atom, one may enquire whether trends in KIEs or, more simply as here, in TS IPFRs might also be reproduced for multiple configurations involving a single ¹⁴C substitution: does a 1-atom extract work? Table 2 and Figure 5 reveal the answer to be no: although the TV factor alone displays a very good linear correlation, both EX and ZP show considerable scatter, leading to an overall IPFR correlation with a slope that is too steep and a significant negative intercept. The same 6-atom extract as above yields a good overall ¹⁴C IPFR correlation but not the excellent correlation obtained for the ³H₃ IPFRs.

The SAM moiety can be truncated to a 7-atom fragment (involving only the transferring methyl attached to S and its adjacent C atoms) without much detriment to the quality of the correlation, as exemplified by the trendline for N_x = 29, but any attempt to truncate the DOP moiety introduces an apparent anomaly for two of the 16 TSs: the N_x-extract IPFRs for these two points lie off the line for the remaining 14. The correlations appear to be improved for smaller extract Hessians if the two “anomalous” structures are removed (n = 14). However, inspection of Figure 5 suggests that it is these two points that lie closer to the best regression line and the other 14 that are anomalous! Inspection of the geometrical structures for the two “anomalous” TSs (shown in green and purple licorice style in Figure 6 and which are, of course, identical for both extract Hessians and full-subset Hessians) reveals that the distance between the nucleophilic oxygen atom (O_nu) of DOP and the Mg²⁺ cation is considerably shorter (2.27 Å) than in the other structures (Figure 6: average values of 3.77 Å for the other 11 also generated within a QM region containing residues within 6 Å of C_α and 4.14 Å for the 3 generated within a 7 Å QM region). Consequently, the distance from Mg²⁺ to Asp169 is longer in these two structures (Table S4). Along with the shorter O···Mg distance, the C_α···O distance is also shorter (1.93 Å) and the C_α···S distance longer (2.22 Å) than in the other TSs (average values of 2.02 and 2.14 Å, respectively, for the other 13 TSs): the “anomalous” TSs are more product-like and have smaller ¹⁴C IPFRs.

Figure 6.

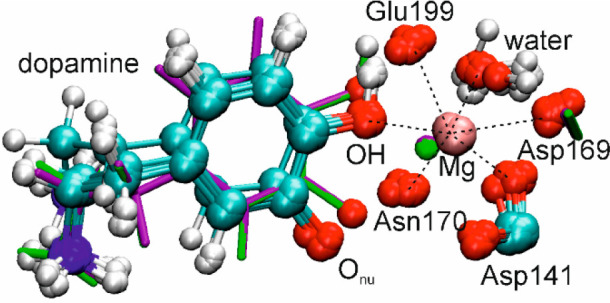
Close-up of the octahedral coordination around Mg²⁺ in an overlay of 13 transition structures of COMT-catalyzed methyl transfer generated within a QM region containing residues within 6 Å of C_α. The green and purple licorice structures are the two apparently anomalous TSs.

The reason for the apparent anomaly is to be found in the EX factor, which arises from the isotopic sensitivity of low-frequency modes. The magnitude of EX increases as the size of the Hessian increases, since larger systems have more and lower frequencies. However, the anomaly exists even in a 3-atom extract comprising only the SC_αO atoms: although EX is very small, one of the bending frequencies is markedly higher in each the two apparently anomalous structures than in the others. Curiously, this feature persists for all extract Hessians that do not contain all the atoms of DOP but not for any that possess the full atomic complement of SAM. The traditional 2-bond cutoff rule for C_α would suggest a 6-atom extract (different from that considered in Table 2 and Figure 5) comprising (C)2SC_αOC; however, in the light of the above discussion, neither this nor a 3-bond cutoff model would provide an adequate approximation to the full subset Hessian.

Ponderal Effects on IPFRs

While investigating the 3-atom extracted Hessians for the SC_αO fragment mentioned above, it was noted that the resulting ¹⁴C IPFR values were much larger (Figure 5) than those obtained from the full subset Hessians for the same TSs. We were curious to enquire whether this might be due purely to the “missing mass” of the other atoms and therefore whether “correct” IPFRs could be obtained simply by adjusting the masses of the S and O atoms. Figure 7a,b shows ¹⁴C IPFRs (plotted as a function of S and O masses in the range from 4 to 80 amu) for both the 3-atom and 6-atom extracted Hessians of a representative TS (whose ¹⁴C IPFR value is close to the mean of the set of 16). Clearly, the elevated ¹⁴C IPFR for the 3-atom fragment cannot be reduced to full subset-Hessian value simply by adjusting the masses of the S and O atoms. However, there is a surprising degree of sensitivity to the O-mass: both the 3-atom and 6-atom surfaces display a cliff-edge, dropping precipitously to lower IPFR values, for O-mass < 16 amu. The 6-atom extract also shows a small degree of sensitivity to the S-mass, with a gradual decrease in IPFR for increasing mass. In both cases the IPFR appears to diminish gradually as both the O- and S-masses increase, to about 1.144 and 1.037 for the 3-atom and 6-atom extracts, respectively, for masses of 1000 amu.

Figure 7.

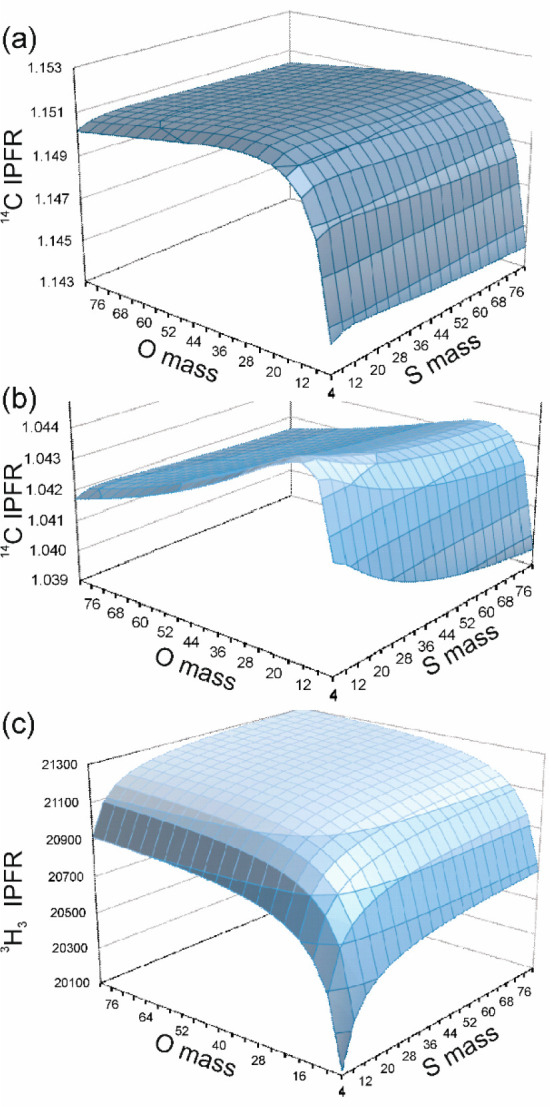
Iso-contour-surface plots of AM1/OPLS-AA/TIP3P α-¹⁴C IPFRs for (a) 3-atom- and (b) 6-atom-extracted Hessians, and (c) α-T₃ IPFRs for the 6-atom-extracted Hessian, of a representative transition structure of COMT-catalyzed methyl transfer (310 K), as a function of the O and S masses in the SC_αO fragment.

Figure 7c shows a similar plot of α-T₃ IPFRs for the 6-atom extract of the same representative TS. This displays a broad plateau, tending to a maximum value of about 21340 for O- and S-masses of 1000 but dropping to much lower values as either mass falls below its respective normal atomic mass.

These are ponderal effects, as originally defined by Ingold and co-workers⁴³ to describe the influences of added masses in reactivity and equilibria⁴⁴ quite apart from steric or electronic effects. Although (despite the existence of lower-mass oxygen radioisotopes) it is physically unrealistic to consider masses for O and S smaller than 16 and 32, respectively, substitution of greater masses is useful in that it mimics one feature of the influence of the larger molecular of supramolecular system of which these atoms are a part, and it does so without the complication of either the bulk volume or the polar properties of the system. The key results from this investigation are that the isotopic sensitivity at C_α tends to a limiting minimum value as the mass of the whole system increases, whereas that for the H_α atoms tends to a limiting maximum value. To the best of our knowledge, this is the first instance of the use of plots, like Figure 7, to explore ponderal effects.

It is important to note that the force constants remain unchanged for each system as the masses alone are varied. The 3-atom-extract Hessian transforms to yield internal valence force constants of 1.56 and 0.81 aJ Å^–2 for SC_α and C_αO stretching and 5.08 aJ rad^–2 for bending. The imaginary frequency for the transition vector arises due to the large magnitude of the SC_α/C_αO coupling constant (1.66 aJ Å^–2) which gives rise to a negative determinant for that 2 × 2 block of the valence force constant matrix. Similar surfaces to those shown in Figure 7 may be plotted for each of the individual EX, ZP, and TV factors contributing to the overall IPFR: perhaps surprisingly, it turns out that each factor displays similar topographical features. EX and ZP are functions of the two real frequencies (symmetric stretching and bending), whereas TV is a function of the imaginary frequency (for asymmetric stretching). Of course, the IM surface is flat and featureless because this factor depends only on the mass at the position of isotopic substitution and not on masses at any other positions.

Transition-Vector Analysis

The unweighted normal coordinate for the transition vector of each of the set of 16 AM1/OPLS-AA/TIP3P TSs, considered in previous sections, may be analyzed in terms of the normalized magnitude of the contribution of the atoms of each residue included within the full subset Hessian, as presented in Table 3. The striking observation is that, for both the 13 TSs and 3 TSs with subset Hessians including 222-atoms or 299-atoms, respectively, the atoms of the SAM and DOP residues together contribute over 99.3% of motion in the transition vector. The next largest contributions are from the Mg²⁺ cation and Lys144 (which deprotonates the nucleophilic O of DOP). Tyr68 and Met40 together contribute only about 0.1%. These residues have both been implicated in the mode of catalytic action by COMT: the former purportedly by exerting a compressive influence along the methyl-transfer axis^14,17 and the latter by hydrogen-bonding to the transferring methyl group.²¹ It was recently suggested⁴⁵ that the reaction coordinate of COMT involves four protein residues: Tyr68, Glu90, Leu198, and Glu199. Unfortunately, the subset Hessians considered in the present study do not include either Glu90 or Leu198, since these residues lie at > 7 Å from C_α. However, it should be noted that the transition vector corresponds to infinitesimal displacements around the stationary point for the transition structure within the harmonic approximation, whereas the reaction coordinate determined by Chen and Schwartz⁴⁵ is obtained by transition path sampling and committor distribution calculations involving the whole pathway between the reactant and product complexes. On the potential-energy hypersurface for a single transition-path trajectory, the transition vector is tangential to the minimum-energy reaction path only at the saddle point. Of course, consideration of only the TS excludes any account of dynamic processes leading to it, but this does not invalidate the analysis.²

Table 3. Residue-Based Analysis of Average Contributions to the Transition Vector from AM1/OPLS-AA TIP3P Hessians for Transition Structures of COMT-Catalyzed Methyl Transfer^a.

		% average
residue	na	6-atom (ns = 16)	222-atom (6 Å, ns = 13)	299-atom (7 Å, ns = 3)
Trp38	24	–	–	0.00
Met40	17	–	0.06	0.05
Asn41	14	–	–	0.01
Gly66	7	–	0.02	0.02
Tyr68	21	–	0.04	0.04
Asp141	12	–	0.09	0.06
His142	17	–	0.03	0.01
Trp143	24	–	0.04	0.01
Lys144	22	–	0.09	0.06
Tyr147	21	–	–	0.01
Asp169	12	–	–	0.01
Asn170	14	–	0.06	0.07
Glu199	15	–	0.05	0.04
Mg	1	–	0.18	0.11
SAM	50	85.80	81.51	82.55
DOP	22	14.20	17.83	16.86
HOH11	3	–	–	0.04
WAT6872	3	–	–	0.02

^an_a is the number of atoms in each residue, and n_s is the number of transition structures.

Table 4 presents the AM1/OPLS-AA/TIP3P transition vector, averaged over the 16 TSs and determined by means of the 6-atom-extracted Hessians, and represented by linear combinations of valence coordinates, as defined qualitatively in Table 5 and Figure 8. Although the trigonal bipyramid does not have strict D_3h symmetry, these local “symmetry” coordinates provide a compact description of the average transition vector, which is clearly shown to be mostly a combination of Walden-inversion “umbrella” bending and asymmetric stretching of the bonds between C_α and the nucleofuge and nucleophile. However, it is of interest to note that there is a small negative contribution from symmetric SC_α/C_αO stretching, consistent with a small degree of contraction between the S and O atoms in this normal mode in the forward direction of methyl transfer from S to O. This should not be regarded as evidence for geometrical compression in the TS because not only would it be an expansion in the reverse phase of the vibration but also the motion oscillates about a TS stationary point, the geometry of which may or may not be compressed relative to that of the reactant complex.

Table 4. Symmetry-Coordinate Representation of the Transition Vector from 6-Atom-Extracted AM1/OPLS-AA/TIP3P Hessians Averaged over 16 Transition Structures of COMT-Catalyzed Methyl Transfer.

coordinate	mean	std dev
umbrella	0.701	0.008
asym SCα/CαO stretch	0.454	0.001
sym SCα/CαO stretch	–0.058	0.003
in-plane SCαO bending	–0.011	0.005
sym CαH3 stretch	–0.009	0.004
CαH3 rocking	–0.007	0.008
CαH3 twisting	0.006	0.007
CαH3 tilting	–0.004	0.002
CαH3 scissoring	0.001	0.004
asym CαH3 stretch (a′)	0.0009	0.0004
out-of-plane SCαO bending	–0.0004	0.0060
asym CαH3 stretch (a″)	–0.0001	0.0008

Table 5. Definition of Symmetry Coordinates for a Trigonal Bipyramidal 6-Atom Fragment; Atom Numbers Defining Stretching Coordinates, and Letters Denoting Angle-Bending Coordinates, Are As in Figure 8^a.

symmetry coordinate	linear combination of valence coordinates
in-plane SCαO bending	a – b – c + d – e – f
out-of-plane SCαO bending	b – c + e – f
umbrella	a + b + c – d – e – f
CαH3 rocking	h – i
CαH3 twisting	b – c – e + f
CαH3 tilting	–a + b + c + d – e – f
CαH3 scissoring	g – h – i
sym SCα/CαO stretch	(1–2) + (2–6)
asym SCα/CαO stretch	(1–2) – (2–6)
sym CαH3 stretch	(2–3) + (2–4) + (2–5)
asym CαH3 stretch (a′)	(2–3) – (2–4) – (2–5)
asym CαH3 stretch (a″)	(2–4) – (2–5)

^aLinear combinations are qualitatively correct but do not show the coefficients for valence-coordinate displacements.

Figure 8.

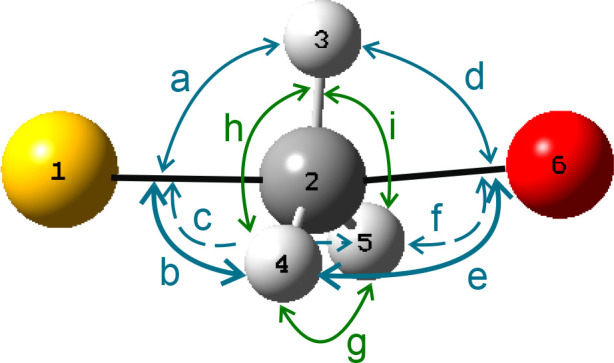
Labeling scheme for valence angle-bending coordinates around the central atom of a trigonal bipyramid. Yellow denotes S, and red denotes O. Valence bond stretching coordinates are defined by pairs of atom numbers.

TS Valence Force Constants

The local symmetry coordinates defined by Table 5 and Figure 8 allow the 6-atom extracted Hessian to be transformed: first, into the nonredundant set of 12 internal symmetry coordinates and second into the redundant set of 14 valence coordinates which includes all 9 of the interbond angles a–i about C_α. In each individual transition structure, the three H atoms of the methyl group may interact with specific active-site residues and are therefore not equivalent. However, since they are readily interchanged by rotation about the SC_αO axis, they cannot be identified separately when average values of C_αH force constants are being considered. It is therefore appropriate to consider average values for C_αH stretching and for HC_αS, HC_αO, and HC_αH angle bending. Table 6 presents AM1/OPLS-AA/TIP3P valence force constants averaged over 16 transition structures of COMT-catalyzed methyl transfer.

Table 6. AM1/OPLS-AA/TIP3P Valence Force Constants and Standard Errors Averaged Over 16 Transition Structures of COMT-Catalyzed Methyl Transfer^a.

valence coordinate	average force constant
⟨CαH⟩48	5.61 ± 0.01
⟨CαS⟩16	1.87 ± 0.02
⟨CαO⟩16	1.88 ± 0.05
⟨SCαH⟩48	2.18 ± 0.04
⟨OCαH⟩48	2.90 ± 0.30
⟨HCαH⟩48	0.346 ± 0.004

^aThe subscript outside the bracket denotes the sample size. Units are aJ Å^–2 for bond stretching and aJ rad^–2 for bending.

It may be noted that the C_αS and C_αO stretching force constants determined from the 6-atom extract are significantly different from those obtained (for a single structure) from the 3-atom extracted Hessian. Furthermore, the SC_αO bending force constant for the 3-atom extract has a larger value than any of the bending force constants in Table 6 because it is, in effect, doing the work of a combination of HC_αS and HC_αO bending coordinates.

Finally, it is of interest to compare these TS force constants with the BEBOVIB estimates of Schowen and co-workers.¹⁰ Their method scaled the C_αS and C_αO stretching force constants by the respective Pauling bond orders for these bonds in the TS: assuming bond orders of 0.5 would have led to values of about 3.2 and 6.2 aJ Å^–2, respectively, which are much higher than the average AM1/OPLS-AA/TIP3P values. Conversely, the HC_αS and HC_αO bending force constants were scaled directly by the corresponding bond orders for C_αS and C_αO: assuming again bond orders of 0.5 would have led to BEBOVIB estimates of 0.31 and 0.44 aJ rad^–2, respectively, which are much lower than the average AM1/OPLS-AA/TIP3P values. As mentioned in the Introduction, it was necessary to employ significantly larger bond orders for the TS of the enzyme-catalyzed reaction than for the TS of uncatalyzed methyl transfer in order to model the more inverse α-D₃ KIE observed for the COMT-catalyzed reaction, leading naturally (but, in our view with hindsight, mistakenly) to the inference of mechanical compression.⁷

Axial and Equatorial Interactions

Nonbonded interatomic distances between key active site residues and the SAM moiety, as obtained by inspection of the optimized TS geometries for the set of 16 structures discussed above, are presented in Table 7.

Table 7. Selected AM1/OPLS-AA/TIP3P Nonbonded Distances (/Å) in 16 Transition Structures of COMT-Catalyzed Methyl Transfer.

TS	SSAM···HBZTyr	SMet···HMe	OAsp···HMe	OAsPD1/D2HMe
1	2.727	2.593	2.436	2.987
2	2.798	3.262	2.238	2.704
3	2.728	2.715	2.354	3.167
4	2.927	3.170	2.232	2.658
5	2.783	2.819	2.333	3.152
6	2.650	2.750	2.364	3.241
7	2.777	2.503	2.468	2.970
8	2.739	2.577	2.492	3.016
9	2.766	2.916	2.319	3.172
10	2.793	2.561	2.460	3.100
11	2.719	2.596	2.468	3.111
12	2.744	2.569	2.455	3.034
13	2.762	2.639	2.397	2.974
14	2.762	2.541	2.506	3.251
15	2.773	2.488	2.434	3.638
16	2.759	2.733	2.362	3.533
mean	2.76	2.71	2.39	3.11
SE	0.01	0.06	0.02	0.06

In view of the proposed role for Tyr68 within the compression hypothesis,¹¹ it is of interest to consider whether there exists any correlation between the SAM···Tyr68 separation and the α-T₃ IPFR. The closest nonbonded contact is between the S atom of SAM and one of the H atoms (H^B2) attached to C_β in the side chain of Tyr68 and has a mean value of 2.76 ± 0.01 Å (Table 7, column 2). As shown in Figure S7, there is no sensible correlation between this distance and the IPFR: variation in the latter is not explained by this parameter. The interaction between SAM and Tyr68 may be described as “axial” in the sense that it may exert force in a direction more-or-less parallel to the methyl transfer axis.

Nonbonded interactions between any of the H atoms of the transferring methyl group and either Met40 or Asp141 may be described as “equatorial”: their forces are directed more-or-less perpendicularly to the methyl-transfer axis around its circumference.^21,25 All TS geometries inspected contain a short contact (mean value 2.39 ± 0.02 Å, Table 7, column 4) between a methyl H atom and the backbone carbonyl O atom of Asp141. The next closest contact is usually with the S atom of Met40 (column 3), but where this is long, a short contact with either O^D1 or O^D2 of the carboxylate side chain of Asp141 is found (column 5). Despite the generality of these interactions in SAM-dependent methyltransferases,⁴⁶ again no correlation is found between these distances and the TS IPFRs (Figure S7).

Summary and Concluding Remarks

(1) The ability of 6-atom-extracted Hessian to reproduce perfectly the α-T₃ IPFR values from the full-subset Hessians of all the TSs demonstrates that the origin of variation in these IPFRs for systems of any size is entirely due to changes in the isotopic sensitivity of the vibrational frequencies of the extracted 6-atom core. This result is consistent with the traditional rule that isotope effects are well approximated by truncated models including only atoms two bonds removed from the site of isotopic substitution; this is expected to be a general result for isotopes of hydrogen. Furthermore, it suggests that α-D₃ or T₃ KIEs could be reliably estimated by Hessian evaluations for only these 6 atoms, provided that the calculations involve an adequate treatment of the surrounding protein environment. A large QM region may be necessary, even though only a small Hessian is required. Of course, there is no reduction in computational effort if a larger (approximate) Hessian has already been used in relaxing a structure to a local stationary point, but there would be if a higher-level QM method were to be employed for Hessian evaluation at a stationary point obtained with a lower-level method or if better results were obtained by averaging over a greater number of Hessians evaluated at instantaneous nonstationary structures from an MD trajectory. (2) Vibrational analysis based upon the 4-atom-extracted Hessian shows that the three CH stretching modes are responsible for the largest part of the overall α-T₃ IPFR but that the external modes should not be neglected. For displacements with similar magnitudes to the mean-square amplitudes of vibration at 310 K, the harmonic approximation is found to be very good for most of the 12 vibrational modes of the transferring methyl group within the framework of its environment. (3) In order to reproduce α-¹⁴C IPFR values from full-subset Hessians by means of Nx-atom extracted Hessians requires all atoms of the DOP moiety to be included. The 6-atoms of the SC_αH₃O fragment are not enough, nor is the traditional 2-bond cutoff rule satisfied simply by addition of an extra atom to either S or O. This feature arises due to the EX factor, which depends heavily on low-frequency modes that are sensitive to isotopic substitution at C_α and which involve a more-extensive chain of atoms. (4) A novel investigation of ponderal effects upon IPFRs suggests that the value for α-¹⁴C tends toward a limiting minimum whereas that for α-T₃ tends toward a limiting maximum as the mass of the rest of the system increases. This analysis is of relevance to the question of how truncated (or cluster) models may relate to full-size systems. (5) The transition vector is dominated by motions of atoms within the SAM and DOP moieties and is very well described as a simple combination of Walden-inversion “umbrella” bending and asymmetric stretching of the SC_α and C_αO bonds. The contribution of atoms of the protein residues Met40, Tyr68, and Asp141 to the transition vector is extremely small. (6) Average AM1/OPLS-AA/TIP3P valence force constants for the COMT TS show significant differences from early BEBOVIB estimates which were used in support of the compression hypothesis for catalysis. The ability to characterize TSs without the need for dubious guesswork is a strong advantage of QM/MM methodology. (7) There appears to be no correlation between TS IPFRs and the nonbonded distances for close contacts between the S atom of SAM and Tyr68 or between any of the H atoms of the transferring methyl group and either Met40 or Asp141. (8) In regard to Hessian size, it is found that the requirements for faithful modeling of transition structures are more demanding than for equilibrium structures. The insights gained from this study provide a firm foundation for DFT-based QM/MM computational studies of KIEs for COMT-catalyzed reactions in progress in our laboratories. While DFT and DFT/MM methods have been employed for structural studies on COMT,^21,47,48 there do not appear to have been published reports of DFT-based KIE calculations for COMT-catalyzed methyl transfer. QM/MM KIEs with AM1, B3LYP, and M06 for WT and mutant COMT will be presented in a forthcoming paper.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c07344.

• Computed PMF, structures for selected QM regions, IPFRs, and selected geometrical parameters for optimized TSs, EX, ZP, and TV factors for full subset, 6-atom and 1-atom-extract Hessians; attempted correlations of IPFRs with selected nonbonded distances; Fortran code, input and output for methyl-group normal-mode PE scans (PDF)

The authors declare no competing financial interest.