Predictions and analyses of RNA nearest neighbor parameters for modified nucleotides

Abstract

The most popular RNA secondary structure prediction programs utilize free energy (ΔG°₃₇) minimization and rely upon thermodynamic parameters from the nearest neighbor (NN) model. Experimental parameters are derived from a series of optical melting experiments; however, acquiring enough melt data to derive accurate NN parameters with modified base pairs is expensive and time consuming. Given the multitude of known natural modifications and the continuing use and development of unnatural nucleotides, experimentally characterizing all modified NNs is impractical. This dilemma necessitates a computational model that can predict NN thermodynamics where experimental data is scarce or absent. Here, we present a combined molecular dynamics/quantum mechanics protocol that accurately predicts experimental NN ΔG°₃₇ parameters for modified nucleotides with neighboring Watson–Crick base pairs. NN predictions for Watson-Crick and modified base pairs yielded an overall RMSD of 0.32 kcal/mol when compared with experimentally derived parameters. NN predictions involving modified bases without experimental parameters (N⁶-methyladenosine, 2-aminopurineriboside, and 5-methylcytidine) demonstrated promising agreement with available experimental melt data. This procedure not only yields accurate NN ΔG°₃₇ predictions but also quantifies stacking and hydrogen bonding differences between modified NNs and their canonical counterparts, allowing investigators to identify energetic differences and providing insight into sources of (de)stabilization from nucleotide modifications.

INTRODUCTION

Over the past several decades, there has been extensive research into the variety of roles RNA plays in vivo. Because structural features dictate function, there has also been immense interest in identifying the tertiary structures that RNA is able to adopt. Experimental high-resolution RNA structures are mostly determined by X-ray crystallography, nuclear magnetic resonance (NMR), and cryogenic electron microscopy (cryo-EM), but these methods cannot match the rate at which new functional RNAs are being discovered, driving the need for improved computational methods that can predict RNA structure from sequence. While great strides have been made with RNA structure prediction, many secondary structure prediction programs take only Watson–Crick (WC) base pairs into account, which remains a key obstacle for predicting tertiary structures for sequences containing non-standard base pairs (1).

Many structure prediction limitations exist due to RNA modifications, which are known to affect stability and structure in vivo by modifying properties such as electrostatics, base-pairing potential, secondary structure, and RNA–protein interactions (2–4). Once thought to be found almost exclusively in functional RNAs, RNA modifications are found in all types of RNA including messenger RNA (mRNA), small nuclear RNA (snRNA) and microRNA (miRNA) and in all domains of life (2,5). RNA base modifications have been shown to affect functional RNAs and their folding, stability and function, but these modifications also have significant implications in mRNA structure. Six unique naturally occurring modifications have been found in mRNA including pseudouridine (Ψ), inosine (I), 5-methylcytidine (m⁵C), N⁶-methyladenosine (m⁶A), N¹-methyladenosine (m¹A) and 5-hydroxy-methylcytidine (hm⁵C) which affect splicing, maturation, stability, expression and degradation (4).

In addition to the many known in vivo effects of modification, RNA modifications are often used in various biochemical applications including the probing of structure, dynamics, folding, and recognition. Due to its fluorescence, the base 2-aminopurine riboside (2AP) is often substituted for the canonical A in structure probing studies (6). Like A–U pairs, 2AP·U pairs contain two hydrogen bonds, so it is assumed 2AP·U pairs do not disrupt typical RNA base pairing or stability. Another adenosine analog, 2,6-diaminopurineriboside (DAP), is used to enhance the stability of duplexed regions containing A–U base pairs and to assess the role of the 2-amino group in certain molecular recognition or solvation contexts (7–9). Inosine has been substituted for G to identify the effect of the exocyclic amino group in G·U wobble pairs on peptide binding (10) and to weaken G–C pairs in the investigation of RNA chaperones, leading to insights about how these chaperones alter free energy landscapes of RNA folding (11).

Recently, Mauger et al. investigated mRNAs with modified uridine residues including Ψ, N¹-methylpseudouridine (m¹Ψ) and 5-methoxyuridine (mo⁵U) to determine the effect of mRNA base modifications on protein expression. Nearest neighbor (NN) free energy (ΔG°₃₇) parameters for A·m¹Ψ and A·mo⁵U were only –0.18 and 0.25 kcal/mol different than A–U NNs, respectively, yet impacted local and global mRNA structures. Expected pairing frequencies (m¹Ψ > U > mo⁵U) and stabilities (m¹Ψ > U > mo⁵U) were consistent with selective 2'-hydroxyl acylation and primer extension (SHAPE) data and RNA structures, respectively, and correlated with derived NN ΔG°₃₇ parameters. While these modifications maintained WC base-pairing potential, the thermodynamic impacts of these modifications led to significant changes in mRNA structure, half-life, and protein expression (12), directly representing how small base modifications can have subtle thermodynamic impacts with profound effects on secondary structure.

RNA base pairing forms faster than and prior to tertiary contacts, causing RNA 3D folds to be largely constrained by their secondary structures (13,14). Because of this, there has been much interest in accurate base pairing predictions for RNAs. While secondary structure can be most accurately predicted by sequence comparison, homologs are not always available, leaving free energy minimization as the most popular secondary structure prediction method (15). Many prediction programs (e.g. the Vienna RNA Package (16), RNAStructure (17) and Mfold (18)) use dynamic programming algorithms to obtain the most probable RNA secondary structures based on a sequence's minimum free energy (MFE). These programs rely on experimental thermodynamic free energies from the NN model (19) but are limited by a lack of non-WC base pairing data. Modified bases can either be entered into these programs as their WC equivalent or can simply be set to be unpaired as a hard constraint in the final structure determination based on prior knowledge or experimental probing data (20). Imposing single-stranded conformations for modified bases makes sense in extensively modified bases (e.g. wyosine, wybutosine, etc.) or bases that prohibit WC base pairing (e.g. N¹-methyladenosine), but forcing modified bases to be unpaired in secondary structure predictions can cause investigators to ignore important base pairing interactions for functional RNAs that contribute to an RNA's secondary structure. For example, Saccharomyces cerevisiae cytosolic tRNA^Phe has four occurrences of three different modified base pairs (G·m⁵C, A·Ψ and m²G·C) that have important hydrogen bonding interactions in stem regions of the structure (Supplementary Figure S1). Other modified bases maintain base-pairing potential and have been shown to adopt WC-like geometry as well (Figure 1).

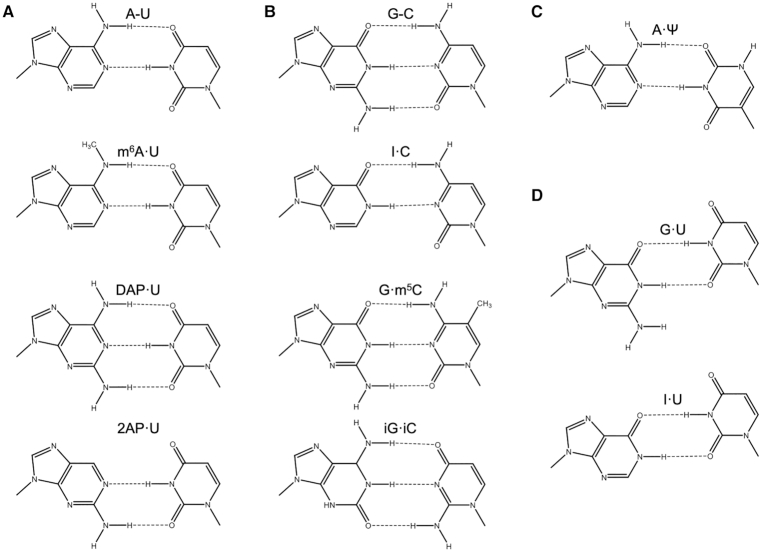
Figure 1.

Base pairs whose nearest neighbor free energy parameters were predicted or utilized for comparison in this work. (A) The Watson–Crick adenosine–uridine base pair (top) and similar modified derivatives: N⁶-methyladenosine·uridine, 2,6-diaminopurineriboside·uridine, and 2-aminopurineriboside·uridine. (B) The Watson-Crick guanosine-cytidine base pair (top) and similar modified derivatives: inosine·cytidine, guanosine·5-methylcytidine, and isoguanosine·isocytidine. (C) The base pair adenosine·pseudouridine that has a stabilizing backbone interaction. (D) Base pairs that result in significant helical distortions to the typical A-form RNA duplex: guanosine·uridine and inosine·uridine wobble pairs. Letter codes are shown above respective base pairs with hyphens representing Watson-Crick base pairing and middle dots representing wobble or modified base pairing. For simplicity, each base is shown capped with a methyl group where bases would connect to the sugar. The base pairs here are drawn to maximize base-base hydrogen bonding and to mimic the conformation of the canonical pairs. In solution within a duplex, it is likely that these pairs adopt this conformation; however, it is possible that they adopt a different hydrogen bonding pattern and/or slightly different conformation in varying sequence contexts.

Because secondary structure formation is thermodynamically driven, computational determination of component energetics should provide a good basis for NN ΔG°₃₇ prediction. Nucleic acid duplex formation is mainly governed by stacking and hydrogen bonding interactions. A prior computational model from the Znosko lab divided these components even further into hydrogen bonding, intrastrand base stacking, and interstrand base stacking in the context of WC NNs (21). A similar model was used to rank I·U nearest neighbor binding energy calculations (22). While these prior works were able to successfully rank nearest neighbor free energies, they both lacked the predictive power to estimate NN ΔG°₃₇ parameters from computational data.

Today, there exists enough experimentally derived NN ΔG°₃₇ parameters with modified nucleotides (12,23–26) to validate and benchmark computational approaches. Thermodynamic work has been done with modified nucleotides in a variety of settings (27–31), but this work focuses on modified nucleotides involved in pairs within RNA helices. Recently, Das and coworkers have shown for the first time that NN ΔG°₃₇ predictions are feasible with current computational methods using a RECCES-Rosetta (reweighting of energy-function collection with conformational ensemble sampling in Rosetta) framework. RECCES-Rosetta predictions were able to recover WC and modified NN free energies with RMSDs <1 kcal/mol (26).

In this work, we offer an alternative molecular dynamics (MD)/quantum mechanical (QM) approach that specifically quantifies the hydrogen bonding and stacking energies for each NN set and allows for simplified and direct comparison to their Watson–Crick counterparts. In this approach, RNA NN geometries are generated from MD simulations on RNA duplexes. Free energy parameters are estimated using computational stacking and hydrogen bonding energies from QM calculations of the nucleobases. A modified base's thermodynamic contributions due to solvation, helical distortion, or rotational isomerization can be estimated from predictions or calculated separately and included in NN ΔG°₃₇ predictions.

MATERIALS AND METHODS

RNA duplex design

RNA heptamer duplexes were designed to have 5′GC/3′CG nearest neighbors on either end with the base pair of interest in the middle of the duplex. By capping both duplex termini with the most stable WC NN combination, we aimed to minimize the effects of terminal base pair dynamics and MD artifacts that could skew the preferred base-pairing structures in the context of duplexed RNA. For example, I·C duplexes were designed as 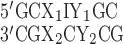where X₁ and Y₁ are A, C, G or U, and X₂ and Y₂ are their WC base pairing complements, respectively, to construct all 16 WC neighboring combinations for internal I·C base pairs. Although the most likely base pairing conformations are illustrated in Figure 1, no restraints were added during MD production runs, allowing base pairs to sample whatever conformational space they preferred. By constructing heptamer duplexes in which the modified pair is situated between all 16 possible Watson–Crick nearest neighbor combinations, the modified base pairs could change conformation based on their immediate surrounding environments (different base pair steps).

Starting structures and force fields

A-form WC duplexes were built using the Nucleic Acid Builder (NAB) in AmberTools18 (http://ambermd.org) while modified duplexes were built by editing the WC NAB structures in Biovia Discovery Studio (https://www.3dsbiovia.com/) to keep starting structures as similar as possible. Leap was used to add sodium counterions and to solvate duplexes with water (TIP3P) in an octahedral box with a 12.0 Å buffer (>4000 water molecules around each duplex). Parameter/topology files were built using the Amber ff99 forcefield (32) with the Barcelona α/γ backbone modification (33) and the χ modification for RNA (34) (ff99bsc0χOL3) as well as the modrna08 forcefield for modified nucleotides (35). For modified nucleotides that did not have force fields available, antechamber was used to create forcefield modification files.

Energy minimization and molecular dynamics simulations

Prior to molecular dynamics simulations, two rounds of minimization were performed with constant volume, periodic boundaries, and a non-bond cutoff of 12.0 Å using sander. A minimization was done with restraints on the RNA (500 kcal/mol Å²) to allow the bulk solvent to relax followed by an unrestrained minimization on the whole system. Both minimizations were carried out with a 10 000-step maximum and the steepest gradient used until 5000 steps had completed.

Following energy minimization, the system was first heated from 0 to 310 K over a period of 20 ps using constant volume periodic boundaries, keeping the RNA duplex weakly restrained with a force constant of 10 kcal/mol Å². The system was then allowed to equilibrate for 100 ps using constant pressure periodic boundaries with an average pressure of 1.0 atm at a temperature of 310 K. Isotropic position scaling was used to maintain pressure with a relaxation time of 2.0 fs. Once the system had reached equilibrium, a 1.0 ns simulation was run using the same setup as the equilibration run. The choice of pressure and temperature (1.0 atm and 310 K, respectively) were chosen to be consistent with experimentally derived thermodynamics.

To ensure that 1 ns MD simulations were of sufficient duration, select modified duplexes were also run for 10, 50 and 100 ns. These yielded very small structural differences that caused <1.5% change in computational nearest neighbor binding energies (E_NN,binding) and resulted in trimer duplex RMSDs <0.2 Å, showing no improvement or significant structural changes from longer simulations. As a result, 1 ns MD simulations were used to conserve computational resources without sacrificing accuracy. For more significantly modified nucleotides that are likely to disrupt traditional WC pairing or alter standard base-backbone interactions, longer MD simulations are likely required.

For all MD simulations, a non-bond cutoff of 12.0 Å was applied, and the SHAKE algorithm was employed to minimize the magnitude of H-involved motions with a timestep of 2.0 fs/step. Langevin dynamics were used to control the temperature with a collision frequency of 1.0 ps⁻¹.

Duplex processing

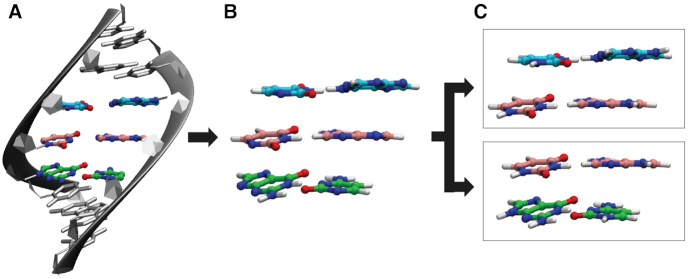
From the MD trajectories, an average structure for each duplex was calculated using cpptraj after removing water, sodium counterions, and hydrogen atoms. Hydrogen atoms from MD trajectories were removed as they were susceptible to the greatest motion and likely to influence the calculations of the average structure of each duplex. Leap was used to add a new set of hydrogen atoms according to residue templates to the average duplex structure. The average structure was stripped of backbone atoms and the two terminal G–C base pairs on either terminus using cpptraj to generate a trimer duplex consisting only of the base pair of interest with both neighboring base pairs. Each nucleobase was then capped with H atoms at the N1 and N9 positions for pyrimidine and purine bases, respectively. Each trimer duplex was divided into two dimer duplexes which were used as the NN geometry for running QM calculations (Figure 2).

Figure 2.

Process of generating nearest-neighbor geometries from MD trajectories. (A) An average structure is calculated from a 1 ns MD trajectory on each RNA duplex using only heavy (non-hydrogen) atoms. (B) Hydrogen atoms are added to the RNA duplex according to residue templates. Terminal base pairs and backbone are removed. (C) Bases are capped with H atoms at N9/N1 for purines/pyrimidines, respectively. From each MD simulation, two nearest neighbor geometries are generated for QM calculations.

The choice to remove the backbone from calculations was validated by small backbone RMSDs when a modified base pair was substituted for a WC pair. For example, m⁶A·U duplexes yielded an average backbone RMSD of 0.40 Å when compared to corresponding A–U duplexes. For duplexes containing G·m⁵C instead of G–C base pairs, backbone atoms yielded an average RMSD of 0.36 Å for the entire heptamer duplex. Because these changes are so small, the backbone atoms can easily be removed to save computational resources without sacrificing important interactions. For modifications that significantly disrupt standard A-form RNA backbone structures (e.g. duplexes containing I·U pairs), backbone alterations should be accounted for and are discussed below in the section Additional Corrections to NN Free Energy Predictions.

Quantum mechanical calculations

Single-point QM calculations were run on each H-capped dimer duplex at the ωB97X-D3 level of theory (36,37) and the def2-TZVP basis set (38) and the def2-TZVP/C auxiliary basis set using the conductor-like polarizable continuum model (CPCM) in Orca 4.1.1 (https://orcaforum.kofo.mpg.de/). The level of theory chosen (ωB97X-D3) was based on the highest correlation with experimental NN parameters when benchmarked against experimental data for Watson–Crick base pairs (Supplementary Figure S2 and Supporting Methods and Supporting Results). For each dimer duplex, six interactions were accounted for: two base-pairing energies (hydrogen bonding, E_HB) and two intra- and inter-strand stacking energies (E_stack) (Figure 3). Basis set superposition errors (BSSE) were minimized using the counterpoise methods of Boys and Bernardi (39). Specifically, dimer and monomer energies were calculated with the basis sets of all four bases of each nearest neighbor set. Accounting for solvent was important for experimental correlation (Supplementary Figure S2), but due to recently discovered rotational discrepancies of CPCM with the DFT methods, the solvent probe radius was increased from the default 1.3 to 1.5 Å to overcome inconsistencies that resulted from the initial DFT implicit solvent calculations (Supplementary Tables S1–S4).

Figure 3.

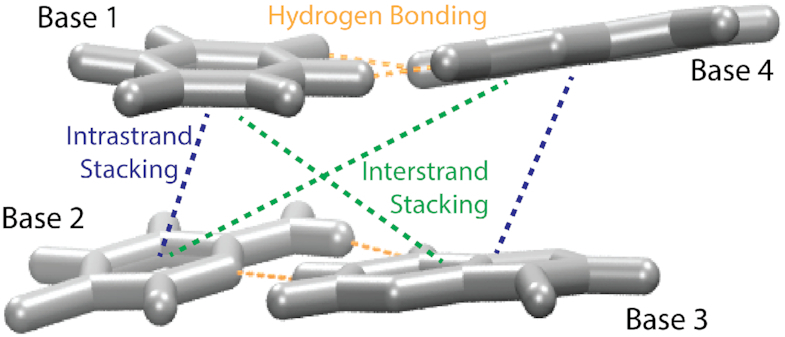
Schematic of bases involved for calculated hydrogen bonding energies and intra- and inter-strand stacking energies. E_HB was calculated for base interactions B1–B4 and B2–B3. Stacking energies (E_stack) include the two intrastrand (B1–B2 and B3–B4) and two interstrand base stacking combinations (B1–B3 and B2–B4).

In the interest of conserving biologically relevant RNA geometries (e.g. propeller twist, stretch, slide, etc.) from the MD simulations, we did not perform a QM optimization of the base fragments that were extracted from the simulation model. Unrestrained QM optimizations with only four bases result in base pair and stacking geometries that are inconsistent with experimental and MD-derived structures. Restrained QM optimizations on these systems that would conserve characteristic RNA features (e.g. helical and propeller twist) often do not properly converge. Full duplex unrestrained optimizations are computationally costly and can also result in optimized but biologically inconsistent geometries. Not performing optimizations allows users to avoid computationally costly calculations and to preserve base step helical twists that are consistent with biologically relevant and experimentally derived nucleic acid structures. The accuracy of the method discussed in the results section validates that QM optimizations are not necessary for this model's predictive power.

Nearest neighbor free energy prediction

Computational nearest neighbor binding energies (E_NN,binding) were calculated according to the equation

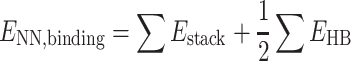as done in previous works (21,22). The hydrogen bonding energies (E_HB) were halved so that the addition of consecutive nearest neighbor energies would result in each E_HB being counted only once in the context of internal base pairs. For the NN geometry 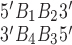where B₁–B₄ and B₂–B₃ are base pairs, the total stacking and hydrogen bonding energies can be expressed as a sum of their interaction energies (E_int) as described in Johnson et al. (21), where 1, 2, 3 and 4 represent B₁, B₂, B₃ and B₄, respectively.

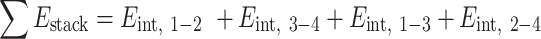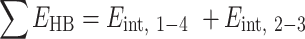Methods for calculating these interaction energies were changed slightly from previous methods so that all interaction energies for each dimer interaction were counterpoise corrected with basis sets for all four monomer basis sets present:

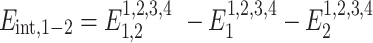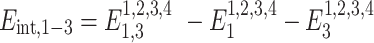etc.

Each E_NN,binding was converted to predicted NN ΔG°₃₇ parameters according to the line of best fit from Watson–Crick experimental free energies versus computational NN binding energies (Figure 4 and Supplementary Tables S5–S6). In select cases, additional terms were added based on rotational isomerization (m⁶A, Supplementary Figure S3) and helical distortion (I·U) and are discussed below. The line of best fit between Watson-Crick experimental and computational NN energies (Figure 4) was used to predict NN free energy parameters (ΔG°_37,predicted) for all modified base pairs.

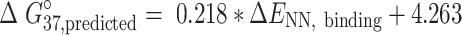Figure 4.

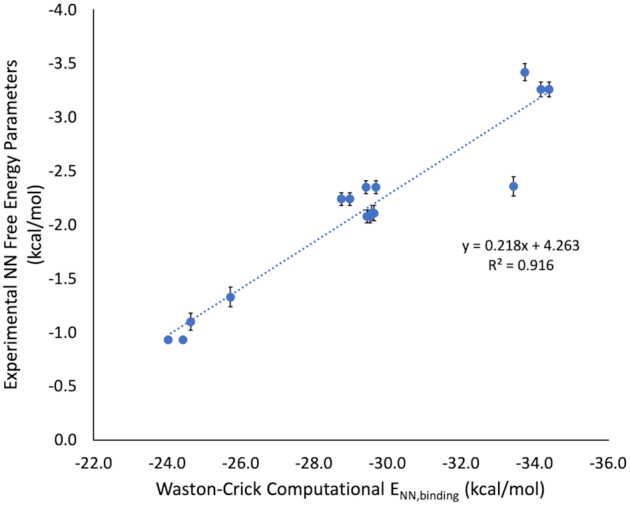
Experimental NN free energy parameters for Watson–Crick nearest neighbor combinations versus computational NN binding energies (ωB97X-D3 with CPCM (water, α = 1.5 Å)) from NN geometries obtained from MD simulations. Average fiber diffraction data was used to benchmark QM methods as described in Supplementary Figure S2. However, because our method to obtain modified base pair NN geometries comes from MD simulations, it was necessary to run the same MD protocol on all A–U and G–C base pair NN combinations to ensure consistency in energy derivation. Therefore, eight A–U and eight G–C computational NN free energies (Supplementary Tables S5 and S6) were mapped to experimental NN free energy parameters (19) using a simple linear regression.

Additional corrections to NN free energy predictions

Calculation of G·U/I·U helical distortion penalty

G·U/I·U base pairs are known to distort the typical A-form RNA helix. Therefore, I·U NN ΔG°_37,predicted were calculated by accounting for this term. On average, NN free energy predictions of G·U base pairs were overestimated by 0.54 kcal/mol. This was assumed to be due to the distortion of the backbone. Corrected G·U/I·U NN free energy parameters were estimated as:

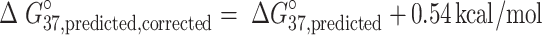Calculation of m⁶A rotamer penalty

N ⁶-Methyladenosine is known to prefer the anti rotamer when unpaired. Adopting the syn conformation is required when base pairing with uridine. Therefore, this energetic penalty was calculated as the difference between these two energies. Both structures were built in Chemcraft (https://www.chemcraftprog.com) and optimized with B3LYP/def2-TZVP. Single-point calculations were carried out on the optimized syn and anti structures using ωB97X-D3/def2-TZVP to remain consistent with NN binding energy methods. The difference between the syn and anti conformations of m⁶A was 1.61 kcal/mol. Therefore, half of this energy (0.81 kcal/mol) was applied as a penalty to each m⁶A·U E_NN,binding such that corrected E_NN,binding were calculated as:

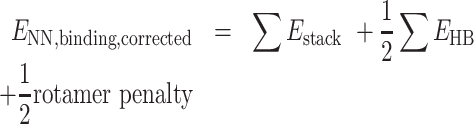or

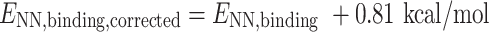Explanation of reported computational errors

For each interaction energy and binding energy, up to four sets of data were included. Sixteen duplexes with varying NNs were simulated for each base pair. For example, in the case of I·C simulations, four 5′AI/3′UC NN geometries were analyzed: 5′AIA/3′UCU, 5′AIC/3′UCG, 5′AIG/3′UCC and 5′AIU/3′UCA. Errors were simply reported as the standard error of this spread as described below.

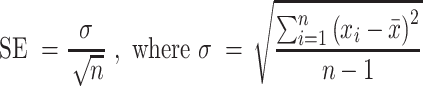RESULTS

In order for this computational approach to produce accurate NN binding energies (E_NN,binding), we had to survey several QM levels of theory and choose appropriate parameters for these calculations. The range-separated functional ωB97X-D3 (37) using implicit solvation with a solvent probe radius of 1.5 Å showed the greatest correlation with experimental data (Supporting Results, Supplementary Tables S1–S4, and Supplementary Figure S2). Because this method uses MD simulations to obtain NN geometries for modified base pairs, it was necessary to use the same approach with Watson–Crick base pairs to map E_NN,binding to NN free energy parameters (Figure 4) and obtain component energies for stacking and hydrogen bonding contributions in Watson–Crick NNs (Supplementary Tables S5–S6). Component energies for modified NNs can be found in Supplementary Tables S7–S15.

Protocol validation with experimental inosine·cytidine free energy parameters

Because this NN prediction method does not take backbone conformation into account, protocol validation initially required testing on a modified base pair with available experimental NN parameters that would incur minimal backbone distortion compared to WC base pairs. For this reason, I·C base pairs were chosen to verify that this method (taking only hydrogen bonding and base stacking into account) could accurately predict a WC-like modified base pair's NN ΔG°₃₇ parameters. All eight I·C NN ΔG°₃₇ predictions with neighboring WC base pairs were within experimental error of parameters derived by Wright et al. (24) (Table 1) with a mean signed error (MSE) of –0.02 kcal/mol, a mean absolute error (MAE) of 0.17 kcal/mol, and a root mean square deviation (RMSD) of 0.21 kcal/mol, indicating a lack of systematic error and a small deviation from experimental parameters. An energetic component analysis of I·C pairs (Supplementary Table S7) revealed that I·C and A–U base pairs, on average, contribute similar thermodynamic contributions to RNA duplex stability. Although I·C E_HB is, on average, 15% more stable than A–U E_HB, A–U pairs generally tend to form stronger stacking interactions with neighboring base pairs (Supplementary Tables S5 and S7).

Table 1.

Nearest neighbor free energy parameters derived experimentally compared to predicted values in this work (ΔG°_{37, predicted}) and from the RECCES-Rosetta framework (ΔG°_{37, Rosetta}) with average differences from A–U and G–C NN ΔG°₃₇ and RMSDs from experimental values. ΔG°_{37,experimental} refers to experimentally derived NN ΔG°₃₇ parameters for Watson–Crick, inosine·cytidine, isoguanosine·isocytidine, 2,6-diaminopurineriboside·uridine, and inosine·uridine obtained from references (19), (24), (25), (26) and (23), respectively. All values are reported in kcal/mol.

	NN	ΔG°37,experimental	ΔG°37,predicted	ΔG°37,Rosetta
Watson–Crick	AA	−0.93 ± 0.03	−1.02 ± 0.12	−1.13 ± 0.17
	UU
	AU	−1.10 ± 0.08	−1.11 ± 0.13	−0.91 ± 0.21
	UA
	UA	−1.33 ± 0.09	−1.34 ± 0.09	−1.26 ± 0.20
	AU
	AG	−2.08 ± 0.06	−2.16 ± 0.08	−2.19 ± 0.11
	UC
	CA	−2.11 ± 0.07	−2.19 ± 0.04	−2.09 ± 0.10
	GU
	AC	−2.24 ± 0.06	−2.03 ± 0.07	−1.95 ± 0.14
	UG
	GA	−2.35 ± 0.06	−2.18 ± 0.07	−2.13 ± 0.09
	CU
	CG	−2.36 ± 0.09	−3.02 ± 0.13	−2.89 ± 0.21
	GC
	CC	−3.26 ± 0.07	−3.21 ± 0.11	−3.29 ± 0.21
	GG
	GC	−3.42 ± 0.08	−3.09 ± 0.11	−2.88 ± 0.17
	CG
	RMSD		0.25	0.28
	MSE		−0.02	0.05
Inosine·cytidine	AI	−1.57 ± 0.44	−1.32 ± 0.11	−1.09 ± 0.14
	UC
	CI	−1.86 ± 0.31	−2.07 ± 0.32	−1.98 ± 0.20
	GC
	GI	−2.62 ± 0.40	−2.31 ± 0.09	−2.07 ± 0.26
	CC
	UI	−0.96 ± 0.40	−1.31 ± 0.14	−0.98 ± 0.25
	AC
	IA	−1.18 ± 0.44	−1.25 ± 0.07	−1.06 ± 0.11
	CU
	IC	−1.89 ± 0.31	−2.03 ± 0.21	−1.96 ± 0.13
	CG
	IG	−2.23 ± 0.40	−2.19 ± 0.22	−2.24 ± 0.16
	CC
	IU	−1.02 ± 0.40	−1.02 ± 0.13	−0.95 ± 0.21
	CA
	RMSD		0.21	0.27
	MSE		−0.02	0.13
	ΔA-U	−0.03	−0.05	0.09
	ΔG-C	0.97	0.95	1.09
Isoguanosine·isocytidine	AiG	N/A	−2.45 ± 0.26	−2.34 ± 0.26
	UiC
	CiG	−2.46 ± 0.08	−3.11 ± 0.23	−3.01 ± 0.39
	GiC
	GiG	−3.07 ± 0.11	−3.43 ± 0.31	−3.48 ± 0.22
	CiC
	UiG	N/A	−2.58 ± 0.27	−1.93 ± 0.24
	AiC
	iGA	N/A	−2.66 ± 0.04	−2.14 ± 0.23
	iCU
	iGC	−4.00 ± 0.09	−3.31 ± 0.27	−2.78 ± 0.18
	iCG
	iGG	−3.46 ± 0.11	−3.68 ± 0.09	−3.23 ± 0.16
	iCC
	iGU	N/A	−2.53 ± 0.26	−1.84 ± 0.27
	iCA
	RMSD		0.52	0.71
	MSE		−0.14	0.12
	ΔG–C	−0.22a	−0.33	0.04
2,6-Diaminopurine·uridine	AD	N/A	−1.42 ± 0.15	−2.32 ± 0.17
	UU
	CD	−2.72 ± 0.20	−2.24 ± 0.11	−3.57 ± 0.21
	GU
	GD	−3.10 ± 0.21	−2.37 ± 0.09	−3.10 ± 0.17
	CU
	UD	N/A	−1.78 ± 0.71	−2.61 ± 0.18
	AU
	DA	N/A	−1.45 ± 0.08	−2.28 ± 0.16
	UU
	DC	−2.62 ± 0.14	−2.35 ± 0.13	−2.80 ± 0.15
	UG
	DG	−2.28 ± 0.22	−2.33 ± 0.04	−3.20 ± 0.13
	UC
	DU	N/A	−1.41 ± 0.08	−1.85 ± 0.19
	UA
	RMSD		0.46	0.63
	MSE		0.36	−0.49
	ΔA–U	−0.49	−0.29	−1.08
	ΔG–C	0.40	0.71	−0.08
	Overall RMSDb		0.33	0.44
	Overall MSEb		0.02	0.00
Inosine·uridine	AI	−0.41 ± 0.47	−0.37 ± 0.17	N/A
	UU
	CI	−0.77 ± 0.39	−0.87 ± 0.14	N/A
	GU
	GI	−1.34 ± 0.33	−1.20 ± 0.34	N/A
	CU
	UI	0.37 ± 0.39	−0.13 ± 0.28	N/A
	AU
	IA	0.43 ± 0.43	−0.04 ± 0.35	N/A
	UU
	IC	−1.03 ± 0.30	−1.17 ± 0.16	N/A
	UG
	IG	−1.22 ± 0.37	−1.32 ± 0.23	N/A
	UC
	IU	−0.50 ± 0.44	−0.36 ± 0.06	N/A
	UA
	RMSD		0.26	N/A
	MSE		−0.12	N/A
	Overall RMSDc		0.32	N/A
	Overall MSEc		–0.01	N/A

^aValue estimated by halving the reported average duplex ΔG–C from (7).

^bOverall root mean square deviation (RMSD) and mean signed error (MSE) are for only WC, I·C, iG·iC, and DAP·U for direct comparisons to RECCES-Rosetta predictions.

^cOverall RMSD and MSE include WC, I·C, iG·iC, DAP·U and I·U data.

After validating the protocol for I·C NN ΔG°₃₇ parameters, NN ΔG°₃₇ predictions of other modified base pairs (Figure 1) were employed for modifications that were either biologically or biochemically relevant. Of the modified base pairs whose experimental NN ΔG°₃₇ parameters have been derived, an overall RMSD of 0.32 kcal/mol was achieved using the NN ΔG°₃₇ predictions in this work. Experimental NN ΔG°₃₇ parameters versus NN ΔG°₃₇ predictions are illustrated in Figure 5 (with panels for individual base pairs shown in Supplementary Figure S4). Predictions for modified base pairs with no available experimental parameters are given in Table 2.

Figure 5.

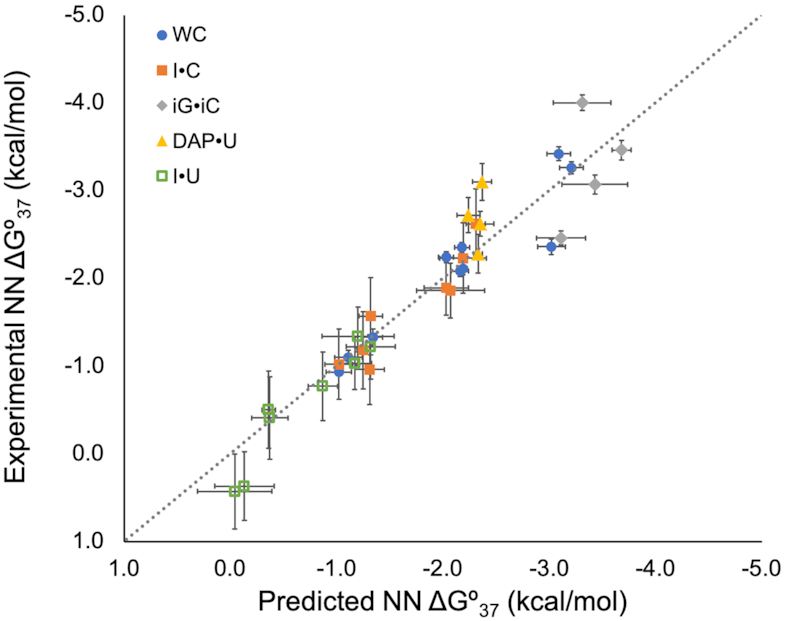
Predicted versus experimental nearest neighbor free energies. The dotted line has a slope of one and an intercept of zero, representing ideal correlation between predicted and experimental data. Watson–Crick (WC), inosine·cytidine (I·C), isoguanosine·isocytidine (iG·iC), 2,6-diaminopurineriboside·uridine (DAP·U) and inosine·uridine (I·U) experimental NN parameters were taken from references (19), (24), (25), (26) and (23), respectively. Individual panels for each modified base pair can be found in Supplementary Figure S4.

Table 2.

Predictions of nearest neighbor free energy parameters for guanosine·5-methylcytidine (G·m⁵C), N⁶-methyladenosine·uridine (m⁶A·U), and 2-aminopurineriboside·uridine (2AP·U) with average differences from comparable Watson–Crick parameters. X·Z base pairs represent the modified base pair in column headings, where X is first nucleotide listed (purine) and Z is the second (pyrimidine)

	m6A·U	G·m5C	2AP·U
AX	−0.91 ± 0.13	−1.86 ± 0.06	−1.03 ± 0.20
UZ
CX	−1.84 ± 0.47	−2.62 ± 0.17	−1.78 ± 0.28
GZ
GX	−1.94 ± 0.06	−2.89 ± 0.07	−1.99 ± 0.08
CZ
UX	−1.15 ± 0.09	−2.00 ± 0.28	−1.21 ± 0.22
AZ
XA	−0.90 ± 0.07	−2.06 ± 0.14	−0.98 ± 0.06
ZU
XC	−1.75 ± 0.03	−3.05 ± 0.86	−2.05 ± 0.25
ZG
XG	−1.84 ± 0.07	−3.02 ± 0.08	−1.92 ± 0.13
ZC
XU	−0.86 ± 0.18	−1.96 ± 0.13	−1.05 ± 0.18
ZA
ΔA-U	N/A	0.24	0.13
ΔG-C	0.20	N/A	N/A

Predicting free energy parameters for modified Watson–Crick-like base pairs

Guanosine·5-methylcytidine

The modified base m⁵C can form a WC-like base pair with guanosine, but G·m⁵C base pairs and their neighbors must adopt a geometry able to accommodate a methyl group at the five position. This results in altered hydrogen bonding energies in a G·m⁵C base pair compared with a canonical G–C pair. G·m⁵C base pairs have stacking energies consistent with G–C pairs; however, the presence of the methyl group affects hydrogen bonding. On average, the E_HB for G·m⁵C base pairs is 8% less than their G–C counterparts (Supplementary Tables S6 and S8). Additionally, the presence of a G·m⁵C base pair slightly weakens the E_HB of neighboring G-C base pairs (6.6%) but does not affect neighboring A–U pairs (<1% difference) (Supplementary Tables S5 and S8). This hydrogen bonding difference leads to G·m⁵C NN ΔG°₃₇ predictions that are 0.20 kcal/mol less stable than G-C base pairs and an average duplex destabilization of 0.41 kcal/mol per G·m⁵C base pair (Table 2), consistent with the reported 0.5 kcal/mol average destabilization measured experimentally (40).

2-Aminopurineriboside·uridine

The modified base 2AP is often substituted for A due to its fluorescence. Because of its hydrogen bonding scheme with U (Figure 1), it is assumed to not affect RNA stability compared to A. Contrary to this assumption, we estimate a slight destabilization due to the shifted base pair stacking in 2AP·U NN geometries. On average, 2AP·U pairs are predicted to destabilize RNA duplexes by 0.27 kcal/mol (0.13 kcal/mol per NN) compared to A-U pairs (Table 2). Calculations showed that the E_HB in 2AP·U is only 3% weaker than A–U base pairs (Supplementary Tables S5 and S9); however, the amino group in the 2-position causes the base pairs to shift in the way they stack with their neighbors (Supplementary Figure S5). This results in slightly stronger intrastrand base stacking compared to A at the 5′ position and weaker stacking in the 3′ position. Interstrand 5′ stacking energies are also weaker compared to A due to the position of the amino group. NN ΔG°₃₇ parameters are not available for 2AP·U base pairs; however, sequence comparisons in DNA show promising performance when compared with 2AP·T base pairs (41) and are discussed later.

2,6-Diaminopurineriboside·uridine

Like G–C pairs, DAP·U pairs can form three hydrogen bonds (Figure 1). While E_HB for G–C pairs is 50% stronger than A–U pairs, component analysis revealed that E_HB for DAP·U pairs is only 18% stronger than A–U pairs (Supplementary Tables S5 and S10). This is consistent with previous literature which showed that a polymer of DAP·U yielded a melting temperature (T_m) only 25°C higher than a comparable A–U polymer while a G–C polymer melt resulted in a T_m 50°C higher than the A–U polymer (42). This suggests that DAP·U pairs contribute only half of the added stability that G-C pairs contribute to an RNA duplex compared to A-U pairs. E_stack for DAP·U pairs was, on average, <0.05 kcal/mol different from A–U NNs (Supplementary Tables S5 and S10), suggesting that most of the increased stabilizing interactions come from E_HB. DAP·U NNs are predicted to be, on average, 0.29 kcal/mol more stable than A–U NNs, corresponding to an estimated 0.57 kcal/mol duplex stabilization per DAP·U pair in an RNA duplex (Table 1). This showed excellent agreement with the DAP·U polymer study, which estimated a 0.6 kcal/mol stabilizing contribution from the additional amino group's hydrogen bond (42). Compared with experimental parameters (26), our predictions yield an RMSD of 0.46 kcal/mol (Table 1).

Isoguanosine·isocytidine

NN ΔG°₃₇ parameters for the unnatural base pair iG·iC derived by Turner et al. showed that iG·iC base pairs were experimentally determined to contribute, on average, 0.44 kcal/mol more stability compared to G-C (43). NN ΔG°₃₇ parameters predicted in this work suggest a slightly stronger (0.67 kcal/mol) average duplex stabilization compared to G–C pairs and result in an RMSD of 0.52 kcal/mol compared to experimental parameters (Supplementary Table S11). A component analysis revealed that iG·iC base pairs contribute E_HB that is 15% stronger than G–C and an interstrand 3′ stacking energy that is 19% stronger with adjacent bases (Supplementary Tables S5 and S11). While the 0.52 kcal/mol RMSD is higher than any of the other modified NN predictions, it is important to note that this MD/QM approach is able to differentiate between iG·iC and G–C energetics, recovering the increased experimental stability in iG·iC versus G–C NNs.

Predictions of modified base pair nearest neighbor free energies involving additional energy correction terms

In order to obtain accurate QM calculations on nearest neighbor systems while keeping time and resources within reason, the sugar-phosphate backbone was removed, leaving only the 50–60 atoms that make up the H-capped RNA nucleobases. As a result, modified base pair interactions that significantly interact with the backbone or disrupt double-helical conformations are not taken into account, nor is the syn/anti rotamer penalty for converting from the preferred syn conformation (where m⁶A's methyl group points toward the WC face) to the anti conformation (where m⁶A's methyl group points away from the WC face) (Supplementary Figure S3) necessary for a two-hydrogen-bond base pair between m⁶A and U (Figure 1). For these cases, additional independent calculations were run to estimate the thermodynamic impact of interactions that are not accounted for with standard hydrogen bonding and stacking calculations. For the case of A·Ψ base pairs, it is necessary to consider the thermodynamic contribution of the coordinating water molecule between the Ψ N1-imino proton and OP2 of the phosphate backbone (Supplementary Figure S6). While the dynamics of this interaction limit the usefulness of standard QM interaction energies, the methods in this work can be used to estimate the stabilizing impact of this coordinated water molecule and are discussed in the SI.

N⁶-Methyladenosine·uridine

Literature suggests that the penalty for m⁶A rotation from the syn to the anti rotamer conformation (Supplementary Figure S3) is ∼1.5 kcal/mol (43), which agrees well with our calculated destabilization of 1.6 kcal/mol (Supplementary Table S16). We applied this 1.6 kcal/mol rotamer penalty to the total E_NN,binding prior to mapping this energy to a predicted ΔG°₃₇. On average, replacing A with m⁶A in a duplex is predicted to cause a destabilization of 0.47 kcal/mol (Table 2). Consistent with previous reports (44), m⁶A participates in stronger intrastrand stacking with neighboring bases by 0.49 kcal/mol (12%) compared with A; however, overall NN geometries led to total stacking energies that were only 0.19 kcal/mol more stable than A–U NNs (Supplementary Tables S5 and S12) due to the adjustment of neighboring base pairs when accommodating m⁶A's methyl group. The E_HB for m⁶A·U base pairs was slightly less (6%) than the E_HB for A–U base pairs, likely due to the increased propeller twist on account of the N⁶-methyl group. There is also a small (6%) destabilization of neighboring G–C E_HB that is not evident in neighboring A–U pairs. Increased stacking with decreased hydrogen bonding energies roughly off-set one another. As a result, most of the predicted destabilization results from the penalty of shifting from the syn to the anti rotameric conformation.

Inosine·uridine

Due to the structural similarity of inosine and guanosine, I·U and G·U pairs adopt the same base pairing geometry (Figure 1). These base pairs are known to cause distortion to the RNA backbone (45–48), which affects their stability in duplexed RNA and, therefore, their NN thermodynamic parameters. For this reason, I·U NN ΔG°₃₇ parameters could not accurately be predicted without explicitly accounting for the energetic impact of helical distortion. G·U NN ΔG°₃₇ parameters were predicted from E_NN,binding, which accounted for the E_stack and E_HB of G·U NNs (Supplementary Table S13). The average difference between the predicted and the experimental ΔG°₃₇ (49) was assumed to be the energetic penalty of helical distortion. This estimated penalty for G·U NNs (0.54 kcal/mol) (Supplementary Table S13) was assumed to be the same for I·U base pairs and was applied to I·U NN ΔG°₃₇ predictions (Supplementary Table S14). The resulting I·U ΔG°₃₇ predictions showed excellent agreement with experimental parameters (23), resulting in an MSE of –0.12 kcal/mol and an RMSD of only 0.26 kcal/mol (Table 1). This level of accuracy validates that independent correction factors based on a known set of data can be used to accurately predict NN ΔG°₃₇ parameters where there are non-stacking and non-hydrogen bonding energetic contributions.

DISCUSSION

Comparison to available NN parameters and other prediction methods

Work out of the Das lab has measured a small set of experimental free energies involving the unnatural base DAP and has predicted ΔG°₃₇ parameters for NN combinations involving DAP·U, iG·iC, I·C and WC base pairs using a RECCES-Rosetta framework (26). This was the first model to demonstrate computational methods were capable of blindly predicting NN ΔG°₃₇ parameters and showed <1 kcal/mol RMSD for all NN prediction sets. A comparison of their blind predictions to ours with experimental reference data is summarized in Table 1. Because our work focused only on base pairs with WC neighbors, NN predictions and experimental free energies containing tandem modified base pairs were ignored for the sake of comparison consistency.

Using the NN parameters reported here, ΔG°₃₇ predictions for the six duplexes containing DAP·U base pairs were, on average, 0.67 kcal/mol closer to the experimental free energies than the RECCES-Rosetta predictions (Supplementary Table S17). RMSDs for DAP·U NN parameters were 0.63 and 0.46 kcal/mol for RECCES-Rosetta and our predictions, respectively (Table 1). Early studies from Howard et al. found that polyDAP·polyU duplexes have melting temperatures half-way between polyA-polyU and polyG-polyC duplexes (42), suggesting that the three hydrogen bonds in DAP·U base pairs are not as strong as the three hydrogen bonds found in G–C base pairs. They estimated the contribution from the additional amino group to be only 0.6 kcal/mol per DAP·U base pair. NN parameters predicted from Das and coworkers suggest a 2.2 kcal/mol duplex stabilization per DAP·U base pair (1.1 kcal/mol per NN) when replacing an A-U base pair. This is more than the contribution of substituting G–C for A–U base pairs, which was not found in the experimental NN ΔG°₃₇ parameters with WC neighbors. Our NN free energies predict a far smaller stabilization of 0.57 kcal/mol per DAP·U base pair (0.29 kcal/mol per NN) when replacing an A–U base pair (Table 1), which aligns well with the experimentally determined 0.6 kcal/mol added stability (42).

Similar to the DAP·U NNs derived, only four experimental iG·iC NN with WC neighbors are available to compare to predicted NN parameters. RMSDs between available experimental and predicted iG·iC NN parameters were 0.71 and 0.52 kcal/mol for RECCES-Rosetta and our predictions, respectively (Table 1). Interestingly, both prediction methods underestimated the stability of two NNs (5′iGC/3′iCG and 5′iGG/3′iCC), and both overestimated the stability of the two others (5′CiG/3′GiC and 5′GiG/3′CiC). iG·iC base pairs were experimentally determined to contribute, on average, 0.44 kcal/mol more stability to RNA duplexes than G-C (25). NN ΔG°₃₇ parameters predicted in this work suggest an average 0.67 kcal/mol duplex stabilization, while average RECESS-Rosetta predictions suggest a slight (0.08 kcal/mol) destabilization (Table 1).

In predicting Watson–Crick and I·C NN free energies, there was no significant difference between RECCES-Rosetta predictions and ours. RMSDs between experimental and predicted free energies for WC and I·C NNs were 0.28 kcal/mol and 0.27 kcal/mol, respectively, for RECCES-Rosetta predictions and 0.25 and 0.21 kcal/mol, respectively, for predictions in this work (Table 1). The I·C NN ΔG°₃₇ parameters had not yet been experimentally derived when the RECCES-Rosetta predictions were published, making their accuracy rather remarkable. One clear advantage of the RECCES-Rosetta framework is the estimation of a terminal contribution for modified base pairs, which were not investigated in this work but are important energetic contributions given the frequency of modifications at terminal positions of tRNA stem regions (Supplementary Figure S1).

Although the RECCES-Rosetta framework demonstrated a significant step forward in computational NN ΔG°₃₇ predictions, an obvious advantage of the method presented here is its simplicity in quantifying the hydrogen bonding and stacking energies for individual stacks and base pairs in NN geometries. These clear-cut breakdowns allow for simple and direct comparisons to their Watson–Crick counterparts, providing insight into sources of (de)stabilization for a modified base compared its corresponding canonical nucleotide. Because no optimizations are necessary and only base atoms (capped with H) are included in the QM calculations, there is relatively little strain on computational resources, allowing NN ΔG°₃₇ parameter sets to be predicted in only 2 days. The better agreement between prediction and experiment for DAP·U and iG·iC NNs also suggests a possible advantage to using our QM-based approach. The Rosetta framework does not rigorously model electrostatic contributions beyond the hydrogen bonding terms, so the RECCES-Rosetta predictions included a new stack_elec term, which represents electrostatics for stacking atoms (26). Average overestimation of DAP·U stability and underestimation of iG·iC stability could result from errors in this type of electrostatic modeling, which was also evident in the inability of the framework to differentiate the significant stacking differences in 5′GC/3′CG compared to 5′CG/3′GC (26). Therefore, for modified bases that are not well-parametrized, our methods may be more generalizable and accurate when quantifying interactions that contribute to NN component energetics (e.g. stacking), which directly correlate with NN ΔG°₃₇ parameters.

Evaluation of NN predictions involving methylated bases

For the methylated base pairs studied in this work, there are no experimentally derived nearest neighbor free energies available in the literature to which our predictions can be compared. However, prior works have performed optical melts with these modified nucleotides with which we can attempt to benchmark our predictions. Work out of the Serra lab has measured an average 0.5 kcal/mol destabilization as the result of a G·m⁵C substitution for the canonical G–C base pair in RNA duplexes (40). This experimental finding aligns very well with our average predicted destabilization of 0.41 kcal/mol (0.20 kcal/mol per NN) (Supplementary Table S8). Roost et al. have melted duplexes with m⁶A·U base pairs and found that duplexes containing m⁶A·U base pairs caused a 0.6 kcal/mol destabilization per modified base pair compared to A-U counterparts (44), which is consistent with the findings of von Hippel who found a 0.5–1.0 kcal/mol destabilization per methylation in polymer studies (50). Our predicted destabilization for m⁶A·U-containing duplexes is 0.47 kcal/mol (Supplementary Table S12) and agrees very well with these experimental findings. While our nearest neighbors cannot currently be benchmarked for all m⁶A·U and G·m⁵C nearest neighbors, the average predicted destabilization from our NN ΔG°₃₇ predictions agrees well with available experimental data. Furthermore, it is interesting to note that while neither methylation directly affected the WC base pairing potential, both modifications resulted in weakened E_HB in their respective base pairs as well as weakened E_HB in neighboring G–C base pairs (Supplementary Tables S5, S6, S8 and S12). The agreement with experiment suggests that not only are the methods here sufficient to predict NN parameters but also to analyze component contributions to NN stabilities and identify trends across modification types.

Potential to predict DNA free energy changes upon modification

A DNA study was performed for the sequence 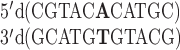and its 2AP counterpart 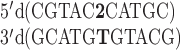where 2 represents 2AP. Law et al. reported that the 2AP·T-containing duplex was destabilized by 0.5 kcal/mol in comparison to the (otherwise) same sequence with an A-T base pair (41). Differing nearest neighbors involved were 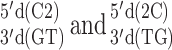. The predicted RNA destabilization for an A–U to 2AP·U substitution in the same sequence context is 0.52 kcal/mol, resulting from 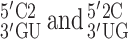nearest neighbors that are 0.33 and 0.19 kcal/mol less stable, respectively, than their A-U NN counterparts (Table 1). Therefore, while the geometry and base stacking of DNA and RNA duplexes may be too different to share the same NN ΔG°₃₇ predictions, it may still be possible to estimate relative free energy differences across nucleic acid duplexes using the parameters predicted here.

In summary, we present and validate nearest neighbor free energy predictions for modified base pairs using a model whose only experimental input is the set of Watson-Crick NN ΔG°₃₇ parameters. These modified base pair predictions include some of the most biologically common and functionally relevant modifications known to occur in vivo including m⁶A and m⁵C. In the case of I·C NNs for which there are experimental NN ΔG°₃₇ parameters to compare, all blind predictions were within experimental error with an RMSD of 0.21 kcal/mol. Watson–Crick and modified base pair NN free energy predictions including I·C, I·U, DAP·U, and iG·iC result in an overall RMSD and MSE of only 0.32 kcal/mol and –0.01 kcal/mol, respectively, indicating small deviation from experimental parameters and a lack of systematic error. Furthermore, while the QM methods here only take base-base interactions into account, we have shown success in approximating helical distortions using a known set of data that adopts a similar geometry, as demonstrated in the predictions of I·U NNs. This MD/QM approach provides simple and useful comparisons of stacking and hydrogen bonding differences between canonical and modified NNs as well as insight into structural causes for stability differences. Given the prediction accuracies and ability to identify energetic component differences, this protocol can not only inform secondary structure predictions but has the potential to provide insight into the effects and mechanisms of specific modifications on RNA stability and structure.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health [2R15GM085699-03 to B.M.Z.]. Funding for open access charge: National Institutes of Health.

Conflict of interest statement. None declared.