Extending the hierarchical decision matrix to incorporate a dominance ranking score for economic systematic reviews

Abstract

As the base of clinical evidence grows, it is increasingly common to conduct economic evaluations in addition to clinical evaluations of effectiveness in order to inform health policies. For economic systematic reviews there is currently no agreed-upon quantitative method to obtain a pooled economic effect size. With no suitable quantitative method available, the hierarchical decision matrix stands out as a tool that enables a visual summary of different types of economic studies, but there are limitations with the hierarchical decision matrix. We extended the hierarchical decision matrix with a weighted scoring system (termed dominance ranking score) to allow for useful information of a study design to be incorporated.

• •The scoring system of the dominance ranking score incorporates weighting factors that are based on sample size and effect size of a study.
• •The dominance ranking score enables a more differentiating analysis of dominance levels.
• •For systematic reviews that include partial economic studies, both the hierarchical decision matrix and the dominance ranking score assist to indicate the level of economic potential for a particular intervention, which facilitates the conduct of subsequent full economic studies.

Graphical abstract

Specifications table

Subject Area	Medicine and Dentistry
More specific subject area:	Economic systematic review
Method name:	Dominance ranking score
Name and reference of original method	Hierarchical decision matrix Nixon J, Khan KS, Kleijnen J. summarising economic evaluations in systematic reviews: a new approach. BMJ. 2001;322(7302):1596–8.
Resource availability	Not applicable

Background

Systematic review of clinical effectiveness has become the gold standard for evidence-based medical research. As the base of clinical evidence grows, it is increasingly common to conduct economic evaluations in addition to clinical evaluations of effectiveness in order to inform health policies [1,2]. Economic evaluations can be classified into two main types: empirical economic evaluations which collect patient-level data on costs and outcomes, and decision model (simulation) based economic analyses [2]. Empirical economic evaluations involve data collection and synthesis of existing evidence using the framework of a systematic review, while economic decision modeling involves the data collection and synthesis of existing evidence in order to generate a new economic evaluation using the framework of a decision model [3]. For either type of economic evaluation, the economic outcomes are expressed using a variety of measures, such as cost effectiveness, cost utility, cost benefit and incremental cost effectiveness ratios (which measure relative efficiency and are expressed as incremental gains in clinical effectiveness, health utility values or monetary valuations) [3], [4], [5].

Systematic reviews of empirical economic studies involve several stages of research which are similar to systematic reviews of clinical effectiveness: defining the review question and inclusion criteria for study eligibility; identifying and collecting data; appraising methodological quality; analyzing collected data and undertaking meta-analysis (where appropriate); and summarizing and presenting results [4,5]. On the other hand, economic decision modelling involves computing the expected costs and outcomes of alternative interventions, based on a synthesis of evidence for the probabilities, costs and outcomes associated with each event in the pathway flow of the intervention [3].

However, in the systematic review of empirical economic studies, there are currently no agreed-upon methods to obtain a pooled economic effect size from included empirical trials using meta-analysis or other quantitative synthesis methods [4,6]. The main reasons are the generalizability of the empirical economic studies. Economic trials are context and time sensitive [3], as resource use and unit costs are dependent on local settings, clinical practices and currency values at a particular time. This generates high heterogeneity if the economic studies in a systematic review come from different clinical contexts in different countries. Only if the studies have similar resource use and unit costs, with economic outcomes expressed in a common metric, then meta-analysis could be appropriate [4].

Given the current lack of quantitative synthesis methods, systematic reviews of economic studies have been restricted to methods of using descriptive narratives (via summaries or tables) [4] or plotting the magnitude and direction of cost and effectiveness using the CE-plane [7], or applying visual summaries in a hierarchical decision matrix [1,5]. Here, we propose methods to extend the hierarchical decision matrix in order to enhance its use and address some of its limitations.

Advantages of the hierarchical decision matrix

The hierarchical decision matrix (also known as dominance ranking framework) [1,5] enables a visual summary of various economic studies that have different economic outcome measures (e.g. cost-effectiveness, cost-utility, cost-benefit), which would otherwise not be possible in a quantitative meta-analysis approach [8]. Although the hierarchical decision matrix is not a quantitative synthesis method, its hierarchical structure enables an interpretation of the dominance levels of an intervention based on assessment of benefits for both cost and health outcomes within a trial. If there are more studies in a certain color band, it would indicate a dominance level which is associated with that band.

Another advantage of the hierarchical decision matrix is that it allows for economic synthesis even when only partial economic data (e.g. cost minimization data) is available. For emerging research areas, basic economic cost data is usually collected in parallel to a trial on clinical effectiveness. These trials do not usually incorporate extensive economic analysis, such as calculations of incremental cost effectiveness ratio or acceptability curves. In such a scenario, the hierarchical decision matrix allows for rudimentary economic studies with only cost minimization data to be synthesized.

Limitations of hierarchical decision matrix/dominance ranking framework

The hierarchical decision matrix shows the distribution of studies in the three different bands, where a predominance of the number of studies in a certain band will indicate the likely implication of the intervention. However, if there are equal numbers of studies across two or three bands, no clear conclusion can be drawn.

Furthermore, this approach also does not take into account sample sizes and effect sizes of the clinical trials, which affect the statistical power of a trial to detect an effect. To illustrate, in an example where there are three studies and one of them is within the band that favors the intervention, while the other two studies are within the band that rejects the intervention. Under the current hierarchical decision matrix, it will imply that the intervention is to be rejected. However, the two studies that reject the intervention could be smaller trials while the study that favors the intervention may have a larger sample size and greater precision. Rejecting the intervention in such a scenario may lead to an inaccurate conclusion. If we can extend the hierarchical decision matrix to incorporate additional study aspects, it may provide more informative analysis of dominance levels.

Methods

We extend the hierarchical decision matrix using a weighted scoring system which is described here. We term this method the dominance ranking score.

The data transformation of the benefit value to make it suitable for use in the dominance ranking score is shown in Table 1. To calculate the traditional dominance ranking we transform the qualitative expression of the benefits in terms of ‘+’ and ‘-‘ into quantitative data that can be calculated. This process of converting qualitative data into quantitative data is called quantitizing[9] and this approach of data transformation is commonly used in mixed method analysis and synthesis [10], [11], [12]. For the dominance ranking score, in order to align the direction of the scoring for health outcome to be the same as the direction for cost outcome, a better health outcome for the intervention of interest is given a negative sign. Note that this is in opposite contrast to the hierarchical decision matrix, where a better health outcome is given a positive sign [1].

Table 1.

Benefit values for dominance ranking score.

Benefit Value	Cost Outcome	Health outcome
−1	Lower	Better
0	Same	Same
+1	Higher	Poorer

We know the sample size of a trial improves the precision of the trial and the larger the sample size, the smaller the confidence interval [13]. We also know that for meta-analysis, studies are weighted by their variance, with larger studies having more weight [14]. To give a similar weighting to larger studies, which should have more precision in their effects, we can modify the existing hierarchical decision matrix by adding a weighting to the cost and health benefits that is based on their sample sizes.

The weighting calculation schema are as follows:

$$\text{Weighted}\text{Benefit}=\frac{n}{N}\times \text{Benefit}\text{Value}$$

Where: n = sample size of a study; N = total sample size of studies in a sub-group analysis; Benefit Value = −1, 0 or +1

$$\text{Overall}\text{Dominance}\text{Ranking}\text{Score}=\left(\sum _{i=1}^{k}WeightedCostBenefit+\sum _{i=1}^{k}WeightedHealthBenefit\right)/2$$

Where: k = number of studies included in a sub-group analysis

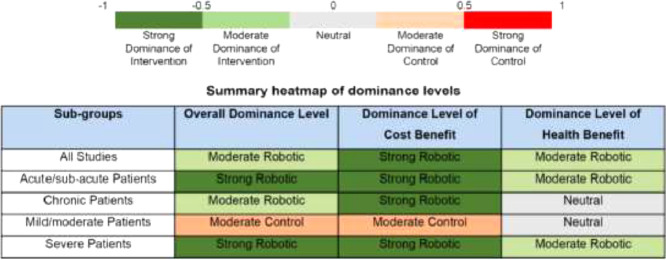
By adding a weighting based on sample size to the cost benefit, the cumulative dominance ranking score will range from −1 to +1. Similarly, by weighting the health benefit, the cumulative ranking score will range from −1 to +1. Assuming that both cost and health benefits play an equal role in determining the overall ranking result, the weighed cost and health benefits can be averaged to obtain the overall dominance ranking score. Based on this approach, we can color-code the dominance ranking scores per Table 2 to visually represent the level of dominance of the intervention.

Table 2.

Dominance ranking score scale.

If the overall score is in the green zone (−1 ≤ score < 0), then the result favors the intervention, with a score in the lighter green zone (−0.5 ≤ score < 0) showing a moderate dominance of the intervention and a score in the deeper green zone (−1 ≤ score < −0.5) showing a strong dominance of the intervention. If the overall score is in the red zone (0 < score ≤1), then the result favors the control, with a score in the lighter red zone (0 < score ≤ 0.5) showing a moderate dominance of the control and a score in the deeper red zone (0.5 < score ≤1) showing a strong dominance of the control. In the case that the overall score is equal to 0, then it would mean that neither the intervention nor control dominates, i.e. a neutral state (indicated by the grey zone).

Results

Using a case study example from a published economic review [15], we illustrate calculations of the dominance ranking score and presentation of its color-coded scale. In the case study example, five studies were included for economic review and Tables 3 and 4 show the results of the original review. From Table 3, there are more studies under the green band, which indicates that the intervention is favored. For the sub-groups analysis (Table 4), all sub-groups except for the sub-group “mild/moderate”, indicate that the intervention is favored. Under the “mild/moderate” sub-group, there is one study favoring the intervention and one study rejecting the intervention, which leads to an inconclusive result.

Table 3.

Hierarchical decision matrix/Dominance ranking framework (all studies) [16], [17], [18], [19], [20].

Table 4.

Summary of dominance levels (based on hierarchical decision matrix).

Using the data transformation key in Table 1, these studies were assigned values of either −1, 0, +1 for their cost and health benefits. Thereafter the cost and health benefits were weighted based on sample sizes of the studies (Table 5).

Table 5.

Dominance ranking score (all studies) [16], [17], [18], [19], [20].

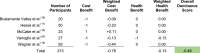The calculations are then repeated for every subgroup and a summary can be tabulated as shown in Table 6. As a comparison, the results using the hierarchical decision matrix and its summary tabulation are shown in Tables 3 and 4 respectively.

Table 6.

Summary heatmap of dominance levels (based on dominance ranking score).

In Table 4, for “mild/moderate” subgroup, as there was one study in each band, no clear interpretation can be drawn; whereas under the dominance ranking score (Table 6), we can glean further analysis. In this case, that overall, for the “mild/moderate” subgroup, there is a moderate dominance for control. For the cost benefit, moderate dominance for control is shown and for the health benefit, a neutral state is shown. Under a dominance ranking score which incorporates sample sizes, we can have not only a more differentiated analysis for overall dominance level, but also analysis which can be specific to dominance levels of cost and health benefits.

Sensitivity analysis

To illustrate changes to the summary heat map, sensitivity analysis of varying the weights of the cost and health outcomes was conducted based on two weight fractions: 25% Cost/75% Health and 75% Cost/25% Health. The resulting heat maps are as shown (Tables 7 and 8).

Table 7.

Summary heatmap of dominance levels (25% Cost/75% Health).

Table 8.

Summary heatmap of dominance levels (75% Cost/25% Health).

Discussion

In the following sections, improvements of the dominance ranking score are described.

Weighting the effects of cost and health outcomes

In the case study example illustrated above, we had assumed that cost and health outcomes had an equal role in determining the overall dominance ranking score. For certain trials this may not be so, for example in certain infectious diseases with high mortality rates, the health outcome might have a larger emphasis. With sufficient evidence and justification provided, reviewers can alter the weights of the cost and health outcomes for the dominance ranking score, thus enabling researchers the flexibility to determine the ranking score that is applicable to their research context. The revised calculation schema incorporating weights to cost and health outcomes is:

$$\begin{array}{ccc}\hfill \text{Overall}\text{Dominance}\text{Ranking}\text{Score}& =& \left(W_{cost}\times \sum _{i=1}^{k}WeightedCostBenefit\right)\hfill \\ & & +\left(W_{health}\times \sum _{i=1}^{k}WeightedHealthBenefit\right)\hfill \end{array}$$

$$W_{cost}+W_{health}=1$$

Where: W_cost = weight applied to cost outcome; W_health = weight applied to health outcome; k = number of studies included in a sub-group analysis

Sensitivity analysis

Weighting fractions were applied for cost and health benefits, and this resulted in slight changes to the summary heatmap. For 25% Cost/75% Health weighting fraction, only the sub-group of ‘severe patients’ was changed. Instead of a strong overall dominance by the robotic intervention, a moderate dominance resulted. This was due to a shift in dominance level towards Health Benefit, which has a moderate robotic dominance. For 75% Cost/25% Health weighting fraction, only the sub-group of ‘all studies’ was changed. Instead of a moderate overall dominance by the robotic intervention, a strong dominance resulted. This was due to a shift in dominance level towards Cost Benefit, which has a strong robotic dominance. The sensitivity analysis demonstrated that varying the weighting fractions would generate slightly different heatmaps, and researchers would need to consider their research context when determining the weighting fractions.

Incorporating multiple weighting factors

With a weighting scheme, various aspects of a study design can be incorporated as multiple weighting factors. In our method, besides the sample sizes, we could incorporate one other weighting factor that mirror key considerations when conducting a systematic review: effect sizes of trials.

Effect size weighting

Effect size data could be an additional weighting factor. Studies that show greater effect sizes will have more weight and the effect size weighting will shift the dominance ranking score towards such studies. The calculation schema to incorporate effect size weighting is:

$$WeightedBenefit\left(\text{Effect}\text{Size}\right)=\frac{\left|e\right|}{E}\times \text{Benefit}\text{Value}$$

$$E={\Sigma }_{i=1}^k\left|e\right|$$

$$\begin{array}{ccc}& & OverallDominanceRankingScore\hfill \\ & & =\left(W_{cost}\times \frac{\left({\sum }_{i=1}^k\frac{n}{N}\times CostBenefit+{\sum }_{i=1}^k{\left[\frac{\left|e\right|}{E}\right]}_{cost}\times CostBenefit\right)}{F}\right)\hfill \\ & & +\left(W_{health}\times \frac{\left({\sum }_{i=1}^k\frac{n}{N}\times HealthBenefit+{\sum }_{i=1}^k{\left[\frac{\left|e\right|}{E}\right]}_{health}\times HealthBenefit\right)}{F}\right)\hfill \end{array}$$

Where: |e| = modulus of effect size of a study; E = sum of effect sizes of studies in a sub-group analysis; ${\left[\frac{\left|e\right|}{E}\right]}_{cost}$ is the effect size weight for cost data; ${\left[\frac{\left|e\right|}{E}\right]}_{health}$ is the effect size weight for health data; F = number of weighting factors applied (here F = 2); n = sample size of a study; N = total sample size of studies in a sub-group analysis; W_cost = weight applied to cost outcome; W_health = weight applied to health outcome; k = number of studies included in a sub-group analysis; Benefit Value = −1, 0 or +1

Note: Effect sizes can have positive or negative values, depending on whether intervention is favored, or control is favored. As the direction of effect size is already indicated by the sign of the benefit value, only the modulus (i.e. absolute value) of the effect size is needed for calculation of effect size weighting. As there are both cost and health (i.e. clinical effectiveness) outcomes, there will also be two effect size data: one for cost outcome and one for health outcome. Note that the presented weighting scheme applies to effect sizes of continuous data (i.e. weighted mean difference, standardized mean difference), as the meta-analysis of such data is centered on a neutral value of “0”, with either side representing effects favoring intervention or control on symmetrical scales.

Increasing the precision of the dominance ranking score

The inclusion of confidence intervals would provide more precision to the dominance ranking score. However, at this early stage of the proposed methodology, it is our intent that varying levels of dominance be easily interpreted via a simple bar scale ranging from −1 to +1. As we gain more experience with the use of the currently proposed dominance ranking score, confidence intervals could be incorporated in the future.

Limitations

Weighting factors

We have shown how weights based on factors relevant and important to most reviews, namely: sample size and effect size of studies can be considered in the analysis. The weighting factors serve to incorporate useful aspects of a study design into the hierarchical decision matrix/dominance ranking framework and helps to provide more information for analysis and understanding of dominance levels. In our example, we have demonstrated a technique to increase discriminatory power in the analysis, through incorporating a weighting scheme that is based on sample sizes of the included studies.

Effect size weighting factor

With an additional weighting factor that incorporates effect size, the dominance ranking score can be further enhanced for a better analysis of dominance levels. However, effect size data for economic cost measures is often not available, as meta-analysis for economic cost data is not encouraged due to resource use and cost data that are sensitive to variability across settings and between countries [8]. Even if economic effect size data is available, the different economic outcome measures used in economic trials (e.g. cost-effectiveness, cost-utility, cost-benefit, cost minimization) also make the comparison of effect sizes currently not possible, so we urge caution when incorporating effect size weighting. For economic studies where the cost setting is similar, with low variability across resource use or clinical practice, and the economic outcome measure is the same, effect size weighting may be appropriate. If only effect size data for clinical effectiveness is available, it is not suggested to conduct effect size weighting for the health benefit without a similar effect size weighting for the cost benefit. Such an approach, while incorporating more information for health benefit analysis, will render an unbalanced weighting approach towards the overall interpretation of dominance levels.

Another consideration to incorporating effect size weighting factor is that outlying studies in a meta-analysis would skew the dominance ranking score towards such studies. Unless the causes for the outlying effect can be explained, such outliers should be viewed with caution and be justified if included.

Sample size weighting factor

The dominance ranking score is flexible to allow multiple weighting factors to be incorporated. However, reviewers might wish to limit their weighting factors and only incorporate those factors that are most relevant to their review. Given that effect size weighting has its limitations and are to be used with caution, we would recommend that sample size weighting be the preferred weighting factor. Sample sizes are usually reported (unlike economic effect sizes) and can be easily extracted from studies. It is also a form of objective data, in that it is not subject to interpretation by reviewers.

Benefit values

It is important to note that the weightings are associated with a benefit value (−1, 0, +1) which is, itself, a categorical expression of the direction of dominance. As such, it may not be appropriate to have too many weighting factors, as the starting point (i.e. the benefit value) is not a precise measure of dominance level. For example, in the scenario that all studies in a review have lower intervention cost outcome than control, this will mean that the cost benefit values assigned would all be −1. In such a case, regardless of the weightings, the calculated cost dominance level would always be −1. Hence the dominance ranking score is useful when studies have heterogeneous benefit values and can help to better differentiate the dominance level. The dominance ranking score is also useful when the hierarchical decision matrix shows an unclear interpretation (such as equal number of studies in each band).

Extending the hierarchical decision matrix

In no sense do we claim that the dominance ranking score is able to perform a quantitative meta-analysis of economic data or that the hierarchical decision matrix is irrelevant. We merely extend the hierarchical decision matrix tool to have more differentiating information incorporated into it and thereby enable a more informed analysis of dominance levels to be performed. In fact, we suggest reviewers conduct a review tabulation using the hierarchical decision matrix and then supplement their analysis with the dominance ranking score.

We also recognize that for decision making, good quality economic trials or models that represent the specific context of the healthcare system is necessary. However, the proposed dominance ranking score and the associated hierarchical decision matrix are still useful when evaluating partial economic studies, such as studies with only cost minimization data. Such cost minimization studies are usually conducted for emergent research areas where basic economic data is collected, in parallel to a trial on clinical effectiveness. On this spectrum of rudimentary economic studies, we see a role for the hierarchical decision matrix and the dominance ranking score to provide some degree of dominance analysis. Through such a ‘pilot’ analysis, it could indicate the level of economic potential and pave the way for a full economic study.

Sub-weighting of weighting factors

If the use of multiple weighting factors is appropriate, it is possible to further weight each individual weighting factor, such that one can assign more priority to a certain factor. For example, if effect size is more relevant to a review, the effect size weighting can be given a higher weight. This will shift the direction of the dominance ranking score towards studies that have larger effect sizes. If such further sub-weights are adopted, it is suggested that justifications for the levels of sub-weightings be reported and that these sub-weights be consistently applied for both cost and health benefit calculations. The sum of the sub-weights should always add up to 1.

Conclusion

For economic systematic reviews there is currently no agreed-upon quantitative method to obtain a pooled economic effect size. With no suitable quantitative method available, the hierarchical decision matrix stands out as a tool that enables a visual summary of different types of economic studies. Extending the hierarchical decision matrix with a weighted scoring system (termed dominance ranking score) allows for useful information of a study design to be incorporated and enables a more differentiating analysis of dominance levels.

Various study characteristics can be incorporated via weighting factors in the dominance ranking score, although the appropriate use of each weighting factor needs to be considered. In this paper, we have incorporated weights based on factors that we deem are relevant to most reviews, namely: sample size and effect size of studies. Given that effect size weighting has its limitations, we would recommend that sample size weighting be the preferred weighting factor, as sample sizes are usually reported and are a more objective form of data.

For systematic reviews that include partial economic studies, we see a role for the hierarchical decision matrix and the dominance ranking score to provide some degree of dominance analysis, which would otherwise not be possible. This analysis could improve the utility of such reviews by indicating the level of economic potential for a particular intervention, which may facilitate the conduct of subsequent full economic studies.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.