Exploring the Free-Energy Landscape and Thermodynamics of Protein-Protein Association

Abstract

We report the free-energy landscape and thermodynamics of the protein-protein association responsible for the drug-induced multimerization of HIV-1 integrase (IN). Allosteric HIV-1 integrase inhibitors promote aberrant IN multimerization by bridging IN-IN intermolecular interactions. However, the thermodynamic driving forces and kinetics of the multimerization remain largely unknown. Here, we explore the early steps in the IN multimerization by using umbrella sampling and unbiased molecular dynamics simulations in explicit solvent. In direct simulations, the two initially separated dimers spontaneously associate to form near-native complexes that resemble the crystal structure of the aberrant tetramer. Most strikingly, the effective interaction of the protein-protein association is very short-ranged: the two dimers associate rapidly within tens of nanoseconds when their binding surfaces are separated by d ≤ 4.3 Å (less than two water diameters). Beyond this distance, the oligomerization kinetics appears to be diffusion controlled with a much longer association time. The free-energy profile also captured the crucial role of allosteric IN inhibitors in promoting multimerization and explained why several C-terminal domain mutations are remarkably resistant to the drug-induced multimerization. The results also show that at small separation, the protein-protein binding process contains two consecutive phases with distinct thermodynamic signatures. First, interprotein water molecules are expelled to the bulk, resulting in a small increase in entropy, as the solvent entropy gain from the water release is nearly cancelled by the loss of side-chain entropies as the two proteins approach each other. At shorter distances, the two dry binding surfaces adapt to each other to optimize their interaction energy at the expense of further protein configurational entropy loss. Although the binding interfaces feature clusters of hydrophobic residues, overall, the protein-protein association in this system is driven by enthalpy and opposed by entropy.

Significance

Elucidating the energetics and thermodynamic aspects of protein-protein association is important for understanding this fundamental biophysical process. Our study provides a more complete physical picture of the protein-protein association responsible for the drug-induced HIV-1 integrase multimerization. The results captured the critical role of the inhibitor and successfully accounted for the effects of mutations on the protein association. Remarkably, the effective range of the protein-protein attractive funnel is found to be very short, at less than two layers of water, despite the fact that the two binding partners carry opposite net charges. Lastly, entropy-enthalpy decomposition suggests that the entropy gain due to solvent release is more than offset by the loss of the solute configurational entropy upon complexation.

Introduction

Noncovalent and specific protein-protein association plays a crucial role in a wide range of fundamentally important biological processes such as signal transduction and antibody-antigen recognition (1). In recent years, protein-protein interactions are increasingly targeted for therapeutics development (2,3). In this work, we characterize at an atomic level of detail the free-energy landscape and the thermodynamic driving forces for the protein-protein association underlying the drug-induced HIV-1 integrase multimerization (4, 5, 6, 7). HIV-1 integrase (IN) is an important therapeutic target for the development of antiviral therapy (2) because of the vital roles IN plays in the life cycle of HIV. Allosteric HIV-1 integrase inhibitors (ALLINIs) bind at the dimer interface of the IN catalytic core domain (CCD) and inhibit HIV-1 by promoting aberrant IN multimers, which impairs both the catalytic activity of IN and virus core maturation (8, 9, 10). The mechanism by which ALLINIs promote aberrant multimerization has previously been revealed by our protein-protein docking simulations, which suggested that the multimerization is mediated by an ALLINI that bridges IN-IN interactions between the CCDs of one IN dimer and the C-terminal domain (CTD) of another dimer. The central prediction from the modeling study of the IN aberrant multimerization, i.e., the CCD and CTD intersubunit interaction bridged by ALLINIs (5), was confirmed by the experimental crystal structure later obtained containing full-length IN and ALLINIs (11).

Despite the progress in understanding the ALLINI-induced aberrant multimerization, several important aspects of the molecular mechanism of the aberrant multimerization need to be better understood to inform rational inhibitor design. What is the predominant thermodynamic driving force for the intermolecular association of CTDs and CCDs bridged by ALLINIs? What does the association free-energy landscape of the IN multimerization look like? At the molecular level, why do specific amino acid substitutions in the CTD such as Y226D and K266A block the ALLINI-induced multimerization? What are the roles of the water molecules in the intervening space between the CCD and CTD in the association? To date, only limited, indirect experimental data regarding the drug-induced IN multimers are available. The only experimental structure of an aberrant multimer was determined at a relatively low resolution of 4.4 Å (11). Although our modeling correctly predicted the central mechanism of action of the drug-induced multimerization, the use of protein-protein docking precludes the characterization of the association mechanism directly influenced by solvent.

To address the mechanistic questions regarding the IN multimerization at an atomic level of detail, here we employ molecular dynamics (MD) simulations in explicit solvent to study the CCD and CTD association mediated by ALLINI. In recent years, because of the advances in methodology, algorithms, and computer hardware, MD simulation and associated techniques have increasingly been successfully used to study the energetics and kinetics of protein-protein binding (12, 13, 14, 15). Here, we first directly simulate the formation of a tetramer starting from two dimers initiated from dissociated states with different separations between the CTD and CCD. The results show that the experimental multimer structure can be obtained using unbiased physical models in explicit aqueous solutions. We then quantitatively explore the free-energy landscape of the protein-protein association using umbrella sampling with varying conditions to investigate the role of ALLINIs and the different amino acid mutations that influence the multimerization. Entropy-enthalpy decomposition of the free energy reveals a detailed thermodynamic picture of protein-protein association that is dominated by favorable overall enthalpy, despite the presence of hydrophobic interactions traditionally believed to be favored by entropy. The study provides a wealth of atomistic information concerning the biophysics of drug-induced IN aberrant multimerization that may inform the design of new allosteric IN inhibitors.

Materials and Methods

The GROMACS program 2016-3 (16,17) was used to perform the MD simulations in this work. The starting structure of the IN dimers (Fig. 1) was taken from the structure of the aberrant tetramer containing the ALLINI BI224436 described in the previous report (4). The protein was modeled by the AMBER parm99ILDN force field (18) and the ligand by the AMBER GAFF (19) and the AM1-bcc charge models (20). TIP3P water (21) was used to solvate the solute, with the distance between any solute atom and the nearest wall of the box being ≥ 10 Å. In the direct simulations starting from the dissociated IN dimers (Fig. 3), a 9.28 nm × 16.99 nm × 11.34 nm solvent box containing 53,748 water molecules is used to solvate the two separated dimers. 91 Na⁺ and 107 Cl⁻ ions are added to the solvent box to neutralize the net charges on the solute and to mimic the experimental ionic concentration of 0.1 M. The entire system contains 179,106 atoms. In the umbrella sampling simulations using the truncated system containing one CCD dimer and one CTD (Fig. 5), a solvent box with the dimension 9.55 nm × 9.00 nm × 7.80 nm containing 20,384 water molecules and 34 Na⁺ and 39 Cl⁻ ions is used to solvate the solute. The entire system contains 67,043 atoms. The electrostatic interactions were treated using the particle mesh Ewald (PME) (22) method with a real-space cutoff of 10 Å and a grid spacing of 1.0 Å. MD simulations were performed in the NPT ensemble with a time step of 2 fs.

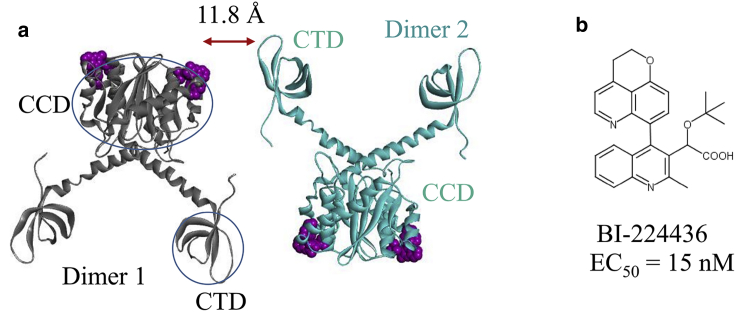
Figure 1.

(a) Two HIV-1 integrase dimers separated by an interfacial gap d = 11.8 Å are solvated in a box of water (not displayed). (b) Chemical structure of the ALLINI BI224436 is given. To see this figure in color, go online.

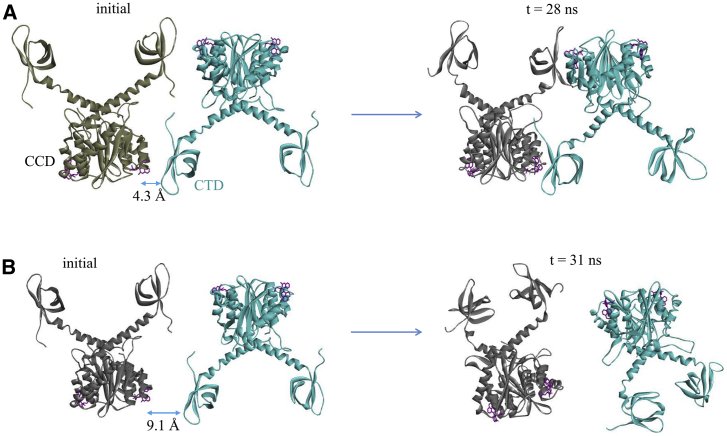
Figure 3.

(A) Representative results of simulation set 1, in which the CTD and CCD on the two dimers are initially separated by an interfacial gap d ≈ 4.3 Å. (B) A trajectory from simulation set 2, in which the closest distance between CTD and CCD in the starting structure is 9.1 Å, is given. To see this figure in color, go online.

Figure 5.

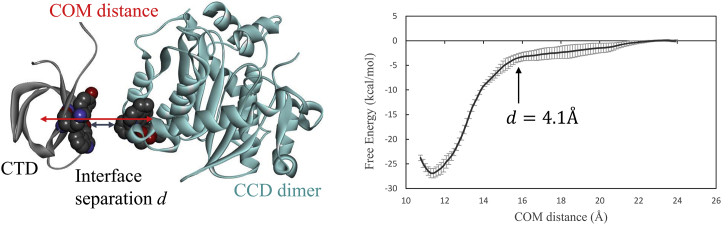
Left: the distance between the COM of the CTD and that of the interface residues on the CCD. Also shown is the interface gap distance d between the two binding surfaces. The residues at the centers of the two binding interfaces (Tyr226 and Trp235 on CTD and BI224436, which binds with CCD) are shown as spheres to illustrate the interface separation d. Right: the PMF of the CTD and BI224436-bound CCD is computed using umbrella sampling on the COM distance. To see this figure in color, go online.

The potentials of mean force were computed using umbrella sampling by applying harmonic biasing potential on the distance between the center of mass (COM) of the CTD (denoted as L1) and center of mass of the following CCD residues (denoted here as P1): 124–128, 131–132, 167–168, and BI224436 (Fig. 5). During the umbrella sampling simulation, weak angular harmonic restraints are also applied to maintain the relative orientation between the two proteins and to ensure that the pulling is done along the predefined axis r_P1-L1 and to accelerate the convergence of the potential of mean force (PMF) calculation. For this purpose, two polar angles (θ, ϕ) and three Euler angles (Θ, Ф, Ψ) (23,24) are defined using the two centers of masses P1 and L1, plus two atoms on each of the binding proteins. The following two CCD atoms (P2, P3) and two CTD atoms (L2, L3) are chosen together with P1 and L1 to define five angles (θ, ϕ, Θ, Φ, Ψ) that determine the ligand orientation: P2, T124-CA; P3, W131-C; L2, D253-CA; and L3, V234-C. The range of the pulling distance is 11.0 Å ≤ |r_P1-L1| ≤ 23.9 Å. The equilibrium values of the five angles are θ₀ = 58.29°, ϕ₀ = −70.92°, Θ₀ = 130.1°, Φ₀ = 77.27°, and Ψ₀ = −57.45°. A single force constant k_r = 23.9 kcal mol⁻¹ Å⁻² is used for the distance restraints in all the umbrella sampling windows. The force constants used in the angular restraints are k_θ = k_ϕ = k_Θ = k_Φ = k_Ψ = 0.0728 kcal degree⁻² mol⁻¹.

To compute the one-dimensional PMF, 24 umbrella windows are used to cover the full range of the distance space. The spacing between adjacent umbrella windows is 0.5–1.0 Å, which we find provides good overlap between the sampled distances. In each umbrella window, a reasonable starting configuration is generated by first running a short 1.2 ns umbrella sampling simulation starting from the last snapshot of the short umbrella sampling simulation in the previous umbrella window. Next, 30 ns umbrella sampling simulations are run in parallel in each window starting from the initial configurations generated above. The last 20 ns trajectory was used to compute the PMF using the WHAM (25) program implemented in the GROMACS 2016.3 package. For each protein-protein complex, four independent umbrella sampling simulations were run for estimating the statistical uncertainties in the calculated PMF. Thus, a total of ∼2.88 μs simulation time is used to compute the PMF for a single protein-protein complex. The binding entropy is estimated using the temperature difference of the free-energy changes at 275, 300, and 320 K. The error bar in the ΔS is estimated using the formula for the standard error of the slope of linear regression, i.e., s(b₁) = $\sqrt{\left(1/n-2\right)\left({\sum }_i{\left(y_i-{\hat{y}}_i\right)}^2/{\sum }_i{\left(x_i-\overline{x}\right)}^2\right)}$. Here, x_i and y_i correspond to the temperature T_i and the free-energy change ΔG_i, respectively. b₁ is the slope of the linear regression (i.e., entropy) and s(b₁) is the standard error of the slope. n is the number of independent (ΔG_i, T_i) measurements. The error bar in the ΔH is estimated using error propagation from the error bars in the TΔS and ΔG.

Results

Direct simulation of the formation of aberrant tetramer from dimers

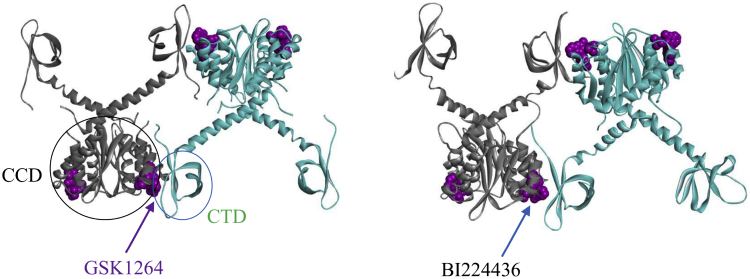
In a previous report, we have used protein-protein docking guided by indirect experimental information from hydrogen-deuterium exchange data as restraints to derive the first structural model of the drug-induced HIV-1 integrase multimer (5). The model accurately predicted that the intermolecular CCD-CTD interaction mediated by bound ALLINIs is the most important feature of the drug-induced IN multimerization. Whereas the structural model predicted using protein-protein docking was confirmed by the subsequently reported crystal structure (11), the docking study was carried out without the aqueous environment and therefore precluded the characterization of the thermodynamics and kinetics of the drug-induced IN aggregation. To explore the association mechanism of the IN multimerization process, here we perform multiple independent MD simulations in explicit solvent without any restraints for a total of 23 μs starting from two dissociated HIV-1 integrase dimers containing ALLINI BI224436 (26,27) with varying initial interfacial separations d (Fig. 1). The starting structure of the two dimers is taken from the structure of the aberrant tetramer containing BI224436 reported previously (4). The interface gap d is calculated based on the distance between the COM of the CTD and the COM of the following interfacial residues on the CCD dimer: 124–128, 131–132, 167–168, and BI224436. To obtain the value of d, we subtract the COM distance corresponding to the bound complex (11.4 Å) from the current COM distance between the two separated dimers. The setup and results of these simulations are summarized in Table 1. In simulation set 1, the initial separation distance between the surfaces of CTD and CCD of the two dimers is d ≈ 4.3 Å, whereas in the simulation set 2, they are initially separated by between 7.8 and 11.8 Å. All the simulations are repeated with different initial velocities, and each lasts on average 500 ns. The structures sampled in the MD trajectories are compared with the crystal structure of the GSK1264-induced aberrant IN tetramer reported by Gupta et al. (11). GSK1264 and BI224436 are very similar (Fig. S1; (28)); the superposition of the crystal structures of the HIV-1 IN dimers in complex with the two ligands (Protein Data Bank, PDB: 4OJR for the GSK1264-IN and PDB: 6NUJ for the BI224436-IN) shows that the two ALLINIs bind the IN with the identical binding mode, with root mean-square deviation ≈ 0.2 Å for the shared atoms (Fig. S2). Therefore, the two ligands are expected to induce the same aberrant tetramer.

Table 1.

Summary of the Direct Simulations of Aberrant Tetramer Formation Starting from Dissociated IN Dimers

Simulation Set	Starting Configuration	Successful Association/Total Trajectories	MFPTa (ns)	Average Trajectory Length (ns)
Set 1	d ≈ 4.3 Å	8/10	∼20	500
Set 2	7.8 Å ≤ d ≤ 11.8 Å	0/10	>500	500

^aMFPT to the formation of the near-native complex.

The experimental aberrant tetramer structure is captured in unbiased MD simulations in explicit solvent starting from separated integrase dimers

We found that in the majority of the trajectories in set 1, the two initially separated dimers (d ≈ 4.3 Å) spontaneously associate to form complexes that resemble the experimental structure of the native aberrant multimer (see Fig. 2), which compares a representative MD snapshot with the experimental structure. A snapshot is considered to have a near-native multimer interface if the following criteria are met: when the central interface residues in the CCD (T124, A128, E170, H171, and T174) are superimposed onto the corresponding residues of the CCD in the crystal structure, the root mean-square deviation between the interface residues of the CTD (Y226, W235, K266 and I268) in the MD structure and those in the crystal structure is less than 3.5 Å. Importantly, the outcome of the simulation is highly sensitive to the starting separation of the two dimers: in contrast to the trajectories in set 1, none of the trajectories in set 2 leads to successful association and the formation of an aberrant tetramer. Note that the only difference between the two sets of simulations is that the two dimers in set 2 have a larger initial separation of 7.8 Å ≤ d ≤ 11.8 Å compared with those in set 1, in which the initial separation d ≈ 4.3 Å (Table 1).

Figure 2.

Left: crystal structure of the IN aberrant tetramer containing the GSK compound GSK1264. Right: a representative MD snapshot taken at 28 ns (starting from two dissociated dimers, each containing the Gilead compound BI224436). To see this figure in color, go online.

The probability for observing the native aberrant tetramer within a timescale of hundreds of nanoseconds is highly sensitive to initial dimer-dimer separation

These results therefore show that there is a very sharp increase in the mean first-passage time (MFPT) to association (Table 1) as the initial separation between the CTD and CCD on the two dimers is increased from ∼4.3 to 7.8 Å: when the two dimers are separated by a gap of d ≤ 4.3 Å, which is less than two water diameters, the association is fast, with MFPT ∼20 ns for reaching the near-native complex (Fig. 3 A). Beyond the critical separation gap of d ≈ 4.3 Å, the association kinetics is characterized by a much longer association timescale (Fig. 3 B) beyond the microsecond range explored in this work. As shown below, this behavior is closely related to the shape of the free-energy landscape of the protein-protein association.

The calculated PMF reveals that the association free-energy landscape is a narrow funnel with the downhill association beginning at a critical separation of ∼4.1 Å

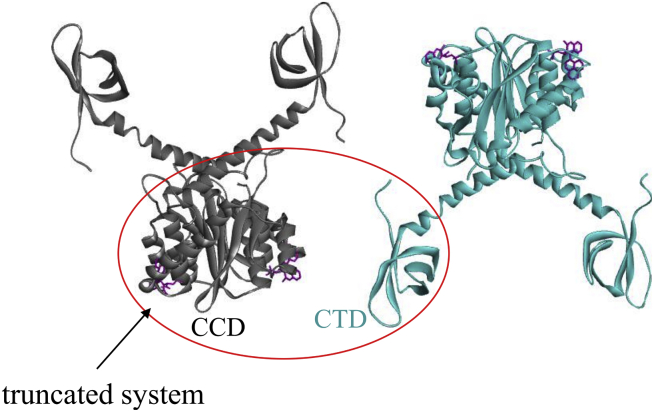
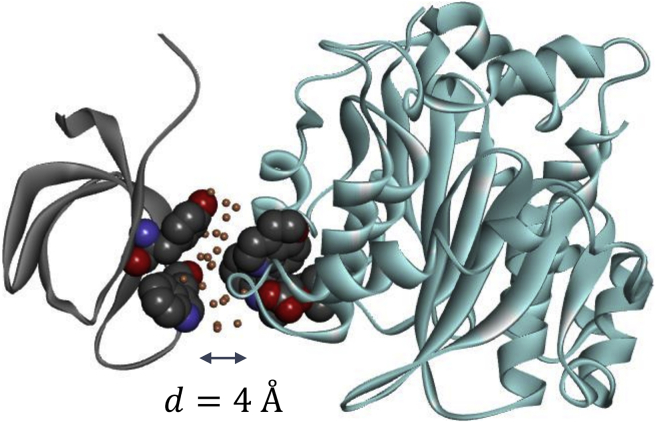
To quantitatively characterize the energy landscape, the strength, and the molecular mechanism of the drug-induced IN aberrant association, we compute the association free-energy profile or PMF (13,29, 30, 31, 32) as a function of the separation distance of the two binding partners. The solvated system of the two dimers has ∼180,000 atoms, which makes the PMF calculation computationally very costly. From Fig. 2, it is noted that in the complexed state, two dimers make two symmetrical contact interfaces that each involve one CTD and one CCD dimer, bridged by one drug molecule. Because the two symmetrical contact interfaces are equivalent, a truncated system of one CCD dimer and one CTD (Figs. 4 and 5) provides a reasonable model system for investigating the free-energy landscape of the association of the full dimer-dimer system. This truncated system (∼67,000 atoms) used in the umbrella sampling calculation of the PMF comprises one CCD dimer with a bound ALLINI and one CTD. We show below that the validity of the truncated computational model is supported by the comparison of the onset of the downhill association from the truncated system with that of the full dimer-dimer system.

Figure 4.

The truncated system (red oval) used to compute the PMF of CTD-CCD association using umbrella sampling. To see this figure in color, go online.

Fig. 5 shows the PMF of the CTD association with an ALLINI-bound CCD dimer, computed from umbrella sampling by applying harmonic bias on the COM distance between the CTD and CCD-ALLINI as defined earlier. The interface separation gap d between the two binding surfaces is also indicated in the left panel of Fig. 5 along with the COM distance. During umbrella sampling, the reversible pulling is carried out along the axis defined by the two COMs, which is perpendicular to the binding interface. This ensures that no intermolecular entanglement or collision between the two binding partners occurs along this pulling pathway. To accelerate the convergence in computing the PMF of protein-protein association, weak angular harmonic restraints on the center of the CTD and its relative orientation with respect to the CCD are applied to the polar angles (θ, ϕ) and three Euler angles (Θ, Ф, Ψ) (23,24) during umbrella sampling; see Materials and Methods.

The PMF is a monotonically decreasing function of the separation. Starting at a critical separation distance of ∼4.1 Å the landscape of the protein-protein association becomes a steep downhill funnel. As shown in Fig. 5, the free energy of bringing the two proteins from far apart to d = 4.1 Å, i.e., ΔG(d: ∞ → 4.1 Å) = −3.6 ± 0.86 kcal/mol, whereas going from d = 4.1 Å to d = 0 Å (corresponding to the bound complex), the free-energy drop is much larger, ΔG(d: 4.1 Å → 0 Å) = −23.3 ± 0.43 kcal/mol. This result coincides with the observations from the unrestrained MD simulations of the full dimer-dimer system, in which the spontaneous association is found to occur at an initial separation distance of d = 4.3 Å (Fig. 3; Table 1). The result therefore confirms that the effective attractive interaction involved in the multimerization is very short range, i.e., it becomes attractive at a distance that can accommodate less than two layers of water molecules. Beyond this critical short separation, the association free-energy landscape is almost flat, and the corresponding association kinetics is largely diffusive. The short-range nature of the effective attraction is likely to have contributed to the slow kinetics for multimerization; for example, as shown by the study from the Kvaratskhelia group, the timescale for the growth of the ALLINI-induced aggregates is on the order of minutes (7).

Justification for using PMF alone as a measure of the strength of association

Although the strength of molecular association is normally measured by the absolute binding free energy of the two binding partners, for reasons given below, we only need to consider the PMF as a measure for the strength of the protein-protein association. The absolute binding free energy can be written as (23,24)

$$G_{bind}^{°}=-\Delta G_{\left(\theta ,\varphi ,\text{Θ},\text{Φ},\text{Ψ}\right)}^{bound}-w\left(r^{\ast }\right)-k_{B}T\ln \frac{\underset{bound}{\int }{e}^{-\frac{w\left(r\right)}{k_{B}T}}dr}{{\left(\frac{2\pi k_{B}T}{k_r}\right)}^{\frac{1}{2}}}-k_{B}T\ln \frac{C^o{r}^{\ast 2}sin{\theta }_{0}sin{\text{Θ}}_0{\left(2\text{π}{k}_B\text{T}\right)}^3}{8{\pi }^2{\left(k_r{k}_{\theta }{k}_{\varphi }{k}_{\text{Θ}}{k}_{\text{Φ}}{k}_{\text{Ψ}}\right)}^{\frac{1}{2}}}=-\Delta G_{\left(\theta ,\varphi ,\text{Θ},\text{Φ},\text{Ψ}\right)}^{bound}-w\left(r^{\ast }\right)-\Delta G_{bound-bulk}^{vibr}+\Delta G_{restr}^{bulk},$$ (1)

where $\Delta G_{restr}^{bulk}$ and $-\Delta G_{\left(\theta ,\varphi ,\text{Θ},\text{Φ},\text{Ψ}\right)}^{bound}$ are the free energy of switching on the polar and orientational restraints (U_θ, U_ϕ, U_Θ, U_Φ, U_Ψ) for the ligand (in this case, CTD) in the bulk solution and the free energy of switching off these angular restraints in the bound state, respectively. w(r^∗) is the reversible work (PMF) of pulling the ligand from the bound state to the bulk location r^∗, computed using umbrella sampling in the presence of the angular restraints (U_θ, U_ϕ, U_Θ, U_Φ, U_Ψ). $-\Delta G_{bound-bulk}^{vibr}$ accounts for the ligand positional fluctuation in the bound state versus when it is harmonically restrained at a bulk location with the force constant k_r (23). k_θ, k_ϕ, k_Θ, k_Φ, and k_ψ are the force constants for the two polar angles (θ, ϕ) and three Euler angles (Θ, Ф, Ψ), respectively, for the ligand in the receptor reference frame (23,24). Table 2 lists the different components of the absolute binding free energy for the CTD association with an ALLINI-bound CCD dimer. The calculated $\Delta G_{bind}^{°}$ = 18.68 ± 0.96 kcal/mol has the same order of magnitude as the experimental affinity for tight protein-protein complexes such as the barnase-barstar ($\Delta G_{bind}^{°}$ = −19.02 kcal/mol) (33).

Table 2.

Components of the Absolute Binding Free Energy for the CTD Association with an ALLINI-Bound CCD Dimer in kcal/mol

$-\Delta G_{\left(\theta ,\varphi ,\Theta ,\Phi ,\Psi \right)}^{bound}$	−w(r∗)	$-\Delta G_{bound-bulk}^{vibr}$	$\Delta G_{restr}^{bulk}$	$\Delta G_{bind}^{°}$
−1.73 ± 0.11	−26.9 ± 0.96	−0.29 ± 0.03	10.24	−18.68 ± 0.96

As can be seen from Table 2, among the different contributions to the absolute binding free energy $G_{bind}^{°}$, $-\mathrm{\Delta }{G}_{\left(\theta ,\varphi ,\text{Θ},\text{Φ},\text{Ψ}\right)}^{bound}$ and $-\mathrm{\Delta }{G}_{bound-bulk}^{vibr}$ are small compared with the PMF term −w(r^∗). In addition, $\Delta G_{restr}^{bulk}$ is a constant term for the various combinations of protein-protein association calculations considered in this work. Therefore, in this work we only need to consider the PMF contribution −w(r^∗) as a measure of the absolute association free energy $G_{bind}^{°}$.

Entropy-enthalpy decomposition of the PMF reveals a two-step association process with distinct thermodynamic signatures

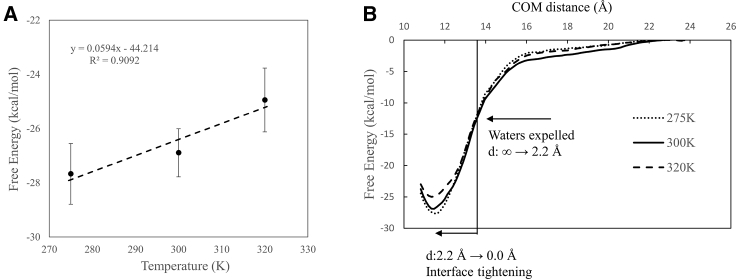
To elucidate the thermodynamic driving forces for the association, we decomposed the free energy of protein-protein association into enthalpic and entropic contributions using the same temperature derivative approach previously used to characterize the thermodynamic signatures of the associations between two graphite-like plates (34) and between a methane-sized sphere and a hemispherical cavity with different charge complementarities (35). Here, the free energy of association is taken to be the value at the contact minimum in the PMF near d = 0 Å that corresponds to the bound complex relative to the separated state. The entropy of association is estimated from the temperature derivative of the free energy, i.e., ΔS = $-{\left(\partial \Delta G/\partial T\right)}_P$, where the ΔG is obtained from the PMF at three temperatures 275, 300, and 320 K. As seen from Fig. 6 A, the temperature dependence of the free energy of association is approximately linear.

Figure 6.

(A) Temperature dependence of the free energy of association. (B) The range of the PMF is divided into two phases: the water expulsion phase and the interface tightening phase.

Table 3 gives the thermodynamic quantities of the protein-protein association at different separations between the two binding partners. The column “d: ∞ to 0 Å” shows the thermodynamic quantities for bringing the CTD and the ALLINI-bound CCD from infinitely apart to the contact minimum. This column therefore gives the total association free energy, entropy, and enthalpy. As seen from Table 3, overall, the association ΔG(∞ → 0 Å) = −26.9 ± 0.96 kcal/mol is driven by a large favorable enthalpic contribution ΔH(∞ → 0 Å) = −45.0 ±5.5 kcal/mol and opposed by an unfavorable entropy change −TΔS(∞ → 0 Å) = 18.0 ± 5.5 kcal/mol. Note that the estimation of the enthalpy and entropy components has much larger statistical uncertainty than that in the free energy, which is expected because the entropy and enthalpy are related to the derivative of free energy (36,37).

Table 3.

Thermodynamic Properties of the CTD-CCD Association at Different Separations at 300 K

Thermodynamic Quantity (kcal/mol)	d: ∞ to 0 Å	d: ∞ to 2.2 Å	d: 2.2 to 0 Å
−TΔS	18.0 ± 5.5	−1.3 ± 6.1	19.1 ± 6.0
ΔH	−45.0 ± 5.5	−10.3 ± 6.1	−34.5 ± 6.1
ΔG	−26.9 ± 0.96	−11.6 ± 0.48	−15.3 ± 0.85

Given the fact that protein-protein association is accompanied by releasing water molecules to the bulk solution from the intervening space between the two proteins, the large unfavorable entropy of association is puzzling. To examine the physical origins of the entropic and enthalpic changes, we divide the entire range of the PMF into two segments and compute the corresponding thermodynamic quantities; see Fig. 6 B. The first phase consists in bringing the dissociated proteins to a separation of d = 2.2 Å, at which all the water molecules from the intervening space are expelled to the bulk. As shown in Table 3, during this phase the corresponding entropy change is weakly favorable, with −TΔS(∞ → 2.2 Å) = −1.3 ± 6.1 kcal/mol. This small favorable entropy is likely to result from releasing the interfacial water molecules to the bulk, and its small magnitude is likely attributable to fact that the increase in solvent entropy is largely offset by the loss of side-chain entropies as the two binding surfaces approach each other to establish intermolecular contact during this phase. For example, during this phase of the association, the Lys266 side chain starts to form a salt bridge with the carboxylate group of the BI224436 at d ≈ 3.8 Å. Such intermolecular interactions are also reflected by the favorable ΔH(∞ → 2.2 Å) = −10.3 ± 6.1 kcal/mol (see Table 3).

The second phase in the association process is from d = 2.2 Å until the contact minimum at d = 0 Å. This phase is characterized by a small change in the separation distance of just 2.2 Å as the two binding surfaces adapt to each other to optimize their interaction energy, which results in a large reduction in enthalpy ΔH(2.2 Å → 0 Å) = −34.4 ± 6.1 kcal/mol, which is gained at the expense of a large entropy loss of −TΔS(2.2 Å → 0 Å) = 19.1 ± 6.0 kcal/mol. Here, the large entropy penalty is likely to originate from the loss of conformational entropy of the binding surface residues because all the intervening waters have already been expelled to the bulk in the previous phase d: ∞ → 2.2 Å (a water molecule has a diameter ∼3.4 Å; therefore, below d = 2.2 Å, no water molecules can be accommodated between the two binding surfaces) Thus, these results suggest that the large unfavorable entropy change for the overall association is likely to be caused by configurational entropy loss partially offset by entropic gains due to the expulsion of interfacial water to the bulk.

The calculated PMF captures the crucial role of ALLINIs in promoting IN multimerization

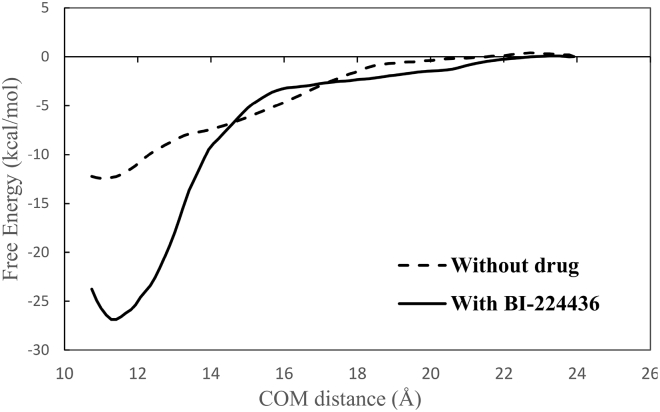
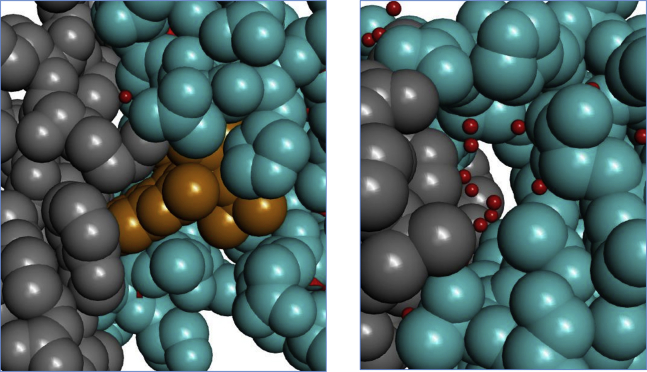
It is known that an ALLINI is required for the aberrant IN multimerization (6,38). Although the low-resolution crystal structure of the IN aberrant tetramer containing an ALLINI provides the structural basis for the multimer (11), it does not by itself contain information on the strengths of the association with or without ALLINIs. Computationally, we have previously used an FEP (Free Energy Perturbation) thermodynamic cycle to compute the relative association free energy to rationalize how different ALLINIs exhibit different potencies in stabilizing the multimer (5). Here, we use PMF calculation to directly quantify the role of ALLINIs in inducing the IN aggregation. Fig. 7 shows the computed PMF of CCD-CTD association with and without the ALLINI BI224436. The PMF of the association without the drug shows a shallow attractive basin that resembles that of a nonspecific protein-protein association. In contrast, the PMF computed with the bound BI224436 features a deep minimum characteristic of specific tight binding. The free energies of association estimated from the PMF in Fig. 7 with and without the drug are −26.9 ± 0.96 kcal/mol and −12.4 ± 0.7 kcal/mol, respectively. The large difference in the association free energy can be understood from the structures of the complexes at their free-energy minima in the PMF; see Fig. 8. The CTD-CCD binding interface in the complex containing the drug shows a significantly greater intermolecular atomic packing than the one without the drug. In addition, in the complex without the drug, the CTD-CCD interfacial space is filled with several water molecules. These water molecules, which are trapped in a narrow space between nonpolar interfacial residues (e.g., W235, Y226, L102, A128, and W132), form a significantly fewer number of hydrogen bonds on average than the number of hydrogen bonds (∼3.5) per molecule formed in bulk water. Therefore, these interfacial water molecules in the complex without the drug likely weaken the association free energy. These simulation results provide a physical explanation for the crucial role of ALLINI binding in promoting the IN aggregation.

Figure 7.

The computed PMF of CCD-CTD association with and without the drug BI224436.

Figure 8.

Representative MD snapshots of the complex of CTD (gray) and CCD (cyan) in the presence (left) and absence (right) of BI224436 (yellow). The snapshots are taken from the lowest free-energy bins in the PMF (Fig. 7). Water molecules are shown as small red dots. To see this figure in color, go online.

The calculated PMF successfully accounts for the resistance to the drug-induced IN multimerization caused by certain amino acid substitutions

Experimentally, a number of engineered amino acid substitutions on the CTD, such as Y226D (11), W235A (11), and K266A (7), are found to abrogate the ALLINI-induced aberrant IN multimerization. Although the low-resolution crystal structure of the IN aberrant tetramer shows that these residues are at the protein-protein interface, the experimental structure itself does not give information on the strength of the multimerization from the mutant proteins. Here, we run PMF calculations on these mutant proteins to directly probe their effects on the association free energy. Fig. 9 shows the calculated PMF for the three mutant proteins. The calculated association free energies for the three mutant proteins, Y226D, W235A, and K266A are −17.5 ± 1.0, −23.4 ± 2.4, and −20.2 ± 2.7 kcal/mol, respectively. Thus, the Y226D mutant and K266A mutant both bind significantly more weakly to the CCD than does the wild-type CTD (ΔG_assoc = −26.9 ± 0.96 kcal/mol), in good agreement with the results of experimental multimerization assays (7,11). In the case of the W235A mutant, although the calculated average free-energy difference ΔΔG_assoc = −3.5 kcal/mol also favors the wild-type over the mutant, which is in agreement with the experiment (11), the free-energy difference is not much larger than the margins of error, so the computational evidence is less clear-cut than the other two mutations Y226D and K266A. One possible reason for the less clear-cut result on the W235A mutation is that this substitution is from a large nonpolar group to a smaller nonpolar group, whose effects may be more subtle to capture in the finite umbrella sampling simulations. In contrast, the other two mutations Y226D and K266A involve modifications between charged groups and neutral nonpolar groups. Overall, these PMF results on the engineered amino acid substitutions provide further support for the validity of the free-energy modeling adopted in this work.

Figure 9.

Free-energy profile of the CTD-CCD binding in which the CTD contains the following single amino acid substitutions: Y226D (left), W235A (center), and K266A (right).

The calculated interaction energies provide insights into the origins of the favorable binding enthalpy

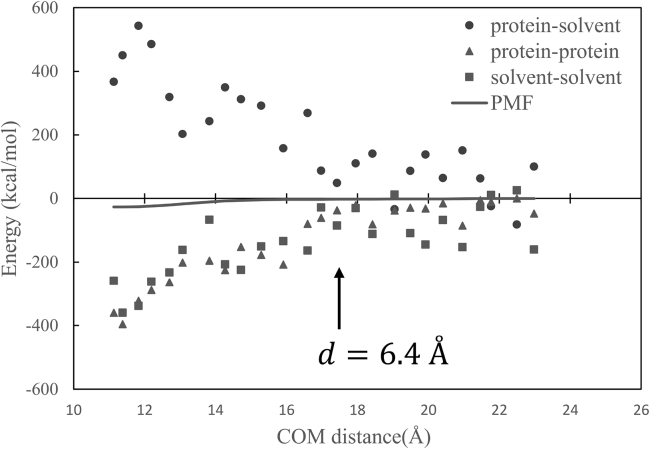
To examine the origins of the favorable enthalpy, we compare the free-energy profile for the CTD and CCD-ALLINI association with the direct interaction energies that make up the total enthalpy of dimerization: the protein-protein, protein-solvent, and solvent-solvent interaction (Fig. 10). The interaction energies plotted in Fig. 10 are much noisier compared with the well-behaved free-energy profile, e.g., a small change in the COM distance can be accompanied by large fluctuations in the interaction energy. For example, when d is increased from 13.8 to 14.2 Å, which is only a fraction of one water diameter, the protein-solvent interaction energy increased by ∼100 kcal/mol. Despite the noisiness in interaction energies, the general trend in these plots is that as the two proteins approach each other, the association is favored by the protein-protein interaction energy and strongly opposed by the loss of protein-solvent interactions. Solvent-solvent interactions also favor dimerization because water molecules expelled from the interprotein space form more hydrogen bonds in the bulk. Note that the solvent-solvent interaction and the protein-protein direct interaction have similar orders of magnitudes.

Figure 10.

The PMF or free energy plotted together with the various interaction energies: protein-protein, solute-solvent, and solvent-solvent.

Discussion

We have applied direct MD simulations and free-energy calculations to explore the energy landscape of the protein-protein interaction responsible for the drug-induced aberrant multimerization of HIV-1 integrase. The PMF results captured the critical role of the ALLINI in promoting the CTD-CCD intersubunit interactions that are the cornerstone of the IN aggregation (Figs. 7 and 8). By showing that all three key substitutions Y226D, W235A, and K266A result in significantly less attractive association than the wild-type protein (Fig. 9), the calculations also successfully account for why these amino acid substitutions block the drug-induced IN multimerization. These results demonstrate the power of free-energy modeling in elucidating the effects of mutations in protein-protein interactions. However, PMF calculations in explicit solvent such as those performed here remain computationally very demanding. In this regard, we note a recent study by Siebenmorgen and Zacharias, who have used a PMF-based binding free-energy method in an implicit solvent to more accurately rerank the docking poses of 20 different protein-protein complexes (15).

In addition to providing a physical basis for the IN multimerization, the work sheds light on the thermodynamic foundation of protein-protein association. We find that the protein-protein association between the CTD and CCD-ALLINI is driven by enthalpy change and opposed by entropy; see Table 3 and Fig. 6. (Note that in the following, we focus on the solvent and solute conformational entropy changes only, which are the values given in Table 3; the external entropy change that includes translational and rotational entropies will not be discussed.) We now discuss these results in the context of hydrophobic and hydrophilic protein-protein association, which can have different thermodynamic signatures. It has been known that the thermodynamic driving force for hydrophobic association is length-scale dependent (39,40). Aggregation of small hydrophobic solutes is driven by favorable entropy change and opposed by unfavorable enthalpy change. This is because the water molecules near small hydrophobic solute can rearrange themselves to maintain the hydrogen-bond network, and therefore, releasing such surface waters to the bulk upon solute association is more or less enthalpy neutral. In this case, the net enthalpy change of association results mainly from the loss of favorable solute-water interactions, which can outweigh the favorable solute-solute interaction. For example, Cui et al. (41) studied the thermodynamics of the rigid body binding between a hydrophobic α-helix with ubiquitin. The size and shape of the buried surface area in this complex suggest that it belongs to the small solute regime. Hence, the binding is driven by entropy and opposed by enthalpy because of the loss of protein-water interactions not compensated by the gain of protein-peptide interactions and solvent-solvent interactions from the desolvation of the solutes (41).

For large hydrophobic solutes (e.g., interface dimension R > 10 Å) association can be favored or disfavored by enthalpy, depending on the strength of the solute-water interaction. This is because unlike the water molecules around a small solute, water molecules near a large hydrophobic surface cannot orient themselves around the surface to maintain the hydrogen-bond network. As a result, the loss of large hydrophobic surface patches upon binding releases energetically frustrated water molecules into the bulk, resulting in a reduction of the enthalpy. For example, using highly hydrophobic plates with weak solute-water interaction parameters, Zangi and Berne (42) found that both entropy and enthalpy favor hydrophobic collapse. However, for graphene plates, which have stronger plate-water interaction parameters, Choudhury and Pettitt (34) found that the collapse of the plates in water is driven only by entropy and opposed by enthalpy. This is because the loss of plate-water interaction upon collapse outweighs the enthalpy gain from the release of water molecules in between the plates and from the increased direct plate-plate attraction.

There have been few computational studies on characterizing the thermodynamic driving forces for hydrophilic protein-protein association (43,44). Helms and co-workers have studied several hydrophilic protein-protein complexes, including the barnase-barstar complex (43), focusing on the calculation of the binding free energy and translation and rotation entropy changes. For the barnase-barstar complex, using the experimental data (45), one can estimate that the protein-protein binding is largely driven by favorable enthalpy with a relatively small favorable entropy contribution. Ben-Naim proposed a model suggesting that in hydrophilic protein-protein association, water molecules can “stitch” the two proteins by forming hydrogen-bond bridges between two hydrophilic groups on the surfaces of two binding partners, resulting in favorable enthalpy at the expense of entropy (46).

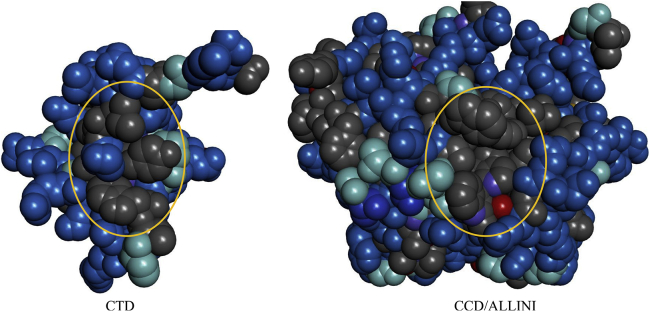
In this study, as shown in Fig. 11, the protein-protein interfaces in the complex contain a mixture of mainly hydrophobic groups and also several hydrophilic residues, with the nonpolar patch roughly surrounded by polar residues. Because both the solvent and solute degrees of freedom are unconstrained, our calculations reveal a more realistic thermodynamic picture of protein-protein association than did previous studies that either used idealized geometry (plates and ellipsoids) or have fixed intramolecular degrees of freedom of the protein. Importantly, we found that when the protein conformational degrees of freedom are accounted for, the entropy of association becomes unfavorable (Table 3). Consistent with previous work, we also found that during the water expulsion phase, the entropy change is weakly favorable because the large increase in the solvent entropy due to interprotein water release is largely canceled by the reduction in the solute entropy. As the two proteins approach the contact minimum, the entropy drops further as the conformational motions are more limited. The configuration entropy loss at the final stage of the complexation of ∼20 kcal/mol is in the same order as those estimated by Chang et al. for the binding of AKAP protein HT31 with the D/D domain of RII α-regulatory subunit of protein kinase A (47).

Figure 11.

The VDW surfaces of the binding interfaces in the two proteins. Gray: hydrophobic. Blue: hydrophilic. Cyan: intermediate between hydrophilic and hydrophobic, e.g., GLY, PRO, and THR. The central contact residues involved in the binding are circled. To see this figure in color, go online.

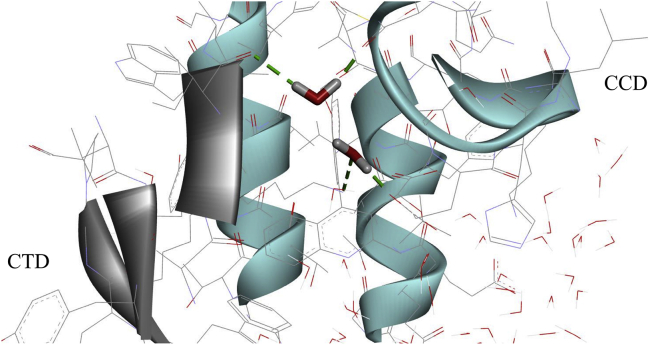
In this study, we find evidence that is consistent with the bridging water effect proposed by Ben-Naim; see Fig. 12. The thermodynamic properties for the association of large hydrophobic and hydrophilic solutes surveyed here are summarized in Table 4. It should be noted that although the signs of the entropy and enthalpy may be generalized for idealized systems, for realistic proteins the situation is more complex and likely to be system dependent because of the presence of many variables, such as the interface composition, curvature, flexibility, and solvent conditions (e.g., ionic concentration and pH).

Figure 12.

An MD snapshot showing two bridging waters forming hydrogen bonds with both proteins. To see this figure in color, go online.

Table 4.

Summary of the Thermodynamic Driving Forces in the Association of Large Solutes Surveyed Here

Superhydrophobic Plates (42)	Normal Hydrophobic Plates (34)	Hydrophilic Proteins (45)	Proteins that Associate Using both Nonpolar and Polar Groups (This Work)
ΔS favorable	ΔS favorable	ΔS small	ΔS unfavorable
ΔH favorable	ΔH unfavorable	ΔH favorable	ΔH favorable

In this work, both the direct simulations and PMF calculations show that the effective range of the attraction between the two binding proteins CTD and ALLINI-bound CCD is very short, at interface distance d ≈ 4 Å or less than two layers of water molecules, even though the two binding partners CTD and CCD carry 9+e and 3−e net charges, respectively. Apparently, the short-ranged effective interaction is the combined result of several factors, including the spatial distribution of the charges and the electrostatic screening from the solvent. To gain more insights into the origin of this short-ranged effective interaction, we analyze the calculated protein-protein PMF in terms of the interaction energy components in Fig. 10. Although all the interaction energies are much noisier compared with the well-behaved free-energy profile, some qualitative trends can be gleaned from such an analysis. First, the short-range protein-protein PMF is the result of a near-complete cancellation of several much larger forces (note that entropy contributions are not included in Fig. 10). Second, the interaction energies have somewhat longer range compared with the free energy. For example, the protein-solvent interaction energy starts to increase at about d = 6.4 Å, whereas the free energy starts its descent at d = 4.1 Å.

Next, we compare the effective range of the protein-protein binding observed in this work with those reported in the literature (13,43,44,48). Helms and co-workers have computed the PMF for several hydrophilic protein-protein complexes, including the barnase-barstar complex (43), for which they report a large effective range of the binding funnel of ∼14 Å. The PMF of the barnase-barstar complex, which is characterized by a highly polar or charged interface in explicit solvent, has also been reported by other groups. For example, Hoefling and Gottschalk (48) reported the width of the binding funnel to be ∼15 Å, similar to the result by Helms and co-workers (43). On the other hand, in a study by Gumbart et al. (13) in which the protein conformational degrees of freedom are constrained, the effective range of attraction in barnase-barstar is ∼6 Å. Overall, the effective range of the association funnels for hydrophilic protein-protein binding is considerably larger than the ∼4 Å for the HIV-1 integrase aggregation studied here. The difference in the width of the binding funnel could be attributed to the more hydrophobic nature of the system studied in this work, as the CTD and drug-bound CCD interface involves several nonpolar residues such as A128, T226, W235, and I268 in addition to the charged K266.

Lastly, some studies of hydrophobic protein-protein association (40,49, 50, 51) have focused on determining the effects of dewetting or cavitation (52), i.e., the cooperative liquid-to-vapor phase transition in the interdomain region that was first observed in idealized plates when the interplate region is still large enough to hold more than two layers of water (40). Although a dewetting transition may occur below a critical separation between idealized nanoscale hydrophobic plates or ellipsoids (53,54), it has rarely been observed in realistic hydrophobic protein association (55). For example, in the hydrophobic collapse of protein domains of 2,3-dihydroxybiphenyl dioxygenase, dewetting is observed only after turning off the protein-water electrostatic interactions in the simulation (50). The only system in which the cooperative drying phase transition has been observed is in the melittin tetramer (49), which was separated to create a nanoscale tube-like channel. Interestingly, Ricci and McCammon (56) recently observed that during the association of a 15-residue hydrophobic MDM2 peptide to a highly hydrophobic cleft of the p53 protein, the water density in the interfacial space starts to drop from the bulk value when the interfacial separation is less than 7.6 Å, which is believed to be the onset of dewetting transition. However, it appears that cavitation in the interprotein space did not occur even in this highly nonpolar system. In our study, we did not observe a dewetting transition in the protein-protein association of the CTD and CCD-ALLINI system. As shown in Fig. 13, within the binding funnel, the intervening region remains well hydrated with water molecules whose occupancy is even higher than that in the bulk water. The small number of hydrophilic groups in the interface region (Fig. 11) that interact strongly with interfacial water molecules is likely canceling any tendency to dewet (55).

Figure 13.

The orange dots represent interfacial water sites whose occupancy is at least 1.5 times the bulk water occupancy. To see this figure in color, go online.

Conclusions

Elucidating the energetics and thermodynamic aspects of protein-protein association is important to our understanding of this fundamental molecular recognition process. Computational characterizations of the thermodynamic signatures of protein-protein association for realistic systems are still scarce. Here, using explicit solvent MD and umbrella sampling, we have provided a more complete picture of the protein-protein association responsible for the drug-induced HIV-1 integrase multimerization. The calculated free-energy profile has correctly captured the critical role of the inhibitor in the integrase multimerization and accounted for the effects of various amino acid substitutions on the protein association. Remarkably, the results reveal that the effective range of the protein-protein attractive funnel is less than two layers of water molecules, which is significantly shorter than those reported for the more hydrophilic protein-protein complexes despite the fact that the two binding partners studied here carry opposite net charges. Lastly, we find that although the majority of the residues forming the contact interface are hydrophobic, the overall association is favored by enthalpy and opposed by entropy. Our analysis suggests that although the solvent release from the interprotein region into the bulk solution results in an increase in entropy, this is more than offset by the loss of the solute configurational entropy due to the complexation.

Author Contributions

N.D., R.L., and E.G. designed the research. C.T., L.W., and N.D. performed the research. M.K. contributed research data. N.D., R.L., E.G, and L.W. analyzed the results. N.D., R.L., and E.G. wrote the manuscript.

Editor: Alan Grossfield.