Abstract
Mechanosensation of cells is an important prerequisite for cellular function, e.g., in the context of cell migration, tissue organization, and morphogenesis. An important mechanochemical transducer is the actin cytoskeleton. In fact, previous studies have shown that actin cross-linkers such as α-actinin-4 exhibit mechanosensitive properties in their binding dynamics to actin polymers. However, to date, a quantitative analysis of tension-dependent binding dynamics in live cells is lacking. Here, we present a, to our knowledge, new technique that allows us to quantitatively characterize the dependence of cross-linking lifetime of actin cross-linkers on mechanical tension in the actin cortex of live cells. We use an approach that combines parallel plate confinement of round cells, fluorescence recovery after photobleaching, and a mathematical mean-field model of cross-linker binding. We apply our approach to the actin cross-linker α-actinin-4 and show that the cross-linking time of α-actinin-4 homodimers increases approximately twofold within the cellular range of cortical mechanical tension, rendering α-actinin-4 a catch bond in physiological tension ranges.
Significance
Mechanosensation of cells is an important prerequisite for cellular function, e.g., in the context of cell migration, tissue organization, or embryogenesis. Previous studies have shown that cytoskeletal cross-linkers, such as α-actinin-4, exhibit mechanosensitive properties in their binding dynamics to actin polymers. Here, we present a, to our knowledge, new technique to quantify the dependence of actin cross-linker unbinding in dependence of mechanical tension in the cytoskeleton. We apply our approach to the actin cross-linker α-actinin-4. Our findings suggest that the cross-linking density of α-actinin-4 homodimers increases approximately twofold within physiological tension ranges.
Introduction
Mechanosensation of cells is pivotal for the regulation of cell adhesion and cytoskeletal force generation. Therefore, it is vital for biological processes such as cell migration, cell shape emergence, tissue organization, and morphogenesis (1, 2, 3, 4). A particularly important role for cellular mechanotransduction is played by the actin cytoskeleton, which connects to the extracellular matrix via focal adhesion complexes (2). Mechanosensation is enabled by mechanosensitive molecules inside cells that transduce mechanical triggers into chemical cues. One way to realize such a mechanochemical transduction is through mechanosensitive bonds; protein-protein bonds subject to mechanical tension may either strengthen (catch bonds) or weaken (slip bonds) in response to tensile mechanical stress. In turn, catch bonds enhance their bond lifetime in response to tension, whereas slip-bond lifetime decreases (5). Furthermore, catch- (slip-) bond dynamics is associated with an increased (decreased) fraction of bound proteins in the presence of mechanical tension.
Previous studies put forward that the actin cross-linker α-actinin-4 forms catch bonds: Yao et al. showed stress-enhanced gelation of in vitro actin networks cross-linked by α-actinin-4, indicating catch-bond behavior (6). Previous studies demonstrated slowed α-actinin-4 turnover in the actin cytoskeleton of HeLa cells in response to compressive stress (7) and accumulation of α-actinin in response to suction pressure from micropipette aspiration in Dictyostelium cells (8). However, to date, there are no studies that showed a quantitative relation between α-actinin-4 cross-linking lifetimes and mechanical tension in the cytoskeleton. The goal of our study is to close this gap by establishing a new technique that combines parallel plate assays of nonadherent cells based on atomic force microscopy (AFM) with photobleaching of fluorescently labeled α-actinin-4 and mathematical modeling of cross-linker binding kinetics.
Like many actin cross-linkers, α-actinin-4 binds at a high affinity to a dumbbell-shaped antiparallel homodimer in the cytoplasm (9). Each monomer inside the homodimer provides an F-actin-binding domain (ABD). In this way, α-actinin-4 homodimers can bind as cross-linkers in actin cytoskeletal networks. Previous studies have characterized the biochemical features of α-actinin-4 actin binding; each α-actinin-4 monomer inside the homodimer contains two N-terminal calponin homology domains. These two domains are normally tethered in a closed conformation, forming the ABD (9,10). An additional actin binding site outside the ABD of α-actinin-4 is present but normally buried inside the molecule in the closed conformation. Alternatively, an open conformation can be adopted by α-actinin-4 with a higher actin-binding affinity; this can be achieved through biochemical modifications such as phosphorylation at Y265 (10). The exposure of this additional actin binding site through mechanical stretching of the cross-linking homodimer has been suggested to be at the heart of mechanosensitive binding dynamics of α-actinin-4 (10). Furthermore, the binding affinity of normal α-actinin-4 is regulated by Ca2+ ions through a C-terminal calmodulin-like Ca2+-binding domain where the presence of Ca2+ reduces the binding affinity of α-actinin-4 to actin (9,10).
In our study, we qualitatively characterize the lifetime of fluorescently labeled α-actinin-4 constructs at the actin cortex in HeLa cells in mitotic arrest. To this end, we combine 1) confocal imaging of the cortex and fluorescence recovery after photobleaching (FRAP) with 2) a parallel plate confinement assay of cells that allows us to measure the momentary mean-field mechanical tension in the actin cortex as described previously (11, 12, 13). We use our results on FRAP-derived cortical residence time at given values of cortical tension to infer the cross-linking lifetime of α-actinin-4 in the cortex using a simple mathematical model of cross-linker binding, as has been previously suggested by (14). We extend this model such that it includes the dependence of cross-linking lifetimes on mechanical tension in the actin cortex and fit model predictions to experimental data. Furthermore, we present passive and active methods to manipulate cortical tension in individual cells and monitor cross-linker concentration concomitantly.
Materials and Methods
Cell culture
We cultured HeLa Kyoto cells expressing a green-fluorescent or red-fluorescent, C-terminally tagged α-actinin-4 construct in Dulbecco’s modified Eagle’s medium (PN:31966-021; Life Technologies, Carlsbad, CA) supplemented with 10% (vol/vol) fetal bovine serum, 100 μg/mL penicillin, 100 μg/mL streptomycin, and 0.5 μg/mL geneticin (all Invitrogen, Carlsbad, CA) at 37°C with 5% CO2. One day before the measurement, 10,000 cells were seeded into a silicon cultivation chamber (0.56 cm2, from ibidi 12-well chamber; ibidi, Martinsried, Germany) that was placed in a 35 mm cell culture dish (fluorodish FD35-100, glass bottom; World Precision Instruments, Sarasota, FL) such that a confluency of ∼30% is reached at the day of measurement.
For AFM experiments, medium was changed to Dulbecco’s modified Eagle’s medium (PN:12800-017; Invitrogen) with 4 mM NaHCO3 buffered with 20 mM HEPES/NaOH (pH 7.2). Mitotic arrest of cells was achieved by addition of S-trityl-l-cysteine (Sigma-Aldrich, St. Louis, MO) 2–8 h before the experiment at a concentration of 2 μM. This allowed conservation of cell mechanical properties during measurement times of up to 30 min for one cell (15). Cells in mitotic arrest were identified by their shape and visibility of condensed DNA in transmitted light images. Pharmacological agents (−)-blebbistatin (B0560-1MG; Sigma-Aldrich), para-nitroblebbistatin (DR-N-111; Optopharma, Budapest, Hungary), Y-27632 (Cay10005583-1; Cayman Chemical, Ann Arbor, MI), gadolinium chloride (4741; Tocris), BAPTA (123311000; Thermo Fisher Scientific, Waltham, MA) or GsMTx4 (141871; Abcam, Cambridge, UK) were added at least 15 min before measurement to indicated concentrations. As opposed to blebbistatin (16), para-nitroblebbistatin is optically stable and allows cell imaging with blue light without activity changes of the drug.
Cell lines
Within this study, three different HeLa cell lines were used, expressing either fluorescently labeled murine Actn4 from Bacterial Artificial Chromosomes (BACs) (see Figs. 3 and 5) or GFP-labeled human Actn4 with a point mutation (K255E) from a plasmid. The K255E mutant was cloned into the plasmid backbone pLGC as described in (17). HeLa Kyoto cells were stably transfected with this plasmid using lipofectamine 2000 (11668030; Invitrogen) according to the protocol of the manufacturer.
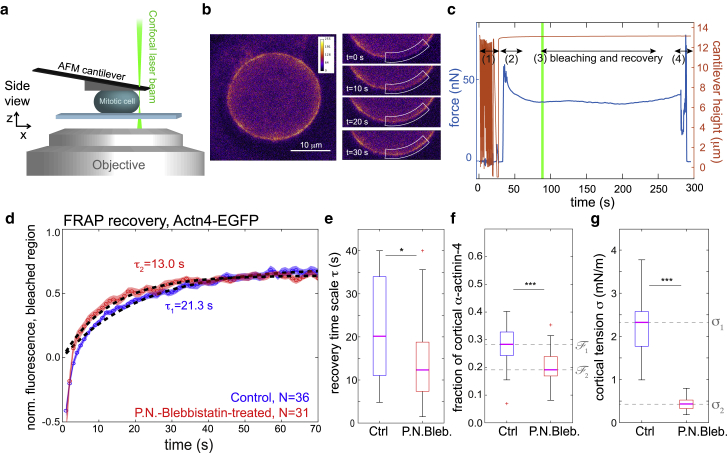
Figure 3.
Photobleaching of α-actinin-4 in the mitotic cortex in combination with an AFM confinement assay. (a) A schematic of the experimental setup. Confocal imaging and photobleaching of cells in mitotic arrest were combined with parallel plate confinement by wedged AFM cantilevers. Confocal imaging was performed in the equatorial plane of the cell (maximum cross-sectional area). The AFM readout was the confinement height and the confinement force of the cell over time. (b) Exemplary confocal image of the equatorial plane of a mitotic cell (left panel) and fluorescence evolution after photobleaching (panels on the right). The bleached region is indicated by a white boundary. (c) Exemplary force and cantilever height readout during the experiment. In phase (1), the cantilever is approached on the glass substrate of the cell culture dish. In phase (2), the retracted cantilever is moved over the cell. At the beginning of phase (3), photobleaching is performed, and the cortex is imaged during fluorescence recovery. In phase (4), the cantilever is removed from the cell and lifted. (d–g) Experimental results from the combined assay on HeLa cells expressing Actn4-EGFP. (d) Averaged recovery curves of normalized fluorescence intensity in control conditions (N = 36, blue curve) and of cells with pharmacologically reduced cortical tension (N = 31, red curve, incubated with para-nitroblebbistatin at 10 μM). Red and blue shaded regions indicate the respective standard error of the mean for each condition. Averaged normalized curves were fitted with an exponential increase (black dashed lines), with fit timescales of τ = 21.3 s (control) and 13.0 s (P.N.Bleb., 10 μM). (e) Recovery times from fits of individual recovery curves in control and blebbistatin-treated conditions corresponding to (a). (f) Corresponding estimated fractions of cortical α-actinin-4. (g) Corresponding cortical tensions in control and para-nitroblebbistatin-treated conditions (measurements are representative for at least two independent experiments. n.s. (not significant), p > 0.05; ∗p < 0.05, ∗∗p < 0.01, ∗∗∗p < 0.001). To see this figure in color, go online.
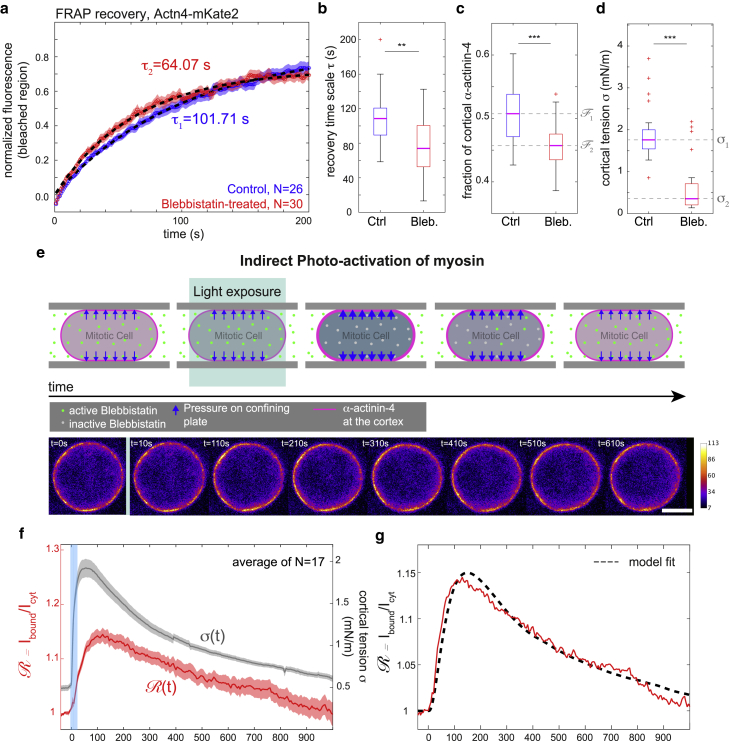
Figure 5.
Experimental results from FRAP and indirect photoactivation of myosin with red fluorescently labeled α-actinin-4 (Actn4-mKate2) in mitotic HeLa cells. (a) Averaged recovery curves of α-actinin-4-mKate2 after photobleaching at the mitotic cortex: control (N = 26, blue curve) and tension-reduced (N = 30, red curve, incubated with blebbistatin at 10 μM). Red and blue shaded regions indicate the respective standard error of the mean for each condition. Fluorescence intensities were normalized. Averaged curves were fitted with an exponential recovery (black dashed lines), with fit timescales of τ = 101.71 s (control) and 64.07 s (Bleb., 10 μM). (b) Recovery times from fits of individual recovery curves in control and blebbistatin-treated conditions corresponding to (a). Median values are 108.5 s (control) and 72.8 s (blebbistatin at 10 μM). (c) Estimated fraction of cortical α-actinin-4 in control and blebbistatin-treated conditions corresponding to (a). Median values of fit recovery timescales are 0.51 (control) and 0.46. (d) Cortical tensions in control and blebbistatin-treated conditions corresponding to measurements presented in (a). (e) Top: schematic of cellular response upon indirect photoactivation of myosin. Bottom: time series of confocal micrographs of the equatorial plane of the cell recorded during the photoactivation experiment. Fluorescence changes are typically too small to be assessed by eye. Scale bar, 10 μm. (f) Time evolution of the cortex/cytoplasm ratio = Ibound/Icyt of Actn4-mKate2 fluorescence (red curve) and corresponding time evolution of cortical tension (gray curve). The blue shaded region indicates the time interval during which cells were scanned with blue laser light (488 nm) to inactivate blebbistatin inside the cell. Averages were taken over 17 cells. Red and grey shaded regions indicate the standard errors of the mean of cortex/cytoplasm ratio and tension, respectively. (g) Averaged time evolution of cortex/cytoplasm ratio (red curve, as in f) with corresponding model fit (black dashed line). Fitting parameters are given in Table 1, fourth row. Curves were averaged over 17 cells. Before averaging, intensity curves were normalized to take the value one before photoinactivation (measurements are representative for at least two independent experiments. n.s., p > 0.05; ∗p < 0.05, ∗∗p < 0.01, ∗∗∗p < 0.001). To see this figure in color, go online.
BACs with Actn4 constructs were prepared as follows: BACs harboring mouse Actn4 (RP23-375C17) were modified by recombineering as described (18). Briefly, using electroporation, both, a plasmid pSC101 carrying two recombinases and gene-specific purified EGFP- or mKate2-tagging cassettes were introduced into the Eschericha coli strains containing the parental BAC vectors. For this purpose, 50-nucleotide-homology arms that match the C-termini of both target genes, respectively, were attached to the BAC tagging cassettes using PCR. Precise incorporation of the tagging cassette was confirmed by PCR and sequencing. Next, tagged BACs were isolated from bacteria using the Nucleobond PC100 kit (Macherey-Nagel, Düren, Germany). Subsequently, HeLa Kyoto cells were transfected using Effectene (Qiagen, Hilden, Germany) and cultivated in selection media containing 400 μg/mL geneticin (G418; Invitrogen). Finally, pools of HeLa cells stably expressing Actn4-EGFP were analyzed by Western blot and immunofluorescence using an anti-GFP antibody (11814460001; Roche, Basel, Switzerland) or to verify correct protein size and localization of the tagged transgene.
Confocal imaging in combination with AFM
The experimental setup consisted of an atomic force microscope (Nanowizard I; JPK Instruments, Berlin, Germany) mounted on a Zeiss LSM700 laser scanning confocal system of the Center for Molecular and Cellular Bioengineering (CMCB) light microscopy facility. For imaging, we used a 20× objective (Plan Apochromat, NA = 0.80; Carl Zeiss, Oberkochen, Germany) and a 555 nm laser line for excitation of mKate2 fluorescence at laser powers between or a 488 nm laser line for excitation of GFP both at laser powers between 0.3 and 1%. During measurements, cell culture dishes were kept in a petri dish heater (JPK Instruments) at 37°C. On every measurement day, the spring constant of the cantilever was calibrated using the thermal noise analysis (built-in software; JPK Instrumetns). Cantilevers were tipless, 200–300 μm long, 35 μm wide, and 2 μm thick (NSC12/tipless/noAl or CSC37/tipless/noAl; Mikromasch, Sofia, Bulgaria), with nominal force constants between 0.3 and 0.8 N/m. Cantilevers were modified with wedges to correct for the 10° cantilever tilt consisting of ultraviolet curing adhesive (Norland 63; Norland Products, East Windsor, NJ) (19).
Before cell confinement, the AFM cantilever was lowered to the dish bottom near the cell until it came into contact with the glass surface and then retracted to ∼14.5 μm above the surface. Thereafter, the free cantilever was moved over the cell. The confocal plane of scanning was adjusted to coincide with the equatorial plane of the cell that exhibits the largest cross-sectional area. To increase fluorescence intensity, the aperture of the pinhole was set to three Airy units, corresponding to an optical section thickness of 6 μm.
Stationary-state AFM forces were used to calculate cortical tension as described previously (12,20). Briefly, as part of this analysis, cell height and cross-sectional area of the cell in the equatorial plane were used to estimate cell volume and other geometrical parameters (contact area, mean curvature) as described in (12).
During the entire experiment, the force acting on the cantilever was continuously recorded at a frequency of 10 Hz. The height of the confined cell was computed as the difference between the height that the cantilever was raised from the dish surface and lowered onto the cell plus the height of spikes at the rim of the wedge (because of imperfections in the manufacturing process (19)) and the force-induced deflection of the cantilever.
Photobleaching experiments
AFM cell confinement of a cell in mitotic arrest was realized as described in the previous section at a height of ∼14.5 μm (retracted AFM cantilever), and recording of AFM force and cantilever height was started. Afterwards, confocal imaging of the chosen cell was set up. For every cell, we scanned a square region of 512 × 512 pixels (side length between 30 and 50 μm) that covered the equatorial cell cross section and part of its surroundings. We recorded a time series at time intervals between 1.5 and 4 s. After imaging of 4–10 initial frames, a small rectangular region of ∼2 × 20 μm2 of the cell cortex was bleached in three iterations with the 555 nm laser at a laser power of 70% and a pixel dwell time 2.55 μs (see Fig. S1 a; green rectangle depicts bleached area). After bleaching, a time interval of 150–250 s was recorded until fluorescence in the bleached area plateaued.
Image analysis of photobleaching experiments
For image analysis of confocal time series, the cell boundary was determined by a MATLAB (The MathWorks, Natick, MA) custom code (see Fig. S1 b for an example cell; the cell boundary is marked in red). Along this cell boundary, 200 orthogonal, equidistant lines were determined extending 4 μm to the cell interior and 2 μm into the exterior (see Fig. S1 b, red lines orthogonal to cell boundary; only every 10th line is plotted out of 200).
To obtain fluorescence recovery curves from the bleached region of the cell cortex, we determined the averaged intensity along the cortex circumference by averaging fluorescence intensity values along 200 shorter radial lines (pink lines in Fig. S1 b, extending 2.4 μm to the interior, 0.8 μm to the exterior). Plotting average intensities along the cortex circumference over time allows to generate a kymograph of cortex fluorescence intensity (see Document S1. Figs. S1–S8, Document S2. Article plus Supporting Material c).
We determined the bleached area of the cortex by identifying the region with more than 40% intensity change from the frame before to the frame after bleaching. The intensity average along pink, radial lines within the bleached cortical area Ibl was calculated for every time point. Furthermore, we determined the averaged intensity in the unbleached cortical region Iun over time t. To estimate the rate of bleaching kbl, we fitted the function Iun(t) by an exponential decay Aexp(−kblt). Correcting now intensity values along the cortex by multiplying it with the factor exp(kblt), we may plot a new kymograph in which bleaching has been corrected (Fig. S1 d) such that the average intensity in the unbleached area remains constant.
The normalized and bleaching-corrected intensity = Ibl(t)exp(kblt)/Ibl,0 was then, in the following, used to analyze fluorescence recovery (see Document S1. Figs. S1–S8, Document S2. Article plus Supporting Material e), where Ibl,0 denotes the intensity bleached region before bleaching. Recovery curves were fitted by an exponential rise
in terms of a least-squares fit. The fit function takes the value at t = 0 but converges to at long times. Recovery is captured by a characteristic timescale τ. The first 5 s of the recovery were excluded from fitting because in this time regime, it was apparent that recovery had a major contribution from cytoplasmic diffusion into the cytoplasmic region next to the bleached cortex area. Renormalized intensities were then averaged for all cells measured to obtain Figs. 3 d and 5 a, main text.
Estimating the fraction of cortical fluorescent protein
Fluorescence intensities of radial lines at the cell periphery (red lines in Fig. S1 b) were averaged for all prebleaching frames to obtain an average intensity profile in radial direction along the cortex (see Fig. S1 f, blue curve). This intensity profile along the red orthogonal line is then fitted by the function
| (1) |
with fit parameters p = {μ, σ1, σ2, Icyt,o, Icor, IBG, α}, to obtain a smoothed variant Ism(r, p) of the intensity profile along the radial coordinate. A respective exemplary fit of Eq. 1 is shown in Fig. S1 f (orange curve). Here, erf(r) denotes the error function and G(r, μ, σ2) denotes a Gaussian function with mean value μ and standard deviation σ2. The term is a corresponding skewed Gaussian function with skewness characterized by parameter α. The parameters Icyt,o and Icor quantify the amplitude of cytoplasmic versus cortical fluorescence, whereas σ1 and σ2 quantify the smearing out of the cytoplasmic or cortical fluorescence distribution, respectively. IBG captures the value of background intensity, and μ is the coordinate for the location of the cell boundary.
The skewed Gaussian contribution in the fitted intensity profile (Fig. S1 f, yellow curve) is interpreted as fluorescence contribution from the cortical proteins, and the remaining part (Fig. S1 f, violet curve) is interpreted as a sum of cytoplasmic fluorescence in the outer rim of the cell Icyt,o and background fluorescence IBG. The skewed Gaussian was then integrated along the radial direction to obtain I2D,cortex as a measure for the two-dimensional concentration of fluorescent protein at the cortex. The integrand was then multiplied with the overall cell surface area estimate Acell to an intensity value that is proportional to the overall number of fluorescent proteins Ncor at the cortex. To estimate the cytoplasmic concentration of fluorescent protein, we determine the average fluorescence intensity in the inner part of the cross section Icyt,i (Fig. S1 b, green disk extending to 70% of the cell radius) and in the outer cytoplasmic region Icyt,o. Icyt,o is the innermost value of Ism of a radial line profile (Fig. S1 b, red lines). To obtain an overall intensity average of the cytoplasmic fluorescence, we calculate Icyt = (0.72Icyt,i + (12 − 0.72)Icyt,o) − Iwedge, where Iwedge is the background intensity from the wedge, which we estimate as 0.46 × IBG (see section below and Fig. S2). Icyt × Vcell is then used as a measure for the number of fluorescent proteins in the cytoplasm Ncyt, where Vcell is the estimated volume of the cell. Therefore, we approximate the fraction of cortical fluorescent protein = Ncor/(Ncyt + Ncor) as (I2D,cort Acell)/(IcytVcell + I2D,cort Acell).
Because of uncertainty in the background fluorescence, we estimate the relative error of Icyt to be ∼20%. Because of error propagation, we estimate a corresponding relative error of up to 10% of .
As previously described (12), we estimated the cell volume Vcell and the overall cell surface area Acell as
which can be derived by regarding the cell as an axisymmetric body of revolution and approximating the profile of the free cell contour by a semicircle with radius h/2. Here, Req is the equatorial radius of the confined cell (obtained from imaging) at confinement height h (obtained as AFM readout).
Blue light inactivation experiments
After moving the cantilever over the cell and a subsequent initial equilibration time of at least 200 s, we started to record a time series of confocal images with the focal plane coinciding with the equatorial plane of the cell, choosing time intervals between 5 and 10 s. After imaging between 5 and 10 initial frames, the frame was laser scanned with blue light (488 nm, diode laser of Zeiss LSM 700) in 10 iterations at a laser power of 8%, speed of 10 (pixel dwell time 1.27 μs) to inactivate blebbistatin in the cell (16). To monitor the concentration of cortex-bound fluorescent protein during photoinactivation of blebbistatin, we determined the averaged intensity at the cell boundary Ibound by integrating fluorescence intensities over all 200 short radial lines at the cortex (pink lines in Fig. S1 b, extending 2.4 μm to the interior, 0.8 μm to the exterior). Here, averaging was performed along the line and over all 200 lines along the circumference. To quantify the cytoplasmic concentration of fluorescent protein, we determined the average fluorescence intensity in the inner part of the cross section Icyt,i (Fig. S1 b, green disk extending to 70% of the cell radius). To estimate the ratio of cortex-bound/cytoplasmic fluorophore concentration in Fig. 5, f and g, we calculated the ratio (Ibound − Iwedge)/(Icyt,i − Iwedge), where Iwedge is the background intensity from the wedge, which we estimated as 0.46 × IBG (see Fig. S2 b and following paragraph).
Fluorescence background analysis
For image analysis, we quantified contributions to background fluorescence by plotting the intensity profile along a straight line spanning the cell diameter and its neighborhood (Fig. S2 a). We identified two contributions to the background fluorescence: 1) autofluorescence of the wedge and 2) autofluorescence of the medium. Estimating average fluorescence values in regions A and B, respectively, as indicated in Fig. S2, a and b, we quantified background fluorescence in the equatorial plane of the cell at a cantilever height of ∼14 μm for six cells. We obtained an average value of 6.7 ± 1.7 (error indicates the standard deviation) in the region outside of the wedge (region A), whereas we quantified an average value 11.2 ± 3.4 in the region underneath the wedge (region B). This indicates that the background fluorescence from the wedge adds ∼46% to the overall fluorescence background, whereas the remaining background is constituted by the autofluorescence of the medium.
Cell-squishing experiments
After moving the retracted cantilever over the cell at a height of h ≈ 14.5 μm, we let the cell equilibrate for an initial equilibration time of at least 200 s. Then, a time series of confocal imaging was started while the cell was still confined by a retracted cantilever. After imaging between 2 and 10 initial frames, cell squishing was started by lowering the cantilever at a speed of 0.5 μm/s down to a nominal height between 9.5 and 11.5 μm. Imaging was performed at time intervals between 1.5 and 5 s. Before the start of the imaging time series, the focal plane was adjusted to coincide with the equatorial plane after cell squishing was finalized. As described above, we determined the ratio of cortex-bound/cytoplasmic fluorophore concentration by calculating the ratio (Ibound − Iwedge)/(Icyt,i − Iwedge), where we estimated Iwedge as 0.64 × IBG for the lower final cantilever heights between 9.5 and 11.5 μm used here.
We registered AFM force curves and imaging time series of the cell in time by setting the following events to be at time zero: 1) the peak of the AFM force curve and 2) the first frame in the imaging series in which the cell cross section does not continue to grow. Images recorded before this time point were not used for analysis. For averaging cortex/cytoplasm ratios from several cells, the measured ratio was normalized for each cell through division by smoothed curve evaluated at time t = 150 s. In this way, averaged normalized cortex/cytoplasm ratios converge to one in the long time limit (see Fig. 4 d). To test the significance of the peak at time t = 30 s after uniaxial compression, we applied a t-test to the distribution of normalized intensity ratios for 10 cells and found that the mean value is significantly different from 1 (p-value: 0.041, mean: 1.04).
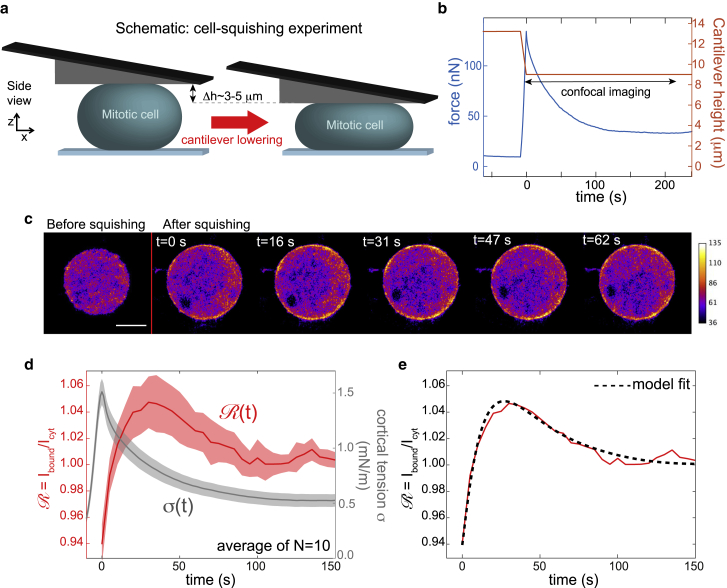
Figure 4.
Cell-squishing experiments: fluorescence of α-actinin-4 (Actn4-EGFP) increases at the cortex after transient mechanically induced increase in actin cortex tension. (a) A schematic of the experimental procedure. Cells were mechanically perturbed by a fast lowering of the AFM cantilever onto the cell (see Materials and Methods). Thereby, a mechanical stretch of cortical area was induced. Cells were in mitotic arrest and treated with the ROCK inhibitor Y27632 (5 μM). ROCK inhibition was necessary to avoid blebbing during mechanical cell squishing. (b) Exemplary force and cantilever height readout during the experiment. As the cantilever is lowered, cellular confinement force increases. Afterwards, the confinement force relaxes to a new steady-state force. (c) An exemplary time series of confocal micrographs of the equatorial plane of the cell recorded during a squishing experiment. Fluorescence changes are typically too small to be assessed by eye. Scale bar, 10 μm. (d) Averaged time evolution of cortical tension (gray curve) and normalized α-actinin-4 fluorescence at the cortex (red curve) during and after mechanical squishing of the cell. Averages were taken over 10 cells. Red and grey shaded regions indicate the respective standard errors of the mean of normalized fluorescence and tension. Mechanical tension peaks right after cantilever lowering has been stopped. Then, tension drops because of viscoelastic relaxation of deformation-induced cortical mechanical tension (12). Concomitantly, we observe a peak of α-actinin-4 fluorescence at the cortex at ∼30 s shortly after the peak in mechanical tension at the actin cortex. (e) Our model on protein dynamics provides an excellent fit (dashed black line) to the measured time evolution of cortical α-actinin-4 fluorescence (as depicted in d). Fitting parameters are given in Table 1, second row. According to our model, the transient peak in cortical intensity at t ≈ 30 s stems from the tension increase and the resulting increase in cross-linking lifetime koff(σ)−1. The elevated stationary-state value at long times can be accounted for by an increase of the surface/volume ratio due to increased cell confinement. To see this figure in color, go online.
Model parameter determination
To determine model parameters for different α-actinin-4 constructs, we used for each construct experimentally measured quantities τ1, τ2, , σ1, and σ2; τ1 and τ2 are measured recovery times of averaged FRAP recoveries in condition 1 (control) or condition 2 (tension-reduced), respectively (Figs. 3 d and 5 a). Correspondingly, and denote the measured median fractions of cortical protein in both conditions as depicted in Figs. 3 f and 5 c. σ1 and σ2 denote respective measured median values of cortical tension as depicted in Figs. 3 g and 5 d.
For the mutant protein Actn4-K255E-GFP, we determined model parameters as presented in Table 1 by directly solving the following equations numerically with respect to kon, kon,2, koff (0), and α:
| (2) |
Table 1.
Estimated Model Parameters for the Binding of Fluorescently Labeled α-Actinin-4 Homodimers for Two Different Cell Lines Expressing either Actn4-EGFP or Actn4-mKate2
| Cell line | kon(μm/s) | kon,2 (1/s) | koff(0) (1/s) | α (103 m/N) | (s) | (s) | Fcor,1 | Fcor,2 |
|---|---|---|---|---|---|---|---|---|
| Actn4-EGFP | 0.036 ± 0.013 | 1.61 ± 2.61 | 0.34 ± 0.20 | 0.55 ± 0.22 | 21.6 | 13 | 0.19 | 0.28 |
| Actn4-EGFP | 0.043 ± 0.003 | 0.035 ± 0.009 | 0.11 ± 0.034 | 0.9 ± 0.19 | 21.6 | 13 | 0.25 | 0.22 |
| Actn4-mKate2 | 0.026 ± 0.004 | 0.009 ± 0.025 | 0.022 ± 0.012 | 0.92 ± 0.43 | 101.7 | 64.1 | 0.51 | 0.46 |
| Actn4-mKate2 | 0.025 ± 0.002 | 0.026 ± 0.01 | 0.027 ± 0.002 | 0.41 ± 0.18 | 101.7 | 64.1 | 0.51 | 0.46 |
For both cell lines, parameters have been estimated according to the simple (green) or elaborate (brown) analysis pathway (see Fig. 6 and Materials and Methods). Here, and denote cortical residence times at tension values of σ1 (control conditions) or σ2 (tension-reduced conditions). Cortical tension values σ1 and σ2 were chosen as median tension values from Fig. 3g as well as Fig. 5d in respective measurement conditions. Error ranges are obtained by error propagation (see Materials and Methods). Parameter values of the brown analysis pathway have to be considered as more accurate.
Here, Fcor(σ1/2) and kdet(σ1/2) are given by Eqs. 5 and 10, respectively. This corresponds to the green analysis pathway as depicted in Fig. 6.
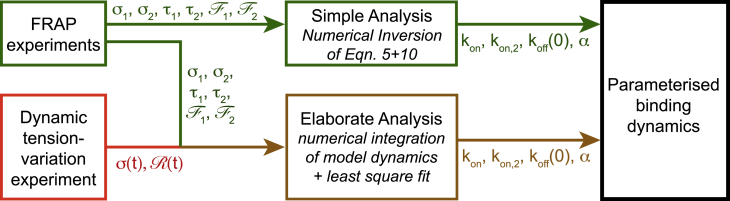
Figure 6.
Analysis scheme of experimental data to obtain a parameterized model of cross-linker binding dynamics. Although the green analysis scheme is simpler, the brown analysis scheme provides smaller error bars of determined model parameters, in particular for model parameter kon,2. To see this figure in color, go online.
For cell lines with BAC constructs (Actn4-EGFP, Actn4-mKate2), we determined model parameters according to the brown pathway as depicted in Fig. 6. There, we used, in addition to the abovementioned experimental quantities (τ1, τ2, , σ1, σ2), the output from cell-measurements with dynamic tension variation (cell squishing or indirect photoactivation). This output includes a time series of cortex/cytoplasm ratio of cross-linkers and cortical tension σ(t). The experimental quantity corresponds to the model quantity R as given in Eq. 6. Using all of these experimentally measured quantities, we performed a least-squares fit to obtain model parameters that provide the best match. A nonlinear least-squares fit was performed using MATLAB and the command lsqnonlin. The least-squares fit was minimizing the following functional:
| (3) |
Here, denotes the averaged normalized fluorescence intensities from measurements, as depicted in Figs. 4 e and 5 g, and the corresponding model predictions of normalized intensity.
was obtained from the numerical integration of defining Eq. 4 in MATLAB using a Euler forward algorithm with time step Δt = 0.1 s in MATLAB. was calculated (csb(t) + ccl(t))/ccyt(t) × ccyt(tend)/(csb(tend) + ccl(tend)), where tend is the biggest time argument under consideration.
For both the green and the brown analysis pathways, errors of estimated model parameters were determined by calculating derivatives of all model parameters with respect to each measured variable. The error of the model parameter was then estimated by the variance formula of error propagation. Accordingly, the error of kon was calculated as
For all other model parameters, the error estimate was performed analogously. The relative errors of σ1, σ2, τ1, and τ2 were estimated as 5%, whereas the relative errors of and were estimated as 10%. We find that the brown analysis pathway reduces error bars, in particular for the attachment parameter kon,2 (see Table 1).
Numerical integration of the model
The numerical integration of model Eq. 4 presented in Fig. 2, a–c was obtained by Mathematica using the command NDSolve.
Figure 2.
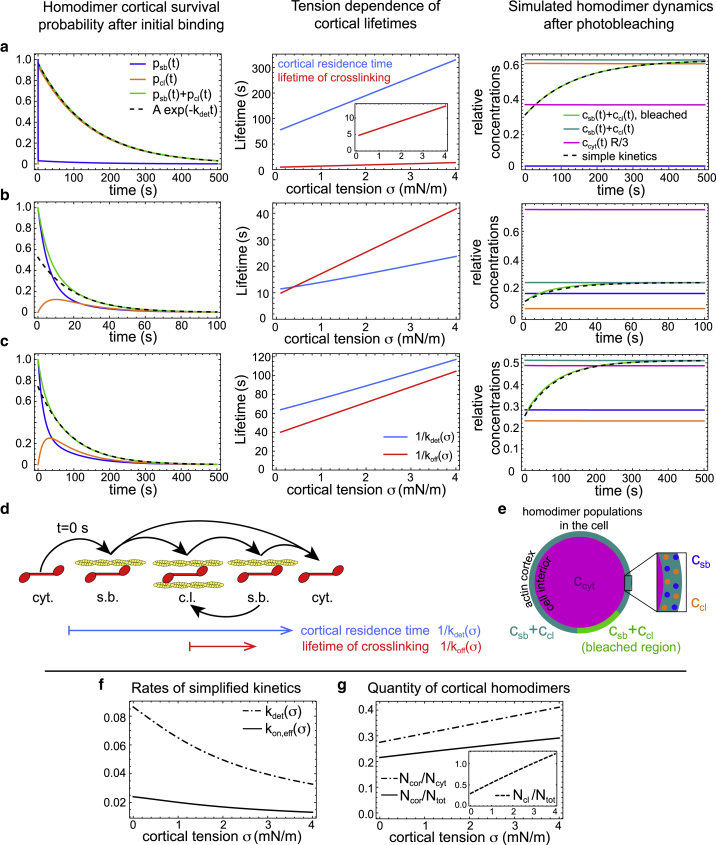
(a–c) Coarse-grained model of homodimer dynamics for three different parameter sets. Left panel column shows the time evolution of homodimer cortical survival probability according to Eq. 8 with the probability to be in a cross-linked (pcl, orange curve) or a single-bound state (psb, blue curve). The event of initial cortical attachment is assumed to be at t = 0 s, i.e., psb(0) = 1 and pcl(0) = 0. The associated exponential decay with the slowest timescale (1/kdet(σ)) of the model dynamics is shown by the dashed line. Central panel column shows cross-linking lifetime (red) and predicted cortical residence time (blue) of homodimers in dependence of cortical tension σ. The total residence time of the homodimer at the cortex follows qualitatively the same trend as the cross-linking lifetime. Right panel column shows simulation of FRAP recovery according to model Eq. 4 after bleaching of a small region of the cortex (green: concentration at the cortex in the bleached region; stationary state concentrations: cytoplasmic scaled (pink), total cortical (turquoise), cortical single-bound (blue), cortical cross-linking (orange)). The corresponding simplified kinetics as described by Eq. 12 is shown by dashed black lines. (d) Illustration of the cascade of possible events after the binding of a cytoplasmic homodimer at t = 0 s (cyt., cytoplasmic; s.b., single-bound; c.l., cross-linking). Associated cortical residence time (blue) and cross-linking time (red) are indicated. (e) An illustration of homodimer populations in the cell relevant for simulated FRAP dynamics presented in (a)–(c), rightmost panels. (f) Attachment and detachment rates of the approximating simplified kinetics in dependence of cortical tension. (g) The fraction of cortex-associated homodimers increases with tension in the scenario of a simple catch-bond behavior because of increased cross-linking times. Inset: fraction of cross-linking homodimers in dependence of tension. Here, Ncor and Ncyt denote the total number of cortex-associated or cytoplasmic homodimers, respectively. Model parameters for (f) and (g) are the same as in (b). Parameters used in simulations corresponding to (a) were R = 10 μm, kon = 0.021 μm/s, kon,2 = 6.6 s−1, koff(0) = 0.22 s−1, α = 0.5 × 103 m/N, σ = 2 mN/m, and koff(σ) = koff(0)/(1 + ασ). Parameters corresponding to plots in (b) and (c) were R = 10 μm, σ = 2 mN/m, and otherwise taken from Table 1, second and fourth row, respectively. In all FRAP simulations, the bleached percentage of the cortex was chosen to be 1%. To see this figure in color, go online.
For data fitting as presented in Figs. 4 e and 5 g, numerically integrated solutions of our model were fitted to measured data by a nonlinear least-squares fit using MATLAB and the command lsqnonlin (see previous section).
For the simulation of cell-squishing experiments, the anticipated squishing-induced increase of cell surface area was taken into account. Experimentally, we identified a typical cell volume of ∼5000 μm3 of mitotic HeLa cells. Therefore, using the assumption of cellular droplet shapes (11), we can predict cellular surface area increase due to squishing to be between ∼6.5 and 15% for an initial cell height of 14.5 μm and final heights between 9.5 and 11.5 μm. For the numerical integration of our model, we assumed an average increase of this ratio by 11%. For simulations of cell-squishing experiments and corresponding data fitting, surface areas were for simplicity approximated to increase linearly from the starting point of cantilever lowering until cantilever halt. Surface area increase of cells through squishing can account for the observed elevated equilibrium intensity of α-actinin-4 after squishing (see Fig. 4 e).
Analysis of fluorescence recovery for the K255E mutant
Recovery curves of the K255E mutant were not fitted well by an exponential recovery with a single timescale. Instead, fluorescence recovery of averaged curves were well captured by a double-exponential recovery of the form 1 − (Af exp(−t/τf) + (1 − Af) exp(−t/τs))B, where τf denotes a fast recovery timescale smaller than 100 s and τs a slow recovery timescale >100 s. Because mutant α-actinin-4 has significantly higher actin-binding affinity (9), mutant homodimers are expected to exhibit a longer cross-linking time and a slower photobleaching recovery time than heterodimers consisting of a mutant and a wild-type protein. In fact, in the framework of our model, heterodimers will exhibit an effective unbinding rate , where and are the unbinding rates of one ABD in the cross-linking state for endogenous and mutant α-actinin-4, respectively. Therefore, the tension-dependent unbinding rate of heterodimers is a mixture of the tension dependence of endogenous and mutant protein. It is noteworthy that in the limit case of small or negligible tension dependence of mutant unbinding, heterodimers would effectively behave as catch-bond cross-linkers. Furthermore, it is possible that the two tension dependences of wild-type and mutant bond effectively cancel each other out. The observation of no significant changes of the fast FRAP recovery time τf upon tension reduction (see Fig. 7 h) is in support of this latter scenario.
Figure 7.
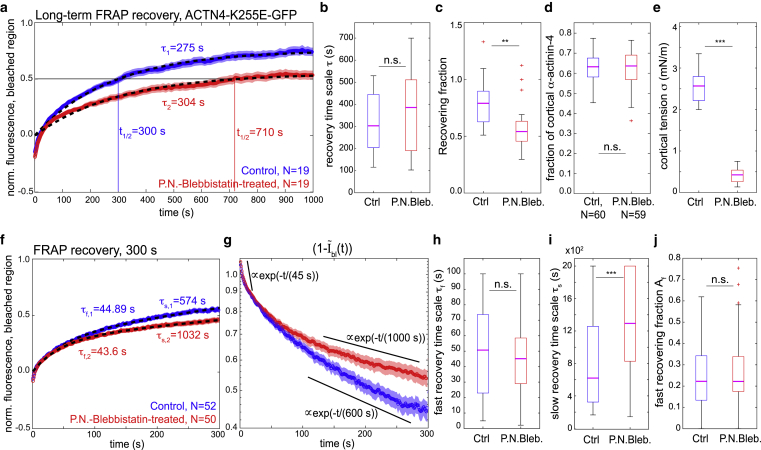
FRAP of the K255E mutant of α-actinin-4 in the mitotic cortex of HeLa cells. (a) Averaged long-term recovery of mutant α-actinin-4-GFP after photobleaching at the mitotic cortex: control (N = 19, blue curve), tension-reduced (N = 19, red curve, incubated with para-nitroblebbistatin at 10 μM). Fluorescence intensities were normalized. Recovery curves were averaged and fitted with an exponential recovery with a single timescale (black dashed lines). Red and blue shaded regions indicate the respective standard error of the mean for each condition. (b and c) Distribution of parameters from fitting individual recovery curves with an exponential function (same data as a): (b) distributions of fit recovery times τ (p-value: 0.6) and (c) distributions of recovering fractions. (d) Estimated fraction of cortical α-actinin-4 in control and tension-reduced conditions for an enlarged data set. Median values of fit recovery timescales are 0.6 in both conditions (control: N = 60, P.N.Bleb.: N = 59, p-value: 0.3). (e) Cortical tensions in control and blebbistatin-treated conditions corresponding to measurements presented in (a). (f) Averaged recovery of mutant α-actinin-4-GFP during 300 s after photobleaching (large data set). Depicted are normalized fluorescence intensities within the bleached cortex region . Recovery curves were averaged and fitted with an exponential recovery with two timescales (black dashed lines; see Materials and Methods). Red and blue shaded regions indicate the respective standard error of the mean for each condition. (g) Decay of the bleached fraction reveals different timescales of relaxations of recovery dynamics (same data as f). Note the logarithmic y axis. (h–j) Distribution of parameters from fitting individual recovery curves with a double-exponential function including a fast and a slow recovery timescale corresponding to data in (f). (h) Distributions of fitted fast recovery times τf are not significantly different in control and tension-reduced conditions (p-value: 0.56). (i) Slow recovery times τs are significantly larger in tension-reduced conditions. (j) Distributions of the amplitude Af of the slow recovering fraction are not significantly changed by cortical tension reduction (p-value: 0.55) (measurements are representative for at least two independent experiments. n.s., p > 0.05; ∗p < 0.05, ∗∗p < 0.01, ∗∗∗p < 0.001). To see this figure in color, go online.
If the fast recovery time τf is associated with heterodimer recovery and the slow recovery time τs with homodimer recovery, the ratio (1 − Af)/Af is expected to increase with the fluorescence intensity of the cell by the following proportionalities:
where and are the cortical concentration of homodimers or heterodimers, chom and chet are the cell-averaged concentrations of homo- and heterodimers, Nmut and NWT are the number of mutant and wild-type α-actinin-4 proteins in the cell, and I is the fluorescence intensity of the cell. This proportionality is confirmed by a significant positive correlation between and absolute cortical fluorescence intensities of cells (Fig. S7).
FRAP in adherent cells
To monitor the turnover of adherent labeled Actn4-EGFP cells, we imaged the cells in a time series using a Zeiss LSM700 confocal microscope of the CMCB light microscopy facility with a Zeiss C-Apochromat 40×/1.2 water objective. At the beginning of the time series, a small region of the stress fiber was photobleached. Afterwards, the GFP fluorescence was recorded for a total time span of 140 s at a time interval of 3 s. Fiji was used for obtaining the intensity profiles of the bleached regions. Averaged fluorescence of the bleached region was then calculated. When necessary, translational motion of the cells during FRAP recovery was removed from the series by the TemplateMatching plugin of Fiji before analysis. Intensity normalization and exponential fitting of recovery curves was performed as described above. We did not correct intensities for bleaching.
Results
Mathematical model of tension-dependent cross-linker binding dynamics
We adapt a coarse-grained description of cross-linker dynamics developed by Mulla et al. (14) that allows us to connect the ensemble-averaged lifetime of a cross-linking protein at the cortex with the lifetime of its cross-linking state. We formally extend the model to include the change of cross-linking lifetimes under mechanical loading. A similar approach has been pursued by Schiffhauer et al. and Kee et al. considering also spatial heterogeneities and diffusion (7,8).
The model includes the dynamic exchange of three populations of cross-linker protein homodimers: 1) a well-stirred cytoplasmic population ccyt(t), 2) homodimers bound at the cortex with a single ABD csb(x,t) (experiencing no mechanical loading), and 3) homodimers bound with two ABDs ccl(x,t) (cross-linking state) (see Fig. 1). Populations csb(x,t) and ccl(x,t) are bound to the cortex and contribute to the fluorescence signal during FRAP measurements. The defining equations of homodimer dynamics are
| (4) |
where Scell and Vcell are the cell surface area and the cell volume, respectively, and denotes the integration of csb over the cell surface. The attachment rate kon characterizes the binding rate of an ABD inside cytosolic homodimers to the actin cortex. The attachment rate kon,2 characterizes the rate of actin binding of the second ABD of a homodimer that is already bound via one ABD. Furthermore, the rate koff(σ) describes the average rate of unbinding of one ABD of a cross-linking homodimer at a mean-field cortical tension of σ. At steady state, the fraction of cortical proteins Fcor(σ) = Ncor/Ntot takes the following form:
| (5) |
where Ncor = (ccl + csb)Scell is the number of cortex-associated homodimers, Ntot = Ncor + Ncyt is the overall number of homodimers, and Ncyt = ccytVcell is the number of cytoplasmic homodimers. The ratio R(σ) = Ncor/Ncyt of cortical/cytoplasmic homodimers is given by
| (6) |
Figure 1.
Schematic of actin cross-linker binding dynamics according to our model. (a) Cytoplasmic (well-stirred) homodimers bind with a rate kon to cortical actin filaments. (b) Homodimers bound via a single ABD either detach from actin filaments at a rate koff(0) or attach via the second ABD with a rate kon,2. (c) Cross-linking homodimers may detach at either binding site with a rate koff(σ), where σ is the mean-field mechanical tension in the actin cortex. To see this figure in color, go online.
In the sequel of this manuscript, we will assume a simple catch-bond behavior of the cross-linker with a linear tension dependence of cross-linking lifetime
| (7) |
This approach can be considered as a Taylor expansion up to the first order of the tension dependence of cross-linker lifetime.
From Eq. 4, we determined the average residence time of a homodimer at the cortex by calculating the time evolution of the probability of a freshly bound homodimer to remain in a single-bound state or a cross-linking state at the cortex. Let psb(t) and pcl(t) denote these probabilities, with psb(0) = 1 and pcl(0) = 0. Then, they evolve in time according to
| (8) |
This set of equations can be solved analytically as
| (9) |
where
| (10) |
and
| (11) |
Solutions for different parameter sets are presented in Fig. 2, a–c, leftmost panels. The dynamics exhibits a slowest relaxation timescale τdet = kdet(σ)−1. This timescale constitutes an approximation to the residence time at the cortex and characterizes the slowest timescale in the recovery after photobleaching (see Fig. 2, a–c, rightmost panels, black dashed lines). In the following, we will refer to kdet(σ)−1 as cortical residence time. In fact, the cortical dynamics can be approximated by a simple reaction kinetics of the kind
| (12) |
where ccor captures the concentration of all homodimers at the cortex (regardless of whether they are single bound or cross-linking). Here, the condition of equal steady-state concentrations at the cortex and in the cytoplasm is used to determine the effective attachment rate
| (13) |
The recovery dynamics of the corresponding simplified reaction kinetics after bleaching is illustrated in Fig. 2, a–c, rightmost panels (black dashed lines). It approximates the full homodimer dynamics closely if either the population of single-bound homodimers or of cross-linking homodimers dominates at the cortex. The latter scenario is realized in the model dynamics in Fig. 2 a. In general, our model predicts that kdet(σ)−1 captures the slowest timescale in recovery of cortical α-actinin-4 fluorescence after photobleaching. It is noteworthy that both the attachment and detachment rates of the simplified reaction kinetics depend now on cortical tension (Fig. 2 f), which is in contrast to the full model.
Our analysis shows that a catch- or slip-bond behavior of a cytoskeletal homodimer is qualitatively reflected in the tension dependence of cortical residence time of the homodimer (see Fig. 2, a–c, central panels). However, cortical residence times kdet(σ)−1 can be smaller or larger than cross-linking lifetimes koff(σ)−1. Furthermore, the slopes of their respective tension dependences may be distinct from each other (see Fig. 2, a–c, central panels). The cortical residence time strongly exceeds the cross-linking lifetime if the fraction of cross-linking homodimers is substantial (see Fig. 2 a, central panel). In this case, homodimers undergo on average several cycles of rebinding from the single-bound to the cross-linking state before they go back into the cytoplasm. By contrast, the average cortical residence time may also be smaller than the average cross-linking lifetime (see Fig. 2 b, central panel). In this case, we have a substantial fraction of single-bound homodimers at the cortex that never go into the cross-linking state but instead drop off quickly into the cytoplasm, thereby bringing down the average cortical residence time. Corresponding to an increased cortical residence time, our model predicts an increased cortex-bound fraction of homodimers at higher cortical tension in the case of catch-bond dynamics (see Fig. 2 g).
It is noteworthy that all four model parameters (kon, kon,2, koff(0), and α) can be determined if the effective detachment rate kdet and fraction of cortically bound homodimers Fcor have been determined for two different known values of cortical tension σ1 and σ2. In this case, the four expressions for Fcor(σ1), Fcor(σ2), kdet(σ1), and kdet(σ2), as given by Eqs. 5 and 10, respectively, can be numerically inverted to obtain the four unknown model parameters.
Experimental results
We now want to use our theoretical insight to extract the cross-linking lifetime of α-actinin-4 from the cortical residence time in the actin cortex of live cells. As a cellular model system, we utilized HeLa cells expressing a fluorescently labeled α-actinin-4 construct (see Materials and Methods). Measured cells were arrested in mitosis to take advantage of the adoption of a well-defined cell-cycle stage and of a round, deadhered cell shape with a largely uniform actin cortex. Further, we and others reported a particularly high active cortical tension in mitosis (11,21,22), which allows us to explore a large cortex tension range in combination with tension-inhibiting drugs. At the beginning of the experiment, cells cultured in a glass-bottomed petri dish were mounted on a confocal microscope in combination with an atomic force microscope (Fig. 3 a, Materials and Methods). We used this setup to quantify the cortical residence time of fluorescent α-actinin-4 by photobleaching and imaging of subsequent fluorescence recovery at the cortex (Fig. 3 b, Materials and Methods). A characteristic timescale τ of the recovery was determined by a fit of the recovering fluorescence intensity with a simple exponential function A(1 − exp(−t/τ)) + B. This timescale was identified with the cortical residence time of α-actinin-4 at the cortex (Materials and Methods). During FRAP measurements, the cell under consideration was confined via the wedged cantilever of an atomic force microscope. In this way, a time series of the AFM force and the cell height was recorded (Materials and Methods) (11,12). An exemplary readout is shown in Fig. 3 c. We previously showed that large cell surface tension in mitosis drives cells into droplet shapes with constant mean curvature in mechanical confinement. Using the previously developed analysis scheme for such droplet-shaped cells, we could determine cortical tension of measured cells from the corresponding AFM readout and cellular imaging (11,12,20,23).
We first investigated a HeLa cell line with GFP-labeled α-actinin-4 (Actn4-EGFP). Corresponding averaged normalized fluorescence recovery curves are presented in Fig. 3 d (blue curve: control conditions, N = 36; red curve: tension-reduced condition, N = 31, para-nitroblebbistatin 10 μM). Fluorescence intensities were normalized before averaging as described in Materials and Methods. Fitting an exponential function, we find recovery times of τ1 = 21.3 s and τ2 = 13 s in control and tension-reduced conditions, respectively. In addition, we fit the recovery curve for each cell individually and find median recovery timescales that are in close correspondence with timescales obtained from averaged recoveries (Fig. 3 e). Median values of active cortical tension in control and tension-reduced conditions were σ1 = 2.3 mN/m and σ2 = 0.43 mN/m, respectively (Fig. 3 g). According to our model, cortical recovery times τ correspond to kdet(σ)−1. Thus, the model predicts an increased cortical residence time at higher tension (Fig. 2, a–c, central panels). This prediction is confirmed by our experimental observations (Fig. 3 e). Further in agreement with our model predictions, we measured decreased actin binding in tension-reduced conditions; we found median values of the fraction of cortical α-actinin-4 to be 0.28 in control conditions and 0.19 in tension-reduced conditions, respectively (Fig. 3 f).
To rule out the possibility that the observed tension-related change in cortical binding affinity is triggered indirectly by tension-induced permeability changes of mechanosensitive ion channels, we measured the cortical fraction of α-actinin-4 in the presence of inhibitors of stretch-activated ion channels (gadolinium chloride 25 μM, GsMTx4 5 μM) (24,25). We found the same trend of reduced cortical α-actinin-4 in tension-reduced conditions that we observed without inhibitors (Fig. S3). Furthermore, chelation of calcium ions in the cell culture medium through 1,2-Bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid (BAPTA: 50 μM) also preserved the phenotype of reduced cortical affinity in tension-reduced conditions (Fig. S3; (26)). Taken together, these findings indicate that ion channel permeability and ion fluxes play no major role in observed changes of cortex association of α-actinin-4.
Furthermore, in a complementary experiment, we also performed FRAP on Actn4-GFP in stress fibers of adherent interphase cells. Indeed, we found the same trend of faster recovery upon pharmacological tension reduction as in the mitotic cortex (Fig. S4).
To test how mechanical tension influences the actin-binding dynamics of α-actinin-4 in the mitotic cortex, we modified mechanical tension over time in the actin cortex of individual cells while jointly monitoring the fraction of cortex-bound protein. According to our model, a catch-bond dynamics of α-actinin-4 would give rise to an increase of cortex-bound protein when cortical tension increases (Fig. 2 g). We manipulated cortical tension in individual cells in two different ways: 1) by inducing additional cortical tension via mechanically dilating the actin cortex through external perturbation (Fig. 4) or 2) by pharmacologically increasing active mechanical tension in the actin cortex by photo-deactivation of the myosin inhibitor blebbistatin (Fig. 5).
We will first discuss the effect of increase of cortical tension by cortex dilation through external perturbation. Cortical dilation was achieved by applying a step of cell squishing using the wedged cantilever of an atomic force microscope (Fig. 4 a, Materials and Methods). We showed previously that confined mitotic cells adopt droplet shapes at a cell volume that is largely independent of cell height (11). Consequently, cell surface area must increase if cells are squished. Compression steps in our experiment reduced cell height by 3–5 μm at a speed of 0.5 μm/s. The corresponding cell surface increase can be estimated to be between 6.5 and 15% at typical cell volumes (11). To avoid cell blebbing upon cell squishing, cells were treated with the ROCK inhibitor Y27632 (5 μM), which leads to a reduction of myosin activity and slowed viscoelastic relaxation of stresses after cortex dilation (12,27). During cantilever lowering over the cell, the measured AFM force quickly rises. Once the cantilever comes to a halt, the force relaxes to a new steady state within a time interval of ∼100 s, indicating the viscoelastic relaxation of deformation-induced cortical mechanical tension over time (Fig. 4 b). We monitored the time evolution of the intensity ratio of cortical/cytoplasmic fluorescence, starting from the moment at which the cantilever came to a halt until mechanical tension had been relaxed. We calculated averaged values of normalized fluorescence ratio for 10 cells (red curve, Fig. 4 d) jointly with averaged tension evolution (gray curve, Fig. 4 d). We see an intermediate peak in the averaged cortex/cytoplasm ratio of fluorescence at a time t ≈ 30 s after the uniaxial compression step (see Materials and Methods). This peak is followed by a relaxation to a new elevated steady-state value. A fit of our model that conforms with measured FRAP recovery times and cortical fractions (Fig. 3, d–f) can account for our observation (Fig. 4 e, black dashed line, model parameters given in Table 1, second row); the intermediate concentration rise stems from the transient peak in cortical tension and a corresponding transient dip in detachment rate koff(σ). Furthermore, the elevated final steady state originates from an increase in the surface/volume ratio during cell squishing and the adoption of a corresponding new equilibrium state of the dynamic system given by Eq. 4.
We wanted to test whether the activity of stretch-sensitive ion channels plays a role for the observed cortex association peak after cell squishing. To this end, we repeated the squishing experiment in the presence of 25 μM gadolinium chloride, an inhibitor of stretch-sensitive ion channels (Fig. S5). We find that the cortex association peak of α-actinin-4 persists under these conditions, rendering the scenario of a causative involvement of tension-induced ion fluxes as unlikely.
As an alternative method to test the tension dependence of α-actinin-4 in single cells, we used the possibility to increase active cortical tension in the cortex of single cells through optical manipulation of the myosin inhibitor blebbistatin (11,12,22). When exposed to blue light, blebbistatin becomes inactive and ceases to reduce myosin activity which gives rise to a boost in myosin activity and cortical tension (12,16). In the following, we will refer to this effect as indirect photoactivation of myosin. To employ indirect photoactivation, we generated a HeLa cell line expressing an mKate2-labeled construct of Actn4 (Materials and Methods) whose fluorescence excitation is not in the range of blue light (28). In turn, for this cell line, fluorescent imaging of Actn4-mKate2 does not affect blebbistatin activity (29).
We first characterized cortical residence time of mKate2-labeled α-actinin-4 by FRAP measurements (Fig. 5, a and b). We find qualitatively analogous results to the GFP-labeled cell line, i.e., cortical residence times and affinity to cortical actin are larger at conditions of high cortical tension (Fig. 5, a–d). Interestingly, we observe significantly longer cortical residence times than for the GFP-labeled construct. We speculate that C-terminal tagging of α-actinin-4 might interfere with C-terminally located Ca2+ binding. This could in turn modify the actin affinity of the α-actinin-4 homodimer in a fluorophore-dependent manner (9).
In a next step, we carried out experiments in which cortical tension was dynamically varied by indirect photoactivation of myosin. To this end, we mechanically confined mitotic cells with the AFM cantilever in the presence of a low dose of blebbistatin in the medium (2.5 μM). During steady confinement, we started a time series of confocal imaging of the equatorial cross section of the cell accompanied by a time series readout of AFM force and cantilever height. After recording 5–10 initial frames in a state of inhibited myosin and reduced cortical tension, we laser scanned the cell for ∼10 s with blue light (see Materials and Methods) and then continued the time series of confocal imaging. The blue light exposure leads to a quick rise of AFM force due to inactivation of blebbistatin in the cell, reflecting an increase of cortical tension by ∼4-fold (Fig. 5, e and f). Over time, active blebbistatin reenters the cell, and cortical tension slowly drops over a time span of 10–20 min. We performed an image analysis of the accompanying confocal time series of the cortical and cytoplasmic α-actinin-4 population and calculated the cortex/cytoplasm ratio of fluorescence intensity (Fig. 5 f, red curve; see Materials and Methods). We find, on average, a trend of a delayed rise of this intensity ratio, indicating a transient increase of α-actinin-4 actin-binding affinity. Our model can account for this observation in terms of the transient tension rise of cortical tension in combination with a catch-bond-binding of α-actinin-4. A corresponding fit of predicted model dynamics is shown in Fig. 5 g (black dashed line).
Finally, using our experimental results in conjunction with our modeling insights, we estimated model parameters for each cell line under consideration (Table 1). Recovery times τ from averaged FRAP recovery curves (Fig. 3 d) and median cortical fractions in control and tension-reduced conditions (Fig. 3 f) were identified with and according to Eqs. 5 and 10 (see Materials and Methods). Numerical inversion then gives an estimate of model parameters kon, kon,2, koff(0), and α (Fig. 6, green analysis pathway, parameter α quantifies the tension dependence of the unbinding rate koff; see Eq. 7). Furthermore, we used a more elaborate analysis scheme in which we employed additional information about the cortex/cytoplasm ratio in dependence of time-dynamic cortical tension σ(t) from either cell-squishing experiments or experiments with indirect photoactivation of myosin (Fig. 6, brown analysis pathway). For the simple green analysis scheme, we find significant error bars for estimated model parameters. In particular, parameter kon,2 must essentially be regarded as undetermined because of errors in the range of 100% and beyond. Also, for parameters koff(0) and α, the green analysis allows only for an order of magnitude estimate. For the brown analysis pathway, error bars are reduced because of the larger set of experimental data fed into the fitting algorithm (Fig. 6). Thus, meaningful estimates can be obtained for all model parameters. Deviations of model parameters between the two analysis pathways can be accounted for by estimated numerical uncertainties. It is noteworthy that our parameter fitting predicts a substantially higher unbinding rate koff(0) for the GFP-labeled protein as compared with the mKate2-labeled construct, which accounts for the lower fraction of cortical Actn4-GFP as compared to Actn4-mKate2 (Figs. 3 f and 5 c). This finding might indicate that unbinding rates are affected by C-terminal tagging of α-actinin-4. Most importantly, we find positive slopes of the tension dependence of the cross-linking time for both α-actinin-4 constructs with slope values ranging between 0.4 and 0.95 mN/m, indicating catch-bond behavior of α-actinin-4-actin bonds. Within physiological ranges of mean-field cortical tension of 0–2 mN/m, these slopes put forward a substantial change of α-actinin-4 cross-linking time by a factor between 1.8 and 2.9.
We were interested in whether the catch-bond tension dependence of α-actinin-4 binding dynamics would be kept in the K255E mutant. The disease-causing mutant K255E of human α-actinin-4 has one amino acid of the protein exchanged and exhibits a higher actin-binding affinity than wild-type α-actinin-4 (9,10,30). Previous studies reported that this mutant is insensitive to Ca2+ regulation (9). Correspondingly, it has been suggested that the K255E mutant of α-actinin-4 adopts an open conformation that exposes the additional actin binding site of α-actinin-4 outside the ABD and thereby mediates enhanced actin-binding affinity. In turn, observations of a lack of a significant mechanosensitive response in the K255E mutant have been reported (7).
To investigate the tension dependence of the K255E mutant further, we transfected HeLa Kyoto cells with a plasmid expressing the GFP-labeled K255E mutant and performed analogous FRAP and AFM measurements (Fig. 7; Fig. S6). Consistent with previous observations (7), we observed fluorescence recoveries of the mutant protein that were substantially slower than that of the wild-type constructs (Fig. 7 a). Further, in accordance with previously reported increased actin-binding affinity of the K255E mutant (9), we observed now elevated fractions of cortical α-actinin-4 in the mutant as compared with the wild-type (Fig. 7 d vs. Figs. 3 f and 5 c). Also different from wild-type α-actinin-4, pharmacological reduction of cortical tension did not result in diminished cortical association of the K255E mutant (Fig. 7 d). Furthermore, recovery in tension-reduced conditions was slower than in control conditions, as reflected by a significantly larger half time of fluorescence recovery (Fig. 7 a, control: t1/2 ≈ 300 s, tension-reduced: t1/2 ≈ 710 s). Fitting of exponential recovery curves gave recovery timescales τ that did not change significantly upon pharmacological reduction of cortical tension (Fig. 7 b). However, the corresponding fitted fraction of recovering fluorescence was significantly lower in tension-reduced conditions (Fig. 7 c). This finding puts forward the presence of a subpopulation of α-actinin-4 dimers that turns over very slowly, the fraction of which is enhanced when cortical tension is diminished.
To take into account the presence of several timescales in fluorescence recovery, we recorded a larger data set of mutant α-actinin-4 FRAP data focusing on the first 300 s of fluorescence recovery (Fig. 7, f–j). We find that fluorescence recovery of averaged curves is well captured by a double-exponential recovery of the form 1 − (Af exp(−t/τf) + (1 − Af)exp(−t/τs))B, where τf denotes a fast recovery timescale smaller than 100 s and τs a long recovery timescale >100 s (Fig. 7 f). Systematic fitting of individual recovery curves yields parameter distributions as presented in Fig. 7, h–j; we observed no significant differences upon tension reduction in the fast recovering timescale τf and in the fraction of fast fluorescence recovery Af (Fig. 7, h and j). By contrast, the slow recovery timescale τs was significantly enlarged upon pharmacological tension reduction (Fig. 7 i).
We conjecture that the existence of two recovery timescales is associated with two distinct fluorescent α-actinin-4 dimers that are expected to be present in the cell: 1) heterodimers that form by dimerization of one (nonfluorescent) endogenous α-actinin-4 and one K255E mutant α-actinin-4 as well as 2) homodimers that form by dimerization of two fluorescent mutant proteins. Because the K255E mutant of α-actinin-4 has significantly higher actin-binding affinity (9), mutant homodimers are expected to exhibit a longer cross-linking time and a slower photobleaching recovery time than heterodimers. Therefore, mutant homodimers are likely associated with recovery timescale τs.
In support of this interpretation scheme, we observed that the ratio of slow/fast recovering fractions (1 − Af)/Af increases with the fluorescence intensity of the cortex. For this ratio, we found an average value of 3.6 (Fig. S7; see Materials and Methods for a derivation). Furthermore, we performed a Western blot quantifying relative amounts of endogenous protein to mutant protein as 1:0.7 averaged over the entire cell population (Fig. S8, second column). Because the fraction of transfected (fluorescent) cells was ∼27%, the average ratio of endogenous protein/K255E mutant protein was approximated as 1:2.6 in transfected cells. We thus estimate the intensity contribution of the mutant homodimers to be 2.6 times higher than the intensity contribution of the heterodimers. This value is reasonably close to our estimate of 3.6 of the slow versus fast recovering intensity fraction (1 − Af)/Af (Fig. S7). The discrepancy in numbers could originate from higher cortex affinity of mutant homodimers and a corresponding cortical overrepresentation of mutant protein.
According to our model, an increase of FRAP recovery time τs upon tension reduction in the actin cortex indicates a slip-bond behavior of mutant homodimers in actin cross-linking (Fig. 7 i). In conclusion, our experimental observations of the K255E mutant of α-actinin-4 hint not only at a loss of the wild-type catch-bond properties of α-actinin-4 but also at a trend reversal of the tension-dependent unbinding rate, i.e., slip-bond behavior.
Discussion
In this study, we present a, to our knowledge, new technique that allows us to quantify the dependence of actin cross-linker binding on mechanical tension (contractility) in the actin cortex of mitotic cells. Therefore, our approach permits us to characterize bonds of actin cross-linkers to be of the slip- or catch-bond type (or tension insensitive) in a physiological range of active tensions in the cellular cortex. As part of our assay, we performed FRAP experiments on fluorescently labeled cross-linker proteins in round mitotic cells in combination with AFM-based cell confinement and a mean-field mathematical model of cross-linker binding dynamics. We applied this technique in an exemplary manner to characterize the binding dynamics of the actin cross-linker α-actinin-4, which is the most abundant actin cross-linker in HeLa cells (31).
In terms of our mathematical model, we could connect cross-linking lifetime of a cross-linker molecule to its overall residence time at the cortex. We showed that there is a qualitative correspondence between the tension dependence of cross-linking lifetime and cortical residence time; if cross-linking lifetime increases in dependence of cortical tension, cortical residence time also increases (catch-bond scenario). On the other hand, if cross-linking time decreases in dependence of tension, our model predicts a corresponding decrease of cortical residence time (slip-bond scenario). However, the respective magnitude of the slopes may differ between cross-linking lifetime and cortical residence time (Fig. 2, a–c, central panels).
We recorded experimental data of FRAP-derived cortical residence times of α-actinin-4 in dependence of cortical tension and used our theoretical derivations to obtain associated actin-binding and unbinding rates of α-actinin-4 (Table 1). We predict intracellular values of the unbinding rate koff(0) ranging between 0.027 and 0.11 s−1 (brown analysis pathway). Interestingly, these unbinding rates are reasonably close to unbinding rates reported for skeletal muscle α-actinin from in vitro experiments with optical tweezers ((32): koff = 0.07 s−1, (33): koff = 0.05 s−1). Furthermore, in combination with insight from our mathematical model, our measurements put forward that cross-linking lifetimes and cross-linking concentrations of wild-type α-actinin-4 increase by a factor of 2–3 within a physiological tension range of cortical tension of 0.1–2 mN/m (Fig. 2, b and c, central panels and Fig. 2 g; (11,12,21,34)). For our measurements with the K255E mutant of α-actinin-4, signatures of catch-bond binding as predicted by our model (higher cortical association and longer cortical residence times at higher cortical tension) were missing. In fact, the observed phenotype of slower FRAP recovery at reduced cortical tension points at a slip-bond behavior of the mutant protein. Taken together, all our findings strongly support the hypothesis that α-actinin-4 acts as a catch-bond cross-linker of F-actin in cells. We cannot, however, at this stage entirely rule out that mechanical tension changes the cortical affinity of α-actinin-4 through secondary effects such as tension-induced structural changes in the actin cortex.
For experimental convenience, we characterized in this study the tension dependence of α-actinin-4 unbinding in the actin cortex of mitotic cells. However, we expect that the same kind of tension-dependent unbinding of α-actinin-4 is at work in stress fibers and focal adhesions. This is supported by our complementary photobleaching experiments on stress fibers of adherent cells (Fig. S4). We conjecture that α-actinin-4 catch bonding might further contribute to reinforcement of focal adhesions and stress fibers at high tension (1,35, 36, 37, 38).
We wondered about the biological function of α-actinin’s catch-bond binding in the actin cortex. First, catch bonding of cross-linkers ensures increased actin network connectivity at higher mechanical tension through increased cross-linker concentration. Previous theoretical and experimental work put forward that growing connectivity is a requirement for active polymer networks to maintain material integrity and mechanical rigidity at growing motor activity (39, 40, 41). Furthermore, catch bonding may assist the generation of high cortical tension in such conditions (42). Therefore, we speculate that tension-increased connectivity of the actin cortex through cross-linker catch bonding assists proper actin cortex function and integrity in the presence of high motor activity. Secondly, cross-linker concentration is a parameter that regulates the mechanical parameters of cross-linked biopolymer networks; the shear stiffness of polymer networks depends sensitively on cross-linker concentration (43, 44, 45). Furthermore, cross-linking lifetime was shown to introduce characteristic timescales into the viscoelastic relaxation of a cross-linked biopolymer network because cross-linker unbinding gives rise to local stress releases (14,46). In particular, catch bonding of actin cross-linkers promotes increased cortical stiffness and a prolonged shape memory (more solid-like nature) of the actin cortex at higher cortical tension (43,46). These changes of material properties may further assist cortical function at high tension.
In summary, the approach presented here allows us to systematically study the tension dependence of actin cross-linker binding in the actin cortex of live cells. We believe that this technique can make a key contribution to our understanding of nonlinear cytoskeletal mechanics and cytoskeletal force generation.
Author Contributions
E.F.-F. designed the research. K.H. and E.F.-F. performed experiments and data analysis. L.S. and E.F.-F. developed MATLAB scripts for image and data analysis. E.F.-F. developed the theoretical underpinning for data analysis and performed numerical simulations. I.P. generated cell lines from BACs. K.H. and E.F.-F. wrote the manuscript.
Acknowledgments
We thank William Brieher for provision of a plasmid expressing ACTN4K255E-GFP. Further, we thank Anthony Hyman for provision of transgenic HeLa cell lines. In addition, we thank the CMCB light microscopy facility for excellent support.
E.F.-F. acknowledges financial support from the Deutsche Forschungsgemeinschaft, project FI 2260/4-1. K.H. and E.F.-F. were further supported by the Deutsche Forschungsgemeinschaft under Germany’s Excellence Strategy, EXC-2068-390729961, Cluster of Excellence Physics of Life of TU Dresden.
Editor: Kathleen Trybus.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.07.031.
Supporting Material
References
- 1.Iskratsch T., Wolfenson H., Sheetz M.P. Appreciating force and shape—the rise of mechanotransduction in cell biology. Nat. Rev. Mol. Cell Biol. 2014;15:825–833. doi: 10.1038/nrm3903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Geiger B., Spatz J.P., Bershadsky A.D. Environmental sensing through focal adhesions. Nat. Rev. Mol. Cell Biol. 2009;10:21–33. doi: 10.1038/nrm2593. [DOI] [PubMed] [Google Scholar]
- 3.Bendix P.M., Koenderink G.H., Weitz D.A. A quantitative analysis of contractility in active cytoskeletal protein networks. Biophys. J. 2008;94:3126–3136. doi: 10.1529/biophysj.107.117960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rivero F., Köppel B., Noegel A.A. The role of the cortical cytoskeleton: F-actin crosslinking proteins protect against osmotic stress, ensure cell size, cell shape and motility, and contribute to phagocytosis and development. J. Cell Sci. 1996;109:2679–2691. doi: 10.1242/jcs.109.11.2679. [DOI] [PubMed] [Google Scholar]
- 5.Thomas W.E., Vogel V., Sokurenko E. Biophysics of catch bonds. Annu. Rev. Biophys. 2008;37:399–416. doi: 10.1146/annurev.biophys.37.032807.125804. [DOI] [PubMed] [Google Scholar]
- 6.Yao N.Y., Broedersz C.P., Weitz D.A. Stress-enhanced gelation: a dynamic nonlinearity of elasticity. Phys. Rev. Lett. 2013;110:018103. doi: 10.1103/PhysRevLett.110.018103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Schiffhauer E.S., Luo T., Robinson D.N. Mechanoaccumulative elements of the mammalian actin cytoskeleton. Curr. Biol. 2016;26:1473–1479. doi: 10.1016/j.cub.2016.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Luo T., Mohan K., Robinson D.N. Molecular mechanisms of cellular mechanosensing. Nat. Mater. 2013;12:1064–1071. doi: 10.1038/nmat3772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Weins A., Schlondorff J.S., Pollak M.R. Disease-associated mutant α-actinin-4 reveals a mechanism for regulating its F-actin-binding affinity. Proc. Natl. Acad. Sci. USA. 2007;104:16080–16085. doi: 10.1073/pnas.0702451104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Thomas D.G., Robinson D.N. The fifth sense: mechanosensory regulation of α-actinin-4 and its relevance for cancer metastasis. Semin. Cell Dev. Biol. 2017;71:68–74. doi: 10.1016/j.semcdb.2017.05.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fischer-Friedrich E., Hyman A.A., Helenius J. Quantification of surface tension and internal pressure generated by single mitotic cells. Sci. Rep. 2014;4:6213. doi: 10.1038/srep06213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fischer-Friedrich E., Toyoda Y., Jülicher F. Rheology of the active cell cortex in mitosis. Biophys. J. 2016;111:589–600. doi: 10.1016/j.bpj.2016.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yoneda M. Tension at the surface of sea-urchin egg: a critical examination of Cole’s experiment. J. Exp. Biol. 1964;41:893–906. doi: 10.1242/jeb.41.4.893. [DOI] [PubMed] [Google Scholar]
- 14.Mulla Y., Wierenga H., Koenderink G.H. Frustrated binding of biopolymer crosslinkers. Soft Matter. 2019;15:3036–3042. doi: 10.1039/c8sm02429d. [DOI] [PubMed] [Google Scholar]
- 15.Skoufias D.A., DeBonis S., Kozielski F. S-trityl-L-cysteine is a reversible, tight binding inhibitor of the human kinesin Eg5 that specifically blocks mitotic progression. J. Biol. Chem. 2006;281:17559–17569. doi: 10.1074/jbc.M511735200. [DOI] [PubMed] [Google Scholar]
- 16.Sakamoto T., Limouze J., Sellers J.R. Blebbistatin, a myosin II inhibitor, is photoinactivated by blue light. Biochemistry. 2005;44:584–588. doi: 10.1021/bi0483357. [DOI] [PubMed] [Google Scholar]
- 17.Kemp J.P., Jr., Brieher W.M. The actin filament bundling protein α-actinin-4 actually suppresses actin stress fibers by permitting actin turnover. J. Biol. Chem. 2018;293:14520–14533. doi: 10.1074/jbc.RA118.004345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Poser I., Sarov M., Hyman A.A. BAC transgeneOmics: a high-throughput method for exploration of protein function in mammals. Nat. Methods. 2008;5:409–415. doi: 10.1038/nmeth.1199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Stewart M.P., Hodel A.W., Helenius J. Wedged AFM-cantilevers for parallel plate cell mechanics. Methods. 2013;60:186–194. doi: 10.1016/j.ymeth.2013.02.015. [DOI] [PubMed] [Google Scholar]
- 20.Hosseini K., Taubenberger A., Fischer-Friedrich E. EMT-induced cell mechanical changes enhance mitotic rounding strength. bioRxiv. 2019 doi: 10.1101/598052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chugh P., Clark A.G., Paluch E.K. Actin cortex architecture regulates cell surface tension. Nat. Cell Biol. 2017;19:689–697. doi: 10.1038/ncb3525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Stewart M.P., Helenius J., Hyman A.A. Hydrostatic pressure and the actomyosin cortex drive mitotic cell rounding. Nature. 2011;469:226–230. doi: 10.1038/nature09642. [DOI] [PubMed] [Google Scholar]
- 23.Mokbel M., Hosseini K., Fischer-Friedrich E. The poisson ratio of the cellular actin cortex is frequency dependent. Biophys. J. 2020;118:1968–1976. doi: 10.1016/j.bpj.2020.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Matthews B.D., Overby D.R., Ingber D.E. Cellular adaptation to mechanical stress: role of integrins, Rho, cytoskeletal tension and mechanosensitive ion channels. J. Cell Sci. 2006;119:508–518. doi: 10.1242/jcs.02760. [DOI] [PubMed] [Google Scholar]
- 25.Han Y., Liu C., Jia Z. Mechanosensitive ion channel Piezo1 promotes prostate cancer development through the activation of the Akt/mTOR pathway and acceleration of cell cycle. Int. J. Oncol. 2019;55:629–644. doi: 10.3892/ijo.2019.4839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ricci A.J., Wu Y.C., Fettiplace R. The endogenous calcium buffer and the time course of transducer adaptation in auditory hair cells. J. Neurosci. 1998;18:8261–8277. doi: 10.1523/JNEUROSCI.18-20-08261.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ramanathan S.P., Helenius J., Müller D.J. Cdk1-dependent mitotic enrichment of cortical myosin II promotes cell rounding against confinement. Nat. Cell Biol. 2015;17:148–159. doi: 10.1038/ncb3098. [DOI] [PubMed] [Google Scholar]
- 28.Shcherbo D., Merzlyak E.M., Chudakov D.M. Bright far-red fluorescent protein for whole-body imaging. Nat. Methods. 2007;4:741–746. doi: 10.1038/nmeth1083. [DOI] [PubMed] [Google Scholar]
- 29.Kolega J. Phototoxicity and photoinactivation of blebbistatin in UV and visible light. Biochem. Biophys. Res. Commun. 2004;320:1020–1025. doi: 10.1016/j.bbrc.2004.06.045. [DOI] [PubMed] [Google Scholar]
- 30.Ward S.M.V., Weins A., Weitz D.A. Dynamic viscoelasticity of actin cross-linked with wild-type and disease-causing mutant alpha-actinin-4. Biophys. J. 2008;95:4915–4923. doi: 10.1529/biophysj.108.131722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hein M.Y., Hubner N.C., Mann M. A human interactome in three quantitative dimensions organized by stoichiometries and abundances. Cell. 2015;163:712–723. doi: 10.1016/j.cell.2015.09.053. [DOI] [PubMed] [Google Scholar]
- 32.Ferrer J.M., Lee H., Lang M.J. Measuring molecular rupture forces between single actin filaments and actin-binding proteins. Proc. Natl. Acad. Sci. USA. 2008;105:9221–9226. doi: 10.1073/pnas.0706124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Miyata H., Yasuda R., Kinosita K., Jr. Strength and lifetime of the bond between actin and skeletal muscle alpha-actinin studied with an optical trapping technique. Biochim. Biophys. Acta. 1996;1290:83–88. doi: 10.1016/0304-4165(96)00003-7. [DOI] [PubMed] [Google Scholar]
- 34.Tinevez J.-Y., Schulze U., Paluch E. Role of cortical tension in bleb growth. Proc. Natl. Acad. Sci. USA. 2009;106:18581–18586. doi: 10.1073/pnas.0903353106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Shams H., Golji J., Mofrad M.R.K. A molecular trajectory of α-actinin activation. Biophys. J. 2012;103:2050–2059. doi: 10.1016/j.bpj.2012.08.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Le S., Hu X., Yan J. Mechanotransmission and mechanosensing of human α-actinin 1. Cell Rep. 2017;21:2714–2723. doi: 10.1016/j.celrep.2017.11.040. [DOI] [PubMed] [Google Scholar]
- 37.Bershadsky A.D., Ballestrem C., Kozlov M.M. Assembly and mechanosensory function of focal adhesions: experiments and models. Eur. J. Cell Biol. 2006;85:165–173. doi: 10.1016/j.ejcb.2005.11.001. [DOI] [PubMed] [Google Scholar]
- 38.Choi C.K., Vicente-Manzanares M., Horwitz A.R. Actin and alpha-actinin orchestrate the assembly and maturation of nascent adhesions in a myosin II motor-independent manner. Nat. Cell Biol. 2008;10:1039–1050. doi: 10.1038/ncb1763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Alvarado J., Sheinman M., Koenderink G.H. Molecular motors robustly drive active gels to a critically connected state. Nat. Phys. 2013;9:591–597. [Google Scholar]
- 40.Alvarado J., Sheinman M., Koenderink G.H. Force percolation of contractile active gels. Soft Matter. 2017;13:5624–5644. doi: 10.1039/c7sm00834a. [DOI] [PubMed] [Google Scholar]
- 41.Koenderink G.H., Dogic Z., Weitz D.A. An active biopolymer network controlled by molecular motors. Proc. Natl. Acad. Sci. USA. 2009;106:15192–15197. doi: 10.1073/pnas.0903974106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ennomani H., Letort G., Blanchoin L. Architecture and connectivity govern actin network contractility. Curr. Biol. 2016;26:616–626. doi: 10.1016/j.cub.2015.12.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gardel M.L., Shin J.H., Weitz D.A. Elastic behavior of cross-linked and bundled actin networks. Science. 2004;304:1301–1305. doi: 10.1126/science.1095087. [DOI] [PubMed] [Google Scholar]
- 44.Gardel M.L., Nakamura F., Weitz D.A. Prestressed F-actin networks cross-linked by hinged filamins replicate mechanical properties of cells. Proc. Natl. Acad. Sci. USA. 2006;103:1762–1767. doi: 10.1073/pnas.0504777103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.MacKintosh F.C., Käs J., Janmey P.A. Elasticity of semiflexible biopolymer networks. Phys. Rev. Lett. 1995;75:4425–4428. doi: 10.1103/PhysRevLett.75.4425. [DOI] [PubMed] [Google Scholar]
- 46.Broedersz C.P., Depken M., MacKintosh F.C. Cross-link-governed dynamics of biopolymer networks. Phys. Rev. Lett. 2010;105:238101. doi: 10.1103/PhysRevLett.105.238101. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.