Abstract
Quantifying chemical substituent contributions to ligand-binding free energies is challenging due to nonadditive effects. Protein allostery is a frequent cause of nonadditivity, but the underlying allosteric mechanisms often remain elusive. Here, we propose a general NMR-based approach to elucidate such mechanisms and we apply it to the HCN4 ion channel, whose cAMP-binding domain is an archetypal conformational switch. Using NMR, we show that nonadditivity arises not only from concerted conformational transitions, but also from conformer-specific effects, such as steric frustration. Our results explain how affinity-reducing functional groups may lead to affinity gains if combined. Surprisingly, our approach also reveals that nonadditivity depends markedly on the receptor conformation. It is negligible for the inhibited state but highly significant for the active state, opening new opportunities to tune potency and agonism of allosteric effectors.
Significance
Understanding the allosteric mechanisms underlying the nonadditivity of substituent contributions to the free energy of protein-ligand binding is a central challenge in biophysical chemistry. Yet, a general methodology to investigate such mechanisms is still lacking, especially for inherently dynamic systems that function as allosteric switches, alternating between inhibition competent and incompetent states. As a first step toward filling this gap, here, we present an NMR-based approach to dissect the allosteric driving forces of substituent nonadditivity. When applied to the HCN4 ion channel, this approach reveals that the determinants of binding nonadditivity include not only a single concerted two-state transition, but also conformation-dependent allosteric frustration.
Introduction
Understanding how ligand substituents control the free energy of binding is a central challenge in chemistry (1, 2, 3, 4, 5). One of the simplest approaches to quantify substituent contributions to the binding free energy relies on the principle of thermodynamic additivity (6, 7, 8, 9). According to it, the ligand-binding free energy change caused by a double substitution is the sum of the changes elicited by the two single substitutions, provided that the two substituents act independently. However, substituents are often not independent and therefore the respective contributions to macromolecule-ligand-binding free energies are nonadditive (10,11). The difference between the change in binding free energy arising from a double substitution and the sum of the changes caused by the two single substitutions is the coupling free energy (Fig. 1, a and b; (8, 9, 10, 11)) and is calculated as:
| (1) |
with
| (2) |
where KAB, KS, KA, and KB are the respective association constants measured for the P:SAB, P:S, P:SA, and P:SB complexes, which define a double-ligand cycle (Fig. 1 a; (11)). Similar to the Q factor originally utilized to quantify the coupling between two different ligands (12,13), when = 1, full additivity applies (Document S1. Sections S1–S5, Figs. S1–S12, and Tables S1 and S2, Document S2. Article plus Supporting Material), whereas > 1 (<1) points to positive (negative) cooperativity between the A and B functional groups. Furthermore, if is within the [e−1, e] range, |ΔGcoupling,AB| does not exceed the thermal room temperature (RT) benchmark (∼0.6 kcal/mol) and therefore the nonadditivity is considered marginal, even when differs from unity beyond experimental uncertainty.
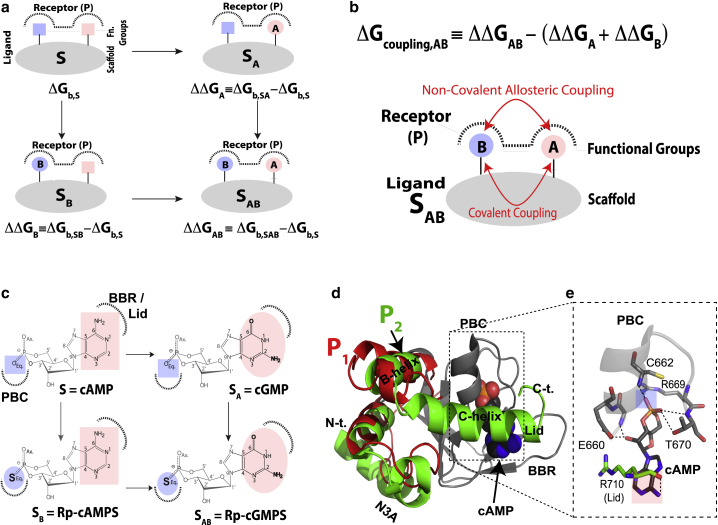
Figure 1.
Nonadditivity between two ligand substituents as defined by double-ligand cycles. (a) General double-ligand cycle for a ligand composed of a scaffold or linker S (gray) and two substituents A (pink) and B (blue). The cycle includes four protein complexes in which the receptor (P) binds either S, the single-substituted ligands (i.e. SA or SB), or the double-substituted ligand SAB. Dotted lines denote binding sites in P. ΔGb,S is the binding free energy for ligand S, whereas ΔΔGA is defined as the contribution to binding arising from substituent A in ligand SA. Similar definitions apply to SB and SAB. If modifications A and B are independent, then ΔΔGAB = ΔΔGA + ΔΔGB, which is the equation defining binding additivity (Fig. S1 a). (b) Definition of the coupling free energy between substituents A and B (ΔGcoupling,AB) and a scheme illustrating the covalent and/or noncovalent double nature of such coupling. (c) Example of the double-ligand cycle including the cyclic nucleotide monophosphates (cNMPs) cAMP, the phosphorothioate Rp-cAMPS, cGMP, and Rp-cGMPS. (d) Autoinhibitory and active conformations accessed by the cNMP-binding domain (CNBD) of HCN4 in the apo and cAMP-bound forms (PDB: 2MNG and PDB: 3OTF; denoted here as P1 and P2, respectively). The invariant β-subdomain is shown as a gray cartoon, whereas the more dynamic α-subdomain is depicted in red (apo) or green (cAMP-bound). Key structural motifs are labeled, including the phosphate-binding cassette (PBC), the base-binding region (BBR), and the N3A. (e) Expanded view of the PBC and part of the lid region of the HCN4 CNBD, highlighting key interactions of these regions with cAMP. Hydrogen bonds are shown as dashed lines. To see this figure in color, go online.
The binding free energy nonadditivity arising from the coupling between substituents A and B severely limits the accuracy of several inherently linear docking scoring functions and classical quantitative structure activity relationship models (9, 10, 11,14). Hence, understanding the mechanisms underlying the cooperativity between simultaneous ligand modifications is crucial for drug design as well as computational and structural biology.
The coupling between substituents A and B may arise covalently (e.g., inductive or electromeric “through-ligand” effects; Fig. 1 b) or as the result of noncovalent changes in the protein and/or ligand (e.g., allosteric conformational changes in the protein receptor P, changes in ligand/protein interactions and/or solvation). Although covalent couplings have been extensively investigated, less is known about the noncovalent mechanisms underlying the coupling between ligand substituents (10,11).
Structural dynamics has been hypothesized to be one of the main noncovalent determinants of substituent couplings (9). Qualitative evidence in support of this hypothesis comes primarily from the comparative analysis of crystal structure B-factors for the complexes formed by a congeneric series of thrombin inhibitors (9). However, the allosteric mechanisms at the basis of nonadditive substituent contributions to binding free energies have not been fully investigated.
Here, using NMR spectroscopy, we elucidate the allosteric mechanisms underlying substituent nonadditivity in an archetypal ligand-dependent conformational switch (15), i.e., the cyclic-nucleotide (cNMP)-binding domain (CNBD) of the hyperpolarization-activated and cNMP-gated ion channel isoform 4 (HCN4; Fig. 1, c–e). The cNMP-dependent gating of HCN4 is critical to control basal heart rates (16), and similar allosteric switches regulate signal transduction pathways and enzymatic catalysis (15,17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36).
The CNBDs adopt a conserved architecture with a contiguous and relatively rigid β-subdomain composed of an eight-stranded β-barrel, as well as a noncontiguous and dynamic α-subdomain that includes an N-terminal helical bundle, denoted as the N-terminal three-helix bundle (N3A) motif, and two C-terminal helices, referred to as B and C (Fig. 1 d; (15,37,38)). The β-subdomain includes the phosphate-binding cassette (PBC) and the base-binding region (BBR), where the cNMP docks and recruits through its base the C-helix as a lid (Fig. 1 d). The closure of the lid over the cNMP base drives a conformational change in the α-subdomain from an autoinhibitory state, in which the N3A is proximal to the β-subdomain (“N3A in” topology), to an active state, in which the N3A is displaced away from the β-barrel (“N3A out” topology).
The apo CNBD dynamically samples both autoinhibitory and active conformations, denoted here as P1 and P2 (Fig. 1 d), which interconvert in the fast exchange regime, as previously shown (15). cAMP-binding selects and stabilizes the active state (26,39), whereas cAMP analogs modulate the position of the autoinhibitory versus active P1 P2 equilibrium. Such modulations correlate with the cNMP-dependent changes in activation voltages (ΔV1/2) measured by electrophysiology for integral full-length ion channels (15). The linkage between the autoinhibitory P1 P2 and ligand-binding equilibria of the CNBD is best described by a classical four-state thermodynamic cycle, where the coupling between the two equilibria depends on the ratio between the state-specific association constants K1j and K2j (Fig. S1 b), which define the P1 vesus P2 state-selectivity of a given ligand Sj (i.e., S, SA, SB, or SAB in the double-ligand cycle of Fig. 1 a).
In the case of HCN4 investigated here, the scaffold ligand S is the endogenous allosteric effector cAMP, whereas the other ligands are built by introducing either a phosphate substitution (e.g., equatorial exocyclic oxygen to sulfur in Rp-cAMPS), a base substitution (e.g., adenine to guanine in cGMP), or a combination of the two (e.g., Rp-cGMPS; Fig. 1 c). The double-ligand cycle for HCN4 (Fig. 1 c) was utilized as a perturbation library for the chemical shift covariance analysis (CHESCA) (40,41). CHESCA takes advantage of the linear chemical shift-averaging typical of fast-exchanging equilibria, as in the case of the HCN4 CNBD P1 P2 equilibrium, and is ideally suited to map residues subject to concerted transitions modulated by a targeted ligand library (40, 41, 42, 43).
Our results for the HCN4 CNBD indicate that, although allostery is an essential driver of binding nonadditivity, the free energy of substituent coupling arises not only from the concerted inhibitory-to-active state P1 P2 transition, but unexpectedly also from the nonadditivity of state-specific binding free energies. We show that active state-specific binding is highly nonadditive because of the presence of allosteric frustration (44,45), which was further probed through molecular dynamics (MD) simulations and mutations. On the contrary, full additivity was observed for the inhibitory state-specific binding, revealing that nonadditivity is surprisingly state-dependent. The state-dependency of the free energy of substituent coupling is a key determinant of partial agonism. Overall, our investigation illustrates how it is possible to elucidate by NMR unprecedented allosteric mechanisms underlying the coupling of substituent contributions to binding free energies. The identification of the key allosteric drivers of substituent nonadditivity is expected to facilitate the constructive exploitation of intersubstituent couplings in medicinal chemistry.
Materials and Methods
Sample preparation
The HCN4 cAMP-binding domain constructs spanning residues 563–724 and 579–707 were prepared as described previously (15,46). The F689A mutants were created using a variation of the Quikchange protocol, as noted previously (46, 47, 48), and prepared similarly to the wild-type (wt) HCN4 samples. The concentration of HCN4 was determined using a Bradford assay and its purity was confirmed by SDS-PAGE. Cyclic AMP and GMP were purchased from Sigma Aldrich (ON, Canada), whereas all other cNMPs were purchased from Axxora (NY, USA). All cNMPs were prepared as 25 mM stock solutions.
Affinity measurements
Measurements of cNMP-binding affinities for HCN4 were achieved via competitive binding with the fluorescent cAMP analog, 8-NBD-cAMP, using an approach similar to the protocols described previously (49, 50, 51). The Kd of 8-NBD-cAMP for each HCN4 construct was initially determined via a titration in which the 8-NBD-cAMP concentration was fixed at 500 nM and the HCN4 construct was added at concentrations ranging from 0.1 to 50 μM. The HCN4 and 8-NBD-cAMP concentrations were then fixed at 5 μM and 500 nM, respectively, and cNMPs were added to outcompete 8-NBD-cAMP from HCN4. Fluorescence data were acquired with a BioTek Cytation Five-Plate Reader (Biotek, VT, USA) using Corning 96-well half-area plates (product no. 3881; Corning, NY, USA). The sample was excited at 485 nm and emission was recorded at 535 nm. Data was normalized relative to the fluorescence of 8-NBD-cAMP in the presence (max fluorescence) and absence (min fluorescence) of HCN4 and scaled according to the fraction of bound 8-NBD-cAMP (<v>) expected in the absence of competing ligand, determined from the equations described below. The Kd-values of the cNMPs were determined by fitting the competition curve with the following equation, as previously described by Wang (49):
where
[A]T, [B]T, and [P]T correspond to the total concentrations of the competing cNMP, 8-NBD-cAMP and HCN4, respectively, whereas and are the dissociation constants of the competing cNMP and the 8-NBD-cAMP ligands, respectively. [PB] represents the concentration of 8-NBD-cAMP bound to HCN4 and <v> defines the fraction of bound 8-NBD-cAMP.
NMR spectroscopy
NMR data were acquired on a Bruker AV 700 spectrometer (Bruker, MA, USA) equipped with a 5-mm TCI cryoprobe. All experiments were acquired at 300 K. Gradient and sensitivity enhanced HSQC spectra were acquired on 100 μM samples of HCN4 constructs with >1 mM concentrations of cNMPs and 50 μM 15N-acetyl glycine, for internal chemical shift referencing. Saturation of HCN4 was confirmed either by performing a full titration and reaching plateau or by acquiring spectra at three consecutive concentrations for which there were no significant chemical shift changes. The HSQC data were processed with NMRpipe, analyzed in Sparky and assigned via comparison with wt spectra or from chemical shift titrations. Chemical shift correlation plots were constructed as described previously (47,52), using the chemical shift difference between wt cAMP-bound and apo states as a reference (x axis) and the chemical shift difference between the perturbed state (cNMP-bound, mutant, etc.) and wt apo state for the y axis, except for the 579–707 construct. For this deletion construct, the y axis of the chemical shift correlation plot was determined from the difference between the perturbed state and the wt cAMP-bound state, as previously described (47). Only residues with an absolute cos (θ), as obtained from a CHESPA analysis, greater than 0.9 were plotted. In addition, all residues comprising the cAMP-binding pocket (i.e., BBR: 641–652; PBC: 658–672; Lid: 707–714) were removed because they sense nearest neighbor effects. The chemical shift projection analysis (CHESPA) was performed as described previously (15,46, 47, 48). The wt cAMP-bound and apo states were used as the reference vector for all analyses, whereas the perturbation vector was constructed from the difference between the perturbed state (cNMP-bound, mutant, etc.) and the wt apo state, unless otherwise stated. The cos (θ) value was only calculated for residues with a combined chemical shift difference greater than the cutoff of 0.025 ppm for the perturbation vector. Alternatively, the fractional shifts measured through the slopes of the chemical shift correlation plots are also obtained through the normalized PC1 components of the CHESCA singular value decomposition. The CHESCA and the chemical shift correlation analyses were performed as previously described (40,41), but the singular value decomposition analysis was performed using the apo chemical shifts as reference rather than those of Rp-cAMPS. This is because Rp-cAMPS is not a reverse agonist for HCN4.
The free ligand chemical shift data utilized to gauge intraligand covalent effects were acquired as follows. Each cNMP was prepared as a 5-mM sample in D2O with 5 mM of TSP. For each sample, 1D 1H, 1D 13C, 1D DEPT, and 2D {1H-13C}-HSQC spectra were acquired. The 1D 1H spectra were acquired with 32,768 complex points and a spectral width of 12 ppm centered at 4.7 ppm, whereas the 1D 13C spectra were acquired with 65,536 complex points and a spectral width of 200 ppm centered at 100 ppm. The 1D 1H spectra were acquired with 32 scans and 16 dummy scans, whereas the 1D 13C spectra were acquired with 2000 scans and 32 dummy scans. The DEPT experiment was acquired with similar conditions to the 1D 13C spectra except with 512 scans and a recycle delay of 1 s. The HSQC spectrum was acquired with 1000 and 128 complex points in the direct and indirect dimensions, respectively, eight scans, 32 dummy scans, and a recycle delay of 1.5 s.
MD simulations
MD simulations in explicit solvent were performed for the Rp-cAMPS-bound monomer of the intracellular region (IR) of human HCN4, which includes the CNBD. The total simulation time was 1.05 μs. The simulations were set up and executed following a protocol previously validated for the apo and cAMP-bound HCN4 IR (53).
Initial structure preparation protocol
The HCN4 IR construct spanning residues 521–717 of the HCN4 intracellular region was used for all MD simulations, as 717 is the last residue in the X-ray crystal structure. An initial cAMP-bound monomer structure was obtained from the x-ray crystal structure of the cAMP-bound IR (Protein Data Bank, PDB: 3OTF) by first deleting all water molecules from the structure and using SwissPDB Viewer to reconstruct partially missing side chains on the protein surface. The corresponding Rp-cAMPS-bound monomer structure was then obtained by editing the PDB text file, changing the equatorial exocyclic phosphate oxygen atom of the bound cAMP to a sulfur atom. Molecular structure topology and parameters data formatted for use with the CHARMM all-atom force field were generated for the Rp-cAMPS molecule using the online SwissParam software, and the topology and parameters data inserted into the respective parameter files for the CHARMM27 force field in preparation for subsequent MD simulation set-up.
MD simulation protocol
The MD simulations were performed in triplicate using the NAMD 2.9 software on the Shared Hierarchical Academic Research Computing Network. The CHARMM27 force field with CMAP correction, supplemented with the molecular structure topology and parameters data computed for the Rp-cAMPS molecule, was implemented. Simulation set-up and execution using the supplemented force field was performed following a protocol similar to that previously utilized for the apo and cAMP-bound HCN4 IR monomer simulations, resulting in a total simulation time of 1.05 μs.
Analysis of HCN4 IR structural dynamics
Structure similarity measures
To assess the propensities of the major HCN4 IR structural components for active- versus inactive-like structural arrangements, the simulations were analyzed through calculation of RMSD-based active-versus-inactive structure similarity measures (SMs) (53), where SM-values approaching 1 or −1 indicate protein conformations with fully active- or inactive-like structural arrangements, respectively. The distributions of SM-values for the HCN4 IR structures generated by the Rp-cAMPS-bound monomer simulations were computed following a protocol similar to that implemented previously (53), compiling the SM-values for all three replicate simulations into a single data set for examination, and using the previously-computed SM-value distributions for the apo and cAMP-bound monomer simulations as benchmarks for comparison (53).
Assessment of steric clashes
Potential energies of steric contact
To assess the suspected steric clash between the PBC and B-C structural elements in the presence of bound Rp-cAMPS, potential energies of steric contact between the PBC and B-C structural elements (i.e., residues 659–671 and 687–711 of HCN4, respectively), and between PBC residue L663 and B-helix residue F689, were computed for the HCN4 IR structures generated by the Rp-cAMPS-bound monomer simulations, with corresponding potential energies calculated from the cAMP-bound monomer simulations used as benchmarks for comparison. For each simulation, van der Waals (VDW) potential energies were computed using NAMD 2.9 with the CHARMM27 force field, implementing the same energy calculation parameters used in the simulations but with no nonbonded cutoff, and during each energy calculation, the portion(s) of the protein to be analyzed were specified using NAMD’s Pair Interaction tool. VDW potential energies were calculated for each aforementioned pair of structural elements/residues, and for the separate structural elements/residues in each pair, and the potential energies of steric contact between the structural elements/residues in each pair were then computed from the VDW potential energies as follows: PEsteric; X vs. Y = VDWX and Y together – VDWX separate – VDWY separate, where “X” and “Y” are the two structural elements/residues in the pair, and the “VDW” terms are the calculated VDW potential energies obtained using NAMD. Boxplots were then constructed using Origin 9.1 (OriginLab Corporation), based on the data from the three replicates for each state.
Results and Discussion
Allostery is a key driver of nonadditive substituent contributions to ligand binding in HCN4
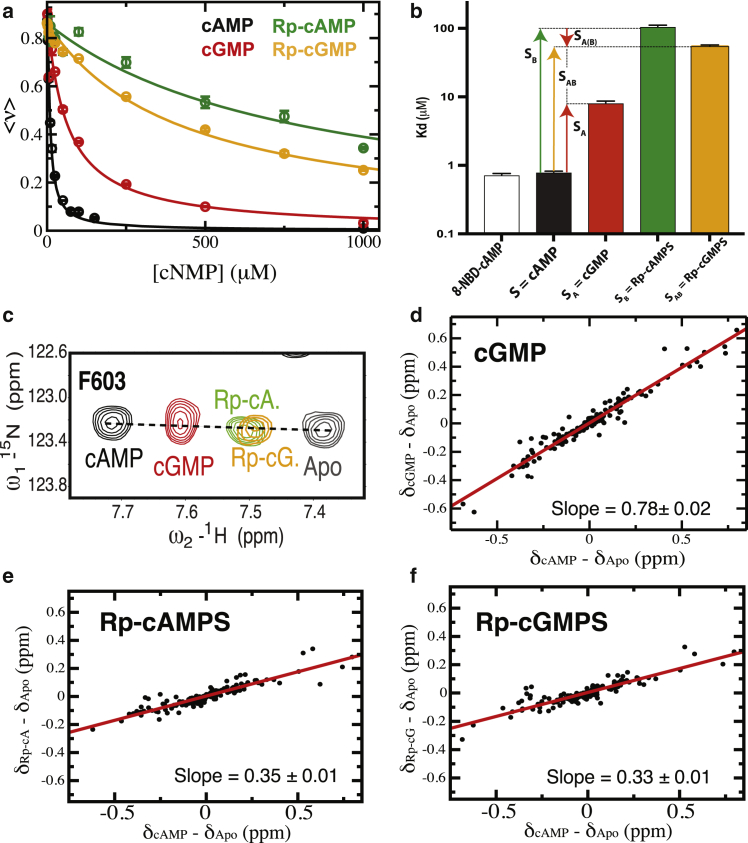
The measurement of affinities through fluorescence competition for the double-ligand cycle in Fig. 1 c reveals that the A-to-G and Rp substitutions in cAMP cause losses of affinity by approximately one and two orders of magnitude, respectively, when implemented in isolation (Fig. 2, a and b; Table S1). However, when the A-to-G replacement is applied to the phosphorothioate Rp-cAMPS analog, it surprisingly leads to a gain of affinity (Fig. 2, a and b; Table S1). Using Eq. 2, the resulting nonadditivity factor is 19.6 ± 1.7 (Table S1), which is significantly above the thermal RT benchmark, pointing to significant positive cooperativity for the double-ligand cycle in Fig. 1 c.
Figure 2.
Nonadditivity in the Rp/G double-ligand cycle for the HCN4 CNBD. (a) Binding competition isotherms for cNMP analogs versus the fluorescent 8-NBD-cAMP ligand. The cAMP analogs are those in the nonadditivity cycle of Fig. 1c. The Rp-cAMP/cGMP and Rp-cAMPS/cGMPS notations are used interchangeably in this paper. (b) Kd-values for the cAMP analogs in the previous panel, shown as a log scale bar plot. The Kd of 8-NBD-cAMP was measured by direct titration. The Kd-values are also reported in Table S1. Error bars were obtained from replicate measurements. The vertical arrows indicate the affinity changes caused by the A, B, A (B), and AB substitutions. The A (B) notation indicates that the A substitution occurs in the presence of B. (c) NH-HSQC spectral expansion of residue F603 in the HCN4 CNBD in the presence of saturating amounts of the cNMP analogs in the double-ligand cycle of Fig. 1c. The F603 position in the HSQC spectrum reports primarily on the shifts in the fast-exchanging HCN4 CNBD autoinhibitory P1 P2 equilibrium relative to the cAMP-bound and apo samples. (d–f) Chemical shift correlation plots for the cNMP analogs in (c). The slopes reflect the fractional activation relative to the cAMP-bound and apo HCN4 CNBD samples. Errors for the slopes were obtained from linear regressions. To see this figure in color, go online.
To check to what extent the nonadditivity in the double-ligand cycle of Fig. 1 c arises from conformational exchange, we extended the measurement of the factor to an allosterically silenced mutant (i.e., HCN4 707X). In HCN4 707X, the inhibitory (P1) versus active (P2) transition is silenced by the removal of an indispensable driver of activation, i.e., the C-terminal lid. The removal of the lid locks HCN4 707X primarily in the P1 state (Fig. S2, a–f). Hence, if the P1 P2 conformational exchange is the key determinant of nonadditivity, we expect that the factor for the lidless mutant should approach unity. The measured affinities do indeed confirm that the factor observed for HCN4 707X is only 1.2 ± 0.1 (Fig. S2, g and h; Table S1), which is close to unity and well within the RT benchmark [e−1, e] range, indicating negligible nonadditivity for the allosterically silenced HCN4 707X mutant.
The HCN4 707X results reveal that the dynamic inhibitory versus active conformational equilibrium of the HCN4 CNBD (i.e., the P1 P2 exchange; Fig. S1 b) is an essential determinant of nonadditivity for the ligand cycle of Fig. 1 c, ruling out significant contributions from intraligand through bond-covalent cross talk (e.g., inductive or electromeric effects). This conclusion is further supported by the absence of significant 1H and 13C chemical shift changes observed for the base upon introduction of the equatorial sulfur in Rp-cAMPS (Fig. S3). Hence, the near unity value of the measured for HCN4 707X and the chemical shift data (Figs. S2 and S3) consistently indicate that the free energy of coupling between the phosphate and base modifications (Fig. 1 c) arises primarily from noncovalent sources beyond the single-P1 state, i.e., the P1 P2 transition and/or contributions specific of the P2 state.
A concerted P1 P2 transition contributes to nonadditive binding but is insufficient alone to fully account for the observed nonadditivity
The contribution to the overall experimental nonadditivity factor arising uniquely from the P1 P2 equilibrium is denoted here as . Because in the assessment of the transition between states 1 and 2 is assumed to be the sole source of nonadditivity, the binding to each state is expected to be additive, i.e., with i = 1 or 2. In this case, the contribution can be estimated starting from the state populations in the P:S, P:SA, and P:SB complexes (Fig. 1 a) using the theory of thermodynamic linkage (8,54) implemented through binding polynomials (55), as shown in Section S1:
| (3) |
where and are the fractions of states P1 and P2, respectively, in the macromolecule P saturated with the Sj ligand in the cycle, i.e., the scaffold ligand S or the singly substituted ligands SA and SB (Figs. 1 a and S1 b). NMR spectroscopy is ideally suited to measure these state fractions.
If the exchange between conformations P1 and P2 is fast, as previously shown for the HCN4 CNBD (15), the relative populations of states P1 and P2 are measured directly from the NMR peak positions, by taking advantage of the fact that the observed chemical shifts are linear averages of the state-specific chemical shifts. For example, the NMR chemical shift changes for HCN4 residues sufficiently distant from the cAMP-binding site report primarily on the two-state inhibitory versus active equilibrium, e.g., F603 in the N3A shows that saturation with Rp-cAMPS or cGMP causes a linear shift away from cAMP and toward the apo position (Fig. 2 c). The fractional shifts reported by F603 are corroborated and quantified through more exhaustive chemical shift correlation analyses (Fig. 2, d–f; (52,56,57)). The slopes of the (δSj – δApo) versus (δcAMP – δApo) plots in Fig. 2, d–f provide fractional activation shifts, denoted as , for P in the P:Sj complexes of the double-ligand cycle in Fig. 1 (Table S1). The values in Table S1 are then converted into state populations, and , using the apo and cAMP-bound wt HNC4 CNBD samples as well as the inhibitory 707X mutant as references (Section S2). If the exchange between states P1 and P2 is slow or intermediate in the NMR chemical shift timescale, the state populations are reliably measured through chemical exchange saturation transfer or NMR dispersion experiments (Fig. S5; (58, 59, 60)).
In the case of the double-ligand cycle in Fig. 1 c, once the and values were determined using the fractional shifts in Fig. 2, d and e, the value was computed based on Eq. 3 to be 9.6 ± 0.7 (Fig. 3; Table S1). This result reveals that, although accounts for a significant fraction of the observed nonadditivity (∼50%; Fig. 3; Table S1), the transition between states 1 and 2 alone is not sufficient to fully recapitulate the observed binding nonadditivity as quantified by . In addition, as explained in Section S3, the residual agonism quantified by the fractional activation observed for the doubly substituted ligand (Fig. 2 f; Table S1) cannot be explained by the P1 P2 equilibrium alone with the assumption of additive state-specific binding (i.e., with i = 1 or 2).
Figure 3.
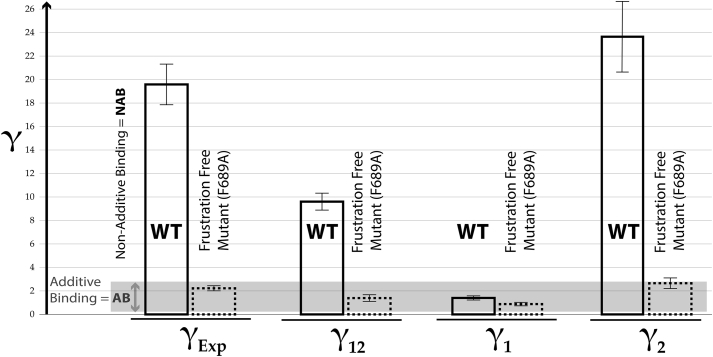
Dissection of the experimental nonadditivity factor () into transition-specific () and state-specific ( and ) contributions. Shown are the-values for the Rp/G cycle of Fig. 1c as applied to the HCN4 CNBD wt (bars with solid lines) and the frustration-free F689A mutant (bars with dotted lines). The gray region indicates -values that fall within the RT-benchmark window [e−1, e], for which deviations from the additivity limit are assumed negligible. Error bars were obtained through error propagation.
To solve these discrepancies, we hypothesized that the observed nonadditivity may arise not only from the P1 P2 transition, but also from nonadditive state-specific binding. To gauge the latter contribution, we defined the state-specific nonadditivity factors, denoted as and , in terms of state-specific association constants as opposed to the overall average association constants utilized in the definition of :
| (4) |
where is the association constant for state i of the receptor macromolecule P and the Sj ligand in the cycle (Fig. S1 b), i.e., S, SA, SB, or SAB.
The P1 P2 equilibrium together with nonadditive state-specific binding is sufficient to fully account for the observed nonadditivity
As shown in Section S4, the and nonadditivity factors are computed as:
| (5) |
| (6) |
where and are the fractions of states P1 and P2, respectively, in the macromolecule P saturated with one of the four Sj ligands in the cycle, i.e., S, SA, SB, and SAB (Figs. 1 c and S1 b). Eqs. 5 and 6 show that the computation of state-specific nonadditivity factors requires not only the state populations of the P:S, P:SA, and P:SB complexes, as in the case of (Eq. 3), but also the value and the state populations of the doubly substituted complex P:SAB. As a result, the inclusion of the state-specific nonadditivity factors and ensures consistency with the observed nonadditivity factor () as well as all fractional activations (), thereby resolving the discrepancy previously encountered when assuming that nonadditivity originates uniquely from the P1 P2 equilibrium.
The and factors offer unique insight on additional mechanisms of intersubstituent allosteric coupling beyond the P1 P2 transition, and they reveal how nonadditivity varies across different states. For example, the and factors computed for the Rp/G cycle (Fig. 1 c) using Eqs. 5 and 6 reveal that state-specific contributions to nonadditivity are highly variable. They arise primarily from conformation P2, as indicated by a value in the [e−1, e] range and a significantly higher ( = 23.6 ± 3.0; Fig. 3; Table S1). Notably, the computed value for the wt HCN4 CNBD is in remarkably good agreement with the experimental nonadditivity factor measured for the lidless 707X mutant, which traps the inhibitory state P1 ( = 1.2 ± 0.1; Table S1). This agreement corroborates our computations and confirms the absence of significant nonadditivity for state P1.
The additivity in conformer P1 is consistent with the disengagement of the cNMP base from the lid in this state, as is typical of autoinhibitory conformations (Fig. 1 d). In marked contrast to , significantly exceeds the RT-based threshold (Fig. 3; Table S1) and explains why the fractional activation observed for the CNBD bound to the doubly substituted Rp-cGMPS ligand is approximately one order of magnitude higher than expected based on the assumption of additivity for both the P1 and P2 states (0.33 ± 0.01 vs. 0.02 ± 0.01; Table S1). Hence, the nonadditivity of state P2 (i.e., the active conformation) is a major driver of both the overall experimental nonadditivity () and of the partial agonism observed for Rp-cGMPS. It is therefore critical to further investigate the determinants of .
Steric frustration is a major determinant of state-specific-binding nonadditivity ()
The high value (23.6 ± 3.0; Fig. 3; Table S1) points to significant nonadditivity arising specifically from conformation P2. Because additivity is observed for P1 (Table S1) and a key P1 versus P2 difference is the engagement of the lid region in the latter state, we computed the free energy of coupling between the lid and the ligand substitutions, i.e., G and Rp (Fig. 1 c). For this purpose, we relied on the mutant/ligand cycle of Document S1. Sections S1–S5, Figs. S1–S12, and Tables S1 and S2, Document S2. Article plus Supporting Material c and the affinities measured for the 707X mutant (Table S1). We found that the lid/G ΔGcoupling is positive (ΔGlid/G coupling ∼1.6 ± 0.1 kcal/mol; Table S2), confirming that the A-to-G replacement destabilizes the interactions between the lid and the base.
Interestingly, we observed an even larger positive value for the lid/Rp ΔGcoupling (ΔGlid/Rp coupling ∼2.4 ± 0.1 kcal/mol; Table S2), indicating that the introduction of the Rp modification in the cAMP phosphate interferes with the lid-base interactions. This result is remarkable because the nucleotide phosphate does not interact directly with the lid and suggests that, when Rp-cAMPS binds to the active conformation of HCN4 (i.e., state P2, with a fully engaged lid; Fig. 1, d and e), it introduces a tension or strain, i.e., the complex of state P2 with Rp-cAMPS is frustrated (44,45).
As a first step toward understanding why the P2:Rp-cAMPS complex is frustrated, we reverted to MD simulations, which suggest that a key determinant of frustration is the steric hindrance between the side chains of F689 in the B-helix and L663 in the PBC (Section S5 and Fig. S6). To confirm this hypothesis and measure the extent of steric frustration arising from the F689 side chain, we engineered the frustration-silencing F689A mutation and measured the affinities of this mutant for the four ligands in the double-ligand cycle (Document S1. Sections S1–S5, Figs. S1–S12, and Tables S1 and S2, Document S2. Article plus Supporting Material a; Table S1). The F689A mutation is anticipated to compensate for the steric hindrance caused by the replacement of the equatorial exocyclic oxygen atom with the bulkier sulfur atom in the Rp-cAMPS:P2 complex, without significantly affecting changes in hydrogen-bond strength resulting from electronic effects, such as the oxygen versus sulfur electronegativity difference. As expected, the affinities of the Rp containing cNMPs (i.e., Rp-cAMPS and Rp-cGMPS) are dramatically increased in the frustration-silenced F689A mutant versus wild-type HCN4 (Document S1. Sections S1–S5, Figs. S1–S12, and Tables S1 and S2, Document S2. Article plus Supporting Material a; Table S1), consistent with the enhanced stability of the F689A HCN4:Rp complex due to the removal of steric frustration induced by the F689 phenyl side chain.
Based on the affinities measured for F689A (Table S1) and the mutant-ligand thermodynamic cycle in Document S1. Sections S1–S5, Figs. S1–S12, and Tables S1 and S2, Document S2. Article plus Supporting Material c, the free energy of coupling between the F689 side chain and the Rp substitution is estimated to be ∼1.7 ± 0.1 kcal/mol (Table S2). This value is of the same order of magnitude as the Rp-cAMPS versus cAMP steric destabilization gauged through MD simulations (Fig. S6 d) and accounts for most of the frustration in the wt HCN4 CNBD arising from the recruitment of the lid in the presence of the Rp substitution, i.e., the ∼2.4 kcal/mol lid/Rp-coupling free energy computed based on the 707X lidless mutant (Table S2). We conclude that the elimination of the F689/L663 steric clash (Fig. S6 f) in the F689A mutant enables a more effective recruitment of the lid region by the cNMP base, as is also confirmed by the marked increase in the fractional activations for both Rp-cNMPS (i.e., Rp-cAMPS and Rp-cGMPS) in going from the wild-type to the F689A HCN4 mutant (Fig. S7, d and e; Table S1). Overall, the F689A versus wt changes in affinities and fractional activation along the double mutant cycle (Fig. S7; Table S1) confirm the steric frustration between the F689 side chain and the Rp substituent predicted by the MD simulations (Fig. S6).
To test our hypothesis that the steric frustration arising from F689 is a key determinant of the elevated value observed for the wt HCN4 CNBD, we measured for the F689A mutant using the affinities and fractional activations of Fig. S7. As anticipated, the F689A versus wt changes in affinities and fractional activations (Table S1) translate into a reduction of by approximately one order of magnitude to values that fall within the RT-benchmark region (Fig. 3; Table S1). This result points to negligible nonadditivity for state P2 of the F689A mutant, confirming our hypothesis that the steric frustration of the P2:Rp-cAMPS complex is a major determinant of . Such frustration is lost in the P1:Rp-cAMPS complex because in the P1 conformer, the B-C helices are disengaged and adopt an “out” orientation that releases the steric hindrance with F689. Hence, the steric frustration hypothesis explains not only the elevated value observed for but also why falls within the additive range in wt HCN4 (Fig. 3; Table S1).
Interestingly, the nonadditivity analysis of the F689A mutant reveals that this mutation reduces not only but also to values within the additive range (Fig. 3; Table S1). This is an interesting observation because, unlike the allosterically silenced 707X mutant, the F689A mutant transitions from the P1 to the P2 state upon cAMP binding, and this transition occurs to an extent comparable to wt HCN4 (<XcAMP,F689A> = 0.90 ± 0.02; Document S1. Sections S1–S5, Figs. S1–S12, and Tables S1 and S2, Document S2. Article plus Supporting Material c; Table S1). This observation implies that the P1 P2 transition alone is insufficient to generate nonadditive binding and other properties of such transition must be considered as well. For example, allosteric sites have been shown to locally violate the principle of minimal frustration (44,45). This notion suggests that the suppression of steric frustration by F689A may also disrupt the allosteric networks that ensure a concerted P1 P2 transition, thus explaining why the value observed for the F689A mutant falls within the RT-benchmark level expected for near-additive binding.
The concerted nature of the P1 P2 transition is a necessary determinant of the nonadditivity factor
To further support the hypothesis that the observed F689A versus wt reduction is caused by a loss of concertedness in the P1 P2 transition because of compromised allosteric networks, we mapped such networks through comparative CHESCA analyses of the F689A versus wt HCN4 CNBD (Fig. 4). CHESCA is ideally suited to identify residue clusters subject to concerted transitions for fast-exchanging systems such as the HCN4 CNBD. Both the wt and F689A CHESCA analyses rely on the same perturbation library, which includes the four ligands that define the double-ligand cycle (Fig. 1 c) as well as the apo HCN4 CNBD.
Figure 4.
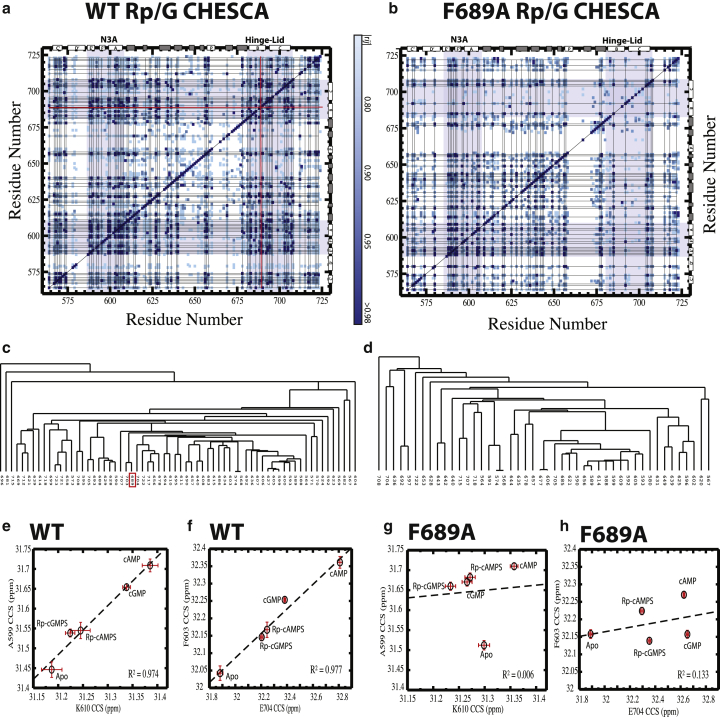
Chemical shift covariance analysis (CHESCA) of the HCN4 CNBD based on the Rp/G double-ligand cycle. (a) CHESCA correlation matrix for wt HCN4 (563–724) generated using the apo sample and the four cNMPs in the Rp/G cycle of Fig. 1c. The secondary structure is shown as white (α-helices) and gray (β-strands) rectangles. The grid lines depict the single-linkage allosteric cluster of (c), whereas the red lines mark the position of F689. Shaded areas mark the N3A and hinge-lid helical regions. (b) As (a) but for the F689A HCN4 (563–724) mutant. (c) Dendrogram of the cluster obtained through single-linkage agglomerative clustering for the wt HCN4 CNBD. A Pearson’s correlation coefficient cutoff ≥0.98 was utilized. F689 is highlighted by a red box. (d) As (c) but for the F689A HCN4 (563–724) mutant. (e and f) Representative pairwise interresidue combined chemical shift correlations for wt HCN4 (563–724). (g and h) Pairwise plots for the same residue pairs in (e) and (f) are shown but for F689A HCN4 (563–724), illustrating the decorrelation caused by the mutation, which perturbs the allosteric networks of wt HCN4. To see this figure in color, go online. Errors in the chemical shifts were assessed as previously described (40,41).
The wt CHESCA-based allosteric map clearly shows that F689 serves as a major allosteric hub for the HCN4 CNBD, involved in multiple pairwise correlations with other residues in both the α- and β-subdomains (Fig. 4 a). As expected, F689 belongs to the main allosteric cluster of the HCN4 CNBD, as consistently indicated by both agglomerative clustering of the chemical shift correlation matrix (Fig. 4, a and c) and by singular value decomposition (Fig. S8, a and b). The allosteric role of the F689 phenyl group is further confirmed by the F689A mutant CHESCA, revealing a significant loss of correlations (Fig. 4, b, d, g, and h) relative to the wt HCN4 CNBD (Fig. 4, a, c, e, and f).
The CHESCA results (Fig. 4) clearly show that the F689 side chain is necessary to ensure a concerted allosteric P1 P2 transition without significant sampling of transition intermediates, explaining why the value for the F689A mutant falls in the near-additivity range (Fig. 3; Table S1). Overall, the comparative CHESCA analyses of Fig. 4 reveal that the concertedness of the P1 P2 transition is a key determinant of the contribution to binding nonadditivity. Furthermore, the one order of magnitude F689A versus wt reduction in the experimental to the RT-benchmark range (Fig. 3; Table S1) confirms the absence of other significant nonadditivity determinants (e.g., covalent ligand-based effects; Fig. 1 b) besides the concerted P1 P2 allosteric transition and the frustration of state P2, as quantified by and , respectively.
Conclusions
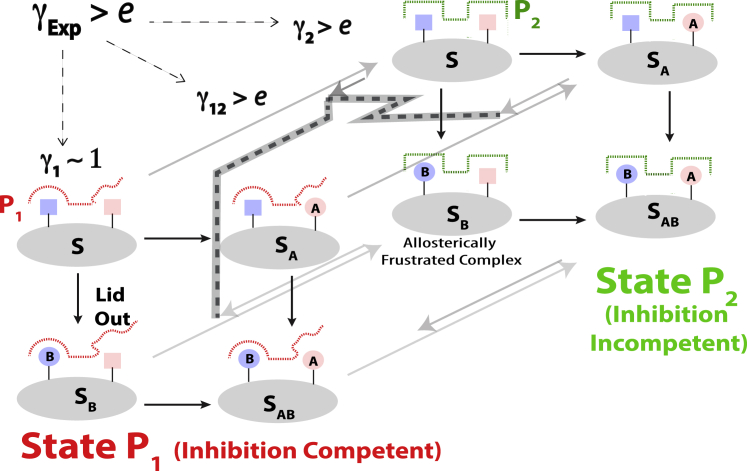
In conclusion, we have proposed an NMR-based approach to elucidate the allosteric mechanisms underlying nonadditive substituent contributions to ligand-binding. We have shown how, using NMR (Fig. S5), it is possible to quantitatively dissect the experimental nonadditivity factor into transition- and state-specific contributions, i.e., , , and (Fig. 3). The dissection of the experimental nonadditivity factor in terms of , , and offers a means to analyze previously elusive mechanisms and driving forces underlying nonadditivity between substituents A and B (Fig. 5).
Figure 5.
Allosteric mechanism of HCN4 nonadditivity for the Rp/G double-ligand cycle. The observed nonadditivity ( > e) for the HCN4 CNBD Rp/G double-ligand cycle is dissected in terms of three main contributions (, , and ), which represent state- and transition-specific terms, respectively. The factor is close to unity because the lid is disengaged from the base in state 1 (wavy red dotted line), resulting in negligible nonadditivity. The factor is >e because both substituents drive the P1 P2 two-state equilibrium in the same direction (black dashed lines) relative to the scaffold S, i.e., the unmodified cAMP ligand, giving rise to significant nonadditivity. The factor is >e primarily because of the allosteric frustration in the P2:Rp-cAMPS complex. To see this figure in color, go online.
The value quantifies the contribution to nonadditivity arising uniquely from ligand-dependent modulations of the concerted P1 P2 transition, and is primarily dictated by whether the two A and B substitutions shift the P1 P2 equilibrium toward the same state (Fig. 5). The contribution to nonadditivity explains why ligand modifications that result in affinity losses when implemented in isolation, may lead to affinity gains when combined (Fig. 2, a and b). However, the term alone may not suffice to fully recapitulate the observed nonadditivity (i.e., ) and the agonism of the doubly substituted ligand. It is, therefore, necessary to consider also the and descriptors of state-specific nonadditivity. They quantify the contributions to that cannot be captured solely by the two-state P1 P2 transition and report on intersubstituent couplings specific of states P1 and P2, respectively (Fig. 5).
The application of the proposed NMR-based approach to the Rp/G double-ligand cycle for the prototypical allosteric HCN4 ion channel reveals that state-specific contributions to nonadditivity may arise from the release of steric frustration and may vary dramatically from state to state. For example, the value specific of the inhibited state points to the absence of significant nonadditivity because of the disengagement of one of the critical binding sites in this state (i.e., the lid; Fig. 5). Unlike , the value measured here indicates the presence of marked nonadditivity arising from the simultaneous engagement of both binding sites in the active state (i.e., the PBC and the lid), which results in steric frustration for the P2:Rp-cAMPS complex (Fig. 5). The versus differential explains the partial agonism of the doubly substituted ligand. Furthermore, the molecular features underlying the versus differential (i.e., the L663/F689 residue pair linked to allosteric frustration) are highly conserved across CNBDs (37), suggesting that the state-specific nonadditivity observed for HCN4 may be a universal property of the ubiquitous cNMP-binding domain.
Overall, the proposed NMR-based analysis of nonadditive substituent contributions to binding free energies provides a widely applicable means to rationalize nonadditivity in mechanistic allosteric terms and constructively exploit it for the design of ligands with improved affinities and agonism. Ultimately, the inclusion of nonadditive effects in docking scoring functions and quantitative SAR models will further enhance these essential medicinal chemistry tools. Furthermore, we anticipate that the analyses and methods proposed here are generally applicable to allosteric receptors and signaling conformational switches, offering a new approach to analyze the molecular determinants that drive substituent nonadditivity.
Author Contributions
S.B., B.V., and G.M. designed research. S.B., K.V., B.V., J.A., and M.A. performed research. S.B., K.V., B.V., J.A., M.A., and G.M. analyzed data. B.V. and G.M. wrote the article.
Acknowledgments
We thank Dr. F. Fogolari, Dr. S.S. Taylor, Dr. G. Veglia, Dr. F.W. Herberg, Dr. A. Moroni, Dr. W. Zagotta, Dr. Pietro Roversi, Romi Lifshitz, Alveena Ahmed, Nishi Parikh, and Rashik Ahmed for helpful discussions.
This work was supported by the Canadian Institutes of Health Research Grant 389522 (to G.M.) and the Natural Sciences and Engineering Research Council of Canada Grant RGPIN-2019-05990 (to G.M.).
Editor: Elizabeth Komives.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.07.038.
Supporting Material
References
- 1.Klebe G. Applying thermodynamic profiling in lead finding and optimization. Nat. Rev. Drug Discov. 2015;14:95–110. doi: 10.1038/nrd4486. [DOI] [PubMed] [Google Scholar]
- 2.Tinberg C.E., Khare S.D., Baker D. Computational design of ligand-binding proteins with high affinity and selectivity. Nature. 2013;501:212–216. doi: 10.1038/nature12443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ye L., Neale C., Prosser R.S. Mechanistic insights into allosteric regulation of the A2A adenosine G protein-coupled receptor by physiological cations. Nat. Commun. 2018;9:1372. doi: 10.1038/s41467-018-03314-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Warne T., Edwards P.C., Tate C.G. Molecular basis for high-affinity agonist binding in GPCRs. Science. 2019;364:775–778. doi: 10.1126/science.aau5595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sormanni P., Aprile F.A., Vendruscolo M. Rational design of antibodies targeting specific epitopes within intrinsically disordered proteins. Proc. Natl. Acad. Sci. USA. 2015;112:9902–9907. doi: 10.1073/pnas.1422401112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dill K.A. Additivity principles in biochemistry. J. Biol. Chem. 1997;272:701–704. doi: 10.1074/jbc.272.2.701. [DOI] [PubMed] [Google Scholar]
- 7.Jencks W.P. On the attribution and additivity of binding energies. Proc. Natl. Acad. Sci. USA. 1981;78:4046–4050. doi: 10.1073/pnas.78.7.4046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Di Cera E., Gill S.J., Wyman J. Binding capacity: cooperativity and buffering in biopolymers. Proc. Natl. Acad. Sci. USA. 1988;85:449–452. doi: 10.1073/pnas.85.2.449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Baum B., Muley L., Klebe G. Non-additivity of functional group contributions in protein-ligand binding: a comprehensive study by crystallography and isothermal titration calorimetry. J. Mol. Biol. 2010;397:1042–1054. doi: 10.1016/j.jmb.2010.02.007. [DOI] [PubMed] [Google Scholar]
- 10.Nasief N.N., Hangauer D. Additivity or cooperativity: which model can predict the influence of simultaneous incorporation of two or more functionalities in a ligand molecule? Eur. J. Med. Chem. 2015;90:897–915. doi: 10.1016/j.ejmech.2014.11.056. [DOI] [PubMed] [Google Scholar]
- 11.Kramer C., Fuchs J.E., Liedl K.R. Strong nonadditivity as a key structure-activity relationship feature: distinguishing structural changes from assay artifacts. J. Chem. Inf. Model. 2015;55:483–494. doi: 10.1021/acs.jcim.5b00018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Reinhart G.D. The determination of thermodynamic allosteric parameters of an enzyme undergoing steady-state turnover. Arch. Biochem. Biophys. 1983;224:389–401. doi: 10.1016/0003-9861(83)90225-4. [DOI] [PubMed] [Google Scholar]
- 13.Mesecar A.D., Nowak T. Metal-ion-mediated allosteric triggering of yeast pyruvate kinase. 1. A multidimensional kinetic linked-function analysis. Biochemistry. 1997;36:6792–6802. doi: 10.1021/bi962869t. [DOI] [PubMed] [Google Scholar]
- 14.Cherkasov A., Muratov E.N., Tropsha A. QSAR modeling: where have you been? Where are you going to? J. Med. Chem. 2014;57:4977–5010. doi: 10.1021/jm4004285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Akimoto M., Zhang Z., Melacini G. A mechanism for the auto-inhibition of hyperpolarization-activated cyclic nucleotide-gated (HCN) channel opening and its relief by cAMP. J. Biol. Chem. 2014;289:22205–22220. doi: 10.1074/jbc.M114.572164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Harzheim D., Pfeiffer K.H., Seifert R. Cardiac pacemaker function of HCN4 channels in mice is confined to embryonic development and requires cyclic AMP. EMBO J. 2008;27:692–703. doi: 10.1038/emboj.2008.3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lolicato M., Bucchi A., Moroni A. Cyclic dinucleotides bind the C-linker of HCN4 to control channel cAMP responsiveness. Nat. Chem. Biol. 2014;10:457–462. doi: 10.1038/nchembio.1521. [DOI] [PubMed] [Google Scholar]
- 18.Stathopulos P.B., Ikura M. Store operated calcium entry: from concept to structural mechanisms. Cell Calcium. 2017;63:3–7. doi: 10.1016/j.ceca.2016.11.005. [DOI] [PubMed] [Google Scholar]
- 19.Doucet N., Savard P.Y., Gagné S.M. NMR investigation of Tyr105 mutants in TEM-1 β-lactamase: dynamics are correlated with function. J. Biol. Chem. 2007;282:21448–21459. doi: 10.1074/jbc.M609777200. [DOI] [PubMed] [Google Scholar]
- 20.Carroll M.J., Mauldin R.V., Lee A.L. Evidence for dynamics in proteins as a mechanism for ligand dissociation. Nat. Chem. Biol. 2012;8:246–252. doi: 10.1038/nchembio.769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Carroll M.J., Gromova A.V., Lee A.L. Direct detection of structurally resolved dynamics in a multiconformation receptor-ligand complex. J. Am. Chem. Soc. 2011;133:6422–6428. doi: 10.1021/ja2005253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Pagano K., Torella R., Ragona L. Direct and allosteric inhibition of the FGF2/HSPGs/FGFR1 ternary complex formation by an antiangiogenic, thrombospondin-1-mimic small molecule. PLoS One. 2012;7:e36990. doi: 10.1371/journal.pone.0036990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tomaselli S., Pagano K., Ragona L. Lipid binding protein response to a bile acid library: a combined NMR and statistical approach. FEBS J. 2015;282:4094–4113. doi: 10.1111/febs.13405. [DOI] [PubMed] [Google Scholar]
- 24.Yu C.H., Yang N., Dmitriev O.Y. The metal chaperone Atox1 regulates the activity of the human copper transporter ATP7B by modulating domain dynamics. J. Biol. Chem. 2017;292:18169–18177. doi: 10.1074/jbc.M117.811752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Fayos R., Melacini G., Jennings P.A. Induction of flexibility through protein-protein interactions. J. Biol. Chem. 2003;278:18581–18587. doi: 10.1074/jbc.M300866200. [DOI] [PubMed] [Google Scholar]
- 26.McNicholl E.T., Das R., Melacini G. Communication between tandem cAMP binding domains in the regulatory subunit of protein kinase A-Ialpha as revealed by domain-silencing mutations. J. Biol. Chem. 2010;285:15523–15537. doi: 10.1074/jbc.M110.105783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Byun J.A., Van K., Melacini G. Mechanism of allosteric inhibition in the Plasmodium falciparum cGMP-dependent protein kinase. J. Biol. Chem. 2020;295:8480–8491. doi: 10.1074/jbc.RA120.013070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Walker C., Wang Y., Veglia G. Cushing’s syndrome driver mutation disrupts protein kinase A allosteric network, altering both regulation and substrate specificity. Sci. Adv. 2019;5:eaaw9298. doi: 10.1126/sciadv.aaw9298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Byun J.A., Akimoto M., Taylor S.S. Allosteric pluripotency as revealed by protein kinase A. Sci. Adv. 2020;6:eabb1250. doi: 10.1126/sciadv.abb1250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wang Y., v S M., Veglia G. Globally correlated conformational entropy underlies positive and negative cooperativity in a kinase’s enzymatic cycle. Nat. Commun. 2019;10:799. doi: 10.1038/s41467-019-08655-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.De Simone A., Aprile F.A., Vendruscolo M. Structure of a low-population intermediate state in the release of an enzyme product. eLife. 2015;4:e02777. doi: 10.7554/eLife.02777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wodak S.J., Paci E., McLeish T. Allostery in its many disguises: from theory to applications. Structure. 2019;27:566–578. doi: 10.1016/j.str.2019.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Meng W., Clerico E.M., Gierasch L.M. Allosteric landscapes of eukaryotic cytoplasmic Hsp70s are shaped by evolutionary tuning of key interfaces. Proc. Natl. Acad. Sci. USA. 2018;115:11970–11975. doi: 10.1073/pnas.1811105115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kumar G.S., Clarkson M.W., Peti W. Dynamic activation and regulation of the mitogen-activated protein kinase p38. Proc. Natl. Acad. Sci. USA. 2018;115:4655–4660. doi: 10.1073/pnas.1721441115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Tzeng S.-R., Kalodimos C.G. Protein activity regulation by conformational entropy. Nature. 2012;488:236–240. doi: 10.1038/nature11271. [DOI] [PubMed] [Google Scholar]
- 36.Long D., Brüschweiler R. Atomistic kinetic model for population shift and allostery in biomolecules. J. Am. Chem. Soc. 2011;133:18999–19005. doi: 10.1021/ja208813t. [DOI] [PubMed] [Google Scholar]
- 37.Berman H.M., Ten Eyck L.F., Taylor S.S. The cAMP binding domain : An ancient signaling module. Proc. Natl. Acad. Sci. USA. 2005;102:4–9. doi: 10.1073/pnas.0408579102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Xu X., Vysotskaya Z.V., Zhou L. Structural basis for the cAMP-dependent gating in the human HCN4 channel. J. Biol. Chem. 2010;285:37082–37091. doi: 10.1074/jbc.M110.152033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Akimoto M., Vanschouwen B., Melacini G. The structure of the apo cAMP-binding domain of HCN4 - a stepping stone toward understanding the cAMP-dependent modulation of the hyperpolarization-activated cyclic-nucleotide-gated ion channels. FEBS J. 2018;285:2182–2192. doi: 10.1111/febs.14408. [DOI] [PubMed] [Google Scholar]
- 40.Boulton S., Selvaratnam R., Melacini G. Implementation of the NMR CHEmical shift covariance analysis (CHESCA): a chemical biologist’s approach to allostery. Methods Mol. Biol. 2018;1688:391–405. doi: 10.1007/978-1-4939-7386-6_18. [DOI] [PubMed] [Google Scholar]
- 41.Selvaratnam R., Chowdhury S., Melacini G. Mapping allostery through the covariance analysis of NMR chemical shifts. Proc. Natl. Acad. Sci. USA. 2011;108:6133–6138. doi: 10.1073/pnas.1017311108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Selvaratnam R., Mazhab-Jafari M.T., Melacini G. The auto-inhibitory role of the EPAC hinge helix as mapped by NMR. PLoS One. 2012;7:e48707. doi: 10.1371/journal.pone.0048707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Chen H., Marsiglia W.M., Mohammadi M. Elucidation of a four-site allosteric network in fibroblast growth factor receptor tyrosine kinases. eLife. 2017;6:e21137. doi: 10.7554/eLife.21137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ferreiro D.U., Komives E.A., Wolynes P.G. Frustration in biomolecules. Q. Rev. Biophys. 2014;47:285–363. doi: 10.1017/S0033583514000092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ferreiro D.U., Komives E.A., Wolynes P.G. Frustration, function and folding. Curr. Opin. Struct. Biol. 2018;48:68–73. doi: 10.1016/j.sbi.2017.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Boulton S., Akimoto M., Melacini G. Free energy landscape remodeling of the cardiac pacemaker channel explains the molecular basis of familial sinus bradycardia. J. Biol. Chem. 2017;292:6414–6428. doi: 10.1074/jbc.M116.773697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Moleschi K.J., Akimoto M., Melacini G. Measurement of state-specific association constants in allosteric sensors through molecular stapling and NMR. J. Am. Chem. Soc. 2015;137:10777–10785. doi: 10.1021/jacs.5b06557. [DOI] [PubMed] [Google Scholar]
- 48.Boulton S., Selvaratnam R., Melacini G. Mechanism of selective enzyme inhibition through uncompetitive regulation of an allosteric agonist. J. Am. Chem. Soc. 2018;140:9624–9637. doi: 10.1021/jacs.8b05044. [DOI] [PubMed] [Google Scholar]
- 49.Wang Z.-X. An exact mathematical expression for describing competitive binding of two different ligands to a protein molecule. FEBS Lett. 1995;360:111–114. doi: 10.1016/0014-5793(95)00062-e. [DOI] [PubMed] [Google Scholar]
- 50.Zhu Y., Chen H., Cheng X. Biochemical and pharmacological characterizations of ESI-09 based EPAC inhibitors: defining the ESI-09 “therapeutic window”. Sci. Rep. 2015;5:9344. doi: 10.1038/srep09344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Shao H., Mohamed H., Melacini G. Mechanism of action of an EPAC1-selective competitive partial agonist. J. Med. Chem. 2020;63:4762–4775. doi: 10.1021/acs.jmedchem.9b02151. [DOI] [PubMed] [Google Scholar]
- 52.Lorieau J.L., Louis J.M., Bax A. pH-triggered, activated-state conformations of the influenza hemagglutinin fusion peptide revealed by NMR. Proc. Natl. Acad. Sci. USA. 2012;109:19994–19999. doi: 10.1073/pnas.1213801109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.VanSchouwen B., Akimoto M., Melacini G. Role of dynamics in the autoinhibition and activation of the hyperpolarization-activated cyclic nucleotide-modulated (HCN) ion channels. J. Biol. Chem. 2015;290:17642–17654. doi: 10.1074/jbc.M115.651877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Weber G. Chapman and Hall; London, UK: 1992. Protein interactions. [Google Scholar]
- 55.Dill K.A., Bromberg S. Garland Science; New York: 2003. Molecular Driving Forces: Statistical Thermodynamics in Chemistry and Biology. [Google Scholar]
- 56.Selvaratnam R., VanSchouwen B., Melacini G. The projection analysis of NMR chemical shifts reveals extended EPAC autoinhibition determinants. Biophys. J. 2012;102:630–639. doi: 10.1016/j.bpj.2011.12.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Cembran A., Kim J., Veglia G. NMR mapping of protein conformational landscapes using coordinated behavior of chemical shifts upon ligand binding. Phys. Chem. Chem. Phys. 2014;16:6508–6518. doi: 10.1039/c4cp00110a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Vallurupalli P., Sekhar A., Kay L.E. Probing conformational dynamics in biomolecules via chemical exchange saturation transfer: a primer. J. Biomol. NMR. 2017;67:243–271. doi: 10.1007/s10858-017-0099-4. [DOI] [PubMed] [Google Scholar]
- 59.Loria J.P., Rance M., Palmer A.G. A relaxation-compensated Carr−Purcell−Meiboom−Gill sequence for characterizing chemical exchange by NMR spectroscopy. J. Am. Chem. Soc. 1999;121:2331–2332. [Google Scholar]
- 60.Vallurupalli P., Hansen D.F., Kay L.E. Structures of invisible, excited protein states by relaxation dispersion NMR spectroscopy. Proc. Natl. Acad. Sci. USA. 2008;105:11766–11771. doi: 10.1073/pnas.0804221105. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.