Amoeboid Swimming Is Propelled by Molecular Paddling in Lymphocytes

Abstract

Mammalian cells developed two main migration modes. The slow mesenchymatous mode, like crawling of fibroblasts, relies on maturation of adhesion complexes and actin fiber traction, whereas the fast amoeboid mode, observed exclusively for leukocytes and cancer cells, is characterized by weak adhesion, highly dynamic cell shapes, and ubiquitous motility on two-dimensional and in three-dimensional solid matrix. In both cases, interactions with the substrate by adhesion or friction are widely accepted as a prerequisite for mammalian cell motility, which precludes swimming. We show here experimental and computational evidence that leukocytes do swim, and that efficient propulsion is not fueled by waves of cell deformation but by a rearward and inhomogeneous treadmilling of the cell external membrane. Our model consists of a molecular paddling by transmembrane proteins linked to and advected by the actin cortex, whereas freely diffusing transmembrane proteins hinder swimming. Furthermore, continuous paddling is enabled by a combination of external treadmilling and selective recycling by internal vesicular transport of cortex-bound transmembrane proteins. This mechanism explains observations that swimming is five times slower than the retrograde flow of cortex and also that lymphocytes are motile in nonadherent confined environments. Resultantly, the ubiquitous ability of mammalian amoeboid cells to migrate in two dimensions or three dimensions and with or without adhesion can be explained for lymphocytes by a single machinery of heterogeneous membrane treadmilling.

Significance

Leukocytes have a ubiquitous capacity to migrate on or in solid matrices and with or without adhesion, which is instrumental to fight infections. The precise mechanisms sustaining migration remain, however, arguable. It is for instance widely accepted that leukocytes cannot crawl on two-dimensional substrates without adhesion. In contrast, we showed that human lymphocytes swim on nonadherent two-dimensional substrates and in suspension. Furthermore, our experiments and modeling suggest that propulsion hardly rely on cell body deformations and predominantly on molecular paddling by transmembrane proteins protruding outside the cell. For physics, this study reveals a new type of microswimmer, and for biology, it suggests that leukocyte’s ubiquitous crawling may have evolved from an early machinery of swimming shared by various eukaryotic cells.

Introduction

Individual living cells developed different strategies to migrate and explore their environment. Bacteria, microalgae or mammalian gametes swim in a fluid under the propulsion of a flagellum (1) or of shape deformations (2), whereas somatic mammalian cells crawl with adhesion on a solid tissue via a continuous sequence of forward pushing of the cell front, strengthening of adhesion at the leading edge, and pulling of the cell rear (3,4). In vivo, mammalian cells crawl either on two-dimensional (2D) substrates, like leukocytes on inner blood vessels and epithelial surfaces, or in three-dimensional (3D) environments within tissues. The critical role of adhesion for crawling motility was recently revised in the case of amoeboid mammalian cells, i.e., white blood cells and cancer cells. Amoeboid cells differ from mesenchymatous cells (e.g., fibroblasts) by a significantly higher speed (typically 5–20 vs. 0.1–1 μm min⁻¹) and by highly dynamic shape deformations. Both amoeboid and mesenchymatous cells crawl on adhering substrates, but only amoeboid cells remain motile without adhesion provided that they are confined by a 3D environment (5, 6, 7, 8). Although different models exist, this motility in confined nonadherent conditions was generally explained by a chimneying (6) mode in which cell-substrate interactions are mediated by friction instead of adhesion (8, 9, 10, 11). It is therefore widely accepted that amoeboid motility of mammalian cells is strictly dependent on adhesion on 2D substrates and on adhesion/friction in 3D media, whereas nonadherent 2D migration and swimming are precluded (5, 6, 7,12, 13, 14, 15, 16, 17, 18, 19).

In contradiction with this paradigm of adhesive or frictional crawling, Barry and Bretscher (20) reported in 2010 that human neutrophils do swim. They discussed that propulsion may result from membrane treadmilling (rearward movement of the cell surface) or shape deformation (protrusions and contractions along the cell body) but provided no experimental or theoretical evidence supporting either of these hypotheses. Swimming studies on nonmammalian eukaryotic cell, the amoeba Dictyostelium discoideum, have later defended a deformation-based propulsion (21), whereas others discarded both treadmilling and shape deformation (22). For tumoral cells, a theoretical model of blebbing mentioned the possibility of migration in suspension by shape changes (23), whereas other modeling efforts validated a swimming mechanism based on shape deformation for the case of amoeba (24, 25, 26), cyanobacteria (27), and microalgae (2). A recent study on leukocytes, a mesenchymatous macrophages cell line RAW 264.7, reported that an amoeboid swimming mode could be artificially triggered by optogenetic activation of actomyosin contractility in cell rear (28). In contrast to previous studies, membrane treadmilling seemed mainly involved in propulsion, whereas the contribution of deformations was not assessed. Altogether, swimming of cells without flagellum remains mostly explained by shape deformation mechanisms. Moreover, swimming of mammalian cells without flagellum remains widely discarded (5,6,12,14,17, 18, 19,29).

Here, we demonstrate the existence of mammalian amoeboid swimming on primary human T lymphocytes and decipher its functioning experimentally and theoretically at the cellular and molecular scales. T lymphocytes are known to crawl on 2D adhering substrates (16,30, 31, 32) and in 3D matrices via adhesion/friction (11,33,34) at typical speeds of 20 μm min⁻¹. We observed swimming motility with an average speed of 5 μm min⁻¹ and show that propulsion can be mainly explained by a heterogeneous treadmilling of cell membrane. Actin-bound transmembrane proteins paddle by retrograde transport at the membrane and are recycled from the rear to front of cells by anterograde vesicular transport, whereas nonactin-bound transmembrane proteins are diffusive and hinder swimming. This molecular description is consistent with a speed significantly lower for swimming cells than for crawling cells and cortex retrograde flow. Interestingly, heterogeneous membrane treadmilling supports also ubiquitous cell motility within nonadhesive solid matrices because environmental friction is necessarily larger with a solid than with a fluid.

Materials and Methods

Cells

Whole blood from healthy adult donors was obtained from the Établissement Français du Sang (Le Mans, France). Peripheral blood mononuclear cells (PBMCs) were recovered from the interface of a Ficoll gradient/“Milieu de separation des lymphocytes” (Eurobio, Les Ulis, France). T lymphocytes were isolated from PBMCs with Pan T Cell Isolation Kit (Miltenyi Biotec, Bergisch Gladbach, Germany) and then were stimulated for 48 h with anti-CD3/anti-CD28 Dynabeads (Gibco by Thermo Fisher Scientific, Waltham, MA), according to the manufacturer’s instructions. T lymphocytes were subsequently cultivated in Roswell Park Memorial Institute Medium 1640 (Gibco by Thermo Fisher Scientific) supplemented with 25 mM GlutaMax (Gibco by Thermo Fisher Scientific), 10% fetal bovine serum (Gibco by Thermo Fisher Scientific) at 37°C, and 5% CO₂ in the presence of IL-2 (50 ng/mL; Miltenyi Biotec) and used 6–10 days after stimulation. At the time of use, the cells were >99% positive for pan T lymphocyte marker CD3 and assessed for activation and proliferation with CD25, CD45RO, CD45RA, and CD69 markers as judged by flow cytometry.

Quantitative cytometry for integrin expression level

For the quantification, we used the CELLQUANT Calibrator kit (ref 7208, Biocytex, Marseille, France). T lymphocytes were stained by indirect immunofluorescence with specific monoclonal antibodies, CD49d (HP2/1) for VLA-4 and CD11a (Hi111) for LFA-1, and then analyzed by quantitative flow cytometry. The expression level of the tested antigen was determined using the kit calibration beads.

Transfection of cells

For single-objective selective plane illumination microscopy (soSPIM) experiments with LifeAct-transduced cells, virus was produced in HEK 293T cells by cotransfecting the lentiviral plasmids pLenti.PGK.LifeAct-Ruby.W (a gift from Rusty Lansford, Addgene plasmid #51009; Watertown, MA) with psPAX2 and pMD2. G (a gift from Didier Trono, Addgene plasmid #12260 and #12259). PBMC were transduced by spinoculation of virus using polybrene, after 48-h activation with CD3-CD28 Dynabeads. The cells were then cultured with IL-2 and used 8 days after activation. The expression of LifeAct-RFP was controlled by flow cytometry. For total internal reflection fluorescence (TIRF)-fluorescence recovery after photobleaching (FRAP) experiments cells, RFP-lentivirus for RFP-actin transduction was bought from Merck (Lentibrite RFP-β-actin lentiviral biosensor; Kenilworth, NJ), and cells were transduced 48 h after activation with a multiplicity of infection of 10. For GFP-actin transfection, plasmid EGFP-Actin-7 from Addgene (ref 56421) was used with the electroporation program Amaxa T20.

Microfluidic channels and surface treatments

Polydimethylsiloxane (PDMS) microchannels were fabricated using standard soft lithography. A positive mold was created with a negative photoresist SU-8 3000 (Microchem Laboratory, Round Rock, TX) on silicon wafers (Sil’tronix, Archamps, France), and then replicas were molded in PDMS elastomer (Sylgard 184, Dow Corning, Midland, MI) and sealed on glass coverslides via plasma activation (Harrick Plasma, Ithaca, NY). The device is composed of one channel with one inlet and one outlet punched with a 2.4-mm puncher (Harris Uni-Core). For adherent crawling experiments, Ibidi channels IV^0.4 (CliniSciences, Nanterre, France) were coated overnight at 4°C with 10 μg/mL human ICAM-1-Fc (R&D Systems, Minneapolis, MN) in phosphate buffer solution (PBS) (Gibco). Channels were subsequently blocked with a solution containing 2.5% bovine serum album (BSA) (w/v; Axday, Dardilly, France) and 2.5% Pluronic acid F-108 (w/v; BASF, Ludwigshafen, Germany) in PBS for 30 min at room temperature and then rinsed three times with PBS and finally with Hank’s balanced salt solution (HBSS). Cells were injected at densities around 1.5 × 10⁶/mL and allowed to equilibrate for 10 min at 37°C before image acquisition. For nonadherent migration or swimming experiments, Ibidi channels IV^0.4 and PDMS microchannels were incubated with Pluronic F-127 (Sigma-Aldrich, St. Louis, MO) for 30 min at room temperature and then rinsed three times with PBS and finally with HBSS. Cells were injected at densities around 0.75 × 10⁶/mL in Ibidi channels and 6 × 10⁶/mL in PDMS microchannels of 40 μm height. Cells were allowed to equilibrate for 10 min at 37°C before image acquisition. For migration in nonadherent confined environment, microfluidic tubes and channels of height 2–4 μm were treated with Pluronics F-127 as described above. The adhesive/antiadhesive patterns were prepared by optical patterning. We used an inverted microscope (TI Eclipse, Nikon, Champigny Sur Marne, France) coupled to an ultraviolet laser source and a Digital Micromirror Device (Primo, Alveole, Paris, France) (35). Ultraviolet was projected on ICAM-1 substrates in the presence of a soluble photoactivator (PLPP, Alveole) to degrade the proteins (36). Samples were then rinsed with PBS solution and passivated with BSA and Pluronics F-127 for 15 min at room temperature.

Cell treatments

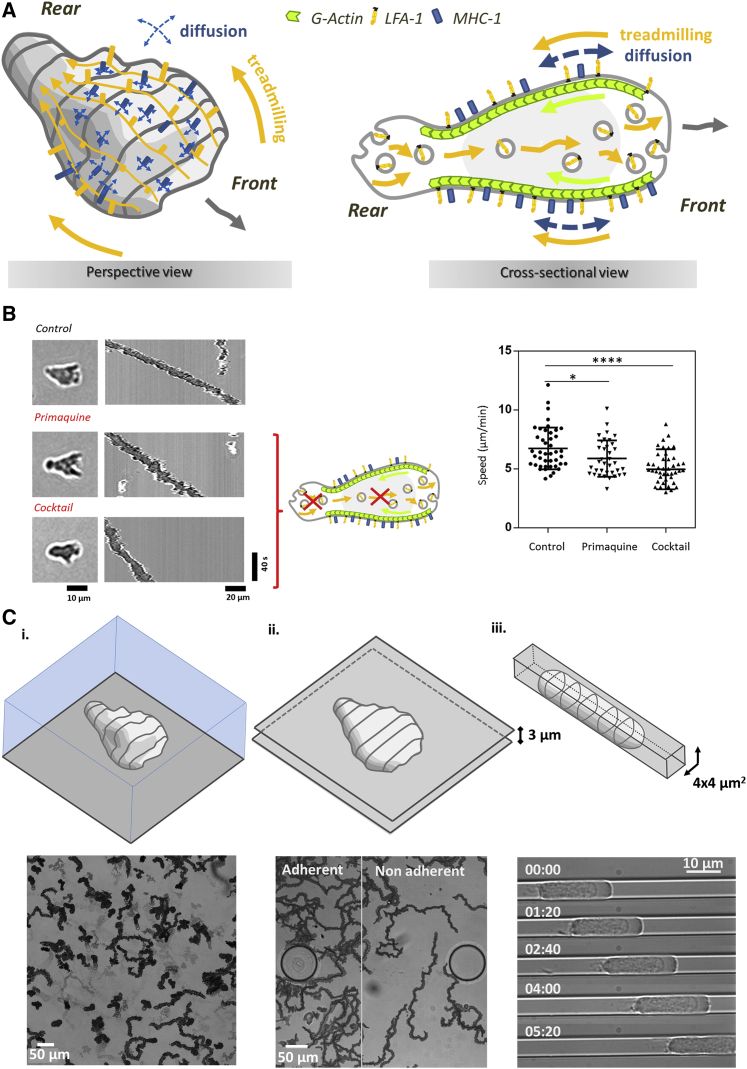
Stock solutions of blebbistatin (Fisher Bioblock Scientific), CK666 (Sigma-Aldrich), latrunculin (L12370; Molecular Probes, Eugene, OR), primaquine (primaquine biphosphate, Sigma-Aldrich), pitstop2 (Sigma-Aldrich), dynasore (dynasore monohydrate, Sigma-Aldrich), and cytohesin (secinH3, Sigma-Aldrich) were prepared in DMSO following manufacturer’s specification, stored at −20°C, and then diluted in culture medium for use in experiments. Cells were resuspended in solutions of 50 μM blebbistatin, 100 μM CK666, 50 nM latrunculin, 100 μM primaquine, or a cocktail of 50 μM pitstop2, 200 μM dynasore, and 20 μM secinH3 and then injected in the microchannels and allowed to settle in the channels for a period of 30 min at 37°C before image acquisition.

Viscosity and osmolarity measurements

Viscosity changes were performed using dextran of average molecular weight of 1500–2800 KDa (Sigma-Aldrich) at concentrations of 50 and 150 g/L. HBSS alone has a viscosity value of 0.001 Pa s, whereas the viscosity for HBSS plus 50 g/L dextran is 0.01, and for HBSS plus 150 g/L dextran, it is 0.1 Pa s. Adding dextran to the media increased the viscosity as well as the osmolarity up to 355 mosm/kg for the solution HBSS plus 150 g/L dextran. Dextrose (Sigma-Aldrich) was then used as an osmolarity control in HBSS media supplemented with 25 mM HEPES. Osmolarity measurements for the different media were performed using the automatic Micro-Osmometer Type 15 (Löser Messtechnik, Berlin, Germany), and calibration was done using standard solutions of 300 and 900 mosm/kg H₂O, according to the manufacturer’s instructions.

Experimental fluidic setup

All experiments were performed in a homemade chamber precisely thermostated at 37° to limit temperature instability, potentially inducing flow drifts within fluidic devices. For swimming close to a surface, we used Ibidi channels for experiments in HBSS, dextrose, and 50 g/L dextran solutions and 40 μm high PDMS microchannels for experiments in 150 g/L dextran to limit the observation range in the z axis because cells did not sediment. To minimize flow, channels were sealed with a plastic cap for Ibidi channels or with a 250 μm thickness PDMS film for the PDMS microchannels. On the microscope stage, the devices were surrounded by a 100% humidity chamber to minimize evaporation through PDMS. For experiments of swimming in suspension, cells were resuspended in 66% Ficoll to limit sedimentation effects and injected in 100 μm high channels. Minimization of drifts for swimming in suspension was more challenging than for the swimming close to a substrate. The microfluidic channel was set vertical (along the gravity axis), and the whole microscope was tilted by 90° to get a side-observation view. The channel was connected to a microfluidic flow control system (Fluigent MFCS-EZ) to control the unidirectional flow toward the bottom, and we used 2-m long tubes of 0.5 μm internal diameter to further limit drift by hydraulic resistance. Cell motion was recorded for at least 100 frames every 10 s.

Cell motion imaging

Experiments were performed with an inverted Zeiss Z1 automated microscope (Carl Zeiss, Oberkochen, Germany) equipped with a CoolSnap HQ CCD camera (Teledyne Photometrics, Tucson, AZ) and piloted by μManager ^1.4. Different objectives were used for bright-field mode (Plan Apochromat 20×/0.8, 63×/1.4 objectives) and for reflection interference contrast microscopy (RICM) mode (Neofluar 63/1.25 antiflex). A narrow band-pass filter (λ = 546 nm ± 12 nm) was used for RICM. 3D imaging was performed on cells stained with a lipophilic tracer DiO (Invitrogen, Carlsbad, CA), and cells were transfected with LifeAct-RFP cells. The imaging was done using a spinning disk (Inverted Nikon Eclilpse TI) equipped with two cameras (Photometrics EMCCD evolve) and controlled by MetaMorph and a home-made soSPIM setup.

soSPIM imaging and analysis

The soSPIM system, for single-objective selective plane illumination microscope, is a recently developed architecture that enables combining the advantages of low phototoxicity and high optical sectioning of light-sheet microscopy techniques with the high sensitivity provided by high numerical aperture objectives (37). The setup is composed of a high numerical aperture objective (CFI Plan Apochromat VC 60× WI 1.27 NA), a beam steering unit, and dedicated microfabricated devices containing mirrors angled at 45° alongside microwells. The soSPIM components are mounted on a conventional inverted microscope (Nikon Ti-E). The microfabricated chambers (see (37) for detailed descriptions of the chambers) are placed on an axial translation piezo stage (Mad City Labs, Madison, WI) within a controlled environment chamber (Tokai Hit, Shizuoka, Japan) for live cell imaging. Fluorescence emission is collected through the same objective used for excitation and is captured on a sCMOS camera (ORCA-Flash 4.0 V2, Hamamatsu, Japan). The whole acquisition process is steered under MetaMorph environment (Molecular Devices, San Jose, CA) using a homemade designed plugin that synchronizes the excitation and acquisition processes. Further details of soSPIM setup, calibration, and synchronization are described in (37). The 3D time series data sets acquired with the soSPIM setup were analyzed using the freely available software UCSF Chimera (38) (developed by the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco (supported by NIGMS P41-GM103311)). This software enables us to render surfaces of equal fluorescence intensity as well as normalization and alignment of whole 3D time series, which enhances the possibility to visualize cell membrane movement in our case.

Molecular motility imaging

For TIRF-FRAP experiments, cells were resuspended in HBSS-dextran 150 g/L solution at a concentration of 4.5 × 10⁶ cells/mL in the presence of CD11a/CD18 (BioLegend, clone M24) and HLA-A,B,C (BioLegend, clone W6/32) primarily conjugated antibodies. Alternatively, cells were labeled with Vybrant DiO by 10-min incubation at 37°C in the presence of 5 μL of dye per 1.5 × 10⁶ cells and then washed twice with HBSS and resuspended in HBSS-dextran. For LifeAct-RFP cells, no further staining was required. Cell suspensions were loaded into the devices and centrifuged for 3 min at 200 RCF. Cells were allowed to equilibrate for at least 10 min at 37°C before image acquisition. Videos were recorded on a Nikon Eclipse Ti microscope, equipped with iLas2 system and controlled by MetaMorph software. For DiO and MHC-1 staining, diffusion coefficients were calculated using the SimFRAP ImageJ plugin. LFA-1 cluster speed values were calculated from kymographs performed along the cell axis, whereas actin flow was calculated measuring the displacement of the frapped region. All values were corrected by the advance of the front edge, measured by a kymograph along the cell axis, to obtain a value relative to the cell front.

Cell tracking

For swimming experiments in the vicinity of a substrate (in 2D), cells were tracked with a homemade program (MATLAB software; The MathWorks, Natick, MA), and raw curvilinear speeds of swimming cells were calculated using trajectory time points every 30 s. Residual flow drift was corrected on each cell trajectory using the mean x- and y-movement values of all cells between two pictures. For high viscosity experiments, the fraction of cells squeezed toward the substrate by depletion force were discarded from the analysis. For swimming experiments in suspension (in 3D), a stack of bright-field images was taken every 10 s across the 100-μm height of the channel with a spatial pitch of 5 μm. To determine the position of a particular cell on the x axis at a given time, we analyzed the intensity distribution of the image of this cell on all images of the x axis stacks. The best focus corresponded to the image with the minimal SD of the intensity, which yielded an x position with a precision of 2.5 μm. Each cell trajectory was fragmented in 30-s steps, and cell-step speed was calculated using coordinates along the x and y axes. The speed component along y was considered negligible because we selected cells with an orientation perpendicular to the y axis. Total cell speed was calculated as the mean of all the 30-s step’s speed for each cell.

The circularity of cells was determined on bright-field images at magnification ×63. Images were first binarized using the Pixel classification workflow of the Ilastik software (39). The binaries images were then analyzed in MATLAB, and the circularity was calculated using the image processing toolbox, Circularity = Perimeter²/(4πArea).

Beads advection experiments

Streptavidin-coupled beads with a diameter of 2.7 μm (Dynabeads M-270 Streptavidin; Invitrogen) were washed three times with 0.1% BSA (w/v) and then incubated with 0.5 μg/mL biotin-coupled Protein-A (Sigma-Aldrich) for 1 h under stirring at room temperature and rinsed with 0.1% BSA. The beads were then incubated with 500 μg/mL ICAM for 2 h at room temperature and rinsed with 0.1% BSA. A final concentration of 0.125 mg/ml Dynabeads was added to the cell suspension. Bright-field images (Plan Apochromat ×20/0.8) were taken every 3 s. Beads were tracked manually from the moment the bead attached to the cell front until it reached the cell rear. Cells are moving in the frame of the laboratory, and cell rear was taken as a reference of bead position. All experiments were performed at least in triplicate for each substrate and/or drug.

Results

Leukocytes are motile on a solid substrate without adhesion or friction

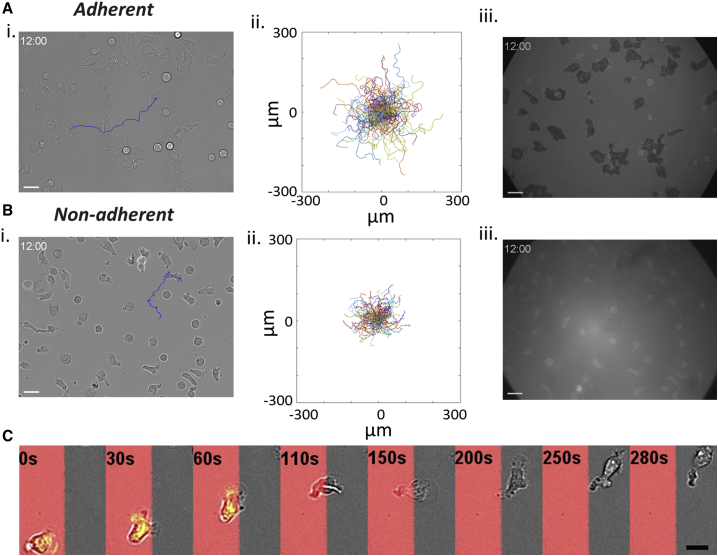
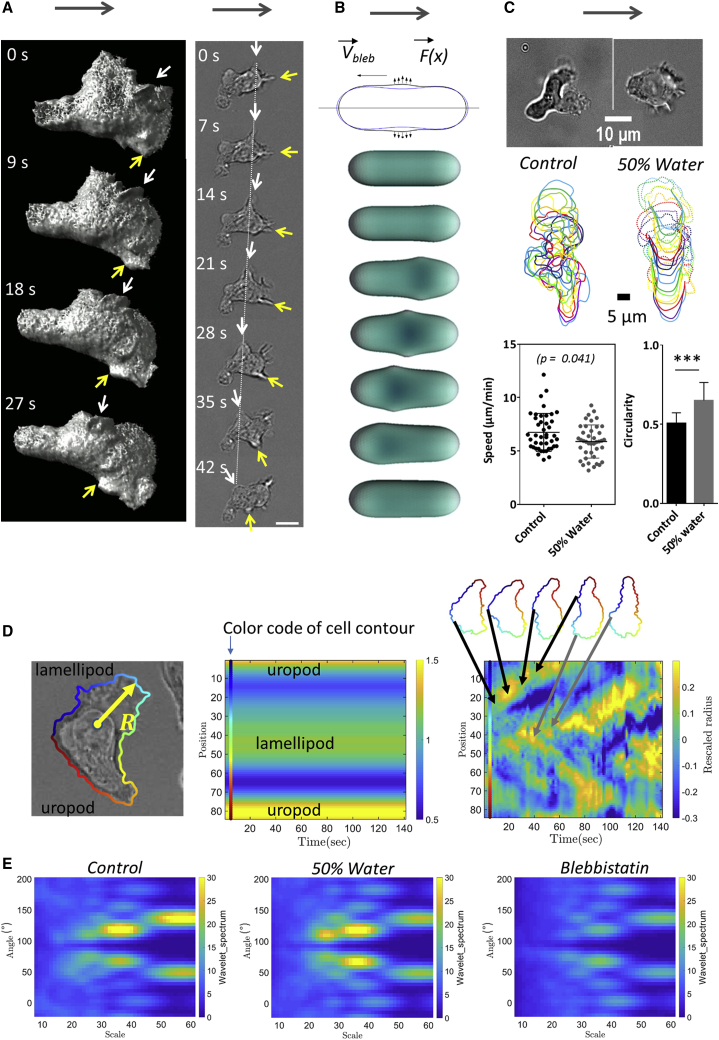
Upon recruitment from the blood stream toward inflammation zones, leukocytes arrest and crawl on the inner surface of blood vessels. This 2D migration, called crawling, was here mimicked in vitro with human primary effector T lymphocytes on glass substrates coated with ICAM-1 molecules, a specific ligand for the integrin adhesion molecules LFA-1. Effector T lymphocytes developed a stable polarization in suspension, with a front pole forming protrusions (lamellipods) under the influence of actin polymerization and a rear pole (uropod) undergoing contraction cycles enforced by actomyosin contractility. When introduced into a chamber coated with ICAM-1, lymphocytes sedimented, adhered to, and migrated on the substrates. They crawled with a random walk pattern (Fig. 1 A; Video S1) of curvilinear speed 14.7 ± SD 7.5 μm min⁻¹, with a widespread lamellipod in front, the nucleus positioned in the cell central zone, and a narrow uropod in rear. To challenge the idea that adhesion is necessary for amoeboid migration on a 2D substrate, we then replaced the ICAM-1 surface treatment by an antiadhesive coating of Pluronic F127 (Fig. 1 B). Without adhesion, cells were highly sensitive to residual flows, which must be dampened to allow observation and characterization of self-propulsion. After sedimentation, cells displayed a random walk with an apparent average curvilinear speed of 5.5 ± SD 2.2 μm min⁻¹ (Fig. 1 Bi; Video S1). To assess the adhesion state of cells versus surface treatment, we performed contrast interferometric imaging, RICM (Fig. 1, A and Biii; Video S1). A dark contact zone of cells on ICAM-1 substrates corresponded to a cell-substrate distance around 50 nm, which is characteristic of tightly adhered cells with extracellular proteins and polysaccharides confined between the substrate and the adherent plasma membrane (40,41). In contrast, a bright contact zone of cells on Pluronics in RICM corresponded to a distance around 100 nm, which is typical of the presence of a thin liquid film separating the substrate from the fluctuating plasma membrane of a cell settling by gravity. According to the RICM assays, 100% of polarized and motile cells were nonadherent on Pluronics (Fig. S1). Nonadherent cells migrating in the vicinity of a nonadherent substrate were further imaged in 3D by spinning disk microscopy (Video S2). Although strong phototoxicity hampered long-term 3D imaging, migration of polarized cells with dynamic 3D shape deformations could be monitored on tens of micrometers. Altogether, these data show that polarized lymphocytes do migrate on a 2D surface in the absence of adhesion.

Figure 1.

From adherent to nonadherent 2D migration. Primary human effector T lymphocytes are shown. (A) Adhesive crawling on ICAM-1-treated substrate and (B) nonadherent migration on Pluronic F127-treated substrate. (i) Bright-field images. Blue lines correspond to the track of a particular cell for 12 min. Scale bars, 20 μm. See also Video S1. (ii) Representative tracks of motile cells in a single experiment (time lag = 20 s, duration 16 min, n > 100 cells). (iii) RICM images. Cell contact zone is dark for cells crawling on ICAM-treated surfaces, revealing an adhesion phenotype, and white for cells on nonadhesive surfaces, attesting the absence of adhesion to the surface (see also Fig. S1). Bars are standard deviations. ****p < 0.0001 (two-tailed Student’s t-test). Scale bars, 20 μm. (C) Image sequence of a cell migrating over adjacent stripes of adhesive ICAM-1 (red) and antiadhesive polyetheleneglycol (gray) prepared by LIMAP (72) with a width of 40 μm. The sequence is a merge of fluorescent images (ICAM-1, red), bright-field images (cell morphology, gray), and RICM images (adhesion zone, green). Scale bars, 20 μm. See also Video S3. To see this figure in color, go online.

Video S1. From Crawling to Swimming in the Vicinity of a Substrate

(Left) Crawling on adhering ICAM-1-treated substrate. (Right) Swimming on Pluronic F127 treated surface. First sequence, 20× bright field transmission microscopy, then 63× bright field transmission microscopy and finally ×63 reflected interference contrast microscopy.

Video S2. 3D Imaging of Primary Human Effector T Lymphocyte Swimming in Spinning Disk Microscopy

Videomicroscopy sequence of swimming T lymphocytes stained with CMFDA (5-chloromethylfluorescein diacetate) on Pluronic F127 treated surface for 14 min 40 s with a time lapse every 20 s and stack of 10 slices taken every 1 μm. Some unpolarized cells do not swim. The arrow points a polarized and swimming cell that crosses the whole field of view. Scale bars, in μm indicated on axis, magnification: 63×.

Cells can switch between adherent and nonadherent migration

To shed light on the transition between adherent and nonadherent migration, we then presented lymphocytes to substrates patterned with alternated stripes of adhesive and antiadhesive coatings (Fig. 1 C; Video S3). Although mesenchymatous cells are known to be strictly confined to adherent stripes in similar experiments (42), lymphocytes showed here a unique capability to transfer repeatedly between adherent and nonadherent zones. The stripes width of 40 μm was chosen to be large enough to allow cells to travel on homogeneous stripes for tens of seconds and small enough to favor the occurrence of transitions between different stripes. Interference microscopy attested that cells traveled across the adhesive zones with adhesive contact to the substrate (green signal) and across antiadhesive zones with a lubrication film separating the cells from the substrate (no green signal). Cells were even found to have the same probability of presence on adherent and antiadherent stripe (43). These observations suggest that the transition between adherent and nonadherent motility modes is fast or that the two phenotypes share the same machinery, which altogether cancels the idea of switch between two modes.

Video S3. Immediate Transition between Crawling and Swimming

Migration on alternative 40 μm wide stripes of adherent ICAM-1 and non-adherent Pluronic F127 prepared by LIMAP (31). Superimposition of fluorescent image (ICAM-1, red), bright filed transmission image (greyscale) and reflection interference contrast microscopy image (bright green corresponds to cells adhesion fingerprints) taken at 63×.

Diffusive versus active motion in nonadherent migration

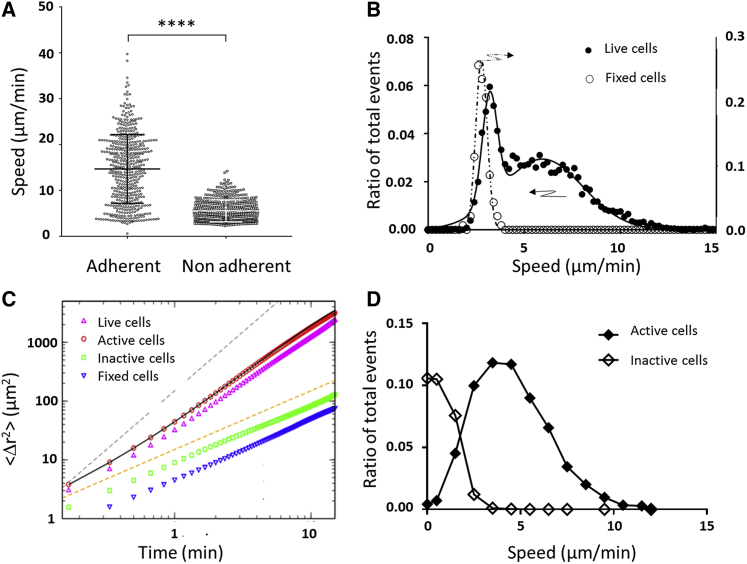
The average speed of cells measured using the average displacements of cell mass center every 30 s was significantly different between adherent and nonadherent cells (Fig. 2 A). However, this estimation of the active motion of cells was biased by several effects for nonadherent cells. First, our system of effector lymphocytes in suspension comprised two populations, one of round and inactive cells with a typical circularity >0.8 and the other of polarized and active cells with a typical circularity <0.8. The average fraction of active cells in suspension is around 48 ± SEM 5%. Fig. 2 B presents the histogram of raw speeds for individual cells in the case of live and fixed lymphocytes (all cell shapes are frozen by paraformaldehyde in the latter case). Although fixed cells were not motile, they displayed an apparent raw curvilinear speed of 2.8 ± 0.3 μm min⁻¹ because of Brownian diffusion. Live cells displayed two populations, one with low speed corresponding to round and inactive cells and one with higher speed corresponding to polarized and active cells. The apparent speed of inactive cells was close to the one of fixed cells, meaning that their movement was close to Brownian motion. In contrast, active cells had a significantly larger average raw curvilinear speed of 5.9 ± 4.2 μm min⁻¹. However, this new estimated speed does not strictly characterize active motility because it still comprises diffusion effects as evidenced by fixed cells or round inactive cells. We therefore performed a more detailed analysis of cell trajectories to discriminate the diffusive contribution from the effective active motion. First, we investigated the mean-square displacement averaged over all cells in the population as a function of time. Second, we fitted the mean-square displacements as a function of time interval by a random walk law, which combines 2D Brownian-like diffusion with persistent motion, and we analyzed the distribution of speeds v_s and diffusion coefficients D_t obtained by the fitting procedure:

$${\left[r\left(t\right)-r\left(0\right)\right]}^2=v_s^2{t}^2+4D_{t}t,$$ (1)

Figure 2.

Active polarized cells migrate without adhesion in 2D at 5 μm min⁻¹. (A) Raw curvilinear speed of cells crawling on adherent ICAM-1-treated substrates and migrating on antiadherent Pluronic F127-treated substrates, estimated by averaging the displacements of cell mass centers over intervals of 30 s. Bars are standard deviations. N = 500 cells, ****p < 0.0001 (two-tailed Student’s t-test). (B) Histogram of raw curvilinear speed of live nonadherent migrating cells (filled dots, left y axis) and fixed cells (hollow dots, right y axis). Data are fitted with a single Gaussian for fixed cells (dotted line) and a double Gaussian for live cells (dark line). Live cells are composed of one population of diffusing cells and one of migrating cells with an average speed of 5.9 μm min⁻¹. (C) Mean-square displacement <[r(t) − r(0)]²> as a function of time for all cells and all steps was combined in the case of live cells (upward pointed triangles) and fixed cells (downward pointed triangles). Fixed cells have purely diffusive behavior corresponding to D_t = 2.34 μm² min⁻¹. Circles and squares show the mean-square displacement for active and inactive cells, respectively. Black line is a fit of active cells using Eq. 9 (Supporting Materials and Methods) with v_s = 4.3 μm min⁻¹, D_r = 0.19 min⁻¹, and D_t = 7.28 μm² min⁻¹. Dashed lines show the limit cases of purely ballistic and diffusive behavior with slopes of, respectively, 2 and 1. (D) Histogram of average speed per cell determined using Eq. 1 as in (C) for active cells (filled diamonds) and inactive cells (hollow diamonds). Root mean-square speed of active cells is equal to 4.9 μm min⁻¹. Lines are guides for the eye. To see this figure in color, go online.

We then separated all cells in the population into two groups. We considered as active the cells that traveled at least a distance of 25 μm (about two cell diameters) during the acquisition time of 13 min and the rest of the cells being referred to as inactive. Fig. 2 C shows the mean-square displacement as a function of time for fixed and live cells, and we also report inactive and active cells separately for live cells. Both inactive and fixed cells had a diffusive behavior, with an average diffusion coefficient of, respectively, 2.3 and 1.1 μm² min⁻¹, whereas active cells had a superdiffusive behavior. A satisfactory fit could not be obtained with Eq. 1, and we extended the model by adding rotational diffusion (with a rotational diffusion coefficient D_r), which accounted for gradual changes in the direction of the cells (see Supporting Materials and Methods). The fitting procedure gave here v_s = 4.3 μm min⁻¹, D_r = 0.19 min⁻¹, and D_t = 7.28 μm² min⁻¹ (black curve in Fig. 2 C). To obtain the distribution of speeds of active cells, we then simplified the analysis and considered only displacements for time intervals of 2 min, which is 3 times smaller than 1/D_r and therefore allowed us to neglect rotational diffusion. As can be observed in Fig. 2 D, most of the active cells had a speed around 3 to 5 μm min⁻¹, and root mean-square speed extracted of individual active cells was finally 4.9 μm min⁻¹ in cell culture medium. This precise determination of cell speed without adhesion will later be instrumental to propose a consistent mechanism.

Active lymphocytes swim in free suspension

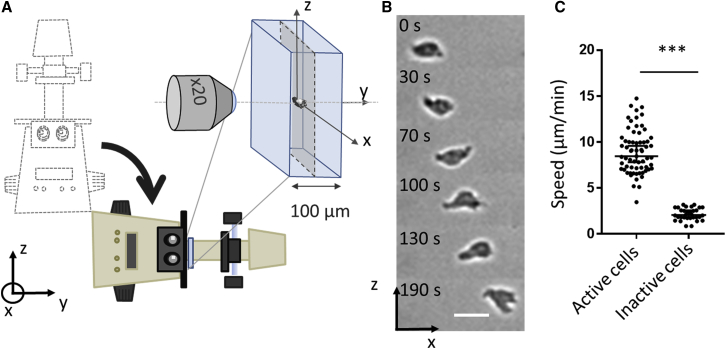
Although active lymphocytes migrated in the vicinity of a surface without adhesion, one may argue that propulsion close to a substrate may be favored by hydrodynamic coupling between cells and substrate. We therefore performed experiments with cells in bulk suspension to test the existence of swimming without hydrodynamic coupling to any solid wall. It appeared quite challenging to cancel artifactual cell displacements in suspension. Conditions of negligible flow were difficult to achieve because of several perturbative effects such as temperature gradients, pressure imbalance between channel outlets, or gravimetric imbalance resulting from cell dispersion inhomogeneity. In the end, we used a microfluidic channel connected to a high-precision pressure controller and highly resistant tubing connections to slow down pressure-driven flows. Besides, cell sedimentation was decreased using Ficoll-supplemented medium to match the average density of cells. Still, cells had dispersed densities, and they exchanged material with the medium, so that sedimentation drifts were changing with each cell and with time. As a consequence, flow and sedimentation drifts could not be totally cancelled, and we decided to merge their combined artifactual effects on a single axis by tilting the microscope by 90° and setting the main axis of the microfluidic channel along the vertical axis (Fig. 3 A and Supporting Materials and Methods for details). In this configuration, the vertical z axis cumulated artifacts because of pressure-driven flow across the microchannel main direction, which was low but non-null, and because of the gravity-induced sedimentation, which was different from one cell to another. Swimming prowess was then measured on the y and x axes (Fig. 3 B; Video S4). Cell position on the y axis was determined from the selection of the best-focused images on y stack scans for each time point. In line with the results on a nonadherent substrate, round cells (circularity >0.8) were used as a negative control for inactive and nonswimming cells, whereas polarized cells (circularity <0.8) were tested as the active and potentially swimming cells. Fig. 3 C shows that inactive cells displayed a curvilinear speed of 2.1 ± SD 0.6 μm min⁻¹, which is close to the value found for diffusive cells in 2D. In contrast, active polarized cells displayed an apparent average curvilinear speed of 8.9 ± SD 2.4 μm min⁻¹. These data confirm the intrinsic capability of polarized lymphocytes to swim in suspension at several μm min⁻¹. Furthermore, experiments showed that the vicinity of a wall within a few micrometers range had no significant effect on swimming speed (Fig. S2). We performed theoretical calculations to get quantitative insight on the influence of substrate on swimming speed down to a distance of 100-nm range, which corresponds to the case of sedimented cells migrating over nonadherent substrates in Figs. 1 and 2. Our calculations support that the vicinity of a single wall has a negligible effect on swimming speed (see Supporting Materials and Methods, Vicinity of a wall is negligible). In what follows, systematic measurements to characterize swimming properties were therefore performed with the more convenient setup of cells close to a nonadherent substrate.

Figure 3.

Lymphocytes swim in free suspension. (A) Schematic of the setup used to image swimming in suspension with a microscope tilted by 90° and a flow channel oriented vertically. (B) Sequence of images of a cell swimming in the center of the channel in the direction of the x axis. Scale bars, 20 μm. See also Video S4. (C) Speed of active and inactive cells for a distance to the wall larger than 40 μm. Experiments N = 6, cells N >16, and steps N >80. ^∗∗∗p < 0.001 (two-tailed Student’s t-test). To see this figure in color, go online.

Video S4. Swimming in Bulk Suspension

Movie of two cells suspended in a medium of matched density using a microscope tilted by 90°and a flow chamber oriented vertically for sideway observations.

Swimming propulsion is oriented along polarization axis toward lamellipod edge

Swimming appears to be a specific property of polarized and active cells, whereas inactive and round cells are just passively diffusing. We further analyzed the angular difference between the direction of polarization of active cells and their instant displacement direction (Video S5). Active cells showed a maximal probability for swimming direction co-linear to cell polarization, whereas fixed cells displayed no preferential orientation of motion (see Fig. S3). This analysis supports further that the process of swimming is specific to active and polarized cells and that swimming propulsion is oriented along the cell’s polarization axis in the direction of lamellipod.

Video S5. Correlation of Swimming Direction with Cell Polarization Axis

T lymphocytes swimming on Pluronic F127 treated surface imaged in bright field at 10× of primary human effector. The red bars direction represents the instant tangent to trajectory, and their norm is proportional to the ratio between instant speed and maximal speed reached by the cells. The yellow bars direction represents the orientation of the ellipse having the same second-moment as the segmented cell, and their norm scales with the value of the ellipse eccentricity, as (exp(ecc)-1)/(exp(1)-1), where ecc is the eccentricity of the ellipse which varies between 0 and 1. (For more details see Fig. S3 and corresponding paragraph).

Viscosity hardly affects swimming speed

Swimming relies necessarily on the coupling between a cell motility machinery and the surrounding fluid. One may therefore expect the viscosity of the fluid to have an effect on the coupling efficiency. Swimming speed was measured versus the different viscosities of the external medium by the addition of dextran of the molecular weight 2000 kDa. Viscosity was increased by 100-fold as compared to normal medium. Higher dextran concentrations were inaccessible because cells were strongly pressed to the substrate by depletion force and consequently immobilized. For a 10-fold viscosity increase, there was a slight decrease of speed by 25%; however, this tendency was not confirmed for a 100-fold viscosity increase, for which speed was similar to control. Hence, counterintuitively, cell swimming speed was hardly affected by a change of viscosity of two orders of magnitude (Fig. S4; Table S1). The insensitivity of cell speed to external viscosity is traced back to the fact that dissipation because of swimming occurs predominately in the cell cortex, which has a much higher viscosity compared to the suspending medium. This means that we expect an effect of external viscosity only when it becomes comparable to that of the cortex.

Actin mediates swimming propulsion by polymerization and, to a lesser extent, contractility

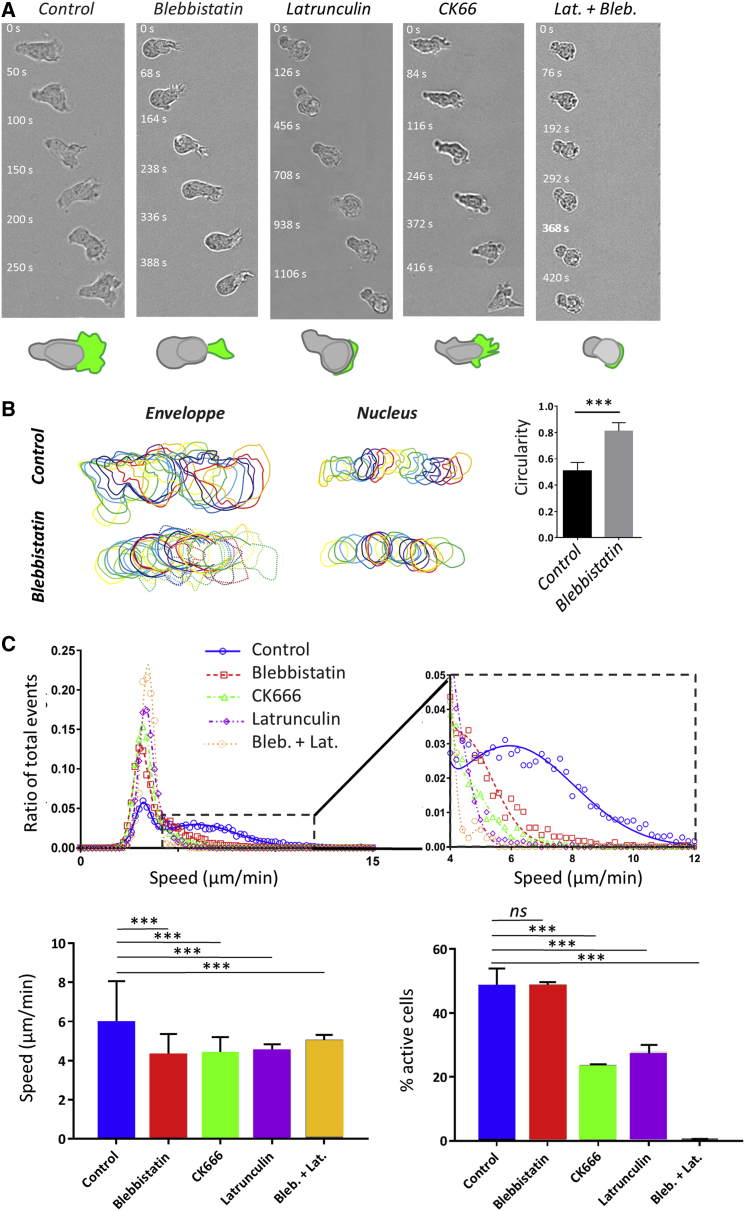
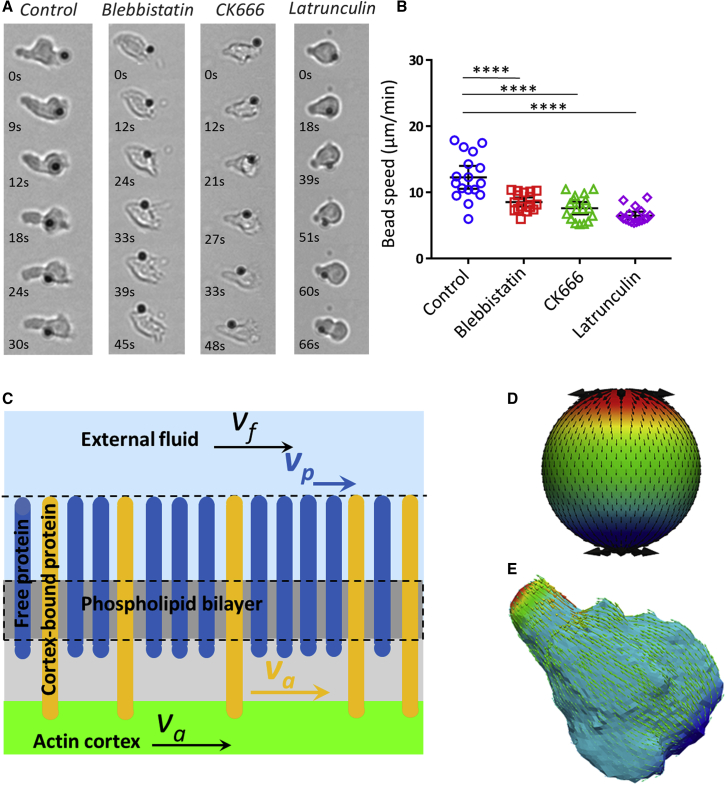
Actin cytoskeleton is widely accepted as the molecular engine propelling cell crawling. Effector T lymphocytes are characterized by a strongly polarized state with actomyosin contractility, mainly in the cell rear (uropod), and actin polymerization, mainly in the cell front (lamellipod). We first perturbed cells with blebbistatin, a potent inhibitor of actomyosin contractility. The uropod was not distinguishable anymore, and the cell body looked devoid of contractile activity, but motile cells displayed a small lamellipod, which attested a conserved front-rear polarization. (Fig. 4, A and B; Video S6). The dampening of cell’s deformations because of contractility inhibition induced a significant increase of the circularity index (Fig. 4 B, right), whereas swimming speed decreased by 25% as compared to control cells (Fig. 4 C; Table S1). Swimming direction and cell polarization were still markedly correlated, even more than for control cells (Fig. S3). These results suggest that actin contractility and contractile cell deformations are not required for swimming and, conversely, that frontal actin polymerization plays a dominant role. We then perturbed actin polymerization in the cell front with latrunculin (Fig. 4 A; Video S6). The dose was chosen low enough to inhibit the lamellipod formation at the cell front while preserving contractility in the cell rear. Latrunculin-treated cells were therefore deprived of lamellipod but conserved a uropod, which is the opposite situation to blebbistatin-treated cells. The fraction of swimming cells was significantly lower than for both control and blebbistatin-treated cells (Fig. 4 C; Table S1), which suggests that actin polymerization plays a more preponderant role than contractility in propulsion. We then treated cells with CK666, an inhibitor of the protein Arp2/3 that mediates branching of the actin network in lamellipods (Fig. 4 A; Video S6). Although the front of migrating leukocytes usually displayed lamellar-shaped protrusions (44), CK666-treated cells formed filopodia and blebs in cell front. The average effect of CK666 on swimming speed was found intermediate between the blebbistatin and latrunculin cases in terms of the fraction of migrating cells. Altogether, swimming was more efficient with a perturbed lamellipod (CK666) than without lamellipod (latrunculin). This correlation between a stronger perturbation of the lamellipod and slower swimming is in line with the lamellipod being important for propulsion. Besides, swimming was more efficient for totally inhibited uropod (blebbistatin) than for partially inhibited lamellipod (CK666), which corroborates the idea that swimming would be mediated to a larger extent by lamellipod rather than by uropod. Finally, swimming was fully abrogated with a combination of blebbistatin and latrunculin (Fig. 4, A and C; Video S6), which suggests that the actin network is the main engine of lymphocyte swimming.

Figure 4.

Actin propels swimming more by polymerization than by contractility. (A) Bright-field image sequences show the shape and dynamics of cells swimming on an antiadhesive substrate versus the addition of actomyosin inhibitors. Shown from left to right: wild-type cells and cells treated with 50 μM blebbistatin, 0.05 μM latrunculin, 100 μM CK666, and combined latrunculin and blebbistatin. See also Video S6. Cartoons at the bottom reproduce the cell in the first image to illustrate in each case the shape of the cell body (rear and nucleus) in gray and of the cell front or lamellipod in green. Blebbistatin-treated cells have a roundish cell body without traveling protrusion and a reduced but active lamellipod; latrunculin-treated cells have almost no lamellipod; and CK666-treated cells have a perturbed lamellipod forming blebs and spikes. Cells treated with blebbistatin and latruculin have a roundish noncontractile cell body and no lamellipod (Scale bars, 10 μm). (B) Left: shown are representative sequences of envelope and nucleus contours of a control cell (top) and of a cell treated with 50 μM blebbistatin (bottom), suggesting a difference of contractile activity. Time lag between each contour is 10 s. Right: shown is the quantification of the circularity of cells envelops for control cells and 50 μM blebbistatin treatment on image sequence taken at magnification ×60 and cell contour determined using Ilastik. Error bars correspond to standard deviation. Cells N >10, and experiments N = 3. ^∗∗∗p < 0.001 (two-tailed Student’s t-test). (C) Top: shown is a histogram of raw curvilinear speeds for swimming cells in response to above-mentioned actin inhibitors treatments. The lines correspond to a fit by a double Gaussian function. Insert presents a zoom of the histogram for the active cells corresponding to the Gaussian of high mean speed. Bottom left: shown is the average speed and SD corresponding to the Gaussian of high mean speed. Bottom right: shown is the percentage of active motile cells, and error bars correspond to SEM. Cells N = 4342 (HBSS), 2353 (blebbistatin), 5582 (CK666), 2255 (latrunculin), and 403 (blebbistatin plus latrunculin). Error bars correspond to SEM. Experiments N >5. ^∗∗∗p < 0.001 with respect to homogeneous substrate, one-way ANOVA followed by the Tukey multiple comparison test. To see this figure in color, go online.

Video S6. Role of Actomyosin Network in Swimming Motion

Movies in bright field at 63× of primary human effector T lymphocytes swimming on Pluronic© F127 treated surface in the presence of actin inhibitors: control, 50 μM blebbistatin, 0.05 μM Latrunculin or 100 μM CK666. Scale bars, 20 μm.

Rearward traveling of membrane protrusions alone seems not efficient enough to propel lymphocyte swimming

Swimming propulsion arises from the interactions of the cell external membrane with the surrounding fluid; therefore, the dynamic properties of the cell external membrane is the key of the swimming mechanism. Like all amoeboid cells, lymphocytes display highly dynamic shape deformations, which are good candidates for generating propulsion. To precisely monitor cell deformations and circumvent the strong photosensitivity issues, we resorted to light-sheet soSPIM microscopy on cells transfected with RFP-Lifeact. The 3D dynamics of cell cytoskeleton (Fig. 5 A, left; Video S7) revealed waves of lamellar protrusions that formed with different orientations in the cell front (44,45) and traveled backward until they vanished in the cell rear. Similar propagating waves of cell membrane were also visible in transmission microscopy (Fig. 5 A, right; Video S8) (18,46,47) together with constriction rings, provoking sudden nucleus movement and important reorganizations of cell’s contours toward the direction of cell motility (see also Video S8). This dynamics of cell contours is qualitatively reminiscent of the shape deformation cycles analyzed in theoretical modeling of amoeboid swimming (2). To get more quantitative insight, we developed a direct numerical simulation of normal active forces applied to the cell membrane (with force-free and torque-free conditions) that generated deformations traveling backward along the cell body (Figs. 5 B and S5 and S6; Video S9). Our model presents the rare advantage of using only parameters accessible experimentally, such as the amplitude and speed of deformation waves. Waves of a few microns amplitude and 10 μm min⁻¹ speed observed experimentally yielded in our simulation a swimming speed 1000 times slower than the experimental swimming speed (Fig. S7). This quantitative analysis suggests strongly that deformations are not efficient enough to propel swimming of lymphocytes. To support this result further, we performed perturbations of cell shapes by osmotic swelling. The addition of 50% of water in medium resulted in an average cell volume increase by 65%, as assessed by the size increase of round cells, and imposed a more roundish shape on motile cells, as assessed by the increase of their circularity index (Fig. 5 C; Video S10). Nevertheless, swimming speed was not significantly affected. This result supports that average shapes are not crucial for swimming, but it says nothing about the role of propagating deformations. We then performed a spatiotemporal analysis of cell’s contours using wavelet transforms (Figs. 5, D and E, S8, and S9). As compared to control cells, the dynamic mode of protrusion that propagated backward was found hardly altered by osmotic swelling but strongly affected by blebbistatin treatment. For osmotic swelling, protrusions paddling and swimming are both hardly perturbed, which yields little information. In contrast, with blebbistatin treatment, the amplitude of propagative protrusions was decreased by a factor larger than two (see also Video S6) so that swimming speed should decrease by more than 80% according to our model of propulsion by deformations (see Fig. S7). In fact, the experimental speed decreased by less than 25%, which further supports that protrusion may not be the main propelling source of swimming. Finally, we reasoned that if micron-scale deformations were not sufficient to propel swimming, sub-micron-scale deformations, typically undetected by optical microscopy, might mediate efficient propulsion. We therefore simulated the effect of submicronic waves by varying their number, shapes, and organization and found an optimum for an idealized case of trains of three waves traveling in phase (see Figs. S10 and S11). Still, swimming speed was more than 10 times slower than the protrusions traveling backward at 10 μm min⁻¹. Altogether, quantitative analysis and perturbations experiments support that cell deformations are not sufficient to propel lymphocytes swimming. This conclusion motivates the search of alternative and more plausible sources of propulsion.

Figure 5.

Protrusion paddling alone seems not efficient enough to propel swimming. (A) Image sequence of swimming cell with micron-scale protrusions traveling along cell body. Left: soSPIM images of a cell transfected with RFP-Lifeact reveals the shape and motion of waves of actin protrusion in three dimensions. White and yellow arrows point to particular protrusions. See also Video S7. Right: bright-field images of a swimming cell show dynamics of protrusions. See also Video S8. Protrusions (white and yellow arrows) travel backward in the frame of the cell and of the lab (white dashed line). Gray arrows indicate swimming direction. Scale bars, 10 μm. (B) Schematic illustrates the model of cell swimming by protrusive blebs. Top: blue and black contours are the initial and deformed configurations of the cell in the model. Bottom: shown is the sequence of cell shapes obtained by the numerical simulation. Simulations yield that a cell propelled by shape waves is 1000 times slower than the protrusion wave (details in Supporting Materials and Methods). (C) Osmotic swelling affects cell shape but not swimming speed. Top: representative images of a cell in medium and in water dilution at 50%. Middle: representative cell contour sequences (time lag is 10 s between each contour). The cell swollen by osmotic stress displays less deformations of cell body (full lines), but lamellipod protrusions are still distinguishable (dotted line). Bottom: shown is the swimming speed in medium and with water dilution at 50%. (cells N >30, p value of t-test) and circularity of cells on image taken at magnification ×60, with cell contours determined using Ilastik. Error bars stand for standard deviation Cell N >10, and experiments N = 3. ^∗∗∗p < 0.001 (two-tailed Student’s t-test). See also Video S10. (D) Measurement of cell protrusion dynamics. Left: Shown is a representative example of an elliptic Fourier contour reconstruction. Radius R definition of edge distance to the center of mass is shown. Middle and right: shown are kymographs of rescaled R versus position along the cell perimeter, either averaged in time (middle) or with time-average contribution subtracted (right). Color scale on the left corresponds to the color code used in contour reconstruction, allowing one to identify the position in kymographs of lamellipod, uropod, and propagating protrusions. See also Fig. S8. (E) Spatiotemporal spectrum of protrusion dynamics by wavelet transform. Shown is the average wavelet spectra of rescaled R kymographs without time-averaged contribution (see also Fig. S9). To see this figure in color, go online.

Video S7. 3D Live Imaging by so-SPIM of the Actin Cytoskeleton of Swimming Primary Human Effector T Lymphocyte

Video microscopy movie of RFP-Lifeact transfected cell, showing lamellar-protrusion forming with random orientation in cell front and traveling backwards at around 10 μm min⁻¹.

Video S8. Live Bright Field Imaging of Swimming Primary Human Effector T Lymphocytes Showing Protrusion Retrograde Motion and Nucleus Forward Squeezing through Constricted Rings

Bright field videomicroscopy at 63× of primary human effector T lymphocytes swimming on Pluronic F127 treated surface. Scale bars, 10 μm.

Video S9. Swimming of a Cell by the Motion of Two Blebs on the Cell Surface

The color here represents the mean curvature of the cell surface.

Video S10. Lymphocytes Swimming with Perturbation of Cell Body Deformation

Bright field videomicroscopy at 63× of primary human effector T lymphocytes swimming on Pluronic F127 treated surface in pure medium (left) and in a medium diluted with water at 50% (right). Osmotic stress cancels the deformations of cell body by swelling but cell speed is 8 μm min⁻¹ like for control cells.

Membrane rearward treadmilling correlates with swimming speed

Normal motion of cell membrane seems to yield insufficient propulsion, but the membrane of amoeboid cells displays also tangential movement triggered by the retrograde flow of the inner actin cortex. To evidence the motion of cell’s external membrane, we incubated swimming cells with ICAM-1-coated beads. When cells encountered beads along their path, beads attached to the cell front via the transmembrane integrins LFA-1 and were carried backward (Fig. 6 A; Video S11). The average speed of beads in the reference frame of the cell was 12 ± 3 μm min⁻¹, which is significantly larger than swimming speed. Similar measurements with inhibitors blebbistatin, CK666, and latrunculin showed a decrease of bead’s speed as compared to control (Fig. 6 B; Video S11). More precisely, the speed changes with blebbistatin, CK666, and latrunculin correlated with the respective changes in swimming speed (Fig. 6 B), which suggests a direct role of tangential membrane motion in swimming.

Figure 6.

External membrane retrograde flow can propel swimming efficiently. (A) Bright-field images of ICAM-coated beads traveling from front to back on the cell membrane of swimming primary human effector T cells in HBSS control media and with 50 μM blebbistatin, 100 μM CK666, and 0.05 μM latrunculin (left to right). Scale bars, 10 μm. See also Video S11. (B) Traveling speed of ICAM-coated beads versus inhibitor type (n = 17 cells for each case, error bar is SD, ^∗∗∗∗p < 0.0001, Dunnet’s multiple comparison test versus control condition). (C) Cartoon of the external and internal structure of the cell membrane considered in the modeling of membrane dynamics. (D and E) Retrograde flow pattern on a model spherical cell (D) and a cell with an experimental shape (E) extracted from soSPIM images of (Fig. 5A). Swimming speed is found in both cases equal to the speed of the membrane at equator. See also Video S12. To see this figure in color, go online.

Video S11. Cell Membrane Retrograde Flow Revealed by Attached Beads

Bright field videomicroscopy of ICAM-coated beads traveling from front to back on the cell membrane of swimming T-cells in HBSS control media, 50 μM blebbistatin, 0.05 μM Latrunculin, or 100 μM CK666.

Retrograde flow of cell membrane can propel swimming

To analyze quantitatively the propulsion strength induced by tangential movements of the cell’s membrane, we developed a basic model of retrograde flow, taking into account an internal actin cortex, a cytoplasmic lipidic membrane, and transmembrane proteins protruding outside the cell (Fig. 6 C). The transfer of movement from the inner cortex to the fluid surrounding the cell can be either total or partial depending on the coupling mechanism between the actin cortex and the lipids and proteins of the membrane, as discussed below. We first considered that the cell surface was made of a homogeneous membrane with an average treadmilling velocity proportional to the velocity of the actin cortex, v_a, and a transmission coefficient denoted β. In the laboratory frame, the velocity of the fluid adjacent to the cell membrane, denoted as v_f, is:

$$v_f\left(r\right)=\beta v_a\left(r\right)+v_s+{\omega }_{s}r,$$ (2)

where ν_s and ω_s are, respectively, the translation and rotation swimming velocities of the cell. They were obtained by solving the Stokes equations (see Supporting Materials and Methods) in the fluid outside the cell, taking as boundary conditions that the flow vanished at large distances away from the cell and that it obeyed Eq. 2 at the cell surface. The obtained flow field was parametrized by the still unknown quantities ν_s and ω_s, which allowed us to express the viscous forces acting on the cell. The system was closed by imposing that the total force and torque acting on the swimmer vanished, yielding the values of ν_s and ω_s. A remarkable observation is that the swimming velocity does not depend on the viscosity of the suspending medium for a given cortex velocity (see Supporting Materials and Methods for a proof), which is consistent with experimental observations. The problem could be solved analytically for a sphere (Fig. 6 D), and the swimming velocity was given by ν_s = βν₀, where ν₀is the retrograde flow velocity at the equator. β is found equal to 1 for a complete transmission between actin retrograde flow and external membrane. A similar result has been obtained by Lighthill for a model-ciliated swimmer (squirmer), which yielded $v_s=\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.v_0$ for the swimming speed (48), the difference of proportionality coefficient being due to the choice of the surface flow. For other shapes, we solved numerically the problem using the boundary integral formulation for the Stokes equations (see Supporting Materials and Methods). In particular, we discretized a shape of T lymphocyte obtained by 3D soSPIM microscopy (Fig. 6 E) and introduced an actin source in a small region at the front of the cell and an actin sink at its rear. The overall flow pattern was similar to the spherical case, and the swimming velocity was close to the velocity of the cell membrane in the central region of the cell (in the cell frame), like for a spherical shape (Video S12). Besides, because most experimental data were obtained for cells close to a rigid wall, we used our numerical simulations to confirm that the swimming velocity was largely insensitive to the distance to the wall (see Fig. S12). Altogether, modeling confirms that swimming speed has the same magnitude as the speed of the external membrane treadmilling, supporting that cortex retrograde flow contributes significantly to lymphocyte swimming and could be the sole propelling source.

Video S12. Numerical Simulation of Swimming by Retrograde Flow

Cell shape is extracted from experiments. The swimming is shown in the laboratory frame. Color code on the surface represents the production/consumption of the cortex material. Small spheres are fictitious tracers moving with the cortex velocity. Transmission coefficient β = 1.

Membrane treadmilling is heterogeneous at the molecular scale

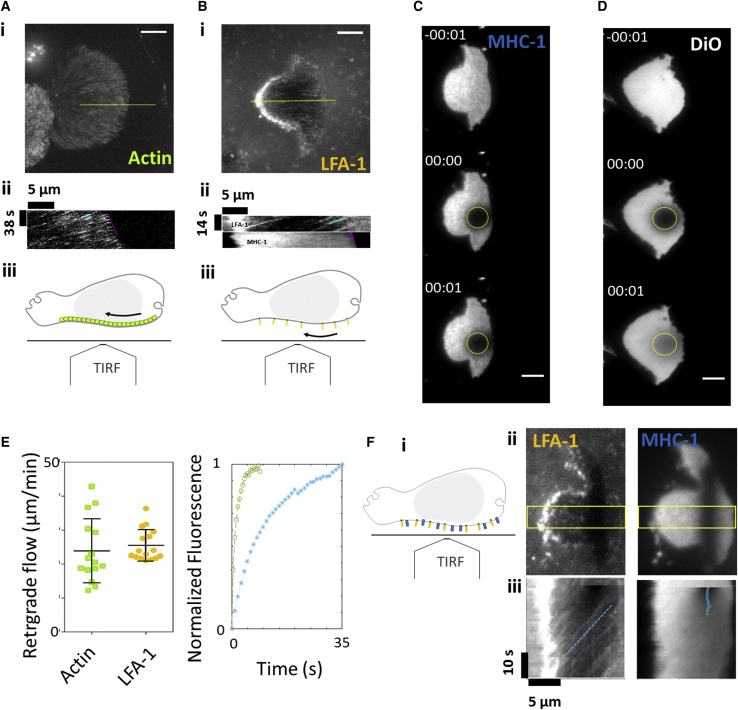
The propulsion model by a treadmilling membrane was considered a total coupling between the external fluid and a homogeneous membrane. This model yielded equal speeds between cell swimming and membrane treadmilling; however, the swimming speed (ν_s ∼5 μm min⁻¹) was found two times smaller than the membrane treadmilling speed (>10 μm min⁻¹) as revealed by beads attached to the membrane. This difference suggests that the coupling between cell membrane and surrounding fluid is not total and/or that the membrane is not homogeneous. Both the composition and the dynamics of a cell cytoplasmic membrane are indeed highly heterogeneous at a molecular level. The external fluid is therefore in contact with numerous lipids and transmembrane proteins and the hydrodynamic coupling between a fluid and such a complex surface is a delicate and hardly considered problem. Also, the molecular dynamics of the cell membrane itself is not fully characterized. If the retrograde flow of actin cortex and actin-bound transmembrane proteins is well attested, the circulation of lipids and of nonactin-bound transmembrane proteins is less documented. To get more insight into the molecular dynamics of the cell membrane at the timescale of tens of seconds and at the spatial scale of the entire cell, which are the relevant scales for cell swimming, we performed live FRAP-TIRF measurements on nonadherent cells maintained in the vicinity of the probing glass/fluid interface using depletion force induced by the addition of dextran in the medium. On RFP-actin-transfected cells, we observed the motion of actin clusters that displayed no detectable diffusion. The actin cortical cytoskeleton behaved like a solid gel (Fig. 7 A; Videos S13 and S14) flowing backward at 24 ± 9 μm min⁻¹ (Fig. 7 E). This result for human lymphocytes is in the top range of literature for other cellular systems (between 6 and 20 μm min⁻¹) (12,19,34,49,50). For transmembrane proteins, different dynamics could be expected whether proteins could bind or not to the actin cortex. To shed light on this issue, we used fluorescent-specific antibodies against an actin-bound protein, the integrin LFA-1 in high affinity state, and a nonactin-bound protein, the ligand of T lymphocyte receptor, MHC-1. Like actin, actin-bound proteins LFA-1 formed clusters that persistently flowed backward (Fig. 7 B; Video S13) with an average speed of 25 ± 5 μm min⁻¹ (Fig. 7 E). The absence of diffusion and similarity of speed with actin retrograde flow are consistent with a strong attachment rate of high affinity integrins to subcortical actin. By contrast, nonactin-bound proteins MHC-1 displayed a diffusive dynamics in FRAP experiments (Fig. 7 C; Video S13) with a characteristic diffusion coefficient of D = 0.26 ± 0.22 μm² s⁻¹ (Fig. 7 E). Similarly, for the lipidic layer, FRAP experiments with Vybrant DiO lypophilic molecules inserted in the cytoplasmic membrane (Fig. 7 D and Video S13) yielded a diffusion coefficient of 3.1 ± 1.8 μm² s⁻¹ (Fig. 7 E). Altogether, these results confirm that the molecular dynamics of the plasma membrane is heterogeneous. Actin-bound transmembrane proteins display ballistic backward motion, whereas lipids and nonactin-bound transmembrane display diffusion. This heterogeneity was not taken into account in simulations and may explain the difference between the speed of cell swimming and actin treadmilling.

Figure 7.

Actin-bound proteins LFA-1 treadmill backward at the cytoplasmic membrane, whereas nonactin-bound protein MHC-1 diffuses without net transport. (A and B) Backward transports of actin and actin-bound LFA-1 transmembrane protein are shown. (i) Maximal intensity projection of TIRF sequences on adhesion-free cells transduced with RFP-actin (A) and stained with antibody M24 that binds the actin-bound integrin LFA-1 in its high-affinity state (B). Scale bars, 5 μm. (ii) Representative kymographs along the yellow line in (i), with the front advance highlighted in magenta and clusters retrograde flow highlighted in blue. See also Videos S13 and S14. (iii) Schematics representing a side view of a nonadherent cell observed with a TIRF objective and highlighting the retrograde flow of internal actin (green units) and external LFA-1 integrins (orange bars). (C and D) Diffusive dynamics of nonactin-bound transmembrane protein MHC-1 and lipidic DiO marker. TIRF-FRAP experiments on adhesion-free cells (C), stained with anti-HLA-ABC that binds the nonactin-bound MHC-1 type I proteins and (D) with membrane lipidic marker DiO. Yellow circles indicate frapped regions used to calculate fluorescence recovery. Scale bars, 5 μm. (E) Quantification of transmembrane proteins advection and diffusion. Left: speed values for retrograding actin were measured by cluster tracking as in (D) (n = 7 cells, 51 clusters tracked) and by FRAP as in Supporting Materials and Methods (n = 8 cells) and for LFA-1 clusters (n = 16 cells, 106 clusters tracked), all normalized to the front of the cell. Error bars stand for standard deviation. Right: shown are the averaged FRAP curves for DiO (blue, n = 10 cells) and MHC-1 (green, n = 14 cells). All values were normalized and corrected by a nonbleached cell. Diffusion coefficient is of 3.1 ± 1.8 μm²/s for DiO and 0.26 ± 0.22 μm²/s for MHC-1. (F) Single cell evidence of average backward advection for actin-bound LFA-1 and average absence of motion for nonactin-bound MHC-1. (i) Schematics representing a side view of a nonadherent cell double stained for LFA-1 (orange) and MHC (blue). (ii) TIRF images after FRAP bleaching of a line pattern reveal actin-bound activated LFA-1 in its high-affinity state (left) and nonactin-bound MHC-1 (right). (iii) Kymographs in the yellow rectangle in (ii) with the motion of clusters and the center of mass of the FRAP region highlighted in blue for, respectively, LFA-1 and MHC-1. See also Video S15. To see this figure in color, go online.

Video S13. Evidence that Actin-Bound Proteins LFA-1 Are Advected Backwards at Cell Membrane, Whereas Non Actin-Bound Proteins MHC-1 Are Diffusive

TIRF-FRAP experiments on primary human effector T-cell (Top left) transfected with a GFP-actin by lentiviral infection, (Top right) stained with membrane lipidic marker DiO, (Bottom left) stained with antibody Mab24 that binds an actin-bound protein, the integrin LFA-1 in its high affinity state, and (Bottom right) stained with anti-HLA-ABC that binds the non-actin-bound MHC-1 type I proteins. Scale bars, 5 μm.

Video S14. Cytoskeleton Retrograde Flow

TIRF imaging of a primary human effector T lymphocyte transfected with GFP-actin and displaying backward traveling of clusters. Scale bars, 5 μm.

Video S15. Single Cell Evidence of Average Backward Advection for Actin-Bound LFA-1 and Average Absence of Motion for Non-Actin-Bound MHC-1

TIRF images after FRAP bleaching of a line pattern revealing actin-bound activated LFA-1 in its high affinity state (left) and non-actin-bound MHC-1 (right). Scale bar 5 μm.

Model of retrograde flow transmission by a heterogeneous membrane

To quantify the effect of partial coupling between the actin retrograde flow and the external fluid through a heterogeneous membrane, we considered the layers of transmembrane proteins protruding in the external fluid as a brush of polymeric molecules and analyzed the flow inside the brush composed of either advected or diffusing molecules. Based on polymer science developments, the brush of proteins was considered as a Brinkman medium (51) with a hydrodynamic penetration length, denoted as${\lambda }^{-1}\sim r/\left[2{\left({\phi }_i^{2D}\right)}^{1/2}\right]$, where ${\phi }_i^{2D}$ is the area fraction occupied by advected transmembrane proteins (e.g., integrins), and r is the typical lateral extent of the proteins on the membrane. The transmission coefficient can be expressed as:

$$\beta =1-2g/\left(1+g^2\right)withg=e^{\lambda h},$$ (3)

where h is the brush thickness. We first considered the effect of advected proteins linked to actin. Integrins LFA-1 and VLA-4, dominant in lymphocytes, were measured with an average occurrence of 25,000 and 15,000 molecules per cell, respectively (Fig. S13). Considering a radius r = 5 nm for each integrin and an excess of membrane in microvilli of 150%, the surface occupancy of LFA-1/VLA-4 corresponds to a mere 0.1%. The fact that integrins are not in high-affinity state at the same time tends to decrease further this value. Conversely, T lymphocytes express other integrins and other transmembrane proteins that link actin (e.g., T cell receptor or CD44), which tends to increase the surface occupancy by advected molecules. All in all, exhaustive experimental data are lacking to determine the exact value of ${\phi }_i^{2D}$. However, assuming ${\phi }_i^{2D}$ of 2% and h of 20 nm, the theoretical coupling value was found at β = 0.2, which is in agreement with the experimental result of a swimming speed five times smaller than the cortex retrograde flow. The effect of diffusing transmembrane proteins was also taken into account by considering that they were indirectly advected by the drag of the external fluid and by viscous interactions within the membrane. Modeling of fluid drag and estimation of membrane viscosity from FRAP measurements allowed us to show that membrane viscosity dominates over the external fluid drag (Supporting Materials and Methods) and that the presence of diffusing transmembrane proteins reduces the value of β (Fig. S14). Altogether, membrane treadmilling can participate in swimming, and heterogeneity of the membrane can significantly modulate the coupling efficiency.

Actin-bound proteins are advected backward at cell membrane, whereas nonactin-bound proteins are not

Simulations show that swimming speed decreases when a fraction of cell membrane has no backward motion. Assessing the average motion of lipids was not possible experimentally because of their fast diffusion. However, for transmembrane proteins, we managed to get more insight by performing line-shaped FRAP experiments on cells with double staining for LFA-1 and MHC-1. On Fig. 7 F, clusters of LFA-1 and the center of mass of the FRAP zone for LFA-1 moved backward at 22 μm min⁻¹, in line with previous measurements. In contrast, the center of mass of the FRAP zone for diffusing MHC-1 was on average immobile. These data are a direct support that a fraction of the membrane is purely diffusive and hinders the propulsion effect of paddling molecules.

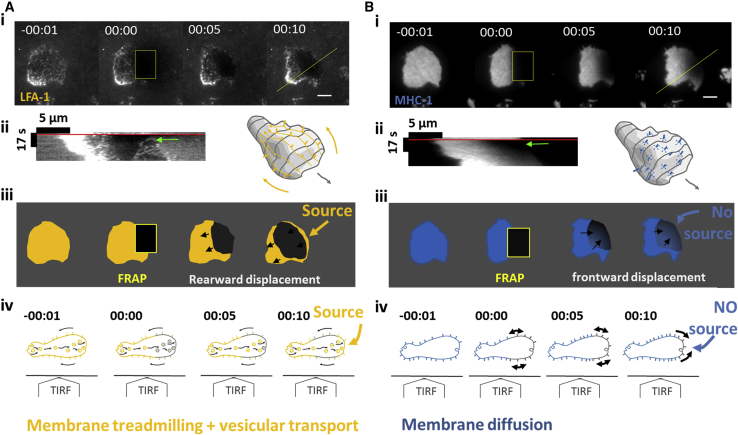
Actin-bound proteins are recycled by internal vesicular extrusion and nonactin-bound proteins are not

A sustainable retrograde flow at the surface of an axisymmetric object requires a source of material at the front and a sink at the back, which therefore implies the existence of an internal anterograde transport to loop a cycle. Conversely, when molecules are not advected backward (and are only diffusive), there must be no internal frontward recycling because a source at the cell front would generate an external retrograde flow. Our swimming model implies therefore the existence and the absence of an internal anterograde recycling of, respectively, actin-bound and nonactin-bound proteins. To support further the relevance and consistency of our model, we then intended to verify these two properties by performing square-shaped FRAP experiments on the cell front (Fig. 8 A; Video S16). In the case of LFA-1, a source of fluorescence at the cell leading edge after photobleaching (Fig. 8 A; Video S16) was consistent with the extrusion of integrins originated from the unbleached cell rear and carried undetected by TIRF by internal vesicular transport. Interestingly, the cycle of extrusion/treadmilling of integrins occurred within a minute, which is consistent with the treadmilling and swimming timescales. These observations validate the existence of a complete cycling of integrins by treadmilling and vesicular transport, whose timescale is consistent with swimming speed. In the case of MHC-1, fluorescence after photobleaching recovered only by diffusion from the cell back (Fig. 8 B; Video S16), and there was no source at the cell front. This confirms that internal recycling is not occurring for this nonactin-binding protein. Altogether, FRAP-TIRF data support that lymphocyte membrane does not treadmill as a whole. Actin-bound proteins undergo retrograde ballistic motion externally and anterograde vesicular transport internally, whereas nonactin-bound proteins undergo diffusion at the cell surface without internal recycling. Some surface molecules treadmill and paddle, whereas others diffuse and hinder motion.

Figure 8.

Treadmilling actin-bound transmembrane protein LFA-1 is recycled by internal vesicular transport, whereas diffusive transmembrane protein MHC-1 is not. (A) Staining of high affinity LFA-1 and (B) of MHC-1. (i) Sequences of TIRF images before FRAP, after FRAP of cell leading edge, and then 5 and 10 s after FRAP. Scale bars, 5 μm. See also Video S16. (ii) Kymographs along yellow lines of figures (A and B), with red lines indicating FRAP time and green arrows pointing at the cell front shortly after FRAP. 3D cartoon illustrates backward treadmilling of LFA-1 and 2D diffusion of MHC-1. (iii) Schematics of experimental results in (i) illustrate that fluorescence recovers from the cell leading edge for LFA-1, revealing a source at cell front, and from the back for MHC-1, revealing the absence of source at cell front. (iv) Side view schematics of nonadherent cells observed with a TIRF objective illustrate the dynamics of transmembrane proteins evidenced in TIRF experiments. For actin-binding LFA-1, the source at cell front reveals internal frontward transport of fresh material exocytosed at cell front, whereas for nonactin-binding MHC-1, purely diffusive transport dominates. To see this figure in color, go online.

Video S16. Evidence that Advected Proteins LFA-1 Are Recycled at the Cell Front by Internal Vesicular Transport, Whereas Diffusive Proteins MHC-1 Are Not

TIRF-FRAP experiments on primary human effector T-cell (Right) stained with antibody Mab24 that binds the actin-bound proteins LFA-1 in high affinity state, and (Left) stained with anti-HLA-ABC that binds the non-actin-bound proteins MHC-1. The cell front is frapped and fluorescence recovers only from the front for LFA-1, in agreement with an internal vesicular recycling of integrins from back to front, and only from the rear for HLA, in accord with a surface diffusion mechanism.

Treadmilling of a heterogeneous membrane can propel ubiquitous locomotion

Cell swimming by molecular paddling of a heterogeneous membrane is illustrated in Fig. 9 A with the treadmilling proteins exerting propulsion (orange), the diffusing proteins hindering propulsion (blue), and the inner recycling of paddling proteins by vesicular transport. To test further the mechanism, we perturbed the molecular cycling machinery without affecting actin treadmilling or actin-driven cell deformations by using inhibitors of endocytosis. Fig. 9 B shows results with primaquine 100 μM (52) and with a cocktail of inhibitors, including a clathrin inhibitor (pitstop2 50 μM), a dynamin inhibitor (dynasore 200 μM), and an inhibitor of the Arf6 GEF cytohesin (secinH3 20 μM) (28). Swimming was significantly slowed down with doses low enough to preserve cell morphological dynamics. The fact that osmotic swelling did not affect swimming speed (Fig. 5) is consistent with heterogeneous treadmilling propulsion because swelling does not affect protein cycle, and cell shape has a marginal influence on propulsion by treadmilling (Fig. 6, E and D). Beyond swimming, it is interesting to underline that the heterogeneous treadmilling mechanism can also foster propulsion on adherent 2D substrates and 3D matrices coated with integrin ligands. In these cases, the integrin-mediated clutch mechanism promotes optimal momentum transfer between internal cortex and external medium, and cell speed is indeed close to actin treadmilling speed. This corresponds to actin-integrin clutch mechanism (10). Furthermore, the heterogeneous treadmilling mechanism can also propel cells through nonadherent confined environments because friction of the cell membrane with a solid substrate is expected to be stronger than with a fluid. We found that cells confined between two plates and in microfluidic tubes were motile (Fig. 9 C; Videos S17 and 18). Between plates, two adjacent zones with adherent and nonadherent coatings were prepared by optical patterning (43), and tube surfaces were treated with Pluronic F107 (14). Cells are slightly faster between plates and significantly faster in tubes as compared to swimming mode. Literature data reported the case of cells in a microfluidic channel displaying treadmilling of membrane but no motion, which was interpreted as an example of null friction and null transmission between membrane and substrate (14). However, an ideal solid/cell interface with perfect slippage or null friction is not physically relevant because hydrodynamics of physical contact always yield friction. The mechanism of heterogeneous membrane treadmilling supports therefore ubiquitous lymphocyte migration in fluid and solids, with and without adhesion.

Figure 9.

Treadmilling of transmembrane proteins recycled from rear to front by internal transport provides ubiquitous propulsion. (A) Schematics of heterogeneous membrane treadmilling mechanism. The perspective view displays a swimming cell on which actin-bound proteins (orange) are advected backward and entangled with nonactin-bound proteins. Swimming is promoted by advected proteins and hindered by diffusing proteins, which results in swimming significantly slower than treadmilling. The cross-sectional view displays the complete cycling of actin-binding proteins (orange), which comprises endocytosis at cell rear, internal advection by vesicles forward, exocytosis at cell front, and advection at cell membrane backward by linkage to retrograde actin flow (green). (B) Specific perturbation of paddling cycle by inhibitors of endocytosis (cartoon). Left: shown are representative images of a cell; middle: shown are representative kymographs of the swimming motion of the corresponding cells; and right: shown is a plot of the raw curvilinear swimming speeds for control conditions, with primaquine at 100 μM and with a cocktail of inhibitors (pitstop2 at 50 μM, dynasore at 200 μM, and secinH3 at 20 μM). N = 30 cells, ∗p < 0.05 and ∗∗∗∗p < 0.0001 (two-tailed Student’s t-test). (C) Heterogeneous treadmilling fosters ubiquitous motility without adhesion. (i) Swimming on a nonadherent surface, (ii) crawling between two surfaces separated by 3 μm, with adherent and nonadherent zones (see also Video S17), and (iii) in a nonadherent tube of cross section 4 × 4 μm² (see also Video S18). Data for cases (i) and (ii) correspond to projected images taken every 10 s for 3 min of a given area with several cells. The round shapes in (ii) correspond to 100-μm diameter glass pillars that sustain the structure. Data for case (iii) show a sequence of images of a single cell for 5 min. To see this figure in color, go online.

Video S17. Lymphocytes Are Motile When Confined between Non-Adherent Plates

Movies in bright field at 20× of primary human effector T lymphocytes moving between two glass substrates patterned with an adherent zone covered with ICAM-1 (left) and an antiadhesive zone (right). The round shapes correspond to 100 μm diameter glass pillars that sustain the structure.

Video S18. Lymphocytes Are Motile When Confined in Tubes

Movies in bright field at 63× of a primary human effector T lymphocytes moving in a non-adherent microfluidic channel of cross-section 4 × 4 μm².

Discussion

Amoeboid migration of mammalian cells, i.e., leukocytes and cancer cells, has attracted intensive interest in the last decade for their ubiquitous ability to migrate at high speed in various 2D and 3D environments. The requirement of adhesion with a substrate remains a widely accepted hallmark for 2D migration (5, 6, 7,12,14, 15, 16, 17, 18, 19), whereas two studies reported nonadherent motility and swimming with leukocytes (20,28). However, Barry and Bretscher (20) did not investigate the mechanisms of neutrophils swimming, and O’Neil et al. (28) considered an original but artificial swimming mode induced by optogenetic activation of contractility in the cell rear. In this context, we provided here direct experimental evidences and quantifications of swimming by primary lymphocytes, together with an original theoretical model of molecular paddling that can explain amoeboid swimming at speeds compatible with precise experimental measurements as well as ubiquitous migration in/on adherent and nonadherent substrates.

In principle, cell swimming without flagella can be propelled either by normal (protrusion) and/or tangential (treadmilling) motion of the cell membrane. Mechanistic studies of swimming by eukaryotic cells have mostly focused on amoeba D. discoideum and favored propulsion by shape deformation rather than treadmilling (21,24, 25, 26). However, most models involve parameters difficult to link to experimental data (26) or yield a swimming speed smaller than the experimental ones (24,25). There is therefore no consensus for swimming propelled by deformation. Interestingly, a recent study by O’Neil et al. (28) put forward original evidence that membrane treadmilling could be involved in propulsion, however without assessing the contributions of deformations in propulsion. Here, we proposed theoretical and experimental evidences that swimming of lymphocytes is barely relying on cell deformations. Modeling based only on parameters accessible experimentally like the micron-scale amplitudes and 10–20 μm min⁻¹ speed of protrusions yielded that cell deformations cannot propel swimming at a speed as high as 5 μm min⁻¹. Experimental perturbations of the average and time-dependent cell deformations were also hardly perturbing swimming prowess. In contrast, experiments and modeling both validated a high efficiency of propulsion by membrane treadmilling, as proposed by O’Neil et al. (28), and we further show that membrane does not treadmill as a whole. Altogether, the effect of shape deformations seems negligible in lymphocyte swimming, whereas membrane treadmilling would be the main propelling machinery.

Actin dynamics acts a priori as a hybrid motor of membrane treadmilling, polymerization at the cell front pushing the nascent cross-linked cortical network backward, and contractility at the cell rear pulling the network backward. It is not clear whether the two mechanisms combine their action on a continuous actin gel or if they act independently on disconnected actin networks at the cell front and rear. However, we found here that lymphocyte swimming relies more on frontal actin polymerization than on rear myosin II contractility. This diverges from the Rho-A-induced swimming mode described by O’Neil et al. (28) as well as from several recent reports on adherent crawling (15,18,53, 54, 55, 56, 57) that attribute a dominant propelling role to a gradient of contractility along cell’s front-rear polarization axis. Our results are more in line with studies proposing that contractility is marginally involved in propulsion and mostly relevant for the detachment of cell rear (for Dictyostelium amoebae) (58) or for the squeezing of cell nucleus through pores (for dendritic cells) (5). Hence, depending on cell types, actin treadmilling may be powered more by actin network contractility (28) or by actin polymerization, but in any case, our results corroborate the idea that membrane treadmilling is an essential player of lymphocyte motility, either by swimming or crawling.

Hydrodynamic coupling between a treadmilling membrane and a surrounding fluid is the key of amoeboid swimming, and we analyzed here its molecular basis experimentally and theoretically. Studies considering that cellular membranes treadmill as a whole yield a theoretical ratio between swimming and membrane speeds ranging between 2/3 and 1 (59). O’Neil et al. (28) measured swimming speeds 2/3 of membrane speeds and observed gradients of several membrane components (lipids and proteins) along cell rear-front axis. This led them to conclude that the cell membrane was treadmilling as a whole and propelling swimming. One may, however, argue that their correlation between speeds of membrane and speed of cell swimming relied on a narrow set of data. Besides, proteins gradients do not strictly imply that proteins treadmill because gradients can also result from a balance between diffusion and drag by surrounding molecules. In contrast, the analysis of lymphocyte swimming motion showed here that swimming speed was 1/3 of membrane treadmilling speed (measured with a bead attached to the membrane) and 1/5 of the actin-bound proteins speed (measured by TIRF) and therefore too low to arise from the treadmilling of a homogeneous membrane. Moreover, direct microscopy experiments showed that membrane dynamics was heterogeneous at the molecular level and that only a fraction of transmembrane protein treadmilled backward. Hence, some membrane molecules treadmill backward, paddle, and promote swimming, whereas others are diffusive and hinder swimming. Simulations of propulsion by a heterogeneous treadmilling support further that a fraction of treadmilling proteins is efficient enough to support swimming at a speed close to internal cortex speed, and also that a fraction of diffusing protein can significantly slow down speed to the observed swimming speed.

Importantly, we also showed that treadmilling of actin and transmembrane proteins, whose essential role has been widely inferred in cell motility, was associated with sophisticated mechanisms of internal vesicular transport to sort proteins that support continuous swimming. Vesicular transport is indeed implemental to complete the cycle of paddling proteins and promote sustained propulsion, and the sorting of proteins transported by vesicles is also necessary to explain heterogeneity of proteins dynamics at cell surface. Internal transport of a treadmilling transmembrane protein and the absence of internal frontward recycling of a diffusion transmembrane protein was evidenced here by FRAP with, respectively, integrin LFA-1 and protein MHC. Mechanisms of internal integrins recycling by anterograde vesicular transport have also been documented in the literature (60, 61, 62, 63, 64). Moreover, the cycle of extrusion/treadmilling of integrins in our experiments occurred within a minute, which is in line with the treadmilling and swimming timescales (in contrast to literature data that reported timescales around 15–30 min (61,62)).

Our swimming model sheds also new light on the ubiquitous motility of amoeboid cells. The adaptation of mammalian amoeboid cells to various environments has repeatedly been attributed to their capability to switch between different migration modes versus the environment (10,14,15,19,33,57). The mode of adherent crawling is generally attributed to a sequence of cell front protrusion/attachment and cell rear pulling/detachment, whereas the more intriguing mode of nonadherent migration in 3D has been explained by various mechanisms depending on cell types (9,19): blebbing in the cell front and transfer of actin cytoskeleton into the novel bleb (54,65,66), intercalation of protrusion into gaps and discontinuities of the matrix to advance like on a ladder (67, 68, 69), chimneying via active gel pushing off the wall (11), cell rear contractility stabilizing a single bleb conformation (18), water permeation throughout the cell body (70), or treadmilling coupled to friction with the substrate (8,9,12). In our case, there was no evidence of a mode switching between crawling and swimming sequences on patterned substrates, and treadmilling of a heterogeneous membrane can propel ubiquitous migration of lymphocytes versus solid (8,12) or liquid environments. In this scheme, speed depends on cell/environment coupling conditions. An adhesive solid environment provides optimal coupling and cell’s speed is close to actin treadmilling speed (unless detachment issues slow down motion); a liquid environment provides a minimal coupling due to the molecular heterogeneity of cell membrane treadmilling (the environment fluidity is not directly responsible for weak coupling, as attested by our model or by the squirmer model (48)); and finally, a nonadherent confined environment provides an intermediate coupling, in which friction relies on surface forces rather than on hydrodynamic lubrication (40). The regime of hydrodynamic friction (or lubrication) appears, indeed, only for objects much faster than crawling cells (71). Interestingly, the propulsion by heterogeneous membrane treadmilling supports systematic migration in nonadherent confined environments because a solid/cell interface with null friction is not physically relevant. Furthermore, nonadherent confined propulsion is expected to be at least as fast as swimming because the coupling of the membrane with a solid can only be more efficient than with a liquid. Altogether, the mechanism of heterogeneous membrane treadmilling is operational in polarized cells displaying backward actin treadmilling. This mechanism can allow ubiquitous adaptation of lymphocytes to various microenvironments via a single mode of migration (10) associated to different friction/adhesion coupling conditions. It may exist for other cell types and coexist with other propulsion mechanisms.

In the end, heterogeneous membrane treadmilling can drive ubiquitous amoeboid migration within fluid and solid and with or without adhesion; however, the physiological role of swimming remains enigmatic for leukocytes. Because the traffic of immune cells (or invasivity of cancer cells) relies mostly on matrix-associated migration and because swimming is clearly relevant to planktonic eukaryotic cells (like amoeba), it is possible that the basic machinery for swimming is an evolutionary conserved ability that has found novel functions for ubiquitous crawling in mammalian cells. Nevertheless, swimming might be instrumental to extend the ubiquitous migration capabilities of immune cells to nonconfining conjunctive tissues or liquid-rich infected niches like postwound edema zones.

Editor: Alexander Dunn.

Author Contributions

L.A. and P.N. worked on all experiments and analysis except TIRF-FRAP section. A.F. developed all modeling and simulations on treadmilling mechanism and contributed to swimming speed analysis. N.G.-S. performed experiments of beads tracking and all FRAP-TIRF assays. M.S.R. performed modeling of shape deformation mechanism. X.L. performed migration assays on patterned substrates. S.T. performed elliptic Fourier reconstruction of contours and wavelet transforms. M.B.-P. managed cell culture, performed transfection with RFP-Lifeact, and made quantitative cytometry. M.-P.V. participated in experiments and analysis. R.G. and J.-B.S. performed 3D live imaging by soSPIM. C.H. and S.D. prepared GFP-actin cells. S.R. performed viscosity measurements and participated in discussions. C.M. supervised and participated in all modeling developments, designed the study, and wrote the article. O.T. supervised and participated in all experiments and analysis, designed the study, and wrote the article.