Potential Biases Arising From Epidemic Dynamics in Observational Seroprotection Studies

Abstract

The extent and duration of immunity following infection with severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) are critical outstanding questions about the epidemiology of this novel virus, and studies are needed to evaluate the effects of serostatus on reinfection. Understanding the potential sources of bias and methods for alleviating biases in these studies is important for informing their design and analysis. Confounding by individual-level risk factors in observational studies like these is relatively well appreciated. Here, we show how geographic structure and the underlying, natural dynamics of epidemics can also induce noncausal associations. We take the approach of simulating serological studies in the context of an uncontrolled or controlled epidemic, under different assumptions about whether prior infection does or does not protect an individual against subsequent infection, and using various designs and analytical approaches to analyze the simulated data. We find that in studies assessing whether seropositivity confers protection against future infection, comparing seropositive persons with seronegative persons with similar time-dependent patterns of exposure to infection by stratifying or matching on geographic location and time of enrollment is essential in order to prevent bias.

Abbreviations

SARS-CoV-2

severe acute respiratory syndrome coronavirus 2

The extent and duration of immunity following infection with severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) are critical outstanding questions about the epidemiology of this novel virus (1). Serological tests, which detect the presence of antibodies, are becoming more widely available (2). However, the presence of antibodies, or seroconversion, does not guarantee immunity to reinfection, and experimental data with other coronaviruses raise concerns that antibodies could in some circumstances enhance future infections (3). Studies are needed to evaluate the short- and long-term effects of seropositivity. Understanding the potential sources of bias and methods for alleviating biases in these studies is important for informing their design and analysis.

Serological studies may be useful for a variety of reasons, including 1) assessment of the cumulative incidence of infection within a community, 2) identification of risk factors for transmission, and 3) determination of the extent of clustering of infections within a community (4, 5). While these types of studies are often cross-sectional and use seroconversion as the endpoint, here we consider longitudinal studies where seroconversion is the exposure of interest.

These seroprotection studies may be conducted by starting with a cross-sectional serological survey, where the tested individuals are then followed to identify future infections. To obtain a sufficient cohort of seropositive persons, enrollment may need to occur on multiple days. Follow-up for identification of future infections depends on regular monitoring of symptoms and/or polymerase chain reaction testing for the virus. Consistent case definitions across the study and tracking of individual enrollment and seroconversion dates are key to reducing the risk of misclassification. If cases are defined on the basis of symptom onset, the study outcome will be the association between seropositivity and progression to symptoms. If cases are based on virological testing, the study outcome will be the association between seropositivity and infection. These endpoints have different public health implications, and the choice should depend on the scientific question of interest (6).

A crude analysis of this longitudinal study would compare time from enrollment to infection between persons who are seropositive at enrollment and those who are seronegative at enrollment. However, because seroprotection studies are observational, since the exposure (i.e., seropositivity) is not assigned at random, investigators must control for potential confounders to obtain unbiased estimates. Studies of seropositivity and its effect on future infection are particularly prone to confounding, because factors that affect someone’s risk of infection and therefore their serostatus prior to enrollment (the exposure) are likely to be similar to factors that affect someone’s risk of infection after enrollment (the outcome). For example, persons in high-risk occupations (e.g., health-care workers) are more likely to become seropositive and more likely to be exposed again once they are seropositive.

Confounding by individual-level risk factors is relatively well appreciated. Less obvious perhaps is that geographic structure (7) or the underlying, natural dynamics of epidemics (8, 9) can induce noncausal associations between an exposure and an outcome. For example, even when seropositivity confers no protection against future infection, if the overall size of an epidemic is very different in different communities, people in communities with small epidemics will have a low prevalence of the exposure (seropositivity) and a low incidence of the outcome (infection after enrollment), while people in communities with larger epidemics will have a higher prevalence of the exposure and a higher incidence of the outcome, biasing estimates of the effect of seroprotection. Bias may also occur if people are enrolled at different times during an epidemic. If enrollment occurs during an upward trajectory (such as the early exponential phase of an epidemic), persons enrolled early in the epidemic will be both less likely to be seropositive (exposure) and less likely to become infected at a given point in time after enrollment (outcome) than those with a later date of enrollment. Moreover, in an epidemic that is controlled (thus with an up-then-down trajectory of incidence), the representation of seropositive individuals will increase with time, but the rate at which these persons experience the outcome will increase and then decrease, creating potential for confounding in either direction.

In this article, we take the approach of simulating such studies in the context of an uncontrolled or controlled epidemic, under different assumptions about whether prior infection does or does not protect an individual against subsequent infection, and using various designs and analytical approaches to analyze the simulated data. By identifying the direction and comparative magnitude of bias of the estimated degree of protection relative to a known true effect of prior infection (known because we have built it into the simulations), we identify means of designing and analyzing such studies that can render them less likely to show bias due to these confounding factors. This framework of simulating studies in the context of an epidemic has been widely used to understand experimental (10) and observational (8, 11) studies of risk factors and prevention interventions for infectious disease.

METHODS

We simulate a stochastic outbreak of a disease in a network of people grouped into communities, with each community’s outbreak seeded by introductions over time (7, 12). For each simulation, we generate a network graph, where individuals are grouped into either 1 community of 10,000 people or 10 communities of 1,000 people each. Individuals are only connected to persons in their own community, with the probability of such a connection being based on an input parameter in the simulation. For “well-mixed” communities, every individual is connected to every other individual in their community, while for simulations with “clustered” communities, people have a limited number of connections within their community, which creates smaller subcommunities, or “clusters,” by chance. In these latter simulations, individuals may have varying numbers of actual connections, but all of them have the same expected number. The network graph of a “well-mixed” community is a complete graph, while that of a “clustered” community is a random graph with uniform edge probability. In simulations with 10 communities, all communities are independent of one another, conditional on the introduction of infection from the outside.

At each time step in the model, each susceptible individual has a daily probability of infection from each of their infectious contacts of 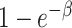, where β is the force of infection. Hence, 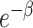is the conditional probability of infection-free survival over a single day among those at risk at the start of the day. If a subject has n infectious contacts on a given day, the force of infection is nβ, and thus the day’s conditional probability of infection is 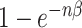. Since the number of contacts per individual varies by simulation, β varies by simulation to keep the reproduction number R fixed (see Web Appendix 1, available at https://academic.oup.com/aje). The outbreak is seeded with stochastic introductions into the communities between days 1 and 50 based on an external force of infection (different from β; see Web Figure 1), which means that in simulations with multiple communities, outbreaks may start at different times in each community, and some communities may avoid infection completely.

The disease natural history follows a susceptible-exposed-infectious-susceptibleʹ model, where under the null hypothesis (i.e., no immunity), persons in the susceptible and susceptibleʹ compartments are equally susceptible, while under the alternative hypothesis, those in the susceptibleʹ compartment are less susceptible (in principle, perhaps completely immune; but in keeping with prior evidence about coronaviruses, we assume that they are partially immune) (13, 14). In simulations with partial immunity, we make the simplifying assumption that susceptibility is immediately decreased following the infectious period and remains constant over time. Seroconversion is assumed to be detectable at the end of the infectious period. We simulate scenarios with limited control measures in place (effective reproduction number (R_E) = 1.5) and scenarios in which control measures that reduce the force of infection per infected individual (β) are implemented on day 120 of the study period, reducing R_E from 2 to 0.8. Beta is set to yield these values of R_E. Table 1 shows the specific numbers corresponding to these parameters of the simulations, and Web Appendix 1 describes the generation of the network and outbreak in more detail.

Table 1.

Parameters for Simulated Serological Studies in the Context of an Uncontrolled or Controlled Epidemic, Under Different Assumptions About Whether Prior Infection Protects an Individual Against Subsequent Infection, and Using Various Designs and Analytical Approaches

Parameter	Value(s)
No. of communities	1 or 10
Average community size, no. of persons	1-community simulations: 10,000
	10-community simulations: 1,000
Probability of connection with someone within the same community	Well-mixed: 1 (everyone is connected to everyone else in their community)
	Clustered: 0.002 probability per edge for 1 community and 0.02 probability per edge for 10 communities
Probability of connection with someone in another community	0
RE a (17)	Controlled: 2.0 → 0.8
	Uncontrolled: 1.5
Latency period, days	5.6 (gamma distribution with shape = 5, rate = 0.9)
Infectious period, days	10 (gamma distribution with shape = 3, rate = 0.3)
No. of days in simulation	200
Day on which epidemic control measures begin	Controlled epidemic: day 120
	Uncontrolled epidemic: never
Reduction in β after control, %	60
Day(s) of enrollment in the serological study	Same day: day 100
	Different days (uncontrolled): days 50, 100, and 150
	Different days (controlled): days 100 and 150
% of persons enrolled (unmatched)	50
Seropositivity protection, %	0 (null)
	50
	95

^a  R_E, effective reproduction number.

For each simulation setting (1 or 10 communities, well-mixed or clustered communities, control measures or not, and seroprotective efficacy), we consider 3 sampling designs: 1) enrolling people on a single day without matching (day 100), 2) enrolling people on multiple days (days 50, 100, and 150) without matching, and 3) enrolling people on multiple days with matching of enrolled seropositive and seronegative individuals. Enrollment on multiple days may occur if, for example, different cross-sectional surveys are conducted, and this study enrolls the participants in those surveys. A random sample of individuals are enrolled in the study at these specified time points over the course of the outbreak.

We classify people as seropositive or seronegative based on their serostatus on the day of enrollment in the study, and then we follow them up until they are infected or until the study period ends at day 200. In the unmatched designs, we enroll half of the people in each community in the study, with an equal number enrolled on each day of enrollment. In the matched designs, for every seropositive individual enrolled on each day of enrollment, we also enroll 1 seronegative individual on that day from the same community. This increases the balance between exposure arms but reduces the overall sample size.

For each simulation setting and sampling design, we conduct 2 analyses. First, we conduct an unstratified analysis in which we calculate the hazard ratio of infection comparing seropositive persons with seronegative persons, using a Cox proportional hazards model with time starting from enrollment (i.e., possibly not the same calendar time if people enroll on different dates). Second, given the potential for stochasticity to generate heterogeneous outbreaks between communities (7), we also conduct an analysis stratified by community and day of enrollment to prevent confounding by these variables. In this analysis, a Cox proportional hazards model with time starting from enrollment is fitted with a separate baseline hazard function for each combination of community and day of enrollment but a common hazard ratio due to seropositivity. R code for the simulations and analysis (R Foundation for Statistical Computing, Vienna, Austria) is available on GitHub (15); additional analyses considered are described in Web Appendix 2 and illustrated in Web Figures 2 and 3.

Figure 1.

Continues

RESULTS

Figure 1 shows the results from 1,000 simulations for each of 36 combinations of parameters (see Table 1). Figure 1A–D shows results from simulations with limited control measures in place (R_E = 1.5). Results shown in Figure 1A and 1C are under the null value (hazard ratio = 1), meaning that seropositivity provides no protection against reinfection (β⁺ = β⁻, where β⁺ is the force of infection for contact between an infectious individual and a seropositive individual and β⁻ is the force of infection for contact between an infectious individual and a seronegative individual). In Figure 1B and 1D, seropositivity reduces susceptibility by 50% (β⁺ = 0.5 × β⁻) and 95% (β⁺ = 0.05 × β⁻), respectively.

Figure 1.

Median estimated hazard ratios for infection (circles) and interquartile ranges (IQRs; bars) comparing seropositive individuals with seronegative individuals in 1,000 simulations for each of 36 combinations of parameters. A) Well-mixed communities, uncontrolled epidemic, no seroprotection; B) well-mixed communities, uncontrolled epidemic, 50% seroprotection; C) clustered communities, uncontrolled epidemic, no seroprotection; D) well-mixed communities, uncontrolled epidemic, 95% seroprotection; E) well-mixed communities, controlled epidemic, no seroprotection; F) well-mixed communities, controlled epidemic, 50% seroprotection. Note the different x-axis scales in the different panels. We considered 3 sampling designs for each simulation setting: 1) enrolling people in a serological study on a single day without matching, 2) enrolling people on multiple days without matching, and 3) enrolling people on multiple days with matching. In the matched designs, for each seropositive individual enrolled on each enrollment day, a seronegative individual from the same community was also enrolled on that day. We compared analyses stratified by enrollment day and community with unstratified analyses. Simulations with 0 events in either the seropositive arm or the seronegative arm were excluded (percentage of simulations excluded in each panel: A, 0.85%; B, 1.6%; C, 0.28%; D, 22.1%; E, 4.7%; F, 6.3%). For analyses with a high infection hazard for any enrolled individuals (e.g., different days of enrollment in panels B, D, and F), the estimated hazard ratio is between the ratio of the force of infection in seropositive persons to the force of infection in seronegative persons (β⁺:β⁻) and the null value (hazard ratio = 1). This occurs because an individual’s hazard is not simply the product of their number of contacts and the force of infection. This is not a bias in the conventional sense, but rather a difference between the ratio β⁺:β⁻ and the parameter that is estimated by the Cox model (see Web Appendix 1 for more details).

The simulations are carried out in well-mixed communities, meaning everyone within a community is connected to each other, except in Figure 1C, which has random clustering within each community. This clustering leads to correlations between the infection statuses of particular individuals close together in the network and may be understood as creating multiple smaller (albeit overlapping) “communities” within each discrete community.

For simulations with 1 well-mixed community with the same day of enrollment for all individuals (top lines of Figure 1A, 1B, and 1D), a crude analysis returns unbiased results. If enrollment occurs on different days (second and third lines of Figure 1A, 1B, and 1D), a crude analysis yields an upwardly biased estimate of the hazard ratio, making seropositivity appear harmful. However, matching on day of enrollment or stratifying the analysis by day of enrollment removes this bias.

With multiple communities (and thus multiple, unconnected epidemics, as in the bottom halves of Figure 1A, 1B, and 1D), an unadjusted analysis creates the same upward bias regardless of whether enrollment is on the same calendar date or multiple calendar dates, as the same calendar date does not mean the same phase of the epidemic in each of the communities. Once again, the bias is upward because people in communities with larger or more advanced epidemics are exposed to higher hazards and are more likely to be seropositive at baseline (Figure 2A–D). As before, the bias can be removed through the use of a matched design or stratified analysis, this time matching or stratifying on both community and day of enrollment. For analyses with a high number of infectious contacts for any enrolled individuals (e.g., see different days of enrollment in Figure 1B and 1D), the estimated hazard ratio is between the ratio β⁺:β⁻ and the null value (hazard ratio = 1). This occurs because an individual’s hazard is not simply the product of their number of contacts and the force of infection. This is not a bias in the conventional sense, but rather a difference between the ratio β⁺:β⁻ and the parameter that is estimated by the Cox model (see details in Web Appendix 1). For settings with a lower force of infection or fewer infectious contacts, this difference is imperceptible.

Figure 2.

Average daily hazard, or proportion of persons in the initial susceptible compartment (i.e., never infected) moving to the exposed compartment in a serological study, in 1,000 outbreak simulations within a single community of 10,000 persons. A) Well-mixed communities, uncontrolled epidemic, no seroprotection; B) well-mixed communities, uncontrolled epidemic, 50% seroprotection; C) clustered communities, uncontrolled epidemic, no seroprotection; D) well-mixed communities, uncontrolled epidemic, 95% seroprotection; E) well-mixed communities, controlled epidemic, no seroprotection; F) well-mixed communities, controlled epidemic, 50% seroprotection. Note the different y-axis scales in the different panels. Horizontal gray bars show the lengths of follow-up for each day of enrollment. The height of each bar indicates the average hazard for that duration of follow-up. In panels A–D, follow-up begins on days 50, 100, and 150, while in panels E and F, follow-up begins on days 100 and 150 only. In panels E and F, the vertical gray dashed lines denote the day on which control measures are implemented, which reduces the force of infection by 60%. The number of infectious individuals continues to grow beyond the day of control for approximately the average length of the latency period (5.6 days) due to the presence of persons who were infected in the days just before implementation of control measures. This causes the hazard to increase again after its initial drop before declining again.

Clustering of contacts within communities (a departure from the assumption of a well-mixed epidemic (Figure 1C)) produces an upward bias even in the matched design and stratified analyses. As we noted above, this reflects the fact that the different parts of the network have different local prevalences at any given time, resulting in a milder form of the same heterogeneity-induced bias as that seen when there are many discrete communities. Because these clusters of high- and low-prevalence areas overlap and arise during the study, there is no a priori way to adjust for them.

In the simulations shown in Figure 1E and 1F, transmission is reduced partway through the outbreak in 1 or more well-mixed communities, representing intensified control measures (R_E = 2 → 0.8). In these simulations, there are fewer reinfections, as reflected in the wider interquartile ranges. As before, the single-community estimates are unbiased when all people enroll on the same day, but when enrollment occurs on different days or there are multiple communities, the estimates are biased. In the single-community simulations with 2 different days of enrollment, the unstratified, nonmatched analysis estimates are slightly biased away from the null, making seropositivity look protective. This occurs because there are more seropositive persons at later enrollment dates when the average hazard over the rest of the study is lowest (Figure 2E and 2F).

Hence, with multiple communities or multiple enrollment dates, confounding can go in either direction depending on the dynamics of the epidemic at the times of enrollment. Matching on enrollment alleviates the different biases, as does stratification in cases where there are infections in both the seropositive and seronegative arms. If there are substantially fewer seropositive persons than seronegative persons and the risk of infection after enrollment is low (i.e., because of effective control measures), there can be settings with no infections among the seropositive enrollees in some or all strata. In these cases, stratified analyses can lead to unstable results because methods of accounting for 1 arm with 0 cases (e.g., adding a case to each arm) can overcorrect when the 0-case arm has far fewer individuals than the other. Matched designs are thus preferable because they remove this imbalance between the 2 exposure arms.

We note that in the simulations under the null scenario with limited control measures (Figure 2A and 2C), the daily hazard (proportion of persons in the susceptible compartment moving to the exposed compartment) continues to increase over time. In simulations with controlled epidemics and/or immunity (Figure 2B and 2D–F), the daily hazard increases and then plateaus or decreases.

DISCUSSION

We find that in studies assessing whether seropositivity confers protection against future infection, comparing seropositive persons with seronegative persons with similar time-dependent patterns of exposure to infection is essential, because otherwise confounding can bias results; accounting for differential exposure among seropositive and seronegative persons is necessary to prevent bias. This bias can arise either from having multiple days of enrollment over the course of the study by design or from having multiple communities where the outbreak stochastically starts at different times (Table 2). Matching in the design or stratifying in the analysis on community and day of enrollment alleviates this bias in well-mixed communities. When there is clustering within communities, a slight upward bias remains, suggesting that the local network structure in a study is an important factor to consider.

Table 2.

Possible Types of Bias in Serological Studies Conducted During an Outbreak of an Infectious Disease

Cause of Bias	Direction of Bias	Ways to Correct
Multiple communities with different timing of epidemics	Upward	Matched design or stratified analysis (matching works better when both number of seropositives and risk of infection are low)
Different days of enrollment	Upward or  downward	Matched design or stratified analysis (matching works better when both number of seropositives and risk of infection are low)
Clustered communities	Upward	Cannot correct a priori but could consider matching on household or neighborhood

While most people are susceptible when they are enrolled in a study, it is possible for people to be exposed or infectious upon enrollment. Excluding persons who are infected soon after enrollment (e.g., within the average latency period) would remove many of these cases. For potentially asymptomatic infections, investigators would not be able to exclude these cases from the study without viral testing for active infection. Small biases may occur if all people enrolled in the study are not susceptible at enrollment.

The results shown here assume perfect specificity of the serological test. As expected (16), imperfect specificity causes bias toward the null (Web Appendix 3 and Web Figure 4). More complex interactions between immunity and infection, including immunity that wanes over the time scale of the study, viral-load–dependent infection, and effects of repeated exposures, such as boosting of titers, may affect these biases as well, or may introduce other potential biases. Further research is needed to understand the effects of these biological mechanisms in the specific context of SARS-CoV-2.

These simulations focus on the bias inherent in some study designs that may be considered, but they do not address the feasibility of implementing these designs. In addition, we do not focus on the statistical power of these studies; this may have important consequences in determining an adequate sample size. Sample-size considerations will be particularly important in balancing the advantage of starting enrollment later, when the cumulative incidence is higher and thus the exposure arms are more likely to be balanced, and avoiding the tail of an outbreak or a setting after control measures have been implemented, which will reduce the infection risk for all participants. We have shown that matching can address these issues, but matching requires exposure status to be known at enrollment. This may be feasible if the study is designed following a serological survey, where people can be enrolled on the basis of their antibody presence from the survey. If the exposure needs to be measured for the seroprotection study, however, matching may require far more serological testing to be conducted, inflating the cost of the study. Investigators will need to consider the relative sample-size requirements and testing burden of these designs in the context of their specific study.

As serological studies begin, understanding potential sources of bias and how to alleviate them is important for accurately estimating the extent and duration of immunity to SARS-CoV-2. Here we have focused on the impact of epidemic dynamics on estimation of seroprotection and have assumed that all people in the model are exchangeable and differ only in whom they contact. Future work could examine additional heterogeneity, such as behaviors or factors that increase risk of infection, which might lead to further biases.